Estructura de la frontera de un conjunto convexo. Los politopos
|
|
|
- Ramona Rojas Castilla
- hace 7 años
- Vistas:
Transcripción
1 Capítulo 2 Estructura de la frontera de un conjunto convexo. Los politopos Cuando hablamos de polígonos y poliedros (cubos, prismas, etc.) es bien conocido por todos el significado de los términos vértice o cara. Sin embargo, estos conceptos resultan menos intuitivos si nos estamos refiriendo a un conjunto convexo (cerrado) genérico. El estudio de la frontera de un conjunto convexo resulta de gran importancia, pues determinados puntos (o estructuras) de la frontera capturan una gran cantidad de información sobre el propio conjunto (tanto en dimensión finita como infinita). Los poliedros (politopos convexos tridimensionales), especialmente los regulares, han fascinado a la humanidad desde la antigüedad. La construcción de los cinco sólidos regulares en R 3 (tetraedro, cubo, octaedro, dodecaedro e icosaedro) en el Libro XIII, fue uno de los puntos más relevantes del famoso Los Elementos de Euclides ( A.C.). Estos poliedros reciben el nombre de sólidos platónicos, debido a que Platón ( A.C.) hace mención expresa de ellos en el Timeo, uno de sus diálogos. En él exponía sus ideas sobre estos sólidos, siendo también conocidos como los cuerpos cósmicos ya que representaban la composición y armonía de las cosas: la Tierra estaba formada por átomos agrupados en forma de cubos, pues éste es el poliedro más sólido de los cinco ; el fuego, de tetraedros, ya que éste es el elemento más pequeño, ligero, móvil y agudo ; el aire, de octaedros, por ser el de tamaño, peso y fluidez, en cierto modo intermedios ; y el agua, de icosaedros: éste es el más móvil y fluido de los elementos; debe tener como forma propia o semilla, el icosaedro, el sólido más cercano a la esfera y, por tanto, el que con mayor facilidad puede rodar ;
2 22 Estructura de la frontera de un conjunto convexo. Los politopos finalmente, el universo (o éter) estaba figurado en el dodecaedro: la forma del dodecaedro es la que los dioses emplean para disponer las constelaciones en los cielos; Dios lo utilizó para todo cuando dibujó el orden final. Figura 2.1: Representación de 5 los elementos en los cuerpos cósmicos, según Platón. La primera demostración conocida del hecho de que sólo existen 5 poliedros regulares en R 3 se remonta a los pitagóricos (Pitágoras, A.C.), y podría resumirse como sigue: Obsérvese en primer lugar que cada vértice debe ser común, al menos, a tres caras para que se forme un sólido. Además, la suma de los ángulos interiores de las caras que se encuentran en cada vértice debe ser menor que 360 (la figura se cierra, no es plana). Así pues, las distintas posibilidades son: Los ángulos del triángulo equilátero miden 60. Por tanto, en un vértice pueden concurrir 3, 4 ó 5 de ellos. Así se obtienen el tetraedro, el octaedro y el icosaedro. Los ángulos del cuadrado miden 90. En consecuencia, sólo pueden concurrir 3 en cada vértice. Esto nos proporciona el cubo. Los ángulos del pentágono regular valen 108. Poniendo 3 de ellos en cada vértice se obtiene un dodecaedro. Con los siguientes polígonos no es posible formar poliedros regulares: los ángulos interiores de una hexágono miden 120 o y no es posible poner tres juntos sin llegar al límite de 360 o ; los ángulos interiores de los siguientes son mayores. Muchos piensan que los pitagóricos fueron los primeros en observar este hecho, aunque su historia es mucho más antigua: los arqueólogos han hallado imágenes de los sólidos en piedra considerablemente más remotas. Figura 2.2: Tierra, fuego, universo, agua y aire. Figuras recogidas en un yacimiento neoĺıtico de Escocia ( A.C.).
3 2.1 La estructura facial de un conjunto convexo. 23 Ya en el siglo XVI, en su tratado Mysterium Cosmographicum, Kepler ( ) defendía la idea de que las órbitas (circulares) de los planetas estaban en proporción con los radios de las esferas inscritas en sólidos platónicos dispuestos uno dentro de otro. Sólo tras conocer los resultados de las observaciones de Tycho Brahe, Kepler concluyó que tal modelo era erróneo y que los planetas se movían describiendo trayectorias elípticas. En los propios comentarios y grabados de la obra de Kepler antes citada se puede observar cómo aún sobrevivía en esta época tan tardía la asociación entre elementos y poliedros establecida por Platón. La investigación de los politopos convexos en dimensión tres ha sido una de las principales fuentes de la Teoría de Figura 2.3: Representación del universo de Grafos Planos, y gracias al buen desarrollo de esta teoría, los Kepler. poliedros son, relativamente, bien conocidos. Sin embargo, los politopos en dimensión cuatro y superior suponen un desafío considerablemente mayor para los matemáticos, lo que ha supuesto el desarrollo de una teoría sorprendentemente profunda y compleja, fundamentalmente de naturaleza algebraica, en un intento por entender su estructura. Además del gran interés que tienen por sí mismos, los politopos juegan un papel esencial en muy diversos campos, como en la ya mencionada Teoría de Grafos, en Cristalografía, para medir conjuntos convexos, en Programación Lineal, en Teoría de Juegos o en Geometría Combinatoria, entre otros La estructura facial de un conjunto convexo. Sumario. Caras i-dimensionales. Caras expuestas. Cono soporte y cono normal de K en un punto x. Vector normal exterior. Puntos r-singulares y puntos regulares Sin duda alguna, todos estamos familiarizados con el término cara cuando éste se aplica a los poliedros convexos, tales como cubos, prismas triangulares, pirámides cuadrangulares, etc. En la presente lección vamos a introducir el concepto de cara para conjuntos convexos (cerrados) arbitrarios, lo que nos permitirá describir la estructura de la frontera relativa de un conjunto convexo. Definición 2.1. Una cara de un conjunto convexo cerrado K de R n es un subconjunto convexo F de K de forma que, siempre que λx + (1 λ)y F, donde x, y K y 0 < λ < 1, entonces ambos puntos x, y F.
4 24 Estructura de la frontera de un conjunto convexo. Los politopos O, dicho de otro modo, una cara de K es un subconjunto convexo F K tal que cada segmento está contenido en F. [x, y] K con F relint[x, y] Se considera que tanto el conjunto vacío como el propio conjunto K son caras de K, denominadas caras impropias de K; todas las demás caras se dicen propias. Además, para hacer referencia a la dimensión de las caras se hablará de i-caras del conjunto. En lo sucesivo, representaremos por F (K) el conjunto de todas las caras del conjunto K, y por F i (K) el conjunto de todas las caras i-dimensionales de K. Algunas propiedades elementales, que se deducen directamente de la definición son las siguientes: Las 0-caras son los puntos extremos del conjunto. Las caras de un conjunto convexo cerrado K son cerradas. Si F K es una cara de K, entonces F relint K =. En particular, F relbd K y dim F < n. Proposición 2.2. Si K es un conjunto convexo cerrado de R n : i) La intersección de cualquier colección no vacía de caras de K es una cara de K. ii) Si F es una cara de K y G es una cara de F, entonces G también es una cara de K. iii) Si F 1, F 2 F (K) son dos caras distintas de K, entonces relint F 1 relint F 2 =. Esto permite deducir además que el sistema { relint F : F F (K) } es una descomposición disjunta de K. Si H es un hiperplano soporte al conjunto K, entonces H K es una cara de K. Esto nos permite establecer la siguiente definición: Definición 2.3. La intersección de un conjunto convexo cerrado K de R n con uno de sus hiperplanos soporte recibe el nombre de cara expuesta de K (o i-cara expuesta de K). De nuevo, los conjuntos y K se consideran caras expuestas y se denominan impropias. Al igual que ocurría para las caras de un conjunto convexo cerrado K (véase la Proposición 2.2), se puede demostrar que: Proposición 2.4. La intersección de cualquier colección no vacía de caras expuestas de K es una cara expuesta de K. Sin embargo, la propiedad (ii) de la Proposición 2.2 no tiene contrapartida para las caras expuestas: una cara expuesta G de una cara expuesta F del conjunto K no tiene por qué ser, necesariamente, una cara expuesta de K.
5 2.1 La estructura facial de un conjunto convexo. 25 Definición 2.5. Sean K un cuerpo convexo y x un punto de K. Definimos el conjunto P (K, x) := { λ(y x) : y K, λ > 0 } = λ>0 λ(k x). Entonces S(K, x) = cl P (K, x) recibe el nombre de cono soporte de K en x. Claramente P (K, x) es un cono convexo, y además, P (K, x) = aff K x si, y sólo si, x relint K. Evidentemente, el cono soporte S(K, x) puede representarse de la forma S(K, x) = H (K, u) x, x H(K,u) donde la intersección se toma sobre todas las direcciones u S n 1 para las que x se encuentra en el hiperplano soporte H(K, u) (si x relint K, se adopta el convenio usual de que la intersección de una familia vacía de subconjuntos de R n es igual a R n ). Definición 2.6. Se define el cono normal de K en x como N(K, x) := { u R n \{O} : x H(K, u) } {O}. Si x K H(K, u), entonces se dice que u es un vector normal exterior a K en x. Por lo tanto, N(K, x) no es otra cosa que el conjunto de todos los vectores normales exteriores a K en x junto con el vector nulo. Claramente, N(K, x) es un cono convexo cerrado, y además N(K, x) = S(K, x), esto es, N(K, x) y S(K, x) son conos convexos duales. Un hecho interesante es que el cono normal está estrechamente relacionado con la proyección métrica: el Lema 1.17 nos aseguraba que si x K, entonces el hiperplano H que pasa por el punto más próximo p(k, x) = p K (x), ortogonal al vector u(k, x), soporta K; de aquí se deduce que N(K, x) = p 1 K (x) x. El siguiente resultado describe el comportamiento de los conos soporte y normal respecto a la suma y la intersección de conjuntos. Teorema 2.7. Sean K y L dos cuerpos convexos de R n. i) Si x K e y L, entonces S(K + L, x + y) = S(K, x) + S(L, y), N(K + L, x + y) = N(K, x) N(L, y). ii) Si x K L y relint K relint L, entonces S(K L, x) = S(K, x) S(L, x), N(K L, x) = N(K, x) + N(L, x).
6 26 Estructura de la frontera de un conjunto convexo. Los politopos Los conos normales conducen, de forma natural, a una clasificación de los puntos singulares de la frontera de un cuerpo convexo. Definición 2.8. Sea K un cuerpo convexo con O int K y sea x un punto de la frontera de K. Decimos que x es un punto r-singular de K si dim N(K, x) n r. Un punto (n 2)-singular se denomina, simplemente, punto singular. En particular, un punto 0-singular verifica que dim N(K, x) = n, y es lo que se conoce comúnmente por un vértice de K. Si el hiperplano soporte a K en x es único, es decir, si x es no singular, entonces x se llama regular. En consecuencia, el cuerpo convexo K se dice regular si todos sus puntos frontera son regulares Los politopos. Sumario. Los k-politopos. Los sólidos platónicos. Paralelotopos, k-símplices y k-crosspolitopos. Vértices, aristas y caras de un politopo. Politopos simpliciales y simples. Zonotopos. Teorema Principal de los Politopos. La fórmula de Euler- Poincaré. Aproximación por politopos. Se define un politopo como la envoltura convexa de un conjunto finito (posiblemente vacío) de puntos en R n. Es por tanto la generalización natural de un polígono en el plano y un poliedro en dimensión tres. De forma más general, se da el nombre de k-politopo a un politopo de dimensión k. Además de los famosos sólidos platónicos, conocemos ya algunos ejemplos sencillos de politopos: i) Los paralelotopos: politopos generados mediante la suma de un número finito de vectores linealmente independientes de R n. Entre ellos, los más sencillos son los cubos: un cubo n-dimensional no es más que el producto cartesiano [ 1, 1] n. ii) Los k-símplices: politopos generados por la envoltura convexa de k + 1 puntos afínmente independientes. iii) Los crosspolitopos: en general, un crosspolitopo k-dimensional es la envoltura convexa de k segmentos linealmente independientes en R n cuyos puntos medios coinciden. Tal crosspolitopo se dice regular si todos los segmentos tienen la misma longitud y son además mutuamente ortogonales. Si P es un politopo, se denominan vértices, los puntos extremos de P, aristas o lados, las 1-caras de P, y simplemente
7 2.2 Los politopos. 27 caras, las caras (n 1)-dimensionales de P. Existen además dos clases muy importantes de politopos: los llamados simpliciales y los simples. Definición 2.9. Un politopo de R n se dice simplicial si todas sus caras (propias) son símplices, es decir, si toda cara (n 1)-dimensional tiene n vértices. Un politopo de R n se dice simple si todo vértice está contenido en n caras (n 1)-dimensionales. Estos dos conceptos están ligados por la polaridad: si dos politopos P y Q son duales, entonces uno de ellos es simple si, y sólo si, el otro es simplicial, y viceversa La estructura facial de un politopo. Los vértices de un politopo P = conv{x 1,..., x k } son los puntos extremos de P, y coincidiesen a su vez con los puntos x 1,..., x k si, y sólo si, para cada i = 1,..., k, x i conv j i x j. Los politopos son los cuerpos convexos que tienen una cantidad finita de puntos extremos. Otras propiedades de los politopos son las siguientes: Si H es un hiperplano soporte de un politopo P = conv{x 1,..., x k }, entonces H P = conv ( H {x 1,..., x k } ), y por tanto la intersección H P es un politopo. Es innecesaria la distinción entre caras y caras expuestas: en efecto; se demuestra que toda cara propia de un politopo P es la intersección de P con algún hiperplano soporte H a P. En particular, cada punto extremo de un politopo es un punto expuesto. Además si F es una cara propia de P, como existe un hiperplano H con F = H P = conv ( H {x 1,..., x k } ), se puede concluir que toda cara es la envoltura convexa de un subconjunto de los vértices. Si P y Q son dos politopos en R n y α R, entonces P + Q y αp son también politopos. En particular: Definición La suma vectorial de un número finito de segmentos en R n es un politopo que recibe el nombre de zonotopo. Un politopo se ha definido como la envoltura convexa de un número finito de puntos. De manera alternativa, se puede ver como la intersección de un número finito de semiespacios:
8 28 Estructura de la frontera de un conjunto convexo. Los politopos Teorema Todo politopo es la intersección de una cantidad finita de semiespacios cerrados. Teorema Toda intersección acotada de una cantidad finita de semiespacios cerrados es un politopo. La caracterización de los politopos establecida por los Teoremas 2.11 y 2.12 suele recibir el nombre de Teorema Principal de los Politopos. Lema El cuerpo polar de un politopo es de nuevo un politopo. Por ejemplo, si consideramos los cinco sólidos platónicos, se tiene que el cubo y el octaedro son politopos duales, que el dodecaedro y el icosaedro son también polares y que el tetraedro es dual de sí mismo. La siguiente elegante construcción, puramente geométrica, del dodecaedro a partir del icosaedro (y viceversa) permite intuir esa dualidad existente entre ambas figuras: Imaginemos dos pentágonos regulares y horizontales, situados uno sobre el otro, y rotemos el superior, dentro de su plano, un ángulo de 36. Conectemos entonces los vértices mediante 10 triángulos isósceles, lo que nos da un poliedro que, usualmente, recibe el nombre de antiprisma. Claramente, para una distancia adecuada entre los pentágonos, dichos triángulos serán equiláteros. Finalmente, sustituyamos los dos pentágonos por sendos capuchones formados por 5 triángulos equiláteros. Hemos construido un icosaedro. Si ahora conectamos los puntos medios de las caras triangulares adyacentes, obtenemos los 12 pentágonos regulares que forman las caras del dodecaedro. Ya sabemos que toda cara de un politopo P es la envoltura convexa de un subconjunto de sus vértices. Sea V el conjunto de los vértices de P. La pregunta surge entonces de forma natural: Qué subconjuntos W del conjunto de los vértices V van a determinar una cara de P? El siguiente resultado proporciona la respuesta a la cuestión anterior: Proposición Sea W un subconjunto del conjunto de los vértices V de un politopo P. Entonces conv W es una cara de P si, y sólo si, (aff W ) conv(v \W ) =. De forma general, se establece el siguiente teorema sobre la estructura facial de los politopos: Teorema 2.15 (La estructura facial). Si F (P ) es el conjunto de todas las caras de un politopo P, entonces: i) Para cualesquiera dos caras F y G de F (P ), la intersección F G es una nueva cara de P que incluye todas las caras que están contenidas tanto en F como en G. ii) Para cualesquiera dos caras F y G de F (P ), existe una cara de P, denominada la cara común de F y G, que contiene a ambas, y que está incluida a su vez en cualquier otra cara que contenga, tanto a F como a G.
9 2.2 Los politopos La fórmula de Euler. En 1752, Euler descubrió que, para los politopos 3-dimensionales, se verificaba la hoy conocida fórmula f e + v = 2, donde f representa el número de caras, e el número de aristas y v el número de vértices del politopo. El caso general fue demostrado por Poincaré en 1899, por lo que dicha relación se conoce a menudo con el nombre de fórmula de Euler-Poincaré. Vamos a representar por f r (P ) el número de r-caras que presenta un n-politopo P de R n para r = 1, 0, 1,..., n, donde f 1 (P ) = f n (P ) = 1. De forma general, si r < 1 ó r > n se considera que f r (P ) = 0. Teorema 2.16 (La fórmula de Euler-Poincaré, ). Sea P un m-politopo no vacío en R n. Entonces m 1 ( 1) r f r (P ) = 1 ( 1) m Aproximación de cuerpos convexos por politopos. r=0 Dado que disponemos de una métrica en la familia K n de los cuerpos convexos de R n, la métrica de Hausdorff, podemos estudiar la aproximación de cuerpos convexos arbitrarios por otros particulares. La aproximación de cuerpos convexos generales por politopos es una herramienta extremadamente útil en numerosas investigaciones. Vamos a señalar aquí únicamente los hechos más básicos referentes a la aproximación por politopos. Teorema Sean K un cuerpo convexo de R n y ε > 0. Entonces, existe un politopo P K n verificando que P K P + εb n, y por tanto, con δ(p, K) ε. Teorema 2.18 (Teorema de aproximación). Sea K un cuerpo convexo de R n que contiene el origen en su interior. Entonces, para cada λ > 1, existe un politopo P K n verificando que P K λp.
10 30 Estructura de la frontera de un conjunto convexo. Los politopos
Los conjuntos convexos y sus propiedades
 Capítulo 1 Los conjuntos convexos y sus propiedades TEMARIO Lección 1.1 Los conjuntos convexos y sus propiedades. Lección 1.2 Proyección métrica, soporte y separación. Lección 1.3 Dualidad. Lección 1.4
Capítulo 1 Los conjuntos convexos y sus propiedades TEMARIO Lección 1.1 Los conjuntos convexos y sus propiedades. Lección 1.2 Proyección métrica, soporte y separación. Lección 1.3 Dualidad. Lección 1.4
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton
 Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Polígonos y poliedros
 Polígonos y poliedros Rojo central (1980). El científico se ocupa de demostrar hechos, para comprobarlos, las mentes más estrictas utilizan ecuaciones matemáticas, luego vienen otros hombres, que aplican
Polígonos y poliedros Rojo central (1980). El científico se ocupa de demostrar hechos, para comprobarlos, las mentes más estrictas utilizan ecuaciones matemáticas, luego vienen otros hombres, que aplican
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
REGULARES.
 Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
 http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
 Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
TEMA 5. Geometría. Teoría. Matemáticas
 1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
GEOMETRÍA POLIEDROS. Los ángulos diedros y los ángulos poliedros determinados por las caras son los ángulos diedros y ángulos poliedros del poliedro.
 GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
Introducción. Este trabajo será realizado con los siguientes fines :
 Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos
 Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
Cuerpos geométricos. Cuerpos redondos Cuerpos de revolución. Poliedros (más importantes)
 Cuerpos geométricos Cuerpos redondos Cuerpos de revolución Poliedros (más importantes) Cuerpo geométrico limitado por caras que son polígonos Cuerpo geométrico que se obtiene a partir de una figura plana
Cuerpos geométricos Cuerpos redondos Cuerpos de revolución Poliedros (más importantes) Cuerpo geométrico limitado por caras que son polígonos Cuerpo geométrico que se obtiene a partir de una figura plana
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
11 CONOCER LOS POLIEDROS Y DIFERENCIAR
 REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
Se dice que un poliedro es regular cuando sus caras son polígonos regulares iguales y sus ángulos poliedros tienen el mismo número de caras.
 LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
TEMA 4. Geometría. Teoría. Matemáticas
 1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
POLIEDROS. POLIEDROS Prof. Annabella Zapattini. Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos.
 POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
Figuras de tres dimensiones
 Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
Figuras de tres dimensiones Poliedros: cuerpos geométricos limitados por 4 o más superficies planas que son polígonos. Poliedros regulares: todas las caras de igual forma y tamaño. Solo existen 5. Prismas
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
Poliedros Regulares Proyectivos
 Poliedros Regulares Proyectivos Jorge Arocha Javier Bracho Luis Montejano Instituto de Matemáticas Universidad Nacional Autónoma de México México, D.F. 04510 La sallita Que es el espacio proyectivo? x
Poliedros Regulares Proyectivos Jorge Arocha Javier Bracho Luis Montejano Instituto de Matemáticas Universidad Nacional Autónoma de México México, D.F. 04510 La sallita Que es el espacio proyectivo? x
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
Dibujo y geometría descriptiva II 2014
 ` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
SISTEMASS DE REPRESENTACIÓNN Geometría Básica
 SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
Conjuntos y funciones convexas
 Conjuntos y funciones convexas Un conjunto X R n se dice convexo si para todo par de puntos x 1 y x 2 en X, λ x 1 + ( 1- λ) x 2 X, para todo λ [0,1] Qué significa esto geométricamente? Un punto λ x 1 +
Conjuntos y funciones convexas Un conjunto X R n se dice convexo si para todo par de puntos x 1 y x 2 en X, λ x 1 + ( 1- λ) x 2 X, para todo λ [0,1] Qué significa esto geométricamente? Un punto λ x 1 +
IES FONTEXERÍA MUROS. 14-II-2014 Nombre y apellidos:.
 IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
Geometría convexa y politopos, día 2
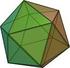 Geometría convexa y politopos, día 2 Alexey Beshenov (cadadr@gmail.com) 9 de agosto de 2016 2. La envolvente convexa 2.1. Definición. Si X R n es cualquier conjunto, entonces la envolvente convexa de X
Geometría convexa y politopos, día 2 Alexey Beshenov (cadadr@gmail.com) 9 de agosto de 2016 2. La envolvente convexa 2.1. Definición. Si X R n es cualquier conjunto, entonces la envolvente convexa de X
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
unidad 10 Cuerpos geométricos
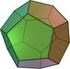 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
Material educativo. Uso no comercial 12.1 NOCIONES BÁSICAS. Definición 72. Ángulo diedro. Definimos el ángulo diedro que notamos P AB.
 12.1 NOCIONES BÁSICAS Definición 72. Ángulo diedro. Sean 1, 2 distintos, AB, P 1, P AB, Q 2, Q AB. Definimos el ángulo diedro que notamos P AB Q a la figura : P : Q AB. Esto es P AB Q : P : Q AB. Ver figura
12.1 NOCIONES BÁSICAS Definición 72. Ángulo diedro. Sean 1, 2 distintos, AB, P 1, P AB, Q 2, Q AB. Definimos el ángulo diedro que notamos P AB Q a la figura : P : Q AB. Esto es P AB Q : P : Q AB. Ver figura
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
INTRODUCCIÓN A LOS POLIEDROS
 INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS.
 TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS. LOS POLÍGONOS El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los vértices.
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS. LOS POLÍGONOS El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los vértices.
ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES
 OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
 EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
Poliedros y cuerpos redondos para imprimir
 Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
Poliedros y cuerpos redondos para imprimir Nombre Curso: Fecha: Escribe en la parte derecha lo que falta. 1. Los cuerpos redondos. La geometría del espacio estudia los cuerpos que tienen tres dimensiones:
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
Optimización lineal. Diego A. Patino. 2 de septiembre de Pontificia Universidad Javeriana 1/ 29
 Optimización lineal Diego A. Patino Pontificia Universidad Javeriana 2 de septiembre de 2016 1/ 29 Introducción Formulación del problema Herramientes del análisis convexo Formas de las restricciones 2/
Optimización lineal Diego A. Patino Pontificia Universidad Javeriana 2 de septiembre de 2016 1/ 29 Introducción Formulación del problema Herramientes del análisis convexo Formas de las restricciones 2/
A mi muy querida profesora que con ansias debe estar esperando mi trabajo. I. Introducción pag. 4
 MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
Poliedros Regulares Convexos
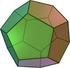 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
1. Poliedros regulares. 2. Fórmula de Euler. 3. Poliedros semiregulares. 4. Poliedros de Catalán. 5. Prismas y antiprismas. 6. Dualidad de poliedros
 7. Poliedros Ámbito científico 1. Poliedros regulares 2. Fórmula de Euler 3. Poliedros semiregulares 4. Poliedros de Catalán 5. Prismas y antiprismas 6. Dualidad de poliedros 7. Dipirámides y deltaedros
7. Poliedros Ámbito científico 1. Poliedros regulares 2. Fórmula de Euler 3. Poliedros semiregulares 4. Poliedros de Catalán 5. Prismas y antiprismas 6. Dualidad de poliedros 7. Dipirámides y deltaedros
UP I Universidad de Palermo
 Poliedros Cuerpos tridimensionales formados por caras planas. Sus caras son siempre figuras geométricas de aristas rectas. En forma de polígonos Sus aristas, segmento que une a las caras, deben tener igual
Poliedros Cuerpos tridimensionales formados por caras planas. Sus caras son siempre figuras geométricas de aristas rectas. En forma de polígonos Sus aristas, segmento que une a las caras, deben tener igual
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO 2º BACH.
 SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
SISTEMA DIÉDRICO POLIEDROS REGULARES DIBUJO TÉCNICO. ANA BALLESTER JIMÉNEZ 0 SISTEMA DIÉDRICO: REPRESENTACIÓN DE POLIEDROS REGULARES DEFINICIÓN DE POLIEDRO: Sólido geométrico limitado por caras planas.
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación
 Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Sistema Diédrico (II). Superficies poliédricas y radiadas: Representación Comenzamos una nueva unidad didáctica en la que desarrollaremos los conceptos y procedimientos sobre superficies poliédricas y
Geometría en el espacio. Poliedros
 Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
GEOMETRÍA. Convexos Llano (Plano) Cóncavo Giro. Consecutivos Adyacentes Diedro Complementario Suplementario
 GEOMETRÍA Angulo.- Es la abertura comprendida entre dos rectas que se encuentran en un punto. Estas rectas se llaman lados del ángulo, y el punto de encuentro se denomina vértice. Un ángulo suele designarse
GEOMETRÍA Angulo.- Es la abertura comprendida entre dos rectas que se encuentran en un punto. Estas rectas se llaman lados del ángulo, y el punto de encuentro se denomina vértice. Un ángulo suele designarse
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
Módulo Tres. Bloque 9 Tema 7
 Ámbito Científico y Tecnológico Módulo Tres. Bloque 9 Tema 7 Las formas y las medidas que nos rodean Educación Secundaria Para Adultos Ámbito Científico y Tecnológico Página 1 de 30 ÍNDICE Presentación
Ámbito Científico y Tecnológico Módulo Tres. Bloque 9 Tema 7 Las formas y las medidas que nos rodean Educación Secundaria Para Adultos Ámbito Científico y Tecnológico Página 1 de 30 ÍNDICE Presentación
A G R. Diédrico 17. Cuerpos 4. Tetraedro
 Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones. 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides.
 Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
ESTALMAT-Andalucía Actividades 05/06 Sesión: nº 22 Fecha: 10 de junio de 2006 Título: Construcción de Poliedros deltaedros-
 Hoja número 0. CONSTRUYENDO POLIEDROS. El material que tienes sobre la mesa se llama CREATOR o POLYDRON. Consta de piezas polígonos regulares- que pueden engarzarse para formar cuerpos como los sólidos
Hoja número 0. CONSTRUYENDO POLIEDROS. El material que tienes sobre la mesa se llama CREATOR o POLYDRON. Consta de piezas polígonos regulares- que pueden engarzarse para formar cuerpos como los sólidos
1. Dualidad de poliedros. 2. Prismas y antiprismas. 3. Estructuras espaciales. 4. Secciones y simetrías de poliedros. 5. Macizamiento del espacio
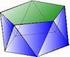 5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
ACTIVIDADES PARA LA SESIÓN PRIMERA
 ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
POLIEDROS. ÁREAS Y VOLÚMENES.
 7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
MATEMÁTICAS Y SU DIDÁCTICA
 MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2009 2010 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2009 2010 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
Perímetros, áreas y volúmenes de figuras y cuerpos geométricos.
 Perímetros, áreas y volúmenes de figuras y cuerpos geométricos. Perímetros y áreas de polígonos Triángulo El triángulo es un polígono con tres lados P = b + c + d ( Perímetro es igual a la suma de las
Perímetros, áreas y volúmenes de figuras y cuerpos geométricos. Perímetros y áreas de polígonos Triángulo El triángulo es un polígono con tres lados P = b + c + d ( Perímetro es igual a la suma de las
Tema 2. Geometría en el espacio
 Tema 2. Geometría en el espacio Matemáticas I La geometría espacial o geometría en el espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio
Tema 2. Geometría en el espacio Matemáticas I La geometría espacial o geometría en el espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
5to Parcial de Geometría Euclidiana. 2) Sea p un polígono tal que se puede descomponer en n polígonos simples
 5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
PÁGINA 98. a) Tetraedro = 2 Cubo = 2 Octaedro = 2 Dodecaedro = 2 Icosaedro = 2
 PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
Capítulo 2: Politopos
 Capítulo 2: Politopos Un politopo es la generalización del concepto Polígono (2D), o poliedro (3D) a cualquier otra dimensión. Geométricamente un politopo es una región finita de un espacio n-dimensional
Capítulo 2: Politopos Un politopo es la generalización del concepto Polígono (2D), o poliedro (3D) a cualquier otra dimensión. Geométricamente un politopo es una región finita de un espacio n-dimensional
Tema 2: Figuras geométricas
 Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
