ELABORACIÓN DE UN ÍNDICE COMPUESTO CAPÍTULO = X
|
|
|
- Ana Isabel Segura Alcaraz
- hace 7 años
- Vistas:
Transcripción
1 5 CAPÍTULO ELABORACIÓN DE UN ÍNDICE COMPUESTO Ls Ídces Cmpuess, expresa de maera resumda la varacó prmed de u cju de varables respec de u períd base. Csderems u Agregad Cmplej "X", csud pr las varables X1, X, X3,..., X (puede ser prec, cadad valr). El ídce elemeal de cada csuv X se defe pr: X I X El prblema se rga al sezar, ls ídces elemeales de las varables e esud e u ídce úc que ega, s es psble, las prpedades de ls ídces elemeales. La csruccó de u ídce séc psee ua sgfcacó ccrea sasfacra, y su erpreacó esá ascada al ccep de u esadígraf de edeca ceral. E ls ídces cmpuess, cada ídce elemeal ee ua pderacó ( ) que refleja la mpraca relava de cada eleme respec del al; dde la suma de las pderaces crrespdee a ds ls íems csderads es gual a la udad. Es represea resrccó algua, ya que dad u cju de valres basa dvdr cada ua de ells ere su suma para beer u ssema de pderaces cuya suma es gual a la udad. 68 Reá uspe Llas Reá uspe Llas 69
2 0 Se ee pues: Dde: 1,,..., varables elemes Pr ejempl, csderad ls valres del perd crree se bee dvded cada valr ( P ) ere la suma de sus valres: P A cuacó se presea las fórmulas para el cálcul de ls dferees ídces csderad pr fes explcavs, sól del p de la Meda Arméca Pderada. 5.1 ÍNDICE DE CANTIDADES Es el prmed pderad de ls ídces elemeales de cadad e la cual el facr de pderacó esá deermad pr ua prprcó de valres respec del al, varad la frma segú ls aures: I I Dde: 1 Smplfcad érms se llega a la expresó: Dde: Z I Z Z : arable de pderacó, que e el cas del cálcul de ls ídces de cadad esá fjadas pr ls precs; la frma varía segú ls dss aures. Ejempl:. Laspeyres... P. Paasche... P. Marshall-... (P + P) Edgewrh. alsh... P x P. Keyes... M(P, P ) I Z Z : Ídce elemeal de cadad del arícul "" : Facr de pderacó que expresa la prprcó del valr de u eleme cmpee respec del al. 5. ÍNDICE DE PRECIOS Es el prmed de ls ídces elemeales de prec, e la cual el facr de pderacó, esá deermad pr ua prprcó de valres respec del al, varad la frma segú ls aures. S se reemplaza el equvalee de e la fórmula: Z I Z IP P P 1 1 IP 70 Reá uspe Llas Reá uspe Llas 71
3 Dde: P IP : Ídce elemeal de precs, del arícul "" P P Z : Facr de pderacó de ls relavs de P Z prec de cada u de ls cmpees que expresa su parcpacó relava respec al al e érms de valr. S se reemplaza el equvalee de e la fórmula escra: P P Z IP P P Z Smplfcad érms llegams a la expresó: P Z IP P Z Dde: Z : arable de pderacó, que e el cas del cálcul de ls ídces de precs, esá fjadas pr cadades, la frma varía segú ls dss aures. Ejempl:. Laspeyres.... Paasche.... Marshall-... Edgewrh. alsh... + x. Keyes... M(, ) 5.3 ÍNDICE DE ALOR Es el prmed pderad de ls ídces smples de valr de u cju de bees y servcs, e el cual el facr de pderacó, esá deermad pr la prprcó de valres e el períd base. Dde: I I 1 I : Ídce elemeal de valr del arícul "" : Facr de pderacó de cada eleme cmpee, represead pr la prprcó e érms de valr de cada cmpee, respec del al e el períd base. Reemplazad e la fórmula: I Smplfcad érms: 1 I E ls úlms añs ha surgd la dea de ls Ídces c la Meda Gemérca y el Ídce de Turqvs-Thel, cm aleravas adcales. 7 Reá uspe Llas Reá uspe Llas 73
4 E geeral, respec a ls ídces expuess es ecesar cmear l sguee: Ls ídces de Laspeyres y Paasche s ls más ulzads. Ambs puede defrse cm medas pderadas de precs cadades relavas, sed las pderaces ls valres de ls dss bees servcs e u u r de ls ds períds que se cmpara. El ídce de precs de Laspeyres ( IP) L se defe cm la meda arméca pderada de ls precs relavs ulzad cm pderaces ls valres del períd base, realzádse la sumara para dferees bees y servcs. El ídce de cadades de Laspeyres ( I) aálga de las cadades relavas. L es ua meda pderada La Meda Gemérca prduce resulads meres guales que la Meda Arméca. La Meda Gemérca se ulza cuad ls das referds a ua msma varable esá expresads e prprces. E el cálcul de ídces se puede ulzar para evaluar el cmprame de varedades cuad es heergéea. Es decr, cuad esá egrada pr arículs que dfere ere sí, per cuad el arícul se muesre cm ua varedad hmgéea. La erpreacó de ua meda gemérca cm precs prmeds es cmúmee usada e el cálcul del Ídce de Precs al Csumdr, para el cálcul de ls precs prmeds ulzads e ls dferees Ssemas de Cueas Nacales de ls países del mud. E las varedades hmgéeas se calcula ls precs prmeds a parr de Medas Armécas. ÍNDICE DE FISHER (F) Se defe c la meda gemérca de ls ídces de Laspeyres y Paasche. ÍNDICE DE PRECIOS. IP ÍNDICE DE CANTIDAD F. L IP. F I. L I.. p IP Fsher calfcó de "deal" ese ídce prque sasface varas pruebas que csderaba mpraes, cm las de "versó del emp" e "versó de ls facres". El ídce de Fsher presea varas caraceríscas aracvas, bsae hay que adverr que ambé ee alguas desveajas, uas práccas y ras eórcas 1/ : - El ídce de Fsher es exgee e sus ecesdades de das, ya que ha de calcularse ls ídces de Laspeyres y Paasche, c l que sól aumea ls css, s que se prduce rerass e ls cálculs y publcacó. - El ídce de Fsher es a fácl de cmpreder cm el de Laspeyres el Paasche, que puede erprearse smplemee cm meddas del camb del valr de ua caasa especfcada de bees y servcs. p I 1 / Naces Udas, Nuev Ssema de Cueas Nacales Meddas de Precs y lume. 74 Reá uspe Llas Reá uspe Llas 75
5 - La fucó parcular de prefereca para la que el ídce de Fsher prprca ua medda exaca del ídce eórc crrespdee es sól u cas especal. - El ídce de Fsher es advamee cgruee. Es decr, puede ulzarse para crear u cju adv de das a "precs csaes". ÍNDICE DE TORNIST (T), O TRANSLOGARÍTMICO Es al gual que el ídce de Fsher, u ídce smérc, dde, para el cas de ls ídces de precs, es ua meda gemérca pderada de las cadades relavas, ulzad cm pderaces las medas armécas de las prprces de valr e ls ds períds, arbuyédles gual mpraca. ÍNDICE DE PRECIOS P. T IP Π 1 P α + α ÍNDICE DE CANTIDADES. T I Π 1 α + α Es de esperar que su valr se aprxme a la meda de ls ídces de Laspeyres y Paasche, cm el de Fsher, especalmee cuad es grade la dspersó ere ells del úmer ídce. La dfereca ere ls valres umércs de ls ídces de Trqvs y Fsher será mer e cmparacó c la dfereca ere ells y ls de Laspeyres y Paasche. 76 Reá uspe Llas
1. Una empresa estudia la evolución de los precios en euros de tres componentes (A, B, C) para una pieza en los últimos 5 años.
 Ejerccos Resuelos Números Ídces Faculad Cecas Ecoómcas y Emresarales Dearameo de Ecoomía Alcada Profesor: Saago de la Fuee Ferádez 1. Ua emresa esuda la evolucó de los recos e euros de res comoees (A,
Ejerccos Resuelos Números Ídces Faculad Cecas Ecoómcas y Emresarales Dearameo de Ecoomía Alcada Profesor: Saago de la Fuee Ferádez 1. Ua emresa esuda la evolucó de los recos e euros de res comoees (A,
CLASIFICACIÓN DE LOS ÍNDICES CAPÍTULO 4.1 PRIMERA CLASIFICACIÓN
 4 CAÍTULO CLASIFICACIÓN DE LOS ÍNDICES Hay varias maeras de clasificar ls ídices, de las cuales las más impraes s de ds ips La primera, aedied a la auraleza de la variable; la seguda, relacada a su grad
4 CAÍTULO CLASIFICACIÓN DE LOS ÍNDICES Hay varias maeras de clasificar ls ídices, de las cuales las más impraes s de ds ips La primera, aedied a la auraleza de la variable; la seguda, relacada a su grad
VOLUMEN IV CAPITULO 3 METODOLOGÍA PARA LA ACTULIZACIÓN DE LAS CURVA DE COSTOS ÓPTIMOS DE RACIONAMIENTO DE ELECTRICIDAD Y GAS NATURAL
 ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
PLAN DE TRABAJO 11 Período 23/10/06 al 3/11/06. Durante estas dos semanas estudiarás los modelos de regresiones lineales.
 Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Reglas para el manejo de los índices de deuda de la BNV. Bolsa Nacional de Valores Version 4.4 13/07/2005
 Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
TEMA 3. Medidas de variabilidad y asimetría. - X mín. X máx
 TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
4.4. La ciudad circular El Modelo de Salop
 4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
Figura 1. Figura 2. Para realizar este análisis asumiremos las siguientes condiciones:
 Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
Introducción a la Estadística Descriptiva
 Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
UNIDAD 7.- Matrices (tema 1 del libro) = MATRICES
 UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
TRANSMISIÓN DE CALOR MULTIDIRECCIONAL Y TRANSITORIA
 Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Estadística. Tema 2: Medidas de Tendencia Central.. Estadística. UNITEC Tema 2: Medidas de Tendencia Central Prof. L. Lugo
 Estadístca Tema : Meddas de Tedeca Cetral. Estadístca. UNITEC Tema : Meddas de Tedeca Cetral 1 Parámetros y Estadístcos Parámetro: Es ua catdad umérca calculada sobre ua poblacó La altura meda de los dvduos
Estadístca Tema : Meddas de Tedeca Cetral. Estadístca. UNITEC Tema : Meddas de Tedeca Cetral 1 Parámetros y Estadístcos Parámetro: Es ua catdad umérca calculada sobre ua poblacó La altura meda de los dvduos
TEMA 5: CAPITALIZACIÓN COMPUESTA ÍNDICE
 Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
1. Introducción, n, concepto y clasificación
 Tema 5: Números índces. Inroduccón, n, concepo y clasfcacón 2. Números índces smples. Defncón y propedades 3. Números índces complejos Números índces complejos sn ponderar Números índces complejos ponderados
Tema 5: Números índces. Inroduccón, n, concepo y clasfcacón 2. Números índces smples. Defncón y propedades 3. Números índces complejos Números índces complejos sn ponderar Números índces complejos ponderados
1.1.- Concepto Definición de cono Definición de función homogénea Interpretación económica de la función homogénea
 Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Una Estrategia de Acumulación de Reservas Mediante Opciones de Venta de Dólares. El Caso de Banco de México
 Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Años I0 t (base 1992 = 100)
 Esadísca y Meodología de la vesgacó Dada cualquer varable de la que coocemos los valores referdos a dsos perodos emporales, eedemos por úmero ídce de esa varable e dchos perodos el resulado de dvdr los
Esadísca y Meodología de la vesgacó Dada cualquer varable de la que coocemos los valores referdos a dsos perodos emporales, eedemos por úmero ídce de esa varable e dchos perodos el resulado de dvdr los
Taller de Preparación para el examen Models Life Contingencies (MLC) de la SOA.
 Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
TEMA 3: EQUIVALENCIA FINANCIERA DE CAPITALES
 Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
1. Introducción 1.1. Análisis de la Relación
 . Itroduccó.. Aálss de la Relacó Ejemplos: Relacoes fucoales de terés Redmeto Doss de fertlzate Redmeto hortícola Desdad de platacó Volume de madera a cortar Desdad de platacó Catdad de suplemeto dado
. Itroduccó.. Aálss de la Relacó Ejemplos: Relacoes fucoales de terés Redmeto Doss de fertlzate Redmeto hortícola Desdad de platacó Volume de madera a cortar Desdad de platacó Catdad de suplemeto dado
Semiconductores ( ) Masa Efectiva. Masa Efectiva. Masa Efectiva. Hueco. Masa Efectiva. v g dk h dk. m * Cualquier electrón está sujeto a fuerzas
 Semdutres Masa Efeta Cualquer eletró está sujet a fuerzas ttal ext + t ma S resams la euaó sól e fuó de las fuerzas exteras ext m a El eletró se mrta m s su masa ambara. Esta es la masa efeta. Masa Efeta
Semdutres Masa Efeta Cualquer eletró está sujet a fuerzas ttal ext + t ma S resams la euaó sól e fuó de las fuerzas exteras ext m a El eletró se mrta m s su masa ambara. Esta es la masa efeta. Masa Efeta
I N D I C E 1 INTRODUCCIÓN... 5 2 ANTECEDENTES... 6
 I N D I C E 1 INTRODUCCIÓN... 5 2 ANTECEDENTES... 6 3 CARACTERÍSTICAS DEL NUEVO SISTEMA DE INDICES DE PRECIOS AL CONSUMIDOR...8 3.1 POBLACIÓN DE REFERENCIA...8 3.2 COBERTURA GEOGRÁFICA DEL SISTEMA DE INDICES
I N D I C E 1 INTRODUCCIÓN... 5 2 ANTECEDENTES... 6 3 CARACTERÍSTICAS DEL NUEVO SISTEMA DE INDICES DE PRECIOS AL CONSUMIDOR...8 3.1 POBLACIÓN DE REFERENCIA...8 3.2 COBERTURA GEOGRÁFICA DEL SISTEMA DE INDICES
MEDIDAS DE FORMA Y CONCENTRACIÓN
 MEDIDAS DE FORMA Y CONCENTRACIÓN 4..- Asmetría: coefcetes de asmetría de Fsher y Pearso. Otros Coefcetes de asmetría. 4.2.- La ley ormal. 4..- Curtoss o aplastameto: coefcete de Fsher. 4.4.- Meddas de
MEDIDAS DE FORMA Y CONCENTRACIÓN 4..- Asmetría: coefcetes de asmetría de Fsher y Pearso. Otros Coefcetes de asmetría. 4.2.- La ley ormal. 4..- Curtoss o aplastameto: coefcete de Fsher. 4.4.- Meddas de
La inferencia estadística es primordialmente de naturaleza
 VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
Metodología Índice de Precios de Edificaciones Nuevas
 Meodología Ídce de recos de Edfcacoes Nuevas COLECCIÓN DOCUMENTOS - ACTUALIZACIÓN 29 Núm. 66 DEARTAMENTO ADMINISTRATIVO NACIONAL DE ESTADÍSTICA HÉCTOR MALDONADO GÓMEZ Drecor CARLOS EDUARDO SEÚLVEDA RICO
Meodología Ídce de recos de Edfcacoes Nuevas COLECCIÓN DOCUMENTOS - ACTUALIZACIÓN 29 Núm. 66 DEARTAMENTO ADMINISTRATIVO NACIONAL DE ESTADÍSTICA HÉCTOR MALDONADO GÓMEZ Drecor CARLOS EDUARDO SEÚLVEDA RICO
En esta sección estudiaremos el caso en que se usa un solo "Predictor" para predecir la variable de interés ( Y )
 Regresó Leal mple. REGREIÓN IMPLE El aálss de regresó es ua herrameta estadístca la cual utlza la relacó, etre dos o más varables de modo que ua varable pueda ser predcha desde la (s) otra (s). Por ejemplo
Regresó Leal mple. REGREIÓN IMPLE El aálss de regresó es ua herrameta estadístca la cual utlza la relacó, etre dos o más varables de modo que ua varable pueda ser predcha desde la (s) otra (s). Por ejemplo
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO Introducción.
 TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
RENTABILIDAD DE LA CUOTA DE CAPITALIZACIÓN INDIVIDUAL.
 Supertedeca de Admstradoras de Fodos de Pesoes CIRCULAR Nº 736 VISTOS: Las facultades que cofere la ley a esta Supertedeca, se mparte las sguetes struccoes de cumplmeto oblgatoro para todas las Admstradoras
Supertedeca de Admstradoras de Fodos de Pesoes CIRCULAR Nº 736 VISTOS: Las facultades que cofere la ley a esta Supertedeca, se mparte las sguetes struccoes de cumplmeto oblgatoro para todas las Admstradoras
CURSO DE ECONOMETRIA BÁSICA
 CURSO DE ECONOMETRIA BÁSICA D. Fracsco Parra Rodríguez. Jefe de Servco de Esadíscas Ecoómcas y Socodemografcas. Isuo Caabro de Esadísca. ICANE, ÍNDICE Tema. Regresó y correlacó leal smple Tema. Regresó
CURSO DE ECONOMETRIA BÁSICA D. Fracsco Parra Rodríguez. Jefe de Servco de Esadíscas Ecoómcas y Socodemografcas. Isuo Caabro de Esadísca. ICANE, ÍNDICE Tema. Regresó y correlacó leal smple Tema. Regresó
MEDIDAS DE CENTRALIZACIÓN
 Educagua.com MEDIDAS DE CETRALIZACIÓ Las meddas de cetralzacó so estadístcos que releja algú valor global de la sere estadístca. Las prcpales meddas de cetralzacó so: Meda artmétca smple. Meda artmétca
Educagua.com MEDIDAS DE CETRALIZACIÓ Las meddas de cetralzacó so estadístcos que releja algú valor global de la sere estadístca. Las prcpales meddas de cetralzacó so: Meda artmétca smple. Meda artmétca
Modelos de Regresión análisis de regresión diagrama de dispersión coeficientes de regresión
 Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Tema 60. PARÁMETROS ESTADÍSTICOS: CÁLCULO, PROPIEDADES Y SIGNIFICADO.
 Tema 60.Parámetros estadístcos. Calculo propedades y sgfcado Tema 60. PARÁMETROS ESTADÍSTICOS: CÁLCULO, PROPIEDADES Y SIGIFICADO.. Itroduccó. Defcó de estadístca. Estadístca descrptva y estadístca ferecal.
Tema 60.Parámetros estadístcos. Calculo propedades y sgfcado Tema 60. PARÁMETROS ESTADÍSTICOS: CÁLCULO, PROPIEDADES Y SIGIFICADO.. Itroduccó. Defcó de estadístca. Estadístca descrptva y estadístca ferecal.
ENCUESTA DE SALARIOS AGRARIOS METODOLOGÍA
 SECRETARÍA GENERAL TÉCNICA MINISTERIO DE AGRICULTURA, ALIMENTACIÓN Y MEDIO AMBIENTE SUBDIRECCIÓN GENERAL DE ESTADÍSTICA ENCUESTA DE SALARIOS AGRARIOS METODOLOGÍA INTRODUCCIÓN: La Ecuesa de Salaros Agraros
SECRETARÍA GENERAL TÉCNICA MINISTERIO DE AGRICULTURA, ALIMENTACIÓN Y MEDIO AMBIENTE SUBDIRECCIÓN GENERAL DE ESTADÍSTICA ENCUESTA DE SALARIOS AGRARIOS METODOLOGÍA INTRODUCCIÓN: La Ecuesa de Salaros Agraros
INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA
 Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
Clasificación de señales. Clasificación de señales. Clasificación de señales. Vectores
 Clasificació de señales Señales de Eergía y Señales de Pecia Señal de Eergía: Señal e fra de puls que ralee exise sól durae u ierval fii de iep, al es la ayr pare de su eergía se ecuera ccerada e u ierval
Clasificació de señales Señales de Eergía y Señales de Pecia Señal de Eergía: Señal e fra de puls que ralee exise sól durae u ierval fii de iep, al es la ayr pare de su eergía se ecuera ccerada e u ierval
TEMAS CUESTIONARIO DE AUTOEVALUACIÓN
 TEMAS 1-2-3 CUESTIOARIO DE AUTOEVALUACIÓ 2.1.- Al realzar los cálculos para obteer el Ídce de G se observa que: p 3 > q 3 y que p 4 >q 4 etoces: La prmera desgualdad es falsa y la seguda certa. La prmera
TEMAS 1-2-3 CUESTIOARIO DE AUTOEVALUACIÓ 2.1.- Al realzar los cálculos para obteer el Ídce de G se observa que: p 3 > q 3 y que p 4 >q 4 etoces: La prmera desgualdad es falsa y la seguda certa. La prmera
Una formulación general de un modelo de regresión paramétrico es la siguiente:
 Esmadores úcleos y polomos locales. Fracsco Parra Rodrguez Docor e Cecas Ecoómcas. UNED. Modelos de regresó o paramércos Los modelos de regresó paramércos supoe ue los daos observados provee de varables
Esmadores úcleos y polomos locales. Fracsco Parra Rodrguez Docor e Cecas Ecoómcas. UNED. Modelos de regresó o paramércos Los modelos de regresó paramércos supoe ue los daos observados provee de varables
RESUMEN. Códigos de campo JEL: F0 C6 SUMMARY
 RESUMEN El ema raado e ese rabao se emarca dero del esquema de Cueas Saéle del Tursmo. Maemácamee se desarrolla u ssema de ecuacoes e dferecas. Se pare de la ecuacó macroecoómca fudameal e equlbro para
RESUMEN El ema raado e ese rabao se emarca dero del esquema de Cueas Saéle del Tursmo. Maemácamee se desarrolla u ssema de ecuacoes e dferecas. Se pare de la ecuacó macroecoómca fudameal e equlbro para
Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores
![Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores](/thumbs/63/49997694.jpg) 1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
Sistemas Productivos
 Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
Tema 16: Modelos de distribución de probabilidad: Variables Continuas
 Aálss de Datos I Esquema del Tema 6 Tema 6: Modelos de dstrbucó de robabldad: Varables Cotuas. EL MODELO RECTANGULAR. EL MODELO NORMAL, N(μ, σ) 3. MODELO CHI-CUADRADO DE PEARSON, χ k 4. MODELO t DE STUDENT,
Aálss de Datos I Esquema del Tema 6 Tema 6: Modelos de dstrbucó de robabldad: Varables Cotuas. EL MODELO RECTANGULAR. EL MODELO NORMAL, N(μ, σ) 3. MODELO CHI-CUADRADO DE PEARSON, χ k 4. MODELO t DE STUDENT,
REGRESIÓN LINEAL SIMPLE
 RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
Estimación de parámetros en ecuaciones diferenciales estocásticas aplicadas a finanzas
 Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
Capítulo 3. Consideraciones sobre métodos numéricos
 3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
CAPITULO TRES MEDIDAS DE TENDENCIA CENTRAL
 CAPITULO TRES MEDIDAS DE TENDENCIA CENTRAL 3. CARACTERISTICAS NUMERICAS DE UNA VARIABLE S tratamos de represetar uestras edades medate u polígoo de frecuecas, y os ubcamos e el tempo: hace 0 años, hoy
CAPITULO TRES MEDIDAS DE TENDENCIA CENTRAL 3. CARACTERISTICAS NUMERICAS DE UNA VARIABLE S tratamos de represetar uestras edades medate u polígoo de frecuecas, y os ubcamos e el tempo: hace 0 años, hoy
1 Estadística. Profesora María Durbán
 Tema 5: Estmacó de Parámetros Tema 5: Estmacó de Parámetros 5. Itroduccó y coceptos báscos 5. Propedades de los estmadores 5.4 Dstrbucó de u estmador e el muestreo Objetvos del tema: Al fal del tema el
Tema 5: Estmacó de Parámetros Tema 5: Estmacó de Parámetros 5. Itroduccó y coceptos báscos 5. Propedades de los estmadores 5.4 Dstrbucó de u estmador e el muestreo Objetvos del tema: Al fal del tema el
VARIABLES ESTADÍSTICAS UNIDIMENSIONALES.
 CONTENIDOS. VARIABLES ESTADÍSTICAS UNIDIMENSIONALES. Itroduccó a la Estadístca descrptva. Termología básca: poblacó, muestra, dvduo, carácter. Varable estadístca: dscretas y cotuas. Orgazacó de datos.
CONTENIDOS. VARIABLES ESTADÍSTICAS UNIDIMENSIONALES. Itroduccó a la Estadístca descrptva. Termología básca: poblacó, muestra, dvduo, carácter. Varable estadístca: dscretas y cotuas. Orgazacó de datos.
SEMINARIO SOBRE ÍNDICES DE PRECIOS DE CONSUMO
 SEMINARIO SOBRE ÍNDICES DE PRECIOS DE CONSUMO Del 23 al 27 marzo 2009 Madrd -España Lla Monoya Sánchez TEMAS 1. Concepos generales: Números índces 2. Objevos y aplcacones del IPC español 3. Méodo general
SEMINARIO SOBRE ÍNDICES DE PRECIOS DE CONSUMO Del 23 al 27 marzo 2009 Madrd -España Lla Monoya Sánchez TEMAS 1. Concepos generales: Números índces 2. Objevos y aplcacones del IPC español 3. Méodo general
Probabilidad y estadística
 Probabldad y estadístca Grupo PM4 Trabajado gráfcas,meddas de tedeca cetral, meddas de dspersó e terpretado resultados Prof. Mguel Hesquo Garduño. Depto. De Igeería Químca Petrolera ESIQIE-IPN hesquogm@yahoo.com.m
Probabldad y estadístca Grupo PM4 Trabajado gráfcas,meddas de tedeca cetral, meddas de dspersó e terpretado resultados Prof. Mguel Hesquo Garduño. Depto. De Igeería Químca Petrolera ESIQIE-IPN hesquogm@yahoo.com.m
Modelación hidrológica empleando isoyetas de relieve, una aproximación geoestadística
 lmae Varably ad hage Hydrologcal Impacs Proceedgs of he Ffh FRIND World oferece held a Havaa uba November 006 IAHS Publ. 308 006. 6 odelacó hdrológca empleado soyeas de releve ua aproxmacó geoesadísca
lmae Varably ad hage Hydrologcal Impacs Proceedgs of he Ffh FRIND World oferece held a Havaa uba November 006 IAHS Publ. 308 006. 6 odelacó hdrológca empleado soyeas de releve ua aproxmacó geoesadísca
CÁLCULO Y COMENTARIOS SOBRE ALGUNAS MEDIDAS DESCRIPTIVAS. de una variable X, la denotaremos por x y la calcularemos mediante la fórmula:
 CÁLCULO Y COMENTARIOS SOBRE ALGUNAS MEDIDAS DESCRIPTIVAS I Meddas de localzacó Auque ua dstrbucó de frecuecas es certamete muy útl para teer ua dea global del comportameto de los datos, es geeralmete ecesaro
CÁLCULO Y COMENTARIOS SOBRE ALGUNAS MEDIDAS DESCRIPTIVAS I Meddas de localzacó Auque ua dstrbucó de frecuecas es certamete muy útl para teer ua dea global del comportameto de los datos, es geeralmete ecesaro
5.3 Estadísticas de una distribución frecuencial
 5.3 Estadístcas de ua dstrbucó frecuecal 5.3. Meddas de tedeca cetral Meddas de tedeca cetral Las meddas de tedeca cetral so descrptores umércos que proporcoa ua dea de los valores de la varable, alrededor
5.3 Estadístcas de ua dstrbucó frecuecal 5.3. Meddas de tedeca cetral Meddas de tedeca cetral Las meddas de tedeca cetral so descrptores umércos que proporcoa ua dea de los valores de la varable, alrededor
Consumo de gas natural en Bolivia: Una aplicación del Sistema Cuadrático Casi Ideal de Demanda
 Cosumo de gas aural e Bolva: Ua alcacó del Ssema Cuadráco Cas Ideal de Demada Medacel Morroy Maurco Agoso 2009 Resume Ese documeo ea cuafcar los osbles macos sobre el cosumo de gas aural reseco a deermadas
Cosumo de gas aural e Bolva: Ua alcacó del Ssema Cuadráco Cas Ideal de Demada Medacel Morroy Maurco Agoso 2009 Resume Ese documeo ea cuafcar los osbles macos sobre el cosumo de gas aural reseco a deermadas
x x x x x Y se seguía operando
 . INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
. INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
Tema 12: Modelos de distribución de probabilidad: Variables Continuas
 Aálss de Datos I Esquema del Tema Tema : Modelos de dstrbucó de robabldad: Varables Cotuas. EL MODELO RECTANGULAR. EL MODELO NORMAL, N(; ) 3. MODELO CHI-CUADRADO DE PEARSON, k 4. MODELO t DE STUDENT, t
Aálss de Datos I Esquema del Tema Tema : Modelos de dstrbucó de robabldad: Varables Cotuas. EL MODELO RECTANGULAR. EL MODELO NORMAL, N(; ) 3. MODELO CHI-CUADRADO DE PEARSON, k 4. MODELO t DE STUDENT, t
CIRCUITOS CON DIODOS.
 ema 3. Crcus cn dds. ema 3 CCUOS CON OOS. 1.- plcacón elemenal..- Crcus recradres (lmadres)..1.- eslucón de un crcu recradr ulzand las cuar aprxmacnes del dd..1.1.- eslucón ulzand la prmera aprxmacón..1..-
ema 3. Crcus cn dds. ema 3 CCUOS CON OOS. 1.- plcacón elemenal..- Crcus recradres (lmadres)..1.- eslucón de un crcu recradr ulzand las cuar aprxmacnes del dd..1.1.- eslucón ulzand la prmera aprxmacón..1..-
Una introducción al concepto de VARIEDAD REAL DIFERENCIABLE Y GRUPO DE LIE
 N NTRODCCÓN L CONCPETO DE VREDD REL DFERENCBLE Y GRPO DE LE CRLOS S. CHNE a trduccó al ccept de VREDD REL DFERENCBLE Y GRPO DE LE 0. Sbre tplgía y espac tplógc. 0. Separabldad. Espacs de Hausdr. 03. El
N NTRODCCÓN L CONCPETO DE VREDD REL DFERENCBLE Y GRPO DE LE CRLOS S. CHNE a trduccó al ccept de VREDD REL DFERENCBLE Y GRPO DE LE 0. Sbre tplgía y espac tplógc. 0. Separabldad. Espacs de Hausdr. 03. El
APLICACIONES TÍPICAS DEL AO
 3 PLIIONES TÍPIS DEL O 3.. INTODUIÓN Exsen nnumerables aplcacnes para ls O, an lneales cm n lneales, muchas de las cuales pueden ser mejradas medane pequeñas aracnes. El gran prblema, es sn duda saber
3 PLIIONES TÍPIS DEL O 3.. INTODUIÓN Exsen nnumerables aplcacnes para ls O, an lneales cm n lneales, muchas de las cuales pueden ser mejradas medane pequeñas aracnes. El gran prblema, es sn duda saber
METODOLOGÍA ÍNDICE DE DISTRIBUCIÓN DE ENERGÍA ELÉCTRICA, GAS POR CAÑERÍA Y AGUA POTABLE (IDEGA) (Preeliminar)
 MEODOLOGÍA ÍNDCE DE DSBUCÓN DE ENEGÍA ELÉCCA, GAS PO CAÑEÍA Y AGUA POABLE (DEGA) (Preelmar) SUBDECCÓN ÉCNCA SUBDECCÓN DE OPEACONES Saago, 26 de Dcembre de 2007 CHDA/GGM/GMA/VM ÍNDCE Págas. roduccó 3 2.
MEODOLOGÍA ÍNDCE DE DSBUCÓN DE ENEGÍA ELÉCCA, GAS PO CAÑEÍA Y AGUA POABLE (DEGA) (Preelmar) SUBDECCÓN ÉCNCA SUBDECCÓN DE OPEACONES Saago, 26 de Dcembre de 2007 CHDA/GGM/GMA/VM ÍNDCE Págas. roduccó 3 2.
ESTADÍSTICA DESCRIPTIVA
 ESTADÍSTICA DESCRIPTIVA A. MEDIDAS DE TENDENCIA CENTRAL B. MEDIDAS DE VARIABILIDAD C. MEDIDAS DE FORMA RESUMEN: A. MEDIDAS DE TENDENCIA CENTRAL So estadígrafos de poscó que so terpretados como valores
ESTADÍSTICA DESCRIPTIVA A. MEDIDAS DE TENDENCIA CENTRAL B. MEDIDAS DE VARIABILIDAD C. MEDIDAS DE FORMA RESUMEN: A. MEDIDAS DE TENDENCIA CENTRAL So estadígrafos de poscó que so terpretados como valores
LOS NÚMEROS COMPLEJOS
 LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
. Si vamos calculando así las potencias n-ésimas de la unidad imaginaria, descubriremos que son cíclicas y que cada 4 términos se repiten: ( )
 Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
Curvas Sistemas Gráficos Ing. Horacio Abbate 1
 Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
3 Metodología de determinación del valor del agua cruda
 3 Metodología de determacó del valor del agua cruda Este aexo de la metodología del valor de agua cruda (VAC), cotee el método de detfcacó de la relacó etre reco y caudal, el cálculo de los estadígrafos
3 Metodología de determacó del valor del agua cruda Este aexo de la metodología del valor de agua cruda (VAC), cotee el método de detfcacó de la relacó etre reco y caudal, el cálculo de los estadígrafos
TEMA 6 MUESTREO POR CONGLOMERADOS MONOETÁPICO
 TEA 6 UESTREO POR COGLOERADOS OOETÁPICO Cotedo 1- Defcó. Aplcacó. Seleccó de ua muestra por Coglomerados. Etapas. otacó. - uestreo mooetápco co coglomerados de gual tamaño. Estmacó de la meda, el total
TEA 6 UESTREO POR COGLOERADOS OOETÁPICO Cotedo 1- Defcó. Aplcacó. Seleccó de ua muestra por Coglomerados. Etapas. otacó. - uestreo mooetápco co coglomerados de gual tamaño. Estmacó de la meda, el total
ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL
 ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL TIPOS DE RELACIONES ENTRE VARIABLES Dos varables puede estar relacoadas por: Modelo determsta Modelo estadístco Ejemplo: Relacó de la altura co la edad e ños.
ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL TIPOS DE RELACIONES ENTRE VARIABLES Dos varables puede estar relacoadas por: Modelo determsta Modelo estadístco Ejemplo: Relacó de la altura co la edad e ños.
Tema 3: Números índice
 Tema : Números índce Los números ndce son ndcadores ue nos ermen ver la evolucón de una o más magnudes a ravés del emo, esaco, ec. Índce smle Dada una varable o magnud X, se defne el número índce de X
Tema : Números índce Los números ndce son ndcadores ue nos ermen ver la evolucón de una o más magnudes a ravés del emo, esaco, ec. Índce smle Dada una varable o magnud X, se defne el número índce de X
V II Muestreo por Conglomerados
 V II Muestreo por Coglomerados Dr. Jesús Mellado 31 Por alguas razoes aturales, los elemetos muestrales se ecuetra formado grupos, como por ejemlo, las persoas que vve e coloas de ua cudad, lo elemetos
V II Muestreo por Coglomerados Dr. Jesús Mellado 31 Por alguas razoes aturales, los elemetos muestrales se ecuetra formado grupos, como por ejemlo, las persoas que vve e coloas de ua cudad, lo elemetos
MUESTREO EN POBLACIONES FINITAS (1) Dos aspectos básicos de la inferencia estadística, no vistos aún:
 A. Morllas - p. - MUESTREO E POBLACIOES FIITAS () Dos aspectos báscos de la fereca estadístca, o vstos aú: Proceso de seleccó de la muestra Métodos de muestreo Tamaño adecuado e poblacoes ftas Fabldad
A. Morllas - p. - MUESTREO E POBLACIOES FIITAS () Dos aspectos báscos de la fereca estadístca, o vstos aú: Proceso de seleccó de la muestra Métodos de muestreo Tamaño adecuado e poblacoes ftas Fabldad
Aproximación a la distribución normal: el Teorema del Límite Central
 Aproxmacó a la dstrbucó ormal: el Teorema del Límte Cetral El teorema del límte cetral establece que s se tee varables aleatoras, X, X,..., X, depedetes y co détca dstrbucó de meda µ y varaza σ, a medda
Aproxmacó a la dstrbucó ormal: el Teorema del Límte Cetral El teorema del límte cetral establece que s se tee varables aleatoras, X, X,..., X, depedetes y co détca dstrbucó de meda µ y varaza σ, a medda
Duración y Convexidad I
 Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
1 i) c) ( 3+ 2i) (1 5i) es una diagonal del paralelogramo de lados z. 1 i) c) ( 3 + 2i)(1 5i) 3 4i e) c) 33
 Ejerccs resuelts en vde http://www.aprendermatematcas.rg 6. De ls sguentes númers cmplejs, calcula:,,,,,, a) = b) = + c) = 7. A) Calcula: a) ( ) + ( + 6) b) ( ) (7 + 5 ) c) ( + ) ( 5). B) Representa gráfcamente,
Ejerccs resuelts en vde http://www.aprendermatematcas.rg 6. De ls sguentes númers cmplejs, calcula:,,,,,, a) = b) = + c) = 7. A) Calcula: a) ( ) + ( + 6) b) ( ) (7 + 5 ) c) ( + ) ( 5). B) Representa gráfcamente,
SISTEMAS DISCRETOS. 1. Qué son?
 SISTEMAS DISCRETOS. Qué sn? Sn sisemas que rabajan cn das muesreads Ess sisemas sn cnrlads pr cmpuadr Ls cnrladres se desarrllan en cmpuadres. Ejempl de das muesreads Prces Reenr Muesreadr D/A Cmpuadr
SISTEMAS DISCRETOS. Qué sn? Sn sisemas que rabajan cn das muesreads Ess sisemas sn cnrlads pr cmpuadr Ls cnrladres se desarrllan en cmpuadres. Ejempl de das muesreads Prces Reenr Muesreadr D/A Cmpuadr
Experimento: TEORÍA DE ERRORES. UNIVERSIDAD DE ATACAMA Facultad de Ciencias Naturales Departamento de Física I. OBJETIVOS
 Epermeto: I. OJETIVOS UNIVERSIDD DE TM Facultad de ecas Naturales Departameto de Físca TEORÍ DE ERRORES Idetfcar errores sstemátcos y accdetales e u proceso de medcó. ompreder los coceptos de eacttud y
Epermeto: I. OJETIVOS UNIVERSIDD DE TM Facultad de ecas Naturales Departameto de Físca TEORÍ DE ERRORES Idetfcar errores sstemátcos y accdetales e u proceso de medcó. ompreder los coceptos de eacttud y
Qué es la estadística? presentación, análisis e interpretación de datos numéricos con e fin de realizar una toma de decisión más efectiva.
 Estadístca Alguos Coceptos Itroduccó Qué es la estadístca? La estadístca, e geeral, es la ceca que trata de la recoplacó, orgazacó presetacó, aálss e terpretacó de datos umércos co e f de realzar ua toma
Estadístca Alguos Coceptos Itroduccó Qué es la estadístca? La estadístca, e geeral, es la ceca que trata de la recoplacó, orgazacó presetacó, aálss e terpretacó de datos umércos co e f de realzar ua toma
TEMA 2.- LA CAPITALIZACIÓN COMPUESTA.
 TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
EJERCICIOS RESUELTOS TEMA 3.
 INTRODUCCIÓN AL ANÁLII DE DATO EJERCICIO REUELTO TEMA 3. 3.1. La ampltud total de la dstrbucó de frecuecas de la tabla 1. es: A) 11; B) 1; C). Tabla 1. Estatura e cetímetros de ños de 1 meses de edad.
INTRODUCCIÓN AL ANÁLII DE DATO EJERCICIO REUELTO TEMA 3. 3.1. La ampltud total de la dstrbucó de frecuecas de la tabla 1. es: A) 11; B) 1; C). Tabla 1. Estatura e cetímetros de ños de 1 meses de edad.
Manual del usuario. Software de Matemáticas Herramientas de Estadística y Probabilidad. HEST Versión 1.9.7
 Maual del usuaro HET Versó.9.7 ofware de Maemácas Herrameas de Esadísca y robabldad Wdows X - Wdows Vsa - Wdows 7 - Wdows 8 - Wdows O F T W R E Refereca: HET www.vaasofware.com EÑOL ÍDICE Iroduccó...3
Maual del usuaro HET Versó.9.7 ofware de Maemácas Herrameas de Esadísca y robabldad Wdows X - Wdows Vsa - Wdows 7 - Wdows 8 - Wdows O F T W R E Refereca: HET www.vaasofware.com EÑOL ÍDICE Iroduccó...3
Inferencia estadística Intervalos de confianza
 Ifereca estadístca Itervals de cfaa Cuad se btee ua estmacó utual de u arámetr es cveete acmañar dcha estmacó r ua medda de la recsó de la estmacó. U md de hacerl es frmar el estmadr y su errr stadard.
Ifereca estadístca Itervals de cfaa Cuad se btee ua estmacó utual de u arámetr es cveete acmañar dcha estmacó r ua medda de la recsó de la estmacó. U md de hacerl es frmar el estmadr y su errr stadard.
Respuesta. Si 100 manzanas es una muestra suficientemente grande podemos ocupar el TCL. Por lo tanto:
 Curso: Estadístca Iferecal (ICO 8306) Profesores: Esteba Calvo, Pablo Huechapa y Omar Ramos Ayudates: José T. Meda, Fabo Salas y Daela Vlches PROBLEMA Cosdere que Ud. es dueño de u campo que produce mazaas,
Curso: Estadístca Iferecal (ICO 8306) Profesores: Esteba Calvo, Pablo Huechapa y Omar Ramos Ayudates: José T. Meda, Fabo Salas y Daela Vlches PROBLEMA Cosdere que Ud. es dueño de u campo que produce mazaas,
Una Propuesta de Presentación del Tema de Correlación Simple
 Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
MEDIDAS DE TENDENCIA CENTRAL
 Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
Estadística Descriptiva
 Estadístca Descrptva Poblacoes y muestras Varables. Tablas de frecuecas Meddas de: tedeca cetral-dspersó ESTADÍSTICA DESCRIPTIVA: Tee por objetvo recoplar, orgazar y aalzar formacó referda a datos de u
Estadístca Descrptva Poblacoes y muestras Varables. Tablas de frecuecas Meddas de: tedeca cetral-dspersó ESTADÍSTICA DESCRIPTIVA: Tee por objetvo recoplar, orgazar y aalzar formacó referda a datos de u
MÉTODOS ESTADÍSTICOS PARA EL CONTROL DE CALIDAD
 UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
Producto y división de dos series a partir de los coeficientes de Fourier.
 Prduc dvsó de ds seres rr de ls cefcees de Furer Frcsc Prr Rdrígue Dcr e Cecs Ecómcs UED PRODUCO Y DIVISIÓ DE DOS SERIES PRIR DE LOS COEFICIEES DE FOURIER Frcsc Prr Rdrígue s lcesed uder Creve Cmms Reccme-Cmercl
Prduc dvsó de ds seres rr de ls cefcees de Furer Frcsc Prr Rdrígue Dcr e Cecs Ecómcs UED PRODUCO Y DIVISIÓ DE DOS SERIES PRIR DE LOS COEFICIEES DE FOURIER Frcsc Prr Rdrígue s lcesed uder Creve Cmms Reccme-Cmercl
Tema 1: Transformada de Laplace. Contenidos Transformada de Laplace
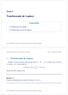 Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AVANZADA Udad I: Prpedade y Leye de la ermdámca Prce reverble e tema cerrad Vlume de ctrl Cted Etrpía Degualdad de Clauu Defcó La ercera Ley de la ermdámca Prce ermdámc Dagrama -S Vlume de
ERMODINÁMICA AVANZADA Udad I: Prpedade y Leye de la ermdámca Prce reverble e tema cerrad Vlume de ctrl Cted Etrpía Degualdad de Clauu Defcó La ercera Ley de la ermdámca Prce ermdámc Dagrama -S Vlume de
Influencia de distribución del tiempo de ocurrencia entre siniestros en la solvencia de las carteras de seguros no vida (*)
 ESTADÍSTICA ESPAÑOLA Vol. 50, úm. 69, 008, págs. 455 a 478 Iflueca de dsrbucó del empo de ocurreca ere sesros e la solveca de las careras de seguros o vda (*) por MAITE MÁRMOL JIMÉNEZ y M. MERCE CLARAMUNT
ESTADÍSTICA ESPAÑOLA Vol. 50, úm. 69, 008, págs. 455 a 478 Iflueca de dsrbucó del empo de ocurreca ere sesros e la solveca de las careras de seguros o vda (*) por MAITE MÁRMOL JIMÉNEZ y M. MERCE CLARAMUNT
Sesión 4: Estadística descriptiva y exportación de resultados
 Curs de trduccó a Stata Jrd Muñz (UAB) Sesó 4: Estadístca descrptva y exprtacó de resultads E esta sesó vams a trabajar c la estadístca descrptva e Stata. Prevamete, presetams ua pequeña trduccó de ls
Curs de trduccó a Stata Jrd Muñz (UAB) Sesó 4: Estadístca descrptva y exprtacó de resultads E esta sesó vams a trabajar c la estadístca descrptva e Stata. Prevamete, presetams ua pequeña trduccó de ls
por SANTIAGO RODRÍGUEZ FEIJOÓ Universidad de Las Palmas de Gran Canaria CARLOS GONZÁLEZ CORREA Consejería de E. y H. del Gobierno de Canarias
 ESTADÍSTICA ESAÑOLA Vol. 44, Núm. 50, 2002, págs. 229 a 255 La eoría de la ardad Relava del oder de Compra ere erroros ecoómcos que ee ua msma moeda: ua aplcacó a las comudades auóomas españolas por SANTIAO
ESTADÍSTICA ESAÑOLA Vol. 44, Núm. 50, 2002, págs. 229 a 255 La eoría de la ardad Relava del oder de Compra ere erroros ecoómcos que ee ua msma moeda: ua aplcacó a las comudades auóomas españolas por SANTIAO
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002
 REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002 UN SISTEMA BASADO EN CASOS PARA LA TOMA DE DECISIONES EN CONDICIONES DE INCERTIDUMBRE Ilaa Guérrez Maríez, Rafael E. Bello Pérez y Adrés Tellería Rodríguez
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002 UN SISTEMA BASADO EN CASOS PARA LA TOMA DE DECISIONES EN CONDICIONES DE INCERTIDUMBRE Ilaa Guérrez Maríez, Rafael E. Bello Pérez y Adrés Tellería Rodríguez
DIFERENCIADORES E INTEGRADORES
 DIFEENIDOES E INTEGDOES En la Fgura enems un amplcadr en el que las ressencas de enrada y realmenacón han sd susudas pr mpedancas, es decr, Z y Z represenan ascacnes de ressencas y cndensadres (raramene
DIFEENIDOES E INTEGDOES En la Fgura enems un amplcadr en el que las ressencas de enrada y realmenacón han sd susudas pr mpedancas, es decr, Z y Z represenan ascacnes de ressencas y cndensadres (raramene
ESTADÍSTICA poblaciones
 ESTADÍSTICA Es la parte de las Matemátcas que estuda el comportameto de las poblacoes utlzado datos umércos obtedos medate epermetos o ecuestas. ESTADÍSTICA La Estadístca tee dos ramas: La Estadístca descrptva:
ESTADÍSTICA Es la parte de las Matemátcas que estuda el comportameto de las poblacoes utlzado datos umércos obtedos medate epermetos o ecuestas. ESTADÍSTICA La Estadístca tee dos ramas: La Estadístca descrptva:
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU
 MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
GRADO EN PSICOLOGIA INTRODUCCIÓN AL ANÁLISIS DE DATOS Código Asignatura: FEBRERO 2010 EXAMEN MODELO A
 Febrero 20 EAMEN MODELO A Pág. 1 GRADO EN PICOLOGIA INTRODUCCIÓN AL ANÁLII DE DATO Códgo Asgatura: 620137 FEBRERO 20 EAMEN MODELO A Tabla 1: Para estudar la relacó etre las putuacoes e u test () y el redmeto
Febrero 20 EAMEN MODELO A Pág. 1 GRADO EN PICOLOGIA INTRODUCCIÓN AL ANÁLII DE DATO Códgo Asgatura: 620137 FEBRERO 20 EAMEN MODELO A Tabla 1: Para estudar la relacó etre las putuacoes e u test () y el redmeto
X / n : proporción de caras ( = frecuencia relativa del suceso A = f A = n A / n ) Se espera que a medida que n crece la frecuencia relativa de cara
 95 Teoremas límte Cosderemos el exermeto aleatoro que cosste e arrojar ua moeda equlbrada veces. Suogamos que se regstra la roorcó de caras. U resultado coocdo es que esta roorcó estará cerca de /. Formalzado
95 Teoremas límte Cosderemos el exermeto aleatoro que cosste e arrojar ua moeda equlbrada veces. Suogamos que se regstra la roorcó de caras. U resultado coocdo es que esta roorcó estará cerca de /. Formalzado
Tema 5: Equilibrio General Parte III OWC Economía para Matemáticos. Fernando Perera Tallo ttp://bit.ly/8l8ddu
 y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
Estadística Descriptiva
 Estadístca Descrptva Poblacó: Es u cojuto de elemetos co ua determada característca. Muestra: Es u subcojuto de la poblacó. Muestreo: Es el proceso para elegr ua muestra que sea represetatva de la poblacó.
Estadístca Descrptva Poblacó: Es u cojuto de elemetos co ua determada característca. Muestra: Es u subcojuto de la poblacó. Muestreo: Es el proceso para elegr ua muestra que sea represetatva de la poblacó.
n t T é c n i c Curso de Estadística con R Autor: Francisco Parra Rodríguez Jefe de Servicio de Estadísticas Económicas y Sociodemográficas ICANE
 D o c u m e Curso de Esadísca co R o s Auor: Fracsco Parra Rodríguez Jefe de Servco de Esadíscas Ecoómcas y Socodemográfcas ICANE DOC. Nº /6 ISSN 444-67 Saader, Caabra T é c c o s . EL MODELO LINEAL GENERAL...3..
D o c u m e Curso de Esadísca co R o s Auor: Fracsco Parra Rodríguez Jefe de Servco de Esadíscas Ecoómcas y Socodemográfcas ICANE DOC. Nº /6 ISSN 444-67 Saader, Caabra T é c c o s . EL MODELO LINEAL GENERAL...3..
Teoría Simplificada de ERRORES Suscriben este documento los coordinadores de Laboratorio de Química, Física I y Física II.
 Teoría Smplfcada de ERRORES Suscrbe este documeto los coordadores de Laboratoro de Químca, Físca I y Físca II. Defcoes Báscas: -Error absoluto (o error): Itervalo xe dode co máxma probabldad se ecuetra
Teoría Smplfcada de ERRORES Suscrbe este documeto los coordadores de Laboratoro de Químca, Físca I y Físca II. Defcoes Báscas: -Error absoluto (o error): Itervalo xe dode co máxma probabldad se ecuetra
