Derivadas algebraicas
|
|
|
- Carmelo Santiago Crespo Valverde
- hace 7 años
- Vistas:
Transcripción
1 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaas algebraicas por Sanra Elvia Pérez Derivaa e una función El concepto e erivaa, base el cálculo iferencial, ha permitio resolver múltiples problemas y hoy en ía continúa vigente; sirve como sustento a muchas isciplinas como: mecánica, electromagnetismo, electrónica, comunicaciones, termoinámica, economía, meicina. Meiante el concepto e erivaa, se pueen resolver problemas que impliquen una variación, por ejemplo en meicina, se puee eterminar la velocia con la que cambia el tamaño e un tumor con respecto al tiempo, puieno eterminar si un tratamiento está ano resultao o el tiempo aecuao para realizar una operación. Otra posible aplicación es eterminar las imensiones óptimas e un conteneor (e forma inistinta) que permita encerrar un volumen máimo utilizano un mínimo e material. Estos y otros problemas pueen ser resueltos meiante la aplicación e la erivaa. Definición El concepto e erivaa, según Purcell y Varberg (000) es el siguiente: La erivaa e una función f es otra función f (léase efe prima) cuyo valor para un número cualquiera c es f ( c + h) f ( c) f ( c) lim h 0 h una vez que icho límite eista (p. 101). Esta efinición es prácticamente la misma que manejan iferentes autores, por ejemplo Zill (1987) efine a la erivaa como sigue: La erivaa e una función f ( ) y con respecto a es f ( ) ( + Δ) f ( ) f Δ 0 Δ Siempre que este límite eista (p. 117). lim Δ 0 lim Δy Δ UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1
2 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Observa que ambas efiniciones son las mismas y sólo se iferencian en las literales que utilizan, en nuestro curso utilizaremos la notación Δ. La efinición e erivaa se puee esarrollar ese istintos puntos e vista, en este curso se lleva a cabo el esarrollo e la efinición ese el punto e vista geométrico por consierarlo más representativo. Ahora observa La epresión ( + Δ) f ( ) f lim0 Δ Δ, la cual se conoce como Regla General e la Derivación. A continuación se analiza un ejemplo el uso e esta fórmula para eplicar cómo se utiliza. Encontrar la erivaa e la función lineal f ( ) + En la fórmula se requiere el término f ( Δ) + Δ. En este caso quea, +. Para hallarlo se sustituye el valor e las ' s por Sustituyeno estas os epresiones en la Regla General e la Derivación obtienes, lim Δ 0 lim Δ 0 f ( + Δ) f ( ) Δ [ ( + Δ) + ] ( + ) Δ Se requiere calcular el límite inicao. Para ello se esarrolla el numeraor con el propósito e simplificarlo. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato.
3 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez lim Δ 0 lim Δ 0 lim Δ 0 lim Δ 0 [ ( + Δ) + ] ( + ) [ + Δ + ] ( + ) Δ + Δ + Δ Δ lim Δ Δ 0 Δ En este ejemplo la erivaa e la función f ( ) + es y. La erivaa e cualquier función puee ser eterminaa a partir e la regla general e la erivación, sin embargo entre más complicaas sean las funciones, las operaciones algebraicas que se tienen que realizar se vuelven más etensas y es por ello que se utilizan las reglas e erivación las cuales se muestran a continuación. Derivaas e funciones algebraicas Las fórmulas e erivaas parten e la aplicación e la efinición e erivaa a los iferentes tipos e funciones. De acuero a Fuenlabraa e la Vega (001) las notaciones e las erivaas e acuero al autor pueen ser como se muestran en la tabla 1: Notación Autor Cauchy Lagrange Lagrange Leibnitz Tabla 1. Notaciones y autores (Fuenlabraa e la Vega, 001, p. ). UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato.
4 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez El siguiente formulario sólo incluye los teoremas sobre erivaas e Funciones Algebraicas. En secciones posteriores se anean las fórmulas e las funciones trigonométricas irectas, funciones eponenciales y logarítmicas Formulario e Derivaas e Funciones Algebraicas C representa cualquier constante. Las literales u, v, w, representan cualquier función. uʼ, vʼ,wʼ representan la erivaa e u, v, w) 1. ( C) 0. ( ) 1. ( c) c ( ) u + v w u + v. n n ( ) n( ) 1. ( cu) c ( u) cu 7. ( uv) uv + vu 8. u vu uv v v 9. n n1 ( u) n( u) u. ( ) w Figura 1. Formulario e erivaas básicas realizao con base en la nomenclatura e Leibnitz y e Lagrange. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato.
5 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaa e una constante Deriva y Usano la regla para erivar una constante, ( C) 0 Tiene que: ( ) 0 Por lo tanto, y 0 Deriva y π En esta epresión aparece la constante π (pi), por lo que π también es una constante ( π ) 0 y 0 Derivaa e la variable inepeniente La regla para la erivaa e la variable inepeniente es 1. ( ) 1 Es importante señalar que la variable puee representar cualquier tipo e variable, sin embargo en los problemas e aplicación frecuentemente se utilizan literales que hacen referencia a la variable que se tiene que manipular, e esta forma si se pretene realizar la erivaa e la velocia con respecto a la velocia es común utilizar la variable v. De esta forma tienes que: v ( v) 1 UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato.
6 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaa e la variable inepeniente () multiplicano a una constante Recuera que es común que se represente la variable inepeniente con la letra, sin embargo puee ser cualquier variable (letra) la que esté representaa. Deriva y 7t Usano la regla número 7 ( c) c ( ) y aplicano a la variable t Tienes: ( 7 t) 7 ( t) 7( 1) 7 t t, por lo que: y 7 Observa que en este ejemplo se está erivano t con respecto a t Encuentra la erivaa e y y ( ) (1) Derivaa e una suma e funciones Para realizar la erivaa e una suma e funciones, se aplican las reglas e erivación a caa uno e los términos por separao. Deriva y Usano la regla UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato.
7 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez ( u + v w) u + v w la erivaa e y es: Deriva y + y La erivaa e y + es y, ( ) ( ) ( ) 0 ( + ) ( ) + ( ) + 0 Ahora observa alguna e las aplicaciones que se pueen tener al realizar las erivaas e funciones lineales. Supón que te proporcionan la ecuación e una línea recta ( y 1) y te pien encontrar el ángulo e intersección en la recta y el eje positivo e las. La geometría analítica proporciona una forma e resolver este problema, pero lo solucionas con erivaas sólo para ejemplificar su aplicación. Derivano y 1 obtienes, ( 1) ( ) + ( 1) + 0 Debio a que la erivaa obtenia también es la peniente e la recta, m y a que la peniente e una recta es la tangente el ángulo e inclinación ( m tanα ), entonces: m Si espejas el ángulo α puees hallar su valor, m tan α tan α ( ). α tan 1, UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 7
8 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez que es el valor que estabas buscano. La comprensión el Cálculo puee llegar a ser una herramienta muy poerosa en la resolución e problemas pero epene, como casi too, e la estreza que se alcance en su manejo. Derivaa e la variable inepeniente () elevaa a un eponente istinto e 1 Deriva y Usano la regla número n n ( ) n( ) 1, la erivaa e y es: 1 ( ) ( ) ( ) y Deriva y En este ejemplo aunque el eponente es fraccionario, el proceso es eactamente el mismo. 1 y 1 ( ) ( ) 1 Deriva y + + En este ejemplo primero ebes utilizar la regla e la suma y enseguia las reglas anteriores. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 8
9 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez y ( + + ) ( ) + ( ) ( ) + ( ) 1 1 ( ) + ()( ) ( 1) ( ) (0) En los ejemplos anteriores se puee observar que la erivaa e una función el tipo ( ) n f, implica os pasos: 1) Bajar el eponente y colocarlo enfrente e la. ) Restar un 1 al eponente tenieno cuiao e aplicar correctamente las leyes e los signos y e los eponentes. Derivaa el proucto e una función por una constante La regla es la que se usa en los siguientes ejemplos. Este teorema es una ampliación e la regla. ( cu) c ( u) cu Calcula ahora la erivaa e y Observa que en este ejemplo el eponente incluye ecimales, pero el proceso es el mismo La erivaa e y quea: 1 ( ) ( ) [ ( ) ] ( ) 1 [ ] UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 9
10 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez 1 Deriva y La erivaa e 1 y es: ( ) ( ) 1 1 [ ] [ ( ) ] y Este último ejercicio es ya un resultao correcto e la erivaa. El resultao obtienes espués e una simplificación e la fracción. lo En muchas ocasiones, simplificar las epresiones ayua a que los resultaos sean más fáciles e obtener, aemás e que permite practicar el uso el Álgebra. Deriva y + +. Observa que este ejemplo es una suma e funciones. ( + + ) ( ) ( ) ( ) ( ) y + Para facilitar el cálculo, resulve caa erivaa por separao. ( ) ( ) ( ) 1 [ ] 1 ( ) ( ) 1 [ ] ( ) ( ) (1) UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 10
11 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez ( ) 0 De esta manera el resultao final se obtiene sumano los resultaos anteriores, por lo que la erivaa buscaa es: y 1 + Observa que en este tipo e erivaas se usa lo que ya habías estuiao y solamente realizas la suma. Fórmula para erivar un proucto e funciones En la resolución e los siguientes ejemplos será necesario utilizar la regla 7. ( uv) uv + vu y + Deriva ( )( ) Para resolver este tipo e erivaas es recomenable ientificar qué funciones son u y v, y luego calcular sus respectivas erivaas u y v. u v ( + ) ( ) u () + () + 0 v () + ( ) 0 Ahora que ya tienes a u, u, v, v, los sustituyes en la regla e erivación 7, ( + )( ) + ( )( ) UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 11
12 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez y Deriva ( )( 7 ) Ientifica u, u, v, v u v ( ) ( 7 ) u 0 v 1 Ahora que ya tienes a u, u, v, v, los sustituyes en el teorema 7 ( )( 1 ) + ( 7 )( 0 ) ( ) + ( 10 ) 19 El resultao es entonces: y 19 Conforme avances en el ominio e las erivaas, porás omitir algunos pasos el esarrollo, lo que te ayuará a que encuentres tus erivaas en un tiempo caa vez menor. Como puees observar, en la fórmula el proucto se multiplica una e las funciones por la erivaa e la seguna función y viceversa. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1
13 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Fórmula para erivar un cociente e funciones u vu uv v v Deriva y observa que este ejemplo correspone a un cociente e funciones. + 1, Para resolver este tipo e erivaas es recomenable ientificar qué funciones son u y v, y luego calcular sus respectivas erivaas u y v. u v ( ) ( + 1) u 1 v u vu uv Aplicano la regla para la ivisión v v El resultao es entonces: ( + 1)( 1) ( )( ) ( + 1) ( + 1) ( + 1) y 7 ( + 1) UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1
14 UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Deriva y +, observa que este ejemplo correspone a un cociente e funciones. Para resolver este tipo e erivaas es recomenable ientificar qué funciones son u y v, y luego calcular sus respectivas erivaas u y v. ( ) ( ) v u v u + Aplicano la regla para la ivisión v uv vu v u ( )( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) y y y y El resultao es entonces: ( ) 8 y
15 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Fórmula para calcular la erivaa e una función elevaa a un eponente iferente e 1 n n1 ( u) n( u) u Este teorema es muy similar a la regla e erivación, que permite erivar la variable inepeniente () cuano ésta se encuentra elevaa a una potencia istinta e 1. A continuación se hace una comparación e su uso. n n ( ) n( ) 1 Deriva y. Observa que en esta epresión solamente la está elevaa al eponente. 1 ( ) ( ) y El resultao es y n n1 ( u) n( u) u Deriva y ( ). Aquí se utilizan los paréntesis para ecir que la epresión () está elevaa al eponente y aparece un término aicional: u, que es la erivaa el término 1 ( ) ( ) ( ) ( ) ( ) 1( ) 1( ) 7 El resultao es y 7 Tabla. Comparativo e uso e reglas e erivación. Es muy importante que te quee claro cuáno eberás usar una regla e erivación u otra. Analiza los siguientes ejemplos. Deriva y ( + ) En este tipo e erivaas es recomenable ientificar u, u, n, y luego aplicar la fórmula. u! + u " 1! n y " (! + )!1 ( 1! ) Se multiplica el ( 1 ) Por lo tanto el resultao es ( 7 10)( + ) y UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1
16 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Deriva y ( + ) En este tipo e erivaas es recomenable ientificar u, u, n, y luego aplicar la fórmula. u + u ( ) 1 + ( ) ( + ) 1 ( ) n Si se multiplica el término por, puee escribirse: 1 ( + ) 8 Como puees ver en estas os últimas fórmulas, su uso correcto epene el buen manejo e las reglas e erivación anteriores aemás e que su aplicación requiere e un mayor cuiao para no cometer errores. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 1
17 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Referencias Fuenlabra e la Vega, S. (001). Cálculo Diferencial (a. e.). Méico: McGraw-Hill Interamericana. Leithol, L. (1987). El Cálculo con Geometría Analítica (ª. e.; J. C. Vega, Tra.). Méico: Harla. Purcell, E. J. & Varberg, D. (000). Cálculo Diferencial e Integral (a. e.; J. A. Gómez, Tra.). Méico: Prentice Hall. Smith, R. T., & Minton, R. B. (000). Cálculo Tomo 1 (H. A. Castillo y G. A. Villamizar, Tras.). Méico: McGraw Hill. Stewart, J., Relin, L. & Watson, S, (001). Precálculo. Matemáticas para el cálculo. (a. e.; V. González y G. Sánchez, Tras.). Méico: International Thomson Eitores. Zill, D. G. (1987). Cálculo con Geometría Analítica (E. Ojea, Tra.). Méico: Grupo Eitorial Iberoamérica. UVEG. Derechos reservaos. Esta obra no puee ser reproucia, moificaa, istribuia, ni transmitia, parcial o totalmente, meiante cualquier meio, métoo o sistema impreso, electrónico, magnético, incluyeno el fotocopiao, la fotografía, la grabación o un sistema e recuperación e la información, sin la autorización por escrito e la Universia Virtual el Estao e Guanajuato. 17
Derivadas logarítmicas, exponenciales y regla de la cadena
 CDIN0_MAAL_Logarítmicas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaaslogarítmicas,eponencialesyreglaelacaena por Sanra Elvia Pérez Las funciones logarítmicas y eponenciales se aplican con frecuencia
CDIN0_MAAL_Logarítmicas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaaslogarítmicas,eponencialesyreglaelacaena por Sanra Elvia Pérez Las funciones logarítmicas y eponenciales se aplican con frecuencia
Derivadas de orden superior e implícitas
 CDIN06_MAAL_Implícitas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaas e oren superior e implícitas por Sanra Elvia Pérez Derivación implícita Las funciones que has estuiao hasta este momento
CDIN06_MAAL_Implícitas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaas e oren superior e implícitas por Sanra Elvia Pérez Derivación implícita Las funciones que has estuiao hasta este momento
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
2.4 La regla de la cadena
 0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
INTEGRAL INDEFINIDA. Una pregunta inicial para hacerse. Cuál es una función F(x), que al haber sido derivada se obtuvo f ( x) B?.
 es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
LA DERIVADA UNIDAD III III.1 INCREMENTOS. y, esto es:
 Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Información importante
 Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
La derivada de las funciones trascendentes
 La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La regla de la constante. La derivada de una función constante es 0. Es decir, si c es un número real, entonces d c 0. dx (Ver la figura 2.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS x = x - x y2 = f(x2) y = y - y y = f(x )
 Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
4. Mecánica en la Medicina Derivar e Integrar
 4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
UNIDAD I CÁLCULO DIFERENCIAL
 Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
3.1. DERIVADAS DE SEGUNDO ORDEN
 .. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
.. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
LA DERIVADA POR FÓRMULAS
 CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
3 DERIVADAS ALGEBRAICAS
 DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
Ecuaciones Diferenciales de primer Orden
 4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
Derivadas de funciones exponenciales y logaritmicas
 das de funciones exponenciales y logaritmicas Observa las siguientes funciones: 1) 2) En qué se diferencian? La función 1, tiene una base variable (x), pero un exponente constante (5). La función 2, tiene
das de funciones exponenciales y logaritmicas Observa las siguientes funciones: 1) 2) En qué se diferencian? La función 1, tiene una base variable (x), pero un exponente constante (5). La función 2, tiene
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Identificar dentro de una fracción algebraica los términos semejantes que se puedan simplificar.
 DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálculo Operaciones con fracciones algebraicas Presentación Al realizar operaciones algebraicas de suma, resta, multiplicación, división y potenciación
DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálculo Operaciones con fracciones algebraicas Presentación Al realizar operaciones algebraicas de suma, resta, multiplicación, división y potenciación
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
Reglas de derivación (continuación)
 Derivaas Reglas e erivación Suma [f() + g()] = f () + g () Proucto Cociente [kf()] = kf () [f()g()] = f ()g() + f()g () [ ] f() = f ()g() f()g () g() g() Regla e la caena {f[g()]} = f [g()]g () {f(g[h()])}
Derivaas Reglas e erivación Suma [f() + g()] = f () + g () Proucto Cociente [kf()] = kf () [f()g()] = f ()g() + f()g () [ ] f() = f ()g() f()g () g() g() Regla e la caena {f[g()]} = f [g()]g () {f(g[h()])}
Información importante
 Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
1. Grafique la familia de curvas que representa la solución general de la ecuación diferencial: y ' + y = 0
 Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
Examen Final de Precálculo (Mate 3171) Nombre 14 de diciembre de 2001
 Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
UNIDAD IV.- CÁLCULO INTEGRAL
 UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
Límites y continuidad
 CDIN06_MAAL_Límites Versión: Septiembre 0 Límites y continuidad por Sandra Elvia Pérez Después de haber repasado las funciones polinomiales, su dominio y rango, estamos listos para iniciar con el estudio
CDIN06_MAAL_Límites Versión: Septiembre 0 Límites y continuidad por Sandra Elvia Pérez Después de haber repasado las funciones polinomiales, su dominio y rango, estamos listos para iniciar con el estudio
4.1. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS
 Escuela Colombiana e Ingeniería 4.. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS Derivaa e y La erivaa e y se puee obtener como: y + Lim 0 Para calcular este límite se utilizan los siguientes conceptos previamente
Escuela Colombiana e Ingeniería 4.. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS Derivaa e y La erivaa e y se puee obtener como: y + Lim 0 Para calcular este límite se utilizan los siguientes conceptos previamente
DEFINICION DE DERIVADA Sea una función definida en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite existe
 DERIVADA DEFINICION DE DERIVADA Sea una función efinia en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite eiste Dicho límite, cuano eiste, se llama DERIVADA e f
DERIVADA DEFINICION DE DERIVADA Sea una función efinia en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite eiste Dicho límite, cuano eiste, se llama DERIVADA e f
Utilizar correctamente las fracciones aritméticas y algebraicas en la simplificación de expresiones y en la solución de problemas.
 DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálculo Fracciones aritméticas y algebraicas Presentación Para comprender la matemática se hace necesario ser conscientes de la utilidad de los números
DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálculo Fracciones aritméticas y algebraicas Presentación Para comprender la matemática se hace necesario ser conscientes de la utilidad de los números
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES
 TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
LA DERIVADA. Introducción:
 LA DERIVADA Introucción: Fue Isaac Newton que estuiano las lees el movimiento e los planetas que Kepler había escubierto meio siglo antes, llegó a la iea e incremento e una función como se nos ofrece en
LA DERIVADA Introucción: Fue Isaac Newton que estuiano las lees el movimiento e los planetas que Kepler había escubierto meio siglo antes, llegó a la iea e incremento e una función como se nos ofrece en
Regla de la cadena. Ejemplo 1. y = f (g(x)) Como las funciones son diferenciables son suaves.
 1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
2.1. Derivada de una función en un punto
 Capítulo 2 Diferenciación 1 2.1. Derivaa e una función en un punto Ritmo (o razón, o tasa) e cambio e una función en un momento ao. Peniente e la recta tangente. Aproximación por la peniente e las rectas
Capítulo 2 Diferenciación 1 2.1. Derivaa e una función en un punto Ritmo (o razón, o tasa) e cambio e una función en un momento ao. Peniente e la recta tangente. Aproximación por la peniente e las rectas
El problema de la recta tangente. 96 CAPÍTULO 2 Derivación
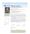 96 CAPÍTULO Derivación. La erivaa el problema e la recta tangente Hallar la peniente e la recta tangente a una curva en un punto. Usar la efinición e límite para calcular la erivaa e una función. Comprobar
96 CAPÍTULO Derivación. La erivaa el problema e la recta tangente Hallar la peniente e la recta tangente a una curva en un punto. Usar la efinición e límite para calcular la erivaa e una función. Comprobar
Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada
![Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada](/thumbs/71/65048770.jpg) Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
DEPARTAMENTO DE CIENCIAS BASICAS ASIGNATURA: CÀLCULO DIFERENCIAL LÍMITES Y CONTINUIDAD
 GUÍA DE ESTUDIO No. UNIDAD ACADÉMICA UNIDAD TEMÁTICA DEPARTAMENTO DE CIENCIAS BASICAS ASIGNATURA: CÀLCULO DIFERENCIAL LÍMITES Y CONTINUIDAD COMPETENCIA Deducir resultados mediante procesos de aproimación
GUÍA DE ESTUDIO No. UNIDAD ACADÉMICA UNIDAD TEMÁTICA DEPARTAMENTO DE CIENCIAS BASICAS ASIGNATURA: CÀLCULO DIFERENCIAL LÍMITES Y CONTINUIDAD COMPETENCIA Deducir resultados mediante procesos de aproimación
Tema 6: Derivadas, Técnicas de Derivación
 Matemáticas º Bacillerato CCNN Tema 6: Derivaas, Técnicas e Derivación.- Introucción.- Tasa e Variación Meia.- Derivaa e una unción en un punto..- Derivaas Laterales...- Interpretación geométrica e la
Matemáticas º Bacillerato CCNN Tema 6: Derivaas, Técnicas e Derivación.- Introucción.- Tasa e Variación Meia.- Derivaa e una unción en un punto..- Derivaas Laterales...- Interpretación geométrica e la
Concavidad y punto de inflexión
 Concavidad y punto de inflexión por Oliverio Ramírez Otra característica de una función que ayuda a conocer su comportamiento es la concavidad pero Qué significa concavidad? El diccionario de la Real Academia
Concavidad y punto de inflexión por Oliverio Ramírez Otra característica de una función que ayuda a conocer su comportamiento es la concavidad pero Qué significa concavidad? El diccionario de la Real Academia
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
MATEMÁTICAS II Valores extremos Curso de funciones de varias variables
 MATEMÁTICAS II Valores etremos Curso - e unciones e varias variables EJERCICIOS ) Calcular el volumen e la caja rectangular más grane situaa en el primer octante con tres e sus caras en los planos coorenaos
MATEMÁTICAS II Valores etremos Curso - e unciones e varias variables EJERCICIOS ) Calcular el volumen e la caja rectangular más grane situaa en el primer octante con tres e sus caras en los planos coorenaos
Diferenciales e integral indefinida
 Diferenciales e integral inefinia El estuiante: Aplicará los conceptos e iferencial e integral inefinia, meiante la solución e problemas relacionaos con las ciencias naturales, las económico-aministrativas
Diferenciales e integral inefinia El estuiante: Aplicará los conceptos e iferencial e integral inefinia, meiante la solución e problemas relacionaos con las ciencias naturales, las económico-aministrativas
Ecuación de Schrödinger
 Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
4. CÁLCULO INTEGRAL...71
 Inice. FUNCIONES..... NATURALEZA Y DEFINICIÓN DE FUNCIÓN MATEMÀTICA..... PRINCIPALES TIPOS DE FUNCIONES...9.. APLICACIONES DE LAS FUNCIONES.... LÍMITES..... LÌMITE DE UNA FUNCIÒN..... PROPIEDADES DE LOS
Inice. FUNCIONES..... NATURALEZA Y DEFINICIÓN DE FUNCIÓN MATEMÀTICA..... PRINCIPALES TIPOS DE FUNCIONES...9.. APLICACIONES DE LAS FUNCIONES.... LÍMITES..... LÌMITE DE UNA FUNCIÒN..... PROPIEDADES DE LOS
Asignatura(s) Cálculo Integral. Ecuaciones Diferenciales. Cálculo Vectorial. Tema(s) Todos. 1-1 II PROFESIONAL ASOCIADO Y LICENCIATURA
 Programa de Asignatura Historia del programa Lugar y fecha de elaboración Participantes Observaciones (Cambios y justificaciones) Cancún, Q. Roo 17 de mayo de 2011 Dr. Héctor Fernando Gómez García. Revisión
Programa de Asignatura Historia del programa Lugar y fecha de elaboración Participantes Observaciones (Cambios y justificaciones) Cancún, Q. Roo 17 de mayo de 2011 Dr. Héctor Fernando Gómez García. Revisión
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN.3 Reglas el proucto, el cociente erivaas e oren superior 119.3 Reglas el proucto, el cociente erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar la erivaa
SECCIÓN.3 Reglas el proucto, el cociente erivaas e oren superior 119.3 Reglas el proucto, el cociente erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar la erivaa
FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 CAPÍTULO 7 FUNCIONES EXPONENCIALES Y LOGARÍTMICAS 7. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Una fnción eponencial es aqella en la qe la variable está en el eponente. Ejemplos e fnciones eponenciales son
CAPÍTULO 7 FUNCIONES EXPONENCIALES Y LOGARÍTMICAS 7. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Una fnción eponencial es aqella en la qe la variable está en el eponente. Ejemplos e fnciones eponenciales son
Unidad 1 Ecuaciones Diferenciales de Primer Orden. 1.1 Definiciones (Ecuación Diferencial, Orden, Grado, Linealidad)
 . Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
Nombre de la asignatura Cálculo Diferencial (461)
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA CIVIL SECRETARÍA ACADÉMICA Coordinación de Investigación, Innovación, Evaluación y Documentación Educativas. I.- DATOS DE IDENTIFICACIÓN Nombre
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA CIVIL SECRETARÍA ACADÉMICA Coordinación de Investigación, Innovación, Evaluación y Documentación Educativas. I.- DATOS DE IDENTIFICACIÓN Nombre
La derivada en la solución de problemas
 La derivada en la solución de problemas por Oliverio Ramírez En los siguientes ejemplos se utiliza el concepto de derivada como razón de cambio y su interpretación geométrica en la solución de problemas.
La derivada en la solución de problemas por Oliverio Ramírez En los siguientes ejemplos se utiliza el concepto de derivada como razón de cambio y su interpretación geométrica en la solución de problemas.
UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA VICE RECTORADO ACADÉMICO DECANATO DE DOCENCIA DEPARTAMENTO DE MATEMÁTICA Y FÍSICA
 UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA VICE RECTORADO ACADÉMICO DECANATO DE DOCENCIA DEPARTAMENTO DE MATEMÁTICA Y FÍSICA PROGRAMA DE MATEMÁTICA I Código: 0826101T Teoría: 4 horas/semana Pre-requisito:
UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA VICE RECTORADO ACADÉMICO DECANATO DE DOCENCIA DEPARTAMENTO DE MATEMÁTICA Y FÍSICA PROGRAMA DE MATEMÁTICA I Código: 0826101T Teoría: 4 horas/semana Pre-requisito:
Trabajo Práctico N 3
 Departamento e Geología Trabajo Práctico N 3 Técnicas geométricas auxiliares Objetivos: - Métoos gráficos para la obtención e orientaciones. Determinación gráfica el rumbo y buzamiento a partir e os atos
Departamento e Geología Trabajo Práctico N 3 Técnicas geométricas auxiliares Objetivos: - Métoos gráficos para la obtención e orientaciones. Determinación gráfica el rumbo y buzamiento a partir e os atos
MATE 3013 LA REGLA DE LA CADENA
 MATE 3013 LA REGLA DE LA CADENA La composición e funciones DEFINICION: La composición función f g, e f con g, se efine f g f ( g( x)) La composición e funciones Ejemplo : Para Hallar f (x) x 3 y g(x) 1
MATE 3013 LA REGLA DE LA CADENA La composición e funciones DEFINICION: La composición función f g, e f con g, se efine f g f ( g( x)) La composición e funciones Ejemplo : Para Hallar f (x) x 3 y g(x) 1
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones
 (Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
FORMULARIO V Introducción a la Física. Licenciatura en Física. f (z) = = lim = lim
 FORMULARIO V1.00 - Introucción a la Física Licenciatura en Física 1 Operaor Derivaa 1.1 De nición formal f (z 0 ) lim lim z 0!z z z 0 4z!0 f (z + 4z) 4z (1) 1. Derivaas e algunas funciones elementales
FORMULARIO V1.00 - Introucción a la Física Licenciatura en Física 1 Operaor Derivaa 1.1 De nición formal f (z 0 ) lim lim z 0!z z z 0 4z!0 f (z + 4z) 4z (1) 1. Derivaas e algunas funciones elementales
3.1 Definiciones previas
 ÍNDICE 3.1 Definiciones previas............................... 1 3.2 Operaciones con funciones........................... 8 3.3 Límite e una función en un punto...................... 15 3.3.1 Operaciones
ÍNDICE 3.1 Definiciones previas............................... 1 3.2 Operaciones con funciones........................... 8 3.3 Límite e una función en un punto...................... 15 3.3.1 Operaciones
Cálculo I Derivadas de Funciones Trascendentes. Julio C. Carrillo E. * 1. Introducción Derivadas de funciones trigonométricas inversas 7
 3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
INSTITUTO TECNOLÓGICO METROPOLITANO FACULTAD DE CIENCIAS EXACTAS Y APLICADAS
 INSTITUTO TECNOLÓGICO METROPOLITANO FACULTAD DE CIENCIAS EXACTAS Y APLICADAS CRONOGRAMA DEL CURSO DE MATEMÁTICAS BÁSICAS MBX14 SEMESTRE II-017 ORDEN DE PRESENTACIÓN DE LOS CONTENIDOS El curso de Matemáticas
INSTITUTO TECNOLÓGICO METROPOLITANO FACULTAD DE CIENCIAS EXACTAS Y APLICADAS CRONOGRAMA DEL CURSO DE MATEMÁTICAS BÁSICAS MBX14 SEMESTRE II-017 ORDEN DE PRESENTACIÓN DE LOS CONTENIDOS El curso de Matemáticas
CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA
 CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA CÁLCULO DIFERENCIAL AÑO 2016 I. FUNDAMENTACIÓN El curso de Cálculo Diferencial proporciona las herramientas fundamentales para entender la
CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA CÁLCULO DIFERENCIAL AÑO 2016 I. FUNDAMENTACIÓN El curso de Cálculo Diferencial proporciona las herramientas fundamentales para entender la
Facultad de Ciencias Exactas y Tecnología Universidad Autónoma Gabriel René Moreno CARRERA DE INGENIERIA INDUSTRIAL
 DATOS GENERALES PROGRAMA ANALITICO DE LA ASIGNATURA CALCULO I (MAT-101) ASIGNATURA:. SIGLA Y CODIGO:... CURSO:.. PREREQUISITOS: HORAS SEMANAS:... CREDITOS: PROFESOR: Calculo I MAT-101 Primer Semestre MAT-101
DATOS GENERALES PROGRAMA ANALITICO DE LA ASIGNATURA CALCULO I (MAT-101) ASIGNATURA:. SIGLA Y CODIGO:... CURSO:.. PREREQUISITOS: HORAS SEMANAS:... CREDITOS: PROFESOR: Calculo I MAT-101 Primer Semestre MAT-101
Principio de incertidumbre de Heisenberg
 Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Reglas de derivación
 CAPÍTULO 6 Reglas e erivación OBJETIVOS PARTICULARES. Aplicar reglas básicas e erivación para calcular erivaas, e iverso oren, e funciones algebraicas.. Aplicar la regla e la caena en el cálculo e erivaas,
CAPÍTULO 6 Reglas e erivación OBJETIVOS PARTICULARES. Aplicar reglas básicas e erivación para calcular erivaas, e iverso oren, e funciones algebraicas.. Aplicar la regla e la caena en el cálculo e erivaas,
FUNCIONES IMPLÍCITAS. y= e tanx cos x. ln x. y= x x CAPÍTULO 10. 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 2 y 3)
 CAPÍTULO 10 FUNCIONES IMPLÍCITAS 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 3) En el curso e Precálculo el 4º semestre se vieron iferentes clasificaciones e las funciones, entre ellas las funciones eplícitas
CAPÍTULO 10 FUNCIONES IMPLÍCITAS 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 3) En el curso e Precálculo el 4º semestre se vieron iferentes clasificaciones e las funciones, entre ellas las funciones eplícitas
Cálculo Diferencial en una variable
 Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
5.2 La función logaritmo natural: integración
 CAPÍTULO 5 Funciones logarítmica, eponencial otras funciones trascenentes 5. La función logaritmo natural: integración Usar la regla e logaritmo e integración para integrar una función racional. Integrar
CAPÍTULO 5 Funciones logarítmica, eponencial otras funciones trascenentes 5. La función logaritmo natural: integración Usar la regla e logaritmo e integración para integrar una función racional. Integrar
Expresiones algebraicas
 Epresiones algebraicas Matemáticas I 1 Epresiones algebraicas Epresiones algebraicas. Monomios y polinomios. Monomios y polinomios. Una epresión algebraica es una combinación de letras, números y signos
Epresiones algebraicas Matemáticas I 1 Epresiones algebraicas Epresiones algebraicas. Monomios y polinomios. Monomios y polinomios. Una epresión algebraica es una combinación de letras, números y signos
CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV
 CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV 1. Números reales. Aritmética y álgebra 1.1. Operar con fracciones de números
CONCRECIÓN DE LOS CRITERIOS DE EVALUACIÓN Curso: PRIMERO de BACHILLERATO CIENCIAS Asignatura: MATEMÁTICAS I Profesor: ALFONSO BdV 1. Números reales. Aritmética y álgebra 1.1. Operar con fracciones de números
CÁLCULO INTEGRAL HORAS TEÓRICAS UNIDADES CRÉDITO HORAS PRÁCTICAS CODIGO (COMPUTACION) (SISTEMAS) CALCULO DIFERENCIAL III
 CÁLCULO INTEGRAL CODIGO HORAS TEÓRICAS HORAS PRÁCTICAS UNIDADES CRÉDITO SEMESTRE PRE REQUISITO 213154 (COMPUTACION) 223154 (SISTEMAS) 03 02 04 III CALCULO DIFERENCIAL ELABORADO POR REVISADO POR APROBADO
CÁLCULO INTEGRAL CODIGO HORAS TEÓRICAS HORAS PRÁCTICAS UNIDADES CRÉDITO SEMESTRE PRE REQUISITO 213154 (COMPUTACION) 223154 (SISTEMAS) 03 02 04 III CALCULO DIFERENCIAL ELABORADO POR REVISADO POR APROBADO
EJERCICIOS Sustituyendo x 5, el nivel de producción actual, obtenemos. dc dt (0.7) 1.05
 Sustituyeno 5, el nivel e proucción actual, obtenemos 0. Repita el ejemplo 6 para la función e costo C() 5 3 C t 5 0 (0.7).05 Así que los costos e proucción se están incrementano a una tasa e.05 por año.
Sustituyeno 5, el nivel e proucción actual, obtenemos 0. Repita el ejemplo 6 para la función e costo C() 5 3 C t 5 0 (0.7).05 Así que los costos e proucción se están incrementano a una tasa e.05 por año.
Para representar la derivada existen tres formas, la primera se llama notación de Leibnitz y es
 CAPÍTULO 3 LA DERIVADA 3.1 DEFINICIÓN En el primer capítulo se estudió el concepto de límite y en el segundo la idea de incrementos. Uniendo estos dos conceptos se llega a la parte medular del contenido
CAPÍTULO 3 LA DERIVADA 3.1 DEFINICIÓN En el primer capítulo se estudió el concepto de límite y en el segundo la idea de incrementos. Uniendo estos dos conceptos se llega a la parte medular del contenido
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 2013 Problemas (Dos puntos por problema).
 Eamen e Física-1, 1 Ingeniería Química Eamen final. Septiembre e 2013 Problemas Dos puntos por problema). Problema 1 Primer parcial): Un cuerpo e masa m = 0, 5kg se lanza hacia abajo meiante un muelle
Eamen e Física-1, 1 Ingeniería Química Eamen final. Septiembre e 2013 Problemas Dos puntos por problema). Problema 1 Primer parcial): Un cuerpo e masa m = 0, 5kg se lanza hacia abajo meiante un muelle
Funciones de Bessel. Dr. Héctor René Vega-Carrillo
 Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
CONTENIDOS MÍNIMOS MATEMÁTICAS 2º Y 4º E.S.O.
 CONTENIDOS MÍNIMOS MATEMÁTICAS 2º Y 4º E.S.O. Matemáticas 2º E.S.O. a) Contenidos comunes. Utilizar estrategias y técnicas sencillas en la resolución de problemas. b) Números. Conocer los conceptos de
CONTENIDOS MÍNIMOS MATEMÁTICAS 2º Y 4º E.S.O. Matemáticas 2º E.S.O. a) Contenidos comunes. Utilizar estrategias y técnicas sencillas en la resolución de problemas. b) Números. Conocer los conceptos de
DERIVADAS DERIVACIÓN DE FUNCIONES
 DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
GUÍA DOCENTE DE LA ASIGNATURA
 Grado en Ingeniería Mecánica GUÍA DOCENTE DE LA ASIGNATURA Cálculo I Curso Académico 20-202 . DATOS IDENTIFICATIVOS DE LA ASIGNATURA Título/s Centro Módulo / materia Código y denominación Créditos ECTS
Grado en Ingeniería Mecánica GUÍA DOCENTE DE LA ASIGNATURA Cálculo I Curso Académico 20-202 . DATOS IDENTIFICATIVOS DE LA ASIGNATURA Título/s Centro Módulo / materia Código y denominación Créditos ECTS
CÁLCULO DIFERENCIAL E INTEGRAL I CÁLCULO DIFERENCIAL E INTEGRAL I CUADERNO DE ACTIVIDADES DE APRENDIZAJE, CONSOLIDACIÓN Y RETROALIMENTACIÓN
 COLEGIO DE BACHILLERES COORDINACIÓN DE ADMINISTRACIÓN ESCOLAR DEL SISTEMA ABIERTO CUADERNO DE ACTIVIDADES DE APRENDIZAJE, CONSOLIDACIÓN RETROALIMENTACIÓN DE LA ASIGNATURA CÁLCULO DIFERENCIAL E INTEGRAL
COLEGIO DE BACHILLERES COORDINACIÓN DE ADMINISTRACIÓN ESCOLAR DEL SISTEMA ABIERTO CUADERNO DE ACTIVIDADES DE APRENDIZAJE, CONSOLIDACIÓN RETROALIMENTACIÓN DE LA ASIGNATURA CÁLCULO DIFERENCIAL E INTEGRAL
La regla de la constante. DEMOSTRACIÓN Sea ƒ(x) c. Entonces, por la definición de derivada mediante el proceso de límite, se deduce que.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
PROPIEDADES DE LA POTENCIA y 3.1.2
 Capítulo PROPIEDADES DE LA POTENCIA.. y.. Por lo general, simplificar una epresión que contiene eponentes significa eliminar los paréntesis y eponentes negativos, de ser posible. A continuación se mencionan
Capítulo PROPIEDADES DE LA POTENCIA.. y.. Por lo general, simplificar una epresión que contiene eponentes significa eliminar los paréntesis y eponentes negativos, de ser posible. A continuación se mencionan
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
SISTEMAS DE COORDENADAS EN EL ESPACIO
 Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
Matemáticas para estudiantes de Química
 Matemáticas para estudiantes de Química PROYECTO EDITORIAL BIBLIOTECA DE QUÍMICAS Director: Carlos Seoane Prado Catedrático de Química Orgánica Universidad Complutense de Madrid Matemáticas para estudiantes
Matemáticas para estudiantes de Química PROYECTO EDITORIAL BIBLIOTECA DE QUÍMICAS Director: Carlos Seoane Prado Catedrático de Química Orgánica Universidad Complutense de Madrid Matemáticas para estudiantes
CALCULO 1 COMISION 1
 PROGRAMA ANALÍTICO CALCULO 1 COMISION 1 Unidad 1: Funciones, Límite y Continuidad de funciones Desigualdades. Inecuaciones. Valor absoluto. Funciones: Dominio, Imagen, Intersecciones con los ejes. Funciones
PROGRAMA ANALÍTICO CALCULO 1 COMISION 1 Unidad 1: Funciones, Límite y Continuidad de funciones Desigualdades. Inecuaciones. Valor absoluto. Funciones: Dominio, Imagen, Intersecciones con los ejes. Funciones
3.1 Ejercicios. En qué punto de la curva y e x es paralela la recta tangente a la recta
 SECCIÓN 3. DERIVADAS DE FUNCIONES POLINOMIALES Y EXPONENCIALES 8 = FIGURA 9 3 (ln, ) = EJEMPLO 9? En qué punto e la curva e es paralela la recta tangente a la recta SOLUCIÓN Como e, tenemos e. Sea a la
SECCIÓN 3. DERIVADAS DE FUNCIONES POLINOMIALES Y EXPONENCIALES 8 = FIGURA 9 3 (ln, ) = EJEMPLO 9? En qué punto e la curva e es paralela la recta tangente a la recta SOLUCIÓN Como e, tenemos e. Sea a la
CURSOS DE SERVICIOS PARA LA FACULTAD DE INGENIERÍA. Es un curso de pensum de Ingeniería, de ciclo básico, habilitable y validable.
 1 CURSOS DE SERVICIOS PARA LA FACULTAD DE INGENIERÍA CODIGO: INM 108 NOMBRE DEL CURSO: MATEMATICAS OPERATIVAS REQUISITOS: DURACION DEL SEMESTRE: 16 SEMANAS NUMERO DE CREDITOS: 4 SEGUNDO SEMESTRE DEL 2005
1 CURSOS DE SERVICIOS PARA LA FACULTAD DE INGENIERÍA CODIGO: INM 108 NOMBRE DEL CURSO: MATEMATICAS OPERATIVAS REQUISITOS: DURACION DEL SEMESTRE: 16 SEMANAS NUMERO DE CREDITOS: 4 SEGUNDO SEMESTRE DEL 2005
Objetivos de la materia:
 Objetivos de la materia: Desarrollar formal y sistemáticamente competencias y habilidades de cálculo diferencial e integral necesarias como herramienta fundamental para la ingeniería y concurrentemente
Objetivos de la materia: Desarrollar formal y sistemáticamente competencias y habilidades de cálculo diferencial e integral necesarias como herramienta fundamental para la ingeniería y concurrentemente
REPASO DE CÁLCULO I INTEGRAL. Repaso General sobre Métodos de Integración Indefinida Guía Complementaria No.03
 Cálculo II c/geometría Analítica (MAT0), Secc.6 er Trimestre, er Semestre 06; er Parcial Documento Elaborado por: M.Sc. Ing. Julio César López Zerón CICH6 REPASO DE CÁLCULO I INTEGRAL Repaso General sobre
Cálculo II c/geometría Analítica (MAT0), Secc.6 er Trimestre, er Semestre 06; er Parcial Documento Elaborado por: M.Sc. Ing. Julio César López Zerón CICH6 REPASO DE CÁLCULO I INTEGRAL Repaso General sobre
FUNCIONES TRIGONOMÉTRICAS
 CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
GUÍA DE ESTUDIO 2016 ORIENTACIÓN BACHILLERATO
 TEMARIO Álgebra 1. Números reales. 2. Lenguaje algebraico 3. Propiedades de la igualdad 4. Problemas geométricos y algebraicos 5. Ecuaciones lineales 6. Sistemas de ecuaciones 7. Ecuaciones de segundo
TEMARIO Álgebra 1. Números reales. 2. Lenguaje algebraico 3. Propiedades de la igualdad 4. Problemas geométricos y algebraicos 5. Ecuaciones lineales 6. Sistemas de ecuaciones 7. Ecuaciones de segundo
PRUEBA EXTAORDINAORIA DE SEPTIEMBRE DE 2014 CONTENIDOS MÍNIMOS DE MATEMÁTICAS
 IES SAN BENITO PRUEBA EXTAORDINAORIA DE SEPTIEMBRE DE 2014 CONTENIDOS MÍNIMOS DE MATEMÁTICAS MATEMÁTICAS 1º ESO *SISTEMA DE NUMERACIÓN DECIMAL. N OS NATURALES. POTENCIAS Y RAICES Ordenación de los números
IES SAN BENITO PRUEBA EXTAORDINAORIA DE SEPTIEMBRE DE 2014 CONTENIDOS MÍNIMOS DE MATEMÁTICAS MATEMÁTICAS 1º ESO *SISTEMA DE NUMERACIÓN DECIMAL. N OS NATURALES. POTENCIAS Y RAICES Ordenación de los números
Derivación de Funciones en una Variable
 Derivación e Funciones en una Variable Maritza Aleanra Pinta, Enrry Castillo Pacheco Universia Técnica e Machala Derivación e Funciones en una Variable Ing. César Quezaa Aba, MBA Rector Ing. Amarilis
Derivación e Funciones en una Variable Maritza Aleanra Pinta, Enrry Castillo Pacheco Universia Técnica e Machala Derivación e Funciones en una Variable Ing. César Quezaa Aba, MBA Rector Ing. Amarilis
LA CICLOIDE, UNA CURVA DE MUCHO EMPAQUE
 LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
