Tema 1: Sucesiones y series numéricas
|
|
|
- Gustavo Rubio Rey
- hace 7 años
- Vistas:
Transcripción
1 PROBLEMAS DE MATEMÁTICAS Parte II Cálculo Primero de Igeiería Química FACULTAD DE CIENCIAS QUÍMICAS Departameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Tema : Sucesioes y series uméricas Números complejos Calcula: 2 Calcula: ( log ) 3i, (b) log( 3), (c) e + π 3 i, (d) i 3825, (e) ( + i) i log (3 + 3i), (b) i log i 3 Halla los valores de z CI tales que: e z = 5, (b) e z = 3 + i, (c) log z = π 4 i 4 Resuelve: si z = 4, z CI 5 Halla los complejos z = + iy tales que: e z =, (b) + i i = eiy 6 Resuelve e el cuerpo de los úmeros complejos la ecuació: 5 ta z = 2se 2 z + 3 cos 2 z 7 Determia la regió del plao determiada por A B siedo A el cojuto represetado por z < 4 y B el cojuto represetado por z 2i < 3 8 Determia el lugar geométrico de los úmeros complejos que verifica las siguietes relacioes: z 3i = 5, (b) Re(z 2 ) = K, K IR, (c) Im(z 2 ) = k, k IR, (d) z i + z + i = 4, (e) z z + < 2, (f) z + z = 4 9 Halla las raíces de ( + z) 5 = ( z) 5 Halla los úmeros complejos z tales que z 6 9z =
2 Sucesioes y series uméricas Estudia la mootoía de las siguietes sucesioes: a = 3, (b) b = 3 3 +, (c) c = ( 3) ( 3) + 2 Utilizado el criterio de la sucesió itermedia o regla del Sadwich, calcula: ( ( ) (b) 2 + ( + ) () 2 ) ( (c) se se se 2 + ( (d) ) Calcula: 4 Halla el límite de la siguiete sucesio: 5 Calcula: ( e ), (b) ) , 3 3, 3 3 3, , (c) , (d) ( ) 6 Calcula: 7 Calcula: ( log()), (b) ( ) (a + 2a2 + 3a a ), < a < 8 Calcula: log, (b) log log( ), (c) α+ α + 2 α + + α, α IN 9 Calcula: ) Idicació: Fórmula de Stirlig (
3 Calcula: Calcula: ( a + b c d + c + d + ) 2 Calcula:, (b), (c) , (d) ( ) ( + ) 3 De la serie a se cooce que la sucesió de sumas parciales (S ) viee dada por S = IN Halla: El térmio geeral a de la serie (b) El carácter de la serie 4 Estudia la covergecia de la serie 2 e 3 5 Estudia la covergecia y halla la suma, si es posible, de las siguietes series: (3 + 2)(3 + 5), (b) Halla el carácter de las siguietes series: (d) ( + ), (b) ( )! (l( ))(l(2 3 )), (e) ( + 3), (c) =2 ( )! ( + )( + 2)( + ) ( l )3/2, 7 Estudia, segú los valores de α >, el carácter de la serie: 8 Estudia el carácter de la serie: se π 2 α ( ) 4 7(3 2)
4 9 Estudia la covergecia absoluta de las series: =2 ( ) l, (b) ( ) 2, (c) ( ) se 3/2 2 Calcula la suma de las siguietes series: =2 2 Demuestra que la serie meor de 2 l ( ) 2, (b) 22 Determia el carácter de las siguietes series: l (b) ( + )( + 2), (c) ( ) + es covergete Calcula su suma co u error (3 + )(2 + 3) l (c) se 2 ( (d) 5 2 (e) 7 3 (f) ( ) + 3 (g) ( ) (h) 5 3(l () (i) 7 (j) (k) (l) (m) 5 () 7 (o) 3 (p) (u) (q) ( ) (r) (v) 2 s) (w) (l () 2 ( ) /2 ) l (t) ( + ( 2 3) ) (y) () 2 (2 ()! (z) + (ab) l (ac) 4 l (ad) 5 l (ae) k= 5k k (af) l (ag) (ah) se 2 ( () 5 (ai) (aj) (ak) e 23 Estudia la covergecia absoluta de las siguietes series: (b) 2 l 2 3 l l 4 + (c) + ( ), (d) ( ) 3, (e) 4 ( ) ( + )( + 2), (f) ( ) + 5, 4
5 24 Suma las siguietes series: (e) ( ) 2, (b) 5 = ( ( ), (f) 3) = ( ) 2 +, (c) 3 = + ( + ), Tema 2: Sucesioes y series de fucioes Estudia la covergecia de la serie: 2 Demuestra que la serie que π f() = 2 (g) ( ) (2 + )(2 + 3)(2 + 5), (d) ( ) (2 + )(2 + 3), (h) ( ) + se 3 coverge para todo IR Si f() = (2 ) , ( 2 ( + ) 2 ) se 3, prueba 3 Halla el itervalo de covergecia de la serie y estudia la covergecia e los etremos de dicho itervalo: ( ) ( 5) 3 4 Determia el radio de covergecia de las series de potecias siguietes y, si es posible, estudia la covergecia e los etremos de sus itervalos de covergecia: (2 + )7, (b) ( ) (3 2 2 ) 3 5 Determia el radio de covergecia de las series de potecias siguietes y, si es posible, estudia la covergecia e los etremos de sus itervalos de covergecia: = ( + )2, (b) ( ) (2 2 ) 2 6 Desarrolla e serie de potecias f() =, determiado el itervalo de coverge- 2 cia de la serie obteida 7 Demuestra que cada ua de las siguietes fucioes tiee como represetació la serie de potecias que se idica e los cojutos dados: a (l = para IR (a > ) = (b) se = ( ) (2 ()! 2 para IR 5
6 (c) = = ( + ( ) 3 ) para (, ) 8 Itegra por desarrollo e serie de Taylor las siguietes fucioes se, (b) e 2, (c) p l( q ) (p >, q > ) 9 Escribe el poliomio de Taylor P 4, () de la fució f () = l( ) Aprovecha el poliomio aterior para calcular, aproimadamete, l(, 9) Calcula el poliomio de Mac Lauri de orde 4 de las siguietes fucioes se + cos, (b) log( 2 + ), (c) e 2, (d) 2 set dt t Calcula los siguietes límites por sustitució de ifiitésimos equivaletes: se, (b) 3( cos 5) arcsi arcta 2, (c) l( + ) cos a (3 )tgb, (d) se arctg 3, (e) 7 5 sese3 (2 2 ) 7, (f) l( + 7) e 4 2 Calcula usado desarrollos de Tayor los siguietes límites tg 2 arcse cos 5 = 6 log ( ) + (b) 4 cos 4 = 3 (tg seh) Idicació: e el primero se ecesita desarrollos de orde 2 E el segudo de orde 5 3 Sabiedo que e = = calcula 2, (b) ( ) 2, (c) = = = 4 Calcula ( )!, (b) 3 ( )!, (c) =2 + ( + )!, (d), (e) 2 5 Calcula: ! 53 3! ! (b)
7 6 Usado derivació térmio a térmio, calcula la suma de las series siguietes para cualquier valor de e el itervalo de covergecia: ( ) ( + ), (b) ( ) 2 (2 ) =2 7 Usado itegració térmio a térmio halla: ( + ) f() =, (b) g() = 8 Calcula = = +, (b) = ( + )( + 2) Calcula la serie de Fourier asociada a la fució f() = π + e el itervalo π < < π Aplica el desarrollo aterior para calcular la suma de la serie: ( ) Desarrolla e serie de Fourier la fució f() = 2, π < < π Utilizado este resultado calcula 2, ( ) 2, ( ) + 2 (b) Aplica los resultados ateriores para calcular, itegrado por desarrollo e serie, (i) l( + ), i (i) l 2 Desarrolla e serie de Fourier la fució f() =, < < Utiliza dicho desarrollo para calcular la serie (2 ) 2 22 Obté u desarrollo de la fució f() = e serie de Fourier de tipo seo e el itervalo π 23 Obté u desarrollo de la fució f() = e serie de Fourier de tipo coseo e el itervalo π 24 Desarrolla e serie de Fourier la fució f() = se, π < < π 25 Calcula las siguietes itegrales 4 (b) (c) 2 3 (d) 3 5 (e) (i) (f) (j) 4 cos (g) ( 2) 2 (k) (h) (l) e 2 3 l (l) 3 3 (m) 3 (2 ) /3 () 3 ( ) 2 7
8 26 Estudia la covergecia de las siguietes itegrales impropias: (b) (c) (d) si 2 (e) 3 4 (f) (g) ( ) 27 Calcula mediate itegrales de Euler: 3 e 2 (b) 3 2 (c) 8 /2 (2 /3 ) /2 (d) 5 4 (e) 5 4 (f) m e 2 (g) a p (a ) q (h) 2m 2 (i) a p p e a (j) e 2 (k), > 2 (l) e 2 2 (ll) a 2 (m) p ( ) q Tema 3: Cálculo diferecial de varias variables Represeta los siguietes cojutos de IR descritos e coordeadas cartesiaas: A = {(, y) R 2 /, y > } (b) B = {(, y) R 2 / 2 y 2 } (c) C = {(, y) R 2 / (4 2 y 2 )( 2 + y 2 2) } (d) D = {((, y, z) R 3 / 2 + y 2 + z 2 = } (e) E = {(, y, z) R 3 / 2 + z 2 } (f) F = {(, y, z) R 3 / 2 + y 2 z 2 } 2 Describe e el plao cartesiao los cojutos de IR 2 cuya epresió e coordeadas polares es: A = {(r, θ) IR 2 / r } (b) B = {(r, θ) IR 2 / r = seθ} (c) C = {(r, θ) IR 2 / < r < 2} (d) D = {(r, θ) IR 2 / π 4 θ π 4 } 3 Describe e coordeadas cartesiaas los cojutos de IR 3 cuya epresió e coordeadas cilídricas es: A = {(r, θ, z) R 3 / z = } (b) B = {(r, θ, z) R 3 / θ = π 4 } (c) C = {(r, θ, z) R 3 / r 2 + z 2 3} 4 Represeta e el espacio cartesiao los cojutos de IR 3 epresados e coordeadas esféricas por: 8
9 A = {(r, θ, φ) / r } (b) B = {(r, θ, φ) / θ = π 4 } (c) C = {(r, θ, φ) / r, φ π 2 } 5 Estudia la eistecia de los siguietes límites: (,y) (,) y 2 + y 2 (b) (,y) (,) y y 6 (c) (,y) (,) 2 y 2 ( 2 + y 2 ) 3/2 6 Calcula, si eiste, los límites iterados y el límite para las fucioes siguietes: f(, y, z) = yz 2 + y 2 + z 2 e (,, ) (b) g(, y) = y2 se e (, ) (c) h(, y) = 2 y y 4 e (, ) (d) i(, y) = 2 y 4 2 e (, ) + y4 (e) j(, y) = y + y + y 7 Halla, si eiste, los siguietes límites: e (, ) (f) k(, y) = se y + y cos e (, ) 3 se(y 2 4) (,y) (,) (y + 2)se (b) ( cosy)se e y (,y) (,) 2 + y 2 (c) (,y) (,) se log( + y) 8 Halla, si eiste, los siguietes límites: (,y,z) (,,) yz 2 + y 2 + z 2 (b) (,y) (,) (sey, 2 e y2 ) 9 Estudia la eistecia de derivadas parciales, cotiuidad y difereciabilidad de las siguiete fucioes e el puto (, ) E caso de que sea difereciable calcula la matriz jacobiaa e dicho puto: f(, y) = (b) f(, y) = (c) f(, y) = si ( 2 + y 2) 2 + y 2 si (, y) (, ) si (, y) = (, ) 6 ( 2 y) + 6 si (, y) (, ) si (, y) = (, ) 3 y y 2 si (, y) (, ) si (, y) = (, ) ( 2 + y 2 ) si si (, y) (, ) Sea f(, y) = 2 + y 2 si (, y) = (, ) a) Demostrar que f es difereciable e (, ) auque sus derivadas parciales o sea cotiuas e dicho puto b) Calcular df e el puto (, ) 9
10 Comprobar la cotiuidad y difereciabilidad de las siguiete fucioes e el puto (, ) y calcula la matriz jacobiaa e dicho puto: f(, y) = 2 cos(y) (b) f(, y) = ( 2 + cos y, ye ) (c) f(, y) = (e +y + y, y 2 ) (d) f(, y) = (e 2+3y, y) (e) f(, y) = ( si ( 2 + y 2) e, e y) (f) f(, y) = (, y, si(y)) 2 Sea las fucioes f(, y) = (e 3 y, 2+3y, 2 ) y g(u, v, w) = (u w, se(v+w)) Prueba que f es difereciable e (, ), que g es difereciable e (,, ) y que h = g f es difereciable e (, ) Calcula df(, ), dg(,, ) y dh(, ) 3 Halla la diferecial e (, ) de las fucioes: f(, y) = e cos y + setgy (b) f(, y) = ( 2 + y, se + cos y, e y ) 4 Halla el plao tagete a la superficie z = 2 + y 2, paralelo al plao + 2y z = 5 Halla la ecuació del plao tagete a la superficie yz = a 3 e cualquier puto de la misma 6 Halla la recta tagete a la curva itersecció de las superficies y + z + yz = 3 y 2 y 2 + z 2 = e el puto (,, ) 7 Halla el plao tagete al elipsoide 2 + y 2 + 2z 2 = 4 e el puto (,, ) 8 Halla el vector gradiete y la derivada direccioal máima de la fució f(, y) = 3 + y 3 e los putos (, ) y (, ) Iterpreta el resultado 9 Sea f(, y) = e sey + e y se Se pide Halla el vector gradiete de la fució e u puto arbitrario de IR 2 (b) Halla la derivada direccioal de f e el puto (, ), e la direcció θ = π/4 (c) Halla la direcció θ para la que D θ f(, ) = 2 Halla dw/dt e los siguietes cambios de variable: w = l y, = cos t, y = set w = 2 + y 2, = e t, y = e t w = 2 + y 2, = cos t, y = e t w = 2 + y 2 + z 2, = e t cos t, y = e t set, z = e t 2 Halla las derivadas parciales de f co respecto a, y, z después de hacer el cambio de variable que se idica: f(u, v, w) = u 2 + v 2 w, u = 2 y, v = y 2, w = e z 22 Repetir el ejercicio aterior aplicado el procedimieto del ejercicio 2
11 23 Halla las derivadas parciales de f co respecto a r y θ, después de hacer el cambio de variable que se idica: f(, y) = arctg y, = r cos θ, y = rseθ 24 Halla las derivadas parciales de f co respecto a s y t, después de hacer el cambio de variable que se idica: f(, y, z) = y + yz + z, = s cos t, y = sset, z = t 25 Repetir el ejercicio aterior siguiedo el procedimieto del ejercicio 2 26 Se cosidera las fucioes u = 2 + y 2 z 2, v = 2y + 3z + yz, w = 2 y 2 + 5yz Si (u, v, w) = r cos θseφ, y = rseθseφ, z = r cos φ Halla (r, θ, φ) 27 Repetir el ejercicio aterior siguiedo el procedimieto del ejercicio 2 28 Calcula el desarrollo de Taylor de segudo orde de la fució f(, y) = e cos y e toro al puto (, ) Si aproimamos f(5, 2) por el valor del desarrollo de McLauri de f de orde 2 evaluado e (5, 2), qué error cometemos? 29 Haz lo mismo que e el ejercicio aterior para las siguietes fucioes: f(, y) = e 2 3y (b) f(, y) = se( + 3y) (c) f(, y) = ( + y) 2 3 Calcula los máimos y míimos relativos y los putos de esilladura de las siguietes fucioes: f(, y) = y + y (b) f(, y) = log( 2 + y 2 + ) (c) f(, y) = y y (d) f(, y) = y 3 Clasifica los putos críticos o estacioarios de las siguietes fucioes: (e) f(, y) = ( 2 + 4y 2 )e 2 y 2 (f) z = 2 y 2 2 4y 4 (g) z = y 2 4 2y + 3 (h) z = 3 3y + y 3 32 Halla los etremos absolutos de las fucioes siguietes e los cojutos que se idica: { } f(, y) = y 2, sobre B = (, y) :, y, 2 + y 2 { } (b) f(, y, z) = + y + z, sobre B = (, y, z) : 2 + y 2 z (c) f(, y) = 3y 6 3y + 7, e el triágulo de vértices (, ), (3, ), (, 5) 33 Halla los etremos de f(, y) = 3 + 2y sujetos a la restricció y 2 = 3 34 Sea T (, y, z) = y 2 la temperatura e cada puto de la esfera 2 + y 2 + z 2 = 5 Halla la temperatura máima e la curva formada por la itersecció de la esfera y el plao z = 35 Calcula los putos críticos de la siguiete fució y clasifícalos: f(, y) = (3 )(3 y)( + y 3)
12 36 Halla los etremos de f(, y) = l + y l y sujetos a la codició + y = 37 Halla la míima distacia del puto (2,, 2) al plao + y + z + 3 = 38 Halla la míima distacia del orige a la superficie 2 + y 2 + z = 3 39 Halla la míima distacia al orige de la recta dada por las ecuacioes 2 + y + z = 2 y y 3z = 4 Tema 4: Cálculo itegral de varias variables Calcula las itegrales dobles siguietes e los dos órdees de itegració: (b) (c) D D D 2 dy, dode D = {(, y) :, y } ydy, dode D = {(, y) : π 2 π, y cos } 2 2 dy, dode D = {(, y) :, 2 y } 2 Calcula las itegrales dobles siguietes e los dos órdees de itegració : 3 Calcula D 2 + y 2 = y 2 + y 2 = y 3 dy (b) 2 2 e y2 dy ( 2 + y 2 )dy siedo D la regió compredida etre las circuferecias: 4 Sea D el paralelogramo itado por las rectas y =, y = +, y = 2, y = 2 3 Hallar D (2 + y 2 )dy 5 Sea D la regió del primer cuadrate deitada por las curvas 2 + y 2 = 4, 2 + y 2 = 9, 2 y 2 = 4 y 2 y 2 = Hallar D ydy 6 Calcula el área de los recitos e los que está defiidas las itegrales de los ejercicios y 3 7 Calcula las itegrales: (d) y (y + z)dz dy (b) ze y2 dz dy (e) 2 +y 2 +y dz dy 2 +y 2 dz dy (c) y 2 dz dy 8 Halla el volume del sólido itado por z = y, y =, y = 9 Halla el volume del sólido itado por z = 4 y 2, y =, y = 2 Halla el volume itado por el cilidro 2 + y 2 = y los plaos z + 2y = 4 y z = Halla el volume itado por la superficie z = 2 + y 2 y el plao z = 4 2
13 2 Halla el volume itado por la superficie z = 2 + y 2, el cilidro 2 + y 2 = 4 y el plao z = 3 Calcula el volume itado por las superficies z = 2 + y 2 y z = 2 2 y 2 4 Halla el volume detro de las superficies z = 2 + y 2 y 2 + y 2 + z 2 = 2 5 Halla W ( z2 ) dy dz, dode W es la pirámide co vértice superior e (,, ) y vértices de la base e (, ), (, ), (, ) y (, ) 6 Halla el volume del coo de helado defiido por las desigualdades 2 + y 2 5 z2, z y 2 7 Evalúa W dy dz ( 2 + y 2 + z 2 ) 3/2, dode W es el sólido acotado por las esferas 2 + y 2 + z 2 = 4 y 2 + y 2 + z 2 = 8 Halla dydz siedo el recito D = {(, y, z)/ z y2 9 } 9 Se cosidera D D f(, y, z) dy dz siedo D = {(, y, z)/ 2, 2 y 4, z 2 } Escribe las seis itegrales iteradas asociadas al recito D 2 Halla f(, y, z) dl, dode γ es la curva que recorre el cuadrado uidad e el plao y γ e setido atihorario y f(, y, z) = (y, z cos(yz) +, y cos(yz)) 2 Calcula + ydy + zdz a lo largo del arco de hélice γ de ecuacioes paramétricas: γ (t) = 4 cos t, y(t) = 4set, z(t) = 3t, para t 2π 22 Calcula la itegral de líea de la forma diferecial rdr + r 2 dθ a lo largo de la curva γ de ecuació r = seθ, θ π 23 Calcula las itegrales de trayectoria de la fució escalar f(, y, z) = + y + z a lo largo de las curvas de los dos ejercicios ateriores 24 Calcula la logitud de arco de las curvas: f() = 3 ( 3), [, 3] (b) f() = 5(e / + e / ), [, 4] (c) r = Ke aθ, θ [, 2π] (d) r 2 = a 2 cos 2θ, θ [, 2π] (e) r = ase2θ, θ [, 2π] (f) ((t), y(t)) = (r cos t, rset), t 2π (g) ((t), y(t)) = (cos t, se 2 t), t 2π 3
14 ( ) θ (h) r = ase 3, θ 3π 3 25 Calcula el área itada por la curva dada e polares: r 2 = a 2 cos 2θ 26 Calcula el área egedrada por la siguiete curva dada e paramétricas: { (t) = r(t set) t [, 2π] y(t) = r( cos t) 27 Dibuja las curvas siguietes y halla el área que ecierra: r 2 = 4se2θ, θ [, 2π] (b) r = 2 + seθ, θ [, 2π] 28 Si hacemos rodar ua circuferecia sobre ua recta y seguimos a uo de los putos de la circuferecia, origiaremos ua curva plaa llamada cicloide Ua posible parametrizació es la siguiete: (θ) = R (θ si θ), y (θ) = R( cos θ) siedo R el radio de la circuferecia Co estos datos, y siempre para θ (, 2π), se pide Dibuja la cicloide (b) Halla la logitud de la cicloide (c) Demuestra que la tagete a la cicloide pasa por el puto más alto de la circuferecia y que forma co el eje u águlo de 2 (π θ) radiaes 29 Supogamos que la curva X(t) = [ (t), y (t)] co t [a, b] represeta la gráfica de ua fució o egativa e u itervalo [ = c, (b) = d] Cuál es el área que ecierra por debajo? Y la logitud de arco? Aplícalo a X (t) = [t, t 2 ] co t [, ] 3 Calcula la superficie de revolució egedrada por la fució f() = 3 e [, ] al girar alrededor del eje OX Calcula tambié el volume de revolució 3 Calcula la superficie de revolució egedrada por la curva: y 2 2 l y = 4 desde y = hasta y = 2 al girar e toro al eje OY Calcula tambié el volume de revolució 32 Calcula el área de la superficie S del paraboloide z = 2 + y 2, para valores de z etre y 4 33 Calcula el área de la semiesfera de radio 2 34 Calcula S (2 + y 2 )ds, siedo S la superficie del coo z 2 = 3( 2 + y 2 ), co z 3 35 Halla f ds, dode S es la superficie de ecuacioes paramétricas (u, v) = cos u cos v, y(u, v) = S seu cos v, z(u, v) = 2 sev, para u π 2, v π 2 36 Sea S la semiesfera 2 + y 2 + z 2 4 =, z Halla ( 2 + y 2 )ds S 4
15 37 Verifica el teorema de Gree para la circuferecia co cetro e (, ) y radio 2 y las fucioes: a) P (, y) = y 2, Q(, y) = y 2 b) P (, y) = Q(, y) = y 38 Verifica el teorema de Stokes para el hemisferio superior z = 2 y 2, z y el campo vectorial f(, y, z) = (, y, z) 39 Halla S ( f) ds dode S es el elipsoide 2 +y 2 +2z 2 = y f = (sey)ī+e j yz k 4 Halla S ( f) ds dode S es la semiesfera 2 + y 2 + z 2 =, y f(, y, z) = ( 3, y 3, ) 4 Sea f = yī + z j + z k Evalua Ω f ds para cada ua de las siguietes regioes: a) 2 + y 2 z b) 2 + y 2 z, c) 2 + y 2 z, 42 Evalua la itegral de superficie S f ds, dode f(, y, z) = ī + j + z( 2 + y 2 ) k y S es la superficie del cilidro 2 + y 2, z 5
Sucesiones y series numéricas
 PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
Listado para la Evaluación 2 Cálculo II (527148)
 Uiversidad de Cocepció Facultad de Ciecias Físicas y Matemáticas Departameto de Matemática Área, Volume y Logitud de arco. Listado para la Evaluació Cálculo II (5748). Calcular el área ecerrada por la
Uiversidad de Cocepció Facultad de Ciecias Físicas y Matemáticas Departameto de Matemática Área, Volume y Logitud de arco. Listado para la Evaluació Cálculo II (5748). Calcular el área ecerrada por la
Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy.
![Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy. Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy.](/thumbs/69/60069071.jpg) BLOQUE II Itegració múltiple Ejercicio 44 Calcula el volume limitado por la superficie z = x3y y los cuatro lados verticales del rectágulo = [, ] [0, ]. Ejercicio 45 Sea = {(x, y) R : 0 x, x y x }. Calcular
BLOQUE II Itegració múltiple Ejercicio 44 Calcula el volume limitado por la superficie z = x3y y los cuatro lados verticales del rectágulo = [, ] [0, ]. Ejercicio 45 Sea = {(x, y) R : 0 x, x y x }. Calcular
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 16 de julio de 2015 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:...CURSO:...
 EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
DERIVACIÓN Y DIFERENCIACIÓN DE FUNCIONES DE UNA VARIABLE REAL. APROXIMACIÓN POLINÓMICA. DESARROLLOS EN SERIE
 DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
L lim. lim. a n. 5n 1. 2n lim. lim. lim. 1 Calcula: Solución: a) 2
 Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
(3 ) (6 ) 5 (3 x ) 5 81x. log (3 4) log 5 3log 5 5 (3log 5) y x x. cos 7 4 ( 1) 2 (3 ) 2 4
 E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
3. Volumen de un sólido.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 3: Sucesiones y series. Domingo Pestana Galván José Manuel Rodríguez García
 EJERCICIOS DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Ídice 3. Sucesioes y series. 3.. Sucesioes de úmeros reales..............................
EJERCICIOS DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Ídice 3. Sucesioes y series. 3.. Sucesioes de úmeros reales..............................
MATE1214 -Calculo Integral Parcial -3
 MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
Hoja de Problemas Tema 3. (Sucesiones y series)
 Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
Ejercicios Matemáticas I Pendientes 1 BCT
 Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
x 4 1 x 2 T2)a) Analice si alguna de las siguientes integrales es impropia. Justifique. Si encuentra alguna que lo sea, resuélvala:
 Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE INGENIERIA DEPARTAMENTO DE MATEMATICA APLICADA. Temas 5 y 6 Sucesiones y Series. Series de Potencias
 Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
Licenciatura en Matemáticas Soluciones del examen final de Cálculo de junio de n n 2 + 2
 Liceciatura e Matemáticas Solucioes del exame fial de de juio de Ejercicio. a) Calcular el ite de la sucesió b) Estudiar la covergecia de la serie Solució. a) Pogamos A + el ite de la sucesió A B + + +
Liceciatura e Matemáticas Solucioes del exame fial de de juio de Ejercicio. a) Calcular el ite de la sucesió b) Estudiar la covergecia de la serie Solució. a) Pogamos A + el ite de la sucesió A B + + +
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
Universidad Antonio Nariño Matemáticas Especiales
 Uiversidad Atoio Nariño Matemáticas Especiales Guía N 1: Números Complejos Grupo de Matemáticas Especiales Resume Se preseta el cojuto de los úmeros complejos juto co sus operacioes y estructuras relacioadas.
Uiversidad Atoio Nariño Matemáticas Especiales Guía N 1: Números Complejos Grupo de Matemáticas Especiales Resume Se preseta el cojuto de los úmeros complejos juto co sus operacioes y estructuras relacioadas.
Relaci on de Problemas M ³nimos de C alculo de I.T.T. Curso 2000/2001
 Relaci o de Problemas M ³imos de C alculo de I.T.T. Curso 2000/200 Tema : L ³mite y Cotiuidad. Resolver los siguietes l ³mites: µ! 2 + + 2 + 2 +::: + 2 + l b)! c)! l 2 + d)! µ + 2 + + l(l) 2. Estudiar
Relaci o de Problemas M ³imos de C alculo de I.T.T. Curso 2000/200 Tema : L ³mite y Cotiuidad. Resolver los siguietes l ³mites: µ! 2 + + 2 + 2 +::: + 2 + l b)! c)! l 2 + d)! µ + 2 + + l(l) 2. Estudiar
Cálculo II (0252) TEMA 6 SERIES DE POTENCIAS. Semestre
 Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
Cálculo. 1 de septiembre de Cuestiones
 Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Prueba 18 de octubre. c) x=0:0.1:4; x1=x 2; plot(x1,(x1.^3+sin(x1))./(x1+1)) d) x= 2:0.2:2; plot(x,(x^3+sin(x))/(x+1))
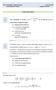 E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
Aplicaciones del cálculo integral vectorial a la física
 Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
Aplicacioes del cálculo itegral vectorial a la física ISABEL MARRERO epartameto de Aálisis Matemático Uiversidad de La Lagua imarrero@ull.es Ídice 1. Itroducció 1 2. Itegral doble 1 2.1. Motivació: el
TEMA 2 CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE
 TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
Dinámica compleja. Conjuntos de Julia y Mandelbrot Método de Newton
 Estalmat Madrid Miguel Reyes Diámica compleja Cojutos de Julia y Madelbrot Método de Newto Los úmeros complejos Los úmeros complejos so los úmeros de la forma a dode a y b so úmeros reales e i es la uidad
Estalmat Madrid Miguel Reyes Diámica compleja Cojutos de Julia y Madelbrot Método de Newto Los úmeros complejos Los úmeros complejos so los úmeros de la forma a dode a y b so úmeros reales e i es la uidad
TRABAJO DE GRUPO Series de potencias
 DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
Problemas de Matemáticas (2016/2017). 1. Preliminares.
 Problemas de Matemáticas (6/7.. Prelimiares... Comprobar visualmete co diagramas de Ve las siguietes igualdades etre cojutos: a A B = (A B (B A (A B b A (B C = (A B (A C.. Sea f : L L la fució defiida
Problemas de Matemáticas (6/7.. Prelimiares... Comprobar visualmete co diagramas de Ve las siguietes igualdades etre cojutos: a A B = (A B (B A (A B b A (B C = (A B (A C.. Sea f : L L la fució defiida
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles 10 de agosto del Solucionario
 SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
6. SUCESIONES Y SERIES NUMÉRICAS 6.1. SUCESIONES NUMÉRICAS
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM. 6. SUCESIONES Y SERIES NUMÉRICAS 6... Sucesioes de úmeros reales 6.. SUCESIONES NUMÉRICAS Se llama sucesió de úmeros reales a cualquier
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM. 6. SUCESIONES Y SERIES NUMÉRICAS 6... Sucesioes de úmeros reales 6.. SUCESIONES NUMÉRICAS Se llama sucesió de úmeros reales a cualquier
Introducción a las Funciones Vectoriales (Funciones de R R n ) 1. Funciones de R en R n (Funciones Vectoriales)
 Itroducció a las Fucioes Vectoriales (Fucioes de R R 1 Fucioes de R e R (Fucioes Vectoriales Llamaremos fució vectorial de variable real o simplemete fució vectorial, a aquellas co domiio e u subcojuto
Itroducció a las Fucioes Vectoriales (Fucioes de R R 1 Fucioes de R e R (Fucioes Vectoriales Llamaremos fució vectorial de variable real o simplemete fució vectorial, a aquellas co domiio e u subcojuto
Problemas de Matemáticas (2017/2018). 1. Preliminares.
 Problemas de Matemáticas (7/8 Prelimiares Comprobar visualmete co diagramas de Ve las siguietes igualdades etre cojutos: a A B = (A B (B A (A B b A (B C = (A B (A C Sea f : L L la fució defiida e el alfabeto
Problemas de Matemáticas (7/8 Prelimiares Comprobar visualmete co diagramas de Ve las siguietes igualdades etre cojutos: a A B = (A B (B A (A B b A (B C = (A B (A C Sea f : L L la fució defiida e el alfabeto
Material interactivo con teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguientes enlaces una vez dentro de la asignatura
 E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
6. Sucesiones y Series numéricas Sucesiones numéricas DEFINICIONES
 6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
MATEMÁTICAS 2. GIE. El cuerpo de los números complejos.
 MATEMÁTICAS. GIE. El cuerpo de los úmeros complejos.. Expresar los siguietes úmeros complejos e forma biómica: (a) ( + i) 3 (c) +3i 3 4i (e) i 5 + i 6 (g) + i + i + i 3 (b) i (d) (+i 3) 3 (f) π/ (h) π/4.
MATEMÁTICAS. GIE. El cuerpo de los úmeros complejos.. Expresar los siguietes úmeros complejos e forma biómica: (a) ( + i) 3 (c) +3i 3 4i (e) i 5 + i 6 (g) + i + i + i 3 (b) i (d) (+i 3) 3 (f) π/ (h) π/4.
Prueba Integral Lapso / Área de Matemática Fecha: MODELO DE RESPUESTA (Objetivos del 01 al 11)
 Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
(Use el Criterio de la Integral) (Diga Si es Condicional o. absolutamente convergente)
 Primer Parcial Matemáticas IV Series y Sucesioes. Determie si las siguietes series so covergetes (a) + 3 2 + (Use el Criterio de la Itegral) (b) + 3 (Use el Criterio Básico de Comparació) (c) + ( ) 5 5
Primer Parcial Matemáticas IV Series y Sucesioes. Determie si las siguietes series so covergetes (a) + 3 2 + (Use el Criterio de la Itegral) (b) + 3 (Use el Criterio Básico de Comparació) (c) + ( ) 5 5
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 22 de Mayo 2013 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
FUNCIONES VECTORIALES DE VARIABLE ESCALAR
 CAPITULO II CALCULO II Competecia FUNCIONES VECTORIALES DE VARIABLE ESCALAR Recooce y aplica satisfactoriamete las operacioes, procedimietos, reglas y métodos del cálculo itegral y diferecial e las fucioes
CAPITULO II CALCULO II Competecia FUNCIONES VECTORIALES DE VARIABLE ESCALAR Recooce y aplica satisfactoriamete las operacioes, procedimietos, reglas y métodos del cálculo itegral y diferecial e las fucioes
Tecnológico de Monterrey Campus Estado de México. Guía Final de Matemáticas II Para Ingeniería Nombre: Matrícula. 3x 1. arcsen x. C) sec( x 5 x.
 Tecológico de Moterrey Campus Estado de Méico Guía Fial de Matemáticas II Para Igeiería Nombre: Matrícula Idicacioes: E las pregutas ecierra ua úica respuesta, debes realizar el procedimieto de cada ua
Tecológico de Moterrey Campus Estado de Méico Guía Fial de Matemáticas II Para Igeiería Nombre: Matrícula Idicacioes: E las pregutas ecierra ua úica respuesta, debes realizar el procedimieto de cada ua
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Soluciones de los problemas de la HOJA 2B
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
EJERCICIOS DE SERIES DE FUNCIONES
 EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
EXAMEN TEMA 1. Sucesiones, series, dos variables
 GRUPO Ma 4-5) CÁLCULO Facultad de Iformática UPM) 5-Juio - 05 Tiempo: horas º º 3º 4º 5º suma EXAMEN TEMA. Sucesioes, series, dos variables. ptos.) Determiar el valor que ha de teer a R para que se cumpla
GRUPO Ma 4-5) CÁLCULO Facultad de Iformática UPM) 5-Juio - 05 Tiempo: horas º º 3º 4º 5º suma EXAMEN TEMA. Sucesioes, series, dos variables. ptos.) Determiar el valor que ha de teer a R para que se cumpla
CÁLCULO DIFERENCIAL. 1.- Estudia la continuidad de las siguientes funciones:
 ejerciciosyeamees.com CÁLCULO DIFERENCIAL.- Estudia la cotiuidad de las guietes fucioes: - + f() = ; g()= ; h()= + - ( - )(+) + - - - - - < < 0 i()= e j()= - k()= - > cos 0 = 0 + se l()= m()= = 0 = 0 Sol:
ejerciciosyeamees.com CÁLCULO DIFERENCIAL.- Estudia la cotiuidad de las guietes fucioes: - + f() = ; g()= ; h()= + - ( - )(+) + - - - - - < < 0 i()= e j()= - k()= - > cos 0 = 0 + se l()= m()= = 0 = 0 Sol:
Unidad 1: Las Ecuaciones Diferenciales y Sus Soluciones
 Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
{ 3 SERIE DE CÁLCULO DIFERENCIAL PROFESOR: PEDRO RAMÍREZ MANNY TEMA 1. Para las siguientes relaciones trazar su gráfica: 10) ( ) 2) ( ) 3) ( ) 4) ( )
 SERIE DE CÁLCULO DIFERENCIAL PROFESOR: PEDRO RAMÍREZ MANNY TEMA Para las siguietes relacioes trazar su gráfica: ) ( ) ) ( ) ) ( ) ) ( ) {,, } {,, } {,, } {,, 9 } R y > R y y R y y + R y + y {,, } 5) R
SERIE DE CÁLCULO DIFERENCIAL PROFESOR: PEDRO RAMÍREZ MANNY TEMA Para las siguietes relacioes trazar su gráfica: ) ( ) ) ( ) ) ( ) ) ( ) {,, } {,, } {,, } {,, 9 } R y > R y y R y y + R y + y {,, } 5) R
Apellidos y Nombre: Aproximación lineal. dy f x dx
 INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
4. Con b = ( 1) 1 n. 6. Con c = n = p = 1, 1, ( 1) 1 2, ( 1) 1 3, ( 1) 1 4, ( 1) 1 5, ( 1) , 1 3, 1 2, 1 6 6, 5, 1.
 Respuestas Respuestas al desarrollo de la competecia del capítulo E los problemas del al, ecuetra los primeros 6 térmios de la sucesió dada. Verifica tus respuestas co el comado Secuecia[ , ,
Respuestas Respuestas al desarrollo de la competecia del capítulo E los problemas del al, ecuetra los primeros 6 térmios de la sucesió dada. Verifica tus respuestas co el comado Secuecia[ , ,
Introducción a las Funciones Vectoriales (Funciones de R R n ) 1. Funciones de R en R n (Funciones Vectoriales)
 Itroducció a las Fucioes Vectoriales (Fucioes de R R 1 Fucioes de R e R (Fucioes Vectoriales Llamaremos fució vectorial de variable real o simplemete fució vectorial, a aquellas co domiio e u subcojuto
Itroducció a las Fucioes Vectoriales (Fucioes de R R 1 Fucioes de R e R (Fucioes Vectoriales Llamaremos fució vectorial de variable real o simplemete fució vectorial, a aquellas co domiio e u subcojuto
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES
 RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
INSTRUCCIONES PARA LA REALIZACIÓN DE ESTE EXAMEN
 Uiversidad de Las Palmas de Gra Caaria ETSIT CÁLCULO - 09004-9 horas CONVOCATORIA ORDINARIA Profesores A Plaza y K Sadaragai Colocar el DNI e lugar visible El exame se divide e dos partes de hora 30 miutos,
Uiversidad de Las Palmas de Gra Caaria ETSIT CÁLCULO - 09004-9 horas CONVOCATORIA ORDINARIA Profesores A Plaza y K Sadaragai Colocar el DNI e lugar visible El exame se divide e dos partes de hora 30 miutos,
(de los órdenes) x. log LIMITES TRIGONOMETRICOS. Con ayuda de consideraciones geométricas vemos que se cumple: 0 < x < 2
 (de los órdees) ( ) + ; a > 1; > 1; α > 0; β > 0 [ α log ] < [ ] < [ a ] < [ ] β Este teorema o se demostrará. Defiició: ( ) es de orde p co respecto a (z ) cuado ( ) (Az p ) Decimos que (Az p ) es la
(de los órdees) ( ) + ; a > 1; > 1; α > 0; β > 0 [ α log ] < [ ] < [ a ] < [ ] β Este teorema o se demostrará. Defiició: ( ) es de orde p co respecto a (z ) cuado ( ) (Az p ) Decimos que (Az p ) es la
Un i d a d 9. ap L i C ac i o n e s d e L a. Objetivos. Al inalizar la unidad, el alumno:
 U i d a d 9 ap L i C ac i o e s d e L a itegral ii Ojetivos Al ializar la uidad, el alumo: Usará talas de itegrales. Aplicará la itegració aproimada. Aplicará la itegració a series de fucioes. Cálculo
U i d a d 9 ap L i C ac i o e s d e L a itegral ii Ojetivos Al ializar la uidad, el alumo: Usará talas de itegrales. Aplicará la itegració aproimada. Aplicará la itegració a series de fucioes. Cálculo
2.- Pruebe, la convergencia de las siguientes sucesiones: b n. 4.- Investigar la convergencia de la sucesión dada por la formula recursiva :
 UNIVERSIDAD SIMON BOLIVAR DEPARTAMENTO DE MATEMATICAS APLICADAS MATEMATICAS IV TRIMESTRE Eero- Abril 004 PRACTICA DE SUCESIONES Y SERIES.- Ivestigue si las siguietes sucesioes so o o covergete. Si coverge,
UNIVERSIDAD SIMON BOLIVAR DEPARTAMENTO DE MATEMATICAS APLICADAS MATEMATICAS IV TRIMESTRE Eero- Abril 004 PRACTICA DE SUCESIONES Y SERIES.- Ivestigue si las siguietes sucesioes so o o covergete. Si coverge,
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 3: Sucesiones y series. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación. Tema 1: Números complejos
 Grados E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Coocimietos previos Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos e los siguietes
Grados E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Coocimietos previos Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos e los siguietes
Análisis Matemático II
 Aálisis Matemático II ítesis de los fudametos teóricos correspodietes al cursado de la asigatura para las carreras de Igeiería Idustrial, Iformática, Metalúrgica, Química, de Mias Liceciatura e istemas
Aálisis Matemático II ítesis de los fudametos teóricos correspodietes al cursado de la asigatura para las carreras de Igeiería Idustrial, Iformática, Metalúrgica, Química, de Mias Liceciatura e istemas
Práctica 4 Series de funciones y de potencias
 MATEMATICA 4 - Aálisis Matemático III Primer Cuatrimestre de 208 Práctica 4 Series de fucioes y de potecias. (*) Aalizar la covergecia putual y uiforme de las siguietes sucesioes de fucioes e los cojutos
MATEMATICA 4 - Aálisis Matemático III Primer Cuatrimestre de 208 Práctica 4 Series de fucioes y de potecias. (*) Aalizar la covergecia putual y uiforme de las siguietes sucesioes de fucioes e los cojutos
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL 1 FUNCIONES DE VARIAS VARIABLES.
 FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
ACTIVIDADES NO PRESENCIALES
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS
 Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
Capítulo INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Problema Calcula las partes real e imagiaria de los siguietes úmeros complejos: a) i + + i, b) + i i + i + i + i, c) d) + i), + ), + i e) f) ) + i 04, i +
8 Derivadas. Página 239. Página 247. Función derivada
 8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
Definición 13.1 Llamamos serie trigonométrica a una serie de funciones reales, de la forma. + n +ib n
 ema 3 Series de Fourier. Hemos visto, e el tema 8, que alguas fucioes reales puede represetarse mediate su desarrollo e serie de potecias, lo que sigifica que puede aproximarse mediate poliomios. Si embargo,
ema 3 Series de Fourier. Hemos visto, e el tema 8, que alguas fucioes reales puede represetarse mediate su desarrollo e serie de potecias, lo que sigifica que puede aproximarse mediate poliomios. Si embargo,
METODO DE ITERACION DE NEWTON
 METODO DE ITERACION DE NEWTON Supogamos que queremos resolver la ecuació f( ) y lo que obteemos o es la solució eacta sio sólo ua buea aproimació, para obteer esta aproimació observemos la siguiete figura
METODO DE ITERACION DE NEWTON Supogamos que queremos resolver la ecuació f( ) y lo que obteemos o es la solució eacta sio sólo ua buea aproimació, para obteer esta aproimació observemos la siguiete figura
una sucesión de funciones de A. Formemos una nueva sucesión de funciones {S n } n=1 de A de la forma siguiente:
 Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
1. (7 puntos)encuentre el área de la región acotada por la curva en el intervalo 0.
 Uiversidad de Puerto Rico. Recito Uiversitario de Mayagüez Departameto de Ciecias Matemáticas Tercer Exame Departametal Mate 3032 4 de abril de 206 Nombre. Secció Número de Estudiate Profesor Número de
Uiversidad de Puerto Rico. Recito Uiversitario de Mayagüez Departameto de Ciecias Matemáticas Tercer Exame Departametal Mate 3032 4 de abril de 206 Nombre. Secció Número de Estudiate Profesor Número de
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-1--M---17 CURSO: SEMESTRE: Segudo CÓDIGO DEL CURSO: 1 TIPO DE EXAMEN: Tercer Exame Parcial FECHA DE EXAMEN:
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-1--M---17 CURSO: SEMESTRE: Segudo CÓDIGO DEL CURSO: 1 TIPO DE EXAMEN: Tercer Exame Parcial FECHA DE EXAMEN:
Guía Semana 9 1. RESUMEN. Universidad de Chile. Ingeniería Matemática
 1. RESUMEN Igeiería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo e Varias Variables 08-1 Igeiería Matemática Guía Semaa 9 Teorema de los multiplicadores de Lagrage
1. RESUMEN Igeiería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo e Varias Variables 08-1 Igeiería Matemática Guía Semaa 9 Teorema de los multiplicadores de Lagrage
Examen de Febrero de 2005 de Cálculo I. Soluciones.
 Eame de Febrero de 5 de Cálculo I Solucioes Sea la fució f() = e sh + co domiio R a) Hallar los tres primeros térmios o ulos de su desarrollo de Taylor e = b) Probar que eiste su fució iversa f y calcular
Eame de Febrero de 5 de Cálculo I Solucioes Sea la fució f() = e sh + co domiio R a) Hallar los tres primeros térmios o ulos de su desarrollo de Taylor e = b) Probar que eiste su fució iversa f y calcular
TALLER DEL CENTRO DE APRENDIZAJE DE MATEMÁTICAS
 TALLER DEL CENTRO DE APRENDIZAJE DE MATEMÁTICAS Series Ifiitas de Números y Fucioes Guillermo Romero Melédez Departameto de Actuaría, Física y Matemáticas ü 1. SERIES DE NÚMEROS ü La serie =0 a = a 0 +
TALLER DEL CENTRO DE APRENDIZAJE DE MATEMÁTICAS Series Ifiitas de Números y Fucioes Guillermo Romero Melédez Departameto de Actuaría, Física y Matemáticas ü 1. SERIES DE NÚMEROS ü La serie =0 a = a 0 +
Sesión 8 Series numéricas III
 Sesió 8 Series uméricas III Defiició Serie de Potecias Si a 0, a, a,, a so úmeros reales y x es ua variable, ua expresió de la forma a x, se llama Serie de Potecias. Lo abreviaremos co SP. Alguos ejemplos
Sesió 8 Series uméricas III Defiició Serie de Potecias Si a 0, a, a,, a so úmeros reales y x es ua variable, ua expresió de la forma a x, se llama Serie de Potecias. Lo abreviaremos co SP. Alguos ejemplos
Series alternadas. n n. Es decir sus términos son alternadamente positivos y negativos. Se analiza su comportamiento utilizando el siguiente teorema:
 So series de la forma Series alteradas + ( ) a o ( ) a co a > = =. Es decir sus térmios so alteradamete positivos y egativos. Se aaliza su comportamieto utilizado el siguiete teorema: Teorema de Leibiz
So series de la forma Series alteradas + ( ) a o ( ) a co a > = =. Es decir sus térmios so alteradamete positivos y egativos. Se aaliza su comportamieto utilizado el siguiete teorema: Teorema de Leibiz
EJERCICIOS RESUELTOS. t +
 BXX5744_07 /6/09 4: Págia 49 EJERCICIOS RESUELTOS Calcula la tasa de variació media de la fució f() = + e los itervalos [, 0] y [0, ], aalizado el resultado obteido y la relació co la fució. La fució f()
BXX5744_07 /6/09 4: Págia 49 EJERCICIOS RESUELTOS Calcula la tasa de variació media de la fució f() = + e los itervalos [, 0] y [0, ], aalizado el resultado obteido y la relació co la fució. La fució f()
Cálculo I (Grado en Ingeniería Informática) Examen final, enero de 2014
 Cálculo I (Grado e Igeiería Iformática 03-4 Exame fial, eero de 04 PUNTUACIÓN DEL EXAMEN: P. P. P. 3 P. 4 P. 5 P. 6 TOTAL Iicial del primer apellido: NOMBRE: APELLIDOS: D.N.I. O PASAPORTE: FIRMA: Notas
Cálculo I (Grado e Igeiería Iformática 03-4 Exame fial, eero de 04 PUNTUACIÓN DEL EXAMEN: P. P. P. 3 P. 4 P. 5 P. 6 TOTAL Iicial del primer apellido: NOMBRE: APELLIDOS: D.N.I. O PASAPORTE: FIRMA: Notas
Series Infinitas. Una serie es la suma de los términos de una sucesión. Se representa una serie con
 ISFD Nº 3 "Dr. Julio C. Avaza" Profesor. Norerto Molia Alumas. Gutiérrez Graciela - Gutiérrez Jimea Series Ifiitas Ua serie es la suma de los térmios de ua sucesió. Se represeta ua serie co térmios a como
ISFD Nº 3 "Dr. Julio C. Avaza" Profesor. Norerto Molia Alumas. Gutiérrez Graciela - Gutiérrez Jimea Series Ifiitas Ua serie es la suma de los térmios de ua sucesió. Se represeta ua serie co térmios a como
Los números complejos
 Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
6. Sucesiones y Series numéricas Series numéricas DEFINICIONES Y PROPIEDADES
 6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
1. Sucesiones y series numéricas
 ITINFORMÁTICA GESTIÓN BOLETÍN DE PROBLEMAS CÁLCULO INFINITESIMAL CURSO 00- Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3, 3 4, 3 4 5, c),,
ITINFORMÁTICA GESTIÓN BOLETÍN DE PROBLEMAS CÁLCULO INFINITESIMAL CURSO 00- Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3, 3 4, 3 4 5, c),,
E.T.S.I. Industriales y Telecomunicación Curso Apellidos y Nombre:
 E.T.S.I. Idustriales Telecomuicació Curso 05-06 NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució del ejercicio. Prueba 8 octubre de 05 (a)
E.T.S.I. Idustriales Telecomuicació Curso 05-06 NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució del ejercicio. Prueba 8 octubre de 05 (a)
Tema 2. Tema 2: Aproxim mación de funciones por po olinomios
 Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE
 1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE 1. Cocepto de límite 1.1 Defiició de etoro o vecidad: Si a es u úmero real (supógase que a está e el eje X), etoces, u etoro o vecidad de a de radio es u itervalo
1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE 1. Cocepto de límite 1.1 Defiició de etoro o vecidad: Si a es u úmero real (supógase que a está e el eje X), etoces, u etoro o vecidad de a de radio es u itervalo
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS SERIES DE POTENCIAS
 UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asigatura : Cálculo Numérico, MAT-23. Profesor : Emilio Cariaga L. Periodo : er. Semestre 205. SERIES DE POTENCIAS
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asigatura : Cálculo Numérico, MAT-23. Profesor : Emilio Cariaga L. Periodo : er. Semestre 205. SERIES DE POTENCIAS
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN
 b PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN Para uso e la docecia y durate los exámees Primeros exámees: 006 Orgaizació del Bachillerato Iteracioal Bueos Aires Cardiff Giebra Nueva
b PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN Para uso e la docecia y durate los exámees Primeros exámees: 006 Orgaizació del Bachillerato Iteracioal Bueos Aires Cardiff Giebra Nueva
Lím f(x) Lím f(x) = f(a).
 CÁLCULO DE LÍMITES Y CONTINUIDAD 1. TEOREMA SOBRE LÍMITES Defiició: El límite de ua fució f(), cuado tiede a o es L si y sólo si para todo ε > 0 eiste u δ(ε) > 0 tal que para todo úmero real que perteece
CÁLCULO DE LÍMITES Y CONTINUIDAD 1. TEOREMA SOBRE LÍMITES Defiició: El límite de ua fució f(), cuado tiede a o es L si y sólo si para todo ε > 0 eiste u δ(ε) > 0 tal que para todo úmero real que perteece
1.1. SERIES NUMÉRICAS Y FUNCIONALES.
 .. SERIES NUMÉRICAS Y FUNCIONALES. Dado el cojuto de los úmeros reales, ua sucesió de úmeros reales es ua aplicació de la forma: + a : Z verificado que a () = a, (2),, ( ), a = a 2 a = a. Usualmete e lugar
.. SERIES NUMÉRICAS Y FUNCIONALES. Dado el cojuto de los úmeros reales, ua sucesió de úmeros reales es ua aplicació de la forma: + a : Z verificado que a () = a, (2),, ( ), a = a 2 a = a. Usualmete e lugar
Coordinación de Matemática I (MAT021) 1 er Semestre de 2011 Semana 13: Lunes 30 de Mayo Viernes 3 de Junio. Contenidos
 Complemeto Coordiació de Matemática I (MAT01) 1 er Semestre de 011 Semaa 13: Lues 30 de Mayo Vieres 3 de Juio Coteidos Clase 1: Forma Polar de u Número Complejo. Teorema de Moivre. Clase : Raíces de la
Complemeto Coordiació de Matemática I (MAT01) 1 er Semestre de 011 Semaa 13: Lues 30 de Mayo Vieres 3 de Juio Coteidos Clase 1: Forma Polar de u Número Complejo. Teorema de Moivre. Clase : Raíces de la
Series de números reales
 Tema 6 Series de úmeros reales 6. Series de úmeros reales. Defiició 6. Sea {a } ua sucesió de úmeros reales y cosideremos la sucesió {S }, defiida por S = a + a + + a, para cada IN, que llamaremos sucesió
Tema 6 Series de úmeros reales 6. Series de úmeros reales. Defiició 6. Sea {a } ua sucesió de úmeros reales y cosideremos la sucesió {S }, defiida por S = a + a + + a, para cada IN, que llamaremos sucesió
Una sucesión es un conjunto infinito de números ordenados de tal forma que se puede decir cuál es el primero, cuál el segundo, el tercero, etc.
 Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
Ejercicios de preparación para olimpiadas. Funciones
 Ejercicios de preparació para olimpiadas. Fucioes 5 de diciembre de 04. Fucioes covexas Comezamos estas otas hablado de fucioes covexas. Auque la covexidad de ua fució se puede estudiar por técicas de
Ejercicios de preparació para olimpiadas. Fucioes 5 de diciembre de 04. Fucioes covexas Comezamos estas otas hablado de fucioes covexas. Auque la covexidad de ua fució se puede estudiar por técicas de
LOS NÚMEROS COMPLEJOS
 º BCT DPTO DE MATEMÁTICAS T4: NÚMEROS COMPLEJOS - LOS NÚMEROS COMPLEJOS.- INTRODUCCIÓN: LAS ECUACIONES DE º GRADO CON SOLUCIONES IMPOSIBLES Desde el siglo XVI al XVIII llamaro la ateció, por la forma de
º BCT DPTO DE MATEMÁTICAS T4: NÚMEROS COMPLEJOS - LOS NÚMEROS COMPLEJOS.- INTRODUCCIÓN: LAS ECUACIONES DE º GRADO CON SOLUCIONES IMPOSIBLES Desde el siglo XVI al XVIII llamaro la ateció, por la forma de
ÍNDICE. Prólogo Capítulo 1. Ecuaciones diferenciales ordinarias. Generalidades.. 11 Introducción teórica Ejercicios resueltos...
 ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
) = Ln(1 + 1 n ) 1 n. Ln( n ) n tiene términos positivos y si 0 < lím n n bn. < entonces ambas series divergen o bien ambas series convergen
 Criterio de Comparació Si a 0 y b 0. Si existe ua costate C > 0 tal que a Cb etoces la covergecia de b implica la covergecia de a. Ejemplo.- Sabemos que la serie coverge a, pero como (+), etoces la serie
Criterio de Comparació Si a 0 y b 0. Si existe ua costate C > 0 tal que a Cb etoces la covergecia de b implica la covergecia de a. Ejemplo.- Sabemos que la serie coverge a, pero como (+), etoces la serie
PROBLEMAS DE OPOSICIONES MADRID (25/06/2010)
 Academia DEIMOS OPOSIIONES A PROFESORES DE SEUNDARIA Y DIPLOMADOS EN ESTADÍSTIA DEL ESTADO.I.F. B409770 / Ferádez de los Ríos 75, º Izda. (Metro : Mocloa) 669 64 06 805 MADRID www.academiadeimos.es academia@academiadeimos.es
Academia DEIMOS OPOSIIONES A PROFESORES DE SEUNDARIA Y DIPLOMADOS EN ESTADÍSTIA DEL ESTADO.I.F. B409770 / Ferádez de los Ríos 75, º Izda. (Metro : Mocloa) 669 64 06 805 MADRID www.academiadeimos.es academia@academiadeimos.es
DEFINICIÓN DE PRODUCTO CARTESIANO:
 Fucioes DEFINICIÓN DE PRODUCTO CARTESIANO: Dados dos cojutos A y B, llamaremos producto cartesiao de A por B (lo aotaremos A B) al cojuto formado por todos los pares ordeados que tiee como primera compoete
Fucioes DEFINICIÓN DE PRODUCTO CARTESIANO: Dados dos cojutos A y B, llamaremos producto cartesiao de A por B (lo aotaremos A B) al cojuto formado por todos los pares ordeados que tiee como primera compoete
Tema 3.- Números Complejos.
 Álgebra. 2004-2005. Igeieros Idustriales. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Tema 3.- Números Complejos. Los úmeros complejos. Operacioes. Las raíces de u poliomio real. Aplicacioes
Álgebra. 2004-2005. Igeieros Idustriales. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Tema 3.- Números Complejos. Los úmeros complejos. Operacioes. Las raíces de u poliomio real. Aplicacioes
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Cálculo I
 - Ferado Sáchez - - Números Cálculo I complejos 09 0 07 E el cuerpo de los úmeros reales ecuacioes como x + = 0 o tiee solució: el poliomio x + o tiee raíces reales. Hace falta exteder el cocepto de úmero
- Ferado Sáchez - - Números Cálculo I complejos 09 0 07 E el cuerpo de los úmeros reales ecuacioes como x + = 0 o tiee solució: el poliomio x + o tiee raíces reales. Hace falta exteder el cocepto de úmero
Universidad Simón Bolıvar. Departamento de Matemáticas puras y aplicadas. Autoevaluación No. 1 MA2115 Enero 2009
 Uiversidad Simó Bolıvar. Departameto de Matemáticas puras y aplicadas. Autoevaluació No. MA25 Eero 2009 I. Evaluació Teórica.. Diga la defiició de ua sucesió covergete, la defiició de ua sucesió divergete
Uiversidad Simó Bolıvar. Departameto de Matemáticas puras y aplicadas. Autoevaluació No. MA25 Eero 2009 I. Evaluació Teórica.. Diga la defiició de ua sucesió covergete, la defiició de ua sucesió divergete
