γ * = D para mostrar el comportamiento de cada
|
|
|
- María Isabel Castellanos Torres
- hace 7 años
- Vistas:
Transcripción
1 "FÓRMULAS PARA CUANTIFICAR EL ARRASTRE EN LA CAPA DE FONDO" JOSÉ ANTONIO MAZA ÁLVAREZ Prf., Diviión de Etudi de Pgrad de la Fa. De Ing., UNAM Gerente de Etudi de Ingeniería Civil, CFE Méxi, D. F. RAFAEL VAL SEGURA Té Aadémi, Intitut de Ingeniería, UNAM Méxi, D. F. TEMA: HIDRÁULICA FUNDAMENTAL RESUMEN En ete trabaj e muetran la prinipale fórmula que han id prpueta para predeir el arratre en la apa de fnd. Tda ella e preentan prurand repetar la expreión riginal del autr, n bjet de que ete erit irva también m un prntuari de ete tip de fórmula. Ademá e explia el ignifiad y valr de ada variable; para que la euaine puedan er apliada. Pr tra parte, e han eleinad d parámetr g g adimeninale G = U y RS τ γ = D para mtrar el mprtamient de ada expreión y la diferenia má imprtante entre l reultad de la fórmula preentada.. INTRODUCCIÓN En l rí y anale e tranprta agua y ediment. Et e enuentran en el fnd y rilla pueden prvenir del lavad de la partíula má fina de la uena. Al tener en mente úniamente al material del fnd, e puede hablar de d frma de tranprte: el que urre en la eranía del fnd, denminad arratre en la apa de fnd, y el que e tranprtad en upenión, entre la frntera uperir de ea apa y la uperfiie del agua. Para uantifiar el tranprte del material del fnd, l métd que e han prpuet e pueden agrupar de tre frma ditinta: en el primer etán l que ól permiten btener el tranprte en la apa de fnd, denminad g ; en el egund l que irven para valuar el tranprte ttal del fnd, denminad g T, eparand g del que e tranprtad en upenión y que e deigna m g S ; n l que e umple que g T = g + g S ; y pr últim, en el terer grup etán l que valuan g T en njunt, in eparar u mpnente. Se ha meninad que exiten vari métd para alular l diferente tip de tranprte, uand n una la euaión, para ada tip, ería ufiiente. Ell e debe al aráter eminentemente empíri de la hidráulia fluvial, y a la falta de preiión de l dat, bre td g ; ea falta de preiión urre tant en el labratri m en la mediine de amp. En 90, Eintein etableió que la apa de fnd tiene un eper igual a d vee el diámetr de la partíula. Pterirmente tr autre han prpuet epere diferente. De ualquier manera, al tratar n el arratre dentr de ea apa, e hae referenia a tda la partíula que ruedan e arratran, aún n pequeñ alt, era del fnd.
2 En ete trabaj e preentan la euaine de l prinipale métd que e han prpuet para uantifiar uniamente el arratre en la apa de fnd g. El ner g e neeari para etimar el tiemp de llenad de prea derivadra, etudiar la etabilidad de aue, para analizar ndiine de erión y edimentaión en tram de rí, uand en ell la velidad de la rriente e baja el material del fnd e grue. A ntinuaión e muetran la prinipale fórmula de arratre en la apa de fnd que e meninan en la bibligrafía epeializada, repetand la frma en que ella fuern preentada pr u autre. Cn bjet de que puedan er utilizada, e india el ignifiad de l parámetr que en ella intervienen y u expreión para alularl.. FÓRMULAS PARA OTENER EL ARRASTRE UNITARIO EN LA CAPA DE FONDO En tda ella g e exprea en kgf/ m a. DUOYS Y STRAU (879, 9). ( γ γ) τ ( τ τ ) g = D Se utiliza D = D 0, y e aplia i τ.0 b. SHOCKLITSCH (9, 90) ( ) g = 00 S qs. x 0 D / 7/ / 7/8 Utiliza D = D 0, y e aplia para ualquier τ. SHIELDS (9) ( τ τ ) g = 0UdS /D Utiliza D = D 0, y e aplia i τ 0. para C a = 9 y τ 0.7 para C a = 8. d. MEYER-PETER Y MÜLLER (98) ( ) ( ) [ τ ] g = 8 g D n'/n 0.07 γ 0.. Utiliza n D = D m, y e aplia para ualquier τ e. KALINSKE (97) τ τ g = γ U D[ f ( τ / τ ) ] Utiliza D = D 0. La funión f ( τ / τ ) vale / f( τ τ ) τ τ / / f( τ τ ) / τ τ f( τ τ ) / / f. LEVI (98). 0. ( ) [ ( ) ] g = 0.00γ U U U / g d D Utiliza D = D m. U e la velidad rítia de la partíula y vale.
3 /7 ( ) ( L d/7d) U =. gd D /D + Sbreetima g uand n 0.0 aprximadamente. g. EINSTEIN 9, EINSTEIN Y ROWN (90) g) EINSTEIN 9 máx ( ) [ τ ] g =.Fγ g D exp 0.9/ n 0. Utiliza D = D 0, y e válida uand 0.0 τ 0.9 g) EINTEIN-ROWN ( g D ) g = 0Fγ τ 0. Utiliza D = D 0, y e válida uand 0.9 τ.0 h. SATO, KIKKAWA Y ASHIDA (98) ( τ τ ) g = U Utiliza D = D m, y e válida uand n 0.0 ( τ τ )( ) g U /0n = E válida uand 0.0 n 0.00 i. ROTTNER (99) ( ) ( ). [ ] [ ] ( ) ( ) g = γ g d 0.7D/d U/ g d.7d/d 0. / 0. / Utiliza D = D m. E la únia fórmula en que g n depende de τ, baj ninguna ndiión rítia de arratre. j. GARDE Y ALERTSON (9) N e muetra pr requerir de una familia de urva para u apliaión. E válida uand 0.08 τ 0. y 8 U U. k. FRIJLINK (9) 0. ( ) [ ] g = γ D µ gds exp0.7/ µτ Utiliza D = D 0, y e válida para ualquier τ. YALIN (9) [ ] ( γ γ ) /a S Ln( a S ) g = 0.S D U + y y y y y Utiliza D = D m, y e válida para ualquier τ ( ) ay =. τ γ / γ ; Sy = τ m. PERNECKER y VOLLMER (9) 0.. ( ) τ ( τ ) g = g g D Utiliza D = D m, y e válida para τ.0 n. INGLIS Y LACEY (98) ( ) g = 0.γ U ν / ω dg / / Utiliza D = D m, y e aplia para τ 0. para C a = 9 y τ 7.0 para C a = 8.. OGARDI (979) ( ) g = 99γ U g D τ Utiliza D = D m, y e aplia uand τ.0. SIGNIFICADO DE LAS VARIALES 0..
4 γ, pe epeífi del agua, en kgf/m ; γ, pe epeífi de la partíula, en kgf/m ;, denidad relativa de la partíula umergida (e btiene de la relaión = (γ - γ)/γ); ν, viidad inemátia del agua, en m /; S, pendiente de la pérdida de arga; d, tirante prfundidad del fluj, en m; U, velidad media de la rriente, en m/; q, gat unitari líquid, en m /.m (e btiene de la relaión q = Ud); g, aeleraión debida a la gravedad, en m/ ; D, diámetr de la partíula, en m; D m, diámetr medi del njunt de partíula, en m( e btiene de la relaión D m = 0.0 (D i p i ); D i, diámetr de la partíula tal que el i% de la muetra e menr que ee tamañ, en m; p i fraión, n repet al ttal de la muetra de partíula, n diámetr D i, e exprea en frma deimal; D máx, diámetr máxim en el material del fnd, en m; ω, velidad de aída de la partíula, en m/ (e btiene de la reaión ω = F (g D) 0. ); F, efiiente de Rubey que e utiliza en u fórmula de la v v velidad de aída (e btiene de la relaión F = + ; τ, g D g D efuerz rtante riti que el fluj ejere en el fnd, en kgf/m (e btiene de la relaión ( ) τ = γ ds ; τ, númer adimeninal de Shield aiad a τ (e btiene de la relaión τ = ds/ D); τ, númer adimeninal de Shield para la ndiión rítia (e btiene de la relaión τ = exp ; uand. D. Para D, D D τ = 0.0; D, númer adimeninal de la partíula (e btiene de la relaión D = D [ ] g /v / ) ; τ efuerz rtante ríti en el fnd para iniiar el mvimient de la partíula (e btiene de la relaión τ = (γ - γ)d τ )n, efiiente de rugidad egún Manning (e btiene de la relaión n = d / S / /U); n', efiiente de rugidad egún Manning aiad a la partíula (e btiene de la relaión n' = D 90 /); µ, efiiente que relaina efiiente de rugidad (e btiene de la relaión µ = C'/C); C, efiiente de rugidad egún Chezy, en m / /, (e btiene de la relaión C = ds/u);c' efiiente de rugidad egún Chezy aiad a la partíula, en m / /, (e btiene de la relaión C = 8 lg (d/d 90 ); C a, efiiente adimeninal de Chezy (e btiene de la relaión C a = C g). En tda la fórmula g e el arratre unitari en la apa de fnd, en kgf/ m.. ANÁLISIS DE LOS MÉTODOS Para viualizar la tendenia de l diferente métd derit y mtrar la direpania que hay entre ell, tda la fórmula preentada e nvirtiern a una relaión, uand men, entre l iguiente númer adimeninale. G = gg / γ U y τ = ds/ D Al efetuar dih ambi de variable, algun de l métd requiriern de tr númer adimeninal adiinal m: n'/n, C a S. Para tmar en uenta ee terer parámetr adimeninal e eleinarn d efiiente de rugidad de Manning n = 0.08 y n 0 = En la fig a e muetran la /
5 urva btenida para τ - G y n = 0.08 y en la fig b, τ ntra G para n = 0.0. En diha figura ól e enuentran algun de l métd. Del análii efetuad y en la figura eñala e berva que l diferente métd e pueden agrupar de la iguiente manera: a) Métd en que G, y pr tant g, ól e funión de τ. Cumplen eta ndiión l de Duby y Straub, Kalinke, Eintein (9), Eintein y rwn (90), Sat et al (uand n > 0.0), Yalin, Perneker y Vllmer, y gardi. Dada la gemetría de la eión, pendiente y la prpiedade del agua y de l ediment del fnd, el arratre en la apa de fnd e independiente de la rugidad ttal del aue y pr ende de la velidad. Eta limitaión hae que l métd e apliquen n reerva. b) Métd en que G e funión de τ y C a. Dentr de ete grup etán l de Shield, Meyer-Peter y Müller (en funión de Cá/Ca), Sat et al (uand n > 0.0), y Frijlink (en funión de Cá/Ca). ) Métd en que G e funión de τ, C a y d/d. Caen dentr de ete grup l de Levi e Ingli Laey. d) Métd en l que G e funión de τ, C a y S. Cumple n eta ndiión úniamente el métd de Shklith. e) Pr últim, métd en que G n e funión de τ. Dentr de ete grup l etá el métd de Rttner; en él, G e l funión de C a. Puet que ademá ubvalua a g e un métd que n e remienda utilizar. Pr tra parte, uand τ > 0.8. e preenta régimen uperir y l métd e pueden agrupar de uatr frma ditinta. ) Aquell en que G Aτ U (A y n ntante para el material y el agua). Et métd dan el tranprte ttal del fnd y n el arratre en la apa del fnd, y pr tant, n e pueden uar para ete prpóit. Dentr de ete grup e enuentran l de: Duy, Shield (para τ > 0.), Perneker y Vllmer, Ingli y Laey, y gardi. ) Aquell en que G ya n depende de τ ; e deir G A U. Sn válid para btener el arratre en la apa de fnd. Dentr de ete grup etán l de: Meyer-Peter y Müller, Sat et al, Kikkawa y Ahida, Rttner, y Yalin. ) Aquell en que G Aτ U. También n válid para btener g, aunque dan valre menre que l del egund grup. Ea diferenia e tant mayr uant mayr e τ, Caen dentr de ete grup l de: Kalinke y Frijlink. ) L que n iguen alguna de la ndiine eñalada; ell n: Shklith, Levi (brevalúa uand n e reduida, n < 0.), y Eintein y rwn (l aplia i τ <.0)
6 Pr últim e pueden meninar aquell métd en que n e limita el tranprte de ediment pr debaj de la ndiión rítia de arratre; e deir, que indian tranprte de ediment para ualquier velidad del fluj, pr reduida que ella ea. L métd que tienen eta limitaión n l de Rttner, Ingli y gardi. Al utilizar et métd primer e debe ner la ndiión rítia de arratre. Gx Gx gardi Ingli y Laey Shield Perneker y Vllmer Duy y Straub Yalin Sat, Kikkawa y Ahida Frijlink Rttner a) b) Fig Repreentaión gráfia de alguna euaine de arratre en la apa de fnd, en el plan G - τ, y d valre del efiiente de rugidad de Manning.
SOLUCIÓN: DETERMINAR: Pérdidas totales en el hierro: P 0, Densidad del hierro ( fe): 7800 Kg/m 3
 niversidad de Ovied Dpt de ngeniería Elétria EJERO Nº TEMA V: Transfrmadres mnfásis OBJETVOS: Revisión nepts básis eletrmagnetism: induión, intensidad de amp magnéti, urva BH et, análisis detallad pérdidas
niversidad de Ovied Dpt de ngeniería Elétria EJERO Nº TEMA V: Transfrmadres mnfásis OBJETVOS: Revisión nepts básis eletrmagnetism: induión, intensidad de amp magnéti, urva BH et, análisis detallad pérdidas
ANEJO 7: CÁLCULO DEL CONTENIDO DE AGUA DE LAS MUETRAS DE SUELO
 ANEJO 7: CÁLCULO DEL CONTENIDO DE AGUA DE LAS UETRAS DE SUELO I 1. INTRODUCCIÓN A cntinuación e expndrán l cncept neceari para el cálcul del grad de aturación de la muetra, para el ca de lucine de epmita.
ANEJO 7: CÁLCULO DEL CONTENIDO DE AGUA DE LAS UETRAS DE SUELO I 1. INTRODUCCIÓN A cntinuación e expndrán l cncept neceari para el cálcul del grad de aturación de la muetra, para el ca de lucine de epmita.
TEMA 20 : Transporte de materiales (II)
 TEMA 0 : Tranporte de materiale (II) JOSÉ LUIS GARCÍA RODRÍGUEZ UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES UNIVERSIDAD POLITÉCNICA DE MADRID
TEMA 0 : Tranporte de materiale (II) JOSÉ LUIS GARCÍA RODRÍGUEZ UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES UNIVERSIDAD POLITÉCNICA DE MADRID
ANÁLISIS Y SÍNTESIS DE CIRCUITOS PROBLEMAS TEMA 3
 ANÁLISIS Y SÍNTESIS DE CICUITOS POBLEMAS TEMA 3 Análii y Síntei de Circuit. Prblema Tema 3 1 POBLEMA 1 Obtener la función de tranferencia de l iguiente circuit: Análii y Síntei de Circuit. Prblema Tema
ANÁLISIS Y SÍNTESIS DE CICUITOS POBLEMAS TEMA 3 Análii y Síntei de Circuit. Prblema Tema 3 1 POBLEMA 1 Obtener la función de tranferencia de l iguiente circuit: Análii y Síntei de Circuit. Prblema Tema
Análisis del lugar geométrico de las raíces
 Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el itema tiene una ganania
Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el itema tiene una ganania
Lugar geométrico de las raíces
 Lugar geométrio de la raíe Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si
Lugar geométrio de la raíe Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si
6. CONTROL PID CLÁSICO. Consideremos el siguiente lazo de control SISO:
 6. CONROL PI CLÁSICO 6. Etructura PI Crrepnde a la etructura de cntrl ma uada en el medi indutrial. La letra PI crrepnden a la accine: Prprcinal, Integral y erivativa. Su implicidad limita el rang de la
6. CONROL PI CLÁSICO 6. Etructura PI Crrepnde a la etructura de cntrl ma uada en el medi indutrial. La letra PI crrepnden a la accine: Prprcinal, Integral y erivativa. Su implicidad limita el rang de la
Dadas las siguientes ecuaciones algebraicas, observe si es posible expresarlas en la forma: 1 K
 Trabaj práctic Nº 5 Ejercici Dada la iguiente ecuacine algebraica, berve i e pible exprearla en la frma: 0 c) k 3 0 b) 3 3 k k 0 ( 4) ( k) 0 d) ( k) ( 3) 0 En ca afirmativ: Halle la cnfiguracine de pl
Trabaj práctic Nº 5 Ejercici Dada la iguiente ecuacine algebraica, berve i e pible exprearla en la frma: 0 c) k 3 0 b) 3 3 k k 0 ( 4) ( k) 0 d) ( k) ( 3) 0 En ca afirmativ: Halle la cnfiguracine de pl
MACROECONOMÍA AVANZADA Ejercicio 1: 17 DE OCTUBRE DE º GECO, Itinerario Análisis Económico, Profs. LUIS PUCH y JESÚS RUIZ APELLIDOS:
 MACROECONOMÍA AVANZADA Ejeriio : 7 DE OCTUBRE DE 06. 4º GECO, Itinerario Análii Eonómio, Prof. LUIS PUCH JESÚS RUIZ APELLIDOS: NOMBRE: GRUPO: El ejeriio onta de do parte. La primera e un tet de 6 pregunta.
MACROECONOMÍA AVANZADA Ejeriio : 7 DE OCTUBRE DE 06. 4º GECO, Itinerario Análii Eonómio, Prof. LUIS PUCH JESÚS RUIZ APELLIDOS: NOMBRE: GRUPO: El ejeriio onta de do parte. La primera e un tet de 6 pregunta.
TEMA 21 : Transporte de materiales (III)
 TEMA : Tranporte e materiale (III JOSÉ LUIS GARCÍA RODRÍGUEZ UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES UNIVERSIDAD POLITÉCNICA DE MADRID
TEMA : Tranporte e materiale (III JOSÉ LUIS GARCÍA RODRÍGUEZ UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES UNIVERSIDAD POLITÉCNICA DE MADRID
CAPÍTULO 2 TEMAS DE DINÁMICA INCLUIDOS
 CAPÍTULO TEMAS DE DINÁMICA INCLUIDOS.1. CONCEPTOS DE DINÁMICA ESTRUCTURAL Dede el punto de vita de la ingeniería ímia, el tema entral de la dinámia e etudiar y entender la vibraión de una etrutura uando
CAPÍTULO TEMAS DE DINÁMICA INCLUIDOS.1. CONCEPTOS DE DINÁMICA ESTRUCTURAL Dede el punto de vita de la ingeniería ímia, el tema entral de la dinámia e etudiar y entender la vibraión de una etrutura uando
CAPÍTULO 3 ESTADO DEL ARTE 3. ESTADO DEL ARTE 9
 ESTADO DEL ATE. ESTADO DEL ATE 9 ESTADO DEL ATE.1. FOMULACIÓN PAA LA PEDICCIÓN DE EBASE La primera frmulaine de rebae empezarn a apareer en la egunda mitad del igl XX. A ntinuaión reviarem algun de l autre
ESTADO DEL ATE. ESTADO DEL ATE 9 ESTADO DEL ATE.1. FOMULACIÓN PAA LA PEDICCIÓN DE EBASE La primera frmulaine de rebae empezarn a apareer en la egunda mitad del igl XX. A ntinuaión reviarem algun de l autre
CAPÍTULO VII CABLES. Figura 7.1. Cable con cargas concentradas.
 PÍULO VII LES 7.1 ables on argas onentradas Sea un able fleible de peso despreiable. ualquier tramo del able entre dos puntos de apliaión de fuerzas onentradas puede onsiderarse omo un elemento sometido
PÍULO VII LES 7.1 ables on argas onentradas Sea un able fleible de peso despreiable. ualquier tramo del able entre dos puntos de apliaión de fuerzas onentradas puede onsiderarse omo un elemento sometido
2006 Avances en la Investigación Científica en el CUCBA
 26 Avance en la Invetigación Científica en el CUCBA 16 ISBN 97-27-145-6 EVALUACIÓN DE COMBINACIÓN DE SUSTRATOS EN TRES CICLOS DE CULTIVO BAJO EL SISTEMA DE SIEMBRA EARTH BOXES DEL PROYECTO THE GROWING
26 Avance en la Invetigación Científica en el CUCBA 16 ISBN 97-27-145-6 EVALUACIÓN DE COMBINACIÓN DE SUSTRATOS EN TRES CICLOS DE CULTIVO BAJO EL SISTEMA DE SIEMBRA EARTH BOXES DEL PROYECTO THE GROWING
Hidráulica de canales
 Laboratorio de Hidráulia Ing. David Hernández Huéramo Manual de prátias Hidráulia de anales o semestre Autores: Guillermo Benjamín Pérez Morales Jesús Alberto Rodríguez Castro Jesús Martín Caballero Ulaje
Laboratorio de Hidráulia Ing. David Hernández Huéramo Manual de prátias Hidráulia de anales o semestre Autores: Guillermo Benjamín Pérez Morales Jesús Alberto Rodríguez Castro Jesús Martín Caballero Ulaje
ANTECEDENTES PARA CÁLCULO DE VIGAS EN PANEL COVINTEC
 ANTECEDENTES PARA CÁLCULO DE IGAS EN PANEL COINTEC Anteedente de Cálulo para iga en Panele Covinte iga Geometría: Fig. 1 Nomenlatura: h: altura total de la viga h : altura del hormigón o mortero uperior
ANTECEDENTES PARA CÁLCULO DE IGAS EN PANEL COINTEC Anteedente de Cálulo para iga en Panele Covinte iga Geometría: Fig. 1 Nomenlatura: h: altura total de la viga h : altura del hormigón o mortero uperior
CAPITULO 2 CONTROLADORES PID
 CAPITULO CONTROLADORES PID. INTRODUCCIÓN El ontrol automátio de un roeo requiere de un itema que ajute automátiamente una variable del roeo ara mantener otra dentro de límite etableido. Una de la forma
CAPITULO CONTROLADORES PID. INTRODUCCIÓN El ontrol automátio de un roeo requiere de un itema que ajute automátiamente una variable del roeo ara mantener otra dentro de límite etableido. Una de la forma
CONCEPTOS DE CINÉTICA ELECTROQUÍMICA
 COOSIÓN (Ingeniería Químia) TEMA 3 Tema 3: CONCEPTOS DE CINÉTICA ELECTOQUÍMICA Ley de Faraday Apeto termodinámio báio de la reaione eletroquímia: Euaión de Nernt Conepto báio de inétia eletroquímia: Euaión
COOSIÓN (Ingeniería Químia) TEMA 3 Tema 3: CONCEPTOS DE CINÉTICA ELECTOQUÍMICA Ley de Faraday Apeto termodinámio báio de la reaione eletroquímia: Euaión de Nernt Conepto báio de inétia eletroquímia: Euaión
Asignatura: Horas: Total (horas): Obligatoria Teóricas 3.0 Semana 3.0 Optativa X Prácticas Semanas 48.0
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO POSGRADO EN INGENIERÍA PROGRAMA DE ESTUDIO HIDRÁULICA FLUVIAL 2 06 Asignatura Clave Semestre Créditos Facultad e Instituto de Ingeniería Ingeniería Civil (Hidráulica)
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO POSGRADO EN INGENIERÍA PROGRAMA DE ESTUDIO HIDRÁULICA FLUVIAL 2 06 Asignatura Clave Semestre Créditos Facultad e Instituto de Ingeniería Ingeniería Civil (Hidráulica)
7. Amplificadores RF de potencia
 7. Amplificadre RF de ptencia 7. ntrducción El amplificadr de ptencia (PA e la última etapa del emir. Tiene la miión de amplificar la ptencia de la eñal (n neceariamente la tenión y tranmitirla a la antena
7. Amplificadre RF de ptencia 7. ntrducción El amplificadr de ptencia (PA e la última etapa del emir. Tiene la miión de amplificar la ptencia de la eñal (n neceariamente la tenión y tranmitirla a la antena
ENSAYO MEDICIÓN NACIONAL Matemática IIº medio Julio 2013
 ENSAYO MEDICIÓN NACIONAL Matemátia IIº medio Julio 0 Ante de omenzar la prueba, lee la iguiente intruione: INSTRUCCIONES Trata de ontetar toda la pregunta de la prueba, inluo i no etá totalmente eguro
ENSAYO MEDICIÓN NACIONAL Matemátia IIº medio Julio 0 Ante de omenzar la prueba, lee la iguiente intruione: INSTRUCCIONES Trata de ontetar toda la pregunta de la prueba, inluo i no etá totalmente eguro
Diego Luis Aristizábal R., Roberto Restrepo A. Profesores, Escuela de Física de la Universidad Nacional de Colombia Sede Medellín
 UNIVRSIDAD NACIONAL D COLOMIA SD MDLLÍN FACULTAD D CINCIAS-SCULA D FÍSICA FÍSICA D OSCILACIONS ONDAS Y ÓPTICA MÓDULO # 19: L SPCTRO LCTROMAGNÉTICO TORÍA CLÁSICA- Dieg Lui Aritizábal R., Rbert Retrep A.
UNIVRSIDAD NACIONAL D COLOMIA SD MDLLÍN FACULTAD D CINCIAS-SCULA D FÍSICA FÍSICA D OSCILACIONS ONDAS Y ÓPTICA MÓDULO # 19: L SPCTRO LCTROMAGNÉTICO TORÍA CLÁSICA- Dieg Lui Aritizábal R., Rbert Retrep A.
El estudio teórico de la práctica se realiza en el problema PTC
 PRÁCTICA LTC-1: REFLEXIONES EN UN PAR TRENZADO 1.- Decripción de la práctica a) Excitar un cable de pare de 50 metro de longitud con un pulo de tenión de 0 a 10 voltio, 100 Khz frecuencia y un duty cycle
PRÁCTICA LTC-1: REFLEXIONES EN UN PAR TRENZADO 1.- Decripción de la práctica a) Excitar un cable de pare de 50 metro de longitud con un pulo de tenión de 0 a 10 voltio, 100 Khz frecuencia y un duty cycle
Controles de Calidad en la Fabricación de un Rodete Pelton. Murray Garcia, Harry Ernesto CAPITULO II MARCO TEORICO
 CAPITULO II MARCO TEORICO Reordemos que las Turbinas Pelton son Turbinas de Aión, y son apropiadas para grandes saltos y pequeños audales; por lo ual sus números espeífios son bajos. Referente a las partes
CAPITULO II MARCO TEORICO Reordemos que las Turbinas Pelton son Turbinas de Aión, y son apropiadas para grandes saltos y pequeños audales; por lo ual sus números espeífios son bajos. Referente a las partes
1 Introducción. Tema B: Hidrología y Gestión del Agua
 Evaluaión de lo fatore que originan eroión hídria y tranporte de edimento en parela agríola ubiada en la uena del río Chirgua Venezuela Márquez Adriana, Guevara Edilberto Ingeniero Civil-MS Ingeniería
Evaluaión de lo fatore que originan eroión hídria y tranporte de edimento en parela agríola ubiada en la uena del río Chirgua Venezuela Márquez Adriana, Guevara Edilberto Ingeniero Civil-MS Ingeniería
5.1 CONTROL DE CORRIENTE DE PICO. Capítulo 5
 Capítulo 5 Análii de pequeña eñal de lo potreguladore de alto rendimiento (III). Apliaión del ontrol modo orriente de pio a lo pot-reguladore de alto rendimiento En ete apitulo e va a realizar el análii
Capítulo 5 Análii de pequeña eñal de lo potreguladore de alto rendimiento (III). Apliaión del ontrol modo orriente de pio a lo pot-reguladore de alto rendimiento En ete apitulo e va a realizar el análii
DISEÑO A TORSIÓN ESTRUCTURAS DE HORMIGÓN 2
 DISEÑO A ORSIÓN ESRUCURAS DE HORMIGÓN 8. DISEÑO A ORSION DEL HORMIGÓN ARMADO 8.1 Intrduión Un mment que atúa alrededr del eje lngitudinal de un element etrutural e denmina mment trr trque y e denta n la
DISEÑO A ORSIÓN ESRUCURAS DE HORMIGÓN 8. DISEÑO A ORSION DEL HORMIGÓN ARMADO 8.1 Intrduión Un mment que atúa alrededr del eje lngitudinal de un element etrutural e denmina mment trr trque y e denta n la
II CONGRESO NACIONAL DE RIEGO Y DRENAJE COMEII 2016
 Artíul: COMEII-16054 II CONGRESO NACIONAL DE RIEGO Y DRENAJE COMEII 016 Caping, Ed. de Méxi, del 08 al 10 de eptiembre MODELACIÓN EN RÉGIMEN PERMANENTE DE POZOS DE INFILTRACIÓN EN SUELOS ESTRATIFICADOS
Artíul: COMEII-16054 II CONGRESO NACIONAL DE RIEGO Y DRENAJE COMEII 016 Caping, Ed. de Méxi, del 08 al 10 de eptiembre MODELACIÓN EN RÉGIMEN PERMANENTE DE POZOS DE INFILTRACIÓN EN SUELOS ESTRATIFICADOS
Laboratorio 4. Piezoelectricidad.
 Laboratorio 4. Piezoelectricidad. Objetivo Analizar el comportamiento de un material piezoeléctrico ometido a un campo eléctrico de frecuencia variable. Etudiar el modelo eléctrico equivalente, determinado
Laboratorio 4. Piezoelectricidad. Objetivo Analizar el comportamiento de un material piezoeléctrico ometido a un campo eléctrico de frecuencia variable. Etudiar el modelo eléctrico equivalente, determinado
El estudio teórico de la práctica se realiza en el problema PTC0004-21
 PRÁCTICA LTC-14: REFLEXIONES EN UN CABLE COAXIAL 1.- Decripción de la práctica a) Excitar un cable coaxial de 50 metro de longitud con un pulo de tenión de 0 a 10 voltio, 100 Khz frecuencia y un duty cycle
PRÁCTICA LTC-14: REFLEXIONES EN UN CABLE COAXIAL 1.- Decripción de la práctica a) Excitar un cable coaxial de 50 metro de longitud con un pulo de tenión de 0 a 10 voltio, 100 Khz frecuencia y un duty cycle
Práctica 5: Control de Calidad
 Práctica 5: Control de Calidad Objetivo epecífico Al finalizar eta práctica deberá er capaz de: Contruir lo gráfico de control para la media, la deviación típica y el rango (gráfico de control por variable).
Práctica 5: Control de Calidad Objetivo epecífico Al finalizar eta práctica deberá er capaz de: Contruir lo gráfico de control para la media, la deviación típica y el rango (gráfico de control por variable).
Laboratorio 4. Piezoelectricidad.
 Laboratorio 4. Piezoelectricidad. Objetivo Analizar el comportamiento de un material piezoeléctrico ometido a un campo eléctrico de frecuencia variable. Etudiar el modelo eléctrico equivalente, determinado
Laboratorio 4. Piezoelectricidad. Objetivo Analizar el comportamiento de un material piezoeléctrico ometido a un campo eléctrico de frecuencia variable. Etudiar el modelo eléctrico equivalente, determinado
ANTECEDENTES PARA CÁLCULO DE LOSAS EN PANEL COVINTEC
 ANTECEDENTES PARA CÁLCULO DE LOSAS EN PANEL COVINTEC Anteedente de Cálulo para Loa en Panele Covinte Loa Geometría: Fig. 1. Nomenlatura : h: altura total de la loa h : altura del hormigón uperior h i :
ANTECEDENTES PARA CÁLCULO DE LOSAS EN PANEL COVINTEC Anteedente de Cálulo para Loa en Panele Covinte Loa Geometría: Fig. 1. Nomenlatura : h: altura total de la loa h : altura del hormigón uperior h i :
SOLUCIONES DE LOS EJERCICIOS DE LA OLIMPIADA DEL FASE LOCAL
 SOLUCIONES DE LOS EJERCICIOS DE LA OLIMIADA DEL 1. FASE LOCAL ución ejercicio nº 1 Una plataforma circular, colocada horizontalmente, gira con una frecuencia de vuelta por egundo alrededor de un eje vertical
SOLUCIONES DE LOS EJERCICIOS DE LA OLIMIADA DEL 1. FASE LOCAL ución ejercicio nº 1 Una plataforma circular, colocada horizontalmente, gira con una frecuencia de vuelta por egundo alrededor de un eje vertical
Hidráulica de canales
 Laboratorio de Hidráulia In. David Hernández Huéramo Manual de prátias Hidráulia de anales 5o semestre Autores: Guillermo enjamín Pérez Morales Jesús Alberto Rodríuez Castro Jesús Martín Caballero Ulaje
Laboratorio de Hidráulia In. David Hernández Huéramo Manual de prátias Hidráulia de anales 5o semestre Autores: Guillermo enjamín Pérez Morales Jesús Alberto Rodríuez Castro Jesús Martín Caballero Ulaje
CONJUNTOS. Según se ha visto en el ejercicio anterior, para que la intersección de dos conjuntos A y B sea A, se tiene que verificar que A B.
 CONJUNTOS 1. Si se umple: a) = b) = ) = (Convoatoria junio 2001. Examen tipo E ) Es laro que la opión orreta es la a). Cuando un onjunto está dentro de otro, la interseión es el onjunto pequeño y la unión
CONJUNTOS 1. Si se umple: a) = b) = ) = (Convoatoria junio 2001. Examen tipo E ) Es laro que la opión orreta es la a). Cuando un onjunto está dentro de otro, la interseión es el onjunto pequeño y la unión
INGENIERIA DE SISTEMAS Y AUTOMATICA Calcular las antitransformadas de Laplace de las siguientes funciones: - +
 . Concepto báico.. Calcular la antitranformada de Laplace de la iguiente funcione: a) b) c) F ( ) F ( ) F ( ) ( ) 3 ( ) 3 ( )( 6 34).. Encontrar la función de tranferencia M()Y()/X() mediante la implificación
. Concepto báico.. Calcular la antitranformada de Laplace de la iguiente funcione: a) b) c) F ( ) F ( ) F ( ) ( ) 3 ( ) 3 ( )( 6 34).. Encontrar la función de tranferencia M()Y()/X() mediante la implificación
FILTROS ACTIVOS CAPÍTULO 3
 FILTOS TIOS PÍTULO ealización ctiva en Matlab. Filtro ctivo. Lo filtro activo también tienen en u configuracione elemento paivo como capacitore, reitencia y elemento activo como el mplificador Operacional,
FILTOS TIOS PÍTULO ealización ctiva en Matlab. Filtro ctivo. Lo filtro activo también tienen en u configuracione elemento paivo como capacitore, reitencia y elemento activo como el mplificador Operacional,
SR(s)=R(s) + E(s) C(s)
 TEMA: EO EN ÉGIMEN PEMANENTE Un apecto importante a tener en cuenta e el comportamiento de un itema ante divera entrada en régimen permanente. En cualquier itema fíico de control exite un error inherente,
TEMA: EO EN ÉGIMEN PEMANENTE Un apecto importante a tener en cuenta e el comportamiento de un itema ante divera entrada en régimen permanente. En cualquier itema fíico de control exite un error inherente,
ESTADÍSTICA RELACIÓN 1: VARIABLES ESTADÍSTICAS UNIDIMENSIONALES.
 ESTADÍSTICA CURSO 2011/12 RELACIÓN 1: VARIABLES ESTADÍSTICAS UNIDIMENSIONALES. 1.- L pe de 150 recién nacid (PRN) aí cm el nivel educativ de la madre (NE) y el númer de part anterire (PA) e agrupan en
ESTADÍSTICA CURSO 2011/12 RELACIÓN 1: VARIABLES ESTADÍSTICAS UNIDIMENSIONALES. 1.- L pe de 150 recién nacid (PRN) aí cm el nivel educativ de la madre (NE) y el númer de part anterire (PA) e agrupan en
EII, MEC. DEL SUELO Y CIMENTACIONES (3º P-98, JULIO 2008) PROBLEMAS. tiempo 1 hora
 EII, ME. DEL SUELO Y IMENTIONES (º P-98, JULIO 8 PROLEMS. tiempo 1 hora pellido y Nombre EJERIIO 1 En el emplazamiento de la figura, e quiere imentar una ontruión on etrutura de hormigón, mediante una
EII, ME. DEL SUELO Y IMENTIONES (º P-98, JULIO 8 PROLEMS. tiempo 1 hora pellido y Nombre EJERIIO 1 En el emplazamiento de la figura, e quiere imentar una ontruión on etrutura de hormigón, mediante una
ESTUDIO DE LAS TEORÍAS DE ARRASTRE DE FONDO SOBRE EL RÍO NEGRO, EN UN TRAMO DE
 ESTUDIO DE LAS TEORÍAS DE ARRASTRE DE FONDO SOBRE EL RÍO NEGRO, EN UN TRAMO DE 100 m AGUAS ARRIBA DEL PUENTE TOBIA LA MONTAÑA, MEDIANTE UN MODELO FÍSICO. ASTRID JULIETH PEÑALOSA OLARTE DIANA CRISTINA ARIAS
ESTUDIO DE LAS TEORÍAS DE ARRASTRE DE FONDO SOBRE EL RÍO NEGRO, EN UN TRAMO DE 100 m AGUAS ARRIBA DEL PUENTE TOBIA LA MONTAÑA, MEDIANTE UN MODELO FÍSICO. ASTRID JULIETH PEÑALOSA OLARTE DIANA CRISTINA ARIAS
AUTÓMATAS Y SISTEMAS DE CONTROL
 º NGENERÍA TELECOMUNCACÓN 2º TT SSTEMAS ELECTRÓNCOS 2º TT SSTEMAS DE TELECOMUNCACÓN AUTÓMATAS Y SSTEMAS DE CONTROL PROBLEMAS DE SSTEMAS PARTE 2: ERRORES EN REG. PERMANENTE LUGAR DE LAS RACES DSEÑO REGULADORES
º NGENERÍA TELECOMUNCACÓN 2º TT SSTEMAS ELECTRÓNCOS 2º TT SSTEMAS DE TELECOMUNCACÓN AUTÓMATAS Y SSTEMAS DE CONTROL PROBLEMAS DE SSTEMAS PARTE 2: ERRORES EN REG. PERMANENTE LUGAR DE LAS RACES DSEÑO REGULADORES
La solución del problema requiere de una primera hipótesis:
 RIOS 9 Cuarto Simpoio Regional obre Hidráulica de Río. Salta, Argentina, 9. CALCULO HIDRAULICO EN RIOS Y DISEÑO DE CANALES ESTABLES SIN USAR ECUACIONES TRADICIONALES Eduardo E. Martínez Pérez Profeor agregado
RIOS 9 Cuarto Simpoio Regional obre Hidráulica de Río. Salta, Argentina, 9. CALCULO HIDRAULICO EN RIOS Y DISEÑO DE CANALES ESTABLES SIN USAR ECUACIONES TRADICIONALES Eduardo E. Martínez Pérez Profeor agregado
Nº de actividad Contenido 1 Calcular la transformada de Laplace, usando calculadora
 Univeridad Diego Portale Primer Semetre 007 Facultad de Ingeniería Intituto de Ciencia Báica Aignatura: Ecuacione Diferenciale Laboratorio Nº 7 Definición de tranformada de Laplace Propiedad de la tranformada
Univeridad Diego Portale Primer Semetre 007 Facultad de Ingeniería Intituto de Ciencia Báica Aignatura: Ecuacione Diferenciale Laboratorio Nº 7 Definición de tranformada de Laplace Propiedad de la tranformada
Fuerza de fricción estática
 Laboratorio de Meánia. Experimento 10 Fuerza de friión etátia Objetivo general Etudiar la fuerza de friión etátia. Objetivo epeífio Determinar lo oefiiente de friión entre diferente pareja de materiale.
Laboratorio de Meánia. Experimento 10 Fuerza de friión etátia Objetivo general Etudiar la fuerza de friión etátia. Objetivo epeífio Determinar lo oefiiente de friión entre diferente pareja de materiale.
ACE Análisis de Circuitos Eléctricos
 Análii de Circuito Eléctrico 010/011 º Ingeniería de Telecomunicación - Ecuela Politécnica Superior Univeridad Autónoma de Madrid ACE Análii de Circuito Eléctrico Práctica Síntei de dipolo. Forma canónica
Análii de Circuito Eléctrico 010/011 º Ingeniería de Telecomunicación - Ecuela Politécnica Superior Univeridad Autónoma de Madrid ACE Análii de Circuito Eléctrico Práctica Síntei de dipolo. Forma canónica
Métodos de Regresión Ciencias y Técnicas Estadísticas Práctica 1. Curso 2007 / 2008
 Método de Regreión Ciencia y Técnica Etadítica Práctica. Curo 2007 / 2008 t-student y Anova F. t-student.. Excel. Se tienen dato experimentale correpondiente a 7 individuo de lo que e ha recogido el valor
Método de Regreión Ciencia y Técnica Etadítica Práctica. Curo 2007 / 2008 t-student y Anova F. t-student.. Excel. Se tienen dato experimentale correpondiente a 7 individuo de lo que e ha recogido el valor
Práctica demostrativa Nº 1 Funciones y series en variable compleja
 Práctica Demotrativa con Matlab 207 Práctica demotrativa Nº Funcione erie en variable compleja Obtener el valor de la iguiente funcione en un punto dado, z 0, a) evaluando la función en el punto, b) calculando
Práctica Demotrativa con Matlab 207 Práctica demotrativa Nº Funcione erie en variable compleja Obtener el valor de la iguiente funcione en un punto dado, z 0, a) evaluando la función en el punto, b) calculando
TEST. EXAMEN DE SISTEMAS ELÉCTRICOS 1 de setiembre de 1999 NOMBRE: 1ª PREGUNTA RESPUESTA 2ª PREGUNTA RESPUESTA 3ª PREGUNTA RESPUESTA
 EXAMEN DE SSTEMAS ELÉCTRCOS de setiembre de 999 TEST ª PREGUNTA RESPUESTA Un iruit magnéti tiene una superfiie transversal S y pérdidas P h. Si se aplia la mitad de rriente y se aumenta la seión del núle
EXAMEN DE SSTEMAS ELÉCTRCOS de setiembre de 999 TEST ª PREGUNTA RESPUESTA Un iruit magnéti tiene una superfiie transversal S y pérdidas P h. Si se aplia la mitad de rriente y se aumenta la seión del núle
Examen final de Cálculo Integral
 xamen final de Cálulo Integral 6 de septiembre de 1 (Soluiones) Cuestiones C 1 Apliando el teorema 1.15 y definiión 1. de los apuntes se onluye inmediatamente que el valor de la integral oinide on la longitud
xamen final de Cálulo Integral 6 de septiembre de 1 (Soluiones) Cuestiones C 1 Apliando el teorema 1.15 y definiión 1. de los apuntes se onluye inmediatamente que el valor de la integral oinide on la longitud
Errores y Tipo de Sistema
 rrore y Tipo de Sitema rror dinámico: e la diferencia entre la eñale de entrada y alida durante el período tranitorio, e decir el tiempo que tarda la eñal de repueta en etablecere. La repueta de un itema
rrore y Tipo de Sitema rror dinámico: e la diferencia entre la eñale de entrada y alida durante el período tranitorio, e decir el tiempo que tarda la eñal de repueta en etablecere. La repueta de un itema
DISEÑO ECONÓMICO DE CARTAS DE CONTROL X ASUMIENDO DISTRIBUCIÓN GAMMA
 DISEÑO ECONÓMICO DE CARTAS DE CONTROL X ASUMIENDO DISTRIBUCIÓN GAMMA I.M. González and E. Vile Ecuela Superior de Ingeniero, Univeridad de Navarra, P. Manuel de Lardizábal, 8 San Sebatián, Epaña. E-mail:
DISEÑO ECONÓMICO DE CARTAS DE CONTROL X ASUMIENDO DISTRIBUCIÓN GAMMA I.M. González and E. Vile Ecuela Superior de Ingeniero, Univeridad de Navarra, P. Manuel de Lardizábal, 8 San Sebatián, Epaña. E-mail:
Apantallamiento magnético
 Apantallamient magnéti María Sledad Nakwaki y Mónia Agüer sle@agr.uba.ar mnagu07@yah.m.ar Labratri5- Marz de 00 Faultad de Cienias Exatas y Naturales Universidad de uens Aires Resumen En el siguiente trabaj
Apantallamient magnéti María Sledad Nakwaki y Mónia Agüer sle@agr.uba.ar mnagu07@yah.m.ar Labratri5- Marz de 00 Faultad de Cienias Exatas y Naturales Universidad de uens Aires Resumen En el siguiente trabaj
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS:
 CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
Aceleración del algoritmo K-NN
 Aceleración del algritm K-NN Günther Rland Universidad Carls III Av. de la Universidad, 30 28911 Leganés (Madrid) g.rland(at)student.tugraz.at RESUMEN En el siguiente trabaj presentaré un algritm K-NN
Aceleración del algritm K-NN Günther Rland Universidad Carls III Av. de la Universidad, 30 28911 Leganés (Madrid) g.rland(at)student.tugraz.at RESUMEN En el siguiente trabaj presentaré un algritm K-NN
CÁLCULO DE CALDERÍN. Autores: Pedro Gea José M. Navalón
 CÁLCULO DE CALDERÍN Autores: Pedro Gea José M. Navalón 1. INTRODUCCIÓN Para determinar el golpe de ariete produido en una instalaión protegida on alderín, en realidad, el problema en su ontexto real se
CÁLCULO DE CALDERÍN Autores: Pedro Gea José M. Navalón 1. INTRODUCCIÓN Para determinar el golpe de ariete produido en una instalaión protegida on alderín, en realidad, el problema en su ontexto real se
2.- Tablas de frecuencias Los datos obtenidos en estadística se organizan en unas tablas, llamadas tablas de frecuencias.
 1º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I TEMA 5.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------------------------------
1º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I TEMA 5.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------------------------------
UPM. la encuesta a. Análisis de Modificado
 Análii de la encueta a egread de mát er de la ETSIT-UPM. Cur 206-7 Unidad de Calidad- ETSIT-U UPM Análii de la encueta a egread de Máterr 206-77 Mdificad el 2 de nviembre de 207 Francica Ra. Análii de
Análii de la encueta a egread de mát er de la ETSIT-UPM. Cur 206-7 Unidad de Calidad- ETSIT-U UPM Análii de la encueta a egread de Máterr 206-77 Mdificad el 2 de nviembre de 207 Francica Ra. Análii de
PARA MEJORAR CARACTERÍSTICAS DE DISEÑO EN FILTROS BICUADRÁTICOS
 EL USO DE LOS SFG PARA MEJORAR ARATERÍSTIAS DE DISEÑO EN FILTROS BIUADRÁTIOS - Lui Abraham Sánchez Gapariano, Joé Joel García Delgado, Arturo Prieto Fuenlabrada 3, Alejandro Díaz Sánchez,3 Intituto Nacional
EL USO DE LOS SFG PARA MEJORAR ARATERÍSTIAS DE DISEÑO EN FILTROS BIUADRÁTIOS - Lui Abraham Sánchez Gapariano, Joé Joel García Delgado, Arturo Prieto Fuenlabrada 3, Alejandro Díaz Sánchez,3 Intituto Nacional
Tema 3. TRABAJO Y ENERGÍA
 Tema 3. TRABAJO Y ENERGÍA Físia, J.. Kane, M. M. Sternheim, Reverté, 989 Tema 3 Trabajo y Energía Cap.6 Trabajo, energía y potenia Cap. 6, pp 9-39 TS 6. La arrera Cap. 6, pp 56-57 . INTRODUCCIÓN: TRABAJO
Tema 3. TRABAJO Y ENERGÍA Físia, J.. Kane, M. M. Sternheim, Reverté, 989 Tema 3 Trabajo y Energía Cap.6 Trabajo, energía y potenia Cap. 6, pp 9-39 TS 6. La arrera Cap. 6, pp 56-57 . INTRODUCCIÓN: TRABAJO
Pruebas de Acceso a Ensen anzas Universitarias Oficiales de Grado (PAEG)
 PAEG junio 016 Propuesta B Matemátias II º Bahillerato Pruebas de Aeso a Ensen anzas Universitarias Oiiales de Grado (PAEG) Matemátias II (Universidad de Castilla-La Manha) junio 016 Propuesta B EJERCICIO
PAEG junio 016 Propuesta B Matemátias II º Bahillerato Pruebas de Aeso a Ensen anzas Universitarias Oiiales de Grado (PAEG) Matemátias II (Universidad de Castilla-La Manha) junio 016 Propuesta B EJERCICIO
4.1 GENERALIDADES DEL ARRASTRE DE SEDIMENTOS
 4. ARRATRE DE EDIMENTO 4.1 GENERALIDADE DEL ARRATRE DE EDIMENTO El material eroionado en una cuenca, parte e arratrado por el flujo y parte e captado por la cobertura vegetal y topografía de la cuenca.
4. ARRATRE DE EDIMENTO 4.1 GENERALIDADE DEL ARRATRE DE EDIMENTO El material eroionado en una cuenca, parte e arratrado por el flujo y parte e captado por la cobertura vegetal y topografía de la cuenca.
UNIVERSIDAD DE SEVILLA
 UNIVERSIDAD DE SEVILLA Ecuela Técnica Superior de Ingeniería Informática PRÁCTICA 4: MUESTREO DE SEÑALES Y DIGITALIZACIÓN Tecnología Báica de la Comunicacione (Ingeniería Técnica Informática de Sitema
UNIVERSIDAD DE SEVILLA Ecuela Técnica Superior de Ingeniería Informática PRÁCTICA 4: MUESTREO DE SEÑALES Y DIGITALIZACIÓN Tecnología Báica de la Comunicacione (Ingeniería Técnica Informática de Sitema
Capítulo 3: Algoritmos Usados por el Generador de Autómatas Finitos Determinísticos
 Capítulo 3: Algoritmo Uado por el Generador de Autómata Finito Determinítico 3.1 Introducción En ete capítulo e preentan lo algoritmo uado por el generador de autómata finito determinítico que irve como
Capítulo 3: Algoritmo Uado por el Generador de Autómata Finito Determinítico 3.1 Introducción En ete capítulo e preentan lo algoritmo uado por el generador de autómata finito determinítico que irve como
Reemplazando la salida C(s) en función de R(s) obtenemos, la expresión para el cálculo del error actuante:
 Cátedra: Sitema de Control Reemplaando la alida C( en función de R( obtenemo, la expreión para el cálculo del error actuante: Ea( = R ( + GH ( ( Ete error actuante, podría coniderare como el que e obtendría
Cátedra: Sitema de Control Reemplaando la alida C( en función de R( obtenemo, la expreión para el cálculo del error actuante: Ea( = R ( + GH ( ( Ete error actuante, podría coniderare como el que e obtendría
INSTRUCCION IV/2003 INFORME COYUNTURA DEL MERCADO DE TRABAJO
 1 INSTRUCCION IV/2003 INFORME COYUNTURA DEL MERCADO DE TRABAJO bervatri cupacinal PROVINCIA DE PONTEVEDRA 1 INSTRUCCION IV/2003 INFORME COYUNTURA DEL MERCADO DE TRABAJO bervatri cupacinal PROVINCIA DE
1 INSTRUCCION IV/2003 INFORME COYUNTURA DEL MERCADO DE TRABAJO bervatri cupacinal PROVINCIA DE PONTEVEDRA 1 INSTRUCCION IV/2003 INFORME COYUNTURA DEL MERCADO DE TRABAJO bervatri cupacinal PROVINCIA DE
SOLUCIONES FÍSICA JUNIO 10 OPCIÓN A
 SOLUCIONES FÍSIC JUNIO 10 OCIÓN 1.- a) Veloidad de esape es la mínima que debe omuniarse a un uerpo, situado en la superfiie de un planeta de masa m p y radio r p, para que salga del ampo gravitatorio.
SOLUCIONES FÍSIC JUNIO 10 OCIÓN 1.- a) Veloidad de esape es la mínima que debe omuniarse a un uerpo, situado en la superfiie de un planeta de masa m p y radio r p, para que salga del ampo gravitatorio.
UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA
 UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA La Universidad Católica de Loja TITULACIÓN INGENIERÍA CIVIL Calibración de una ecuación para el transporte de sedimentos en la Cuenca El Limón, en el Río Zamora Trabajo
UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA La Universidad Católica de Loja TITULACIÓN INGENIERÍA CIVIL Calibración de una ecuación para el transporte de sedimentos en la Cuenca El Limón, en el Río Zamora Trabajo
HIDRÁULICA DE ALCANTARILLAS. Amilkar E. ILAYA AYZA
 HIRÁULICA E ALCANTARILLAS INGENIERÍA SANITARIA II CIV 9 B M.Sc.Ing.. Amilkar Ernesto ILAYA AYZA INTROUCCIÓN En sistemas de alcantarillado el escurrimiento debe ser sin presión para: Evitar el reflujo de
HIRÁULICA E ALCANTARILLAS INGENIERÍA SANITARIA II CIV 9 B M.Sc.Ing.. Amilkar Ernesto ILAYA AYZA INTROUCCIÓN En sistemas de alcantarillado el escurrimiento debe ser sin presión para: Evitar el reflujo de
# La capacidad mínima del condensador de filtro que garantice que el valor de la tensión de rizado está por debajo del máximo admisible.
 Cálculo del condenador de filtro El problema de cálculo del condenador de filtro en cualquiera de lo rectificadore etudiado e, en definitiva, una problema de teoría de circuito cuya reolución emplea cálculo
Cálculo del condenador de filtro El problema de cálculo del condenador de filtro en cualquiera de lo rectificadore etudiado e, en definitiva, una problema de teoría de circuito cuya reolución emplea cálculo
Número Reynolds. Laboratorio de Operaciones Unitarias Equipo 4 Primavera México D.F., 12 de marzo de 2008
 Número Reynold Laboratorio de Operacione Unitaria Equipo 4 Primavera 2008 México D.F., 12 de marzo de 2008 Alumno: Arlette Mayela Canut Noval arlettecanut@hotmail.com Francico Joé Guerra Millán fjguerra@prodigy.net.mx
Número Reynold Laboratorio de Operacione Unitaria Equipo 4 Primavera 2008 México D.F., 12 de marzo de 2008 Alumno: Arlette Mayela Canut Noval arlettecanut@hotmail.com Francico Joé Guerra Millán fjguerra@prodigy.net.mx
Ondas. Velocidad de fase. Velocidad de grupo.
 Onda. Veloidad de ae. Veloidad de rupo. Suponao do onda arónia uya euaione on: iendo, uy pareida a. ( t x) y Ao( t x) y Ao π T Si eta do onda e uperponen π T π π Y A o [ ( t x) + o( t x) ] ( + ) x( + )
Onda. Veloidad de ae. Veloidad de rupo. Suponao do onda arónia uya euaione on: iendo, uy pareida a. ( t x) y Ao( t x) y Ao π T Si eta do onda e uperponen π T π π Y A o [ ( t x) + o( t x) ] ( + ) x( + )
EJERCICIOS RESUELTOS TEMA 5
 Fundaento Quíio 1º Ineniería énia Aríola EJECICIO EUELO EMA 5 1.- A 2 ºC la preión de vapor del éter etílio (C 4 H 1 O) e iual a 44 H. Calular la preión de vapor de una dioluión que ontiene 54 de anilina
Fundaento Quíio 1º Ineniería énia Aríola EJECICIO EUELO EMA 5 1.- A 2 ºC la preión de vapor del éter etílio (C 4 H 1 O) e iual a 44 H. Calular la preión de vapor de una dioluión que ontiene 54 de anilina
CÁLCULO DEL SISTEMA DE PUESTA A TIERRA
 FPP / REV.3 PROYECTO: INGENIERÍA BÁSICA Y TALLE LOCALIZACIÓN Y VÍA ACCESO L POZO TALADRO ESCUELA PROYECTO NO. UNIDAD CÓDIGO L DOCUMENTO PROGRESIVO REVISIÓN HOJA Project No. Unit Document Code Serial No.
FPP / REV.3 PROYECTO: INGENIERÍA BÁSICA Y TALLE LOCALIZACIÓN Y VÍA ACCESO L POZO TALADRO ESCUELA PROYECTO NO. UNIDAD CÓDIGO L DOCUMENTO PROGRESIVO REVISIÓN HOJA Project No. Unit Document Code Serial No.
E s t r u c t u r a s
 t r u c t u r a epartamento de tructura de dificación cuela Técnica Superior de Arquitectura de adrid iagrama de efuerzo de una viga quebrada uo: 4,5 k/m I AA 15/16 12-4-2016 jemplo peo propio: 4,5 k/m
t r u c t u r a epartamento de tructura de dificación cuela Técnica Superior de Arquitectura de adrid iagrama de efuerzo de una viga quebrada uo: 4,5 k/m I AA 15/16 12-4-2016 jemplo peo propio: 4,5 k/m
XXI CONGRESO LATINOAMERICANO DE HIDRAULICA SÃO PEDRO, ESTADO DE SÃO PAULO, BRASIL, OCTUBRE 2004 TRANSPORTE DE SEDIMENTOS EN RIOS Y CANALES
 Hidráulia Fluvial y MarítimaMonferrer IAHR AIPH XXI CONGRESO LATINOAMERICANO DE HIDRAULICA SÃO PEDRO, ESTADO DE SÃO PAULO, BRASIL, OCTUBRE 004 TRANSPORTE DE SEDIMENTOS EN RIOS Y CANALES Julián Aguirre-Pe,
Hidráulia Fluvial y MarítimaMonferrer IAHR AIPH XXI CONGRESO LATINOAMERICANO DE HIDRAULICA SÃO PEDRO, ESTADO DE SÃO PAULO, BRASIL, OCTUBRE 004 TRANSPORTE DE SEDIMENTOS EN RIOS Y CANALES Julián Aguirre-Pe,
Tema 3. Muestreo Aleatorio Estratificado Contenido
 Tema 3. Muetre Aleatri Etratificad teid Defiició, vetaja, cm frmar l etrat, elecció y tació. Etimadre de la media y el ttal. 3 ariaza. Límite de cfiaza. 4 Aigació de la muetra (tamañ de la muetra 5 Muetre
Tema 3. Muetre Aleatri Etratificad teid Defiició, vetaja, cm frmar l etrat, elecció y tació. Etimadre de la media y el ttal. 3 ariaza. Límite de cfiaza. 4 Aigació de la muetra (tamañ de la muetra 5 Muetre
ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES
 CAPITULO 3 ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES 3. INTRODUCCIÓN La etabilidad relativa y la repueta tranitoria de un itema de control en lazo cerrado etán directamente relacionada con la localización
CAPITULO 3 ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES 3. INTRODUCCIÓN La etabilidad relativa y la repueta tranitoria de un itema de control en lazo cerrado etán directamente relacionada con la localización
Reguladores y Redes de Compensación
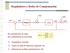 Reguladore y Rede de Compenaión l(t) r(t) e(t) x(t) Reg() G() n(t) y(t) l(t): perturbaión de arga n(t): perturbaión en la medida R ( ) ( + zi ) ( + pi ) Ø Ø Ø Reguladore enillo Seguir la eñal de referenia
Reguladore y Rede de Compenaión l(t) r(t) e(t) x(t) Reg() G() n(t) y(t) l(t): perturbaión de arga n(t): perturbaión en la medida R ( ) ( + zi ) ( + pi ) Ø Ø Ø Reguladore enillo Seguir la eñal de referenia
Comportamiento de Cimentaciones en Suelos Expansivos
 III.- ESTIMACIÓN DE MOVIMIENTOS En a la atualidad existen varis predimients apliables a la prediión del fenómen de expansión y ntraión de las arillas, ests ls pdems lasifiar en tres amplias ategrías: métds
III.- ESTIMACIÓN DE MOVIMIENTOS En a la atualidad existen varis predimients apliables a la prediión del fenómen de expansión y ntraión de las arillas, ests ls pdems lasifiar en tres amplias ategrías: métds
Compensación en adelanto
 UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FAULAD DE INENIEÍA MEANIA Y ELÉIA ONOL LÁSIO M.. JOSÉ MANUEL OHA NUÑEZ ompenaión en adelanto ompenador eletrónio en adelanto on amplifiadore operaionale () () E E i 0,,
UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FAULAD DE INENIEÍA MEANIA Y ELÉIA ONOL LÁSIO M.. JOSÉ MANUEL OHA NUÑEZ ompenaión en adelanto ompenador eletrónio en adelanto on amplifiadore operaionale () () E E i 0,,
FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control LABORATORIO DE SISTEMAS DE CONTROL DISCRETO PRÁCTICA N 3
 FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control LABORATORIO DE SISTEMAS DE CONTROL DISCRETO 1. TEMA PRÁCTICA N 3 EQUIVALENTES DISCRETOS 2. OBJETIVOS 2.1. Analizar
FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control LABORATORIO DE SISTEMAS DE CONTROL DISCRETO 1. TEMA PRÁCTICA N 3 EQUIVALENTES DISCRETOS 2. OBJETIVOS 2.1. Analizar
TP "Estudio de Variaciones en los Parámetros de la Función Trigonométrica Tangente"
 TP "Estudio de Variaiones en los Parámetros de la Funión Trigonométria Tangente" Condiiones de entrega: Este TP está diseñado para ser elaorado usando programas de omputaión tipo "Geogera" Pueden realizarlo
TP "Estudio de Variaiones en los Parámetros de la Funión Trigonométria Tangente" Condiiones de entrega: Este TP está diseñado para ser elaorado usando programas de omputaión tipo "Geogera" Pueden realizarlo
ICNC: Longitudes de pandeo de columnas: Método riguroso
 CC: ongitudes de pandeo de olumnas: método riguroso S008a-S-U CC: ongitudes de pandeo de olumnas: Método riguroso sta CC proporiona informaión respeto al álulo de la longitud de pandeo de olumnas, para
CC: ongitudes de pandeo de olumnas: método riguroso S008a-S-U CC: ongitudes de pandeo de olumnas: Método riguroso sta CC proporiona informaión respeto al álulo de la longitud de pandeo de olumnas, para
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO
 CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
( s) ( ) CAPITULO II 2.1 INTRODUCCIÓN. 1 ss. θ θ K = θ θ. θ θ 0, ) 2-1. Fig.2.1: Diagrama de bloques de. : Amplificador + motor T
 -1 CAPITULO II.1 INTRODUCCIÓN Fig..1: Diagrama de bloque de donde: A J : Momento de inercia B : Coeficiente de roce T() Torque : Amplificador + motor T J B W G FTLC 1 J ( + ) θ θ o i B J. ( ) ( ) + + Donde
-1 CAPITULO II.1 INTRODUCCIÓN Fig..1: Diagrama de bloque de donde: A J : Momento de inercia B : Coeficiente de roce T() Torque : Amplificador + motor T J B W G FTLC 1 J ( + ) θ θ o i B J. ( ) ( ) + + Donde
Resolver. 2. Inecuaciones de segundo grado. La expresión ax bx c puede ser mayor, menor o igual que 0. Esto es, podemos plantearnos: 2
 1 Inecuacines Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines se clasifican pr su grad
1 Inecuacines Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines se clasifican pr su grad
CIRCUNFERENCIA. x 2 + y 2 + mx + p = 0 Circunferencia centrada en el eje OY. C(0,b)
 CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Discontinuidades en un Punto 1 - Tiene ramas infinitas en un punto
 LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Disontinuidades en un Punto - Tiene ramas infinitas en un punto y 5 La reta 5 es una asíntota vertial - Presenta un salto en un punto, si y
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Disontinuidades en un Punto - Tiene ramas infinitas en un punto y 5 La reta 5 es una asíntota vertial - Presenta un salto en un punto, si y
EJERCICIOS DE TEORÍA DE CONTROL AUTOMÁTICO (SOLUCIONES) 1 BOLETIN V: SISTEMAS DISCRETOS (I)
 EJERCICIOS DE TEORÍA DE CONTROL AUTOMÁTICO (SOLUCIONES) C. En primer lugar habría ue omprobar i el itema e etable. En ao afirmativo, bata on alular la ganania etátia de la funión de tranferenia direta
EJERCICIOS DE TEORÍA DE CONTROL AUTOMÁTICO (SOLUCIONES) C. En primer lugar habría ue omprobar i el itema e etable. En ao afirmativo, bata on alular la ganania etátia de la funión de tranferenia direta
1 2 +! $ = # 1$ $ Pensamiento Algebraico GUÍA DE PARA LOS ASPIRANTES A LA MME Temas que debe dominar:
 Pensamiento lgebraio Temas que debe dominar: GUÍ DE PR LOS SPIRNTES L MME-06 Definiión, operaiones y propiedades de: Números Naturales Números Enteros Números raionales Números irraionales Números omplejos
Pensamiento lgebraio Temas que debe dominar: GUÍ DE PR LOS SPIRNTES L MME-06 Definiión, operaiones y propiedades de: Números Naturales Números Enteros Números raionales Números irraionales Números omplejos
CARGA Y DESCARGA DE UN CONDENSADOR
 Laboratorio de Fíica de Proceo Biológico AGA Y DESAGA DE UN ONDENSADO Fecha: 3/2/2006. Objetivo de la práctica Etudio de la carga y la decarga de un condenador; medida de u capacidad 2. Material Fuente
Laboratorio de Fíica de Proceo Biológico AGA Y DESAGA DE UN ONDENSADO Fecha: 3/2/2006. Objetivo de la práctica Etudio de la carga y la decarga de un condenador; medida de u capacidad 2. Material Fuente
Figura 6.1 Sistema de flujo con atraso por transporte
 6. TIEMPO MUERTO 6.1 INTRODUCCION Un fenómen que se presenta muy a menud en ls sistemas de fluj es el del atras pr transprte, que se cnce también cm tiemp muert. Para explicar dich fenómen, se cnsidera
6. TIEMPO MUERTO 6.1 INTRODUCCION Un fenómen que se presenta muy a menud en ls sistemas de fluj es el del atras pr transprte, que se cnce también cm tiemp muert. Para explicar dich fenómen, se cnsidera
ANÁLISIS PARAMÉTRICO DE COLECTORES SOLARES PLANOS OPERANDO EN SERIE
 195 TCSD 03-05 ANÁLISIS PARAMÉTRICO DE COLECTORES SOLARES PLANOS OPERANDO EN SERIE Ignaio R. Martín Domínguez y Ma. Teresa Alarón Herrera Centro de Investigaión en Materiales Avanzados, S.C. Miguel de
195 TCSD 03-05 ANÁLISIS PARAMÉTRICO DE COLECTORES SOLARES PLANOS OPERANDO EN SERIE Ignaio R. Martín Domínguez y Ma. Teresa Alarón Herrera Centro de Investigaión en Materiales Avanzados, S.C. Miguel de
DEPARTAMENTO DE ELECTRÓNICA Y AUTOMÁTICA CARRERAS: BIOINGENIERÍA E INGENIERÍA ELECTRÓNICA GUÍA DE APRENDIZAJE Y AUTOEVALUACIÓN Nº 1
 DEPARTAMENTO DE ELECTRÓNICA Y AUTOMÁTICA CARRERAS: BIOINGENIERÍA E INGENIERÍA ELECTRÓNICA ÁREA: CONTROL ASIGNATURA: CONTROL II GUÍA DE APRENDIZAJE Y AUTOEVALUACIÓN Nº Análii de Etabilidad de lo Sitema
DEPARTAMENTO DE ELECTRÓNICA Y AUTOMÁTICA CARRERAS: BIOINGENIERÍA E INGENIERÍA ELECTRÓNICA ÁREA: CONTROL ASIGNATURA: CONTROL II GUÍA DE APRENDIZAJE Y AUTOEVALUACIÓN Nº Análii de Etabilidad de lo Sitema
. 1. La función de transferencia de una planta es:
 Univeridad de Navarra Nafarroako Unibertitatea Ecuela Superior de Ingeniero Ingeniarien Goi Mailako Ekola ASIGNATURA GAIA Ingeniería de Control I 4º CURSO URTSOA NOMBRE IZENA FECHA DATA 9 de enero de 3
Univeridad de Navarra Nafarroako Unibertitatea Ecuela Superior de Ingeniero Ingeniarien Goi Mailako Ekola ASIGNATURA GAIA Ingeniería de Control I 4º CURSO URTSOA NOMBRE IZENA FECHA DATA 9 de enero de 3
3.11 Intervalos de confianza basados en una población con distribución normal pero con muestras pequeñas
 3. Intervalo de confianza baado en una población con ditribución normal pero con muetra pequeña Cuando n < 30 no e poible uar el teorema central del límite habría que hacer una upoición epecífica acerca
3. Intervalo de confianza baado en una población con ditribución normal pero con muetra pequeña Cuando n < 30 no e poible uar el teorema central del límite habría que hacer una upoición epecífica acerca
SYMBOLIC ANALYSIS IN ACTIVE GM-C TRANSCONDUCTANCE NETWORKS. ABSTRACT
 SYMBOLI ANALYSIS IN ATIVE GM- TRANSONDUTANE NETWORKS. Lui Abraham Sánchez Gapariano luianchez@correo.de Facultad de iencia de la Electrónica, Benemérita Univeridad Autónoma de Puebla, Puebla, México. M..
SYMBOLI ANALYSIS IN ATIVE GM- TRANSONDUTANE NETWORKS. Lui Abraham Sánchez Gapariano luianchez@correo.de Facultad de iencia de la Electrónica, Benemérita Univeridad Autónoma de Puebla, Puebla, México. M..
