Problemas de optimización de funciones
|
|
|
- Julián Cáceres Valverde
- hace 7 años
- Vistas:
Transcripción
1 Problemas de optimización de funciones 1Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm. 2Un triángulo isósceles de perímetro 30 cm, gira alrededor de su altura engendrando un cono. Qué valor debe darse a la base para que el volumen del cono sea máximo? 3Se pretende fabricar una lata de conserva cilíndrica (con tapa) de 1 litro de capacidad. Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de metal? 4Descomponer el número 44 en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo. 5Se tiene un alambre de 1 m de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima. 6Hallar las dimensiones del mayor rectángulo inscrito en un triángulo isósceles que tiene por base 10 cm y por altura 15 cm. 7Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen ha de ser 9 m 3, su altura 1 m y el coste de su construcción por m 2 es de 50 para la base; 60 para la etapa y 40 para cada pared lateral. 8Recortando convenientemente en cada esquina de una lámina de cartón de dimensiones 80 cm x 50 cm un cuadrado de lado x y doblando convenientemente (véase figura), se construye una caja. Calcular x para que volumen de dicha caja sea máximo. 9Una hoja de papel debe tener 18 cm 2 de texto impreso, márgenes superior e inferior de 2 cm de altura y márgenes laterales de 1 cm de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel. 10El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función: B(x)= 1.2x (0.1x) 3 donde x es el número de autobuses fabricados en un mes. 1. Calcula la producción mensual que hacen máximo el beneficio. 2. El beneficio máximo correspondiente a dicha producción. 11Una huerta tiene actualmente 25 árboles, que producen 600 frutos cada uno. Se calcula que por cada árbol adicional plantado, la producción de cada árbol disminuye en 15 frutos. Calcular: 1. La producción actual de la huerta. 2. La producción que se obtendría de cada árbol si se plantan x árboles más. 3. La producción a la que ascendería el total de la huerta si se plantan x árboles más. 4. Cuál debe ser el número total de árboles que debe tener la huerta para qué la producción sea máxima? 12Un sector circular tiene un perímetro de 10 m. Calcular El radio y la amplitud del sector de mayor área. 1
2 Solución problemas de optimización de funciones 1 Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm. 2 Un triángulo isósceles de perímetro 30 cm, gira alrededor de su altura engendrando un cono. Qué valor debe darse a la base para que el volumen del cono sea máximo? 2
3 3 Se pretende fabricar una lata de conserva cilíndrica (con tapa) de 1 litro de capacidad. Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de metal? 3
4 4 Descomponer el número 44 en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo. 5 Se tiene un alambre de 1 m de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima. 4
5 6 Hallar las dimensiones del mayor rectángulo inscrito en un triángulo isósceles que tiene por base 10 cm y por altura 15 cm. Al tener dos triángulos semejantes se cumple que: 7 Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen ha de ser 9 m 3, su altura 1 m y el coste de su construcción por m 2 es de 50 para la base; 60 para la etapa y 40 para cada pared lateral. 5
6 8 Recortando convenientemente en cada esquina de una lámina de cartón de dimensiones 80 cm x 50 cm un cuadrado de lado x y doblando convenientemente (véase figura), se construye una caja. Calcular x para que volumen de dicha caja sea máximo. 9 Una hoja de papel debe tener 18 cm 2 de texto impreso, márgenes superior e inferior de 2 cm de altura y márgenes laterales de 1 cm de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel. 6
7 10 El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función: B(x)= 1.2x (0.1x) 3 donde x es el número de autobuses fabricados en un mes. 1. Calcula la producción mensual que hacen máximo el beneficio. 2. El beneficio máximo correspondiente a dicha producción. 11 Una huerta tiene actualmente 25 árboles, que producen 600 frutos cada uno. Se calcula que por cada árbol adicional plantado, la producción de cada árbol disminuye en 15 frutos. Calcular: 1. La producción actual de la huerta. Producción actual: = frutos. 2. La producción que se obtendría de cada árbol si se plantan x árboles más. Si se plantan x árboles más, la producción de cada árbol será: x. 3. La producción a la que ascendería el total de la huerta si se plantan x árboles más. P(x) = (25 +x)(600 15x) = 15 x x Cuál debe ser el número total de árboles que debe tener la huerta para qué la producción sea máxima? P (x) = 30 x x = 0 x = 7. 5 P (x) = 30 < 0 La producción será máxima si la huerta tiene = 32 ó = 33 árboles 12 Un sector circular tiene un perímetro de 10 m. Calcular El radio y la amplitud del sector de mayor área. 7
8 8
Optimización de funciones
 Optimización de funciones Pasos para la resolución de problemas de optimización 1. Se plantea la función que hay que maximizar o minimizar. 2. Se plantea una ecuación que relacione las distintas variables
Optimización de funciones Pasos para la resolución de problemas de optimización 1. Se plantea la función que hay que maximizar o minimizar. 2. Se plantea una ecuación que relacione las distintas variables
Ejercicios de Funciones: Optimización. L'Hôpital
 Matemáticas 2ºBach CNyT. Ejercicios Funciones: Optimización. L'Hôpital. Pág 1/8 Ejercicios de Funciones: Optimización. L'Hôpital 1. Obtener el triángulo isósceles de área máxima inscrito en un círculo
Matemáticas 2ºBach CNyT. Ejercicios Funciones: Optimización. L'Hôpital. Pág 1/8 Ejercicios de Funciones: Optimización. L'Hôpital 1. Obtener el triángulo isósceles de área máxima inscrito en un círculo
EJERCICIOS VERANO. Matemáticas Bachiller 1ºCCSS
 EJERCICIOS VERANO Matemáticas Bachiller 1ºCCSS 1ª SESIÓN REPASO Semana:... 2. Representa las siguientes funciones, sabiendo que: a) Tiene pendiente 3 y ordenada en el origen 1. b) Tiene por pendiente 4
EJERCICIOS VERANO Matemáticas Bachiller 1ºCCSS 1ª SESIÓN REPASO Semana:... 2. Representa las siguientes funciones, sabiendo que: a) Tiene pendiente 3 y ordenada en el origen 1. b) Tiene por pendiente 4
Resolución de problemas de optimización con ayuda de la calculadora gráfica.
 Autor: José Manuel Jiménez Cobano Correo: jmjcobano@gmail.com D.N.I.: 14317912-K Palabras Clave: Calculadora gráfica, nuevas tecnologías, matemáticas, problemas, aplicaciones. Resumen Este pequeño artículo,
Autor: José Manuel Jiménez Cobano Correo: jmjcobano@gmail.com D.N.I.: 14317912-K Palabras Clave: Calculadora gráfica, nuevas tecnologías, matemáticas, problemas, aplicaciones. Resumen Este pequeño artículo,
Problemas Tema 3 Enunciados de problemas de Derivabilidad
 página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
EJERCICIOS PARA VERANO. MATEMÁTICAS I 1º BACH
 Desarrollar los siguiente valores absolutos f(x) = x² + 5x 4 - x - 2 f(x) = x² -4x + 3 + x - 3 f(x) = x x f(x) = x / x Resolver las ecuaciones exponenciales: Resolver los sistemas de ecuaciones exponenciales:
Desarrollar los siguiente valores absolutos f(x) = x² + 5x 4 - x - 2 f(x) = x² -4x + 3 + x - 3 f(x) = x x f(x) = x / x Resolver las ecuaciones exponenciales: Resolver los sistemas de ecuaciones exponenciales:
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES.
 APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
Jueves 17 de noviembre, Clase #11 y Tarea UTN ISOA. UTN Cálculo I Prof. Milagro Tencio. Clase 11
 UTN ISOA Cálculo I Prof. Milagro Tencio Clase 11 Problemas de Optimización Introducción a Integrales 1 Clase #11 y Tarea UTN Cálculo I Prof. Milagro Tencio Problemas de Optimización Máximos y mínimos 2
UTN ISOA Cálculo I Prof. Milagro Tencio Clase 11 Problemas de Optimización Introducción a Integrales 1 Clase #11 y Tarea UTN Cálculo I Prof. Milagro Tencio Problemas de Optimización Máximos y mínimos 2
PROBLEMAS DE RECTA TANGENTE. 6 en el punto de abscisa 2. Halla la ecuación de la recta tangente a. ( en el punto de abscisa. x 3x
 PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
MATEMÁTICAS 1º BAC Aplicaciones de las derivadas
 . Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
. Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
12. Una caja con base cuadrada y parte superior abierta debe tener un. 14. Un recipiente rectangular de almacenaje con la parte superior
 328 CAPÍTULO 4 APLICACIONES DE LA DERIVACIÓN 4.7 EJERCICIOS 1. Considere el problema siguiente. Encuentre dos números cuya suma es 23 y cuyo producto es un máximo. (a) Formule una tabla de valores, como
328 CAPÍTULO 4 APLICACIONES DE LA DERIVACIÓN 4.7 EJERCICIOS 1. Considere el problema siguiente. Encuentre dos números cuya suma es 23 y cuyo producto es un máximo. (a) Formule una tabla de valores, como
APLICACIONES DE LAS DERIVADAS. 1. Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican:
 Matemáticas Aplicaciones de las derivadas APLICACIONES DE LAS DERIVADAS Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican: 5 a) f, c) f lntg, en en 8 b) f, en d)
Matemáticas Aplicaciones de las derivadas APLICACIONES DE LAS DERIVADAS Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican: 5 a) f, c) f lntg, en en 8 b) f, en d)
Problemas de optimización
 Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
EXAMEN DE LA UNIDAD 1: POLINOMIOS Y FRACCIONES ALGEBRAICAS. 1. Halla el máximo común divisor y el mínimo común múltiplo de los siguientes polinomios:
 COLEGIO SAN ALBERTO MAGNO º BACHILLERATO EXAMEN DE LA UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. Halla el máimo común divisor y el mínimo común múltiplo de los siguientes polinomios: 0 ) ( 8 ) ( Q P.
COLEGIO SAN ALBERTO MAGNO º BACHILLERATO EXAMEN DE LA UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. Halla el máimo común divisor y el mínimo común múltiplo de los siguientes polinomios: 0 ) ( 8 ) ( Q P.
1) ( ) 2 ( 1) 2) ( ) ( 2 )( ) 3) ( ) 4 4) ( ) = 8 5) ( ) = 4 6) ( ) = 4. 6 x
 MATEMÁTICA II (MECÁNICA) EXAMEN II I PARTE: APLICAR EL CRITERIO DE LA PRIMERA DERIVADA A LAS SIGUIENTES FUNCIONES: Determinar: a.) Intervalos donde la función Crece b.) Intervalos donde la función Decrece.
MATEMÁTICA II (MECÁNICA) EXAMEN II I PARTE: APLICAR EL CRITERIO DE LA PRIMERA DERIVADA A LAS SIGUIENTES FUNCIONES: Determinar: a.) Intervalos donde la función Crece b.) Intervalos donde la función Decrece.
a) El beneficio es el resultado de restar los ingresos y gastos. Esto es,
 Análisis: Máimos, mínimos, optimización 1. Una multinacional ha estimado que anualmente sus ingresos en euros vienen dados por la función I( ) 8 6000, mientras que sus gastos (también en euros) pueden
Análisis: Máimos, mínimos, optimización 1. Una multinacional ha estimado que anualmente sus ingresos en euros vienen dados por la función I( ) 8 6000, mientras que sus gastos (también en euros) pueden
Ejercicios propuestos
 Ejercicios propuestos 1. Encuentre el área total y el volumen de un cubo si la diagonal de una de sus caras mide 6 cm. 2. Encuentre el volumen de un cubo si la longitud de su diagonal mayor mide 8 cm.
Ejercicios propuestos 1. Encuentre el área total y el volumen de un cubo si la diagonal de una de sus caras mide 6 cm. 2. Encuentre el volumen de un cubo si la longitud de su diagonal mayor mide 8 cm.
Problemas de optimización
 Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
Optimización. MATE 3031 Cálculo 1. 19/02/2016 Prof. José G. Rodríguez Ahumada 1 de 17
 Optimización MATE 3031 Cálculo 1 19/0/016 Prof. José G. Rodríguez Ahumada 1 de 17 Actividades.6 Referencia: Sección 3.7 Problemas de Optimización, Ver ejemplos 1 al 5; Ejercicios de Práctica: Impares 1-3;
Optimización MATE 3031 Cálculo 1 19/0/016 Prof. José G. Rodríguez Ahumada 1 de 17 Actividades.6 Referencia: Sección 3.7 Problemas de Optimización, Ver ejemplos 1 al 5; Ejercicios de Práctica: Impares 1-3;
PLAN DE RECUPERACIÓN 1º EVALUACIÓN CURSO º BACHILLERATO MODALIDAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS NOMBRE:... CURSO:...
 PLAN DE RECUPERACIÓN 1º EVALUACIÓN CURSO 17-18 º BACHILLERATO MODALIDAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS NOMBRE:... CURSO:... CRITERIOS DE EVALUACIÓN Los criterios de evaluación seleccionados para
PLAN DE RECUPERACIÓN 1º EVALUACIÓN CURSO 17-18 º BACHILLERATO MODALIDAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS NOMBRE:... CURSO:... CRITERIOS DE EVALUACIÓN Los criterios de evaluación seleccionados para
TEMA 10. CÁLCULO DIFERENCIAL
 TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
TEMA 10 FUNCIÓN DERIVADA. REPRESETACIÓN y aplicaciones.
 A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN
 1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
S = x y = x(500 2x) = 500x 2x 2
 .7. OPTIMIZACIÓN 09.7. Optimización Problema 4 Tenemos 500 metros de alambre para vallar un campo rectangular, uno de cuyos lados da a un río. Calcular la longitud que deben tener estos lados para que
.7. OPTIMIZACIÓN 09.7. Optimización Problema 4 Tenemos 500 metros de alambre para vallar un campo rectangular, uno de cuyos lados da a un río. Calcular la longitud que deben tener estos lados para que
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar.
 C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
, hallar su dominio, los puntos de corte con los ejes y la pendiente de la recta x 2-4 tangente a la gráfica de la función en x = 1.
 . [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
. [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
c) Demuestra que la función f(x) anterior y g(x) = 2x 1 se cortan al menos en un punto. (1 punto) 2
 Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Profesor: Fernando Ureña Portero
 Optimización de funciones P a s o s p a r a l a r e s o l u c i ó n d e p ro b l e m a : 1. S e p l a n t e a l a f u n c i ón que hay que maximizar o minimizar. 2. S e p l a n t e a u n a e c u a c i
Optimización de funciones P a s o s p a r a l a r e s o l u c i ó n d e p ro b l e m a : 1. S e p l a n t e a l a f u n c i ón que hay que maximizar o minimizar. 2. S e p l a n t e a u n a e c u a c i
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Ejercicios de Matemáticas I - Relación 5
 Ejercicios de Matemáticas - Relación 5. Calcula y simplifica todo lo que puedas las derivadas de las siguientes funciones: / f./d sen. C 3/ 2/f./D cos 2. 3 / 3/ f./d cos p 5/ f./d 2 C r C 4/ f./d 3p 6/
Ejercicios de Matemáticas - Relación 5. Calcula y simplifica todo lo que puedas las derivadas de las siguientes funciones: / f./d sen. C 3/ 2/f./D cos 2. 3 / 3/ f./d cos p 5/ f./d 2 C r C 4/ f./d 3p 6/
GEOMETRÍA DEL ESPACIO: PRISMA
 FICHA DE TAAJO Nº Nombre Nº orden imestre IV 4ºgrado - sección A C D Ciclo IV Fecha: - - 1 Área Matemática Tema GEOMETÍA DEL ESPACIO: PISMA TEMA: PISMA Es el sólido que se encuentra limitado por dos polígonos
FICHA DE TAAJO Nº Nombre Nº orden imestre IV 4ºgrado - sección A C D Ciclo IV Fecha: - - 1 Área Matemática Tema GEOMETÍA DEL ESPACIO: PISMA TEMA: PISMA Es el sólido que se encuentra limitado por dos polígonos
FORMULARIO (ÁREAS DE FIGURAS PLANAS)
 FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN
 APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN 1. Calcular, aplicando la definición de derivada: f (), siendo f (x) = 3x 1 1 f ( ), siendo f (x) = x 1 Solución: 1; 4. Determinar el dominio y la expresión de
APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN 1. Calcular, aplicando la definición de derivada: f (), siendo f (x) = 3x 1 1 f ( ), siendo f (x) = x 1 Solución: 1; 4. Determinar el dominio y la expresión de
Cálculo Diferencial y Geometría Analítica Agosto 2016
 Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
Cálculo Diferencial y Geometría Analítica Enero 2015
 Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
MATEMÁTICAS. TEMA 7 Aplicaciones de la Derivada
 MATEMÁTICAS TEMA 7 Aplicaciones de la Derivada ÍNDICE MATEMÁTICAS º BACHILLERATO CCSS. TEMA 7: APLICACIONES DE LA DERIVADA 1. Introducción. Máximos y mínimos. 3. Monotonía (Crecimiento y Decrecimiento).
MATEMÁTICAS TEMA 7 Aplicaciones de la Derivada ÍNDICE MATEMÁTICAS º BACHILLERATO CCSS. TEMA 7: APLICACIONES DE LA DERIVADA 1. Introducción. Máximos y mínimos. 3. Monotonía (Crecimiento y Decrecimiento).
RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA.
 RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA. 1. Sea f : IR IR definida por f() = 2 + 1, IR. Probar, utilizando la definición, que f es derivable en cualquier punto de IR. Encontrar los
RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA. 1. Sea f : IR IR definida por f() = 2 + 1, IR. Probar, utilizando la definición, que f es derivable en cualquier punto de IR. Encontrar los
Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3
![Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3 Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3](/thumbs/74/71283356.jpg) Relación Ecuaciones Matemáticas Ecuaciones de primer grado Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 5x + 9 + x + 8 [] [(x ) ] } = 1 [] x + 1 x + x + 5 7 [] 5x (x 8) = (x + ) [5] x + [] 5x
Relación Ecuaciones Matemáticas Ecuaciones de primer grado Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 5x + 9 + x + 8 [] [(x ) ] } = 1 [] x + 1 x + x + 5 7 [] 5x (x 8) = (x + ) [5] x + [] 5x
Universidad Autónoma de Querétaro
 TAREA 1 1. En cada gráfico señala los puntos donde la función no es derivable, explicar por qué. TAREA 1 2. Deriva las siguientes funciones, utiliza la definición geométrica. f(x) = 3x f(x) = x 2 f(x)
TAREA 1 1. En cada gráfico señala los puntos donde la función no es derivable, explicar por qué. TAREA 1 2. Deriva las siguientes funciones, utiliza la definición geométrica. f(x) = 3x f(x) = x 2 f(x)
Matemáticas 3º E.S.O. 2014/15
 Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
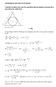 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
I.E. CENTRO FORMATIVO DE ANTIOQUIA CEFA GEOMETRÍA GRADO DÉCIMO
 I.E. CENTRO FORMATIVO DE ANTIOQUIA CEFA GEOMETRÍA GRADO DÉCIMO 1. Calcula el número de baldosas cuadradas que hay en un salón rectangular de 9m de largo y 3 m de ancho. Cada baldosa mide 30 cm de lado.
I.E. CENTRO FORMATIVO DE ANTIOQUIA CEFA GEOMETRÍA GRADO DÉCIMO 1. Calcula el número de baldosas cuadradas que hay en un salón rectangular de 9m de largo y 3 m de ancho. Cada baldosa mide 30 cm de lado.
PAIEP. Valores máximos y mínimos de una función
 Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Valores máximos y mínimos de una función Diremos que la función f : D R R, alcanza un máximo absoluto en el punto
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Valores máximos y mínimos de una función Diremos que la función f : D R R, alcanza un máximo absoluto en el punto
f (x) = 3(1 + x2 cos x)(x sin x 1) 2 x ( x + 7x) 2/3 cos 4 (tan x) ) 1/5 f (x) = 3x4 + 6x 3 9x 2 + 3x + 3 x(x 3 + 3x 1)
 1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
Departamento de Matemáticas I.E.S. Juan García Valdemora. Ejercicios de repaso. 2. Expresa como una potencia de exponente fraccionario: x x.
 Ejercicios de repaso. Epande las siguientes epresiones: + + d) +. Epresa como una potencia de eponente fraccionario: a a a a a. Opera y simplifica. ( + ) ( + ) ( ) ( ) ( )( ) + + +. Realiza las siguientes
Ejercicios de repaso. Epande las siguientes epresiones: + + d) +. Epresa como una potencia de eponente fraccionario: a a a a a. Opera y simplifica. ( + ) ( + ) ( ) ( ) ( )( ) + + +. Realiza las siguientes
EJERCICIOS de REPRESENTACIÓN DE FUNCIONES
 EJERCICIOS de REPRESENTACIÓN DE FUNCIONES º BACH. INTERVALOS DE CRECIMIENTO. M Y m:. Hallar los intervalos de crecimiento y decrecimiento y los M y m de las siguientes funciones. Aplicar para ello, alternativamente,
EJERCICIOS de REPRESENTACIÓN DE FUNCIONES º BACH. INTERVALOS DE CRECIMIENTO. M Y m:. Hallar los intervalos de crecimiento y decrecimiento y los M y m de las siguientes funciones. Aplicar para ello, alternativamente,
Apuntes Matemáticas 2º de bachillerato. Tema 6. Optimización
 Apuntes Tema 6 Optimización 6.1 Problemas de optimización El cálculo de máximos y mínimos no solo se usa en Matemáticas, sino en muchas otras disciplinas. Precisamente este tipo de problemas fue el que
Apuntes Tema 6 Optimización 6.1 Problemas de optimización El cálculo de máximos y mínimos no solo se usa en Matemáticas, sino en muchas otras disciplinas. Precisamente este tipo de problemas fue el que
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Actualizado en el curso 2008/2009
 1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. 2. Calcula dos números que cumplan que al sumarlos
1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. 2. Calcula dos números que cumplan que al sumarlos
Clase 21 Tema: Área lateral y área total de un cilindro
 Matemáticas 9 Bimestre: III Número de clase: 21 Clase 21 Tema: Área lateral y área total de un cilindro Actividad 52 1 Lea la siguiente información. Un cilindro y un prisma tienen en común que ambos tienen
Matemáticas 9 Bimestre: III Número de clase: 21 Clase 21 Tema: Área lateral y área total de un cilindro Actividad 52 1 Lea la siguiente información. Un cilindro y un prisma tienen en común que ambos tienen
ECUACIONES DE 1º GRADO =2x-(10-4x) 2. 5(x-1)+10(x+2)= x+3(2x-4)= x-3(x+5)=3x (2-x)=18x (x-3)=3(x+1) 5-2x.
 ECUACIONES DE 1º GRADO 1. 0=(10). 5(1)10()=5. 1()=0. (1)= 5. (5)= 0. [(1)]=1 7. (5)=10 8. ()=181 9. 105()=(1) 10. ()=[5()] 11. (1)(11)=9 1. = 1. 8 = 1. 7 = 1 5 5 15. 10 = ( ) 9 1. 5 8 5 ( 0)= 18 7 17.
ECUACIONES DE 1º GRADO 1. 0=(10). 5(1)10()=5. 1()=0. (1)= 5. (5)= 0. [(1)]=1 7. (5)=10 8. ()=181 9. 105()=(1) 10. ()=[5()] 11. (1)(11)=9 1. = 1. 8 = 1. 7 = 1 5 5 15. 10 = ( ) 9 1. 5 8 5 ( 0)= 18 7 17.
Derivadas. Problemas de Optimización.
 Departamento de Análisis Matemático Derivadas. Problemas de Optimización. Problema 1. Sea f : R + 0 R la función definida por: 2 si 0 < 4 2 E ( ) 6 si 4 Estudiar la continuidad y derivabilidad de f. Problema
Departamento de Análisis Matemático Derivadas. Problemas de Optimización. Problema 1. Sea f : R + 0 R la función definida por: 2 si 0 < 4 2 E ( ) 6 si 4 Estudiar la continuidad y derivabilidad de f. Problema
. (Nota: ln x denota el logaritmo neperiano de x).
 e - si 0. [04] [ET-A] Sea la función f() = k si = 0 a) Determine razonadamente el valor del parámetro k para que la función sea continua para todos los números reales. b) Estudie si esta función es derivable
e - si 0. [04] [ET-A] Sea la función f() = k si = 0 a) Determine razonadamente el valor del parámetro k para que la función sea continua para todos los números reales. b) Estudie si esta función es derivable
Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (h)
 Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (a) y 6 ; (b) y ( )( ) + ; (c) (e) y + 6 ; + 4; (d) y ( ) 9 + 5 5; (f) 4 y y 9 ; ; (h) y ( + ) ; 4 (g)
Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (a) y 6 ; (b) y ( )( ) + ; (c) (e) y + 6 ; + 4; (d) y ( ) 9 + 5 5; (f) 4 y y 9 ; ; (h) y ( + ) ; 4 (g)
o Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 )
![o Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 ) o Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 )](/thumbs/74/70685188.jpg) Aplicaciones de la derivada MATEMÁTICAS II CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN Definiciones Se dice que una función f es creciente en un punto si para cualquier punto de un entorno de, (, + ) se
Aplicaciones de la derivada MATEMÁTICAS II CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN Definiciones Se dice que una función f es creciente en un punto si para cualquier punto de un entorno de, (, + ) se
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
EJERCICIOS PAU MATEMÁTICAS II ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVABILIDAD 1- Considere la función: 3 2 a) Determine las asíntotas, horizontales, verticales y oblicuas, que tenga la función f(x). b) Determine los intervalos de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVABILIDAD 1- Considere la función: 3 2 a) Determine las asíntotas, horizontales, verticales y oblicuas, que tenga la función f(x). b) Determine los intervalos de
( x) ( ) = D) k( x) ( ) = es una función: 3 x. = + + es una función: h x e + = C) ( ) g x A) B) Sesión 2
 Sesión Unidad I Clasificación dibujo de gráfica de funciones. D. Clasificación de funciones. h ( ) 0.- La función es una función: Creciente Trascendente Irracional Constante Logarítmicas.- Una función
Sesión Unidad I Clasificación dibujo de gráfica de funciones. D. Clasificación de funciones. h ( ) 0.- La función es una función: Creciente Trascendente Irracional Constante Logarítmicas.- Una función
( ) Para comprobar que el extremo calculado es un máximo, se utiliza el criterio de la segunda derivada. ( ) Máximo
 Modelo 01. Problema B.- Calificación máima: puntos) El coste de fabricación de una serie de hornos microondas viene dado por la función C) + 0 + 0000, donde representa el número de hornos fabricados. Supongamos
Modelo 01. Problema B.- Calificación máima: puntos) El coste de fabricación de una serie de hornos microondas viene dado por la función C) + 0 + 0000, donde representa el número de hornos fabricados. Supongamos
PROBLEMAS DE REPASO. Solución: Si llamamos x e y a las longitudes de cada uno de los catetos, sabemos que: x 2 y 2 1 y 2 1 x 2 El volumen del cono es:
 PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
VOLÚMENES DE POLIEDROS PRISMA:
 VOLÚMENES DE POLIEDROS CONCEPTO: El volumen es la medida de la capacidad que posee un sólido. Todo sólido requiere tres dimensiones: largo, ancho y altura (profundidad ó espesor), es por ello que el volumen
VOLÚMENES DE POLIEDROS CONCEPTO: El volumen es la medida de la capacidad que posee un sólido. Todo sólido requiere tres dimensiones: largo, ancho y altura (profundidad ó espesor), es por ello que el volumen
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
(26)2x(3x 4) (1 3x)$(1 +x) = 2
 Resuelve las siguientes ecuaciones ECUACIONES, INECUACIONES Y SISTEMAS. (1)25x 4 29x 2 +4 =0 (2)x 4 5x 2 +4 =0 (3)x 4 a(a +b)x 2 +a 3 b =0 (4)(x 2 5)$(x 2 3) =0 (5)x +2 = 4x +13 (6) x 1 12 = 2 x+1 (7)
Resuelve las siguientes ecuaciones ECUACIONES, INECUACIONES Y SISTEMAS. (1)25x 4 29x 2 +4 =0 (2)x 4 5x 2 +4 =0 (3)x 4 a(a +b)x 2 +a 3 b =0 (4)(x 2 5)$(x 2 3) =0 (5)x +2 = 4x +13 (6) x 1 12 = 2 x+1 (7)
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1
![x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1 x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1](/thumbs/80/80474947.jpg) Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
2. Obtener la longitud de la base de un triángulo isósceles cuyos lados iguales miden 17 cm y su altura 8 cm.
 ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA
 RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
ECUACIONES CUADRÁTICAS CON UNA VARIABLE
 www.matebrunca.com Prof. Waldo Márquez González Ecuaciones de 2 do Grado 1 ECUACIONES CUADRÁTICAS CON UNA VARIABLE OBJETIVO Resolver ecuaciones de segundo grado con una variable, para aplicarlos en la
www.matebrunca.com Prof. Waldo Márquez González Ecuaciones de 2 do Grado 1 ECUACIONES CUADRÁTICAS CON UNA VARIABLE OBJETIVO Resolver ecuaciones de segundo grado con una variable, para aplicarlos en la
Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7
 página 1/6 Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7 Hoja 1. Problema 1 Resuelto por Curro García Olmedo (noviembre 2014) 1. Obtener la derivada de f (
página 1/6 Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7 Hoja 1. Problema 1 Resuelto por Curro García Olmedo (noviembre 2014) 1. Obtener la derivada de f (
Problemas Tema 4 Enunciados de problemas de Repaso y Ampliación de la primera evaluación
 página 1/15 Problemas Tema 4 Enunciados de problemas de Repaso y Ampliación de la primera evaluación Hoja 1 1. Estudia y representa f ()=ln(tg ) 2. Estudia y representa f ()= 52 2+1 4 +6 3. Estudia y representa
página 1/15 Problemas Tema 4 Enunciados de problemas de Repaso y Ampliación de la primera evaluación Hoja 1 1. Estudia y representa f ()=ln(tg ) 2. Estudia y representa f ()= 52 2+1 4 +6 3. Estudia y representa
Conceptos generales.
 Titulación: Ingeniero en Telecomunicación Asignatura: Cálculo Relación de problemas número Conceptos generales RECTA REAL Y PLANO COMPLEJO SUCESIONES Problema Supuesto que s t < x y, donde s,x R, t,y R+,
Titulación: Ingeniero en Telecomunicación Asignatura: Cálculo Relación de problemas número Conceptos generales RECTA REAL Y PLANO COMPLEJO SUCESIONES Problema Supuesto que s t < x y, donde s,x R, t,y R+,
PROBLEMAS ALGEBRAICOS (SISTEMAS NO LINEALES) 1.- Calcular dos números positivos sabiendo que la diferencia es 12 y la suma de sus cuadrados es 170.
 Problemas algebraicos 1 PROBLEMAS ALGEBRAICOS (SISTEMAS NO LINEALES) 1.- Calcular dos números positivos sabiendo que la diferencia es 1 y la suma de sus cuadrados es 170..- Hallar dos números naturales
Problemas algebraicos 1 PROBLEMAS ALGEBRAICOS (SISTEMAS NO LINEALES) 1.- Calcular dos números positivos sabiendo que la diferencia es 1 y la suma de sus cuadrados es 170..- Hallar dos números naturales
Departamento de Matemática Aplicada y Estadística Ampliación de Matemáticas Hoja 5. Optimización no lineal
 Departamento de Matemática Aplicada y Estadística Ampliación de Matemáticas Hoja 5. Optimización no lineal 1. Si Ω 1 y Ω 2 son dos subconjuntos convexos no vacíos de R,demuestraque a) Ω 1 ± Ω = {x 1 ±
Departamento de Matemática Aplicada y Estadística Ampliación de Matemáticas Hoja 5. Optimización no lineal 1. Si Ω 1 y Ω 2 son dos subconjuntos convexos no vacíos de R,demuestraque a) Ω 1 ± Ω = {x 1 ±
PONTIFICIA UNIVERSIDAD JAVERIANA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS. Ejercicios de Cálculo Diferencial
 PONTIFICIA UNIVERSIDAD JAVERIANA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS Ejercicios de Cálculo Diferencial Fabio Germán Molina Focazzio molinaf@javeriana.edu.co Índice 1. Inecuaciones Halle el
PONTIFICIA UNIVERSIDAD JAVERIANA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS Ejercicios de Cálculo Diferencial Fabio Germán Molina Focazzio molinaf@javeriana.edu.co Índice 1. Inecuaciones Halle el
EJERCICIOS GRUPO 1 DERIVADAS. 1. Usando la definición calcule la derivada de las siguientes funciones.
 INSTRUCCIÓN. Resuelve los problemas propuestos del modo siguiente: primero en forma individual, luego en forma grupal y por último preséntalo en forma grupal en un máimo de cinco (05) integrantes. EJERCICIOS
INSTRUCCIÓN. Resuelve los problemas propuestos del modo siguiente: primero en forma individual, luego en forma grupal y por último preséntalo en forma grupal en un máimo de cinco (05) integrantes. EJERCICIOS
Clase 5: Modelando con funciones
 Clase 5: Modelando con funciones Formular en término de funciones lineales un problema y calcular su solución. Resolver problemas de mínimos/máimos formulados en términos de funciones cuadráticas. Formular
Clase 5: Modelando con funciones Formular en término de funciones lineales un problema y calcular su solución. Resolver problemas de mínimos/máimos formulados en términos de funciones cuadráticas. Formular
Gráfica de la función f de X en Y El conjunto X se llama dominio de la función f.
 FUNCIONES Y SUS GRÁFICAS Funciones y notación de funciones Una relación entre dos conjuntos X e Y es un conjunto de pares ordenados, cada uno de la forma (, y) donde es un elemento del conjunto X e y,
FUNCIONES Y SUS GRÁFICAS Funciones y notación de funciones Una relación entre dos conjuntos X e Y es un conjunto de pares ordenados, cada uno de la forma (, y) donde es un elemento del conjunto X e y,
Lic. Saúl Villamizar Valencia 53 SÓLIDOS DE REVOLUCIÓN Y ESFERA
 Lic. Saúl Villamizar Valencia 53 SÓLIDOS DE REVOLUCIÓN Y ESFERA 54 Actualización Permanente en el Área Matemática 1. Cilindro Definiciones Se llama superficie cilíndrica la engendrada por una recta que
Lic. Saúl Villamizar Valencia 53 SÓLIDOS DE REVOLUCIÓN Y ESFERA 54 Actualización Permanente en el Área Matemática 1. Cilindro Definiciones Se llama superficie cilíndrica la engendrada por una recta que
CUARTA LISTA DE EJERCICIOS CALCULO DIFERENCIAL E INTEGRAL LCC Semestre Resuelva los siguientes problemas de razones de cambio relacionadas
 CUARTA LISTA DE EJERCICIOS CALCULO DIFERENCIAL E INTEGRAL LCC Semestre 017-1. Resuelva los siguientes problemas de razones de cambio relacionadas a) Todas las aristas de un cubo están creciendo cm/seg.
CUARTA LISTA DE EJERCICIOS CALCULO DIFERENCIAL E INTEGRAL LCC Semestre 017-1. Resuelva los siguientes problemas de razones de cambio relacionadas a) Todas las aristas de un cubo están creciendo cm/seg.
Derivadas Parciales. Aplicaciones.
 RELACIÓN DE PROBLEMAS FUNDAMENTOS MATEMÁTICOS DE LA INGENIERÍA Curso 2004/2005 Escuela Universitaria de Ingeniería Técnica Agrícola Departamento de Matemática Aplicada I Tema 3. Derivadas Parciales. Aplicaciones.
RELACIÓN DE PROBLEMAS FUNDAMENTOS MATEMÁTICOS DE LA INGENIERÍA Curso 2004/2005 Escuela Universitaria de Ingeniería Técnica Agrícola Departamento de Matemática Aplicada I Tema 3. Derivadas Parciales. Aplicaciones.
ESCUELA MILITAR DE INGENIERIA CÁLCULO II Misceláneas de problemas 2013
 ESCUELA MILITAR DE INGENIERIA CÁLCULO II Misceláneas de problemas 2013 Tema: Aplicaciones de las Derivadas Parciales. 1. Demuestre que el plano tangente al cono z = a 2 x 2 + b 2 y 2 pasa por el origen.
ESCUELA MILITAR DE INGENIERIA CÁLCULO II Misceláneas de problemas 2013 Tema: Aplicaciones de las Derivadas Parciales. 1. Demuestre que el plano tangente al cono z = a 2 x 2 + b 2 y 2 pasa por el origen.
TEMA 9: CUERPOS GEOMÉTRICOS
 1 TEMA 9: CUERPOS GEOMÉTRICOS CUERPOS GEOMETRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos.
1 TEMA 9: CUERPOS GEOMÉTRICOS CUERPOS GEOMETRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos.
Práctica 5 Máximos y Mínimos. Multiplicadores de Lagrange. Escuela de Matemática Instituto Tecnológico de Costa Rica
 Práctica 5 Máximos y Mínimos. Multiplicadores de Lagrange. Escuela de Matemática Instituto Tecnológico de Costa Rica http://www.cidse.itcr.ac.cr 7 de junio de 008 . Para cada una de las funciones que se
Práctica 5 Máximos y Mínimos. Multiplicadores de Lagrange. Escuela de Matemática Instituto Tecnológico de Costa Rica http://www.cidse.itcr.ac.cr 7 de junio de 008 . Para cada una de las funciones que se
GUÍA DE ESTUDIO Exámenes a Título de Suficiencia 2013/2
 Eámenes a Título de Suficiencia 01/ PLAN DE ESTUDIOS 008 009 JUNIIO, 01. Unidad de aprendizaje: SUBDIRECCIÓN ACADÉMICA 01, Año de la Lealtad Institucional y Centenario del Ejército Meicano 80 Aniversario
Eámenes a Título de Suficiencia 01/ PLAN DE ESTUDIOS 008 009 JUNIIO, 01. Unidad de aprendizaje: SUBDIRECCIÓN ACADÉMICA 01, Año de la Lealtad Institucional y Centenario del Ejército Meicano 80 Aniversario
TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros)
 3 TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros) Ejemplo 1: Un rectángulo tiene 60 m de área y 3m de perimetro. Hallar sus dimensiones.. Ejemplo : La base de un rectángulo es el triple de su altura
3 TALLER DE POLÍGONOS Y CÍRCULOS (Areas y Perímetros) Ejemplo 1: Un rectángulo tiene 60 m de área y 3m de perimetro. Hallar sus dimensiones.. Ejemplo : La base de un rectángulo es el triple de su altura
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
( x) = D) k( x) ( ) = es una función: x = = 3 x es una función: = C) ( ) g x A) B) Sesión 4. Unidad II Funciones. D. Clasificación de funciones.
 Sesión Unidad II Funciones. D. Clasificación de funciones. h ( ) 0.- La función es una función: Creciente Trascendente Irracional D) Constante Logarítmicas.- Una función creciente en todo su dominio es:
Sesión Unidad II Funciones. D. Clasificación de funciones. h ( ) 0.- La función es una función: Creciente Trascendente Irracional D) Constante Logarítmicas.- Una función creciente en todo su dominio es:
ACTIVIDADES INCLUIDAS EN LA PROPUESTA DIDÁCTICA: DE AMPLIACIÓN
 Pág. ENUNCIADOS Se desea fabricar un tubo de 2 m de largo y 5 cm de diámetro soldando los dos bordes de un rectángulo. Cuáles deben ser las dimensiones del rectángulo si en las soldaduras se solapan 5
Pág. ENUNCIADOS Se desea fabricar un tubo de 2 m de largo y 5 cm de diámetro soldando los dos bordes de un rectángulo. Cuáles deben ser las dimensiones del rectángulo si en las soldaduras se solapan 5
MATEMÁTICA Seminario Introductorio 2019 ECUACIÓN CUADRÁTICA
 ECUACIÓN CUADRÁTICA Una ecuación como x + 3x 10 = 0 se dice que es de segundo grado porque el exponente de la x (que es la incógnita) está elevado a la dos. La forma general de una ecuación de este tipo
ECUACIÓN CUADRÁTICA Una ecuación como x + 3x 10 = 0 se dice que es de segundo grado porque el exponente de la x (que es la incógnita) está elevado a la dos. La forma general de una ecuación de este tipo
PROBLEMAS DE MÁXIMOS Y MÍNIMOS.
 PROBLEMAS DE MÁXIMOS Y MÍNIMOS. Los métodos para determinar los máximos y mínimos de las funciones se pueden aplicar a la solución de problemas prácticos, para resolverlos tenemos que transformar sus enunciados
PROBLEMAS DE MÁXIMOS Y MÍNIMOS. Los métodos para determinar los máximos y mínimos de las funciones se pueden aplicar a la solución de problemas prácticos, para resolverlos tenemos que transformar sus enunciados
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
