Universidad Rey Juan Carlos Curso 2009/10. Ingeniería Técnica en Informática de Gestión + LADE Ingeniería Técnica en Informática de Gestión
|
|
|
- Marina Rey Botella
- hace 7 años
- Vistas:
Transcripción
1 Universi Rey Jun Crlos Curso 2009/0 Ingenierí Téni en Informáti e Gestión + LADE Ingenierí Téni en Informáti e Gestión Asigntur: Estrutur e Dtos y e l Informión Práti 2A: Grfos + Vores NORMAS PARA LA ENTREGA DE LA PRÁCTICA L entreg e est práti es oligtori y su relizión ee herse en grupos e os persons. El lenguje e progrmión utilizo eerá ser A 95. Aemás e entregr el mteril soliito, los lumnos porán ser onvoos un entrevist personl en l que eerán explir, orlmente, el trjo relizo. L opi e prátis (totl o pril) será snion, l menos, on el suspenso glol e l signtur. Dih snión fetrá tnto l grupo que opi l práti, omo l opio. A este respeto, too lumno que pier informión reltiv su práti (en ulquier formto: ppel, us, orenor, et) eerá omunirlo l profesor e prátis. Se vierte emás e que el proeso e eteión e opis está reforzo meinte menismos utomtizos. Herrmient e orreión utomáti L signtur ispone e un herrmient e orreión utomáti e prátis, esile en l URL Se reomien su uso pr relizr prues e funionmiento e los pquetes y progrms peios, unque ihs prues eerán ir preeis por el iseño e implementión por prte e los lumnos e sus propios tálogos y progrms prue. Qué hy que entregr Un memori en ppel on el siguiente ontenio: Nomre y pellios e uno e los utores. Ároles e sos e prue iseños pr un e ls iferentes prtes e l práti. Listo on el óigo ompleto e toos los fiheros utilizos pr l resoluión e l práti, slvo los que se proporionn y implementos. Toos los fiheros fuente y los sos e prue peios en el enunio. Estos fiheros eerán entregrse e form utomáti trvés e l URL Los fiheros fuente eerán ser e texto plno (ningún formto: ni Wor, ni PDF, et) y no porán ontener rteres espeiles (en prtiulr ni eñes ni entos).
2 Comentrios generles. Antes e utilizr el orretor utomátio es impresinile:.. Diseñr los sos e prue oportunos y relizr ls prues e funionmiento orresponientes ejeutno los progrms e prue soliitos en el enunio..2. Leer el fihero e yu el orretor utomátio pr entener el funionmiento el mismo. Se ee él siguieno el link? que pree en l pliión..3. Asegurrse e que se respet estritmente el formto esrito en el enunio pr el fihero e sli: no es lo mismo un espio en lno que os, ni un líne on un espio en lno que un sin espio en lno l finl, ni un líne ví (ontenieno sólo un retorno e rro) que un líne on un espio en lno, et. Por ejemplo, eerá ponerse espeil tenión en l form en l que se esrien números enteros, reorno, en prtiulr, que l esritur trvés el triuto Imge olo un ráter justo elnte el primer ígito (un signo menos si el entero es negtivo y un espio en lno si el entero es positivo)..4. Asegurrse e que se respet estritmente tnto el nomre omo el tipo (funión o proeimiento) e ls operiones, sí omo el moo (IN, OUT o IN OUT) e los prámetros y el oren en el que éstos preen en l list e prámetros. 2. L págin We e l signtur ispone e un prto inluyeno soluiones pregunts freuentes (FAQ) reltivs l uso el orretor utomátio. 3. Deerá inirse (en el.) l ompleji e ls operiones e los TADs implementos. 4. Deerá tenerse en uent que pr l evluión el funionmiento e l práti se usrán sos e prue iionles los isponiles en el orretor. 5. L no entreg o iseño efiiente e los sos e prue porá ser us e suspenso e l práti unque su funionmiento se orreto. Por otr prte, es posile pror l práti unque no se psen toos los sos e prue isponiles en el orretor. Plzo máximo pr l entreg Pr l onvotori e myo: l feh límite pr l entreg utomáti será el 8 e myo e 200 (hst ls 23:55 hors) y pr l memori en ppel será el iniio el exmen e myo. Pr l onvotori e junio: l feh límite pr l entreg utomáti será el 25 e junio e 200 (hst ls 23:55 hors) y pr l memori en ppel será el iniio el exmen e junio. 2
3 CONTENIDO DE LA PRÁCTICA Est práti tiene por ojetivo implementr el lgoritmo e Dijkstr según el esquem e lgoritmos vores estuio en lse. Este lgoritmo resuelve el siguiente prolem sore grfos vloros: Hllr los minos mínimos ese un etermino noo hst el resto e noos el grfo El mino mínimo entre un pr e noos es quel mino entre esos noos que tiene el oste más pequeño. El oste e un mino es igul l sum e los ostes e sus ros. Tenemos, por tnto, os tos e entr: un grfo vloro y un noo. Pr que el prolem teng soluión se tienen que umplir os oniiones: () que el noo que tommos omo origen e los minos pertenez l grfo, y (2) que el grfo se onexo (en otro so, sólo porímos hllr los minos mínimos que tienen omo extremo finl ulquier e los noos e l omponente onex l que pertenee el noo origen). Otr restriión iionl, impuest por el lgoritmo e Dijkstr, es (3) que los ostes e los ros el grfo sen myores o igules que ero. Representremos los minos e un grfo meinte un seueni e vérties v..v n, one v es el origen el mino y v n el extremo finl. Por ejemplo, o el siguiente grfo: si tommos omo origen el noo, l soluión l prolem onsistirí en el siguiente onjunto e minos: {,,}, on ostes e, 3 y 7 unies, respetivmente. Y si prtimos el noo, el onjunto {,,}, on ostes e 3, 2 y 5 unies. Básimente, el lgoritmo e Dijkstr está estruturo en un serie e iteriones, en un e ls ules se trt e eterminr el mino mínimo pr un nuevo noo. De est form, el onjunto e noos el grfo se estrutur en os suonjuntos U y V-U (one V es el onjunto e vérties el grfo): el formo por los noos pr los ules y se h enontro su mino mínimo, y el formo por quellos pr los que no, respetivmente. Iniilmente, U={o}, one o es el vértie que se tom omo origen. En iterión mpliremos el onjunto U on un vértie w que se enuentre enlzo on lgún miemro v e U meinte un ro e oste. En onreto, el vértie w elegio será quel que se enuentre oneto on el origen trvés e v meinte un mino e oste mínimo, es eir, quel uyo vlor oste(mino(o,v)) + se el más pequeño. A ontinuión se muestrn los psos que permiten otener l soluión l ejemplo nterior. Los vérties e U se enuentrn resltos en negrit. Los ros que unen los vérties e U son los que posiilitron en iterión extener el onjunto, y muestrn por tnto los minos mínimos omputos hst el momento. Los ros punteos representn los istintos nitos pr mplir U en l siguiente iterión (entre préntesis se muestr l sum e su oste más el el mino mínimo l que se une; este vlor, y no simplemente el oste, es el que permite seleionr el siguiente ro). Como en el lgoritmo e Prim. 3
4 () 6(6) 6(6) 2(3) 2 2 6(7) 6(7) 5(8) 6 A ontinuión se ofree un interpretión el lgoritmo e Dijkstr en términos el esquem e lgoritmos vores estuio en lse: - Tipo e l soluión. Ls soluiones e un lgoritmo vorz están ompuests por un etermino número e omponentes. En nuestro so, ests omponentes son los istintos minos ese el noo origen uno e los noos restntes el grfo. - Tipo e los nitos. Se refieren los istintos omponentes nitos formr prte e l soluión que se onsiern en un e ls iteriones el lgoritmo. Según se e eir, estos nitos son los istintos minos lterntivos. No ostnte, pr simplifir l esripión, se onsierrá que ihos nitos son los últimos ros e uno e los minos. El oste e ihos ros no será el que posee en el grfo, sino el el mino que represent. - Es soluión? Est operión onsiste en ompror si hemos enontro un mino pr uno e los noos el grfo. - Seleión e nitos. En fse e l iterión se seleion, e entre los istintos ros nitos, quel que represent el mino on un oste más pequeño. - Es ftile? Est operión omprue que no se hy lulo ún el mino mínimo pr uno e los extremos el ro. Esto no sueerá si el primer mino que se inluyó en l oleión e nitos pr uno e sus extremos, no fue el e oste mínimo. - Atulizión e l oleión e nitos. Si el nito seleiono no es ftile, simplemente se elimin e l oleión e nitos. Si es ftile, eso quiere eir que tenemos un nuevo mino y, por tnto, un nuevo noo. L tulizión, en este so, onsiste en ñir l onjunto e nitos toos los ros que prtn e ese noo hi otros pr los ules no se hy etermino el mino óptimo toví. - Añir el nito l soluión. Consiste en ñir el nuevo mino otenio. Poemos utilizr l siguiente tl pr esriir los psos el lgoritmo: Es Soluión? Seleionr Cnito Es Ftile? Soluión Cnitos Iniilizión <<sol. Iniil>> <<nitos ini.>> ª iterión SI NO <<n>> SI NO <<sol. Atuliz>> <<nitos tulizos>> 2ª iterión n-ésim iter. SI 4
5 Por ejemplo, l siguiente tl muestr el proeso e otenión e l soluión pr el ejemplo nterior: Es Soluión? Seleionr Cnito Es Ftile? Soluión Cnitos Iniilizión {} {(,,),(,,6)} ª iterión No (,,) Sí {} {(,,3),(,,6),(,,7)} 2ª iterión No (,,3) Sí {,} {(,,6),(,,8),(,,7)} 3ª iterión No (,,6) No {(,,8),(,,7)} 4ª iterión No (,,7) Sí {,,} {(,,8)} 5ª iterión Sí Se pie: PARTE I. EJEMPLO DE LA APLICACIÓN DEL ALGORITMO Desriir l ejeuión el lgoritmo e Dijkstr pr hllr los minos mínimos ese el vértie A l resto e noos el siguiente grfo: 2 A B C D E F G PARTE II. IMPLEMENTACIÓN EN ADA95 Implementr en A95 el lgoritmo e Dijkstr. Se eerán tener en uent los siguientes spetos: - El suprogrm eerá tener en uent los posiles sos nómlos meinte exepiones. Estos sos serán que el grfo no se onexo, que el noo origen no pertenez l grfo o que lgunos e los ros el grfo teng un oste negtivo. - Se reomien lmenr los nitos en un list oren. - Con respeto l soluión, se utilizrá un vetor uyo rngo esté formo por los noos poteniles el grfo, y que lmene en posiión el mino que tiene omo extremo finl ese noo. En el so el noo origen el mino será vío. - L implementión eerá estr estrutur en términos e l interpretión vorz el lgoritmo esrit en el prto nterior. - L implementión el lgoritmo e Dijkstr se relizrá en un pquete hijo el pquete Grfos, uy interfz es l siguiente ( flt e inluir omentrios, pre, post, exepiones, ). L funión CosteCmino lul el oste totl e un mino (es eir, l sum e los ostes e sus ros). 5
6 GENERIC WITH PACKAGE ListNoos IS NEW Lists(TipoNoo); TYPE TipoSoluion IS ARRAY (TipoNoo) OF ListNoos.TipoList; PACKAGE Grfos.Cminos IS NooNoPertenee: EXCEPTION; NoConexo: EXCEPTION; CosteNegtivo: EXCEPTION; FUNCTION CosteCmino(g: IN TipoGrfo; mino: IN ListNoos.TipoList) RETURN Flot; PROCEDURE Dijkstr(g: IN TipoGrfo; n: IN TipoNoo; soluion: IN OUT TipoSoluion); END Grfos.Cminos; PARTE III. PRUEBA DEL ALGORITMO DE DIJKSTRA Est prte e l práti tiene por ojetivo iseñr un tálogo e sos e prue pr l implementión el lgoritmo e Dijkstr reliz en l prte nterior. El tálogo e prues estrá formo por el número e sos que los lumnos ren onvenientes. El so e prue I- ésimo el tálogo onstrá e os fiheros enominos so_i.in y so_i.out, uyos ontenios se justrán l siguiente formto: so_i.in. Este fihero ontenrá un grfo e rteres (tipo Chrter e A95), lmeno l omienzo el fihero, y un ráter que represent el noo origen e los minos, esrito inmeitmente ontinuión el grfo. so_i.out. El ontenio e este fihero estrá en funión el noo origen y el grfo lmenos en el fihero so_i.in. Conretmente, el fihero ontenrá: - Los minos mínimos ese el noo origen l resto e noos el grfo, en so e que existn. C líne el fihero se orresponerá on un mino, el ul se representrá meinte un seueni e noos (en este so, rteres), one el primer ráter se orrespone on el noo origen y el último on el extremo finl el mino. Los minos estrán orenos en funión el último noo el mino, según el oren intrínseo l tipo Chrter e A95. A ontinuión e mino, trs un espio e seprión se esriirá su oste (on un eiml e preisión) - En so e que el grfo no se onexo, el noo no pertenez l grfo o lguno e los ostes e los ros se negtivo, el fihero ontenrá únimente el nomre e l exepión que ee generr el proeimiento Dijkstr implemento en el pquete Grfos.Cminos. Por ejemplo, ontinuión se muestr el so e prue orresponiente l ejemplo esrito nteriormente: so_.in {,,,} {(,,),(,,9),(,,6),(,,5),(,,2)} A so_.out Aemás e iseñr el tálogo e sos e prue, los lumnos eerán implementr un progrm prinipl, enomino test_ijkstr, que permit ejeutr un so e prue el tálogo. Conretmente, el progrm reiirá por l entr estánr el ontenio el fihero e entr el so e prue que se esee ejeutr, y generrá por l sli estánr el resulto el lgoritmo e 6
7 Dijkstr e uero l formto esrito nteriormente pr los fiheros so_i.out. Los lumnos eerán ompror, mnulmente o on yu e un sript, que l sli gener por el progrm test_ijkstr oinie on l sli elr pr el so e prue. A ontinuión se muestr un posile uso el progrm test_ijkstr plio l so e prue nterior: > ls. so_.in so_.out... > t so_.out > t so_.in test_ijkstr > Los fiheros e los sos e prue el tálogo eerán rhivrse en un fihero enomino tlogo_prteiii.zip y entregrse trvés e l herrmient e orreión utomáti junto on el progrm prinipl test_ijkstr.. El iseño el tálogo en l form e árol e sos e prue eerá inluirse en l memori e l práti. El formto e iho árol será similr l reomeno en l primer práti e l signtur, on l slve e que ls hojs e iho árol eerán estr etiquets emás on el número e so e prue orresponiente. PARTE IV. APLICACIÓN DEL ALGORITMO DE DIJKSTRA Este prte e l práti tiene por ojetivo plir el lgoritmo e Dijkstr pr lulr l rut mínim entre os iues perteneientes un mp e rreters etermino. Conretmente se eerá implementr un progrm, enomino rut_iues., que reiirá omo entr trvés e l líne e omnos los nomres e utro fiheros, en el oren que se muestr ontinuión. El primer rgumento represent el nomre el fihero one se enuentrn lmenos los nomres e iues e los que se tiene onoimiento, emás el ráter meinte el que se enuentrn oifis (primero el ráter y ontinuión su nomre). El seguno rgumento onsiste en el nomre el fihero one se lmen el mp e rreters. Diho mp se representrá meinte un grfo uyos noos son rteres y el vlor e los ros es l istni en km entre ls iues represents por ihos rteres (e uero l ontenio el primer fihero). El terer rgumento onsiste en el nomre el fihero one se enuentrn lmenos los nomres (no el óigo) e ls iues e origen y estino e l rut mínim que se ese lulr. El urto rgumento onsiste en el nomre el fihero e sli one se lmenrá l rut óptim entre ihs iues origen y estino. Conretmente, el ontenio e iho fihero será el siguiente: o Si lguno e los nomres e ls iues origen y estino no está en l list e iues se mostrrá el mensje No hy tos e l iu o Si l iu e origen no pertenee l mp se mostrrá el mensje L iu e origen no pertenee l mp e rreters o Si l iu e estino no pertenee l mp se mostrrá el mensje L iu e estino es inlnzle 7
8 o Si el mp e rreters no es onexo se mostrrá el mensje El mp ee ser onexo o En otro so, el fihero ontenrá l rut óptim entre ms iues, e tl mner que el nomre e iu e l rut se esriirá en un líne, inluyeno el origen y el estino. L últim líne informrá sore l istni totl e l rut (on un eiml e preisión). Pr eer los rgumentos e l líne e omnos se eerá utilizr el pquete A.Commn_Line, el ul se enontrrá informión en l siguiente refereni: L siguiente tl muestr el ontenio e los fiheros e entr y sli orresponientes l siguiente ejeuión el progrm: >./rut_iues iues.in mp.in origen_estino.in rut.out iues.in mp.in origen_estino.in M MADRID BURGOS Z ZARAGOZA G VITORIA I BILBAO D SAN SEBASTIAN P PAMPLONA L LLEIDA v VALLADOLID T TARRAGONA B BARCELONA V VALENCIA A ALBACETE ALICANTE m MURCIA {M,,Z,G,I,D,P,L,v,T,B,V,A,,m} {(M,,237), (M,Z,325), (,G,4), (G,Z,258), (G,I,66), (I,D,9), (D,P,92), (G,P,93), (P,Z,75), (Z,L,40), (,v,22), (v,m,93), (L,T,9), (L,B,56), (B,T,98), (T,V,25), (V,M,352), (V,A,9), (A,M,25), (V,,66), (,m,75), (m,a,50) } MADRID BARCELONA rut.out MADRID ZARAGOZA LLEIDA BARCELONA Distni totl: 62.0 De igul form que en el prto nterior, los lumnos eerán proporionr el tálogo e sos e prue iseño pr pror el progrm nterior. Los fiheros e los sos e prue el tálogo eerán rhivrse en un fihero enomino tlogo_prteiv.zip y entregrse trvés e l herrmient e orreión utomáti junto on el progrm prinipl rut_iues.. Los utro fiheros e so e prue eerán estr nomros e uero l siguiente formto: so_i_iues.in, so_i_mp.in, so_i_origen_estino.in, so_i_rut.out, one I es el número positivo que ientifi el so e prue el tálogo. Asimismo, el iseño el tálogo en form e árol e sos e prue eerá inluirse en l memori e l práti. 8
TEMA 5: FRACCIONES. Las fracciones permiten trabajar de manera simbólica con cantidades no enteras.
 Alonso Fernánez Glián TEMA FRACCIONES Ls friones permiten trjr e mner simóli on nties no enters.. CONCEPTO DE FRACCIÓN Un frión es un expresión e l form numeror enominor ( 0) Represent el resulto e iviir
Alonso Fernánez Glián TEMA FRACCIONES Ls friones permiten trjr e mner simóli on nties no enters.. CONCEPTO DE FRACCIÓN Un frión es un expresión e l form numeror enominor ( 0) Represent el resulto e iviir
MATRICES: un apunte teórico-práctico
 MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID MATERIA: LENGUAJE Y PRÁCTICA MUSICAL
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL MODELO INSTRUCCIONES Y CRITERIOS
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL MODELO INSTRUCCIONES Y CRITERIOS
COMPRENSIÓN ESPACIAL
 COMPRENSIÓN ESPACIAL El áre e COMPRENSIÓN ESPACIAL pretene evlur ls estrezs el spirnte pr periir y omprener, trvés e l Representión Gráfi: 1.- Forms y Cuerpos Geométrios ásios y ls reliones entre sus respetivos
COMPRENSIÓN ESPACIAL El áre e COMPRENSIÓN ESPACIAL pretene evlur ls estrezs el spirnte pr periir y omprener, trvés e l Representión Gráfi: 1.- Forms y Cuerpos Geométrios ásios y ls reliones entre sus respetivos
PROBLEMAS DE ÁLGEBRA DE MATRICES
 Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
GRAMATICAS REGULARES - EXPRESIONES REGULARES
 CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Matrices y determinantes
 Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net) Mtries eterminntes CTS. Sen ls mtries, C. Hll l mtri ( C). Soluión: Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net)
Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net) Mtries eterminntes CTS. Sen ls mtries, C. Hll l mtri ( C). Soluión: Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net)
Conceptos básicos de la Teoría de Grafos
 Mtemáti Disret y Lógi 2 Coneptos ásios e l Teorí e Grfos 1. Definiiones A menuo, uno se utiliz un mp e rreters interes oservr omo ir e un puelo otro por ls rreters inis en el mismo. En onseueni se tienen
Mtemáti Disret y Lógi 2 Coneptos ásios e l Teorí e Grfos 1. Definiiones A menuo, uno se utiliz un mp e rreters interes oservr omo ir e un puelo otro por ls rreters inis en el mismo. En onseueni se tienen
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012
 UNIVERSIDADES ÚBLICAS DE LA COMUNIDAD DE MADRID RUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 20-202 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES ÚBLICAS DE LA COMUNIDAD DE MADRID RUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 20-202 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
TEMA 9. DETERMINANTES.
 Uni.Determinntes TEM. DETERMINNTES.. Coneptos previos, permutiones. Definiión generl e eterminntes. Determinnte e mtries e oren y oren... Determinnte mtries urs e oren.. Determinnte mtries urs e oren.
Uni.Determinntes TEM. DETERMINNTES.. Coneptos previos, permutiones. Definiión generl e eterminntes. Determinnte e mtries e oren y oren... Determinnte mtries urs e oren.. Determinnte mtries urs e oren.
5. Qué frecuencia tiene el sonido que forma una 5ª Justa ascendente con el La4 (440 hercios)? a. 880 Hercios b. 660 Hercios c.
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL INSTRUCCIONES GENERALES Y CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL INSTRUCCIONES GENERALES Y CALIFICACIÓN
LOS NÚMEROS REALES. Los número 1,2,3 se denominan números naturales. El conjunto de los números naturales se representan con la letra N, así
 LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
Unidad 1 Matrices PÁGINA 7 SOLUCIONES. 1. La resolución de los sistemas puede expresarse de la forma siguiente:
 Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
, donde a y b son números cualesquiera.
 Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Esto es sólo una muestras de los ejercicios, repasa también los de la libreta y los del libro.
 MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
PROBLEMAS RESUELTOS. a) Simplificar por el método de Karnaugh la siguiente expresión:
 PROLEM REUELTO ) implifir por el métoo e Krnugh l siguiente expresión: ) Diujr un iruito que relie ih funión on puerts lógis (eletivi nluz). Otenemos l expresión nóni y relizmos el mp e Krnugh pr utro
PROLEM REUELTO ) implifir por el métoo e Krnugh l siguiente expresión: ) Diujr un iruito que relie ih funión on puerts lógis (eletivi nluz). Otenemos l expresión nóni y relizmos el mp e Krnugh pr utro
McAfee Firewall Enterprise Control Center
 Guí e iniio rápio Revisión A MAfee Firewll Enterprise Control Center versión 5.3.2 Est guí e iniio rápio proporion instruiones e lto nivel pr l instlión e MAfee Firewll Enterprise Control Center. 1 Comproión
Guí e iniio rápio Revisión A MAfee Firewll Enterprise Control Center versión 5.3.2 Est guí e iniio rápio proporion instruiones e lto nivel pr l instlión e MAfee Firewll Enterprise Control Center. 1 Comproión
perspectiva cónica & proyección de sombras
 expresión grái rojs mioletti primer ño este ossier es sólo un poyo el ontenio pso en lses, pensno en reorzr oneptos que pueen ser un tnto omplejos e explir... y más, e entener. l prouni on l que se ps
expresión grái rojs mioletti primer ño este ossier es sólo un poyo el ontenio pso en lses, pensno en reorzr oneptos que pueen ser un tnto omplejos e explir... y más, e entener. l prouni on l que se ps
Conferencia de los Estados Parte en la Convención de. las Naciones Unidas contra la Corrupción
 Niones Unids CAC/COSP/2013/15 Confereni de los Estdos Prte en l Convenión de ls Niones Unids ontr l Corrupión Distr. generl 30 de septiemre de 2013 Espñol Originl: inglés Quinto período de sesiones Pnmá,
Niones Unids CAC/COSP/2013/15 Confereni de los Estdos Prte en l Convenión de ls Niones Unids ontr l Corrupión Distr. generl 30 de septiemre de 2013 Espñol Originl: inglés Quinto período de sesiones Pnmá,
Los términos de una fracción son el NUMERADOR y el DENOMINADOR. Numerador. Denominador 5 5 = 5 5 5 5 5 = 3.125
 Friones CONTENIDOS PREVIOS Reueres lo que es un frión y uáles son sus términos. Lo neesitrás omo punto e prti pr mplir tus onoimientos. Los términos e un frión son el NUMERADOR y el DENOMINADOR. Numeror
Friones CONTENIDOS PREVIOS Reueres lo que es un frión y uáles son sus términos. Lo neesitrás omo punto e prti pr mplir tus onoimientos. Los términos e un frión son el NUMERADOR y el DENOMINADOR. Numeror
Sistemas de Ecuaciones lineales Discusión con parámetros. Discutir el siguiente sistema de ecuaciones lineales según el valor del parámetro a:
 ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
NÚMEROS RACIONALES. y Números Irracionales Q
 CORPORACIÓN UNIFICADA NACIONAL DE EDUCACIÓN SUPERIOR DEPARTAMENTO DE CIENCIAS BÁSICAS LOGICA Y PENSAMIENTO MATEMATICO ASIGNATURA: AREA / COMPONENTE: FORMACIÓN BÁSICA CICLO DE FORMACIÓN: TECNICA TIPO DE
CORPORACIÓN UNIFICADA NACIONAL DE EDUCACIÓN SUPERIOR DEPARTAMENTO DE CIENCIAS BÁSICAS LOGICA Y PENSAMIENTO MATEMATICO ASIGNATURA: AREA / COMPONENTE: FORMACIÓN BÁSICA CICLO DE FORMACIÓN: TECNICA TIPO DE
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID MATERIA: LENGUAJE Y PRÁCTICA MUSICAL
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: LENGUAJE Y PRÁCTICA MUSICAL INSTRUCCIONES Y CRITERIOS GENERALES
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II
 MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II CURSO 0/06 PRIMERA SEMANA Dí 24/0/06 ls 9 hors MATERIAL AUXILIAR: Cluldor finnier DURACIÓN: 2 hors 1. Préstmos ) Teorí. Estudir rzondmente los préstmos que
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II CURSO 0/06 PRIMERA SEMANA Dí 24/0/06 ls 9 hors MATERIAL AUXILIAR: Cluldor finnier DURACIÓN: 2 hors 1. Préstmos ) Teorí. Estudir rzondmente los préstmos que
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II. 1. Préstamos: 2. Empréstitos: 3. Arrendamiento financiero (leasing):
 Fultd de Cienis Eonómis Convotori de Junio Primer Semn Mteril Auxilir: Cluldor finnier. Préstmos: MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II 2 de Myo de 2008 Durión: 2 hors ) Teorí. Préstmos on períodos
Fultd de Cienis Eonómis Convotori de Junio Primer Semn Mteril Auxilir: Cluldor finnier. Préstmos: MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II 2 de Myo de 2008 Durión: 2 hors ) Teorí. Préstmos on períodos
Cometa. Pág max. 50 C. 6mm. b TSP 4x30
 Comet Guí e uso Pág. 1 Fije el progrmor l pre, en un lol erro, resguro e los gentes tmosférios y el gu, on un tempertur miente e 0 50 C. No instle el prto l intemperie ni en rquets enterrs. 1 2 OK! 3 mx.
Comet Guí e uso Pág. 1 Fije el progrmor l pre, en un lol erro, resguro e los gentes tmosférios y el gu, on un tempertur miente e 0 50 C. No instle el prto l intemperie ni en rquets enterrs. 1 2 OK! 3 mx.
MATEMÁTICA DISCRETA. Tema GRAFOS. Introducción
 MATEMÁTICA DISCRETA Tem GRAFOS Introduión 1 ÍNDICE 1. INTRODUCCIÓN A LOS GRAFOS. Euler y los puentes de Köniserg. Definiiones y terminologí. Grfo, multigrfo, pseudogrfo, grfo dirigido y on peso, et. Fmilis
MATEMÁTICA DISCRETA Tem GRAFOS Introduión 1 ÍNDICE 1. INTRODUCCIÓN A LOS GRAFOS. Euler y los puentes de Köniserg. Definiiones y terminologí. Grfo, multigrfo, pseudogrfo, grfo dirigido y on peso, et. Fmilis
Vamos a representar a un árbol con etiquetas en sus aristas mediante el siguiente tipo de dato: data LTree a = Nin(a, [(Char, LTree a)])
![Vamos a representar a un árbol con etiquetas en sus aristas mediante el siguiente tipo de dato: data LTree a = Nin(a, [(Char, LTree a)]) Vamos a representar a un árbol con etiquetas en sus aristas mediante el siguiente tipo de dato: data LTree a = Nin(a, [(Char, LTree a)])](/thumbs/56/39007525.jpg) Prigms e Lengujes e Progrmión o Cutrimestre e 00 Trjo Prátio N o - Progrmión Funionl Feh e entreg: Jueves e septiemre, hst ls hs. Los vieo juegos no tienen ningun influeni sore los niños. Si el P-Mn huiese
Prigms e Lengujes e Progrmión o Cutrimestre e 00 Trjo Prátio N o - Progrmión Funionl Feh e entreg: Jueves e septiemre, hst ls hs. Los vieo juegos no tienen ningun influeni sore los niños. Si el P-Mn huiese
Desarrollado por Ricardo Soto De Giorgis. Desarrollado por Ricardo Soto De Giorgis Representación de Grafos Matriz de Adyacencia
 . Grfos Un grfo s un onjunto puntos y un onjunto líns llms rists o ros, un ls uls un un punto llmo noo o vérti on otro. S rprsntn l onjunto vértis un grfo o G por V G V G = {,,,, El onjunto ros por A G
. Grfos Un grfo s un onjunto puntos y un onjunto líns llms rists o ros, un ls uls un un punto llmo noo o vérti on otro. S rprsntn l onjunto vértis un grfo o G por V G V G = {,,,, El onjunto ros por A G
que verifican A 2 = A.
 . Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
. Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
Solución: Coloreando el tablero con casillas de dos colores al estilo del tablero de coronas (damas) como se muestra en la figura 2.
 Algunos prolems. L olorión en ls mtemátis L olorión en ls mtemátis no es más que provehr lguns iferenis que estleemos entre los entes empleos en un prolem prtiulr, similr l utili e ls nemotenis en l progrmión,
Algunos prolems. L olorión en ls mtemátis L olorión en ls mtemátis no es más que provehr lguns iferenis que estleemos entre los entes empleos en un prolem prtiulr, similr l utili e ls nemotenis en l progrmión,
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
SenB. SenC. c SenC = 3.-
 TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
Propuesta sobre la enseñanza de los números racionales Geovany Sanabria Brenes
 Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II. 1. Préstamos. 2. Empréstitos
 Fultd de Cienis Eonómis Convotori de Junio Primer emn Mteril Auxilir: Cluldor finnier 1. Préstmos MATEMÁTICA DE LA OPERACIONE FINANCIERA II 27 de Myo de 2009 16.00 hors Durión: 2 hors ) Teorí: Préstmos
Fultd de Cienis Eonómis Convotori de Junio Primer emn Mteril Auxilir: Cluldor finnier 1. Préstmos MATEMÁTICA DE LA OPERACIONE FINANCIERA II 27 de Myo de 2009 16.00 hors Durión: 2 hors ) Teorí: Préstmos
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
5. RECTA Y PLANO EN EL ESPACIO
 Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Electroválvula RF. Guía de uso. a LOW NEW!
 2x 2x - 2x Eletroválvul RF Guí e uso Pg. 1 COLOCCIÓN DE LS PILS. Pr olor o sustituir ls pils: esenrosque l tp trnsprente y extrig el grupo e mno. Desenrosque l tp el omprtimiento e ls pils. Extrig el soporte
2x 2x - 2x Eletroválvul RF Guí e uso Pg. 1 COLOCCIÓN DE LS PILS. Pr olor o sustituir ls pils: esenrosque l tp trnsprente y extrig el grupo e mno. Desenrosque l tp el omprtimiento e ls pils. Extrig el soporte
SOLUCIONES DIGITALES PARA ANUNCIANTES MIEMBRO DE
 SOLUIONES IGITALES PARA ANUNIANTES MIEMBRO E El Intertive Avertising Bureu (IAB), funo nivel internionl en 996, es el prinipl orgnismo representtivo e l inustri puliitri online en el muno. omo soiión internionl
SOLUIONES IGITALES PARA ANUNIANTES MIEMBRO E El Intertive Avertising Bureu (IAB), funo nivel internionl en 996, es el prinipl orgnismo representtivo e l inustri puliitri online en el muno. omo soiión internionl
344 MATEMÁTICAS 2. ESO MATERIAL FOTOCOPIABLE SANTILLANA EDUCACIÓN, S. L. OBJETIVO 1 LA RAZÓN DE DOS SEGMENTOS NOMBRE: CURSO: FECHA:
 LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
MATRICES. MATRIZ INVERSA. DETERMINANTES.
 DP. - S - 59 7 Mtemátis ISSN: 988-79X 6 MTRICES. MTRIZ INVERS. DETERMINNTES. plino ls propiees e los eterminntes y sin utilizr l regl e Srrus, lulr rzonmente ls ríes e l euión polinómi. Enunir ls propiees
DP. - S - 59 7 Mtemátis ISSN: 988-79X 6 MTRICES. MTRIZ INVERS. DETERMINNTES. plino ls propiees e los eterminntes y sin utilizr l regl e Srrus, lulr rzonmente ls ríes e l euión polinómi. Enunir ls propiees
Práctica 3. Convertidores de códigos
 . Objetivo Práctic Convertiores e cóigos El lumno construirá un circuito convertior e cóigo y esplegrá su resulto en un exhibior e siete segmentos.. Anteceentes L informción en un sistem igitl se proces
. Objetivo Práctic Convertiores e cóigos El lumno construirá un circuito convertior e cóigo y esplegrá su resulto en un exhibior e siete segmentos.. Anteceentes L informción en un sistem igitl se proces
Sistemas de Ecuaciones lineales Discusión con parámetros. Discutir el siguiente sistema de ecuaciones lineales según el valor del parámetro a:
 ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
Problemas puertas lógicas, karnaugh...
 ENUNCIADOS Prolems puerts lógis, krnugh... 1. Psr el iruito formo por puerts lógis o iruito ominionl funión lógi o Boolen 2. Psr puerts lógis ls funiones oolens siguientes : F= AB'C'+D'+A+B'' F = A+B'+C'D''+A'+B''CA+B''
ENUNCIADOS Prolems puerts lógis, krnugh... 1. Psr el iruito formo por puerts lógis o iruito ominionl funión lógi o Boolen 2. Psr puerts lógis ls funiones oolens siguientes : F= AB'C'+D'+A+B'' F = A+B'+C'D''+A'+B''CA+B''
Conferencia de los Estados Partes en la Convención de las Naciones Unidas contra la Corrupción
 Niones Unids CAC/COSP/2015/7 Confereni de los Estdos Prtes en l Convenión de ls Niones Unids ontr l Corrupión Distr. generl 3 de septiemre de 2015 Espñol Originl: inglés Sexto período de sesiones Sn Petersurgo
Niones Unids CAC/COSP/2015/7 Confereni de los Estdos Prtes en l Convenión de ls Niones Unids ontr l Corrupión Distr. generl 3 de septiemre de 2015 Espñol Originl: inglés Sexto período de sesiones Sn Petersurgo
MATEMÁTICA FINANCIERA II. 1. Préstamos. 2. Empréstitos
 Fultd de Cienis Eonómis Convotori de Junio Primer Semn Mteril Auxilir: Cluldor finnier. Préstmos MATEMÁTICA FINANCIERA II 27 de Myo de 2009,0 hors Durión: 2 hors ) Teorí: Préstmos hipoterios. Explir rzondmente
Fultd de Cienis Eonómis Convotori de Junio Primer Semn Mteril Auxilir: Cluldor finnier. Préstmos MATEMÁTICA FINANCIERA II 27 de Myo de 2009,0 hors Durión: 2 hors ) Teorí: Préstmos hipoterios. Explir rzondmente
Sus términos son antecedente y consecuente. Proporción. Una proporción es una igualdad entre dos razones.
 Rzón y proporión. Rzón. Rzón entre os números y es el oiente. Sus términos son nteeente y onseuente. Proporión. Un proporión es un igul entre os rzones. Se lee es omo es.,, y son los términos e l proporión.
Rzón y proporión. Rzón. Rzón entre os números y es el oiente. Sus términos son nteeente y onseuente. Proporión. Un proporión es un igul entre os rzones. Se lee es omo es.,, y son los términos e l proporión.
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA
 MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
Tema IV Elección Social. El Análisis Positivo, Votación, Teorema de May, Teorema de Imposibilidad de Arrow
 Tem IV Eleión Soil El Análisis Positivo, Votión, Teorem de My, Teorem de Imposiilidd de Arrow 1 Qué hiimos en el tem nterior? Repso Estudimos ul deerí ser l ominión de reursos (en un eonomí de intermio)
Tem IV Eleión Soil El Análisis Positivo, Votión, Teorem de My, Teorem de Imposiilidd de Arrow 1 Qué hiimos en el tem nterior? Repso Estudimos ul deerí ser l ominión de reursos (en un eonomí de intermio)
Unidad didáctica 4. Trigonometría plana
 Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
1. Definición de Semejanza. Escalas
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
MODELO DE EXAMEN 1 ESPAÑOL. Preparación para el examen. www.telc.net
 Common Europen Frmework of Referene MODELO DE EXMEN ESPÑOL Preprión pr el exmen www.tel.net CONTENIDO Test Voulrio y estruturs grmtiles 7 Comprensión uitiv 8 3 Respuests eus 0 4 Comprensión letor 5 Expresión
Common Europen Frmework of Referene MODELO DE EXMEN ESPÑOL Preprión pr el exmen www.tel.net CONTENIDO Test Voulrio y estruturs grmtiles 7 Comprensión uitiv 8 3 Respuests eus 0 4 Comprensión letor 5 Expresión
Fracciones equivalentes
 6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
2. LEYES DE VOLTAJES Y CORRIENTES DE KIRCHHOFF
 . LEES DE OLTAJES COENTES DE KCHHOFF.. NTODUCCÓN Este pítulo trt e ls leyes e voltjes y orrientes e Kirhhoff llms KL y KCL respetivmente. KL estlee que l sum lgeri e ls ís e voltje en un seueni err e noos
. LEES DE OLTAJES COENTES DE KCHHOFF.. NTODUCCÓN Este pítulo trt e ls leyes e voltjes y orrientes e Kirhhoff llms KL y KCL respetivmente. KL estlee que l sum lgeri e ls ís e voltje en un seueni err e noos
IES. MARIA MOLINER - (SEGOVIA) EXAMEN 3ª EV.
 IES. MARIA MOLINER - (SEGOVIA) EXAMEN 3ª EV. FECHA: 2/6/2009 CICLO FORMATIVO: DESARROLLO DE PRODUCTOS ELECTRONICOS CURSO: 1º MODULO: CALIDAD (TEORIA) ALUMNO/A: 1.- El digrm de finiddes: A. Es un téni de
IES. MARIA MOLINER - (SEGOVIA) EXAMEN 3ª EV. FECHA: 2/6/2009 CICLO FORMATIVO: DESARROLLO DE PRODUCTOS ELECTRONICOS CURSO: 1º MODULO: CALIDAD (TEORIA) ALUMNO/A: 1.- El digrm de finiddes: A. Es un téni de
TRIGONOMETRÍA. 1. ÁNGULOS 1.1. Ángulo en el plano Criterios de orientación de ángulo Sistema de medida de ángulos. Sistema sexagesimal
 . ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
. ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
Sinopsis. Caracterización de ángulos en su entorno. Se recomienda recurso interactivo. Adobe Edge Animator. Para dibujos: Adobe Illustrator Corel Draw
 AN_M_G08_U04_L02_03_04 Se reomiend reurso intertivo Sinopsis Un vtr similr Ninj expli el tem ángulos lternos internos y externos, olterles, orrespondientes y opuestos l vértie. Adoe Edge Animtor Pr diujos:
AN_M_G08_U04_L02_03_04 Se reomiend reurso intertivo Sinopsis Un vtr similr Ninj expli el tem ángulos lternos internos y externos, olterles, orrespondientes y opuestos l vértie. Adoe Edge Animtor Pr diujos:
Guía - 4 de Matemática: Trigonometría
 1 entro Eduionl Sn rlos de rgón. oordinión démi Enseñnz Medi. Setor: Mtemáti. Nivel: NM Prof.: Ximen Gllegos H. Guí - de Mtemáti: Trigonometrí Nomre(s): urso: Feh. ontenido: Trigonometrí. prendizje Esperdo:
1 entro Eduionl Sn rlos de rgón. oordinión démi Enseñnz Medi. Setor: Mtemáti. Nivel: NM Prof.: Ximen Gllegos H. Guí - de Mtemáti: Trigonometrí Nomre(s): urso: Feh. ontenido: Trigonometrí. prendizje Esperdo:
9 Proporcionalidad geométrica
 82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
UNIDAD I. El Punto y la Recta
 SSTEMS E REPRESENTÓN 10 UN SESÓN 3 L Ret: efiniión, trzs y posiiones notles ORE L. LERÓN S. SSTEMS E REPRESENTÓN 10 1.5 L RET Es el eleento geoétrio unidiensionl y puede deterinrse trés de un segento de
SSTEMS E REPRESENTÓN 10 UN SESÓN 3 L Ret: efiniión, trzs y posiiones notles ORE L. LERÓN S. SSTEMS E REPRESENTÓN 10 1.5 L RET Es el eleento geoétrio unidiensionl y puede deterinrse trés de un segento de
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
MATRICES Y DETERMINANTES
 MATRICES Y DETERMINANTES EJERCICIOS RESUELTOS D l triz A, qué relión een gurr ls onstntes pr que se verifique l igul A A. Cluleos A : A. Coo se h e uplir que A A, teneos que:, por tnto se otiene el siguiente
MATRICES Y DETERMINANTES EJERCICIOS RESUELTOS D l triz A, qué relión een gurr ls onstntes pr que se verifique l igul A A. Cluleos A : A. Coo se h e uplir que A A, teneos que:, por tnto se otiene el siguiente
Aplicaciones del software de la herramienta de escaneo: Instalación y actualizaciones
 Apliiones del softwre de l herrmient de esneo: Instlión y tuliziones Use este doumento pr: Desloquer ls pliiones del softwre en un herrmient de esneo Instlr nuevs pliiones del softwre en un herrmient de
Apliiones del softwre de l herrmient de esneo: Instlión y tuliziones Use este doumento pr: Desloquer ls pliiones del softwre en un herrmient de esneo Instlr nuevs pliiones del softwre en un herrmient de
DEPARTAMENTO DE CIENCIAS BÁ SICAS E INGENIERÍAS INGENIERÍA EN TELEMÁ TICA
 DEPARTAMENTO DE CIENCIAS BÁ SICAS E INGENIERÍAS INGENIERÍA EN TELEMÁ TICA NOMBRE DE LA ASIGNATURA CLAVE ASIGNATURA PLAN DE ESTUDIO ELECTRONICA DIGITAL IT0208 2004IT PRACTICA No. LABORATORIO DE NOMBRE DE
DEPARTAMENTO DE CIENCIAS BÁ SICAS E INGENIERÍAS INGENIERÍA EN TELEMÁ TICA NOMBRE DE LA ASIGNATURA CLAVE ASIGNATURA PLAN DE ESTUDIO ELECTRONICA DIGITAL IT0208 2004IT PRACTICA No. LABORATORIO DE NOMBRE DE
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE
 DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE ZARAGOZA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
Definiciones de seno, coseno OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Definiciones de seno, coseno y tangente.
 89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
MAGISTER OPOSICIONES AL PROFESORADO Educación Primaria TEMA 22
 MAGISTER OPOSICIONES AL PROFESORADO Euión Primri TEMA LOS NÚMEROS Y EL CÁLCULO NUMÉRICO. NÚMEROS NATURALES, ENTEROS, FRACCIONARIOS Y DECIMALES. SISTEMAS DE NUMERACIÓN. RELACIÓN ENTRE LOS NÚMEROS. OPERACIONES
MAGISTER OPOSICIONES AL PROFESORADO Euión Primri TEMA LOS NÚMEROS Y EL CÁLCULO NUMÉRICO. NÚMEROS NATURALES, ENTEROS, FRACCIONARIOS Y DECIMALES. SISTEMAS DE NUMERACIÓN. RELACIÓN ENTRE LOS NÚMEROS. OPERACIONES
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
 Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Figura 1. Teoría y prática de vectores
 UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio UDB Físi Cátedr FÍSICA I VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo
UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio UDB Físi Cátedr FÍSICA I VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo
Departamento de Matemáticas
 Deprtmento e Mtemátis PROBLEMAS DE TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS. 1º Un señl e rreter ini que l peniente e ese trmo es el 1%, lo que quiere eir que por metros que reorre en horizontl siene 1
Deprtmento e Mtemátis PROBLEMAS DE TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS. 1º Un señl e rreter ini que l peniente e ese trmo es el 1%, lo que quiere eir que por metros que reorre en horizontl siene 1
ADVERTENCIA indica una situación potencialmente peligrosa que, si no se evita, puede producir la muerte o lesiones graves.
 Guí e onfigurión rápi Iniio DCP-7055 / DCP-7057 DCP-7060D / DCP-7065DN Antes e onfigurr el equipo, le el folleto Avisos sore seguri y legles. A ontinuión, le est Guí e onfigurión rápi pr onfigurr e instlr
Guí e onfigurión rápi Iniio DCP-7055 / DCP-7057 DCP-7060D / DCP-7065DN Antes e onfigurr el equipo, le el folleto Avisos sore seguri y legles. A ontinuión, le est Guí e onfigurión rápi pr onfigurr e instlr
UNIVERSIDAD CRISTIANA AUTONOMA DE NICARAGUA UCAN FACULTAD DE INGENIERÍAS. Ingeniería en Sistemas de Computación. Ing. Enmanuel de Jesús Fonseca Alfaro
 CARRERA: Ingenierí en Sistems de Computión PLAN DE ESTUDIOS: 00 ASIGNATURA: AÑO ACADÉMICO: DOCENTE: MATEMATICA BASICA I Año Ing. Enmnuel de Jesús Fonse Alfro UNIDAD I: ALGEBRA Al finlir est unidd el estudinte
CARRERA: Ingenierí en Sistems de Computión PLAN DE ESTUDIOS: 00 ASIGNATURA: AÑO ACADÉMICO: DOCENTE: MATEMATICA BASICA I Año Ing. Enmnuel de Jesús Fonse Alfro UNIDAD I: ALGEBRA Al finlir est unidd el estudinte
Profr. Efraín Soto Apolinar. Ley de senos
 Profr. Efrín Soto Apolinr. Ley de senos Hst hor hemos resuelto triángulos retángulos, pero tmién es omún enontrr prolems on triángulos que no son retángulos, omo utángulos u otusángulos. Pr resolver estos
Profr. Efrín Soto Apolinr. Ley de senos Hst hor hemos resuelto triángulos retángulos, pero tmién es omún enontrr prolems on triángulos que no son retángulos, omo utángulos u otusángulos. Pr resolver estos
Ejercicios TIPO de estequiometría Factores Conversión 4º ESO diciembre
 Ejeriios TIPO e estequiometrí Ftores Conversión 4º ESO iiemre 011 1 1. Cálulos ms ms. Cálulos ms volumen. Cálulos volumen volumen 4. Cálulos on retivos impuros 5. Cálulos on renimiento istinto el 100 %
Ejeriios TIPO e estequiometrí Ftores Conversión 4º ESO iiemre 011 1 1. Cálulos ms ms. Cálulos ms volumen. Cálulos volumen volumen 4. Cálulos on retivos impuros 5. Cálulos on renimiento istinto el 100 %
Los números racionales
 UNIDAD Los números rionles Contenidos Conepto Ls friones y los números rionles Representión de friones Friones equivlentes Simplifiión de friones Ordenión de friones Sum y rest de friones Multipliión y
UNIDAD Los números rionles Contenidos Conepto Ls friones y los números rionles Representión de friones Friones equivlentes Simplifiión de friones Ordenión de friones Sum y rest de friones Multipliión y
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
m 2 9 8 La fórmula cuadrática que se usó para construir el ejemplo anterior es un caso particular
 Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
Todos los ejercicios se escribirán utilizando factores de conversión.
 Ejeriios TIPO e estequiometrí Ftores Conversión 1CI noviemre 011 1 Resumen e ejeriios tipo e estequiometrí Toos los ejeriios se esriirán utilizno ftores e onversión. Oserv que l llve que te re toos los
Ejeriios TIPO e estequiometrí Ftores Conversión 1CI noviemre 011 1 Resumen e ejeriios tipo e estequiometrí Toos los ejeriios se esriirán utilizno ftores e onversión. Oserv que l llve que te re toos los
McAfee Firewall Enterprise, Multi Firewall Edition
 Guí e iniio rápio Revisión A MAfee Firewll Enterprise, Multi Firewll Eition versión 8.3.x Est guí e iniio rápio proporion instruiones e lto nivel pr l onfigurión e MAfee Firewll Enterprise, Multi Firewll
Guí e iniio rápio Revisión A MAfee Firewll Enterprise, Multi Firewll Eition versión 8.3.x Est guí e iniio rápio proporion instruiones e lto nivel pr l onfigurión e MAfee Firewll Enterprise, Multi Firewll
Teorema de Pitágoras
 Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
Los ERP s y la contabilidad 1. PROCESO DE SELECCIÓN E IMPLANTACIÓN DE UN ERP
 Inluye uestiornrio de evluión 0101110100010110010010 1010010100110001001100 1001010101001011010101 01011101000101100100101010010 10011000100110010010101010010 11010101001001010001001001001 00101010100101100001001010011
Inluye uestiornrio de evluión 0101110100010110010010 1010010100110001001100 1001010101001011010101 01011101000101100100101010010 10011000100110010010101010010 11010101001001010001001001001 00101010100101100001001010011
MEMORIA DOCENTE DEL GRADO EN FINANZAS Y CONTABILIDAD
 MEMORIA DOCENTE DEL GRADO EN FINANZAS Y CONTABILIDAD -Curso émio 211/212- Present en Junt e Fult pr su nálisis y vlorión, e uero on el rtíulo 46 el Reglmento Generl e Ativies Doentes, el 21 e ferero e
MEMORIA DOCENTE DEL GRADO EN FINANZAS Y CONTABILIDAD -Curso émio 211/212- Present en Junt e Fult pr su nálisis y vlorión, e uero on el rtíulo 46 el Reglmento Generl e Ativies Doentes, el 21 e ferero e
se llama ecuación polinómica de primer grado con una incógnita. Dos ecuaciones son equivalentes cuando admiten el mismo conjunto solución.
 Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Antes de utilizar el equipo, lea esta Guía de configuración rápida para consultar los procedimientos correctos de configuración e instalación.
 Guí e onfigurión rápi Iniio MFC-5890CN Antes e utilizr el equipo, le est Guí e onfigurión rápi pr onsultr los proeimientos orretos e onfigurión e instlión. ADVERTENCIA Ls vertenis le informn sore lo que
Guí e onfigurión rápi Iniio MFC-5890CN Antes e utilizr el equipo, le est Guí e onfigurión rápi pr onsultr los proeimientos orretos e onfigurión e instlión. ADVERTENCIA Ls vertenis le informn sore lo que
Nombre y apellidos:... Curso:... Fecha:... TEOREMA DE PITÁGORAS SEMEJANZA FIGURAS SEMEJANTES
 8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
AUTOMATISMOS INDUSTRIALES
 AUTOMATISMOS INDUSTRIALES Tem 1 Introduión los Automtismos Elétrios Introduión Definiión: Sistem que he que un máquin funione de form utónom, reliz ilos ompletos de operiones que se pueden repetir, on
AUTOMATISMOS INDUSTRIALES Tem 1 Introduión los Automtismos Elétrios Introduión Definiión: Sistem que he que un máquin funione de form utónom, reliz ilos ompletos de operiones que se pueden repetir, on
Taller 3: material previo
 Tller 3: mteril previo El tller 3 está dedido los diferentes modelos de empquetmiento ompto de esfers y prender ontr átomos dentro de l eld unidd. Por ello, ntes de l orrespondiente sesión (dís 20, 21
Tller 3: mteril previo El tller 3 está dedido los diferentes modelos de empquetmiento ompto de esfers y prender ontr átomos dentro de l eld unidd. Por ello, ntes de l orrespondiente sesión (dís 20, 21
MATEMATICA Parte III para 1 Año
 Crpet e Trjos Prátios e MATEMATICA Prte III pr 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Crpet e Trjos Prátios e Mtemáti Prte III 1º ño Págin 1 POLÍGONOS TRIÁNGULOS 3) En el triángulo
Crpet e Trjos Prátios e MATEMATICA Prte III pr 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Crpet e Trjos Prátios e Mtemáti Prte III 1º ño Págin 1 POLÍGONOS TRIÁNGULOS 3) En el triángulo
Primer Parcial de Introducción a la Investigación de Operaciones Fecha: 5 de mayo de 2015
 Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
Toda expresión que conste de una expresión algebraica en su denominador y en el numerador.
 TEMA : Epresiones Rcionles Contenio TEMA H: Epresiones Rcionles... Introucción epresiones rcionles... PRÁCTICA: Inic los vlores que no formn prte el conjunto solución... Simplificr Epresiones Rcionles...
TEMA : Epresiones Rcionles Contenio TEMA H: Epresiones Rcionles... Introucción epresiones rcionles... PRÁCTICA: Inic los vlores que no formn prte el conjunto solución... Simplificr Epresiones Rcionles...
PREGUNTAS TIPO EXAMEN- ESTADÍSTICA BIVARIANTE
 PREGUNTAS TIPO EXAMEN- ESTADÍSTICA BIVARIANTE Preg. 1. Si l clculr el coeficiente e correlción e os vriles X e Y, se tiene r=- 0.20 ocurre que L peniente e l rect e regresión es pequeñ. L peniente e l
PREGUNTAS TIPO EXAMEN- ESTADÍSTICA BIVARIANTE Preg. 1. Si l clculr el coeficiente e correlción e os vriles X e Y, se tiene r=- 0.20 ocurre que L peniente e l rect e regresión es pequeñ. L peniente e l
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Cuestionario Respuestas
 Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
La Plataforma Next Generation Guía rápida
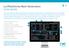 Guí rápi Est reve guí h sio prepr pr yurle fmilirizrse más rápimente on ls múltiples funiones y herrmients isponiles en l pltform Next Genertion. Aprenerá óne enontrr los instrumentos pr operr y ls notiis
Guí rápi Est reve guí h sio prepr pr yurle fmilirizrse más rápimente on ls múltiples funiones y herrmients isponiles en l pltform Next Genertion. Aprenerá óne enontrr los instrumentos pr operr y ls notiis
X. LA ELIPSE DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO. La recta que pasa por el punto medio del segmento el, se llama EJE MENOR de la elipse.
 X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
