1. Desafío inicial Cálculo de dosis, concentraciones y disoluciones Conceptos previos: Actividades... 9
|
|
|
- José Carlos Torres Poblete
- hace 7 años
- Vistas:
Transcripción
1 Índice 1. Desfío inicil Qué es un rzón? Ejemplos Ts: un rzón especil usd en el áre de l slud Qué es un proporción? Propiedd fundmentl en un proporción Otrs propieddes de ls proporciones Proporción direct (vriciones directmente proporcionles) Proporción indirect (vriciones inversmente proporcionles) Proporcionlidd compuest Ejemplo Ejercicios Porcentjes(=Tnto por ciento) Qué es? Frcciones y porcentjes Cálculo de porcentjes Porcentje de un número Incrementr/disminuir un número en un porcentje Qué porcentje represent un número de otro Cálculo de dosis, concentrciones y disoluciones Conceptos previos: Actividdes Bibliogrfi (dicionl l del curso) 10 1
2 1. Desfío inicil En un ciert poblción el 40 % de los hombres están csdos y el 30 % de ls mujeres están csds. Qué porcentje de l poblción dult está csd? Qué es un rzón? Un rzón entre dos cntiddes es un comprción por cuociente. Asi, l rzón entre los números y b, correspponde b o bien : b lo que se lee: es b Not: En l rzón, se llm ntecedente y b consecuente. b 2.2. Ejemplos Se el número de hombres presentes y b el de mujeres, entonces es l rzón entre ls cntiddes b indicds. Qué represent? 40 uniddes de un medicmento se deben se deben reprtir en dos hbitciones en l rzón 3 : 7. Cuántos medicmentos se llevn cd hbitción? En hospitl con 380 enfermos y 95 enfermers, l rzón serí: rzón de enfermos enfermers = = 4 1 = 4 : 1 lo que indic que hy 4 enfermos por cd enfermer, o bien rzón de enfermers enfermos = = 1 4 = 1 : 4 lo que indic que hy un enfermer por cd enfermo Ts: un rzón especil usd en el áre de l slud El concepto de ts es similr l de un rzón, con l diferenci de que ls tss llevn incorpordo el concepto de tiempo. Tomn todos los csos de un evento (enfermedd o muerte) por un cus, pertenecientes un poblción totl, en un lugr y período determindo. Ejemplos, En nuestro pís: Ts de mortlidd por ccidentes de tránsito (2009): Ncimiento de niños con bjo peso (2009): 5, ,
3 Mtemátic (2015-1) Médicos por hbitntes (2009): Enfermers (trbjndo en el sector público) por hbitntes (2009): Relción del número de enfermers por médico (2009): 1 2 Tss de ntlidd Qué es un proporción? Un proporción es l iguldd entre dos rzones. Asi entonces, 4 números, b, c y d conformn un proporción, siempre y cundo, se cumpl que: b = c d Propiedd fundmentl en un proporción b = c d d = bc Otrs propieddes de ls proporciones Si 4 números, b, c y d conformn un proporción, es decir, entonces tmbien constituyen un proporción: 1) + b b 2) b b = c + d d = c d d b = c d, 1 Número de ncidos vivos ocurridos en un territorio por cd mil hbitntes del mismo, en un período ddo. 3
4 Mtemátic (2015-1) 3) + b 4) b = c + d c = c d c 5) + b b = c + d c d 6) Si b = c d = e f entonces b = c d = e f = + c + d b + d + f 2.5. Proporción direct (vriciones directmente proporcionles) Dos mgnitudes son directmente proporcionles (DP) cundo l umentr un de ells, l otr tmbién ument en l mism proporción; y si un disminuye, l otr tmbién disminuye en l mism proporción Dos cntiddes A y B se dicen DP cundo su cuociente es constnte, es decir A B = k, o bien A = kb donde k es l constnte, que usulmente recibe el nombre de constnte de proporcionlidd. Por ejemplo, l longitud de un circunferenci es DP (o, simplemente proporcionl) l rdio. En efecto L r = k donde k, en este cso, es igul 2π Proporcionr otros ejemplos Proporción indirect (vriciones inversmente proporcionles) Dos mgnitudes son inversmente proporcionles (IP) cundo l umentr (disminuir) un de ells, l otr disminuye (ument) en l mism proporción. Dos cntiddes A y G se dicen IP cundo su producto es constnte, es decir donde k es constnte. AB = k, o bien A = k B Por ejemplo, pr el recorrido en uto de un mism distnci, l velocidd y el tiempo son cntiddes IP. En efecto: vt = k donde k, en este cso, es igul igul l distnci (constnte). Proporcionr otros ejemplos. 4
5 2.7. Proporcionlidd compuest En l proporcionlidd compuest hy vribles que se relcionn medinte proporcionlidd direct y otrs trvés de proporcionlidd invers. Pr resolver los ejercicios de este tem, en primer lugr se debe revisr qué tipo de proporcionlidd existe entre cd pr de vribles. Posteriormente, se debe determinr l constnte de proporcionlidd Ejemplo Se necesitn 20 persons pr pvimentr 2 km de cmino en 5 dís. Cuánts persons se necesitn pr pvimentr 5 km en 10 dís? Metodo 1 En primer lugr, determinremos qué tipo de proporcionlidd existe entre ls vribles: Persons (P) longitud del cmino (L): están en proporcionlidd direct (entre más persons, más km de cmino se pvimentrán) Persons (P) tiempo (T) están en proporcionlidd invers (entre más persons, menos tiempo se demorrán en pvimentr el cmino) Luego, P fijo T fijo T fijo P L T respuest Metodo 2 Se prte de un tbl como l siguiente: P L T x 5 10 Se estudin si ls vribles son direct o inversmente proporcionles. Si son DP, si combinn con un flech oblicu, en cso contrrio, con un flech horizontl. Hciéndolo, l tbl nterior qued: P L T x
6 Mtemátic (2015-1) Luego, se formn e iguln los productos que siguen ls flechs con los otros, en este cso, qued: = x 2 10 se donde, x = 25, que y hbímos obtenido con el método 1. Not: Es clro que pr situciones de más de 3 vribles, el método 2 es mucho más práctico Ejercicios Siguiendo los 2 métodos nteriores, resolver: 1) Pr clentr 2 litros de gu desde 0 o C 20 o C se hn necesitdo 1000 clorís. Si de quieren clentr 3 litros de gu de 10 o C 60 o C Cuánts clorís son necesris? 2) Seis fotocopidors trdn 5 minutos en hcer 600 fotocopis. Si se ponen en funcionmiento 2 fotocopidors y se quieren hcer 1800 fotocopis, cuánto minutos trdrán? 3. Porcentjes(=Tnto por ciento) Not. El PIB en nuestro pís el ño 2010 fue de millones de euros Qué es? Comentr l informción 2 : 2 6
7 Lo destcble es que myor riquez los píses gstn proporcionlmente más en slud. Así, USA gst el 17,6 % de su PIB en slud, mientrs que los píses europeos más desrrolldos gstn cerc del 12 % del PIB. Chile gst el 8 % de su PIB en el rubro y el promedio en l OECD es de un 9,5 %. Cómo se clcul el por ciento de b?. Qué represent? 3.2. Frcciones y porcentjes 1) Porcentje frcción: 20 %=??? 2) Frcción porcentje: 1=??? % 2 3) Porcentje deciml: 58 %=??? 4) Deciml porcentje: 2.16=??? % 3.3. Cálculo de porcentjes Porcentje de un número Clculr el 15 % de 85. 1) Solución 1: 15 % de 85 = = 12, ) Solución 2: % x 15 % x = = 12,75 por tnto, el 15 % de 85 es 12, Incrementr/disminuir un número en un porcentje Un pciente tom un 50mg de un medicmento l 8 de l mñn, si el pciente elimin un 10 % del medicmento presente en su cuerpo, por cd hor trnscurrid. Qué prte del medicmento tendrá el pciente l 1 de l trde? 7
8 Qué porcentje represent un número de otro qué porcentje represent 24 de 1200? 1) Solución 1: 2) Solución 2: x % de 1200 = 24 x 1200 = 24 x = por tnto, 24 represent el 2 % de 1, % 24 x % x = = 2 4. Cálculo de dosis, concentrciones y disoluciones 4.1. Conceptos previos: Dosis 3 : es l cntidd de medicmento que se debe dministrr pr producir el efecto terpéutico desedo. L dosis hce referenci l cntidd de medicmento dministrr de un sol vez. En cso contrrio es necesrio especificr l put de dosificción: dosis/dí, dosis/ciclo. Cntidd totl de medicmento: Indic l cntidd totl de medicmento que hy que dministrr durnte un trtmiento completo. Disolución: es l mezcl homogéne resultnte trs disolver culquier sustnci en un líquido. En un disolución, es posible distinguir entre el soluto (l sustnci que se disuelve en l mezcl y que suele precer en menor cntidd) y el disolvente o solvente (l sustnci donde se disuelve el soluto). Concentrción de l disolución: es l relción entre l cntidd de soluto y l cntidd de disolvente. A myor proporción de soluto disuelto, myor concentrción, y vicevers. 1) Porcentje peso en peso: es cundo tnto l cntidd de soluto como l de l disolución se expres en peso. Se represent por p/p. Ejemplo: Glucos 5 % p/p = 5 g de glucos en 100 g de solución. 2) Porcentje peso en volumen: es cundo l cntidd de soluto se expres en peso y l disolución en volumen. Se represent por p/v. Ejemplo: Glucos 5 % p/v = 5 g de glucos en 100 ml de solución. 3) Porcentje volumen en volumen: es cundo l cntidd de soluto y l disolución se expresn en volumen. Se represent por v/v. Ejemplo: Glicerin 5 % v/v = 5 ml de glicerin en 100 ml de disolución. Dilución de medicmentos: Es el procedimiento medinte el cul se obtienen, concentrciones y dosis requerids de medicmentos trvés de fórmuls mtemátics. 3 Est sección h seguido el punte: Cálculo básicos en frmci hospitlri uxilires/re5.pdf 8
9 4.2. Actividdes 1) Cntidd de medicmento que hy en un cntidd determind de solución Se hn dministrdo un niño 7,5ml de un solución de digoxin que tiene un concentrción del 0,25mg / 5ml. Qué cntidd de digoxin se le h ddo l niño? Respuest: 0,375mg de digoxin 2) Cntidd de solución que se debe tomr de modo que ell conteng l cntidd de medicmento que se requiere. Es necesrio dministrr un niño 375mg de mpicilin. El vil de mpicilin contiene 2ml de solución con 500mg de mpicilin. Qué volumen de solución de mpicilin se debe tomr pr dministrr los 375mg de mpicilin? Respuest: 1,5ml de solución. 3) Cntidd de medicmento y de disolvente que se tiene que mezclr pr preprr un determind solución. Hy que dministrr un pciente 375mg de ácido cetilslicílico (AAS). Si un comprimido de 3gr de AAS tiene un concentrción de 500mg/2g. Qué cntidd de comprimido hy que dministrr? Respuest: 1 comprimido y medio 4) Conversión de un concentrción expresd en form de rzón en porcentje y vicivers Un vil de mpicilin contiene un solución del fármco l concentrción de 250mg/ml. Cuál es l concentrción de mpicilin expresd en porcentje? Not: El porcentje de concentrción se expres en g/100ml. Respuest: 25 % 5) Cntidd de un solución determind que se debe tomr pr preprr otr solución con distint concentrción Cómo se preprn 500ml de un solución de lidocín l 2 %, si se dispone de un solución de este fármco l 5 %? Respuest: 200ml de l solución l 5 % más 300ml de gu destild. 6) Cálculo de un dosis según el peso del pciente Se precis dministrr gentmicin un pciente de 65kg de peso. L dosis hbitul de gentmicin es de 1,5 mg/kg cd 8 hors. Qué dosis hy que dministrr l pciente? Respuest: 97,5mg 7) Clculo de dosis según l edd En este cso, usulmente se estblecen dosis por grupos de edd. Por ejemplo: 9
10 Rngo edd entre 2 y 6 ños entre 6 y 12 ños entre 6 y 15 ños Sobre 15 ños dosis 1/2 comprimido/di (ó 250mg/d) 1 comprimido/di (ó 500mg/d) 1,5 comprimido/di (ó 750mg/d) 2 comp/d (ó 1g/d) Not: Tmbién se estblecen dosis en función del áre superficil del pciente. 5. Bibliogrfi (dicionl l del curso) Cálculo de dosis. tller %20c %C3 %A1lculo %20de %20dosis.pdf. %20 %5B1 %5D9mte.pdf Números y proporcionlidd. %C3 %BAmeros %20y % 20Proporcionlidd %20Modulo %201.pdf Tss. Pnorm de Slud 2011 Informe sobre Chile y comprción con píses miembros. generl/elementos/oecdchl2011.pdf Indicdores de l slud en Chile y su cpcidd pr evlur l clidd de l gestión públic en slud. DEPESEX/BCN/SERIE ESTUDIOS AÑO XIV, No pdf estudios/nro303.pdf Cálculo básicos en frmci hospitlri 10
PROPORCIONALIDAD DIRECTA E INVERSA
 PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
a b y se lee a es a b ; a se denomina antecedente y b consecuente.
 1 Centro Educcionl Sn Crlos de Argón. Dpto. de Mtemátic. Prof.: Ximen Gllegos H. Guí Nº 5 PSU NM 4: Proporcionlidd Nombre: Curso: Fech: Aprendizje Esperdo: Plnte y resuelve problems que requieren plicr
1 Centro Educcionl Sn Crlos de Argón. Dpto. de Mtemátic. Prof.: Ximen Gllegos H. Guí Nº 5 PSU NM 4: Proporcionlidd Nombre: Curso: Fech: Aprendizje Esperdo: Plnte y resuelve problems que requieren plicr
Tutorial MT-b12. Matemática Tutorial Nivel Básico. Proporcionalidad
 12345678901234567890 M te m átic Tutoril MT-b12 Mtemátic 2006 Tutoril Nivel Básico Proporcionlidd Mtemátic 2006 Tutoril Proporcionlidd Mrco Teórico 1. Rzón: Cuociente entre 2 cntiddes homogénes. b = k
12345678901234567890 M te m átic Tutoril MT-b12 Mtemátic 2006 Tutoril Nivel Básico Proporcionlidd Mtemátic 2006 Tutoril Proporcionlidd Mrco Teórico 1. Rzón: Cuociente entre 2 cntiddes homogénes. b = k
Una magnitud es cualquier propiedad que se puede medir numéricamente.
 Etueri Clses Prticulres Online Tem 4. Proporcionlidd Mgnitudes Un mgnitud es culquier propiedd que se puede medir numéricmente. Ejemplos: longitud, cpcidd de un recipiente, peso, Rzón L rzón es el cociente
Etueri Clses Prticulres Online Tem 4. Proporcionlidd Mgnitudes Un mgnitud es culquier propiedd que se puede medir numéricmente. Ejemplos: longitud, cpcidd de un recipiente, peso, Rzón L rzón es el cociente
TEMA 3: PROPORCIONALIDAD Y PORCENTAJES.
 TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
Magnitudes proporcionales I
 Mgnitudes proporcionles I Mgnitud: Es todo quello que puede ser medido. Mgnitudes proporcionles: Dos mgnitudes son proporcionles si son dependientes entre sí, es decir, si un de ells vrí, l otr tmbién
Mgnitudes proporcionles I Mgnitud: Es todo quello que puede ser medido. Mgnitudes proporcionles: Dos mgnitudes son proporcionles si son dependientes entre sí, es decir, si un de ells vrí, l otr tmbién
ENCUENTRO # 5 TEMA: Resolución de problemas de razones y proporciones. DESARROLLO
 ENCUENTRO # 5 TEMA: Resolución de problems de rzones y proporciones. CONTENIDOS:. Mgnitudes proporcionles (direct e invers). 2. Regl de tres simple. DESARROLLO Ejercicio Reto Cntiddes proporcionles cntiddes
ENCUENTRO # 5 TEMA: Resolución de problems de rzones y proporciones. CONTENIDOS:. Mgnitudes proporcionles (direct e invers). 2. Regl de tres simple. DESARROLLO Ejercicio Reto Cntiddes proporcionles cntiddes
UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIONES
 C u r s o : Mtemátic Mteril N GUÍA TEÓRICO PRÁCTICA Nº 8 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIONES DEFINICIÓN Sen A B conjuntos no vcíos. Un función de A en B es un relción que sign cd elemento del conjunto
C u r s o : Mtemátic Mteril N GUÍA TEÓRICO PRÁCTICA Nº 8 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIONES DEFINICIÓN Sen A B conjuntos no vcíos. Un función de A en B es un relción que sign cd elemento del conjunto
open green road Guía Matemática RAZONES Y PROPORCIONES tutora: Jacky Moreno .co
 Guí Mtemátic RAZONES Y PROPORCIONES tutor: Jcky Moreno.co 1. Rzones Al resolver distintos problems mtemáticos nos costumbrmos relcionr dos o más cntiddes medinte ls operciones básics de dición, sustrcción,
Guí Mtemátic RAZONES Y PROPORCIONES tutor: Jcky Moreno.co 1. Rzones Al resolver distintos problems mtemáticos nos costumbrmos relcionr dos o más cntiddes medinte ls operciones básics de dición, sustrcción,
PROPORCIÓN AÚREA. NÚMERO AÚREO. PROPORCIONALIDAD 2º E.S.O. a = 2 b = 5 1. b 2
 PROPORCIÓN AÚREA. NÚMERO AÚREO. PROPORCIONALIDAD 1 1 1 5 1 1 1 1 5 1 2º E.S.O. = 2 = 5 1 1+ 5 Φ = = = 1,6180339887... 2 PROPORCIÓN AÚREA PROPORCIÓN AÚREA PROPORCIÓN AÚREA RAZONES Y PROPORCIONES L rzón
PROPORCIÓN AÚREA. NÚMERO AÚREO. PROPORCIONALIDAD 1 1 1 5 1 1 1 1 5 1 2º E.S.O. = 2 = 5 1 1+ 5 Φ = = = 1,6180339887... 2 PROPORCIÓN AÚREA PROPORCIÓN AÚREA PROPORCIÓN AÚREA RAZONES Y PROPORCIONES L rzón
a) Decimales finitos: Corresponden a los cuocientes exactos entre el numerador y el denominador. Ejemplo: : 8 = (b)
 Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
RAZONES Y PROPORCIONES I)
 Aritmétic de Secundri: III Trimestre XVI: RAZONES Y PROPORCIONES I) Rzón o Relción.- ) Hllndo en cunto excede un cntidd respecto de otr (rest). Ejem: 6- = 4 ) Hllndo en cunto contiene un cntidd otr (división).
Aritmétic de Secundri: III Trimestre XVI: RAZONES Y PROPORCIONES I) Rzón o Relción.- ) Hllndo en cunto excede un cntidd respecto de otr (rest). Ejem: 6- = 4 ) Hllndo en cunto contiene un cntidd otr (división).
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 9 EJERCICIOS Ls relciones de proporcionlidd 1 Indic, entre los siguientes pres de mgnitudes, los que son directmente proporcionles, los que son inversmente proporcionles y los que no gurdn
Pág. 1 PÁGINA 9 EJERCICIOS Ls relciones de proporcionlidd 1 Indic, entre los siguientes pres de mgnitudes, los que son directmente proporcionles, los que son inversmente proporcionles y los que no gurdn
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
MATEMÁTICAS PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 25 AÑOS LOGARITMOS
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
UNIDAD DIDÁCTICA 4: LOGARITMOS
 Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
VOLUMETRIA ACIDO-BASE ó DE NEUTRALIZACIÓN
 Químic Anlític VOLUMETRIA ACIDO-BASE ó DE NEUTRALIZACIÓN Medinte l volumetrí ácido-bse se pueden vlorr sustncis que ctúen como ácidos o como bses y ls recciones que trnscurren según los csos pueden formulrse
Químic Anlític VOLUMETRIA ACIDO-BASE ó DE NEUTRALIZACIÓN Medinte l volumetrí ácido-bse se pueden vlorr sustncis que ctúen como ácidos o como bses y ls recciones que trnscurren según los csos pueden formulrse
EJERCICIOS DE VERANO DE MATEMÁTICAS
 EJERCICIOS DE VERANO DE MATEMÁTICAS º E.S.O. ES OBLIGATORIA LA RESOLUCIÓN COMPLETA DE CADA EJERCICIO PLANTEAMIENTO, DESARROLLO Y SOLUCIÓN DE FORMA CLARA Y CONCISA NÚMEROS. Reliz ls siguientes operciones
EJERCICIOS DE VERANO DE MATEMÁTICAS º E.S.O. ES OBLIGATORIA LA RESOLUCIÓN COMPLETA DE CADA EJERCICIO PLANTEAMIENTO, DESARROLLO Y SOLUCIÓN DE FORMA CLARA Y CONCISA NÚMEROS. Reliz ls siguientes operciones
Matemáticas Empresariales I. Integral Definida
 Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
Ecuación de la circunferencia de centro el origen C(0, 0) y de
 CÓNICAS EN EL PLANO. CIRCUNFERENCIA, ELIPSE, HIPÉRBOLA Y PARÁBOLA centrds en el origen CIRCUNFERENCIA Aunque segurmente se sep, recordmos que l circunferenci es el conjunto de puntos que distn un cntidd
CÓNICAS EN EL PLANO. CIRCUNFERENCIA, ELIPSE, HIPÉRBOLA Y PARÁBOLA centrds en el origen CIRCUNFERENCIA Aunque segurmente se sep, recordmos que l circunferenci es el conjunto de puntos que distn un cntidd
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Números reales. 1. Números y expresiones decimales. página El conjunto de los números reales página La recta real. Intervalos página 9
 Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
Logaritmos y exponenciales de otras bases. La función. Tipo III: Si u y v son funciones diferenciables en x y u > 0,
 Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
CONTENIDO PROGRAMÁTICO
 CONTENIDO PROGRAMÁTICO Fech Emisión: 2011/09/15 Revisión No. 1 AC-DO-F-8 Págin 1 de 6 MATEMÁTICAS CÓDIGO 1724101 PROGRAMA Tecnologí en Atención Prehospitlri ÁREA DE FORMACIÓN Fundmentos de Biomédics -
CONTENIDO PROGRAMÁTICO Fech Emisión: 2011/09/15 Revisión No. 1 AC-DO-F-8 Págin 1 de 6 MATEMÁTICAS CÓDIGO 1724101 PROGRAMA Tecnologí en Atención Prehospitlri ÁREA DE FORMACIÓN Fundmentos de Biomédics -
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
IES. SIERRA DE LAS VILLAS Departamento de Matemáticas
 Informe pr lumnos pendientes de Mtemátics º de E.S.O. IES. SIERRA DE LAS VILLAS Deprtmento de Mtemátics Nombre:.. Alumno/ de º de E.S.O. tendrá que relizr l prueb extrordinri de Mtemátics, en el mes de
Informe pr lumnos pendientes de Mtemátics º de E.S.O. IES. SIERRA DE LAS VILLAS Deprtmento de Mtemátics Nombre:.. Alumno/ de º de E.S.O. tendrá que relizr l prueb extrordinri de Mtemátics, en el mes de
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Razones y Proporciones
 Instituto Ncionl de Chile Deprtmento de Mtemátic Prof. Luis Arncibi Año 2008 Rzones y Proporciones Definición Rzón: Cociente entre dos cntiddes; : b como rzón debe leerse es b, y l rzón es el cociente;
Instituto Ncionl de Chile Deprtmento de Mtemátic Prof. Luis Arncibi Año 2008 Rzones y Proporciones Definición Rzón: Cociente entre dos cntiddes; : b como rzón debe leerse es b, y l rzón es el cociente;
Bloque II: Equilibrios Químicos. Profesor: Mª del Carmen Clemente Jul
 Bloque II: Equilibrios Químicos Profesor: Mª del Carmen Clemente Jul LEY DE EQUILIBRIO QUÍMICO. CONSTNTE DE EQUILIBRIO, EQ L LEY DE EQUILIBRIO QUÍMICO ES L EXPRESIÓN MTEMÁTIC DE L LEY DE CCIÓN DE MSS QUE
Bloque II: Equilibrios Químicos Profesor: Mª del Carmen Clemente Jul LEY DE EQUILIBRIO QUÍMICO. CONSTNTE DE EQUILIBRIO, EQ L LEY DE EQUILIBRIO QUÍMICO ES L EXPRESIÓN MTEMÁTIC DE L LEY DE CCIÓN DE MSS QUE
DESIGUALDADES < d < En el campo de los números reales tenemos una. Un momento de reflexión muestra que una
 DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
Nombre y apellidos:... Curso:... Fecha:... PROPORCIONALIDAD. Una proporción es la igualdad de... a. b c a. = c. d 21 EJEMPLO: EJERCICIO: = 8 x =...
 4 Proporcionlidd y porcentjes Esquem de l unidd Curso:... Fech:... PROPORCIONALIDAD PROPORCIÓN Un proporción es l iguldd de...... b = Los términos y d se llmn... Los términos b y c se llmn... c d EJEMPLO:
4 Proporcionlidd y porcentjes Esquem de l unidd Curso:... Fech:... PROPORCIONALIDAD PROPORCIÓN Un proporción es l iguldd de...... b = Los términos y d se llmn... Los términos b y c se llmn... c d EJEMPLO:
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
La elipse es el lugar geométrico de todos los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante.
 LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
FUNDAMENTOS DE ANÁLISIS INSTRUMENTAL. 6ª RELACIÓN DE PROBLEMAS.
 EPARTAMENTO E QUÍMICA ANALÍTICA Y TECNOLOGÍA E ALIMENTOS FUNAMENTOS E ANÁLISIS INSTRUMENTAL. 6ª RELACIÓN E PROBLEMAS..- Considerndo que un determindo compuesto AB present un vlor de 0 pr un sistem prticulr
EPARTAMENTO E QUÍMICA ANALÍTICA Y TECNOLOGÍA E ALIMENTOS FUNAMENTOS E ANÁLISIS INSTRUMENTAL. 6ª RELACIÓN E PROBLEMAS..- Considerndo que un determindo compuesto AB present un vlor de 0 pr un sistem prticulr
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
Cuál es su valor de CRF? Es normal? Qué enfermedad le sugiere esta valor de CRF?
 1 Bloque 1 Problem 1. Un niño es conectdo, después de un espirción norml, un bols conteniendo 2 litros de 8% He, 92% O 2. Respir de l bols hst que l mezcl es complet, y en ese momento l concentrción de
1 Bloque 1 Problem 1. Un niño es conectdo, después de un espirción norml, un bols conteniendo 2 litros de 8% He, 92% O 2. Respir de l bols hst que l mezcl es complet, y en ese momento l concentrción de
Desarrollos para planteamientos de ecuaciones de primer grado
 1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
SECCIÓN 3 DESCRIPCIÓN DE LOS NÚMEROS REALES
 SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
DETERMINANTES. Determinante es la expresión numérica de una matriz. Según el orden de la matriz el determinante se resuelve de distintas formas:
 ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
LICENCIATURA EN KINESIOLOGÍA Y FISIATRÍA FÍSICA BIOLÓGICA. TRABAJO PRACTICO Nº 2 Dinámica
 LICECIATURA E KIESIOLOGÍA Y ISIATRÍA TRABAJO PRACTICO º Dinámic LICECIATURA E KIESIOLOGÍA Y ISIATRÍA TRABAJO PRACTICO º Dinámic Ing. ROIO GUAYCOCHEA Ing. MARCO DE ARDI Ing. ESTEBA LEDROZ Ing. THELMA AURORA
LICECIATURA E KIESIOLOGÍA Y ISIATRÍA TRABAJO PRACTICO º Dinámic LICECIATURA E KIESIOLOGÍA Y ISIATRÍA TRABAJO PRACTICO º Dinámic Ing. ROIO GUAYCOCHEA Ing. MARCO DE ARDI Ing. ESTEBA LEDROZ Ing. THELMA AURORA
Relación entre el cálculo integral y el cálculo diferencial.
 Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES
 71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
 TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
PROPORCIONALIDAD. PROPORCIÓN: Es una igualdad entre dos PORCENTAJES. Relación entre porcentajes y: o Proporciones o Fracciones o Números decimales
 PROPORCIONALIDAD RAZÓN entre dos números y b: Es el cociente b PROPORCIÓN: Es un iguldd entre dos c rzones: b d RELACIÓN DE PROPORCIONALIDAD entre mgnitudes: o Mgnitudes directmente proporcionles o Mgnitudes
PROPORCIONALIDAD RAZÓN entre dos números y b: Es el cociente b PROPORCIÓN: Es un iguldd entre dos c rzones: b d RELACIÓN DE PROPORCIONALIDAD entre mgnitudes: o Mgnitudes directmente proporcionles o Mgnitudes
Es una función exponencial con base 2. Veamos con la rapidez que crece:
 Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 QUÍMICA TEMA 6: EQUILIBRIOS ÁCIDO-BASE
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 016 QUÍMICA TEMA 6: EQUILIBRIOS ÁCIDO-BASE Junio, Ejercicio 4, Opción A Reserv 1, Ejercicio 4, Opción B Reserv, Ejercicio 6, Opción A Reserv, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 016 QUÍMICA TEMA 6: EQUILIBRIOS ÁCIDO-BASE Junio, Ejercicio 4, Opción A Reserv 1, Ejercicio 4, Opción B Reserv, Ejercicio 6, Opción A Reserv, Ejercicio 4, Opción
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Álgebra Lineal. 1) (Junio-96) Considérese el sistema de ecuaciones lineales (a, b y c son datos; las incógnitas son x, y, z):
 Mtemátics II Álgebr Linel (Junio-96 Considérese el sistem de ecuciones lineles ( b c son dtos; ls incógnits son : b c c b b c Si b c son no nulos el sistem tiene solución únic. Hllr dich solución. (Sol:
Mtemátics II Álgebr Linel (Junio-96 Considérese el sistem de ecuciones lineles ( b c son dtos; ls incógnits son : b c c b b c Si b c son no nulos el sistem tiene solución únic. Hllr dich solución. (Sol:
TEMA VI: ACIDOS Y BASES
 www.selectividd-cgrnd.com TEMA VI: ACIDOS Y BASES 1.- El ácido clorocético (ClCH COOH) en concentrción 0,01M y 5 C se encuentr disocido en 1%. Clculr: ) L constnte de disocición de dicho ácido. b) El ph
www.selectividd-cgrnd.com TEMA VI: ACIDOS Y BASES 1.- El ácido clorocético (ClCH COOH) en concentrción 0,01M y 5 C se encuentr disocido en 1%. Clculr: ) L constnte de disocición de dicho ácido. b) El ph
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 4: Lunes 1 - Viernes 5 de Abril. Contenidos
 Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
a Y = X donde a 1 siendo Lg el logaritmo y
 Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
1.- Cálculo del coeficiente de autoinducción.
 Trbjo Práctico 8 1.- Cálculo del coeficiente de utoinducción. Describ el fenómeno de utoinducción en un bobin. Encuentre l expresión del coeficiente de utoinducción en un solenoide lrgo de N s = 1 espirs
Trbjo Práctico 8 1.- Cálculo del coeficiente de utoinducción. Describ el fenómeno de utoinducción en un bobin. Encuentre l expresión del coeficiente de utoinducción en un solenoide lrgo de N s = 1 espirs
Optimización de funciones
 Tem 5 Optimizción de funciones 5.1. Extremos de funciones de vris vribles Definición 5.1.1. Sen f : D R n R, x 0 D y el problem de optimizción: mximizr / minimizr f(x 1, x,, x n ), (x 1, x,, x n ) D en
Tem 5 Optimizción de funciones 5.1. Extremos de funciones de vris vribles Definición 5.1.1. Sen f : D R n R, x 0 D y el problem de optimizción: mximizr / minimizr f(x 1, x,, x n ), (x 1, x,, x n ) D en
5. Integral y Aplicaciones
 Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Capítulo 5. Medición de la Distancia por Medio de Triangulación
 Cpítulo 5. Medición de l Distnci por Medio de Tringulción 5.1 Introducción Hemos visto cómo medir l distnci de un objeto un cámr cundo dicho objeto es cptdo por un sol cámr; sin embrgo, cundo el objeto
Cpítulo 5. Medición de l Distnci por Medio de Tringulción 5.1 Introducción Hemos visto cómo medir l distnci de un objeto un cámr cundo dicho objeto es cptdo por un sol cámr; sin embrgo, cundo el objeto
MATEMÁTICAS-FACSÍMIL N 9
 MTEMÁTIS-FSÍMIL N 9. b b b ) - b ) b - ) b D) E) 6 cm ( b) =. El triángulo está inscrito en l mitd de l circunferenci. Si h c = cm y el ldo = 5cm. El rdio de l circunferenci es: ) cm ) 6 cm ) 6 cm O D)
MTEMÁTIS-FSÍMIL N 9. b b b ) - b ) b - ) b D) E) 6 cm ( b) =. El triángulo está inscrito en l mitd de l circunferenci. Si h c = cm y el ldo = 5cm. El rdio de l circunferenci es: ) cm ) 6 cm ) 6 cm O D)
60º L = 5 cm. q 1. q 2. b = 6 cm. q 4. q 3
 UNIVERSIDAD NACIONAL EXERIMENTAL FRANCISCO DE MIRANDA COMLEJO DOCENTE EL SABINO DEARTAMENTO DE MATEMÁTICA Y FÍSICA UNIDAD CURRICULAR: FÍSICA II ROFESORA CARMEN ADRIANA CONCECIÓN 1 Considere tres crgs en
UNIVERSIDAD NACIONAL EXERIMENTAL FRANCISCO DE MIRANDA COMLEJO DOCENTE EL SABINO DEARTAMENTO DE MATEMÁTICA Y FÍSICA UNIDAD CURRICULAR: FÍSICA II ROFESORA CARMEN ADRIANA CONCECIÓN 1 Considere tres crgs en
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
Teorema fundamental del Cálculo.
 Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
Clase 2: Expresiones algebraicas
 Clse 2: Expresiones lgebrics Operr expresiones lgebrics usndo ls propieddes lgebrics de ls operciones sum y producto, propieddes de ls potencis, regls de signos y préntesis. Evlur expresiones lgebrics
Clse 2: Expresiones lgebrics Operr expresiones lgebrics usndo ls propieddes lgebrics de ls operciones sum y producto, propieddes de ls potencis, regls de signos y préntesis. Evlur expresiones lgebrics
accés a la universitat dels majors de 25 anys MATEMÀTIQUES UNIDAD DIDÁCTICA 4: LOGARITMOS
 Unitt d ccés ccés l universitt dels mjors de 25 ns Unidd de cceso cceso l universidd de los mores de 25 ños UNIDAD DIDÁCTICA 4: LOGARITMOS ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función
Unitt d ccés ccés l universitt dels mjors de 25 ns Unidd de cceso cceso l universidd de los mores de 25 ños UNIDAD DIDÁCTICA 4: LOGARITMOS ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función
(2132) Repuestos de maquinaria 80.000
 3. Norms prticulres sobre el inmovilizdo mteril 80.000 25.000 800 (2131) Mquinri. Motores (75.000 + 5.000) (28132) Amortizción cumuld. Repuestos de mquinri (motores) (100.000/8) x 2 (472) Hciend Públic,
3. Norms prticulres sobre el inmovilizdo mteril 80.000 25.000 800 (2131) Mquinri. Motores (75.000 + 5.000) (28132) Amortizción cumuld. Repuestos de mquinri (motores) (100.000/8) x 2 (472) Hciend Públic,
TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS
 TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. POTENCIAS L epresión n se llm potenci de bse y eponente n: Si n es un número nturl: n =, n veces. 0 =, = n m n n m = y = n Ejercicios: º)
TEMA 7: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. POTENCIAS L epresión n se llm potenci de bse y eponente n: Si n es un número nturl: n =, n veces. 0 =, = n m n n m = y = n Ejercicios: º)
5 2 B) C) o 16 1 C) 2 D) 16 E)-2. Sesión Si una progresión geométrica tiene primer término 243 y el quinto término es
 Sesión.- Si un progresión geométric tiene primer término y el quinto término es entonces l rzón r es igul : Unidd I Progresiones y series. D. Progresión geométric..- L poblción de un ciudd h umentdo de
Sesión.- Si un progresión geométric tiene primer término y el quinto término es entonces l rzón r es igul : Unidd I Progresiones y series. D. Progresión geométric..- L poblción de un ciudd h umentdo de
TEMA 3 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Matemáticas CCSSII 2º Bachillerato 1
 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
XII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN FLUJO EN CONDUCTOS
 XII.- TANSMISIÓN DE CALO PO CONVECCIÓN FLUJO EN CONDUCTOS XII.1.- FLUJO ISOTÉMICO EN CONDUCTOS CICULAES; ECUACIÓN DE POISEUI- LLE En un flujo lminr l corriente es reltivmente lent y no es perturbd por
XII.- TANSMISIÓN DE CALO PO CONVECCIÓN FLUJO EN CONDUCTOS XII.1.- FLUJO ISOTÉMICO EN CONDUCTOS CICULAES; ECUACIÓN DE POISEUI- LLE En un flujo lminr l corriente es reltivmente lent y no es perturbd por
TEMA8: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS
 TEMA8: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. LA FUNCIÓN EXPONENCIAL Ejercicio: º) Resuelve ls siguientes ecuciones plicndo ls propieddes de ls potencis:. = 8 + 6 9. 5. = = 0. + = 6 8
TEMA8: FUNCIONES EXPONENCIALES, LOGARÍTMICAS Y TRIGONOMÉTRICAS. LA FUNCIÓN EXPONENCIAL Ejercicio: º) Resuelve ls siguientes ecuciones plicndo ls propieddes de ls potencis:. = 8 + 6 9. 5. = = 0. + = 6 8
Geodesia Física y Geofísica
 Geodesi Físic y Geofísic I semestre, 016 Ing. José Frncisco Vlverde Clderón Emil: jose.vlverde.clderon@un.cr Sitio web: www.jfvc.wordpress.com Prof: José Fco Vlverde Clderón Geodesi Físic y Geofísic I
Geodesi Físic y Geofísic I semestre, 016 Ing. José Frncisco Vlverde Clderón Emil: jose.vlverde.clderon@un.cr Sitio web: www.jfvc.wordpress.com Prof: José Fco Vlverde Clderón Geodesi Físic y Geofísic I
Aplicación del Cálculo Integral para la Solución de. Problemáticas Reales
 Aplicción del Cálculo Integrl pr l Solución de Problemátics Reles Jun S. Fierro Rmírez Universidd Pontifici Bolivrin, Medellín, Antioqui, 050031 En este rtículo se muestr el proceso de solución numéric
Aplicción del Cálculo Integrl pr l Solución de Problemátics Reles Jun S. Fierro Rmírez Universidd Pontifici Bolivrin, Medellín, Antioqui, 050031 En este rtículo se muestr el proceso de solución numéric
a n =b Si a es múltiplo de b, entonces b es divisor de a. Números primos: son números cuyos únicos divisores son ellos mismos y el 1.
 1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA. Objetivos
 UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
UNGS - Elementos de Matemática Práctica 7 Matriz insumo producto
 UNGS - Elementos de Mtemátic Práctic 7 Mtriz insumo producto El economist W. Leontief es el utor del modelo o l tbl de insumo producto. Est tbl refle l interrelción entre distintos sectores de l economí
UNGS - Elementos de Mtemátic Práctic 7 Mtriz insumo producto El economist W. Leontief es el utor del modelo o l tbl de insumo producto. Est tbl refle l interrelción entre distintos sectores de l economí
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
XI. LA HIPÉRBOLA LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO
 XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
MOVIMIENTO DE RODADURA
 E.T.S.. Agrónomos. U.P.. OVENTO DE ODADUA Cuerpos rodntes. Considermos el moimiento de cuerpos que, debido su geometrí, tienen l cpcidd de rodr: eser, ro, disco, supericie eséric, cilindro poydo sobre
E.T.S.. Agrónomos. U.P.. OVENTO DE ODADUA Cuerpos rodntes. Considermos el moimiento de cuerpos que, debido su geometrí, tienen l cpcidd de rodr: eser, ro, disco, supericie eséric, cilindro poydo sobre
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
3 Sistemas de ecuaciones lineales
 Solucionrio Sistems de ecuciones lineles CTIVIDDES INICILES.I. Resuelve los siguientes sistems de ecuciones. ) c) 6 ), λ, λλ R, c) Sistem incomptible,.ii. En cd cso, escribe un sistem de ecuciones cu solución
Solucionrio Sistems de ecuciones lineles CTIVIDDES INICILES.I. Resuelve los siguientes sistems de ecuciones. ) c) 6 ), λ, λλ R, c) Sistem incomptible,.ii. En cd cso, escribe un sistem de ecuciones cu solución
MATRICES DE NÚMEROS REALES
 MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
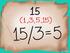 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
DINÁMICA Y LAS LEYES DE NEWTON
 DINÁMICA Y LAS LEYES DE NEWTON EXPERIENCIA N 7 Un propiedd de los cuerpos mteriles es su ms inercil. L fuerz es otro concepto nuevo, útil cundo se trt de describir ls intercciones entre cuerpos mteriles.
DINÁMICA Y LAS LEYES DE NEWTON EXPERIENCIA N 7 Un propiedd de los cuerpos mteriles es su ms inercil. L fuerz es otro concepto nuevo, útil cundo se trt de describir ls intercciones entre cuerpos mteriles.
Taller de Matemáticas I
 Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
RESOLUCIÓN DE PROBLEMAS DE CRECIMIENTO DE UNA POBLACIÓN BACTERIAS Y VIRUS QUE SIGUEN UN PATRÓN DE CRECIMIENTO SEGÚN UNA FUNCIÓN EXPONENCIAL
 2º ESPA! I.E.S Slmedin (Chipion) RESOLUCIÓN DE PROBLEMAS DE CRECIMIENTO DE UNA POBLACIÓN BACTERIAS Y VIRUS QUE SIGUEN UN PATRÓN DE CRECIMIENTO SEGÚN UNA FUNCIÓN EXPONENCIAL N=No t/tr tiempo trnscurrido/tiempo
2º ESPA! I.E.S Slmedin (Chipion) RESOLUCIÓN DE PROBLEMAS DE CRECIMIENTO DE UNA POBLACIÓN BACTERIAS Y VIRUS QUE SIGUEN UN PATRÓN DE CRECIMIENTO SEGÚN UNA FUNCIÓN EXPONENCIAL N=No t/tr tiempo trnscurrido/tiempo
recta numérica U Figura 1.1
 Cpítulo 1 Rect numéric L rect numéric es un objeto mtemático que formliz l cint de medir o ls regls. En un rect ilimitd se elige un punto que se llm origen y un unidd, es decir decimos que el segmento
Cpítulo 1 Rect numéric L rect numéric es un objeto mtemático que formliz l cint de medir o ls regls. En un rect ilimitd se elige un punto que se llm origen y un unidd, es decir decimos que el segmento
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL
 3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
73 ESO. E = m c 2. «El que pregunta lo que no sabe es ignorante un. día. El que no lo pregunta será ignorante toda la vida»
 73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
LICENCIATURA EN OBSTETRICIA FÍSICA BIOLÓGICA. TRABAJO PRACTICO Nº 2 Dinámica
 LICECIATURA E OBSTETRICIA TRABAJO PRACTICO º Dinámic LICECIATURA E OBSTETRICIA TRABAJO PRACTICO º Dinámic Ing. ROIO GUAYCOCHEA Ing. MARCO DE ARDI Ing. ESTEBA LEDROZ Ing. THELMA AURORA ZAO AÑO 014 Ing.
LICECIATURA E OBSTETRICIA TRABAJO PRACTICO º Dinámic LICECIATURA E OBSTETRICIA TRABAJO PRACTICO º Dinámic Ing. ROIO GUAYCOCHEA Ing. MARCO DE ARDI Ing. ESTEBA LEDROZ Ing. THELMA AURORA ZAO AÑO 014 Ing.
