FUNDAMENTOS DE MECÁNICA ESTADÍSTICA
|
|
|
- Ana Muñoz Padilla
- hace 7 años
- Vistas:
Transcripción
1 Departamento de Físca Aplcada III Capítulo : Físca estadístca Capítulo FUNDAMENTOS DE MECÁNICA ESTADÍSTICA.- INTRODUCCIÓN A LA MECÁNICA ESTADÍSTICA CLÁSICA. La mecánca está basada en certos prncpos fundamentales, como la conservacón de la energía y de la cantdad de movmento, que son aplcables al movmento de partículas en nteraccón. En estas líneas extenderemos los prncpos de la mecánca a sstemas de muchas partículas, enfatzando los métodos utlzados para obtener propedades colectvas o macroscópcas del sstema, sn consderar al movmento detallado de cada partícula. Esta técnca se denomna mecánca estadístca (Alonso, M., Fnn,E. 976).
2 Departamento de Físca Aplcada III Capítulo : Físca estadístca Usaremos aquí el concepto de partícula en un sentdo amplo que ncluye a las partículas fundamentales, como el electrón, o a las asocacones de partículas fundamentales, como los átomos o las moléculas. Una partícula será entonces cada una de las undades defndas y estables que componen un sstema físco determnado. Es posble darse cuenta fáclmente de que necestamos un tratamento estadístco de las propedades macroscópcas de la matera s recordamos que en un centímetro cúbco de gas a temperatura y presón normales hay unas x 0 9 moléculas. Es práctcamente mposble a la vez que nnecesaro tener en cuenta el movmento de cada molécula en detalle para determnar las propedades macroscópcas del gas, tales como su presón o su temperatura. Por otra parte, para hacer un análss estadístco de un sstema con muchas partículas, tenemos que hacer una estmacón razonable acerca del estado dnámco de cada partícula, basada en las propedades generales de las partículas. Hacemos esta estmacón ntroducendo el concepto de probabldad de dstrbucón de las partículas entre los dversos estados dnámcos en que pueden encontrarse. Al ntroducr la dea de probabldad no estamos mplcando que suponemos que las partículas se mueven al azar o en forma caótca, sn obedecer nnguna ley defnda. El concepto de probabldad surge de nuestro método de estmar los estados dnámcos de las partículas de un sstema, y no del mecansmo por el cual las partículas del sstema se dstrbuyen en la naturaleza entre los posbles estados dnámcos como resultado de sus nteraccones. Luego la valdez del análss estadístco de un sstema de muchas partículas está drectamente relaconada con la de nuestras hpótess acerca de la probabldad de dstrbucón de las partículas.
3 Departamento de Físca Aplcada III Capítulo : Físca estadístca.- EQUILIBRIO ESTADÍSTICO. Consderemos un sstema aslado compuesto de un gran número N de partículas, en el cual cada partícula tene a su dsposcón varos estados de energía E, E, E...Los estados de energía pueden estar cuantzados (como los estados rotaconales y vbraconales de una molécula) o pueden formar un espectro práctcamente contnuo (como la energía cnétca traslaconal de las moléculas de una gas). En un nstante dado las partículas están dstrbudas entre los dferentes estados, de modo que n partículas tene energía E, n partículas energía E, y así sucesvamente. El número total de partículas es: N n + n + n +... = n = Además, suponemos que permanece constante durante todos los procesos que ocurren en el sstema. La energía total del sstema es: U = n E n E n E... n E = (.) Esta expresón de la energía total del sstema supone mplíctamente que las partículas no nteractúan ( o que sólo lo hacen lgeramente ), por lo que podemos atrbur a cada partícula una energía que depende solamente de sus coordenadas. S consderamos las nteraccones debemos agregar a la ecuacón (.) térmnos de la forma E P + E P E P +... correspondentes a la energía potencal de nteraccón entre pares de partículas. Cada térmno ncluye las coordenadas de ambas partículas nteractuantes. En este caso no podemos hablar de la energía de cada partícula sno solamente de la del sstema. 4
4 Departamento de Físca Aplcada III Capítulo : Físca estadístca Puede parecer que este tratamento no está de acuerdo con la realdad, ya que todas las partículas que componen los sstemas físcos están en nteraccón. Sn embargo, en condcones especales podemos usar una técnca denomnada del campo autocompatble, en la que se consdera que cada partícula está sujeta a una nteraccón promedo debda a las otras, tenendo un energía potencal promedo que sólo depende de sus coordenadas; podemos entonces segur escrbendo U como en le ec.(.), sólo que ahora : E = E + E k p En los casos en que es necesaro consderar explíctamente las nteraccones entre partículas hay que usar otras técncas, como con los gases reales. S el sstema está aslado, la energía total U debe ser constante. Sn embargo, puede cambar la dstrbucón de las partículas entre los estados dsponbles de energía debdo a sus nteraccones y colsones. Por ejemplo, en un gas, una molécula rápda puede chocar con una lenta; después del choque la molécula rápda puede haberse frenado y la lenta puede haberse acelerado. O un átomo exctado puede chocar nelástcamente con otro átomo, transfrendo su energía de exctacón como energía cnétca de ambos átomos. En ambos ejemplos las partículas están en estados dferentes después de la colsón. En otras palabras: los números n, n, n...que dan la partcón de las N partículas entre los estados dsponbles de energía pueden estar cambando. Es razonable suponer que para cada estado macroscópco de un sstema de partículas hay una partcón que es más probable que cualquer otra. De otro modo: podemos decr que, dadas las condcones físcas del sstema de partículas ( el número de partículas, la energía total y la estructura de cada partícula) hay una partcón mucho más probable. Una vez alcanzada esta partcón, se dce que el sstema está en equlbro estadístco. 5
5 Departamento de Físca Aplcada III Capítulo : Físca estadístca Un sstema en equlbro estadístco no se apartará de la partcón más probable (excepto por fluctuacones estadístcas) a no ser que sea perturbado por un agente externo. Queremos sgnfcar con esto que los números de partcón n, n, n... pueden fluctuar alrededor de los valores correspondentes a la partcón más probable sn que se produzcan efectos macroscópcos. Supongamos, por ejemplo, que tenemos un gas en equlbro estadístco, una de cuyas moléculas con energía E choca con otra de energía E j ; después de la colsón sus energías son E s, E r. Podemos suponer que después de un corto tempo otro par de moléculas sale de los estados de energía E s y E r y que el msmo par u otro va a los estados E y E j, de modo que estadístcamente la partcón no ha cambado. El problema clave de la mecánca estadístca es hallar la partcón (o ley de dstrbucón ) más probable de un sstema aslado, dada su composcón. Una vez hallada la partcón más probable, el problema sguente es dear métodos para obtener de dcha partcón las propedades observadas macroscópcamente. Es necesaro hacer alguna hpótess para obtener la ley de dstrbucón. Se puede probar con varas hpótess razonables hasta obtener una ley de dstrbucón que esté de acuerdo con los resultados expermentales. Una es la que se denomna ley de dstrbucón de Maxwell- Boltzmann, que es la base de la estadístca clásca y que veremos a contnuacón, y las dos leyes de dstrbucón restantes, la de Ferm-Drac y la de Bose-Ensten, pertenecen a la estadístca cuántca..- LEY DE DISTRIBUCIÓN DE MAXWELL-BOLTMANN Consderemos un sstema compuesto de un gran número de partículas déntcas y dstngubles. Por déntcas entendemos que las partículas tenen la msma estructura y composcón. Por dstngubles entendemos que es posble dstngur, o decr cuál es la dferenca, entre una partícula déntca y otra. A prmera vsta, parece exstr una contradccón entre déntca y dstnguble y realmente es así! más tarde consderaremos esta aparente falta de lógca. 6
6 Departamento de Físca Aplcada III Capítulo : Físca estadístca Representemos una partcón determnada n, n, n... medante el ordenamento geométrco mostrado en la fgura. Cada línea representa un estado partcular de energía E y el número de puntos ndca el número n de partículas que hay en cada estado de energía. En nuestro ejemplo, n =, n,=0,n =,n 4 =,etc.. Fgura Nuestra prmera suposcón es que todos los estados de energía son gualmente accesbles a las partículas del sstema, es decr que todos los estados de energía tenen la msma probabldad de ser ocupados. Supondremos entonces que: la probabldad de una partcón determnada es proporconal al número de maneras dferentes en que las partículas pueden dstrburse entre los estados dsponbles de energía para producr la partcón. 7
7 Departamento de Físca Aplcada III Capítulo : Físca estadístca Tengamos el caso más general de N partículas dsponbles que pueden llenar una sere de estados de energía E, E, E,etc. La expresón general del número total de modos dstngubles dferentes de colocar n partículas en el estado E es entonces: N! n!( N )! n (.) Esto es justamente el número de permutacones de N objetos tomados de n por prmera vez. Al pasar al segundo estado E, sólo dsponemos de N- n partículas; luego, s queremos colocar n partículas en el estado E, debemos emplear la ec.(.) con N- n en vez de N y n en vez de n, resultando: ( N n n )! n!( N n n )! (.) Se puede contnuar el proceso hasta agotar todos los estados de energía. El número total de modos dferentes dstngubles de obtener la partcón n, n, n... se obtene multplcando las expresones (.) y (.) y las sguentes correspondentes a los estados de energía restantes. Al hacer esto, se puede comprobar que muchos factores se cancelan y nos queda que: N! P = (.4) n! n!!... n que da el número de modos dferentes dstngubles en que se puede obtener la partcón n, n, n... 8
8 Departamento de Físca Aplcada III Capítulo : Físca estadístca Hasta ahora hemos supuesto que todos los estados dsponbles tenen la msma probabldad de ser ocupados. Puede ocurrr que los estados tengan probabldades ntrínsecas g dferentes(alonso, M., Fnn,E. 976). Por ejemplo, un certo estado de energía puede ser compatble con más estados dferentes de momento angular que otros estados por lo que es más probable que sea ocupado. S se tene en cuenta esta probabldad ntrínseca, la probabldad P de una partcón determnada es dferente de la ec.(.4). Es evdente que s g es la probabldad de encontrar un partícula en el nvel de energía E, la probabldad de encontrar n partículas es g x g x g x g = g n. Luego la probabldad de una partcón determnada, en vez de estar dada por la ec.(.4), es: N! g g g... P = n! n! n!... n n n Levantemos fnalmente la condcón de dstngubldad. S todas las partículas son déntcas e ndstngubles no podemos, por ejemplo, darnos cuenta de la dferenca provenente de ntercambar las partículas a y p en la partcón de la fgura. En consecuenca, todas las N! permutacones entre las partículas que ocupan los estados dferentes dan la msma partcón. Esto sgnfca que debemos dvdr la ecuacón anteror entre N!, resultando: n n n = n g g g... C n g P = = (.5) n! n! n!... n! Esta es la expresón que da la probabldad de una dstrbucón en la estadístca de Maxwell-Boltzmann. 9
9 Departamento de Físca Aplcada III Capítulo : Físca estadístca Podemos obtener el estado de equlbro, que corresponde a la dstrbucón más probable, determnando el máxmo P compatble con las condcones dadas por las ec.(.5). El método es una técnca matemátca smple, y tene como resultado que la máxma probabldad está dada por: n α βe = g e (.6) donde a y ß son dos parámetros que, como se verá, están relaconados con las propedades físcas del sstema. Se defne tambén la cantdad, denomnada funcón de partcón, que es una expresón muy mportante que aparece frecuentemente en muchos cálculos. = g e βe (.7) La ec.(.6) puede ponerse entonces tambén en funcón de de la sguente forma: n N g e β E = (.8) La expresón anteror consttuye la ley de dstrbucón de Maxwell-Boltzmann. La cantdad ß está relaconada con la energía del sstema, o más precsamente con la energía meda de una partícula, como se verá más adelante. 0
10 Departamento de Físca Aplcada III Capítulo : Físca estadístca 4.- EL CONCEPTO ESTADÍSTICO DE TEMPERATURA. El parámetro ß de la ecuacones (.6), (.7), (.8) está drectamente relaconado con una cantdad físca, la temperatura, que fue orgnalmente más para descrbr una experenca sensoral que como propedad estadístca de una coleccón de partículas. Usando la ec.(.8), tenemos que la energía total de un sstema de partículas en equlbro estadístco es: U βe βe βe ( g e + g e + g e...) N = n E + ne + ne +... = + es decr, U N = g Ee βe Usando la defncón de la funcón de partcón dada por la ec.(.7), podemos escrbr U de forma equvalente: U N d = ge dβ βe = N d dβ d = N (Ln) dβ Esta es una relacón muy mportante entre la energía total y la funcón de partcón de un sstema en equlbro estadístco. La energía meda de una partícula es, por tanto: E = U N d = (Ln) dβ
11 Departamento de Físca Aplcada III Capítulo : Físca estadístca Podemos observar que podemos usar el parámetro ß para caracterzar la energía nterna de un sstema. Sn embargo, se ha encontrado que es más convenente ntroducr una nueva cantdad físca en vez de ß. Esta cantdad se denomna temperatura absoluta, se desgna por T y se defne conforme a la relacón: = (.9) β Es evdente que se debe expresar la cantdad en undades de energía, como Julos o electronvoltos. La constante k se denomna constante de Boltzmann, y su valor está determnado por la eleccón de undades de T. Queda por demostrar aquí que la temperatura que se ha defndo concde con la temperatura medda, dgamos con un termómetro de gas. En realdad es así, pero no lo demostraremos, baste decr que cuando se expresa T en una undad denomnada kelvn, que se desgna por K, el valor de la constante de Boltzmann es: k = J K Asmsmo, se demuestra que la cantdad ß es postva, por lo que la temperatura absoluta T es postva. La temperatura más baja es cero, y corresponde a lo que se denomna cero absoluto. De esta forma, ntroducendo la ec.(.9) de temperatura en la ec.(.7) podemos escrbr la funcón de partcón de equlbro en la forma: = g e E (.0)
12 Departamento de Físca Aplcada III Capítulo : Físca estadístca Análogamente, sabendo que dβ = dt, podemos escrbr: n = N g e E U = knt d dt ( Ln) d E = ( Ln) (.) dt Observamos que la ec.(.) establece una relacón entre la energía meda por partícula de un sstema en equlbro estadístco y la temperatura del msmo. La relacón exacta depende evdentemente de la estructura mcroscópca del sstema, expresada por la funcón de partcón, y es dferente para un gas deal, un gas real, un líqudo o un sóldo. Podemos decr entonces que la temperatura de un sstema en equlbro estadístco es una cantdad relaconada con la energía meda por partícula del sstema, dependendo dcha relacón de la estructura del sstema. Por últmo, en caso general, el valor medo de cualquer propedad F(E) asocada con las partículas, se converte ahora en : F = g F( E ) e E y es, por tanto, funcón de la temperatura.
13 Departamento de Físca Aplcada III Capítulo : Físca estadístca 5.- LEY DE MAXWELL-BOLTMANN PARA UN GAS IDEAL. Nuestro próxmo caso es determnar s hay algún sstema de partículas en la naturaleza cuyo comportamento colectvo se parezca a las predccones de la ley de dstrbucón de Maxwell- Boltznmann. Hasta ahora hemos presentado esta dstrbucón solamente como una construccón teórca más o menos razonable. La experenca confrma que se puede descrbr la mayoría de los gases con la estadístca de Maxwell- Boltzmann en un ntervalo de temperaturas muy amplo (Brey J.,de la Ruba,J. 00). Para smplfcar, consderaremos ahora los gases deales compuestos de moléculas monoatómcas. De este modo no tenemos que nclur n la energía potencal de las fuerzas ntermoleculares n la energía asocada con los movmentos nternos de rotacón o de vbracón de las moléculas; por lo tanto, toda la energía molecular es traslaconal; es decr, la E que aparece en la ec (.8). es: E = p = m mv Como podemos consderar que la energía cnétca de un gas deal que ocupa un volumen sufcentemente grande no está cuantzada, sno que tene un espectro contnuo, debemos entonces volver a escrbr la ec.(.0), reemplazando la suma por una ntegral, en la forma: E = g( E) e 0 de donde g(e) reemplaza a g y representa el número de estados moleculares en el ntervalo de energía entre E y E+dE. Este número provene de las dferentes orentacones que puede tener la cantdad de movmento p para un energía determnada. 4
14 Departamento de Físca Aplcada III Capítulo : Físca estadístca Para calcular g(e) necestamos recurrr a la solucón de un problema de mecánca cuántca que más adelante analzaremos: la partícula en una caja de potencal trdmensonal (Levne I. 986) Adelantaremos que los estados de energía posbles para este caso son: ( n + n y n ) h E = x + z n x, n y, nz = 0,,,,... (.) 8ma Hay una correspondenca bunívoca entre los estados de energía dados por la ec.(.) y los puntos en un espaco trdmensonal con coordenadas dadas por valores enteros postvos (Mc Quarre,D. 97). En la fgura tenemos una versón en dmensones. Fgura 5
15 Departamento de Físca Aplcada III Capítulo : Físca estadístca La ec. (.) equvale a una ecuacón para una esfera de rado R = ( 8ma E / h ) en el espaco trdmensonal. Nosotros queremos calcular el número de puntos que se encuentran a una dstanca fja al orgen de este sstema de coordenadas. Lo que haremos será tratar R y E como una varable contnua y preguntarnos por el número de puntos comprenddos entre E y E+dE. Para calcular dcha cantdad, es convenente prmero calcular el número de puntos cuya energía es menor que E. Así, para valores grandes de E, es una aproxmacón excelente gualar el número de dchos puntos con energía menor que E con el volumen de un octante ( pues de esfera de rado R. n x n y,, n han de ser postvos) z S llamamos a dcho número de estados F(E), entonces: ( 4πa π 8ma E ) 8 6 E = = h φ (.) El número de estados entre E y E+dE será entonces: [( ) ] π 8ma g( E) E = φ ( E + de) φ( E) = E E + O E 4 h (.4) En la expresón anteror podemos desprecar los térmnos de orden cuadrado de cometendo un error nferor al % para la mayoría de los casos habtuales. E, La ecuacón anteror puede expresarse de la forma: ( m ) E de 4πV ( E) de = (.5) h g donde V representa el volumen ocupado por el gas.por lo tanto: 6
16 Departamento de Físca Aplcada III Capítulo : Físca estadístca = 4πV h ( m ) 0 E e E de Se puede demostrar que la ntegral del segundo membro tene el valor luego: π ( ), V (m ) = (.6) h Esta expresón da la funcón de partcón de un gas deal monoatómco en funcón de la temperatura y del volumen del gas. Ya tenemos todos los ngredentes necesaros para hallar lo que deseamos: la dstrbucón de moléculas en las dferentes energías. Reemplazando g por g(e)de dado por la ecuacón: n = N g e E tenemos: dn N N 4πV ( m ) E e E de E = e g ( E ) de = h (.7) donde dn es el número de moléculas con energía entre E y E+dE. Introducendo el valor de dado por la ec.(.6) tenemos: dn de πn = E e ( π) E 7
17 Departamento de Físca Aplcada III Capítulo : Físca estadístca que es la fórmula de Maxwell para la dstrbucón de energía de las moléculas de un gas deal. Nosotros en este trabajo utlzaremos la dstrbucón de velocdades en vez de la dstrbucón de energía. Tenendo en cuenta que : E = p = m mv dn dn = mv dv de y susttuyendo en la ec.(.7) ambas expresones se llega a la solucón fnal: m mv π N v e (.8) dn = 4 dv π Esta es la fórmula de Maxwell para la dstrbucón de velocdades de las moléculas en un gas deal : la msma da el número de moléculas que se mueven con una velocdad entre v y v+dv ndependentemente de la dreccón de movmento. La dstrbucón de velocdades en el oxígeno a dos temperaturas dferentes está representada en la fgura Fgura 8
18 Departamento de Físca Aplcada III Capítulo : Físca estadístca Una prueba crucal y drecta de la aplcabldad de la estadístca de Maxwell- Boltzmann a los gases deales consstría en contar realmente el número de moléculas que hay en cada ntervalo de velocdad o de energía. Con este fn han sdo utlzados varos dspostvos expermentales. La fgura 4 lustra un método que usa un selector de velocdades o cortadora. Dos dscos D y D, cada uno con una muesca, rotan con velocdad angular ω. Las muescas están desplazadas un ángulo θ. De las moléculas de gas que escapan de un horno a certa temperatura (proceso denomnado efusón) sólo pasan por las dos muescas e ncden en el detector aquellas cuya velocdad es : v = sω /θ Fgura 4 En realdad, como ambas muescas tenen un ancho fnto, las moléculas transmtdas tenen velocdades dentro de certo ntervalo en el entorno del valor dado. Se puede cambar la velocdad de las moléculas recbdas en el detector varando θ o ω. Hacendo varas observacones para dversas velocdades v se obtenen las dstrbucones de velocdades y de energía. Los resultados expermentales confrman la predccón de la estadístca de Maxwell-Boltzmann expresada por las ecuacones (.7) y (.8). 9
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
Electricidad y calor
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electricidad y calor. Un repaso... Temas. 4. Primera ley de la Termodinámica. Webpage: Algunas definiciones
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
10. VIBRACIONES EN SISTEMAS CON N GRADOS DE LIBERTAD
 10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
TRABAJO Y ENERGÍA INTRODUCCIÓN. requiere como varia la fuerza durante el movimiento. entre los conceptos de fuerza y energía mecánica.
 TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Centro de Masa. Sólido Rígido
 Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Problemas donde intervienen dos o más variables numéricas
 Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
Teoría cinético molecular
 5//00 Teoría cnétco molecular Químca 404 Ileana ees Martínez Tería Cnétco molecular Termodnámca (empírco) Macroscópco: P, V, ρ, T Independente de modelo molecular Teoría atómca molecular Interpretacón
5//00 Teoría cnétco molecular Químca 404 Ileana ees Martínez Tería Cnétco molecular Termodnámca (empírco) Macroscópco: P, V, ρ, T Independente de modelo molecular Teoría atómca molecular Interpretacón
3. VARIABLES ALEATORIAS.
 3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemático y dinámico de un mecanismo plano articulado con un grado de libertad.
 Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
Mecánica Clásica ( Partículas y Bipartículas )
 Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
Métodos específicos de generación de diversas distribuciones discretas
 Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Campo eléctrico. Líneas de campo. Teorema de Gauss. El campo de las cargas en reposo. Campo electrostático
 qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
TERMODINÁMICA AVANZADA
 TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
Ejemplo: Consumo - Ingreso. Ingreso. Consumo. Población 60 familias
 Ejemplo: Consumo - Ingreso Ingreso Consumo Poblacón 60 famlas ( YX ) P = x [ YX ] E = x Línea de regresón poblaconal 80 60 Meda Condconal 40 20 00 [ X = 200] EY o o o o [ X = 200] EY 80 o o o 60 o 40 8
Ejemplo: Consumo - Ingreso Ingreso Consumo Poblacón 60 famlas ( YX ) P = x [ YX ] E = x Línea de regresón poblaconal 80 60 Meda Condconal 40 20 00 [ X = 200] EY o o o o [ X = 200] EY 80 o o o 60 o 40 8
CESMA BUSINESS SCHOOL
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Mecánica del Sólido Rígido
 Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Y ahora observamos que lo que está entre paréntesis es la derivada de un producto, de modo que
 Estas son ms notas para las clases del curso Mecánca Raconal (62.11) en la Facultad de Ingenería-UBA. Están aún en proceso de ser completadas, no tenen carácter de texto acabado, por el contraro seguramente
Estas son ms notas para las clases del curso Mecánca Raconal (62.11) en la Facultad de Ingenería-UBA. Están aún en proceso de ser completadas, no tenen carácter de texto acabado, por el contraro seguramente
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA
 EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
Población: Es el conjunto de todos los elementos cuyo conocimiento nos interesa y serán objeto de nuestro estudio.
 Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6a)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
Departamento de Señales, Sistemas y Radicomunicaciones Comunicaciones Digitales, junio 2011
 Departamento de Señales, Sstemas y Radcomuncacones Comuncacones Dgtales, juno 011 Responder los problemas en hojas ndependentes. No se permte el uso de calculadora. Problema 1 6 p.) En este ejercco se
Departamento de Señales, Sstemas y Radcomuncacones Comuncacones Dgtales, juno 011 Responder los problemas en hojas ndependentes. No se permte el uso de calculadora. Problema 1 6 p.) En este ejercco se
Consideremos un sólido rígido sometido a un sistema de fuerzas en equilibrío, es decir
 1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION
 Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
ESTADÍSTICA. Definiciones
 ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
Modelos unifactoriales de efectos aleatorizados
 Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
Variables Aleatorias. Variables Aleatorias. Variables Aleatorias. Objetivos del tema: Al final del tema el alumno será capaz de:
 Varables Aleatoras Varables Aleatoras Objetvos del tema: Concepto de varable aleatora Al fnal del tema el alumno será capaz de: Varables aleatoras dscretas y contnuas Funcón de probabldad Funcón de dstrbucón
Varables Aleatoras Varables Aleatoras Objetvos del tema: Concepto de varable aleatora Al fnal del tema el alumno será capaz de: Varables aleatoras dscretas y contnuas Funcón de probabldad Funcón de dstrbucón
Termodinámica y Mecánica Estadística II serra/termoii 2016.html Guía 4 - Setiembre de 2016
 Termodnámca y Mecánca Estadístca II http://www.famaf.unc.edu.ar/ serra/termoii 2016.html Guía 4 - Setembre de 2016 Problema 1: Utlce el prncpo varaconal de Gbbs para obtener la expresón para la densdad
Termodnámca y Mecánca Estadístca II http://www.famaf.unc.edu.ar/ serra/termoii 2016.html Guía 4 - Setembre de 2016 Problema 1: Utlce el prncpo varaconal de Gbbs para obtener la expresón para la densdad
16.21 Técnicas de diseño y análisis estructural. Primavera 2003 Unidad 8 Principio de desplazamientos virtuales
 16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
Capítulo V. Teoremas de Fermat, Euler y Wilson
 Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
Una Reformulación de la Mecánica Clásica
 Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Reconciliación de datos experimentales. MI5022 Análisis y simulación de procesos mineralúgicos
 Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
INSTITUTO DE FÍSICA MECÁNICA ESTADÍSTICA
 INSTITUTO DE FÍSICA ECÁNICA ESTADÍSTICA Curso 0 Práctco IV Ensemble Canónco y Gases Ideales. Fecha de Entrega: 5 de Novembre de 0 Parte A: Ejerccos Teórco: Ejercco N o (*) Teorema de Equpartcón. H x x
INSTITUTO DE FÍSICA ECÁNICA ESTADÍSTICA Curso 0 Práctco IV Ensemble Canónco y Gases Ideales. Fecha de Entrega: 5 de Novembre de 0 Parte A: Ejerccos Teórco: Ejercco N o (*) Teorema de Equpartcón. H x x
H 0 : La distribución poblacional es uniforme H 1 : La distribución poblacional no es uniforme
 Una hpótess estadístca es una afrmacón con respecto a una característca que se desconoce de una poblacón de nterés. En la seccón anteror tratamos los casos dscretos, es decr, en forma exclusva el valor
Una hpótess estadístca es una afrmacón con respecto a una característca que se desconoce de una poblacón de nterés. En la seccón anteror tratamos los casos dscretos, es decr, en forma exclusva el valor
Universidad Diego Portales Facultad de Economía y Empresa
 Unversdad Dego Portales Profesor: Carlos R. Ptta Hasta este momento nos hemos enfocado en juegos en los cuales cualquer nformacón que es conocda por un jugador es conocda por todos los demás (es decr,
Unversdad Dego Portales Profesor: Carlos R. Ptta Hasta este momento nos hemos enfocado en juegos en los cuales cualquer nformacón que es conocda por un jugador es conocda por todos los demás (es decr,
Efectos fijos o aleatorios: test de especificación
 Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Físca General 1 Proyecto PMME - Curso 2007 Insttuto de Físca Facultad de Ingenería UdelaR ANÁLISIS E INFLUENCIA DE DISTINTOS PARÁMETROS EN EL ESTUDIO DE LA ESTÁTICA DE CUERPOS RÍGIDOS. Sebastán Bugna,
Físca General 1 Proyecto PMME - Curso 2007 Insttuto de Físca Facultad de Ingenería UdelaR ANÁLISIS E INFLUENCIA DE DISTINTOS PARÁMETROS EN EL ESTUDIO DE LA ESTÁTICA DE CUERPOS RÍGIDOS. Sebastán Bugna,
Tema 8 - Estadística - Matemáticas CCSSI 1º Bachillerato 1
 Tema 8 - Estadístca - Matemátcas CCSSI 1º Bachllerato 1 TEMA 8 - ESTADÍSTICA 8.1 NOCIONES GENERALES DE ESTADÍSTICA 8.1.1 INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para
Tema 8 - Estadístca - Matemátcas CCSSI 1º Bachllerato 1 TEMA 8 - ESTADÍSTICA 8.1 NOCIONES GENERALES DE ESTADÍSTICA 8.1.1 INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para
Modelos triangular y parabólico
 Modelos trangular y parabólco ClassPad 0 Prof. Jean-Perre Marcallou INTRODUCCIÓN La calculadora CASIO ClassPad 0 dspone de la Aplcacón Prncpal para realzar los cálculos correspondentes a los modelos trangular
Modelos trangular y parabólco ClassPad 0 Prof. Jean-Perre Marcallou INTRODUCCIÓN La calculadora CASIO ClassPad 0 dspone de la Aplcacón Prncpal para realzar los cálculos correspondentes a los modelos trangular
Aplicación de la termodinámica a las reacciones químicas Andrés Cedillo Departamento de Química Universidad Autónoma Metropolitana-Iztapalapa
 Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
INGENIERÍA DE TELECOMUNICACIÓN BLOQUE 1
 INGENIERÍA DE TELECOMUNICACIÓN BLOQUE En el Aula Vrtual se encuentra dsponble: Materal nteractvo con teoría y ejerccos resueltos. Para acceder a ello deberá pulsar sobre los sguentes enlaces una vez dentro
INGENIERÍA DE TELECOMUNICACIÓN BLOQUE En el Aula Vrtual se encuentra dsponble: Materal nteractvo con teoría y ejerccos resueltos. Para acceder a ello deberá pulsar sobre los sguentes enlaces una vez dentro
Mª Dolores del Campo Maldonado. Tel: :
 Mª Dolores del Campo Maldonado Tel: : 918 074 714 e-mal: ddelcampo@cem.mtyc.es Documentacón de referenca nternaconalmente aceptada ISO/IEC GUIDE 98-3:008 Uncertanty of measurement Part 3: Gude to the n
Mª Dolores del Campo Maldonado Tel: : 918 074 714 e-mal: ddelcampo@cem.mtyc.es Documentacón de referenca nternaconalmente aceptada ISO/IEC GUIDE 98-3:008 Uncertanty of measurement Part 3: Gude to the n
PRÁCTICA 10 CINÉTICA QUÍMICA I: DETERMINACIÓN DEL ORDEN DE REACCIÓN Y DE LA CONSTANTE DE VELOCIDAD
 PRÁCTICA 10 CINÉTICA QUÍMICA I: DETERMINACIÓN DEL ORDEN DE REACCIÓN Y DE LA CONSTANTE DE VELOCIDAD OBJETIVOS. Estudar la cnétca de una reaccón químca por el método de las velocdades ncales. Determnar los
PRÁCTICA 10 CINÉTICA QUÍMICA I: DETERMINACIÓN DEL ORDEN DE REACCIÓN Y DE LA CONSTANTE DE VELOCIDAD OBJETIVOS. Estudar la cnétca de una reaccón químca por el método de las velocdades ncales. Determnar los
OSCILACIONES 1.- INTRODUCCIÓN
 OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
5ª Lección: Sistema de fuerzas gravitatorias. Cálculo de centros de gravedad de figuras planas: teoremas de Guldin.
 Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Fundamentos de Física Estadística: Problema básico, Postulados
 Fundamentos de Físca Estadístca: Problema básco, Postulados y Formalsmos. Problema básco de la Mecánca Estadístca del Equlbro (MEE) El problema básco de la MEE es la determnacón de la relacón termodnámca
Fundamentos de Físca Estadístca: Problema básco, Postulados y Formalsmos. Problema básco de la Mecánca Estadístca del Equlbro (MEE) El problema básco de la MEE es la determnacón de la relacón termodnámca
ESTADÍSTICA DESCRIPTIVA
 Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
Física Curso: Física General
 UTP IMAAS ísca Curso: ísca General Sesón Nº 14 : Trabajo y Energa Proesor: Carlos Alvarado de la Portlla Contendo Dencón de trabajo. Trabajo eectuado por una uerza constante. Potenca. Trabajo eectuado
UTP IMAAS ísca Curso: ísca General Sesón Nº 14 : Trabajo y Energa Proesor: Carlos Alvarado de la Portlla Contendo Dencón de trabajo. Trabajo eectuado por una uerza constante. Potenca. Trabajo eectuado
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Primer Semestre - Otoño 2014. Omar De la Peña-Seaman. Instituto de Física (IFUAP)
 MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
Tema 3. Sólido rígido.
 Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
TEMA 4. TRABAJO Y ENERGIA.
 TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
CARTAS DE CONTROL. Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones para el control del proceso.
 CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
La mecánica de Newton
 8 La mecánca de Newton Contendos del módulo 8.1 Espaco y tempo 8.2 Ley de la nerca 8.3 Momentum 8.4 Centro de masa de un sstema de partículas 8.5 Momentum de un sstema de partículas 8.6 Teorema de conservacón
8 La mecánca de Newton Contendos del módulo 8.1 Espaco y tempo 8.2 Ley de la nerca 8.3 Momentum 8.4 Centro de masa de un sstema de partículas 8.5 Momentum de un sstema de partículas 8.6 Teorema de conservacón
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL
 EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA
 LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
A. Una pregunta muy particular que se puede hacer a una distribución de datos es de qué magnitud es es la heterogeneidad que se observa.
 MEDIDA DE DIPERIÓ A. Una pregunta muy partcular que se puede hacer a una dstrbucón de datos es de qué magntud es es la heterogenedad que se observa. FICHA º 18 Las meddas de dspersón generalmente acompañan
MEDIDA DE DIPERIÓ A. Una pregunta muy partcular que se puede hacer a una dstrbucón de datos es de qué magntud es es la heterogenedad que se observa. FICHA º 18 Las meddas de dspersón generalmente acompañan
Es el movimiento periódico de un punto material a un lado y a otro de su posición en equilibrio.
 1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED
 Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA.
 Programacón en Pascal 5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA. Exsten numerosas stuacones que pueden representarse medante relacones de recurrenca; entre ellas menconamos las secuencas y las
Programacón en Pascal 5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA. Exsten numerosas stuacones que pueden representarse medante relacones de recurrenca; entre ellas menconamos las secuencas y las
EJERCICIO 1 1. VERDADERO 2. VERDADERO (Esta afirmación no es cierta en el caso del modelo general). 3. En el modelo lineal general
 PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
EXPERIMENTACIÓN COMERCIAL(I)
 EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
PRÁCTICA Nº 5. CIRCUITOS DE CORRIENTE CONTINUA
 PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA
 INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA LABORATORIO 1-008 PRACTICA 4: LEYES DE LOS GASES 1. OBJETIVOS ) Comprobacón expermental de las leyes de los gases. En este caso nos vamos a concentrar en el estudo
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA LABORATORIO 1-008 PRACTICA 4: LEYES DE LOS GASES 1. OBJETIVOS ) Comprobacón expermental de las leyes de los gases. En este caso nos vamos a concentrar en el estudo
Cinemática del Brazo articulado PUMA
 Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Vida Util, características de la Fiabilidad e Inviabilidad y distribuciones teóricas en el terreno de la fiabilidad
 Vda Utl, característcas de la Fabldad e Invabldad y dstrbucones teórcas en el terreno de la fabldad Realzado por: Mgter. Leandro D. Torres Vda Utl Este índce se refere a una vda útl meda nomnal y se puede
Vda Utl, característcas de la Fabldad e Invabldad y dstrbucones teórcas en el terreno de la fabldad Realzado por: Mgter. Leandro D. Torres Vda Utl Este índce se refere a una vda útl meda nomnal y se puede
Mecánica del Sólido Rígido
 Mecánca del Sóldo ígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, otacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Mecánca del Sóldo ígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, otacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Variable aleatoria: definiciones básicas
 Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
Estadísticos muéstrales
 Estadístcos muéstrales Una empresa dedcada al transporte y dstrbucón de mercancías, tene una plantlla de 50 trabajadores. Durante el últmo año se ha observado que 5 trabajadores han faltado un solo día
Estadístcos muéstrales Una empresa dedcada al transporte y dstrbucón de mercancías, tene una plantlla de 50 trabajadores. Durante el últmo año se ha observado que 5 trabajadores han faltado un solo día
ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO.
 ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO..- PERSPECTIVA HISTÓRICA MATERIA { MOLÉCULAS } { ÁTOMOS}, sendo los átomos y/o moléculas estables por la nteraccón electromagnétca. Desde la perspectva electromagnétca
ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO..- PERSPECTIVA HISTÓRICA MATERIA { MOLÉCULAS } { ÁTOMOS}, sendo los átomos y/o moléculas estables por la nteraccón electromagnétca. Desde la perspectva electromagnétca
Pregunta Hoy está nublado, cuál es la probabilidad de que mañana continúe nublado? cuál es la probabilidad de que está nublado pasado mañana?
 Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Teoría de Modelos y Simulación Enrique Eduardo Tarifa Facultad de Ingeniería - Universidad Nacional de Jujuy. Generación de Números Aleatorios
 Teoría de Modelos y Smulacón Enrque Eduardo Tarfa Facultad de Ingenería - Unversdad Naconal de Jujuy Generacón de Números Aleatoros Introduccón Este capítulo trata sobre la generacón de números aleatoros.
Teoría de Modelos y Smulacón Enrque Eduardo Tarfa Facultad de Ingenería - Unversdad Naconal de Jujuy Generacón de Números Aleatoros Introduccón Este capítulo trata sobre la generacón de números aleatoros.
TEMA 3. VARIABLE ALEATORIA
 TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
Coordenadas Curvilíneas
 Departamento: Físca Aplcada III Mecánca Raconal (Ingenería Industral) Curso 007-08 Coordenadas Curvlíneas 1. Introduccón a. Obetvo: Generalar los tpos de coordenadas conocdos. Cartesanas. Clíndrcas, Esfércas,
Departamento: Físca Aplcada III Mecánca Raconal (Ingenería Industral) Curso 007-08 Coordenadas Curvlíneas 1. Introduccón a. Obetvo: Generalar los tpos de coordenadas conocdos. Cartesanas. Clíndrcas, Esfércas,
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS
 CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
Reconocimiento de Locutor basado en Procesamiento de Voz. ProDiVoz Reconocimiento de Locutor 1
 Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
ESTADÍSTICA BIDIMENSIONAL ÍNDICE GENERAL
 ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
Tema 3. Trabajo, energía y conservación de la energía
 Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
3.- Programación por metas.
 Programacón Matemátca para Economstas 1 3.- Programacón por metas. Una vez menconados algunos de los nconvenentes de las técncas generadoras, la ncorporacón de nformacón se va a traducr en una accón del
Programacón Matemátca para Economstas 1 3.- Programacón por metas. Una vez menconados algunos de los nconvenentes de las técncas generadoras, la ncorporacón de nformacón se va a traducr en una accón del
Matemáticas Discretas
 Coordnacón de Cencas Computaconales - INAOE Matemátcas Dscretas Cursos Propedéutcos 2010 Cencas Computaconales INAOE Dr. Lus Vllaseñor Pneda vllasen@naoep.mx http://ccc.naoep.mx/~vllasen Algo de nformacón
Coordnacón de Cencas Computaconales - INAOE Matemátcas Dscretas Cursos Propedéutcos 2010 Cencas Computaconales INAOE Dr. Lus Vllaseñor Pneda vllasen@naoep.mx http://ccc.naoep.mx/~vllasen Algo de nformacón
1.Variables ficticias en el modelo de regresión: ejemplos.
 J.M.Arranz y M.M. Zamora.Varables fctcas en el modelo de regresón: ejemplos. Las varables fctcas recogen los efectos dferencales que se producen en el comportamento de los agentes económcos debdo a dferentes
J.M.Arranz y M.M. Zamora.Varables fctcas en el modelo de regresón: ejemplos. Las varables fctcas recogen los efectos dferencales que se producen en el comportamento de los agentes económcos debdo a dferentes
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
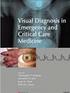 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
i=1 Demuestre que cumple los axiomas de norma. Calcule el límite Verifiquemos cada uno de los axiomas de la definición de norma: i=1
 CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
6.1 EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS
 TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y A c se les ha asociado los sucesos B y B c.
 Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
