CAMPOS ESCALARES TEMA 11 Y VECTORIALES
|
|
|
- Gabriel Luna Gil
- hace 7 años
- Vistas:
Transcripción
1 MATEMÁTICAS I (Ing. Téc. Sistemas de Telecomunicación) CÁLCULO DIFERENCIAL E INTEGRAL (Ing. Téc. Telemática) CAMPOS ESCALARES TEMA 11 Y VECTORIALES En términos abstractos un campo vectorial definido en un abierto U de R n no es otra cosa que una aplicación de U en R m. La teoría que exponemos aquí va dirigida a proporcionar un formalismo más adecuado a los modelos de la Física y de la Técnica, así como la interpretación en este contexto particular de los conceptos que se definen relacionados con la derivación, cuando esas aplicaciones representan magnitudes escalares o vectoriales. Aunque algunas definiciones y propiedades se enuncian en espacios R n de dimensión arbitraria, el lector que lo prefiera puede pensar en los casos de aplicación habitual, es decir, R 2 y R 3. 1 CAMPOS. OPERADORES DIFERENCIALES. Definición Sea U un conjunto abierto de R n. i) Un campo escalar de clase C k en U es una función f: U R de clase C k. ii) Un campo vectorial de clase C k en U es una aplicación F : U R m, m>1, de clase C k. El índice k recorre el conjunto de los números enteros positivos, entendiéndose que las aplicaciones de clase C 0 son las continuas. Ejemplos: 1) Son campos escalares la temperatura o la celeridad. 2) Son campos vectoriales la velocidad o cualquier campo de fuerzas (gravitatorio, eléctrico, magnético, etc.). Notación: Sea U un abierto de R n. Al conjunto de las aplicaciones f de clase C k definidas en U con valores en R p, f: U R p, lo denotaremos por C k (U, R p ). No es difícil comprobar que estos espacios, dotados de la suma habitual de funciones y el producto de números reales por funciones, son espacios vectoriales. La palabra operador se utiliza para designar las aplicaciones lineales entre este tipo de espacios vectoriales, en distinción con el caso de los espacios euclídeos. Cuando la imagen de un campo por un operador se define en términos de las derivadas parciales de sus componentes, se dice que el operador es diferencial.
2 Campos escalares y vectoriales 2 Ejemplo: La aplicación que a cada función f de clase C 1 en un abierto U de R n le asigna la función continua f/x 1 es un operador diferencial definido en C 1 (U, R). A continuación se presentan los operadores usuales que se manejan en la Física y sus propiedades básicas. Gradiente de un campo escalar Definición Sea f un campo escalar de clase C 1 en un abierto U de R n. Se denomina gradiente de f al campo vectorial definido por ( f f(x) = (x), f (x),..., f ) (x), x U. x 1 x 2 x n Propiedades Sean f,g campos escalares de clase C 1 en un abierto U de R n y c un número real. Se verifica: i) (f + g) = f + g. ii) (cf)=c f. iii) (f g)=f g + g f. iv) Si g(x) 0,x U, ( f/g) = (g f f g)/g 2. Observación De las propiedades i) y ii) se deduce que el gradiente es un operador definido en el espacio de los campos escalares de clase C 1 en un abierto U que toma valores en el espacio de los campos vectoriales continuos en U, f C 1 (U, R) f C 0 (U, R n ). Formalmente escribiremos = ( x 1, x 2,..., ). x n Definición Sea U un abierto de R n y F : U R n un campo vectorial continuo. Se dice que F es conservativo si existe un campo escalar f de clase C 1 en U tal que f(x) =F (x) para cada x U. En este caso, se dice que el campo f es una función potencial de F. Observaciones i) En ciertos modelos físicos, si f = F, se dice que f es una función potencial de F. Esto no debe causar ningún trastorno o confusión, es simplemente otro convenio de notación.
3 Campos escalares y vectoriales 3 ii) Veremos más adelante, al estudiar el concepto de integral curvilínea, que el adjetivo conservativo tiene un significado físico preciso. Observación Si F es el gradiente de un campo escalar f de clase C 2 en un abierto U de R n, entonces se sigue del lema de Schwarz que F i (x) = 2 f (x) = 2 f (x) = F j (x), 1 i, j n, x U. x j x j x i x i x j x i Sin embargo, el recíproco no es necesariamente cierto, a no ser que se impongan condiciones adicionales sobre la geometría de U. Definición Sea U un subconjunto abierto de R n. i) Se dice que U es estrellado respecto de un punto a U si para cualquier elemento x de U el segmento de extremos a y x, dado por {t x +(1 t)a : t [0, 1]}, está contenido en U. Se dice que U es estrellado si lo es respecto de alguno de sus puntos. ii) Se dice que U es convexo si para cada par de elementos x, y de U el segmento de extremos x e y, dado por {t x +(1 t)y : t [0, 1]}, está contenido en U. Obviamente un abierto convexo es estrellado respecto de cualquiera de sus puntos. Proposición (Lema de Poincaré) Sea F un campo vectorial de clase C 1 definido en un abierto estrellado U de R n. Entonces F es el gradiente de un campo escalar en U si, y sólo si, F i (x) = F j (x), x U, i,j=1, 2,...,n. (1) x j x i Observaciones i) La demostración teórica de la existencia de potenciales requiere de la noción de integral curvilínea que veremos más adelante, aunque la resolución práctica se reduce en la mayoría de los casos a un cálculo elemental de primitivas. Se puede mostrar que dos potenciales de un mismo campo conservativo (en general, en un abierto conexo) difieren en una constante. ii) Aunque el resultado anterior sigue siendo válido para una familia más amplia de abiertos, los denominados simplemente conexos, no se verifica para abiertos arbitrarios.
4 Campos escalares y vectoriales 4 Rotacional de un campo vectorial Definición Sea F =(F 1,F 2,F 3 ) un campo vectorial de clase C 1 en un abierto U de R 3. Se define el rotacional de F como el campo vectorial ( F3 rot F (x) = y (x) F 2 z (x), F 1 z (x) F 3 x (x), F 2 x (x) F ) 1 y (x), x U. Observaciones i) En la terminología anglosajona se denota rot F = curl F. ii) El siguiente determinante simbólico es útil para recordar la fórmula que define el rotacional: i j k rot F = x y z. F 1 F 2 F 3 Por esta razón el rotacional del campo F también se representa por F. Propiedades Sean F =(F 1,F 2,F 3 ), G =(G 1,G 2,G 3 ) dos campos vectoriales y f un campo escalar, todos ellos de clase C 1 en un abierto U de R 3. i) rot(f + G) =rotf + rot G. ii) Si c R, rot(c F )=c rot F. iii) rot(f F )=f rot F + f F. Observación De lo anterior se deduce que rot es un operador diferencial de C k (U, R 3 ) en C k 1 (U, R 3 ). Proposición Sea f un campo escalar de clase C 2 en un abierto U de R 3, entonces rot( f) =0. Definición Se dice que un campo F =(F 1,F 2,F 3 ) de clase C 1 en un abierto U de R 3 es irrotacional si su rotacional es idénticamente nulo en U, es decir, rot F (x) =0 para cada x U. Un campo conservativo de clase C 1 es, en virtud de la proposición anterior, irrotacional. El recíproco viene dado por el lema de Poincaré, que en este caso se escribe: Proposición Sea F =(F 1,F 2,F 3 ) un campo vectorial de clase C 1 definido en un abierto estrellado U de R 3. Entonces F es conservativo si, y sólo si, es irrotacional.
5 Campos escalares y vectoriales 5 Divergencia de un campo vectorial Definición Sea F =(F 1,F 2,...,F n ) un campo vectorial de clase C 1 en un abierto U de R n. Se define la divergencia de F como el campo escalar n F j div F (x) = (x) = F 1 (x)+ F 2 (x)+ + F n (x), x U. x j x 1 x 2 x n Formalmente, j=1 div F = F = ( x 1, x 2,..., razón por la cuál también se denota div F = F. ) (F 1,F 2,...,F n ), x n Propiedades Sean F, G: U R n dos campos vectoriales y f un campo escalar, todos ellos de clase C 1 en el abierto U de R n. i) div(f + G) = div F + div G. ii) Si c R, div(c F )=c div F. iii) div(f F )=f div F + f F. Observación De lo anterior se deduce que div es un operador diferencial de C k (U, R n ) en C k 1 (U, R). Proposición Si F =(F 1,F 2,F 3 ) es un campo vectorial de clase C 2 en un abierto U de R 3, entonces div(rot F )=0. Definición Se dice que un campo F =(F 1,F 2,F 3 ) de clase C 1 en un abierto U de R 3 es solenoidal o incompresible si su divergencia es idénticamente nula en U, div F (x) = 0 para cada x U. Según 1.21 el rotacional de un campo vectorial es solenoidal. Recíprocamente: Proposición Sea F =(F 1,F 2,F 3 ) un campo vectorial de clase C 1 definido en un abierto estrellado U de R 3. Entonces F es el rotacional de un campo vectorial G si, y sólo si, F es solenoidal. Observaciones i) Si F =(F 1,F 2,F 3 ), G =(G 1,G 2,G 3 ) son campos vectoriales en un abierto de R 3 tales que rot G = F (G al menos de clase C 1 ) se dice que G es un potencial vectorial de F. Nótese la analogía que existe entre los resultados 1.17 y 1.23.
6 Campos escalares y vectoriales 6 ii) Al igual que sucede con los potenciales escalares, la búsqueda de potenciales vectoriales en el caso de que el abierto U sea conexo se reduce al cálculo de primitivas. Si el campo F =(F 1,F 2,F 3 ) es de clase C 1 y solenoidal en el intervalo U de R 3,la ecuación rot G = F es el sistema de ecuaciones en derivadas parciales G 3 y G 2 z F 1 G 1 z G 3 x F 2 G 2 x G 1 y F 3 Gracias al resultado 1.15, podemos suponer, por ejemplo, que G 3 0; entonces, es posible dar unas primeras expresiones para G 1 y G 2 a partir de las dos primeras ecuaciones: G 2 z F 1 G 2 = F 1 dz + C 2 (x, y), G 1 z F 2 G 1 = F 2 dz + C 1 (x, y), siendo C 1 y C 2 las correspondientes constantes (respecto de z) de integración. Podemos suponer a continuación, por la misma razón que antes, que C 2 0, con lo que ya hemos determinado G 3 y G 2. Para concluir, basta determinar C 1 a partir de la tercera ecuación. Así se ha encontrado un potencial vectorial de F ; los demás se obtienen sumando a éste gradientes.
ROTACIONAL y DIVERGENCIA Campos vectoriales: Campo escalar: Campo vectorial: Campo vectorial:
 ROTACIONAL DIVERGENCIA Campos vectoriales: Los campos vectoriales son uno de los conceptos fundamentales de la física. Sin ellos es imposible entender el electromagnetismo, la óptica, o ramas más avanzadas
ROTACIONAL DIVERGENCIA Campos vectoriales: Los campos vectoriales son uno de los conceptos fundamentales de la física. Sin ellos es imposible entender el electromagnetismo, la óptica, o ramas más avanzadas
Divergencia y rotacional
 SESIÓN 2 Divergencia y rotacional 2.1 Introducción En esta sesión se revisan dos operaciones sobre campos vectoriales, de frecuente uso el resto del curso. Una de ellas produce un campo escalar (divergencia)
SESIÓN 2 Divergencia y rotacional 2.1 Introducción En esta sesión se revisan dos operaciones sobre campos vectoriales, de frecuente uso el resto del curso. Una de ellas produce un campo escalar (divergencia)
Derivadas Parciales de Orden Superior
 Capítulo 9 Derivadas Parciales de Orden Superior La extensión a funciones de varias variables del concepto de derivada de orden superior, aunque teóricamente no ofrece ninguna dificultad, presenta ciertas
Capítulo 9 Derivadas Parciales de Orden Superior La extensión a funciones de varias variables del concepto de derivada de orden superior, aunque teóricamente no ofrece ninguna dificultad, presenta ciertas
Campos Vectoriales y Operadores Diferenciales
 Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
Campos escalares vectoriales Sesión 1
 Campos escalares vectoriales Sesión 1 E. Cuesta 1 1 Departamento de Matemática Aplicada E.T.S.I. de Telecomunicaciones Universidad de Valladolid (España) Ampliación de Matemáticas Outline Campos escalares
Campos escalares vectoriales Sesión 1 E. Cuesta 1 1 Departamento de Matemática Aplicada E.T.S.I. de Telecomunicaciones Universidad de Valladolid (España) Ampliación de Matemáticas Outline Campos escalares
Comenzaremos repasando la Fórmula de Taylor para funciones reales de una variable real.
 Tema 5 Aplicaciones 5.1 Introducción Dedicaremos este tema a estudiar algunas aplicaciones del Cálculo Diferencial en varias variables, particularmente la Fórmula de Taylor, el cálculo de extremos locales
Tema 5 Aplicaciones 5.1 Introducción Dedicaremos este tema a estudiar algunas aplicaciones del Cálculo Diferencial en varias variables, particularmente la Fórmula de Taylor, el cálculo de extremos locales
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Comenzamos recordando algunos conceptos de la topología de l - R 2. Dado a lc y ɛ > 0 se llama bola abierta de centro a y radio ɛ al conjunto
 Capítulo 2 Funciones analíticas. Funciones armónicas. En este capítulo iniciamos el estudio de las funciones de variable compleja. Comenzamos con los conceptos de límite y continuidad en lc, conceptos
Capítulo 2 Funciones analíticas. Funciones armónicas. En este capítulo iniciamos el estudio de las funciones de variable compleja. Comenzamos con los conceptos de límite y continuidad en lc, conceptos
TEMA 0: Herramientas matemáticas
 1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
El diferencial exterior
 Capítulo 8 El diferencial exterior 1. El diferencial exterior En esta sección estudiaremos el operador diferencial entre formas. Definición 8.1. Sea ω una k-forma en R n, ω = ω dx. El diferencial dω es
Capítulo 8 El diferencial exterior 1. El diferencial exterior En esta sección estudiaremos el operador diferencial entre formas. Definición 8.1. Sea ω una k-forma en R n, ω = ω dx. El diferencial dω es
Definición. Tema 12: Teoremas de Integración del Cálculo Vectorial. Gradiente de un campo escalar. Rotacional de un campo vectorial.
 Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
ECUACIONES EN DERIVADAS PARCIALES Tópicos previos
 ECUACIONES EN DERIVADAS PARCIALES Tópicos previos Para tomar el curso de ecuaciones en derivadas parciales es importante la familiaridad del alumno con los conceptos que se detallan a continuación. Sugerimos
ECUACIONES EN DERIVADAS PARCIALES Tópicos previos Para tomar el curso de ecuaciones en derivadas parciales es importante la familiaridad del alumno con los conceptos que se detallan a continuación. Sugerimos
Parte II. Cálculo Diferencial para Funciones de Varias Variables Reales
 Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
1. Límites de sucesiones en R n
 1. Límites de sucesiones en R n Definición 1 (Límite de una sucesión). Dada {A k } k=1 = {a1 k,... an k } Rn decimos que el límite de A k cuando k tiende a infinito es L si: lím A k = L ε > 0, N N : A
1. Límites de sucesiones en R n Definición 1 (Límite de una sucesión). Dada {A k } k=1 = {a1 k,... an k } Rn decimos que el límite de A k cuando k tiende a infinito es L si: lím A k = L ε > 0, N N : A
x, y = x 0 y 0 + x 1 y 1 + x 2 y 2 + x 3 y 3. Es fácil ver que verifica 1. Es simétrica. x, y = y, x para todo x, y R 4.
 1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
Campos conservativos. f(x) = f (x) = ( f x 1
 Capítulo 1 Campos conservativos En este capítulo continuaremos estudiando las integrales de linea, concentrándonos en la siguiente pregunta: bajo qué circunstancias la integral de linea de un campo vectorial
Capítulo 1 Campos conservativos En este capítulo continuaremos estudiando las integrales de linea, concentrándonos en la siguiente pregunta: bajo qué circunstancias la integral de linea de un campo vectorial
Tema 6: Cinética de la partícula
 Tema 6: Cinética de la partícula FISICA I, 1º Grado en Ingeniería Civil Departamento Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice Introducción Trabajo mecánico
Tema 6: Cinética de la partícula FISICA I, 1º Grado en Ingeniería Civil Departamento Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice Introducción Trabajo mecánico
Funciones de varias variables
 Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Ecuaciones diferenciales lineales
 Ecuaciones diferenciales lineales Ecuaciones diferenciales lineales de orden n Una ecuación diferencial lineal de orden n es una expresión del tipo a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
Ecuaciones diferenciales lineales Ecuaciones diferenciales lineales de orden n Una ecuación diferencial lineal de orden n es una expresión del tipo a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Diferenciciación en R n
 Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
ELEMENTOS DE ANÁLISIS FUNCIONAL
 ELEMENTOS DE ANÁLISIS FUNCIONAL Guillermo Ames Universidad Tecnológica Nacional - Facultad Regional Córdoba 2011 TEMA 1: NOCIONES BÁSICAS DE ESPACIOS MÉTRICOS Espacios métricos: definición y ejemplos Definición
ELEMENTOS DE ANÁLISIS FUNCIONAL Guillermo Ames Universidad Tecnológica Nacional - Facultad Regional Córdoba 2011 TEMA 1: NOCIONES BÁSICAS DE ESPACIOS MÉTRICOS Espacios métricos: definición y ejemplos Definición
Capítulo 3. Funciones con valores vectoriales
 Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
Espacios Vectoriales
 Espacios Vectoriales Pedro Díaz Navarro * Abril de 26. Vectores en R 2 y R 3 2. Espacios Vectoriales Definición (Espacio vectorial) Decimos que un conjunto no vacío V es un espacio vectorial sobre un cuerpo
Espacios Vectoriales Pedro Díaz Navarro * Abril de 26. Vectores en R 2 y R 3 2. Espacios Vectoriales Definición (Espacio vectorial) Decimos que un conjunto no vacío V es un espacio vectorial sobre un cuerpo
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2018
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Cálculo diferencial e integral 3
 Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 12 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor, que vimos en el capítulo anterior, es el estudio de los extremos relativos de una función escalar. Aunque la analogía
Capítulo 12 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor, que vimos en el capítulo anterior, es el estudio de los extremos relativos de una función escalar. Aunque la analogía
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1. CÁLCULO DIFERENCIAL EN VARIAS VARIABLES
 TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
Análisis Matemático I: La integral de Riemann
 Contents : La integral de Riemann Universidad de Murcia Curso 2006-2007 Contents 1 Definición de la integral y propiedades Objetivos Definición de la integral y propiedades Objetivos 1 Definir y entender
Contents : La integral de Riemann Universidad de Murcia Curso 2006-2007 Contents 1 Definición de la integral y propiedades Objetivos Definición de la integral y propiedades Objetivos 1 Definir y entender
TEMA 2. ESPACIOS VECTORIALES
 TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
Teoría del potencial. Capítulo 5. Objetivos Introducción. Campos conservativos y solenoidales. Campos armónicos.
 Capítulo 5 Teoría del potencial Objetivos Campos conservativos y solenoidales. Campos armónicos. Representación integral de funciones. Teorema de Helmholtz. Ecuación de Poisson. 5.1. Introducción La teoría
Capítulo 5 Teoría del potencial Objetivos Campos conservativos y solenoidales. Campos armónicos. Representación integral de funciones. Teorema de Helmholtz. Ecuación de Poisson. 5.1. Introducción La teoría
PUBLICACIONES ETSIN Página 1
 MÉTODOS MATEMÁTICOS DE LA INGENIERÍA I La asignatura Métodos Matemáticos de la Ingeniería I comprende en su temario contenidos muy diversos, que van desde el análisis en varias variables a la ecuaciones
MÉTODOS MATEMÁTICOS DE LA INGENIERÍA I La asignatura Métodos Matemáticos de la Ingeniería I comprende en su temario contenidos muy diversos, que van desde el análisis en varias variables a la ecuaciones
UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS
 UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS Código: CNM- 517 Nombre: Análisis vectorial Prerrequisitos: CNM-295 Duración del semestre: 16 semanas Intensidad
UNIVERSIDAD DE ANTIOQUIA FACULTAD DE CIENCIAS EXACTAS Y NATURALES PREGRADO EN MATEMÁTICAS Código: CNM- 517 Nombre: Análisis vectorial Prerrequisitos: CNM-295 Duración del semestre: 16 semanas Intensidad
DERIV. DE UNA FUNC. EN UN PUNTO
 DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
Programa de Campos I
 Programa de Campos I Alejandro Kunold 28 de marzo de 2006 1. Bibliografía 1. Francis B. Hildebrand, Advanded Calculus for Applications (Prentice-Hall, New Jersey, 1976) 2. G. Arfken, Mathematical Methods
Programa de Campos I Alejandro Kunold 28 de marzo de 2006 1. Bibliografía 1. Francis B. Hildebrand, Advanded Calculus for Applications (Prentice-Hall, New Jersey, 1976) 2. G. Arfken, Mathematical Methods
Raíz cuadrada. Superficies de Riemann
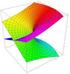 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
Chapter 1. Matrices. 1.1 Introducción y definiciones
 Chapter 1 Matrices 1.1 Introducción y definiciones Los conceptos de las matrices y determinantes se remonta al siglo segundo BC, incluso antes. Pero no es hasta el siglo XVII cuando las ideas reaparecen
Chapter 1 Matrices 1.1 Introducción y definiciones Los conceptos de las matrices y determinantes se remonta al siglo segundo BC, incluso antes. Pero no es hasta el siglo XVII cuando las ideas reaparecen
7 Teoremas de la divergencia y de Stokes
 7 Teoremas de la divergencia y de Stokes Si X es una hipersuperficie en R n que admite una normal unitaria continua ν : X R n, escribiremos X, ν) para indicar la variedad orientada formada por X y la orientación
7 Teoremas de la divergencia y de Stokes Si X es una hipersuperficie en R n que admite una normal unitaria continua ν : X R n, escribiremos X, ν) para indicar la variedad orientada formada por X y la orientación
CÁLCULO DIFERENCIAL Muestras de examen
 CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
ÍNDICE INTRODUCCIÓN... 9 INSTRUCCIONES PARA EL LECTOR... 13
 ÍNDICE INTRODUCCIÓN 9 INSTRUCCIONES PARA EL LECTOR 13 CAPÍTULO 1 GENERALIDADES TEOREMA DE LAGRANGE I Grupos 17 II Subgrupos 25 III Orden de un grupo 36 IV Índice de un subgrupo 40 Ejercicios correspondientes
ÍNDICE INTRODUCCIÓN 9 INSTRUCCIONES PARA EL LECTOR 13 CAPÍTULO 1 GENERALIDADES TEOREMA DE LAGRANGE I Grupos 17 II Subgrupos 25 III Orden de un grupo 36 IV Índice de un subgrupo 40 Ejercicios correspondientes
Unidad 1: Integrales Múltiples
 Unidad 1: Integrales Múltiples 1.1 Integrales dobles y triples. (1) Definir qué es una función integrable Riemann. (2) Decidir cuándo una función es integrable Riemann. (3) Enunciar y aplicar las propiedades
Unidad 1: Integrales Múltiples 1.1 Integrales dobles y triples. (1) Definir qué es una función integrable Riemann. (2) Decidir cuándo una función es integrable Riemann. (3) Enunciar y aplicar las propiedades
Diferenciales de Orden Superior
 Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
NOCIONES DE CALCULO VECTORIAL
 NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
Matemáticas III Tema 5 Integrales de ĺınea
 Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Análisis Matemático I
 Análisis Matemático I Los Teoremas de Valor Medio. Aplicaciones de clase C r Francisco Montalvo Departamento de Matemáticas. UEX Curso 2011/12 Contenido 1 Los teoremas de valor medio Los teoremas en una
Análisis Matemático I Los Teoremas de Valor Medio. Aplicaciones de clase C r Francisco Montalvo Departamento de Matemáticas. UEX Curso 2011/12 Contenido 1 Los teoremas de valor medio Los teoremas en una
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2017
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Capítulo 4: Conjuntos
 Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
1. Funciones diferenciables
 1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
Espacios normados y espacios métricos
 Lección 2 Espacios normados y espacios métricos Abstrayendo las propiedades básicas que tiene la norma de un espacio pre-hilbertiano, definiremos ahora lo que se entiende por una norma en un espacio vectorial,
Lección 2 Espacios normados y espacios métricos Abstrayendo las propiedades básicas que tiene la norma de un espacio pre-hilbertiano, definiremos ahora lo que se entiende por una norma en un espacio vectorial,
CÁLCULO III. Pablo Torres. Parte 4: Integrales curvilíneas. Facultad de Ciencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario
 ÁLULO III Pablo Torres Facultad de iencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario Parte 4: Integrales curvilíneas URVAS Una trayectoria o camino en R n es una función α : [a,b]
ÁLULO III Pablo Torres Facultad de iencias Exactas, Ingeniería y Agrimensura - Universidad Nacional de Rosario Parte 4: Integrales curvilíneas URVAS Una trayectoria o camino en R n es una función α : [a,b]
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
Teorema del valor medio
 Tema 10 Teorema del valor medio Podría decirse que hasta ahora sólo hemos sentado las bases para el estudio del cálculo diferencial en varias variables. Hemos introducido el concepto general o abstracto
Tema 10 Teorema del valor medio Podría decirse que hasta ahora sólo hemos sentado las bases para el estudio del cálculo diferencial en varias variables. Hemos introducido el concepto general o abstracto
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Preliminares. 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros.
 CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Una operación interna: Suma Una operación externa: Multiplicación por un escalar
 El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
El conjunto R n Es el conjunto de las n-adas formadas por el producto cartesiano RRR.R, donde R es el conjunto de los números reales. Así pues, dos elementos X y Y de R n serán iguales si y solo si tienen
CAMPOS VECTORIALES CONSERVATIVOS
 1 CAMPOS VECTORIALES CONSERVATIVOS DEFINICION DE CAMPO VECTORIAL. Sean M y N funciones de las variables x e y definidas en una región R del plano. La función definida por F(x, y) = Mi + Nj se llama campo
1 CAMPOS VECTORIALES CONSERVATIVOS DEFINICION DE CAMPO VECTORIAL. Sean M y N funciones de las variables x e y definidas en una región R del plano. La función definida por F(x, y) = Mi + Nj se llama campo
Tema 4 Diferenciación de funciones de una y varias
 Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Gabriela Jeronimo, Juan Sabia y Susana Tesauri. Álgebra lineal
 Gabriela Jeronimo, Juan Sabia y Susana Tesauri Álgebra lineal Buenos Aires, agosto de 2008 Prefacio El álgebra lineal es una herramienta básica para casi todas las ramas de la matemática así como para
Gabriela Jeronimo, Juan Sabia y Susana Tesauri Álgebra lineal Buenos Aires, agosto de 2008 Prefacio El álgebra lineal es una herramienta básica para casi todas las ramas de la matemática así como para
1. Ecuaciones lineales en cuerpos finitos
 1. Ecuaciones lineales en cuerpos finitos Un cuerpo es un conjunto F dotado de dos operaciones suma y producto, usualmente denotadas por + y que satisfacen los axiomas de los números reales, exceptuando
1. Ecuaciones lineales en cuerpos finitos Un cuerpo es un conjunto F dotado de dos operaciones suma y producto, usualmente denotadas por + y que satisfacen los axiomas de los números reales, exceptuando
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal.
 Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Apuntes y Ejercicios de Cálculo. Prácticas con Mathematica
 Marzo de 2010, Número 21, páginas 199-205 ISSN: 1815-0640 Apuntes y Ejercicios de Cálculo. Prácticas con Mathematica Autor de la Aplicación: Dirección: http://www.ugr.es/~fjperez/ El profesor es profesor
Marzo de 2010, Número 21, páginas 199-205 ISSN: 1815-0640 Apuntes y Ejercicios de Cálculo. Prácticas con Mathematica Autor de la Aplicación: Dirección: http://www.ugr.es/~fjperez/ El profesor es profesor
Rotacional, Divergencia, Gradiente, Laplaciano
 Rotacional, Divergencia, Gradiente, Laplaciano Denición 1. Rotacional Supongamos un campo F : U R 3 R 3, F, y, z = F 1, y, z, F, y, z, F 3, y, z diferenciable denido en el conjunto abierto U de R 3. Se
Rotacional, Divergencia, Gradiente, Laplaciano Denición 1. Rotacional Supongamos un campo F : U R 3 R 3, F, y, z = F 1, y, z, F, y, z, F 3, y, z diferenciable denido en el conjunto abierto U de R 3. Se
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2016
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
FUNCIONES DE VARIAS VARIABLES
 CAPITULO III CALCULO II FUNCIONES DE VARIAS VARIABLES 3.1 DEFINICIÓN Se denomina función de varias variables a la función que tiene n variables independientes y m variables dependientes. Una función de
CAPITULO III CALCULO II FUNCIONES DE VARIAS VARIABLES 3.1 DEFINICIÓN Se denomina función de varias variables a la función que tiene n variables independientes y m variables dependientes. Una función de
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
INDICE Capitulo 1. Leyes generales del campo electromagnético Capitulo 2. Divisiones de Electromagnetismo
 INDICE Acerca del autor XIII Prólogo XV Al estudiante XIX Agradecimientos XXI Capitulo 1. Leyes generales del campo electromagnético 1 1.1. Introducción 1 1.2. Definición de magnitudes fundamentales 2
INDICE Acerca del autor XIII Prólogo XV Al estudiante XIX Agradecimientos XXI Capitulo 1. Leyes generales del campo electromagnético 1 1.1. Introducción 1 1.2. Definición de magnitudes fundamentales 2
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Apuntes de Física II TERMODINÁMICA
 Apuntes de Física II TERMODINÁMICA Dr. Ezequiel del Río Departamento de Física Aplicada E.T.S. de Ingeniería Aeronáutica y del espacio Universidad Politécnica de Madrid 14 de febrero de 2017 ÍNDICE GENERAL
Apuntes de Física II TERMODINÁMICA Dr. Ezequiel del Río Departamento de Física Aplicada E.T.S. de Ingeniería Aeronáutica y del espacio Universidad Politécnica de Madrid 14 de febrero de 2017 ÍNDICE GENERAL
Matrices y sistemas de ecuaciones
 Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
GF = I V. G(v ) = v 1
 7- Inversas a Izquierda y Derecha Sea F : V V una transformación lineal. G : V V lineal se denomina inversa a izquierda de F si GF = I V donde I V : V V denota el operador identidad en V. En tal caso F
7- Inversas a Izquierda y Derecha Sea F : V V una transformación lineal. G : V V lineal se denomina inversa a izquierda de F si GF = I V donde I V : V V denota el operador identidad en V. En tal caso F
Tema 4: Integración en el plano complejo. Trayectorias (I) Trayectorias (II) Marisa Serrano, José Ángel Huidobro
 Índice Tema 4: en el plano complejo Marisa Serrano, José Ángel Huidobro Universidad de Oviedo 2 3 email: mlserrano@uniovi.es email: jahuidobro@uniovi.es Tema 4: en el plano complejo Tema 4: en el plano
Índice Tema 4: en el plano complejo Marisa Serrano, José Ángel Huidobro Universidad de Oviedo 2 3 email: mlserrano@uniovi.es email: jahuidobro@uniovi.es Tema 4: en el plano complejo Tema 4: en el plano
VECTORES 1.2 CONCEPTOS Y DEFINICIONES FUNDAMENTALES. En este capítulo estudiaremos los vectores y su álgebra.
 CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
Ignacio Romero 20 de Septiembre de 2004. Notación indicial
 INGENIERÍA GEOLÓGICA: MECÁNICA DE MEDIOS CONTINUOS Ignacio Romero 20 de Septiembre de 2004 Notación indicial En Mecánica de Medios Continuos los objetos matemáticos más empleados son los escalares, vectores
INGENIERÍA GEOLÓGICA: MECÁNICA DE MEDIOS CONTINUOS Ignacio Romero 20 de Septiembre de 2004 Notación indicial En Mecánica de Medios Continuos los objetos matemáticos más empleados son los escalares, vectores
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 5 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 5 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 5 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Teorema de Kirk y estructura normal en espacios de Banach
 Teorema de Kirk y estructura normal en espacios de Banach Introducción En el anterior artículo se comentaron los llamados problemas del milenio de las matemáticas [8]. Sólo uno de ellos se ha podido resolver
Teorema de Kirk y estructura normal en espacios de Banach Introducción En el anterior artículo se comentaron los llamados problemas del milenio de las matemáticas [8]. Sólo uno de ellos se ha podido resolver
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
ESPACIOS VECTORIALES
 01 de Junio de 2011 ESPACIOS VECTORIALES (Clase 02) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Combinación lineal 2. Subespacio vectorial
01 de Junio de 2011 ESPACIOS VECTORIALES (Clase 02) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela 1 Puntos a tratar 1. Combinación lineal 2. Subespacio vectorial
P r o g r a m a s S i n t é t i c o s y A n a l í t i c o s d e l a c a r r e r a d e I n g e n i e r í a M e c a t r ó n i c a TERCER SEMESTRE
 Programas Analíticos TERCER SEMESTRE A) Nombre del Curso Cálculo Vectorial B) Datos básicos del curso Semestre Horas de teoría por semana Horas de práctica por semana Horas trabajo adicional estudiante
Programas Analíticos TERCER SEMESTRE A) Nombre del Curso Cálculo Vectorial B) Datos básicos del curso Semestre Horas de teoría por semana Horas de práctica por semana Horas trabajo adicional estudiante
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES CUAUTITLÁN LICENCIATURA: INGENIERÍA MECÁNICA ELÉCTRICA.
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES CUAUTITLÁN LICENCIATURA: INGENIERÍA MECÁNICA ELÉCTRICA PROGRAMA DE LA ASIGNATURA DE: Cálculo Vectorial IDENTIFICACIÓN DE LA ASIGNATURA
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES CUAUTITLÁN LICENCIATURA: INGENIERÍA MECÁNICA ELÉCTRICA PROGRAMA DE LA ASIGNATURA DE: Cálculo Vectorial IDENTIFICACIÓN DE LA ASIGNATURA
101. Se ha visto que en los campos conservativos la divergencia era siempre distinta de cero, I 0 y por otra parte en dichos campos I
 Campos 6S. Se ha visto que en los campos conservativos la divergencia era siempre distinta de cero, I por otra parte en dichos campos I V, de lo que I V V, esta epresión así simbolizada que no es mas que
Campos 6S. Se ha visto que en los campos conservativos la divergencia era siempre distinta de cero, I por otra parte en dichos campos I V, de lo que I V V, esta epresión así simbolizada que no es mas que
MATEMATICA IV Carácter: Obligatoria
 UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE INGENIERIA CIVIL MATEMATICA IV Carácter: Obligatoria PROGRAMA: Ingeniería Civil DEPARTAMENTO: Ciencias Básicas CODIGO SEMESTRE UNIDAD DE CREDITO
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE INGENIERIA CIVIL MATEMATICA IV Carácter: Obligatoria PROGRAMA: Ingeniería Civil DEPARTAMENTO: Ciencias Básicas CODIGO SEMESTRE UNIDAD DE CREDITO
