* * * GEOMETRÍA DESCRIPTIVA * * *

Transcripción

1 4.- SISTEMA CÓNICO. Figura 42. El sistema cónico está formado por dos planos que se cortan bajo ángulo recto que reciben los nombres de plano del cuadro, PC, (el PV de diédrico) y plano geometral, PG, (el PH de diédrico). Ambos planos se cortan en la línea de tierra, LT. También hay un punto que es el punto de vista, PV, lugar desde donde se proyecta el espacio sobre el plano del cuadro. Existen dos planos mas que son, un plano paralelo al geometral trazado por el punto de vista que recibe el nombre de plano del horizonte y corta al plano del cuadro en la linea del horizonte, LH, y otro plano paralelo al plano del cuadro y que pasa por el punto de vista que recibe el nombre de plano de desvanecimiento, recibe este nombre porque, cualquier punto contenido en este plano no tiene representación (está en el infinito) ya que la recta definida por este punto y el PV es una recta paralela al cuadro y por tanto no corta a este plano, por lo cual no puede tener representación tan solo obtendremos la dirección en la que se encuentra. El plano de desvanecimiento tiene un gran interés ya que una circunferencia que tenga un punto en este plano tendrá una representación con un punto en e infinito (parábola) y si tuviera dos puntos en común con este plano, su representación tendrá dos puntos en el infinito (hipérbola). Figura 42 Página nº 35

2 El único punto que no tiene representación es el PV por ser un elemento propio del sistema. Para poder representarlo lo haremos por sus proyecciones diédricas sobre el plano del cuadro y el geometral, obteniéndose las proyecciones P y V. De esta manera podemos pasar de diédrico a cónico y viceversa. Para representar un punto (A) trazaremos la recta definida por PV y (A), donde esta recta corte al plano del cuadro, tendremos la perspectiva directa A. Seguidamente proyectaremos el punto (A) ortogonalmente sobre el PG obteniéndose el punto ((A)) Figura 43 y este punto se vuelve a proyectar sobre el PC desde PV, obteniéndose la perspectiva de la proyección, a. Así de esta manera a cada punto del espacio (A) le corresponde una pareja de puntos A, a sobre el PC. Figura 43. En la representación plana haremos coincidir el PG con el PC mediante un giro en sentido horario y el PC con el plano del papel, de esta manera solamente tenemos la LT y la LH así como las proyecciones diédricas del PV (P y V), (punto principal). Página nº 36

3 Figura 44. Figura 44 La distancia de V a LT es la separación entre el PV y el PC y la distancia entre LH y LT es la altura del PV respecto del PG. Representación del punto. Figura 45. Consideremos un punto A dado por sus proyecciones diédricas, para realizar su representación en el sistema cónico procederemos de la siguiente manera. En la imagen de la izda se ha representado un punto A perteneciente al segundo cuadrante y en la imagen de la dcha se han representado dos puntos, el A del segundo cuadrante y el B del primero. Observemos la imagen de la izda. Para determinar la perspectiva directa A, basta con calcular la traza vertical de la recta R definida por los puntos (A) y PV. Uniendo V con (a) nos corta a LT en m, levantando por m una perpendicular a LT donde esta recta corte a la P(a ) tendremos la perspectiva buscada A. Para determinar la perspectiva de la proyección bastará con trazar la recta definida por los puntos n Página nº 37

4 Figura 46 E por detrás del PC y por debajo del PG. Figura 45 y P donde corte a la perpendicular a LT trazada por A tendremos la perspectiva de la proyección a. Para tener una idea de la profundidad del dibujo consideremos que los puntos son corchos que van de la proyección A a la a y que estamos en una playa donde hemos colocado un cristal sobre la orilla de la misma, así quedan perfectamente definido la linea del horizonte (LH) la linea de tierra (orilla del mar) y el plano del cuadro (cristal). Figura 46. En la figura se han representado los puntos: A por detrás del PC y por encima del PG. B por delante del PC y por encima del PG. C por delante del PC y por debajo del PG. D en el PC y por encima del PG. Página nº 38

5 F Por detrás del PC, por encima del PG y en el infinito. Representación de la recta. Sabemos que una recta queda definida por dos puntos de ella, conociendo las proyecciones de dos puntos basta con unirlas y tendremos las proyecciones de la recta. Figura 47. Dados los puntos A,a y B,b la recta Rr queda definida uniendo las perspectivas A y B (R) y a y b (r). Son puntos importantes de determinar en la recta los de interección con el PC y con el PG así como su punto del infinito, punto que adquiere una gran importancia ya que cualquier recta que sea paralela con ella tendrá el mismo punto del infinito. Para determinar el corte con el PG, GR, basta buscar el punto en común de ambas Figura 47 perspectivas R y r. El punto de corte con el PC queda definido al determinar el punto tr, intersección de r con la LT y el punto del infinito LR, al determinar el punto lr, intersección de r con LH. Figura 48. Para determinar el punto del infinito de una recta dada, R, por sus proyecciones diédricas, (r )-(r), basta con trazar una recta paralela por el punto de vista PV y determinar su traza vertical y para determinar su traza con el PC basta con calcular la traza vertical de la recta dada, uniendo ordenadamente estos puntos tendremos la perspectiva cónica de la recta. Observando la figura, hemos calculado la traza vertical de la recta (r )-(r) que es el punto TR-tr y hemos trazado una paralela a esta recta por el punto de vista obteniéndose el punto LR-lr, la unión de estos puntos nos da la perspectiva cónica de la recta R, R-r. La recta S-s es paralela a la R-r ya que ambas tienen el mismo punto del infinito. Página nº 39

6 Figura 48 Posiciones particulares de la recta. Una recta puede adoptar seis posiciones que son: a). Recta paralela al plano geometral. Recta horizontal. b). Recta perpendicular al plano geometral. Recta vertical. c). Recta contenida en el plano geometral. d). Recta paralela al plano del cuadro. Recta frontal. e). Recta perpendicular al plano del cuadro. Recta de punta. f). Recta contenida en el plano del cuadro. a). Recta paralela al PG. Recta horizontal. Recta R. Figura 49. b). Recta perpendicular al PG. Recta vertical. Recta S. Figura 49. c). Recta contenida en el PG. Recta T. Figura 49. Página nº 40

7 a). Recta R. Una recta paralela al plano geometral (recta horizontal) se caracteriza por tener su punto límite en LH. b). Recta S. La recta perpendicular al PG se caracteriza por carecer de punto límite. Caso particular del d). Por tanto cualquier recta paralela a ella mantendrá el paralelismo entre sus perspectivas. c). Recta T. La recta contenida en el PG es un caso particular del a), tendrá sus perspectivas confundidas. Figura 49 d). Recta paralela al PC. Recta frontal. Recta R. Figura 50. e). Recta perpendicular al PC. Recta de punta. Recta S. Figura 50. f). Recta contenida en el PC. Recta T. Figura 50. d). Recta R. La recta paralela al PC se caracteriza por carecer de punto límite y la perspectiva r se mantiene paralela a LT. Por tanto cualquier recta paralela a ella mantendrá el paralelismo entre sus perspectivas. e). Recta S. La recta perpendicular al PC se caracteriza por tener su punto límite en el punto principal. Es un caso particular del a). f). Recta T. La recta contenida en el PC es un caso particular del d). Además de no tener punto límite, su perspectiva t coincide con LT. Figura 50 Página nº 41

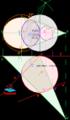
8 Haces de rectas. Figura 51. En diédrico vimos que el paralelismo entre rectas se conservaba (ver página 50 y siguientes de diédrico). En el sistema cónico, como los puntos del infinito tienen representación en los puntos límites, todas las rectas que compartan el mismo punto del infinito, son paralelas entre si. En el gráfico se han representado cuatro haces de rectas paralelas, las R, S y T; las U y V; y las X e Y. Obsérvese que estas últimas mantienen el paralelismo entre si por ser rectas paralelas al PC. Rectas que forman un ángulo dado con el PC. Figura 52. Figura 51 Vamos a determinar el lugar geométrico de todos los puntos límites de haces de rectas que forman un cierto ángulo con el PC. Recordemos que el punto límite de una recta se determina calculando la traza vertical de la recta paralela a la dada y que pase por el punto de vista. Puesto que el problema planteado se reduce a determinar única y exclusivamente puntos límites, trabajaremos con las paralelas trazadas por el punto de vista, y por pasar estas por dicho punto, trabajaremos en diédrico. Para determinar el lugar geométrico de todos los puntos del infinito de todos los haces de rectas que formen α grados con el PC, trazaremos por V una recta horizontal que forme con LT α grados y le calculamos su traza vertical, L3-l3. La circunferencia de centro P y radio PL3 será el lugar geométrico buscado. Cualquier recta que tenga por punto límite los puntos L1-l1, L2-l2 o L3-l3 serán haces de rectas paralelas entre si y formarán con el PC α grados. El punto L3-l3 es el punto límite de las rectas que además de cumplir lo anterior son paralelas al PG. Página nº 42

9 Figura 52 Unos puntos muy importantes y especiales son aquellos que forman 45º con PC, la circunferencia tendrá por radio la distancia que hay entre V y LT. Determinación del ángulo que una recta forma con el PC. Figura 53. Figura 53 Este problema se resuelve basándonos en el procedimiento anteriormente expuesto. Trazaremos la circunferencia de centro P y radio PL, esta cortará a LH en el punto L1-l1 que será la traza vertical de la recta paralela a la dada y que pasa por el punto de vista, recta (X)- (x), determinando la proyección (x) tendremos el ángulo buscado. Obsérvese que el procedimiento es el mismo que aplicábamos en diédrico (ver página 68 de diédrico). Página nº 43

10 Representación del plano. A igual que en diédrico, un plano lo representaremos en el sistema cónico por sus trazas, estas no son mas que las intersecciones del plano dado con el PC, PT, y con el PG, PS. Además todo plano posee una recta límite que se obtendrá calculando la traza vertical del plano paralelo al dado y que pase por el punto de vista. Como el paralelismo de planos en diédrico se conserva (ver página 51 de diédrico), esta recta límite será paralela a la traza con el PC. Figura 54. Figura 54 Téngase en cuenta que la traza PT es una recta que pertenece al PC por tanto cualquier punto, T, situado en PT tendrá su otra perspectiva sobre LT y cualquier punto, G, situado sobre PS tendrá su otra perspectiva confundida con él ya que PS es una recta perteneciente al PG, y cualquier punto, A, situado sobre la recta límite PL tendrá su otra perspectiva sobre LH. Piénsese que A es un punto del infinito. Pertenencia entre puntos y planos. Para situar un punto en un plano basta con situarlo en una recta que pertenezca al Página nº 44

11 plano y una recta pertenece a un plano si las trazas de la recta están sobre las trazas del plano. Figura 55. Figura 55 El punto B representado pertenece al plano P ya que el punto B-b pertenece a la recta R-r y esta al plano PT-PS-PL por tener la recta R su traza T-t sobre la traza PT del plano y su punto límite A-a sobre la recta límite PL del plano. Obsérvese que también podríamos haber situado el punto B-b sobre la recta U-u que al ser paralela al PC sus perspectivas serán paralelas a la traza PT del plano y a LT respectivamente. Posiciones particulares del plano. Un plano puede adoptar cuatro posiciones que son: a). Plano paralelo al plano del cuadro. Plano frontal. b). Plano perpendicular al plano del cuadro. Plano de canto. c). Plano paralelo al plano geometral. Plano horizontal. d). Plano perpendicular al plano geometral. Plano vertical. Página nº 45

12 a). Plano paralelo al PC. Plano P. Plano frontal. Figura 56. b). Plano perpendicular al PC. Plano Q. Plano de canto. Figura 56. a). Plano P. El plano paralelo al PC se caracteriza por poseer una sola traza, carece de traza con el plano del cuadro y de recta límite, la única traza que posee se mantiene paralela a LT. b). Plano Q. El plano perpendicular al PC se caracteriza porque su recta límite pasa por el punto principal. Figura 56 c). Plano paralelo al PG. Plano horizontal. Figura 57. d). Plano perpendicular al PG. Plano vertical. Figura 57. a). Plano P. El plano paralelo al PG se caracteriza por carecer de traza con él y su traza con el PC y su recta límite se mantienen paralelas a LT. b). Plano Q. El plano perpendicular al PG se caracteriza por tener su traza con el PC y su recta límite perpendicular a LT. Haces de planos. Obtención del que pasa por el punto de vista. Como hemos dicho, en diédrico el paralelismo entre planos se conserva (ver página 51 de diédrico). En el sistema cónico como la recta del infinito de un Figura 57 Página nº 46

13 plano tiene representación en su recta límite, todos los planos que compartan la misma recta límite serán paralelos entre si. De todos los planos que comparten una misma recta límite el que pasa por el punto de vista será aquél en el que sus tres trazas estén confundidas, plano V. Figura 58. Figura 58 Intersecciones de planos. Figura 59. A igual que en diédrico (ver página 30 y siguiente de diédrico) la intersección de dos planos es una recta y la determinábamos calculando las trazas de la misma que deberán estar sobre las trazas y rectas límites del plano. Además la traza con el PG de la recta debe coincidir con la traza con el PG del plano. Figura 59 La traza con el PC de la recta R es el punto, TR-tr, intersección de las trazas de los planos PT y QT y el punto del infinito de la recta R, LR-lr, es el punto de intersección de las rectas límites PL y QL de ambos planos. Página nº 47

14 Intersección de recta y plano. Figura 60. Como quedó expuesto tanto en diédrico como en axonométrico (ver página 32 y siguientes de diédrico y página 25 de axonométrico) se resuelve considerando un plano auxiliar Q que contenga a la recta R, resolviendo la intersección, S, del plano Q y el plano dado P y la intersección buscada será la intersección de las rectas R y S. Observando la figura, hemos considerado un plano vertical QL- QS-QT que contiene a la recta R-r, nótese que la traza QS está confundida con r. Seguidamente hemos calculado la intersección de los planos P y Q, para ello hemos obtenido la traza con PC de S, el punto TS-ts, y su punto límite LSls, la unión de TS y LS y ts y ls nos dan las perspectivas de la recta S- s. Donde S corta a R tendremos el punto I buscado. La otra perspectiva del punto I, estará situada sobre la recta r y la perpendicular trazada por I a LT. Figura 60 División de un segmento en partes iguales o proporcionales. Vamos a considerar tres casos, que son: a). Segmento horizontal. Paralelo al PG. b). Segmento frontal. Paralelo al PC. c). Segmento cualquiera. Página nº 48

15 a). Segmento horizontal. Paralelo al PG. Figura 61. Al ser el segmento paralelo al PG es indiferente trabajar con la perspectiva directa o con la perspectiva de la proyección. Aplicaremos el teorema de Thales 2, al determinar el haz de rectas paralelas, estas tendrán un punto límite, determinamos este punto y por él trazaremos las rectas paralelas interceptando, en la perspectiva de la proyección, segmentos que son iguales o proporcionales. Consideremos el segmento AB. Para dividirlo en partes iguales o proporcionales vamos a trabajar con la perspectiva de la proyección. Trazaremos por uno de sus extremos, por ejemplo el a, una recta paralela a LT y sobre ella llevaremos n segmentos iguales o proporcionales a partir de a. En la figura hemos considerado dividirlo en cuatro partes, obteniéndose los puntos 1', 2', 3' y 4', seguidamente unimos el punto 4' con el extremo b que al prolongarlo corta a LT en el Figura 61 punto l, punto del infinito del haz de rectas paralelas que trazaremos por los puntos anteriores, estas paralelas cortan al segmento ab en los puntos 1, 2 y 3, quedando así divido el segmento en cuatro partes iguales, que son a1, 12, 23 y 3b. Levantando perpendiculares a LT por estos puntos obtendremos la división en el segmento AB. Análogamente se procedería si en lugar de trabajar con la perspectiva de la proyección trabajásemos con la perspectiva directa AB. b). Segmento frontal. Paralelo al PC. Figura 62. Dado un segmento AB frontal, por ser paralelo al PC, el problema se resuelve 2 Un haz de rectas paralelas cortadas por dos rectas concurrentes interceptan en estas segmentos que son iguales o proporcionales. Página nº 49

16 directamente. Figura 62 Sea el segmento AB, podemos trabajar con cualquiera de las dos perspectiva, hemos elegido la perspectiva de la proyección. Trazamos por uno de sus extremos, por ejemplo el a, una recta cualquiera y sobre ella llevaremos n segmentos iguales o proporcionales, en el ejemplo hemos considerado cuatro partes, obteniéndose los puntos 1', 2', 3' y 4'. Unimos el punto 4' con el otro extremo b y por los puntos 1', 2', y 3' trazaremos paralelas a la recta 4'b obteniéndose sobre ab los puntos 1, 2 y 3 que dividen al segmento en cuatro partes iguales, a1, 12, 23 y 3b. Levantando perpendiculares a LT por estos puntos obtendremos en el segmento AB la división. Análogamente se procedería si trabajásemos con la perspectiva directa AB. c). Segmento cualquiera. Figura 63. Para dividir un segmento cualquiera en partes iguales o proporcionales trabajaremos con la perspectiva de la proyección ya que es mas fácil que si trabajásemos con la perspectiva directa. El proceso es análogo al caso a). Figura 63 Página nº 50

17 Existe otro procedimiento aplicable a los casos a) y c). Este método consiste en abatir sobre el PC el PG. y por tanto obtendremos el abatido, (a)(b), del segmento ab, procederemos a dividir este segmento en partes iguales y luego procederemos a deshacer el abatimiento. Pero antes de realizar este método vamos a ver como podemos encontrar el abatido de un punto que esté en el PG. Abatimiento del PG. sobre el PC. Abatimiento de un punto. Figura 64. Figura 64 Consideremos el punto A-a, cuya perspectiva a queremos abatir sobre el PC. Antes de empezar obtendremos los puntos límites de las rectas que forman 45º y 90º con el PC (véase páginas 42 y 43). Para ello trazaremos por el punto de vista V una recta que forme 45º con LT y le determinaremos su traza vertical obteniéndose los puntos F45º, para la que forma 90º su punto límite es P. Un punto podemos considerarlo como la intersección de dos rectas. Tracemos dos rectas cualesquiera que pasen por a, las mas fáciles de trazar serán una que forme 45º con PC y otra que forme 90º con PC. La primera tendrá su punto límite en F45º (dcha) y la segunda lo tendrá en P. Estas rectas cortan a LA en los puntos m y n respectivamente, Página nº 51

18 trazando por ellos una recta a 45º con respecto a LT y otra a 90º con respecto a la misma línea, donde ambas rectas se corten tendremos el punto buscado (a). De esta manera podemos determinar el abatimiento de cualquier figura contenida en el PG. Asimismo este proceso nos servirá para determinar la perspectiva de la proyección de cualquiera figura plana. Por ejemplo, vamos a determinar la perspectiva de la proyección de un exágono regular paralelo al PG siendo el punto O-o su centro, teniendo dos lados perpendiculares a LT y teniendo un vértice en LT. Figura 65. Figura 65 Para empezar vamos a determinar los puntos límites de las rectas que forman 30º con el PC ya que los lados del exágono forman 30º con la LT. Procedamos a encontrar Página nº 52

19 los puntos límites de las rectas que forman 30º y 90º con PC. Para ello trazaremos por V una recta que forme 30º con LT y le calculamos su traza vertical obteniendo los puntos F30º, el punto límite de las rectas que forman 90º es el punto P. Tracemos por o dos rectas una que forme 30º con PC y otra 90º, (uniendo o con F30º dcha y o con P), prolongando estas rectas obtendremos los puntos m y n respectivamente y trazando por estos puntos dos rectas una que forme 30º con LT y otra 90º, en su intersección, tendremos el punto (o), centro del exágono. Por tener dos lados perpendiculares a LT y un vértice en LT, la construcción es fácil. Una vez obtenida el abatimiento del exágono, procedamos a desabatir los puntos (a), (b), (c), (d) y (e), para ello trazaremos por estos puntos rectas a 30º con respecto a LT y 90º obteniéndose los puntos r, ñ, p y q. Los puntos r, ñ y n lo uniremos con P (rectas perpendiculares a PC) y los p y q con F30º (izda), (rectas a 30º con respecto al PC), en las respectivas intersecciones de estas líneas obtendremos los puntos a, b, c, d, e y n. La unión de estos nos dará la perspectiva de la proyección del exágono buscado. Obsérvese que los lados cd y an pasan por F30º (izda) y los ne y bc por F30º (dcha), por el paralelismo de dichos lados. Para determinar la perspectiva directa trazaremos rectas a 30º con respecto al cuadro por el punto O, estas rectas pasarán por los puntos límites F30º y sobre ellas estarán los vértices AD y BE respectivamente, levantando perpendiculares a LT por a, d, b y e donde corten a las rectas anteriores tendremos los vértices A, D, B y E. Para determinar los N y C como la recta NC es perpendicular al PC bastará con unir O con P y sobre esta recta estarán dichos vértices. Ahora estamos en condiciones de poder dividir un segmento cualquiera en partes iguales. Este proceso quedó expuesto en el inicio de la página 51. Figura 66. Previamente calcularemos los puntos límites de rectas a 45º con respecto al PC y 90º obteniéndose los puntos F45º y P respectivamente. A continuación procederemos a encontrar el punto (b), abatido de b. La unión de (b) con n nos dará el abatido de la recta que define el segmento ab. Para encontrar el punto (a) trazaremos por a una recta perpendicular al PC (uniendo a con P) donde esta recta corte a LT, trazaremos una perpendicular a ella y encontraremos el punto (a). Conocido el segmento (a)(b) procedamos a dividirlo en, por ejemplo, cuatro partes iguales, obteniéndose los puntos (1), (2) y (3). Para encontrar los desabatidos de estos puntos trazaremos rectas perpendiculares a LT por ellos, encontrado los puntos 3', 2' y 1' respectivamente. Estas rectas, por ser perpendiculares al PC, pasarán por P, donde estas corten al segmento ab obtendremos los puntos 3, 2 y 1 Página nº 53

20 respectivamente que dividen al segmento ab en partes iguales b3, 32, 21 y 1a. Para determinar las divisiones en la perspectiva directa bastará con trazar por 1, 2 y 3 rectas perpendiculares a LT y tendremos la perspectiva directa divida en partes iguales. Figura 66 Verdadera magnitud de un segmento. Vamos a determinar las verdaderas magnitudes de segmentos. Consideraremos casos que son: a). Segmento perpendicular al plano geometral. Recta vertical. b). Segmento paralelo al plano geometral. Recta horizontal. c). Segmento perpendicular al plano del cuadro. Recta de punta. d). Segmento paralelo al plano del cuadro. Recta frontal. e). Segmento cualquiera. Página nº 54

21 a). Segmento perpendicular al plano geometral. Recta vertical. Figura 67. Consideremos el segmento AB de la figura cuya magnitud queremos calcular. Sabemos que las únicas verdaderas magnitudes son las de los segmentos contenidos en el PC El segmento AB que nos dan es paralelo al PC, traslademos este segmento, paralelamente a si mismo, hasta que esté contenido en el PC. La forma mas fácil es trazando dos rectas paralelas al PC por los extremos del segmento hasta que corten al PC, obteniéndose los puntos C y D, la distancia entre estos dos puntos serán la verdadera magnitud del Figura 67 segmento AB. Para ello tomaremos un punto límite cualquiera, L-l situado sobre LH, y por él trazaremos las rectas la, LA y LB, la recta la corta a LT en el punto m, punto que está situado en el PC, levantando por m una perpendicular a LT donde corte a las rectas LA y LB tendremos los puntos C y D respectivamente. Basta con medir la distancia entre C y D y tendremos la verdadera magnitud del segmento AB. b). Segmento paralelo al plano geometral. Recta horizontal. Figura 68. Sea el segmento AB. Al ser paralelo al PG es indistinto trabajar con la perspectiva directa como con la perspectiva de la proyección, ya que, al ser paralelo al PG ambas perspectivas medirán lo mismo. Trabajaremos con la perspectiva de Figura 68 Página nº 55

22 la proyección por ser mas fácil. El proceso que vamos a seguir es abatir el PC sobre el PG, de esta manera podremos calcular la verdadera magnitud del segmento ab. Para empezar determinaremos los puntos límites de las rectas que forman 45º y 90º con el PC, la primera es el punto F45º y la segunda el punto P. Seguidamente trazaremos por el punto a dos rectas, una que forme 45º y otra 90º con el PC, la primera resulta de la unión de F45º con a y la segunda de a con P, estas rectas cortan a LT en los puntos m y n respectivamente, trazaremos por estos puntos una recta a 45º y otra a 90º con respecto a LT y en su intersección tendremos la perspectiva abatida (a) del punto a. Para obtener el abatido del punto b, trazaremos una recta perpendicular al PC y que pase por él, esta recta corta a LT en el punto p, trazando por p la perpendicular a LT donde se corte con la recta m(a) tendremos el punto (b) buscado. La verdadera magnitud del segmento AB será (a)(b). c). Segmento perpendicular al plano del cuadro. Recta de punta. Este problema es un caso particular del b). d). Segmento paralelo al plano del cuadro. Recta frontal. Figura 69. Este ejercicio es un caso particular del a). Procederemos de la misma manera, es decir, trasladaremos el segmento AB paralelamente a si mismo hasta que esté en el PC. Determinaremos el punto límite de las rectas que forman 90º con PC. (punto P) y trazaremos por él las rectas PG, PA y PB; la recta PG corta a LT en m, punto que está situado en el PC, por él trazaremos una recta paralela a la AB donde esta recta corte a las PA y PB tendremos los puntos C y D Figura 69 respectivamente que son los que nos dan la verdadera magnitud buscada. Obsérvese que por estar situado por delante del PC el segmento se reduce de magnitud mientras que en el caso a) por estar situado por detrás del PC aumenta. Página nº 56

23 e). Segmento cualquiera. Figuras 70 y 71. Observando la figura 70, vemos que la verdadera magnitud del segmento AB se puede obtener construyendo un triángulo rectángulo cuya hipotenusa sea el segmento AB y sus catetos los OB y OA, siendo OB paralelo a ab y el OA perpendicular al plano que contiene al segmento ab. Este es el método que vamos a aplicar para Figura 70 calcular la verdadera magnitud de un segmento cualquiera AB. El proceso será obtener la verdadera magnitud de la perspectiva de la proyección ab y la verdadera magnitud de la diferencia de alturas entre los puntos A y B, seguidamente construiremos el triángulo rectángulo y la hipotenusa nos dará la magnitud buscada. Existen otros métodos para realizar este cálculo pero debido al hecho de que hay conocimientos de este sistema que no vamos a abordar, como son los abatimientos y los cambios de sistema de referencia, aplicaremos el que acabamos de exponer. Figura 71. En primer lugar determinaremos los puntos límites de las rectas que forman 45º y 90º con el PC (F45º y P respectivamente). Seguidamente procederemos a abatir PG sobre PC con lo cual encontraremos la verdadera magnitud del segmento (a)(b). Para abatir el segmento (a)(b) trazaremos por el punto (b) dos rectas una que forme 45º con el PC (unión de F45º dcha con a) y otra 90º (unión de P con a), ambas rectas cortan a LT en los puntos m y n respectivamente, a continuación trazaremos por estos puntos dos rectas una a 45º con respecto a LT y la otra a 90º, donde ambas rectas se corten tendremos el punto (b). Para obtener el punto (a) trazaremos una perpendicular al PC por él y corta a LT en ñ, trazando por n una perpendicular a LT donde esta recta se corte con la t(b) tendremos el punto buscado y con ello, la verdadera magnitud del segmento ab. Vamos a determinar ahora la diferencia de alturas entre los puntos A y B. Para ello trazaremos dos rectas que pasando por estos puntos sean paralelas al PG (rectas horizontales), estas rectas tendrán su punto límite coincidente con l. Uniendo l con A y l con B tendremos, sobre la perpendicular por A, la diferencia de alturas AC Página nº 57

24 entre los puntos AB. A continuación calcularemos la verdadera magnitud de este segmento, que por ser paralelo al PC los trasladaremos paralelamente a si mismo hasta que esté situado en el PC. Uniendo a y l nos corta a LT en t, punto que está sobre PC y trazando la perpendicular por este punto a LT intercepta con las rectas la y lb el segmento DE, verdadera magnitud de la diferencia de alturas entre ambos puntos. Construyendo el triángulo rectángulo cuyos catetos son (a)(b) y DE respectivamente, en la hipotenusa, tendremos el valor del segmento AB buscado. La construcción de este triángulo podemos hacerla sobre el segmento (a)(b) abatido con lo cual evitamos tener que construirlo aparte. En el gráfico se ha realizado aparte para mayor claridad del trazado. Figura 71 Nota: Catetos ab y AC. Verdaderas magnitudes de estos catetos, (a)(b) y DE. Página nº 58

25 Perspectiva de figuras planas. En la página 52 hemos desarrollado la construcción de un exágono regular contenido en un plano paralelo al PG. Vamos a estudiar ahora el trazado de la circunferencia que, como quedó expuesto en la página 35, puede dar lugar a una elipse, parábola o hipérbola según que la circunferencia no toque, sea tangente o corte al plano de desvanecimiento. De estos tres casos solo vamos a exponer cuando sea una elipse. a). Circunferencia situada en el PG y por detrás del PC. Figura 72. Figura 72 Nos dan el punto O-o que es centro de una circunferencia contenida en el PG y es tangente al PC. Procedemos a abatir el PG sobre el PC y con ello encontramos el centro abatido (O), trazamos la circunferencia y le circunscribimos un cuadrado trazándole las diagonales y los ejes paralelo y perpendicular a LT. Las rectas que son perpendiculares a LT tendrán por punto límite P y las que son a 45º con respecto a LT tendrán a F45º. Observando la figura vemos el proceso de obtención de los ocho puntos de la elipse. Obsérvese que las tangentes en los puntos 2, 4, 6 y 8 son rectas Página nº 59

26 a 45º por tanto, irán a los puntos límites F45º, las tangentes en los puntos 1 y 5 serán paralelas a LT y las que lo son en los puntos 3 y 7 irán al punto P. Téngase presente que el centro de la elipse NO ES el centro de la circunferencia (O). Métodos para realizar perspectivas cónicas. Vamos a exponer dos métodos de poner objetos en perspectiva cónica, que son: a). Método Reile. b). Método de la homología. a). Método Reile. Cuando miramos un objeto lo hacemos variando nuestros ojos hacia los puntos característicos de este. Esto es debido a que el ángulo de visión del ojo humano es aproximadamente un cono de semiángulo 30º, cuyo eje es el rayo principal. Por lo tanto, todo aquello que quede fuera del cono de visión se verá deformado. Generalmente dirigimos la vista al centro de gravedad del objeto. Aplicando este concepto a la perspectiva cónica, vemos que una vez elegido el punto de vista, el rayo principal será el que va directamente al c.d.g. del objeto y el plano del cuadro será perpendicular a dicho rayo (no es necesario que el rayo principal pase por el c.d.g. del objeto). Desde el punto de vista, proyectaremos cónicamente el objeto sobre el plano del cuadro. Es evidente que si queremos representarlo totalmente y sin deformación, tendrá que estar comprendido dentro del cono de visión. Veamos el proceso a seguir para realizar una perspectiva cónica por este método. Consideremos el edificio dado por su Figura 73 planta y alzado de la figura 73. Página nº 60

27 Figura 74 Una vez fijado el PV, la inclinación del objeto con respecto al rayo principal, la situación del PC y de la LH, procederemos a determinar los puntos límites de las líneas principales del objeto. Figura 74. Para ello trazaremos por el PV rectas paralelas a las direcciones principales del objeto y le calcularemos sus trazas verticales obteniéndose los puntos límites de ambas direcciones, F1 y F2. La altura de la LH con respecto a PC la tomaremos de las proyecciones diédricas. Figura 75. Procedamos a proyectar la arista a, (recta vertical), para ello unimos PV con a y vemos que corta al PC en el punto 1, giremos 90º esta arista y la veremos como la línea A. Figura 76. Seguidamente vamos a determinar la magnitud de esta arista, para ello vamos al alzado y medimos la distancia que hay desde La LH hasta los extremos de dicha arista. Tomamos una de las dos direcciones que pasan por a y la prolongamos hasta que corte al PC en 2, la giramos 90º y la arista se verá como la línea (A) y como esta línea se encuentra en el PC, sobre ella podemos tomar las magnitudes anteriores. Uniendo estos extremos con el punto límite, de la dirección que hemos prolongado (F1), nos intercepta en la recta A la magnitud que tendrá dicha arista. Figura 77. Ahora vamos a determinar la arista b, siguiendo un proceso idéntico al descrito. Una vez encontrada la posición de esta arista (la veremos como B), procedemos a unir los extremos anteriormente hallados en A con el punto límite correspondiente a la línea ab, F1, y nos dará el tamaño de la arista B. Obsérvese que no hace falta calcular las distancias desde la LH hasta los extremos de la arista b. Página nº 61

28 Figura 75 Figura 76 Página nº 62

29 Figura 77 Figura 78. Repitiendo este proceso para la arista c y así sucesivamente con todos los elementos de la figura obtendremos la perspectiva de la misma. Figura 78 En las figuras 79 y 80 tenemos el resultado final de la perspectiva. Página nº 63

30 Figura 79 Figura 80 Página nº 64

31 Figura 81. Hay que tener en cuenta en este método que, si la figura está por delante del PC la perspectiva aumenta de tamaño mientras que si está por detrás del cuadro la perspectiva disminuye de tamaño, en el primer caso la figura se encuentra situada en el primer cuadrante y en el segundo caso estaría situada en el segundo cuadrante. Figura 81 Figura 82. El hecho de que la figura quede situada en el primer cuadrante implica que su proyección sobre el PG, (al girar el PG hasta que coincida con el PC), quedará por debajo de LT y la perspectiva quedará por encima de LT y mas pequeña, mientras que si la figura está en el segundo cuadrante su proyección sobre PG, (al girar el PG hasta que coincida con el PC), quedará por encima de LT y la perspectiva quedaría por debajo de LT y mas grande y se confundirá con la planta de la figura. Generalmente al aplicar este método se suele colocar la figura en el primer cuadrante para evitar que se superpongan la perspectiva y la planta de la figura. b). Método de la homología. Figura 82. Este método implica una variación en la configuración de los elementos del sistema, es decir, la LT y la LH quedarán invariantes pero el punto de vista quedaría por encima de la LH, ya que para hacer coincidir el PG con el PC se realizaría mediante un giro en sentido antihorario quedando el punto de vista V por encima de LH. Página nº 65

32 Figura 82 La forma de trabajar con este método es idéntica a lo expuesto hasta ahora. Veamos como se realiza la perspectiva de una figura por este método. Sea la figura dada en diédrico por su planta y alzado de la figura 83. Figura 83 Aquí tenemos que tener presente que entre la perspectiva buscada, la planta de la figura y el punto de vista V existe una homología siendo V el centro de la homología, LT el eje y LH la recta límite, por tanto, aplicando los conocimientos de la homología podemos obtener la perspectiva. Figura 84. Una vez situada la LT, la LH, el PV y la planta de la figura, procederemos a obtener los puntos límites de las direcciones principales de la misma. Para ello, trazaremos por el punto V paralelas a las direcciones principales de la figura, obteniéndose los puntos F1 y F2. Página nº 66

33 Figura 84 Figura 85. Después de haber obtenido los puntos límites, F1 y F2, procederemos a obtener la perspectiva de la planta de la figura. Recordemos que, en la homología, rectas homólogas se cortan en el eje, procedamos a prolongar las aristas de la planta hasta cortar a LT uniendo estos puntos con F1 y F2 tendremos la perspectiva de la planta. Figura 86. A continuación procederemos a dar alturas a cada una de las aristas que integran la figura. Consideremos la arista a, cuya perspectiva es A, levantando por ella una perpendicular a LT tendremos la posición de la misma lo que falta es darle el tamaño que tenga. Para darle la altura, siendo la arista a una recta vertical, la trasladaremos paralelamente a si misma hasta que esté contenida en PC, (obtenemos el punto 1), sobre esta línea podemos colocar su magnitud, (punto 2),y trazaremos una paralela por este último punto interceptando a la arista A en el punto 3, que nos da su magnitud, A3. Figura 87. Vamos a determinar la altura de la arista b, cuya perspectiva es B, uniendo el extremo superior de A con F1 interceptará a la perpendicular trazada por B en el punto 2, siendo B2 la altura de la arista B. Página nº 67

34 Figura 85 Figura 86 Página nº 68

35 Figura 87 Figura 88 Página nº 69

36 Figuras 88 y 89. Repitiendo este proceso obtendremos la perspectiva de la figura. Figura 89 Cuando se aplica este método, si la figura se encuentra situada en el primer cuadrante su planta queda situada por encima de la LT y su perspectiva quedará por debajo de la LT y de mayor tamaño mientras que, si se encuentra situada en el segundo cuadrante, su planta quedará por debajo de la LT y su perspectiva por encima de LT y de menor tamaño. Generalmente se suelen colocar las figuras en el segundo cuadrante. Válido para ambos métodos es la siguiente consideración: Figura 90. Si tenemos líneas que no son paralelas al PG, su punto límite, no está situado en la LH, no obstante podemos encontrar su punto límite sin mas que trazar por el punto de vista (P proyección vertical y V proyección horizontal) una recta paralela a esta línea calculándose su traza vertical que será su punto límite. Hay que Página nº 70

37 tener en cuenta que, generalmente, nos dan la planta y el alzado de la figura en diédrico y la posición para realizar la perspectiva está girada con respecto a LT, NO PODEMOS, pues, trazar la paralela a la línea en cuestión tomándola de la representación diédrica, sino que tenemos que determinarla en función de la representación que tenemos girada. Figura 90 Nos dan la recta R (r -r) por sus proyecciones diédricas, vemos que está situada en el primer cuadrante. Tanto en la representación de la izda (homología) como en la de la dcha la postura de la recta rg está girada con respecto al dato r. Obsérvese que en la homología queda por encima de LT y en la otra por debajo, esto es debido a la forma en que se gira el PG para que coincida con el PC (ver páginas 65 y 66). Procedemos a realizar un giro en la representación diédrica para colocar la recta en la misma posición que tienen en ambas perspectivas. Seguidamente trazamos por V una paralela a rg y por P una paralela a rg, le hallamos su traza vertical y hemos obtenido el punto límite, L-l, de la recta R. Nótese que en ambos casos la solución es la misma, pero en la homología, la paralela a rg por V es la simétrica de rg respecto de LT, (compárese con las proyecciones diédricas). Página nº 71

38 ÍNDICE 3.- SISTEMA AXONOMÉTRICO Clases de sistemas axonométricos....2 El triángulo de trazas....3 Concepto de coeficiente de reducción....4 Determinación de los coeficientes de reducción y de los ángulos que forman los ejes con el plano del cuadro....5 Determinación de los coeficientes de reducción....5 Determinación de los ángulos que forman los ejes con el plano del cuadro....7 Alfabeto del punto. Proyecciones del punto....9 Puntos situados en los planos de proyección y en los ejes....9 Alfabeto de la recta. Proyecciones de la recta Posiciones particulares de la recta a). Recta paralela a uno de los ejes del sistema b). Recta paralela a uno de los planos del sistema c). Recta perpendicular a uno de los planos del sistema d). Perpendicular al plano del cuadro Alfabeto del plano. Proyecciones del plano Posiciones particulares del plano a). Paralelo a uno de los ejes del sistema b). Paralelo a uno de los planos del sistema c). Plano que contiene a uno de los ejes del sistema d). Plano que contiene al origen del sistema e). Plano perpendicular a uno de los ejes del sistema f). Plano perpendicular a uno de los planos del sistema g). Plano paralelo al plano del cuadro h). Plano perpendicular al plano del cuadro Intersecciones de planos Traza natural u ordinaria de un plano Traza natural u ordinaria de una recta Determinación de secciones planas de figuras Intersección de recta y plano Representación de figuras planas a). Aplicando los coeficientes de reducción b). Abatiendo el plano que contiene a la figura Representación de la circunferencia Representación en axonométrico de figuras dadas por sus proyecciones diédricas...30 Paso de diédrico a axonométrico Paso de axonométrico a diédrico Sistema axonométrico oblicuo. Perspectiva caballera Página nº 72

39 4.- SISTEMA CÓNICO Representación del punto Representación de la recta Posiciones particulares de la recta a). Recta paralela al PG. Recta horizontal. Recta R b). Recta perpendicular al PG. Recta vertical. Recta S...40 c). Recta contenida en el PG. Recta T...40 d). Recta paralela al PC. Recta frontal. Recta R e). Recta perpendicular al PC. Recta de punta. Recta S f). Recta contenida en el PC. Recta T Haces de rectas Rectas que forman un ángulo dado con el PC Determinación del ángulo que una recta forma con el PC Representación del plano Pertenencia entre puntos y planos Posiciones particulares del plano a). Plano paralelo al PC. Plano P. Plano frontal b). Plano perpendicular al PC. Plano Q. Plano de canto c). Plano paralelo al PG. Plano horizontal d). Plano perpendicular al PG. Plano vertical Haces de planos. Obtención del que pasa por el punto de vista Intersecciones de planos Intersección de recta y plano División de un segmento en partes iguales o proporcionales a). Segmento horizontal. Paralelo al PG b). Segmento frontal. Paralelo al PC c). Segmento cualquiera Abatimiento del PG. sobre el PC. Abatimiento de un punto Verdadera magnitud de un segmento a). Segmento perpendicular al plano geometral. Recta vertical b). Segmento paralelo al plano geometral. Recta horizontal c). Segmento perpendicular al plano del cuadro. Recta de punta d). Segmento paralelo al plano del cuadro. Recta frontal e). Segmento cualquiera Perspectiva de figuras planas a). Circunferencia situada en el PG y por detrás del PC Métodos para realizar perspectivas cónicas a). Método Reile...60 b). Método de la homología Página nº 73