Funciones trigonométricas
|
|
|
- Raúl Miranda Iglesias
- hace 7 años
- Vistas:
Transcripción
1 Tema 0 Funciones trigonométricas Para estudiar esta nueva familia de funciones utilizamos una estrategia similar a la seguida en el tema anterior. Igual que ocurrió con el logaritmo, una integral indefinida de una función racional bien conocida nos llevará a la función arco-tangente, cuyas principales propiedades se probarán fácilmente, usando el Teorema Fundamental del Cálculo y el Teorema del Valor Medio. Su función inversa, extendida por periodicidad, será la función tangente, a partir de la cual estudiaremos con facilidad el seno, el coseno y el resto de las funciones trigonométricas. 0.. El arco-tangente La función t /( + t 2 ) es continua en R, lo que nos permite considerar su integral indefinida con origen en 0. La función arco-tangente, o simplemente el arco-tangente, es la función arctg : R R definida por: arctg x = x 0 dt +t 2 x R Su primera propiedad, clave para obtener las demás, es la siguiente: (A.) El arco-tangente es la única función f D(R) tal que f (0) = 0 y f (x) = /( + x 2 ) para todo x R. Por tanto, es una función estrictamente creciente. Es obvio que arctg 0 = 0 y el Teorema Fundamental del Cálculo nos da arctg (x) = /(+x 2 ) para todo x R. Unicidad y crecimiento estricto se deducen del Teorema del Valor Medio. Podemos reducir el estudio del arco-tangente al de su restricción a R + : (A.2) El arco-tangente es una función impar: arc tg( x) = arc tg x para todo x R. En efecto, basta usar la sustitución t = s: arctg( x) = x 0 dt x +t 2 = ds = arctg x x R + s2 0 82
2 0. Funciones trigonométricas 83 Para proseguir nuestro estudio del arco-tangente, es conveniente, aunque no imprescindible, introducir el número π. Su definición puede resultar sorprendente, pero está motivada por ideas básicas de trigonometría: si un ángulo mide π/4 radianes, su tangente debe ser. Así pues, por definición, el número π viene dado por: π = 4 arctg = 4 0 dt +t 2 Puesto que /2 / ( + t 2) para todo t [0,], y ambas desigualdades son estrictas para t ]0,[, tenemos 2 < π < 4. A continuación relacionamos este número con la imagen del arco-tangente. (A.3) Se verifica que arctg x + arctg(/x) = π/2 para todo x R +. Como consecuencia se tiene que lím arctg x = π y lím x + 2 arctg x = π x 2 Por tanto, la imagen del arco-tangente es el intervalo abierto ] π/2,π/2[. Para obtener la primera igualdad observamos que, para x R +, se tiene /x dt +t 2 = x ds/s 2 + (/s) 2 = x ds + s 2 donde hemos hecho la sustitución t = /s con s R +. La aditividad de la integral nos da dt x arctg x + arctg(/x) = 2 0 +t 2 + dt /x +t 2 + dt +t 2 = π 2 El límite en + se calcula ahora convirtiéndolo en un límite por la derecha en el origen: lím arctg x = lím arctg(/x) = π x + x 0+ 2 lím arctg x = π x 0+ 2 Para el límite en basta usar que el arco-tangente es una función impar y, por tratarse de una función estrictamente creciente, su intervalo imagen no podrá ser otro que ] π/2,π/2[. Revisamos ahora las propiedades de la función inversa del arco-tangente, a la que no vamos a dar un nombre especial, pues enseguida la extenderemos para obtener la función que realmente nos interesa. Sea J =] π/2,π/2[. La función τ = arctg : J R tiene las siguientes propiedades: (i) Es derivable en J con τ (x) = + τ(x) 2 para todo x J. (ii) Es una función impar: τ( x) = τ(x) para todo x J. (iii) Es una biyección estrictamente creciente de J sobre R, con τ(x) (x π/2), τ(x) + (x π/2) τ( π/4) =, τ(0) = 0, τ(π/4) = Sólo (i) merece comentario. El teorema de la función inversa nos da: τ (x) = arctg ( τ(x) ) = + τ(x)2 x J
3 0. Funciones trigonométricas La tangente A partir de la inversa del arco-tangente vamos a definir la función tangente haciendo una extensión por periodicidad, es decir, repitiendo sus valores en sucesivos intervalos abiertos de longitud π. La periodicidad es una propiedad clave de varias funciones trigonométricas, así que conviene aclarar algunas ideas al respecto. Dada una función f : A R, decimos que T R es un periodo de f cuando se verifican las dos condiciones siguientes {x + T : x A} = A y f (x + T ) = f (x) x A Trivialmente, 0 es un periodo de cualquier función. Decimos que la función f es periódica cuando tiene un periodo T 0, y si queremos explicitar dicho periodo, podemos decir que f es T -periódica. Es evidente que entonces T es otro periodo de f, luego toda función periódica posee un periodo positivo. De hecho, se comprueba claramente por inducción que k T también es un periodo de f, para todo k Z. Toda función definida en un conjunto acotado admite una extensión por periodicidad, es decir, se puede extender para obtener una función periódica. Trataremos solamente el caso que realmente nos interesa. Como la función τ = arctg está definida en J =] π/2,π/2[, un intervalo de longitud π, es natural intentar extenderla, para obtener una función π-periódica. El conjunto de definición de dicha extensión deberá contener todos los puntos de la forma x + kπ con x J y k Z. Dichos puntos forman el conjunto A t = ] kπ π 2, kπ + π [ 2 k Z unión de intervalos abiertos consecutivos. Por tanto, R \ A t está formado precisamente por los extremos de dichos intervalos, es decir, R \ A t = {kπ (π/2) : k Z} = {(2k )π/2 : k Z} Así que A t se obtiene al suprimir de R los múltiplos enteros impares de π/2. Para que la extensión que buscamos estuviera definida en algún punto de R \ A t, debería estarlo en π/2, pero sabemos que τ diverge en π/2, luego ninguna extensión suya puede ser siquiera continua en dicho punto. En resumen, si queremos extender la función τ para obtener una función periódica, sin perder la continuidad, la extensión ha de estar definida en A t. Para definir dicha extensión, dado x A t, bastará encontrar k Z de forma que x kπ J, y el valor de la nueva función en el punto x deberá ser τ(x kπ). Pero esto es fácil, ya que: π 2 < x kπ < π 2 kπ < x + π 2 < (k + )π k < x π + 2 < k + ) Obsérvese que, precisamente por ser x A t tenemos que x π + ( x 2 / Z, luego k = E π + 2 es el único entero que verifica la condición anterior. Queda así explicada la siguiente definición.
4 0. Funciones trigonométricas 85 Sea A t = R \ {(2k )π/2 : k Z}. La función tangente, o simplemente la tangente, es la función tg : A t R, definida por tg x = arctg (x k(x)π ) ( x donde k(x) = E π + ) x A t 2 Conviene recordar que k(x) es el único número entero que verifica π/2 < x k(x)π < π/2. Anotemos las propiedades que caracterizan a la función tangente: (T.) La tangente es la única función π-periódica, definida en A t, cuya restricción al intervalo ] π/2,π/2[ es la función inversa del arco-tangente. Queda pues determinada por: tg : A t R, tg(x + π) = tg x x A t, tg(arctg x) = x x R También conviene anotar algunos valores concretos de la tangente: para m Z tenemos claramente que tg ( mπ (π/4) ) =, tg(mπ) = 0 y tg ( mπ + (π/4) ) =. Las propiedades de la función inversa del arco-tangente, se extienden fácilmente usando la periodicidad, para obtener las correspondientes propiedades de la tangente. (T.2) La tangente es derivable en A t, con tg (x) = + tg 2 x para todo x A t. Podemos aplicar directamente la regla de la cadena. La función parte entera es derivable en R \ Z con E (y) = 0 para todo y R \ Z, luego la función k : A t Z también es derivable en A t con k (x) = 0 para todo x A t. Por tanto, tg (x) = τ ( x k(x)π ) = + τ ( x k(x)π ) 2 = + tg 2 x x A t (T.3) La tangente es una función impar: tg( x) = tg x para todo x A t. En efecto, para x A t tenemos π/2 < x k(x)π < π/2 y basta usar la periodicidad de la tangente junto con la imparidad de la función τ: tg( x) = tg ( k(x)π x ) = τ ( k(x)π x ) = τ ( x k(x)π ) = tg x (T.4) Para cada m Z, la restricción de la tangente al intervalo J m =]mπ (π/2),mπ+(π/2)[ es una biyección estrictamente creciente de J m sobre R. Por tanto, la tangente diverge positivamente por la izquierda, y negativamente por la derecha, en todo punto de R \ A t. Finalmente, para todo y R se tiene: {x A t : tg x = y} = {arctg y + mπ : m Z}. La primera afirmación se comprueba usando que, si m Z, para todo x J m se tiene k(x) = m y tg x = τ(x mπ), con lo que basta aplicar las propiedades de τ ya conocidas. Dado z R \ A t, existe m Z tal que z = mπ (π/2) = ínf J m con m Z, y trabajando en J m obtenemos que tg x (x z+). Pero como también z = sup J m, trabajando en J m obtenemos que tg x + (x z ). Nótese que tg x + (x z). Veamos la última igualdad, que aclara la relación entre tangente y arco-tangente. Para y R y m Z tenemos tg ( arctg y + mπ ) = tg(arctg y) = y, lo que nos da una inclusión. Para la otra, si x A t, de y = tg x = arctg ( x k(x)π ), deducimos que arctg y = x k(x)π, luego x = arctg y + mπ con m = k(x) Z.
5 0. Funciones trigonométricas El seno y el coseno A partir de la tangente, definiremos directamente estas dos funciones, sin duda las funciones trigonométricas más relevantes. Consideramos el conjunto B = R \ {(2k )π : k Z}, que se obtiene al suprimir de R los múltiplos enteros impares de π, y observamos su relación con el conjunto de definición de la tangente: A t = {x/2 : x B}. Pues bien, el seno y el coseno son las funciones sen : R R y cos : R R definidas por sen x = 2 tg(x/2) + tg 2 (x/2) cos x = tg2 (x/2) + tg 2 (x/2) x B, sen x = 0 x R \ B x B, cos x = x R \ B De la continuidad de la tangente deducimos que ambas funciones son continuas en B. Además, como la tangente diverge en todo punto de R \ A t, para todo x R \ B tenemos que tg(y/2) + (y x), de donde 2 lím sen y = lím ( ) = 0 = sen x y x y x /tg(y/2) + tg(y/2) ( /tg 2 (y/2) ) lím cos y = lím ( y x y x /tg 2 (y/2) ) = = cos x + Esto explica la definición del seno y el coseno en R \ B: se ha hecho de forma que ambas funciones sean continuas en todo R. De hecho, probamos enseguida algo mucho mejor: (SC.) Las funciones seno y coseno son derivables en R con sen (x) = cos x, cos (x) = sen x x R El carácter local de la derivada y las reglas básicas de derivación nos dan la derivabilidad en B. Para x B se tiene que tg (x/2) = + tg 2 (x/2), de donde sen (x) = tg (x/2) ( + tg 2 (x/2) ) 2 tg 2 (x/2) tg (x/2) ( + tg 2 (x/2) ) 2 = tg2 (x/2) + tg 2 (x/2) = cos x cos (x) = tg(x/2) tg (x/2) ( + tg 2 (x/2) + tg 2 (x/2) ) ( + tg 2 (x/2) ) 2 = 2tg(x/2) + tg 2 (x/2) = sen x Sea ahora a R \ B y consideremos el intervalo J =]a 2π, a + 2π[, que verifica J \ {a} B. Sabemos que el seno y el coseno son funciones continuas en J, y acabamos de ver que son derivables en J \ {a}. Usando otra vez la continuidad de ambas en el punto a, tenemos lím x a sen (x) = lím cos x = cos a, x a lím cos (x) = lím ( sen x) = sen a x a x a Una consecuencia del Teorema del Valor Medio, estudiada en su momento, nos dice que el seno y el coseno son derivables en a verificándose que sen (a) = cos a y cos (a) = sen a.
6 0. Funciones trigonométricas 87 Conviene anotar algunos valores del seno y el coseno, que se deducen directamente de las definiciones, usando valores conocidos de la tangente: sen( π) = 0, sen( π/2) =, sen 0 = 0, sen(π/2) =, sen π = 0 cos( π) =, cos( π/2) = 0, cos 0 =, cos(π/2) = 0, cos π = Probamos ahora una relación entre el seno y el coseno que es la más famosa de las llamadas identidades trigonométricas. De ella se deduce la imagen de ambas funciones. (SC.2) Se verifica que cos 2 x + sen 2 x = para todo x R. Como consecuencia, la imagen, tanto del seno como del coseno, es el intervalo [,]. Se puede deducir directamente de las definiciones, pero usemos una idea alternativa: definiendo h(x) = cos 2 x + sen 2 x para todo x R, vemos inmediatamente que h D(R) con h = 0, luego h es constante, pero es claro que h(0) =. Por tanto, tenemos sen x y cos x para todo x R, pero sabemos que ambas funciones toman los valores y, luego su imagen no puede ser otra que [,]. Las identidades trigonométricas más importantes son sin duda las siguientes: (SC.3) Fórmulas de adición para el seno y el coseno. Para cualesquiera x,y R se tiene: sen(x + y) = sen x cos y + cos x sen y cos(x + y) = cos x cos y sen x sen y Fijado y R, consideramos las funciones f,g : R R definidas por f (x) = sen(x + y) sen x cos y cos x sen y x R g(x) = cos(x + y) cos x cos y + sen x sen y x R y queremos probar que ambas son idénticamente nulas. Es claro que f,g D(R) con f (x) = g(x), g (x) = f (x) x R Consideremos ahora la función h : R R dada por h(x) = f (x) 2 + g(x) 2 para todo x R. Entonces h D(R) con h (x) = 2 f (x) f (x) + 2g(x)g (x) = 2 f (x)g(x) 2g(x) f (x) = 0 x R luego h es constante. De sen 0 = 0 y cos 0 = deducimos que f (0) = g(0) = 0, luego h(0) = 0. Por tanto, h(x) = 0 para todo x R, es decir, f (x) = g(x) = 0 para todo x R, como queríamos demostrar. A partir de las fórmulas de adición deduciremos otras propiedades básicas del seno y el coseno. En primer lugar obtenemos una relación aún más directa entre ambas funciones, de la que se deduce su periodicidad:
7 0. Funciones trigonométricas 88 (SC.4) Para cualesquiera x R y m Z, se verifican las siguientes igualdades: sen ( x + (π/2) ) = cos x, cos ( x + (π/2) ) = sen x () sen(x + mπ) = ( ) m sen x, cos(x + mπ) = ( ) m cos x (2) En particular, el seno y el coseno son funciones 2π-periódicas, así que no tienen límite en + y tampoco en. Puesto que sen(π/2) = y cos(π/2) = 0, las fórmulas de adición, con y = π/2, nos dan (). Aplicando dos veces () obtenemos (2) para m =, lo que también puede usarse dos veces, para conseguir la periodicidad. Entonces, para todo k Z, tenemos que 2kπ también es un periodo del seno y el coseno. Esto demuestra (2) cuando m es par y, usando de nuevo el caso m =, lo probamos también para m impar. Con respecto al comportamiento en y + basta observar que sen ( (π/2) + mπ ) = cos(mπ) = ( ) m para todo m Z. (SC.5) El coseno es una función par, mientras que el seno es impar: cos( x) = cos x, sen( x) = sen x x R Para probarlo, dado x R, las fórmulas de adición nos dan: = cos ( x + ( x) ) = cos x cos( x) sen x sen( x) 0 = sen ( x + ( x) ) = sen x cos( x) + cos x sen( x) Multiplicando en la primera igualdad por cos x, en la segunda por sen x, y sumando las igualdades resultantes, obtenemos cos x = ( cos 2 x + sen 2 x ) cos( x) = cos( x). También podemos multiplicar la primera igualdad por sen x y la segunda por cos x, con lo que al sumar obtenemos: sen x = ( sen 2 x + cos 2 x ) sen( x) = sen( x) Arco-seno y arco-coseno La periodicidad del seno y el coseno permite reducir el estudio de dichas funciones al de sus restricciones a un intervalo de longitud 2 π. Pero teniendo en cuenta que sen(x + π) = sen x y cos(x + π) = cos x para todo x R, podemos de hecho restringirnos a un intervalo de longitud π. Es habitual usar el intervalo [ π/2,π/2] para el seno y [0,π] para el coseno. En ambos casos, la restricción es una función inyectiva y toma los mismos valores que la función de partida, más concretamente: (SC.6) La restricción del seno al intervalo [ π/2, π/2] es una biyección estrictamente creciente de dicho intervalo sobre [, ]. La restricción del coseno al intervalo [0, π] es una biyección estrictamente decreciente de dicho intervalo sobre [,].
8 0. Funciones trigonométricas 89 Para x ] π/2,π/2[ tenemos x/2 < π/4, luego tg(x/2) <, de donde cos x > 0, es decir, sen (x) > 0. Así pues, el seno es estrictamente creciente en [ π/2,π/2], luego transforma dicho intervalo en [sen( π/2), sen(π/2)] = [, ]. Análogamente, para x ]0,π[ tenemos 0 < x/2 < π/4, luego tg(x/2) > 0, de donde sen x > 0, es decir, cos (x) < 0. Vemos que el coseno es estrictamente decreciente en [0,π] y transforma dicho intervalo en [cos π,cos 0] = [,]. Es natural considerar ahora las funciones inversas de las dos biyecciones recién conseguidas. El arco-seno es, por definición, la inversa de la restricción del seno al intervalo [ π/2,π/2] y se denota por arcsen. Así pues, para cada x [,], arcsen x es el único y [ π/2,π/2] que verifica sen y = x. Análogamente, el arco-coseno es la inversa de la restricción del coseno al intervalo [0, π] y se denota por arccos, de modo que para x [,], arccos x es el único z [0,π] tal que cos z = x. Tomando entonces y = (π/2) z [ π/2,π/2] tenemos sen y = x, con lo que y = arcsen x y obtenemos la relación directa entre las dos funciones recién definidas: arcsen x + arccos x = π 2 x [,] Las propiedades básicas de estas dos funciones se deducen fácilmente de su definición: El arco-seno es una biyección estrictamente creciente de [, ] sobre [ π/2, π/2] y el arco-coseno es una biyección estrictamente decreciente de [, ] sobre [0, π]. Ambas funciones son continuas en [, ] y derivables en ], [ con arcsen (x) = pero no son derivables en los puntos y. x 2 = arccos (x) x ],[ Basta trabajar con el arco-seno, que es biyectiva, estrictamente creciente y continua, como inversa de una función definida en un intervalo que tiene esas mismas propiedades. Para la derivabilidad, dado x [,], escribimos y = arcsen x [ π/2,π/2]. Si x = ±, tenemos y = ±(π/2), luego sen (y) = cos y = 0 y la regla de derivación de la función inversa nos dice que el arco-seno no es derivable en x. Si por el contrario x ],[, tenemos cos y > 0 y la misma regla nos dice que arcsen (x) = sen (y) = cos y = sen 2 y = x 2 El arco-seno y el arco-coseno nos permiten determinar el conjunto de puntos donde el seno y el coseno toman cada uno de sus valores: Para todo x [, ] se tiene: {z R : cos z = x} = {± arccos x + 2k π : k Z} {y R : sen y = x} = {arcsen x + 2k π : k Z} {π arcsen x + 2k π : k Z}
9 0. Funciones trigonométricas 90 De la primera igualdad, una inclusión se deduce de la periodicidad y paridad del coseno: para k Z se tiene cos(± arccos x + 2k( π) = cos(± ) arccos x) = x. Para la otra inclusión, sea z + π z R tal que cos z = x, sea k = E Z y pongamos z 0 = z 2k π, que también 2π verifica cos z 0 = x pero ahora con π z 0 < π. Entonces cos z 0 = x con 0 z 0 π, de donde z 0 = arccos x, luego z = ± arccos x + 2k π. En cuanto a la segunda igualdad, basta pensar que, para y R, se tiene: sen y = x cos ( y (π/2) ) = x y (π/2) = ± arccos x + 2k π con k Z { y = (π/2) + arccos x + 2k π = π arcsen x + 2k π, o bien, y = (π/2) arccos x + 2k π = arcsen x + 2k π y esta equivalencia es precisamente la igualdad de conjuntos buscada Coordenadas polares en el plano Veamos ahora un resultado que conecta las funciones seno y coseno con las nociones básicas de la trigonometría. Para cada t R, el punto del plano (a,b) = (cos t,sen t) R 2 verifica que a 2 + b 2 =, es decir, (a,b) está en la circunferencia con centro en el origen y radio, a la que suele llamarse circunferencia unidad. Pues bien, lo interesante es que el recíproco también es cierto: todo punto de la circunferencia unidad puede expresarse en la forma (cos t,sen t) con t R. Veamos antes la relación entre dos posibles valores de t : Si s, t R verifican cos s = cos t y sen s = sen t, entonces s t = 2k π con k Z. En efecto, tenemos claramente cos(s t) = cos 2 s + sen 2 s =, pero conocemos los puntos donde el coseno toma el valor, luego: s t = ± arccos + 2k π = 2k π con k Z Probamos ya el resultado anunciado, con la condición adicional que asegura la unicidad: Si a,b R y a 2 + b 2 =, existe un único t ] π,π] tal que (a,b) = (cos t, sen t). Podemos dar explícitamente el valor de t : si b 0, basta tomar t = sgn(b) arccos a y es obvio que cos t = a, luego sen 2 t = a 2 = b 2. Además, por ser a <, tenemos 0 < arccos a < π, es decir, 0 < t < π. Entonces es claro que sgn(sen t) = sgn(t) = sgn(b), y deducimos que sen t = b. En el caso b = 0 tenemos a = con lo que basta tomar t = arccos a {0,π}. Obsérvese que este segundo caso queda englobado en el primero, si convenimos que sgn 0 =. La unicidad se deduce del resultado anterior: si s verifica las mismas condiciones que t, deberá ser s t = 2k π con k Z. Pero sumando miembro a miembro las desigualdades π < s π y π t < π, obtenemos 2π < 2k π < 2π, luego k = 0 y s = t. De manera ligeramente más general, podemos ahora obtener:
10 0. Funciones trigonométricas 9 Para cada (x,y) R 2 \ {(0,0)}, existe un único ρ R + y un único t ] π,π], tales que (x,y) = (ρ cos t, ρ sen t). La igualdad buscada implica que x 2 + y 2 = ρ 2, luego es obligado tomar ρ = x 2 + y 2. Basta ahora aplicar el resultado anterior, que nos proporciona un único t ] π,π] verificando que cos t = x/ρ y sen t = y/ρ. Hemos obtenido las coordenadas polares de cualquier punto del plano, excluido el origen: se dice que ρ es el radio polar y t el ángulo polar del punto (x,y). La interpretación geométrica es clara: ρ es la longitud del segmento que une el origen con el punto (x,y) y t es la medida en radianes del ángulo (orientado) que forma dicho segmento con la dirección positiva del eje de abscisas, entendiendo que dicha medida es positiva o negativa según que el punto (x,y) esté situado en el semiplano superior o en el inferior. Cuando y = 0, estamos en el eje de abscisas y tenemos t = 0 o t = π según el signo de x Otras funciones trigonométricas Observemos la relación entre el conjunto de definición de la tangente y los ceros del coseno: A = R \ {(2k )π/2 : k Z} = {x R : cos x 0} Pues bien, vamos a recuperar la tangente a partir del seno y el coseno: Se verifica que tg x = sen x cos x para todo x A. Para x A, como 2x no es múltiplo impar de π, tenemos y concluimos que cos(2x) = tg2 x + tg 2 x = 2 2 tg x + tg 2 y sen(2x) = x + tg 2 x tg x = sen(2x) + cos(2x) = 2 sen x cos x + cos 2 x sen 2 x donde hemos usado las fórmulas de adición. = 2 sen x cos x 2 cos 2 x = sen x cos x En claro paralelismo con la última expresión de la tangente, pasamos a comentar brevemente otras tres funciones trigonométricas. La función secante tiene el mismo conjunto de definición que la tangente y viene dada por: sec : A R, sec x = cos x x A Por otra parte, podemos considerar el conjunto de los puntos donde no se anula el seno, que sabemos se obtiene al suprimir de R los múltiplos enteros de π: B = {x R : sen x 0} = R \ {k π : k Z}
11 0. Funciones trigonométricas 92 Pues bien, en el conjunto B se definen las funciones cotangente y cosecante: cotg, cosec : B R, cotg x = cos x sen x, cosec x = sen x x B No haremos un estudio detallado de estas nuevas funciones, pues sus propiedades básicas (periodicidad, paridad o imparidad, derivabilidad, etc.) se deducen rutinariamente de las que ya conocemos para el seno y el coseno Algunos contraejemplos Para una función f : I R, donde I es un intervalo no trivial, recordemos tres afirmaciones que ya habíamos relacionado: (i) f es continua (ii) f admite una primitiva (iii) f tiene la propiedad del valor intermedio Sabemos que (i) (ii) (iii). Usando la funciones trigonométricas, probaremos ahora con comodidad que esas implicaciones no son reversibles. El coseno no tiene límite en + ni en, pero conviene precisar esa afirmación: para todo y [,], el conjunto {x R : cos x = y} no está mayorado ni minorado, luego si S R es cualquier semirrecta, se tendrá que cos(s) = [,]. Un obvio cambio de variable nos proporciona una función que tiene el mismo tipo de comportamiento en el origen, tanto por la derecha como por la izquierda: La función f : R R definida por f (x) = cos x x R (3) verifica que f ( ]0,δ[ ) = f ( ] δ,0[ ) = [,] para todo δ > 0. Por tanto, f no tiene límite por la izquierda, ni por la derecha, en el origen. Basta pensar que f ( ]0,δ[ ) = cos ( ]/δ,+ [ ) y f ( ] δ,0[ ) = cos ( ], /δ[ ). Ya podemos dar ejemplos de funciones que tienen la propiedad del valor intermedio, sin ser continuas: Fijado λ [,], la función f λ : R R definida por: f λ (x) = cos x x R, f λ (0) = λ (4) tiene la propiedad del valor intermedio, pero no es continua.
12 0. Funciones trigonométricas 93 Vemos que f λ extiende a la función f definida en (3), así que f λ no es continua en 0. Si J es un intervalo no trivial y 0 / J, f λ es continua en J, luego f λ (J) es un intervalo. Si 0 J, podemos encontrar δ > 0 de forma que ]0,δ[ J, o bien ] δ,0[ J. En ambos casos deducimos que f (J \ {0}) = [,], luego f λ (J) = f (J \ {0}) {λ} = [,]. Con respecto a las afirmaciones consideradas al principio, hemos visto que (iii) (i), pero queremos ver que (iii) (ii). Encontraremos el contraejemplo casi al mismo tiempo que probamos que (ii) (i). La función h : R R, definida por h(x) = x 2 sen x para todo x R y h(0) = 0, es derivable en R pero su derivada no es continua: h D(R) pero h / C (R). Usaremos también la función g : R R dada por g(x) = x sen x x R, g(0) = 0 Es evidente que g es continua en R pero, al tratarse del producto de una función acotada por otra que tiene límite 0 en el origen, tenemos lím x 0 g(x) = 0 = g(0), luego g C(R). Claramente h es derivable en R, con h (x) = 2x sen x cos x = 2g(x) f (x) x R (5) donde f es la función definida en (3). Pero h también es derivable en 0, ya que h(x) lím x 0 x = lím x 0 g(x) = 0 así que h (0) = 0. Como también g(0) = 0, si en (5) sustituimos f por su extensión f 0 (definida en (4) para λ = 0), hacemos que la igualdad sea válida en todo R. Anotémosla para uso posterior: f 0 (x) = 2g(x) h (x) x R (6) Como g es continua en el origen, pero f 0 no lo es, deducimos que h tampoco puede serlo. Ya tenemos una función derivable en un intervalo, cuya derivada no es continua. Pero aprovechando los razonamientos anteriores, encontraremos también una función que tiene la propiedad del valor intermedio pero no admite primitiva. Sen f 0, f : R R las funciones definidas en (4), con λ = 0 y λ = respectivamente. Entonces, f 0 admite una primitiva, pero f no. Para la primera afirmación, recordemos la igualdad (6). Como g C(R), existe G D(R) tal que g = G. Basta entonces tomar F 0 = 2G h para tener una primitiva de f 0. Supongamos, por reducción al absurdo, que f también admite una primitiva: F D(R) tal que F = f. Como F 0 y F coinciden en R, el Teorema del Valor Medio nos dice que F 0 F es constante en R +, y también en R, pero al ser continua en 0, será constante en todo R. Entonces F 0 = F, es decir, f 0 = f, flagrante contradicción.
13 0. Funciones trigonométricas Ejercicios. Dados a,b R +, estudiar el comportamiento en el origen y en el infinito de las funciones f,g : R R definidas por ( a ) ( ) b f (x) = arc tg + arc tg, g(x) = x f (x) x R x x 2. Calcular la imagen de la función f : R R definida por f (x) = arc tg(log x ) x R 3. Sea f : R \ {} R la función definida por f (x) = arc tg + x x x R \ {} Estudiar la continuidad de f y su comportamiento en, + y. Calcular su imagen. 4. Probar que, si a,b R verifican que ab <, entonces: 5. Calcular las siguientes integrales: arctg a + arctg b = arctg a + b ab (a) 0 dx ( + x 2 ) 2 (b) 0 x 2 3x + 4 x 3 x 2 + 3x + 5 dx 6. Calcular la imagen de las funciones F,G : R + R definidas por: F(x) = x t t (t + )(t 2 + ) dt, G(x) = +(x )2 arctg t t 2 dt x R + 7. Probar que existe una única función f : R R que verifica f (x) + exp ( f (x) ) = arctg ( f (x) ) + x x R Probar también que f D(R) y calcular f (). 8. Si A es el conjunto de definición de la tangente, probar que el conjunto {x A : tg x = x} es infinito y numerable. 9. Probar que el arco-tangente es uniformemente continua, pero su inversa no. 0. Probar que, para todo x ]0, π/2[ se tiene: 2x π < sen x < x < tg x.. Dado x R, estudiar la convergencia de las sucesiones { sen(nx) } y { cos(nx) }.
14 0. Funciones trigonométricas Estudiar la convergencia de las siguientes sucesiones: { ( )} n { ( (a) n sen n 2 (b) cos 2 nπ )} + 2 (c) { (log n)cos } n 2 + n arctg n 3. Dado α R, estudiar la convergencia de las siguientes series (( e /n ) arctg(/n) (a) n2 cos(nα) ( ) α n(log n) 2 (b) sen(/n) (c) n n3 4. Sea f : R R la función definida por f (x) = sen x sen ( ) x x R, f (0) = 0 log n Estudiar la continuidad y derivabilidad de f, así como su comportamiento en + y. 5. Sea α R y f : R + 0 R la función definida por ( ) f (x) = x α cos x R +, f (0) = 0 x Estudiar la continuidad y derivabilidad de f, así como la continuidad de su derivada. 6. Para x R, discutir la validez de cada una de las siguientes afirmaciones: (a) tg(arctg x) = x (c) sen(arcsen x) = x (e) cos(arccos x) = x (b) arctg(tg x) = x (d) arcsen(sen x) = x (f) arccos(cos x) = x 7. Sea f :]0, π/2[ R la función definida por ( ) sen x f (x) = x ]0,π/2[ tg x Puede extenderse f para obtener una función continua en [0,π/2]? 8. Sea f :]0, π/2[ R la función definida por f (x) = ( + sen x) cotgx x ]0,π/2[ Estudiar la continuidad de f y su comportamiento en 0 y π/2. 9. Sean J = [ / 2,/ 2] y g : J [ π/2,π/2] la función definida por g(x) = arc sen ( 2x x 2) x J Probar que g es biyectiva, continua en J y estrictamente creciente. Dar una expresión explícita para la función inversa de g. 20. Dado a R +, calcular la imagen de la función G : [0,a] R definida por x G(x) = a 2 t 2 dt x [0,a] x ) α
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Funciones convexas Definición de función convexa. Tema 10
 Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Reglas de derivación Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
12.1. Definición de las derivadas sucesivas
 Tema 12 Derivadas sucesivas El proceso de derivación de funciones reales de variable real puede obviamente iterarse, obteniendo la segunda y sucesivas derivadas de una función. Como es lógico, para n N,
Tema 12 Derivadas sucesivas El proceso de derivación de funciones reales de variable real puede obviamente iterarse, obteniendo la segunda y sucesivas derivadas de una función. Como es lógico, para n N,
Práctica 1. Continuidad Ejercicios resueltos
 Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Tema 7: Funciones de una variable. Límites y continuidad.
 Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Funciones convexas Definición de función convexa. Tema 14
 Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Cálculo:Notas de preliminares
 Cálculo:Notas de preliminares Antonio Garvín Curso 04/05 1 Recordando cosas Recordaremos los conjuntos con los que vamos a trabajar, en especial R y R n. A fin de cuentas el cálculo trata basicamente de
Cálculo:Notas de preliminares Antonio Garvín Curso 04/05 1 Recordando cosas Recordaremos los conjuntos con los que vamos a trabajar, en especial R y R n. A fin de cuentas el cálculo trata basicamente de
Figura 1. Círculo unidad. Definición. 1. Llamamos número π (pi) al valor de la integral
 ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Sucesiones monótonas Monotonía. Tema 6
 Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real
 Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real En la primera parte de este tema vamos a tratar con funciones reales de variable real, esto es, funciones
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real En la primera parte de este tema vamos a tratar con funciones reales de variable real, esto es, funciones
Derivadas de las funciones trigonométricas
 Tema 8 Derivadas de las funciones trigonométricas Completamos en este tema la derivación de las principales funciones reales de variable real que venimos manejando, estudiando la derivabilidad de las funciones
Tema 8 Derivadas de las funciones trigonométricas Completamos en este tema la derivación de las principales funciones reales de variable real que venimos manejando, estudiando la derivabilidad de las funciones
La siguiente definición es muy intuitiva. Se dice que una sucesión {x n } es:
 Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
DERIV. DE UNA FUNC. EN UN PUNTO
 DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
Universidad Autónoma de México
 Universidad Autónoma de México Hernández Ortiz Cuauhtémoc Funciones circulares y sus inversas 9 de marzo del 2005 Las funciones trigonométricas circulares. Las funciones trigonométricas básicas son el
Universidad Autónoma de México Hernández Ortiz Cuauhtémoc Funciones circulares y sus inversas 9 de marzo del 2005 Las funciones trigonométricas circulares. Las funciones trigonométricas básicas son el
DERIVADA DE UNA FUNCIÓN
 DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
Funciones trigonométricas
 Tema 4 Funciones trigonométricas Va a aparecer aquí una nueva familia de funciones reales de variable real: las funciones trigonométricas. Existen varias formas de introducir estas funciones, ninguna de
Tema 4 Funciones trigonométricas Va a aparecer aquí una nueva familia de funciones reales de variable real: las funciones trigonométricas. Existen varias formas de introducir estas funciones, ninguna de
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
FUNCIONES ELEMENTALES.
 Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
Continuidad Funciones reales de variable real. Tema 12
 Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
Cálculo infinitesimal Grado en Matemáticas Curso 20014/15 Clave de soluciones n o 6. Derivadas de orden superior
 Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Funciones (continuación)
 Nivelación de Matemática MTHA UNLP Funciones (continuación) Funciones trigonométricas Consideremos un ángulo x y seleccionemos un punto (a, b) sobre el rayo que determina dicho ángulo Sea R = a + b, la
Nivelación de Matemática MTHA UNLP Funciones (continuación) Funciones trigonométricas Consideremos un ángulo x y seleccionemos un punto (a, b) sobre el rayo que determina dicho ángulo Sea R = a + b, la
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Por ser un cociente entre dos longitudes, el radián no tiene dimensión. De la definición obtenemos la relación entre radianes y grados:
 E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
11.1. Funciones uniformemente continuas
 Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Límite Funcional Puntos de acumulación. Tema 1
 Tema 1 Límite Funcional Estudiamos en este tema el concepto de límite para funciones reales de variable real, que guarda una estrecha relación con la continuidad. 1.1. Puntos de acumulación Pretendemos
Tema 1 Límite Funcional Estudiamos en este tema el concepto de límite para funciones reales de variable real, que guarda una estrecha relación con la continuidad. 1.1. Puntos de acumulación Pretendemos
Teorema del Valor Medio
 Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
El teorema del valor intermedio
 Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Conexión Motivación. Lección 10
 Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL.
 EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
Propiedades de las funciones continuas
 Tema 13 Propiedades de las funciones continuas Estudiamos en este tema los dos resultados fundamentales sobre funciones continuas, que se refieren a funciones continuas en intervalos. Primero veremos que
Tema 13 Propiedades de las funciones continuas Estudiamos en este tema los dos resultados fundamentales sobre funciones continuas, que se refieren a funciones continuas en intervalos. Primero veremos que
Curso Propedéutico de Cálculo Sesión 3: Derivadas
 Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Acotación y compacidad
 Lección 8 Acotación y compacidad Para subconjuntos de un espacio métrico, estudiamos ahora la noción de acotación, que como ocurría con la complitud, no es una noción topológica, pero se conserva en un
Lección 8 Acotación y compacidad Para subconjuntos de un espacio métrico, estudiamos ahora la noción de acotación, que como ocurría con la complitud, no es una noción topológica, pero se conserva en un
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Teorema del Valor Medio
 Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Propiedades de las funciones continuas
 Tema 13 Propiedades de las funciones continuas Estudiamos en este tema los dos resultados fundamentales sobre la continuidad de funciones reales de variable real, que se refieren a funciones continuas
Tema 13 Propiedades de las funciones continuas Estudiamos en este tema los dos resultados fundamentales sobre la continuidad de funciones reales de variable real, que se refieren a funciones continuas
1º Bachillerato Matemáticas I Tema 3: Trigonometría Ana Pascua García
 . MEDIDAS DE ÁNGULOS. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO Para medir los ángulos solemos utilizar las siguientes unidades: el grado sexagesimal y el radián. Grado sexagesimal: Se denomina grado
. MEDIDAS DE ÁNGULOS. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO Para medir los ángulos solemos utilizar las siguientes unidades: el grado sexagesimal y el radián. Grado sexagesimal: Se denomina grado
Aplicaciones de las derivadas. El teorema del valor medio
 Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
x y = x x y = x
 FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
Reglas de l Hôpital Teorema del Valor Medio Generalizado. Tema 7
 Tema 7 Reglas de l Hôpital Estudiamos en este tema el método práctico más efectivo para calcular ites de funciones en los que se presenta una indeterminación del tipo [0/0], o [ / ]. Este método se atribuye
Tema 7 Reglas de l Hôpital Estudiamos en este tema el método práctico más efectivo para calcular ites de funciones en los que se presenta una indeterminación del tipo [0/0], o [ / ]. Este método se atribuye
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Soluciones de los ejercicios del examen de Cálculo del 29 de junio de 2007 Primero de Ingeniería de Telecomunicación
 Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
Cálculo: Notas sobre diferenciabilidad en una variable
 Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. f : R R
 TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Convergencia Sucesiones convergentes
 Lección 6 Convergencia Vamos a estudiar la noción de convergencia de sucesiones en un espacio métrico arbitrario, generalizando la que conocemos en R. La definimos de forma que quede claro que se trata
Lección 6 Convergencia Vamos a estudiar la noción de convergencia de sucesiones en un espacio métrico arbitrario, generalizando la que conocemos en R. La definimos de forma que quede claro que se trata
Reglas de l Hôpital Teorema del Valor Medio Generalizado. Tema 5
 Tema 5 Reglas de l Hôpital Estudiamos en este tema un método práctico para resolver indeterminaciones del tipo [0/0] o [ / ], que lleva el nombre de un aristócrata y matemático francés, el marqués de l
Tema 5 Reglas de l Hôpital Estudiamos en este tema un método práctico para resolver indeterminaciones del tipo [0/0] o [ / ], que lleva el nombre de un aristócrata y matemático francés, el marqués de l
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9.1 DERIVADA DE UNA FUNCIÓN EN UN PUNTO
 TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
Funciones continuas e inyectivas
 Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Examen de Cálculo infinitesimal PROBLEMAS. 1 + a + a a n a n+1
 Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
C alculo Septiembre 2010
 Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Funciones. A.1 Definiciones. Dominio, rango e imagen A.1.1
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
TRIGONOMETRÍA. 1. Ángulos. 2. Razones trigonométricas de ángulos agudos
 TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
Capítulo 2: Cálculo diferencial de una y varias variables
 Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Contenidos. Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada
 Contenidos Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada Máximo, mínimo Función par o impar Función periódica Función Potencial
Contenidos Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada Máximo, mínimo Función par o impar Función periódica Función Potencial
Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García. UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior
 INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
Capítulo 2. Derivación de funciones.
 Capítulo 2. Derivación de funciones. Objetivos del tema Concepto matemático de derivada. Interpretaciones del concepto de derivada. Cálculo de derivadas de funciones y funciones definidas a trozos. Propiedades
Capítulo 2. Derivación de funciones. Objetivos del tema Concepto matemático de derivada. Interpretaciones del concepto de derivada. Cálculo de derivadas de funciones y funciones definidas a trozos. Propiedades
Divergencia de sucesiones
 Tema 7 Divergencia de sucesiones Nuestro próximo objetivo es prestar atención a ciertas sucesiones no acotadas de números reales, que llamaremos sucesiones divergentes. Estudiaremos su relación con los
Tema 7 Divergencia de sucesiones Nuestro próximo objetivo es prestar atención a ciertas sucesiones no acotadas de números reales, que llamaremos sucesiones divergentes. Estudiaremos su relación con los
Por extensión, también se puede hablar de la preimagen de un conjunto. Si B 0 B, la preimagen de B 0 es
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
MATEMÁTICAS II. Apuntes
 MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
Funciones elementales. A.1 Funciones potenciales. A.2 Función exponencial
 Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
UNIVERSIDAD CARLOS III DE MADRID. Departamento de Matemáticas CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
Tema 1: Repaso de conocimientos previos. Funciones elementales y sus gráficas. Límites. Continuidad.
 Tema 1: Repaso de conocimientos previos.... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Outline Relaciones trigonométricas 1 Relaciones trigonométricas 2 3 4 5 6 Outline Relaciones
Tema 1: Repaso de conocimientos previos.... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Outline Relaciones trigonométricas 1 Relaciones trigonométricas 2 3 4 5 6 Outline Relaciones
Funciones, Límites y Continuidad
 Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
Funciones de Variable Real
 Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Derivabilidad de funciones de una
 Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
Funciones continuas Motivación
 Lección 9 Funciones continuas Generalizando la noción que conocemos para funciones reales de variable real, vamos a estudiar la continuidad para funciones entre dos espacios métricos cualesquiera. La definimos
Lección 9 Funciones continuas Generalizando la noción que conocemos para funciones reales de variable real, vamos a estudiar la continuidad para funciones entre dos espacios métricos cualesquiera. La definimos
Trigonometría. 1. Ángulos
 Trigonometría Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, la medida de un ángulo está comprendida
Trigonometría Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, la medida de un ángulo está comprendida
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria) TEMA 3 FUNCIONES CIRCULARES E HIPERBÓLICAS Y SUS RECÍPROCAS. SITUACIONES REALES EN LAS QUE APARECEN.. Introducción.. Funciones circulares... Funciones de
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria) TEMA 3 FUNCIONES CIRCULARES E HIPERBÓLICAS Y SUS RECÍPROCAS. SITUACIONES REALES EN LAS QUE APARECEN.. Introducción.. Funciones circulares... Funciones de
FUNCIONES ELEMENTALES Y PROPIEDADES
 . NOCIONES INTRODUCTORIAS.. Concepto de función. Dominio e Imagen. Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente x, le asocia un único valor de
. NOCIONES INTRODUCTORIAS.. Concepto de función. Dominio e Imagen. Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente x, le asocia un único valor de
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
La propiedad de compacidad
 En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
Continuidad Funciones reales de variable real. Tema 12
 Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
Funciones Hiperbólicas. Who? Verónica Briceño V. When? noviembre 2013
 Funciones Hiperbólicas Funciones Hiperbólicas Who? Verónica Briceño V. When? noviembre 2013 En esta Presentación... En esta Presentación veremos: Definición de Funciones Hiperbólicas En esta Presentación...
Funciones Hiperbólicas Funciones Hiperbólicas Who? Verónica Briceño V. When? noviembre 2013 En esta Presentación... En esta Presentación veremos: Definición de Funciones Hiperbólicas En esta Presentación...
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS
 CONTINUIDAD Y DERIVABILIDAD. DERIVADAS. Dada la función f (), (, ), definir f () y f () de forma que f sea continua sen(π ) en todo el intervalo cerrado [, ]. : f () f () π 5 si. Estudiar la continuidad
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS. Dada la función f (), (, ), definir f () y f () de forma que f sea continua sen(π ) en todo el intervalo cerrado [, ]. : f () f () π 5 si. Estudiar la continuidad
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
CÁLCULO. GRADO EN INGENIERÍA INFORMÁTICA SEGUNDA PRUEBA PARCIAL. GRUPO A.
 CÁLCULO. GRADO EN INGENIERÍA INFORMÁTICA SEGUNDA PRUEBA PARCIAL. GRUPO A.. (2.5 puntos) Se considera la función F : [0, [ R definida por F() := 0 sen(t 2 ) dt 0. Demostrar que F es derivable en [0, [ y
CÁLCULO. GRADO EN INGENIERÍA INFORMÁTICA SEGUNDA PRUEBA PARCIAL. GRUPO A.. (2.5 puntos) Se considera la función F : [0, [ R definida por F() := 0 sen(t 2 ) dt 0. Demostrar que F es derivable en [0, [ y
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
π = π rad º? 3 α.180
 1 TEMA 5 RESOLUCIÓN DE TRIÁNGULOS Y FÓRMULAS TRIGONOMÉTRICAS 5.1 DEFINICIÓN DE ÁNGULO Y UNIDADES DE MEDIDA DE LOS ÁNGULOS Ángulo es la parte del plano comprendida entre dos semirrectas que se encuentran
1 TEMA 5 RESOLUCIÓN DE TRIÁNGULOS Y FÓRMULAS TRIGONOMÉTRICAS 5.1 DEFINICIÓN DE ÁNGULO Y UNIDADES DE MEDIDA DE LOS ÁNGULOS Ángulo es la parte del plano comprendida entre dos semirrectas que se encuentran
Cociente incremental. Mide la variación media de f(x) en (x 0, x 0 + x)
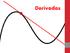 Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Espacios normados y espacios métricos
 Lección 2 Espacios normados y espacios métricos Abstrayendo las propiedades básicas que tiene la norma de un espacio pre-hilbertiano, definiremos ahora lo que se entiende por una norma en un espacio vectorial,
Lección 2 Espacios normados y espacios métricos Abstrayendo las propiedades básicas que tiene la norma de un espacio pre-hilbertiano, definiremos ahora lo que se entiende por una norma en un espacio vectorial,
Funciones reales de variable real
 Capítulo 2 Funciones reales de variable real 2.. Definición. Dominio, imagen y gráfica. Informalmente, una función entre dos conjuntos A y B es una regla que a ciertos elementos del conjunto A les asigna
Capítulo 2 Funciones reales de variable real 2.. Definición. Dominio, imagen y gráfica. Informalmente, una función entre dos conjuntos A y B es una regla que a ciertos elementos del conjunto A les asigna
Límites en el infinito, funciones divergentes
 Tema 2 Límites en el infinito, funciones divergentes Nuestro próximo objetivo es usar las sucesiones divergentes para ampliar la noción de límite funcional en dos sentidos. Por una parte, analizaremos
Tema 2 Límites en el infinito, funciones divergentes Nuestro próximo objetivo es usar las sucesiones divergentes para ampliar la noción de límite funcional en dos sentidos. Por una parte, analizaremos
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
Matemáticas CÁLCULO DE DERIVADAS
 Matemáticas Derivada de un cociente de funciones CÁLCULO DE DERIVADAS Considérense, como en los casos precedentes, dos funciones f y g definidas y derivables en un punto x. Además, en este caso, se tiene
Matemáticas Derivada de un cociente de funciones CÁLCULO DE DERIVADAS Considérense, como en los casos precedentes, dos funciones f y g definidas y derivables en un punto x. Además, en este caso, se tiene
Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:
![Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como: Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:](/thumbs/71/66199093.jpg) Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
Tema 6: Derivada de una función
 Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
f : R R Definición 2. Se llama dominio de una función f (lo denotaremos por Dom f) al conjunto de valores para los que está bien definida f(x) :
 Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
