INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA
|
|
|
- Fernando Álvarez Castillo
- hace 6 años
- Vistas:
Transcripción
1 Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez
2 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad.. PRONÓSTICOS EN ACTIVOS REPARABLES INTRODUCCIÓN U ssema reparable es aquel que acepa reparacoes y le puede ser resauradas sus fucoes medae el uso de cualquer méodo de reparacó dferee al reemplazo del ssema compleo. E el aálss de ssemas reparables hay cco posble esados e los cuales dcho ssemas puede quedar después de ua reparacó. Esos esados so: Ta bueo como uevo Ta malo como aes de reparar Mejor que aes de reparar pero peor que cuado esaba uevo Mejor que cuado esaba uevo Peor que aes de reparar Los modelos probablíscos ulzados radcoalmee para esmar o predecr el úmero esperado de fallas asume alguo de los dos prmeros esados pero o cubre los úlmos res, los cuales parecera acercarse más a la realdad. E esa seccó se presea ua revsó de los modelos radcoales de predccó del úmero de fallas e u empo msó para ssemas reparables, así como alguos ejemplos de aplcacoes. Adcoalmee se presea la formulacó de u modelo probablísco que oma e cuea los cco esados e los que puede quedar u ssema ua vez reparado, el cual se deoma Proceso Geeralzado de Resauracó (PGR) y se demuesra que el PGR es la eoría más geeral para predecr el úmero de fallas e acvos reparables.... VARIABLES PROBABILÍSTICAS DE INTERÉS EN ANÁLISIS DE CONFIABILIDAD DE ACTIVOS REPARABLES Como se mecoó prevamee u equpo reparable es aquel cuya codcó operava puede resaurarse después de fallar, co ua reparacó. Esa cosderacó mplca que e su vda puede ocurrr mas de ua falla y es esa la dfereca fudameal co los equpos o reparables e cuya vda solo puede ocurrr ua úca falla. E la seccó.. se esudó exesamee como raar la varable probablísca de erés para acvos o reparables, es decr, el empo para la falla; y los dcadores o fguras de méro ulzados para descrbrla; ales como la asa de fallas h( m ), la cofabldad C( m ) y la probabldad de falla F( m ) para u empo msó m ; o obsae como se demosrara mas adelae, esos cocepos, dcadores y ecuacoes, al como fuero defdos e la mecoada seccó, o aplca cuado hablamos de equpos reparables. E esa seccó, se raará exesamee el ema de la varable probablísca que 87
3 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad se esuda para equpos reparables y los dcadores o fguras de méro para caracerzarla. Cuado se raa de equpos reparables y se habla de empo para la falla, surge medaamee la pregua empo para cual falla? ; (empo para la prmera falla?; o empo para la seguda falla?; o empo para la ésma falla?), ya que para u empo msó m puede ocurrr mas de ua falla. S se habla por ejemplo la probabldad de falla e el empo msó m, surge las pregua, probabldad de cuaas fallas?; probabldad de ua falla e u perodo m?; o probabldad de fallas e u empo m?; o probabldad de fallas e u empo m?. E la fgura.-a se esquemaza ua proyeccó o esmado de u proceso de operacó de u equpo reparable, e el que se sabe que puede ocurrr fallas que será resauradas co reparacoes. Al mecoado esquema se asoca la omeclaura que se ulzara e lo sucesvo. Nóese que se maejara dos escalas de empo:.- Ua escala relacoada al empo de operacó ere fallas; para la cual se usara subídces; por ejemplo empo de operacó ere la prmera y la seguda falla..- Ora escala relacoada co el empo acumulado de operacó hasa las fallas o hasa u eveo específco; para la cual se usara superídces; por ejemplo ] empo acumulado de operacó hasa la seguda falla. Nóese que ] ra falla da falla ra falla a falla (-) - h falla () h falla K ] ] ] ] ]... ]... ] K Tempo msó T... K Fgura.-A: Proceso de fallas sucesvas. Nomeclaura Aalzado la fgura.-a y recordado que el empo para la falla se cosdera como ua varable aleaora por exceleca, se cocluye que los varables (empo de operacó hasa la prmera falla), (empo de operacó ere la prmera y la seguda falla), (empo de operacó ere la seguda y la ercera falla); hasa (empo de operacó ere la (-) h y la falla ), so odas varables aleaoras; es decr varables que puede omar múlples valores y que 88
4 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad por ede cada ua puede ser represeada co ua dsrbucó de probabldades. De la msma maera, y recordado los cocepos de operacoes co varables aleaoras dscudos e el Capíulo III, se cocluye que las varables ] (empo acumulado de operacó hasa la seguda falla), ] (empo acumulado de operacó hasa la ercera falla), ] (empo acumulado de operacó hasa la cuara falla), hasa ] (empo acumulado de operacó hasa la falla), so ambé varables aleaoras ya que las msmas resula de la suma de oras varables aleaoras; al como puede verse e la fgura. A. E la fgura.-b se represea la probabldad de fallas F( ), que como puede oarse aumea desde 0 a ere la falla - y la falla ; para,,,.., y e la fgura.-c se represea la cofabldad del ssema C( ), que dsmuye desde hasa 0 ere la falla - y la falla ; para,,,..,. F( ) Probabldad de Fallas ere la (-) h falla y la h falla 0 ra falla da falla ra falla a falla (-) - h falla () h falla K a] empo acumulado e operacó 0 k] Fgura.-B: Probabldad de Fallas e Acvos Reparables C( ) Cofabldad ere la (-) h falla y la h falla 0 ra falla da falla ra falla a falla (-) - h falla () h falla K a] empo acumulado e operacó 0 k] Fgura.-C: Cofabldad e Acvos Reparables 89
5 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad Las fguras.-b y.-c muesra claramee que o ee mucho sedo hablar de probabldad de falla o cofabldad e u empo acumulado de operacó k] o empo msó, ya que e ese perodo esos valores flucúa ere 0 y varas veces, y para dferees valores del empo e operacó puede darse el msmo valor de probabldad de falla. Por esa razó esos dcadores so poco usados e el aálss de acvos reparables. El aálss de la fgura.-d perme defcar la varable aleaora que caracerza a los equpos reparables coocda como Número Acumulado de Fallas N( m] ), para u empo acumulado de operacó o empo msó m]. N( a] ) No acumulado de fallas e el empo acumulado de operacó a] N( k] ) 95% f(n( k] )) µn( k] )Λ( k] ) N( k] ) 5%... ra falla da falla ra falla a falla ] ] ] ] Hsora (pasado) Hoy m Predccó (fuuro) a] empo acumulado e operacó ] m Tempo msó m Fgura.-D: Número Acumulado de Fallas e el Tempo Acumulado de Operacó Para la mejor compresó de ése ema es mporae explcar dos zoas claramee dferecadas e la fgura.-d:.- Ua zoa correspodee a la Hsora o al pasado; que comprede fallas acumuladas, que ha ocurrdo e forma sucesva y co ervalos,, y. Los valores,, y o so varables aleaoras; porque so coocdos; así como ampoco es ua varable aleaora el úmero acumulado de fallas e el empo de operacó ]. Esos valores so daos que se usara para hacer predccoes del umero de fallas para empos mayores a ]..- La ora es la llamada zoa de Predccó y correspode al fuuro. E esa zoa odo es aleaoro, y el objevo es saber cuaas fallas mas puede ocurrr 90
6 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad desde ] hasa m] ] m. Como el lecor puede ferr, la varable Número Acumulado de Fallas N( m] ), puede omar múlples valores para u empo acumulado de operacó o empo msó m] m ; es decr, es ua varable aleaora que puede y debe ser modelada maemácamee co ua dsrbucó de probabldades, a la cual se le puede calcular ua meda y uos perceles; al como se muesra e la fgura. Resumedo, la predccó del úmero acumulado de fallas para cada valor del empo de operacó dara como resulado ua dsrbucó de probabldades. La meda o valor esperado de esa dsrbucó se cooce como Número Esperado de Fallas y se deoa como Λ( m] ), como se muesra claramee e la fgura. La varable aleaora Número Acumulado de Fallas N( m] ), para u empo acumulado de operacó m] es la varable probablísca objeo de esudo e aálss de acvos reparables, y la fgura de méro Número Esperado de Fallas Λ( m] ) es el dcador por exceleca ulzado para caracerzarla. Además de Λ( m] ), exse oras fguras de mero o dcadores de gra uldad para aálss de equpos reparables; esos so: λ( m] ) asa de ocurreca de fallas al empo acumulado de operacó m] TEPPF empo esperado para la próxma falla, después del empo acumulado de operacó hasa la úlma falla E las seccoes sucesvas, se defrá los modelos maemácos para esmacó de los dcadores probablíscos de erés e ssemas reparables; co especal éfass e la esmacó del Número Esperado de Fallas Λ( m] ).... MODELOS PROBABILÍSTICOS PARA LA ESTIMACIÓN O PREDICCIÓN DEL NÚMERO DE FALLAS (N(T M] )) EN UN PERIODO DE OPERACIÓN T M], PARA SISTEMAS REPARABLES La fgura.-e muesra u resume de las eorías o procesos esocáscos para el modelaje de cofabldad de ssemas reparables. El Proceso Ordaro de Resauracó, el cual asume que el ssema vuelve a la codcó de a bueo como uevo y el Proceso No Homogéeo de Posso, el cual asume que queda a malo como esaba, so los méodos más comúmee ulzados para la evaluacó de ssemas reparables. El Proceso Geeralzado de Resauracó (PGR), el cual o asume gú esado e parcular y cosdera que los 5 esados so posbles, ha sdo receemee de gra erés debdo a la ecesdad de eer aálss y predccoes que esé suseados sobre bases más realsas. 9
7 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad Aálss de Cofabldad para Equpos Reparables Resaurar a la codcó orgal Reparacó míma posble Resaurar parcalmee Proceso Ordaro de Resauracó (POR) Proceso o Homogeeo de Posso (PNHP) Proceso Geeralzado de Resauracó (PGR) Ta bueo como uevo Ta malo como vejo Mejor que como esaba pero peor que uevo Fgura.-E: Teorías para Modelaje de acvos reparables... PROCESO ORDINARIO DE RESTAURACIÓN (POR) Se defe como Proceso Ordaro de Resauracó a u modelo maemáco que cosdera que los dferees empos ere fallas sucesvas de u acvo reparable so varables aleaoras depedees e décamee dsrbudas (es decr que puede represearse co la msmo modelo de dsrbucó paramérca probablísca). Esas cosderacoes puede ser valdas s se asume que el ssema es resaurado a su codcó orgal cada vez que se repara; es decr el equpo queda a bueo como uevo. S eso se asume como cero, los empos (,,...) ere fallas sucesvas so depedees, ya que al haber ua reparacó perfeca el empo de operacó o ee gú efeco e el empo. De gual forma, s cuado ocurre la falla e el empo (,,.), el equpo es resaurado a su codcó orgal, es razoable pesar que la varable aleaora, se comporara de maera smlar a la varable aleaora ya que al co de ambos perodos, el equpo esa eórcamee e la msma codcó; por lo que puede asumrse que ambas varables puede caracerzarse co la msma dsrbucó de probabldades; es decr, puede cosderarse décamee dsrbudas. 9
8 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad Por supueso, cosderar que cuado ocurre ua falla el equpo es resaurado a su codcó orgal represea u escearo deal, por lo que el POR es u modelo que ee lmacoes e su aplcacó e el aálss de ssemas reparables. Ese modelo esa resrgdo para equpos cosudos por alguos pocos compoees prcpales o reparables los cuales so reemplazables dvdualmee al fallar. Eso es, cuado ua pare prcpal del equpo falla, esa será reemplazada por ua ueva. Los compoees so o reparables ; pero el equpo es reparable. També es valda esa asucó, cuado la políca de reparacó sea revsar odo el equpo y reemplazar odo lo que ese deerorado cada vez que el equpo falle. Co base e el POR, y asumedo que los empos ere fallas sucesvas sgue ua dsrbucó Webull, las ecuacoes para los dcadores probablíscos de erés, para u valor del empo de operacó m], so las sguees: m] Probabldad de Fallas: ( ) m] Cofabldad: ( ) m F e Ecuacó.6 m C e Ecuacó.7 m] Tasa de Ocurreca de Fallas: ( ) m λ Ecuacó.8 Tempo Esperado para la próxma Falla: TEPPF. Γ Ecuacó.9 Número Esperado de Fallas: El cálculo de la varable Número Esperado de Fallas (Λ( m] )), revse especal erés y complejdad; por esa razó, se propoe ua solucó por smulacó de Moecarlo para esa varable. Para el POR a parr de la ecuacó.6, se sabe que: ( ( ( )) ) / lf Ecuacó.0 Dode represea empos ere fallas sucesvas geerados desde la ecuacó de Probabldad de Falla del POR. Co la ecuacó.0, podemos calcular el 9
9 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad úmero Esperado de Fallas Λ(T) al empo acumulado de operacó m] T; sguedo el dagrama de flujo que se muesra e la fgura.. El flujo-grama de la fgura. es fáclmee programable, y e cuesó de segudos es posble realzar mles de eracoes para obeer u cálculo umérco de Λ(T). INICIO SELECCIONE EL PERIODO DE ANALISIS T INGRESE EL VALOR DE LOS PARAMETROS y SELECCIONE EL NUMERO DE ITERACIONES m j T j 0 GENERAR ALEATORIAMENTE, UN VALOR X j ENTRE 0 y Tempo para la Falla () 0 F() 0,9 0,8 0,7 0,6 0,5 0, 0, 0, 0, 0 F () e 0,0 50,0 00,0 50,0 00,0 50,0 empo (hrs) j / ( l ( X )) j T j T j j SI <m? N Fallas j NO T j <T? SI jj NO NUMERO ESPERADO DE FALLAS AL TIEMPO T m Λ(T ) m STOP Fgura.: Flujograma de la Smulacó de Moecarlo para el cálculo del N Esperado de Fallas Λ(T) e acvos reparables basado e el POR Nóese que para el cálculo de cualquera de los dcadores probablíscas de erés, es ecesaro eer calculados los valores de los parámeros de escala () y de forma (). Ecuacoes para los Parámeros del POR Caso : Equpo Fallado La esmacó se hace e u momeo e el que acaba de ocurrr la falla, y el equpo o esa operado. E esas ecuacoes represea los empos ere fallas sucesvas observados y es el úmero oal de fallas observadas. 9
10 ˆ Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad ( ) Ecuacó.. l( )] l ( ) Ecuacó.. Ecuacoes para los Parámeros del POR Caso : Equpo Operado La esmacó o predccó se realza cuado el equpo esa operado ha rascurrdo u empo c (ver fgura.-a) desde la ocurreca de la úlma falla. Para el cálculo de parámeros es ecesaro resolver el sguee ssema de ecuacoes: ˆ ( ) ( ) l( )] ( ) ( ) c c l(c c ) l ( ) Ecuacó.. Ecuacó.. E ese puo es mporae desacar que el valor c puede clasfcarse como u dao cesado; al como se defó e la seccó... Como se dca e la fgura.-a, los parámeros se calcula co los valores de empos ere fallas y empos cesados que ya ha ocurrdo; es decr co la Hsora ; y los msmos so usados para predecr las fallas que ocurrrá a fuuro. 95
11 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad N( a] ) No acumulado de fallas e el empo acumulado de operacó a] N( k] ) 95% f(n( k] )) µn( k] )Λ( k] ) N( k] ) 5% Daos para esmar parámeros y... ra falla da falla ra falla a falla c ] ] ] ] Hsora (pasado) ] m Tempo msó Hoy c m m Predccó (fuuro) a] empo acumulado e operacó Fgura.-A: Esmacó de Parámeros, equpo operado... PROCESO NO HOMOGÉNEO DE POISSON (PNHP) U proceso de resauracó que pueda modelarse co el llamado Proceso No Homogéeo de Posso es aquel e el que los dferees empos para la falla ( ) de u compoee o ssema so cosderados varables aleaoras depedees e décamee dsrbudas. Esa cosderacó es válda s se asume que al fallar, el ssema es somedo a ua reparacó míma, y que por lo ao el equpo queda a malo como esaba juso aes de la falla. Ese modelo es váldo para equpos muy complejos, co múlples compoees, cuado la políca de reparacó es hacer la míma reparacó requerda para poer al equpo a operar uevamee. Asumedo que se cumple las asucoes prevamee descras, y que los empos sucesvos para fallar sgue ua dsrbucó de Webull, las ecuacoes de cálculo para las varables probablíscas de erés, para el PNHP so las sguees: 96
12 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad 97 Probabldad de Fallas: ( ) e F Ecuacó. ( ) e f Ecuacó. Cofabldad: ( ) e C Ecuacó.5 Número Esperado de Fallas: ( ) ( ) ( ) ] Λ ] m ] ] m ] Ecuacó.6 Tasa de Ocurreca de Fallas: ( ) m ] m ] λ Ecuacó.7 : ( ) ( ) ] m m ] TEPPF Ecuacó.8 Al gual que para el caso del POR, para el caso del PNHP debe obeerse dos expresoes dferees para los parámeros y de las ecuacoes aerores. Ecuacoes para los Parámeros del PNHP Caso : Equpo Fallado Ese caso se refere a esmacoes que se hace e u momeo e el que acaba de ocurrr la falla, y el equpo o esa operado. Las ecuacoes de los parámeros para ese caso so las sguees: ( ) ] ˆ Ecuacó.9
13 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad ˆ l ] ( ) ( ) ] Ecuacó.0 Dode ] es el empo de operacó acumulado hasa que ocurró la ulma falla, ] es el empo acumulado de operacó hasa que ocurre la falla y es el úmero oal de fallas. Ecuacoes para los Parámeros del PNHP Caso : Equpo Operado La esmacó se realza cuado el equpo esa operado y ha rascurrdo u empo c desde la ocurreca de la úlma falla. ˆ m ] ( ) Ecuacó.-A ˆ K ] ( ) ( ) Ecuacó.-B l ] Dode ] es el empo acumulado de operacó hasa la falla, m] es el empo de aálss o perodo de erés, c es el empo rascurrdo desde que ocurró la úlma falla hasa el momeo e que desea realzarse el cálculo y es el úmero oal de fallas observadas.... SIMULACIÓN DE MONTECARLO PARA EL PROCESO NO HOMOGÉNEO DE POISSON (PNHP) A pesar de que para el PNHP la esmacó del úmero esperado de fallas puede hacerse aalícamee s mayor dfculad co la ecuacó.6, esa esmacó ambé puede hacerse sguedo el msmo procedmeo ulzado e el POR. La prcpal dfereca es se ulza ua dsrbucó Webull codcoal. Eso es: F ( ) e, obeédose: ( ) l F( )]) /, para, Ecuacó. 98
14 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad Co la ecuacó., podemos calcular el Número Esperado de Fallas al empo T (Λ(T)), sguedo el dagrama de flujo que se muesra a e la fgura.. INICIO SELECCIONE EL PERIODO DE ANALISIS T INGRESE EL VALOR DE LOS PARAMETROS y SELECCIONE EL NUMERO DE ITERACIONES m j T GENERAR ALEATORIAMENTE, UN VALOR X j ENTRE 0 y Tempo para la Falla () 0 F() 0,9 0,8 0,7 0,6 0,5 0, 0, 0, 0, 0 F ( ) e 0,0 50,0 00,0 50,0 00,0 50,0 j empo (hrs) ( ) ( ) / l X j j T j T j- j SI <m? N Fallas j NO T j <T? SI jj NO NUMERO ESPERADO DE FALLAS AL TIEMPO T m Λ(T ) m STOP Fgura.: Smulacó de Moecarlo N Esperado de Fallas Λ(T) PNHP El flujo-grama de la fgura., al gual que el de la fgura., es fáclmee programable, y e cuesó de segudos es posble realzar mles de eracoes para obeer u cálculo umérco de Λ(T).... PROCESO GENERALIZADO DE RESTAURACIÓN (PGR) El proceso geeralzado de resauracó provee la plaaforma para calcular las varables probablíscas de erés para equpos reparables s la ecesdad de hacer asucoes acerca del esado del equpo después de la reparacó. Es u proceso geeral que coee a los casos de POR y NHPP como casos exremos; pero que perme modelar casos ermedos, es decr, reparacoes e las que el equpo queda mejor que como esaba pero peor que cuado 99
15 Yañez Meda, Medardo - Gómez de la Vega, Herado Valbuea Chouro, Geebel Igeería de Cofabldad y Aálss Probablísco de Resgo Capíulo IV: Igeería de Cofabldad uevo ; es decr veles parcales de resauracó. Como el lecor urá, ese proceso perme modelar casos mas reales que el POR y el PNHP. El PGR es u desarrollo muy recee, de cosderable complejdad maemáca que au puede cosderarse u área de vesgacó. Por esa razó, e aras de la fludez de la lecura de ese exo, se prefró dejarlo para lecores parcularmee eresados e el ema. 00
{ a 1, a 2,..., a } n. Cualquier vector n
 Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
Ingeniería de Confiabilidad - Equipos
 SECCION 4. Igeería de Cofabldad-Equpos Igeería de Cofabldad - Equpos Seccó 4 Medardo Yañez Herado Gómez de la Vega Kara Semeco Soo Nayrh Meda Esa seccó esa dedcada al esudo de los aspecos físcos y aleaoros
SECCION 4. Igeería de Cofabldad-Equpos Igeería de Cofabldad - Equpos Seccó 4 Medardo Yañez Herado Gómez de la Vega Kara Semeco Soo Nayrh Meda Esa seccó esa dedcada al esudo de los aspecos físcos y aleaoros
PLAN DE TRABAJO 11 Período 23/10/06 al 3/11/06. Durante estas dos semanas estudiarás los modelos de regresiones lineales.
 Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Álgebra Manuel Hervás Curso
 Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Introducción a la Econometría Curso 2009/ Serie de Problemas 21
 Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
LECTURA 3 Confiabilidad de Equipos No Reparables
 LECTURA 3 Cofabldad de Equpos No Reparables INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Góez de
LECTURA 3 Cofabldad de Equpos No Reparables INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Góez de
Figura 1. Figura 2. Para realizar este análisis asumiremos las siguientes condiciones:
 Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
UNIDAD 7.- Matrices (tema 1 del libro) = MATRICES
 UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
7. Contrastes de Hipótesis
 7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
TEMA 5: CAPITALIZACIÓN COMPUESTA ÍNDICE
 Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Taller de Preparación para el examen Models Life Contingencies (MLC) de la SOA.
 Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS.
 09- ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS. Iroduccó. Para obeer la ecuacó geeral que descrbe el comorameo del flujo de fludos a ravés de medos orosos, se hace uso de dferees rcos
09- ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS. Iroduccó. Para obeer la ecuacó geeral que descrbe el comorameo del flujo de fludos a ravés de medos orosos, se hace uso de dferees rcos
Una Estrategia de Acumulación de Reservas Mediante Opciones de Venta de Dólares. El Caso de Banco de México
 Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
TRANSMISIÓN DE CALOR MULTIDIRECCIONAL Y TRANSITORIA
 Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
4 METODOLOGIA ADAPTADA AL PROBLEMA
 4 MEODOLOGA ADAPADA AL PROBLEMA 4.1 troduccó Báscamete el problema que se quere resolver es ecotrar la actuacó óptma sobre las tesoes de los geeradores, la relacó de tomas de los trasformadores y el valor
4 MEODOLOGA ADAPADA AL PROBLEMA 4.1 troduccó Báscamete el problema que se quere resolver es ecotrar la actuacó óptma sobre las tesoes de los geeradores, la relacó de tomas de los trasformadores y el valor
1.1 MEDIA Y VARIANZA. Demostración: NOTAS: 1 n
 . TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
. TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
Modelos de Regresión análisis de regresión diagrama de dispersión coeficientes de regresión
 Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
F = = 0. 64, que es la eficiencia del test de signo relativa al
 Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
x independiente y dependiente 0301a) Concepto de Cambio Fenómenos F( t + t Generalidades Cambio Ejemplo: crecimiento exponencial Cambio de F Positivo
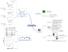 = ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
= ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
4.4. La ciudad circular El Modelo de Salop
 4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
VOLUMEN IV CAPITULO 3 METODOLOGÍA PARA LA ACTULIZACIÓN DE LAS CURVA DE COSTOS ÓPTIMOS DE RACIONAMIENTO DE ELECTRICIDAD Y GAS NATURAL
 ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
1.1.- Concepto Definición de cono Definición de función homogénea Interpretación económica de la función homogénea
 Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Una formulación general de un modelo de regresión paramétrico es la siguiente:
 Esmadores úcleos y polomos locales. Fracsco Parra Rodrguez Docor e Cecas Ecoómcas. UNED. Modelos de regresó o paramércos Los modelos de regresó paramércos supoe ue los daos observados provee de varables
Esmadores úcleos y polomos locales. Fracsco Parra Rodrguez Docor e Cecas Ecoómcas. UNED. Modelos de regresó o paramércos Los modelos de regresó paramércos supoe ue los daos observados provee de varables
2. Movimiento Browniano.
 Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
Estimación de parámetros en ecuaciones diferenciales estocásticas aplicadas a finanzas
 Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
Capítulo 3. Consideraciones sobre métodos numéricos
 3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
La Docencia y la importancia de la investigación en Ingeniería
 a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
V II Muestreo por Conglomerados
 V II Muestreo por Coglomerados Dr. Jesús Mellado 31 Por alguas razoes aturales, los elemetos muestrales se ecuetra formado grupos, como por ejemlo, las persoas que vve e coloas de ua cudad, lo elemetos
V II Muestreo por Coglomerados Dr. Jesús Mellado 31 Por alguas razoes aturales, los elemetos muestrales se ecuetra formado grupos, como por ejemlo, las persoas que vve e coloas de ua cudad, lo elemetos
Introducción a la Inferencia Estadística. Dept. of Marine Science and Applied Biology Jose Jacobo Zubcoff
 Itroduccó a la Ifereca Estadístca Dept. of Mare cece ad Appled Bology Jose Jacobo Zubcoff Modelos de Regresó mple Que tpo de relacó exste etre varables Predccó de valores a partr de ua de ellas Varable
Itroduccó a la Ifereca Estadístca Dept. of Mare cece ad Appled Bology Jose Jacobo Zubcoff Modelos de Regresó mple Que tpo de relacó exste etre varables Predccó de valores a partr de ua de ellas Varable
Flujo en acuífero libre
 SESIÓN PRÁCTICA EDP PARABÓLICA CON MÉTODO FTCS Flujo e acuíero lbre E esa sesó se aalza medae el méodo eplíco de derecas as la evolucó emporal del vel reáco sobre ua geomería de acuíero lbre alerada por
SESIÓN PRÁCTICA EDP PARABÓLICA CON MÉTODO FTCS Flujo e acuíero lbre E esa sesó se aalza medae el méodo eplíco de derecas as la evolucó emporal del vel reáco sobre ua geomería de acuíero lbre alerada por
1.3. Longitud de arco.
 .. Logtud de arco. Defcó. Sea C ua curva suave defda paramétrcamete por la fucó vectoral f : R R / f () t = ( f() t, f() t,, f ( t) ) e el espaco R, co t [ a, b], que se recorre exactamete ua vez cuado
.. Logtud de arco. Defcó. Sea C ua curva suave defda paramétrcamete por la fucó vectoral f : R R / f () t = ( f() t, f() t,, f ( t) ) e el espaco R, co t [ a, b], que se recorre exactamete ua vez cuado
Comportamiento Mecánico de Sólidos Capítulo II. Introducción al análisis tensorial. Tensores. x 3 A 3. Figura 1. Componentes de un vector.
 Comportameto Mecáco de Sóldos Capítulo II. Itroduccó al aálss tesoral. Itroduccó al aálss tesoral esores Es aquella catdad físca que después de ua trasformacó de coordeadas (que obedezca certas reglas),
Comportameto Mecáco de Sóldos Capítulo II. Itroduccó al aálss tesoral. Itroduccó al aálss tesoral esores Es aquella catdad físca que después de ua trasformacó de coordeadas (que obedezca certas reglas),
NOMBRE Apellido Paterno Apellido Materno Nombre(s)
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
REGRESIÓN LINEAL SIMPLE
 RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores
![Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores](/thumbs/63/49997694.jpg) 1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
Cuatro medidas de inflación subyacente para Uruguay
 Cuaro meddas de flacó subyacee para Uruguay Rosaa Ferádez 002-2005 688-7565 CUATRO MEDIDAS DE INFLACIÓN SUBYACENTE PARA URUGUAY Rosaa Ferádez Casro Área de Ivesgacoes Ecoómcas Baco Ceral del Uruguay Julo
Cuaro meddas de flacó subyacee para Uruguay Rosaa Ferádez 002-2005 688-7565 CUATRO MEDIDAS DE INFLACIÓN SUBYACENTE PARA URUGUAY Rosaa Ferádez Casro Área de Ivesgacoes Ecoómcas Baco Ceral del Uruguay Julo
MODELO CIR. Nota Técnica RESUMEN EJECUTIVO
 Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
TEMA 3: EQUIVALENCIA FINANCIERA DE CAPITALES
 Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Método de depreciación de reducción de saldos y saldos decrecientes sin error residual
 esó Jove Revsa de la Agrupacó Jove Iberoamercaa de oabldad y Admsracó de Empresas (AJOIA) º 7 07 I 988-90 pp 60-75 Méodo de deprecacó de reduccó de saldos y saldos decrecees s error resdual uevo méodo
esó Jove Revsa de la Agrupacó Jove Iberoamercaa de oabldad y Admsracó de Empresas (AJOIA) º 7 07 I 988-90 pp 60-75 Méodo de deprecacó de reduccó de saldos y saldos decrecees s error resdual uevo méodo
Vida media residual de mixturas finitas y aplicaciones a sistemas coherentes
 Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Navarro Camacho, Jorge jorgeav@umes Deparameo de Esadísca e Ivesgacó Operava Uversdad
Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Navarro Camacho, Jorge jorgeav@umes Deparameo de Esadísca e Ivesgacó Operava Uversdad
3 = =. Pero si queremos calcular P (B) 2, ya que si A ocurrió, entonces en la urna
 arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
Introducción a la Estadística Descriptiva
 Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
CURSO DE ECONOMETRIA BÁSICA
 CURSO DE ECONOMETRIA BÁSICA D. Fracsco Parra Rodríguez. Jefe de Servco de Esadíscas Ecoómcas y Socodemografcas. Isuo Caabro de Esadísca. ICANE, ÍNDICE Tema. Regresó y correlacó leal smple Tema. Regresó
CURSO DE ECONOMETRIA BÁSICA D. Fracsco Parra Rodríguez. Jefe de Servco de Esadíscas Ecoómcas y Socodemografcas. Isuo Caabro de Esadísca. ICANE, ÍNDICE Tema. Regresó y correlacó leal smple Tema. Regresó
Intensificación en Estadística
 GRADO EN VETERINARIA DEPARTAMENTO DE ESTADÍSTICA E IO 0-0 IV Curso Cero Itesfcacó e Estadístca Itroduccó a la fucó Sumatoro Itroduccó Cocepto de fucó sumatoro Aplcacoes Itroduccó Cocepto de fucó sumatoro
GRADO EN VETERINARIA DEPARTAMENTO DE ESTADÍSTICA E IO 0-0 IV Curso Cero Itesfcacó e Estadístca Itroduccó a la fucó Sumatoro Itroduccó Cocepto de fucó sumatoro Aplcacoes Itroduccó Cocepto de fucó sumatoro
LOS NÚMEROS COMPLEJOS
 LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
Reglas para el manejo de los índices de deuda de la BNV. Bolsa Nacional de Valores Version 4.4 13/07/2005
 Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
TEMA 2.- LA CAPITALIZACIÓN COMPUESTA.
 TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
Influencia de distribución del tiempo de ocurrencia entre siniestros en la solvencia de las carteras de seguros no vida (*)
 ESTADÍSTICA ESPAÑOLA Vol. 50, úm. 69, 008, págs. 455 a 478 Iflueca de dsrbucó del empo de ocurreca ere sesros e la solveca de las careras de seguros o vda (*) por MAITE MÁRMOL JIMÉNEZ y M. MERCE CLARAMUNT
ESTADÍSTICA ESPAÑOLA Vol. 50, úm. 69, 008, págs. 455 a 478 Iflueca de dsrbucó del empo de ocurreca ere sesros e la solveca de las careras de seguros o vda (*) por MAITE MÁRMOL JIMÉNEZ y M. MERCE CLARAMUNT
Test de Hipótesis. Error de tipo I: Rechazar H 0 siendo H 0 Verdadera. Error de tipo II: No rechazar H 0 siendo H 0 Falsa
 Error tpo I: Rechazar H sedo H Verdara Test Hpótess Error tpo II: No rechazar H sedo H Falsa Nvel Sgfcacó: = P(error tpo I = P(Rechazar H sedo H Verdara Probabldad error tpo II: = P(error tpo II = P(No
Error tpo I: Rechazar H sedo H Verdara Test Hpótess Error tpo II: No rechazar H sedo H Falsa Nvel Sgfcacó: = P(error tpo I = P(Rechazar H sedo H Verdara Probabldad error tpo II: = P(error tpo II = P(No
TEMA 3. Medidas de variabilidad y asimetría. - X mín. X máx
 TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
Análisis de Regresión y Correlación Lineal
 Aálss de Regresó y Correlacó Leal 2do C. 2018 Mg. Stella Fgueroa Clase Nº 14 Tpos de relacoes etre varables Exste u compoete aleatoro por lo que las predccoes tee asocado u error de predccó. Modelo determsta
Aálss de Regresó y Correlacó Leal 2do C. 2018 Mg. Stella Fgueroa Clase Nº 14 Tpos de relacoes etre varables Exste u compoete aleatoro por lo que las predccoes tee asocado u error de predccó. Modelo determsta
x x x x x Y se seguía operando
 . INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
. INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA
 MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA José Rgobero Parada Daza Uversdad de Cocepcó, Chle Regsro Propedad Ielecual Nº.798 I.S.B.N. 956-89-9- Auor: José Rgobero Parada Daza ÍNDICE CAPÍTULO I OPTIMIZACIÓN
MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA José Rgobero Parada Daza Uversdad de Cocepcó, Chle Regsro Propedad Ielecual Nº.798 I.S.B.N. 956-89-9- Auor: José Rgobero Parada Daza ÍNDICE CAPÍTULO I OPTIMIZACIÓN
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN
 VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
Orden de la tirada. Figura 1: Frecuencia relativa de cara para una sucesión de 400 tiradas.
 Estadístca (Q) Dra. Daa M. Kelmasky 99. Teoremas límte Frecueca Relatva 0.5 0.6 0.7 0.8 0.9.0 0 00 00 300 400 Orde de la trada Fgura : Frecueca relatva de cara para ua sucesó de 400 tradas. La fgura muestra
Estadístca (Q) Dra. Daa M. Kelmasky 99. Teoremas límte Frecueca Relatva 0.5 0.6 0.7 0.8 0.9.0 0 00 00 300 400 Orde de la trada Fgura : Frecueca relatva de cara para ua sucesó de 400 tradas. La fgura muestra
Tarificación de bonos sobre catástrofes (cat bonds) con desencadenantes de índices de pérdidas. Modelación mediante un proceso de Ornstein-Uhlenbeck
 REVISTA DE MÉTODOS CUANTITATIVOS PARA LA ECONOMÍA Y LA EMPRESA (24). Págas 340 361. Dcembre de 2017. ISSN: 1886-516X. D.L: SE-2927-06. www.upo.es/revsas/dex.php/revmecua/arcle/vew/2891 Tarfcacó de boos
REVISTA DE MÉTODOS CUANTITATIVOS PARA LA ECONOMÍA Y LA EMPRESA (24). Págas 340 361. Dcembre de 2017. ISSN: 1886-516X. D.L: SE-2927-06. www.upo.es/revsas/dex.php/revmecua/arcle/vew/2891 Tarfcacó de boos
Método Matemático para las Series Uniformes o Anualidades
 Mg Mao Aoo Plaza Vdaue Méodo Maemáo paa las Sees Ufomes o Aualdades E el pesee doumeo ulzaemos es méodos paa halla las fómulas que se ulza paa efeua álulos faeos e las aualdades vedas Pmeo se hallaá la
Mg Mao Aoo Plaza Vdaue Méodo Maemáo paa las Sees Ufomes o Aualdades E el pesee doumeo ulzaemos es méodos paa halla las fómulas que se ulza paa efeua álulos faeos e las aualdades vedas Pmeo se hallaá la
ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL
 ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL TIPOS DE RELACIONES ENTRE VARIABLES Dos varables puede estar relacoadas por: Modelo determsta Modelo estadístco Ejemplo: Relacó de la altura co la edad e ños.
ANÁLISIS DE REGRESIÓN Y CORRELACIÓN LINEAL TIPOS DE RELACIONES ENTRE VARIABLES Dos varables puede estar relacoadas por: Modelo determsta Modelo estadístco Ejemplo: Relacó de la altura co la edad e ños.
Supongamos que hemos aplicado el test F y hemos rechazado la H0.
 Comparacó de medas tomadas de a pares CONDICION Meda s --------- ---------- ------ ---------- 0.00 3.0000 0.00 3.73 3 97.00 3.0000 4 93.00.44 TOTAL 98.73.6036 Supogamos que hemos aplcado el test F y hemos
Comparacó de medas tomadas de a pares CONDICION Meda s --------- ---------- ------ ---------- 0.00 3.0000 0.00 3.73 3 97.00 3.0000 4 93.00.44 TOTAL 98.73.6036 Supogamos que hemos aplcado el test F y hemos
CAPÍTULO III TÉCNICAS DE SIMULACIÓN ESTADÍSTICA. Los datos sintéticos son elementos de suma importancia en los sistemas de diseño en
 CAPÍTULO III TÉCNICAS DE SIMULACIÓN ESTADÍSTICA 3. Itroduccó Los datos stétcos so elemetos de suma mportaca e los sstemas de dseño e presas de almaceameto, ya que se evalúa el propósto del sstema co sumo
CAPÍTULO III TÉCNICAS DE SIMULACIÓN ESTADÍSTICA 3. Itroduccó Los datos stétcos so elemetos de suma mportaca e los sstemas de dseño e presas de almaceameto, ya que se evalúa el propósto del sstema co sumo
7. Muestreo con probabilidades desiguales.
 7. Muestreo co probabldades desguales. 7. Itroduccó. 7.. Probabldades de clusó. 7.. Pesos del dseño muestral. 7.. Alguos métodos co probabldades desguales. 7. Estmacó de la meda, proporcó total poblacoales.
7. Muestreo co probabldades desguales. 7. Itroduccó. 7.. Probabldades de clusó. 7.. Pesos del dseño muestral. 7.. Alguos métodos co probabldades desguales. 7. Estmacó de la meda, proporcó total poblacoales.
CAPÍTULO 6. CINEMÁTICA DIFERENCIAL DEL ROBOT PARALELO
 CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
Análisis amortizado. Técnicas Avanzadas de Programación - Javier Campos 205
 Aálss amortzado Téccas Avazadas de Programacó - Javer Campos 205 Aálss amortzado El pla: Coceptos báscos: Método agregado Método cotable Método potecal Prmer ejemplo: aálss de tablas hash dámcas Motículos
Aálss amortzado Téccas Avazadas de Programacó - Javer Campos 205 Aálss amortzado El pla: Coceptos báscos: Método agregado Método cotable Método potecal Prmer ejemplo: aálss de tablas hash dámcas Motículos
7. Contrastes de Hipótesis
 7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
MEDIDAS DE TENDENCIA CENTRAL
 Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
02 ) 2 0 en el resto. Tiempo (meses) Ventilador adicional No No Si No Si Si Si Si No Si Tipo carcasa A C B A B A B C B C
 Ua empresa motadora de equpos electrócos está realzado u estudo sobre aluos de los compoetes que utlza. E partcular mde el tempo de vda e meses reales de los procesadores que mota, dode a aluos de ellos
Ua empresa motadora de equpos electrócos está realzado u estudo sobre aluos de los compoetes que utlza. E partcular mde el tempo de vda e meses reales de los procesadores que mota, dode a aluos de ellos
ÍNDICE DE INVENTARIOS DEL COMERCIO BASE DICIEMBRE 2014=100
 ÍNDICE DE INVENTARIOS DEL COMERCIO BASE DICIEMBRE 2014=100 DOCUMENTO METODOLÓGICO INSTITUTO NACIONAL DE ESTADÍSTICAS Marzo / 2017 DEPARTAMENTO DE ESTUDIOS ECONÓMICOS COYUNTURALES SUBDEPARTAMENTO DE ESTADÍSTICAS
ÍNDICE DE INVENTARIOS DEL COMERCIO BASE DICIEMBRE 2014=100 DOCUMENTO METODOLÓGICO INSTITUTO NACIONAL DE ESTADÍSTICAS Marzo / 2017 DEPARTAMENTO DE ESTUDIOS ECONÓMICOS COYUNTURALES SUBDEPARTAMENTO DE ESTADÍSTICAS
Estimación de Parámetros de Sistemas Lineales vía Matrices Operacionales
 Esmacó de Parámeros de Ssemas Leales vía Marces Operacoales Isdro I. Lázaro, Salvador Ramírez lazaro@zeus.umch.mx szavala@zeus.umch.mx Faculad de Igeería Elécrca-Uversdad Mchoacaa de Sa Ncolás de Hdalgo
Esmacó de Parámeros de Ssemas Leales vía Marces Operacoales Isdro I. Lázaro, Salvador Ramírez lazaro@zeus.umch.mx szavala@zeus.umch.mx Faculad de Igeería Elécrca-Uversdad Mchoacaa de Sa Ncolás de Hdalgo
VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS *
 Revsa Igeerías Uversdad de Medellí VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS * Carlos Alexáder Grajales Correa ** Fredy Ocars Pérez Ramírez *** Recbdo: 6//009 Acepado: 08/0/00 RESUMEN
Revsa Igeerías Uversdad de Medellí VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS * Carlos Alexáder Grajales Correa ** Fredy Ocars Pérez Ramírez *** Recbdo: 6//009 Acepado: 08/0/00 RESUMEN
ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO 1 (NOVALES 2.1)
 ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO (NOVALES.) Cosideremos P P e g. Dado que dicha fució es coiua y que exise y so coiuas las derivadas de odos los órdees, podemos aplicar Taylor
ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO (NOVALES.) Cosideremos P P e g. Dado que dicha fució es coiua y que exise y so coiuas las derivadas de odos los órdees, podemos aplicar Taylor
Estadística. Tema 2: Medidas de Tendencia Central.. Estadística. UNITEC Tema 2: Medidas de Tendencia Central Prof. L. Lugo
 Estadístca Tema : Meddas de Tedeca Cetral. Estadístca. UNITEC Tema : Meddas de Tedeca Cetral 1 Parámetros y Estadístcos Parámetro: Es ua catdad umérca calculada sobre ua poblacó La altura meda de los dvduos
Estadístca Tema : Meddas de Tedeca Cetral. Estadístca. UNITEC Tema : Meddas de Tedeca Cetral 1 Parámetros y Estadístcos Parámetro: Es ua catdad umérca calculada sobre ua poblacó La altura meda de los dvduos
La inferencia estadística es primordialmente de naturaleza
 VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
ERRORES EN LAS MEDIDAS (Conceptos elementales)
 ERRORES E LAS MEDIDAS (Coceptos elemetales). Medda y tpos de errores ormalmete, al realzar varas meddas de ua magtud físca, se obtee e ellas valores dferetes. E muchas ocasoes, esta dfereca se debe a causas
ERRORES E LAS MEDIDAS (Coceptos elemetales). Medda y tpos de errores ormalmete, al realzar varas meddas de ua magtud físca, se obtee e ellas valores dferetes. E muchas ocasoes, esta dfereca se debe a causas
Números Complejos PREGUNTAS MÁS FRECUENTES
 Repaso de º de Bachllerato Números Complejos PREGUNTAS MÁS FRECUENTES. Qué es la udad magara? Es u elemeto del que coocemos úcamete su cuadrado:.obvamete, o se trata de u úmero real.. Qué es u úmero complejo?
Repaso de º de Bachllerato Números Complejos PREGUNTAS MÁS FRECUENTES. Qué es la udad magara? Es u elemeto del que coocemos úcamete su cuadrado:.obvamete, o se trata de u úmero real.. Qué es u úmero complejo?
n t T é c n i c Curso de Estadística con R Autor: Francisco Parra Rodríguez Jefe de Servicio de Estadísticas Económicas y Sociodemográficas ICANE
 D o c u m e Curso de Esadísca co R o s Auor: Fracsco Parra Rodríguez Jefe de Servco de Esadíscas Ecoómcas y Socodemográfcas ICANE DOC. Nº /6 ISSN 444-67 Saader, Caabra T é c c o s . EL MODELO LINEAL GENERAL...3..
D o c u m e Curso de Esadísca co R o s Auor: Fracsco Parra Rodríguez Jefe de Servco de Esadíscas Ecoómcas y Socodemográfcas ICANE DOC. Nº /6 ISSN 444-67 Saader, Caabra T é c c o s . EL MODELO LINEAL GENERAL...3..
Inferencia Estadística
 Ifereca Estadístca Poblacó y muestra Coceptos y defcoes Muestra Aleatora Smple (MAS) Cosderemos ua poblacó, cuya fucó de dstrbucó esta dada por F(), la cual está costtuda por u úmero fto de posbles valores,
Ifereca Estadístca Poblacó y muestra Coceptos y defcoes Muestra Aleatora Smple (MAS) Cosderemos ua poblacó, cuya fucó de dstrbucó esta dada por F(), la cual está costtuda por u úmero fto de posbles valores,
Análisis de supervivencia. Albert Sorribas Grup de Bioestadística I Biomatemàtica Departament de Ciències Mèdiques Bàsiques Universitat de Lleida
 Análss de supervvenca Alber Sorrbas Grup de Boesadísca I Bomaemàca Deparamen de Cènces Mèdques Bàsques Unversa de Lleda Esquema general Inroduccón al análss de supervvenca Tpos de esudos El concepo de
Análss de supervvenca Alber Sorrbas Grup de Boesadísca I Bomaemàca Deparamen de Cènces Mèdques Bàsques Unversa de Lleda Esquema general Inroduccón al análss de supervvenca Tpos de esudos El concepo de
1. Los postulados de la Mecánica Cuántica. 2. Estados Estacionarios. 3. Relación de Incertidumbre de Heisenberg. 4. Teorema de compatibilidad.
 Parte : MECÁNICA CUÁNTICA 1. Los postulados de la Mecáca Cuátca.. Estados Estacoaros. 3. Relacó de Icertdumbre de Heseberg. 4. Teorema de compatbldad. 1 U breve repaso de Mecáca Clásca 1. Partícula clásca:
Parte : MECÁNICA CUÁNTICA 1. Los postulados de la Mecáca Cuátca.. Estados Estacoaros. 3. Relacó de Icertdumbre de Heseberg. 4. Teorema de compatbldad. 1 U breve repaso de Mecáca Clásca 1. Partícula clásca:
Aplicaciones de Balances de Energía en Reactores Batch
 plcacoes de Balaces de Eergía e Reactores Batch Para u reactor batch, el BdeM se epresa como la ecuacó para determar el tempo de resdeca: t N ( rv Separado varables: V N Esta es ua ecuacó dferecal ordara
plcacoes de Balaces de Eergía e Reactores Batch Para u reactor batch, el BdeM se epresa como la ecuacó para determar el tempo de resdeca: t N ( rv Separado varables: V N Esta es ua ecuacó dferecal ordara
Estimación de parámetros Tema 2. Propiedades de los buenos estimadores. 2. Estimación por intervalos
 Uverdad Auóoma de Madrd Emacó de parámero Tema. Emacó puual Propedade de lo bueo emadore. Emacó por ervalo.. Coruccó del ervalo de cofaza. íme cofdecale. Nvel de cofaza y vel de rego... Iervalo de cofaza
Uverdad Auóoma de Madrd Emacó de parámero Tema. Emacó puual Propedade de lo bueo emadore. Emacó por ervalo.. Coruccó del ervalo de cofaza. íme cofdecale. Nvel de cofaza y vel de rego... Iervalo de cofaza
Modelos de Regresión Simple
 Itroduccó a la Ifereca Estadístca Dept. of Mare cece ad Appled Bology Jose Jacobo Zubcoff Modelos de Regresó mple Que tpo de relacó exste etre varables Predccó de valores a partr de ua de ellas Varable
Itroduccó a la Ifereca Estadístca Dept. of Mare cece ad Appled Bology Jose Jacobo Zubcoff Modelos de Regresó mple Que tpo de relacó exste etre varables Predccó de valores a partr de ua de ellas Varable
Serie de Gradiente (Geométrico y Aritmético) y su Relación con el Presente.
 Sere de radete (eométrco y rtmétco) y su Relacó co el resete. Certos proyectos de versó geera fluos de efectvo que crece o dsmuye ua certa catdad costate cada período. or eemplo, los gastos de matemeto
Sere de radete (eométrco y rtmétco) y su Relacó co el resete. Certos proyectos de versó geera fluos de efectvo que crece o dsmuye ua certa catdad costate cada período. or eemplo, los gastos de matemeto
REVISTA INVESTIGACION OPERACIONAL Vol. 22, No. 2, 2001
 REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
ANÁLISIS DE CIRCUITOS EN RÉGIMEN POLIARMÓNICO
 A.4. EORÍA DE CRCUOS CAPÍULO 3 ANÁLSS DE CRCUOS EN RÉGEN POLARÓNCO Cáedra de eoría de Crcuos Edcó 3 ANÁLSS DE CRCUOS EN RÉGEN POLARÓNCO 3. roduccó El desarrollo de las éccas de aálss de Fourer posee ua
A.4. EORÍA DE CRCUOS CAPÍULO 3 ANÁLSS DE CRCUOS EN RÉGEN POLARÓNCO Cáedra de eoría de Crcuos Edcó 3 ANÁLSS DE CRCUOS EN RÉGEN POLARÓNCO 3. roduccó El desarrollo de las éccas de aálss de Fourer posee ua
. Si vamos calculando así las potencias n-ésimas de la unidad imaginaria, descubriremos que son cíclicas y que cada 4 términos se repiten: ( )
 Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
2.5. Área de una superficie.
 .5. Área de ua superfce. Sea g ua fucó co prmeras dervadas parcales cotuas, tal que z g( x y), 0 e toda la regó D del plao xy. Sea S la parte de la gráfca de g cuya proyeccó e el plao xy es como se lustra
.5. Área de ua superfce. Sea g ua fucó co prmeras dervadas parcales cotuas, tal que z g( x y), 0 e toda la regó D del plao xy. Sea S la parte de la gráfca de g cuya proyeccó e el plao xy es como se lustra
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO POSGRADO EN ECONOMIA UNAM FACULTAD DE ECONOMÍA ECONOMETRIA. Proceso Estocástico. Mtro. Horacio Catalán Alonso
 UNIVERSIDAD NACIONAL AUÓNOMA DE MÉXICO POSGRADO EN ECONOMIA UNAM FACULAD DE ECONOMÍA ECONOMERIA Proceso Esocásico Mro. Horacio Caalá Aloso Proceso esocásico Defiició.- U Proceso Esocásico (PE es ua secuecia
UNIVERSIDAD NACIONAL AUÓNOMA DE MÉXICO POSGRADO EN ECONOMIA UNAM FACULAD DE ECONOMÍA ECONOMERIA Proceso Esocásico Mro. Horacio Caalá Aloso Proceso esocásico Defiició.- U Proceso Esocásico (PE es ua secuecia
INSTITUTO POLITÉCNICO NACIONAL
 INTITUTO POLITÉCNICO NACIONAL ECUELA UPERIOR DE FÍICA Y MATEMÁTICA APLICACIONE EN FINANZA DE MODELO AUTORREGREIVO TEI QUE, PARA OBTENER EL TITULO DE INGENIERO MATEMÁTICO, PREENTA. CLAUDIA VIRIDIANA VÁZQUEZ
INTITUTO POLITÉCNICO NACIONAL ECUELA UPERIOR DE FÍICA Y MATEMÁTICA APLICACIONE EN FINANZA DE MODELO AUTORREGREIVO TEI QUE, PARA OBTENER EL TITULO DE INGENIERO MATEMÁTICO, PREENTA. CLAUDIA VIRIDIANA VÁZQUEZ
El MÉTODO MATEMÁTICO PARA LAS SERIES VARIABLES CON GRADIENTE ARITMÉTICO DECRECIENTE
 Mg Mrco oo Plz Vdurre El MÉTODO MTEMÁTIO PR LS SERIES VRIBLES ON RDIENTE RITMÉTIO DEREIENTE El presee documeo desrroll e delle el méodo ulzdo por Jme rcí e su lro Memács cers co ecucoes e dferec f, sedo
Mg Mrco oo Plz Vdurre El MÉTODO MTEMÁTIO PR LS SERIES VRIBLES ON RDIENTE RITMÉTIO DEREIENTE El presee documeo desrroll e delle el méodo ulzdo por Jme rcí e su lro Memács cers co ecucoes e dferec f, sedo
EJERCICIOS SISTEMA FINANCIERO COMPUESTO
 UNIVERSIDAD DE LOS ANDES FAULTAD DE IENIAS EONÓMIAS Y SOIALES DEPARTAMENTO DE IENIAS ADMINISTRATIVAS ÁTEDRA: ANÁLISIS DE LA INVERSIÓN ASIGNATURA: MATEMÁTIA FINANIERA PROFESOR: MIGUEL A. OLIVEROS V. EJERIIOS
UNIVERSIDAD DE LOS ANDES FAULTAD DE IENIAS EONÓMIAS Y SOIALES DEPARTAMENTO DE IENIAS ADMINISTRATIVAS ÁTEDRA: ANÁLISIS DE LA INVERSIÓN ASIGNATURA: MATEMÁTIA FINANIERA PROFESOR: MIGUEL A. OLIVEROS V. EJERIIOS
SISTEMAS DE ECUACIONES NO LINEALES
 SISTEMAS DE ECUACIONES NO INEAES Capítulo 7 Sstemas de ecuacoes o leales c Elzabeth Vargas 7 INTRODUCCIÓN os métodos teratvos para resolver ua ecuacó o leal se puede eteder para ecotrar la solucó de u
SISTEMAS DE ECUACIONES NO INEAES Capítulo 7 Sstemas de ecuacoes o leales c Elzabeth Vargas 7 INTRODUCCIÓN os métodos teratvos para resolver ua ecuacó o leal se puede eteder para ecotrar la solucó de u
METODOLOGÍA DE CÁLCULO DEL INDICADOR DE FLOTA EN OPERACIÓN (IFO)
 METODOLOGÍA DE CÁLCULO DEL INDICADOR DE FLOTA EN OPERACIÓN (IFO) I. Descrpcó del cálculo de los dcadores IFO CIFO La flota e operacó se medrá a través de los mecasmos IFO y CIFO, de acuerdo a lo establecdo
METODOLOGÍA DE CÁLCULO DEL INDICADOR DE FLOTA EN OPERACIÓN (IFO) I. Descrpcó del cálculo de los dcadores IFO CIFO La flota e operacó se medrá a través de los mecasmos IFO y CIFO, de acuerdo a lo establecdo
Curvas Sistemas Gráficos Ing. Horacio Abbate 1
 Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO Introducción.
 TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
2.4 Pruebas estadísticas para los números pseudoaleatorios
 Capítulo Números pseudoaleatoros.4 Pruebas estadístcas para los úmeros pseudoaleatoros 34 E la seccó. se presetaro dversos algortmos para costrur u cojuto r, pero ése es sólo el prmer paso, ya que el cojuto
Capítulo Números pseudoaleatoros.4 Pruebas estadístcas para los úmeros pseudoaleatoros 34 E la seccó. se presetaro dversos algortmos para costrur u cojuto r, pero ése es sólo el prmer paso, ya que el cojuto
estimación de la estructura de Tasas nominales de chile: aplicación del modelo dinámico nelson-siegel
 Volume 4 - º / dcembre 0 estmacó de la estructura de Tasas omales de chle: aplcacó del modelo dámco elso-segel Rodrgo Alaro A. * Sebasá Becerra C. ** Adrés Sager T. *** I. IroduccIó La esmacó de la esrucura
Volume 4 - º / dcembre 0 estmacó de la estructura de Tasas omales de chle: aplcacó del modelo dámco elso-segel Rodrgo Alaro A. * Sebasá Becerra C. ** Adrés Sager T. *** I. IroduccIó La esmacó de la esrucura
2. Censura y truncamiento
 2. Cesura y trucameto Los datos de tempo de fallo se preseta e dferetes formas que crea problemas especales cuado se aalza. E muchas ocasoes o se cooce co exacttud el valor del tempo de fallo y úcamete
2. Cesura y trucameto Los datos de tempo de fallo se preseta e dferetes formas que crea problemas especales cuado se aalza. E muchas ocasoes o se cooce co exacttud el valor del tempo de fallo y úcamete
CAPITULO 2º FUNCIONES DE VECTORES Y MATRICES_01. Ing. Diego Alejandro Patiño G. M.Sc, Ph.D.
 CPIULO 2º FUNCIONES DE VECORES Y MRICES_ Ig. Dego lejadro Patño G. M.Sc, Ph.D. Fucoes de Vectores y Matrces Los operadores leales so fucoes e u espaco vectoral, que trasforma u vector desde u espaco a
CPIULO 2º FUNCIONES DE VECORES Y MRICES_ Ig. Dego lejadro Patño G. M.Sc, Ph.D. Fucoes de Vectores y Matrces Los operadores leales so fucoes e u espaco vectoral, que trasforma u vector desde u espaco a

 cocetrac0,,4,6,8,0, fluo
cocetrac0,,4,6,8,0, fluo