CARACTERISTICAS DE LOS CAMPOS CONSERVATIVOS
|
|
|
- Francisco Javier Ramírez Ponce
- hace 6 años
- Vistas:
Transcripción
1 CARACTERISTICAS DE LOS CAMPOS CONSERVATIVOS Paa los inteeses de la Física, los Campos Vectoiales se clasifican en dos gupos: -CAMPOS VECTORIALES CONSERVATIVOS.CAMPOS VECTORIALES NO CONSERVATIVOS Los de más inteés en la Física son los pimeos. Po ello iniciamos definiéndolos: Los Campos Vectoiales Consevativos, son aquéllos paa los cuales la Integal de Línea del Campo Vectoial vale ceo paa una tayectoia ceada. Los Campos Vectoiales Consevativos, son aquéllos paa los cuales la Integal de Línea del Campo Vectoial tiene el mismo valo paa tayectoias que tienen los mismos puntos límites Una condición suficiente paa que la integal de línea tenga las popiedades anteioes, es que el campo vectoial sea deivable de una Función Escala Potencial, es deci, si (x, es el Ca mpovectoial, existe una función escala φ ( x, que cumple la elación: F(x, = ϕ (x, F = 0. Un Campo Vectoial seá deivable de una Función Potencial si se cumple que su Rotacional es nula, es deci se cumple que:. F En la jega de las Matemáticas, se demuesta que el hecho de asevea que Un Campo Vectoial es Consevativo, es equivalente a deci que ese campo es IRROTACIONAL. Y un campo es Iotacional cuando se cumple: F = 0. Realicemos un pequeño ecodatoio: El Campo Vectoial VECTOR DE POSICION, es el Campo vectoial que a cada punto del espacio le asocia el vecto cuyo oigen se encuenta anclado al oigen del sistema coodenado, y donde el extemo está colocado en el punto al que está elacionado. Se dice que este vecto dá la posición de cualquie punto especto al obsevado, a quien se le considea anclado en el oigen del sistema coodenado. Si el punto P: (x, es un punto cualquiea del espacio, su vecto de posición es dado po la expesión: = xiˆ + yj ˆ + zkˆ
2 La Figua 4 pesenta ese vecto de posición paa el punto P:(x, cualquiea. La función Vecto de Posición puede deivase y difeenciase. La difeencial de esa función es dada según el Cálculo Vectoial po: d = dx iˆ + dy ˆj + dz kˆ y su intepetación es la de un desplazamiento infinitesimal hacia cualquie diección a pati del punto P: (x,z,), la Figua 5 muesta a ese vecto.
3 El Opeado Nabla o Del, dado po = iˆ Escalaes. + x ˆj + kˆ, se puede aplica a Campos Vectoiales o Cuando se aplica a Campos Escalaes se obtiene la función GRADIENTE DE LA FUNCION ESCALAR. Si se tiene el Campo Escala ϕ ( x,, al aplicale el opeado Nabla, se obtiene la función Gadiente de φ, dada po: ϕ = iˆ + ˆj + kˆ La aplicación del Opeado Nabla nos inteesa cuando se efectúa sobe Campos Vectoiales. La aplicación es a tavés de las opeaciones poducto escala y poducto vectoial. La aplicación po medio del poducto escala da como esultado la Función Divegencia. La aplicación po medio del poducto vectoial da como esultado la Función Rotacional. Si la Función que da el Campo Vectoial es (x,, entonces la Divegencia esulta de la Opeación: F F F = cuando la Función 1 ( x, + F F (x, cumple: ( x, + F 3 ( x, F(x, = F ( x, iˆ F ( x, ˆ 1 + j + F3 ( x, kˆ F (x, donde las funciones F 1, F, F 3, son las Funciones Escalaes Componentes de la Función. En los países Euopeos, en luga del símbolo div ( F ). utilizan el símbolo F
4 Del mismo modo, si la Función que da el Campo Vectoial es (x,, entonces la Rotacional esulta de la Opeación: F F = iˆ F ˆj kˆ 1 F F3 En los países Euopeos, se usa la notación: También se utiliza: -ot ( F (x, ), paa epesenta -cul( F (x, ). F. INTERPRETACION FISICA DEL GRADIENTE. UN PRODUCTO MUY INTERESANTE! La clave de la intepetación Física del Gadiente se encuenta en el poducto: d φ en donde φ es un Campo Escala. Al ealiza ese poducto encontamos: d φ = ( dxiˆ + dy ˆj + dz kˆ) ( iˆ + ˆj + kˆ) al desaolla el poducto escala tenemos: d φ = dx + dy + dz
5 Paa una función Escala de tes vaiables independientes y una dependiente como la función φ(x,, es bien conocido que su difeencial cumple: dφ = dx+ En consecuencia, se obtiene la siguiente elación: dy + d φ = d φ dz Esta última expesión seá de vital impotancia paa la intepetación Física del Gadiente que daemos más adelante. Hagamos antes un poco más de matemáticas! Una Función ψ (x, y), es una función escala de dos vaiables independientes y una dependiente. La gáfica de ella es una Supeficie en el espacio de tes dimensiones, algunos ejemplos son: Paa ψ (x, y) = x + y tenemos: Que es la gáfica paa un dominio ectangula de 0 unidades po lado. Esta figua fue ceada con el paquete DERIVE paa Windows 95, así como todas las siguientes.
6 Paa ψ (x, y) = sin(x) sin(y) la Figua 7 da la gáfica. El dominio en este caso es un ectángulo de 10 unidades po lado. sin( Cuando Ψ ( x, y) = gáfica es dada en la figua 8: x x + y + y )
7 Las funciones del tipo anteio, φ (x, y ), tienen la popiedad siguiente: Al igualalas con una constante, se obtiene una ecuación de la foma: φ (x, y) = C que constituye una ECUACION IMPLICITA DE DOS VARIABLES. Este tipo de Ecuaciones pemite a pimea instancia despeja la vaiable y en téminos de la vaiable x, oiginando una función de la foma y = f (x) La cual constituye la ecuación de la gáfica de la función f (x), la Geometía Analítica nos pemite ecoda que la Gáfica espectiva, es el luga geomético de una cuva en el plano catesiano. Es evidente que pa (x, y) = C bien deteminada. a cada valo elegido de la constante C, la ecuación φ, genea una cuva Esa cuva se denomina cuva de nivel de la función φ (x, y) paa el valo C. Esta denominación está fundada en el hecho (muy impotante), q (x, y) existentes en la cuva de nivel. Consideamos pudente ejemplifica este hecho con funciones concetas: Sea φ ( x, y) = x + y ue la función φ (x, y) toma el mismo valo C paa todos los puntos A esta función la podemos iguala con una constante C positiva paa que tenga sentido la búsqueda de la gáfica, en especial podemos pensa que esa constante es el cuadado de un númeo k φ( x, y) = x + y = k Esa ecuación se conviete en la ecuación de una cicunfeencia centada en el oigen y de adio k. Gafiquemos las ecuaciones esultantes cuando k toma los valoes enteos 1,, 3 y 4, es deci busquemos las cuvas de nivel de las siguientes ecuaciones: φ(x, y) = x + y = 1 φ(x, y) = x + y = φ(x, y) = x + y = 3 φ(x, y) = x + y = 4
8 Las cuvas de nivel obtenidas, paa esos valoes se epesentan gáficamente en la Figua 9: En la siguiente figua se ha desaollado la gáfica de la función φ ( x, y) dento del dominio del plano catesiano compendido po el cículo de adio =3. Al mismo tiempo se dan 3 cuvas de nivel coespondientes a los valoes de la constante k = 1,, y 3. Esa Figua se geneó con ayuda del paquete de CAD Cadwin Statégies. Paa hacelo, se tazó la paábola geneatiz de la Gáfica supeficie de gáfica. Las cuvas de nivel, se poyectaon sobe la paa todos los puntos de la cuva de nivel. de φ ( x, y) en el plano ZX, enseguida po otación alededo del eje Z se geneó la gáfica, utilizando la popiedad que ellas tienen la misma imagen Paa el caso de la cuva caacteizada po k=1, se usó la elevación de poyección z=1, paa la cuva con k=, se usó la elevación z=4, y finalmente paa k=3, se usó z=9. Esta altua de elevación se eligió, poque po ejemplo, paa k=1, la cuva de nivel contiene al punto (1,0), el cual tiene la imagen φ (1,0) = =1 + 0 =1 y como to misma imagen, entonces la elevación aconsejada es pecisamente z=1. dos los puntos de esa cuva tienen la Evidentemente, paa k=, la cuva de nivel pasa po el punto (,0) cuya imagen es φ (,0)= + 0 = 4, povocando una altua de elevación de z=4. Mientas que paa k=3, uno de los puntos de la cuva es (3,0) cuya imagen es φ (3,0) = 9, dimensiones (el plano Catesiano). siendo ésta la elevación elegida. Este poceso, nos pemite demosta que las cuvas de nivel, constituyen ota foma de caacteiza las funciones φ ( x, y ), sin necesida d de ecui a la gáfica en 3 dimensiones, haciéndolo en el espacio de
9 Las Cuvas de Nivel pemiten epesenta de una manea muy conveniente, las funciones φ ( x, y) po medio de una familia de cuvas del Plano Catesiano. Ellas epesentan zonas en las que la función φ ( x, y) toma valoes constantes, y donde además, todos los puntos de una misma cuva de nivel, tienen la misma imagen, es deci tienen asociado el mismo escala. REPRESENTACION DE CAMPOS ESCALARES En el caso de las funciones de tes vaiables independientes univaluadas, que hemos llamado Campos Escalaes, y son funciones de la foma φ (x, z ), apaece un poble espacio de 4 dimensiones, no pudiendo epesentase esquemáticamente. Este poblema de epesentación, se puede ebasa po medio de un atificio: G ma inteesante, su gáfica está en el enealiza lo que sucede con las funciones φ (x, y) de dos vaiables independientes univaluadas. En efecto, las cuvas de nivel constituyen una epesentación en el espacio de dos dimensiones de una función cuya gáfica es un subconjunto del Espacio Tidimensional.
10 El atificio consiste en lo siguiente: Pimeo, la gáfica de una función φ (x, es una hipesupeficie subconjunto del espacio tetadimensional R 4, no se puede dibuja poque simplemente, no podemos epesenta 4 ejes pependiculaes ente sí. Segundo, si genealizamos el concepto de Cuvas de Nivel en el Plano Catesiano, debemos tene las Hipecuvas de Nivel de la fun 3 supeficies en el espacio R. ción φ (x, en el espacio de Tes dimensiones, que no son ota cosa que Podía pensase que la genealización de una cuva en el Plano Catesiano seía ota cuva peo en el espacio de tes dimensiones, sin embago, una cuva en el espacio es epesentada po un conjunto de tes ecuaciones paaméticas x y z = x ( t) = y ( t) = z( t), las cuales son la genealización lógica, del conjunto de ecuaciones paaméticas, que epesentan un cuva en el plano, ellas tienen la foma: x = x ( t) y = y( t) Las funciones φ (x, tienen asociadas paa su epesentación, SUPERFICIES DE NIVEL, las cuale se obtienen al iguala con una constante la función φ (x,, es deci, se obtienen de las ecuaciones:. s φ (x, = C donde C puede toma valoes dento del intevalo ] + [ del conjunto de los númeos eales R.,, es deci, toma valoes cualesq Po ello, el númeo de Supeficies de Nivel es infinito. uiea dento Se asevea que las Supeficies de Nivel son en ealidad, supeficies del espacio tidimensional, poque a pati de la ecuación φ (x, = C, podemos despe ja la vaiable z, ya que esa ecuación es en ealidad una Función Implícita de tes vaiables del tipo F ( x, = 0, y de la teoía de funciones implícitas, se sabe que al tene una de esas funciones, es posible despeja una de esas vaiables en téminos de las otas dos. Es deci, se pueden obtene las ecuaciones: x = x( y, y = y( x, z = z( x, y) Nuesto inteés va diigido hacia la última ecuación, z = z(x, y), que es la ecuación de la gáfica de una función f (x, y), donde z = f (x, y), y esulta como vimos ya antes, una supeficie en el espacio de tes dimensiones. Po simple genealización, todos los puntos de una supeficie de nivel tienen el mismo valo de imagen, y ese valo es pecisamente la constante C a la qu e se iguala φ (x, paa obtene la ecuación:
11 que es la ecuación de la supeficie de nivel. φ (x, = C Así, un Campo Escala φ (x,, puede epesentase po una familia de Supeficies de Nivel, cuya ecuación geneal toma la foma: Demos un ejemplo paa conceta estas popiedades: φ (x, = C y la cual, sobe todos los puntos de cada supeficie de nivel, la función φ (x, tiene el mismo valo. Sea φ (x, = x + y + z mostemos que foma tienen sus Supeficies de Nivel: Igualemos φ (x, = x + y + z co que el despeje nos daía z n una constante C. Obligatoiamente ella debe se positiva, ya = C x y, y cuando C es negativa, se tata de busca la aíz de un númeo negativo eal, el cual no existe. En consecuencia, sólo son pemisibles los valoes positivos de la constante C, de ahí que podemos supone que esa constante es el esultado de eleva al cuadado una constante k, es deci se pemite el despeje:
12 z = k x y En la Figua 31 se muestan las Supeficies de Nivel paa los valoes de k = 10, 0, 30 y 40, cuando k es la constante que cumple: φ ( x, = x + y + z = k donde se ha substituido po la constante C, la constante k. Desde luego, las ecuaciones φ ( x, = x + y + z = k coesponden a esfeas tidimensionales centadas en el oigen del sistema coodenado con adio k. Nota: Las flechas amaillas indican los adios de las geneatices que oiginaon las supeficies de nivel en el paquete Cadwin Statégies. INTERPRETACION DE L A FUNCION GRADIENTE Pasaemos ahoa a analiza la Función Gadiente de un Campo Escala: φ ( x, = iˆ + ˆj + kˆ p obtenemos: aa ello, patiendo de un punto P: (x 0, y 0, z 0 ), y si en ese punto evaluamos la función gadiente, x0, y φ ( x0, y0, z 0 ) = ( 0, z 0 ) 0, y0, z0 ) ( x0, y0, z 0 ( x iˆ + esa función evidentemente le asocia al punto P: (x 0, y 0, z 0 ), un vecto, de ese vecto no atibutos pincipales, a sabe, magnitud, diección y sentido. Paa ayudanos a enconta esos atibutos, es necesaio utiliza la expesión fundamental: d φ = d φ ˆj + ) kˆ s inteesaán sus donde d φ es el cambio sufido po la imagen del punto (x,, bajo la función φ (x,, cuando n os desplazamos del punto de la siguiente difeencia: ( x, y, ( x + dx, y + dy, z + d, hacia el punto φ ( x + dx, y + d z + d ϕ ( x,, es deci es el valo
13 la cual se identifica con d φ. Como ya hemos analizado, φ (x, es tal que, sobe una supeficie de nivel, φ tiene al mismo valo paa todos los puntos de ella. Así, si nos desplazamos sobe una de las supeficies de nivel, tenemos: ϕ ( x + dx, y + d z + d ϕ ( x, = 0 poque el punto inicial ( x, y, y el punto final ( x + dx, y + dy, z + d tienen ambos, la misma imagen. El vecto de desplazamiento que va del punto vecto: En consecuencia, como d ( x, y, ( x + dx, y + dy, z + d al punto = dx iˆ + dy ˆj + dz kˆ d φ = d φ, es el, entonces paa un desplazamiento sobe la supeficie de una d φ es nula, implicando a su vez que el poducto d φ Su peficie de Nivel, se cumple que sea igual a ceo, es deci: d como d φ = 0 φ no son vectoes nulos, como se ve en la Figua 3, entonces, el hecho Po oto lado, tanto que su poducto escala sea ceo, significa que ellos son pependiculaes.
14 Además como el desplazamiento es sobe la supeficie, plano tangente a la Supeficie de Nivel en el punto (x,. Y como d escogidos, entonces ϕ ϕ d es paalelo a la supeficie, po ello está sobe un ϕ es pependicula a los vectoes, es obligatoiamente pependicula al plano tangente a la Supeficie de Nivel, esto significa que es pependicula a la Supeficie de Nivel en el Punto (x,. Esto da un significado de gan inteés paa el Gadiente de una función: El Gadiente de una Función da un Vecto Nomal a la supeficie de Nivel, en el punto exacto donde se da el valo de esa función gadiente. Es deci, si en el punto P de Coodenadas (x 0, y 0, z 0 ), se calcula el gadiente ϕ de la función ϕ, el Vecto esultante es un Vecto Nomal a la Supeficie de Nivel que pasa po el punto P: (x 0, y 0, z 0 ), y la cual petenece a la familia de supeficies que epesenta a la función φ (x,. En la Figua 33 se muestan los vectoes Siempe este vecto es pependicula a la supeficie. ϕ paa difeentes puntos sobe una Supeficie de Nivel. Figua 33
15
r u,v ( ) = x u,v ( )î + y u,v ( ) ĵ + z u,v ( ) ˆk
 Supeficies Se ha visto que una cuva en el espacio se puede epesenta po una ecuación paamética del tipo: t = x t î + y t ĵ + z t ˆk En donde inteviene un solo paámeto t. La epesentación paamética de cuvas
Supeficies Se ha visto que una cuva en el espacio se puede epesenta po una ecuación paamética del tipo: t = x t î + y t ĵ + z t ˆk En donde inteviene un solo paámeto t. La epesentación paamética de cuvas
Las imágenes de la presentación han sido obtenidas del libro:
 Las imágenes de la pesentación han sido obtenidas del libo: Physics fo Scientists and Enginees Paul A. Tiple Gene Mosca Copyight 2004 by W. H. Feeman & Company Supongamos una función f = f ( x, y, z) Con
Las imágenes de la pesentación han sido obtenidas del libo: Physics fo Scientists and Enginees Paul A. Tiple Gene Mosca Copyight 2004 by W. H. Feeman & Company Supongamos una función f = f ( x, y, z) Con
Apunte FII-1-RM: Repaso de Matemática
 Física II Física B - Electomagnetismo Pofesoa: Da. C. Caletti : Repaso de Matemática I. Gadiente A fin de compende mejo el concepto de gadiente comenzaemos po las bases, analizando, peviamente, qué tipo
Física II Física B - Electomagnetismo Pofesoa: Da. C. Caletti : Repaso de Matemática I. Gadiente A fin de compende mejo el concepto de gadiente comenzaemos po las bases, analizando, peviamente, qué tipo
LEY DE GAUSS. Este enunciado constituye en realidad una de las principales leyes del Electromagnetismo.
 LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO
 FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO Los campos magnéticos pueden genease po imanes pemanentes, imanes inducidos y po coientes elécticas. Ahoa inteesaá enconta la fueza sobe una
FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO Los campos magnéticos pueden genease po imanes pemanentes, imanes inducidos y po coientes elécticas. Ahoa inteesaá enconta la fueza sobe una
Fig. 1 Esquema para el cálculo de B
 P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
VECTORES EN DIFERENTES SISTEMAS DE COORDENADAS. TRANSFORMACIONES ENTRE SISTEMAS
 VECTRES EN DIFERENTES SISTEMAS DE CRDENADAS. TRANSFRMACINES ENTRE SISTEMAS Sistema ectangula Se explica especto de tes ejes pependiculaes ente sí (,,) que se cotan fomando un tiedo y sobe los que están
VECTRES EN DIFERENTES SISTEMAS DE CRDENADAS. TRANSFRMACINES ENTRE SISTEMAS Sistema ectangula Se explica especto de tes ejes pependiculaes ente sí (,,) que se cotan fomando un tiedo y sobe los que están
Diferencia de potencial y potencial eléctricos. En el campo gravitatorio.
 Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
El potencial en un punto de un campo de fuerzas eléctrico es la energía potencial que poseería la unidad de carga situada en dicho punto:
 Campo eléctico Hemos visto hasta ahoa un tipo de inteacción, la gavitatoia, siendo siempe una fueza atactiva. En la mateia, además de esta, nos encontamos con: inteacción eléctica, inteacción débil,...
Campo eléctico Hemos visto hasta ahoa un tipo de inteacción, la gavitatoia, siendo siempe una fueza atactiva. En la mateia, además de esta, nos encontamos con: inteacción eléctica, inteacción débil,...
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CAMPOS ELECTROMAGNÉTICOS
 CAMPOS ELECTROMAGNÉTICOS GRADO EN INGENIERÍA AEROESPACIAL EN AERONAVEGACIÓN UNIVERSIDAD RE JUAN CARLOS «ANÁLISIS VECTORIAL» CURSO ACADÉMICO 15/16 Índice 1. Escalaes vectoes 2 1.1. Nociones básicas de análisis
CAMPOS ELECTROMAGNÉTICOS GRADO EN INGENIERÍA AEROESPACIAL EN AERONAVEGACIÓN UNIVERSIDAD RE JUAN CARLOS «ANÁLISIS VECTORIAL» CURSO ACADÉMICO 15/16 Índice 1. Escalaes vectoes 2 1.1. Nociones básicas de análisis
0.2.4 Producto de un escalar por un vector. Vector unitario. 0.3 Vectores en el sistema de coordenadas cartesianas.
 VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
GEOMETRÍA. 1. Sin resolver el sistema, determina si la recta 2x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia
 Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO Geometría lineal Recta y Plano
 LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
TEMA10. VECTORES EN EL ESPACIO.
 TEMA0. VECTORES EN EL ESPACIO..- Coodenadas en el espacio: En el espacio tidimensional, un punto P iene deteminado po tes coodenadas P(x, y, z) que epesentan las distancias diigidas desde los planos de
TEMA0. VECTORES EN EL ESPACIO..- Coodenadas en el espacio: En el espacio tidimensional, un punto P iene deteminado po tes coodenadas P(x, y, z) que epesentan las distancias diigidas desde los planos de
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS
 TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
CUERPOS REDONDOS. LA ESFERA TERRESTRE
 IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
Apuntes de Electrostática Prof. J. Martín ETSEIT ELECTROESTÁTICA I CAMPO ELECTRICO EN EL ESPACIO LIBRE
 LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
Teoremas Integrales. V(x j ) ds
 Semana 2 - Clase 5 24/03/09 Tema : Algeba ectoial Teoemas Integales. Teoema de la Divegencia o de Gauss Sea = x j ) un campo vectoial definido sobe un volumen cuya fontea es la supeficie y ˆn el vecto
Semana 2 - Clase 5 24/03/09 Tema : Algeba ectoial Teoemas Integales. Teoema de la Divegencia o de Gauss Sea = x j ) un campo vectoial definido sobe un volumen cuya fontea es la supeficie y ˆn el vecto
2.5 Vectores cartesianos
 .5 VECTORES CRTESINOS 43.5 Vectoes catesianos Las opeaciones del álgeba vectoial, cuando se aplican a la esolución de poblemas en tes dimensiones, se simplifican consideablemente si pimeo se epesentan
.5 VECTORES CRTESINOS 43.5 Vectoes catesianos Las opeaciones del álgeba vectoial, cuando se aplican a la esolución de poblemas en tes dimensiones, se simplifican consideablemente si pimeo se epesentan
200. Hallar la ecuación de la simetría ortogonal respecto de la recta:
 Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Problemas de la Unidad 1
 Poblemas de la Unidad.- Dado el vecto a = i + 5 j - k, calcula: a) Sus componentes catesianas, b) Módulo de las componentes catesianas, c) Módulo del vecto a, d) Los cosenos diectoes, e) Ángulo que foma
Poblemas de la Unidad.- Dado el vecto a = i + 5 j - k, calcula: a) Sus componentes catesianas, b) Módulo de las componentes catesianas, c) Módulo del vecto a, d) Los cosenos diectoes, e) Ángulo que foma
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
LECCIÓN 5: CINEMÁTICA DEL PUNTO
 LECCIÓN 5: CINEMÁTICA DEL PUNTO 5.1.Punto mateial. 5.. Vecto de posición. Tayectoia. 5.3. Vecto velocidad. 5.4. Vecto aceleación. 5.5. Algunos tipos de movimientos. 5.1. PUNTO MATERIAL. Un punto mateial
LECCIÓN 5: CINEMÁTICA DEL PUNTO 5.1.Punto mateial. 5.. Vecto de posición. Tayectoia. 5.3. Vecto velocidad. 5.4. Vecto aceleación. 5.5. Algunos tipos de movimientos. 5.1. PUNTO MATERIAL. Un punto mateial
ˆk, donde f 1. son funciones escalares, entonces su producto cruz o vectorial del operador con la función es: y f 2
 Rotacional de una función vectoial Si una función vectoial es f = f 1 î + f 2 ĵ + f 3 ˆk, donde f 1, f 2, f 3 son funciones escalaes, entonces su poducto cuz o vectoial del opeado con la función es: f
Rotacional de una función vectoial Si una función vectoial es f = f 1 î + f 2 ĵ + f 3 ˆk, donde f 1, f 2, f 3 son funciones escalaes, entonces su poducto cuz o vectoial del opeado con la función es: f
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA
 LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
Derivando dos veces respecto del tiempo obtenemos la aceleración del cuerpo:
 MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
CAPITULO 3 MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES
 CAPÍTULO : METODO DE RESOLUCIÓN MEDIANTE INTEGRALES CAPITULO MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES. Resumen En este capítulo se encuenta solución analítica mediante el método de sepaación de vaiables
CAPÍTULO : METODO DE RESOLUCIÓN MEDIANTE INTEGRALES CAPITULO MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES. Resumen En este capítulo se encuenta solución analítica mediante el método de sepaación de vaiables
Vectores Presentanción basada en el material contenido en: Serway, R. Physics for Scientists and Engineers. Saunders College Pub. 3rd edition.
 Vectoes Pesentanción basada en el mateial contenido en: Seway, R. Physics fo Scientists and Enginees. Saundes College Pub. 3d edition. Sistemas de Coodenadas Se usan paa descibi la posición de un punto
Vectoes Pesentanción basada en el mateial contenido en: Seway, R. Physics fo Scientists and Enginees. Saundes College Pub. 3d edition. Sistemas de Coodenadas Se usan paa descibi la posición de un punto
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
1. MECÁNICA GENERAL 1.3. CINEMÁTICA DEL SÓLIDO RÍGIDO
 Fundamentos y Teoías Físicas ETS Aquitectua 1. MECÁNICA GENERAL 1.3. CINEMÁTICA DEL SÓLIDO RÍGIDO Se define sólido ígido como un sistema de puntos mateiales cuyas distancias son inaiables. Cuando un cuepo
Fundamentos y Teoías Físicas ETS Aquitectua 1. MECÁNICA GENERAL 1.3. CINEMÁTICA DEL SÓLIDO RÍGIDO Se define sólido ígido como un sistema de puntos mateiales cuyas distancias son inaiables. Cuando un cuepo
5. ROTACION; CINEMATICA Y DINAMICA
 73 5. OTACION; CINEMATICA Y DINAMICA Los movimientos cuvilíneos se dan en el plano o en el espacio, son, po tanto, movimientos bi o incluso tidimensionales. Ello hace que paa expesa la posición sea necesaio
73 5. OTACION; CINEMATICA Y DINAMICA Los movimientos cuvilíneos se dan en el plano o en el espacio, son, po tanto, movimientos bi o incluso tidimensionales. Ello hace que paa expesa la posición sea necesaio
Leyes de Kepler. Antes de demostrar las tres leyes de Kepler, haré un análisis matemático de lo que es una elipse.
 Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
MATEMÁTICAS 2º Bach Tema 5: Vectores José Ramón BLOQUE 2: GEOMETRÍA DEL ESPCACIO. Tema 5: Vectores
 MATEMÁTICAS º Bach Tema 5: Vectoes José Ramón BLOQUE : GEOMETRÍA DEL ESPCACIO Tema 5: Vectoes MATEMÁTICAS º Bach Tema 5: Vectoes José Ramón Definición de vecto Un sistema de ejes tidimensional se constuye
MATEMÁTICAS º Bach Tema 5: Vectoes José Ramón BLOQUE : GEOMETRÍA DEL ESPCACIO Tema 5: Vectoes MATEMÁTICAS º Bach Tema 5: Vectoes José Ramón Definición de vecto Un sistema de ejes tidimensional se constuye
Existe la costumbre de dividir el estudio de la Mecánica en tres partes:
 U I.- T : Cinemática del Punto Mateial 3 1.- LA MECÁNICA Y SUS PARTES Existe la costumbe de dividi el estudio de la Mecánica en tes pates: + Cinemática: es una descipción geomética del movimiento + Dinámica:
U I.- T : Cinemática del Punto Mateial 3 1.- LA MECÁNICA Y SUS PARTES Existe la costumbe de dividi el estudio de la Mecánica en tes pates: + Cinemática: es una descipción geomética del movimiento + Dinámica:
RELACION DE ORDEN: PRINCIPALES TEOREMAS
 RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
SERIE # 3 CÁLCULO VECTORIAL
 SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 7 POTENCIAL ELECTROSTÁTICO
 EL POTENCIAL ELÉCTRICO. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA II Pofeso: José Fenando Pinto Paa UNIDAD 7 POTENCIAL ELECTROSTÁTICO Dos cagas en la misma posición tienen dos veces más enegía
EL POTENCIAL ELÉCTRICO. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA II Pofeso: José Fenando Pinto Paa UNIDAD 7 POTENCIAL ELECTROSTÁTICO Dos cagas en la misma posición tienen dos veces más enegía
Profesor BRUNO MAGALHAES
 POTENCIL ELÉCTRICO Pofeso RUNO MGLHES II.3 POTENCIL ELÉCTRICO Utilizando los conceptos de enegía impatidos en Física I, pudimos evalua divesos poblemas mecánicos no solo a tavés de las fuezas (vectoes),
POTENCIL ELÉCTRICO Pofeso RUNO MGLHES II.3 POTENCIL ELÉCTRICO Utilizando los conceptos de enegía impatidos en Física I, pudimos evalua divesos poblemas mecánicos no solo a tavés de las fuezas (vectoes),
INSTITUTO DE FÍSICA MECÁNICA NEWTONIANA
 INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
Junio 2010 OPCIÓN A. A vemos que se diferencian en el cuadrado de la matriz unitaria. Dado que en este caso. por ser la matriz nula.
 Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
3 y un vector director Supongamos también que P x, y,
 . Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
. Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
Tema 1: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 4/7 Flujo, divergencia y teorema de Gauss
 Tema 1: Fundamentos Matemáticos 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Flujo, divegencia y teoema de Gauss Concepto
Tema 1: Fundamentos Matemáticos 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Flujo, divegencia y teoema de Gauss Concepto
Solución al examen de Física
 Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Orbital atómico Ψ 4f (Ψ/r) radio/ bohr. Fig.
 ORBITALES ATÓMICOS HIDROGENOIDES tipo f ( pimea pate) Po lo geneal en el bachilleato, los pofesoes dejan al magen de sus explicaciones los obitales f. Desciben los d, estudian los poblemas que enciean,
ORBITALES ATÓMICOS HIDROGENOIDES tipo f ( pimea pate) Po lo geneal en el bachilleato, los pofesoes dejan al magen de sus explicaciones los obitales f. Desciben los d, estudian los poblemas que enciean,
Flujo eléctrico. Michael Faraday, septiembre de íd. 25 de agosto de 1867) fue un físico y químico inglés)
 Flujo eléctico Michael Faaday, (Londes, 22 de septiembe de 1791 - íd. 25 de agosto de 1867) fue un físico y químico inglés) Flujo eléctico (Φ) 2 N m φ E da A C Flujo eléctico (Φ) Cuál es el flujo eléctico
Flujo eléctico Michael Faaday, (Londes, 22 de septiembe de 1791 - íd. 25 de agosto de 1867) fue un físico y químico inglés) Flujo eléctico (Φ) 2 N m φ E da A C Flujo eléctico (Φ) Cuál es el flujo eléctico
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Circuitos de Corriente Continua
 Fundamentos Físicos y Tecnológicos de la Infomática Cicuitos de Coiente Continua -Caga eléctica. Ley de Coulomb. Campo eléctico. -Potencial eléctico. Conductoes en euilibio electostático. Agustín Álvaez
Fundamentos Físicos y Tecnológicos de la Infomática Cicuitos de Coiente Continua -Caga eléctica. Ley de Coulomb. Campo eléctico. -Potencial eléctico. Conductoes en euilibio electostático. Agustín Álvaez
Cátedra de Física 1. Autor: Ing. Ricardo Minniti. Sábado 10 de Febrero de 2007 Página 1 de 14. Índice
 Cáteda de Física Índice Figua - Enunciado Solución Ecuación - Momento de inecia definición Figua - Sistema de estudio 3 Ecuación - Descomposición del momento de inecia3 Figua 3 - Cálculo del momento de
Cáteda de Física Índice Figua - Enunciado Solución Ecuación - Momento de inecia definición Figua - Sistema de estudio 3 Ecuación - Descomposición del momento de inecia3 Figua 3 - Cálculo del momento de
Tema 7 Geometría en el espacio Matemáticas II 2º Bachillerato 1
 Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
SUPERPOSICIÓN DE M. A.S.
 SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
CAPÍTULO II LEY DE GAUSS
 Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
Trabajo, Energía, Potencial y Campo Eléctrico
 Cáteda de Física Expeimental II Física III Tabajo, Enegía, Potencial y Campo Eléctico Pof. D. Victo H. Rios 2010 Contenidos - El concepto físico de tabajo. - Enegía potencial eléctica. - Enegía paa la
Cáteda de Física Expeimental II Física III Tabajo, Enegía, Potencial y Campo Eléctico Pof. D. Victo H. Rios 2010 Contenidos - El concepto físico de tabajo. - Enegía potencial eléctica. - Enegía paa la
Tema 1: Análisis vectorial
 Tema 1: Análisis vectoial Campos Electomagnéticos º Cuso Ingenieía Industial Dpto.Física Aplicada III Cuso 010/011 Dpto. Física Aplicada III - Univ. de Sevilla Joaquín Benal Ménde 1 Tema 1: Índice (I)
Tema 1: Análisis vectoial Campos Electomagnéticos º Cuso Ingenieía Industial Dpto.Física Aplicada III Cuso 010/011 Dpto. Física Aplicada III - Univ. de Sevilla Joaquín Benal Ménde 1 Tema 1: Índice (I)
Facultad de C. E. F. y N. Departamento de FÍSICA Cátedra de FÍSICA II SOLENOIDE
 U N IV ESID A D NACIONA de CÓ DO BA Facultad de C. E. F. y N. Depatamento de FÍSICA Cáteda de FÍSICA II caeas: todas las ingenieías auto: Ing. ubén A. OCCHIETTI Capítulo VI: Campo Magnético: SOENOIDE El
U N IV ESID A D NACIONA de CÓ DO BA Facultad de C. E. F. y N. Depatamento de FÍSICA Cáteda de FÍSICA II caeas: todas las ingenieías auto: Ing. ubén A. OCCHIETTI Capítulo VI: Campo Magnético: SOENOIDE El
Lección 2. El campo de las cargas en reposo: campo electrostático.
 Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
GUIA Hallar el módulo del vector de origen en (20,-5,8) y extremo en (-4,-3,2).
 GUIA 0 1 - Halla el módulo del vecto de oigen en (20,-5,8) etemo en (-4,-3,2). 2 - a) Halla las componentes catesianas de los siguientes vectoes: (i) A (ii) A = 4 A = θ = 30º 4 θ =135º A (iii) (iv) A θ
GUIA 0 1 - Halla el módulo del vecto de oigen en (20,-5,8) etemo en (-4,-3,2). 2 - a) Halla las componentes catesianas de los siguientes vectoes: (i) A (ii) A = 4 A = θ = 30º 4 θ =135º A (iii) (iv) A θ
IV. Geometría plana. v v2 2. u v = u v cos α
 Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
TEMA 3. CAMPO MAGNÉTICO.
 Física º Bachilleato TEMA 3. CAMPO MAGNÉTICO. 0. INTRODUCCIÓN. NATURALEZA DEL MAGNETISMO. Hasta ahoa en el cuso hemos estudiado dos tipos de inteacciones: gavitatoia y electostática. La pimea se manifestaba
Física º Bachilleato TEMA 3. CAMPO MAGNÉTICO. 0. INTRODUCCIÓN. NATURALEZA DEL MAGNETISMO. Hasta ahoa en el cuso hemos estudiado dos tipos de inteacciones: gavitatoia y electostática. La pimea se manifestaba
CAMPO ELÉCTRICO Y POTENCIAL
 CMPO ELÉCTRICO Y POTENCIL INTERCCIONES ELECTROSTÁTICS (CRGS EN REPOSO) Caga eléctica: popiedad intínseca de la mateia ue se manifiesta a tavés de fuezas de atacción o epulsión Ley de Coulomb: expesa la
CMPO ELÉCTRICO Y POTENCIL INTERCCIONES ELECTROSTÁTICS (CRGS EN REPOSO) Caga eléctica: popiedad intínseca de la mateia ue se manifiesta a tavés de fuezas de atacción o epulsión Ley de Coulomb: expesa la
Tema 7 Problemas métricos
 Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
CASTILLA Y LEÓN / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS II / EXAMEN COMPLETO PRUEBA A
 CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
z a3 Ecuaciones continuas de la recta: eliminando el parámetro de (2) = = u u u
 Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
MATEMÁTICAS I Grupos F, H
 MATEMÁTICAS I Gupos F, H 2--2 APELLIDOS: NOMBRE: En cada pegunta no sólo se valoaá la coección del pocedimiento y el esultado, sino también, en la misma medida, la coección en la expesión de los cálculos
MATEMÁTICAS I Gupos F, H 2--2 APELLIDOS: NOMBRE: En cada pegunta no sólo se valoaá la coección del pocedimiento y el esultado, sino también, en la misma medida, la coección en la expesión de los cálculos
GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO
 SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
Análisis de respuesta en frecuencia
 Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
ALGEBRA Y GEOMETRÍA I
 FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
CAMPOS ELECTROMAGNÉTICOS Tema 1. Cálculo Vectorial y Coordenadas Cartesianas, Cilíndricas y Esféricas
 ETS. Ingenieía de Telecomunicación Dpto. Teoía de la Señal Comunicaciones CAMPOS ELECTROMAGNÉTICOS Tema. Cálculo Vectoial Coodenadas Catesianas, Cilíndicas Esféicas P.- Dado un vecto A = + (a) su magnitud
ETS. Ingenieía de Telecomunicación Dpto. Teoía de la Señal Comunicaciones CAMPOS ELECTROMAGNÉTICOS Tema. Cálculo Vectoial Coodenadas Catesianas, Cilíndicas Esféicas P.- Dado un vecto A = + (a) su magnitud
Cálculo diferencial e integral en una variable. Examen Febrero de 2018
 Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
 FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES
 EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
( ) y ( ) = CAMPOS: OPERADOR NABLA ( ) ( )
 CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
87. Un cierto campo de fuerzas viene dado por la expresión F 4y
 Campos 5 81. El témino potencial, es elativamente modeno, dado que tampoco existía el de enegía potencial, que Helmholtz, denominaba tensión. Fue Rankine el que en 1842 (algunos histoiadoes de la ciencia,
Campos 5 81. El témino potencial, es elativamente modeno, dado que tampoco existía el de enegía potencial, que Helmholtz, denominaba tensión. Fue Rankine el que en 1842 (algunos histoiadoes de la ciencia,
Trabajo y Energía I. r r = [Joule]
![Trabajo y Energía I. r r = [Joule] Trabajo y Energía I. r r = [Joule]](/thumbs/62/47291103.jpg) C U R S O: FÍSICA MENCIÓN MATERIAL: FM-11 Tabajo y Enegía I La enegía desempeña un papel muy impotante en el mundo actual, po lo cual se justifica que la conozcamos mejo. Iniciamos nuesto estudio pesentando
C U R S O: FÍSICA MENCIÓN MATERIAL: FM-11 Tabajo y Enegía I La enegía desempeña un papel muy impotante en el mundo actual, po lo cual se justifica que la conozcamos mejo. Iniciamos nuesto estudio pesentando
L Momento angular de una partícula de masa m
 Campo gavitatoio Momento de un vecto con especto a un punto: M El momento del vecto con especto al punto O se define como el poducto vectoial M = O Es un vecto pependicula al plano fomado po los vectoes
Campo gavitatoio Momento de un vecto con especto a un punto: M El momento del vecto con especto al punto O se define como el poducto vectoial M = O Es un vecto pependicula al plano fomado po los vectoes
Situaciones 1: Dada una carga eléctrica puntual, determine el campo eléctrico en algún punto dado. r u r. r 2. Esmelkys Bonilla
 Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
. Estos vectores unitarios apuntan siempre en la misma dirección y en el mismo sentido, y no cambian, por tanto, de un punto a otro del espacio.
 CAPÍTUL 7.01 ÁLGEBRA VECTRIAL Sistemas de coodenadas Un sistema de coodenadas es un conjunto de valoes numéicos que deteminan unívocamente la posición de un punto en el espacio euclidiano. Las coodenadas
CAPÍTUL 7.01 ÁLGEBRA VECTRIAL Sistemas de coodenadas Un sistema de coodenadas es un conjunto de valoes numéicos que deteminan unívocamente la posición de un punto en el espacio euclidiano. Las coodenadas
Adenda Electrones en potencial periódico
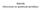 Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
Instituto de Ayuda Politécnica
 Instituto de yuda Politécnica Quisquís 100 ente venida del Ejécito y Gacía Moeno (0) 8705 1.5.. Poducto ente vectoes. Hay fenómenos en la natualeza que se explican de una manea muy concisa con el poducto
Instituto de yuda Politécnica Quisquís 100 ente venida del Ejécito y Gacía Moeno (0) 8705 1.5.. Poducto ente vectoes. Hay fenómenos en la natualeza que se explican de una manea muy concisa con el poducto
Movimientos rectilíneos o de trayectoria recta. Movimientos curvilíneos o de trayectoria curva (circular, elíptica, parabólica, etc.).
 1.- Clasificación de movimientos. 1. Tomando como efeencia la tayectoia: Movimientos ectilíneos o de tayectoia ecta. Movimientos cuvilíneos o de tayectoia cuva (cicula, elíptica, paabólica, etc.). 2. Tomando
1.- Clasificación de movimientos. 1. Tomando como efeencia la tayectoia: Movimientos ectilíneos o de tayectoia ecta. Movimientos cuvilíneos o de tayectoia cuva (cicula, elíptica, paabólica, etc.). 2. Tomando
Campos 5. W C, por lo A. I, C dr A. , mientras que C I dr. , de lo que A. , Como que la única respuesta válida es la b
 Campos 5 81. El témino potencial, es elativamente modeno, dado que tampoco existía el de enegía potencial, que Helmholtz, denominaba tensión. Fue Rankine el que en 184 (algunos histoiadoes de la ciencia,
Campos 5 81. El témino potencial, es elativamente modeno, dado que tampoco existía el de enegía potencial, que Helmholtz, denominaba tensión. Fue Rankine el que en 184 (algunos histoiadoes de la ciencia,
Potencial Escalar - Integrales de superposición. 2010/2011
 Potencial Escala - Integales de supeposición. / Electostática Definición os conductoes en electostática. Campo de una caga puntual. Aplicaciones de la ey de Gauss Integales de supeposición. Potencial electostático
Potencial Escala - Integales de supeposición. / Electostática Definición os conductoes en electostática. Campo de una caga puntual. Aplicaciones de la ey de Gauss Integales de supeposición. Potencial electostático
Temas teóricos. Lino Spagnolo
 1 Temas teóicos Electomagnetismo Teoema de Helmholtz. Lino Spagnolo La teoía electomagnética de Maxwell, e incluso las modenas elaboaciones como la electodinámica cuántica y la como dinámica, utilizan
1 Temas teóicos Electomagnetismo Teoema de Helmholtz. Lino Spagnolo La teoía electomagnética de Maxwell, e incluso las modenas elaboaciones como la electodinámica cuántica y la como dinámica, utilizan
Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).
![Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ). Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).](/thumbs/76/73987868.jpg) Electomagnetismo I Semeste: 25-2 Pof. Alejando Reyes Coonado Ayud. Calos Albeto Maciel Escudeo Ayud. Chistian Espaza López Solución a la Taea 5 Solución po Calos Maciel Escudeo. Poblema: 2pts El potencial
Electomagnetismo I Semeste: 25-2 Pof. Alejando Reyes Coonado Ayud. Calos Albeto Maciel Escudeo Ayud. Chistian Espaza López Solución a la Taea 5 Solución po Calos Maciel Escudeo. Poblema: 2pts El potencial
Ejemplos 2. Cinemática de los Cuerpos Rígidos
 Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS
 INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
: TEORÍA DE CAMPOS ELECTROMAGNÉTICOS
 UNVERSDAD NACONAL DEL CALLAO FACULTAD DE NGENERÍA ELÉCTRCA Y ELECTRÓNCA ESCUELA PROFESONAL DE NGENERÍA ELÉCTRCA CURSO : TEORÍA DE CAMPOS ELECTROMAGNÉTCOS PROFESOR : ng. JORGE MONTAÑO PSFL PROLEMAS RESUELTOS
UNVERSDAD NACONAL DEL CALLAO FACULTAD DE NGENERÍA ELÉCTRCA Y ELECTRÓNCA ESCUELA PROFESONAL DE NGENERÍA ELÉCTRCA CURSO : TEORÍA DE CAMPOS ELECTROMAGNÉTCOS PROFESOR : ng. JORGE MONTAÑO PSFL PROLEMAS RESUELTOS
Introducción al cálculo vectorial
 GRADUADO EN INGENIERÍA Y CIENCIA AGRONÓMICA GRADUADO EN INGENIERIA ALIMENTARIA GRADUADO EN INGENIERÍA AGROAMBIENTAL Intoducción al cálculo vectoial Magnitudes escalaes y vectoiales Tipos de vectoes Opeaciones
GRADUADO EN INGENIERÍA Y CIENCIA AGRONÓMICA GRADUADO EN INGENIERIA ALIMENTARIA GRADUADO EN INGENIERÍA AGROAMBIENTAL Intoducción al cálculo vectoial Magnitudes escalaes y vectoiales Tipos de vectoes Opeaciones
Soluciones de la Tarea #6 de Física I
 Soluciones de la Taea #6 de Física I Tomás Rocha Rinza 4 de octube de 006 1. Puesto que la tayectoia del satélite alededo de la Tiea es cicula, entonces ocue en un plano. Si se considea a la Tiea fija
Soluciones de la Taea #6 de Física I Tomás Rocha Rinza 4 de octube de 006 1. Puesto que la tayectoia del satélite alededo de la Tiea es cicula, entonces ocue en un plano. Si se considea a la Tiea fija
