La ecuación de equilibrio dinámico del sistema de 1 grado de libertad dinámico (1 GLD) sin amortiguamiento indicado en la Figura 1 se expresa como:
|
|
|
- María Luisa Fuentes Montoya
- hace 6 años
- Vistas:
Transcripción
1 Respuesta a exctacones sísmcas La ecuacón de equlbro dnámco del sstema de grado de lbertad dnámco ( GLD) sn amortguamento ndcado en la Fgura se expresa como: () M y() t 0 K u t + = () M K u( t ) y( t) Fgura. Osclador smple sujeto a movmento de apoyo El térmno nulo de la derecha ndca que no exste una fuerza Pt () externa conocda aplcada drectamente sobre la masa. La fuerza elástca K u() t es sólo funcón del movmento relatvo entre los extremos del resorte es decr entre la masa y el apoyo. La aceleracón absoluta yt () es gual a la suma de la aceleracón relatva ut () y de la aceleracón del apoyo correspondente al ssmo u S () t que se consdera como un dato del problema. Con estas defncones la ecuacón de equlbro dnámco resulta: ( ) ( ) ( ) K u t + M u t = M u t () El segundo membro de esta expresón M u ( t) S S cumple el rol de una fuerza externa equvalente en las ecuacones de equlbro dnámco expresadas en funcón del desplazamento relatvo ut (). En otras palabras la solucón de la ecuacón () no dfere en nada de la determnacón de la respuesta ut () para una carga exteror conocda gual a S ( t) M u. Una partculardad de la ecuacón () es que para el nstante en que el desplazamento relatvo pasa por su valor máxmo u la fuerza que soporta el resorte K es máxma y dado que no hay otro térmno en la ecuacón tambén debe ser máxma la aceleracón absoluta de la masa yt () y alcanzar su valor y es decr que: K u = M y o sea y u (3) = ω donde ω es la frecuenca natural del sstema. Esta expresón tene una forma muy partcular ya que es smlar a la dervada segunda de una accón armónca de frecuenca ω de ampltud u. Debe destacarse que se trata de una concdenca formal ya que la respuesta sísmca ut () a una exctacón sísmca no armónca u () t no resulta en general armónca. S
2 De acuerdo con la defncón de Espectro de Respuesta Elástca ya vsto el valor del desplazamento relatvo máxmo u se denomna habtualmente Desplazamento Espectral S d. De esta manera resulta que la máxma aceleracón de la masa M puede obtenerse como el producto del desplazamento espectral S d por el cuadrado de la frecuenca natural ω. Nótese que en matera de exctacones sísmcas el hstograma de aceleracones u S () t puede consderarse con su sgno o con el sgno opuesto ya que se trata de un proceso de orgen aleatoro cuyo sgno podría ser ntercambable entre + y. En el análss de la respuesta sísmca en partcular cuando se trata de determnar el valor máxmo se consderará con el sgno ± en todos los casos. En el caso que el amortguamento no sea nulo como ocurre en la nmensa mayoría de estructuras cvles la expresón (3) no representa el valor exacto de la aceleracón máxma sno sólo una aproxmacón de ella ya que además de las fuerzas elástcas K u() t coexsten contemporáneamente las fuerzas de amortguamento f D. Para el caso de fuerzas vscosas lneales resulta: fd = Cut (). De esta forma la máxma aceleracón absoluta no está rgurosamente dada por la expresón (3) pero de todos modos ésta representa una muy buena aproxmacón de la máxma aceleracón absoluta y para estructuras cvles en que el amortguamento típco es del orden del 5% del crítco. El valor de y dado por la ec. (3) para el caso de amortguamento dferente de cero se conoce como Pseudo-aceleracón de la masa y representa una muy buena aproxmacón de la aceleracón máxma cuando el amortguamento es dstnto de cero. La pseudo-aceleracón se expresa habtualmente con la notacón S a que en todos los casos está dada por la expresón (gnorando el sgno): S a = ω Sd (4) De todos modos vale la pena destacar que a pesar que la pseudo-aceleracón S a es una aproxmacón de la máxma aceleracón absoluta la fuerza elástca máxma nducda por el ssmo es exactamente la dada por la expresón: K u = M S (5) a Por lo antes expuesto dado que el análss sísmco centra su nterés en los desplazamentos y esfuerzos máxmos los valores espectrales de desplazamento S d o de pseudo-aceleracón S a pueden utlzarse en forma ndstnta con las expresones anterores para evaluar los desplazamentos o esfuerzos máxmos nducdos por un ssmo utlzando expresones de formato estátco; es decr sn tener que nclur en forma explícta las fuerzas de nerca o de amortguamento propas de un problema dnámco. Cuando se utlzan los valores espectrales (S a y S d ) la dnámca del problema está tenda en cuenta en forma mplícta en la dependenca de S a y S d en funcón del período natural (o frecuenca) del sstema consderado. De todo lo expresado surge que el análss sísmco lneal de un sstema elástco puede ser realzado utlzando expresones que son de tpo estátco y que esta stuacón no consttuye una aproxmacón del problema sno que es una solucón exacta para el sstema de GLD. Para estructuras con múltples grados de lbertad dnámcos (MGLD) este tpo de enfoque del problema lleva naturalmente a certas aproxmacones dervadas del hecho que el análss es sólo exacto para un grado de lbertad dnámco ya que las máxmas respuestas dnámcas de los modos naturales desacoplados entre sí en el campo lneal no concden en el tempo y por lo tanto no pueden superponerse como s se tratara de exctacones estátcas.
3 Por lo antes comentado el Método Modal Espectral de análss sísmco que se presenta a contnuacón resulta ser una aproxmacón que permte el cálculo de los esfuerzos y desplazamentos máxmos nducdos por el ssmo que es aplcable para el dseño de estructuras cvles en una gran cantdad de casos de la ngenería práctca y que está ncorporado en los códgos o reglamentos de dseño de obras cvles bajo accones sísmcas. Las prncpales lmtacones del método están relaconadas con la forma en que las estructuras desarrollan comportamento nelástco o plástco durante la accón sísmca. Los reglamentos normalmente establecen condcones que deben cumplr el dseño de la estructura para que el método modal espectral tenga sufcente precsón y resulte aplcable para la verfcacón del dseño. Análss sísmco modal espectral El método modal espectral requere como dato de partda para su aplcacón conocer los modos y frecuencas naturales del sstema de múltples grados de lbertad es decr que se conocen los valores de las frecuencas ω y de los modos Φ. Las ecuacones de movmento de un sstema de N grados de lbertad dnámcos (N GLD) para la exctacón sísmca son: () () ( ) ( ) KUt + MUt + CUt = us t M B El vector de carga equvalente a la accón sísmca es el dado en el segundo membro de la ecuacón (6). Este vector representa la carga dnámca equvalente a la accón sísmca que debe utlzarse para calcular la respuesta en el tempo Ut () cuando se defne como dato que descrbe la exctacón sísmca al hstograma de las aceleracones u S () t. Para resolver la ec. (6) se puede utlzar el método de descomposcón modal ya vsto para cualquer otro tpo de cargas dnámcas Pt () en el Capítulo 5 de la parte Dnámca Estructural. Este análss váldo sempre que el sstema sea lneal y elástco no será abordado en más detalle ya que no dfere en nada al correspondente a solctacones dnámcas en general ya vsto. De todos modos el concepto de descomposcón modal resulta de utldad para el análss sísmco en el caso general de la ec. (6). Se propone la descomposcón modal en la forma: (6) N () q () t U t = Φ = (7) donde q (t) es el desplazamento generalzado del modo. Substtuyendo la ec. (7) en la ec. (6) y premultplcando ambos membros de la ec. (6) por la transpuesta del vector Φ que representa los desplazamentos modales del modo se obtene la expresón de la ecuacón de equlbro dnámco del modo en la forma: ( ) ( ) ( ) ( ) T T T T Φ K Φ q t +Φ M Φ q t +Φ C Φ q t = us t Φ M B (8) T Introducendo la notacón: K = Φ K Φ T M = Φ M Φ y T C =Φ C Φ y dvdendo ambos membros de la ec. (8) por M se obtene: 3
4 T ( ) ( ) ξ ω ( ) ( ) ( ) ω q t + q t + q t = u t Φ M B M S (9) Comparando la ecuacón (9) con la correspondente a la exctacón sísmca de un sstema de GLD: ( ) ( ) ξ ω ( ) ( ) ω u t + u t + u t = u t (0) S surge que ambas expresones presentan una correspondenca drecta en todos sus térmnos en T los respectvos valores de q(t) y de u(t) salvo el factor ( Φ M B) M que aparece en la ec. (9) y no aparece en la ec. (0). Este factor que se expresa: T ( M B) Γ = Φ M se denomna factor de partcpacón modal del modo. De este análss surge que s se conoce el desplazamento máxmo que ocurre en un sstema de GLD denomnado como S d el valor máxmo de la coordenada modal respectva q (t) q será gual al producto Γ Sd: () q =Γ S () d Por lo tanto los desplazamentos relatvos máxmos asocados con el modo están dados por la expresón: U = q Φ =Γ S Φ d De manera smlar el vector de pseudo-aceleracón cuenta que q =Γ S resulta: a s U (3) debdo al modo tenendo en U = q Φ =Γ S Φ s a Como ya se ndcó anterormente para un sstema de GLD el producto de la pseudoaceleracón de cada grado de lbertad dnámco por su respectva masa representa la fuerza que produce como respuesta estátca el valor de la máxma respuesta dnámca del modo es decr que el vector de cargas equvalentes Peq estará dado por (4) P = M U s eq (5) que consttuye un vector de cargas tal que s se calcula la respuesta estátca a ellas se obtene el desplazamento máxmo en el modo vector que se denomna U en la ec. (3): P = K U eq (6) 4
5 En realdad la expresón de la ec. (6) no es necesara para calcular U ya que la contrbucón del modo a los desplazamentos de los nudos puede obtenerse drectamente a través de la ec. (3). Sn embargo la ec. (6) pone en evdenca que la respuesta dnámca máxma en un modo puede ser obtenda a través del vector de fuerzas máxmas estátcas equvalentes Peq y que dchos valores no consttuyen una aproxmacón a la respuesta sísmca de ese modo sno que representan la solucón exacta de los desplazamentos relatvos máxmos U los que a su vez permten el cálculo de los respectvos esfuerzos máxmos de la estructura en ese modo. De todo lo expuesto surge que el vector de los desplazamentos máxmos debdos a la respuesta de un modo puede calcularse en forma exacta a partr del conocmento de la frecuenca natural del modo ω de su forma modal Φ y de la ordenada espectral S d (o S a ) que es funcón de la frecuenca natural ω (o del período T ). Una de las lmtacones nherentes al método modal espectral es que es aplcable a sstemas lneales; es decr sempre que la estructura se mantenga dentro del campo elástco y de pequeños desplazamentos. Otra lmtacón mportante del método espectral es que sólo da como resultado el valor máxmo del desplazamento de la estructura (o los esfuerzos máxmos) pero sn ndcar en qué nstante del tempo se produce dcho máxmo. Como lo que nteresa es el valor máxmo de los desplazamentos (o esfuerzos) resultante de la superposcón de todos los modos la falta de smultanedad de la respuesta máxma en los dstntos modos mpde que se pueda obtener el valor exacto del máxmo de la superposcón de todos los modos. De esta lmtacón surge la necesdad de realzar certas hpótess sobre cómo sumar los máxmos de los dstntos modos. Una manera de estmar el máxmo de la superposcón de todos los modos que se utlza con bastante frecuenca en las aplcacones práctcas del método consste en consderar la respuesta en cada modo como estadístcamente ndependente de la correspondente a los restantes modos. Sobre esta base que es sólo una prmera aproxmacón al problema se puede justfcar que los máxmos modales no se suman en forma algebraca drecta sno a través de la suma cuadrátca (Ptagórca) es decr que el vector desplazamentos máxmos de todos los modos puede aproxmarse para cada componente j por la expresón: u j N = j ( u ) (7) Para el cálculo de los esfuerzos (nternos y reaccones) máxmos combnados de todos los modos utlzando esta hpótess de ndependenca estadístca de la respuesta en cada modo es necesaro recurrr a las reglas del análss estátco para el vector de fuerzas equvalentes Peq de cada modo. Denomnando con E al valor máxmo del esfuerzo genérco en un punto de la estructura en el modo la superposcón de los valores de los dstntos modos para obtener una aproxmacón al máxmo de todos los modos está dada por: E N = ( E ) (8) 5
6 El cálculo de las componentes modales de los esfuerzos máxmos de dos maneras dferentes en el caso de estructuras regulares en altura: E puede realzarse En funcón del vector de desplazamentos modales máxmos U como es característco en el Método de Rgdez (estátco) multplcando las matrces de rgdez elementales de cada componente por los desplazamentos de los extremos de cada barra contendos en el vector U. Por consderacones estátcas a partr del vector de cargas equvalentes del modo Peq. A los efectos del cálculo manual resulta más smple este procedmento aunque los valores resultantes de ambos métodos son déntcos. La prncpal condcón o lmtacón a la valdez de la respuesta estadístcamente ndependente de los modos es que las frecuencas de dchos modos sean sufcentemente dferentes. En térmnos generales se tende a aceptar la hpótess de ndependenca estadístca cuando las frecuencas de los modos consderados dferen en al menos un 0 o 30 %. Esta condcón se cumple en la mayoría de las construccones de confguracón estructural ordenada y smple ndependentemente de las dmensones de la estructura. Como se ha vsto en los ejerccos práctcos la frecuenca del segundo modo de un pórtco smple de dos psos es típcamente próxma a 3 veces la frecuenca fundamental. En el caso de una chmenea o vga en voladzo la frecuenca del segundo modo es típcamente 5 o más veces la del modo fundamental. En el caso de edfcos de varos psos de hormgón armado típcos de las construccones locales la frecuenca del segundo modo se encuentra entre 3 y 5 veces la frecuenca fundamental según la confguracón de la estructura y sus fundacones. Estas consderacones generales no resultan aplcables para edfcos en altura que presentan reduccones a su seccón en funcón de la altura como ocurre típcamente para respetar los retros oblgatoros en las fachadas de construccones urbanas. De ahí que sea necesaro tener en cuenta las lmtacones de las reglas de superposcón modal que se utlcen para casos que no cumplen con las premsas requerdas aunque en la mayoría de las construccones regulares en planta y elevacón la regla de la ndependenca estadístca es aplcable. Otro aspecto mportante que no ha sdo analzado todavía en detalle se refere a cuántos modos naturales de vbracón es necesaro consderar en el cálculo de la respuesta sísmca. Naturalmente s se trata de un edfco de dos plantas es muy probable que se pueda utlzar un modelo de GLD para representar la respuesta sísmca en cada dreccón suponendo que la confguracón en planta está orentada en dos dreccones ortogonales no acopladas por un efecto de torsón. Un edfco de N psos puede representarse con un modelo de N GLD y por lo tanto tene en cada dreccón horzontal N modos y frecuencas naturales de vbracón. Se debe recordar que una estructura puede tener propedades dnámcas (frecuencas y modos) muy dferentes en dos dreccones horzontales en planta y estos modos están en general desacoplados en ambas dreccones cuando no hay excentrcdad de la masa de cada pso respecto al centro de torsón. Ahora ben s se trata de un edfco de 0 psos cabe preguntarse: es necesaro consderar los 0 modos naturales de vbracón en cada dreccón horzontal en planta para tener una buena aproxmacón de la respuesta sísmca?. La respuesta a esta pregunta es un categórco NO. La prncpal razón es que los modos que se exctan más fáclmente con el ssmo son los modos de menor frecuenca no sólo por su frecuenca y la posble resonanca 6
7 con el ssmo sno porque los modos superores generan fuerzas dnámcas equvalentes Peq que se cancelan parcalmente en altura y tenden a dar una resultante acumulada haca la base que no aportan demasado a los esfuerzos y aún en menor medda a los desplazamentos. Para estmar la mportanca de la contrbucón de un certo modo a la respuesta sísmca resulta de gran utldad ntroducr el concepto de Masa Modal. Para ello consdérese la estructura de varos psos representada en la Fgura. El concepto se desarrolla para un modo cualquera por ejemplo el modo fundamental pero su valdez resulta aplcable a cualquer modo. En la fgura se lustran las componentes del vector de fuerzas equvalentes del modo Peq que producen la máxma respuesta en ese modo. La fuerza total de corte acumulada en la base del edfco está dada por la suma algebraca de las componentes ndvduales del vector Peq. La reaccón en la base para el modo expresada en funcón de los desplazamentos de j los psos u y de la masa de cada pso m j donde representa el número del modo y j el pso consderado resulta: N N N j s j j = eq = j =Γ a j j= j= j= R P m u S m u (9) P eq P eq P 3 eq P 4 eq R Fgura. Fuerzas equvalentes del modo genérco Dvdendo la reaccón en la base para el modo por la aceleracón espectral S a se obtene una magntud con dmensones de masa desgnada Masa Modal del modo : T ( Φ M B) T ( M ) M = (0) Φ Φ Se puede aprecar que la masa modal es sempre postva y su valor es tal que la suma de la M de todos los modos es exactamente gual al 00 % de masa de toda la estructura. Sobre la base de este concepto es posble decdr s el número de modos consderados es sufcente a partr que la suma de las masas modales de todos los modos ncludos en el análss alcance un certo porcentaje de la masa total. Habtualmente se consdera que es sufcente cuando la suma de la masa modal de los modos ncludos en el análss alcanza o supera el 90% de la masa total de la estructura. 7
8 Método estátco equvalente Dsposcones reglamentaras A los efectos de smplfcar el cálculo de los esfuerzos y deformacones de una estructura debdos a la accón sísmca los reglamentos de dseño de estructura de edfcos típcamente dan una sere de pautas a través de las cuales es posble aproxmar la solucón del problema a través de la respuesta del modo fundamental. Más aún para estructuras regulares en plan y elevacón tal como aquellas para las cuales está orentado este método es normal consderar que los desplazamentos horzontales asocados al modo fundamental varían lnealmente en funcón de la altura del pso. Por lo tanto sobre la base de esta hpótess n squera resulta necesaro calcular con precsón el modo fundamental ya que se supone una ley lneal en altura y sólo es necesaro estmar la frecuenca fundamental a los efectos de la determnacón del valor de la aceleracón espectral S a de dcho modo. Una manera de estmar el valor de ω es a través del cocente de Raylegh tomando como forma modal a una ley lneal en altura Φ. Se defne como cocente de Raylegh a la relacón: ω Φ K Φ T T Φ M Φ S la forma supuesta Φ fuera exactamente el modo fundamental el valor dado por la ec. () para el modo fundamental sería el valor exacto de ω. Con el valor de T = π / ω se obtene del espectro de pseudo-aceleracón la ordenada espectral S a y se procede a calcular el vector de fuerzas estátcas equvalentes desgnado Peq y la masa modal M. Como es de esperar la masa modal M es nferor al 00% de la masa total del edfco. Típcamente para un edfco regular en altura y con la forma lneal del modo fundamental el valor de la masa modal M resulta aproxmadamente cerca del 85% del total. En otras palabras s el análss se hcera sólo con el prmer modo aproxmado en forma lneal habría un faltante de masa del 5% del total. Para corregr esa masa faltante pero mantenendo la ley lneal de varacón del modo (y de las fuerzas estátcas equvalentes que producen la respuesta dnámca máxma) los reglamentos ntroducen un factor de amplfcacón de la respuesta del prmer modo calculada sobre la hpótess de varacón lneal de los desplazamentos en altura de forma tal que la masa modal sea gual al 00% de la masa de la estructura. Esto se logra multplcando la fuerzas estátcas equvalentes antes calculadas y defndas según el método modal espectral general Peq por el factor mayor a la undad: M total M. En síntess el método estátco equvalente de análss sísmco ncorporado a los reglamentos de dseño sísmco de edfcos consste en una aproxmacón del método modal espectral general ya vsto en el que se ntroducen las sguentes aproxmacones adconales: La forma del modo fundamental presenta una varacón lneal en altura desde un valor nulo en correspondenca con la fundacón hasta un valor máxmo en correspondenca con el techo del últmo pso. () 8
9 La frecuenca fundamental se calcula con el cocente de Raylegh para esa forma aproxmada del prmer modo y se determna la ordena espectral correspondente S a. Se calcula el vector de cargas estátcas equvalentes P eq y se lo multplca por el factor mayor a la undad gual a M total M. Con el vector de cargas así factorzado se calculan los esfuerzos y deformacones de la estructura como s fuera un problema estátco tal como se ha desarrollado para el método modal espectral en general. Consderacones sobre el comportamento elasto-plástco El análss modal espectral desarrollado en las seccones precedentes es aplcable sólo a estructuras que permanecen elástcas durante la accón sísmca. Sn embargo la ntensdad de los ssmos de dseño prescrptos por los reglamentos actuales se corresponde con una accón sísmca cuyo período de recurrenca es 475 años consttuyendo una accón extrema es decr una accón que se acepta puede dejar daños permanentes en la estructura aunque sn llegar a provocar su colapso. Aceptando que las accones sísmcas corresponden a un modelo probablístco de Posson se demuestra que dcho período de recurrenca corresponde a una probabldad de excedenca de 0% en 50 años para el ssmo de dseño asocado al espectro S a. Algunos reglamentos recomendan consderar además del espectro así defndo para evaluar la segurdad de la estructura otro ssmo de mayor frecuenca de ocurrenca y menor ntensdad que se denomna ssmo de operacón normal cuya probabldad de excedenca resulta de 50% en 00 años lo que corresponde a un período medo de recurrenca de 44 años. Para este nvel de accones sísmcas se espera que el comportamento de la estructura se mantenga dentro del campo elástco. En la Fgura 3 se muestra el espectro de pseudo-aceleracón para la zona sísmca dado por el Reglamento INPRES-CIRSOC 03 en correspondenca con un perfl de suelo de rgdez ntermeda (suelo tpo II). Sa [%g] Zona Sísmca - Suelo Tpo II Perodo [seg] Fgura 3. Espectro elástco de pseudo-aceleracones con ξ = 5% 9
10 La manera prevsta en este reglamento para tener en cuenta el comportamento nelástco de las estructuras bajo el ssmo consste en efectuar el cálculo como s fuera elástca pero corrgendo la repuesta por medo de un factor de reduccón R que varía según el período fundamental de la estructura T según se lustra en la Fgura 4. La varacón del coefcente de reduccón R ndcada por el reglamento es una ley formada por dos rectas. Para estructuras cuyo período fundamental es gual o nferor al período al valor defndo como T en el reglamento el coefcente R varía entre para T = 0 hasta R = µ para T = T donde µ es la ductldad máxma nomnal que el reglamento permte asgnar a la estructura según sus característcas. Para estructuras cuyo período T es mayor que T el reglamento permte adoptar el valor máxmo de R = µ ndependentemente del valor de T. R µ Fgura 4. Varacón del coefcente de reduccón R en funcón del período natural Esta manera de consderar el efecto del comportamento nelástco de las estructuras frente a las accones sísmcas responde a observacones empírcas del comportamento de estructuras en escala natural frente a ssmos como así tambén a smulacones numércas sobre el efecto de las deformacones plástcas en la respuesta dnámca frente a dferentes ssmos. S ben se trata de recomendacones que responden a una lógca ntutva no resultan de una ley natural exacta como la ley de Newton de la conservacón de la energía o de la cantdad de movmento y por lo tanto deben ser tomadas como de valdez estadístca aunque no aplcable a todos los casos en forma exacta. A pesar de estas lmtacones en la metodología ndcada por el reglamento las accones sísmcas que pueden ncdr sobre una estructura dada presentan una sere de ncertdumbres que llevan a la necesdad de contar con reglas smples aunque sean aproxmadas sobre los efectos del comportamento nelástco frente a dchas accones que son de muy baja probabldad de ocurrenca y con períodos de recurrenca de ser superadas que según el reglamento son de aproxmadamente una vez cada 475 años para el ssmo destructvo de dseño. La dea detrás de las recomendacones reglamentaras es que el análss de las deformacones y esfuerzos sísmcos tenendo en cuenta el comportamento nelástco puede realzarse como s el sstema fuera lneal y elástco pero ntroducendo factores de correccón a los resultados lneales. La lógca utlzada se descrbe a contnuacón. Esfuerzos máxmos. T Para estructuras relatvamente rígdas aquellas cuyo período fundamental es mucho menor que el período T del espectro las aceleracones máxmas que sufre la masa de un sstema de GLD por efecto del ssmo no dferen sustancalmente 0 T [seg]
11 de las del sstema elástco y por lo tanto la reduccón del esfuerzo máxmo respecto al correspondente al comportamento elástco a través del factor R es muy pequeña y resulta aproxmadamente gual a la undad. Estrctamente para una estructura muy rígda en relacón a su masa con período natural cercano a 0 los benefcos del comportamento nelástco no se traducen en una reduccón del esfuerzo máxmo en el resorte K. Por el contraro para estructuras cuyo período fundamental es cercano a T del espectro la reduccón del esfuerzo máxmo es próxma al valor de la ductldad máxma µ que puede desarrollar sn colapso y en este caso el coefcente de reduccón R tende al límte máxmo R = µ. Para períodos ntermedos entre 0 y T el reglamento ntroduce una ley lneal de varacón de R. Para estructuras relatvamente flexbles cuyo período fundamental es superor al límte T del espectro se consdera que se produce una sgnfcatva reduccón del esfuerzo máxmo que sente el resorte como consecuenca del comportamento nelástco frente al ssmo y esa reduccón se estma dvdendo el esfuerzo máxmo que sufrría la estructura s fuera elástca por el factor de reduccón R con su valor máxmo (R = µ). Desplazamentos máxmos. Consstente con la reduccón de los esfuerzos máxmos en la estructura por efecto de la ductldad resulta necesaro consderar que los desplazamentos relatvos máxmos nducdos por el ssmo deben ser corregdos a partr del valor que tendrían s el comportamento fuese lneal elástco sguendo para ello la sguente regla práctca: Para estructuras relatvamente flexbles (T > T ) los desplazamentos máxmos son aproxmadamente guales a los que corresponden a una estructura lneal elástca y por lo tanto no resulta necesaro corregr los valores de desplazamento basados en la hpótess de comportamento lneal elástco. Para estructuras relatvamente rígdas (T < T ) los desplazamentos máxmos consstentes con el comportamento nelástco se obtenen de multplcar los desplazamentos elástcos máxmos por la relacón µ / R. Por lo tanto para estructuras muy rígdas (R ) los desplazamentos máxmos de un sstema elastoplástco serán aproxmadamente µ veces más grandes que los desplazamentos elástcos máxmos. Esta consderacón se expresa en forma clara en los gráfcos (a) y (b) de la Fgura 5. F (a) Estr. relatvamente flexble F (b) Estr. relatvamente rígda F elas F elas F nel K F nel K u calc u elas u nel u u calc u elas u nel u Fgura 5. Comparacón de esfuerzos y desplazamentos elástcos y elasto-plástcos
12 A manera de comentaro fnal resulta de nterés señalar que las tres zonas característcas en cualquer espectro de respuesta elástca S a son las sguentes: Zona controlada por las aceleracones máxmas: segmento del espectro que corresponde a estructuras relatvamente rígdas donde las aceleracones máxmas no presentan una reduccón marcada respecto a las elástcas como consecuenca del comportamento nelástco. Zona controlada por las velocdades máxmas: segmento donde las aceleracones espectrales son máxmas que se extende entre los períodos desgnados como T y T por el reglamento INPRES-CIRSOC 03. En este sector se produce la máxma amplfcacón dnámca de la respuesta de la estructura respecto a las que se producrían s las msmas aceleracones debdas al ssmo generaran una respuesta estátca o cas estátca (lo que ocurre esencalmente cuando el período fundamental T es muy bajo frente a T ). De todos modos a pesar de la amplfcacón dnámca que se produce en esta zona por el efecto de una certa resonanca entre la exctacón y el modo fundamental de la estructura el comportamento nelástco produce una notable reduccón del efecto del esfuerzo que se producría en un sstema elástco. Zona controlada por los desplazamentos máxmos: segmento que corresponde a las estructuras relatvamente flexbles en las que el desplazamento máxmo nducdo por el ssmo resulta ndependente a s el comportamento es elástco o nelástco. Naturalmente s los desplazamentos máxmos son ndependentes de las deformacones plástcas los esfuerzos máxmos se reducen respecto a los elástcos a través del factor R por la expresón Fnel = F elas µ.
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
Apéndice A: Metodología para la evaluación del modelo de pronóstico meteorológico
 Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
CARTAS DE CONTROL. Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones para el control del proceso.
 CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CAPÍTULO 3 METODOLOGÍA. En el siguiente capítulo se presenta al inicio, definiciones de algunos conceptos actuariales
 CAPÍTULO 3 METODOLOGÍA En el sguente capítulo se presenta al nco, defncones de algunos conceptos actuarales que se utlzan para la elaboracón de las bases técncas del Producto de Salud al gual que la metodología
CAPÍTULO 3 METODOLOGÍA En el sguente capítulo se presenta al nco, defncones de algunos conceptos actuarales que se utlzan para la elaboracón de las bases técncas del Producto de Salud al gual que la metodología
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Organización y resumen de datos cuantitativos
 Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
5ª Lección: Sistema de fuerzas gravitatorias. Cálculo de centros de gravedad de figuras planas: teoremas de Guldin.
 Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
TERMODINÁMICA AVANZADA
 TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Créditos Y Sistemas de Amortización: Diferencias, Similitudes e Implicancias
 Crédtos Y Sstemas de Amortzacón: Dferencas, Smltudes e Implcancas Introduccón Cuando los ngresos de un agente económco superan su gasto de consumo, surge el concepto de ahorro, esto es, la parte del ngreso
Crédtos Y Sstemas de Amortzacón: Dferencas, Smltudes e Implcancas Introduccón Cuando los ngresos de un agente económco superan su gasto de consumo, surge el concepto de ahorro, esto es, la parte del ngreso
Las acciones a considerar en el proyecto de una estructura o elemento estructural se pueden clasificar según los criterios siguientes:
 CAÍTULO III ACCIONES Artículo 9º Clasfcacón de las accones Las accones a consderar en el proyecto de una estructura o elemento estructural se pueden clasfcar según los crteros sguentes: - Clasfcacón por
CAÍTULO III ACCIONES Artículo 9º Clasfcacón de las accones Las accones a consderar en el proyecto de una estructura o elemento estructural se pueden clasfcar según los crteros sguentes: - Clasfcacón por
Comparación entre distintos Criterios de decisión (VAN, TIR y PRI) Por: Pablo Lledó
 Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
OPERACIONES ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS
 P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
Histogramas: Es un diagrama de barras pero los datos son siempre cuantitativos agrupados en clases o intervalos.
 ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
CESMA BUSINESS SCHOOL
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
Resumen de los teoremas fundamentales del análisis estructural aplicados a celosías
 Resumen de los teoremas fundamentales del análss estructural aplcados a celosías INTRODUCCIÓN Fuerzas aplcadas y deformacones de los nudos (=1,n) ESTICIDD Tensón =Ν/Α. Unforme en cada seccón de la arra.
Resumen de los teoremas fundamentales del análss estructural aplcados a celosías INTRODUCCIÓN Fuerzas aplcadas y deformacones de los nudos (=1,n) ESTICIDD Tensón =Ν/Α. Unforme en cada seccón de la arra.
TEMA 8: PRÉSTAMOS ÍNDICE
 TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
Análisis de error y tratamiento de datos obtenidos en el laboratorio
 Análss de error tratamento de datos obtendos en el laboratoro ITRODUCCIÓ Todas las meddas epermentales venen afectadas de una certa mprecsón nevtable debda a las mperfeccones del aparato de medda, o a
Análss de error tratamento de datos obtendos en el laboratoro ITRODUCCIÓ Todas las meddas epermentales venen afectadas de una certa mprecsón nevtable debda a las mperfeccones del aparato de medda, o a
APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES
 APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES Documento Preparado para la Cámara de Fondos de Inversón Versón 203 Por Rodrgo Matarrta Venegas 23 de Setembre del 204 2 Análss Industral
APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES Documento Preparado para la Cámara de Fondos de Inversón Versón 203 Por Rodrgo Matarrta Venegas 23 de Setembre del 204 2 Análss Industral
TÉCNICAS AUXILIARES DE LABORATORIO
 TÉCNICAS AUXILIARES DE LABORATORIO I.- ERRORES 1.- Introduccón Todas las meddas epermentales venen afectadas de una mprecsón nherente al proceso de medda. Puesto que en éste se trata, báscamente, de comparar
TÉCNICAS AUXILIARES DE LABORATORIO I.- ERRORES 1.- Introduccón Todas las meddas epermentales venen afectadas de una mprecsón nherente al proceso de medda. Puesto que en éste se trata, báscamente, de comparar
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Análisis de Weibull. StatFolio de Muestra: Weibull analysis.sgp
 Análss de Webull Resumen El procedmento del Análss de Webull está dseñado para ajustar una dstrbucón de Webull a un conjunto de n observacones. Es comúnmente usado para analzar datos representando tempos
Análss de Webull Resumen El procedmento del Análss de Webull está dseñado para ajustar una dstrbucón de Webull a un conjunto de n observacones. Es comúnmente usado para analzar datos representando tempos
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
Rentas o Anualidades
 Rentas o Anualdades Patrca Ksbye Profesorado en Matemátca Facultad de Matemátca, Astronomía y Físca 10 de setembre de 2013 Patrca Ksbye (FaMAF) 10 de setembre de 2013 1 / 31 Introduccón Rentas o Anualdades
Rentas o Anualdades Patrca Ksbye Profesorado en Matemátca Facultad de Matemátca, Astronomía y Físca 10 de setembre de 2013 Patrca Ksbye (FaMAF) 10 de setembre de 2013 1 / 31 Introduccón Rentas o Anualdades
Unidad II: Análisis de la combustión completa e incompleta. 2. 1. Aire
 4 Undad II: Análss de la combustón completa e ncompleta. 1. Are El are que se usa en las reaccones de combustón es el are atmosférco. Ya se djo en la Undad I que, debdo a que n el N n los gases nertes
4 Undad II: Análss de la combustón completa e ncompleta. 1. Are El are que se usa en las reaccones de combustón es el are atmosférco. Ya se djo en la Undad I que, debdo a que n el N n los gases nertes
Economía de la Empresa: Financiación
 Economía de la Empresa: Fnancacón Francsco Pérez Hernández Departamento de Fnancacón e Investgacón de la Unversdad Autónoma de Madrd Objetvo del curso: Dentro del contexto de Economía de la Empresa, se
Economía de la Empresa: Fnancacón Francsco Pérez Hernández Departamento de Fnancacón e Investgacón de la Unversdad Autónoma de Madrd Objetvo del curso: Dentro del contexto de Economía de la Empresa, se
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Primer Semestre - Otoño 2014. Omar De la Peña-Seaman. Instituto de Física (IFUAP)
 MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
2.2 TASA INTERNA DE RETORNO (TIR). Flujo de Caja Netos en el Tiempo
 Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Diseño y Análisis de Experimentos en el SPSS 1
 Dseño y Análss de Expermentos en el SPSS EJEMPLO. Los sguentes datos muestran las meddas de hemoglobna (gramos por 00 ml) en la sangre de 40 ejemplares de una espece de truchas marrones. Las truchas se
Dseño y Análss de Expermentos en el SPSS EJEMPLO. Los sguentes datos muestran las meddas de hemoglobna (gramos por 00 ml) en la sangre de 40 ejemplares de una espece de truchas marrones. Las truchas se
ESTADÍSTICA (GRUPO 12)
 ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
Procedimiento de Calibración. Metrología PROCEDIMIENTO DI-010 PARA LA CALIBRACIÓN DE COMPARADORES MECÁNICOS
 Procedmento de Calbracón Metrología PROCEDIMIENTO DI-00 PARA LA CALIBRACIÓN DE COMPARADORES MECÁNICOS La presente edcón de este procedmento se emte exclusvamente en formato dgtal y puede descargarse gratutamente
Procedmento de Calbracón Metrología PROCEDIMIENTO DI-00 PARA LA CALIBRACIÓN DE COMPARADORES MECÁNICOS La presente edcón de este procedmento se emte exclusvamente en formato dgtal y puede descargarse gratutamente
El análisis de desviaciones sobre el resultado previsto
 Tema 6 El análss de desvacones sobre el resultado prevsto Trabajar con presupuestos supone, como fase fnal lógca, el comparar las cfras prevstas con las reales, y proceder a un «análss de desvacones».
Tema 6 El análss de desvacones sobre el resultado prevsto Trabajar con presupuestos supone, como fase fnal lógca, el comparar las cfras prevstas con las reales, y proceder a un «análss de desvacones».
Cálculo y diseño sismorresistente de edificios. Aplicación de la norma NCSE-02
 CENTRO INTERNACIONAL DE MÉTODOS NUMÉRICOS EN INGENIERÍA Monografías de Ingenería Sísmca Edtor A. H. Barbat Cálculo y dseño ssmorresstente de edfcos. Aplcacón de la norma NCSE-02 H. Barbat S. Oller J. C.
CENTRO INTERNACIONAL DE MÉTODOS NUMÉRICOS EN INGENIERÍA Monografías de Ingenería Sísmca Edtor A. H. Barbat Cálculo y dseño ssmorresstente de edfcos. Aplcacón de la norma NCSE-02 H. Barbat S. Oller J. C.
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA
 LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
T. 9 El modelo de regresión lineal
 1 T. 9 El modelo de regresón lneal 1. Conceptos báscos sobre el análss de regresón lneal. Ajuste de la recta de regresón 3. Bondad de ajuste del modelo de regresón Modelos predctvos o de regresón: la representacón
1 T. 9 El modelo de regresón lneal 1. Conceptos báscos sobre el análss de regresón lneal. Ajuste de la recta de regresón 3. Bondad de ajuste del modelo de regresón Modelos predctvos o de regresón: la representacón
Unidad I. 1. 1. Definición de reacción de combustión. 1. 2. Clasificación de combustibles
 2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
Correlación y regresión lineal simple
 . Regresón lneal smple Correlacón y regresón lneal smple. Introduccón La correlacón entre dos varables ( e Y) se refere a la relacón exstente entre ellas de tal manera que a determnados valores de se asocan
. Regresón lneal smple Correlacón y regresón lneal smple. Introduccón La correlacón entre dos varables ( e Y) se refere a la relacón exstente entre ellas de tal manera que a determnados valores de se asocan
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
REGRESION LINEAL SIMPLE
 REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL
 EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
Código Sísmico de Costa Rica Edición 2002
 Edcón 2002 Resumen Ejecutvo Presentado a la Asamblea de Representantes del CFIA Preparado por Ing. Gullermo Santana, Ph.D. e Ing. Jorge Gutérrez, Ph.D.(LANAMME, UCR) 20 de novembre 2002 Nota: Referencas
Edcón 2002 Resumen Ejecutvo Presentado a la Asamblea de Representantes del CFIA Preparado por Ing. Gullermo Santana, Ph.D. e Ing. Jorge Gutérrez, Ph.D.(LANAMME, UCR) 20 de novembre 2002 Nota: Referencas
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
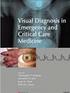 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
Perturbación de los valores propios simples de matrices de polinomios dependientes diferenciablemente de parámetros
 Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Investigación y Técnicas de Mercado. Previsión de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): Ajustes de Tendencia
 Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
CAPITULO 3.- ANÁLISIS CONJUNTO DE DOS VARIABLES. 3.1 Presentación de los datos. Tablas de doble entrada.
 Introduccón a la Estadístca Empresaral Capítulo - Análss conjunto de dos varables Jesús ánchez Fernández CAPITULO - AÁLII COJUTO DE DO VARIABLE Presentacón de los datos Tablas de doble entrada En el capítulo
Introduccón a la Estadístca Empresaral Capítulo - Análss conjunto de dos varables Jesús ánchez Fernández CAPITULO - AÁLII COJUTO DE DO VARIABLE Presentacón de los datos Tablas de doble entrada En el capítulo
EXPERIMENTACIÓN COMERCIAL(I)
 EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
MÉTODOS PARA PROBAR NUMEROS
 Capítulo 3 ALEATORIOS MÉTODOS PARA PROBAR NUMEROS III.1 Introduccón Exsten algunos métodos dsponbles para verfcar varos aspectos de la caldad de los números pseudoaleatoros. S no exstera un generador partcular
Capítulo 3 ALEATORIOS MÉTODOS PARA PROBAR NUMEROS III.1 Introduccón Exsten algunos métodos dsponbles para verfcar varos aspectos de la caldad de los números pseudoaleatoros. S no exstera un generador partcular
Convertidores Digital-Analógico y Analógico-Digital
 Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS
 CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
i=1 Demuestre que cumple los axiomas de norma. Calcule el límite Verifiquemos cada uno de los axiomas de la definición de norma: i=1
 CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
TEMA 6 CONTROL DE VIBRACIONES. Control de Vibraciones
 Control de Vbracones ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 6. - ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 6. - 6. Introduccón y metodologías En la práctca, exsten un gran número de stuacones en las que es
Control de Vbracones ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 6. - ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 6. - 6. Introduccón y metodologías En la práctca, exsten un gran número de stuacones en las que es
TEMA 6 AMPLIFICADORES OPERACIONALES
 Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Econometría. Ayudantía # 01, Conceptos Generales, Modelo de Regresión. Profesor: Carlos R. Pitta 1
 Escuela de Ingenería Comercal Ayudantía # 01, Conceptos Generales, Modelo de Regresón Profesor: Carlos R. Ptta 1 1 cptta@spm.uach.cl Escuela de Ingenería Comercal Ayudantía 01 Parte 01: Comentes Señale
Escuela de Ingenería Comercal Ayudantía # 01, Conceptos Generales, Modelo de Regresón Profesor: Carlos R. Ptta 1 1 cptta@spm.uach.cl Escuela de Ingenería Comercal Ayudantía 01 Parte 01: Comentes Señale
El costo de oportunidad social de la divisa ÍNDICE
 El Costo de Oportundad Socal de la Dvsa El costo de oportundad socal de la dvsa ÍNDICE. INTRODUCCIÓN. EL MARCO TEÓRICO 3. CÁLCULO DEL COSTO DE OPORTUNIDAD SOCIAL DE LA DIVISA 3. Nvel agregado 3. Nvel desagregado
El Costo de Oportundad Socal de la Dvsa El costo de oportundad socal de la dvsa ÍNDICE. INTRODUCCIÓN. EL MARCO TEÓRICO 3. CÁLCULO DEL COSTO DE OPORTUNIDAD SOCIAL DE LA DIVISA 3. Nvel agregado 3. Nvel desagregado
Pruebas Estadísticas de Números Pseudoaleatorios
 Pruebas Estadístcas de Números Pseudoaleatoros Prueba de meda Consste en verfcar que los números generados tengan una meda estadístcamente gual a, de esta manera, se analza la sguente hpótess: H 0 : =
Pruebas Estadístcas de Números Pseudoaleatoros Prueba de meda Consste en verfcar que los números generados tengan una meda estadístcamente gual a, de esta manera, se analza la sguente hpótess: H 0 : =
PORTAFOLIO DE TRES ACTIVOS FINANCIEROS
 PORTAFOLIO DE TRES ACTIVOS FINANCIEROS Contendo:. Introduccón.. Fondos Mutuos. Rendmento y Resgo.. Parámetros estadístcos de un Portafolo de Tres Actvos. a) El Retorno de un Portafolo. b) El Resgo de un
PORTAFOLIO DE TRES ACTIVOS FINANCIEROS Contendo:. Introduccón.. Fondos Mutuos. Rendmento y Resgo.. Parámetros estadístcos de un Portafolo de Tres Actvos. a) El Retorno de un Portafolo. b) El Resgo de un
AMPLIFICADORES CON BJT.
 Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
GUIA DE ALCANCE FINANCIERO CAE OPERACIONES DE CRÉDITO HIPOTECARIO
 INTRODUCCIÓN La ley 2.555 publcada el día 5 de dcembre de 211 y que entró en vgenca el día 4 de marzo de 212, que modca la ley 19.496 Sobre Proteccón de los Derechos de los Consumdores (LPC, regula desde
INTRODUCCIÓN La ley 2.555 publcada el día 5 de dcembre de 211 y que entró en vgenca el día 4 de marzo de 212, que modca la ley 19.496 Sobre Proteccón de los Derechos de los Consumdores (LPC, regula desde
UNIVERSIDAD DE LOS ANDES FACULTAD DE INGENIERÍA DOCTORADO EN CIENCIAS APLICADAS
 UNIVERSIDAD DE LOS ANDES FACULTAD DE INGENIERÍA DOCTORADO EN CIENCIAS APLICADAS Modelo smplfcado para el comportamento dnámco de pórtcos con vgas plana-columna de concreto armado consderando el deslzamento
UNIVERSIDAD DE LOS ANDES FACULTAD DE INGENIERÍA DOCTORADO EN CIENCIAS APLICADAS Modelo smplfcado para el comportamento dnámco de pórtcos con vgas plana-columna de concreto armado consderando el deslzamento
Oferta de Trabajo Parte 2. Economía Laboral Julio J. Elías LIE - UCEMA
 Oferta de Trabajo Parte 2 Economía Laboral Julo J. Elías LIE - UCEMA Curva de oferta de trabajo ndvdual Consumo Salaro por hora ($) G w=$20 F w=$25 25 Curva de Oferta de Trabajo Indvdual w=$14 20 14 w
Oferta de Trabajo Parte 2 Economía Laboral Julo J. Elías LIE - UCEMA Curva de oferta de trabajo ndvdual Consumo Salaro por hora ($) G w=$20 F w=$25 25 Curva de Oferta de Trabajo Indvdual w=$14 20 14 w
Equilibrio termodinámico entre fases fluidas
 CAPÍTULO I Equlbro termodnámco entre fases fludas El conocmento frme de los conceptos de la termodnámca se consdera esencal para el dseño, operacón y optmzacón de proyectos en la ngenería químca, debdo
CAPÍTULO I Equlbro termodnámco entre fases fludas El conocmento frme de los conceptos de la termodnámca se consdera esencal para el dseño, operacón y optmzacón de proyectos en la ngenería químca, debdo
Cálculo y EstadísTICa. Primer Semestre.
 Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
6.1 EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS
 TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
PRUEBAS DE ACCESO A LAS UNIVERSIDADES DE ANDALUCÍA PARA MAYORES DE 25 AÑOS MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
 PRUEBAS DE ACCESO A LAS UNIVERSIDADES DE ANDALUCÍA PARA MAYORES DE AÑOS EXÁMENES PROPUESTOS Y RESUELTOS DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES CONVOCATORIAS DE --- F Jménez Gómez Este cuaderno
PRUEBAS DE ACCESO A LAS UNIVERSIDADES DE ANDALUCÍA PARA MAYORES DE AÑOS EXÁMENES PROPUESTOS Y RESUELTOS DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES CONVOCATORIAS DE --- F Jménez Gómez Este cuaderno
Aplicación de la termodinámica a las reacciones químicas Andrés Cedillo Departamento de Química Universidad Autónoma Metropolitana-Iztapalapa
 Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Leyes de tensión y de corriente
 hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
Análisis de Regresión y Correlación
 1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
CANTIDADES VECTORIALES: VECTORES
 INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, son números ordenados en filas y columnas.
 MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y A c se les ha asociado los sucesos B y B c.
 Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Media es la suma de todas las observaciones dividida por el tamaño de la muestra.
 Estadístcos Los estadístcos son valores calculados con los datos de una varable cuanttatva y que mden alguna de las característcas de la dstrbucón muestral. Las prncpales característcas son: tendenca central,
Estadístcos Los estadístcos son valores calculados con los datos de una varable cuanttatva y que mden alguna de las característcas de la dstrbucón muestral. Las prncpales característcas son: tendenca central,
Una Reformulación de la Mecánica Clásica
 Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
EVALUACIÓN PROBABILISTA DEL RIESGO SÍSMICO DE EDIFICIOS DE HORMIGÓN ARMADO CON BASE EN LA DEGRADACIÓN DE LA RIGIDEZ RESUMEN
 EVALUACIÓN PROBABILISTA DEL RIESGO SÍSMICO DE EDIFICIOS DE HORMIGÓN ARMADO CON BASE EN LA DEGRADACIÓN DE LA RIGIDEZ Barbat A.H. 1, Vargas Y.F. 2, Pujades L.G. 3 y Hurtado J.E. 4 RESUMEN El análss dnámco
EVALUACIÓN PROBABILISTA DEL RIESGO SÍSMICO DE EDIFICIOS DE HORMIGÓN ARMADO CON BASE EN LA DEGRADACIÓN DE LA RIGIDEZ Barbat A.H. 1, Vargas Y.F. 2, Pujades L.G. 3 y Hurtado J.E. 4 RESUMEN El análss dnámco
CAPITULO 7. METODOLOGÍA DEL PLAN DE PENSIONES ALTERNATIVO. Como se explica en el capítulo 4, una anualidad es una serie de pagos que se realizan
 CAPITULO 7. METODOLOGÍA DEL PLAN DE PENSIONES ALTERNATIVO 7. Anualdad de Vda Como se elca en el caítulo 4, una anualdad es una sere de agos que se realzan durante un temo determnado, nombrándose a esta
CAPITULO 7. METODOLOGÍA DEL PLAN DE PENSIONES ALTERNATIVO 7. Anualdad de Vda Como se elca en el caítulo 4, una anualdad es una sere de agos que se realzan durante un temo determnado, nombrándose a esta
LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION
 Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
La planificación financiera
 Tema 5 La planfcacón fnancera 5.1 El paso de prevsones económcas a prevsones fnanceras Entre el plan fnancero de una empresa y su plan económco hay dferencas de la msma naturaleza que las estentes conceptualmente
Tema 5 La planfcacón fnancera 5.1 El paso de prevsones económcas a prevsones fnanceras Entre el plan fnancero de una empresa y su plan económco hay dferencas de la msma naturaleza que las estentes conceptualmente
REGRESION Y CORRELACION
 nav Estadístca (complementos) 1 REGRESION Y CORRELACION Fórmulas báscas en la regresón lneal smple Como ejemplo de análss de regresón, descrbremos el caso de Pzzería Armand, cadena de restaurantes de comda
nav Estadístca (complementos) 1 REGRESION Y CORRELACION Fórmulas báscas en la regresón lneal smple Como ejemplo de análss de regresón, descrbremos el caso de Pzzería Armand, cadena de restaurantes de comda
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
TEMA 4 Amplificadores realimentados
 TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
Documento Básico SE-C Cimientos
 5 Cmentacones profundas 5.1 Defncones y tpologías 5.1.1 Defncones 1 A efectos de este DB se consderará que una cmentacón es profunda s su extremo nferor, en el terreno, está a una profunddad superor a
5 Cmentacones profundas 5.1 Defncones y tpologías 5.1.1 Defncones 1 A efectos de este DB se consderará que una cmentacón es profunda s su extremo nferor, en el terreno, está a una profunddad superor a
UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE. Dpto. de Métodos Cuantitativos e Informáticos. Universidad Politécnica de Cartagena.
 UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE COURNOT. Autores: García Córdoba, José Antono; josea.garca@upct.es Ruz Marín, Manuel; manuel.ruz@upct.es Sánchez García, Juan Francsco; jf.sanchez@upct.es
UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE COURNOT. Autores: García Córdoba, José Antono; josea.garca@upct.es Ruz Marín, Manuel; manuel.ruz@upct.es Sánchez García, Juan Francsco; jf.sanchez@upct.es
4 Estabilidad de taludes. Introducción 2
 4 Establdad de taludes Introduccón 2 Deslzamento de Thstle en 1983 En Chle un caso smlar ocurró en Rñhue durante el terremoto de 1960 en las cercanías de Valdva. Deslzamentos de terra están asocados a
4 Establdad de taludes Introduccón 2 Deslzamento de Thstle en 1983 En Chle un caso smlar ocurró en Rñhue durante el terremoto de 1960 en las cercanías de Valdva. Deslzamentos de terra están asocados a
Métodos específicos de generación de diversas distribuciones discretas
 Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Oligopolio. Un mercado oligopólico se define como una estructura de mercado en donde
 Olgopolo Defncón y característcas Un mercado olgopólco se defne como una estructura de mercado en donde exste un número reducdo de frmas y que se caracterza por una sgnfcatva nterdependenca entre las frmas
Olgopolo Defncón y característcas Un mercado olgopólco se defne como una estructura de mercado en donde exste un número reducdo de frmas y que se caracterza por una sgnfcatva nterdependenca entre las frmas
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
