Capítulo 1: Secciones Cónicas
|
|
|
- Ricardo Fernández Villalobos
- hace 6 años
- Vistas:
Transcripción
1 Capítulo : Secciones Cónicas Resumen En este apartado se trata sobre la definición, caractrización graficación de las Secciones Cónicas. Primero se definen las secciones cónicas como la curva de intersección entre un cono doble un plano. Posteriormente se definencomolagrafica de una ecuación general de segundo gradoporúltimocomoelconjuntodepuntosque satisface cierta propiedad geométrica. Contenidos Secciones Cónicas. Laparábola Ecuacióncanónicadelaparábola.... Lacircunferencia Elipse Laecuacióncanónicadelaelipse:.... Lahipérbola Laecuacióncanónicadeunahipérbola:... 0
2 Jorge Monge Fallas Secciones Cónicas Las secciones cónicas se pueden definer de tres formas distintas: En forma visual, en la cual las secciones cónicas se pueden ver como la curva que se obtienen de la intersección entre un plano un cono doble. En una forma análitica, en esta las secciones cónicas correspoden general de segundo grado. a la gráfica de la ecuación Como un conjunto de puntos en el plano que satisfacen cierta propiedad geométrica. La primera de ellas se muestra en las figuras,, 3, a cada una de las curvas que resaltan se le llama una sección cónica. Figura. Parábola Figura. Elipse Figura 3. Hipérbola Figura. Circunferencia Las figuras anteriores nos dan una idea visual de lo que llamamos secciones cónicas, además nos muestran las distintas secciones cónicas que llamaremos: parábola, circunferencia, elipse e hipérbola. Otradelasformasenquesedefinen las secciones cónicas es a partir de la ecuación general de segundo grado A + B + C + D + E + F =0 () para A, B, C, D, E, F R con A B ambos no nulos. La gráfica correspondiente al conjunto de puntos (, ) que satisfacen () corresponde a una sección cónica. Como ejemplo de ello consideremos la ecuación + + 5=0es decir A =,B =0, C =,D =,E = F = 5 la gráfica correspondiente a esta ecuación se muestra en la figura 5
3 . La parábola Jorge Monge Fallas Figura =0 corresponde a una elipse. Por último las cónicas se pueden definir como un locus (colección) de puntos en el plano que satisfacen cierta propiedad geométrica. Esta propiedad geométrica nos lleva a obtener una ecuación canónica, la ecuación canónica es una ecuación que caracteriza en forma completa los elementos que se destacan en la gráfica de la cónica. Acontinuación definimos cada una de las secciones cónicas.. La parábola Definición Una parábola es el conjunto de puntos del plano que están a distancias iguales de un punto fijo llamado foco unarectafija llamada directriz. En la figura 6 se muestran los elementos característicos de la parábola, tales como el foco F, el vértice V, la directriz, el eje de simetría. Y la condición que deben satisfacer los puntos que pertenecen a la parábola. Figura 6. En la figura 7 se establecen las coordenadas generales del vértice V =(h, k), las coordenadas del foco F =(h, k + c), donde c es la distancia del vértice al foco del vértice a la directriz. La ecuación de la directriz en este caso viene dada por = k c la ecuación del eje de simetría = h. 3
4 . La parábola Jorge Monge Fallas Figura 7. Además al segmento AB cuos etremos pertenecen a la parábola, pasa por el foco es perpendicular al eje de simetría se le llama lado recto mide c. A partir de los datos en la figura (7) del hecho que la distancia de cualquier punto P =(, ) al foco es igual a la distancia del punto P a la directriz, es decir, d (P, F) = d (P, L) con P =(, ),F =(h, k + c) L : = k c q q ( h) +( (k + c)) = ( ) +( (k c)) ( h) +( (k + c)) = ( ) +( (k c)) ( h) + c +ck c + k k + = c ck +c + k k + ( h) +ck c = ck +c ( h) = ck +c ( h) = c ( k) A esta última ecuación se la llama ecuación canónica, esta la detallamos a continuación... Ecuación canónica de la parábola. La forma canónica de la ecuación de una parábola con vértice V =(h, k) directriz = k c como las mostradas en las figuras anteriores viene dada por ( h) =c ( k) Eje de simetría vertical. La forma canónica de la ecuación de una parábola con vértice V =(h, k) directriz = h c como se muestra en la figura 8, viene dada por ( k) =c ( h) Eje de simetría horizontal
5 . La parábola Jorge Monge Fallas Figura 8. Ejemplo Consideremos la parábola con ecuación canónica ( ) =8( ) podemos observar que c =,c>0por lo que la parábola es cóncava hacia arriba. La distancia del foco F =(, 3) al vértice V =(, ) es c =ladirectrizesunarectaparalelaalejex seubica a c =por debajo del vértice, esto es =. En la ecuación ( ) =8( ) si se desarolla el cuadrado se deja igualada a cero obtenemos + = = 0 que corresponde a una ecuación general de segundo grado como en () con A =,B =0,C =0,D =,E = 8 F =. La gráfica de esta parábola se ve como en la siguiente figura 5
6 . La parábola Jorge Monge Fallas Figura 9. ( ) =8( ) Ejemplo De igual forma veamos la parábola con ecuación canónica ( +) = podemos obaservar que c =, c<0. La distancia del foco F =(, ) al vértice V =(0, ) es c =ladirectrizesunarectaparalelaalejey seubicaa c =aladerechadelvértice,estoes =. En la ecuación ( +) = si se desarolla el cuadrado se deja igualada a cero obtenemos + + = = 0 que corresponde a una ecuación general de segundo grado como en () con A =0,B =0,C =,D =,E = F =. La gráfica de esta parábola se ve como en la siguiente figura 6
7 . La parábola Jorge Monge Fallas Figura 0. ( +) = Ejemplo 3 Ahora tomamos la ecuación de una parábola que no está en su forma canónica + 6 =5 enestecasoaplicaremoselprocesoinversoparaobtenerlaformacanónicadelaparábola. Además podemos observar que la gráfica de esta parábola es una función de, por lo que esta se abre ahacia la derecho o hacia la izquierda. Completando cuadrados para se tiene + 6 = 5 6 = = = + ( 3) = ( +7) De esta manera la ecuación ( 3) =( +7) corresponde a la ecuación canónica de una parábola con c =, c>0indica que la parábola se abre hacia la derecha, con vértice V =( 7, 3), foco F = 3, 3 directriz = 5. La gráfica de esta parábola se ve como en la siguiente figura 7
8 . La parábola Jorge Monge Fallas Figura. ( 3) =( +7) - Ejemplo También podemos determinar la ecuación de una parábola a partir de cierta información, por ejemplo: Determinar la ecuación de la parábola con foco en (3, ) ecuación de la directriz =. DadoqueladirectrizesunarectaparalelaalejeX, significaquelaparábolaescóncavahaciaarribao concava hacia abajo. Para este tipo de parábola el foco tiene coordenadas F =(h, k + c) la directriz es = k c con esta información tenemos de donde concluimos que h =3que (h, k + c) =(3, ) k c = k + c = k c = resolviendo se tiene k =0 c =. Por lo tanto la ecuación canónica de la parábola que cumple las condiciones establecidas inicialmente viene dada por ( 3) = Realice la gráfica para que verifique que todo esté correcto. Ejemplo 5 Ahora determinenos la ecuación de la parábola que satisface estas nuevas condiciones; el ejedesimetríaesparaleloalejex, vértice en (, 3) contienealpunto(, ). Cuando se dice que el eje es paralelo al eje X, serefiere al eje de simetría. Por tanto la parábola se abre hacia la derecha o hacia la izquierda la ecuación correspondiente tendría la forma ( 3) =c ( ) lo único que queda por determinar es la constante c. La última condición dice que la parábola contiene al punto (, ), esta condición nos permitirá determinar c. Dado que si un punto pertenece a una 8
9 . La circunferencia Jorge Monge Fallas curva entonces, satisface su ecuación así ( 3) = c ( ) sustituendo =, = 6 = c ( ) c = De esta forma queda completamente determinada la ecuación de la parábola ( 3) = 8( ) nos confirma que la parábola se abre hacia la izquierda.. La circunferencia Definición Una circunferencia es el lugar geométrico de los puntos del plano que están a una distancia constante de un punto fijo (llamado centro), como se muestra en la figura (), ala distancia fija se le llama radio(r). De acuerdo con la figura podemos determinar q la ecuación canónica de la circunferencia aplicando pitágoras para determinar la longitud r, r = ( h) +( k) r =( h) +( k) Eje Y (,) r k C=(h,k) h Eje X Figura. Por tanto la ecuación canónica de una circunferencia de centro (h, k) radior viene dada por ( h) +( k) = r Ejemplo 6 Veamos ahora la circunferencia con ecuación canónica ( +) +( ) = dado que la circunferencia queda completamente determinada al saber el radio r = su centro c =(, ), para este caso particular podemos ver la gráfica en la figura(3) 9
10 . La circunferencia Jorge Monge Fallas Figura 3. ( +) +( ) = Ejemplo 7 Ahora tomamos la ecuación de una cirncunferencia que no está en su forma canónica + =6 en este caso aplicaremos el proceso inverso para obtener la forma canónica de la circunferencia. Completando cuadrados para e se tiene + = = = = 9 +( 3) = 9 ( 0) +( 3) = 9 De esta forma la ecuación ( 0) +( 3) =9corresponde a la ecuación canónica de una circunferencia con centro C =(0, 3) radio3. La gráfica se muestra en la figura () 0
11 .3 Elipse Jorge Monge Fallas Figura. + =6.3 Elipse Definición 3 La elipse es el conjunto de puntos del plano cua suma de las distancias a dos puntos fijos de ese plano es constante, a los puntos fijos se les llama focos. En la figura (5), se establece la condición para que un punto P,pertenezcaalaelipse.Setieneque d (P, F) + d (P, F) = a Donde a es la distancia del centro al vértice como se muetra en la figura (6) Figura 5.
12 .3 Elipse Jorge Monge Fallas En la figura (6), c es la distancia del centro al foco. Al segmento que une los vértices se le llama eje maor al segmento cua longitud es b pasa por el centro se le llama eje menor. Además a, b c están relacionados por la ecuación b = a c.3. La ecuación canónica de la elipse: Figura 6.. La ecuación canónica para una elipse con eje maor horizontal de centro C =(h, k) viene dada por ( h) ( k) a + b =,a>b Eje maor horizontal (Figura 6). La ecuación canónica para una elipse con eje maor vertical de centro C =(h, k) viene dada por ( h) ( k) b + a =,a>b Eje maor vertical (Figura 7) La figura (7), corresponde a una elipse cuo eje maor es vertical.
13 .3 Elipse Jorge Monge Fallas Figura 7. Losfocosestánenelejemaoraunadistanciac del centro, con b = a c centro al foco. c es la distancia del Definición Eentricidad: Mide el achatamiento de la elipse viene dada por Si e< la elipse se aplana Si e 0 la elipse tiende a una circunferencia e = c a Como se puede ver, la ecuación de la elipse requiere un número maor de constantes por determinar en consecuencia para caracterizarla se necesitan los dos focos, los dos vértices, el centro las dimensiones tanto del eje maor como el eje menor. Además es importante reconocer si el eje maor es horizontal o vertical la relación entre a, b c que para el caso de una elipse, estas constantes están relacionados por medio de la ecuación b = a c esto implica que en una elipse a>c>0 a>b. Cuando a = b entonces la elipse degenera en una circunferencia de radio a = b. Ejemplo 8 Consideremos la elipse con ecuación canónica ( ) + ( ) 9 dado que a>bse tiene que a =3 b =. Como a que es el maor está sobre la variable esto indica que el eje maor de la elispe es vertical con centro C =(, ), vértices V =(, ± 3).Como para los focos se es necesario c utilizamos la reclación b = a c para determinarla = =3 c c = 5 así los focos serían F =, ± 5, la dimensión del eje maor es a =6 la del eje b =. menor es 3
14 .3 Elipse Jorge Monge Fallas Al igual como se hizo con las ecuaciones de las cónicas anteriores, podemos desarrollar los cuadrados para obtener ( ) ( ) + 9 = = multiplicando por = = 0 que corresponde a una ecuación general de segundo grado como en () con A =9,B =0,C =,D = 36,E = 8 F =. La gráfica de esta elipse se ve como en la figura(8) Figura 8. ( ) + ( ) 9 = Ejemplo 9 De igual forma veamos la elipse con ecuación canónica ( +) + = podemos obaservar que a = b =.Comoaque es el maor está sobre la variable esto indica que el eje maor de la elispe es horizontal con centro c =(0, ), vértices V =(0±, ).Como para los focos se es necesario c utilizamos la reclación b = a c para determinarla = c c = 3 así los focos serían F = 0 ± 3,, la dimensión del eje maor es a = la del eje menor es b =. Al igual como se hizo con las ecuaciones de las cónicas anteriores podemos desarrollar los cuadrados
15 .3 Elipse Jorge Monge Fallas para obtener ( +) + = = multiplicando por = = 0 que corresponde a una ecuación general de segundo grado como en () con A =,B =0,C =,D = 0,E =8 F =0. La gráfica de esta elipse se ve como en la figura(9) Figura 9. ( +) + = Ejemplo 0 Ahora tomamos la ecuación de una elipse que no está en su forma canónica Completando cuadrados para e se tiene = = + 8 = + + = ( ) + + = ( ) = ( ) +( ) = 6 dividiendo entre 6 ( ) ( ) + 6 = 5
16 .3 Elipse Jorge Monge Fallas se tiene que a = b =. La elispe es horizontal con centro C =(, ), vértices V =(±, ).Calculamos c utilizando la reclación b = a c, = c c = así los focos serían F = ±,, la dimensión del eje maor es a =8 la del eje b =. La gráfica de esta parábola se ve como en la figura menor es Figura 0. ( ) 6 + ( ) = Ejemplo También podemos determinar la ecuación de una elipse a partir de cierta información, por ejemplo: Determinar la ecuación de la elipse con centro en (5, ), un vértice está en (5, ) un etremo del eje menor en (3, ). Dado que el centro el foco son colineales están sobre una recta ( =5)paralela al eje Y la elipse es una elipse vertical. Como a es la distancia del centro al vértice se tiene que a =3 la distancia del centro a los etremos del eje menor es b =. Como b = a c de esta forma la ecuación canónica de la elipse es =3 c c = 5 ( 5) + ( ) 9 Ejemplo Ahora determinenos la ecuación de la elipse que satisface esta nuevas condiciones; Los ejes de la elipse están en los ejes coordenados, los puntos (, 3) (, ) pertenecen a la elipse. Cuando se dice que los ejes de la elipse están en los ejes coordenado se conclue que el centro C, es C =(0, 0). Que los puntos (, 3) (, ) pertenezcanalaelipse,nonosdicenadasobrelaforma de la elipse si es horizontal o vertical. Una alternativa puede ser dibujar los puntos así decidir cual ecuación canónica corresponde. En la figura están representados el centro los dos puntos = 6
17 .3 Elipse Jorge Monge Fallas Figura. Se conclue que la elipse es horizontal debido que la elipse es simetrica tanto al eje maor como al eje menor, como se puede ver en la figura es imposible lograr la simetría sobre el eje Y con una elipse vertical. Por lo tanto la ecuación canónica tiene la forma de a + b = Para determinar a b utilizamos el hecho de que los puntos (, 3) (, ) deben satisfacer la ecuación de la elipse. Para (, 3) se tiene Para (, ) se tiene a + 3 b = 6 a = 9 b 6 a = b 9 b a 6 = ( ) b b 9 a = µ b a + b = a = 6 b a = b 6 b a b = b 6 b 9 6 7
18 . La hipérbola Jorge Monge Fallas Igualando resolviendo para b se tiene b b 6 b 6 = = µ b b 9 6 b 9 6 como b 6= 0 b 9 = 6b 56 5b = 7 b = 7 5 a = 7 7 La ecuación canónica correspondien es En la figura se muestran los puntos (, 3) (, ), elcentroc =(0, 0) la elipse que satisface las condiciones planteadas. = La hipérbola Figura Definición 5 Una hipérbola es el lugar geométrico de todos los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos (llamados focos)de ese plano es constante. De acuerdo con la figura (3) ladefinición de hipérbola, P pertenece a la hipérbola si d (P, F) d (P, F) = a, dondea es la distancia del centro al vértice, igual que en la elipse, de igual forma para c. = 8
19 . La hipérbola Jorge Monge Fallas Figura 3. En la figura (), c es la distancia del centro al foco. A la recta que pasa por los vértices se le llama eje transversal a la recta que pasa por el centro es perpendicualar al eje transversal se le llama eje conjugado. Además a, b c están relacionados por la ecuación b = c a Figura. En la figura (5), c es la distancia del centro al foco. Además a, b c están relacionados por la ecuación b = c a 9
20 . La hipérbola Jorge Monge Fallas.. La ecuación canónica de una hipérbola : Figura 5.. La ecuación canónica para una hipérbola con eje transversal horizontal de centro C =(h, k) viene dada por ( h) a ( k) b = Eje transversal horizontal (Figura ) Asíntotas de la Hipérbola = k + b ( h) a = k b ( h) a. La ecuación canónica para una hipérbola con eje transversal vertical de centro C =(h, k) viene dada por ( k) a ( h) b = Eje transversal vertical (Figura 6) Asíntotas de la Hipérbola = k + a ( h) b = k a ( h) b La figura (6), corresponde a una hipérbola cuo eje transversal es vertical. 0
21 . La hipérbola Jorge Monge Fallas Figura 6. Definición 6 Eentricidad: Mide el achatamiento de la hipérbola viene dada por e = c a Si e> las ramas de la hipérbola son casi planas. Si e las ramas de la hipérbola son más puntiagudas. Al igual que la ecuación de la elipse, la ecuación de la hipérbola requiere un número igual de constantes por determinar para caracterizarla se necesitan además de los focos, los vértices el centro, las ecuaciones de las asíntotas. Destacamos el eje transversal el eje conjugado, la relación entre a, b c que está dada por ecuación b = c a esto implica que en una hipérbola c>a>0 a b o b a. Ejemplo 3 Consideremos la hipérbola con ecuación canónica ( ) ( ) = 9 como la variable positiva es (o bien el signo negativo está sobre ) se tiene una hipérbola con eje transversal horizontal con a = b =3. El centro es C =(, ), vértices V =(±, ).Para los focos es necesario c, utilizamos la reclación b = c a para determinarla 3 = c c = 3 así los focos serían F = ± 3,, como se ve en la figura, las dimensiones del rectángulo para nuestra hipérbola son a = b =6. Las ecuaciones de las asíntotas vienen dadas por como se muestra en la figura (7). = + 3 ( ) = 3 ( )
22 . La hipérbola Jorge Monge Fallas Ejemplo Desarrollando los cuadrados podemos obtener ( ) ( ) 9 = = multiplicando por = = 0 que corresponde a una ecuación general de segundo grado como en () con A =9,B =0,C =,D = 36,E =8 F =. La gráfica de esta hipérbola se ve como en la siguiente figura Figura 7. ( ) ( ) 9 = Ejemplo 5 De igual forma veamos la hipérbola con ecuación canónica ( +) = la variable positiva es (o bien el signo negativo está sobre ) se tiene una hipérbola con eje transversal vertical con a = b =. El centro es c =(0, ), vértices V =(0, ± ).Determinamos c utilizando la reclación b = c a = c c = 5 así los focos serían F = 0, ± 5, como se ve en la figura(0) las dimensiones del rectángulo para nuestra hipérbole son a = b =.
23 . La hipérbola Jorge Monge Fallas Desarrollando los cuadrados podemos obtener ( +) = + + = multiplicando por = 8 + = 0 que corresponde a una ecuación general de segundo grado como en () con A =,B =0,C =,D = 0,E =8 F =0. La gráfica de esta hipérbola se ve como en la siguiente figura Figura 8. ( +) = Ejemplo 6 Ahora tomamos la hipérbola dada por la ecuación de segundo grado + 8 =6 3
24 . La hipérbola Jorge Monge Fallas Completando cuadrados para e se tiene + 8 = = = 6 ( ) + + = 6 ( ) = 6 ( ) + + = 9 ( ) ( +) = 9 dividiendo entre 9 ( ) ( +) 9 9 = como 9 = 9 se tiene ( ) ( +) 9 9 = se tiene que a =3b = 3. La hipérbola es horizontal con centro C =(, ), vértices V = ( ± 3, ).Calculamos c utilizando la reclación b = c a µ 3 = c (3) r 9 5 = c 9 c = Ã r! 5 así los focos serían F = ±,, la dimensión del eje maor es a =8 la del eje menor es b =. La gráfica de esta hipérbola se ve como en la siguiente figura Figura =6
25 . La hipérbola Jorge Monge Fallas Ejemplo 7 También podemos determinar la ecuación de unahipérbolaapartirdeciertainforma- ción, por ejemplo: Determinar la ecuación de la hipérbola con asíntotas =3; = 3 vértices en (, 0) (, 0). Dadoµ que el centro es el punto medio del segmento que une los vértices(o los focos) se tiene que + c =, 0+0 =(0, 0) además tenemos que a =. Por la posición de los vértices el centro, la hipérbola es una hipérbola horizontal las ecuaciónes de las asíntotas están dadas por = k ± b a ( h), es decir = ± b como las ecuaciones de nuestra hipérbola son = ±3 a concluimos que b =3comoa = b = a de esta forma la ecuación canónica de la hipérbola es 6 = Ejemplo 8 Sean P =(, ), A =( 3, 0), B =( 3, 3).Determine la ecuación de la hipérbola que contiene los puntos P, para los cuales d(p, A) d(p, B) = Lo que se establece con la epresión d(p, A) d(p, B) =es la definición de la hiperbola, esto es, el conjunto de puntos P cua diferencia de las distancias a dos puntos fijosllamadosfocos es constante(a). LoqueimplicaquelospuntosA B corresponde a los focos de nuestra hipérbola el centro es el punto medio del segmento que une los focos(o los vértices) se tiene que C = µ 3+ 3, 0+3 µ = 3, 3 además tenemos que c = 3.Por la posición de los focos el centro, la hipérbola es una hipérbola vertical. Por otro lado como la diferencia de las distancias es igual a a, setienequea = a = µ r 3 b = () 5 b = de esta forma se tiene µ 3 ( +3) 5 = 5
26 . La hipérbola Jorge Monge Fallas Figura 30. µ 3 ( +3) 5 = El siguiente teorema nos permite sin necesidad de completar cuadrados, saber que gráfica le corresponde a una ecuación general de segundo grado, claro que es sólo para saber qué es, pués si se tiene que graficar, la ecuación canónica es fundamental. Teorema Ecuación general: La gráfica de A + C + D + E + F =0 es una de las siguientes cónicas a. La circunferencia si A = C b. Parábola si AC =0 A =0 o C =0pero no ambos c. Elipse si AC > 0 A C tienen el mismo signo d. Hipérbola si AC < 0 A C tienen diferente signo Podemos a partir de la ecuación general obtener la forma canónica de cualquiera de las cónicas, esto por medio del procedimiento de completar cuadrados, como se ha hecho en los ejemplos anteriores. Ejemplo 9 Dadas las ecuaciones, determine la forma canónica de la cónica e indique todas sus características. Dibuje la cónica a) =0 De acuerdo con el teorema anterior podemos confirmar que la ecuación = 0 corresponde a la ecuación de una hipérbola, dado que A = C = 9 por lo que AC < 0. Completando cuadrados 6
27 . La hipérbola Jorge Monge Fallas ( + ) 9( + ) = 3 ( ) 6 9( ) +9= 3 ( ) 9( ) = 36 ( ) ( ) 9 = Tenemos que C =(, ) a = b =3 c = 3 V =(, +),V =(, ) F =(, + 3),F =(, 3) La gráfica de la hipérbola viene dada por Asíntotas =± 3 ( ) e = Figura 3. ( ) ( ) 9 = b) = 0 De acuerdo con el teorema anterior podemos confirmar que la ecuación =0corresponde a la ecuación de una elipse, dado que A =9 C =por lo que AC > 0. Completando cuadrados 7
28 . La hipérbola Jorge Monge Fallas 9( + ) + = 0 9( ) 36 + = 0 9( ) + =6 9( ) = ( ) = C =(, 0) a = b = 3 c = 8 9 V =(, 0+),V =(, 0 ) F =(, ),F =(, ) e = 8 9 = 9 La gráfica de la elipse viene dada por Figura 3. ( ) = 8
Introducción La Circunferencia Parábola Elipse Hiperbola. Conicas. Hermes Pantoja Carhuavilca
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
GEOMETRÍA ANALÍTICA LA CIRCUNFERENCIA
 LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
7. Cónicas. Propiedades métricas y ópticas
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
IX. LA PARÁBOLA 9.1. LA PARÁBOLA COMO LUGAR GEOMÉTRICO 9.2. CONSTRUCCIÓN DE UNA PARÁBOLA CON REGLA Y COMPÁS
 IX LA PARÁBOLA 9 LA PARÁBOLA COMO LUGAR GEOMÉTRICO Definición: Se llama parábola al lugar geométrico de un punto P que se mueve en un plano, en forma tal que su distancia a un punto fijo F (llamado foco)
IX LA PARÁBOLA 9 LA PARÁBOLA COMO LUGAR GEOMÉTRICO Definición: Se llama parábola al lugar geométrico de un punto P que se mueve en un plano, en forma tal que su distancia a un punto fijo F (llamado foco)
3. La circunferencia.
 UNIDAD 8: RESOLVAMOS CON GEOMETRÍA ANALITICA. 3. La circunferencia. Objetivos conceptuales. Definir el concepto de circunferencia. Objetivos procedimentales. Calular el radio, el centro, algunos puntos
UNIDAD 8: RESOLVAMOS CON GEOMETRÍA ANALITICA. 3. La circunferencia. Objetivos conceptuales. Definir el concepto de circunferencia. Objetivos procedimentales. Calular el radio, el centro, algunos puntos
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos)
 CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta llamada directriz.
 UNIDAD IV: LA PARABOLA. 4.1. Caracterización geométrica. 4.1.1. La parábola como lugar geométrico. Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta
UNIDAD IV: LA PARABOLA. 4.1. Caracterización geométrica. 4.1.1. La parábola como lugar geométrico. Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
MATEMÁTICAS UNIDAD 4 GRADO 10º. Cónicas y repaso de funciones
 1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 10º Cónicas y repaso de funciones 1 Franklin Eduardo Pérez Quintero LOGRO: Reconoce la formación y características básicas de las secciones
1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 10º Cónicas y repaso de funciones 1 Franklin Eduardo Pérez Quintero LOGRO: Reconoce la formación y características básicas de las secciones
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO PLANTEL IGNACIO RAMÍREZ CALZADA DE LA ESCUELA PREPARATORIA PROBLEMARIO GEOMETRÍA ANALÍTICA
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO PLANTEL IGNACIO RAMÍREZ CALZADA DE LA ESCUELA PREPARATORIA PROBLEMARIO GEOMETRÍA ANALÍTICA ELABORO: ING. ROBERTO MERCADO DORANTES SEPTIEMBRE 2008 Sistemas coordenados
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO PLANTEL IGNACIO RAMÍREZ CALZADA DE LA ESCUELA PREPARATORIA PROBLEMARIO GEOMETRÍA ANALÍTICA ELABORO: ING. ROBERTO MERCADO DORANTES SEPTIEMBRE 2008 Sistemas coordenados
La representación gráfica de una función cuadrática es una parábola.
 Función Cuadrática A la función polinómica de segundo grado +bx+c, siendo a, b, c números reales y, se la denomina función cuadrática. Los términos de la función reciben los siguientes nombres: La representación
Función Cuadrática A la función polinómica de segundo grado +bx+c, siendo a, b, c números reales y, se la denomina función cuadrática. Los términos de la función reciben los siguientes nombres: La representación
La definición de una parábola es el conjunto de puntos equidistantes de un punto llamado foco y una línea llamada la directriz.
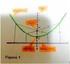 Materia: Matemática de 5to Tema: La Parábola Marco Teórico Cuando se trabajaste con parábolas en el pasado probablemente estés acostumbrado a ver la parábola en forma de vértice y analizado el gráfico
Materia: Matemática de 5to Tema: La Parábola Marco Teórico Cuando se trabajaste con parábolas en el pasado probablemente estés acostumbrado a ver la parábola en forma de vértice y analizado el gráfico
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA
 De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
Profesorado de Nivel Medio y Superior en Biología Matemática - 1º Cuatrimestre Año 2013 FUNCIÓN CUADRÁTICA
 Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
La recta se define como el lugar geométrico de todos los puntos de un plano que al tomarse de dos en dos se obtiene la misma pendiente.
 Formas de la ecuación de una recta. Hasta el momento, se han dado algunas características de la recta tales como la distancia entre dos puntos, su pendiente, su ángulo de inclinación, relación entre ellas,
Formas de la ecuación de una recta. Hasta el momento, se han dado algunas características de la recta tales como la distancia entre dos puntos, su pendiente, su ángulo de inclinación, relación entre ellas,
Dibujo Técnico Curvas cónicas-parábola
 22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
O -2-1 1 2 X -1- -2- de coordenadas, y representamos los números sobre cada eje, eligiendo en ambos ejes la misma unidad, como muestra la figura.
 MATEMÁTICA I Capítulo 1 GEOMETRÍA Plano coordenado Para identificar cada punto del plano con un par ordenado de números, trazamos dos rectas perpendiculares que llamaremos eje y eje y, que se cortan en
MATEMÁTICA I Capítulo 1 GEOMETRÍA Plano coordenado Para identificar cada punto del plano con un par ordenado de números, trazamos dos rectas perpendiculares que llamaremos eje y eje y, que se cortan en
Problema a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente.
 Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
5x + 4y 20 = 0! 5 ( x) + 4 ( y) 20 = 0! 5x 4y 20 = 0. al origen O. En resumen, la ecuación 5x + 4y 20 = 0 no tiene ninguna simetría.
 Geometría Analítica; C. H. Lehmann. Ejercicio, grupo, capítulo II, página 0.. Discute la ecuación + 0 = 0, estudiando las intersecciones, las simetrías la etensión. Después traza la grá ca correspondiente.
Geometría Analítica; C. H. Lehmann. Ejercicio, grupo, capítulo II, página 0.. Discute la ecuación + 0 = 0, estudiando las intersecciones, las simetrías la etensión. Después traza la grá ca correspondiente.
APUNTES DE GEOMETRÍA ANALÍTICA
 CAPÍTULO 1: LA RECTA EN EL PLANO Conceptos Primitivos: Punto, recta, plano. APUNTES DE GEOMETRÍA ANALÍTICA Definición 1 (Segmento) Llamaremos segmento a la porción de una línea recta comprendida entre
CAPÍTULO 1: LA RECTA EN EL PLANO Conceptos Primitivos: Punto, recta, plano. APUNTES DE GEOMETRÍA ANALÍTICA Definición 1 (Segmento) Llamaremos segmento a la porción de una línea recta comprendida entre
LA CIRCUNFERENCIA. x y r. (x h) (y k) r. d(p; 0) x y r. d(p; C) (x h) (y k) r. Definición. Ecuación de la circunferencia. Geometría Analítica 3
 Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
UNIDAD IV DISTANCIA ENTRE DOS PUNTOS
 UNIDAD IV DISTANCIA ENTRE DOS PUNTOS Dados los puntos: P(x1, y1) y Q(x2, y2), del plano, hallemos la distancia entre P y Q. Sin pérdida de generalidad, tomemos los puntos P y Q, en el primer cuadrante
UNIDAD IV DISTANCIA ENTRE DOS PUNTOS Dados los puntos: P(x1, y1) y Q(x2, y2), del plano, hallemos la distancia entre P y Q. Sin pérdida de generalidad, tomemos los puntos P y Q, en el primer cuadrante
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Tema 7: Geometría Analítica. Rectas.
 Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES
 UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
IES Fco Ayala de Granada Septiembre de 2011 (Septiembre Modelo 2) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
SUPERFICIES CUÁDRICAS
 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
Precálculo 1 - Ejercicios de Práctica. 1. La pendiente de la línea (o recta) que pasa por los puntos P(2, -1) y Q(0, 3) es:
 Precálculo 1 - Ejercicios de Práctica 1. La pendiente de la línea (o recta) que pasa por los puntos P(2, -1) y Q(0, 3) es: a. 2 b. 1 c. 0 d. 1 2. La ecuación de la línea (recta) con pendiente 2/5 e intercepto
Precálculo 1 - Ejercicios de Práctica 1. La pendiente de la línea (o recta) que pasa por los puntos P(2, -1) y Q(0, 3) es: a. 2 b. 1 c. 0 d. 1 2. La ecuación de la línea (recta) con pendiente 2/5 e intercepto
ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE G E O M É T R Í A GUÍA A N A L Í T I C A
 CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
DISTANCIA ENTRE DOS PUNTOS EN EL PLANO CARTESIANO.
 RAZONAMIENTO Y DEMOSTRACIÓN Determina la distancia entre pares de puntos. Calcula las coordenadas del punto medio del segmento cuyos extremos son dos puntos dados. Halla la pendiente de una recta. COMUNICACIÓN
RAZONAMIENTO Y DEMOSTRACIÓN Determina la distancia entre pares de puntos. Calcula las coordenadas del punto medio del segmento cuyos extremos son dos puntos dados. Halla la pendiente de una recta. COMUNICACIÓN
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
Funciones 1. D = Dom ( f ) = x R / f(x) R. Recuerda como determinabas los dominios de algunas funciones: x x
 Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones Cuadráticas en una Variable Real
 en una Variable Real Carlos A. Rivera-Morales Precálculo I Tabla de Contenido Contenido adrática : Contenido Discutiremos: qué es una función cuadrática : Contenido Discutiremos: qué es una función cuadrática
en una Variable Real Carlos A. Rivera-Morales Precálculo I Tabla de Contenido Contenido adrática : Contenido Discutiremos: qué es una función cuadrática : Contenido Discutiremos: qué es una función cuadrática
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
21. Círculo y recta Matemáticas II, 2012-II. Por qué el círculo y la recta son tan importantes?
 . Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
. Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
Función cuadrática. Ecuación de segundo grado completa
 Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
En la notación C(3) se indica el valor de la cuenta para 3 kilowatts-hora: C(3) = 60 (3) = 1.253
 Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
GIMNASIO VIRTUAL SAN FRANCISCO JAVIER Valores y Tecnología para la Formación Integral del Ser Humano UNIDAD I FUNCIONES
 UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
Geometria Analítica Laboratorio #1 Sistemas de Coordenadas
 1. Verificar las identidades siguientes: 1) P (3, 3), Q( 1, 3), R(4, 0) Laboratorio #1 Sistemas de Coordenadas 2) O( 10, 2), P ( 6, 3), Q( 5, 1) 2. Demuestre que los puntos dados forman un triángulo isósceles.
1. Verificar las identidades siguientes: 1) P (3, 3), Q( 1, 3), R(4, 0) Laboratorio #1 Sistemas de Coordenadas 2) O( 10, 2), P ( 6, 3), Q( 5, 1) 2. Demuestre que los puntos dados forman un triángulo isósceles.
5.5 LÍNEAS TRIGONOMÉTRICAS
 5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
PARÁBOLA UNIDAD IX IX.1 DEFINICIÓN DE PARÁBOLA
 PARÁBOLA UNIDAD IX IX.1 DEFINICIÓN DE PARÁBOLA La parábola se define como el lugar geométrico de los puntos que equidistan de un punto fijo en el plano llamado foco de una recta también fija en el plano
PARÁBOLA UNIDAD IX IX.1 DEFINICIÓN DE PARÁBOLA La parábola se define como el lugar geométrico de los puntos que equidistan de un punto fijo en el plano llamado foco de una recta también fija en el plano
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Función Cuadrática: Es toda función de la forma: f() = a ² + b + c con a, b, c números Reales Puede suceder que b ó c sean nulos, por ej: f() = ½ ² + 5 f() = 5 ² ¾ Pero a no puede ser = 0, de los contrario
Función Cuadrática: Es toda función de la forma: f() = a ² + b + c con a, b, c números Reales Puede suceder que b ó c sean nulos, por ej: f() = ½ ² + 5 f() = 5 ² ¾ Pero a no puede ser = 0, de los contrario
AYUDAS SOBRE LA LINEA RECTA
 AYUDAS SOBRE LA LINEA RECTA AYUDA : Grafiquemos la función Solución: Se debe escoger algunos números que representan a la variable x, para obtener el valor de la variable y respectivamente así: El proceso:
AYUDAS SOBRE LA LINEA RECTA AYUDA : Grafiquemos la función Solución: Se debe escoger algunos números que representan a la variable x, para obtener el valor de la variable y respectivamente así: El proceso:
EJERCICIOS PROPUESTOS
 EJERCICIOS PROPUESTOS ) Se dan los siguientes puntos por sus coordenadas: A(3, 0), B(, 0), C(0, ) y sea P un punto variable sobre el eje. i) Hallar la ecuación de la recta (AC) y de la recta (r) perpendicular
EJERCICIOS PROPUESTOS ) Se dan los siguientes puntos por sus coordenadas: A(3, 0), B(, 0), C(0, ) y sea P un punto variable sobre el eje. i) Hallar la ecuación de la recta (AC) y de la recta (r) perpendicular
Aplicación: cálculo de áreas XII APLICACIÓN: CÁLCULO DE ÁREAS
 XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS
 V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS 134 5.1. DISCUSIÓN DE UNA ECUACIÓN Discutir una ecuación algebraica representada por una epresión en dos variables de la forma f (, y) = 0, significa analizar algunos
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS 134 5.1. DISCUSIÓN DE UNA ECUACIÓN Discutir una ecuación algebraica representada por una epresión en dos variables de la forma f (, y) = 0, significa analizar algunos
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES
 SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
Ecuaciones Lineales en Dos Variables
 Ecuaciones Lineales en Dos Variables Una ecuación lineal en dos variables tiene la forma general a + b + c = 0; donde a, b, c representan números reales las tres no pueden ser iguales a cero a la misma
Ecuaciones Lineales en Dos Variables Una ecuación lineal en dos variables tiene la forma general a + b + c = 0; donde a, b, c representan números reales las tres no pueden ser iguales a cero a la misma
LUGARES GEOMÉTRICOS. CÓNICAS
 9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
Funciones y sus gráficas
 y sus gráficas Marzo de 2006 Índice 1 polinómicas función constante función lineal función afín función cuadrática 2 racionales función de proporcionalidad inversa función racional 3 exponenciales 4 Ejemplos
y sus gráficas Marzo de 2006 Índice 1 polinómicas función constante función lineal función afín función cuadrática 2 racionales función de proporcionalidad inversa función racional 3 exponenciales 4 Ejemplos
#Desarrollo. Evaluación Actividad:2 Producto: Investigación. Puntaje: Saberes. Investiga la aplicación de la parábola en su entorno.
 #Desarrollo Actividad: En equipo, investiga cinco aplicaciones de la parábola, describe cada una de ellas, añade las imágenes correspondientes y entrega un reporte escrito a tu profesor. El reporte deberá
#Desarrollo Actividad: En equipo, investiga cinco aplicaciones de la parábola, describe cada una de ellas, añade las imágenes correspondientes y entrega un reporte escrito a tu profesor. El reporte deberá
Ejemplos resueltos: CIRCUNFERENCIA Y ELIPSE
 Ejeplo : Deterina la ecuación de la circunferencia con centro en (,) y que pasa por el punto (,5) Respuesta: ( x + ) + ( y ) 0 Ejeplo : Deterina centro, radio y grafica de x 6x + y + y (x- )² + (y + /)²
Ejeplo : Deterina la ecuación de la circunferencia con centro en (,) y que pasa por el punto (,5) Respuesta: ( x + ) + ( y ) 0 Ejeplo : Deterina centro, radio y grafica de x 6x + y + y (x- )² + (y + /)²
Lección 12: Sistemas de ecuaciones lineales
 LECCIÓN 1 Lección 1: Sistemas de ecuaciones lineales Resolución gráfica Hemos visto que las ecuaciones lineales de dos incógnitas nos permiten describir las situaciones planteadas en distintos problemas.
LECCIÓN 1 Lección 1: Sistemas de ecuaciones lineales Resolución gráfica Hemos visto que las ecuaciones lineales de dos incógnitas nos permiten describir las situaciones planteadas en distintos problemas.
EJERCICIOS RESUELTOS DE CÓNICAS
 EJERCICIOS RESUELTOS DE CÓNICAS 1. Hallar la ecuación de la circunferencia que tiene: a) el centro en el punto (, 5) y el radio es igual a 7. b) un diámetro con extremos los puntos (8, -) y (, 6). a) La
EJERCICIOS RESUELTOS DE CÓNICAS 1. Hallar la ecuación de la circunferencia que tiene: a) el centro en el punto (, 5) y el radio es igual a 7. b) un diámetro con extremos los puntos (8, -) y (, 6). a) La
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
PROF: Jesús Macho Martínez
 DIBUJO TÉCNICO ELEMENTAL PROF: Jesús Macho Martínez 1º.- Trazar la perpendicular a r por el punto P. 2º.- Trazar la bisectriz del ángulo que forman r y s. P * r r s 3º.- Trazar las tangentes interiores
DIBUJO TÉCNICO ELEMENTAL PROF: Jesús Macho Martínez 1º.- Trazar la perpendicular a r por el punto P. 2º.- Trazar la bisectriz del ángulo que forman r y s. P * r r s 3º.- Trazar las tangentes interiores
Universidad de la Frontera. Geometría Anaĺıtica: Departamento de Matemática y Estadística. Cĺınica de Matemática. J. Labrin - G.
 Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 CTIVIDDES DE GEMETRÍ PR 4º ES DE EPV Nombre y apellidos: Curso: TEM 1: TRZDS BÁSICS. 1. RECTS PRLELS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar. 1.1. Trazado
CTIVIDDES DE GEMETRÍ PR 4º ES DE EPV Nombre y apellidos: Curso: TEM 1: TRZDS BÁSICS. 1. RECTS PRLELS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar. 1.1. Trazado
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
Distancia entre un punto y una recta
 Distancia entre un punto una recta Frecuentemente en geometría nos encontramos con el problema de calcular la distancia desde un punto a una recta. Distancia de un punto a una recta La fórmula para calcular
Distancia entre un punto una recta Frecuentemente en geometría nos encontramos con el problema de calcular la distancia desde un punto a una recta. Distancia de un punto a una recta La fórmula para calcular
Parciales Matemática CBC Parciales Resueltos - Exapuni.
 Parciales Matemática CBC 2012 Parciales Resueltos - Exapuni www.exapuni.com.ar Compilado de primeros parciales del 2012 Parcial 1 1) Sea. Hallar todos los puntos de la forma, tales que la distancia entre
Parciales Matemática CBC 2012 Parciales Resueltos - Exapuni www.exapuni.com.ar Compilado de primeros parciales del 2012 Parcial 1 1) Sea. Hallar todos los puntos de la forma, tales que la distancia entre
VII. ECUACIÓN GENERAL DE SEGUNDO GRADO
 VII. ECUACIÓN GENERAL DE SEGUNDO GRADO 7.. SECCIONES CÓNICAS Cuando un plano corta a un cono circular recto de dos mantos, la sección que resulta de dicho corte determina ciertas curvas llamadas CÓNICAS.
VII. ECUACIÓN GENERAL DE SEGUNDO GRADO 7.. SECCIONES CÓNICAS Cuando un plano corta a un cono circular recto de dos mantos, la sección que resulta de dicho corte determina ciertas curvas llamadas CÓNICAS.
GEOMETRÍA ANALÍTICA: CÓNICAS
 GEOMETRÍA ANALÍTICA: CÓNICAS 1.- GENERALIDADES Se define lugar geométrico como el conjunto de puntos que verifican una propiedad conocida. Las cónicas que estudiaremos a continuación se definen como lugares
GEOMETRÍA ANALÍTICA: CÓNICAS 1.- GENERALIDADES Se define lugar geométrico como el conjunto de puntos que verifican una propiedad conocida. Las cónicas que estudiaremos a continuación se definen como lugares
B22 Homología. Geometría plana
 Geometría plana B22 Homología Homología y afinidad Homología: es una transformación biunívoca e inequívoca entre los puntos de dos figuras F y F'. A cada punto y recta de la figura F le corresponde un
Geometría plana B22 Homología Homología y afinidad Homología: es una transformación biunívoca e inequívoca entre los puntos de dos figuras F y F'. A cada punto y recta de la figura F le corresponde un
1 er Problema. 2 Problema
 Facultad de Contaduría Administración. UNAM Lugares geométricos Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS LUGARES GEOMÉTRICOS Eisten dos problemas fundamentales en la Geometría Analítica:.
Facultad de Contaduría Administración. UNAM Lugares geométricos Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS LUGARES GEOMÉTRICOS Eisten dos problemas fundamentales en la Geometría Analítica:.
Función lineal Ecuación de la recta
 Función lineal Ecuación de la recta Función constante Una función constante toma siempre el mismo valor. Su fórmula tiene la forma f()=c donde c es un número dado. El valor de f() en este caso no depende
Función lineal Ecuación de la recta Función constante Una función constante toma siempre el mismo valor. Su fórmula tiene la forma f()=c donde c es un número dado. El valor de f() en este caso no depende
*SIMETRAL DE UN TRAZO.: perpendicular en el punto medio.
 *DISTANCIA ENTRE DOS PUNTOS EN EL PLANO: P(x a, y b ). Q(x a, y b ) 2 b + ya yb d= ( ) ( ) 2 x a x *SIMETRAL DE UN TRAZO.: perpendicular en el punto medio. *ALTURA: perpendicular bajada del vértice al
*DISTANCIA ENTRE DOS PUNTOS EN EL PLANO: P(x a, y b ). Q(x a, y b ) 2 b + ya yb d= ( ) ( ) 2 x a x *SIMETRAL DE UN TRAZO.: perpendicular en el punto medio. *ALTURA: perpendicular bajada del vértice al
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
LA RECTA. Ax By C 0. y y m x x. y mx b. Geometría Analítica 2 ECUACIÓN GENERAL. Teorema: ECUACIÓN PUNTO - PENDIENTE .
 LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
GEOMETRIA ANALITICA- GUIA DE EJERCICIOS DE LA RECTA Y CIRCUNFERENCIA PROF. ANNA LUQUE
 Ejercicios resueltos de la Recta 1. Hallar la ecuación de la recta que pasa por el punto (4. - 1) y tiene un ángulo de inclinación de 135º. SOLUCION: Graficamos La ecuación de la recta se busca por medio
Ejercicios resueltos de la Recta 1. Hallar la ecuación de la recta que pasa por el punto (4. - 1) y tiene un ángulo de inclinación de 135º. SOLUCION: Graficamos La ecuación de la recta se busca por medio
IES Fco Ayala de Granada Junio de 2012 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS
 CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS Yuli Andrea Rodríguez Rodríguez 1 Universidad Pedagógica Nacional yulyarr@gmail.co Benjamin R. Sarmiento Lugo 2 Universidad Pedagógica Nacional bsarmiento@pedagogica.edu.co
CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS Yuli Andrea Rodríguez Rodríguez 1 Universidad Pedagógica Nacional yulyarr@gmail.co Benjamin R. Sarmiento Lugo 2 Universidad Pedagógica Nacional bsarmiento@pedagogica.edu.co
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
FUNCIONES CUADRÁTICAS
 FUNCIONES CUADRÁTICAS A la función polinómica de segundo grado f(x) = ax 2 + bx + c, siendo a, b, c, números reales y a 0 se la denomina función cuadrática. Dominio de una función cuadrática es el conjunto
FUNCIONES CUADRÁTICAS A la función polinómica de segundo grado f(x) = ax 2 + bx + c, siendo a, b, c, números reales y a 0 se la denomina función cuadrática. Dominio de una función cuadrática es el conjunto
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
El plano cartesiano y Gráficas de ecuaciones. Copyright 2013, 2009, 2006 Pearson Education, Inc. 1
 El plano cartesiano y Gráficas de ecuaciones Copyright 2013, 2009, 2006 Pearson Education, Inc. 1 Sistema de coordenadas rectangulares En el cap 2 presentamos la recta numérica real que resulta al establecer
El plano cartesiano y Gráficas de ecuaciones Copyright 2013, 2009, 2006 Pearson Education, Inc. 1 Sistema de coordenadas rectangulares En el cap 2 presentamos la recta numérica real que resulta al establecer
Ángulos 1º = 60' = 3600'' 1' = 60''
 Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
IES Fco Ayala de Granada Sobrantes de 2011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
EJERCICIOS Nº 10: GEOMETRIA ANALITICA. se extiende hacia cada extremo en una longitud igual a su longitud original. Halle las coordenadas de
 EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
Vectores y rectas. 4º curso de E.S.O., opción B. Modelo de examen (ficticio)
 demattematicaswordpresscom Vectores y rectas º curso de ESO, opción B Modelo de examen (ficticio) Sean los vectores u = (,5) y v = (, ) a) Analiza si tienen la misma dirección No tienen la misma dirección
demattematicaswordpresscom Vectores y rectas º curso de ESO, opción B Modelo de examen (ficticio) Sean los vectores u = (,5) y v = (, ) a) Analiza si tienen la misma dirección No tienen la misma dirección
Solución: Las rectas paralelas a estas tienen la misma pendiente, es decir 2; por tanto la ecuación es:
 Representa las rectas y = x + e y = x y calcula el punto que tienen en común El punto que tienen en común estas dos rectas se obtiene resolviendo el siguiente sistema de ecuaciones: y = x + y = x 3 x =,
Representa las rectas y = x + e y = x y calcula el punto que tienen en común El punto que tienen en común estas dos rectas se obtiene resolviendo el siguiente sistema de ecuaciones: y = x + y = x 3 x =,
INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA
 INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA Los hombres y pueblos en decadencia viven acordándose de dónde vienen; los hombres geniales y pueblos fuertes sólo necesitan saber
INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA Los hombres y pueblos en decadencia viven acordándose de dónde vienen; los hombres geniales y pueblos fuertes sólo necesitan saber
