1. Números reales. Resuelve BACHILLERATO. Página 29
|
|
|
- Luz Macías Gómez
- hace 6 años
- Vistas:
Transcripción
1 . Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin 9 A l F B d C. Demuestr que los triángulos ABF y EBD son semejntes (es decir, demuestr que sus ángulos son respectivmente igules).. Si llmmos l l ldo del pentágono y d su digonl, bsándote en l semejnz de los triángulos que cbs de demostrr, hll l relción d y comprueb que es el número áureo: l E D d l + ϕ El ángulo B^ en el triángulo ABF, y B^ en el triángulo EBD. Por otr prte los triángulos DAB y EBD son igules, luego el ángulo A^ en el triángulo ABF, y D^ en el triángulo EBD son igules. Por tnto los triángulos son semejntes. El ldo AF d l. Por l semejnz de los triángulos ABF y EBD; BD ED ; es decir, BF AF Operndo, d(d l) l, por tnto d dl l 0. d l l d l Ls soluciones posibles pr d son l ± l + l d l ± Como d no puede ser negtiv, d l +, y d l + ϕ
2 Unidd. Números reles Lenguje mtemático: conjuntos y símbolos Págin Verddero o flso? A B El conjunto coloredo de l izquierd se puede designr A B. Verddero, porque l prte colored está formd por todos los elementos de A que no están en B. El conjunto coloredo de l izquierd se puede designr A B'. Verddero, porque l prte colored está formd por todos los elementos de A que no están en B, y que B' es el complementrio de B. El conjunto coloredo de l derech se puede designr: (A B) (B A) Verddero, porque pr que un elemento esté en el conjunto coloredo, o está en A y no está en B, o está en B y no está en A. d) El conjunto coloredo de l derech se puede designr: (A B) (A B) Verddero, porque pr que un elemento esté en el conjunto coloredo, tiene que estr en A o en B, pero no puede estr en los dos l vez (A B). e) El conjunto coloredo de l derech se puede designr (A B' ) (A' B). Verddero, porque pr que un elemento esté en el conjunto, o está en A y no está en B, o está en B y no está en A. f ) x Z x Q Verddero, porque todos los números enteros son rcionles. g) [x ( ) y x ( )] x ( ) ( n) es el conjunto de los múltiplos de n. Verddero, porque si un número es l vez múltiplo de y de, entonces es múltiplo de. h) ( ) ( ) ( ) Es l mism firmción nterior. i) x A B x A B' Verddero, porque los elementos de A B están en A y no están en B, luego están en A y en B'. j) (x A x B ) es lo mismo que decir A B. Verddero, porque l implicción indic que todo elemento de A es un elemento de B. k) (x A x B ) A B Tenemos que comprobr que ls dos siguientes firmciones son cierts: (x A x B) A B que es l firmción del prtdo j) A B x A x B, pero si B contiene A, es porque todos los elementos de A están en B, luego son equivlentes y es verdder l firmción. l) (x A x B ) B A Flso, porque puede existir lgún elemento de B que no esté en A. A B
3 Unidd. Números reles m) x (0, ) x Á y 0 < x < Verddero, porque los intervlos representn conjuntos de números reles y el intervlo (0, ) está formdo por los números comprendidos entre 0 y que son myores que 0 y menores que, luego son firmciones equivlentes. n) (Á Q) (0, ) pero / (Á Q) (0, ) Verddero, porque es un número rel que no es rcionl y es myor que, sin embrgo / tmbién es irrcionl, pero está entre 0 y. ñ) 0, (Á Q) (0, ) Flso, porque 0, es rcionl. o) ( Á Q) (0, ) es el conjunto de los números irrcionles positivos menores que. Verddero, porque son los números reles que no son rcionles, es decir, irrcionles, y demás tienen que ser myores que cero, por tnto positivos, y menores que. p) {x Z / < x } {, 0,,,,, } Verddero, porque los únicos números enteros myores que y menores o igules que son los del conjunto indicdo. q) El conjunto de los números enteros myores que y menores que 7 es Z (, 7). Verddero, porque, de los números enteros myores que y menores que 7, están en el intervlo (, 7) y demás son enteros. r) (x es un número rel pero no es rcionl) x Á Q Verddero, porque Á Q es el conjunto de todos los números reles menos los rcionles, que es equivlente decir los números reles que no son rcionles.
4 Unidd. Números reles Números reles. L rect rel Págin Reflexion y resuelve Observ cómo se sitún estos números en los conjuntos numéricos:, Ahor, en tu cuderno, sitú los siguientes números en un digrm similr: ;,; ; 0; ; ; 7/; 7/ 7, 0 7 7, 7 8, 7 N, 7, Z ; 7 ; ;,; 7 Q ; 7 ; ;,; 7 ; 0; Á, no es rel Págin Represent los siguientes conjuntos: (, ) [, + ) (, 9] d) (, 0) e) {x / x < } f ) [, ) (, 7] g) (, 0) (, + ) h) (, ) (, + ) e) g) d) f) h) Averigu y represent pr qué vlores de x se cumplen ls siguientes relciones: x x x d) x e) x > f ) x + > y x ; [, ] y d) x ; [, ] e) x < o x > ; (, ) (, + ) f) x < 9 o x > ; (, 9) (, + )
5 Unidd. Números reles Rdicles. Propieddes Págin Simplific. 9 x x 8 y d) 8 e) f ) 8 9 x x 8 Se dividen índice y exponente entre. x x 0 y y d) e) f) 8 Cuál es myor, o? Reducimos índice común: 979; 8 Por tnto, es myor. Reduce índice común. y y ; 9 9 ; 0 Simplific. kk 8 x 0 ( x) ` k j k x x x x Págin Reduce. 8 9 d) 8 e) f ) d) 8 ( ) ( ) e) Se fctorizn los rdicndos y se reduce índice común: $ $ f) Se fctorizn los rdicndos y se reduce índice común: 8 $ ( )
6 Unidd. Números reles Simplific. x x x x b b x x d) b b b c b c b bc c bc d) b c b c 7 Reduce d) d) 79 8 Sum y simplific. x+ x+ x d) e) 0 8 f) x d) e) f) Se fctorizn los rdicndos y se scn fctores de l ríz: Págin Rcionliz denomindores y simplific cunto pueds. e) i) e) g) i) f) j) g) d) f) 0 h) j) 7 8 d) h)
7 Unidd. Números reles 0 Rcionliz denomindores y simplific cunto pueds. x+ y + x+ y e) + f ) g) d) h) x+ y x y + x y x+ y ( )( + ) ( x+ y)( x ) ( )( ) y x+ y x y x x x y+ y x y y ( x + y)( x y) x y x y ( )( + ) ( )( ) + ( )( + ) ( ) + ( x+ y)( x+ y) x y xy d) + + ( x y )( x+ y ) x y ( + ) e) + + ( )( + ) 7 f) ( + ) g) h) + + ( )( ) ( ) ( ) ( ) ( )( + ) ( ) x + y+ x y x x y x y 7
8 Unidd. Números reles Logritmos. Propieddes Págin 9 Hll. log log 0, log 9 d) log 0 0, e) log f ) log 7 9 g) ln e h) ln e / i) log 0,0 j) log c m log log log 0, log log 9 0 d) log 0 0, log 0 0 e) log log f) log 7 9 log 7 7 g) ln e h) ln e / i) log 0,0 log j) log Hll l prte enter de c m log log 0. log 700. log d) log 0 0,08. e) log 9 0. f ) ln e. g) log h) log, 900. ; ; < 0 < < log 0 < log 0, ; ; < 700 < < log 700 < log 700, ; ; < 000 < < log < log 0 000, d) 0 0,0 ; 0 0, ; 0,0 < 0,08 < 0, < log 0 0,08 < log 0 0,08, e) 9 9 ; 9 8 ; 9 < 0 < 8 < log 9 0 < log 9 0, f) ln e g) log ; ; Como < < < log <. L prte enter de log es. h) log, 900,07, 80,;, 9,7 Como, 80, < 900 < 9,7, < log, 900 <. L prte enter de log, 900 es. 8
9 Unidd. Números reles Aplic l propiedd 8 pr obtener los siguientes logritmos con l yud de l clculdor: log 00 log 00 log d) log 00 0 En cd cso, comprueb el resultdo utilizndo l potencición. log 00 0,; 0, 00 log log 00,9;,9 00 log log 00,; 00, log 0 00 d) 0,80; 00 0,80 0 log 00 log 00 Clcul sbiendo que log A,8 y log B,. log log A B log A B A [ log B A log log B] [,8,] 0, 8 0,7 log A B log + log A log B +,8, +,7,8, Averigu l relción que hy entre x e y, sbiendo que se verific: ln y x ln ln y x ln ln y ln e x ln ln y ln e x y e x 9
10 Unidd. Números reles Expresión deciml de los números reles. Números proximdos Págin Verddero o flso? I. El precio de est viviend es, proximdmente, de , con un error menor que II. El precio del menú del dí es, proximdmente, de, con un error menor que. En I el error bsoluto es mucho myor que en II, pero el error reltivo es menor. I. E.R. < 0000, 0 0,0 E.R. <, % II. E.R. < 8, 0 0,08 E.R. < 8, % El error bsoluto nos lo dicen y es myor en I que en II. Hemos clculdo el error reltivo en cd cso y vemos que es verdder l firmción. Di un cot del error bsoluto y otr del error reltivo en ls siguientes mediciones: Dniel le dice su hermn Mrí que l superficie de su cs es de 9, m. Por l gripe se hn perdido 7 millones de hors de trbjo. Jun gn unos l ño. E.A. < 0,0 m ; E.R. < 00,,87 0 0,00087 E.R. < 0,0 % 9, E.A. < 0, millones de hors hors E.R. < 0, < 0,0, % 7 Si suponemos que los tres ceros finles se hn utilizdo pr poder expresr l cntidd (es decir, que se trt de 9 mil, redondendo los miles de euros ), entonces: E.A. < 0, miles de 00 E.R. < 0, < 0,07,7 % 9 Si suponemos que es 9000 exctmente: E.A. < 0, E.R. < 0, < 0, ,007 % 9000 Págin Clcul en notción científic sin usr l clculdor: ( : 0,000) 0, 0 0, ( : 0,000) 0, 0 ((8 0 ) : ( 0 )) 0 ( 0 9 ) , , , Oper con l clculdor: (,87 0,9 0 9 ) : (,9 0 ) 8, , 0 0, 0 9, 0 7, 0 (,87 0,9 0 9 ) : (,9 0 ),8 0 8, , 0 0, 0 9,
11 Unidd. Números reles Ejercicios y problems resueltos Págin. Conjuntos numéricos Hzlo tú. Clsific los siguientes números: ; 7; 0,; ; 8 ; ; ;,! 0, 7 8,. Intervlos y vlor bsoluto Hzlo tú. Indic, en cd cso, qué números cumplen ests condiciones: x + x < x + x x + 8 * 8 ) x (, 7] [, + ) x + x 7 x < 8 < x< 8 7< x < Cmbimos de signo: < x < 7 x (, 7). Simplificción de rdicles Hzlo tú. Simplific. 7 x 7 : 8 x x x x 7 8 x x x Págin. Operciones con rdicles Hzlo tú. Oper y simplific: b b Fctorizmos y scmos fctores de ls ríces: Reducimos los rdicles índice común y scmos fctores de ls ríces: 7 8b b 8 b ( ) b b b b b
12 Unidd. Números reles. Rcionlizción de denomindores Hzlo tú. Rcionliz: + Multiplicmos numerdor y denomindor por : Multiplicmos numerdor y denomindor por : ( ) ( ) + ( + )( ) 9. Problems con rdicles Hzlo tú. El volumen de un pirámide cudrngulr regulr es rist.. Hll l longitud de su B l H l l C O l L rist de l cr tringulr es igul l rist de l bse. V Pirámide A bse H l H L distnci OC es l mitd de l digonl del cudrdo OC l. L rist es l hipotenus del triángulo rectángulo de ctetos l ltur H y el ldo OC. Por ser l rist igul l ldo de l bse, H l e lo l V Pirámide l l l Por tnto, l l l & 8 & Págin 7. Definición de logritmo Hzlo tú. Clcul x : log x / log x / log 8 x 8 x 8 x x log x 8 0 x 8 x 8 x 8 x
13 Unidd. Números reles 8. Logritmos sin clculdor Hzlo tú. Hll el vlor de log 0, y de log! 0, 8 log log log log 8 / sin utilizr l clculdor Propieddes de los logritmos Hzlo tú. Si ln k,8, clcul: ln (k e ) ln c m e k ln ( k e) ln k+ ln e ln k+ ln e / ( 8, ) +, ln ck m ln k ( ln k ln e) (, 8 ) 8, e e 0. Propieddes de los logritmos Hzlo tú. Clcul x en estos csos: ln x log x log log ln x Aplicmos l propiedd de los logritmos: log m n nlog m. ( x ) ln 8 x 8 8, ln x + ln x log x log log Aplicmos ls propieddes de los logritmos: log x log log log x log 9; x 9 Soluciones: x, x Pero como no se pueden tomr logritmos de números negtivos, l únic solución válid es x. Págin. Errores y notción científic Hzlo tú. Expres el resultdo de ests operciones en notción científic y cot el error bsoluto y el error reltivo cometidos: ( : 0,000) (0,008), 0 8 +, 0 7 (, 0 ) ( : 0, 000) ( 0, 008) e 0 o ( 80 ) 0 ( ) 0 ( ) , E.A. < 0, E.R. < 0 80, 0, , %
14 Unidd. Números reles, 0 8 +, 0 7 (, 0 ), 0 8 +, 0 7, 0 8, , 0 8 (, +,) 0 8,0 0 8,0 0 7 E.A. < 0, E.R. < 0, Reprtos proporcionles, , ,0 % Hzlo tú. Reprte 00 en prtes inversmente proporcionles, 0 y Pr x 8 x , Pr 0 x 0 8 x, Pr x 8 x ,
15 Unidd. Números reles Ejercicios y problems guidos Págin 7. Simplificción de rdicles Simplificr est expresión: 08. Vlor de un exponente Clculr x pr que se cumpl l iguldd: x 7 log x log 7; (x )log log 7 x log 7,9; x,9 +,9. Extrcción de fctores de un rdicl Extrer fuer del rdicl los fctores que se posible. cd + 8bcd + b cd cd + 8bcd + b cd cd( + 8b+ b ) cd( + ( + cd ( + cd. Propieddes de los logritmos Averigur l relción que existe entre M, x e y si sbemos que: ln M ( ln x + ln y ln ) ln M x y x y ( ln x+ ln y ln ) ( ln x+ ln y ln ) ln ln M x y. Cots de error bsoluto y reltivo Acotr el error que se comete l tomr, como proximción del número de oro, ϕ. E.A. < 0,00 0, 00 E.R. <, ,00 + Corresponde un error reltivo menor que 0, %.
16 Unidd. Números reles Ejercicios y problems propuestos Págin 8 Pr prcticr Números rcionles e irrcionles Clsific los siguientes números indicndo cuáles de los conjuntos N, Z, Q o Á, pertenecen: ; 7;, ; 8 ; ; ; 7,! ; 8 N, 8, 7 Z ; π 8 ; 7;! ; 7, Q ; Cuáles de estos números son irrcionles? Expres como frcción los que se posible.,888 7,! 8 d), e),0 f ) 8 g),999 h) π, ! 7, Irrcionl. d), Irrcionl. e), f) 8 Irrcionl. 8 ; 7;! ; 7, ; ; ; π Á g), h) π Irrcionl. Qué números irrcionles representn los puntos: A, B, C y D? Justific l respuest. 0 A B C 7 D A + 0 B + 9 C + D Indic cuál, de cd pr de números, es myor: 0 y 0, & y 0, 99 $ 89, y d),098 y, Redonde ls centésims los números nteriores. 0, # 89, d),098
17 Unidd. Números reles Intervlos y vlor bsoluto Represent gráficmente y expres como intervlo o como semirrect los números que cumplen l condición dd en cd cso. x es menor que. es menor o igul que x. x está comprendido entre y. d) x está entre y 0, mbos incluidos. e) x es myor o igul que y menor que. x < ; (, ) x; [, + ) < x < ; (, ) d) x 0; [, 0] e) [, ); x < Escribe l desiguldd que verific todo número x que pertenece estos intervlos o semirrects: [, 7] [, + ) (, 0) d) (, 0] e) [/, ) f ) (0, + ) x 7 x x < 0 d) < x 0 e) x < f) 0 < x < + 7 Expres en form de intervlo los números que cumplen cd un de ests expresiones: x < 7 x x < 8 d) x e) x + > 9 f ) x ( 7, 7) [, ] [, + ] (, ) d) [, 7] e) (, 7) f) (, ] [, + ) 8 Escribe medinte intervlos los posibles vlores de x pr que se pued clculr l rí z en cd cso. x x + x d) x e) x f ) + x x 0 x ; [, + ) x + 0 x x ; <, + F x 0 x 0; (, 0] d) x 0 x x ; c, F e) x 0 x; (, ] f) + x 0 + x 0 x ; [, + ) 9 Expres como un único intervlo. (, ] [, ) [, ) (0, ] (, ] [, 7) d) [, ) (0, ) e) [, ] [0, ] f ) [, + ) (0, 0) (, ] [, ) (, ] [, ) (0, ] [, ] (, ] [, 7) [, ] d) [, ) (0, ) (0, ) e) [, ] [0, ] [0, ] f) [, + ) (0, 0) [, 0) 7
18 Unidd. Números reles 0 Se llm entorno de centro y rdio r l intervlo ( r, + r). Expres como intervlos los siguientes entornos: centro y rdio 0,; centro y rdio. Describe como entornos los siguientes intervlos: I (, ); I (,,). Centro y rdio 0, ( 0,; + 0,) (,7;,) Centro y rdio (, + ) (, ) I (, ); centro: + ; rdio I es un entorno de centro y rdio. I (,,); centro:, + ( ), ; rdio, (,) 0,8 I es un entorno de centro, y rdio 0,8. Potencis Expres los siguientes rdicles medinte potencis de exponente frccionrio y simplific: / / 90 / 0 9 / x x x x / / / x x Resuelve, sin utilizr clculdor: d) 0, e) 8 f ) 0, d) 0, e) f) 0, 0, Expres como un potenci de bse : ( ) / 8 ( ) / ( ) / /8 / Clcul utilizndo potencis de bse, y : c m c m c m 9 8 ( ) ( 8 ) ( 9 ) 0 ( ) ( ) ( ) ( ) ( ) d) ( 0 ) 0 d) 00 8
19 Unidd. Números reles Expres en form de potenci, efectú ls operciones y simplific: / / 7 / ( ) / ( ) / ( ) / / / 0 / 7 Simplific, utilizndo ls propieddes de ls potencis: d) b c b c d) c c 8 78 b b 8 c b Págin 9 Rdicles 7 Introduce los fctores dentro de cd ríz. d) 9 x x 8 e) f ) x d) x x e) 8 f) 8 Sc de l ríz el fctor que pueds d) 8 e) g) f ) + b 9 h) + i) d) e) f) b b g) h) ( + ) + i) 9 9
20 Unidd. Números reles 9 Simplific los siguientes rdicles: 7 08 d) y e) g) 007, h) 000, 8 8 f ) : 8 i) 9 + / / d) y y y y e) 8 f) : : g) 0, h) 8 0, i) Reduce índice común y orden de menor myor.,,,, 0 d) 0, 9, 00,, ;, 8, < <, < , < 0 d) 0, 9, 00 9 < 00 < 0 ; tenemos 0 000; ; 8000 Reliz l operción y simplific, si es posible d) ( ) e) ( ) f ) : d) ` j 8 e) k f) : : Efectú y simplific, si es posible. 08 f 9 f p d) : 8 p e o d) : : Expres con un únic ríz k:
21 Unidd. Números reles Rcionliz los denomindores y simplific. 8 d) + e) 7 8 f ) ( ) ( ) 9 ( ) d) 9 e) f) 7 8 Multiplicmos numerdor y denomindor por 7 8 ( 7 8) ( ) 8 Simplific. Multiplicmos numerdor y denomindor por ( + ) ( + ) ( + ) + ( + ) Simplific ls siguientes expresiones: c + 7 m 7 7 c m ( 7 Efectú y simplific. ( + )( ) ( )( + ) ( ) d) ( )( + ) d) ( )
22 Unidd. Números reles 8 Rcionliz y simplific. d) 8 e) + 0 f ) ( ) + + ( ) ( ) + + ( + ) + + ( + ) + + ( )( + ) ( ) ( + ) ( ) d) + ( + ) + ( )( + ) + e) 0 ( + ) 0( + ) + 78 ( + ) 9 f) ( + )( ) ( + )( ) 7 9 Efectú y simplific ( + ) ( ) + + ( )( + ) + ( 7 ) ( 7+ ) ( )( 7 7 ) 7( ) ( 7+ )( 7 ) 7 Logritmos 0 Expres como potenci de l bse y clcul plicndo l definición de logritmo. log 0 log 0,00 log d) log e) log f ) log 8 g) log / h) log π i) ln log 0 0 log 0 log d) log ( ) e) log / f) log / / g) log / c m h) 0 i) ln e / Clcul l bse de estos logritmos: log x log x 9 log x d) log x e) log x 0,0 f ) log x e x x x 9 x x x d) x / x e) x 0,0 x f) x / x
23 Unidd. Números reles Clcul el vlor de x en ests igulddes: log x log x 7 x d) x e) log 7 x 0, f ) + x 7 x 9, log x x log x, 8 log 0 log 7 log d) x 0, 8 e) 7 log 0, x x 7 Hll con l clculdor y comprueb el resultdo medinte potencición. log 8 ln (, 0 ) ln (7, 0 ) d) log,9 e) log,9 f ) log 0,0 f) + x log 7 x log 7,08 ln (, 0 ), e,, 0 ln (7, 0 ) 9, e 9, 7, 0 d),,,9 e) 0, 0,,9 f),88,88 0,0 Págin 0 Desrroll ls siguientes expresiones: log b 00c log b ln x e y log 00c log + log b log 0 log c log + log b log c ln x e ln xe ln y ln x+ ln e ln y ln x+ ln y y Sbiendo que log x 0,8 clcul el vlor de: log x 00 log 000x log log x log x / log x / log 00 log x 08,, log000x log log x log log x + 08, 8, log log log x / 0 log x 08, 0, x d) log0x + log log0 log x log log x 0, , 0, 7 x Hll el vlor de x en ests expresiones: ln x ln 7 + ln log x log log 9 d) log 0x + log x x ln x ln ln 0 d) log x log log ln x ln (7 ) x 7 log x log 9 x 9 ln x ln ln 0 ; ln x ln ; x 0 ; x d) log x log log / ; log x log log ; log x log 8 ; x 8
24 Unidd. Números reles 7 Si log k x, escribe en función de x. log 00k log k 000 log k d) log 0k e) log k f ) (log k) / log 00 + log k + x log k log 000 x log k x d) (log 0 + log k) ( + x) e) log log k 0 x x f) x 8 Averigu, en cd cso, l relción entre x, y, z. log z log x log y log z log x log y log z (log x log y) d) ln z ln x + ln y log z log x log y; log z log x ; z y x y log z log 0 log x log y ; log z log 00 ; z 00 x y x y log z log 0 log x ; log z log 0 log y d) ln z ln e ln x + ln y e ; ln z ln y e y x ; z x Notción científic y errores x ; log z log y 0 0 ; z x x y 9 Efectú y d el resultdo en notción científic con tres cifrs significtivs. Determin tmbién, en cd cso, un cot del error bsoluto y otr del error reltivo cometidos. 8 (, 0 + 7, 0 0 ) 8, 0, (, )(, 0 8) 9, 0, 0, , 0 0, 0 ; E.A. < 0,00 0 0, E.R. < 0, < 0,00,8 0 ; E.A. < 0, E.R. < 0 <, 0 80,, 0 ; E.A. < 0, E.R. < 0 0, <,89 0 y 0 Expres en notción científic y clcul: ( 0 ) ( 0 ) 0 70, ( 0 ) , , 000
25 Unidd. Números reles Orden de myor menor los números de cd prtdo. Pr ello, ps notción científic los que no lo estén.,7 0 ; 8,7 0 ; 0,9 0 9 ; 0,0 0 7 ; ,7 0 >, 0 >, > 0 9 >,9 0 9 Pr resolver Un depósito de gu tiene dos grifos. Si los brimos l vez, el depósito se llen en dos hors. Si brimos solo el primero, se llen en seis hors. Cuánto trdrá en llenrse el depósito si brimos solmente el segundo grifo? Llmmos x n.º de hors que trd en llenr el depósito el segundo grifo. El primer grifo llen del depósito en un hor. El segundo grifo llen del depósito en un hor. x Los dos juntos llenn del depósito en un hor. Por otr prte, los dos juntos, en un hor, llenn +. Por tnto: x + 8 x x + 8 x x 8 x x x x x + El segundo grifo trd hors en llenr el depósito. En un concurso se reprten entre ls tres persons que hn trddo menos tiempo en relizr un prueb. L primer h trddo minutos; l segund, minutos, y l tercer, 8 minutos. Cuánto dinero le corresponde cd un si el reprto es inversmente proporcionl l tiempo invertido? Debemos reprtir de form inversmente proporcionl l tiempo empledo: trdrín entre los tres Al primero le corresponde , Al segundo le corresponde , Al tercero le corresponde ,8 Vrios migos se reúnen en un br, tomn refrescos y pgn 8,7 en totl. Uno de ellos tomó solo un refresco, otro tomó dos y el resto tomron refrescos cd uno. Cuántos migos fueron y cuánto tuvo que pgr cd uno? 8,7 :, por refresco., pg el primero;, pg el segundo,7 entre los dos. Los restntes tomn refrescos. : migos, y cd uno pg,7. Son en totl. Pgn,,, y los otros cutro,,7 cd uno.
26 Unidd. Números reles En un grnj hy 7 gllins que consumen 0 kg de míz en 0 dís. Pr umentr l producción de huevos, se ument el número de gllins 00 y se comprn 800 kg de míz. Cuántos dís se podrá dr de comer ls gllins? 0 : 0 ; : 7 0, kg de míz es lo que come un gllin en un dí. 00 0, 0 kg por dí pr limentr 00 gllins. 800 : 0 0 dís podrán comer ls gllins. Un empledo puede hcer los / de un trbjo en 8 dís trbjndo hors diris, y otro, los / del mismo trbjo en dís de 7 hors de trbjo. Cuánto tiempo trdrán los dos juntos en hcer el trbjo, dedicndo hors diris? Pr hcer todo el trbjo el primero trd: 8 0 hors. Y el segundo: 7 hors. En hor los dos juntos hcen: Pr hcer todo el trbjo trdn: 80 8, 9 hors. 9 8,9 : dís hors 8 minutos 7 Dos migs, trbjndo junts, emplerín dís pr hcer un trbjo. Después del primer dí, un de ls dos lo tiene que dejr. Continú l otr sol y trd dís en cbr el trbjo. En cuántos dís hrí el trbjo cd un isldmente? Después del primer dí quedn por hcer los / y como l segund mig trd dís, pr hcer todo el trbjo trdrí 9 dís. L primer hce por dí del trbjo. 9 9 Por tnto, trdrí en hcer todo el trbjo 9, dís. 8 Dos poblciones A y B distn 0 km. A l mism hor sle un utobús de A hci B un velocidd de 80 km/h y un turismo de B hci A 0 km/h. Cuándo se cruzrán? Si se proximn km/h, en recorrer 0 km trdrán: t 0 7, hors hor y minutos Un utomóvil trd hors en ir de A B y otro trd hors en ir de B A. Clcul el tiempo que trdrán en encontrrse si slen simultánemente cd uno de su ciudd. El primero recorre / del cmino en hor. El segundo recorre / del cmino en hor. Entre los dos recorren: + 8 del cmino en hor. Trdrán 8 h h ' 0'' en encontrrse.
27 Unidd. Números reles 0 Hll el áre de l prte colored de est figur en el que el ldo del cudrdo mide m. Expres el áre en decímetros cudrdos con tres cifrs significtivs y cot el error cometido. r d El áre pedid es el áre del cudrdo, menos cutro veces el áre verde y menos el áre roj. Cutro veces el áre verde es el áre de un círculo de rdio, es decir, AVerde π c m Llmmos d l digonl del cudrdo: d + Clculmos el rdio: r d El áre roj es el áre del círculo de rdio A Roj πe o π π. Áre pedid A Cudrdo A Verde A Roj π c π π m E.A. < 0,00 dm E.R. < π π + 7, m 7,98 dm 0, 00 7, 989 0,8 0 0,08, que equivle l, %. π Págin L estción espcil Mir estuvo en órbit csi ños y durnte ese tiempo dio, proximdmente, 8 00 vuelts lrededor de l Tierr, un ltur medi de 00 km. Clcul l distnci totl recorrid por l Mir en esos ños. Redonde el resultdo ls decens de millón y d un cot del error bsoluto y un cot del error reltivo cometidos. El rdio medio de l Tierr es de 7 km. L longitud de un vuelt del stçelite es π (00 + 7) π km. El totl de kilómetros recorridos es: E.A. < 0, 0 7 E.R. < π 8 00, decens de millón 7 00, 80, 9, , 00 0, % 7
28 Unidd. Números reles L longitud de un brr metálic después de clentrl es l l 0 ( + kt) donde l 0 es l longitud 0 C, t l tempertur finl y k el coeficiente de diltción linel. Si un brr de plomo mide m 800 C, cuál es su longitud 00 C? (En el plomo k 0 ). Clculmos l 0 prtir de l longitud de l brr 800 C: l l 0 ( + kt) l 0 ( ) l 0 c8 m, luego l 0 8 Clculmos hor l longitud de l brr 00 ºC: l l 0 ( + kt) ( ) ,98 m L estrell R, descubiert recientemente, está 000 ños-luz y tiene un ms ctul equivlente veces l ms del Sol. Expres l distnci en kilómetros y l ms en kilogrmos. D, en cd cso, cots del error bsoluto y del error reltivo. Un ño luz es proximdmente 9, 0 km. L distnci de l estrell R l Tierr es: d 000 9, 0, km E.A. < 0 km E.R. < 0,0 0 0,0000, que equivle l 0,00 %., L ms del Sol es, proximdmente,, kg. L ms de l estrell R es: m, ,7 0 kg E.A. < 0 7 kg E.R. < 7 0, 7 0 El volumen de un cubo es cm. Hll: 9,87 0 0, , que equivle l 0,0009 %. Su rist. L digonl de un cr. L digonl del cubo. D, en cd cso, el vlor excto. V cubo 8 Digonl de un cr + + Digonl del cubo L superficie de un tetredro es 9 cm. Clcul su rist y su volumen. D el vlor excto. Un tetredro tiene cutro crs igules. Llmmos l rist. L superficie de cd cr es 9 cm. Cd cr es un triángulo equilátero cuy ltur es b l. L superficie de cd cr es: S cr. Por tnto, ±. Como es un longitud, cm. L ltur del tetredro es: h V Abse h 9 9 cm. h 8
29 Unidd. Números reles Cuestiones teórics Explic si ests frses son verdders o flss: Hy números irrcionles que son enteros. Todo número irrcionl es rel. Todos los números decimles son rcionles. d) Entre dos números rcionles hy infinitos números irrcionles. Flso. Los números irrcionles tienen infinits cifrs decimles no periódics. Verddero. Flso. El número π es deciml pero no es rcionl, puesto que no puede expresrse como cociente de dos números enteros. d) Verddero. 7 Si x 0, explic si ests firmciones son verdders o flss: x es negtivo si lo es x. x tiene el mismo signo que x. Si x > 0 entonces x < x. Fls, x x siempre es positivo por ser el exponente pr, independientemente del signo de x. Verdder, porque el índice de l ríz es impr. Fls, > 8 Cuáles de ests igulddes son verdders? Explic por qué: log m + log n log (m + n) log m log m log n log n log m log n log n m d) log x log x + log x e) log ( b ) log ( + + log ( Flso. log m + log n log (m n) log (m + n) Flso. log m log n log m log m b l n log n Verddero. Por un propiedd de los logritmos. d) Verddero. log x log (x x) log x + log x e) Verddero. log ( b ) log [( + ( ] log ( + + log ( 9
30 Unidd. Números reles Autoevlución Clsific los siguientes números indicndo cuáles de los conjuntos N, Z, Q o Á pertenecen: 8 ; ; π ; ; 8; ;, 07 7! N: Z: ; 8 Q: ; Expres en form de intervlo. ; 8 ; 07,! Á: ; 8 7 x es myor que y menor o igul que. x < x (, ] x (, 9) Escribe como potenci y simplific. ( ):( ; / / / + / / / / / 7 / ( ):( ( ):( ) ( ):( ) ( ):( ) Clcul y simplific: 7 Rcionliz ( + )( ) ( )( ) ( + ) ( )( + ) 9 Simplific: ; 07,! ; π ; 7 Si A, 0 ; B, 0 ; C,8 0 y D, 0, clcul c A + Cm D. Expres B el resultdo con tres cifrs significtivs y d un cot del error bsoluto y otr del error reltivo cometidos. c A + C m D f 0, + 80, p 0, e, , o 0, B 0,, E.A. < 0, 0 E.R. < ( 0, 9 + 8, ) 0 0,, 0, 7, , 70,,799 0,7 0, , , % 0
31 Unidd. Números reles 8 Aplic l definición de logritmo y obtén x. log x log x, ln x log x 8 x 8 x log x, 8 x 0, 8 x 0 / ln x x e 9 Clcul x en cd cso., x 0,0087,00 x log 0, 0087 xlog, log 0, x, 8 log,,00 x Tommos logritmos: log log, 00 x log 8 xlog, 00 log 8 x,8 log, 00 0 Expres como un solo logritmo y di el vlor de A: log + log log log A log+ log log log + log log logc9 m 8 A Si log k 0,8, cuál es el vlor de log 0k k + log 00? log0k+ log k log0 + log k+ log k log 00 + log k+ log k + 08, + 08,, 8 00 El áre totl de un cubo es cm. Cuál es el áre totl del cilindro inscrito en el cubo? D el vlor excto. El áre totl del cubo es. El rdio del cilindro inscrito es r. El áre de un bse del cilindro es π e o π. El áre lterl del cilindro es π π. El áre totl del cilindro es π + π c + m π cm.
1. Números reales. Resuelve BACHILLERATO. Página 25
 . Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
. Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Números reales. 1. Números y expresiones decimales. página El conjunto de los números reales página La recta real. Intervalos página 9
 Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero. TEMA 2: actividades
 º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
TEMA 1: NÚMEROS REALES. 2. Indica el menor conjunto numérico al que pertenecen los siguientes números:
 I.E.S. Tierr de Ciudd Rodrigo Deprtmento de Mtemátics Conjuntos numéricos. Relción entre ellos.. Complet: TEMA : NÚMEROS REALES Números reles. Indic el menor conjunto numérico l que pertenecen los siguientes
I.E.S. Tierr de Ciudd Rodrigo Deprtmento de Mtemátics Conjuntos numéricos. Relción entre ellos.. Complet: TEMA : NÚMEROS REALES Números reles. Indic el menor conjunto numérico l que pertenecen los siguientes
Multiplicar por la potencia de 10 adecuada para convertirlo en entero. Despejar N 119. Simplificar la fracción, si es posible N = 50
 .0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
.0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
4º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- Escrie un número que cumpl: ) Pertenece N y I. ) Pertenece R pero no Q. c) No pertenece R. d) Pertenece Q pero no N. ) IMPOSIBLE
º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- Escrie un número que cumpl: ) Pertenece N y I. ) Pertenece R pero no Q. c) No pertenece R. d) Pertenece Q pero no N. ) IMPOSIBLE
Ejercicios. Números enteros, fraccionarios e irracionales.
 CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
1. Utilizando las propiedades de las potencias simplifica las siguientes expresiones: c) 2. d) 0,001 e) 0, f) 0,
 TEMA POTENCIAS, RADICALES A) POTENCIAS Y NOTACIÓN CIENTÍFICA.. Utilizndo ls propieddes de ls potencis simplific ls siguientes expresiones: ) ) ) ) c) 0 e) f) g) h) 0) ) ) ). Expres con un potenci de se
TEMA POTENCIAS, RADICALES A) POTENCIAS Y NOTACIÓN CIENTÍFICA.. Utilizndo ls propieddes de ls potencis simplific ls siguientes expresiones: ) ) ) ) c) 0 e) f) g) h) 0) ) ) ). Expres con un potenci de se
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
IES Fernando de Herrera 23 de octubre de 2013 Primer trimestre - Primer examen 4º ESO NOMBRE:
 IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN:
 TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
LITERATURA Y MATEMÁTICAS. El código Da Vinci
 Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
Si la base de una potencia es positiva y el exponente es negativo de qué signo es el resultado. Pon un ejemplo. Expresa como potencia única de 10:
 Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
17532 = Hemos usado el 10 como base, pero podíamos haber usado cualquiera. Por ejemplo el 9, entonces.
 Tem 1.- V de números 1.1.- Números pr contr. Un de ls primers ctividdes intelectules que reliz el ser humno es l de contr: el número de flechs, el número de ovejs, el número de enemigos, etc. En Mtemátics
Tem 1.- V de números 1.1.- Números pr contr. Un de ls primers ctividdes intelectules que reliz el ser humno es l de contr: el número de flechs, el número de ovejs, el número de enemigos, etc. En Mtemátics
NÚMEROS REALES, R. Es el conjunto de números que se obtiene al unir el conjunto de los números racionales con el conjunto de los números irracionales.
 NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
Apellidos: Nombre: Curso: 1º Grupo: C Día: 10 - XI- 14 CURSO Resuelve las siguientes ecuaciones y comprueba las soluciones obtenidas:
 EXAMEN DE MATEMÁTICAS ALGEBRA Apellidos: Nombre: Curso: º Grupo: C Dí: - XI- 4 CURSO 4-5. Hll el vlor de log log ), 4 log log b) log4 6 -log -log log 7 4 6. Clcul x pr que se cumpl: ) log 6,45,5 b) 5 +,58.
EXAMEN DE MATEMÁTICAS ALGEBRA Apellidos: Nombre: Curso: º Grupo: C Dí: - XI- 4 CURSO 4-5. Hll el vlor de log log ), 4 log log b) log4 6 -log -log log 7 4 6. Clcul x pr que se cumpl: ) log 6,45,5 b) 5 +,58.
a n =b Si a es múltiplo de b, entonces b es divisor de a. Números primos: son números cuyos únicos divisores son ellos mismos y el 1.
 1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
SOLUCIONES DE LAS ACTIVIDADES Págs. 4 a 21
 TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA
 EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
Números reales NÚMEROS REALES RADICALES APROXIMACIONES ERRORES EN LA APROXIMACIÓN NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES
 Números reles NÚMEROS REALES NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES RADICALES APROXIMACIONES TRUNCAMIENTO REDONDEO POR EXCESO ERRORES EN LA APROXIMACIÓN 8 Mi desconocido migo L misiv
Números reles NÚMEROS REALES NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES RADICALES APROXIMACIONES TRUNCAMIENTO REDONDEO POR EXCESO ERRORES EN LA APROXIMACIÓN 8 Mi desconocido migo L misiv
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
IES Capellanía 4º ESOB Departamento de Matemáticas. Alumno: Ejercicios Temas 1 y 2: Números Reales. Potencias y Radicales
 IES Cpellní º ESOB Deprtmento de Mtemátics Alumno: Efectú el cociente Ejercicios Tems y : Números Reles Potencis y Rdicles,,0, 0, psndo frcciones genertrices Represent en l rect rel, utilizndo el teorem
IES Cpellní º ESOB Deprtmento de Mtemátics Alumno: Efectú el cociente Ejercicios Tems y : Números Reles Potencis y Rdicles,,0, 0, psndo frcciones genertrices Represent en l rect rel, utilizndo el teorem
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Potencias y radicales
 Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
SECCIÓN 3 DESCRIPCIÓN DE LOS NÚMEROS REALES
 SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
MATEMATICAS 3º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION
 MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
1 Agrupa aquellos monomios de los que siguen que sean semejantes, y halla su suma: , cuando:
 Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
MATEMÁTICAS-FACSÍMIL N 9
 MTEMÁTIS-FSÍMIL N 9. b b b ) - b ) b - ) b D) E) 6 cm ( b) =. El triángulo está inscrito en l mitd de l circunferenci. Si h c = cm y el ldo = 5cm. El rdio de l circunferenci es: ) cm ) 6 cm ) 6 cm O D)
MTEMÁTIS-FSÍMIL N 9. b b b ) - b ) b - ) b D) E) 6 cm ( b) =. El triángulo está inscrito en l mitd de l circunferenci. Si h c = cm y el ldo = 5cm. El rdio de l circunferenci es: ) cm ) 6 cm ) 6 cm O D)
IES. SIERRA DE LAS VILLAS Departamento de Matemáticas
 Informe pr lumnos pendientes de Mtemátics º de E.S.O. IES. SIERRA DE LAS VILLAS Deprtmento de Mtemátics Nombre:.. Alumno/ de º de E.S.O. tendrá que relizr l prueb extrordinri de Mtemátics, en el mes de
Informe pr lumnos pendientes de Mtemátics º de E.S.O. IES. SIERRA DE LAS VILLAS Deprtmento de Mtemátics Nombre:.. Alumno/ de º de E.S.O. tendrá que relizr l prueb extrordinri de Mtemátics, en el mes de
de Thales y Pitágoras
 8 Teorems de Thles y Pitágors 8.1. Cuents y problem del dí 1. Reliz l siguiente operción: 874,53 + 3 607,8 + 875,084 2. Reliz l siguiente operción, obtén dos decimles en el cociente y hz l prueb de l división:
8 Teorems de Thles y Pitágors 8.1. Cuents y problem del dí 1. Reliz l siguiente operción: 874,53 + 3 607,8 + 875,084 2. Reliz l siguiente operción, obtén dos decimles en el cociente y hz l prueb de l división:
Matemáticas. José María Arias Cabezas Ildefonso Maza Sáez EDUCACIÓN SECUNDARIA OBLIGATORIA
 S O L U C I O N A R I O Mtemátics José Mrí Aris Cbezs Ildefonso Mz Sáez EDUCACIÓN SECUNDARIA OBLIGATORIA B Dirección del proyecto editoril Antonio Díz Autores José Mrí Aris Cbezs e Ildefonso Mz Sáez Coordinción
S O L U C I O N A R I O Mtemátics José Mrí Aris Cbezs Ildefonso Mz Sáez EDUCACIÓN SECUNDARIA OBLIGATORIA B Dirección del proyecto editoril Antonio Díz Autores José Mrí Aris Cbezs e Ildefonso Mz Sáez Coordinción
pág. 71 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
1. NÚMEROS RACIONALES
 IES Jun Grcí Vldemor Deprtmento de Mtemátics 4º ESO Mtemátics B. NÚMEROS RACIONALES Desde l prición de ls socieddes humns los números desempeñn un ppel fundmentl pr ordenr y contr los elementos de un conjunto.
IES Jun Grcí Vldemor Deprtmento de Mtemátics 4º ESO Mtemátics B. NÚMEROS RACIONALES Desde l prición de ls socieddes humns los números desempeñn un ppel fundmentl pr ordenr y contr los elementos de un conjunto.
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Matemáticas Nivel Medio Matemáticas Ap.CC.SS.I
 Mtemátics Nivel Medio Mtemátics Ap.CC.SS.I Mrtes 0 de noviembre de 01 1 hor NOMBRE APELLIDOS CALIFICACIÓN 1. Oper medinte notción rdicl y simplific l máximo: (0 puntos). Resuelv ls siguientes cuestiones
Mtemátics Nivel Medio Mtemátics Ap.CC.SS.I Mrtes 0 de noviembre de 01 1 hor NOMBRE APELLIDOS CALIFICACIÓN 1. Oper medinte notción rdicl y simplific l máximo: (0 puntos). Resuelv ls siguientes cuestiones
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
LÁMINA No. 1.1 LECTURA Y ESCRITURA DE UN NÚMERO
 6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
Unidad 2. Fracciones y decimales
 Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
1 La recta principal, en el plano, mide 44 cm. Cuánto mide en la realidad?
 PÁGIN 164 El director del equipo nliz un plno en el cul 1 cm corresponde 20 m en l relidd. Su mquet de l moto es l décim prte de lrg que l moto rel. L moto de l fotogrfí es l mism que se ve en l mquet.
PÁGIN 164 El director del equipo nliz un plno en el cul 1 cm corresponde 20 m en l relidd. Su mquet de l moto es l décim prte de lrg que l moto rel. L moto de l fotogrfí es l mism que se ve en l mquet.
PROPORCIONALIDAD DIRECTA E INVERSA
 PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
PROPORCIONALIDAD DIRECTA E INVERSA Rzón entre dos números Siempre que hblemos de Rzón entre dos números nos estremos refiriendo l cociente (el resultdo de dividirlos) entre ellos. Entonces: Rzón entre
IES Fernando de Herrera 13 de enero de 2014 Primer trimestre Examen de autoevaluación 1º Bach CCSS NOMBRE:
 IES Fernndo de Herrer de enero de 04 Primer trimestre Exmen de utoevlución º Bch CCSS NOMBRE: 7 ) ) Representr en l rect rel: b) Qué número es el indicdo en el gráfico? 0 ) Clculr el resultdo simplificdo
IES Fernndo de Herrer de enero de 04 Primer trimestre Exmen de utoevlución º Bch CCSS NOMBRE: 7 ) ) Representr en l rect rel: b) Qué número es el indicdo en el gráfico? 0 ) Clculr el resultdo simplificdo
Regla de Sarrus: Para recordar con mayor facilidad el desarrollo del determinante de orden 3, podemos usar esta regla:
 UNIDD 8: Determinntes. DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) = = = Definición: Pr un mtriz cudrd de orden, not por det( ) ó, l siguiente
UNIDD 8: Determinntes. DETERMINNTES DE ORDEN Y Definición: Pr un mtriz cudrd de orden, por det( ) ó, l siguiente nº rel: det( ) = = = Definición: Pr un mtriz cudrd de orden, not por det( ) ó, l siguiente
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
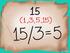 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
ENCUENTRO # 5 TEMA: Resolución de problemas de razones y proporciones. DESARROLLO
 ENCUENTRO # 5 TEMA: Resolución de problems de rzones y proporciones. CONTENIDOS:. Mgnitudes proporcionles (direct e invers). 2. Regl de tres simple. DESARROLLO Ejercicio Reto Cntiddes proporcionles cntiddes
ENCUENTRO # 5 TEMA: Resolución de problems de rzones y proporciones. CONTENIDOS:. Mgnitudes proporcionles (direct e invers). 2. Regl de tres simple. DESARROLLO Ejercicio Reto Cntiddes proporcionles cntiddes
Multiplicar y dividir radicales
 Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
ACTIVIDADES INCLUIDAS EN LA PROPUESTA DIDÁCTICA: DE AMPLIACIÓN
 Pág. 1 ENUNCIADOS 1 En el punto C hy td un cuerd de 5 m que sujet un cbr. Hll l superficie de l cs y l superficie de hierb que puede comer l cbr. m CASA m 10 m C 45 Investig: Qué relción hy entre ls superficies
Pág. 1 ENUNCIADOS 1 En el punto C hy td un cuerd de 5 m que sujet un cbr. Hll l superficie de l cs y l superficie de hierb que puede comer l cbr. m CASA m 10 m C 45 Investig: Qué relción hy entre ls superficies
EJERCICIOS DE VERANO DE MATEMÁTICAS
 EJERCICIOS DE VERANO DE MATEMÁTICAS º E.S.O. ES OBLIGATORIA LA RESOLUCIÓN COMPLETA DE CADA EJERCICIO PLANTEAMIENTO, DESARROLLO Y SOLUCIÓN DE FORMA CLARA Y CONCISA NÚMEROS. Reliz ls siguientes operciones
EJERCICIOS DE VERANO DE MATEMÁTICAS º E.S.O. ES OBLIGATORIA LA RESOLUCIÓN COMPLETA DE CADA EJERCICIO PLANTEAMIENTO, DESARROLLO Y SOLUCIÓN DE FORMA CLARA Y CONCISA NÚMEROS. Reliz ls siguientes operciones
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
c Ejemplo: 25 9x 2 = 0 x
 1.- ECUACIONES POLINÓMICAS Ecuciones de º grdo Son ecuciones donde l incógnit está elevd. Ecuciones de º grdo complets Son del tipo x + bx + c = 0, con b, c 0. Pr resolverls usmos l fórmul b b 4c x L expresión
1.- ECUACIONES POLINÓMICAS Ecuciones de º grdo Son ecuciones donde l incógnit está elevd. Ecuciones de º grdo complets Son del tipo x + bx + c = 0, con b, c 0. Pr resolverls usmos l fórmul b b 4c x L expresión
3º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
( ) ( ) ( ) ( ) 4. Aplique las propiedades de la potenciación y la radicación para simplificar las siguientes expresiones.
 DEPARTAMENTO DE MATEMÁTICAS ÁREA DE MATEMÁTICAS TEMA: PERÍODO: ORIENTADOR: ESTUDIANTE: E-MAIL: FECHA: TEORÍA DE LOS EXPONENTES, LOS RADICALES Y LOS LOGARITMOS PRIMERO UNIDAD TEORÍA DE LOS EXPONENTES, LOS
DEPARTAMENTO DE MATEMÁTICAS ÁREA DE MATEMÁTICAS TEMA: PERÍODO: ORIENTADOR: ESTUDIANTE: E-MAIL: FECHA: TEORÍA DE LOS EXPONENTES, LOS RADICALES Y LOS LOGARITMOS PRIMERO UNIDAD TEORÍA DE LOS EXPONENTES, LOS
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Conjuntos numéricos. Intervalos. Operaciones en el conjunto de números reales.
 Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
56 CAPÍTULO 2. CÁLCULO ALGEBRAICO. SECCIÓN 2.4 Resolución de Ecuaciones de Segundo Grado
 56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
La raíz cuadrada de un número es otro nº que al elevarlo al cuadrado nos da el radicando La raíz cuadrado de 9 es 3. Pues 3 2 es
 Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
Ejercicios de números reales
 Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
(lo podemos visualizar como el área de un cuadrado de lado 4) Pues bien, diremos que la base de dicha potencia, 4, es su raíz cuadrada exacta: 16 = 4.
 Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
pág. 87 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
EJERCICIOS DE RAÍCES
 EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
O(0, 0) verifican que. Por tanto,
 Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
1.- Simplificar las siguientes fracciones: h) 28/36 i) 84/126 j) 54/96 k) 510/850 l) 980/140
 ACTIVITATS DE N ESO PER A ESTIU ACTIVIDADES CON NÚMEROS ENTEROS º ESO. Reliz ls siguientes operciones. + + + d + + b + + 6 e + 6 c + f 6 + + + 6. Reliz ls siguientes operciones. ( + + ( + + ( + d + ( +
ACTIVITATS DE N ESO PER A ESTIU ACTIVIDADES CON NÚMEROS ENTEROS º ESO. Reliz ls siguientes operciones. + + + d + + b + + 6 e + 6 c + f 6 + + + 6. Reliz ls siguientes operciones. ( + + ( + + ( + d + ( +
a b y se lee a es a b ; a se denomina antecedente y b consecuente.
 1 Centro Educcionl Sn Crlos de Argón. Dpto. de Mtemátic. Prof.: Ximen Gllegos H. Guí Nº 5 PSU NM 4: Proporcionlidd Nombre: Curso: Fech: Aprendizje Esperdo: Plnte y resuelve problems que requieren plicr
1 Centro Educcionl Sn Crlos de Argón. Dpto. de Mtemátic. Prof.: Ximen Gllegos H. Guí Nº 5 PSU NM 4: Proporcionlidd Nombre: Curso: Fech: Aprendizje Esperdo: Plnte y resuelve problems que requieren plicr
TEMA 3: PROPORCIONALIDAD Y PORCENTAJES.
 TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Resolución de triángulos
 8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
Se desea calcular la longitud de un lado de una pista de baile de forma cuadrada, cuya área es 16 u 2. Sustituyendo el valor del área
 Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
Portal Fuenterrebollo XXXVI OLIMPIADA MATEMÁTICA ESPAÑOLA, PALMA DE MALLORCA (2000)
 Portl Fuenterrebollo XXXVI OLIMPIADA MATEMÁTIA ESPAÑOLA, PALMA DE MALLORA (000) Problem. Sen los polinomios: P(x) = x 4 + x + bx + cx + ; Q(x) = x 4 + cx + bx + x +. Hll ls condiciones que deben cumplir
Portl Fuenterrebollo XXXVI OLIMPIADA MATEMÁTIA ESPAÑOLA, PALMA DE MALLORA (000) Problem. Sen los polinomios: P(x) = x 4 + x + bx + cx + ; Q(x) = x 4 + cx + bx + x +. Hll ls condiciones que deben cumplir
El conjunto de los números reales se forma mediante la unión del conjunto de los números racionales y el conjunto de los números irracionales.
 El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
MATEMÁTICAS PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 25 AÑOS LOGARITMOS
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
TEMA 3: Polinomios y fracciones algebraicas. Tema 3: Polinomios y fracciones algebraicas 1
 TEMA Polinomios y frcciones lgerics Tem Polinomios y frcciones lgerics ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum y rest de polinomios...- Producto de polinomios...- División de polinomios..-
TEMA Polinomios y frcciones lgerics Tem Polinomios y frcciones lgerics ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum y rest de polinomios...- Producto de polinomios...- División de polinomios..-
