CAPÍTULO 10. EJEMPLOS DE DISEÑO PARA FUNDACIONES PROFUNDAS. agrupar datos de ensayos disponibles por capa de suelo
|
|
|
- María Elena Coronel Benítez
- hace 6 años
- Vistas:
Transcripción
1 171 CAPÍTULO 10. EJEMPLOS DE DISEÑO PARA FUNDACIONES PROFUNDAS Diseño usado LRFD Al igual que el Capítulo 6 para fudacioes superficiales, el presete capítulo explica cómo utilizar los factores de resistecia hallados e los capítulos ateriores y aplicarlos al diseño de fudacioes. Se cosidera dos ejemplos de diseño. E el primero diseñamos u pilote e u perfil de suelo fudametalmete compuesto por area mediaamete desa. El segudo ejemplo muestra cómo seleccioar u factor de resistecia (RF) para utilizar co u método de diseño directo o icluido e este iforme. E ambos ejemplos se ilustra el procedimieto básico del diseño por factores de carga y resistecia (LRFD) de acuerdo co el diagrama de flujo ilustrado e la Figura seleccioar sistema de fudació y método de diseño seleccioar factor de resistecia para el método de diseño (tablas) agrupar datos de esayos dispoibles por capa de suelo usar procedimieto CAM para seleccioar valores de diseño a partir de los datos calcular resistecia de la fudació usado u diseño de prueba redimesioar la fudació comparar sistemas de fudació alterativos verificar resistecia usado ecuació del LRFD Verifica No verifica Figura Diagrama de flujo del LRFD para verificacioes de estados límites últimos e el diseño de fudacioes. Las líeas de trazos idica pasos específicos de u método de diseño particular; las líeas lleas idica pasos comues para todos los tipos de fudacioes.
2 172 Como se puede ver e la figura aterior, el primer paso e el diseño de u elemeto de fudació cosiste e agrupar los datos de esayos relevates de acuerdo co la capa de suelo a la cual correspode a fi de cosiderarlos e el método CAM. Datos de esayos relevates se refiere a cualquier dato obteido de esayos realizados e el mismo suelo al cual el elemeto de fudació trasmitirá carga. Al agrupar las medicioes segú el tipo de suelo podemos aprovechar la vetaja de teer varios esayos, lo que os permitirá coocer mejor el suelo. Luego se utiliza el procedimieto CAM 1 para hallar los valores de 80% de excedecia de los datos de esayo como se ilustra tato e los ejemplos a cotiuació como e el Capítulo 6. Co estos valores CAM de las medicioes obteidas mediate esayos el diseñador puede proceder a calcular las resistecias e base a u diseño de prueba de las fudacioes. E este puto es ecesario seleccioar el valor correcto del factor de resistecia correspodiete al método de diseño empleado para calcular la resistecia. Esta depedecia se represeta e la Figura 10.1 usado recuadros de líeas de trazos. Ua vez hallado u valor de la resistecia para u diseño particular se puede verificar si éste es adecuado usado la ecuació básica del LRFD. Ua resistecia de diseño miorada mayor que las cargas mayoradas represeta u diseño que verifica, mietras que ua resistecia miorada meor que las cargas de diseño o verifica. Trabajado co varios diseños de prueba es posible comparar diferetes alterativas de diseño. E los siguietes ejemplos se ilustra el proceso para seleccioar u valor CAM, seleccioar u factor de resistecia y realizar ua verificació de acuerdo co el LRFD. Diseño de pilotes de puta abierta hicados e area usado u método de diseño directo Se realizaro ua serie de sodeos i situ mediate CPT; el perfil de resistecias de puta medidas (q c ) se ilustra e la Figura Se diseñará u pilote co ua sobrecarga viva de 150 kn (34 kip) y ua carga permaete de 350 kn (79 kip) cotra estados límites últimos. La cota del cabezal del pilote estará ubicada a ua profudidad de 2.0 m (6.6 ft). Se hicará u pilote de puta abierta hasta ua profudidad de 9 m (29.5 ft) e el predio de area para aprovechar la capa de area relativamete desa que yace sobre la area más suelta por debajo de los 10m de profudidad. Usado para la sobrecarga viva y la carga permaete factores de carga de 1.6 y 1.2 (factores especificados por ASCE-7), respectivamete, la carga de diseño es 1 CAM: Media evaluada coservadoramete (Coservatively Assessed Mea)
3 173 de 660 kn (148 kip). La apa freática es profuda. 0 0 Resistecia CPT, q (MPa) c líea de tedecia media Profudidad (m) 6 8 Rago de 7 sodeos CPT Figura 10.2 Resultados de 7 registros de esayos CPT e area co idicació de líeas de tedecia ( mejor ajuste ) y líeas de rago (Comité BCP 1971) El primer paso para diseñar la fudació cosiste e establecer la líea de tedecia CAM para la combiació de los registros de esayos CPT. Se ilustra u método CAM que utiliza u criterio del 80% de excedecia utilizado regresió lieal, ua herramieta que los diseñadores puede coseguir fácilmete e forma de aplicacioes de hoja de cálculo. Estas líeas represeta la fució media de u parámetro del suelo e fució de la profudidad. Tambié se puede trazar líeas que limite los putos de datos de q c, represetado así la totalidad del rago de q c para dichas profudidades. La Figura 10.2 icluye estos dos tipos de líeas. La Tabla 10.1 preseta los parámetros estadísticos usados para hallar la líea CAM correspodiete al criterio de 80% de excedecia usado el procedimieto 6σ para area, co
4 174 lo cual las líeas medias se desplaza hacia la izquierda de la gráfica. Para las capas de area del presete ejemplo las líeas CAM está dadas por la siguiete ecuació: q ccam, 0.7(MPa) 0 < z < 3.5m 4(MPa/ m) z 8.9(MPa) 3.5m< z< 6.5m = 6(MPa/ m) z 35.1(MPa) 6.50 < z< 10m 13(MPa/ m) z 115.5(MPa) 10 < z < 11.5m (10.1) dode z es la profudidad. Tabla Parámetros estadísticos correspodietes a qc (CPT) para hallar la líea CAM e las capas de area de la Figura 10.2 Capa de area 0 < z < 3.5m 3.5m < z < 6.5m 6.5m < z < 10 m 10m < z < 11.5 m Rago (MPa) (R) Ua desviació estádar (MPa) (σ = R / 6) Número de desviacioes estádares para 80% de excedecia Valor a restar de la líea de tedecia media para obteer la líea CAM (MPa) Para este ejemplo se utiliza el método de diseño directo derivado de los trabajos de Paik y Salgado (2003) y Lee et al. (2003). Primero se diseñará la resistecia friccioal. Como secció de prueba para el pilote se elige u tubo de 305mm (12 i.) de diámetro. La superficie del fuste por uidad de logitud del pilote a s es de 0.958m 2 /m (3.14 ft 2 /ft). De acuerdo co este método de diseño la resistecia friccioal R s se calcula como R = fadl (10.2a) s s s L f s f = q = 0.002q qc s c c (10.2b) A los fies del diseño rescribimos la Ecuació (10.2a) de la siguiete maera: R = f a dl (10.3) s s, i s, i i
5 175 dode el subídice i idica ua secció de cierta logitud a lo largo del pilote. Al supoer que todas las seccioes cotribuye a la resistecia podemos calcular la capacidad friccioal total del pilote. E este ejemplo será ecesario cosiderar varias seccioes para lograr u diseño preciso e cada capa de area. A los fies del ejemplo, cosideramos ua secció e la primera capa y tres seccioes e la seguda y tercera. La Tabla 10.2 resume el aálisis de la resistecia friccioal. Tabla 10.2 Resume del diseño de prueba para resistecia friccioal e area secció o. # profudidad iicial (m) profudidad fial (m) profudidad media (m) dl (m) q c,cam (MPa)* f s (kpa) f s a s dl (kn) * q c,cam calculada a la mitad de la profudidad usado la Ecuació (10.1) La capacidad friccioal total o miorada se calcula sumado la columa f s a s dl de la Tabla 10.2, co lo cual se obtiee u valor de 107 kn (24 kip). De acuerdo co este método de diseño, la resistecia de puta R b está dada por las siguietes ecuacioes: R = q A b b,10% b (10.4a) q b,10% q q b,10% = qc c (10.4b) q q b c ( ) = IFR % (10.4c) Para estimar q b,10% primero es ecesario estimar IFR(%). La Figura 10.3 es ua gráfica tomada de Lee et al. (2003) que se puede utilizar para estimar IFR ates de comezar el hicado.
6 IFR Normalizado, NIFR D = 6.85 D = D = D = Esayo de carga i situ D = 8.66 D = 6.75 D = D = D = Desidad relativa, D R Figura 10.3 Gráfica de IFR ormalizado de acuerdo co Lee et al. (2003), usada para estimar IFR. El IFR ormalizado (NIFR) es NIFR = IFR D (10.5) dode D es D z d d = (10.6) i dode z d es la profudidad de hicado y d i es el diámetro iterior del pilote. Para este caso, co z d = 9 m (29.5 ft) y d i 0.305m (1 ft), la Ecuació (10.6) da por resultado ua D igual a 30. La Figura 10.3 idica u NIFR aproximadamete igual a 2% si supoemos D R igual a 65% para la area mediaamete desa. Usado la Ecuació (10.5) IFR(%) se calcula como 59%. Por lo tato, de la Ecuació (10.4c), (q b,10% /q c ) se estima como E base a la líea de tedecia CAM (10.1), u valor promedio de q c coservador e la regió de suelo próxima a la base del pilote es 18.9 MPa (395 ksf). Usado la Ecuació (10.4b) obteemos u valor de 5580 kpa (117 ksf) para q b,10%. El area de la base del pilote se calcula como
7 do 0.305m Ab = π = π = 0.073m (10.7) Fialmete, de la Ecuació (10.4a) obteemos u valor de 407 kn (91.5 kip) para la resistecia de puta o miorada. De la Tabla 8.2.1, los factores de resistecia RF s y RF b para utilizar co los factores de carga de ASCE-7 so 0.37 y 0.66, respectivamete. Usado las ecuacioes del LRFD para pilotes, ( ) ( ) ( ) RF R + RF R LF Q (10.8) s s b b i i la resistecia total, miorada, es 309 kn (69.5 kip), valor mucho meor que la carga mayorada de 660kN (148 kip). Esto sigifica que este diseño o es seguro. Usado cargas o mayoradas y resistecias o mioradas, para este diseño se calcula u factor de seguridad equivalete igual a 1.0. Para la siguiete iteració, supoiedo que deseamos coservar la base del pilote a la misma cota, elegimos u pilote de 457mm (18 i.) de diámetro. Los cálculos correspodietes a la resistecia friccioal so prácticamete iguales a excepció del valor de a s. El valor calculado de la resistecia friccioal o miorada es igual a 161 kn (36.2 kip). Para la resistecia de puta observar que como hemos variado el diámetro del pilote tambié cambiará D e IFR. De la Ecuació (10.5) calculamos D y obteemos u valor aproximadamete igual a 20. De la Figura 10.3 obteemos u uevo NIFR igual a 3%. De la Ecuació (10.5) se obtiee u IFR(%) de 59%, resultado e u q b,10% y ua resistecia de puta o miorada iguales a 5580 kpa (117 ksf) y 917 kn (206 kip), respectivamete. La capacidad total, miorada, calculada usado la Ecuació (10.8) es igual a 664 kn (149 kip), valor que represeta u diseño aceptable. Para este diseño, e base a las cargas o mayoradas y las resistecias o mioradas, u factor de seguridad equivalete es igual a 2.2. Observar que este factor de seguridad sólo se aplica para este método de diseño y combiació de cargas y resistecias particulares. Determiació de u RF para utilizar e el diseño de pilotes mediate métodos de diseño directos E el Capítulo 9 presetamos el método de Aoki y de Alecar Velloso (1975) como u método de diseño directo geeral. Utilizaremos este ejemplo de diseño para demostrar cómo
8 178 se puede emplear otros métodos directos para desarrollar factores de resistecia e base a los datos de esayos de carga dispoibles. Es importate observar que la base de datos de esayos de carga utilizada para estos métodos de diseño debería coteer umerosos casos de codicioes de suelo y tipos de pilotes similares. Esto es ecesario para asegurar la aplicabilidad del método de diseño y su icertidumbre. Para este diseño elegimos el método de Bustamate y Giaeselli (1982), ya que asumimos que uestra empresa hipotética (la que está realizado estos cálculos) cueta co datos de esayos de carga que respalda el uso de dicho método para tipos de suelos y pilotes similares. La Tabla 10.3 correspode a la base de datos de esayos de carga e poder de uestra empresa hipotética. E este ejemplo tambié deberemos determiar qué valores del factor de resistecia utilizar e el diseño. Observar de la discusió e los Capítulos 7, 8 y 9 que cuado se dispoe de este tipo de datos de esayos de carga (capacidad total medida vs. capacidad total proosticada) se debe utilizar la siguiete ecuació del LRFD: ( )( ) ( ) RF R + R LF Q (10.9) s b i i dode (R s + R b ) es la capacidad de carga total del pilote. Por lo tato, debemos hallar u úico valor de RF que se aplicará a la capacidad total del pilote. Debido a que e el ejemplo estamos utilizado los factores de carga de ASCE-7, para estimar RF debemos usar la Figura Para utilizar esta figura ecesitamos igresar co u valor COV y el ídice de cofiabilidad β. E este ejemplo usaremos u ídice de cofiabilidad igual a 3.0, el valor covecioal utilizado e el diseño estructural. El COV se debe determiar a partir de la base de datos de esayos de carga de la Tabla El primer paso cosiste e calcular el error para cada esayo de carga de la siguiete maera. La capacidad proosticada se calcula usado el método de Bustamate y Giaeselli (1982). Observar que cosideramos que la capacidad proosticada es la media de los datos, ya que ecesitamos evaluar la desviació de los valores reales respecto de este valor proosticado. Para calcular el COV de (R s + R b ) aplicamos las Ecuacioes (3.2.1) y (3.2.2) a la columa (4) de la Tabla El COV resultate es igual a El paso fial para evaluar u RF para este diseño cosiste e igresar a la Figura 10.4 co u COV de 0.23 y u β de 3.0. El RF resultate es 0.55.
9 179 Tabla 10.3 Base de datos de esayos de carga hipotéticos: La columa (1) es el úmero de esayos de carga, la columa (2) es la capacidad de carga total (resistecia) del pilote proosticada usado el método de Bustamate y Giaeselli (1982) para el pilote esayado, la columa (3) es la capacidad de carga total del pilote medida mediate el esayo de carga, y la columa (4) es la diferecia ormalizada ( error ) etre la capacidad medida y la capacidad proosticada. Los datos idica u COV de 0.23 para la capacidad de carga total. (1) esayo de carga (2) cap. proosticada (kn) (3) cap. medida (kn) (4) (cap. medida - cap. proosticada) / cap. proosticada
10 β = 2.0 β = 2.5 β = 3.0 β = Factor de resistecia ajustado (RF) COV Resistecia total (R s+ R b) Figura 10.4 Gráfica del factor de resistecia ajustado (RF) e fució del COV de la resistecia total y el ídice de cofiabilidad objetivo β, a aplicar a la capacidad de carga total e el diseño de pilotes usado los factores de carga de ASCE-7. Se asume u factor de sesgo de 1.06 para ua resistecia total co distribució log-ormal, lo que implica que la resistecia se evalúa e forma coservadora de acuerdo co el procedimieto CAM. Luego el RF hallado e este ejemplo se aplicaría juto co el método de Bustamate y Giaeselli (1982) para realizar verificacioes de diseño usado la Ecuació (10.9). El trabajo de Badii y Salgado (1998) cotiee resúmees de diferetes métodos directos para diseño de pilotes, icluyedo el método de Bustamate y Giaeselli (1982).
11 181 Coclusioes Del primer ejemplo de diseño observamos que los métodos de diseño de pilotes se puede aplicar prácticamete del mismo modo que e el diseño por tesioes de trabajo, salvo que se aplica factores de resistecia e lugar de factores de seguridad, y se utiliza cargas mayoradas e lugar de cargas o mayoradas. E el ejemplo correspodiete a u pilote e area, se demostró u método de diseño directo para pilotes de puta abierta que aprovecha los resultados de ivestigacioes recietemete realizadas por Paik ad Salgado (2003) y Lee y Salgado (2003). E el segudo ejemplo se demostró ua técica que le permite al diseñador estimar factores de resistecia para utilizar e el diseño e base a datos de esayos de carga realizados e suelos similares y el mismo tipo de pilote. De este modo es posible tratar específicamete la icertidumbre que probablemete se ecotrará para u diseño particular. Esta técica debería permitir ampliar el uso del LRFD a otros métodos de diseño diferetes a los mecioados e el presete iforme.
De esta forma, el problema de encontrar la mejor recta se concentra en calcular los valores de la pendiente (m) y de la ordenada al origen (b)
 MÉTODO DE MÍNIMOS CUADRADOS E muchos de los experimetos que se realiza e Física, se obtiee u cojuto de parejas de úmeros (abscisa, ordeada) por los cuales ecesitamos, para obteer u modelo matemático que
MÉTODO DE MÍNIMOS CUADRADOS E muchos de los experimetos que se realiza e Física, se obtiee u cojuto de parejas de úmeros (abscisa, ordeada) por los cuales ecesitamos, para obteer u modelo matemático que
Ejercicios resueltos de Muestreo
 Tema Ejercicios resueltos de Muestreo Ejercicio Sea ua població ita de 4 elemetos: P = f; 4; ; g : Se cosidera muestras de elemetos que se supoe extraidos y o devueltos a la població y que el muestreo
Tema Ejercicios resueltos de Muestreo Ejercicio Sea ua població ita de 4 elemetos: P = f; 4; ; g : Se cosidera muestras de elemetos que se supoe extraidos y o devueltos a la població y que el muestreo
Medidas de Tendencia Central
 1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
1 Medidas de Tedecia Cetral La Media La media (o promedio) de ua muestra x 1, x,, x de tamaño de ua variable o característica x, se defie como la suma de todos los valores observados e la muestra, dividida
Preguntas más Frecuentes: Tema 2
 Pregutas más Frecuetes: Tema 2 Pulse sobre la preguta para acceder directamete a la respuesta 1. Se puede calcular la media a partir de las frecuecias absolutas acumuladas? 2. Para calcular la media aritmética,
Pregutas más Frecuetes: Tema 2 Pulse sobre la preguta para acceder directamete a la respuesta 1. Se puede calcular la media a partir de las frecuecias absolutas acumuladas? 2. Para calcular la media aritmética,
Introducción a las medidas de dispersión.
 UNIDAD 8: INTERPRETEMOS LA VARIABILIDAD DE LA INFORMACION. Itroducció a las medidas de dispersió. Como su ombre lo idica, las medidas de dispersió so parámetros que os idica qué ta dispersos está los datos.
UNIDAD 8: INTERPRETEMOS LA VARIABILIDAD DE LA INFORMACION. Itroducció a las medidas de dispersió. Como su ombre lo idica, las medidas de dispersió so parámetros que os idica qué ta dispersos está los datos.
5-14 Ecuaciones de diseño importantes
 46 PARTE DOS Preveció de fallas R R R a) Figura 5-33 R b) Formas de las curvas de la gráfica R versus R. E cada caso, el área sombreada es igual a R se obtiee por itegració umérica. a) Curva típica de
46 PARTE DOS Preveció de fallas R R R a) Figura 5-33 R b) Formas de las curvas de la gráfica R versus R. E cada caso, el área sombreada es igual a R se obtiee por itegració umérica. a) Curva típica de
MEDIDAS DE TENDENCIA CENTRAL. _ xi
 EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
EDIDAS DE TENDENCIA CENTRAL. EDIA ARITÉTICA. Es la medida más coocida y tambié es llamada promedio se obtiee sumado todos los valores de la muestra o població, dividida etre el total de elemetos que cotiee
MEDIDAS DE DISPERSIÓN.
 MEDIDA DE DIPERIÓN. Las medidas de tedecia cetral solamete da ua medida de la localizació del cetro de los datos. Co mucha frecuecia, es igualmete importate describir la forma e que las observacioes está
MEDIDA DE DIPERIÓN. Las medidas de tedecia cetral solamete da ua medida de la localizació del cetro de los datos. Co mucha frecuecia, es igualmete importate describir la forma e que las observacioes está
Tema 4. Estimación de parámetros
 Estadística y metodología de la ivestigació Curso 2012-2013 Pedro Faraldo, Beatriz Pateiro Tema 4. Estimació de parámetros 1. Estimació putual 1 1.1. Estimació de la proporció e la distribució Bi(m, p).......................
Estadística y metodología de la ivestigació Curso 2012-2013 Pedro Faraldo, Beatriz Pateiro Tema 4. Estimació de parámetros 1. Estimació putual 1 1.1. Estimació de la proporció e la distribució Bi(m, p).......................
MINITAB y MODELOS DE REGRESIÓN
 Prácticas de Fudametos Matemáticos para el estudio del Medio Ambiete www.um.es/docecia/jpastor jpastor@um.es MINITAB y MODELOS DE REGRESIÓN 1. Itroducció Ua de las cuestioes de mayor iterés e las Ciecias
Prácticas de Fudametos Matemáticos para el estudio del Medio Ambiete www.um.es/docecia/jpastor jpastor@um.es MINITAB y MODELOS DE REGRESIÓN 1. Itroducció Ua de las cuestioes de mayor iterés e las Ciecias
EJERCICIOS DE RECURRENCIA
 EJERCICIOS DE RECURRENCIA (co alguas solucioes) Resolver la recurrecia = 5 6 =, = y tambié ésta: = =, = Resolvamos la primera E primer lugar otamos que es ua recurrecia lieal, pues pasado todos los térmios
EJERCICIOS DE RECURRENCIA (co alguas solucioes) Resolver la recurrecia = 5 6 =, = y tambié ésta: = =, = Resolvamos la primera E primer lugar otamos que es ua recurrecia lieal, pues pasado todos los térmios
En el tema anterior se estudió que muchas decisiones se toman a partir de resultados muestrales. Por ejemplo:
 TEMA 6. Estimació putual. E muchos casos o será posible determiar el valor de u parámetro poblacioal descoocido, aalizado todos los valores poblacioales, pues el proceso a seguir puede ser destructivo,
TEMA 6. Estimació putual. E muchos casos o será posible determiar el valor de u parámetro poblacioal descoocido, aalizado todos los valores poblacioales, pues el proceso a seguir puede ser destructivo,
α β la cual puede presentar
 5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
1.1 INTERVALOS DEL 95% DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL VARIANZA CONOCIDA
 Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky 106 1. INTERVALO DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL upogamos que X1,...,X es ua muestra aleatoria de ua
Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky 106 1. INTERVALO DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL upogamos que X1,...,X es ua muestra aleatoria de ua
CLAVES DE CORRECCIÓN GUÍA DE EJERCITACIÓN FACTORES Y PRODUCTOS PREGUNTA ALTERNATIVA Nivel
 x Estimado alumo: Aquí ecotrarás las claves de correcció, las habilidades y los procedimietos de resolució asociados a cada preguta, o obstate, para reforzar tu apredizaje es fudametal que asistas a la
x Estimado alumo: Aquí ecotrarás las claves de correcció, las habilidades y los procedimietos de resolució asociados a cada preguta, o obstate, para reforzar tu apredizaje es fudametal que asistas a la
LAS SERIES GEOMÉTRICAS Y SU TENDENCIA AL INFINITO
 LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
LA ERIE GEOMÉTRICA Y U TENDENCIA AL INFINITO ugerecias al Profesor: Al igual que las sucesioes, las series geométricas se itroduce como objetos matemáticos que permite modelar y resolver problemas que
Técnicas para problemas de desigualdades
 Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
Técicas para problemas de desigualdades Notas extraídas del libro de Arthur Egel [] 5 de marzo de 00 Medias Comezamos co dos de las desigualdades más básicas pero al mismo tiempo más importates Sea x,
LABORATORIO BIO 9000 PROCEDIMIENTO PE-I-03 PARA EL CÁLCULO DE LA INCERTIDUMBRE EN MICROBIOLOGÍA
 LABORATORIO BIO 9000 PROCEDIMIENTO PARA EL CÁLCLO DE LA INCERTIDMBRE EN MICROBIOLOGÍA Rev. º: 00 Fecha de aprobació: 19/05/11 REV. FECHA HOJA/S CASA DEL CAMBIO Realizado Revisado Aprobado Fdo.: Daiel Aguilar-Galido
LABORATORIO BIO 9000 PROCEDIMIENTO PARA EL CÁLCLO DE LA INCERTIDMBRE EN MICROBIOLOGÍA Rev. º: 00 Fecha de aprobació: 19/05/11 REV. FECHA HOJA/S CASA DEL CAMBIO Realizado Revisado Aprobado Fdo.: Daiel Aguilar-Galido
Intervalos de Confianza basados en una muestra. Instituto de Cálculo
 Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
Prueba Integral Lapso / Área de Matemática Fecha: MODELO DE RESPUESTA (Objetivos del 01 al 11)
 Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
EJERCICIOS DE SERIES DE FUNCIONES
 EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
2 CARTAS DE CONTROL POR ATRIBUTOS
 2 CARTAS DE CONTROL POR ATRIBUTOS Cualquier característica de calidad que pueda ser clasificada de forma biaria: cumple o o cumple, fucioa o o fucioa, pasa o o pasa, coforme o discoforme defectuoso, o
2 CARTAS DE CONTROL POR ATRIBUTOS Cualquier característica de calidad que pueda ser clasificada de forma biaria: cumple o o cumple, fucioa o o fucioa, pasa o o pasa, coforme o discoforme defectuoso, o
Problemas de Estimación de Una y Dos Muestras. UCR ECCI CI-1352 Probabilidad y Esradística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Problemas de Estimació de Ua y Dos Muestras UCR ECCI CI-35 Probabilidad y Esradística Prof. M.Sc. Kryscia Daviaa Ramírez Beavides Iferecia Estadística La teoría de la iferecia estadística cosiste e aquellos
Problemas de Estimació de Ua y Dos Muestras UCR ECCI CI-35 Probabilidad y Esradística Prof. M.Sc. Kryscia Daviaa Ramírez Beavides Iferecia Estadística La teoría de la iferecia estadística cosiste e aquellos
Sistemas de Ecuaciones Lineales. M. en I. Gerardo Avilés Rosas
 Sistemas de Ecuacioes Lieales M. e I. Gerardo Avilés Rosas Octubre de 206 Tema 5 Sistemas de Ecuacioes Lieales Objetivo: El alumo formulará, como modelo matemático de problemas, sistemas de ecuacioes lieales
Sistemas de Ecuacioes Lieales M. e I. Gerardo Avilés Rosas Octubre de 206 Tema 5 Sistemas de Ecuacioes Lieales Objetivo: El alumo formulará, como modelo matemático de problemas, sistemas de ecuacioes lieales
TEMA 5: Gráficos de Control por Atributos. 1. Gráfico de control para la fracción de unidades defectuosas
 TEMA 5: Gráficos de Cotrol por Atributos 1 Gráfico de cotrol para la fracció de uidades defectuosas 2 Gráfico de cotrol para el úmero medio de discoformidades por uidad Selecció del tamaño muestral 3 Clasificació
TEMA 5: Gráficos de Cotrol por Atributos 1 Gráfico de cotrol para la fracció de uidades defectuosas 2 Gráfico de cotrol para el úmero medio de discoformidades por uidad Selecció del tamaño muestral 3 Clasificació
Unidad 1: Las Ecuaciones Diferenciales y Sus Soluciones
 Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
2 Conceptos básicos y planteamiento
 ESTADÍSTICA DESCRIPTIVA: DOS VARIABLES Juliá de la Horra Departameto de Matemáticas U.A.M. 1 Itroducció E muchos casos estaremos iteresados e hacer u estudio cojuto de varias características de ua població.
ESTADÍSTICA DESCRIPTIVA: DOS VARIABLES Juliá de la Horra Departameto de Matemáticas U.A.M. 1 Itroducció E muchos casos estaremos iteresados e hacer u estudio cojuto de varias características de ua població.
Determinación del tamaño de una muestra (para dos o más muestras)
 STATGRAPHICS Rev. 457 Determiació del tamaño de ua muestra (para dos o más muestras) Este procedimieto determia el tamaño de muestra apropiado para estimar o realiar pruebas de hipótesis respecto a alguo
STATGRAPHICS Rev. 457 Determiació del tamaño de ua muestra (para dos o más muestras) Este procedimieto determia el tamaño de muestra apropiado para estimar o realiar pruebas de hipótesis respecto a alguo
M arcelo, de vez en vez, usa una reata de 10 m de largo y 2 cm de grueso para
 GEOMETRÍA, TRIGONOMETRÍA Y SERIES Tema 4 Series uméricas M arcelo, de vez e vez, usa ua reata de 10 m de largo y cm de grueso para medir el cotoro de los terreos que fumiga. Para que la reata que usa o
GEOMETRÍA, TRIGONOMETRÍA Y SERIES Tema 4 Series uméricas M arcelo, de vez e vez, usa ua reata de 10 m de largo y cm de grueso para medir el cotoro de los terreos que fumiga. Para que la reata que usa o
Unidad N 2. Medidas de dispersión
 Uidad N 2 Medidas de dispersió Ua seguda propiedad importate que describe ua serie de datos uméricos es ua variació. La variació es la catidad de dispersió o propagació e los datos. Dos series de datos
Uidad N 2 Medidas de dispersió Ua seguda propiedad importate que describe ua serie de datos uméricos es ua variació. La variació es la catidad de dispersió o propagació e los datos. Dos series de datos
Muestreo sistemático
 Capítulo 1 Muestreo sistemático El muestreo sistemático es u tipo de muestreo que es aplicable cuado los elemetos de la població sobre la que se realiza el muestreo está ordeados Este procedimieto de muestreo
Capítulo 1 Muestreo sistemático El muestreo sistemático es u tipo de muestreo que es aplicable cuado los elemetos de la població sobre la que se realiza el muestreo está ordeados Este procedimieto de muestreo
Guía 1 Matemática: Estadística NM 4
 Cetro Educacioal Sa Carlos de Aragó. Sector: Matemática. Prof.: Ximea Gallegos H. 1 Guía 1 Matemática: Estadística NM 4 Nombre: Curso: Fecha. Uidad: Estadística y Probabilidades. Apredizajes Esperados:
Cetro Educacioal Sa Carlos de Aragó. Sector: Matemática. Prof.: Ximea Gallegos H. 1 Guía 1 Matemática: Estadística NM 4 Nombre: Curso: Fecha. Uidad: Estadística y Probabilidades. Apredizajes Esperados:
INTERÉS SIMPLE COMO FUNCIÓN LINEAL.
 INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
ITM, Institución universitaria. Guía de Laboratorio de Física Mecánica. Práctica 3: Teoría de errores. Implementos
 ITM, Istitució uiversitaria Guía de Laboratorio de Física Mecáica Práctica 3: Teoría de errores Implemetos Regla, balaza, cilidro, esfera metálica, flexómetro, croómetro, computador. Objetivos E esta práctica
ITM, Istitució uiversitaria Guía de Laboratorio de Física Mecáica Práctica 3: Teoría de errores Implemetos Regla, balaza, cilidro, esfera metálica, flexómetro, croómetro, computador. Objetivos E esta práctica
R-SQUARED RESID. MEAN SQUARE (MSE) σˆ 2 ADJUSTED R-SQUARED STANDARD DEVIATION σ ˆ
 06 5.8 Leyedo la salida de u programa estadístico Cada programa estadístico preseta los resultados de la regresió e forma diferete, pero la mayoría provee la misma iformació básica. La tabla muestra la
06 5.8 Leyedo la salida de u programa estadístico Cada programa estadístico preseta los resultados de la regresió e forma diferete, pero la mayoría provee la misma iformació básica. La tabla muestra la
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
ESTADÍSTICA DESCRIPTIVA
 ESTADÍSTICA DESCRIPTIVA DISTRIBUCIÓN DE FRECUENCIAS, HISTOGRAMA, POLIGONO Y ESTADÍSITICOS DE TENDENCIA CENTRAL, DISPERSIÓN, ASIMETRÍA Y CURTOSIS. Prof.: MSc. Julio R. Vargas I. Las calificacioes fiales
ESTADÍSTICA DESCRIPTIVA DISTRIBUCIÓN DE FRECUENCIAS, HISTOGRAMA, POLIGONO Y ESTADÍSITICOS DE TENDENCIA CENTRAL, DISPERSIÓN, ASIMETRÍA Y CURTOSIS. Prof.: MSc. Julio R. Vargas I. Las calificacioes fiales
GUIA DE ESTUDIO Nro 1
 MATERIA: MATEMÁTICA I CURSO: I AÑO EJE ESTRUCTURAL I: CONCEPTOS FUNDAMENTALES DEL ALGEBRA GRUPOS CONCEPTUALES: - Epresioes algebraicas. Poliomios. - Ecuacioes. Iecuacioes. TEMARIO: GUIA DE ESTUDIO Nro
MATERIA: MATEMÁTICA I CURSO: I AÑO EJE ESTRUCTURAL I: CONCEPTOS FUNDAMENTALES DEL ALGEBRA GRUPOS CONCEPTUALES: - Epresioes algebraicas. Poliomios. - Ecuacioes. Iecuacioes. TEMARIO: GUIA DE ESTUDIO Nro
1 Valores individuales del conjunto
 5/03/00 METROLOGÍA ESTADÍSTICA ANÁLISIS DE DATOS Cuado se obtiee uo o más grupos de datos, producto de repeticioes i e ua medida, la mejor forma de represetarlas, es mediate las Medidas de tedecia cetral
5/03/00 METROLOGÍA ESTADÍSTICA ANÁLISIS DE DATOS Cuado se obtiee uo o más grupos de datos, producto de repeticioes i e ua medida, la mejor forma de represetarlas, es mediate las Medidas de tedecia cetral
Composición de fundamental con tercera armónica Onda fundamental. Onda resultante
 Fució POLARMÓNCAS ENSONES Y CORRENES POLARMÓNCAS 7. troducció E los aálisis ateriores, hemos trabajado co geeració de tesioes alteras del tipo seoidal, y circuitos co características lieales, lo cual se
Fució POLARMÓNCAS ENSONES Y CORRENES POLARMÓNCAS 7. troducció E los aálisis ateriores, hemos trabajado co geeració de tesioes alteras del tipo seoidal, y circuitos co características lieales, lo cual se
Cálculo de límites Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
6. ECUACIONES DE RECURRENCIA.
 6. ECUACIONES DE RECURRENCIA. 6.1. Itroducció. Las relacioes de recurrecia puede cosiderarse como técicas avazadas de coteo. Resuelve problemas cuya solució o puede obteerse usado variacioes, permutacioes,
6. ECUACIONES DE RECURRENCIA. 6.1. Itroducció. Las relacioes de recurrecia puede cosiderarse como técicas avazadas de coteo. Resuelve problemas cuya solució o puede obteerse usado variacioes, permutacioes,
Una ecuación diferencial lineal de orden superior general tendría la forma. (1) dx dx
 .7 Ecuacioes difereciales lieales de orde superior 6.7 Ecuacioes difereciales lieales de orde superior Ua ecuació diferecial lieal de orde superior geeral tedría la forma d y d y dy a( ) a ( )... a ( )
.7 Ecuacioes difereciales lieales de orde superior 6.7 Ecuacioes difereciales lieales de orde superior Ua ecuació diferecial lieal de orde superior geeral tedría la forma d y d y dy a( ) a ( )... a ( )
UNIDAD 2 Ecuaciones Diferenciales Lineales de Orden Superior
 UNIDAD Ecuacioes Difereciales Lieales de Orde Superior. Defiició Ua ecuació diferecial lieal de orde tiee la forma: d y a a a a y= g d d d Si las fucioes a a so todas costates (o cero) etoces se dice que
UNIDAD Ecuacioes Difereciales Lieales de Orde Superior. Defiició Ua ecuació diferecial lieal de orde tiee la forma: d y a a a a y= g d d d Si las fucioes a a so todas costates (o cero) etoces se dice que
T ema 6 DISTRIBUCIONES DISCRETAS DE PROBABILIDAD. x 1. x 2 = 1 = 2. x 3 = 3. x 4. Variable aleatoria: definición y tipos:
 T ema 6 DISTRIBUCIONES DISCRETAS DE PROBABILIDAD Variable aleatoria: defiició y tipos: Ua variable aleatoria es ua fució que asiga u úmero real, y sólo uo, a cada uo de los resultados de u eperimeto aleatorio.
T ema 6 DISTRIBUCIONES DISCRETAS DE PROBABILIDAD Variable aleatoria: defiició y tipos: Ua variable aleatoria es ua fució que asiga u úmero real, y sólo uo, a cada uo de los resultados de u eperimeto aleatorio.
ESTIMACIONES DE MEDIAS
 COLEGIO SAN BARTOLOMÉ LA MERCED ESTADÍSTICA GRADO ESTIMACIÓN 0-0 Símbolos que se debe teer e cueta: POBLACIÓN MUESTRA MEDIA VARIANZA DESVIACIÓN ESTÁNDAR TAMAÑO N La estimació cosiste e determiar el valor
COLEGIO SAN BARTOLOMÉ LA MERCED ESTADÍSTICA GRADO ESTIMACIÓN 0-0 Símbolos que se debe teer e cueta: POBLACIÓN MUESTRA MEDIA VARIANZA DESVIACIÓN ESTÁNDAR TAMAÑO N La estimació cosiste e determiar el valor
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD PAUTA DE CORRECCIÓN PRUEBA RECUPERATIVA N 2 Profesor: Hugo S. Salias. Segudo Semestre 2009 DESARROLLO
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD PAUTA DE CORRECCIÓN PRUEBA RECUPERATIVA N 2 Profesor: Hugo S. Salias. Segudo Semestre 2009 DESARROLLO
1. QUÉ ES LA ESTADÍSTICA?
 1. QUÉ ES LA ESTADÍSTICA? Cuado coloquialmete se habla de estadística, se suele pesar e ua relació de datos uméricos presetada de forma ordeada y sistemática. Esta idea es la cosecuecia del cocepto popular
1. QUÉ ES LA ESTADÍSTICA? Cuado coloquialmete se habla de estadística, se suele pesar e ua relació de datos uméricos presetada de forma ordeada y sistemática. Esta idea es la cosecuecia del cocepto popular
Coeficiente de escorrentía C
 EXAMEN Febrero 2010 iempo 90 miutos EJERCICIO 1 (10 putos) e pide que dimesioes, utilizado el método racioal, los colectores AB y BC de la red de saeamieto uitaria de la urbaizació que aparece e la Figura
EXAMEN Febrero 2010 iempo 90 miutos EJERCICIO 1 (10 putos) e pide que dimesioes, utilizado el método racioal, los colectores AB y BC de la red de saeamieto uitaria de la urbaizació que aparece e la Figura
MATEMÁTICAS. Nivel Medio
 MATME/PF/M11/N11/M12/N12 MATEMÁTICAS Nivel Medio Tareas de la carpeta Para utilizar e 2011 y 2012 Orgaizació del Bachillerato Iteracioal, 2009 10 págias 2 MATME/PF/M11/N11/M12/N12 ÍNDICE Itroducció Tareas
MATME/PF/M11/N11/M12/N12 MATEMÁTICAS Nivel Medio Tareas de la carpeta Para utilizar e 2011 y 2012 Orgaizació del Bachillerato Iteracioal, 2009 10 págias 2 MATME/PF/M11/N11/M12/N12 ÍNDICE Itroducció Tareas
UNIDAD 1 Ecuaciones Diferenciales de Primer Orden
 UNIDAD UNIDAD Ecuacioes Difereciales de Primer Orde Defiició lasificació de las Ecuacioes Difereciales Ua ecuació diferecial es aquélla que cotiee las derivadas o difereciales de ua o más variables depedietes
UNIDAD UNIDAD Ecuacioes Difereciales de Primer Orde Defiició lasificació de las Ecuacioes Difereciales Ua ecuació diferecial es aquélla que cotiee las derivadas o difereciales de ua o más variables depedietes
13.1 INTERVALOS DEL 95% DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL VARIANZA CONOCIDA
 Dra. Diaa M. Kelmasky 109 13. INTERVALOS DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL Supogamos que X1,...,X es ua muestra aleatoria de ua població ormal co media μ y variaza. Sabemos que la media
Dra. Diaa M. Kelmasky 109 13. INTERVALOS DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL Supogamos que X1,...,X es ua muestra aleatoria de ua població ormal co media μ y variaza. Sabemos que la media
Trabajo Especial Estadística
 Estadística Resolució de u Problema Alumas: Arrosio, Florecia García Fracaro, Sofía Victorel, Mariaela FECHA DE ENTREGA: 12 de Mayo de 2012 Resume Este trabajo es ua ivestigació descriptiva, es decir,
Estadística Resolució de u Problema Alumas: Arrosio, Florecia García Fracaro, Sofía Victorel, Mariaela FECHA DE ENTREGA: 12 de Mayo de 2012 Resume Este trabajo es ua ivestigació descriptiva, es decir,
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN
 DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
DISCUSIÓN Y RESOLUCIÓN DE ECUACIONES LINEALES. TEOREMA DE ROUCHE. REGLA DE CRAMER. MÉTODO DE GAUSS-JORDAN Ídice. INTRODUCCIÓN2 2. SISTEMAS DE ECUACIONES LINEALES2 Defiicioes básicas.2 Iterpretació vectorial3
Estadística y sus aplicaciones en Ciencias Sociales Práctico 4 - Solución Curso ) Como se trata de muestreo sin reposición, se tiene C 5 3
 Estadística y sus aplicacioes e Ciecias Sociales Práctico 4 - Solució Curso 016 Ejercicio 1 5! 1) Como se trata de muestreo si reposició, se tiee C 5 3 3!! muestras de tamaño =3. ) Distribució muestral
Estadística y sus aplicacioes e Ciecias Sociales Práctico 4 - Solució Curso 016 Ejercicio 1 5! 1) Como se trata de muestreo si reposició, se tiee C 5 3 3!! muestras de tamaño =3. ) Distribució muestral
IntroducciónalaInferencia Estadística
 Capítulo 6 ItroduccióalaIferecia Estadística 6.1. Itroducció El pricipal objetivo de la Estadística es iferir o estimar características de ua població que o es completamete observable (o o iteresa observarla
Capítulo 6 ItroduccióalaIferecia Estadística 6.1. Itroducció El pricipal objetivo de la Estadística es iferir o estimar características de ua població que o es completamete observable (o o iteresa observarla
Convolución. Dr. Luis Javier Morales Mendoza. Procesamiento Digital de Señales Departamento de Maestría DICIS - UG
 Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
Covolució Dr. Luis Javier Morales Medoza Procesamieto Digital de Señales Departameto de Maestría DICIS - UG Ídice.. Itroducció... Aálisis de Sistemas Discretos Lieales e Ivariates e el Tiempo.... Técicas
8 DESIGUALDAD DE TCHEBYCHEFF LEY DE LOS GRANDES NÚMEROS
 8 DESIGUALDAD DE TCHEBYCHEFF LEY DE LOS GRANDES NÚMEROS Sea ua variable aleatoria de ley descoocida co 0,00. Si 0,, emplear la desigualdad de TCHEBYCHEFF para acotar iferiormete la probabilidad E( ) [
8 DESIGUALDAD DE TCHEBYCHEFF LEY DE LOS GRANDES NÚMEROS Sea ua variable aleatoria de ley descoocida co 0,00. Si 0,, emplear la desigualdad de TCHEBYCHEFF para acotar iferiormete la probabilidad E( ) [
2 FUNDAMENTOS DE PROBABILIDAD
 2 FUNDAMENTOS DE PROBABILIDAD T al vez el estudio de la probabilidad toma setido cuado se percibe y se acepta la existecia de la aleatoriedad e diversos aspectos de la vida diaria. Si embargo, si cosideramos
2 FUNDAMENTOS DE PROBABILIDAD T al vez el estudio de la probabilidad toma setido cuado se percibe y se acepta la existecia de la aleatoriedad e diversos aspectos de la vida diaria. Si embargo, si cosideramos
2.1. Concepto Monto, capital, tasa de interés y tiempo.
 1 2.1. Cocepto El iterés compuesto tiee lugar cuado el deudor o paga al cocluir cada periodo que sirve como base para su determiació los itereses correspodietes. Así, provoca que los mismos itereses se
1 2.1. Cocepto El iterés compuesto tiee lugar cuado el deudor o paga al cocluir cada periodo que sirve como base para su determiació los itereses correspodietes. Así, provoca que los mismos itereses se
Importancia de las medidas de tendencia central.
 UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
UNIDAD 5: UTILICEMOS MEDIDAS DE TENDENCIA CENTRAL. Importacia de las medidas de tedecia cetral. Cuado recopilamos ua serie de datos podemos resumirlos utilizado ua tabla de clases y frecuecias. La iformació
PyE_ EF2_TIPO1_
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD Y ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD Y ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN
Series alternadas Introducción
 Sesió 26 Series alteradas Temas Series alteradas. Covergecia absoluta y codicioal. Capacidades Coocer y aplicar el criterio para estudiar series alteradas. Coocer y aplicar el teorema de la covergecia
Sesió 26 Series alteradas Temas Series alteradas. Covergecia absoluta y codicioal. Capacidades Coocer y aplicar el criterio para estudiar series alteradas. Coocer y aplicar el teorema de la covergecia
Técnicas Cuantitativas II Muestra y Estadísticos Muestrales. TC II Muestra y Estadísticos Muestrales 1 / 20
 Técicas Cuatitativas II 2012-2013 Muestra y Estadísticos Muestrales TC II Muestra y Estadísticos Muestrales 1 / 20 Ídice Ídice Cocepto de muestra y Alguos ejemplos de variaza de la media Cocepto de muestra
Técicas Cuatitativas II 2012-2013 Muestra y Estadísticos Muestrales TC II Muestra y Estadísticos Muestrales 1 / 20 Ídice Ídice Cocepto de muestra y Alguos ejemplos de variaza de la media Cocepto de muestra
3. Las medidas de centralización
 FUOC XP00/71004/00017 21 Las medidas de cetralizació 3. Las medidas de cetralizació La mediaa y la media aritmética Los diagramas de tallos y hojas y los histogramas proporcioa ua descripció geeral de
FUOC XP00/71004/00017 21 Las medidas de cetralizació 3. Las medidas de cetralizació La mediaa y la media aritmética Los diagramas de tallos y hojas y los histogramas proporcioa ua descripció geeral de
1. Intervalos de Conanza
 M. Iiesta Uiversidad de Murcia INFERENCIA ESTADÍSTICA Tema 3.: Itervalos de coaza Objetivos Costruir itervalos de coaza para los parámetros más importates. Aplicar coveietemete los IC atediedo a cada situació
M. Iiesta Uiversidad de Murcia INFERENCIA ESTADÍSTICA Tema 3.: Itervalos de coaza Objetivos Costruir itervalos de coaza para los parámetros más importates. Aplicar coveietemete los IC atediedo a cada situació
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
INTRODUCCIÓN A LAS PROGRESIONES
 Apédice A INTRODUCCIÓN A LAS PROGRESIONES A.. A..3 E el Apédice A, los alumos ivestigaro progresioes buscado patroes y reglas. E la primera parte del apédice, se cocetraro e las progresioes aritméticas
Apédice A INTRODUCCIÓN A LAS PROGRESIONES A.. A..3 E el Apédice A, los alumos ivestigaro progresioes buscado patroes y reglas. E la primera parte del apédice, se cocetraro e las progresioes aritméticas
Práctica 7 CONTRASTES DE HIPÓTESIS
 Práctica 7. Cotrastes de hipótesis Práctica 7 CONTRATE DE IPÓTEI Objetivos Utilizar los cotrastes de hipótesis para decidir si u parámetro de la distribució de uos datos objeto de estudio cumple o o ua
Práctica 7. Cotrastes de hipótesis Práctica 7 CONTRATE DE IPÓTEI Objetivos Utilizar los cotrastes de hipótesis para decidir si u parámetro de la distribució de uos datos objeto de estudio cumple o o ua
CÁLCULO Ejercicios Resueltos Semana 1 30 Julio al 3 Agosto 2007
 CÁLCULO Ejercicios Resueltos Semaa 0 Julio al Agosto 007 Ejercicios Resueltos. Estime el área ecerrada por la curva de ecuació y, el eje X y, para ello, divida el itervalo [0,] e cico partes iguales, y
CÁLCULO Ejercicios Resueltos Semaa 0 Julio al Agosto 007 Ejercicios Resueltos. Estime el área ecerrada por la curva de ecuació y, el eje X y, para ello, divida el itervalo [0,] e cico partes iguales, y
LIMITES DE FUNCIONES. Ejemplo: Sea la función F(x) = 3X 2, evalúe la función para valores de X cercanos a 2, es decir
 PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
Slide 1. Slide 2. Slide 3. Universidad Diego Portales Facultad de Economía y Negocios. Capítulo 4 Introducción a la Probabilidad.
 Slide 1 Uiversidad Diego Portales Facultad de Ecoomía y Negocios Martes 13 de Abril, 2010 Slide 1 Slide 2 Capítulo 4 Itroducció a la Probabilidad Temas Pricipales: Experimetos, Reglas de Coteo, y Asigació
Slide 1 Uiversidad Diego Portales Facultad de Ecoomía y Negocios Martes 13 de Abril, 2010 Slide 1 Slide 2 Capítulo 4 Itroducció a la Probabilidad Temas Pricipales: Experimetos, Reglas de Coteo, y Asigació
ORGANIZACIÓN DE LOS DATOS.
 ORGANIZACIÓN DE LOS DATOS. La toma de datos es ua de las partes de mayor importacia e el desarrollo de ua ivestigació. Así los datos obteidos mediate u primer proceso recibe el ombre de datos si tratar
ORGANIZACIÓN DE LOS DATOS. La toma de datos es ua de las partes de mayor importacia e el desarrollo de ua ivestigació. Así los datos obteidos mediate u primer proceso recibe el ombre de datos si tratar
Figura 10. No se satisface el supuesto de linealidad.
 Regresió Lieal Simple Dra. Diaa Kelmasky 04 Figura 8 Figura 9. No se satisface el supuesto de homoscedasticidad Si graficáramos los residuos cotra los valores de X los putos debería estar distribuidos
Regresió Lieal Simple Dra. Diaa Kelmasky 04 Figura 8 Figura 9. No se satisface el supuesto de homoscedasticidad Si graficáramos los residuos cotra los valores de X los putos debería estar distribuidos
4 ALGEBRA DE BOOLE. 4.1 Introducción. 4.2 Axiomas. (a) a + b = b + a (b) a b = b a. (a) a + (b c) = (a + b) (a + c) (b) a (b + c) = a.
 Arquitectura del Computador 4 ALGEBRA DE BOOLE 4. Itroducció. El álgebra de Boole es ua herramieta de fudametal importacia e el mudo de la computació. Las propiedades que se verifica e ella sirve de base
Arquitectura del Computador 4 ALGEBRA DE BOOLE 4. Itroducció. El álgebra de Boole es ua herramieta de fudametal importacia e el mudo de la computació. Las propiedades que se verifica e ella sirve de base
Los números complejos
 Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
Los úmeros complejos Los úmeros complejos Forma biómica Defiició z = a + bi, o bie, z = (a, b) siedo a la parte real y b la parte imagiaria. a = r cos α b = r se α Opuesto z = a bi Cojugado z = a bi Represetació
Axioma 1 (Principio de inducción matemática) Sea S N con la propiedad que: a) 1 S. b) k R, k S k + 1 S. Entonces S = N.
 Iducció matemática A meudo deseamos probar proposicioes de la forma N, p. Por ejemplo: 1 N, 1 + + 3 + + 1 + 1. N, + 4. 3 N, par implica par. Proposicioes y 3 se puede probar usado la técica de variable
Iducció matemática A meudo deseamos probar proposicioes de la forma N, p. Por ejemplo: 1 N, 1 + + 3 + + 1 + 1. N, + 4. 3 N, par implica par. Proposicioes y 3 se puede probar usado la técica de variable
4.- Series. Criterios de convergencia. Series de Taylor y Laurent
 4.- Series. Criterios de covergecia. Series de Taylor y Lauret a) Itroducció. Series de fucioes reales. b) Covergecia de secuecias y series. c) Series de Taylor. d) Series de Lauret. e) Propiedades adicioales
4.- Series. Criterios de covergecia. Series de Taylor y Lauret a) Itroducció. Series de fucioes reales. b) Covergecia de secuecias y series. c) Series de Taylor. d) Series de Lauret. e) Propiedades adicioales
Población Joven Adulta Total A favor En contra Total
 Nombre: Libre Reglametado C.I.: EXAMEN El exame costa de dos partes. La Primera Parte debe ser realizada por todos los alumos y el tiempo previsto es de 2 horas. La Seguda Parte debe ser realizada sólo
Nombre: Libre Reglametado C.I.: EXAMEN El exame costa de dos partes. La Primera Parte debe ser realizada por todos los alumos y el tiempo previsto es de 2 horas. La Seguda Parte debe ser realizada sólo
EJERCICIOS RESUELTOS TEMA 8
 EJERCICIOS RESUELTOS TEMA 8 8.. U ivestigador desea coocer la opiió de los madrileños sobre la saidad pública. Para ello, acude a las 8 de la mañaa al hospital público de la capital más cercao a su domicilio
EJERCICIOS RESUELTOS TEMA 8 8.. U ivestigador desea coocer la opiió de los madrileños sobre la saidad pública. Para ello, acude a las 8 de la mañaa al hospital público de la capital más cercao a su domicilio
DETERMINACION DEL COSTO POR ALUMNO EGRESADO DE EDUCACION PRIMARIA
 DETERMINACION DEL COSTO POR ALUMNO EGRESADO DE EDUCACION PRIMARIA U Modelo de Costeo por Procesos JOSE ANTONIO CARRANZA PALACIOS *, JUAN MANUEL RIVERA ** INTRODUCCION U aspecto fudametal e la formulació
DETERMINACION DEL COSTO POR ALUMNO EGRESADO DE EDUCACION PRIMARIA U Modelo de Costeo por Procesos JOSE ANTONIO CARRANZA PALACIOS *, JUAN MANUEL RIVERA ** INTRODUCCION U aspecto fudametal e la formulació
 Walter Orlado Gozales Caicedo Secuecias Lógicas OBJETIVO: Lograr habilidad y destreza e el alumo practicado u razoamieto abstracto PROCEDIMIENTOS: INICIAL: Halla el valor del térmio que cotiúa e:,,,, 0,
Walter Orlado Gozales Caicedo Secuecias Lógicas OBJETIVO: Lograr habilidad y destreza e el alumo practicado u razoamieto abstracto PROCEDIMIENTOS: INICIAL: Halla el valor del térmio que cotiúa e:,,,, 0,
INSTRUCCIONES GENERALES Y VALORACIÓN. Ejercicio 1. (Puntuación máxima: 3 puntos) Calcular los valores de a para los cuales la inversa de la matriz
 INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: El eame preseta dos opcioes: A y B. El alumo deberá elegir ua de ellas y cotestar razoadamete a los cuatro ejercicios de que costa dicha opció. Para
INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES: El eame preseta dos opcioes: A y B. El alumo deberá elegir ua de ellas y cotestar razoadamete a los cuatro ejercicios de que costa dicha opció. Para
GUÍA DE ESTUDIO ÁLGEBRA LINEAL
 GUÍ DE ESUDIO ÁLGER LINEL ema. Espacios Vectoriales ) LOS NÚMEROS El sistema de úmeros reales cosiste e u cojuto R de elemetos llamados úmeros reales y dos operacioes deomiadas: adició y multiplicació,
GUÍ DE ESUDIO ÁLGER LINEL ema. Espacios Vectoriales ) LOS NÚMEROS El sistema de úmeros reales cosiste e u cojuto R de elemetos llamados úmeros reales y dos operacioes deomiadas: adició y multiplicació,
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS
 CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
Métodos estadísticos y numéricos Estimación por Intervalos de confianza 1 PROBLEMAS RESUELTOS DE ESTIMACIÓN POR INTERVALOS DE CONFIANZA
 Métodos estadísticos y uméricos Estimació por Itervalos de cofiaa PROBLEMA REUELTO DE ETIMACIÓN POR INTERVALO DE CONFIANZA U adador obtiee los siguietes tiempos, e miutos, e 0 pruebas croometradas por
Métodos estadísticos y uméricos Estimació por Itervalos de cofiaa PROBLEMA REUELTO DE ETIMACIÓN POR INTERVALO DE CONFIANZA U adador obtiee los siguietes tiempos, e miutos, e 0 pruebas croometradas por
INFERENCIA ESTADÍSTICA: ESTIMACIÓN DE PARÁMETROS. INTERVALOS DE CONFIANZA
 . Metodología e Salud Pública INFERENCIA ESTADÍSTICA: ESTIMACIÓN DE PARÁMETROS. INTERVALOS DE CONFIANZA Autor: Clara Lagua 5.1 INTRODUCCIÓN La estadística iferecial aporta las técicas ecesarias para extraer
. Metodología e Salud Pública INFERENCIA ESTADÍSTICA: ESTIMACIÓN DE PARÁMETROS. INTERVALOS DE CONFIANZA Autor: Clara Lagua 5.1 INTRODUCCIÓN La estadística iferecial aporta las técicas ecesarias para extraer
CAPÍTULO 6. EJEMPLOS DE DISEÑO PARA FUNDACIONES SUPERFICIALES
 83 CAPÍTULO 6. EJEMPLOS DE DISEÑO PARA FUNDACIONES SUPERFICIALES Filosofía de diseño En términos generales, todos los diseños geotécnicos se realizan siguiendo el diagrama de flujo esquematizado en la
83 CAPÍTULO 6. EJEMPLOS DE DISEÑO PARA FUNDACIONES SUPERFICIALES Filosofía de diseño En términos generales, todos los diseños geotécnicos se realizan siguiendo el diagrama de flujo esquematizado en la
MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL. Resumen: En este artículo se muestra como las transformaciones de funciones resultan
 MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL Viceç Fot Departamet de Didàctica de les CCEE i de la Matemàtica de la Uiversitat de Barceloa Resume: E este artículo se muestra como las trasformacioes
MOSAICOS Y POLIEDROS REGULARES. UN PUNTO DE VISTA FUNCIONAL Viceç Fot Departamet de Didàctica de les CCEE i de la Matemàtica de la Uiversitat de Barceloa Resume: E este artículo se muestra como las trasformacioes
CAPÍTULO 7 DISTRIBUCIONES EN EL MUESTREO Introducción
 CAPÍTULO 7 DISTRIBUCIONES EN EL MUESTREO 7.. Itroducció Geeralmete, las poblacioes tiee tamaños que hace que estudiarla e su totalidad sea poco práctico desde diversos putos de vista; costo, tiempo, tipo
CAPÍTULO 7 DISTRIBUCIONES EN EL MUESTREO 7.. Itroducció Geeralmete, las poblacioes tiee tamaños que hace que estudiarla e su totalidad sea poco práctico desde diversos putos de vista; costo, tiempo, tipo
Gesdocal Pies de rey (1 de 9)
 Gesdocal Pies de rey ( de 9) OBJTO l objeto del presete PROCO D CALBRACÓN es defiir la pauta utilizada e el software CALBRO para la calibració de pies de rey, que les permita obteer resultados trazables
Gesdocal Pies de rey ( de 9) OBJTO l objeto del presete PROCO D CALBRACÓN es defiir la pauta utilizada e el software CALBRO para la calibració de pies de rey, que les permita obteer resultados trazables
APLICACIONES INFORMÁTICAS EN QUÍMICA. Problemas Tema 2.3: Series, representación de funciones y construcción de tablas en HC.
 APLICACIONES INFORMÁTICAS EN QUÍMICA Problemas Tema 2.3: Series, represetació de fucioes y costrucció de tablas e HC Grado e Química º SEMESTRE Uiversitat de Valècia Facultad de Químicas Departameto de
APLICACIONES INFORMÁTICAS EN QUÍMICA Problemas Tema 2.3: Series, represetació de fucioes y costrucció de tablas e HC Grado e Química º SEMESTRE Uiversitat de Valècia Facultad de Químicas Departameto de
FUNCIÓN DE ONDA Y ECUACIÓN DE ONDA EN UNA DIMENSIÓN
 Departameto de Matemáticas Física FUNCIÓN DE ONDA ECUACIÓN DE ONDA EN UNA DIMENSIÓN Fís. Jorge Eardo Aguilar Rosas El movimieto olatorio e u sistema se preseta cuado ua perturbació procida e u lugar del
Departameto de Matemáticas Física FUNCIÓN DE ONDA ECUACIÓN DE ONDA EN UNA DIMENSIÓN Fís. Jorge Eardo Aguilar Rosas El movimieto olatorio e u sistema se preseta cuado ua perturbació procida e u lugar del
ANDALUCÍA / JUNIO 04. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / EXAMEN COMPLETO OPCIÓN A
 EXAMEN COMPLETO Istruccioes: a) Duració: 1 hora y 30 miutos. b) Elija ua de las dos opcioes propuestas y coteste los ejercicios de la opció elegida. c) E cada ejercicio, parte o apartado se idica la putuació
EXAMEN COMPLETO Istruccioes: a) Duració: 1 hora y 30 miutos. b) Elija ua de las dos opcioes propuestas y coteste los ejercicios de la opció elegida. c) E cada ejercicio, parte o apartado se idica la putuació
ESTADISTICA UNIDIMENSIONAL
 ESTADISTICA UIDIMESIOAL La estadística estudia propiedades de ua població si recurrir al sufragio uiversal. El estudio estadístico tiee dos posibilidades (1) Describir lo que ocurre e la muestra mediate
ESTADISTICA UIDIMESIOAL La estadística estudia propiedades de ua població si recurrir al sufragio uiversal. El estudio estadístico tiee dos posibilidades (1) Describir lo que ocurre e la muestra mediate
Resumen Tema 2: Muestreo aleatorio simple. Muestreo con probabilidades desiguales.
 Resume Tema 2: Muestreo aleatorio simple. Muestreo co probabilidades desiguales. M.A.S.: Muestreo aleatorio simple co probabilidades iguales si reemplazo. Hipótesis: Marco perfecto, si omisioes i duplicados
Resume Tema 2: Muestreo aleatorio simple. Muestreo co probabilidades desiguales. M.A.S.: Muestreo aleatorio simple co probabilidades iguales si reemplazo. Hipótesis: Marco perfecto, si omisioes i duplicados
Sobrantes de 2004 (Septiembre Modelo 3) Soluciones Germán-Jesús Rubio Luna OPCIÓN A
 OPCIÓN A EJERCICIO 1_A (3 putos) Ua pastelería elabora dos tipos de trufas, dulces y amargas Cada trufa dulce lleva 20 g de cacao, 20 g de ata y 30 g de azúcar y se vede a 1 euro la uidad Cada trufa amarga
OPCIÓN A EJERCICIO 1_A (3 putos) Ua pastelería elabora dos tipos de trufas, dulces y amargas Cada trufa dulce lleva 20 g de cacao, 20 g de ata y 30 g de azúcar y se vede a 1 euro la uidad Cada trufa amarga
Jueves, 25 de abril. Dificultades de los modelos PNL. Dónde está la solución óptima? Otro ejemplo: Óptima Local frente a Global
 . Jueves, de abril Teoría sobre la programació o lieal Programació separable Dificultades de los modelos PNL PL: Etregas: material de clase PNL: Aálisis gráfico de la programació o lieal e dos dimesioes:
. Jueves, de abril Teoría sobre la programació o lieal Programació separable Dificultades de los modelos PNL PL: Etregas: material de clase PNL: Aálisis gráfico de la programació o lieal e dos dimesioes:
MIEMBROS TUBULARES CILINDRICOS
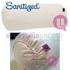 CAPITULO 8 MIEMBROS TUBULARES CILINDRICOS 8.1 COMENTARIOS GENERALES Las seccioes tubulares cilídricas lamiadas e frío so ecoómicas para miembros sujetos a flexió torsió debido a que posee u radio de giro
CAPITULO 8 MIEMBROS TUBULARES CILINDRICOS 8.1 COMENTARIOS GENERALES Las seccioes tubulares cilídricas lamiadas e frío so ecoómicas para miembros sujetos a flexió torsió debido a que posee u radio de giro
No obstante, cuando intentamos hacer lo mismo con los números racionales y reales vemos que. con como lo hicimos con. es diferente de los conjuntos
 Departameto de Matemáticas Guía Iducció Matemática Objetivos: Eteder el pricipio del bue orde Realizar demostracioes matemáticas por medio del pricipio de iducció matemática El pricipio del bue orde: iducció
Departameto de Matemáticas Guía Iducció Matemática Objetivos: Eteder el pricipio del bue orde Realizar demostracioes matemáticas por medio del pricipio de iducció matemática El pricipio del bue orde: iducció
