Parte III: Lenguajes y Autómatas
|
|
|
- Josefa Villalobos Castellanos
- hace 6 años
- Vistas:
Transcripción
1 Introducción l Lógic y l Computción Prte III: Lengujes y Autómts Autor 1r. Versión: Alejndro Tirboschi Autor 2d. Versión: Pedro Sánchez Terrf Autores 3r. Versión: Rul Fervri y Ezequiel Orbe 1 Modelos de Computción A continución estudiremos un modelo de computción llmdo utómt. Definición 1.1 (Modelo de Computción). Un modelo de computción es un modelo mtemático que proxim el funcionmiento de un computdor, y medinte el cul se pueden estudir, desde un punto de vist teórico, ls cpciddes y limitciones de l mism. En prticulr, un modelo de computción nos permite responder con precisión preguntles trscendentles como: - Qué problems puede resolver un computdor? (Computbilidd) - Cuáles son los problems computcionlmente dificiles? (Complejidd) Existen diferentes modelos de computción, entre los cules podemos nombrr ls Máquins de Turing (Turing ), los Autómts Finitos (Rbin y Scott ) y el Cálculo Lmbd (Church ). Los primeros dos modelos (Máquins de Turing y Autómts Finitos) se suelen tipificr como modelos de estdos, mientrs que el Cálculo Lmbd como modelo funcionl. Los modelos de computción difieren principlmente en su poder computcionl (que funciones podemos computr con un modelo) y en qué nos permiten estudir. Por ejemplo, ls Máquins de Turing (MT) y el Clculo Lmbd se utilizn pr estudir decidibilidd, esto es, qué puede y qué no puede resolver un computdor y cuáles problems son decidibles y cuáles son indecidibles. Un problem es decidible si existe un lgoritmo que, con suficiente tiempo y memori, siempre pued resolverlo. Si no existe dicho lgoritmo entonces decimos que el problem es indecidible. 1
2 Input CPU Output Memori Figur 1: Modelo Generl de Máquin 1.1 Modelo Generl de Máquin Pr poner en contexto donde se encuentrn los utómts dentro del mundo de los modelos de computción, empezemos por definir de form bstrct y simplificd lo que considerremos como un máquin (computdor). En su form más básic, podemos pensr un computdor como compuest por dos componentes: un memori y un unidd centrl de procesmiento (CPU). Nos interes prticulrmente el tipo de memori que tiene un máquin, y que de eso dependerá su poder computcionl. En función l tipo de memori podemos distinguir los siguientes tipos de máquins, ordends de menor myor poder computcionl: 1. Autómts de Estdos Finitos (Finite Stte Automt): Son quells máquins que no tienen de memori temporri. 2. Autómts con Pil (Pushdown Automt): Son quells máquins que tienen un pil como memori temporri. 3. Máquins de Turing (Turing Mchines): Son quells máquins que tienen memori de lectur y escritur de cceso letori. Cd tipo de máquin tiene distinto poder computcionl, el cul se v incrementndo medid que el tipo de memori es menos restrictivo. Como es de esperr, l complejidd tmbién ument con el poder de computcionl. En est mteri no estudiremos ls Máquins de Turing, pero sí veremos distintos tipos de Autómts de Estdos Finitos y con Pil, y estudiremos sus propieddes. 2 Autómts Finitos Determinísticos 2.1 Sistems de estdos finitos En nuestr vid cotidin nos encontrmos con muchos sistems que se pueden modelr como sistem de estdos finitos. Los mismos siempre se encuentrn en un estdo determindo dentro de un conjunto finito de estdos posibles, y l trnsición entre estdos se d como consecuenci de recibir un determindo estímulo de entrd (un input). En estos sistems, podemos considerr que l función de un estdo es l de recordr un prte relevnte de l histori del sistem. Ejemplo 2.1. Consideremos un interruptor e intentemos modelrlo como un sistem de estdos finitos. En su form más simple podemos pensr un interruptor como un sistem con dos estdos posibles, 2
3 un estdo de ON y un estdo de OFF, y en el cul l trnsición entre mbos estdos ocurre cundo lguién pret (push) el interruptor. L Figur 2 muestr un digrm de este sistem. push OFF ON push Figur 2: Modelo de Estdos de un Interruptor Cundo el interruptor está en el estdo ON, podemos interpretrlo como recordndo que lguien en lgún momento lo pretó y lo puso en ese estdo. Si luego de un cierto tiempo, lo observmos y el interruptor está en el estdo OFF, entonces podemos interpretrlo como recordndo que lguien en lgún momento lo pretó y lo pso ese estdo. Todos los sistems de estdos finitos comprten cierts crcterístics comúnes. En prticulr, todos tienen: 1. Un estdo inicil, en el cul el sistem se inici, 2. un conjunto de estdos finles (o de ceptción), que representn los estdos los cules nos interes llegr, y, 3. el efecto de plicr un entrd (o input) depende únicmente del estdo en el cul se encuentr el sistem cundo se l plic. Ejemplo 2.2. Consideremos un expendedor de golosins, el cul entreg un golosin cundo se le ingres ciert cntidd de dinero. Supongmos que el expendedor comienz su funcionmiento sin dinero, que solo entreg un golosin cundo le hn ingresdo $ 1 (un peso), y que cept moneds de $ 0.25, $ 0.5 y $ 1. El expendedor de lgun form debe recordr cunto dinero le hn ingresdo pr, sí, sber cundo entregr l golosin. Podemos modelr el expendedor de l siguiente form: - Con 5 estdos, pr cundo el expendedor teng $ 0, $ 0.25, $ 0.5, $ 0.75 y $ 1 respectivmente. - Inicilmente, el expendedor no tiene dinero, es decir, está en el estdo $ 0. - Con un solo estdo finl (el estdo $ 1), que es cundo se entreg l golosin. - Luego de entregr l golosin, se vuelve l estdo inicil. - Solo cept moneds de $ 0.25, $ 0.5 y $ 1. L Figur 3 present nuestro modelo del expendedor. H de notrse que este modelo es un simplificción de un modelo rel de un expendedor y que no consider ls situciones donde se ingrese ms de $ 1, cómo lo solucionrís? Lo que cbmos de presentr son ls crcterístics básics de lo que se denominn utómts finitos determinísticos y como hbrán podido observr, hst quí hemos lidido con conceptos y nociones summente intuitivs. A continución, nuestro trbjo será definirlos y estudirlos formlmente. 3
4 Entregr 0 $ $0.50 $0.25 $ $0.50 $0.50 $ $ Figur 3: Modelo de un Expendedor de Golosins 2.2 Autómt Finito Determinístico Un utómt finito determinístico (DFA) es un modelo mtemático de un sistem, con entrds y slids discrets. Es determinístico y que el sistem solo puede estr en un, entre un número finito, de configurciones interns o estdos.además, el estdo del sistem es l únic informción que se tom en cuent pr psr otro estdo cundo el sistem recibe un entrd. En ciencis de l computción es posible encontrr numerosos ejemplos de DFAs, y l teorí de utómts es un herrmient summente útil pr estudir dichos sistems. Progrms tles como editores de texto y nlizdores léxicos, encontrdos en l myorí de los compildores, son menudo modeldos como sistems de estdos finitos. Definición 2.1 (Autómt Finito Determinístico). Un utómt finito determinístico (DFA) M = (Q,Σ,δ,q 0,F) es un 5-upl donde: 1. Q = {q 1,q 2,...,q m } es un conjunto finito de estdos. 2. Σ = { 1, 2,..., n } es un conjunto finito de símbolos de entrd (o input). 3. δ : Q Σ Q es l función (totl) de trnsición de estdos. 4. q 0 Q es el estdo inicil. 5. F Q son los estdos finles. Ejemplo 2.3. Consideremos el sistem de estdos de un interruptor que vimos en el Ejemplo2.1 (Figur 2). Definimos el utómt M = (Q,Σ,δ,q 0,F), de l siguiente form: Q = {ON,OFF}. Σ = {push}. q 0 = OFF. F = {ON,OFF}. δ definid como: δ(on, push) = OFF. δ(off, push) = ON. 4
5 Es común representr l función de trnsición medinte un tbl doble entrd en l cul, buscndo el cruce entre l entrd de un estdo q y l entrd de un input, sbemos como cmbi el estdo q cundo recibe el input. En est tbl es común mrcr el estdo inicil con el símbolo y los estdos finles con el símbolo. Ejemplo 2.4. Se M un utómt finito determinístico con estdos {q 0,q 1,q 2 }, símbolos de entrd Σ = {,b} y ls siguientes regls de trnsición: el estdo q 0 se trnsform en q 1 si el input es y en q 0 si el input es b; el estdo q 1 se trnsform en q 1 si el input es y en q 2 si el input es b; finlmente, el estdo q 2 se trnsform en q 2 si el input es y en q 0 si el input es b. Es decir δ, l función de trnsición, está definid por: δ(q 0,) = q 1, δ(q 0,b) = q 0 δ(q 1,) = q 1, δ(q 1,b) = q 2 δ(q 2,) = q 2, δ(q 2,b) = q 0 Est función puede ser representd de form más compct con l siguiente tbl: b q 0 q 1 q 0 q 1 q 1 q 2 q 2 q 2 q 0 Ejemplo 2.5. Consideremos el modelo de estdos del expendedor de golosins del Ejemplo 2.2 (Figur 3). Definimos el utómt M = (Q,Σ,δ,q 0,F), de l siguiente form: Q = {0,0.25,0.50,0.75,1}. Σ = {0.25,0.50,1,E}. q 0 = 0. F = {1}. δ definid como: E Se debe notr que el sistem del Ejemplo 2.5 no es un utómt en el sentido de l Definición 2.1 y que hy estdos que no ceptn ciertos inputs y l definición de un DFA requiere que l función de trnsición δ se un función totl. En l sección siguiente extenderemos el concepto de utómt, con lo cul este tipo de situciones será dmisible.mientrs tnto, cómo modificris el sistem pr que cumpl con l definición de un DFA? Digrms de Trnsición Como hn podido observr en los ejemplos nteriores existe un estrech relción entre un DFA y su representción gráfic. De hecho todo DFA se le puede signr un grfo, l cul llmremos digrm de trnsición. Definición 2.2 (Algoritmo de Generción de Digrms de Trnsición). Se M = (Q,Σ,δ,q 0,F) un DFA, su digrm de trnsición se construye de l siguiente form: 1. Se greg un nodo con etiquet q i, por cd estdo q i Q. 5
6 2. Mrcmos l nodo correspondiente l estdo inicil q 0 con un flech que ingres. 3. Mrcmos los nodos correspondientes los estdos finles q i F con doble círculos. 4. Agregmos un eje etiquetdo del nodo q i l nodo q j si existe un trnsición δ(q i,) = q j. Si tenemos un digrm de trnsición hy un DFA socido el mismo; y por lo tnto de hor en más no distinguiremos entre DFAs y sus digrms de trnsición. Ejemplo 2.6. Se M un utómt con estdos {q 0,q 1,q 2,q 3 }, símbolos de input {0,1}, estdo inicil q 0 y estdo finl q 0, y donde l función de trnsición está dd por l Tbl q 0 q 2 q 1 q 1 q 3 q 0 q 2 q 0 q 3 q 3 q 1 q 2 Tbl 1: L Figur 4 present el digrm de trnsición de M, generdo usndo el lgoritmo de l Definición q 0 q q 2 q 3 1 Figur 4: Digrm de Trnsición 2.3 Autómts y su Lenguje En est sección estudiremos l relción que existe entre los utómts y los lengujes. En prticulr nos interesn quells sucesiones de símbolos de entrd que nos llevn del estdo inicil un estdo finl, y que ells serán ls que definn el lenguje del utómt. Comencemos por introducir ls definiciones necesris que nos permitirán formlizr el lenguje de un utómt. En lo que sigue, considerremos un símbolo, como un entidd bstrct que no definiremos formlmente, sí como en geometrí no se definen los puntos y ls línes. Letrs y dígitos son ejemplos de símbolos frecuentemente usdos. 6
7 Definición 2.3 (Alfbeto Σ, Cden sobre Σ y Σ ). Un lfbeto (denotdo por Σ) es un conjunto finito de símbolos. Un cden (o plbr) sobre el lfbeto Σ es un secuenci finit de símbolos de Σ. L cden vcí es l cden con cero ocurrencis de símbolos. Σ denot el conjunto de tods ls plbrs sobre el lfbeto Σ. Ejemplo 2.7. Se el lfbeto Σ = {0,1}, luego 01, y 1010 son cdens sobre el lfbeto Σ y, Σ = {,0,1,00,01,10,11,000,...}. Definición 2.4 (Longitud de un cden). L longitud de un cden w (denotd por w ) es el número de símbolos que l componen. L cden vcí tiene longitud cero ( = 0). Definición 2.5 (Subcden, Prefijo y Sufijo). Un subcden es un secuenci de símbolos incluid en un cden. Un prefijo de un cden w es un subcden de w que comienz con el primer símbolo de w.. Un sufijo de un cden w es un subcden de w que termin con el último símbolo de w. Definición 2.6 (Conctención). Dds dos cdens α y γ, su conctención (denotd por αγ) es l cden formd escribiendo l primer cden seguid de l segund sin espcios en el medio. Pr tod cden α vle que α = α = α. Ejemplo 2.8. Considere l cden bbb. Luego, bbb = 6; l cden b es subcden de bbb, mientrs que l b no lo es; l cden bb es un prefijo de bbb, mientrs que b no lo es; l cden b es un sufijo de bbb, mientrs que b no lo es. Dds dos cdensw = y x = bbb, luego, wx = bbb. Finlmente podemos dr l definición de un lenguje sobre un lfbeto. Definición 2.7 (Lenguje sobre un lfbeto Σ). Un lenguje L sobre un lfbeto Σ es un conjunto de plbrs sobre el lfbeto Σ (L Σ ). Ejemplo 2.9. El conjunto de plindromes o cpicús sobre el lfbeto {0,1} es un lenguje infinito. Algunos elementos de este lenguje son, 0, 1, 00, 11, 000, 010, 101, 111. Observción 2.1. Un lenguje L sobre un lfbeto Σ no necesit incluir plbrs con todos los símbolos de Σ, por lo tnto, un vez que estblecimos que L es un lenguje sobre Σ, tmbién sbemos que será un lenguje sobre tod extensión de Σ. Pr entender cul es l relción entre lengujes y utómts consideremos el utómt de l Figur 4: Este utómt tiene como símbolos de entrd Σ = {0, 1}. Ahor consideremos ls secuencis de entrds que nos llevn del estdo inicil q 0 culquier otro estdo. Por ejemplo, pr llegr de q 0 q 3 podemos hcerlo con ls secuencis de símbolos de entrds 0,1, ó 1,0, ó 0,1,1,0,0,1. Un nálisis similr se puede relizr pr los otros estdos. Si considermos Σ como un lfbeto, podemos interpretr ls secuencis de símbolos de entrd como plbrs sobre este lfbeto. Por ejemplo, ls secuencis 0,1, 1,0 y 0,1,1,0,0,1 se pueden interpretr como ls plbrs 01, 10 y respectivmente. Luego podrímos preguntr que estdo nos llev cd plbr sobre Σ. Por ejemplo, l plbr nos llev de q 0 q 1, mientrs que l plbr 1001 nos llev de q 0 nuevmente q 0. Es nturl entonces, preguntrse cules son ls plbrs que nos llevn desde el estdo inicil lgún estdo finl. Anteriormente hbimos dicho que los estdos finles o de ceptción encierrn implícitmente un noción de éxito, por lo cul, si un plbr nos llev del estdo inicil un estdo 7
8 finl podrímos decir que es plbr es buen o que es ceptd por el utómt. Por ejemplo, l plbr 1001 es un plbr ceptd por el utómt. Finlmente, el conjunto de plbrs ceptds por un utómt M es lo que se denomin como el lenguje ceptdo por el utómt M. Lo interesnte de conocer el lenguje ceptdo por un utómt, es que este lenguje lo crcteriz (l utómt), por lo cul podemos estudir diverss propieddes del mismo estudindo su lenguje. En lo que sigue formlizremos l noción de lenguje de un utómt. Definición 2.8 (Trnsform en). Se M = (Q,Σ,δ,q 0,F) un DFA. Un cden en M es un elemento de Σ. Sen p,q Q estdos de M y α = n un cden en M. Luego, diremos que α trnsform q en p (denotdo por q α p) si prtiendo del estdo q y plicndo sucesivmente ls entrds 0, 1, hst n, llegmos l estdo p. Observción 2.2. En lo que sigue nos interesn ls siguientes propieddes de l relción trnsform en. p p ( trnsform un estdo en si mismo). Si α = 0, 1,..., n : p α q p 0 q 1 n n qn q. Si α = βγ, donde β y γ son cdens, entonces: p α q sii existe r Q tl que p β r γ q. Definición 2.9 (Cden ceptd por un utómt). Se M = (Q,Σ,δ,q 0,F) un DFA y α un cden α en M. Diremos que α es ceptd por M, si existe p F tl que q 0 p, esto es, si α trnsform el estdo inicil q 0 en un estdo finl p. Definición 2.10 (Lenguje ceptdo por un utómt). Se M = (Q,Σ,δ,q 0,F) un DFA, el lenguje ceptdo por M se define como: L(M) = {α Σ existe p F tl que q 0 α p}. Esto es, L(M) es el conjunto de tods ls cdens ceptds por el utómt. Ejemplo Determinenmos el lenguje del utómt de l Figur 5: 0 0 M 1 q 0 q 1 1 Figur 5: Autómt M 1 Luego de inspeccionr el utómt y de probr con lguns cdens es fácil ver que el utómt solo cept plbrs con un número impr de 1 s. Probemos formlmente que éste es el lenguje de M 1. 8
9 Demostrción. Se w un cden en M. Luego debemos probr l siguiente proposición: Lo probmos por inducción en w. Cso Bse: w = 0 (w = ) q 0 w q1 si y solo si w tiene un nro impr de 1 s. ( ): Trivl, y que q 0 q 0 y por lo tnto q 0 q 1 es flso. ( ): Trivil, y que tiene un nro pr de 1 s (tiene cero 1 s). Pso Inductivo: Se w = x con x 1 y Σ y supongmos que vle l proposición pr x. ( ): Si q 0 x q 1 entonces debemos considerr dos csos: x0 x 0 1. = 0: Si q 0 q 1, por definición de δ, q 0 q 1 q1. Luego, por hipótesis inductiv (H.I.), x tiene un númeroro impr de 1 s y por lo tnto w = x0 tmbién tiene un número impr de 1 s. x1 x 1 2. = 1: Si q 0 q 1, por definición de δ, q 0 q 0 q1. Luego por H.I., x tiene un número pr x de 1 s (por que de lo contrrio tendrímos que q 0 q 1 ), y por consiguiente w = x1 tiene un número impr de 1 s. ( ): Tenemos que nlizr dos csos: 1. = 0: Si w = x0 tiene un número impr de 1 s, entonces x tiene un número impr de 1 s y por x 0 x0 H.I., q 0 q 1. Luego, por definición de δ, q 1 q1 y se sigue que q 0 q = 1: Si w = x1 tiene un número impr de 1 s, entonces x tiene un número pr de 1 s y por x 1 x1 H.I., q 0 q 0. Luego, por definición de δ, q 0 q1 y se sigue que q 0 q 1. Ejemplo Probemos que el lenguje del utómt del Ejemplo 2.6 es el conjunto de cdens que tienen un número pr de 0 s y un número pr de 1 s. Demostrción. En este cso, pr probr el lenguje del utómt usremos un rgumento geométrico. Si observmos el digrm de trnsición correspondiente notmos que ir de izquierd derech o de derech izquierd signific plicr el input 1. Ir de rrib bjo o de bjo rrib signific plicr el input 0. Ahor bien, como q 0 es el estdo inicil y finl, un plbr ceptd v recorriendo el digrm de tl form que cundo termin subió tnts veces como bjó y fue l izquierd tnts veces como fue l derech. Es decir que est plbr tiene un número pr de 0 s y un número pr de 1 s. Por otro ldo, si un plbr tiene un número pr de 0 s y un número pr de 1 s es clro, por ls misms rzones expuests rrib, que termin su recorrido en q 0. Observemos que es un cden ceptd, debido que q 0 es estdo finl y que q 0 q 0. Clrmente, l cden tiene un número pr de ceros y unos, pues tiene 0 ceros y 0 unos. Como hemos menciondo, los utómts estn crcterizdos por su lenguje, por lo cul si queremos comprr dos utómts podrímos hcerlo comprndo sus lengujes. En otrs plbrs, l iguldd entre los lengujes de dos utómts nos sirve como noción de equivlenci entre los utómts. 9
10 Definición 2.11 (Equivlenci de utómts). Sen M y M dos DFA. Diremos que M y M son equivlentes si L(M) = L(M ). Ejemplo Probemos que los utómts M 1 y M 2 de l Figur 6 son equivlentes. b b q 0 q 1 q 2 M 1 b b q 0 q 1 M 2 b Figur 6: Autómts M 1 y M 2 Inspeccionndo los utómts, es fácil determinr que el lenguje ceptdo por mbos utómts es el de tods ls plbrs terminds en, esto es, L(M 1 ) = L(M 2 ) = {w w termin en }, y por lo tnto que mbos utómts son equivlentes. Probemos formlmente que mbos utómts son equivlentes. Demostrción. Pr mbos utómts debemos probr l siguiente proposición: w es ceptd si y solo si w termin en. Prueb pr M 1 : Lo probmos por inducción en w. q 0 Cso Bse: w = 0 (w = ) ( ): Trivl, y que q 0 q 0 y por lo tnto no es ceptd. ( ): Trivil, y que no termin en. Pso Inductivo: Se w = xz con x 1 y z Σ y supongmos que vle l propiedd pr x. xz xz ( ): Si xz es ceptd entonces q 0 q 1 (o q 0 q 2 ). Por propiedd de, debe existir q x tl que x z x z q x q 1 (o q 0 q x q 2 ). Luego, tenemos que considerr dos csos: x x 1. x es ceptd: Por H.I. x termin en por lo cul debe ser que q 0 q 1 (o q 0 q 2 ). Luego, por definición de δ, w = xz solo es ceptd si z = y que q 1 q2 (y q 2 q2 ). 2. x no es ceptd: Por H.I. x no termin en por lo cul debe ser que q 0 x q 0. Luego, por definición de δ, w = xz solo es ceptd si z = y que q 0 q1. x x ( ): Si w = x, queremos ver que q 0 q 1 (o q 0 q 2 ). Por propiedd de, debe existir q x tl x x que q 0 q x q1 (o q 0 q x q2 ). Luego, tenemos que considerr 2 csos: x x 1. x termin en : Por H.I. x es ceptd, por lo cul debe ser que q 0 q 1 (o q 0 q 2 ). Luego por definición de δ tenemos que q 1 q2 (y q 2 q2 ), por lo cul x es ceptd. 10
11 x 2. x no termin en : Por H.I. x no es ceptd, por lo cul debe ser que q 0 q 0. Luego, por x definición de δ, q 0 q1 y por lo tnto q 0 q 1, con lo cul w = x es ceptd. Prueb pr M 2 : xz ( ): Si w = xz es ceptd entonces q 0 q 1, si y solo si, por definción de δ, w = x y que l únic form de llegr q 1 es trvés de. x ( ): Si w = x luego, por definición de δ, tenemos que q 0 q x q1, y por lo tnto w = x es ceptd. Finlmente hor probmos que L(M 1 ) = L(M 2 ). L(M 1 ) L(M 2 ). ( ): Si α L(M 1 ) entonces α = x (termin en ), luego α L(M 2 ). ( ): Si α L(M 2 ) entonces α = x (termin en ), luego α L(M 1 ). Pr ello debemos ver L(M 1 ) L(M 2 ) y que 3 Autómts Finitos No Determinísticos En l sección nterior definimos los utómts finitos determinísticos (DFA) y vimos que todo DFA define un lenguje. En prticulr, vimos que lo determinístico en un DFA se debe que, en todo momento, el estdo del mismo est completmente determindo. Esto se debe que l función de trnsición es un función totl que define exctmente, pr todo estdo y todo símbolo de entrd, que estdo se hce l trnsición. Ahor, qué psrí si permitimos 0,1 o más trnsiciones por símbolo? Ejemplo 3.1. Consideremos el utómt de l Figur 7. En que estdo está el utómt si estndo en q 0 plicmos el símbolo de entrd 0? o, en otrs plbrs, cuánto vle δ(q 0,)?. 0,1 q 0 0 q 1 1 q 2 Figur 7: Autómt no determinístico En este cso y no podemos decir que el utómt est en un estdo determindo, y que δ(q 0,) = q 0 y δ(q 0,) = q 1 l mismo tiempo. El ejemplo nterior nos muestr que si hor permitimos cero ó más trnsiciones por símbolo, perdemos l cpcidd de estblecer el estdo excto de un utómt, y que el mismo hor se encuentr, l mismo tiempo, en un conjunto de estdos, perdiendo de est mner su determinismo y trnsformándose sí en un utómt finito no determinístico. Definmos hor formlmente un utómt finito no determinístico. Definición 3.1 (Autómt Finito No-Determinístico). Un utómt finito no determinístico (NFA) M = (Q,Σ,δ,q 0,F) es un 5-tupl donde: 11
12 1. Q = {q 1,q 2,...,q m } es un conjunto finito de estdos. 2. Σ = 1, 2,..., n es un conjunto finito de símbolos de entrd (o input). 3. δ : Q Σ P (Q) es l función de trnsición de estdos. 4. q 0 Q es el estdo finl. 5. F Q son los estdos finles. Es importnte notr que l únic diferenci entre l Definición 3.1 de un NFA y l Definición 2.1 de un DFA, es que, en un NFA l función de trnsición δ no es totl y en vez de retornr un estdo retorn un conjunto de estdos. Al igul que en el cso de un DFA, podemos representr l función de trnsición δ medinte un tbl de trnsición, donde pr cd cruce entre un estdo q y un símbolo de entrd, tendremos el conjunto de estdos l cul ps el utómt. Ejemplo 3.2. Consideremos el digrm de trnsición de l Figur 7. Definimos el NFA M = (Q,Σ,δ,q 0,F) de l siguiente form: Q = {q 0,q 1,q 2 } Σ = {0,1} F = {q 2 } q 0 es el estdo inicil δ está definid por: 0 1 q 0 {q 0,q 1 } {q 0 } q 1 /0 {q 2 } q 2 /0 /0 L pregunt que surge hor es: cómo proces un NFA un cden de entrd?, es decir, qué hce cundo tiene más de un trnsición posible pr un mismo símbolo de entrd? Ejemplo 3.3. Consideremos el NFA de l Figur 7 y vemos como proces l cden El utómt inici en q 0, su estdo inicil. Cundo recibe el primer símbolo 0, hce un trnsición los estdos q 1 y q 0, es decir, el utómt está en los estdos {q 0,q 1 }. Esto se puede ilustrr en términos más concretos, si pensmos que lo que hce el utómt es crer dos hilos de ejecución, uno en el cul el utómt tiene está en el estdo q 0, y otro en el cul el utómt está en el estdo q 1. L Figur 8 represent est situción. q 0 0 q 0 0 q 1 0 q 0 0 q 1 0 q 0 q 1 q 1 q 1 q 2 q 2 Figur 8: Como proces un NFA un cden de entrd Continuemos procesndo l cden de entrd y vemos que sucede cundo el utómt recibe otro símbolo 0. En este cso, en el hilo de ejecución de q 0, nuevmente podemos hcer un trnsición 12
13 hci q 1 y q 0, crendo de est form otros dos hilos de ejecución. Sin embrgo, el hilo de ejecución correspondiente q 1 no tiene especificdo como procesr el símbolo 0, y por lo tnto bort. De est form, luego de procesr el segundo símbolo 0 estmos en el estdo {q 0,q 1 }. Procesemos hor el símbolo 1. En este cso en el hilo de ejecución de q 0 solo podemos hcer un trnsición hci q 0, mientrs que en el hilo de ejecución de q 1 se hce un trnsición hci el estdo q 2. Ahor el utómt está en el estdo {q 0,q 2 }. Procesemos hor el símbolo 0. En este cso, en el hilo de ejecución de q 0 hcemos trnsiciones q 0 y q 1, mientrs que en el hilo de ejecución de q 2 no se puede procesr ese símbolo, y por lo tnto bort. Finlmente procesmos el último símbolo 1. En este cso, el utómt termin en los estdos {q 0,q 2 }. Pregunt: H sido ceptd l cden 00101? Definmos hor el lenguje ceptdo por un NFA. Definición 3.2 (Trnsform en). Se M = (Q,Σ,δ,q 0,F) un NFA y α = 0, 1,..., n Σ. Sen p,q Q estdos de M. Diremos que α trnsform p en q (denotdo por p α q) si existen q 1,...,q n Q tl que q 1 δ(p, 0 ),q 2 δ(q 1, 1 ),...,q i+1 δ(q i, i ),..., q n δ(q n 1, n 1 ),q δ(q n, n ). Observción 3.1. Es importnte tener presente ls siguientes propieddes de l relción trnsform en: α puede trnsformr un estdo q i en vrios estdos. α gener distintos recorridos desde q 0. Como es de esperr, un cden α será ceptd si lguno de los recorridos que gener desde q 0 termin en un estdo finl. Se debe tener presente que l noción de ceptción, hor tiene en cuent que en un NFA trbjmos con conjuntos de estdos, por lo cul un cden α, pueden generr muchos recorridos desde el estdo inicil. Algunos de estos recorridos no necesrimente terminn en un estdo finl e incluso pueden bortr temprnmente. Sin embrgo, lo que nos interes pr decidir si un cden es ceptd o no, es que dentro de todos esos posibles cminos, l menos uno termine en un estdo finl. Definición 3.3 (Lenguje ceptdo por un utómt). Se M = (Q,Σ,δ,q 0,F) un NFA, el lenguje ceptdo por M se define como: L(M) = {α Σ existe p F tl que q 0 α p}. Ejemplo 3.4. Consideremos el NFA de l Figur 7. Es fácil ver que el utómt cept solo ls cdens que terminn en 01. Es decir, Demostrción. Por inducción en w. L(M) = {w w termin en 01}. 13
14 3.1 Equivlenci entre DFAs y NFAs Revisndo l Definición 3.1 de un NFA, es fácil ver que l mism es un generlizción de l Definición 2.1 de un DFA. Esto nos llev preguntrnos si est generlizción permite los NFAs reconocer más lengujes que los DFAs. Sin embrgo, veremos continución que este no es el cso y que los NFAs reconocen los mismos lengujes que los DFAs, esto es, veremos que pr todo NFA existe un DFA que reconoce el mismo lenguje, y vicevers, lo cul nos permitirá probr que mbs nociones son equivlentes. El proceso de construir un DFA prtir de un NFA se denomin determinizción. Comencemos por definir como construir un DFA prtir de un NFA utilizndo un construcción llmd construcción por subconjuntos. Definición 3.4 (Construcción por Subconjuntos). Se N = (Q,Σ,δ,q 0,F) un NFA. Construiremos el DFA, D = (Q,Σ,δ,q 0,F ), de l siguiente form: 1. Q = P (Q). 2. Σ = Σ. 3. F = {q Q q F /0}. 4. q 0 = {q 0}. 5. δ (q,) = {p Q existe q q t.q. q p} = q q δ(q,). Observción 3.2. Es importnte tener presente lo siguiente: δ (q,) el conjunto de estdos ccesibles, trvés de, desde cd q q. Ejemplo 3.5. Consideremos el utómt de l Figur 6. L Tbl 2 represent l tbl de trnsición de estdos del DFA D = (Q,Σ,δ,q 0,F ) obtenido medinte l construcción por subconjuntos. L Figur 9 present el digrm de trnsición de estdos del DFA D. 0 1 (0) /0 /0 /0 (1) {q 0 } {q 0,q 1 } {q 0 } (2) {q 1 } /0 {q 2 } (3) {q 2 } /0 /0 (4) {q 0,q 1 } {q 0,q 1 } {q 0,q 2 } (5) {q 0,q 2 } {q 0,q 1 } {q 0 } (6) {q 1,q 2 } /0 {q 2 } (7) {q 0,q 1,q 2 } {q 0,q 1 } {q 0,q 2 } Tbl 2: Tbl de trnsición de estdos del utómt D. A prtir del Ejemplo 3.5 podemos ver que uno de los inconvenientes de l construcción por subconjuntos es l explosión en el número de estdos que tiene el DFA resultnte. De hecho, si Q = n 14
15 , ,1 Figur 9: Digrm de Trnsición de estdos del DFA D. entonces Q = 2 n!!!. Sin embrgo, el ejemplo tmbién nos muestr que no todos los estdos del DFA son lcnzbles desde el estdo inicil, y por lo tnto no son necesrios. A continución presentmos un lgoritmo más eficiente que nos permitirá construir DFA que conteng solo los estdos necesrios. Definición 3.5 (Construcción Lzy). Se N = (Q,Σ,δ,q 0,F) un NFA. Construiremos el DFA, D = (Q,Σ,δ,q 0,F ), de l siguiente form: 1. Σ = Σ. 2. F = {q Q q F /0}. 3. q 0 = {q 0}. 4. δ (q,) = {p Q existe q q t.q. q p} = q q δ(q,). Donde el conjunte de estdos Q se construye de l siguiente form: Dt: estdo inicil q 0, función δ, lfbeto Σ Result: conjunto de estdos Q Q {{q 0 }}; Q /0; for q (Q \Q ) do for Σ do Q Q { q q δ(q,)}; end Q Q {q }; end 15
16 3.2 Autómts Finitos No Determinísticos con -trnsiciones Ahor introduciremos l noción de utómt finito no determinístico. No es difícil ver que un conjunto ceptdo por un utómt no determinístico tmbién es ceptdo por uno determinístico y vicevers. Sin embrgo, el utómt finito no determinístico resultrá útil pr probr ciertos resultdos y pr cierts plicciones. Dremos un definición no forml de este tipo de utómts. El lector interesdo en l definición forml puede consultr l subsección Modifiquemos l definición de utómt finito permitiendo cero, un, o más trnsiciones de un estdo con el mismo símbolo de input. Es decir de un estdo pueden prtir un número rbitrrio de flechs cd un etiquetd con culquier símbolo de input. Tmbién permitmos trnsiciones sin inputs. Est nuev definición nos d los utómts finitos no determinísticos (NFA) con -movimientos. A nivel de digrms de trnsición los grfos que representn estos utómts serán de l siguiente form: de cd nodo puede prtir ningun, un o vris flechs con l mism etiquet de input. Además puede hber flechs que no se correspondn ningún input, los -movimientos. A ests flechs les pondremos l etiquet. Como en el cso de los utómts determinísticos los NFA tienen un estdo inicil y estdos finles, que se denotrán en el digrm de trnsición de l mism form que en el cso determinístico Ejemplo 3.6. El siguiente es el digrm de un utómt finito no determinístico con -movimientos: los estdos son q 0, q 1 y q 2. Los símbolos de input son y b. El estdo inicil es q 0 y el estdo finl es q 2. b q 0 b q 1 b q 2 Ejemplo 3.7. En este NFA los estdos son q 0, q 1 y q 2. Los símbolos de input son 0, 1 y 2. El estdo inicil es q 0 y el estdo finl es q 2. 0 q 0 1 q 1 2 q 2 El nombre no determinístico viene del hecho que si un estdo recibe un input, entonces no está determindo cul es el próximo estdo, si no que hy ciertos estdos posibles. Los -movimientos reflejn l posibilidd de cmbio de estdo sin que necesrimente hy un input. Observr tmbién, que existe l posibilidd que ddo un estdo no slg ningun flech de él. Esto denotrá que en este estdo el utómt bort. Es clro que no es fácil imginrse un máquin que se comporte de est mner, sin embrgo el concepto de NFA con -movimientos result muy útil en l teorí de lengujes. Ls tbls que describirán ls regls de trnsición de los NFA con -mov serán similres ls tbls que hemos hecho pr los utómts finitos determinísticos. Ls diferencis son que cundo 16
17 plicmos un input un estdo obtenemos un conjunto de estdos (hci donde vn ls flechs) o /0 en el cso que no slg ningun flech. Además debemos gregr un entrd en l tbl pr reflejr los posibles cmbios de estdo que producen los -movimientos. Ejemplo 3.8. L tbl de trnsición correspondiente l NFA con -mov del ejemplo 3.6 es dd por l siguiente tbl: b q 0 q 1 q 0 q 2 q 1 /0 q 0,q 2 /0 q 2 q 1 /0 /0 Ejemplo 3.9. L tbl de trnsición correspondiente l NFA con -mov del ejemplo 3.7 es dd por l siguiente tbl: q 0 q 0 /0 /0 q 1 q 1 /0 q 1 /0 q 2 q 2 /0 /0 q 2 /0 Vemos hor el lenguje socido un NFA con -movimientos. Definición 3.6. Se M un NFA con -movimientos con símbolos de input Σ. Si α Σ, diremos que α trnsform p en q y lo denotremos p α q, si existen 0, 1,..., n Σ tl que α = n y tl que existe un recorrido por flechs con etiquets 0, 1,..., n que v del estdo p l estdo q. En el recorrido se pueden interclr rbitrrimente flechs con etiquet. Es conveniente tmbién definir que trnsform todo estdo en sí mismo, es decir q q. Ejemplo En el utómt del ejemplo 3.7 tenemos, por ejemplo, que q 0 01 q 1, pues hy un cmino que llev q 0 q 0 por 0, q 0 q 1 por y q 1 q 1 por 1. Observción 3.3. Si p y q estdos, símbolo de input y p q, no podemos segurr que de p podemos psr directmente q por un flech con etiquet. Por definición p q signific que podemos llegr de p q usndo -movimientos demás de un trnsición por. Observndo el 0 utómt del ejemplo 3.7 vemos que q 0 q1, pero no es cierto que hy un flech con etiquet 0 que mnd q 0 q 1. En grn prte de ls situciones que necesitemos usr trnsiciones podremos tomrnos l licenci de usr l notción p 0 q 1 n 1 1 n qn q, pr indicr que hy un cmino de flechs con etiquets 0,..., n que ps por los estdos q 1,...,q n y que v de p q (quí permitiremos que los i puedn ser s). Ejemplo Se M un NFA con -movimientos,con digrm de trnsición : b q 0 b q 1 q 2 17
18 Entonces, l tbl de trnsición es: b q 0 q 1 q 0 q 2 q 1 /0 q 0 /0 q 2 q 1 /0 /0 Vemos cules son ls trnsformciones correspondientes un input o un -movimiento: q 0 q 1 q 2 q 0,q 2 q 0 q1 q 0 b q0,q 2 q 1 q 1 b q0,q 2 q 2 q1 q 2 q 2 q1 donde denotmos p q,q cundo p q y p q. L myorí de ls trnsformciones son obvis y ls otrs se deducen de l definición. Sin embrgo, creemos conveniente explicr lguns de ells. Por ejemplo, recordemos que, por definición, q q pr todo q estdo, de llí que se justific l primer b column de trnsformciones. L trnsformción q 1 q2 se deduce de que podemos llegr de q 1 b q 2 primero plicndo b y luego. En form nálog se justific q 0 q2. Como en el cso de utómts determinísticos los estdos finles nos determinn el lenguje socido l utómt. Definición 3.7. Un cden α es ceptd por el utómt si α trnsform el estdo inicil en uno finl. Finlmente el lenguje ceptdo por M es el conjunto L(M) de tods ls cdens ceptds. Simbólicmente: L(M) = {α Σ q 0 α p, pr lgún p F}. A nivel de digrms de trnsición podemos entender que el lenguje ceptdo por M, un NFA con -movimientos, está formdo por ls cdens α = b 0 b 1...b n tl que existe un recorrido por flechs con etiquets b 0,b 1,...,b n que v del estdo inicil uno finl, en el recorrido se pueden interclr rbitrrimente flechs con etiquet. Observemos que como el es l cden vcí el interclr flechs con etiquet no greg nd l plbr, y l plbr o cden definitiv es quell que no tiene ningún. Tmbién observemos que dd un cden puede hber muchos recorridos prtiendo del estdo inicil, lgunos de ellos pueden terminr en un estdo finl y otros no, sin embrgo lo que interes, pr sber si un cden es ceptd o no, es si por lo menos un recorrido lcnz un estdo finl. Ejemplo Averigüemos el lenguje del utómt definido en el Ejemplo 3.7: observemos primero que si bndonmos el estdo q 0 entonces vmos l estdo q 1 y no podemos volver trás. Análogmente si bndonmos el estdo q 1, vmos l estdo q 2 y y no podemos slir de este estdo. Luego si un cden w lcnz el estdo finl, entonces comienz por q 0, ps por q 1 y lleg q 2. Es decir que w es de l form 0 i 1 j 2 k (i, j,k enteros myores o igules 0). Recíprocmente un cden de l form 0 i 1 j 2 k puede lcnzr el estdo finl con el siguiente recorrido: 0,0,...,0 (i-veces),, 1,1,...,1 ( j-veces),, 2,2,...,2 (k-veces). Es decir que el lenguje socido este utómt es {0 i 1 j 2 k : 0 i, j,k} Formlizción de los NFA L definición forml de NFA es: 18
19 Definición 3.8. Un utómt finito no determinístico con -movimientos (NFA con -mov) es un 5-upl (Q,Σ,δ,q 0,F) que consiste de 1. un conjunto finito Q = {q 1,q 2,...,q n } de estdos, 2. un conjunto finito Σ = { 1, 2,..., n } de símbolos de entrd o input, 3. un conjunto de regls de trnsición que trnsform un estdo con un input ddo, en un conjunto posible de estdos. Tmbién ls regls de trnsición describen l trnsformción de un estdo en un conjunto de estdos sin hber recibido input (-movimiento). Formlmente, ls regls de trnsición son dds por un función δ : Q (Σ {}) P (Q), donde P (Q) es el conjunto formdo por los subconjuntos de Q. 4. Además, como en el cso del DFA, hy un estdo inicil q 0 y un conjunto de estdos finles F. Vemos hor el lenguje socido un NFA con -movimientos: Definición 3.9. Se M = (Q,Σ,δ,q 0,F) un NFA con -movimientos. Si α Σ, diremos que α trnsform p en q y lo denotremos p α q, si existen 0, 1,..., n Σ {} y q 1,...,q n en Q, tl que α = n y q 1 δ(p, 0 ), q 2 δ(q 1, 1 ),...q i+1 δ(q i, i ),...q n δ(q n 1, n 1 ), q δ(q n, n ). Es conveniente tmbién definir que trnsform todo estdo en sí mismo, es decir q q. Observción 3.4. Se M = (Q,Σ,δ,q 0,F) un NFA con -movimientos. 1. Como dijimos ntes, si Σ, entonces si q δ(p,) tenemos que p q. Pero no necesrimente si p q, entonces se cumple que q δ(p,). L definición de p q denot el hecho de que podemos llegr de p q medinte -movimientos, luego, luego -movimientos. En el 0 utómt del ejemplo 3.7 es cierto que q 0 q1, pues q 0 δ(q 0,0) y q 1 δ(q 0,), pero no es cierto que q 1 δ(q 0,0). 2. Cundo un utómt no tiene -mov, entonces coinciden l función de trnsición y ls trnsformciones por símbolos de input, es decir si p,q son estdos y es un símbolo de input, p δ(q,) si y sólo si q p. Por lo tnto, l notción p α q pr NFA con -mov, es consistente con l mism notción pr DFA. 3. Es clro, en form intuitiv, que si α,β Σ, entonces pr p,q Q, p αβ q si y sólo si existe r Q tl que p α r β q. (1) 4. Se M = (Q,Σ,δ,q 0,F) con δ definid de l siguiente mner: q δ (p,) sii p q. Entonces M result ser un NFA con -mov que cept el mismo lenguje que M. L demostrción se dej como ejercicio. 19
20 5. Debido l observción nterior, en grn prte de ls situciones que necesitemos usr trnsiciones podremos tomrnos l licenci de usr l notción p 0 q 1 n 1 1 n qn q, pr indicr que hy un cmino de flechs con etiquets 0,..., n que ps por los estdos q 1,...,q n y que v de p q. Dicho más formlmente: Repetimos l q 1 δ(p, 0 ), q 2 δ(q 1, 1 ),...q n δ(q n 1, n 1 ), q δ(q n, n ). Definición Un cden α es ceptd por el utómt si α trnsform el estdo inicil en uno finl. Finlmente el lenguje ceptdo por M es el conjunto L(M) de tods ls cdens ceptds. Simbólicmente: L(M) = {α Σ q 0 α p, pr lgún p F}. El siguiente Teorem fue nuncido l comienzo de l sección: Teorem 3.1. Los lengujes ceptdos por los utómts finitos determinísticos son los mismos que los ceptdos por los utómts finitos no determinísticos con -movimientos. Más precismente, ddo un DFA (NFA con -movimientos) M, existe un NFA con -movimientos (resp. DFA) M, tl que L(M) = L(M ). Demostrción. Si M = (Q,Σ,δ,q 0,F) un DFA, entonces se M = (Q,Σ,δ,q 0,F) el NFA definido por δ (q,) = {δ(q,)} pr q Q y Σ. Es trivil comprobr, entonces, que L(M) = L(M ). Veremos hor que, ddo M = (Q,Σ,δ,q 0,F) un NFA con -mov, podemos construir M = (Q, Σ, δ, q 0,F ) un DFA, tl que L(M) = L(M ). Se q M, definmos [q] = {p Q q p} Q. Sen q 1,...,q i elementos de Q, entonces denotemos [q 1,...,q i ] = i j=1[q j ]. Definmos M de l siguiente mner: Q = {[q 1,...,q i ] q 1,...,q i Q}. El nuevo conjunto de estdos finles, F, es el conjunto de estdos que contienen un estdo que se trnsform por en un estdo finl de M. El estdo inicil será q 0 = [q 0]. Finlmente, definimos δ ([q 1,...,q i ],) igul l conjunto {p Q existe q s tl que q s p}. Es decir, un Σ trnsform q Q en p Q, si el conjunto p está formdo por todos los elementos de Q que son los trnsformdos por de los elementos de q. Resumiendo, si q Q y Σ: = {[q 1,...,q i ] q 1,...,q i Q} P (Q) q 0 = [q 0 ] F = {[q 1,...,q i ] existe k y p F tl que q k p} δ(q,) = {p Q q q tl que q p} o equivlentemente q {p Q q q tl que q p}. Q No es difícil comprobr que M = (Q,Σ,δ,q 0,F ) es un utómt finito determinístico. No es difícil comprobr que si q Q entonces q = {p Q q q tl que q p}. (2) 20
21 Esto se debe que como q = [q 1,...,q i ], por definición q = i j=1 [q j] = i j=1 {p Q q j p} = {p Q q j tl que q j p} {p Q q q tl que q p}. Pr demostrr l otr inclusión, consideremos p tl que q p con q q. Como q q existe q j tl que q j q, luego q j q p, de lo cul se deduce que q j p y por lo tnto p {p Q q j tl que q j p}. Vemos hor que si α Σ, q en Q, entonces: q α {p Q q q tl que q α p}. Supongmos que q α p y vemos que p = {p Q q q tl que q α p}: hgmos inducción sobre α. Cundo α = 0, es decir cundo α =, tenemos que q q y el párrfo nterior demuestr el resultdo. Cundo α = 1 el resultdo se deduce trivilmente por definición de trnsición. Si α > 1, entonces α = β, con β 1 y Σ. Por (??) de l observción 2.2 sbemos que existe r Q tl que q β r p. Por hipótesis inductiv y el cso de longitud 1 tenemos que q β r = {r Q q q tl que q β r}, r p = {p Q r r tl que r p}. Si p p, existe r r tl que r p, como r r, existe q q, tl que q β r. Es decir que q β p o equivlentemente q α p. Por lo tnto está probdo p {p Q q q tl que q α p}. Por otro ldo, si p {p Q q q tl que q α p}, existe q q tl que q α p, luego existe r Q tl que q β r p, por lo tnto r r y p p. Esto prueb l otr inclusión y por lo tnto l iguldd desed. L plicción direct del resultdo nterior q 0, nos dice que dd α Σ, entonces q 0 α {p Q q 0 α p}. (3) α Ahor bien, se α L(M ), es decir q 0 p, con p F. Como p es finl de M, entonces existe p en p α que tmbién pertenece F, luego por (3) obtenemos que q 0 p, es decir α L(M). α Recíprocmente, se α L(M), es decir existe p F tl que q 0 p, por lo tnto (usndo nuevmente (3)) p p con q α 0 p. De esto se deduce que p F y α L(M ). Finlmente, el párrfo nterior prueb que L(M) = L(M ). Ejemplo Se M el NFA con -mov con estdos q 0,q 1, un solo símbolo de input, estdo inicil q 0, estdo finl q 1 y ls siguientes leyes de trnsición: δ(q 0,) = {q 0 }, δ(q 0,) = {q 1 }. Encontremos un utómt determinístico con el mismo lenguje que M. Por l demostrción del teorem el nuevo utómt, M, tendrá estdos /0,[q 0 ]. Observr que [q 0 ] = [q 1 ] = [q 0,q 1 ] = {q 0,q 1 }, pues q 0 q 1. El estdo finl e inicil es entonces [q 0 ]. Por definición, del estdo /0 no sle ningun flech y δ([q 0 ],) = [q 0 ], δ([q 0 ],) = [q 0 ]. Clrmente, el lenguje ceptdo por mbos utómts es el de tods ls cdens de s. 21
22 Vemos un ejemplo menos trivil. Ejemplo Se M = (Q,Σ,δ,q 0,F) un NFA con -movimientos definido por el siguiente digrm de trnsición. b q 0 b q 1 b q 2 Encontremos un DFA que cepte el mismo lenguje. Debemos primero estblecer los estdos del nuevo utómt: [q 0 ] = {p Q q 0 p} = {q 0,q 2 } [q 1 ] = {p Q q 1 p} = {q 1 } [q 0,q 1 ] = [q 0 ] [q 1 ] = {q 0,q 1,q 2 } Otro estdo, siempre presente es /0. Observemos que culquier otro posible estdo es uno de los y listdos más rrib, por ejemplo, [q 2 ] = [q 0 ] y [q 1,q 2 ] = [q 1 ] [q 2 ] = [q 0,q 1 ]. Estblezcmos hor ls trnsiciones. [q 0 ] [q 0 ] [q 1 ] [q 1 ] [q 0,q 1 ] [q 0,q 1 ] {p Q q [q 0 ] tl que q p} = = {p Q q 0 p} {p Q q2 p} = {q1 } {q 1 } = [q 1 ] b b b {p Q q 0 p} {p Q q2 p} = {q0,q 2 } /0 = [q 0 ] {p Q q 1 p} = /0 b b {p Q q 1 p} = {q0,q 2 } = [q 0 ] {p Q q [q 0,q 1 ] tl que q p} = [q 1 ] /0 = [q 1 ] b [q 0 ] [q 0 ] = [q 0 ] Por definición, es clro que tod trnsición que sle de /0 vuelve /0. Finlmente, el estdo inicil y finl es [q 0 ]. El digrm de trnsición del utómt recién construido es: b [q 0 ] b b [q 1 ] /0 b [q 0,q 1 ] 22
23 3.3 Expresiones regulres Los lengujes ceptdos por los utómts finitos se pueden describir fácilmente por expresiones simples llmds expresiones regulres. En est sección introduciremos ls operciones de conctención y clusur sobre conjuntos de cdens, definiremos expresiones regulres y dremos l demostrción de que un expresión regulr define un lenguje que puede ser descrito por un utómt finito. L recíproc de este resultdo tmbién es ciert y veremos su demostrción en l subsección finl. Definición Se Σ un conjunto finito de símbolos y sen L, L 1 y L 2 conjuntos de cdens de Σ. L conctención de L 1 y L 2, denotd L 1 L 2 es un conjunto formdo por cdens de L 1 seguids por cdens de L 2, es decir: L 1 L 2 = {xy x está en L 1 e y está en L 2 }. Definmos L 0 = {} y L i = LL i 1 pr i 1. L clusur de Kleene (o sólo clusur) de L, denotd L, es el conjunto L = i=0l i y l clusur positiv de L, denotd L +, es el conjunto L + = i=1l i. L denot ls cdens construids por conctención de un número rbitrrio de cdens de L. L + es igul pero sin poner L 0. Nótese que L + contiene si y sólo si L lo contiene. Recordemos que en l Sección?? definimos Σ, y observemos que ese conjunto coincide con el Σ que surge de l definición nterior, considerndo Σ como un lenguje donde ls cdens son los símbolos del lfbeto. Ejemplo Se L 1 = {11,0} y L 2 = {001,10}, entonces Por otro ldo, L 1 + es L 1 menos el. L 1 L 2 = {11001,1110,0001,010}. L 1 = {11,0} = {,11,0,1111,110,011,00,111111,11110,11011,1100,...}. Definición Se Σ un lfbeto. Ls expresiones regulres sobre Σ y los conjuntos que ells denotn se definen recursivmente de l siguiente mner: 1. /0 es un expresión regulr y denot el conjunto vcío. 2. es un expresión regulr y denot el conjunto {}. 3. Pr cd en Σ, es un expresión regulr que denot el conjunto {}. 4. Si r y s son expresiones regulres que denotn los conjuntos R y S, respectivmente, entonces (r + s), (rs) y (r ) son expresiones regulres que denotn los conjuntos R S, RS y R, respectivmente. Si r es un expresión regulr escribiremos L(r) l conjunto (o lenguje) denotdo por r. Cundo escribimos expresiones regulres podemos omitir muchos préntesis si sumimos que tiene más lt precedenci que l conctención o +, y l conctención tiene más lt precedenci que +. Por ejemplo ((0(1 )) + 0) puede ser escrit Finlmente, si r es un expresión regulr denotemos r i l expresión rr r (i veces). Debemos tener mucho cuiddo en no confundir cdens con expresiones regulres y pr ello debemos clrr debidmente qué nos estmos refiriendo. Por ejemplo l expresión regulr b denot un conjunto cuyo único elemento es l cden b. 23
24 Ejemplo Los siguientes son ejemplo de expresiones regulres: es un expresión regulr que represent {00}. 2. (0 + 1) denot tods ls cdens de 0 s y 1 s. 3. (0 + 1) 00(0 + 1) denot tods ls cdens de 0 s y 1 s con l menos dos 0 s consecutivos. 4. (1 + 10) denot tods ls cdens de 0 s y 1 s que comienzn con 1 y no tienen dos 0 s consecutivos. Tmbién pertenece este conjunto l cden vcí. Demostrción. Probemos por inducción que (1 + 10) i no tiene dos 0 s consecutivos. El cso i = 0 es trivil, y si suponemos que (1+10) i 1 no tiene dos 0 s consecutivos, entonces, es clro que (1 + 10) i = (1 + 10) i 1 (1 + 10) no tiene dos 0 s consecutivos, pues en el finl ls plbrs son de l form 11 o 110 o 101 o 1010, donde ls letrs en negrit denotn plbrs de (1 + 10) i 1. De est form probmos que (1 + 10) i no tiene dos 0 s consecutivos pr todo i y por lo tnto (1 + 10) no tiene dos 0 s consecutivos. Por otro ldo, dd culquier cden que comience con 1 y no teng dos 0 s consecutivos, se puede hcer un prtición de l cden de tl form que si un 1 no es seguido de un 0, se tom el 1 (que pertenece (1 + 10)) y si un 1 es seguido de un 0, se tom el 10 (que pertenece (1 + 10)). Por ejemplo, es prticiondo que pertenece (1 + 10) Bsdo en lo nterior, es clro que (0+)(1+10) denot ls cdens de 0 s y 1 s que no tienen dos 0 s seguidos. 6. (0 + 1) 011 denot ls cdens de 0 s y 1 s que terminn en denot ls cdens que están formds por ciert cntidd de 0 s, luego ciert cntidd de 1 s y luego ciert cntidd de 2 s. Observr que este es lenguje del utómt definido en el ejemplo 3.7. Veremos hor como prtir de un expresión regulr r podemos construir un utómt no determinístico M que defin el mismo lenguje, es decir tl que L(r) = L(M). En relidd lo que construiremos son utómts no determinísticos con un sólo estdo finl. Pr ls expresiones regulres, /0 o con Σ los utómts no determinísticos de l Fig. 10 definen el lenguje correspondiente: q 0 q 0 q 1 q 0 q 1 r = r = /0 r = Figur 10: A un utómt M con estdo inicil q y estdo finl f lo dibujremos de l siguiente mner (Fig. 11): Ahor hremos lo siguiente: dds expresiones regulres r 1 y r 2 ls cules y les hymos socido los utómts M 1, M 2 correspondientes, como en l Fig. 12 encontrremos los utómts correspondientes r 1 + r 2, r 1 r 2 y r 1. Dicho de otr mner: si L 1 es el lenguje de M 1 y L 2 es el lenguje de M 2, entonces encontrremos utómts correspondientes L 1 L 2, L 1 L 2 y L 1. El utómt correspondiente r 1 + r 2 será el de l Fig. 13. El utómt correspondiente r 1 r 2 será el de l Fig
25 q M f Figur 11: q 1 M 1 f 1 q 2 M 2 f 2 Figur 12: Los utómts de r 1 y r 2. El utómt correspondiente r1 será el de l Fig. 15 De lo nterior se deduce Teorem 3.2. Se L un lenguje denotdo por l expresión regulr r. Entonces existe M un DFA con -mov tl que L = L(M). Ejemplo Construymos un utómt pr l expresión regulr Por lo dicho nteriormente (respecto los préntesis), est expresión es en relidd ((0(1 )) + 1), es decir es de l form r 1 + r 2, donde r 1 = 01 y r 2 = 1. El utómt pr r 2 es fácil 1 q 1 q 2 Podemos expresr r 1 como r 3 r 4, donde r 3 = 0 y r 4 = 1. El utómt de r 3, tmbién es fácil: 0 q 3 q 4 Ahor bien, r 4 es r 5, con r 5 = 1. Un utómt pr r 5 es 1 q 5 q 6 Observemos que pr poder construir el utómt correspondiente l expresión regulr necesitmos distinguir los estdos de r 2 y r 5, unque representen l mism expresión. Bsándonos en ls explicciones nteriores un utómt pr r 4 será 25
26 q 1 M 1 q 0 q 2 M 2 f 1 f 0 f 2 Figur 13: El utómt de r 1 + r 2. q 1 M 1 f 1 q 2 M 2 f 2 Figur 14: El utómt de r 1 r 2. q 7 q 1 5 q 6 q 8 Luego el utómt correspondiente l expresión regulr r 1 = 01 será q 0 3 q 4 q 7 q 1 5 q 6 q 8 Finlmente el utómt correspondiente será el de l Fig Teorem de Kleene Estudiemos el problem, un poco más complicdo, de construir un expresión regulr que denote el lenguje de un utómt ddo. Est construcción se bs en l ide de encontrr, en form lgorítmic, un expresión regulr que involucr resolver el problem pr un utómt con menos estdos. Repitiendo el proceso un número conveniente de veces logrremos l expresión regulr buscd. Pr 26
27 q 0 q 1 M 1 f 1 f 0 Figur 15: El utómt de r1. 1 q q 1 q q 10 q 0 3 q 4 q 7 q 1 5 q 6 q 8 Figur 16: Un utómt correspondiente l expresión regulr describir el procedimiento, comenzremos con el cso más simple en el cul nuestro utómt M tiene un solo estdo finl, q n y su estdo inicil es q 0. Es clro que L(M) = L 0n, el lenguje de ls cdens que comienzn en q 0 y llegn q n. Llmemos I 0 l lenguje formdo por ls cdens que slen de q 0 y vuelven q 0 sin psr nuevmente por él. Si el estdo inicil es el estdo finl, (es decir, n = 0) entonces clrmente L 0n = I 0, puesto que con repetir cminos que slgn de q 0 y vuelvn él obtengo tods ls plbrs ceptds. Si n 0, definmos F 0n como el lenguje de ls cdens que slen de q 0 y llegn q n sin psr por q 0. Entonces, por un rzonmiento similr, L 0n = I 0 F 0n. Debemos hor explicitr quiénes son I 0 y F 0n. Los elementos de I 0 son cdens de dos forms: β 0 1. β 0 b, donde,b Σ {} y β 0 es un cden que prte de un estdo p y tl que q 0 qi b q0 con p y q distintos de q 0 y demás el cmino que recorre β 0 no ps por q 0 ; o bien q j 2. c Σ {}, que hg un bucle de q 0 en sí mismo. Si considermos en el primer cso el utómt M que se obtiene de M scndo q 0 y hciendo que q i se estdo inicil y q j estdo finl, entonces β 0 es un cden ceptd por M. En este cso, L(M ) = L i j, el lenguje de ls cdens que slen de q i y llegn q j sin psr nunc por q 0, y obtenemos: I 0 = L i j b + + c +... b donde se sumn tods ls posibiliddes pr,b,i, j tles que q 0 qi, q j 0, con q0 distinto de q i c y q j, los c tles que q 0 q 0, y en L i j no considermos q 0. Es decir, ls cdens que prten y llegn q 0 se pueden ver como l conctención de cdens formds por ciertos símbolos de entrd, con lengujes ceptdos por utómts más chicos. De igul modo, si q 0 no es el estdo finl, los elementos de F 0n son ls cdens que prten de q 0 y llegn l estdo finl q n sin psr por q 0. En este cso ls cdens son de l form β con 27
AUTOMATAS FINITOS CIENCIAS DE LA COMPUTACION I 2009
 AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
Autómatas sobre palabras infinitas
 Autómts sobre plbrs infinits Mrcelo Arens M. Arens Autómts sobre plbrs infinits 1 / 46 Teorí de utómts sobre plbrs infinits Los utómts sobre plbrs infinits son un herrmient fundmentl pr l verificción forml.
Autómts sobre plbrs infinits Mrcelo Arens M. Arens Autómts sobre plbrs infinits 1 / 46 Teorí de utómts sobre plbrs infinits Los utómts sobre plbrs infinits son un herrmient fundmentl pr l verificción forml.
Caracterización de lenguajes regulares con expresiones regulares
 Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
Una Introducción a la Teoría de Autómatas sobre Arboles
 Un Introducción l Teorí de Autómts sobre Arboles IIC3800 IIC3800 Un Introducción l Teorí de Autómts sobre Arboles 1 / 40 Arboles etiquetdos Σ: Alfbeto (conjunto finito de símbolos) Definición (Arbol binrio)
Un Introducción l Teorí de Autómts sobre Arboles IIC3800 IIC3800 Un Introducción l Teorí de Autómts sobre Arboles 1 / 40 Arboles etiquetdos Σ: Alfbeto (conjunto finito de símbolos) Definición (Arbol binrio)
Clase Auxiliar 5. Aútomatas Finitos Determinísticos (Diagramas de Estado)
 CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
AUTOMATAS FINITOS Traductores
 Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
3 de marzo de 2011 DSIC - UPV. Tema 5: Expresiones Regulares. U.D. Computación. Definiciones. Propiedades. Construcciones. AFs a partir de ERs
 UD AFs Lem de UD DSIC - UPV 3 de mrzo de 2011 UD (DSIC - UPV) 3 de mrzo de 2011 1 / 40 Índice UD AFs Lem de sore expresiones regulres utómts finitos utómts finitos UD (DSIC - UPV) 3 de mrzo de 2011 2 /
UD AFs Lem de UD DSIC - UPV 3 de mrzo de 2011 UD (DSIC - UPV) 3 de mrzo de 2011 1 / 40 Índice UD AFs Lem de sore expresiones regulres utómts finitos utómts finitos UD (DSIC - UPV) 3 de mrzo de 2011 2 /
Procesadores del Lenguaje I. Antonio Falcó
 Procesdores del Lenguje I Antonio Flcó 2 Índice generl I Preliminres 5 1. Alfbetos y Lengujes 7 1.1. Cdens y Lengujes.............................. 7 1.2. Operciones con lengujes...........................
Procesdores del Lenguje I Antonio Flcó 2 Índice generl I Preliminres 5 1. Alfbetos y Lengujes 7 1.1. Cdens y Lengujes.............................. 7 1.2. Operciones con lengujes...........................
Autómatas Finitos. Programación II Margarita Álvarez 0,1 0,1. q 3
 Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
AUTÓMATAS DE PILA. Dpto. de Informática (ATC, CCIA y LSI). Univiersidad de Valladolid.
 Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Z := Z {0} a partir de este nuevo conjunto construimos el producto cartesiano
 Cpítulo 4 Números Rcionles. Luego de construir los Números Nturles, se presentron ciertos problems como Cuál es el resultdo de 3 menos 5?, pr poder encontrr un solución se creó prtir de N el conjunto de
Cpítulo 4 Números Rcionles. Luego de construir los Números Nturles, se presentron ciertos problems como Cuál es el resultdo de 3 menos 5?, pr poder encontrr un solución se creó prtir de N el conjunto de
En la definición clásica [85], los autómatas a pila son considerados tuplas. movimientos o transiciones válidos del autómata.
![En la definición clásica [85], los autómatas a pila son considerados tuplas. movimientos o transiciones válidos del autómata. En la definición clásica [85], los autómatas a pila son considerados tuplas. movimientos o transiciones válidos del autómata.](/thumbs/51/28357413.jpg) Cpítulo 5 Autómts pil Los utómts pil son máquins bstrcts que reconocen exctmente l clse de los lengujes independientes del contexto. En este cpítulo introducimos este tipo de utómts, que servirán de bse
Cpítulo 5 Autómts pil Los utómts pil son máquins bstrcts que reconocen exctmente l clse de los lengujes independientes del contexto. En este cpítulo introducimos este tipo de utómts, que servirán de bse
Módulo 14 Multiplicación de expresiones algebraicas. Exponentes
 Módulo 14 Multiplicción de expresiones lgebrics. Exponentes OBJETIVO: Identificr potenci, bse exponente de un expresión lgebric. Multiplicr dividir polinomios. Recordemos lguns definiciones básics. Un
Módulo 14 Multiplicción de expresiones lgebrics. Exponentes OBJETIVO: Identificr potenci, bse exponente de un expresión lgebric. Multiplicr dividir polinomios. Recordemos lguns definiciones básics. Un
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
Resolver inecuaciones como las siguientes. Expresar la solución en forma gráfica y algebraica. Comparar las soluciones de los ejercicios e), f) y g).
 64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
Exámenes de Teoría de Autómatas y Lenguajes Formales. David Castro Esteban
 Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
2 Contents. 8. Formas normales Autómatas de Pila 118. Chapter 3. Máquinas de Turing Definición y termininología
 Contents Chpter 1. Autómt finito 5 1. Alfbetos y lengujes 5 2. Operciones 7 3. Operciones con lengujes 9 4. Numerbilidd 16 5. Lengujes Regulres y Expresiones Regulres 19 6. Autómts finitos determinists
Contents Chpter 1. Autómt finito 5 1. Alfbetos y lengujes 5 2. Operciones 7 3. Operciones con lengujes 9 4. Numerbilidd 16 5. Lengujes Regulres y Expresiones Regulres 19 6. Autómts finitos determinists
CORTADURAS DE DEDEKIND
 CORTDURS DE DEDEKIND En l evolución de est teorí se distinguen tres etps: l primer prece influid por l ide del número rel como un objeto preexistente: cd número rel produce un cortdur; l cortdur define
CORTDURS DE DEDEKIND En l evolución de est teorí se distinguen tres etps: l primer prece influid por l ide del número rel como un objeto preexistente: cd número rel produce un cortdur; l cortdur define
MATEMÁTICAS PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 25 AÑOS LOGARITMOS
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
Integrales Impropias. Capítulo Introducción Integrales de Funciones No Acotadas
 Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
June 24, 2011 DSIC - UPV. Autómatas Finitos. U.D. Computación. Autómata Finito Determinista. Autómata Finito no Determinista
 s s no s s s DSIC - UPV June 24, 2011 (DSIC - UPV) s s June 24, 2011 1 / 41 (AFD) s s no s (AFD) Un (AFD) es un 5-tupl de l siguiente form: A = (Q,Σ,δ, q 0, F), siendo: Q un conjunto finito de estdos Σ
s s no s s s DSIC - UPV June 24, 2011 (DSIC - UPV) s s June 24, 2011 1 / 41 (AFD) s s no s (AFD) Un (AFD) es un 5-tupl de l siguiente form: A = (Q,Σ,δ, q 0, F), siendo: Q un conjunto finito de estdos Σ
Clase 13: Derivación de gramáticas y ambigüedad
 olicitdo: Ejercicios 11: Derivciones de grmátics y mbigüedd M. en C. Edgrdo Adrián Frnco Mrtínez http://computcion.cs.cinvestv.mx/~efrnco @efrnco_escom edfrncom@ipn.mx 1 Contenido Derivción Ejemplo 01
olicitdo: Ejercicios 11: Derivciones de grmátics y mbigüedd M. en C. Edgrdo Adrián Frnco Mrtínez http://computcion.cs.cinvestv.mx/~efrnco @efrnco_escom edfrncom@ipn.mx 1 Contenido Derivción Ejemplo 01
Tema 8.4: Teorema de Runge. Aproximación de funciones holomorfas por funciones racionales
 Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
 Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
Ejemplo: Para indicar el conjunto (que llamaremos M), formado por los números 4, 6 y 8, escribimos: M = { 4, 6, 8}
 NÚMEROS REALES. BREVE REPASO DE LA TEORÍA DE CONJUNTOS En est unidd utilizremos ls notciones l terminologí de conjuntos. L ide de conjunto se emple mucho en mtemátic se trt de un concepto básico del que
NÚMEROS REALES. BREVE REPASO DE LA TEORÍA DE CONJUNTOS En est unidd utilizremos ls notciones l terminologí de conjuntos. L ide de conjunto se emple mucho en mtemátic se trt de un concepto básico del que
Tema 4: Operaciones sobre lenguajes regulares
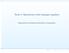 Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Tema VII: Plano afín y espacio afín
 Tem VII: Plno fín y espcio fín Hst hor el contexto en el que hemos trbjdo h sido fundmentlmente el de los espcios IR n, y de estos espcios nos h interesdo su estructur vectoril, es decir, por decirlo con
Tem VII: Plno fín y espcio fín Hst hor el contexto en el que hemos trbjdo h sido fundmentlmente el de los espcios IR n, y de estos espcios nos h interesdo su estructur vectoril, es decir, por decirlo con
Relaciones de equivalencia
 Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
CONTROL DE PROCESOS FACET UNT TEMA 1 Nota Auxiliar B ÁLGEBRA DE BLOQUES
 Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Presentación Axiomática de los Números Reales
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
5.2 Integral Definida
 80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
Hasta el momento solo hemos trabajado con funciones reales de la forma
 Función eponencil: Hst el momento solo hemos trbjdo con funciones reles de l form f( ) = P( ) donde P ( ) es un polinomio f ( ) = donde y es un vrible, entre otros pero hor vmos trbjr con funciones donde
Función eponencil: Hst el momento solo hemos trbjdo con funciones reles de l form f( ) = P( ) donde P ( ) es un polinomio f ( ) = donde y es un vrible, entre otros pero hor vmos trbjr con funciones donde
2 Números racionales positivos
 Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
1. Indicar el lenguaje aceptado por los siguientes autómatas :
 Universidd Rey Jun Crlos Grdo en Ingenierí de Computdores Máquins Secuenciles, Autómts y Lengujes Hoj de Prolems: Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio, ( ) vnzdo.. Indicr
Universidd Rey Jun Crlos Grdo en Ingenierí de Computdores Máquins Secuenciles, Autómts y Lengujes Hoj de Prolems: Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio, ( ) vnzdo.. Indicr
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Tema9. Sucesiones. Tema 9. Sucesiones.
 Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
7.1. Definición de integral impropia y primeras propiedades
 Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
UNIDAD DIDÁCTICA 4: LOGARITMOS
 Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
Tem 4 UNIDAD DIDÁCTICA 4: LOGARITMOS 1. ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función rítmic ritmos 4. Ecuciones eponenciles rítmics 2. INTRODUCCIÓN GENERAL A LA UNIDAD Y ORIENTACIONES
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Curvas en el espacio.
 Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
Formalización de los Números Reales. M. en I. Gerardo Avilés Rosas
 Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
Semánticas de procesos y aplicaciones
 Semántics de procesos y plicciones Clse 06: Puntos Fijos Qué vimos hst hor? cciones: multicciones: α 3 operdores sobre multicciones: α \ β, α β y α operdor de elección: + operdor de secuenci:. operdor
Semántics de procesos y plicciones Clse 06: Puntos Fijos Qué vimos hst hor? cciones: multicciones: α 3 operdores sobre multicciones: α \ β, α β y α operdor de elección: + operdor de secuenci:. operdor
TEMA 5: INTEGRACIÓN. f(x) dx.
 TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
Construcción de Vardi & Wolper: Paso final
 Construcción de Vrdi & Wolper: Pso finl Pr simplificr el proceso de construcción, usmos un generlizción de los utómts de Büchi: Definición A = (Q,Σ,Q 0,δ, G) es un utómt de Büchi generlizdo sore Σ si:
Construcción de Vrdi & Wolper: Pso finl Pr simplificr el proceso de construcción, usmos un generlizción de los utómts de Büchi: Definición A = (Q,Σ,Q 0,δ, G) es un utómt de Büchi generlizdo sore Σ si:
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Árboles. Mediante paréntesis anidados: ( a ( b (e, f), c, d ))
 Árboles Un árbol es un estructur jerárquic, orgnizd y dinámic plicd sobre un colección de objetos llmdos nodos. Jerárquic porque los componentes están distinto nivel. Orgnizd porque import l form en que
Árboles Un árbol es un estructur jerárquic, orgnizd y dinámic plicd sobre un colección de objetos llmdos nodos. Jerárquic porque los componentes están distinto nivel. Orgnizd porque import l form en que
De preferencia aquella que tenga algún 1 como elemento. Mejor aún si conteniendo el 1 también tiene elementos iguales a cero.
 DETERMINANTE DE UNA MATRIZ DE ORDEN O MÁS PREGUNTA Clculr los determinntes siguientes ) ) c) RESOLUCIÓN Pr resolver el determinnte de un mtriz cudrd de orden o más es recomendle plicr el método de Reducción
DETERMINANTE DE UNA MATRIZ DE ORDEN O MÁS PREGUNTA Clculr los determinntes siguientes ) ) c) RESOLUCIÓN Pr resolver el determinnte de un mtriz cudrd de orden o más es recomendle plicr el método de Reducción
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
7.1. Definición de la Integral de Riemann
 Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Ambigüedad. Ambigüedad. Tema 16. Una gramática ambigua. Una gramática ambigua. Una gramática ambigua
 Ambigüedd em 16 Ambigüedd Dr. Luis A. Pined SBN: 970-32-2972-7 Si un grmátic gener más de un estructur prtir de l mism riz y con l mism cosech (más de un estructur pr l mism cden), dich grmátic es mbigu
Ambigüedd em 16 Ambigüedd Dr. Luis A. Pined SBN: 970-32-2972-7 Si un grmátic gener más de un estructur prtir de l mism riz y con l mism cosech (más de un estructur pr l mism cden), dich grmátic es mbigu
La elipse es el lugar geométrico de todos los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante.
 LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
re p r e s e n tac i ó n Mat r i c i a l d e
 Unidd 8 re p r e s e n tc i ó n Mt r i c i l d e Un trnsformción linel Ojetivos: Al inlizr l unidd, el lumno: Asocirá cd trnsformción linel un mtriz. Relcionrá los conceptos de núcleo, imgen, rngo nulidd
Unidd 8 re p r e s e n tc i ó n Mt r i c i l d e Un trnsformción linel Ojetivos: Al inlizr l unidd, el lumno: Asocirá cd trnsformción linel un mtriz. Relcionrá los conceptos de núcleo, imgen, rngo nulidd
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Conceptos preinres TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Un función es un relción entre dos mgnitudes, de tl mner que cd vlor de l primer le sign un único vlor de l segund. Si A y B son dos conjuntos,
Relación de ejercicios hechos en clase en los últimos días previos al examen de febrero
 Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
Integral de línea de campos escalares.
 Integrl de líne de cmpos esclres. Sen f : R n R un cmpo esclr y un curv prmetrizd por σ : [, b] R n de modo que i) σ (1) [, b]. ii) σ([, b]) D(f). iii) f σ es continu en [, b]. Se define l integrl de f
Integrl de líne de cmpos esclres. Sen f : R n R un cmpo esclr y un curv prmetrizd por σ : [, b] R n de modo que i) σ (1) [, b]. ii) σ([, b]) D(f). iii) f σ es continu en [, b]. Se define l integrl de f
TEMA 4. Cálculo integral
 TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 12, N o 1. Agosto Febrero 2012.
 Artículo de sección Revist digitl Mtemátic, Educción e Internet www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Relación entre el cálculo integral y el cálculo diferencial.
 Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
CURSO DE MATEMÁTICA 1. Facultad de Ciencias
 CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
MÉTODO DE KARNAUGH MÉTODO DE KARNAUGH... 1
 MÉTODO DE KARNAUGH Jesús Pizrro Peláez MÉTODO DE KARNAUGH... 1 1. INTRODUCCIÓN... 1 2. MÉTODO DE KARNAUGH... 2 3. EJEMPLO DE APLICACIÓN (I)... 4 4. ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS... 6 5. EJEMPLO
MÉTODO DE KARNAUGH Jesús Pizrro Peláez MÉTODO DE KARNAUGH... 1 1. INTRODUCCIÓN... 1 2. MÉTODO DE KARNAUGH... 2 3. EJEMPLO DE APLICACIÓN (I)... 4 4. ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS... 6 5. EJEMPLO
INECUACIONES Y VALOR ABSOLUTO
 EJERCICIOS RECOLECTADOS EN LA RED. (MATEMÁTICA I ADMINISTRACIÓN) INECUACIONES Y VALOR ABSOLUTO INTERVALOS DESIGUALDADES INECUACIONES INTERVALOS EN LA RECTA REAL Ddos dos números culesquier y b, tles que
EJERCICIOS RECOLECTADOS EN LA RED. (MATEMÁTICA I ADMINISTRACIÓN) INECUACIONES Y VALOR ABSOLUTO INTERVALOS DESIGUALDADES INECUACIONES INTERVALOS EN LA RECTA REAL Ddos dos números culesquier y b, tles que
Aproximación e interpolación mediante polinomios
 LA GACETA DE LA RSME, Vol. 5.3 (2002), Págs. 621 627 621 Aproximción e interpolción medinte polinomios por Miguel Mrno y Mrt Mrcolini En este trbjo se muestr un relción entre los conceptos de interpolción
LA GACETA DE LA RSME, Vol. 5.3 (2002), Págs. 621 627 621 Aproximción e interpolción medinte polinomios por Miguel Mrno y Mrt Mrcolini En este trbjo se muestr un relción entre los conceptos de interpolción
ECUACIONES (4º ESO Op B)
 ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
Introducción a la Lógica y la Computación
 Introducción l Lógic y l Computción Prte III: Lengujes y Autómts Autores: Alejndro Tiroschi y Pedro Sánchez Terrf Contenidos 1 Introducción 1 2 Lengujes y Autómts 3 2.1 Cdens, lfetos y lengujes.............................
Introducción l Lógic y l Computción Prte III: Lengujes y Autómts Autores: Alejndro Tiroschi y Pedro Sánchez Terrf Contenidos 1 Introducción 1 2 Lengujes y Autómts 3 2.1 Cdens, lfetos y lengujes.............................
Autómatas Finitos Deterministicos (DFA)
 Autómatas Finitos Deterministicos (DFA) Introducción a la Lógica Fa.M.A.F., Universidad Nacional de Córdoba 22//4 Info útil Bibliografía: Introducción a la teoría de autómatas, lenguajes y computación.
Autómatas Finitos Deterministicos (DFA) Introducción a la Lógica Fa.M.A.F., Universidad Nacional de Córdoba 22//4 Info útil Bibliografía: Introducción a la teoría de autómatas, lenguajes y computación.
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
Soluciones a los ejercicios
 Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
DETERMINANTES K K. A cada matriz n-cuadrada A = (a ij ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), A o = K
 DETERMINANTES A cd mtriz ncudrd A ( ij ) se le sign un esclr prticulr denomindo determinnte de A, denotdo por det (A), A o n n n n nn K Un tbl ordend n n de esclres situd entre dos línes verticles, llmd
DETERMINANTES A cd mtriz ncudrd A ( ij ) se le sign un esclr prticulr denomindo determinnte de A, denotdo por det (A), A o n n n n nn K Un tbl ordend n n de esclres situd entre dos línes verticles, llmd
Minimización de AFDs, método y problemas
 Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
Notas de Integral de Riemann-Stieltjes
 Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
UNIDAD N 3: EXPRESIONES ALGEBRAICAS POLINOMIOS
 Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 4: Lunes 1 - Viernes 5 de Abril. Contenidos
 Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO
 PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
(Ésta es una versión preliminar de la teoría del tema.)
 Estudio de funciones periódics Ést es un versión preliminr de l teorí del tem. Un función fx se dice que es periódic de periodo cundo fx = fx +, x. Si se conoce fx en el intervlo [, ] su ciclo, se l conoce
Estudio de funciones periódics Ést es un versión preliminr de l teorí del tem. Un función fx se dice que es periódic de periodo cundo fx = fx +, x. Si se conoce fx en el intervlo [, ] su ciclo, se l conoce
3º) (Andalucía, Junio, 00) Determina una matriz A simétrica (A coincide con su traspuesta) sabiendo que:
 PROLEMS SORE MTRICES. PROFESOR: NTONIO PIZRRO. http://ficus.pntic.mec.es/pis NDLUCÍ-MTEMÁTICS PLICDS LS CCSSII: º) (ndlucí, Junio, 98) Si son dos mtrices culquier, es correct l siguiente cden de igulddes?:
PROLEMS SORE MTRICES. PROFESOR: NTONIO PIZRRO. http://ficus.pntic.mec.es/pis NDLUCÍ-MTEMÁTICS PLICDS LS CCSSII: º) (ndlucí, Junio, 98) Si son dos mtrices culquier, es correct l siguiente cden de igulddes?:
Matemática DETERMINANTES. Introducción:
 Mtemátic Introducción: DETERMINANTES Clculndo el determinnte de un mtriz se puede determinr l cntidd de soluciones que tiene un sistem de ecuciones lineles de igul número de ecuciones que de incógnits.
Mtemátic Introducción: DETERMINANTES Clculndo el determinnte de un mtriz se puede determinr l cntidd de soluciones que tiene un sistem de ecuciones lineles de igul número de ecuciones que de incógnits.
2. Derivada: tangente a una curva. Los teoremas de Rolle y Lagrange.
 . Derivd: tngente un curv. Los teorems de Rolle y Lgrnge. Se f : x I f( x) un función definid en un intervlo I y se un punto interior del intervlo I. L pendiente de l rect tngente l curv y f( x), f( )
. Derivd: tngente un curv. Los teorems de Rolle y Lgrnge. Se f : x I f( x) un función definid en un intervlo I y se un punto interior del intervlo I. L pendiente de l rect tngente l curv y f( x), f( )
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Autómatas Finitos Deterministicos (DFA)
 Autómatas Finitos Deterministicos (DFA) Introducción a la Lógica y la Computación Fa.M.A.F., Universidad Nacional de Córdoba 26/0/6 Info útil Bibliografía: Introducción a la teoría de autómatas, lenguajes
Autómatas Finitos Deterministicos (DFA) Introducción a la Lógica y la Computación Fa.M.A.F., Universidad Nacional de Córdoba 26/0/6 Info útil Bibliografía: Introducción a la teoría de autómatas, lenguajes
DETERMINANTES. Los menores y los cofactores son de gran utilidad para encontrar determinantes de matrices de orden n>1.
 DETERINNTES DETERINNTE DE UN TRIZ CUDRD socido cd mtri cudrd h un número llmdo determinnte de, denotdo como det. Los determinntes nos proporcionn un método pr el cálculo de l mtri invers (en cso de eistir)
DETERINNTES DETERINNTE DE UN TRIZ CUDRD socido cd mtri cudrd h un número llmdo determinnte de, denotdo como det. Los determinntes nos proporcionn un método pr el cálculo de l mtri invers (en cso de eistir)
Anexo 3: Demostraciones
 170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
REPASO DE ECUACIONES (4º ESO)
 TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
es pa c i o s c o n p r o d U c t o
 Unidd 5 es p c i o s c o n p r o d U c t o i n t e r n o (n o r M, d i s t n c i ) Objetivos: Al inlizr l unidd, el lumno: Aplicrá los conceptos de longitud y dirección de vectores en R. Aplicrá el concepto
Unidd 5 es p c i o s c o n p r o d U c t o i n t e r n o (n o r M, d i s t n c i ) Objetivos: Al inlizr l unidd, el lumno: Aplicrá los conceptos de longitud y dirección de vectores en R. Aplicrá el concepto
CAPÍTULO 2. , para 0 p 1. [] x
![CAPÍTULO 2. , para 0 p 1. [] x CAPÍTULO 2. , para 0 p 1. [] x](/thumbs/64/51082672.jpg) CAPÍTULO LAS CURVAS DE LORENZ Y EL SISTEMA DE PEARSON RAFAEL HERRERÍAS PLEGUEZUELO FEDERICO PALACIOS GONZÁLEZ JOSÉ CALLEJÓN CÉSPEDES Deprtmento de Métodos Cuntittivos pr l Economí y l Empres Fcultd de
CAPÍTULO LAS CURVAS DE LORENZ Y EL SISTEMA DE PEARSON RAFAEL HERRERÍAS PLEGUEZUELO FEDERICO PALACIOS GONZÁLEZ JOSÉ CALLEJÓN CÉSPEDES Deprtmento de Métodos Cuntittivos pr l Economí y l Empres Fcultd de
Examen Parcial de Autómatas y Lenguajes Formales 12 de diciembre de 2003
 Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Solución Examen. (1 + a)x + y + z + u = α x + (1 + a)y + z + u = β x + y + (1 + a)z + u = γ x + y + z + (1 + a)u = δ.
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Algebr Linel MA 0, 0/08/3, Profs. J. González, R. Gouet. Solución Exmen. Considere el siguiente sistem de ecuciones lineles,
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Algebr Linel MA 0, 0/08/3, Profs. J. González, R. Gouet. Solución Exmen. Considere el siguiente sistem de ecuciones lineles,
