Números reales NÚMEROS REALES RADICALES APROXIMACIONES ERRORES EN LA APROXIMACIÓN NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES
|
|
|
- María Jesús López Alcaraz
- hace 6 años
- Vistas:
Transcripción
1 Números reles NÚMEROS REALES NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES RADICALES APROXIMACIONES TRUNCAMIENTO REDONDEO POR EXCESO ERRORES EN LA APROXIMACIÓN 8
2 Mi desconocido migo L misiv precí urgente y el generl Pernety, l que le uní un profund mistd con Sophie Germin, dejó un ldo sus despchos y ordenó su yudnte que hicier psr su mig. Trs tomr mbos siento, el generl comenzó hblr: Ahor, Sophie, cuéntme qué es eso tn importnte. L gitción volvió l mujer que, con voz nervios, comenzó hblr de mner tropelld: No permits que le pse lo mismo que Arquímedes! L guerr no respet ndie y él no h hecho ningún ml; su pérdid serí irreprble. De qué hbls? l interrumpió el generl. No entiendo nd. L guerr con Prusi! El ejército imperil invdirá l ciudd de Brunswick y llí vive un sbio que nd sbe de guerrs, se llm Guss. Protégelo cundo tus trops entren en l ciudd! Trnquil, me encrgré de que ningún ml le suced tu migo. Tiempo después, trs l cmpñ, de vuelt en Prís el generl Pernety volvió reunirse con Sophie: Estrás content, cumplí tu encrgo; sin embrgo, hubo lgo muy extrño, pues cundo le dije quién er su benefctor, él seguró no conocerte. Los mtemáticos son muy rros! Sophie sonrió, le dio ls grcis y le explicó que solo conocí Guss por correspondenci y que ell firmb sus crts con otro nombre: Le Blnc. En un de ess crts precen los números primos de Germin, son los números primos tles que su doble más un unidd tmbién es un número primo. Encuentr 0 números primos de Germin. Los primeros 0 números primos de Germin son:,,,,, 9,,, 8 y 89 + = + = 0
3 Números reles EJERCICIOS 00 Consider ls ríces cudrds de los números nturles desde hst 0, indic cuáles de ells son números rcionles y cuáles son números irrcionles. Son rcionles: =, =, 9 = y =. El resto son números irrcionles, porque no son cudrdos perfectos. 00 Escribe cutro números irrcionles, explicndo por qué lo son.,, y son irrcionles, porque no son cudrdos perfectos. 00 Indic de qué tipo son los números. ), 0,80 ) Rcionl, periódico puro. Rcionl, deciml excto. Irrcionl. 00 Rzon si ests firmciones son cierts. ) L sum de dos números irrcionles es siempre un número irrcionl. L ríz cudrd de un frcción es un número irrcionl. ) Es flso, por ejemplo: + y + + = 8 Es flso, cundo el numerdor y el denomindor son cudrdos perfectos. 9 = 00 Represent los siguientes números reles. ),,, π F F F G 0, 00 Hll con l clculdor los números, y 0, y represéntlos de mner proximd en l rect. 0 F F 0 G 0
4 SOLUCIONARIO 00 Observ est rect rel y escribe. A B C D 0 ) Dos números enteros entre A y C. Tres números rcionles no enteros entre B y C. Tres números irrcionles entre C y D. ) 0 y 0,; y 0,, y 008 Sc fctor común, oper y simplific l expresión resultnte. ) ) + = + = = + = + = 0 = = ( ) = = 009 Clcul el opuesto y el inverso de los siguientes números reles. ) 0, e) π f) 8 8 ) Opuesto: Inverso: Opuesto: Inverso: 8 Opuesto: Inverso: e) Opuesto: Inverso: 0 Opuesto: 0, Inverso:, f) Opuesto: π Inverso: = π 00 Clcul el inverso de 0,0. 0 0, 0 = = 990 0,
5 Números reles 0 Expres medinte intervlos el conjunto de números reles que verificn que: ) Son menores que. Son myores que 0. Son menores o igules que. Son myores o igules que. ) (0, + ) +,,, 0 Represent sobre l rect rel y usndo l notción mtemátic. ) { x, x } { x, x< } { x, x> } { x, < x< 9} ) (, ] (, + ) [, ) (, 9) Expres como intervlo estos conjuntos numéricos. ) x < x < x ) (, ) No tiene solución. (, + ) 0 Hll ls proximciones de,9 ls centésims y ls milésims, por defecto y por exceso. Decide cuál de ells es el redondeo. Centésims Milésims Defecto,, (redondeo) Exceso, (redondeo), 0 Aproxim ls centésims por truncmiento y por redondeo. ),8,9 e),,0,8 f), ) e) f) Redondeo Truncmiento,8,,,0,,,9,9,9,8,,,,,,,,
6 SOLUCIONARIO 0 Un profesor decide redonder ls nots de 0 lumnos. Qué nots les pondrá?,8, 9,,,8 8, 9,,,8, Les pondrá ests nots:,, 0,,, 8, 0,, y. 0 Clcul l digonl de un rectángulo cuyos ldos miden 8 cm y 0 cm. Qué clse de número se obtiene? Redonde el resultdo ls milésims. Es un número irrcionl: d= =, Obtén el error bsoluto y reltivo cometido: ) Al redonder, ls milésims. Al truncr, ls diezmilésims. Al redonder ls centésims. Al truncr ls décims. e) Al proximr por defecto, ls milésims. ) E =,, =0 E r =,,, = 0 0 % E =,, =0,0000 E r =,,, = 0, ,009 % E =, =0,008 E r =, = 0, 008 0, % E 0,00 = 0, = 0, E 0,009 r = = 0,99 % e) E =,, =0,000 E r =,,, = 0, ,0 %
7 Números reles 09 L cntidd de ntibiótico en un cápsul es de, g ± 0, %. ) Qué signific est firmción? Entre qué vlores oscil l cntidd de ntibiótico en cd cápsul? ) Signific que un cápsul contiene, grmos, con un error reltivo del 0, %. 0,, 0, 0, % de, = = = 0, L cntidd oscil entre: (, 0,00;, + 0,00) = (,9;,0) 00 Escribe dos proximciones de, que tengn el mismo error reltivo. Por ejemplo, ls proximciones, y,. 0 Trnsform ls potencis en ríces. ) =.09 ( ) = = ( ) 8 = ) =. 09 = = 8 = 0 Clcul el vlor numérico, si existe, de los siguientes rdicles. ) 8 00 ) y No existe. 0 Hll, con l clculdor, el vlor numérico de ests expresiones. ) + ( ) ) +,989 =,989,89 =,88 No existe. 0 Pon dos ejemplos de rdicles cuys ríces sen y. Existe un rdicl con ríces y? Ejemplos: 9 y 8 No es posible que un rdicl teng como ríces y, y que en el cso de tener dos ríces, ests deben ser opuests.
8 SOLUCIONARIO 0 Expres ls siguientes potencis como rdicles y hll su vlor numérico. ) e) ( ) ( ) f) ( ) ) =, no existe. =,990 e) =,80 f) =,88 ( ) =,99 0 D dos rdicles equivlentes cd uno. ) ) y 8 y 0 y 0 0 Rzon si son equivlentes estos rdicles. 0 ) y y 0 y y 0 ) = Equivlentes No equivlentes 0 No equivlentes = = Equivlentes 08 Expres en form de potenci. ) x xy x x x x ) ( xy ) x = ( 8x) 09 Compr los siguientes rdicles., y 0 = 0 = 0 = 0 < < 00 Simplific estos rdicles. ) ) b b b
9 Números reles 0 Introduce fctores dentro del rdicl. ) ) = = 8 =. 9 = 0 0 Simplific, si es posible. ).. 0 ) = 0 = = 0 Oper y simplific. ) + + ) + = + = =. 8 = = 0 0 Clcul. ( ) ) 9 ) = = = = ( ) ( ) = = 8 = = Hz est operción. 9 9 ( ) ( ) + = + = = = 9
10 SOLUCIONARIO ACTIVIDADES Rzon cuáles de los siguientes números decimles son rcionles y cuáles son irrcionles. ), e),, f),, g),, h), ) Rcionl, periódico puro. e) Rcionl, periódico mixto. Rcionl, deciml excto. f) Rcionl, periódico puro. Irrcionl. g) Rcionl, periódico mixto. Irrcionl. h) Rcionl, deciml excto. Indic cuáles de los números son rcionles y cuáles son irrcionles. ) 0 g) 9 e) h) f) i) Son rcionles los números de los prtdos y h), y el resto son irrcionles. Averigu cuáles de los siguientes números son rcionles y cuáles son irrcionles. ) + 9 e) 8+ 0 f) Son rcionles los números de los prtdos, e) y f). Son irrcionles los números de los prtdos ), y. Escribe tres números rcionles y otros tres irrcionles. Explic cómo lo relizs. Los números rcionles son el resultdo de frcciones de números enteros; por ejemplo:,;, y,09. Los números irrcionles son números cuy prte deciml no tiene período; por ejemplo:, ;, ;, Escribe un número irrcionl comprendido entre: ) y 0, y 0, 0, y 0,, y, ), 0,0 0,,
11 Números reles 0 Clcul y determin qué tipo de número es, en un triángulo equilátero: h ) L ltur, si el ldo mide 0 cm. El áre, si el ldo mide cm. L ltur y el áre si el ldo mide cm. ) h= 0 = cm Es irrcionl. h= Es irrcionl. 9 h= = = cm A= = cm Son irrcionles. l = cm A= = cm 0 Orden, de menor myor, yudándote de l clculdor < < < + < < 8 < + < + 0 Clsific los siguientes números reles en nturles, enteros, rcionles o irrcionles. Di de qué tipo es su expresión deciml. ), e) π g) f) h) 90 ) Rcionl, deciml excto. e) Irrcionl. Rcionl, periódico puro. f) Rcionl, periódico mixto. Rcionl, deciml excto. g) Entero. Irrcionl. h) Entero. 8
12 SOLUCIONARIO 0 0 Compr estos pres de números. ), y, 9 y ( ), y 9 ), >, 9 = ( ), < 9 Orden, de menor myor, los siguientes conjuntos de números reles. ),,,,...,,88,, 8, 8, 8, 8, y > ), <, <, <,, <,88 <, <, 8, < 8, < 8, < 8, 0 Clcul el inverso y el opuesto de: ) g) e)π h), f), i) 0, ) Inverso: = 0, Opuesto: Inverso: = 0, Opuesto: Inverso: = 0, Opuesto: =, Inverso: = 0, Opuesto: e) Inverso: Opuesto: π =,9 π =, f) Inverso: = 0, 8 Opuesto:, g) Inverso: = 0, 09 Opuesto: =, h) Inverso: = 0,9 0 Opuesto:, 90 i) Inverso: = 8,8 Opuesto: 0, =, 9
13 Números reles 0 Rzon si ls firmciones son verdders o flss. ) Hy números enteros que no son rcionles. Existen números irrcionles que no son números reles. Un número rel es rcionl o irrcionl. Culquier número deciml es un número rel. ) Fls, y que culquier número entero se puede expresr en form de frcción de números enteros: el mismo número dividido entre l unidd. Fls, pues los números irrcionles están incluidos en el conjunto de los números reles. Verdder. Verdder, porque los números decimles son rcionles o irrcionles, y todos son números reles. 08 Indic si son verdders o flss ls firmciones. Rzon tu respuest. ) Todos los números decimles se pueden escribir en form de frcción. Todos los números reles son rcionles. Un número irrcionl es rel. Existen números enteros que son irrcionles. e) Hy números reles que son rcionles. f) Culquier número deciml es rcionl. g) Un número rcionl es entero. h) Los números irrcionles tienen infinits cifrs decimles. i) Todos los números rcionles tienen infinits cifrs decimles que se repiten. ) Fls, pues solo se pueden escribir como frcción los números rcionles. Fls, y que los números irrcionles no son rcionles. Verdder. Fls. e) Verdder. f) Fls, porque los números irrcionles no son rcionles. g) Fls, y que es el cociente de dos números enteros. h) Verdder. i) Fls, pues los números decimles exctos tienen un número finito de cifrs. 80
14 SOLUCIONARIO 09 Reliz ls operciones, scndo fctor común. ) ) ( ) = = 9 ( ) = =. + = = + 9 = = 00 Si y b son dos números reles y < b, qué sucede con sus opuestos? Y con sus inversos? Contest rzondmente. Inversos: > b Opuestos: > b 0 A qué número corresponde est representción? + = = 0 0 Utiliz el teorem de Pitágors pr representr en l rect rel estos números. ) 8 9 ) 8 0 G 0 8 G 0 8
15 Números reles 0 G 9 0 G 9 0 Orden, de menor myor, y represent estos números. 0, < < 0, < < < 0, F F F G G 0 0 Orden, de menor myor, y represent, de form exct o proximd., +, <, <, < < +,, F F G G 0 G + 8
16 SOLUCIONARIO 0 Describe y represent los siguientes intervlos en l rect rel. ) (0, 0) (, ) e) [, 0) (, ] [, ] f) [, + ) ) 0 < x < 0 < x 0 0 x < 8 x 0 e) x < f) x 0 Escribe el intervlo que corresponde los vlores de x. ) < x< x e) x> g) x< 9 < x x< f) x h) 0 x ) (, ) (, ] e) (, + ) g) [, 9) (, ] (, ) f) [, + ) h) [0, ] 0 Expres medinte intervlos ests situciones. ) L ltur de ls css es menor que 8 m. El descuento se plic niños con eddes comprendids entre y ños, mbos incluidos. L trjet sirve pr menores de ños. L entrd es grtuit pr menores de ños o myores de ños. e) L tempertur osciló entre C y C. ) (0, 8) (0, ) (, + ) [, ] e) [, ] (0, ) 8
17 Números reles 08 Represent los intervlos (0, ) y (, ) en l mism rect, y señl el intervlo intersección. 0 El intervlo intersección es (0, ). 09 Represent los intervlos (, 8) y [, + ) en l mism rect, y señl medinte un intervlo los puntos que pertenecen mbos. 0 8 El intervlo intersección es [, 8). 00 Escribe dos intervlos cuy intersección se [, ]. Por ejemplo: [, ) ( 8, ] = [, ] 0 Escribe dos números rcionles y otros dos irrcionles contenidos en el intervlo [0, ]. Rcionles:, y, Irrcionles: y 0 HAZLO ASÍ CÓMO SE CALCULA EL INTERVALO QUE CONTIENE EL RESULTADO DE UNA OPERACIÓN? Si x pertenece l intervlo (, ) e y pertenece (, ), indic qué intervlo pertenece el resultdo de ests operciones. ) x+y x y PRIMERO. Se tomn los extremos de los intervlos y se oper como se indic en cd cso. Extremos inferiores Extremos superiores ) x+y + = x+y + = x y = x y = 0 SEGUNDO. Se tomn los resultdos como los extremos de los nuevos intervlos. ) x+ypertenecerá l intervlo (, ). x ypertenecerá l intervlo (, 0). 0 Si dos números reles, x e y, pertenecen los intervlos (, ) y [0, ], respectivmente, qué intervlo pertenece el resultdo de ls operciones? ) x+y x y y x x y ) (, ) (, ) (, ) (, ) 8
18 SOLUCIONARIO 0 Con yud de l clculdor, escribe en form deciml y sus proximciones por exceso y por defecto ls diezmilésims. =, Aproximción por exceso:, Aproximción por defecto:, Redonde ls milésims el número. Clcul sus proximciones por exceso y por defecto. Qué observs? Aproximción por exceso:, Aproximción por defecto:, Aproxim por exceso y por defecto con dos cifrs decimles. ), ) Aproximción por exceso: 0, Aproximción por exceso:, Aproximción por defecto: 0, Aproximción por defecto:, Aproximción por exceso:,0 Aproximción por exceso:, Aproximción por defecto:,09 Aproximción por defecto:, Qué precerá en l pntll de l clculdor científic, l introducir cd uno de estos números, si previmente pulsmos l secuenci de tecls necesri pr fijr decimles? Y si fijmos? ),89,8 0, e) 8,0009 8,98 f), ) ) e) f) decimles decimles,89,89,898 0, 0, 0, 8,98 8,98 8,98,8,, 8,0009 8,00 8,00,908009,9080, Escribe un número: ) Deciml periódico puro, cuyo redondeo ls milésims es,. Deciml periódico mixto, con truncmiento ls centésims 0,9. Irrcionl, cuyo redondeo ls diezmilésims se 0,00. ), 0,9 0,008 8
19 Números reles Existe lgún cso en el que ls proximciones por exceso y por defecto coincidn? Y si considermos el redondeo, puede coincidir con l proximción por exceso y por defecto? Ls proximciones por exceso y por defecto coinciden cundo proximmos un orden y tods ls cifrs, distints de cero, del número son de órdenes superiores. El redondeo siempre coincide con uno de los csos nteriores; luego puede coincidir con uno o con los dos csos. Obtén el error bsoluto y reltivo cometido l redonder y truncr: ) ls centésims. 9,8 ls milésims. 0, ls décims. ) Redonder Truncr Error bsoluto 0,00 0,008 Error reltivo 0, ,00088 Redonder Truncr Error bsoluto 0,000 0,0008 Error reltivo 0, ,00008 Redonder Truncr Error bsoluto 0,0 0,0 Error reltivo 0 0, , Si proximmos 0,9 por 0,, qué error se comete? Y si lo proximmos por 0,? Cuál es l mejor proximción? Por qué? Al proximr por 0,; el error bsoluto es de 0,0. Al proximr por 0,; el error bsoluto es de 0,09. Es mejor proximción 0,; y que se comete un error menor. Un proximción por defecto de 8,9 es 8,. Hll el error bsoluto y el error reltivo. Error bsoluto: 0,009 Error reltivo: 0,00098 Escribe el número en form deciml con l mínim cntidd de cifrs pr que el error se menor que centésim. 0, 0, < 0, 00 8
20 SOLUCIONARIO 0 Aproxim el número,, de form que el error bsoluto se menor que 0,00. Es válid culquier de ests proximciones:, o, 0 Consider el número de oro o número áureo: Φ= + =, 80 Aproxímlo por redondeo hst ls centésims, y hll el error bsoluto y reltivo. Φ, Error bsoluto: +, = 0,00900 Error reltivo: + +, = 0, Reliz ests operciones y redonde los resultdos ls décims. Después, redonde cd número ls décims y resuelve l operción. Por qué procedimiento se comete menor error? ), + 8,, 8,9,, 0,9 :, ), + 8, =,0,, + 8, =,8 Se comete myor error redondendo cd sumndo., 8,9 =,9,, 8,9 =, Se comete el mismo error.,, =,,,, =, Se comete myor error redondendo el resultdo. 0,9 :, =,0, 0,9 :, =,98 Se comete myor error redondendo el resultdo. 8
21 Números reles 0 Siguiendo los psos de l ctividd nterior, hll un proximción por defecto. ), +,89,8,9,,9 00, : 8, ), +,89 = 8,99 8,, +,8 = 8, Se comete el mismo error.,8,9 = 00, 00,,8,9 = 00, Se comete myor error proximndo el resultdo.,,9 =,,,,9 =, Se comete el mismo error. 00, : 8, =,0, 00, : 8, =,09 Se comete myor error proximndo los fctores. 08 Obtén l proximción por redondeo hst ls diezmilésims. ) ) + =,, + =, 089, 09 = 0, 00 0, =, 0909, Qué error se comete l proximr el resultdo de,9 + 0, + 0,8 por el número 0,9?,9 + 0, + 0,8 = 0,8 E = 0,8 0,9 =0, Pr qué número serí., un proximción ls milésims por defecto? Es únic l respuest? Cuánts hy? L proximción es del número.,. L solución no es únic; hy infinits soluciones, tnts como números decimles que empiezn por., Se puede escribir π=? Justific l respuest y clcul el orden del error cometido. π=,9 =, 99 Es posible escribirlo, y que el error que se comete es menor que millonésim. E = π =,9,99 =0,
22 SOLUCIONARIO Rzon si es verddero o flso. ) Si el ldo de un cudrdo es un número rcionl, l digonl es irrcionl. Si el ldo de un cudrdo es un número irrcionl, el áre es rcionl. Si l digonl de un cudrdo es rcionl, el áre es rcionl. ) Verddero, por ejemplo: Ldo = Digonl = Flso, por ejemplo: Ldo =π Áre =π Verddero, por ejemplo: Digonl = Ldo = Clcul, si es posible, el vlor numérico de los siguientes rdicles. ) 8 g) j) e). 9 h) f) i) 8 )± ± g) No es posible. j) ± e) ± h) f) 0 i) Indic en estos rdicles cuáles son el índice y el rdicndo. Después, expréslos como potenci de exponente frccionrio. Áre= ) e) 9 f) ) Índice:, rdicndo: Índice:, rdicndo: Índice:, rdicndo: Índice: 9, rdicndo: e) Índice:, rdicndo: f) Índice:, rdicndo: ( ) 9 ( ) 08 Trnsform los rdicles en potencis y ls potencis en rdicles. ) g) 0 j) e) h) f) i) ) f) j) e) g) h) i) 0 89
23 Números reles 08 De estos rdicles, cuáles son equivlentes? ) e) g) i) f) h) Son equivlentes: = = = 0 = 08 Extre fctores en cd uno de los siguientes rdicles. ) b 0 g) b j) b b c e) b 8 h) b k) b f) b i) l) b ) b g) b j) bc b e) b h) b k) f) b i) l) b b b b b b No tiene solución, por ser ríz pr de un número negtivo. 088 HAZLO ASÍ CÓMO SE EXTRAEN FACTORES DE UN RADICAL DESCOMPONIENDO EL RADICANDO EN FACTORES PRIMOS? Simplific el rdicl PRIMERO. Se fctoriz el rdicndo = SEGUNDO. Se expres el rdicl como potenci de exponente frccionrio = ( ) = TERCERO. Si lgun de ls frcciones de los exponentes es impropi, se pone como l sum de un número entero y un frcción. + = CUARTO. Se expres como producto de potencis y se vuelve trnsformr en rdicl. + = = = = 0 = 90
24 SOLUCIONARIO 089 Extre fctores de ls ríces. ) 8 98 g) 8 e) h) 0 f) i) ) e) f) g) 0 h) i) 090 Simplific estos rdicles. ) g) e) 8 h) 8 f) i) 8 ) e) f) g) h) i) 09 Introduce fctores en el rdicl. ) g) 0 e) h) f) i) 8 ) 0 g). 80 e) 8 h). f) i) 8 9
25 Números reles 09 Introduce fctores en el rdicl, si es posible. b ) e) 8 c + f) b c b 8 b ) e) b c No es posible. f) 8 b 09 Efectú ls siguientes operciones. ) ) 09 Reliz ests operciones. ) ) = = 9 + = 09 Oper y simplific. ) e) : g) : 8 f) : h) : ) e) g) 8 f) 0 h) 9
26 SOLUCIONARIO 09 Clcul. ) ( + ) ( ) ( ) e) f) ( ) 8 ( ) ( 9 ) ( 8 ) ) e) f) Oper y simplific. ( ) ( ) ) + ( ) ( + ) ( + ) ( ) ( 0) + 0 ) = 0 9 = = 0 = 0 Clcul y simplific. ( ) ( ) + ( + ) ) ( + ) ( ) ( ) ( + ) ) ( ) + ( + + ) = ( ) ( + ) = ( ) ( + + ) = + 9
27 Números reles 099 Hz ls operciones y simplific. ( ) ( ) ) ( ) ( ) ( + ) ( ) ( ) ( + ) + ) + = = + = = = = 0+ 0 = + 00 Clcul. ) b b + + ) = = b : b b b b b = b = b b 9 9 b : b = b 0 0 b b = b = b 0 Efectú y simplific. ( ) ( ) ) + ( + ) ( + ) ( ) ( + ) ( ) + ( ) ( + ) ( + ) ( + ) ) (9 ) + ( 80) = ( 0+ ) ( ) = = = ( ) = + + ( ) = = 0 8 9
28 SOLUCIONARIO 0 Efectú y expres el resultdo como potenci. ( ) ) 8 8 ( ) = ) 0 0 = = = = 0 Escribe los siguientes rdicles como potencis de exponente frccionrio. ) g) = = e) h) = f) i) 0 Expres medinte un solo rdicl. ) e) f) 0 0 ) = = e) 8 f) 9
29 Números reles 0 Rzon si son verdders o flss ests igulddes. ) n m n m b = b n m n b = ( e) f) g) h) n m n+ m b = b n n n + b = + b b = b b 8 = b b+ c = b+ c m + b = + b n m n m m ) b m n n n m b m b n n m = = b Fls. n m n+ m n m n m m b m n n = b = m b n b Fls. Fls, excepto cundo n=. Y se comprueb probndo con culquier vlor de, b y n. n m n b n b m n m m = b Fls, excepto si n=m. e) Fls, y que si elevmos l cudrdo los términos: ( ) = = + + b b b b ( b ) f) b = b = b Verdder. 8 g) b = b = b b Fls. h) b+ c = b+ c b+ c Fls, excepto pr =. 0 Clcul el ldo de un cudrdo inscrito en un circunferenci de rdio cm. El número obtenido, es rcionl o irrcionl? L digonl del cudrdo coincide con el diámetro. Ldo = x Digonl = x x = 0 x= El ldo mide cm, que es un número irrcionl. 0 Hll l digonl de un cudrdo de ldo 8 cm. Si construimos un cudrdo cuyo ldo es es digonl, cuál es el áre del segundo cudrdo? Digonl = 8 cm Áre = ( 8 ) = 8 cm 9
30 SOLUCIONARIO 08 L bse de un rectángulo mide b=8 cm y su ltur es = b. Clcul l longitud de l circunferenci circunscrit este rectángulo y expres el resultdo con tres decimles. El diámetro de l circunferenci es l digonl del rectángulo. Digonl = 8 + = 0 cm, rdio = cm L longitud de l circunferenci es, cm. 09 Clcul el volumen del edificio y redonde el resultdo ls milésims. 0, m,9 m, m ) Redonde sus dimensiones ls décims, y clcul el volumen de nuevo. Qué relción tiene con el resultdo nterior? Hll el error bsoluto y reltivo cometido en cd cso. El vlor excto del volumen es: Volumen =,9, 0, = 8.9, m Si redondemos el resultdo ls milésims: Volumen = 8.9, m ) Volumen =,,8 0, = 8.98, m El resultdo es myor que el resultdo nterior. Volumen =,9, 0, = 8.9, m E = 8.9, 8.9, =0,000 E r = 8. 9, 8. 9, 8. 9, = 0, Volumen =,,8 0, = 8.98, m E = 8.9, 8.98, =,8 E r = 8. 9, 8. 98, 8. 9, = 0, 00 9
31 Números reles 0 Hll l longitud de los ldos y el áre de cd un de ls piezs del tngrm. Suponemos que el ldo del cudrdo es l. l b c es l mitd de l digonl del cudrdo: = l + l = l l b b b c b es l mitd de : b= = c es l mitd de l: c= l l c c Vmos clculr hor el perímetro y el áre de cd figur. P = + l= l+ l= ( + ) l Figur : A= l l = = P = + l= l+ l= ( + ) l Figur : A= l l = = P= b+ c= + = l l + l Figur : l l A= c = 8 l + P= b+ c= + = l l Figur : b b A= l = P= b= l Figur : l A= b = 8 98
32 SOLUCIONARIO + l P= b+ c= + = l l Figur : b b A= l = P= b+ c= + = l l + l Figur : c c A= l = 8 Cuánto mide el áre de l cr de un cubo cuyo volumen es 9 cm? Expres el resultdo como rdicl y como potenci. Arist = 9 m Arist= 9 m Áre de l cr= 9 9 = 9 = 8 m = m Cuánto mide l rist de un cubo cuyo volumen es m? Expres el resultdo en form de rdicles. Arist = m Arist= m Si el volumen de un cubo es 0 cm, hll el vlor de l sum de sus rists. Arist = 0 cm Arist= 0 cm Sum de rists = 0 Con los dtos de l ctividd nterior, clcul l superficie lterl del cubo. Arist = 0 cm Arist= 0 cm Áre de l cr= 0 cm cm Áre lterl= 0 = 0 cm Generliz los resultdos de ls ctividdes nteriores, dndo el vlor de l rist y l superficie lterl de un cubo en función de su volumen. Arist = Volumen Arist= Volumen Áre de l cr Áre lterl = Volumen = Volumen Consider que A, B, C y D son cutro locliddes. L distnci entre A y B es 8 km, con un error de 00 m, y l distnci entre C y D es 00 m, con un error de, m. Qué medid es más decud? Por qué? 00 Comprmos los errores reltivos: = 0,00, < = 0, Es más decud l medid de l distnci entre C y D por tener menor error reltivo. 99
33 Números reles Escribe proximciones decimles del número,, con ls siguientes cots del error bsoluto. ) 0,00 0,0 0,000 0, ),,,,8 8 Justific de qué orden tendrímos que tomr el redondeo de un número irrcionl pr que l cot del error bsoluto fuer menor que un millonésim. El orden del redondeo serí ls diezmillonésims. 9 Reflexion y responde. ) En qué csos ocurre que <? Y en qué csos ocurre que >? ) <, cundo 0< <. >, cundo >. 0 Rcionliz. ) + ) + = + ( + ) ( + ) = + + = + + ( ) ( + + ) = + + Explic cómo se rcionlizn ls frcciones del tipo n n. b n n Volvemos rcionlizr hst que eliminmos totlmente ls ríces del denomindor. n n b b = = n n n ( + b n n n n ( ) = + n n n ( ) + b b n n ( ) + b n n b = ( ) n n n n ( ) ( + + b = n n ( ) ( + ) ( + ) n n n n + b b = b b b b 00
34 SOLUCIONARIO EN LA VIDA COTIDIANA Un equipo de ingenieros eronáuticos v presentr un proyecto pr l construcción de un nuevo vión. Por ello quieren construir un mquet. Sin embrgo, se hn encontrdo con un problem. Te hs fijdo en est piez? Es un rectángulo de cm de lrgo, pero su ncho Sí, es cierto; debe medir cm. Pr no cometer errores en l construcción, se plnten cómo trzr un segmento que mid exctmente Así, el equipo h resuelto el problem pr poder relizr l mquet. cm. Podemos trzr un triángulo rectángulo cuyos ctetos midn cm y cm, y utilizr el teorem de Pitágors. Otr de ls piezs v ser un rectángulo que mid + cm de lrgo y cm de ncho. Cómo conseguirán dibujrlo con precisión? Un vez conocido el segmento de cm, trzmos el segmento de cm medinte un triángulo rectángulo, de ctetos cm y cm, y se hce lo mismo con el segmento de cm con un triángulo de ctetos cm y cm. Teniendo el segmento de con lo que result un segmento de cm, le ñdimos cm prolongndo l rect, + cm. 0
35 Números reles Trzmos l meditriz del segmento y conseguimos un segmento + de cm. Pr el otro ldo del rectángulo, trzmos primero un segmento de cm, medinte un triángulo rectángulo de ctetos cm, y proyectmos cutro veces el segmento utilizndo un compás, por lo que conseguimos un segmento de cm. En un cmpmento, los monitores hn pedido los chicos que se grupen, pinten un murl y, después, lo enmrquen. El grupo de Jun h hecho un murl cuy áre mide m y quiere enmrcrlo. Necesitn clculr l longitud del ldo, pero no disponen de regls pr medir ni clculdors. Vmos relcionrlo con, que es l longitud de l digonl de un cudrdo cuyo ldo mide m. Y cómo medimos? El monitor les pide que den l longitud con precisión de milímetros, por lo que deben determinr los tres primeros decimles de. Los chicos piensn en rectángulos cuy áre coincid con el áre del murl y en dimensiones cd vez más precids entre sí. Empezmos con un rectángulo de m de bse y m de ltur. A continución, tomn un rectángulo cuy bse es l medi entre l bse + y l ltur del nterior: = ; sí, l ltur debe ser : =, y tenemos que: < <. 0
36 SOLUCIONARIO Continundo este proceso, como l diferenci entre l bse y l ltur de estos rectángulos es cd vez menor y siempre está comprendido entre ells, Jun procede sí hst que ls tres primers cifrs de l bse y l ltur del rectángulo sen igules. Cuántos psos debe dr Jun pr logrrlo? PRIMER PASO: < < Cot de error: SEGUNDO PASO: + = : = < < Cot de error: 0 TERCER PASO: + = : = < < Cot de error: 08. L cot es y menor que milímetro. =, 08 0
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Potencias y radicales
 Potencis y rdicles POTENCIAS DE EXPONENTE ENTERO NOTACIÓN CIENTÍFICA RADICALES EQUIVALENTES SEMEJANTES OPERACIONES CON RADICALES SUMA Y RESTA PRODUCTO Y COCIENTE POTENCIA Y RAÍZ RACIONALIZACIÓN DENOMINADOR
Potencis y rdicles POTENCIAS DE EXPONENTE ENTERO NOTACIÓN CIENTÍFICA RADICALES EQUIVALENTES SEMEJANTES OPERACIONES CON RADICALES SUMA Y RESTA PRODUCTO Y COCIENTE POTENCIA Y RAÍZ RACIONALIZACIÓN DENOMINADOR
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero. TEMA 2: actividades
 º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
LITERATURA Y MATEMÁTICAS. El código Da Vinci
 Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
Multiplicar por la potencia de 10 adecuada para convertirlo en entero. Despejar N 119. Simplificar la fracción, si es posible N = 50
 .0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
.0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
SOLUCIONES DE LAS ACTIVIDADES Págs. 4 a 21
 TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN:
 TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Ejercicios. Números enteros, fraccionarios e irracionales.
 CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
4º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- Escrie un número que cumpl: ) Pertenece N y I. ) Pertenece R pero no Q. c) No pertenece R. d) Pertenece Q pero no N. ) IMPOSIBLE
º ESO ACADÉMICAS NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- Escrie un número que cumpl: ) Pertenece N y I. ) Pertenece R pero no Q. c) No pertenece R. d) Pertenece Q pero no N. ) IMPOSIBLE
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
11 Perímetros y áreas de figuras planas
 86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
86464 _ 0371-0384.qxd 1//07 09:4 Págin 371 Perímetros y áres de figurs plns INTRODUCCIÓN En est unidd repsmos ls uniddes de longitud y superficie. Se introducen tmbién lguns uniddes de medid del sistem
1. NÚMEROS RACIONALES
 IES Jun Grcí Vldemor Deprtmento de Mtemátics 4º ESO Mtemátics B. NÚMEROS RACIONALES Desde l prición de ls socieddes humns los números desempeñn un ppel fundmentl pr ordenr y contr los elementos de un conjunto.
IES Jun Grcí Vldemor Deprtmento de Mtemátics 4º ESO Mtemátics B. NÚMEROS RACIONALES Desde l prición de ls socieddes humns los números desempeñn un ppel fundmentl pr ordenr y contr los elementos de un conjunto.
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
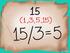 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
pág. 87 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 + + + + 4 4 n n + es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de
REPASO DE ECUACIONES (4º ESO)
 TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
1. Números reales. Resuelve BACHILLERATO. Página 25
 . Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
. Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
11. Triángulos SOLUCIONARIO 1. CONSTRUCCIÓN DE TRIÁNGULOS 2. MEDIANAS Y ALTURAS DE UN TRIÁNGULO
 SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
LÁMINA No. 1.1 LECTURA Y ESCRITURA DE UN NÚMERO
 6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
pág. 71 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
Presentación Axiomática de los Números Reales
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
ECUACIONES (4º ESO Op B)
 ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
1 Agrupa aquellos monomios de los que siguen que sean semejantes, y halla su suma: , cuando:
 Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Conceptos generales de triángulos GUICEN023MT22-A16V1
 GUÍ DE EJERITIÓN VNZD onceptos generles de triángulos rogrm Entrenmiento Desfío GUIEN023MT22-16V1 Mtemátic En l figur, RQ = 24 cm, RS SQ y RM SN. Si M es el punto medio de SQ y N es el punto medio de RQ,
GUÍ DE EJERITIÓN VNZD onceptos generles de triángulos rogrm Entrenmiento Desfío GUIEN023MT22-16V1 Mtemátic En l figur, RQ = 24 cm, RS SQ y RM SN. Si M es el punto medio de SQ y N es el punto medio de RQ,
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
EJERCICIOS DE RAÍCES
 EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
Clasifica los siguientes polígonos. a) b) c) d)
 1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
Las matemáticas son una ciencia experimental que basa su desarrollo en la intuición y la lógica.
 L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
MATEMATICAS 3º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION
 MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
Se desea calcular la longitud de un lado de una pista de baile de forma cuadrada, cuya área es 16 u 2. Sustituyendo el valor del área
 Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
Pág. 1 PÁGINA 06 EJERCICIOS Tipos de poliedros 1 Di, justificdmente, qué tipo de poliedro es cd uno de los siguientes: A B C D E Hy entre ellos lgún poliedro regulr? A Prism pentgonl recto. Su bse es un
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES 2º PARCIAL
 Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
El conjunto de los números reales se forma mediante la unión del conjunto de los números racionales y el conjunto de los números irracionales.
 El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
Las matemáticas son una ciencia experimental que basa su desarrollo en la intuición y la lógica.
 L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
L plbr mtemátics proviene del término griego mthemtiké o cienci por excelenci, pues los sbios de Greci opinbn que tods ls leyes de l vid y del mundo físico se podín expresr por medio de los números. Ls
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
Resolución de triángulos
 8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
Razones trigonométricas
 LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
(lo podemos visualizar como el área de un cuadrado de lado 4) Pues bien, diremos que la base de dicha potencia, 4, es su raíz cuadrada exacta: 16 = 4.
 Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN. 3. Trigonometría I
 Evlución NMBRE PELLIDS CURS GRUP FECH CLIFICCIÓN 4 L solución de l ecución sen 0,5 es: ) 0 y 50 b) 50 y 0 c) 0 y 0 Si sen 0 0,4, entonces cos 0 será: ) 0,4 b) 0,94 c) 0,4 Un estc de longitud, clvd verticlmente
Evlución NMBRE PELLIDS CURS GRUP FECH CLIFICCIÓN 4 L solución de l ecución sen 0,5 es: ) 0 y 50 b) 50 y 0 c) 0 y 0 Si sen 0 0,4, entonces cos 0 será: ) 0,4 b) 0,94 c) 0,4 Un estc de longitud, clvd verticlmente
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
8. Calcule el área de la superficie lateral y total de los sólidos construidos en los numerales 1, 2, 3, 4, 6 y 7.
 8 CAPÍTULO OCHO Ejercicios propuestos 8. Cuerpos geométricos 1. Construy un tetredro regulr con rist de 10cm de longitud. 2. Construy un hexedro regulr con rist de 12cm de longitud.. Construy un octedro
8 CAPÍTULO OCHO Ejercicios propuestos 8. Cuerpos geométricos 1. Construy un tetredro regulr con rist de 10cm de longitud. 2. Construy un hexedro regulr con rist de 12cm de longitud.. Construy un octedro
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
de Thales y Pitágoras
 8 Teorems de Thles y Pitágors 8.1. Cuents y problem del dí 1. Reliz l siguiente operción: 874,53 + 3 607,8 + 875,084 2. Reliz l siguiente operción, obtén dos decimles en el cociente y hz l prueb de l división:
8 Teorems de Thles y Pitágors 8.1. Cuents y problem del dí 1. Reliz l siguiente operción: 874,53 + 3 607,8 + 875,084 2. Reliz l siguiente operción, obtén dos decimles en el cociente y hz l prueb de l división:
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA. Objetivos
 UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA
 EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
12. Los polígonos y la circunferencia
 l: ldo SLUINI 107 1. Los polígonos y l circunferenci 1. PLÍGNS PIENS Y LUL lcul cuánto mide el ángulo centrl mrcdo en los siguientes polígonos:? l: ldo? 4. ivide un circunferenci de de rdio en seis prtes
l: ldo SLUINI 107 1. Los polígonos y l circunferenci 1. PLÍGNS PIENS Y LUL lcul cuánto mide el ángulo centrl mrcdo en los siguientes polígonos:? l: ldo? 4. ivide un circunferenci de de rdio en seis prtes
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
Tema9. Sucesiones. Tema 9. Sucesiones.
 Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
3º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
IES Fernando de Herrera 13 de enero de 2014 Primer trimestre Examen de autoevaluación 1º Bach CCSS NOMBRE:
 IES Fernndo de Herrer de enero de 04 Primer trimestre Exmen de utoevlución º Bch CCSS NOMBRE: 7 ) ) Representr en l rect rel: b) Qué número es el indicdo en el gráfico? 0 ) Clculr el resultdo simplificdo
IES Fernndo de Herrer de enero de 04 Primer trimestre Exmen de utoevlución º Bch CCSS NOMBRE: 7 ) ) Representr en l rect rel: b) Qué número es el indicdo en el gráfico? 0 ) Clculr el resultdo simplificdo
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
Ejercicios de números reales
 Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
10.- Teoremas de Adición.
 Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
PSU Matemática NM-4 Guía 22: Congruencia de Triángulos
 Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
Las expresiones algebraicas provienen de fórmulas físicas, geométricas, de economía, etc. Son expresiones
 Definición de Polinomio Epresiones Algerics Epresión lgeric es tod cominción de números letrs ligdos por los signos de ls operciones ritmétics: dición, sustrcción, multiplicción, división potencición.
Definición de Polinomio Epresiones Algerics Epresión lgeric es tod cominción de números letrs ligdos por los signos de ls operciones ritmétics: dición, sustrcción, multiplicción, división potencición.
Fórmulas de cuadratura.
 PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 3 1. NÚMEROS RACIONALES UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números
Números reales NÚMEROS REALES APROXIMACIONES ERRORES EN LA APROXIMACIÓN NÚMEROS NÚMEROS RACIONALES RELACIÓN DE ORDEN IRRACIONALES
 Números reales NÚMEROS REALES NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES APROXIMACIONES TRUNCAMIENTO REDONDEO POR EXCESO ERRORES EN LA APROXIMACIÓN Mi desconocido amigo La misiva parecía
Números reales NÚMEROS REALES NÚMEROS RACIONALES RELACIÓN DE ORDEN NÚMEROS IRRACIONALES APROXIMACIONES TRUNCAMIENTO REDONDEO POR EXCESO ERRORES EN LA APROXIMACIÓN Mi desconocido amigo La misiva parecía
Propiedades de la Potencia. Observación: La potencia no es distributiva con respecto a la suma ni a la resta.
 Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
GUÍA DE MATEMÁTICAS V. Ciclo escolar B determina:
 Elbor: Preprtori Págin 1 de 14 Ciclo escolr 014-015 Docente: Fernndo Vivr Mrtínez I) Producto Crtesino, Relciones y Funciones B determin: 1) Ddos los conjuntos A 0,1,,3 y 4,5,6,7 ) El Producto Crtesino
Elbor: Preprtori Págin 1 de 14 Ciclo escolr 014-015 Docente: Fernndo Vivr Mrtínez I) Producto Crtesino, Relciones y Funciones B determin: 1) Ddos los conjuntos A 0,1,,3 y 4,5,6,7 ) El Producto Crtesino
Problemas de fases nacionales e internacionales
 Problems de fses ncionles e interncionles 1.- (Chin 1993). Ddo el prlelogrmo ABCD, se considern dos puntos E, F sobre l digonl AC e interiores l prlelogrmo. Demostrr que si existe un circunferenci psndo
Problems de fses ncionles e interncionles 1.- (Chin 1993). Ddo el prlelogrmo ABCD, se considern dos puntos E, F sobre l digonl AC e interiores l prlelogrmo. Demostrr que si existe un circunferenci psndo
a) Decimales finitos: Corresponden a los cuocientes exactos entre el numerador y el denominador. Ejemplo: : 8 = (b)
 Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
UNIDAD N 3: EXPRESIONES ALGEBRAICAS POLINOMIOS
 Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
1.- Simplificar las siguientes fracciones: h) 28/36 i) 84/126 j) 54/96 k) 510/850 l) 980/140
 ACTIVITATS DE N ESO PER A ESTIU ACTIVIDADES CON NÚMEROS ENTEROS º ESO. Reliz ls siguientes operciones. + + + d + + b + + 6 e + 6 c + f 6 + + + 6. Reliz ls siguientes operciones. ( + + ( + + ( + d + ( +
ACTIVITATS DE N ESO PER A ESTIU ACTIVIDADES CON NÚMEROS ENTEROS º ESO. Reliz ls siguientes operciones. + + + d + + b + + 6 e + 6 c + f 6 + + + 6. Reliz ls siguientes operciones. ( + + ( + + ( + d + ( +
73 ESO. E = m c 2. «El que pregunta lo que no sabe es ignorante un. día. El que no lo pregunta será ignorante toda la vida»
 73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
Se traza la paralela al lado a y distancia la altura h a.
 Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
