Ejercicios y problemas de ecuaciones Índice de contenido
|
|
|
- Roberto Franco Moya
- hace 6 años
- Vistas:
Transcripción
1 Ejercicios y problemas de ecuaciones Índice de contenido Ejercicios y problemas de ecuaciones...1 Ejercicios de Ecuaciones...2 Problemas...4 Ejercicios y problemas de sistemas...6
2 Ejercicios de Ecuaciones 1. Escribe la expresión algebraica correspondiente a cada uno de los enunciados: a. Un hermano tiene x años y otro tres más. La altura de un edificio de 5 plantas es h metros. Cuál es la altura de cada planta? c. En un país viven n personas. Cuantas viven en otro país con el triple de población? d. Una mercancía cuesta a p /kg. Cuánto nos costarán 3 kg 400 g? e. En una prenda que cuesta p nos hacen un descuento del d %. Cuánto tenemos que pagar? f. El doble del siguiente de un número x. 2. Escribe un enunciado para las siguientes expresiones algebraicas: a. La relación entre la edad de dos hermanos es y=x+2 La relación entre dos números es p=2q 3 c. La densidad es d= m V 3. Traduce a una ecuación los siguientes enunciados: a. La cuarta parte de mis libros más cuatro es igual al total de libros que tengo menos dos. El producto de dos números consecutivos es igual a su suma al cuadrado c. Los cuatro goles que ha marcado un equipo son cinco novenos de todos los goles del partido. 4. Calcula el valor de a para que x=2 sea solución de la ecuación 3(x 2)=x+a 5. Resuelve: a. 5x+ 3 2 = 3x+1 2 4x 12 =x 15 c Resuelve las siguientes ecuaciones por el método más adecuado: a. x 2 1=0 80=20x 2 c. x 2 +1=0 x+1 8 x x+3 5 =0 d. x x 2 =0 e. 4x 2 75=25 f. 4x x=4x g. (3x+1) 2 =3x 2 +4x +1 h. 8x 2 10x+3=0 i. 4x+1= 4 x 2 7. Resuelve las siguientes ecuaciones bicuadradas a. x 4 +2 x 3 3=0 x 4 5x 2 +4=0 c. x 4 4 x 2 =0 d. x 4 13x 2 +36=0 e. 4x 4 257x 2 +64=0 f. x 4 25x =0 8. Resuelve las siguientes ecuaciones racionales: a. 3 x 13 =1+ x 6 1 x 2 x 1 x 1 =0 c. 1 x x+2 = 1 x 2 4
3 d. 3 x x+2 x 1 = x x+1 e. 7+x x+5 = x+3 x+2 9. Resuelve las siguientes ecuaciones irracionales a. x+5=8 x+5= 2x c. x 2 +5= 2x+40 d. x 2x+9=3 e. 4x+5 3x+1=1 f. x 3 2 x= x g. 3 x=x +1 h. x+1= x +9 i. 3 x = 6 3x Resuelve la siguiente ecuación en x: 11. Resuelve pensando un poco: f. j. 3x+10=1+ 4x+1 1 x+a + 1 x a = 1 x 2 a 2 1+ x+1 x 1 2 x 1 =2 x+1 a. 2 log 2 x=10 log x 625=4 c. 3 log x= 6 d. ln(3 x)=0 12. Calcula el valor de m para que las siguientes ecuaciones tengan solo una solución: a. 2x 2 4x m=0 mx 2 2x 1=0 c. x 2 m x 36=0 13. Escribe una ecuación de segundo grado en cuyas raíces tienen las siguientes sumas y productos: a. S=7, P=0 S=6, P=8 c. S=1, P=-2 d. S=-2, P=-15
4 Problemas 14. Las edades actuales de una mujer y su hijo son 49 y 25 años. Hace cuántos años el producto de sus edades era 640? 15. La edad de una madre es el triple que la de su hijo y dentro de 10 años solo será el doble. Qué edad tiene cada uno ahora? 16. Un grupo de amigos se reparte el bote que ha sobrado de una quedada y sucede lo siguiente: si cada uno se lleva 1 sobran 15 cts, pero faltan 35 cts para que cada uno se pueda llevar 1,25. Cuántos son? Cuánto dinero ha sobrado? 17. Dos fincas rectangulares tienen la misma superficie. En la primera el largo es de 70 m y el ancho de 30 m, mientras que en la segunda el largo es 10 m menor que en la primera. Cuáles son las dimensiones de la segunda? 18. La leche desnatada de una determinada marca contiene un 0,25% de materia grasa, y la leche entera 4%. Calcula la cantidad que hay que mezclar de cada tipo para conseguir tres litros de leche semidesnatada con un 1,5% de grasa. 19. Un peluquero quiere conseguir una disolución de agua oxigenada al 6%. Dispone de dos botellas, una al 3% y otra al 33%. Cómo debe realizar la mezcla para obtener 10 litros de la disolución que desea? 20. Halla un número entero sabiendo que la suma con su inverso es Dos grifos A y B llenan juntos una piscina en dos horas, A lo hace por sí solo en tres horas menos que B. Cuántas horas tarda a cada uno separadamente? 22. Un grifo tarda dos horas más que otro en llenar un depósito y abriendo los dos juntos se llena en 1 hora y 20 minutos. Cuánto tiempo tardará en llenarlo cada uno por separado? 23. Tres personas son capaces de pintar una habitación en dos horas. Una de ellas es capaz de hacerlo sola en 5 horas y otra en 6 horas. Cuánto tardará la tercera persona en hacerlo sola? 24. Un grifo vierte un caudal que es 1,5 veces el de otro grifo. Si entre los dos juntos con capaces de llenar un depósito en 6 horas, cuánto tarda cada grifo por separado? 25. Todas las personas que asistieron a una reunión se estrecharon la mano. Una de ellas advirtió que los apretones de mano fueron 66. Cuántas personas concurrieron a la reunión? 26. En la civilización egipcia, debido a las periódicas inundaciones del Nilo, se borraban los lindes de separación de la tierra y, para la reconstrucción de las fincas, necesitaban saber construir ángulos rectos. En un viejo papiro se puede leer lo siguiente: La altura del muro, la distancia al pie del mismo y la línea que une ambos extremos son tres números consecutivos. Halla dichos números. 27. Una ebanista quiere partir un listón de madera de 30 centímetros de longitud en tres trozos para construir una escuadra, de manera que el trozo de mayor longitud mida 13 centímetros. Cuál es la longitud de los otros dos trozos? 28. Si a uno de los lados de un cuadrado se le aumenta su longitud en 5 centímetros y a su lado contiguo en 3 centímetros, el área de la figura aumenta en 71 centímetros cuadrados. Calcula el lado del cuadrado inicial. 29. Un coche sale de una ciudad A hacía una ciudad B a una velociadad de 80 Km/h. En
5 el mismo instante sale otro coche haciendo el recorrido inverso a una velocidad de 60 km/h. Si la distancia entre A y B es de 60 Km, Cuánto tiempo tardan en encontrarse? A que distancia de de A se encontrarán? 30. Juan sale de su casa a comprar el pan a una velocidad de 4 km/h. A los 6 min su madre se da cuenta de que también tendría que comprar otras cosas, y sale a su encuentro a una velocidad de 6 km/h. Cuánto tiempo tardará en alcanzarle? 31. Un motociclista pasa por un semáforo con velocidad constante de 50 km/h, en el mismo momento un camión pasa por el mismo lugar y con igual sentido a una velocidad constante de 80 km/h, cuánto tiempo después estarán separados por 300 m?. 32. Un tren sale de Barcelona a Madrid con una velocidad constante de 150 km/h, mientras que a la misma hora sale otro de Madrid a Barcelona con una velocidad constante de 200 km/h. Si la distancia entre las dos ciudades es de 600 km, a que distancia de Madrid se encontraran? 33. Observa la siguiente resolución de una ecuación: 2x+3 =2 2x+3=8x +12 6x=9 x= 3 Pero si realizamos la comprobación vemos 4x+6 2 que no se cumple. Serías capaz de decir cual es el problema?
6 Ejercicios y problemas de sistemas 34. Resuelve los siguientes sistemas no lineales x+ y=10 a. x 2 + y 2 =68 x 3y=12 x 2 y 2 =7 c. ( x+ y)2 =269 x 2 + y 2 =169 x+ y=7 d. 1 x + 1 y = 7 12 g. x2 +4y x= y 1 x y= 1 e. x+ y= xy x+ y=5x 5y f. 3 x + 1 y = x + 4 y =10 3 xy=240 h. x 2 20x 16y xy=22 16 y=360 i. x y=1 35. Un gramo de oro pierde, al introducirlo en agua, 0,051 g de su peso, y un gramo de plata 0,095 g. Calcula la cantidad de oro y de plata que tiene un objeto de 6 g, si pierde 0,35 g al meterlo en agua. 36. Una finca, cuya forma es un triángulo isósceles, tiene un perímetro perímetro de 160 m y la altura sobre el lado desigual es de 4 m. Halla los lados de dicha finca. 37. El área de un triángulo rectángulo es 120 dm 2. Si la hipotenusa mide 26 dm, cuáles son las longitudes de los catetos? 38. La suma de los radios de dos círculos es 70 cm y la suma de las áreas de éstos es igual al área de un tercer círculo de 50 cm de radio. Cuál es el radio de los círculos? 39. Los lados paralelos de un trapecio miden 15 cm y 36 cm, respectivamente, y los no paralelos 13 y 20 cm. Calcula la altura del trapecio. 40. La diferencia de las diagonales de un rombo es de 2 dm. Si a las dos las aumentamos en 2 dm, el área aumenta en 16 dm 2. Busca las diagonales, el perímetro y el área de dicho rombo. 41. Halla dos números tales que su suma, producto y cociente sean iguales entre sí.
7 Inecuaciones 42. Resuelve las siguientes inecuaciones de primer grado: a. 4(x 4) 3(x 2) 7 d. x+5 3 2x 3 >5 x e. 2x 3 +x <16 c. 3x 8 5x+2 x 10 >4x Resuelve los siguientes sistemas de inecuaciones de primer grado: 2x 3> x 2 a. x 1 3 x+3 2 x 3x 7< x 1 4x 2 x 1 c. x 1 3 x x x 2 0 d. x+ 1 5 >0 e. x+2 2x+3( x 1)< x+1 3 x 2( x+3)>x Resuelve las siguientes inecuaciones de segundo grado: a. 4 2x 5x x 2 6x 2 >12 x c. 8x x 2 15 d. (x+2) 2 +3x 2(x 2 +1) e. x 2 4x 12 0 f. x 2 +6x 7<0 45. Resuelve x 2>0 a. x 2 4x 3<0 x2 3x>0 x 3x 2 <0 f.
Ecuaciones de 1er y 2º grado
 Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos
 TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos Resuelve mentalmente las siguientes ecuaciones: 1 5 5, 5 9 7, 7 4 5 5 1, 1 Resuelve las siguientes ecuaciones: 6 6, 6 7 16 4, 8 7 9 5 + 6, 10 +
TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos Resuelve mentalmente las siguientes ecuaciones: 1 5 5, 5 9 7, 7 4 5 5 1, 1 Resuelve las siguientes ecuaciones: 6 6, 6 7 16 4, 8 7 9 5 + 6, 10 +
8. Ecuaciones de 1. er y 2. o grado
 0 Solucionario. Ecuaciones de. er y. o grado. Ecuaciones de. er grado piensa y calcula Resuelve mentalmente: a) + = b) = c) = d) = a) = b) = c) = d) = CARNÉ CALCULISTA, : C =,; R = 0, APLICA LA TEORÍA
0 Solucionario. Ecuaciones de. er y. o grado. Ecuaciones de. er grado piensa y calcula Resuelve mentalmente: a) + = b) = c) = d) = a) = b) = c) = d) = CARNÉ CALCULISTA, : C =,; R = 0, APLICA LA TEORÍA
RESOLVER LAS ECUACIONES DE PRIMER GRADO
 RESOLVER LAS ECUACIONES DE PRIMER GRADO 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) PROBLEMAS DE ECUACIONES DE PRIMER GRADO 1 Un padre tiene 35 años y su hijo 5. Al cabo de cuántos años será la
RESOLVER LAS ECUACIONES DE PRIMER GRADO 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) PROBLEMAS DE ECUACIONES DE PRIMER GRADO 1 Un padre tiene 35 años y su hijo 5. Al cabo de cuántos años será la
ECUACIONES E INECUACIONES
 ECUACIONES E INECUACIONES 1.- Escribe las expresiones algebraicas que representan los siguientes enunciados: a) Número de ruedas necesarias para fabricar x coches. b) Número de céntimos para cambiar x
ECUACIONES E INECUACIONES 1.- Escribe las expresiones algebraicas que representan los siguientes enunciados: a) Número de ruedas necesarias para fabricar x coches. b) Número de céntimos para cambiar x
Ejercicios y problemas
 Ejercicios y problemas. Ecuaciones de er y º grado Resuelve mentalmente las siguientes ecuaciones: 55 5 0 5/, 5/ 6 6 + /, 8 ( ) + ( ) 56 ( )( + ) 0, 57 ( ) + 0 0, / 58 6 5 0, 65 66 + + 5 ( + )( ) + 7,
Ejercicios y problemas. Ecuaciones de er y º grado Resuelve mentalmente las siguientes ecuaciones: 55 5 0 5/, 5/ 6 6 + /, 8 ( ) + ( ) 56 ( )( + ) 0, 57 ( ) + 0 0, / 58 6 5 0, 65 66 + + 5 ( + )( ) + 7,
= 10. = 2 h) 2x 5 = 3 4. = 1 3x. = 3 3 7x. Ecuaciones de primer y segundo grado y problemas. 1. Resuelve las siguientes ecuaciones de primer grado:
 Hoja de Ejercicios Ecuaciones de primer y segundo grado y problemas 1. Resuelve las siguientes ecuaciones de primer grado: a) x x1 b) x c) x 10 x d) 1x 1 1 x e) x 0 x1 f) x g) x1 x1 h) x x i) x x 1 j)
Hoja de Ejercicios Ecuaciones de primer y segundo grado y problemas 1. Resuelve las siguientes ecuaciones de primer grado: a) x x1 b) x c) x 10 x d) 1x 1 1 x e) x 0 x1 f) x g) x1 x1 h) x x i) x x 1 j)
ECUACIONES. Ejercicio nº 1.- Dada la ecuación: responde razonadamente:
 ECUACIONES Ejercicio nº 1.- Dada la ecuación: x 1 x 1 x 5 3x 7 responde razonadamente: a Qué valor obtienes si sustituyes x 3 en el primer miembro? b Qué obtienes si sustituyes x 3 en el segundo miembro?
ECUACIONES Ejercicio nº 1.- Dada la ecuación: x 1 x 1 x 5 3x 7 responde razonadamente: a Qué valor obtienes si sustituyes x 3 en el primer miembro? b Qué obtienes si sustituyes x 3 en el segundo miembro?
PROBLEMAS ALGEBRAICOS. 2) La diferencia entre los cuadrados de dos números consecutivos es 71. Calcula dichos números.
 PROBLEMAS ALGEBRAICOS 1) La suma de un número y su cuadrado es 4. Calcula dicho número. Sea dicho número La suma del nº y su cuadrado es 4: + = 4 1+ 13 1 = = 6 1± 1 4 ( 4) 1± 13 + 4 = 0 = = = 1 13 = =
PROBLEMAS ALGEBRAICOS 1) La suma de un número y su cuadrado es 4. Calcula dicho número. Sea dicho número La suma del nº y su cuadrado es 4: + = 4 1+ 13 1 = = 6 1± 1 4 ( 4) 1± 13 + 4 = 0 = = = 1 13 = =
Ecuaciones de Primer Grado
 Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
19 f) = (Sol: x = -3 )
 EJERCICIOS REPASO ÁLGEBRA con soluciones 1.- Resuelve las siguientes ecuaciones: x + a = 1 (Sol: x = 1 5x + 1 x + 5 x b = (Sol: x = 5 14 5 x x + 1 x + c + = (Sol: x = 0 6 x x + 1 x d = (Sol: x = -1 4 6
EJERCICIOS REPASO ÁLGEBRA con soluciones 1.- Resuelve las siguientes ecuaciones: x + a = 1 (Sol: x = 1 5x + 1 x + 5 x b = (Sol: x = 5 14 5 x x + 1 x + c + = (Sol: x = 0 6 x x + 1 x d = (Sol: x = -1 4 6
EJERCICIOS DE REPASO DE MATEMÁTICAS 1º ESO
 EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO EJERCICIOS DE NÚMEROS NATURALES. ( + 7) + 0. ( 0 ). 6 + 7 + 8. 8 + 6 + ( 6 ) +. 6 ( 70 + 0) 600 6. : + 7 7. + 9 + 8 8. 7 ( ) 66 9. ( + 7) 8 7 0. + 6 0. + ( 9 7)
EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO EJERCICIOS DE NÚMEROS NATURALES. ( + 7) + 0. ( 0 ). 6 + 7 + 8. 8 + 6 + ( 6 ) +. 6 ( 70 + 0) 600 6. : + 7 7. + 9 + 8 8. 7 ( ) 66 9. ( + 7) 8 7 0. + 6 0. + ( 9 7)
Departamento de Matemáticas. Nombre:.Grupo:..
 I.E.S. Mar Mediterráneo Matemáticas º E.S.O e) 2 [5 (7 2)] f) 22 - [5 - (8 - )] - 6 g) (-5) 2 - (-2) + (-) 6 h) 8 0 : 5 + 6 : 2 i) 5 : [2 + (2-7) + 5] j) 5 (8 - ) (2-7) 5 ( - 6) k) + 6 : 9 50 : [2 + (7
I.E.S. Mar Mediterráneo Matemáticas º E.S.O e) 2 [5 (7 2)] f) 22 - [5 - (8 - )] - 6 g) (-5) 2 - (-2) + (-) 6 h) 8 0 : 5 + 6 : 2 i) 5 : [2 + (2-7) + 5] j) 5 (8 - ) (2-7) 5 ( - 6) k) + 6 : 9 50 : [2 + (7
EJERCICIOS DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO. 2ª PARTE
 EJERCICIOS DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO. 2ª PARTE CURSO 2015/2016 NOMBRE: IES ALCARRIA BAJA. MONDÉJAR UNIDAD 5. LENGUAJE ALGEBRAICO 1º) Traduce a lenguaje algebraico los siguientes enunciados:
EJERCICIOS DE RECUPERACIÓN DE MATEMÁTICAS 2º ESO. 2ª PARTE CURSO 2015/2016 NOMBRE: IES ALCARRIA BAJA. MONDÉJAR UNIDAD 5. LENGUAJE ALGEBRAICO 1º) Traduce a lenguaje algebraico los siguientes enunciados:
El producto de dos números es 4, y la suma de sus cuadrados 17. Cuáles son esos números?
 TEMA 4: INECUACIONES Y SISTEMAS SISTEMAS DE ECUACIONES NO LINEALES Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado. La resolución de estos sistemas se
TEMA 4: INECUACIONES Y SISTEMAS SISTEMAS DE ECUACIONES NO LINEALES Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado. La resolución de estos sistemas se
1. 1. Calcula todos los divisores de los siguientes números, a partir de su descomposición en factores primos: a) 150 b) 60 c) 54 d) 196
 1. 1. Calcula todos los divisores de los siguientes números, a partir de su descomposición en factores primos: a) 150 b) 60 c) 54 d) 196 2. Opera usando las propiedades de las potencias: a) ( 5) 4 ( 2)
1. 1. Calcula todos los divisores de los siguientes números, a partir de su descomposición en factores primos: a) 150 b) 60 c) 54 d) 196 2. Opera usando las propiedades de las potencias: a) ( 5) 4 ( 2)
En la granja. En el centro comercial
 En la granja 1. En una granja se crían gallinas y conejos. Si se cuentan las cabezas, son 50, si las patas, son 134. Cuántos animales hay de cada clase? 2. Un granjero cuenta con un determinado número
En la granja 1. En una granja se crían gallinas y conejos. Si se cuentan las cabezas, son 50, si las patas, son 134. Cuántos animales hay de cada clase? 2. Un granjero cuenta con un determinado número
6Soluciones a los ejercicios y problemas PÁGINA 141
 PÁGINA Pág. E cuaciones sencillas Resuelve mentalmente. a) b) 6 c) 0 d) e) f) 9 g) h)9 i) 9 a) b) 9 c) d) e) 6 f) g) h) 6 i) Resuelve. a) b) 0 c) 9 9 d) e) 6 f) 8 g) 6 0 h) 8 i) 6 j) 9 6 k) l) 8 m) 6 n)
PÁGINA Pág. E cuaciones sencillas Resuelve mentalmente. a) b) 6 c) 0 d) e) f) 9 g) h)9 i) 9 a) b) 9 c) d) e) 6 f) g) h) 6 i) Resuelve. a) b) 0 c) 9 9 d) e) 6 f) 8 g) 6 0 h) 8 i) 6 j) 9 6 k) l) 8 m) 6 n)
Problemas. En la granja
 Problemas 1. Escribir una ecuación de segundo grado cuyas soluciones son: 3 y 2. 2. Determinar k de modo que las dos raíces de la ecuación x 2 kx+36=0 sean iguales. 3. La suma de dos números es 5 y su
Problemas 1. Escribir una ecuación de segundo grado cuyas soluciones son: 3 y 2. 2. Determinar k de modo que las dos raíces de la ecuación x 2 kx+36=0 sean iguales. 3. La suma de dos números es 5 y su
1.OPERACIONES CON NÚMEROS
 1.OPERACIONES CON NÚMEROS DECIMALES Y FRACCIONES 1. Expresa en forma de fracción: a) 37 6. b) 5 23. c) 7 0 38. OPERACIONES CON FRACCIONES 2. a) 8 ( 1 6 + 4 3 ) b) 3 4 1 2 5 8 + 3 16 c) 1 1 3 5 4 1 2 d)
1.OPERACIONES CON NÚMEROS DECIMALES Y FRACCIONES 1. Expresa en forma de fracción: a) 37 6. b) 5 23. c) 7 0 38. OPERACIONES CON FRACCIONES 2. a) 8 ( 1 6 + 4 3 ) b) 3 4 1 2 5 8 + 3 16 c) 1 1 3 5 4 1 2 d)
4.- Realiza las siguientes operaciones: a) 3,25 (8,23 4,2)
 MATEMÁTICAS.- PRIMER CURSO ESO. Repasa durante el verano estos objetivos, realiza estos ejercicios y preséntalos el día del examen de recuperación en Septiembre. La prueba de Septiembre serán ejercicios
MATEMÁTICAS.- PRIMER CURSO ESO. Repasa durante el verano estos objetivos, realiza estos ejercicios y preséntalos el día del examen de recuperación en Septiembre. La prueba de Septiembre serán ejercicios
EJERCICIOS Y PROBLEMAS PARA LA PREPARACIÓN DE LA PRUEBA DE MATEMÁTICAS CDI DE 3º ESO.
 EJERCICIOS Y PROBLEMAS PARA LA PREPARACIÓN DE LA PRUEBA DE MATEMÁTICAS CDI DE 3º ESO. INSTRUCCIONES Estos ejercicios y problemas se realizarán en casa para preparar las pruebas CDI, cada alumno dedicará
EJERCICIOS Y PROBLEMAS PARA LA PREPARACIÓN DE LA PRUEBA DE MATEMÁTICAS CDI DE 3º ESO. INSTRUCCIONES Estos ejercicios y problemas se realizarán en casa para preparar las pruebas CDI, cada alumno dedicará
1. Números naturales y enteros
 . Números naturales y enteros EJERCICIO. Resuelve las siguientes operaciones con números enteros: 7 9 + + 7 + = 7 + + 8 = EJERCICIO. Calcula los siguientes productos y divisiones de números enteros: (
. Números naturales y enteros EJERCICIO. Resuelve las siguientes operaciones con números enteros: 7 9 + + 7 + = 7 + + 8 = EJERCICIO. Calcula los siguientes productos y divisiones de números enteros: (
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA
 RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
RELACIÓN DE EJERCICIOS DE GEOMETRÍA PLANA 1. Halla el perímetro y el área de las siguientes figuras: 2. Entre las dos diagonales de un rombo suman 100 cm, siendo la menor 20 cm más corta que la mayor.
(26)2x(3x 4) (1 3x)$(1 +x) = 2
 Resuelve las siguientes ecuaciones ECUACIONES, INECUACIONES Y SISTEMAS. (1)25x 4 29x 2 +4 =0 (2)x 4 5x 2 +4 =0 (3)x 4 a(a +b)x 2 +a 3 b =0 (4)(x 2 5)$(x 2 3) =0 (5)x +2 = 4x +13 (6) x 1 12 = 2 x+1 (7)
Resuelve las siguientes ecuaciones ECUACIONES, INECUACIONES Y SISTEMAS. (1)25x 4 29x 2 +4 =0 (2)x 4 5x 2 +4 =0 (3)x 4 a(a +b)x 2 +a 3 b =0 (4)(x 2 5)$(x 2 3) =0 (5)x +2 = 4x +13 (6) x 1 12 = 2 x+1 (7)
1f 2v 3v 4f 5v 6f 7v 8v 9v 10v 11v 12v 13f 14f 15v 16v 17v 18f 19v 20f 21v 22f 23v 5 - ( ) = -2 3(2 + 3(-7) + 25) = -27
 I CUESTIONES TEÓRICAS: 1f v 3v 4f 5v 6f 7v 8v 9v 10v 11v 1v 13f 14f 15v 16v 17v 18f 19v 0f 1v f 3v 4v 5f 6v 7f 8f 9v 30v 31f 3f 33v 34v 35f II OPERACIONES CON NÚMEROS RACIONALES. 1.- Calcula, paso a paso,
I CUESTIONES TEÓRICAS: 1f v 3v 4f 5v 6f 7v 8v 9v 10v 11v 1v 13f 14f 15v 16v 17v 18f 19v 0f 1v f 3v 4v 5f 6v 7f 8f 9v 30v 31f 3f 33v 34v 35f II OPERACIONES CON NÚMEROS RACIONALES. 1.- Calcula, paso a paso,
ACTIVIDADES INCLUIDAS EN LA PROPUESTA DIDÁCTICA: DE REFUERZO
 Pág. 1 ENUNCIADOS 1 Piensa, tantea y encuentra una solución para estas ecuaciones: a) 5 5 b) 5 1 c) 1 4 d) 1 e) 1 f ) 6 1 Despeja la incógnita y encuentra la solución: a) 6 b) 4 c) 7 d) 7 4 Resuelve las
Pág. 1 ENUNCIADOS 1 Piensa, tantea y encuentra una solución para estas ecuaciones: a) 5 5 b) 5 1 c) 1 4 d) 1 e) 1 f ) 6 1 Despeja la incógnita y encuentra la solución: a) 6 b) 4 c) 7 d) 7 4 Resuelve las
DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA SEPTIEMBRE. A los padres del alumno/a.. de 2º
 DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA SEPTIEMBRE A los padres del alumno/a.. de º de ESO Puesto que su hijo no ha superado los objetivos de º de ESO en el área de Matemáticas, es necesario que
DEPARTAMENTO DE MATEMÁTICAS PLAN DE TRABAJO PARA SEPTIEMBRE A los padres del alumno/a.. de º de ESO Puesto que su hijo no ha superado los objetivos de º de ESO en el área de Matemáticas, es necesario que
PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS
 PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS Matemáticas 2 Secundaria 5 Bimestre Prof. Héctor Lagunes Espinosa FECHA DE ENTREGA: 29 DE MAYO DEL 2015 Nombre: - Grado y Grupo: Nota: Escribe todos
PROYECTO # 2 SISTEMAS DE ECUACIONES CON LOS 4 MÉTODOS Matemáticas 2 Secundaria 5 Bimestre Prof. Héctor Lagunes Espinosa FECHA DE ENTREGA: 29 DE MAYO DEL 2015 Nombre: - Grado y Grupo: Nota: Escribe todos
Sistema de ecuaciones e inecuaciones
 5 Sistema de ecuaciones e inecuaciones 1. Sistemas lineales. Resolución gráfica Piensa y calcula Indica, en cada caso, cómo son las rectas y en qué puntos se cortan: c) r r s P r s s Las rectas r y s son
5 Sistema de ecuaciones e inecuaciones 1. Sistemas lineales. Resolución gráfica Piensa y calcula Indica, en cada caso, cómo son las rectas y en qué puntos se cortan: c) r r s P r s s Las rectas r y s son
Ejercicios de ecuaciones y sistemas
 Ejercicios de ecuaciones y sistemas 1 Resuelve las siguientes ecuaciones: 1 7x 2 + 21x 28 = 0 2 x 2 + 4x 7 = 0 3 12x 2 3x = 0 4 2 Halla las soluciones de las ecuaciones: 1 2 3Resuelve: 4 1 x 61x 2 + 900
Ejercicios de ecuaciones y sistemas 1 Resuelve las siguientes ecuaciones: 1 7x 2 + 21x 28 = 0 2 x 2 + 4x 7 = 0 3 12x 2 3x = 0 4 2 Halla las soluciones de las ecuaciones: 1 2 3Resuelve: 4 1 x 61x 2 + 900
π. C. Calcula la fracción generatriz de los siguientes decimales periódicos:
 NÚMEROS RACIONALES e IRRACIONALES A. Clasifica los siguientes números situándolos en el siguiente diagrama en el conjunto correspondiente:!!. π Q R Z B. Calcula y simplifica: C. Calcula la fracción generatriz
NÚMEROS RACIONALES e IRRACIONALES A. Clasifica los siguientes números situándolos en el siguiente diagrama en el conjunto correspondiente:!!. π Q R Z B. Calcula y simplifica: C. Calcula la fracción generatriz
NOMBRE: 1. Redondea a las centenas de mil los siguientes números:
 NOMBRE: 1. Redondea a las centenas de mil los siguientes números: a) 6 342 567 b) 12 535 000 c) 542 657 000 d) 67 584 000 2. Si a = 2 3 3 5 7; b = 2 4 3 2 5 7 y c = 2 3 5 7, averigua: a) Si b es múltiplo
NOMBRE: 1. Redondea a las centenas de mil los siguientes números: a) 6 342 567 b) 12 535 000 c) 542 657 000 d) 67 584 000 2. Si a = 2 3 3 5 7; b = 2 4 3 2 5 7 y c = 2 3 5 7, averigua: a) Si b es múltiplo
MATEMÁTICAS PENDIENTES 3º ESO EJERCICIOS PRUEBA I
 Ejercicio nº 1.- MATEMÁTICAS PENDIENTES º ESO EJERCICIOS PRUEBA I a) Clasifica como naturales, enteros, racionales o irracionales los siguientes números: ) 1 1, 1, b) Representa sobre la recta los números:
Ejercicio nº 1.- MATEMÁTICAS PENDIENTES º ESO EJERCICIOS PRUEBA I a) Clasifica como naturales, enteros, racionales o irracionales los siguientes números: ) 1 1, 1, b) Representa sobre la recta los números:
NOMBRE Y APELLIDOS: debe medir el tercero para que ese triángulo sea un triángulo rectángulo?
 FICHA REFUERZO TEMA 8: TEOREMA DE PITAGORAS. SEMEJANZA. CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Los dos lados menores de un triángulo miden 8 cm y 15 cm. Cuánto debe medir el tercero para que
FICHA REFUERZO TEMA 8: TEOREMA DE PITAGORAS. SEMEJANZA. CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Los dos lados menores de un triángulo miden 8 cm y 15 cm. Cuánto debe medir el tercero para que
MATEMÁTICAS 2º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: Ejercicio nº 2.-
 MATEMÁTICAS º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: 5 6 1, 45 7 19 4 5, 5 1 4 9 Ejercicio nº.- Sitúa cada número (entero o natural) en el conjunto que
MATEMÁTICAS º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: 5 6 1, 45 7 19 4 5, 5 1 4 9 Ejercicio nº.- Sitúa cada número (entero o natural) en el conjunto que
Geometría. 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento?
 Geometría 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento? 2 a.- Qué originan dos puntos en una recta?. Cuántas rectas pasan por dos puntos?, y por un punto?
Geometría 1 a.- Qué diferencia hay entre una recta y una semirrecta?, y entre una semirrecta y un segmento? 2 a.- Qué originan dos puntos en una recta?. Cuántas rectas pasan por dos puntos?, y por un punto?
Ecuaciones de 1er y 2º grado
 Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Problemas (ecuaciones de primer grado)
 Problemas (ecuaciones de primer grado) 1. La suma de tres números naturales consecutivos es igual al quíntuplo del menor menos 11. Qué números son? 2. Reparte 721 entre 3 personas teniendo en cuenta que
Problemas (ecuaciones de primer grado) 1. La suma de tres números naturales consecutivos es igual al quíntuplo del menor menos 11. Qué números son? 2. Reparte 721 entre 3 personas teniendo en cuenta que
MATEMÁTICAS 2º ESO 1. a) x+2 = 5 b) x+3 = 2 c) x-1 = 5 d) x-3 = 4 e) x-1 = 1 f) 3x = 6 g) 5x = 15 h) i)
 MATEMÁTICAS 2º ESO 1 1) Asocia cada enunciado con la ecuación que lo epresa algebraicamente: a) La tercera parte de un número es igual a su cuarta parte más una unidad. b) La edad de Antonio es el triple
MATEMÁTICAS 2º ESO 1 1) Asocia cada enunciado con la ecuación que lo epresa algebraicamente: a) La tercera parte de un número es igual a su cuarta parte más una unidad. b) La edad de Antonio es el triple
7. Sistemas de ecuaciones lineales
 76 SOLUCIONARIO 7. Sistemas de ecuaciones lineales 1. SISTEMAS LINEALES. RESOLUCIÓN GRÁFICA PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul del dibujo? s r 3. Aplica el criterio que relaciona
76 SOLUCIONARIO 7. Sistemas de ecuaciones lineales 1. SISTEMAS LINEALES. RESOLUCIÓN GRÁFICA PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul del dibujo? s r 3. Aplica el criterio que relaciona
Ecuación de primer grado con una incógnita. Ejercicios y Solucionario
 Ecuación de primer grado con una incógnita. Ejercicios y Solucionario 1. Traduce al lenguaje algebraico las siguientes frases: a) la mitad de un número más ocho. b) el doble de un número menos su mitad
Ecuación de primer grado con una incógnita. Ejercicios y Solucionario 1. Traduce al lenguaje algebraico las siguientes frases: a) la mitad de un número más ocho. b) el doble de un número menos su mitad
TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS...
 TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS... 1ª Realizar las siguientes divisiones: a) 345,83 : 6 = b) 23 : 0, 5 = c) 0,18 : 0,12 = d) 34,15 : 5 = e) 2,16 : 1,8 = f) 13,02 : 0,25=
TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS... 1ª Realizar las siguientes divisiones: a) 345,83 : 6 = b) 23 : 0, 5 = c) 0,18 : 0,12 = d) 34,15 : 5 = e) 2,16 : 1,8 = f) 13,02 : 0,25=
MATEMÁTICAS 6º PRIMARIA
 CUADERNO DE ACTIVIDADES MATEMÁTICAS 6º PRIMARIA Nombre: Curso: 1 Descompón estos números. Fíjate en el ejemplo. 4.168 = 4 UM + 1 C + 6 D + 8 U 51.245 = 754.390 = 3.790.050 = 2 Rodea con rojo los múltiplos
CUADERNO DE ACTIVIDADES MATEMÁTICAS 6º PRIMARIA Nombre: Curso: 1 Descompón estos números. Fíjate en el ejemplo. 4.168 = 4 UM + 1 C + 6 D + 8 U 51.245 = 754.390 = 3.790.050 = 2 Rodea con rojo los múltiplos
Proporcionalidad y porcentaje
 160.- Resuelve como en el ejemplo. 5 x 5 = 5 2 = 25 4 x 4 = = 7 x 7 = = 12 x 12 = = 9 x 9 = = 13 x 13 = = Proporcionalidad y porcentaje 161.- Completa las tablas de proporcionalidad.... 12 14 16 18 20
160.- Resuelve como en el ejemplo. 5 x 5 = 5 2 = 25 4 x 4 = = 7 x 7 = = 12 x 12 = = 9 x 9 = = 13 x 13 = = Proporcionalidad y porcentaje 161.- Completa las tablas de proporcionalidad.... 12 14 16 18 20
EJERCICIOS DE REPASO DE MATEMÁTICAS 2º ESO GEOMETRÍA
 EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO GEOMETRÍA. Halla el área de un triángulo equilátero de lado cm. R) A 0, cm. Halla el área de un hexágono regular de lado cm. R) A,6 cm. La superficie de una mesa
EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO GEOMETRÍA. Halla el área de un triángulo equilátero de lado cm. R) A 0, cm. Halla el área de un hexágono regular de lado cm. R) A,6 cm. La superficie de una mesa
2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I. 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es?
 2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I PÁGINA 142 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es? 3x 8 = 25 Solución: 11 Si a cierta cantidad le restas su tercera parte y le sumas
2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I PÁGINA 142 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es? 3x 8 = 25 Solución: 11 Si a cierta cantidad le restas su tercera parte y le sumas
Matemáticas 3º E.S.O. 2014/15
 Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
Matemáticas 3º E.S.O. 2014/15 TEMA 5: Figuras planas Ficha número 16 1.- Calcula la altura del siguiente triángulo: (Sol: 12,12 cm) 2.- En un triángulo isósceles la altura sobre el lado desigual mide 50
Actividades de la 1ª Evaluación para alumnos con Matematicas Pendientes de 2º ESO
 Actividades de la 1ª Evaluación para alumnos con Matematicas Pendientes de º ESO FECHA DEL EXAMEN: 17 DE NOVIEMBRE DE 01 A LAS 10:1 (En el salón de actos) Las actividades realizadas deben entregarse obligatoriamente
Actividades de la 1ª Evaluación para alumnos con Matematicas Pendientes de º ESO FECHA DEL EXAMEN: 17 DE NOVIEMBRE DE 01 A LAS 10:1 (En el salón de actos) Las actividades realizadas deben entregarse obligatoriamente
DIVERSIFICACIÓN CURRICULAR
 ECUACIONES DE SEGUNDO GRADO Una ecuación de segundo grado es aquella que puede reducirse a la forma. donde no se anula a. Si observamos los coeficientes b y c, las podemos clasificar en incompletas si
ECUACIONES DE SEGUNDO GRADO Una ecuación de segundo grado es aquella que puede reducirse a la forma. donde no se anula a. Si observamos los coeficientes b y c, las podemos clasificar en incompletas si
PROBLEMAS. 2. La diferencia entre los cuadrados de dos números consecutivos es 17. Cuáles son dichos números?. Sol: 8 y 9
 PROBLEMAS. 1. Una pluma y su carga cuestan juntas 6 euros. La pluma cuesta cuatro euros más que la carga. Cuánto cuesta la pluma y cuánto cuesta la carga?. Sol: 5, 1 euros 2. La diferencia entre los cuadrados
PROBLEMAS. 1. Una pluma y su carga cuestan juntas 6 euros. La pluma cuesta cuatro euros más que la carga. Cuánto cuesta la pluma y cuánto cuesta la carga?. Sol: 5, 1 euros 2. La diferencia entre los cuadrados
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 167 EJERCICIOS Resolución gráfica 1 Observa el gráfico y responde: + y = 15 + y = 1 + y = 1 + y = 7 a) Escribe un sistema de ecuaciones lineales que tenga por solución = 5, y = 6. Escribe
Pág. 1 PÁGINA 167 EJERCICIOS Resolución gráfica 1 Observa el gráfico y responde: + y = 15 + y = 1 + y = 1 + y = 7 a) Escribe un sistema de ecuaciones lineales que tenga por solución = 5, y = 6. Escribe
1. Calcula: a) = b) : 82 =
 MATEMÁTICAS 1º ESO ACTIVIDADES de REPASO 1. Calcula: a) 906 5437 b) 572934 : 82 2. Un transportista carga en su motocarro 4 televisores y 3 minicadenas musicales. Si cada televisor pesa como 3 minicadenas
MATEMÁTICAS 1º ESO ACTIVIDADES de REPASO 1. Calcula: a) 906 5437 b) 572934 : 82 2. Un transportista carga en su motocarro 4 televisores y 3 minicadenas musicales. Si cada televisor pesa como 3 minicadenas
Ecuaciones. 2x + 3 = 5x 2. 2x + 1 = 2 (x + 1) 2x + 1 = 2x x + 2 = 2 (x + 1) 2x + 2 = 2x = 2. x + 1 = 2 x = 1
 Ecuaciones Igualdad Una IGUALDAD se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2. Cierta 2x + 2 = 2 (x + 1)
Ecuaciones Igualdad Una IGUALDAD se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2. Cierta 2x + 2 = 2 (x + 1)
2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6
 ACTIVIDADES TEMA 1 1.- Escribe con palabras los siguientes números: 1.034.456: 20.004.080: 100.060.201: 35.001.001: 2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6 3.- Ordena de
ACTIVIDADES TEMA 1 1.- Escribe con palabras los siguientes números: 1.034.456: 20.004.080: 100.060.201: 35.001.001: 2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6 3.- Ordena de
Tema: Ecuaciones, inecuaciones y sistemas
 y sistemas. MateB ºESO Tema: Ecuaciones, inecuaciones y sistemas 1. Las siguientes ecuaciones tienen alguna solución entera. Intenta encontrarlas tanteando. Qué tipo de ecuación es cada una?. a) x + 6
y sistemas. MateB ºESO Tema: Ecuaciones, inecuaciones y sistemas 1. Las siguientes ecuaciones tienen alguna solución entera. Intenta encontrarlas tanteando. Qué tipo de ecuación es cada una?. a) x + 6
SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD
 SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD Ejercicio nº 1.- Subraya los pares de magnitudes que sean proporcionales: a) El peso de las naranjas compradas y el precio pagado por ellas. b) La estatura
SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD Ejercicio nº 1.- Subraya los pares de magnitudes que sean proporcionales: a) El peso de las naranjas compradas y el precio pagado por ellas. b) La estatura
Tema 15. Perímetros y áreas
 Matemáticas Ejercicios 1º ESO BLOQUE V: GEOMETRÍA Tema 15. Perímetros y áreas 1. Expresa en metros: a) 2000 mm b) 2 hm c) 1 dm e) 0,1 km c) 50 dam 2 d) 0,02 km 2 2. Transforma las siguientes unidades:
Matemáticas Ejercicios 1º ESO BLOQUE V: GEOMETRÍA Tema 15. Perímetros y áreas 1. Expresa en metros: a) 2000 mm b) 2 hm c) 1 dm e) 0,1 km c) 50 dam 2 d) 0,02 km 2 2. Transforma las siguientes unidades:
MATEMÁTICAS 1º ESO. Operaciones con números enteros y fraccionarios, potencias y raíces
 COLEGIO MARÍA INMACULADA - CARCAIXENT DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 1º ESO Operaciones con números enteros y fraccionarios, potencias y raíces 1. Realiza las siguientes operaciones: 2. Realiza
COLEGIO MARÍA INMACULADA - CARCAIXENT DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 1º ESO Operaciones con números enteros y fraccionarios, potencias y raíces 1. Realiza las siguientes operaciones: 2. Realiza
1º.- Halla el área y el perímetro de las siguientes figuras, calculando previamente el elemento que falta:
 Matemáticas 3º E.S.O. pág. 1 HOJA 1: GEOMETRÍA 1º.- Halla el área y el perímetro de las siguientes figuras, calculando previamente el elemento que falta: 2º.- Halla el área de las figuras marcadas: 3º.-
Matemáticas 3º E.S.O. pág. 1 HOJA 1: GEOMETRÍA 1º.- Halla el área y el perímetro de las siguientes figuras, calculando previamente el elemento que falta: 2º.- Halla el área de las figuras marcadas: 3º.-
Tema 1 Fracciones y decimales
 Código 80986 Curso 016-17 MATEMÁTICAS ACADÉMICAS º ESO (EJERCICIOS DE REPASO) Tema 1 Fracciones y decimales 1. que sean mayores que 1 o menores que 1 en parte entera y parte fraccionaria. fracciones que
Código 80986 Curso 016-17 MATEMÁTICAS ACADÉMICAS º ESO (EJERCICIOS DE REPASO) Tema 1 Fracciones y decimales 1. que sean mayores que 1 o menores que 1 en parte entera y parte fraccionaria. fracciones que
1. a) Qué significa una potencia de exponente negativo?... ; b)
 MATEMÁTICAS - SEPTIEMBRE TAREA DE VERANO 4º E.S.O.-B 1. a) Qué significa una potencia de eponente negativo?..... b) Simplificar: b 1) : b 4 ) b ) 9 1 b 4) 1 4. Simplificar potencias: a) 4 ( ) d) 9000 0'000000006
MATEMÁTICAS - SEPTIEMBRE TAREA DE VERANO 4º E.S.O.-B 1. a) Qué significa una potencia de eponente negativo?..... b) Simplificar: b 1) : b 4 ) b ) 9 1 b 4) 1 4. Simplificar potencias: a) 4 ( ) d) 9000 0'000000006
GUÍA DE TRABAJO N 3 ECUACIONES
 GUÍA DE TRABAJO N ECUACIONES Durante cientos de años, uno de los tópicos mas importantes en Álgebra ha sido la resolución de ecuaciones; sobre todo por las aplicaciones que tienen en campos científicos
GUÍA DE TRABAJO N ECUACIONES Durante cientos de años, uno de los tópicos mas importantes en Álgebra ha sido la resolución de ecuaciones; sobre todo por las aplicaciones que tienen en campos científicos
EJERCICIOS DE SISTEMAS DE ECUACIONES
 EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
EJERCICIOS RECUPERACIÓN MATEMÁTICAS 2º ESO
 NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
1 Descomponer en factores
 Divisibilidad (T 1 ) SOLUCIONES 1 Descomponer en factores 1 216 216 = 2 3 3 3 2 360 360 = 2 3 3 2 5 3 432 432 = 2 4 3 3 2 Descomponer en factores 12250 2250 = 2 3 2 5 3 23500 3500 = 2 2 5 3 7 32520 2 520
Divisibilidad (T 1 ) SOLUCIONES 1 Descomponer en factores 1 216 216 = 2 3 3 3 2 360 360 = 2 3 3 2 5 3 432 432 = 2 4 3 3 2 Descomponer en factores 12250 2250 = 2 3 2 5 3 23500 3500 = 2 2 5 3 7 32520 2 520
SISTEMAS DE ECUACIONES Y DE INECUACIONES
 Sistemas de Ecuaciones de Inecuaciones Departamento de Matemáticas SISTEMAS DE ECUACIONES Y DE INECUACIONES SISTEMAS LINEALES. - Resuelve por sustitución e igualación los siguientes sistemas: a) c) b)
Sistemas de Ecuaciones de Inecuaciones Departamento de Matemáticas SISTEMAS DE ECUACIONES Y DE INECUACIONES SISTEMAS LINEALES. - Resuelve por sustitución e igualación los siguientes sistemas: a) c) b)
NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO
 NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO 1. Responde a las preguntas y justifica tu respuesta: a) El número 14 es divisor de 56? Explica por qué. b) El número 310 es múltiplo de 31? Explica por qué.
NOMBRE Y APELLIDOS REPASO DE MATEMÁTICAS 1ºESO 1. Responde a las preguntas y justifica tu respuesta: a) El número 14 es divisor de 56? Explica por qué. b) El número 310 es múltiplo de 31? Explica por qué.
2º. Rellena los huecos que faltan y determina la constante de proporcionalidad:
 TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO ª EVALUACIÓN CURSO: 3º ESO PROPORCIONALIDAD NUMÉRICA 1º. Busca los valores para que las siguientes proporciones sean ciertas:... 0 45 5 45 5............,...
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO ª EVALUACIÓN CURSO: 3º ESO PROPORCIONALIDAD NUMÉRICA 1º. Busca los valores para que las siguientes proporciones sean ciertas:... 0 45 5 45 5............,...
ECUACIONES DE PRIMER GRADO
 ECUACIONES DE PRIMER GRADO 1.- Comprueba si los valores indicados son soluciones de las ecuaciones correspondientes: a) x 2 de 3x + 3 1 b) x l de + x 2 3x + 5 x + 2 1 x c) x 2 de 1 3 3 x 2 6 d) x 6 de
ECUACIONES DE PRIMER GRADO 1.- Comprueba si los valores indicados son soluciones de las ecuaciones correspondientes: a) x 2 de 3x + 3 1 b) x l de + x 2 3x + 5 x + 2 1 x c) x 2 de 1 3 3 x 2 6 d) x 6 de
10 SEMEJANZA. TEOREMA DE PITÁGORAS EJERCICIOS
 0 SEMEJNZ. TEOREM DE PITÁGORS EJERCICIOS Indica qué rectángulos son semejantes: a) ase cm, altura cm y base 0 cm, altura cm. b) ase 0 m, altura m y base 0 m, altura 8 m. c) ase 0,7 dm, altura 0, dm y base,0
0 SEMEJNZ. TEOREM DE PITÁGORS EJERCICIOS Indica qué rectángulos son semejantes: a) ase cm, altura cm y base 0 cm, altura cm. b) ase 0 m, altura m y base 0 m, altura 8 m. c) ase 0,7 dm, altura 0, dm y base,0
tema 6: ecuaciones curso 2010/2011
 nombre: ecuaciones apellidos: Una ecuación es un igualdad entre expresiones algebraicas expresión algebraica 1 = expresión algebraica 2 En una ecuación hay dos miembros separados por un signo igual =.
nombre: ecuaciones apellidos: Una ecuación es un igualdad entre expresiones algebraicas expresión algebraica 1 = expresión algebraica 2 En una ecuación hay dos miembros separados por un signo igual =.
REFUERZO - MATEMÁTICAS OBJETIVOS MÍNIMOS
 OBJETIVOS MÍNIMOS Realizar operaciones con números enteros [ ] a) 18 ( 8 ) b) [ 1 ( 1 ) ] c) [ ( 8 9) ] 7 ( ) [ ] Realizar operaciones con fracciones 7 1 a) 1 1 b) c) : 1 7 7 1 1 d) : 1 1 e) 1 : 10 1 f)
OBJETIVOS MÍNIMOS Realizar operaciones con números enteros [ ] a) 18 ( 8 ) b) [ 1 ( 1 ) ] c) [ ( 8 9) ] 7 ( ) [ ] Realizar operaciones con fracciones 7 1 a) 1 1 b) c) : 1 7 7 1 1 d) : 1 1 e) 1 : 10 1 f)
3º ESO. ACTIVIDADES DE RECUPERACIÓN
 º ESO. ACTIVIDADES DE RECUPERACIÓN. Opera: [ 7 ( )] (7 ) ( ) :( ) ( ) f) 7 9 c) d) e) 9 : 9 : g) h). Calcula utilizando las propiedades de las potencias. Deja el resultado en forma de potencia: 8 9 9 c)
º ESO. ACTIVIDADES DE RECUPERACIÓN. Opera: [ 7 ( )] (7 ) ( ) :( ) ( ) f) 7 9 c) d) e) 9 : 9 : g) h). Calcula utilizando las propiedades de las potencias. Deja el resultado en forma de potencia: 8 9 9 c)
I.E.S. Miguel de Cervantes (Granada) Departamento de Matemáticas GBG 1
 ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
TRABAJO DE REPASO PARA 2º ESO
 TRABAJO DE REPASO PARA º ESO NOTA: EL TRABAJO SE ENTREGARÁ EL DÍA DEL EXAMEN DE SEPTIEMBRE. PUEDE SUBIR HASTA UN PUNTO LA NOTA, SIEMPRE Y CUANDO EN EL EXAMEN TENGAS UNA NOTA ENTRE 4 Y. RECUERDA QUE TAMBIÉN
TRABAJO DE REPASO PARA º ESO NOTA: EL TRABAJO SE ENTREGARÁ EL DÍA DEL EXAMEN DE SEPTIEMBRE. PUEDE SUBIR HASTA UN PUNTO LA NOTA, SIEMPRE Y CUANDO EN EL EXAMEN TENGAS UNA NOTA ENTRE 4 Y. RECUERDA QUE TAMBIÉN
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
Problemas Tema 1 Enunciados de problemas de Repaso 4ºESO
 página / Problemas Tema Enunciados de problemas de Repaso 4ºESO Hoja. Calcula las medidas de un rectángulo cuya superficie es de 40 metros cuadrados, sabiendo que el largo es 6 metros mayor que el triple
página / Problemas Tema Enunciados de problemas de Repaso 4ºESO Hoja. Calcula las medidas de un rectángulo cuya superficie es de 40 metros cuadrados, sabiendo que el largo es 6 metros mayor que el triple
Solución: a) x = 5 b) x = 4 c) x = ± 9 d) x = 0, x = 2. 3x + 7 24. Solución: x = 1. 2x 2 3x = 0. Solución: = 0, x 2. 5x 2 14x 3 = 0.
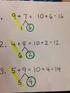
 Resolución de ecuaciones. Ecuaciones de er y º grado Resuelve mentalmente las siguientes ecuaciones: a) + 8 b) 0 c) 8 d) ( ) 0 P I E N S A Y C A L C U L A a) b) c) ± 9 d) 0, Resuelve las siguientes ecuaciones:
Resolución de ecuaciones. Ecuaciones de er y º grado Resuelve mentalmente las siguientes ecuaciones: a) + 8 b) 0 c) 8 d) ( ) 0 P I E N S A Y C A L C U L A a) b) c) ± 9 d) 0, Resuelve las siguientes ecuaciones:
TEMA 05 - EXPRESIONES ALGEBRAICAS
 º ESO TEMA 05 - EXPRESIONES ALGEBRAICAS 1º. Indica las expresiones algebraicas correspondientes a los siguientes enunciados, utilizando una sola letra (x): a) El siguiente de un número, más tres unidades.
º ESO TEMA 05 - EXPRESIONES ALGEBRAICAS 1º. Indica las expresiones algebraicas correspondientes a los siguientes enunciados, utilizando una sola letra (x): a) El siguiente de un número, más tres unidades.
EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 2007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B
 EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B ) Clasifica los siguientes números como naturales, enteros, racionales e irracionales,
EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B ) Clasifica los siguientes números como naturales, enteros, racionales e irracionales,
EJERCICIOS DE MATEMÁTICAS PENDIENTES DE 3º ESO (BLOQUE I)
 -- EJERCICIOS DE MATEMÁTICAS PENDIENTES DE º ESO (BLOQUE I.- Ordena las fracciones 0 0 y.- Simplifica 000 000 0 0 8 0.- Representa gráficamente 0.- Calcula y simplifica ( ( h g f e d c b a.- Una revista
-- EJERCICIOS DE MATEMÁTICAS PENDIENTES DE º ESO (BLOQUE I.- Ordena las fracciones 0 0 y.- Simplifica 000 000 0 0 8 0.- Representa gráficamente 0.- Calcula y simplifica ( ( h g f e d c b a.- Una revista
4. Escribe la fracción generatriz e indica de que tipo es cada número decimal. a. 7. b. 0.16
 REPASO NÚMEROS REALES, POTENCIAS Y RAÍCES 3ºESO Alumno/a : 1. Dibuja un diagrama que exprese las relaciones existentes entre cada uno de los conjuntos numéricos. Indica el conjunto numérico más pequeño
REPASO NÚMEROS REALES, POTENCIAS Y RAÍCES 3ºESO Alumno/a : 1. Dibuja un diagrama que exprese las relaciones existentes entre cada uno de los conjuntos numéricos. Indica el conjunto numérico más pequeño
TRABAJO DE RECUPERACIÓN MATEMÁTICAS 1º ESO TEMA 1 : LOS NÚMEROS NATURALES. 1. Escribe en números romanos las siguientes cantidades: a) 42.
 TRABAJO DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO: TEMA 1 : LOS NÚMEROS NATURALES 1. Escribe en números romanos las siguientes cantidades: a) 42 b) 159 c) 520 2. Escribe como se leen estas cantidades:
TRABAJO DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO: TEMA 1 : LOS NÚMEROS NATURALES 1. Escribe en números romanos las siguientes cantidades: a) 42 b) 159 c) 520 2. Escribe como se leen estas cantidades:
EJERCICIOS DE RECUPERACIÓN
 EJERCICIOS DE RECUPERACIÓN EJERCICIOS DE RECUPERACIÓN DE LA 1ª EVALUACIÓN Números Enteros 1º. Haz las siguientes sumas: a) (+10) + (+5) = b) (+7) + (+6) = c) ( 4) + ( 6) = d) ( 10) + ( 5) = e) ( 7) + (
EJERCICIOS DE RECUPERACIÓN EJERCICIOS DE RECUPERACIÓN DE LA 1ª EVALUACIÓN Números Enteros 1º. Haz las siguientes sumas: a) (+10) + (+5) = b) (+7) + (+6) = c) ( 4) + ( 6) = d) ( 10) + ( 5) = e) ( 7) + (
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 2º E.S.O. PENDIENTES 2º PARCIAL
 de º de E.S.O. (º Parcial) EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE º E.S.O. PENDIENTES º PARCIAL Fecha tope para entregarlos: 17 de abril de 015 Examen el 3 de abril de 015 I.E.S.
de º de E.S.O. (º Parcial) EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE º E.S.O. PENDIENTES º PARCIAL Fecha tope para entregarlos: 17 de abril de 015 Examen el 3 de abril de 015 I.E.S.
Halla los siguientes perímetros y áreas:
 73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
a) Las mediatrices de un triángulo se cortan en un punto llamado... b) Las bisectrices de un triángulo se cortan en un punto llamado...
 Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
Geometría Plana 3º E.S.O. PARTE TEÓRICA 1.- Define para un triángulo los siguientes conceptos: Mediatriz: Bisectriz: Mediana: Altura: 2.- Completa las siguientes frases: a) Las mediatrices de un triángulo
6Soluciones a los ejercicios y problemas PÁGINA 133
 PÁGINA 33 Pág. P RACTICA Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = 4 3x 4y = 0 a) b) 5x + y = 0 4x + 3y = 5 x y = 4 a) ( ) = 5? 4 No es solución. 5x + y = 0 5 =
PÁGINA 33 Pág. P RACTICA Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = 4 3x 4y = 0 a) b) 5x + y = 0 4x + 3y = 5 x y = 4 a) ( ) = 5? 4 No es solución. 5x + y = 0 5 =
PROBLEMAS DE SISTEMAS DE ECUACIONES
 PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
2.- Ecuaciones de primer grado
 3º ESO E UNIDAD 8.- ECUACIONES. SISTEMAS DE ECUACIONES PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------
3º ESO E UNIDAD 8.- ECUACIONES. SISTEMAS DE ECUACIONES PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------
EJERCICIOS DE EXPRESIONES ALGEBRAICAS
 EJERCICIOS DE EXPRESIONES ALGEBRAICAS Ejercicio nº.- Epresa en lenguaje algebraico cada uno de los siguientes enunciados: a El 0% de un número. b El área de un rectángulo de base cm y altura desconocida.
EJERCICIOS DE EXPRESIONES ALGEBRAICAS Ejercicio nº.- Epresa en lenguaje algebraico cada uno de los siguientes enunciados: a El 0% de un número. b El área de un rectángulo de base cm y altura desconocida.
TEMA 5 ECUACIONES 2 2, 17
 TEMA ECUACINES.1 Ecuaciones. Solución de una ecuación. ACTIVIDADES DE LA PÁGINA 94 1. Es solución de alguna de las siguientes ecuaciones?. Justifica tu respuesta. a. x 3 11x 1 Sustituimos la incógnita
TEMA ECUACINES.1 Ecuaciones. Solución de una ecuación. ACTIVIDADES DE LA PÁGINA 94 1. Es solución de alguna de las siguientes ecuaciones?. Justifica tu respuesta. a. x 3 11x 1 Sustituimos la incógnita
DEPARTAMENTO DE MATEMATICAS
 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
2. Un padre tiene 35 años y su hijo 5. Al cabo de cuántos años será la edad del padre tres veces mayor que la edad del hijo?
 TEMA 5: ECUACIONES Y SISTEMAS LINEALES DE ECUACIONES ECUACIONES DE PRIMER GRADO Una ecuación es una igualdad algebraica en la que interviene una letra llamada incógnita. El objetivo es descubrir el valor
TEMA 5: ECUACIONES Y SISTEMAS LINEALES DE ECUACIONES ECUACIONES DE PRIMER GRADO Una ecuación es una igualdad algebraica en la que interviene una letra llamada incógnita. El objetivo es descubrir el valor
CENAFE MATEMÁTICAS POLÍGONOS
 POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
Colegio Portocarrero. Curso Departamento de matemáticas. CUADERNO DE VERANO MATEMÁTICAS 1º ESO ALUMNO:
 Colegio Portocarrero Curso 0-0 CUADERNO DE VERANO MATEMÁTICAS º ESO ALUMNO: Cuaderno de verano º ESO Colegio Portocarrero Curso 0-0 Antes de realizar el refuerzo, repasa los apuntes tomados en clase, pásalos
Colegio Portocarrero Curso 0-0 CUADERNO DE VERANO MATEMÁTICAS º ESO ALUMNO: Cuaderno de verano º ESO Colegio Portocarrero Curso 0-0 Antes de realizar el refuerzo, repasa los apuntes tomados en clase, pásalos
EJERCICIOS PARA PREPARAR LA CDI. Prof: F. López- D. Legal: M /2009 1
 EJERCICIOS PARA PREPARAR LA CDI. Rellena la tabla siguiente: Horas Minutos Segundos ½ hora y 0 minutos 90 minutos 600 segundos hora y cuarto 80 minutos 80 segundos horas 0 minutos 0 segundos 5 minutos
EJERCICIOS PARA PREPARAR LA CDI. Rellena la tabla siguiente: Horas Minutos Segundos ½ hora y 0 minutos 90 minutos 600 segundos hora y cuarto 80 minutos 80 segundos horas 0 minutos 0 segundos 5 minutos
TRABAJO DE MATEMÁTICAS B
 TRABAJO DE MATEMÁTICAS B º ESO NOTA: EL TRABAJO SE ENTREGARÁ EL DÍA DEL EXAMEN DE SEPTIEMBRE. PUEDE SUBIR HASTA UN PUNTO LA NOTA, SIEMPRE Y CUANDO EN EL EXAMEN TENGAS UNA NOTA ENTRE Y. RECUERDA QUE TAMBIÉN
TRABAJO DE MATEMÁTICAS B º ESO NOTA: EL TRABAJO SE ENTREGARÁ EL DÍA DEL EXAMEN DE SEPTIEMBRE. PUEDE SUBIR HASTA UN PUNTO LA NOTA, SIEMPRE Y CUANDO EN EL EXAMEN TENGAS UNA NOTA ENTRE Y. RECUERDA QUE TAMBIÉN
ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II. Unidad 1: Percibimos y representamos los objetos
 ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II Unidad 1: Percibimos y representamos los objetos 1.- Descripción de las figuras geométricas en el plano. Clasificación de triángulos y cuadriláteros.
ESPA: Ámbito Científico Tecnológico Nivel I - Módulo II Unidad 1: Percibimos y representamos los objetos 1.- Descripción de las figuras geométricas en el plano. Clasificación de triángulos y cuadriláteros.
