1.1.- Concepto Definición de cono Definición de función homogénea Interpretación económica de la función homogénea
|
|
|
- Eduardo Coronel Castilla
- hace 8 años
- Vistas:
Transcripción
1 Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas) Suma de fucoes homogéeas Produco de u escalar por ua fucó homogéea Combacó leal de fucoes homogéeas Produco de fucoes homogéeas Cocee de fucoes homogéeas Dervacó de ua fucó homogéea Reduccó a ua fucó de (-) varables.- Teorema de Euler. Ierpreacó ecoómca...- Teorema de Euler..- Teorema de Euler y eoría de la dsrbucó Problemas resuelos Problemas propuesos Bblografía - -
2 Fucoes homogéeas FUNCIONES HOMOGÉNEAS. Cocepo y Propedades..- Cocepo Defcó de coo (e u espaco vecoral real) Se llama coo a odo cojuo C R que cumple la sguee codcó: Defcó de fucó homogéea C, C, >0. Dada ua fucó real de varables al que f: D R R, e dode su domo es u coo, se dce que es homogéea de grado r s verfca: f( ) r f(), D co >0, r R NOTA : Se ege que D sea u coo para garaar que D. NOTA : Jusfcacó de > 0: - Eva problemas de fala de defcó o eseca: Ejemplo : S f( ) r f(). r y < 0 f( ) R. - Ierpreacó ecoómca: Al rabajar co deermadas varables ecoómcas (cadades a cosumr, a emplear o a producr, por ejemplo), el sedo ecoómco mpoe su o egavdad, por lo que co > 0 se ee garaado que va a segur maeedo ese msmo sedo ecoómco. 0 y > 0 0 (sedo ecoómco). NOTA 3: r R r puede ser posvo o egavo; eero, racoal o rracoal. S r es eero (posvo o egavo), > 0 es ua resrccó superflua. El valor de r ee mporaca a la hora de la erpreacó ecoómca de fucoes homogéeas. Ejemplo : f(,y,) 3 + y. - -
3 Fucoes homogéeas Al raarse de ua fucó polómca, su domo es R 3, y por ao es u coo. f(, y, ) 3 + ( y)( ) (3 + y ). Esa fucó o es homogéea. Ejemplo : f(, y) + y. Su domo es el cojuo D{(,y) R /+y 0}, que es u coo, pues mulplcado la resrccó que cumple los puos (,y) D por ua cadad posva, >0, el sedo de la resrccó o camba (+y) 0 + y 0 ( )+( y) 0 (, y) D. Esudado s es homogéea:. f(, y) + y (+ y) + y f(,y) La fucó es homogéea de grado r. Ejemplo 3: y f(, y). + 3 y Su domo es el cojuo D R - {(0,0)}, que es u coo. Se esuda s es homogéea: ( ) ( y) f(, y) ( ) + 3( y) y + 3 y f(,y) Por ao, la fucó es homogéea de grado 0. Ejemplo : y y y ( + 3 y ) f(,y), (,y) D, > 0 r 0. f(, y) + y. Su domo ambé es el cojuo D {R - (0,0) }, que es u coo. - 3-
4 Fucoes homogéeas f(, y) ( ) + ( y) + y ( + y ) - f(,y) (,y) D, > 0 r -. Por ao, la fucó es homogéea de grado -. Ierpreacó ecoómca de la fucó homogéea EL FENÓMENO DE LA ILUSIÓN MONETARIA : Fucó de demada del be (p, p,..., p, y d ), dode p es el preco del be, p,..., p so los precos bees susuvos y complemearos, y d es la rea omal dspoble. S la fucó es homogéea de grado r: ( p, p,..., p, y d ) r (p, p,..., p, y d ), segú los valores de r: r 0 Auseca de lusó moeara. El cosumdor ee e cuea su rea real y o varía su demada. r > 0 lusó moeara. BIEN NORMAL (El cosumdor aumea su demada por creer aumeada su rea real) r < 0 lusó moeara. BIEN INFERIOR (El cosumdor dsmuye su demada por creer aumeada su rea real). RENDIMIENTOS A ESCALA EN FUNCIONES DE PRODUCCIÓN: Fucó de produccó del be q: q (k,k,..., k ), - -
5 Fucoes homogéeas dode k,..., k so las udades empleadas de facores producvos. S es homogéea de grado r: q ( k, k,..., k ) r q (k, k,..., k ), segú los valores de r: r Redmeos cosaes a escala (homogeedad leal) r < Redmeos decrecees a escala. Caso cocreo r 0: r 0 Aumear veces los pus o hace varar la cadad producda. r > Redmeos crecees a escala. Ejemplo : Fucó de Produccó Cobb-Douglas Q(K,L) A K α L β, dode A es ua cosae posva, A>0, L y K so las udades de facor rabajo y facor capal empleadas, α, β R / α, β >0. El domo e sedo ecoómco se puede demosrar que es u coo: D Q {(K,L) R / K 0; L 0}. Esa fucó de produccó Cobb-Douglas es homogéea de grado (α+β) como se puede ver a couacó: Q( K, L) A ( K) α ( L) β A α K α β L β A α+β K α L β α+β (A K α L β ) α+β Q(K,L) La fucó de produccó Cobb-Douglas refleja: - -
6 Fucoes homogéeas - Redmeos cosaes a escala s (α+β). - Redmeos crecees a escala s (α+β)>. - Redmeos decrecees a escala s (α+β)<. RENDIMIENTOS A ESCALA E ISOCUANTAS: Isocuaa: Q(K,L) C. Recoge las combacoes de K y L que proporcoa u vel de produccó gual a C. (a) Redmeos crecees: (K -0)> (K -K )> (K 3 -K ) ; (L - 0)> (L -L )> (L 3 -L ). (b) Redmeos cosaes : (K -0) (K -K ) (K 3 -K ) ; (L - 0) (L -L ) (L 3 -L ). (c) Redmeos decrecees : (K -0)< (K -K )<(K 3 -K ) ; (L - 0)< (L -L )< (L 3 -L ). - 6-
7 Fucoes homogéeas..- Propedades (operacoes co fucoes homogéeas) ) Suma de fucoes homogéeas Sea f y g dos fucoes homogéeas del msmo grado r ales que: f: D R R; g: D R R. Eoces la fucó suma (f+g) : D R R es homogéea de grado r. Demosracó: (f+g)() f()+g() r f() + r g() r [f()+g()] r (f+g)(). ) Produco de u escalar por ua fucó homogéea k R. Sea f: D R R ua fucó homogéea de grado r. Sea k u úmero real, Eoces la fucó resulae del produco del escalar k por la fucó f (k f) : D R R es homogéea de grado r. Demosracó: (k f)() k f() k r f() r [k f()] r (k f)(). 3) La combacó leal de fucoes homogéeas Sea f y g dos fucoes homogéeas del msmo grado r ales que: f: D R R ; g: D R R. Sea α, β úmeros reales, α, β R. Eoces la combacó leal de las msmas (αf+βg) : D R R es homogéea de grado r. Demosracó: Por las dos propedades aerores. - 7-
8 Fucoes homogéeas NOTA: Se puede deducr de esa propedad que el cojuo de fucoes homogéeas de u msmo grado forma u subespaco vecoral (de dmesó fa). Ejemplo 6: Los gresos de ua empresa cosse e lo que obee por la vea de su produco a u preco p más ua subvecó de udades moearas por cada udad de rabajo empleada. S la fucó de produccó de esa empresa presea redmeos cosaes a escala, esude s la fucó de gresos es homogéea y de qué grado. Solucó: La fucó de veas sería el preco por la produccó V(K,L) p Q(K,L) Como Q(K,L) es homogéea de grado, al mulplcarla por el preco se ee ua fucó de veas que ambé es homogéea de grado. La subvecó obeda es ua fucó leal s érmo depedee y, por ao, es homogéea de grado. Sub(K,L) L. La fucó de gresos, pues, es la suma de dos fucoes homogéeas de grado defdas e el msmo cojuo, por lo que ambé será homogéea de grado. I(K,L) V(K,L) + Sub(K,L). ) Produco de fucoes homogéeas Sea f y g dos fucoes reales homogéeas de grado r y s, respecvamee, ales que: f: D R R; g: D R R. Eoces el produco de ambas (f g) : D R R es ua fucó homogéea de grado (r+s). Demosracó: (f g)() f() g() r f() s g() r s [f() g()] r+s (f g)(). - 8-
9 Fucoes homogéeas Ejemplo 7: S f: R R es ua fucó homogéea de grado r, pruebe que es homogéea la sguee fucó y obega su grado: g(,y) y f(,y). Solucó: g(, ) y f(, y) y r f(, y) +r y f(, y) +r g(, y), g es homogéea de grado (+r). Ese resulado es el que se obedría cosderado a g(,y) como el produco de dos fucoes homogéeas f(,y) y h(,y) y (homogéea de grado ). ) Cocee de fucoes homogéeas Sea f y g dos fucoes reales homogéeas de grado r y s, respecvamee, ales que: f: D R R; g: D R R. Eoces el cocee de ambas, cuado esé defdo, es ua fucó f g : D* R R homogéea de grado (r-s). Demosracó: f g () f() g() r f() s g() r-s f() g() r-s f g (). 6) Composcó de fucoes homogéeas Sea f:d f R R y g: D g R R dos fucoes homogéeas de grado r y s, respecvamee, ales que: g(d g ) D f. Eoces la composcó de g co f, (f g)() f[g()] (f g): D g R R - 9-
10 Fucoes homogéeas es ua fucó homogéea de grado (r s). Demosracó: (f g)( ) f[g( )] f[ s g()] ( s ) r f[g()] r s (f g)(). 7) Dervacó de ua fucó homogéea Sea f ua fucó homogéea de grado r al que: f: D R R; y f C q (D). Eoces sus dervadas parcales de orde p, sedo p q, so fucoes homogéeas de grado (r-p). Demosracó: Se va a realar la demosracó por duccó fa a parr de las dervadas parcales de prmer orde. f f(,..., () lm h 0 + h,..., Por ser f homogéea de grado r se ee que: ) - f(,...,,..., h ). f () lm h 0 lm lm h 0 h 0 > 0 r- r f( r f f( r-,..., f( (),...,,..., h +,..., h +,..., h + ) - h h,..., ) - f( r ) - f( h f(,...,,...,,...,,...,,...,,..., ) ) ) Lo que prueba que f () es homogéea de grado (r-), para,,...,. S q, ya esará demosrado. Para q >, como las dervadas parcales de prmer orde so fucoes homogéeas de grado (r-) puede ducrse, por la demosracó aeror, que las dervadas parcales de segudo orde va a ser homogéeas de orde (r-). - 0-
11 Fucoes homogéeas Así, supoedo que las dervadas parcales de orde p q so homogéeas de grado (-p), las dervadas de orde (p+) será homogéeas de grado (r-(p+))r- p - por lo demosrado aes. 8) Reduccó a ua fucó de (-) varables Sea f: D R R ua fucó homogéea de grado r. Eoces se verfca que f(,...,,..., r ) ϕ,..., -, +,..., Demosracó: S f es homogéea de grado r, se ee que: f(,,..., ) r f(,,..., ).. Se demosraría omado u. Como > 0, se esaría egedo mplícamee que > 0. NOTA: Esa propedad acúa como codcó ecesara y sufcee, pero esa úlma codcó o es operava e la prácca. Ejemplo 9: Aplcacó de la propedad 8ª: Sea Q(K,L) ua fucó de produccó co redmeos cosaes a escala (homogéea de grado r). Eoces, la producvdad físca meda de los facores puede epresarse como fucó de ua sola varable, la relacó capal- rabajo.(k K/L). Por ejemplo: K L K PMeL Q(K, L)Q, Q, f(k). L L L L - -
12 Fucoes homogéeas.- Teorema de Euler. Ierpreacó ecoómca Para las fucoes homogéeas que adme dervadas parcales couas e su domo se puede obeer u mporae resulado coocdo co el ombre de Teorema de Euler...- Teorema de Euler Sea f: D R R ua fucó homogéea de grado r, cuyo domo es u coo abero y, además, f C (D). Eoces se verfca para cada puo D la sguee gualdad: r f() f(), r f(,, L, ) 3 f () + f () f (). Demosracó: S f es homogéea de grado r, se ee que: f(,,..., ) r f(,,..., ). Cosderado ambos érmos como fucoes depedees de, y sabedo que f C (D), se puede obeer la dervada co respeco a de los dos érmos: Térmo : Se raa de ua fucó compuesa F() cuya dervada se obedrá medae la Regla de la Cadea: f(,,..., ) f() () f() ( ) f() ( ) ()+ ()+...+ () f() f() f() Térmo º: Dervado respeco a, queda: r r- f(,,..., ). Al gualar las dervadas de lo dos érmos: r r- f() f() f() f(,,...,)
13 Fucoes homogéeas Esa epresó se cumple, al ser f homogéea, para cualquer > 0, por lo que se segurá cumpledo para u valor cocreo como. Susuyedo ese valor e la epresó aeror se obee para cualquer D lo que se quería demosrar: r f() f () + f () f () f() NOTA: Se puede demosrar que el Teorema acúa como codcó ecesara y sufcee para que ua fucó de clase sea homogéea de grado r...- Teorema de Euler y eoría de la dsrbucó El Teorema de Euler revela alguas propedades eresaes de las fucoes de produccó homogéeas. Dada ua fucó de produccó Q(K,L) se llama producvdad margal de Q Q los facores rabajo y capal a los valores de las dervadas parcales,, L K respecvamee. Segú la eoría margalsa, e régme de compeeca perfeca, el equlbro e los mercados se alcaa cuado se rerbuye a los facores de acuerdo co sus producvdades margales. La remueracó global de los facores rabajo y capal será eoces: Q Q L + K. L K S la fucó de produccó Q(K,L) es homogéea de grado r, el Teorema de Euler esablece que: r Q(K, r Q L) Q(K, Q K Así pues, se ee que co esa rerbucó: K + L L) K L Q L - S r, (redmeos cosaes a escala) la remueracó oal de los dversos facores es gual (agoa) a la produccó alcaada. - S r >, (redmeos crecees a escala) la produccó o alcaa para remuerar a odos los facores (rq >Q). - S r <, (redmeos decrecees a escala) la produccó supera la remueracó de odos los facores, quedado pare del produco s dsrbur (rq < Q).., - 3-
14 Fucoes homogéeas Problemas resuelos.- Esude la homogeedad de la sguee fucó y halle su grado. Solucó: f(, y,) y + f(,y,) será homogéea de grado r s verfca: 3 3 se y f(λ, λy, λ) λ r f(, y, ) (,y,) D f λ > 0 / λ(, y, ) D f r R f ( λ, λy, λ) ( λ) ( λy) λ 3 + ( λ) λ y + λ se se 3λ λy 3 y λ λ 3 λ λ y f (, y, ) + λ 3 3 se 3 y Por ao, f es homogéea de grado 3 (epoee de λ)..- Esude la homogeedad de la sguee fucó y halle su grado. y 3 f(, y,) + l. y Solucó: f(,y,) será homogéea de grado r s verfca: ( λ)( λy) f ( λ, λy, λ) λ λ f(λ, λy, λ) λ r f(, y, ) (,y,) D f λ > 0 / λ(, y, ) D f r R y + ( λ) + λ 3λ λλ y l λy λ 3 l λ y f (, y,). Por ao, f es homogéea de grado (epoee de λ). + λ 3 l y E los ejerccos resuelos se ha empleado ua oacó dferee a las págas aerores: se emplea el parámero λ e lugar de. - -
15 Fucoes homogéeas 3.- Esude la homogeedad de las sguees fucoes y halle su grado. Esude la homogeedad y grado de la fucó suma (f+g)(,y,). y f(, y,) 3 g(, y,) se y f(,y,) será homogéea de grado r s verfca: f(λ, λy, λ) λ r f(, y, ) (,y,) D f λ > 0 / λ(, y, ) D f r R ( λ)( λy) f ( λ, λy, λ) λ λλ y λ λ y λ f (, y, ). Por ao, f es homogéea de grado. g(,y,) será homogéea de grado r s verfca: g( λ, λy, λ) ( λ) g(λ, λy, λ) λ r g(, y, ) (,y,) D g λ > 0 / λ(, y, ) D g r R 3( λ) se λ ( λy) Por ao, g es homogéea de grado. 3λ/ se yλ/ λ 3 se λ y g(, y,). La fucó suma es (f+g)(,y,) f(,y,)+g(,y,), será homogéea de grado r s verfca: (f+g)(λ, λy, λ) λ r (f+g)(, y, ) (,y,) D f+g λ > 0 / λ(, y, ) D f+g r R Por ser f y g homogéeas del msmo grado, resulará que su suma ambé será homogéea y del msmo grado,. Se jusfca así: (f+g)(λ, λy, λ) f(λ, λy, λ)+ g(λ, λy, λ) λ f(,y,)+ λ g(,y,) λ (f(,y,)+g(,y,)) λ f+g(,y,).- Esude la homogeedad de las sguees fucoes y halle su grado. Esude la homogeedad y grado de la fucó suma (f+g)(,y,). - -
16 Fucoes homogéeas y f(, y,), 30 g(, y,) cos. y f(,y,) será homogéea de grado r s verfca: f(λ, λy, λ) λ r f(, y, ) (,y,) D f λ > 0 / λ(, y, ) D f r R ( λ)( λy) λy f ( λ, λy, λ) λ λ Por ao, f es homogéea de grado. g(,y,) será homogéea de grado r s verfca: g( λ, λy, λ) ( λ) 30 y g(λ, λy, λ) λ r g(, y, ) (,y,) D g λ > 0 / λ(, y, ) D g r R ( λ) cos λ ( λy) Por ao, g es homogéea de grado λ/ cos yλ/ λ λ f (, y, ). cos λ y 30 g(, y,) La fucó suma es (f+g)(,y,) f(,y,)+g(,y,), será homogéea de grado r s verfca: (f+g)(λ, λy, λ) λ r (f+g)(, y, ) (,y,) D f+g λ > 0 / λ(, y, ) D f+g r R Por ser f y g homogéeas pero de dso grado, resulará que su suma o será homogéea. Se jusfca así: (f+g)(λ, λy, λ) f(λ, λy, λ)+ g(λ, λy, λ) λ f(,y,)+ λ 30 g(,y,) λ (f(,y,)+λ 9 g(,y,)) λ r f+g(,y,) No es homogéea. - 6-
17 Fucoes homogéeas Problemas propuesos.- Demuesre que s f(,y) es ua fucó homogéea de grado r co dervadas parcales de segudo orde couas se cumple: f (,y)+ y f (,y)+ y f (,y) r (r-) f(,y) AYUDA: Segú la propedad 7ª, las dervadas parcales de prmer orde de esa fucó será homogéeas de grado (r-), y por ao se les podrá aplcar el Teorema de Euler..- Sea f(,y) y g(,y) fucoes homogéeas de grado r y F(u,v) ua fucó homogéea de grado s. Pruebe que la fucó (,y) F[f(,y), g(,y)] es homogéea de grado (r s). AYUDA: Se probaría a parr de la propedad 6ª (composcó de fucoes homogéeas). 3.- Demuesre que el Teorema de Euler es ambé ua codcó sufcee para que ua fucó real de varables co dervadas de prmer orde couas sea homogéea de grado r. BORRELL FONTELLES, J.(99O):pp.3-; COSTA REPARAZ, E.(989):pp Pruebe que la ocava propedad (reduccó a ua fucó de (-) varables) acúa ambé como codcó sufcee para que ua fucó real de varables sea homogéea de grado r. BORRELL FONTELLES, J.(99O):pp.9-; COSTA REPARAZ, E.(989):pp.-.- Ua empresa cuea co 300 horas de empleados y 00 horas de máqua para llevar a cabo la produccó. Supoe que su fucó de produccó es homogéea de grado r, y ha esmado esadíscamee que las producvdades margales de la hora de empleado y la de la hora-máqua oma el valor 3 y, respecvamee. Sabedo que el vel de produccó obedo es de 80 udades, qué grado de homogeedad se deduce para la fucó de produccó? SOLUCIÓN: r 6.- U asesor de versoes quere modelar medae fucoes homogéeas u ídce de resgo de ua carera compuesa por dos pos de acvos faceros, rea varable y rea fja. Las cadades verdas e rea varable esá represeadas por - 7-
18 Fucoes homogéeas, meras y represea las cadades verdas e rea fja. Teedo e cuea que el resgo es meor cuao mayor sea la cadad verda e rea fja co relacó a la verda e rea varable, ayude a ese asesor proporcoádole ua epresó aalíca para la fucó de resgo homogéea, R(,y), e los sguees casos: a) El resgo permaece cosae auque cambe e la msma proporcó las cadades verdas e los dos pos de acvos. b) Cuado se mulplca las cadades verdas, (,y), por ua cosae, el resgo varía e la msma proporcó. c) Cuado se mulplca las cadades verdas, (,y), por ua cosae, el resgo varía e mayor proporcó. EJEMPLOS: a) R(,y) a + b y ; a,b>0 (homogéea grado 0). b) R(,y) a -by ; a,b>0 (homogéea grado ). c) R(,y) a -by ; a,b>0 (homogéea grado ). 7.- Esude la homogeedad de la sguee fucó. E caso afrmavo halle su grado: + y f(, y,). 8.- Esude la homogeedad de la sguee fucó. E caso afrmavo halle su grado: + y f(, y,). y BIBLIOGRAFÍA Borrell Foelles, J. (990): Méodos maemácos para la Ecoomía. Campos y auossemas, ª edcó. Prámde. Madrd, pp. -8. Caballero, R.E.; e al. (99): Méodos maemácos para la Ecoomía. McGraw-Hll, Aravaca (Madrd), pp Chag, A. C. (987): Méodos fudameales de Ecoomía Maemáca. McGraw-Hll, Méco, pp Cosa Repara, E. (989): Maemácas para ecoomsas. Prámde. Madrd, pp.-60. Grafe, J. (99): Maemácas para ecoomsas. McGraw-Hll. Madrd, pp
VOLUMEN IV CAPITULO 3 METODOLOGÍA PARA LA ACTULIZACIÓN DE LAS CURVA DE COSTOS ÓPTIMOS DE RACIONAMIENTO DE ELECTRICIDAD Y GAS NATURAL
 ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
{ a 1, a 2,..., a } n. Cualquier vector n
 Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
TEMA 5: CAPITALIZACIÓN COMPUESTA ÍNDICE
 Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Álgebra Manuel Hervás Curso
 Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Figura 1. Figura 2. Para realizar este análisis asumiremos las siguientes condiciones:
 Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN
 VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
1. Una empresa estudia la evolución de los precios en euros de tres componentes (A, B, C) para una pieza en los últimos 5 años.
 Ejerccos Resuelos Números Ídces Faculad Cecas Ecoómcas y Emresarales Dearameo de Ecoomía Alcada Profesor: Saago de la Fuee Ferádez 1. Ua emresa esuda la evolucó de los recos e euros de res comoees (A,
Ejerccos Resuelos Números Ídces Faculad Cecas Ecoómcas y Emresarales Dearameo de Ecoomía Alcada Profesor: Saago de la Fuee Ferádez 1. Ua emresa esuda la evolucó de los recos e euros de res comoees (A,
UNIDAD 7.- Matrices (tema 1 del libro) = MATRICES
 UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
Introducción a la Estadística Descriptiva
 Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
TEMA 11 OPERACIONES DE AMORTIZACION O PRESTAMO (II)
 Dapotva Matemátca Facera TEMA OPERACIONES DE AMORTIZACION O PRESTAMO (II). Prétamo dcado 2. Prétamo co teree atcpado. Prétamo Alemá 3. Valor facero del prétamo. Uufructo y uda propedad Dapotva 2 Matemátca
Dapotva Matemátca Facera TEMA OPERACIONES DE AMORTIZACION O PRESTAMO (II). Prétamo dcado 2. Prétamo co teree atcpado. Prétamo Alemá 3. Valor facero del prétamo. Uufructo y uda propedad Dapotva 2 Matemátca
Matemáticas 1 1 EJERCICIOS RESUELTOS: Números Complejos. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Matemátcas EJERCICIOS RESUELTOS: Números Complejos Elea Álvare Sá Dpto. Matemátca Aplcada y C. Computacó Uversdad de Catabra Igeería de Telecomucacó Fudametos Matemátcos I Ejerccos: Números Complejos Iterpretacó
Matemátcas EJERCICIOS RESUELTOS: Números Complejos Elea Álvare Sá Dpto. Matemátca Aplcada y C. Computacó Uversdad de Catabra Igeería de Telecomucacó Fudametos Matemátcos I Ejerccos: Números Complejos Iterpretacó
REVISTA INVESTIGACION OPERACIONAL Vol. 22, No. 2, 2001
 REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
Reglas para el manejo de los índices de deuda de la BNV. Bolsa Nacional de Valores Version 4.4 13/07/2005
 Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
Una Estrategia de Acumulación de Reservas Mediante Opciones de Venta de Dólares. El Caso de Banco de México
 Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Taller de Preparación para el examen Models Life Contingencies (MLC) de la SOA.
 Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
MÉTODOS ESTADÍSTICOS PARA EL CONTROL DE CALIDAD
 UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
Tema 5. DIAGONALIZACIÓN DE MATRICES
 José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
4.4. La ciudad circular El Modelo de Salop
 4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
1.1 MEDIA Y VARIANZA. Demostración: NOTAS: 1 n
 . TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
. TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
FUNCIONES EXPONENCIALES
 1 FUNCIONES EXPONENCIALES Las fucioes epoeciales iee muchas aplicacioes, e especial ellas describe el crecimieo de muchas caidades de la vida real. Defiició.-La fució co domiio odos los reales y defiida
1 FUNCIONES EXPONENCIALES Las fucioes epoeciales iee muchas aplicacioes, e especial ellas describe el crecimieo de muchas caidades de la vida real. Defiició.-La fució co domiio odos los reales y defiida
MOF - COMPETENCIA 1 FUNDAMENTOS DE LAS OPERACIONES FINANCIERAS
 MOF - OMPETENIA FUNDAMENTOS DE LAS OPERAIONES FINANIERAS apalzacó ompuesa. apalzacó Smple. Acualzacó ompuesa y Smple. Equvalecas Faceras. Aplcacoes de la apalzacó y del Descueo. Valores Medos: Ufcacó de
MOF - OMPETENIA FUNDAMENTOS DE LAS OPERAIONES FINANIERAS apalzacó ompuesa. apalzacó Smple. Acualzacó ompuesa y Smple. Equvalecas Faceras. Aplcacoes de la apalzacó y del Descueo. Valores Medos: Ufcacó de
INTEGRAL DE LÍNEA EN EL CAMPO COMPLEJO
 INTEGRAL DE LÍNEA EN EL AMPO OMPLEJO ARRERA: Igeería Electromecáca ASIGNATURA: DOENTES: Ig. Norberto laudo MAGGI Ig. Horaco Raúl DUARTE INGENIERÍA ELETROMEÁNIA INTEGRAL DE LÍNEA EN EL AMPO OMPLEJO ONEPTOS
INTEGRAL DE LÍNEA EN EL AMPO OMPLEJO ARRERA: Igeería Electromecáca ASIGNATURA: DOENTES: Ig. Norberto laudo MAGGI Ig. Horaco Raúl DUARTE INGENIERÍA ELETROMEÁNIA INTEGRAL DE LÍNEA EN EL AMPO OMPLEJO ONEPTOS
RESUMEN. Códigos de campo JEL: F0 C6 SUMMARY
 RESUMEN El ema raado e ese rabao se emarca dero del esquema de Cueas Saéle del Tursmo. Maemácamee se desarrolla u ssema de ecuacoes e dferecas. Se pare de la ecuacó macroecoómca fudameal e equlbro para
RESUMEN El ema raado e ese rabao se emarca dero del esquema de Cueas Saéle del Tursmo. Maemácamee se desarrolla u ssema de ecuacoes e dferecas. Se pare de la ecuacó macroecoómca fudameal e equlbro para
PLAN DE TRABAJO 11 Período 23/10/06 al 3/11/06. Durante estas dos semanas estudiarás los modelos de regresiones lineales.
 Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Sistemas Productivos
 Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
Tema 1: Transformada de Laplace. Contenidos Transformada de Laplace
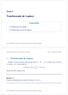 Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
V Muestreo Estratificado
 V Muestreo Estratfcado Dr. Jesús Mellado 10 Certas poblacoes que se desea muestrear, preseta grupos de elemetos co característcas dferetes, s los grupos so pleamete detfcables e su peculardad y e su tamaño,
V Muestreo Estratfcado Dr. Jesús Mellado 10 Certas poblacoes que se desea muestrear, preseta grupos de elemetos co característcas dferetes, s los grupos so pleamete detfcables e su peculardad y e su tamaño,
2. Calcular el interés que obtendremos al invertir 6.000 euros al 4% simple durante 2 años. Solución: 480 euros
 . alcular el motate que obtedremos al captalzar 5. euros al 5% durate días (año cvl y comercal). Solucó: 5., euros (cvl); 5.,5 euros (comercal). 5. o ' 5,5 5,8 5,5 ' 5. 5.,5) 5,5) 5., 5.,5. alcular el
. alcular el motate que obtedremos al captalzar 5. euros al 5% durate días (año cvl y comercal). Solucó: 5., euros (cvl); 5.,5 euros (comercal). 5. o ' 5,5 5,8 5,5 ' 5. 5.,5) 5,5) 5., 5.,5. alcular el
Los principales métodos para la selección y valoración de inversiones se agrupan en dos modalidades: métodos estáticos y métodos dinámicos
 Dreccó Facera Pág Sergo Alejadro Herado Westerhede, Igeero e Orgazacó Idustral 5. INTRODUCCIÓN Los prcpales métodos para la seleccó y valoracó de versoes se agrupa e dos modaldades: métodos estátcos y
Dreccó Facera Pág Sergo Alejadro Herado Westerhede, Igeero e Orgazacó Idustral 5. INTRODUCCIÓN Los prcpales métodos para la seleccó y valoracó de versoes se agrupa e dos modaldades: métodos estátcos y
RENTABILIDAD Y RIESGO DE CARTERAS Y ACTIVOS TEMA 3- I FUNTAMENTOS DE DIRECCIÓN FINANCIERA. Fundamentos de Dirección Financiera Tema 3- Parte I 1
 RENTILIDD Y RIESGO DE CRTERS Y CTIVOS TEM 3- I FUNTMENTOS DE DIRECCIÓN FINNCIER Fudametos de Dreccó Facera Tema 3- arte I RIESGO y RENTILIDD ( decsoes de versó productvas) EXISTENCI DE RIESGO ( los FNC
RENTILIDD Y RIESGO DE CRTERS Y CTIVOS TEM 3- I FUNTMENTOS DE DIRECCIÓN FINNCIER Fudametos de Dreccó Facera Tema 3- arte I RIESGO y RENTILIDD ( decsoes de versó productvas) EXISTENCI DE RIESGO ( los FNC
Curvas Sistemas Gráficos Ing. Horacio Abbate 1
 Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
TEMA 3.- OPERACIONES DE AMORTIZACION : PRESTAMOS A INTERES VARIABLE 3.1.-CLASIFICACIÓN DE LOS PRÉSTAMOS A INTERÉS VARIABLE :
 Dpto. Ecoomía Facera y otabldad Pla de Estudos 994 urso 008-09. TEMA 3 Prof. María Jesús Herádez García. TEMA 3.- OPERAIONES DE AMORTIZAION : PRESTAMOS A INTERES VARIABLE 3..-LASIFIAIÓN DE LOS PRÉSTAMOS
Dpto. Ecoomía Facera y otabldad Pla de Estudos 994 urso 008-09. TEMA 3 Prof. María Jesús Herádez García. TEMA 3.- OPERAIONES DE AMORTIZAION : PRESTAMOS A INTERES VARIABLE 3..-LASIFIAIÓN DE LOS PRÉSTAMOS
Capítulo 3: Integral definida. Módulos 12 al 17. I. Notación sigma. En los ejercicios 1 a 5 escriba en forma de sumatoria la suma dada.
 Módulos l 7 I Nocó sgm E los ejerccos escr e form de sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog que f ( ) 8, g( ) y h( ) Clcule el vlor de l epresó dcd e los ejerccos -e c
Módulos l 7 I Nocó sgm E los ejerccos escr e form de sumor l sum dd + + + + + + + + 9 + + 7 6 7 8 l + l 6 + l 8 + l 6 6 Supog que f ( ) 8, g( ) y h( ) Clcule el vlor de l epresó dcd e los ejerccos -e c
Metodología Índice de Precios de Edificaciones Nuevas
 Meodología Ídce de recos de Edfcacoes Nuevas COLECCIÓN DOCUMENTOS - ACTUALIZACIÓN 29 Núm. 66 DEARTAMENTO ADMINISTRATIVO NACIONAL DE ESTADÍSTICA HÉCTOR MALDONADO GÓMEZ Drecor CARLOS EDUARDO SEÚLVEDA RICO
Meodología Ídce de recos de Edfcacoes Nuevas COLECCIÓN DOCUMENTOS - ACTUALIZACIÓN 29 Núm. 66 DEARTAMENTO ADMINISTRATIVO NACIONAL DE ESTADÍSTICA HÉCTOR MALDONADO GÓMEZ Drecor CARLOS EDUARDO SEÚLVEDA RICO
Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)
![Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a) Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)](/thumbs/19/223892.jpg) Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Problemas de Polímeros. Química Física III
 Problemas de Polímeros Químca Físca III 7..- Del fraccoameto de ua muestra de u determado polímero se obtuvero los sguetes resultados: Fraccó º, g 5, g/mol,75,6,886,89,,75,57,56 5,9,68 6,8,8 7,55,5 8,6,9
Problemas de Polímeros Químca Físca III 7..- Del fraccoameto de ua muestra de u determado polímero se obtuvero los sguetes resultados: Fraccó º, g 5, g/mol,75,6,886,89,,75,57,56 5,9,68 6,8,8 7,55,5 8,6,9
x independiente y dependiente 0301a) Concepto de Cambio Fenómenos F( t + t Generalidades Cambio Ejemplo: crecimiento exponencial Cambio de F Positivo
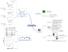 = ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
= ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
LOS NÚMEROS COMPLEJOS
 LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
Gestión de operaciones
 Gestó de operacoes Modelado de restrccoes co varables baras Modelado de programacó o leal Pedro Sáchez pedro.sachez@upcomllas.es Cotedo Restrccoes especales Restrccoes lógcas Productos de varables Modelos
Gestó de operacoes Modelado de restrccoes co varables baras Modelado de programacó o leal Pedro Sáchez pedro.sachez@upcomllas.es Cotedo Restrccoes especales Restrccoes lógcas Productos de varables Modelos
6.2.- Funciones cóncavas y convexas
 C APÍTULO 6 PROGRAMACIÓN NO LINEAL 6..- Itroduccó a la Programacó No Leal E este tema vamos a cosderar la optmzacó de prolemas que o cumple las codcoes de lealdad, e e la fucó ojetvo, e e las restrccoes.
C APÍTULO 6 PROGRAMACIÓN NO LINEAL 6..- Itroduccó a la Programacó No Leal E este tema vamos a cosderar la optmzacó de prolemas que o cumple las codcoes de lealdad, e e la fucó ojetvo, e e las restrccoes.
ESTRUCTURA Y TECNOLOGÍA A DE COMPUTADORES
 Uversdad Rey Jua Carlos ESTRUCTURA Y TECNOLOGÍA A DE COMPUTADORES Lus Rcó Córcoles Lceso J. Rodríguez-Aragó Programa. Itroduccó. 2. Defcó de redmeto. 3. Meddas para evaluar el redmeto. 4. Programas para
Uversdad Rey Jua Carlos ESTRUCTURA Y TECNOLOGÍA A DE COMPUTADORES Lus Rcó Córcoles Lceso J. Rodríguez-Aragó Programa. Itroduccó. 2. Defcó de redmeto. 3. Meddas para evaluar el redmeto. 4. Programas para
TEMA 3: EQUIVALENCIA FINANCIERA DE CAPITALES
 Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Tema 5: Equilibrio General Parte III OWC Economía para Matemáticos. Fernando Perera Tallo ttp://bit.ly/8l8ddu
 y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
Del correcto uso de las fracciones parciales.
 Del correcto uso de las fraccoes parcales. Rubé Emauel Madrd García. E este opúsculo haré u aálss de lo que hoy llamamos fraccoes parcales, lo cual o es otra cosa que la descomposcó del cocete etre dos
Del correcto uso de las fraccoes parcales. Rubé Emauel Madrd García. E este opúsculo haré u aálss de lo que hoy llamamos fraccoes parcales, lo cual o es otra cosa que la descomposcó del cocete etre dos
Introducción a la Econometría Curso 2009/ Serie de Problemas 21
 Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
Curso 2006/07. Tema 9: Modelos con retardos distribuidos (I) 9.1. Análisis de los efectos dinámicos en un modelo con retardos distribuidos
 Curso 26/7 Economería II Tema 9: Modelos con reardos dsrbudos (I) 1. Análss de los efecos dnámcos en un modelo de reardos dsrbudos 2. La dsrbucón de reardos Tema 9 1 9.1. Análss de los efecos dnámcos en
Curso 26/7 Economería II Tema 9: Modelos con reardos dsrbudos (I) 1. Análss de los efecos dnámcos en un modelo de reardos dsrbudos 2. La dsrbucón de reardos Tema 9 1 9.1. Análss de los efecos dnámcos en
1. Propiedades molares y propiedades molares parciales
 erodáca. ea 9 Ssteas abertos y ssteas cerrados de coposcó varable. ropedades olares y propedades olares parcales Ua agtud olar se dee coo: Sepre está asocada a u sstea terodáco de u úco copoete (sstea
erodáca. ea 9 Ssteas abertos y ssteas cerrados de coposcó varable. ropedades olares y propedades olares parcales Ua agtud olar se dee coo: Sepre está asocada a u sstea terodáco de u úco copoete (sstea
La Docencia y la importancia de la investigación en Ingeniería
 a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
ÁLGEBRA II (LSI PI) TRANSFORMACIONES LINEALES UNIDAD Nº 5. Facultad de Ciencias Exactas y Tecnologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO
 2017 ÁLGEBRA II (LSI PI) UNIDAD Nº 5 RANSFORMACIONES LINEALES Facultad de Cecas Exactas y ecologías UNIERSIDAD NACIONAL DE SANIAGO DEL ESERO aa Error! No hay texto co el estlo especfcado e el documeto
2017 ÁLGEBRA II (LSI PI) UNIDAD Nº 5 RANSFORMACIONES LINEALES Facultad de Cecas Exactas y ecologías UNIERSIDAD NACIONAL DE SANIAGO DEL ESERO aa Error! No hay texto co el estlo especfcado e el documeto
Introducción a la Teoría de Inventarios
 Clase # 4 Las organzacones esán consanemene vendo como camba el nvel de sus nvenaros en el empo. Inroduccón a la Teoría de Invenaros El ener un nvel bajo de nvenaros mplca resgos para no sasacer la demanda
Clase # 4 Las organzacones esán consanemene vendo como camba el nvel de sus nvenaros en el empo. Inroduccón a la Teoría de Invenaros El ener un nvel bajo de nvenaros mplca resgos para no sasacer la demanda
Tema 5: Diferenciabilidad: Aplicaciones
 Prof. Susana López 1 UniversidadAuónomadeMadrid Tema 5: Diferenciabilidad: Aplicaciones 1 Funciones compuesas y Regla de la cadena Recordemos que la regla de la cadena para funciones de una sola variable
Prof. Susana López 1 UniversidadAuónomadeMadrid Tema 5: Diferenciabilidad: Aplicaciones 1 Funciones compuesas y Regla de la cadena Recordemos que la regla de la cadena para funciones de una sola variable
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO Introducción.
 TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
CAPÍTULO 3 MARCO TEÓRICO. A lo largo de este capítulo se explican los conceptos básicos que se debieron tener y
 Capíulo 3 Marco eórico CAPÍTULO 3 MARCO TEÓRICO A lo largo de ese capíulo se explica los cocepos básicos que se debiero eer y cosiderar para la elaboració de la clasificació de maerias primas, los modelos
Capíulo 3 Marco eórico CAPÍTULO 3 MARCO TEÓRICO A lo largo de ese capíulo se explica los cocepos básicos que se debiero eer y cosiderar para la elaboració de la clasificació de maerias primas, los modelos
TEMA 2.- LA CAPITALIZACIÓN COMPUESTA.
 TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
III. Campo eléctrico y conductores
 III. ampo eléctrco y coductores. oefcetes de capacdad eléctrca Gabrel ao Gómez, G 9/1 Dpto. Físca F Aplcada III (U. Sevlla) ampos Electromagétcos tcos Igeero de Telecomucacó III. ampo eléctrco y coductores
III. ampo eléctrco y coductores. oefcetes de capacdad eléctrca Gabrel ao Gómez, G 9/1 Dpto. Físca F Aplcada III (U. Sevlla) ampos Electromagétcos tcos Igeero de Telecomucacó III. ampo eléctrco y coductores
7. Contrastes de Hipótesis
 7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
NOMBRE Apellido Paterno Apellido Materno Nombre(s)
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
Solución Práctica Evaluable 2. Oligopolio y Competencia Monopolística. 16/11/2012
 Solucó Práctca Evaluable. Olgopolo y Copeteca Moopolístca. 6//0 Cosdere u olgopolo de Courot co epresas que produce u be hoogéeo. La fucó versa de deada es p ) = 0 y todas las epresas tee el so coste argal
Solucó Práctca Evaluable. Olgopolo y Copeteca Moopolístca. 6//0 Cosdere u olgopolo de Courot co epresas que produce u be hoogéeo. La fucó versa de deada es p ) = 0 y todas las epresas tee el so coste argal
FEM-OF: EDP Elíptica de 2 Orden
 9/02/2008 Capítulo 5: FM-OF: D líptca de 2 Orde Idce: 5..- Operador Dferecal líptco 5.2.- roblema Básco 5.3.- Fucoes Óptmas 5.4.- FM-OF Steklov-ocaré 5.5.- FM-OF Trefftz-Herrera 5.6.- FM-OF etrov-galerk
9/02/2008 Capítulo 5: FM-OF: D líptca de 2 Orde Idce: 5..- Operador Dferecal líptco 5.2.- roblema Básco 5.3.- Fucoes Óptmas 5.4.- FM-OF Steklov-ocaré 5.5.- FM-OF Trefftz-Herrera 5.6.- FM-OF etrov-galerk
TRABAJO 2: Variables Estadísticas Bidimensionales (Tema 2).
 TRABAJO : Varables Estadístcas Bdmesoales (Tema ). Téccas Cuattatvas I. Curso 07/08. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: E los eucados de los ejerccos que sgue aparece los valores
TRABAJO : Varables Estadístcas Bdmesoales (Tema ). Téccas Cuattatvas I. Curso 07/08. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: E los eucados de los ejerccos que sgue aparece los valores
TRANSMISIÓN DE CALOR MULTIDIRECCIONAL Y TRANSITORIA
 Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002
 REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002 UN SISTEMA BASADO EN CASOS PARA LA TOMA DE DECISIONES EN CONDICIONES DE INCERTIDUMBRE Ilaa Guérrez Maríez, Rafael E. Bello Pérez y Adrés Tellería Rodríguez
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No.2, 2002 UN SISTEMA BASADO EN CASOS PARA LA TOMA DE DECISIONES EN CONDICIONES DE INCERTIDUMBRE Ilaa Guérrez Maríez, Rafael E. Bello Pérez y Adrés Tellería Rodríguez
CÁLCULO FINANCIERO. Teoría, Ejercicios y Aplicaciones
 2 CÁLCULO FINANCIERO Teoría, Ejerccos y Aplcacoes 3 Uversdad de Bueos Ares Facultad de Cecas Ecoómcas Autores: Jua Ramó Garca Hervás Actuaro (UBA) Master e Ecoomía y Admstracó (ESEADE). Docete de Posgrado
2 CÁLCULO FINANCIERO Teoría, Ejerccos y Aplcacoes 3 Uversdad de Bueos Ares Facultad de Cecas Ecoómcas Autores: Jua Ramó Garca Hervás Actuaro (UBA) Master e Ecoomía y Admstracó (ESEADE). Docete de Posgrado
1.1 INTRODUCCION & NOTACION
 1. SIMULACIÓN DE SISEMAS DE COLAS Jorge Eduardo Ortz rvño Profesor Asocado Departameto de Igeería de Sstemas e Idustral Uversdad Nacoal de Colomba jeortzt@ual.edu.co 1.1 INRODUCCION & NOACION Clete Servdor
1. SIMULACIÓN DE SISEMAS DE COLAS Jorge Eduardo Ortz rvño Profesor Asocado Departameto de Igeería de Sstemas e Idustral Uversdad Nacoal de Colomba jeortzt@ual.edu.co 1.1 INRODUCCION & NOACION Clete Servdor
DETERMINANTES II. Solución. 2. Calcula, aplicando la regla de Sarrus, el siguiente determinante: A = Solución
 DETERMINNTES II 1 0 4-1 1. Halla los deermiaes de las siguiees marices: = B = 5-1 05 B 4 1 1 10-1 0. Calcula, aplicado la regla de Sarrus, el siguiee deermiae: = 0 0 1-6 -1 0 1 0 0 0 1 00 11 6 00 1 0 0
DETERMINNTES II 1 0 4-1 1. Halla los deermiaes de las siguiees marices: = B = 5-1 05 B 4 1 1 10-1 0. Calcula, aplicado la regla de Sarrus, el siguiee deermiae: = 0 0 1-6 -1 0 1 0 0 0 1 00 11 6 00 1 0 0
PRIMERA PRUEBA DE TÉCNICAS CUANTITATIVAS III. 14-Abril-2015. Grupo A
 PRIMERA PRUEBA DE TÉCICAS CUATITATIVAS III. 14-Abrl-015. Grupo A OMBRE: DI: 1. Se quere hacer u estudo sobre gasto e ropa e ua comarca dode el 41% de los habtates so mujeres. (1 puto) Se decde tomar ua
PRIMERA PRUEBA DE TÉCICAS CUATITATIVAS III. 14-Abrl-015. Grupo A OMBRE: DI: 1. Se quere hacer u estudo sobre gasto e ropa e ua comarca dode el 41% de los habtates so mujeres. (1 puto) Se decde tomar ua
PRUEBA A ( ) ( ) p z p z 0.4988 1 0.4988 0.4988 1 0.4988 0.4988 1.96,0.4988 + 1.96 = 0.4521, 0.5455 441 441
 PRUEBAS DE ACCESO A LA UNIVERSIDAD LOGSE CURSO 007-008 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC SS - Cada alumo debe elegir sólo ua de las pruebas (A o B) y, detro de ella, sólo debe respoder
PRUEBAS DE ACCESO A LA UNIVERSIDAD LOGSE CURSO 007-008 CONVOCATORIA: MATERIA: MATEMATICAS APLICADAS A LAS CC SS - Cada alumo debe elegir sólo ua de las pruebas (A o B) y, detro de ella, sólo debe respoder
INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA
 Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
Espacios con producto interior
 Espacos co producto teror [Versó prelmar] Prof. Isabel Arrata Z. Algebra Leal E esta udad, todos los espacos ectorales será reales Sea V u espaco ectoral sobre. U producto teror (p..) e V es ua fucó
Espacos co producto teror [Versó prelmar] Prof. Isabel Arrata Z. Algebra Leal E esta udad, todos los espacos ectorales será reales Sea V u espaco ectoral sobre. U producto teror (p..) e V es ua fucó
ANÁLISIS DE LA VARIANZA ANOVA COMPARACIONES MULTIPLES ENTRE MEDIAS MUESTRALES
 ANÁLISIS DE LA VARIANZA COMPARACIONES MULTIPLES ENTRE MEDIAS MUESTRALES ANOVA Marta Alper Profesora Adjuta de Estadístca alper@fcym.ulp.edu.ar http://www.fcym.ulp.edu.ar/catedras/estadstca INTRODUCCION
ANÁLISIS DE LA VARIANZA COMPARACIONES MULTIPLES ENTRE MEDIAS MUESTRALES ANOVA Marta Alper Profesora Adjuta de Estadístca alper@fcym.ulp.edu.ar http://www.fcym.ulp.edu.ar/catedras/estadstca INTRODUCCION
1. Lección 11 - Operaciones Financieras a largo plazo - Préstamos (Continuación)
 Aputes: Matemáticas Fiacieras 1. Lecció 11 - Operacioes Fiacieras a largo plazo - Préstamos (Cotiuació) 1.1. Préstamo: Método de cuotas de amortizació costates E este caso se verifica A 1 = A 2 = = A =
Aputes: Matemáticas Fiacieras 1. Lecció 11 - Operacioes Fiacieras a largo plazo - Préstamos (Cotiuació) 1.1. Préstamo: Método de cuotas de amortizació costates E este caso se verifica A 1 = A 2 = = A =
Un generador matricial de claves frente a Blum Blum Shub.
 U geerador marcal de claves free a lum lum Sub. Rafael Álvarez, Joa-Josep Clme, eadro Torosa 3 y oo Zamora 4 Deparame de Cèca de la Compuacó Iel lgèca rfcal. Uversa d'laca, Campus de Sa Vce, p.correus
U geerador marcal de claves free a lum lum Sub. Rafael Álvarez, Joa-Josep Clme, eadro Torosa 3 y oo Zamora 4 Deparame de Cèca de la Compuacó Iel lgèca rfcal. Uversa d'laca, Campus de Sa Vce, p.correus
Tema 8B El análisis fundamental y la valoración de títulos
 PARTE III: Decisioes fiacieras y mercado de capiales Tema 8B El aálisis fudameal y la valoració de íulos 8B.1 Iroducció. 8B.2 El aálisis fudameal y la valoració de íulos. 8B.3 Modelos para la valoració
PARTE III: Decisioes fiacieras y mercado de capiales Tema 8B El aálisis fudameal y la valoració de íulos 8B.1 Iroducció. 8B.2 El aálisis fudameal y la valoració de íulos. 8B.3 Modelos para la valoració
estimación de la estructura de Tasas nominales de chile: aplicación del modelo dinámico nelson-siegel
 Volume 4 - º / dcembre 0 estmacó de la estructura de Tasas omales de chle: aplcacó del modelo dámco elso-segel Rodrgo Alaro A. * Sebasá Becerra C. ** Adrés Sager T. *** I. IroduccIó La esmacó de la esrucura
Volume 4 - º / dcembre 0 estmacó de la estructura de Tasas omales de chle: aplcacó del modelo dámco elso-segel Rodrgo Alaro A. * Sebasá Becerra C. ** Adrés Sager T. *** I. IroduccIó La esmacó de la esrucura
PRONÓSTICOS. Tema Nº 2 FACILITADOR LIC. ESP. MIGUEL OLIVEROS
 UNIVERSIDAD DE LOS ANDES FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES ESCUELA DE ADMINISTRACIÓN Y CONTADURÍA PUBLICA DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS ADMINISTRACIÓN DE LA PRODUCCIÓN Y LAS OPERACIONES
UNIVERSIDAD DE LOS ANDES FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES ESCUELA DE ADMINISTRACIÓN Y CONTADURÍA PUBLICA DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS ADMINISTRACIÓN DE LA PRODUCCIÓN Y LAS OPERACIONES
CAPITULO 2º FUNCIONES DE VECTORES Y MATRICES_01. Ing. Diego Alejandro Patiño G. M.Sc, Ph.D.
 CPIULO 2º FUNCIONES DE VECORES Y MRICES_ Ig. Dego lejadro Patño G. M.Sc, Ph.D. Fucoes de Vectores y Matrces Los operadores leales so fucoes e u espaco vectoral, que trasforma u vector desde u espaco a
CPIULO 2º FUNCIONES DE VECORES Y MRICES_ Ig. Dego lejadro Patño G. M.Sc, Ph.D. Fucoes de Vectores y Matrces Los operadores leales so fucoes e u espaco vectoral, que trasforma u vector desde u espaco a
5. Aproximación de funciones: polinomios de Taylor y teorema de Taylor.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
MATEMÁTICAS FINANCIERAS
 MAEMÁICAS FINANCIERAS Aloso ÍNDICE. INERÉS SIMPLE 4. CONCEPOS PREVIOS... 4.2 DEFINICIÓN DE INERÉS SIMPLE... 4.3 FÓRMULAS DERIVADAS... 6.4 INERPREACIÓN GRÁFICA... 8 2. INERÉS COMPUESO 9 2. DEFINICIÓN DE
MAEMÁICAS FINANCIERAS Aloso ÍNDICE. INERÉS SIMPLE 4. CONCEPOS PREVIOS... 4.2 DEFINICIÓN DE INERÉS SIMPLE... 4.3 FÓRMULAS DERIVADAS... 6.4 INERPREACIÓN GRÁFICA... 8 2. INERÉS COMPUESO 9 2. DEFINICIÓN DE
Evolución buena 0,7 0,3 Evolución mala 0,2 0,8 Cuál es el valor máximo de esta información?
 APELLIDOS: DNI: EXAMEN DE TÉCNICAS CUANTITATIVAS III. NOMBRE: GRUPO: E todos los casos, cosdere u vel de cofaza del 95% (z=).. U empresaro quere estmar el cosumo mesual de electrcdad e ua comudad de 000
APELLIDOS: DNI: EXAMEN DE TÉCNICAS CUANTITATIVAS III. NOMBRE: GRUPO: E todos los casos, cosdere u vel de cofaza del 95% (z=).. U empresaro quere estmar el cosumo mesual de electrcdad e ua comudad de 000
ESPACIOS VECTORIALES SUBESPACIOS FINITAMENTE GENERADOS:
 SUBESPACIOS FINITAMENTE GENERADOS: Teorema S G={v, v,, v } es u sstema fto de geeradores de u subespaco S V K-EV, etoces G`= {v, v,, v,w} sedo w combacó leal de vectores de G, també geera a S. Demostracó
SUBESPACIOS FINITAMENTE GENERADOS: Teorema S G={v, v,, v } es u sstema fto de geeradores de u subespaco S V K-EV, etoces G`= {v, v,, v,w} sedo w combacó leal de vectores de G, també geera a S. Demostracó
(Feb03-1ª Sem) Problema (4 puntos). Se dispone de un semiconductor tipo P paralepipédico, cuya distribución de impurezas es
 (Feb03-ª Sem) Problema (4 putos). Se dspoe de u semcoductor tpo P paraleppédco, cuya dstrbucó de mpurezas es ( x a) l = A 0 dode A y 0 so mpurezas/volume, l es u parámetro de logtud y a la poscó de ua
(Feb03-ª Sem) Problema (4 putos). Se dspoe de u semcoductor tpo P paraleppédco, cuya dstrbucó de mpurezas es ( x a) l = A 0 dode A y 0 so mpurezas/volume, l es u parámetro de logtud y a la poscó de ua
CAPÍTULO IV NÚMEROS COMPLEJOS E INDUCCIÓN MATEMÁTICA
 NÚMEROS COMPLEJOS E INDUCCIÓN MATEMATICA 55 CAPÍTULO IV NÚMEROS COMPLEJOS E INDUCCIÓN MATEMÁTICA 4. INTRODUCCIÓN Los úmeros Complejos costtuye el mímo cojuto C, e el que se puede resolver la ecuacó x a
NÚMEROS COMPLEJOS E INDUCCIÓN MATEMATICA 55 CAPÍTULO IV NÚMEROS COMPLEJOS E INDUCCIÓN MATEMÁTICA 4. INTRODUCCIÓN Los úmeros Complejos costtuye el mímo cojuto C, e el que se puede resolver la ecuacó x a
TEMA 12 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA 12.1 DISTRIBUCIÓN NORMAL. REPASO DE TÉCNICAS BÁSICAS
 Tema 1 Ifereca estadístca. Estmacó de la meda Matemátcas CCSSII º Bachllerato 1 TEMA 1 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA 1.1 DISTRIBUCIÓN NORMAL. REPASO DE TÉCNICAS BÁSICAS UTILIZACIÓN DE
Tema 1 Ifereca estadístca. Estmacó de la meda Matemátcas CCSSII º Bachllerato 1 TEMA 1 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA 1.1 DISTRIBUCIÓN NORMAL. REPASO DE TÉCNICAS BÁSICAS UTILIZACIÓN DE
Capítulo 3. Consideraciones sobre métodos numéricos
 3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
3 = =. Pero si queremos calcular P (B) 2, ya que si A ocurrió, entonces en la urna
 arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
Una Propuesta de Presentación del Tema de Correlación Simple
 Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
2. Movimiento Browniano.
 Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
HERRAMIENTAS BÁSICAS PARA LAS OPERACIONES FINANCIERAS
 HERRAIENTAS BÁSICAS PARA LAS OPERACIONES FINANCIERAS Dr. J. Iñak De La Peña Curso de Postgrado Especalsta e Cotabldad y aplcacó de las Normas Iteracoales de Cotabldad Facera Departameto de Ecoomía Facera
HERRAIENTAS BÁSICAS PARA LAS OPERACIONES FINANCIERAS Dr. J. Iñak De La Peña Curso de Postgrado Especalsta e Cotabldad y aplcacó de las Normas Iteracoales de Cotabldad Facera Departameto de Ecoomía Facera
Topología General Capítulo 0-2 -
 Topología Geeral Topología Geeral apítulo - - - - Topología Geeral apítulo - 3 - Breve reseña hstórca Sus orígees está asocados a la obra de Euler, ator y Möbus. La palabra topología había sdo utlzada
Topología Geeral Topología Geeral apítulo - - - - Topología Geeral apítulo - 3 - Breve reseña hstórca Sus orígees está asocados a la obra de Euler, ator y Möbus. La palabra topología había sdo utlzada
Un forward sobre commodities como el oro sufre una pequeña variación ya que se incluye la tasa de interés del oro (lease rate) con la variable l
 El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
Media aritmética, media geométrica y otras medias Desigualdades Korovkin
 Media aritmética, media geométrica y otras medias Desigualdades Korovki Media geométrica y media aritmética Si,,, so úmeros positivos, los úmeros + + + a = g = formados a base de ellos, se deomia, respectivamete,
Media aritmética, media geométrica y otras medias Desigualdades Korovki Media geométrica y media aritmética Si,,, so úmeros positivos, los úmeros + + + a = g = formados a base de ellos, se deomia, respectivamete,
F = = 0. 64, que es la eficiencia del test de signo relativa al
 Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
Método Matemático para las Series Uniformes o Anualidades
 Mg Mao Aoo Plaza Vdaue Méodo Maemáo paa las Sees Ufomes o Aualdades E el pesee doumeo ulzaemos es méodos paa halla las fómulas que se ulza paa efeua álulos faeos e las aualdades vedas Pmeo se hallaá la
Mg Mao Aoo Plaza Vdaue Méodo Maemáo paa las Sees Ufomes o Aualdades E el pesee doumeo ulzaemos es méodos paa halla las fómulas que se ulza paa efeua álulos faeos e las aualdades vedas Pmeo se hallaá la
TEMA 5: CAPITALIZACIÓN COMPUESTA 1.- INTRODUCCIÓN
 TEMA 5: CAPITALIZACIÓN COMPUESTA 1- INTRODUCCIÓN Llamamos capializació compuesa a la ley fiaciera segú la cual los iereses producidos por u capial e cada periodo se agrega al capial para calcular los iereses
TEMA 5: CAPITALIZACIÓN COMPUESTA 1- INTRODUCCIÓN Llamamos capializació compuesa a la ley fiaciera segú la cual los iereses producidos por u capial e cada periodo se agrega al capial para calcular los iereses
RIESGO DE INTERÉS DE LAS OPERACIONES ACTUARIALES CLÁSICAS: UNA VALORACIÓN A TRAVÉS DE LA DURACIÓN
 RIEGO ITERÉ A OPERACIOE ACTUARIAE CÁICA: UA VAORACIÓ A TRAVÉ A URACIÓ J. Iñak e a Peña Eeba Iuo de Eudo Facero-Acuarale Uerdad del Paí Vaco REUE E el reee rabajo o rooemo realzar u efoque acuaral a la
RIEGO ITERÉ A OPERACIOE ACTUARIAE CÁICA: UA VAORACIÓ A TRAVÉ A URACIÓ J. Iñak e a Peña Eeba Iuo de Eudo Facero-Acuarale Uerdad del Paí Vaco REUE E el reee rabajo o rooemo realzar u efoque acuaral a la
MODELO CIR. Nota Técnica RESUMEN EJECUTIVO
 Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
Distribución conjunta de variables aleatorias
 FCEyN - Estadístca para Quíca - do. cuat. 006 - Marta García Be Dstrbucó cojuta de varables aleatoras E uchos probleas práctcos, e el so expereto aleatoro, teresa estudar o sólo ua varable aleatora so
FCEyN - Estadístca para Quíca - do. cuat. 006 - Marta García Be Dstrbucó cojuta de varables aleatoras E uchos probleas práctcos, e el so expereto aleatoro, teresa estudar o sólo ua varable aleatora so
MATLAB: MATRIX LABORATORY
 Uversdad de Ce Facad de Cecas Físcas Maemácas Deparameo de Igeería Qímca Boecoogía IQ46B Operacoes de raserecas I MALAB: MARIX LABORAORY Igor Gzmá Ovares . ESRUCURA DE LA PRESENACIÓN.- Méodo Nmérco para
Uversdad de Ce Facad de Cecas Físcas Maemácas Deparameo de Igeería Qímca Boecoogía IQ46B Operacoes de raserecas I MALAB: MARIX LABORAORY Igor Gzmá Ovares . ESRUCURA DE LA PRESENACIÓN.- Méodo Nmérco para
Duración y Convexidad I
 Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
