FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables (x 0 ). x ik. x ik 1
|
|
|
- Julio Cáceres González
- hace 6 años
- Vistas:
Transcripción
1 1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio. Consideemos puntos x, y en un conjunto abieto Ω Ê N tales que x, y] := {x + t(y x) / t 0, 1]} (el segmento ente x e y) está contenido en Ω. Sea f : Ω Ê una función difeenciable. Entonces existe ξ ]0, 1 tal que f(y) f(x) = f(x + ξ(y x)) (x y). Regla de la cadena. Sean Ω Ê N, Λ Ê m, abietos, f : Ω Ê m, g : Λ Ê k. Supongamos que f es difeenciable en x 0, que f(x) Λ paa cada x Ω, y que g es difeenciable en f(x 0 ). Entonces la composición g f : Ω Ê N Ê k es difeenciable en x 0 y (g f) (x 0 ) = g (f(x 0 ))f (x 0 ). Si escibimos f(x) = (f 1 (x),..., f m (x)) y si h(x) = g(f 1 (x),..., f m (x)), se tiene que h m g (x 0 ) = (f(x 0 )) i (x 0 ). j i j j=1 Deivadas de oden supeio. De segundo oden: 2 f (x 0 ) := ( ) (x 0 ). i j i j De oden k: k f i1 i2 ik (x 0 ) := i1 ( i2 ( ik 1 2. EJERCICIOS PROPUESTOS Regla de la Cadena ( ik ) )) (x 0 ). P1.- Sean las funciones de clase C 1, f : Ê 4 Ê, g : Ê 2 Ê, h : Ê Ê, l : Ê Ê 2 y sea: Calcula m m(x, y) = f(g(x, y 2 ), h(xy) + g(y, x), l(h(yx 2 )) y m, explicitando su desaollo tanto como pueda. P2.- Mosta que la función f : Ê 2 Ê definida po: f(x, y) = { sen(x+y) x+y x + y (0, 0) 1 x + y = (0, 0) es difeenciable en Ê 2 y calcula su matiz jacobiana en Ê 2. 1
2 P3.- Ingenieía Matemática Univesidad de Chile a) Suponga que u(τ, x) satisface u τ + u u = 0, sobe una cuva donde la vaiable x se escibe como función difeenciable de τ, paa la cual: dx = u(τ, x) dτ Puebe entonces que u(τ, x(τ)) es constante. b) Sea f : Ê 2 Ê una función difeenciable y g : Ê 3 Ê 2 donde g(x, y, z) = (g 1 (x, y, z), g 2 (x, y, z) con g 1 (x, y, z) = (x, y, z) 2 y g 2 (x, y, z) = x + y + z. Sea h = f g. Puebe que: h 2 = 4 ( ) 2 g ( ) 2 u u g P4.- Sea g = (g 1, g 2 ) : Ê 3 Ê 2 y f : Ê 2 Ê 2 donde g(1, 1, 1) = (2, 3) y Df(2, 3) = ] ] xy y f g(x, y, z) = 2 z 2 x 2 y 2 z Calcule: g 2 (1, 1, 1) P5.- Definimos g(x) = { (x 2 y) 2 y 2 x si 0 < x, 0 < y < x 2 0 si no Sea γ(t) = (t, 1 2 t2 ). Es g γ(t) difeenciable en t = 0?. A pati de la egla de la cadena Qué puede conclui de la difeenciabilidad de g en (0, 0)?. P6.- Si u, v y w son las funciones de (x, y, z) definidas po: u = e x cos(y) v = e x sen(y) w = x + y + z Halla el Jacobiano de (u, v, w) especto al cambio de vaiables en coodenadas esféicas, θ, ϕ; a sabe: x = cos(ϕ)sen(θ), y = sen(ϕ)sen(θ), z = cos(θ) 2
3 P7.- a) Sea f : Ê 3 Ê definida po: f(x, y, z) = que: x + y + z z = 0 (x, y, z) (0, 0, 0) Ingenieía Matemática Univesidad de Chile ( x y+z n. x+y z) Puebe b) Sean f : Ê 2 Ê y g : Ê 2 Ê 2 funciones difeenciables. Se define: z(u, v) = e g(u,v) f2 (u,v). (i) Detemine las deivadas paciales de z. Es z difeenciable? (ii) Si f(u, v) = uv y g(u, v) = 1 v. Compuebe la fomula obtenida en la pate anteio (en donde f y g son difeenciables). P8.- Sean f, g : Ê Ê tales que f y g existen. Sea F(x, y) = f(x+g(y)). Calcula 2 F y 2 F 2 Dónde están evaluadas? P9.- a) Una función f : Ê n Ê se dice homogénea de gado m si satisface que f(tx) = t m f(x) x Ê n, t > 0. Demueste que si f es difeenciable en Ê n y homogénea de gado m, entonces se tiene la identidad: mf(x) = f(x), x, x Ê n. Hint: Deive de dos fomas la función φ(t) = f(tx). b) Un abieto Ω Ê n se dice conexo po caminos si paa todo pa de puntos x, y Ω, existe una función γ : 0, 1] Ê n difeenciable en 0, 1] tal que: γ(0) = x, γ(1) = y y γ(t) Ω t 0, 1], esto es, un camino difeenciable que une los puntos x e y dento de Ω. Demueste que si Ω es conexo po caminos y f : Ω Ê es difeenciable en Ω y tal que f(x) = 0, Ω, entonces f es constante. De un contaejemplo a esta afimación si Ω no es conexo po caminos. Hint: Fije un punto x 0 Ω y considee paa y Ω un camino difeenciable γ(t) con γ(0) = x 0, γ(1) = y. Defina φ(t) = f(γ(t)). Deivadas de oden supeio 3
4 P10.- Sea E = x 2 2 z + 2xy 2 z 2 po: ( y ( y z(x, y) = xϕ + ψ x) x) + y2 2 z Ingenieía Matemática Univesidad de Chile 2 donde z : Ê 2 Ê está definida donde ϕ, ψ : Ê Ê dos veces difeenciables. Detemine el valo de E. Paa los siguientes poblemas considee la definición del laplaciano: Sea f : Ê N R una función 2 veces difeenciable. Se define el laplaciano de f como: N f = i Y la ecuación de Laplace: i=1 f = 0 P11.- Detemine cuales de las siguientes funciones satisface la ecuación de Laplace: a) u(x, y) = x 3 3xy 2. b) u(x, y) = sen(x) cosh(y) (ecuede que cosh(x) = ex +e x 2 ). c) u(x, y) = e x sen(y). P12.- Suponga que u : R 2 R, función dos veces difeenciable, satisface la ecuación de Laplace. Puebe que v(s, t) = u(st, 1 2 (s2 t 2 )) también satisface la Ecuación de Laplace. P13.- a) Calcule el Laplaciano usando el cambio de vaiables en coodenadas cilíndicas: x(, θ, z) = cos(θ), y(, θ, z) = sen(θ), z(, θ, z) = z b) Repita lo anteio peo usando coodenadas esféicas. P14.- Sea u : Ê 2 Ê de clase C 2 (Ê 2 ). Demueste que la ecuación x 2 2 u 2 + y2 2 u 2 + x u + y u = 0 toma la foma 2 u u s 2 = 0 bajo el cambio de vaiables x = e, y = e s. 4
5 3. PROBLEMAS RESUELTOS Ingenieía Matemática Univesidad de Chile P15.- Sean f(x, y) y g(x, y) 2 funciones difeenciables a valoes en Ê. Sean ahoa u y v definidas po: u(, ϕ) = cos(ϕ)f( cos(ϕ), sen(ϕ)) + sen(ϕ)g( cos(θ), sen(θ)) v(, ϕ) = sen(ϕ)f( cos(ϕ), sen(ϕ)) + cos(ϕ)g( cos(θ), sen(θ)) Puebe que: + v + 1 u Solución: ϕ = g g( cos(θ), sen(θ)) ( cos(θ), sen(θ)) Calculemos los téminos involucados en el lado izquiedo: = sen(ϕ) = v = sen(ϕ) f + cos(ϕ) g 1 u ϕ = 1 = sen(ϕ) g g cos(ϕ) + ] cos(ϕ) + sen(ϕ) + cos(ϕ) sen(ϕ) cos(ϕ) sen2 (ϕ) + g cos2 (ϕ) + g ] sen(ϕ) cos(ϕ) sen(ϕ) { ] sen(ϕ)f + cos(ϕ) ( sen(ϕ)) + ( cos(ϕ)) ]} cos(ϕ)g + sen(ϕ) g g ( sen(ϕ)) + ( cos(ϕ)) f cos(ϕ) g + sen(ϕ) cos(ϕ) cos2 (ϕ) + g sen2 (ϕ) g sen(ϕ) cos(ϕ) Finalmente, basta suma todas las expesiones anteioes paa obtene: + v + 1 u ϕ = g Es necesaio tene en cuenta que en ésta expesión tanto g como están en función de las vaiables y ϕ (como se pedía en el enunciado). P16.- (P3 C2 OT 2007, M. del Pino) La tempeatua T(x, y) en equilibio, en una egión Ω de Ê 2 satisface en condiciones ideales la ecuación de Laplace. Suponga que Ω es la egión anula: Ω = {(x, y) 1 < x 2 + y 2 < 4} y que se sabe que la tempeatua es una función que sólo depende de la distancia al oigen, esto es T(x, y) = u( x 2 + y 2 ) paa una 5
6 Ingenieía Matemática Univesidad de Chile función u() dos veces deivable en 1, 2]. Si adicionalmente se conoce la tempeatua en la fontea de esta egión: u(1) = T 1, u(2) = T 2 se le pide enconta la tempeatua en todo punto de Ω. Hint: Mueste que u() satisface la ecuación difeencial odinaia: u () + u () = 0, 1, 2] Solución: Calculamos las deivadas paciales de T usando la egla de la cadena, que es posible utiliza pues la noma es difeenciable paa (x, y) 0. Nota además que como la función es simética basta calcula las deivadas paciales con especto a una componente: 2 T 2 = u ( x 2 + y 2 ) T = u ( x 2 + y 2 x ) x2 + y 2 ( ) 2 x + u ( x2 + y 2 x 2 + y 2 ) x 2 +y 2 x 2 + y 2 = u ( x 2 + y 2 ) x 2 x 2 +y 2 + u ( x 2 + y 2 ) Entonces el Laplaciano de T satisface: u ( x 2 + y 2 ) + u ( x 2 + y 2 ) y 2 x 2 +y 23 1 x2 + y 2 = T = 0 x2 x 2 +y 2 Como x 2 + y 2 ecoe todos los valoes en (1, 2), la ecuación difeencial odinaia: u () + u () = 0, 1, 2] es válida, con lo que se pueba el hint. Ahoa utilizaemos factoes integantes paa esolve esta E.D.O., multiplicando la ecuación po : 0 = u () + u () = (u ()) Po lo tanto u () = cte. = A. Dividiendo po e integando nuevamente: u() = A ln() + B con A y B constantes a detemina po las condiciones en los bodes. Recodamos que: T 1 = u(1) = A ln(1) + B = B, T 2 = u(2) = A ln(2) + B Finalmente: B = T 1 y A = T2 B ln(2) y: u() = T 2 B ln(2) ln() + T 1 = T(x, y) = T 2 B ln(2) ln( x 2 + y 2 ) + T 1 6
Guía Regla de la Cadena(1 er Orden)
 UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
PAUTA CONTROL 3 CÁLCULO EN VARIAS VARIABLES, 2014/1
 PAUTA CONTROL CÁLCULO EN VARIAS VARIABLES, 14/1 (1) (a) Demueste que el máximo de la función x y z sobe la esfea x + y + z = a es (a /) y que el mínimo de la función x + y + z sobe la supeficie x y z =
PAUTA CONTROL CÁLCULO EN VARIAS VARIABLES, 14/1 (1) (a) Demueste que el máximo de la función x y z sobe la esfea x + y + z = a es (a /) y que el mínimo de la función x + y + z sobe la supeficie x y z =
CÁLCULO Primer curso de Ingeniero de Telecomunicación Segundo Examen Parcial. 13 de Junio de 2001 Primera parte. ; y = u v ; z = u2 v 2
 CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
. Esta segunda función es posible que no pueda explicitarse: no pueda encontrarse la fórmula y f (x)
 1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
Apuntes de Electrostática Prof. J. Martín ETSEIT ELECTROESTÁTICA I CAMPO ELECTRICO EN EL ESPACIO LIBRE
 LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
SOLUCIÓN EXAMEN PARCIAL II Ecuaciones Diferenciales II
 SOLUCIÓN EXAMEN PARCIAL II Ecuaciones Difeenciales II D. Miguel Angel Uh Zapata 29 de octube de 215 2 hoas) Ejecicio III.1 Dado los siguientes poblemas indica y agumenta si son o no poblemas del tipo Stum-
SOLUCIÓN EXAMEN PARCIAL II Ecuaciones Difeenciales II D. Miguel Angel Uh Zapata 29 de octube de 215 2 hoas) Ejecicio III.1 Dado los siguientes poblemas indica y agumenta si son o no poblemas del tipo Stum-
Plano Tangente a una superficie
 Plano Tangente a una supeficie Plano Tangente a una supeficie Sea z f ( una función escala con deivadas paciales continuas en (a b del dominio de f. El plano tangente a la supeficie en el punto P( a b
Plano Tangente a una supeficie Plano Tangente a una supeficie Sea z f ( una función escala con deivadas paciales continuas en (a b del dominio de f. El plano tangente a la supeficie en el punto P( a b
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
FLUJO POTENCIAL BIDIMENSIONAL (continuación)
 Pof. ALDO TAMBURRINO TAVANTZIS Pof. ALDO TAMBURRINO TAVANTZIS FLUJO POTENCIAL BIDIMENSIONAL (continuación) RESUMEN DE LA CLASE ANTERIOR Si un flujo es iotacional, V 0, entonces eiste una función escala
Pof. ALDO TAMBURRINO TAVANTZIS Pof. ALDO TAMBURRINO TAVANTZIS FLUJO POTENCIAL BIDIMENSIONAL (continuación) RESUMEN DE LA CLASE ANTERIOR Si un flujo es iotacional, V 0, entonces eiste una función escala
( ) y ( ) = CAMPOS: OPERADOR NABLA ( ) ( )
 CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
F =. Calcule F d S donde S es. Exprese una integral de una variable que permita calcular., S es la porción del elipsoide
 egio Yansen Núñez Teoema de tokes y Gauss Actividad Nº Considee el campo vectoial F( x, y, z) ( y, x, z ). Calcule F d donde C es C la intesección ente el plano x + y + z y el cilindo x + y. Actividad
egio Yansen Núñez Teoema de tokes y Gauss Actividad Nº Considee el campo vectoial F( x, y, z) ( y, x, z ). Calcule F d donde C es C la intesección ente el plano x + y + z y el cilindo x + y. Actividad
. Estos vectores unitarios apuntan siempre en la misma dirección y en el mismo sentido, y no cambian, por tanto, de un punto a otro del espacio.
 CAPÍTUL 7.01 ÁLGEBRA VECTRIAL Sistemas de coodenadas Un sistema de coodenadas es un conjunto de valoes numéicos que deteminan unívocamente la posición de un punto en el espacio euclidiano. Las coodenadas
CAPÍTUL 7.01 ÁLGEBRA VECTRIAL Sistemas de coodenadas Un sistema de coodenadas es un conjunto de valoes numéicos que deteminan unívocamente la posición de un punto en el espacio euclidiano. Las coodenadas
INSTITUTO DE FÍSICA MECÁNICA NEWTONIANA
 INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS
 TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
Tema 2: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 4/7 Leyes de la electrostática
 Tema : Pincipios de la electostática 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Leyes de la electostática Leyes de la electostática:
Tema : Pincipios de la electostática 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Leyes de la electostática Leyes de la electostática:
APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 7 POTENCIAL ELECTROSTÁTICO
 EL POTENCIAL ELÉCTRICO. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA II Pofeso: José Fenando Pinto Paa UNIDAD 7 POTENCIAL ELECTROSTÁTICO Dos cagas en la misma posición tienen dos veces más enegía
EL POTENCIAL ELÉCTRICO. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA II Pofeso: José Fenando Pinto Paa UNIDAD 7 POTENCIAL ELECTROSTÁTICO Dos cagas en la misma posición tienen dos veces más enegía
Series de Polinomios Ortogonales
 Semana - Clase 6 9/0/0 Tema : Seies Seies de Polinomios Otogonales Enunciaemos un teoema debido a Weiestass el cual gaantiza que una función contínua en un intevalo [a, b puede se apoximada unifomemente
Semana - Clase 6 9/0/0 Tema : Seies Seies de Polinomios Otogonales Enunciaemos un teoema debido a Weiestass el cual gaantiza que una función contínua en un intevalo [a, b puede se apoximada unifomemente
Teoremas Integrales. V(x j ) ds
 Semana 2 - Clase 5 24/03/09 Tema : Algeba ectoial Teoemas Integales. Teoema de la Divegencia o de Gauss Sea = x j ) un campo vectoial definido sobe un volumen cuya fontea es la supeficie y ˆn el vecto
Semana 2 - Clase 5 24/03/09 Tema : Algeba ectoial Teoemas Integales. Teoema de la Divegencia o de Gauss Sea = x j ) un campo vectoial definido sobe un volumen cuya fontea es la supeficie y ˆn el vecto
CAPÍTULO II LEY DE GAUSS
 Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
5 El colectivo macrocanónico.
 5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
Guía Semana 7 1. RESUMEN 2. EJERCICIOS PROPUESTOS. Universidad de Chile. Ingeniería Matemática
 . RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
. RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
SERIE # 3 CÁLCULO VECTORIAL
 SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) f(x, y) = x 2 y 2 ln(x 2 + y 2 ) y determine si satisface o no la ecuación en derivadas parciales:
 GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) CÁLCULO III (OTOÑO 207) - Calcule las derivadas parciales f x y f y i) ln(y + x 2 + y 2 ) xy ii) +x 2 +y 2 iii) arcsin(x/y) iv) (x 2 + y 2 )e xy v) x2 y 2 x 2 +y
GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) CÁLCULO III (OTOÑO 207) - Calcule las derivadas parciales f x y f y i) ln(y + x 2 + y 2 ) xy ii) +x 2 +y 2 iii) arcsin(x/y) iv) (x 2 + y 2 )e xy v) x2 y 2 x 2 +y
Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).
![Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ). Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).](/thumbs/76/73987868.jpg) Electomagnetismo I Semeste: 25-2 Pof. Alejando Reyes Coonado Ayud. Calos Albeto Maciel Escudeo Ayud. Chistian Espaza López Solución a la Taea 5 Solución po Calos Maciel Escudeo. Poblema: 2pts El potencial
Electomagnetismo I Semeste: 25-2 Pof. Alejando Reyes Coonado Ayud. Calos Albeto Maciel Escudeo Ayud. Chistian Espaza López Solución a la Taea 5 Solución po Calos Maciel Escudeo. Poblema: 2pts El potencial
y 2 dy dx = 1 x 2 dx y 2 dy = 1 9 sen 1. 0 x 3 y dy dx = 0 dx = 0. 6 = y=x 2 1 y [y 2 y 3 ] dy = 1 [ 1 1 e = cos y x sen x dx + π
![y 2 dy dx = 1 x 2 dx y 2 dy = 1 9 sen 1. 0 x 3 y dy dx = 0 dx = 0. 6 = y=x 2 1 y [y 2 y 3 ] dy = 1 [ 1 1 e = cos y x sen x dx + π y 2 dy dx = 1 x 2 dx y 2 dy = 1 9 sen 1. 0 x 3 y dy dx = 0 dx = 0. 6 = y=x 2 1 y [y 2 y 3 ] dy = 1 [ 1 1 e = cos y x sen x dx + π](/thumbs/67/57337196.jpg) Solciones de poblemas de Cálclo (gpo - /6). Integales múltiples. a) b) c) ( + ) d d = e d d = [ e ] d d + d = d d = d + d =. [ e ] d = e = e. () cos d d = [ sen ] d = sen d = 9 sen.. a) log() d d = log
Solciones de poblemas de Cálclo (gpo - /6). Integales múltiples. a) b) c) ( + ) d d = e d d = [ e ] d d + d = d d = d + d =. [ e ] d = e = e. () cos d d = [ sen ] d = sen d = 9 sen.. a) log() d d = log
Tema 1: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 4/7 Flujo, divergencia y teorema de Gauss
 Tema 1: Fundamentos Matemáticos 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Flujo, divegencia y teoema de Gauss Concepto
Tema 1: Fundamentos Matemáticos 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Flujo, divegencia y teoema de Gauss Concepto
Consideremos dos placas paralelas en contacto, con sus correspondientes espesores y conductividades.
 Continuación: Tansfeencia de calo a tavés de placas compuestas: Consideemos dos placas paalelas en contacto, con sus coespondientes espesoes y conductividades. En la supeficie de contacto la tempeatua
Continuación: Tansfeencia de calo a tavés de placas compuestas: Consideemos dos placas paalelas en contacto, con sus coespondientes espesoes y conductividades. En la supeficie de contacto la tempeatua
SELECTIVIDAD SEPTIEMBRE 2004 MATEMÁTICAS II
 Depatament de Matemàtiques Ieslaasuncionog/matematicas SELECTIVIDAD SEPTIEMBRE MATEMÁTICAS II EJERCICIO A PROBLEMA Obtene todos los valoes eales x, y, z, t paa los que se veifica AX XA, siendo X y A z
Depatament de Matemàtiques Ieslaasuncionog/matematicas SELECTIVIDAD SEPTIEMBRE MATEMÁTICAS II EJERCICIO A PROBLEMA Obtene todos los valoes eales x, y, z, t paa los que se veifica AX XA, siendo X y A z
Fuerza magnética sobre conductores.
 Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Lección 2. El campo de las cargas en reposo: campo electrostático.
 Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
PRÁCTICA 7. b) Elabore un archivo de Excel que calcule la cantidad que va a producir esta empresa (no es obligatorio).
 1.- Suponga una empesa que actúa como competitiva a pesa de que es la única empesa del secto. A coto plazo, tiene la siguiente función de costes totales (donde epesenta la cantidad de bien): 56 a) Si la
1.- Suponga una empesa que actúa como competitiva a pesa de que es la única empesa del secto. A coto plazo, tiene la siguiente función de costes totales (donde epesenta la cantidad de bien): 56 a) Si la
VECTORES EN DIFERENTES SISTEMAS DE COORDENADAS. TRANSFORMACIONES ENTRE SISTEMAS
 VECTRES EN DIFERENTES SISTEMAS DE CRDENADAS. TRANSFRMACINES ENTRE SISTEMAS Sistema ectangula Se explica especto de tes ejes pependiculaes ente sí (,,) que se cotan fomando un tiedo y sobe los que están
VECTRES EN DIFERENTES SISTEMAS DE CRDENADAS. TRANSFRMACINES ENTRE SISTEMAS Sistema ectangula Se explica especto de tes ejes pependiculaes ente sí (,,) que se cotan fomando un tiedo y sobe los que están
GEOMETRÍA. 1. Sin resolver el sistema, determina si la recta 2x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia
 Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Una nueva teoría electromagnetica I. Propiedades del electrón en reposo: masa, carga, spin y estabilidad.
 Una nueva teoía electomagnetica I. Popiedades del electón en eposo: masa, caga, spin y estabilidad. Manuel Henández Rosales. 18 de Junio de 215 Abstact En este atículo a pati de nuevas ecuaciones paa el
Una nueva teoía electomagnetica I. Popiedades del electón en eposo: masa, caga, spin y estabilidad. Manuel Henández Rosales. 18 de Junio de 215 Abstact En este atículo a pati de nuevas ecuaciones paa el
CLASE #2 de Bessel: Modos normales de una membrana circular (Continuación):
 CLASE #2 de Bessel: Modos nomales de una membana cicula (Continuación): Intoducción En la clase anteio esolvimos usando el Método de Sepaación de Vaiables, la ecuación de ondas paa una membana cicula de
CLASE #2 de Bessel: Modos nomales de una membana cicula (Continuación): Intoducción En la clase anteio esolvimos usando el Método de Sepaación de Vaiables, la ecuación de ondas paa una membana cicula de
Ayudantía Regla de la Cadena. Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática
 / 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
/ 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
Aplicación de los Residuos al cálculo de Integrales Reales
 Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
Capítulo 8. Sistemas de partículas idénticas
 Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Aplicaciones de la Optimización Convexa al análisis de redes
 Aplicaciones de la Optimización Convea al análisis de edes Intoducción Repaso de conceptos básicos de unciones de vaias vaiables y conveidad Repaso : Función deivada pacial La deivada pacial de con especto
Aplicaciones de la Optimización Convea al análisis de edes Intoducción Repaso de conceptos básicos de unciones de vaias vaiables y conveidad Repaso : Función deivada pacial La deivada pacial de con especto
Ecuaciones del movimiento de un fluido
 Ecuaciones del movimiento de un fluido 1 Foma fundamental El tenso de tensiones Relación constitutiva paa un fluido Newtoniano La ecuación de Navie-Stokes El tenso de tensiones paa flujos incompesibles
Ecuaciones del movimiento de un fluido 1 Foma fundamental El tenso de tensiones Relación constitutiva paa un fluido Newtoniano La ecuación de Navie-Stokes El tenso de tensiones paa flujos incompesibles
Robótica Industrial. Robótica Industrial
 TEMA 3: HERRAMIENTAS MATEMÁTICAS PARA LA LOCALIZACIÓN INDUSTRIAL Ingenieía de Sistemas y Automática Contol de Robots y Sistemas Sensoiales Robótica Industial Robótica Industial ISA.- Ingenieía de Sistemas
TEMA 3: HERRAMIENTAS MATEMÁTICAS PARA LA LOCALIZACIÓN INDUSTRIAL Ingenieía de Sistemas y Automática Contol de Robots y Sistemas Sensoiales Robótica Industial Robótica Industial ISA.- Ingenieía de Sistemas
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO Geometría lineal Recta y Plano
 LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
EXAMEN ORDINARIO DE TECNOLOGÍAS DE ALTA FRECUENCIA DPTO. DE TEORÍA DE LA SEÑAL Y COMUNICACIONES
 (hay que entega la hoja de cada enunciado, duación total 3 hoas y 5 minutos) PROBLEMA 2 DE ANÁLISIS DE CIRCUITOS DE MICROONDAS (75 minutos, 35 puntos, tiene que entega la hoja de enunciado con el nombe)
(hay que entega la hoja de cada enunciado, duación total 3 hoas y 5 minutos) PROBLEMA 2 DE ANÁLISIS DE CIRCUITOS DE MICROONDAS (75 minutos, 35 puntos, tiene que entega la hoja de enunciado con el nombe)
Lección 4. Funciones de varias variables. Derivadas. 4. Las reglas de la cadena.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 11 1. Lección 4. Funciones de aias aiables. Deiadas paciales. 4. Las eglas de la cadena. Las eglas de la cadena nos pemien calcula las deiadas paciales de una función
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 11 1. Lección 4. Funciones de aias aiables. Deiadas paciales. 4. Las eglas de la cadena. Las eglas de la cadena nos pemien calcula las deiadas paciales de una función
MAGNITUDES ESCALARES Y VECTORIALES
 U R S O: FÍSI OMÚN MTERIL: F-01 Sistema intenacional de medidas MGNITUDES ESLRES VETORILES En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales. El sistema
U R S O: FÍSI OMÚN MTERIL: F-01 Sistema intenacional de medidas MGNITUDES ESLRES VETORILES En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales. El sistema
Ecuación de Laplace y Ecuación de Poisson Teorema de Unicidad. Métodos de las Imágenes. Campos y Ondas UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA
 Electostática táti Clase 3 Ecuación de Laplace y Ecuación de Poisson Teoema de Unicidad. Métodos de las Imágenes Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA 2 E V m
Electostática táti Clase 3 Ecuación de Laplace y Ecuación de Poisson Teoema de Unicidad. Métodos de las Imágenes Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA 2 E V m
Potencial Escalar - Integrales de superposición. 2010/2011
 Potencial Escala - Integales de supeposición. / Electostática Definición os conductoes en electostática. Campo de una caga puntual. Aplicaciones de la ey de Gauss Integales de supeposición. Potencial electostático
Potencial Escala - Integales de supeposición. / Electostática Definición os conductoes en electostática. Campo de una caga puntual. Aplicaciones de la ey de Gauss Integales de supeposición. Potencial electostático
Tema 7 Geometría en el espacio Matemáticas II 2º Bachillerato 1
 Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
GUIA Hallar el módulo del vector de origen en (20,-5,8) y extremo en (-4,-3,2).
 GUIA 0 1 - Halla el módulo del vecto de oigen en (20,-5,8) etemo en (-4,-3,2). 2 - a) Halla las componentes catesianas de los siguientes vectoes: (i) A (ii) A = 4 A = θ = 30º 4 θ =135º A (iii) (iv) A θ
GUIA 0 1 - Halla el módulo del vecto de oigen en (20,-5,8) etemo en (-4,-3,2). 2 - a) Halla las componentes catesianas de los siguientes vectoes: (i) A (ii) A = 4 A = θ = 30º 4 θ =135º A (iii) (iv) A θ
z Región III Región II Región I
 Capacito de placas ciculaes - solución completa amos a calcula el potencial electostático en todo el espacio paa un capacito de placas ciculaes y paalelas. Las placas conductoas están ubicadas en z = ±l/2,
Capacito de placas ciculaes - solución completa amos a calcula el potencial electostático en todo el espacio paa un capacito de placas ciculaes y paalelas. Las placas conductoas están ubicadas en z = ±l/2,
Potencial gravitomagnético producido por una esfera en rotación
 5 Potencial gavitomagnético poducido po una esfea en otación 1.5 Cálculo del potencial gavitomagnético poducido en el exteio de un cuepo esféico en otación Obtenidos los fundamentos de la teoía gavitoelectomagnética,
5 Potencial gavitomagnético poducido po una esfea en otación 1.5 Cálculo del potencial gavitomagnético poducido en el exteio de un cuepo esféico en otación Obtenidos los fundamentos de la teoía gavitoelectomagnética,
Capitulo III. Capítulo III
 Cinemática y Dinámica de Máquinas. III. Métodos analíti de análisis cinemático Capitulo III Métodos analíti de análisis cinemático. 1 R Sancibián y. de Juan. Ing. Mecánica Cinemática y Dinámica de Máquinas.
Cinemática y Dinámica de Máquinas. III. Métodos analíti de análisis cinemático Capitulo III Métodos analíti de análisis cinemático. 1 R Sancibián y. de Juan. Ing. Mecánica Cinemática y Dinámica de Máquinas.
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS
 IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES.
 OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES. 1 Intoducción Los movimientos de choos de líquido en el seno del mismo líquido, la estela de cuepos en el seno de una coiente
OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES. 1 Intoducción Los movimientos de choos de líquido en el seno del mismo líquido, la estela de cuepos en el seno de una coiente
ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3. Página para el curso:
 ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3 DANIEL LABARDINI FRAGOSO DANIEL BALAM CRUZ HUITRÓN Página paa el cuso: www.matem.unam.mx/labadini/teaching.html A lo lago de los siguientes ejecicios, seá un campo.
ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3 DANIEL LABARDINI FRAGOSO DANIEL BALAM CRUZ HUITRÓN Página paa el cuso: www.matem.unam.mx/labadini/teaching.html A lo lago de los siguientes ejecicios, seá un campo.
MECANICA APLICADA I. EXAMEN PARCIAL PRIMER EJERCICIO TIEMPO: 75. cuando
 MECNIC PLICD I. EXMEN PCIL. 17-04-99. PIME EJECICI TIEMP: 75 1. btene la expesión de la velocidad de ω V s ω V s sucesión del cento instantáneo de otación cuando =. 2 2. Indica qué afimaciones son cietas
MECNIC PLICD I. EXMEN PCIL. 17-04-99. PIME EJECICI TIEMP: 75 1. btene la expesión de la velocidad de ω V s ω V s sucesión del cento instantáneo de otación cuando =. 2 2. Indica qué afimaciones son cietas
Diferencia de potencial y potencial eléctricos. En el campo gravitatorio.
 Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Fundamentos de Química Terma3 2
 Tema 3: Estuctua atómica (II): Estuctua electónica del átomo 3.1 Intoducción a la mecanica cuántica 3. Ecuación de Schödinge. 3.3 Modelo mecanocuántico del átomo 3.4 Átomos polielectónicos y configuación
Tema 3: Estuctua atómica (II): Estuctua electónica del átomo 3.1 Intoducción a la mecanica cuántica 3. Ecuación de Schödinge. 3.3 Modelo mecanocuántico del átomo 3.4 Átomos polielectónicos y configuación
LEY DE COULOMB. INTENSIDAD DE CAMPO ELÉCTRICO. DENSIDAD DE FLUJO ELÉCTRICO. LEY DE GAUSS. DIVERGENCIA. ENERGÍA. POTENCIA. CORRIENTE Y CONDUCTORES.
 REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN UNIVERSITARIA UNIVERSIDAD POLITÉCNICA TERRITORIAL DE ARAGUA FEDERICO BRITO FIGUEROA PROGRAMA NACIONAL DE FORMACIÓN EN ELECTRÓNICA
REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN UNIVERSITARIA UNIVERSIDAD POLITÉCNICA TERRITORIAL DE ARAGUA FEDERICO BRITO FIGUEROA PROGRAMA NACIONAL DE FORMACIÓN EN ELECTRÓNICA
r r 3 producido por una carga Q localizada en el origen, con ε constante. a. Demuestre que (3 puntos)
 U..V. F.I.U..V. ÁLULO VETORIAL (54) PRIMER PARIAL (3%) 5/1/9 MATEMÁTIA APLIADA Pof. 1. Sean el campo posición (x,, z) = (x,, z) el campo eléctico E = ε Q poducido po una caga Q localizada en el oigen,
U..V. F.I.U..V. ÁLULO VETORIAL (54) PRIMER PARIAL (3%) 5/1/9 MATEMÁTIA APLIADA Pof. 1. Sean el campo posición (x,, z) = (x,, z) el campo eléctico E = ε Q poducido po una caga Q localizada en el oigen,
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
Problemas Tema 8 Sistemas singulares de Sturm-Liouville. Funciones de Bessel
 Ingenieo Industial Tansfomadas Integales y Ecuaciones en Deivadas Paciales Cuso 1/11 J.A. Muillo Poblemas Tema 8 Sistemas singulaes de Stum-Liouville. Funciones de Bessel 4. Encuenta la solución de la
Ingenieo Industial Tansfomadas Integales y Ecuaciones en Deivadas Paciales Cuso 1/11 J.A. Muillo Poblemas Tema 8 Sistemas singulaes de Stum-Liouville. Funciones de Bessel 4. Encuenta la solución de la
Paredes Delgadas. Clase 6 Recipiente de Revolución de Paredes Delgadas. Facultad de Ingeniería - UNA
 Paedes Delgadas Clase 6 Recipiente de Revolución de Paedes Delgadas Impotancia páctica de la evolución de los cálculos Catedal de San Pedo, edificada en el siglo XVI, Luz 40 m, espeso pomedio de 3 metos
Paedes Delgadas Clase 6 Recipiente de Revolución de Paedes Delgadas Impotancia páctica de la evolución de los cálculos Catedal de San Pedo, edificada en el siglo XVI, Luz 40 m, espeso pomedio de 3 metos
DIVISIBILIDAD DE POLINOMIOS
 DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
Adenda Electrones en potencial periódico
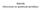 Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
200. Hallar la ecuación de la simetría ortogonal respecto de la recta:
 Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Medición de la conductividad térmica de materiales aislantes en el CENAM Dr. Leonel Lira Cortés Dr. Edgar Mendez Lango
 Medición de la conductividad témica de mateiales aislantes en el CENAM D. Leonel Lia Cotés D. Edga Mendez Lango ÁREA DE METROLOGÍA ELECTRÍCA DIVISIÓN DE TERMOMETRÍA CONTENIDO INTRODUCCION ECUACION DE CONDUCCION
Medición de la conductividad témica de mateiales aislantes en el CENAM D. Leonel Lia Cotés D. Edga Mendez Lango ÁREA DE METROLOGÍA ELECTRÍCA DIVISIÓN DE TERMOMETRÍA CONTENIDO INTRODUCCION ECUACION DE CONDUCCION
Apunte FII-1-RM: Repaso de Matemática
 Física II Física B - Electomagnetismo Pofesoa: Da. C. Caletti : Repaso de Matemática I. Gadiente A fin de compende mejo el concepto de gadiente comenzaemos po las bases, analizando, peviamente, qué tipo
Física II Física B - Electomagnetismo Pofesoa: Da. C. Caletti : Repaso de Matemática I. Gadiente A fin de compende mejo el concepto de gadiente comenzaemos po las bases, analizando, peviamente, qué tipo
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
Tema 4.-Potencial eléctrico
 Tema 4: Potencial eléctico Fundamentos Físicos de la Ingenieía Pime cuso de Ingenieía Industial Cuso 6/7 Dpto. Física plicada III Univesidad de Sevilla 1 Índice Intoducción: enegía potencial electostática
Tema 4: Potencial eléctico Fundamentos Físicos de la Ingenieía Pime cuso de Ingenieía Industial Cuso 6/7 Dpto. Física plicada III Univesidad de Sevilla 1 Índice Intoducción: enegía potencial electostática
ANEJO 2 CÁLCULO DE DEPÓSITOS CILÍNDRICOS CIRCULARES SEGÚN LA TEORIA DE LÁMINAS A2.1.- INTRODUCCIÓN
 Anejo ANEJO CÁLCULO DE DEPÓSITOS CILÍNDRICOS CIRCULARES SEGÚN LA TEORIA DE LÁMINAS A.1.- INTRODUCCIÓN En el capítulo 3 se ha desaollado una fomulación paa el dimensionamiento y compobación de depósitos
Anejo ANEJO CÁLCULO DE DEPÓSITOS CILÍNDRICOS CIRCULARES SEGÚN LA TEORIA DE LÁMINAS A.1.- INTRODUCCIÓN En el capítulo 3 se ha desaollado una fomulación paa el dimensionamiento y compobación de depósitos
Su objetivo: Cuantificar los flujos de transporte de calor en procesos naturales y de Ingeniería.
 TRANSFERENCIA DE CALOR La Tansfeencia de Calo es una Ciencia de la Ingenieía, una disciplina páctica Su objetivo: Cuantifica los flujos de tanspote de calo en pocesos natuales y de Ingenieía. Temodinámica:
TRANSFERENCIA DE CALOR La Tansfeencia de Calo es una Ciencia de la Ingenieía, una disciplina páctica Su objetivo: Cuantifica los flujos de tanspote de calo en pocesos natuales y de Ingenieía. Temodinámica:
LEY DE GAUSS. Este enunciado constituye en realidad una de las principales leyes del Electromagnetismo.
 LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
Examen de Física-1, 1 Ingeniería Química Diciembre de 2010 Cuestiones (Un punto por cuestión).
 Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
CAMPOS ELECTROMAGNÉTICOS
 CAMPOS ELECTROMAGNÉTICOS GRADO EN INGENIERÍA AEROESPACIAL EN AERONAVEGACIÓN UNIVERSIDAD RE JUAN CARLOS «ANÁLISIS VECTORIAL» CURSO ACADÉMICO 15/16 Índice 1. Escalaes vectoes 2 1.1. Nociones básicas de análisis
CAMPOS ELECTROMAGNÉTICOS GRADO EN INGENIERÍA AEROESPACIAL EN AERONAVEGACIÓN UNIVERSIDAD RE JUAN CARLOS «ANÁLISIS VECTORIAL» CURSO ACADÉMICO 15/16 Índice 1. Escalaes vectoes 2 1.1. Nociones básicas de análisis
Guía Semanas 13 y RESUMEN. Universidad de Chile. Ingeniería Matemática. Triedro de vectores y factores escalares. Supongamos que r.
 1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
Cálculo de integrales reales impropias mediante teoría de residuos
 Análisis III B - Tuno mañana - Integales impopias 1 Cálculo de integales eales impopias mediante teoía de esiduos Teoema 1. Sea f : C C tal que a) f es holomofa en Im(z) > salvo en un númeo finito de puntos
Análisis III B - Tuno mañana - Integales impopias 1 Cálculo de integales eales impopias mediante teoía de esiduos Teoema 1. Sea f : C C tal que a) f es holomofa en Im(z) > salvo en un númeo finito de puntos
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES
 TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desaollo de facciones paciales es establecida paa cuida todos los casos sistemáticamente. Hay 4 clases de poblemas, dependiendo
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desaollo de facciones paciales es establecida paa cuida todos los casos sistemáticamente. Hay 4 clases de poblemas, dependiendo
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO
 SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
Combinación de operadores.
 Electicidad Magnetismo so / Tema : Intodcción oncepto de campo Repaso de álgeba vectoial istemas de coodenadas atesiano vilíneas genealiadas: cilíndico esféico. Opeadoes vectoiales. Gadiente Divegencia
Electicidad Magnetismo so / Tema : Intodcción oncepto de campo Repaso de álgeba vectoial istemas de coodenadas atesiano vilíneas genealiadas: cilíndico esféico. Opeadoes vectoiales. Gadiente Divegencia
Derivando dos veces respecto del tiempo obtenemos la aceleración del cuerpo:
 MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
Matemáticas II Hoja 6: Puntos, rectas y planos en el espacio
 Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
2. CURVAS EN EL SISTEMA POLAR
 2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES
 EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
Reflexiones sobre las Leyes de la ELECTROSTÁTICA
 Reflexiones sobe las Leyes de la ELECTROSTÁTICA todo empezo con la le Ley de Coulomb... eceta paa calcula E: dada la densidad de caga ρ, se puede (en pincipio) intega y obtene E Luego, desaollamos dos
Reflexiones sobe las Leyes de la ELECTROSTÁTICA todo empezo con la le Ley de Coulomb... eceta paa calcula E: dada la densidad de caga ρ, se puede (en pincipio) intega y obtene E Luego, desaollamos dos
BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION
 FACULTAD DE CIENCIAS CURSO DE INTRODUCCION A LA METEOROLOGIA 11 BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El oigen de la dinámica se emonta a los pimeos expeimentos
FACULTAD DE CIENCIAS CURSO DE INTRODUCCION A LA METEOROLOGIA 11 BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El oigen de la dinámica se emonta a los pimeos expeimentos
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
Funciones Compuestas.
 CAPÍTULO 4 Funciones Compuestas. En este capítulo trabajaremos con funciones compuestas. Aprendemos el equivalente multidimensional de la regla de la cadena que en varias variables adquiere una dimensión
CAPÍTULO 4 Funciones Compuestas. En este capítulo trabajaremos con funciones compuestas. Aprendemos el equivalente multidimensional de la regla de la cadena que en varias variables adquiere una dimensión
Tema 4.- La economía abierta
 Tema 4.- La economía abieta -Intoducción -Los flujos intenacionales de capitales y mecancías -El ahoo y la invesión en una pequeña economía abieta -Los tipos de cambio La economía ceada popociona modelos
Tema 4.- La economía abieta -Intoducción -Los flujos intenacionales de capitales y mecancías -El ahoo y la invesión en una pequeña economía abieta -Los tipos de cambio La economía ceada popociona modelos
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
Electrostática Clase 2 Vector Desplazamiento o densidad de flujo eléctrico. Ley de Gauss..
 Electostática Clase 2 Vecto Desplazamiento o densidad de flujo eléctico. Ley de Gauss.. Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA En cietos casos que se analizan
Electostática Clase 2 Vecto Desplazamiento o densidad de flujo eléctico. Ley de Gauss.. Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA En cietos casos que se analizan
Electromagnetismo II
 Electomagnetismo II emeste: 15-1 EXAMEN FINAL D. A. Reyes-oonado Ayud. J. astejón-figueoa Ayud. P. E. Roman-Taboada Elaboó: Pedo Eduado Roman Taboada 1.- Poblema: (pts) (a) Escibe las cuato ecuaciones
Electomagnetismo II emeste: 15-1 EXAMEN FINAL D. A. Reyes-oonado Ayud. J. astejón-figueoa Ayud. P. E. Roman-Taboada Elaboó: Pedo Eduado Roman Taboada 1.- Poblema: (pts) (a) Escibe las cuato ecuaciones
2λ λ. La ecuación del plano que buscamos es p: 5x 2y + 2z
 Poducto escala 060 Halla la ecuación de la ecta que cota a y s pependiculamente. x = 1 x = 6 µ : y = 11+ s: y = + µ z = 1+ z = + µ Hallamos un punto P y un punto Q s de modo que el vecto PQ sea pependicula
Poducto escala 060 Halla la ecuación de la ecta que cota a y s pependiculamente. x = 1 x = 6 µ : y = 11+ s: y = + µ z = 1+ z = + µ Hallamos un punto P y un punto Q s de modo que el vecto PQ sea pependicula
Coulomb. 2.2 La ley de Gauss. Gauss. 2.4 La discontinuidad de E n. conductores.
 CAPÍTULO Campo eléctico II: distibuciones continuas de caga Índice del capítulo.1 Cálculo del campo eléctico mediante la ley de Coulomb.. La ley de Gauss..3 Cálculo del campo eléctico mediante la ley de
CAPÍTULO Campo eléctico II: distibuciones continuas de caga Índice del capítulo.1 Cálculo del campo eléctico mediante la ley de Coulomb.. La ley de Gauss..3 Cálculo del campo eléctico mediante la ley de
