CONFIGURACIÓN ELECTRÓNICA
|
|
|
- María Rosa Domínguez Espinoza
- hace 6 años
- Vistas:
Transcripción
1 Cpítulo CONFIGURACIÓN ELECTRÓNICA CONFIGURACIÓN ELECTRÓNICA L form omo los ltrons s istriuyn n los ifrnts oritls un átomo s su onfigurión ltróni. L onfigurión ltróni más stl, o sl, un átomo s qull n l qu los ltrons stán n los stos nrgí más jos posils. PRINCIPIO DE EXCLUSIÓN DE PAULI Estl qu os ltrons n un mismo átomo no pun tnr los mismos stos uántios, s ir, no pun tnr l mismo onjunto númros uántios. Por onsiguint, n un oritl tómio pun xistir omo máximo os ltrons pr lo ul n tnr spins opustos. PRINCIPIO DE MÁXIMA MULTIPLICIDAD DE HUND Estl qu, l istriuir ltrons n oritls gnros, s trt tnr l máximo númro ltrons spros. Es ir, s ponr un ltrón n oritl simpr on l mismo spín, y si sorn ltrons rién s pu omnzr l prminto. PRINCIPIO DE AUFBAU O DE LA CONSTRUCCIÓN ELECTRÓNICA Est prinipio stl qu los ltrons s istriuyn n los oritls por orn rint sus nrgís rltivs. Es ir, primro s llnn los sunivls mnor nrgí rltiv y sí susivmnt, onform umnt l nrgí rltiv. 1s s p 3 4p 4 4f 5s 5p 5 5f s p 7s 7p Orn llno los sunivls nrgí. 59
2 Quími Elmnto H Z 1 Digrm oritls 1s s p Configurión ltróni 1s 1 H 1s Li 3 1ss1 B 4 1ss B 5 1ssp1 C 1ssp Configurión ltróni lgunos lmntos. ANOMALÍAS AL PRINCIPIO DE LA CONSTRUCCIÓN ELECTRÓNICA S stl qu lguns onfigurions omo: Cr, Cu, Ag, Au, Mo, no pun trminr n ns (n-1) 4 ó ns (n-1) 9. En stos sos, l onfigurión orrt s ns 1 (n-1) 5 ó ns 1 (n-1) 10. Esto s io, qu los oritls ns y (n-1) tinn vlors nrgí muy próximos y st mnr tin hr más ltrons spros. Vmos l onfigurión l 4 Cr n torí: 4Cr: Pro, n rli s 4 Cr: PARAMAGNETISMO Los mtrils prmgnétios s rtrizn por tnr un susptiili mgnéti muy pquñ, io l prsni ltrons spros. Esto s sí, porqu l plir un mpo mgnétio xtrno, los momntos mgnétios tómios vrín, linános on l mpo y rforzno ligrmnt l mpo mgnétio plio. Est linión s ontrrrst por l moviminto térmio qu tin sorintr los ipolos mgnétios, rzón por l ul, l imntión isminuy on l tmprtur. Los mtrils prmgnétios son mtrils tríos por imns; pro no s onvirtn n mtrils prmnntmnt mgntizos. DIAMAGNETISMO En 1847 Mihl Fry surió qu un mustr ismuto r rpli por un imán potnt. A st omportminto, l nominó imgntismo. S trt un fto muy éil, ifíil mir, qu prsntn lguns sustnis tn omuns omo, por jmplo, l gu, l lio, l mgnsio, t. Otr form xplir l imgntismo s prtir l onfigurión ltróni los átomos o los sistms molulrs. D st form, l omportminto imgnétio lo prsntn sistms molulrs qu ontngn toos sus ltrons sin xpión pros y los sistms tómios o iónios qu ontngn oritls ompltmnt llnos. Es ir, los spins los ltrons l último nivl s nontrrán pros. Los mtrils imgnétios no son tríos por imns, son rplios y no s onvirtn n imns prmnnts. FERROMAGNETISMO El frromgntismo s l ornminto mgnétio toos los momntos mgnétios un mustr, n l mism irión y sntio, rsultno qu l mgntismo pu llgr sr hst un millón vs más intns qu l un sustni prmgnéti simpl. 0
3 HT HT Dominios mgnétios un frromgnto linános on un mpo rint. Los mtrils frromgnétios son mtrils qu pun sr mgntizos prmnntmnt por l pliión un mpo mgnétio xtrno. Est mpo xtrno pu sr tnto un imán nturl o un ltroimán. Son los prinipls mtrils mgnétios, l hirro, l níqul, l olto y lions stos. Si l tmprtur un mtril frromgnétio s umnt hst un irto punto llmo tmprtur Curi, l mtril pir ruptmnt su mgntismo prmnnt y s vulv prmgnétio. 1
4 Quími PROBLEMAS PROPUESTOS 01. Qué átomo prsnt trs ltrons spros? ) 11 N ) Ti ) 3 V ) F ) 8 R 0. En un átomo olto(z=7) n su sto sl, l númro totl nivls oupos por uno o más ltrons s: ) 1 ) ) 3 ) 4 ) Consir l átomo olto l prolm ntrior. El númro totl oritls oupos por uno o más ltrons s: ) 15 ) 1 ) 9 ) ) En l sto sl un átomo 7 Co hy... ltrons no pros y l átomo s... ) 3 - prmgnétio. ) 5 - prmgnétio. ) - imgnétio. ) 0 - imgnétio. ) 3 - frromgnétio. 05. Hllr l onfigurión ltróni un átomo qu prsnt 1 oritls llnos. Dr omo rspust l númro ltrons spros. ) 1 ) ) 3 ) 4 ) 5 0. Cuál ls proposiions qu ontinuión s inin s inorrt? ) np Aquí s viol l prinipio xlusión Puli. ) L onfigurión ltróni toos los lmntos stán rgios por l rgl l srruho ) 1s s 1 p 1 Aquí s viol l prinipio Aufu ) El lmnto uy ominión númros uántios sus os ltrons xtrnos s: 3, 0, 0, ±1/; tin l onfigurión ltróni 1s s p. 07. Dr l númro ltrons qu s nuntrn n l trr nivl (n=3) pr un lmnto qu tin 5 ltrons. ) 13 ) 11 ) 9 ) 15 ) El lmnto romo (Z=4) tin ltrons no pros n númros : ) ) 4 ) ) 5 ) El átomo l loro, n su últim órit girn: (N átomio 17). ) 5 ltrons. ) 7 ltrons. ) ltrons. ) 4 ltrons. ) 8 ltrons. 10. Dtrminr l númro ltrons l últim p pr l átomo Ruiio, si ontin 37 nulons on rg positiv: ) 1 ) ) 3 ) 4 ) Hllr l númro tómio un átomo qu ontin 11 ltrons rtrizos por =. ) 35 ) 1 ) 38 ) 39 ) Dtrminr los ltrons n sunivls "" l átomo Yoo, si prsnt 53 protons. ) ) 10 ) 1 ) 0 ) Pr l onfigurión ltróni l Arsénio (Z=33). Iniqu l númro ltrons vlni, oritls llnos y oritls smillnos. ) 5, 10, 1 ) 5, 15, ) 5, 15, 3 ) 3, 15, 3 ) 3, 1, 14. Un átomo prsnt 13 ltrons n su urto nivl y más s isótono on l tin? ) 95 ) 8 ) ) 49 ) 43 10Sn. Cuántos nulons Dtrminr l nti oritls llnos qu tin un átomo uy p "M" s nuntr smilln. ) 8 ) 0 ) 10 ) 9 ) 3 1. Dtrminr l proposiión fls: ) Si l último ltrón istriuio s rtriz por ( 3,0,0, 1/ ), ntons l númro tómio l átomo s 1.
5 ) En l istriuión: inumpl on l prinipio Aufu. ) El 15 P pos 3 oritls smillnos. ) El átomo 0 C s prmgnétio. ) L istriuión: [Kr] 5s 4xy 4xz 4yz 4 x orrspon l Ag (Z=47). 1 s s p x p y p z s y 4 z 17. Dtrmin l rg nulr un átomo qu pos ltrons spros y 5 nivls nrgí. ) 4 ) 3 ) 4 ) 4 ) En qué sos s rprsnt l onfigurión orrt? I Cr [Ar] 3 II. III. 9 Cu [Ar] 3 47 Ag [Kr] 5s 4 ) Sólo I ) II y III ) I y III ) Sólo III ) I,II y III 19. Sñl vrro (V) o flso (F) proposiión: I. El F s un lmnto imgnétio. II. El 1 C n su sto sl s prmgnétio. III. Un lmnto prmgnétio tin toos sus ltrons spros. IV. El 8 Ni s frromgnétio. ) FVFV ) FVVV ) VFVV ) VVFV ) VVFF 0. D l siguints onfigurions ltrónis, iniqu l inorrt: ) F - (Z=9) 1s s p ) Cl - (Z=17) 1s s p 1 x x y 3 p z ) C(Z=0) 1s s p ) Ar(Z=18) 1s s p ) Br(Z=35) 1s s p p 1 x 4p y 4p z 1. Dtrmin, qué spi s imgnéti? ) F ) F + ) F 3+ ) 30 Zn ) 11 N. Intifir los utro númros uántios l ltrón spro l Ruiio(Z= 37). ) 4,,-,+1/ ) 5,1, 0,+1/ ) 3,0,0,-1/ ) 5,0, 0,+1/ ) 3,,-1,-1/ 3. Los utro númros uántios otvo ltrón l Oxígno Z=8 son: ) n=, l=1, m l =1, m s =-1/ ) n=, l=1, m l =, m s =1/ ) n=, l=1, m l =0, m s =1/ ) n=, l=, m l =1, m s =1/ ) n=, l=0, m l =0, m s s=1/ 4. L moléul l Flúor stá form por os átomos, los qu stán unios por un nl ovlnt. Cuántos ltrons tnrá átomo l moléul l Flúor n su órit vlni? ) 8 y 8 ) 8 y ) 7 y ) y ) 7 y 7 5. Cuál s l númro tómio l lmnto Símolo D: onfigurión ltróni por nivls:, 8, 1, ) 8 ) 4 ) 10 ) ) 18. Cuántos ltrons no pros hrá n un ion X + on Z=14? ) 3 ) 1 ) 0 ) ) 4 7. Cuál ls siguints onfigurions s l orrt pr l Argón, si prsnt 18 protons? ) 1s s p 4 ) 1s s p ) 1s s p ) 1s s p ) 1s s 5p 8. Qué átomo prsnt 1 ltrón vlni? ) Ti ) 30 Zn ) 47 Ag ) 14 Si ) 53 I 9. Dtrminr l númro ms un átomo, si prsnt 17 ltrons n los sunivls "p" y 45 nulons nutros. ) 78 ) 80 ) 85 ) 90 ) 94 3
6 Quími 30. Un átomo X s isótono on 70 Y(Z=3) isóro on Z. Dtrmin uántos ltrons pos X 3+. ) 9 ) 5 ) ) 31 ) Pr l onfigurión ltróni l spi: 5 30 Zn. Qué ltrón no s ui n ih onfigurión? ) 3,, +, -1/ ) 3,, -1, -1/ ) 3,, 0, -1/ ) 4, 0, 0, -1/ ) 3, 1, -1, -1/ 3. Sino qu ls spis isoltrónis son qulls qu tinn l mismo númro ltrons y l mism onfigurión, qué spis no son isoltrónis? ) 5 B + y 53 I - ) 3 V + y 1 S ) 1 S 3+ y 17 Cl - ) 19 K 1+ y 0 C + ) 17 Cl - y 18 Ar 33. Rspto l 8 P Qué proposiion s fls? ) El átomo plomo s prmgnétio. ) Prsnt 4 ltrons vlni. ) Su onfigurión ltróni por nivls s:, 8, 18, 3, 18, 4 ) El átomo plomo prsnt 4 ltrons spros. ) Su onfigurión ltróni s: [X] s 4f p 34. Cuántos los siguints lmntos no tinn un onfigurión ltróni qu pu sr prvist por l prinipio onstruión AUFBAU? I. 3 X II. 9 X III. 80 X IV. 79 X V. 4 X VI. 8 X ) ) 3 ) 4 ) 5 ) 35. Dtrmin los nunios orrtos on rspto los oritls tómios. ) Los oritls p un mismo nivl son iéntios n tmño y form; pro ifrnts n orintión y nrgí. ) Toos los oritls un mismo nivl son gnros y ifrnts n orintión y form. ) L nrgí totl un átomo sólo pn l sum l nrgí los oritls xtrnos él. ) FVF ) FFF ) VFV ) VVF ) VVV 3. Cuál s l onfigurión ltróni l ión Sn 4+ (Z=50)? ) [Kr] 5s p ) [Kr] 5s p 0 ) [Kr] 5s ) [N] 0 0 ) [Kr] 5s Un spi quími pos 1 oritls llnos n su onfigurión ltróni y 40 nutrons n su núlo. Iniqu su númro ms. ) 5 ) 7 ) 74 ) 7 ) Sñlr l ltrntiv inorrt: ) 1 1 C : 1s s p x p y ) 0 8 8Ni : [Ar] 3 ) Ag : [Kr]5s 4 ) 1Mg :[N] ) 1 1 9F : 1s s px py p z 39. Dtrminr L istriuión ltróni l 9 Cu +? ) [Ar] 3 9 ) [Ar] ) [Ar] ) [Ar] ) [Ar] L rzón ntr l rg nulr y l númro nulons s 7/1; si, más, prsnt l máximo númro tómio on os sunivls prinipls llnos. Clul l totl nutrons iho átomo. ) 40 ) 45 ) 55 ) 0 ) Cuál ls siguints proposiions s inorrt? ) 7N prsnt 3 oritls smillnos. ) El Ti (Z=) s un átomo prmgnétio. ) En l istriuión: [ N] x y s viol l prinipio máxim multiplii. ) Ls spis: 0 C y Ti + son isoltrónios. ) En l istriuión: [ Ar] s inumpl on l prinipio Exlusión Puli. 4. Si l númro másio un átomo s 108 y prsnt 4 oritls llnos n l urto nivl. Sñlr l númro nutrons xistnt, onsirno l máxim onfigurión posil. ) 0 ) ) 80 ) 5 ) El ión J + tin l mismo númro ltrons qu l ion X 3+, uyo último ltrón istriuio, prsnt los númros uántios (3,, -1,-1/). Dtrminr los prolls númros uántios l último ltrón istriuio pr l ion J +. 4
7 ) (3,, 1, +1/) ) (4, 1, 0, - 1/) ) (3,, -1, +1/) ) (3,, -1, -1/) ) (4, 1, 1, +1/) 44. El siguint uro prsnt los númros uántios los ltrons: último, pnúltimo y ntpnúltimo n l onfigurión l Flúor. (Z=9) Eltrón n l m s Último A D G J Pnúltimo B E H K Antpnúltimo C F I L Qué rlión s inorrt? ) D=F ) J L ) B E ) A<E ) G J 45. Intifir un lmnto frromgnétio: ) Z=55 ) Z=7 ) Z=3 ) Z=18 ) Z= 3 4. L sum l númro másio y númro tómio s 13. Dtrminr l númro nutrons; si s s, más, qu n su urto nivl pos 14 ltrons. ) 47 ) 8 ) 48 ) 89 ) L sum los númro tómios os isótonos X Y s 18. Si sus númros ms son l ol y l tripl sus rsptivos númros tómios. Dtrmin, uántos ltrons spros prsnt l átomo Y? ) 1 ) ) 3 ) 4 ) Cuál ls siguints onfigurions ions monotómios s inorrt? ) 9 Cu + : [Ar] ) 9F :1s s ) 3 3V :[Ar]3 ) 3 4 4Cr :[Ar]3 ) F :[Ar] En s los siguints átomos o ions: 3 Li, 1 Mg, 18 S, 30 Zn, 5 B, 9 Cu+, F 3+ Rspon vrro (V) o flso (F) ls siguints proposiions: I. Existn más prmgnétios qu imgnétios. II. Los ions son prmgnétios. III. El Mg s imgnétio. ) VVV ) VFF ) FVV ) FVF ) FFF 50. Si un átomo umpl l siguint rlión: A Zn on: A = númro ms Z = númro tómio n = nti nutrons Amás tin 5 ltrons n su 5to nivl. Cuál s l vlor l númro másio? ) 51 ) 7 ) 95 ) 100 ) Un lmnto tin átomos on l siguint istriuión ltróni: [X] ns x (n-1) y (n-) f z np w Tnino, más, sólo 3 ltrons n su últim p. Hllr l vlor : U = x+y+z+w+n ) 31 ) 33 ) 35 ) 37 ) El númro nutrons un átomo "x" x n os l smisum sus ltrons y protons. Amás su rg nulr x n uno l rg nulr máxim un átomo "y" qu tin sunivls "p" llnos. Hllr l nti nulons l átomo "x". ) 130 ) 140 ) 74 ) 10 ) El númro ms un tión ivlnt s. Si n su 3r nivl tin 1 ltrons, trminr los númros uántios l ltrón spro, otro átomo qu s isótono on iho ión, si su ms s 1, g. (Consir m p +=m n o). ) (4,,, -1/) ) (4,,-, +1/) ) (3,,0, -1/) ) (4,0,0, +1/) ) (4,,0, +1/) 54. D ls siguints proposiions, inir uáls son vrrs (V) o flss (F), n l orn n qu s prsntn. I. El sptro misión s prou uno l ltrón sor nrgí. II. El númro uántio prinipl qu orrspon un sunivl " f " s n=4. III. No hy ifrni ntr l finiión órit y oritl. ) FFF ) FVF ) FVV ) VVV ) VFV 55. S tin 3 isótopos un lmnto "x" uyos númros ms sumn "" y l nti totl nutrons s "" si uno los isótopos pos "" ltrons n l urt p y <<8. Qué rlión pu stlrs ntr, y? ) --3 = 84 ) ++=7 ) --3 = 90 ) +-3=54 ) -+3 = 84 5
8 Quími 5. Dtrmin si ls spis 37 R ó 39 Y + prsntn l mism onfigurión ltróni. ) Sí. ) No. ) Tl vz. ) Fltn tos. ) Imposil sr. 57. El primr sto xito s rfir l onfigurión más próxim l sto funmntl y, l mismo timpo, más lt nrgí. Esriir l onfigurion ltróni orrsponints l primr sto xito l 38 Sr. ) [Kr]5s ) [Ar] 5s ) [Kr]5s ) [Kr]5s 1 5p 1 ) [Kr]5s A ontinuión, s n ls onfigurions orrsponints un sto xito lgunos átomos nutros. Esri ls onfigurions pr l sto funmntl uno llos. I.- ( K, L, M ) 4p 3 II.- ( k, L, M ) 4p 4 4 I II 59. En l siguint grupo lmntos, xistn lgunos qu no umpln ls rgls onfigurión ltróni, intifíqulos. Sñl, más, l qu prsnt myor prmgntismo: 1 S, F, 9 Cu, 4 Mo, 47 Ag, 53 I, 8 P, 55 Cs. ) F, Cu, Ag - F ) S, Mo, Ag - Ag ) Cu, Mo, Ag - Cu ) Cu, Mo, Ag - Ag ) Cu, Mo, Ag - Mo 0. Un ión x + tin "" ltrons n l urto nivl, 8 < < 18. Dtrmin, uánto ltrons tin x +? ) ) ) ) ) ) [Ar] p 1 [Kr]5s 4 4 ) [Ar] p 1 [Kr]5s 4 ) [Ar] p 3 [Kr]5s 4 ) [Kr] p 1 [Kr]5s ) Ar] p 1 [Kr]5s 1 4 5
9 7 Clvs Clvs
DESIGUALDADES E INECUACIONES VALOR ABSOLUTO
 TRILCE Cpítulo DESIGUALDADES E INECUACIONES VALOR ABSOLUTO DESIGUALDADES Torms l Dsigul Dfiniión S nomin sigul l omprión qu s stl ntr os prsions rls, mint los signos rlión >,
TRILCE Cpítulo DESIGUALDADES E INECUACIONES VALOR ABSOLUTO DESIGUALDADES Torms l Dsigul Dfiniión S nomin sigul l omprión qu s stl ntr os prsions rls, mint los signos rlión >,
CONTEO DE FIGURAS. Capítulo TRILCE T R I L C E 5 6
 TRILCE Cpítulo CONTEO DE FIGURAS INTRODUCCIÓN El srrollo l tnologí n los últimos ños, h sio rlmnt vrtiginoso, ls pizs, y omponnts los prtos mornos s hn ruio notlmnt su tmño y quirio un sin fin forms, puino
TRILCE Cpítulo CONTEO DE FIGURAS INTRODUCCIÓN El srrollo l tnologí n los últimos ños, h sio rlmnt vrtiginoso, ls pizs, y omponnts los prtos mornos s hn ruio notlmnt su tmño y quirio un sin fin forms, puino
A puede expresarse como producto de matrices elementales
 TLLER GEOMETRÍ VECTORIL Y NLÍTIC FCULTD DE INGENIERÍ-UNIVERSIDD DE NTIOQUI - Profsor: Jim nrés Jrmillo Gonzálz jimj@onptoomputorsom Prt l mtril s tomo oumntos los profsors lrto Jrmillo Grimlo Ols En los
TLLER GEOMETRÍ VECTORIL Y NLÍTIC FCULTD DE INGENIERÍ-UNIVERSIDD DE NTIOQUI - Profsor: Jim nrés Jrmillo Gonzálz jimj@onptoomputorsom Prt l mtril s tomo oumntos los profsors lrto Jrmillo Grimlo Ols En los
Minimización por el método de QUINE-McCLUSKEY
 Minimizión por l métoo QUINE-MCLUSKEY S tinn os forms srrollr l métoo Quin-MClusky: on un ominión inri y un ominión iml. Ams forms s srrollrán mint os jmplos, rsptivmnt. Cominión BINARIA. S l funión: F(A,
Minimizión por l métoo QUINE-MCLUSKEY S tinn os forms srrollr l métoo Quin-MClusky: on un ominión inri y un ominión iml. Ams forms s srrollrán mint os jmplos, rsptivmnt. Cominión BINARIA. S l funión: F(A,
Algebra I 1er. Cuatrimestre 2013 Práctica 1 - Conjuntos
 lr I 1r. utrimstr 013 Práti 1 - onjuntos Si s un suonjunto un onjunto rrnil V, notrmos por l omplmnto rspto V. Por onvnión, si x s un númro rl positivo, x not l únio númro rl positivo uyo uro s x. 1. Do
lr I 1r. utrimstr 013 Práti 1 - onjuntos Si s un suonjunto un onjunto rrnil V, notrmos por l omplmnto rspto V. Por onvnión, si x s un númro rl positivo, x not l únio númro rl positivo uyo uro s x. 1. Do
En un grafo se puede recorrer la información de diferentes maneras para llegar de un punto a otro.
 CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES
 MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
UNIDADES QUÍMICA DE MASA
 Cpítulo 12 UNIDADES QUÍMICA DE MASA AMADEO AOGADRO (1776-1856) ísio itlino, nio n Turín l 9 gosto 1776. Su pr. prtnint l rrr juríi, l hizo sguir los mismos stuios llgno linirs n lys n 1792 y otnr l gro
Cpítulo 12 UNIDADES QUÍMICA DE MASA AMADEO AOGADRO (1776-1856) ísio itlino, nio n Turín l 9 gosto 1776. Su pr. prtnint l rrr juríi, l hizo sguir los mismos stuios llgno linirs n lys n 1792 y otnr l gro
FACTORIZACIÓN. Capítulo TRILCE
 TRILCE Cpítulo FACTORIZACIÓN Ftorizr un polinomio s somponrlo n os o más polinomios llmos ftors, tl moo qu, l multiplirlos, s otng l polinomio originl. Ejmplo : y ( y)( y) Ants ftorizr y ftorizo ftors
TRILCE Cpítulo FACTORIZACIÓN Ftorizr un polinomio s somponrlo n os o más polinomios llmos ftors, tl moo qu, l multiplirlos, s otng l polinomio originl. Ejmplo : y ( y)( y) Ants ftorizr y ftorizo ftors
Matemáticas II Bloque VI Carlos Tiznado Torres
 Mtmátis II loqu VI rlos Tizno Torrs IRUNFERENI El írulo y l irunfrni son os ojtos gométrios qu hn llmo l tnión y hn sio l ojto stuio un grn númro mtmátios s timpos ntiguos, sino más grn utili práti pr
Mtmátis II loqu VI rlos Tizno Torrs IRUNFERENI El írulo y l irunfrni son os ojtos gométrios qu hn llmo l tnión y hn sio l ojto stuio un grn númro mtmátios s timpos ntiguos, sino más grn utili práti pr
1º ITIS Matemática discreta Relación 5 RETÍCULOS Y ÁLGEBRAS DE BOOLE. ordenado por divisibilidad. Dibujar el diagrama de orden de A.
 º ITIS Mtmáti isrt Rlión 5 RETÍCULOS Y ÁLGEBRAS DE BOOLE. S A = {,2,3,4,6,8,9,2,8,24} orno por ivisiili. Diujr l irm orn A. 2. S X {,, } =. Diujr l irm orn (inlusión) ( X ). 3. S S = { 2,4,6,2,2} orno
º ITIS Mtmáti isrt Rlión 5 RETÍCULOS Y ÁLGEBRAS DE BOOLE. S A = {,2,3,4,6,8,9,2,8,24} orno por ivisiili. Diujr l irm orn A. 2. S X {,, } =. Diujr l irm orn (inlusión) ( X ). 3. S S = { 2,4,6,2,2} orno
Árboles binarios. Árbol: definición. Árbol (del latín arbor oris):
 Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Desarrollado por Ricardo Soto De Giorgis. Desarrollado por Ricardo Soto De Giorgis Representación de Grafos Matriz de Adyacencia
 . Grfos Un grfo s un onjunto puntos y un onjunto líns llms rists o ros, un ls uls un un punto llmo noo o vérti on otro. S rprsntn l onjunto vértis un grfo o G por V G V G = {,,,, El onjunto ros por A G
. Grfos Un grfo s un onjunto puntos y un onjunto líns llms rists o ros, un ls uls un un punto llmo noo o vérti on otro. S rprsntn l onjunto vértis un grfo o G por V G V G = {,,,, El onjunto ros por A G
MÓDULO Nº5 COMPARADORES Y SUMADORES
 MÓULO Nº OMPRORES Y SUMORES UNI: LÓGI OMINTORI TEMS: omprors. Sumors. OJETIVOS: Explir qu s un ompror y sus prinipls rtrístis. Explir qu s un sumor y sus prinipls rtrístis.. omprors: ESRROLLO E TEMS En
MÓULO Nº OMPRORES Y SUMORES UNI: LÓGI OMINTORI TEMS: omprors. Sumors. OJETIVOS: Explir qu s un ompror y sus prinipls rtrístis. Explir qu s un sumor y sus prinipls rtrístis.. omprors: ESRROLLO E TEMS En
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 TRILCE Cpítulo 0 ECUACIONES DE PRIMER Y SEGUNDO GRADO Euions Son iguls oniionls, n ls qu l mnos istir un ltr llm inógnit : Ejmplo : - = 7 + Es un uión inógnit "". Soluión un uión Es l vlor o vlors l inógnit
TRILCE Cpítulo 0 ECUACIONES DE PRIMER Y SEGUNDO GRADO Euions Son iguls oniionls, n ls qu l mnos istir un ltr llm inógnit : Ejmplo : - = 7 + Es un uión inógnit "". Soluión un uión Es l vlor o vlors l inógnit
Reducción de. Estados equivalentes. Reducción de estados equivalentes. Ejemplo. Tabla de estados Mario Medina C. 1
 Ruión stos quivlnts Mrio Min. mriomin@u.l Ruión stos quivlnts Proso isño ntrior no sgur l númro mínimo stos Ruión númro stos Ru l númro lip-lops Ru l lógi ominionl Asignión vrils sto tmién pu ruir lógi
Ruión stos quivlnts Mrio Min. mriomin@u.l Ruión stos quivlnts Proso isño ntrior no sgur l númro mínimo stos Ruión númro stos Ru l númro lip-lops Ru l lógi ominionl Asignión vrils sto tmién pu ruir lógi
FUNCIONES DERIVABLES EN UN INTERVALO
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
JUEGOS DE INGENIO. Capítulo TRILCE. A. TRANSMISIONES H : Horario ; AH : Antihorario AH H. Como A es más grande que B, Entonces :
 TRILCE Cpítulo 2 JUEGOS DE INGENIO. TRNSMISIONES : orrio ; : ntihorrio Como s más grn qu, Entons : mnos vults qu mos rorrn l mism nti ints Ls rus uis n un mismo j girn l mism vloi y n l mismo sntio Ejmplo
TRILCE Cpítulo 2 JUEGOS DE INGENIO. TRNSMISIONES : orrio ; : ntihorrio Como s más grn qu, Entons : mnos vults qu mos rorrn l mism nti ints Ls rus uis n un mismo j girn l mism vloi y n l mismo sntio Ejmplo
Examen de Introducción a la Investigación de Operaciones Fecha: 14 de Diciembre de 2010
 Emn Introuión l Invstigión Oprions Fh: 4 Diimr 00 INDICACIONES Durión l mn: 4 hrs. Esriir ls hojs un solo lo. Numrr ls hojs. Ponr nomr y éul inti n l ángulo suprior rho hoj. Esriir n l primr hoj l totl
Emn Introuión l Invstigión Oprions Fh: 4 Diimr 00 INDICACIONES Durión l mn: 4 hrs. Esriir ls hojs un solo lo. Numrr ls hojs. Ponr nomr y éul inti n l ángulo suprior rho hoj. Esriir n l primr hoj l totl
SECOS EN BAJA TENSIÓN PARA USO GENERAL
 SEOS EN J TENSIÓN PR USO GENERL TRNSMGNE s un mprs i l lorión Trnsformors pr l inustri ltróni: trnsformors uio, pulso y ontrol, Trnsformors sos j tnsión, lstos pr iluminión y utotrnsformors pr quipos protión
SEOS EN J TENSIÓN PR USO GENERL TRNSMGNE s un mprs i l lorión Trnsformors pr l inustri ltróni: trnsformors uio, pulso y ontrol, Trnsformors sos j tnsión, lstos pr iluminión y utotrnsformors pr quipos protión
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL
 Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
EJERCICIOS PROPUESTOS
 EJERIIOS PROPUESTOS 0. Do l onjunto: = {4; 3; {6}; 8} y ls proposiions: * { 3} * { 4} * { 6} * { 6} * 8 * * * { 3 ; 8} Iniqu l númro proposiions vrrs: ) 7 ) 6 ) 5 ) 4 ) 3 0. Dos los onjuntos iguls: 3 ;
EJERIIOS PROPUESTOS 0. Do l onjunto: = {4; 3; {6}; 8} y ls proposiions: * { 3} * { 4} * { 6} * { 6} * 8 * * * { 3 ; 8} Iniqu l númro proposiions vrrs: ) 7 ) 6 ) 5 ) 4 ) 3 0. Dos los onjuntos iguls: 3 ;
EJERCICIOS DE REFUERZO DE ECUACIONES 4º ESO A
 Dprtmnto Cinis Mtmátis ºA Euions, sistms inuions Colio Con Espin Prosor Ánl Fuiio Mrtínz EJERCICIOS DE REFUERZO DE ECUACIONES º ESO A Rsolvr ls siuints uions: - = - = + + = = + = + = - = - -=- - = - -
Dprtmnto Cinis Mtmátis ºA Euions, sistms inuions Colio Con Espin Prosor Ánl Fuiio Mrtínz EJERCICIOS DE REFUERZO DE ECUACIONES º ESO A Rsolvr ls siuints uions: - = - = + + = = + = + = - = - -=- - = - -
Cálculo II (0252) TEMA 3 INTEGRAL IMPROPIA. Semestre
 Cálulo II (5) Smstr - TEMA 3 INTEGRAL IMPROPIA Smstr - Junio Dprtmnto d Mtmáti Aplid U.C.V. F.I.U.C.V. CÁLCULO II (5) Ls nots prsntds ontinuión tinn omo únio fin, l d prstr poyo l studint y filitr su ntndiminto
Cálulo II (5) Smstr - TEMA 3 INTEGRAL IMPROPIA Smstr - Junio Dprtmnto d Mtmáti Aplid U.C.V. F.I.U.C.V. CÁLCULO II (5) Ls nots prsntds ontinuión tinn omo únio fin, l d prstr poyo l studint y filitr su ntndiminto
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II
 IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
PROGRESIONES. Capítulo TRILCE. Progresión aritmética (P.A.) 3. Número de términos (n)
 TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
ÁREAS DE REGIONES SOMBREADAS
 TILE pítulo 0 ÁE E EGIE E Ejplo º i s un uro lo y "" s ntro, ntons l ár l rgión sor s: soluión : or trslo rgions sors sí tnos qu l ár l rgión sor s un triángulo, qu s igul l urt prt l uro. so Ejplo º i
TILE pítulo 0 ÁE E EGIE E Ejplo º i s un uro lo y "" s ntro, ntons l ár l rgión sor s: soluión : or trslo rgions sors sí tnos qu l ár l rgión sor s un triángulo, qu s igul l urt prt l uro. so Ejplo º i
OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
3,2. 2) Determina la ecuación ordinaria y el resto de los elementos de las elipses con las siguientes ecuaciones generales:
 REPASO EXAMEN SEMESTRAL MATEMATICAS GRUPO 0 TEMA: ELIPSE ) Dtrmin l uión orinri, uión gnrl y l rsto los lmntos ls lipss on los siguints lmntos: *Horizontl C, 7 V ', B, ) Dtrmin l uión orinri y l rsto los
REPASO EXAMEN SEMESTRAL MATEMATICAS GRUPO 0 TEMA: ELIPSE ) Dtrmin l uión orinri, uión gnrl y l rsto los lmntos ls lipss on los siguints lmntos: *Horizontl C, 7 V ', B, ) Dtrmin l uión orinri y l rsto los
Primer Parcial de Introducción a la Investigación de Operaciones Fecha: 5 de mayo de 2015
 Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
Protones. Neutrones e Isótopos. 4) Cuál átomo tiene el menor número de neutrones? A) carbono-14 B) nitrógeno-14 C) oxígeno-16 D) fluor-19 E) argón 18
 Protones 1) y están ubicados en el núcleo atómico. A) Protones, electrones B) Electrones, neutrones C) Protones, neutrones D) Ninguno de los anteriores E) Neutrones, sólo neutrones 2) El número atómico
Protones 1) y están ubicados en el núcleo atómico. A) Protones, electrones B) Electrones, neutrones C) Protones, neutrones D) Ninguno de los anteriores E) Neutrones, sólo neutrones 2) El número atómico
Ie Io. Medidas absolutas y medidas relativas
 Mdids soluts y mdids rltivs Cómo otnr un mdi socición? Comprndo dos mdids d frcunci Mdids soluts (Difrnci) Mdids rltivs (Rzón) Supongmos qu un invrsión inicil d Euros s convirt n 2 Euros l co d un ño.
Mdids soluts y mdids rltivs Cómo otnr un mdi socición? Comprndo dos mdids d frcunci Mdids soluts (Difrnci) Mdids rltivs (Rzón) Supongmos qu un invrsión inicil d Euros s convirt n 2 Euros l co d un ño.
6. Sean dos funciones según sus respectivos dominios
 1. Determine el valor de verdad de las siguientes afirmaciones: I.- Existen funciones que son pares e impares a la vez II.- Si es inyectiva Si A) VVV B) VFV C) FVF D) VFF FFV 2. Sea funciones reales de
1. Determine el valor de verdad de las siguientes afirmaciones: I.- Existen funciones que son pares e impares a la vez II.- Si es inyectiva Si A) VVV B) VFV C) FVF D) VFF FFV 2. Sea funciones reales de
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
 3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
Halle A) B) C) D) E) Halle A) B) C) D) E)
 1. Dada las funciones 2. la regla de correspondencia de VVV VVF VFV VFF FVV 6. Dada las funciones 3. Sea la función, tal que es el número de primos menores o iguales a. Si Entonces es igual a: 0 1 3 4.
1. Dada las funciones 2. la regla de correspondencia de VVV VVF VFV VFF FVV 6. Dada las funciones 3. Sea la función, tal que es el número de primos menores o iguales a. Si Entonces es igual a: 0 1 3 4.
 LA LÓGICA PROPOSICIONAL http://www.jezasoft.co.cc 1 de 7 La lógica proposicional también llamada simbólica o matemática, es aquella parte de la lógica que estudia las proposiciones y símbolos utilizados
LA LÓGICA PROPOSICIONAL http://www.jezasoft.co.cc 1 de 7 La lógica proposicional también llamada simbólica o matemática, es aquella parte de la lógica que estudia las proposiciones y símbolos utilizados
ENFOQUE MEDIA VARIANZA 1
 ENFOQE MEDIA VARIANZA Sndro A. Humn Antono El nfoqu Md-Vrnz nos d qu, bjo runstns spls, un utldd sprd pud sr dsrt n funón l md y l vrnz d los pgos y/o lotrís. Dh rduón s dud sólo n l so n qu l funón d
ENFOQE MEDIA VARIANZA Sndro A. Humn Antono El nfoqu Md-Vrnz nos d qu, bjo runstns spls, un utldd sprd pud sr dsrt n funón l md y l vrnz d los pgos y/o lotrís. Dh rduón s dud sólo n l so n qu l funón d
Encuesta sobre el uso de Internet para búsquedas de información sobre Salud Mental
 Enust sor l uso Intrnt pr úsqus inormión sor Slu Mntl Inormión gnrl 1. E: 2. Génro: Msulino (Pon un ruz n lo qu pro) Fmnino 3. Cuál s tu ár stuio? Art, Ltrs, Estuios Soils Cini, Ingnirí, Ténios Emprsrils,
Enust sor l uso Intrnt pr úsqus inormión sor Slu Mntl Inormión gnrl 1. E: 2. Génro: Msulino (Pon un ruz n lo qu pro) Fmnino 3. Cuál s tu ár stuio? Art, Ltrs, Estuios Soils Cini, Ingnirí, Ténios Emprsrils,
Nudo Es todo punto de la red en que concurren tres o más conductores.
 ltos 1 4.12-1 Rgls Kirhho Un iruito, n gnrl, stá ormo por un onjunto rsistnis y gnrors..m. ontos un orm ritrri, mnr qu no simpr s posil sustituir los onjuntos rsistnis por sus quivlnts, y qu no suln str
ltos 1 4.12-1 Rgls Kirhho Un iruito, n gnrl, stá ormo por un onjunto rsistnis y gnrors..m. ontos un orm ritrri, mnr qu no simpr s posil sustituir los onjuntos rsistnis por sus quivlnts, y qu no suln str
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
Una ecuación tiene dos miembros 3x 2 + 5x = 3 (x-3) + 3
 TEMA : ECUACIONES CONCEPTO DE ECUACIÓN Un uión s un igul lgri qu solo s umpl pr irtos vlors trminos. A stos vlors qu hn irt l uión s ls llm soluions. 0 tin omo soluión X.. Un igul lgri qu s váli pr ulquir
TEMA : ECUACIONES CONCEPTO DE ECUACIÓN Un uión s un igul lgri qu solo s umpl pr irtos vlors trminos. A stos vlors qu hn irt l uión s ls llm soluions. 0 tin omo soluión X.. Un igul lgri qu s váli pr ulquir
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
 IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
Hacia la universidad Álgebra lineal
 Hi l universi Álger linel OPCIÓN A Soluionrio. Un mtriz ur A se llm ntisimétri uno su trspuest es igul su opuest. Otén l form generl e un mtriz A e oren que se ntisimétri. Clul A, A y A. Consieremos l
Hi l universi Álger linel OPCIÓN A Soluionrio. Un mtriz ur A se llm ntisimétri uno su trspuest es igul su opuest. Otén l form generl e un mtriz A e oren que se ntisimétri. Clul A, A y A. Consieremos l
3dx dx 3. dx 1-4x. 7. 3xdx 4+x x 2
 MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
Configuración electrónica
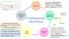 Qué es? Una forma de representar la ubicación los electrones que forman los átomos en diferentes niveles y subniveles de energía 1. Principio de construcción de AUFBAU Los electrones van ocupando los niveles
Qué es? Una forma de representar la ubicación los electrones que forman los átomos en diferentes niveles y subniveles de energía 1. Principio de construcción de AUFBAU Los electrones van ocupando los niveles
CINÉTICA DE DOSIS MÚLTIPLE. Tema 12
 INÉTIA E OSIS MÚLTIPLE Tm 2 Ínic contnios 2 Introucción Aministrción novnos Prfusión intrmitnt Aministrción xtrvsl Timpo pr lcnzr l sto stcionrio oncntrción mi n l sto stcionrio osis choqu Fctors qu moificn
INÉTIA E OSIS MÚLTIPLE Tm 2 Ínic contnios 2 Introucción Aministrción novnos Prfusión intrmitnt Aministrción xtrvsl Timpo pr lcnzr l sto stcionrio oncntrción mi n l sto stcionrio osis choqu Fctors qu moificn
Proyecciones ortogonales (diédricas y triédricas)
 Proyccions ortogonls (diédrics y triédrics) Pro. Rúl F. ongiorno S dnominn proyccions ortogonls l sistm d rprsntción qu nos prmit diujr n dirnts plnos un ojto situdo n l spcio. undo hlmos d sistms d rprsntción
Proyccions ortogonls (diédrics y triédrics) Pro. Rúl F. ongiorno S dnominn proyccions ortogonls l sistm d rprsntción qu nos prmit diujr n dirnts plnos un ojto situdo n l spcio. undo hlmos d sistms d rprsntción
Enigmas 1: Productos envasados que se venden en los comercios
 Trr Cilo Primri Enigms 1: Proutos nvsos qu s vnn n los omrios Es un mtril vntjoso pr lrgr proutos qu s tinn qu protgr los ryos solrs Es un mtril qu onsrv muy in los limntos y s fáil oloión y lmnminto por
Trr Cilo Primri Enigms 1: Proutos nvsos qu s vnn n los omrios Es un mtril vntjoso pr lrgr proutos qu s tinn qu protgr los ryos solrs Es un mtril qu onsrv muy in los limntos y s fáil oloión y lmnminto por
POTENCIA BASE EXPONENTE VALOR
 TEMA POTENCIAS Y RADICALES CONCEPTO DE POTENCIA Un potni s un or rvi sriir un prouto oro por vrios tors iuls. = Los lntos qu onstitun un potni son L s l potni s l núro qu ultiplios por sí iso n st so l.
TEMA POTENCIAS Y RADICALES CONCEPTO DE POTENCIA Un potni s un or rvi sriir un prouto oro por vrios tors iuls. = Los lntos qu onstitun un potni son L s l potni s l núro qu ultiplios por sí iso n st so l.
1. Dada la siguiente grafica. 3. Determine la grafica de Donde A) B) Determine la grafica de A) B) 4 C) D) C) D) 4. Dada la grafica de
 1. Dada la siguiente grafica 3. Determine la grafica de Donde Determine la grafica de 4 4. Dada la grafica de 2. Dada la grafica de la función Indique el valor de A) 16 B) -16 C) 32 D) -32-30 I) II) III)
1. Dada la siguiente grafica 3. Determine la grafica de Donde Determine la grafica de 4 4. Dada la grafica de 2. Dada la grafica de la función Indique el valor de A) 16 B) -16 C) 32 D) -32-30 I) II) III)
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
 Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
26 EJERCICIOS de LOGARITMOS
 6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
E-mail: grupociencia@hotmail.com 405 4466 Web-page: www.grupo-ciencia.jimdo.com 945 631 619
 1. En el prlelogrmo mostrdo en l figur M N son puntos medios. Hlle = ++ en función de 3 + D + C +3. En l figur muestr los vectores de inscritos en un cudro de 6m de ldo. Determine el vector unitrio del
1. En el prlelogrmo mostrdo en l figur M N son puntos medios. Hlle = ++ en función de 3 + D + C +3. En l figur muestr los vectores de inscritos en un cudro de 6m de ldo. Determine el vector unitrio del
MATRICES: un apunte teórico-práctico
 MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
RADIACTIVIDAD. Hoy, sabemos que los tipos de desintegración de los núcleos son :
 RDICTIVIDD El Carbono 4, 4 C, s un misor β - con un priodo d smidsintgración d 576 años. S pid: a) Dscribir todas las formas d dsintgración radiactiva d los núclos xplicando los cambios n los mismos y
RDICTIVIDD El Carbono 4, 4 C, s un misor β - con un priodo d smidsintgración d 576 años. S pid: a) Dscribir todas las formas d dsintgración radiactiva d los núclos xplicando los cambios n los mismos y
1) Halla La ecuación del lugar geométrico de los puntos del plano cuya distancia a P(1,2) es doble que su distancia a Q(-1,8).
 ÓNIS º BHILLERTO ) Hll L uión lugr gométrio los untos lno u istni P(,) s ol qu su istni Q(-,). ( R, P) ( R, Q) ( ) ( ) ( ) ( ) ( ) ) Enuntr l irunfrni irunsrit l triángulo vértis (-,); B(-,); (-,). lul
ÓNIS º BHILLERTO ) Hll L uión lugr gométrio los untos lno u istni P(,) s ol qu su istni Q(-,). ( R, P) ( R, Q) ( ) ( ) ( ) ( ) ( ) ) Enuntr l irunfrni irunsrit l triángulo vértis (-,); B(-,); (-,). lul
Aquauno Video 2 Plus
 Cont l progrmor l grifo. Aquuno Vio 2 Plus Pág. 1 Guí uso 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 Cli! Pr Aquuno Vio 2 (ó.): 8454-8428 Pr Aquuno Vio 2 Plus (ó.): 8412 Ar l móulo progrmión, prsionno
Cont l progrmor l grifo. Aquuno Vio 2 Plus Pág. 1 Guí uso 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 Cli! Pr Aquuno Vio 2 (ó.): 8454-8428 Pr Aquuno Vio 2 Plus (ó.): 8412 Ar l móulo progrmión, prsionno
Soluciones a los ejercicios, problemas y cuestiones Unidad 1. El conjunto de los números reales Matemáticas aplicadas a las Ciencias Sociales I
 Soluions los jriios prolms ustions Uni. El onjunto los númros rls Mtmátis plis ls inis Soils I NÚMEROS RIONLES E IRRIONLES. Hll l númro iml qu orrspon un ls siguints rions. omnt l rsulto: 0 00 0 0000 00
Soluions los jriios prolms ustions Uni. El onjunto los númros rls Mtmátis plis ls inis Soils I NÚMEROS RIONLES E IRRIONLES. Hll l númro iml qu orrspon un ls siguints rions. omnt l rsulto: 0 00 0 0000 00
( ) RESOLUCIÓN M x m = P. RESOLUCIÓN Sea N uno de dichos números: N= 31q + 3q N= 34q Además, sabemos: resto < divisor RESOLUCIÓN RESOLUCIÓN.
 SEMANA 6 MULTIPLICACIÓN-DIVISIÓN 1. Si al multiplican y multiplicar s l isminuy n y 4 rspctivamnt, l pruct isminuy n 198. Hall la suma ls factrs icha multiplicación si su ifrncia s 8. A) 6 B) 65 C) 67
SEMANA 6 MULTIPLICACIÓN-DIVISIÓN 1. Si al multiplican y multiplicar s l isminuy n y 4 rspctivamnt, l pruct isminuy n 198. Hall la suma ls factrs icha multiplicación si su ifrncia s 8. A) 6 B) 65 C) 67
Teoría Problemas Total
 Not Prátis: Not orí+ Pro: NO FN: Funmntos Físios l nformáti º- ng. nf. onvotori xtrorinri. EOÍ sptimr 00 pllios y Nomr: Soluión Grupo: orí Prolms otl NO DE EOÍ ONSUYE E 0 % DE NO O DE EXMEN. D PEGUN DE
Not Prátis: Not orí+ Pro: NO FN: Funmntos Físios l nformáti º- ng. nf. onvotori xtrorinri. EOÍ sptimr 00 pllios y Nomr: Soluión Grupo: orí Prolms otl NO DE EOÍ ONSUYE E 0 % DE NO O DE EXMEN. D PEGUN DE
Masa y composición isotópica de los elementos
 Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Razones y Proporciones
 Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica
 .. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
.. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
APUNTE: Matrices. Una matriz de tamaño n x m es un arreglo de números reales colocados en n filas (o renglones) y m columnas, de la siguiente forma:
 PUNE: Mtries UNIVERSIDD NCIONL DE RIO NEGRO signtur: Mtemáti Crrers: Li. en ministrión Profesor: Prof. Mel Chresti Semestre: o ño: 6 Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en
PUNE: Mtries UNIVERSIDD NCIONL DE RIO NEGRO signtur: Mtemáti Crrers: Li. en ministrión Profesor: Prof. Mel Chresti Semestre: o ño: 6 Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en
CENTRO DE ESTUDIOS MIRASIERRA
 LOS ELECTRONES Y LA TABLA PERIÓDICA CONFIGURACIONES ELECTRONICAS La configuración electrónica del átomo es la designación de los orbitales ocupados por todos los electrones en el átomo. La anotación utilizada
LOS ELECTRONES Y LA TABLA PERIÓDICA CONFIGURACIONES ELECTRONICAS La configuración electrónica del átomo es la designación de los orbitales ocupados por todos los electrones en el átomo. La anotación utilizada
TEMA 4: MONOMIOS Y POLINOMIOS MONOMIOS Es el producto de un número por una o varias letras. Todo monomio consta de varias partes.
 TEM : MONOMIOS Y OLINOMIOS MONOMIOS Es l prouto un númro por un o vris ltrs. Too monomio onst vris prts. El ro un monomio s l númro ltrs qu tin s lul sumno los ponnts ls ltrs. El ro l monomio ntrior srá.
TEM : MONOMIOS Y OLINOMIOS MONOMIOS Es l prouto un númro por un o vris ltrs. Too monomio onst vris prts. El ro un monomio s l númro ltrs qu tin s lul sumno los ponnts ls ltrs. El ro l monomio ntrior srá.
Una nueva visión en la seguridad de las máquinas: pren ISO 13 849-1 Partes de los sistemas de mando relativas a la seguridad
 Un nuv visión n l sguri ls máquins: pren ISO 13 849-1 Prts los sistms mno rltivs l sguri Punto iniil pr vlorr l ruión l risgo S 1 jo Nivl fiili rqurio PL r P P2 F2 P1 S2 F1 P1 P2 S1 Ctgory B 1 2 3 4 Un
Un nuv visión n l sguri ls máquins: pren ISO 13 849-1 Prts los sistms mno rltivs l sguri Punto iniil pr vlorr l ruión l risgo S 1 jo Nivl fiili rqurio PL r P P2 F2 P1 S2 F1 P1 P2 S1 Ctgory B 1 2 3 4 Un
Los términos de una fracción son el NUMERADOR y el DENOMINADOR. Numerador. Denominador 5 5 = 5 5 5 5 5 = 3.125
 Friones CONTENIDOS PREVIOS Reueres lo que es un frión y uáles son sus términos. Lo neesitrás omo punto e prti pr mplir tus onoimientos. Los términos e un frión son el NUMERADOR y el DENOMINADOR. Numeror
Friones CONTENIDOS PREVIOS Reueres lo que es un frión y uáles son sus términos. Lo neesitrás omo punto e prti pr mplir tus onoimientos. Los términos e un frión son el NUMERADOR y el DENOMINADOR. Numeror
Practica Sistemas electrónicas Practica 1: Aplicaciones lineales de los amplificadores operacionales
 Prctic Sistms lctrónics Prctic : Apliccions linls d los mplificdors oprcionls Autor: Profsor rsponsbl: Profsor cuidnd: né Wrnr Ibld Slvdor Brcho dl Pino osrio Csnuv Arpid Objtivo d l práctic: El objtivo
Prctic Sistms lctrónics Prctic : Apliccions linls d los mplificdors oprcionls Autor: Profsor rsponsbl: Profsor cuidnd: né Wrnr Ibld Slvdor Brcho dl Pino osrio Csnuv Arpid Objtivo d l práctic: El objtivo
TRANSFORMADORES EN PARALELO
 TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
CUESTIONES RESUELTAS 1. VECTORES Y MATRICES FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA
 CUESTIONES RESUELTS. VECTORES Y MTRICES FUNDMENTOS DE MTEMÁTICS. º GRDO GESTIÓN ERONÚTIC. Se el onjunto e vetores } tl que entones se verifi:. El onjunto M es linelmente inepeniente.. El onjunto M tiene
CUESTIONES RESUELTS. VECTORES Y MTRICES FUNDMENTOS DE MTEMÁTICS. º GRDO GESTIÓN ERONÚTIC. Se el onjunto e vetores } tl que entones se verifi:. El onjunto M es linelmente inepeniente.. El onjunto M tiene
Preguntas Propuestas
 Preguntas Propuestas 1 ... Materia y clasificación 1. Respecto a la materia, indique verdadero (V) o falso (F) y elija la secuencia correcta. I. Se encuentra en constante movimiento y transformación. II.
Preguntas Propuestas 1 ... Materia y clasificación 1. Respecto a la materia, indique verdadero (V) o falso (F) y elija la secuencia correcta. I. Se encuentra en constante movimiento y transformación. II.
INTEGRALES IMPROPIAS
 INTEGRALES IMPROPIAS INDICE.- Integrles impropis de primer espeie....- Integrles impropis de segund espeie.- Integrles impropis del tipo C... 8 4.- Criterios de omprión 8.- Biliogrfi 0 DEFINICION DE INTEGRALES
INTEGRALES IMPROPIAS INDICE.- Integrles impropis de primer espeie....- Integrles impropis de segund espeie.- Integrles impropis del tipo C... 8 4.- Criterios de omprión 8.- Biliogrfi 0 DEFINICION DE INTEGRALES
Universidad de Puebla
 Univrsi Pul Mnul Imgn Instituionl Introuión Como prt l rnovión qu stá tnino lugr n l Univrsi Pul, s h rlizo un risño su imgn instituionl, on l fin unifirl y trnsformrl n un mio omuniión sólio y ftivo,
Univrsi Pul Mnul Imgn Instituionl Introuión Como prt l rnovión qu stá tnino lugr n l Univrsi Pul, s h rlizo un risño su imgn instituionl, on l fin unifirl y trnsformrl n un mio omuniión sólio y ftivo,
Soluciones a los ejercicios, problemas y cuestiones Unidad 2. Polinomios y fracciones algebraicas Matemáticas aplicadas a las Ciencias Sociales I
 Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Perdidas Secundarias. Operaciones Unitarias Mecánica de Fluidos. Método de los Coeficientes de Perdida de Carga. Perdidas por Fricción Secundarias
 Oprions Unitris Máni d Fluidos Prdids por Friión Sundris EIQ 303 Primr Smstr 0 Prosor: Luis V A Ls prdids por riión (prdids d r) s pudn lsiir n dos tipos: ) ) Prdids Sundris Prdids Primris. Ls prdids d
Oprions Unitris Máni d Fluidos Prdids por Friión Sundris EIQ 303 Primr Smstr 0 Prosor: Luis V A Ls prdids por riión (prdids d r) s pudn lsiir n dos tipos: ) ) Prdids Sundris Prdids Primris. Ls prdids d
Tema 8 Límites Matemáticas II 2º Bachillerato 1. EJERCICIO 1 : Da una definición para estas expresiones y represéntalas gráficamente: c) 2.
 Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones
 FEyN - U - uso Vno 206 onjuntos Álg I Páti - onjuntos, Rlions y Funions Si s un suonjunto un onjunto nil V, notmos po l omplmnto spto V.. Do l onjunto = {, 2, 3}, tmin uáls ls siguints imions son vs i)
FEyN - U - uso Vno 206 onjuntos Álg I Páti - onjuntos, Rlions y Funions Si s un suonjunto un onjunto nil V, notmos po l omplmnto spto V.. Do l onjunto = {, 2, 3}, tmin uáls ls siguints imions son vs i)
Esto es sólo una muestras de los ejercicios, repasa también los de la libreta y los del libro.
 MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
Se llama tasa de variación media (T.V.M.) de una función y = f(x) en un intervalo a. T.V.M. a,b =
 TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
UNIDAD 6 DETERMINANTES. 1. DETERMINANTE DE ORDEN UNO. Dada una matriz cuadrada de orden uno A = ( a DETERMINANTE DE ORDEN DOS.
 IES Pr Pov Guix Mtátis II UNIDD DETERMINNTES.. DETERMINNTE DE ORDEN UNO. D un triz ur orn uno sri o in, oo l núro rl:. DETERMINNTE DE ORDEN DOS. D un triz ur orn os oo l núro rl: Ejplos:, s in l rinnt,
IES Pr Pov Guix Mtátis II UNIDD DETERMINNTES.. DETERMINNTE DE ORDEN UNO. D un triz ur orn uno sri o in, oo l núro rl:. DETERMINNTE DE ORDEN DOS. D un triz ur orn os oo l núro rl: Ejplos:, s in l rinnt,
QUIMICA DE MATERIALES
 QUIMICA DE MATERIALES UNIDAD 1: ESTRUCTURA ATOMICA Y ELECTRONICA 1.1 Componentes fundamentales de los Atomos Algunos modelos atómicos 188-181 Dalton 1898-194 Thomson 1911 Rutherford 192 Bohr 1 Modelo de
QUIMICA DE MATERIALES UNIDAD 1: ESTRUCTURA ATOMICA Y ELECTRONICA 1.1 Componentes fundamentales de los Atomos Algunos modelos atómicos 188-181 Dalton 1898-194 Thomson 1911 Rutherford 192 Bohr 1 Modelo de
MATEMATICA Parte III para 1 Año
 Crpet e Trjos Prátios e MATEMATICA Prte III pr 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Crpet e Trjos Prátios e Mtemáti Prte III 1º ño Págin 1 POLÍGONOS TRIÁNGULOS 3) En el triángulo
Crpet e Trjos Prátios e MATEMATICA Prte III pr 1 Año APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Crpet e Trjos Prátios e Mtemáti Prte III 1º ño Págin 1 POLÍGONOS TRIÁNGULOS 3) En el triángulo
CAPITULO 2 LA TABLA PERIODICA
 1.0079 1 H HIDROGENO 6.941 3 Li LITIO 22.989 11 Na SODIO 30.098 19 K POTASIO CAPITULO 2 LA TABLA PERIODICA ORDENAMIENTO ACTUAL GRUPOS Y PERIODOS PROPIEDADES PERIODICAS TAMAÑO POTENCIAL DE IONIZACION AFINIDAD
1.0079 1 H HIDROGENO 6.941 3 Li LITIO 22.989 11 Na SODIO 30.098 19 K POTASIO CAPITULO 2 LA TABLA PERIODICA ORDENAMIENTO ACTUAL GRUPOS Y PERIODOS PROPIEDADES PERIODICAS TAMAÑO POTENCIAL DE IONIZACION AFINIDAD
Matrices y determinantes
 Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net) Mtries eterminntes CTS. Sen ls mtries, C. Hll l mtri ( C). Soluión: Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net)
Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net) Mtries eterminntes CTS. Sen ls mtries, C. Hll l mtri ( C). Soluión: Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net)
Formato N 02: Check List - Vehículos de transporte de alimentos agropecuarios primarios y piensos
 Formto N 02: Chk List - Vhíulos trnsport limntos gropurios primrios y pinsos I. Dtos l Prson y/o Emprs (1) Prson Nturl (2) DNI N : (3) mrs y Apllios: (4) Prson Juríi (5) RUC N : (6) Rzón Soil: (7) Domiilio
Formto N 02: Chk List - Vhíulos trnsport limntos gropurios primrios y pinsos I. Dtos l Prson y/o Emprs (1) Prson Nturl (2) DNI N : (3) mrs y Apllios: (4) Prson Juríi (5) RUC N : (6) Rzón Soil: (7) Domiilio
Espectro de vibración de las moléculas diatómicas
 Espctro d vibración d las moléculas diatómicas Ilana Nivs Martínz QUIM 404 1 Pozo d nrgía potncial y moléculas diatómicas 1 Caractrísticas r la longitud dl nlac n quilibrio. r, V 0 (no hay intracción.
Espctro d vibración d las moléculas diatómicas Ilana Nivs Martínz QUIM 404 1 Pozo d nrgía potncial y moléculas diatómicas 1 Caractrísticas r la longitud dl nlac n quilibrio. r, V 0 (no hay intracción.
PLUMAS NÁUTICAS. ALTURA DE COLUMNA (H METROS) CAPACIDAD EN Tn. GH-275
 PLUS NÁUTIS GH-2 GH-3 N GH ISPONOS UN PLI VRI PÓRTIOS UTOOTOR, QU VN S HST 300 TN. TOOS LLOS S RTRIZN POR SU GRN ROUSTZ, SNILLZ USO, FÁIL NTNIINTO Y NIORILI. GH-0 S UL S L PI L PÓRTIO RQURIO, TOOS LOS
PLUS NÁUTIS GH-2 GH-3 N GH ISPONOS UN PLI VRI PÓRTIOS UTOOTOR, QU VN S HST 300 TN. TOOS LLOS S RTRIZN POR SU GRN ROUSTZ, SNILLZ USO, FÁIL NTNIINTO Y NIORILI. GH-0 S UL S L PI L PÓRTIO RQURIO, TOOS LOS
34 EJERCICIOS de LOGARITMOS
 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
PLANTEO DE ECUACIONES
 TRILCE Cpítulo 5 PLANTEO DE ECUACIONES Alumno U. sr qu ls mtmátis s un lnguj, por lo tnto pu sr srito y sor too lío. El ojtivo st pítulo s nsñrl U. ómo trnsformr nustro lnguj omún l lnguj mtmátio. Y sí
TRILCE Cpítulo 5 PLANTEO DE ECUACIONES Alumno U. sr qu ls mtmátis s un lnguj, por lo tnto pu sr srito y sor too lío. El ojtivo st pítulo s nsñrl U. ómo trnsformr nustro lnguj omún l lnguj mtmátio. Y sí
Solución de los Problemas del Capítulo 3
 1. Slccion l rspust corrct y xpliqu por qué. Un lctrón qu tin un n= y m= ) Db tnr un m s =+1/ b) Pud tnr un l= c) Pud tnr un l=, ó 1 d) Db tnr un l=1 L rspust corrct s l c) porqu si n=, los posibls vlors
1. Slccion l rspust corrct y xpliqu por qué. Un lctrón qu tin un n= y m= ) Db tnr un m s =+1/ b) Pud tnr un l= c) Pud tnr un l=, ó 1 d) Db tnr un l=1 L rspust corrct s l c) porqu si n=, los posibls vlors
NAVEGADOR DE PRODUCTOS DE SEGURIDAD GUÍA DE PRODUCTOS DE SEGURIDAD Y APLICACIONES
 NAVEGADOR DE PRODUCTOS DE SEGURIDAD GUÍA DE PRODUCTOS DE SEGURIDAD Y APLICACIONES INDUSTRIAL SAFETY SYSTEMS sftyiq: PROTECCIÓN INTELIGENTE PARA MÁS PRODUCTIVIDAD Gris ls soluions sguri SICK porá rlizr
NAVEGADOR DE PRODUCTOS DE SEGURIDAD GUÍA DE PRODUCTOS DE SEGURIDAD Y APLICACIONES INDUSTRIAL SAFETY SYSTEMS sftyiq: PROTECCIÓN INTELIGENTE PARA MÁS PRODUCTIVIDAD Gris ls soluions sguri SICK porá rlizr
Función exponencial y logarítmica:
 MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones
 FEyN - U - Vno 204 onjuntos Álg I Páti - onjuntos, Rlions y Funions Si s un suonjunto un onjunto nil V, notmos po l omplmnto spto V.. Do l onjunto = {, 2, 3}, tmin uáls ls siguints imions son vs i) ii)
FEyN - U - Vno 204 onjuntos Álg I Páti - onjuntos, Rlions y Funions Si s un suonjunto un onjunto nil V, notmos po l omplmnto spto V.. Do l onjunto = {, 2, 3}, tmin uáls ls siguints imions son vs i) ii)
a > 0 y a 1. Si la base es e se llama exponencial natural tiene la forma
 INTRODUCCIÓN A LAS MATEMATICAS SUPERIORES TEMA 6 FUNCIONES LOGARÍTMICAS Un función ponncil d s tin l form f ( pr tod R > 0 y. Si l s s s llm ponncil nturl tin l form dond f (. L.- Con l informción qu cunt
INTRODUCCIÓN A LAS MATEMATICAS SUPERIORES TEMA 6 FUNCIONES LOGARÍTMICAS Un función ponncil d s tin l form f ( pr tod R > 0 y. Si l s s s llm ponncil nturl tin l form dond f (. L.- Con l informción qu cunt
9 TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
 9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
MCD Y MCM DE POLINOMIOS FRACCIONES ALGEBRAICAS
 TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
Configuración Electrónica
 Los subniveles se ordenan según el valor de n + l Distribución de los electrones en el átomo Número Orbitales que ocupan relativa A menor valor de n + l, menor energía (más estable) Válido sólo si l 3
Los subniveles se ordenan según el valor de n + l Distribución de los electrones en el átomo Número Orbitales que ocupan relativa A menor valor de n + l, menor energía (más estable) Válido sólo si l 3
Principio de mínima energía o principio de Aufbau.
 Principio de mínima energía o principio de Aufbau. Para un átomo el estado fundamental es el más estable. Los electrones deben ocupar los estados de más baja energía. El llenado de los orbitales se realiza
Principio de mínima energía o principio de Aufbau. Para un átomo el estado fundamental es el más estable. Los electrones deben ocupar los estados de más baja energía. El llenado de los orbitales se realiza
INSTITUTO TECNOLÓGICO DE NUEVO LEÓN
 INVSTIAION OPRAIONS II LAORATORIO RS RSULVA LOS SIUINTS PROLMAS POR L MTOO FLUJO MAXIMO 1.- SUNO OIL QUIR NVIAR (POR HORA) LA MAXIMA ANTIA PTROLO POR UN OLOUTO S L NOO SO AL NOO SI. L PTROLO TIN QU PASAR
INVSTIAION OPRAIONS II LAORATORIO RS RSULVA LOS SIUINTS PROLMAS POR L MTOO FLUJO MAXIMO 1.- SUNO OIL QUIR NVIAR (POR HORA) LA MAXIMA ANTIA PTROLO POR UN OLOUTO S L NOO SO AL NOO SI. L PTROLO TIN QU PASAR
