R (3 coordenadas) y tres ángulos que definen la rotación del sistema de coordenadas ligada con el cuerpo
|
|
|
- Francisco José Ortiz de Zárate Figueroa
- hace 6 años
- Vistas:
Transcripción
1 . Velocdad y Aceleracón en Marcos de Referenca en Movmento.. Cnemátca de un cuerpo rígdo... Ángulos de Euler.. Teorema de Euler..4 Marcos de Referenca en Movmentos Traslaconal y Rotaconal..5 Dervada de un Vector en Marco de Referenca en Movmento..6 Teoremas de adcón de velocdades y de aceleracones Bblografía: H: Goldsten, Captulo IV.. Cnemátca de un cuerpo rígdo. Para descrbr el movmento de un cuerpo rígdo hay que saber el vector de poscón del centro de masa R ( coordenadas) y tres ángulos que defnen la rotacón del sstema de coordenadas lgada con el cuerpo (x,y,z), sstema de coordenadas móvl respecto de un sstema de referenca fa (X,Y;Z),sstema de coordenadas absoluta. Cualquer movmento de un cuerpo rígdo puede consderarse como una superposcón de dos movmentos: del traslaconal y rotaconal. El sstema de coordenadas móvl con el orgen en el punto O, lgada con el cuerpo rígdo partcpa en un movmento traslaconal el cual se descrbe a través del vector R y en un movmento rotaconal unto con el cuerpo alrededor del punto O (Fg.) Fg. Consderemos el movmento del punto P del cuerpo rígdo defndo a través del vector r '. El vector r ' en el sstema de referenca absoluta esta rotándose mentras que en el sstema de coordenadas móvl es una constante r e ' puesto que este últmo vector esta lgado con el cuerpo rígdo. Entre los vectores r ' y r e ' exste la sguente relacón: r' Âr ' (..) e donde  es la matrz de transcón desde sstema de coordenadas móvl xyz al sstema de coordenadas absoluta. La poscón de un punto P del cuerpo rígdo en el sstema de coordenada absoluta se defne a través del vector r que esta relaconado con los vectores R y r e ' :
2 r R Âre ' (..) donde el prmer térmno descrbe el movmento traslaconal R R t y el segundo rotaconal Ât Â. La matrz Â, la cual defne la transcón de un sstema ortogonal a otra es una matrz untara, es decr su producto con la matrz transpuesta es la matrz undad:   T  T  Ê;   T (..) Esta propedad de la matrz  es consecuenca del hecho que en las rotacones la longtud de cualquer vector a no se camba. En efectvo, sea el vector a en sstema de referenca móvl la relacón a Âa', la cual para los elementos puede escrbrse como: a ' entre ellos debe exstr a A a ' Como longtudes de los vectores a y a ' son guales: (..4) a A,,p A a ' a ' p p a' esta gualdad se cumpla para cualquer par de los vectores solo cuando: A A p p (..5) Esta últma ecuacón muestra que no todos los elementos de la matrz  no son ndependentes. Estos elementos están relaconados según (..5) a través de 6 relacones ndependentes: suma de los productos de los elementos de cada fla es gual a uno, y suma de los productos de los correspondentes elementos de cada par dferentes flas es gual a cero. De esta manera entre los nueve elementos de la matrz  hay solo tres elementos ndependentes y por eso toda la matrz  puede defnrse a través de solo tres parámetros los cuales pueden consderarse como coordenadas generalzadas de un cuerpo rígdo. Estas coordenadas pueden escogerse de dferente manera, pero con mas frecuenca la orentacón de un cuerpo rígdo en mecánca teórca se defne por medo de tres ángulos de Euler... Ángulos de Euler Los llamados ángulos de Euler se escogen de manera sguente. El plano Oxy del sstema coordenadas lgada con el cuerpo se nterseca con el plano XOY del sstema de coordenadas absoluta a lo largo de la línea NN que se llama la línea de los nodos (Fg.). El ángulo entre el ee OX y la lnea de los nodos se denota y se llama el ángulo de precesón. El ángulo entre ees OZ y Oz se denota y se llama el ángulo de nutacón. El ángulo entre ee Ox y la línea de los nodos se denota y se llama el ángulo de la rotacón propa.
3 Fg. Tres ángulos y, son ndependentes y pueden tomar cualquer valor dentro de los ntervalos: ; ; ; (..6) La transcón desde el sstema de coordenadas xyz al sstema XYZ se realza a través de tres rotacones sucesvas: prmera rotacón al ángulo alrededor del ee OZ, segunda al ángulo alrededor de la línea de nodos NN y la últma al ángulo alrededor del ee Oz... Teorema de Euler V V r P O ) En el cualquer momento del tempo las proyeccones de las velocdades de dos puntos de un cuerpo rígdo sobre la recta que une estos dos puntos son guales ) Las velocdades de la cualquera tres puntos que no están ubcados sobre una recta de defnen unformemente las velocdades de todos los puntos de un cuerpo rígdo. ) S las velocdades de algunos tres puntos de un cuerpo rígdo que no están ubcados sobre una recta en algún nstante del tempo son guales entonces el cuerpo en este momento del tempo partcpa en un movmento traslaconal. 4) S en algún momento del tempo las velocdades de unos dos puntos del cuerpo rígdo son guales a cero entonces el cuerpo o está en un reposo nstantáneo o partcpa en este momento en un movmento rotatoro alrededor de la recta que une estos dos puntos. 5) S la velocdad de un punto de un cuerpo rígdo en algún momento del tempo es gual a cero entonces el cuerpo o está en un reposo nstantáneo o en este momento partcpa en un movmento rotatoro alrededor de una ee que atravesa este punto.
4 6) En el caso general el movmento nstantáneo de cualquer cuerpo rígdo se puede presentar como la superposcón traslaconal con la velocdad de algún punto del cuerpo rígdo (polo) y de un movmento rotaconal alrededor de un ee que atravesa este punto que descrbe el desplazamento de cada partícula dr ' respecto de centro de masa como el resultado de rotacón a un ángulo nfntésmo d. Este últmo desplazamento es gual d r' r' d y por eso el desplazamento total de cada partícula de un cuerpo rígdo respecto de sstema de referenca fa es: dr dr d r' (5.) dr dr S ahora ntroducremos las velocdades: absolutav a, de centro de masas V c y angular d obtenemos la relacón entre ellos V V r' (5.) a c Cambaremos la poscón del sstema coordenadas, relaconada con el cuerpo suponendo que ésta ya no esta ubcada en el centro de masa. En este caso en (5.) hay que susttur R por R a y r' por r' a y la formula (5.) se transforma en la sguente: V V a r' (5.4) a c Comparando (5.) y (5.4) uno puede relaconar las velocdades de dos centros de coordenadas y velocdades angulares Vc ' Vc a; ' (5.5) Dos resultados mportantes puede ver desde la formula (5.5): ) La velocdad angular en todos sstemas de referenca relaconados con el cuerpo es la msma; La velocdad de centro de sstema de coordenadas relaconada con el cuerpo vara con el cambo de la poscón del orgen de estos coordenadas y exste un punto dondev. Este punto se llama el centro nstantáneo de rotacón. El movmento del cuerpo respecto de este punto puede consderarse como pura rotacón. c ' 5. Mecánca de cuerpos rígdos 5. Tensor de nerca y Energía cnétca El cuerpo rígdo en mecánca se defne como un sstema de partículas, con las dstancas entre ellas constantes. La masa de un cuerpo rígdo puede consderarse como suma de masas de las partículas o como una ntegral: M m dv (5.)
5 Para descrbr el movmento de un cuerpo rígdo hay que saber el vector de poscón del centro de masa R ( coordenadas) y tres ángulos que defnen la rotacón del sstema de coordenadas lgada con el cuerpo (x,y,z) respecto de un sstema de referenca fa (X,Y;Z). Cualquer movmento de un cuerpo rígdo puede consderarse como una superposcón de dos movmentos: del traslaconal del centro de masa dr y rotaconal que descrbe el desplazamento de cada partícula dr ' respecto de centro de masa como el resultado de rotacón a un ángulo nfntésmo d. Este últmo desplazamento es gual dr' r' d y por eso el desplazamento total de cada partícula de un cuerpo rígdo respecto de sstema de referenca fa es: dr dr d r' (5.) Fg. dr dr d S ahora ntroducremos las velocdades: absolutav a, de centro de masas V c y angular obtenemos la relacón entre ellos V a Vc r' (5.) Cambaremos la poscón del sstema coordenadas, relaconada con el cuerpo suponendo que ésta ya no esta ubcada en el centro de masa. En este caso en (5.) hay que susttur R por R a y r' por r' a y la formula (5.) se transforma en la sguente: V a Vc a r' (5.4) Comparando (5.) y (5.4) uno puede relaconar las velocdades de dos centros de coordenadas y velocdades angulares Vc ' Vc a; ' (5.5) Dos resultados mportantes puede ver desde la formula (5.5): ) La velocdad angular en todos sstemas de referenca relaconados con el cuerpo es la msma; ) La velocdad de centro de sstema de coordenadas relaconada con el cuerpo vara con el cambo de la poscón del orgen de estos coordenadas y exste un punto dondev ' c. Este punto se llama el centro nstantáneo de rotacón. El movmento del cuerpo respecto de este punto puede consderarse como pura rotacón. Ahora calcularemos la energía cnétca de un cuerpo rígdo, suponendo que el punto C esta ubcado en el centro de masa. Denotaremos m, r,v las masas vectores de poscón y de la velocdad para las partículas que forman un cuerpo rígdo. La energía cnétca total es: m V m m T Vc m Vc r' r' El segundo térmno usando la conmutacón cíclca en un producto vectoral mxto puede reducrse a la forma sguente Vc m r' y es gual a cero debdo a que los vectores tenen orgen en el centro de masa. Tenendo en cuenta que cualquer producto vectoral al cuadrado cumple la gualdad a b a b sn a b a b cos a b ab obtenemos la formula fnal para la energía cnétca de un cuerpo rígdo: MVc T m r' r' ; M m (5.6) De esta manera la energía cnétca de un cuerpo rígdo puede representarse como suma de dos partes: de la energía del movmento traslaconal de centro de masa (M es la masa total del cuerpo) y de la energía del movmento rotaconal alrededor de este punto.
6 La formula (5.6) en las anotacones tensorales obtene una forma mas smétrca. Introducremos los,, ; r' x ;,, se puede reducr la formula (5.6) a la sguente: vectores MV T c I ; ; I x x x m Aquí y en adelante para los ndexes repetdas se realza sumacón, por eemplo x x x x x y z ; I I El tensor,,, I se llama el Tensor de Inerca y en la forma explícta puede ser representado como: J yy J zz J xy J xz I J xy J xx J zz J yz ; J m( )x x x x dv (5.8) J J J J xz yz xx yy Como cualquer tensor smétrco tensor de nerca puede reducrse a una forma dagonal, usando una transformacón canónca cambando ees x, y, z por ~ x, ~ y, ~ z : J ~ J ~ y~ ~ y z~ z I ~ I J ~ J ~ x~ ~ x z~ ~ z I J ~ J ~ (5.9) I x~ ~ y~ ~ x y Los nuevos ees x~, y~, ~ z en los cuales el tensor de nerca es dagonal se llaman ees prncpales del cuerpo y los elementos dagonales de este tensor se llaman momentos prncpales de nerca. Momentos prncpales de nerca son valores propos de la matrz (5.8) y la transformacón canónca desde ees x, y, z haca ees x~, y~, ~ z se realza a través de la matrz formada por vectores propos de la matrz (5.8). Algunas propedades del tensor de nerca: ) El cuerpo con dos guales momentos prncpales de nerca ( I I I ) se llama el trompo smétrco y el cuerpo cono todos tres momentos prncpales dferentes se llama el trompo asmétrco. Cuando todos tres momentos son guales se llama el trompo esférco. ) I I I, suma dos momentos prncpales sempre no es menor del tercero ) Todo plano de smetría es perpendcular a un ee prncpal 4) Todo ee de smetría es un ee prncpal 5) Para un cuerpo plano (ubcado en el plano XOY) I m( )y ~ ( ) y~ dv ; I m( )x ~ ( ) x~ dv ; I I. (5.) I En conclusón escrbremos la expresón de la funcón de Lagrange para un cuerpo rígdo: c MV L I U (5.) Problemas. ) Demuéstrese que momentos prncpales de nerca de una molécula lneal formada por los átomos con las masas m,m,,,,,..., n son guales a: y las dstancas relatvas entre ellos, n n I m m, M m ; I M I ) Demuéstrese que los momentos prncpales de nerca de una molécula de tres átomos con las masas m,m, m, que forman un trangulo sósceles con la base a y altura h, son guales a: mm m I h, I a, I I I M 5. Momento angular de un cuerpo rígdo. Ecuacones de Euler. Calcularemos el momento angular de un cuerpo rígdo respecto del punto que concde con la poscón de centro de masa. En este sstema de coordenadas según la formula (5.) la velocdad de cada partícula V r' ( ) y el momento angular es gual: M' m( )r' r' m( ) r' r' r' (5.7)
7 En las denotacones tensorales esta msma formula puede reducrse a la sguente: x x x m x x x M' m( ) Tenendo en cuenta la defncón (5.7) obtenemos defntvamente M' I ; M' Î (5.) La últma relacón esta escrta en las denotacones vectorales, consderando el tensor de nerca como una matrz de orden tres. En las coordenadas con los ees orentadas a lo largo de ees prncpales x~, y~, ~ z esta formula da: M ' I; M' I; M' I (5.) Anotemos que el valor del momento angular depende del sstema de referenca escogda. Las formulas (5.) y (5.) son correctas solo en las coordenadas de centro de masa pegadas al cuerpo las cuales están rotándose unto con el cuerpo con la frecuenca angular. Se sabe que la dervada de cualquer vector A respecto del tempo calculadas en sstema de referenca que esta en reposo respecto de la prmera con la frecuenca angular están relaconadas como: da y la dervada da' en sstema que esta rotándose da da' A' La ecuacón dnámca para el momento angular dm N, donde N es el momento de las fuerzas externas (el tórque) respecto el orgen del sstema de coordenadas en reposo utlzando esta relacón puede ser escrta en la forma sguente: dm' M' N; (5.4) d Î Î N (5.5) Esta ecuacón tene una forma más senclla en coordenadas donde ees ~ x, ~ y, ~ z están orentadas a lo largo de ees prncpales del cuerpo rígdo en los cuales el tensor de nerca tene una forma dagonal: d I I I N; d I I I N ; (5.6) d I I I N; Estas son ecuacones de Euler para el movmento de un cuerpo rígdo. Partendo de estas ecuacones se puede deducr el teorema de la energía. Con esta fn multplcaremos ambas partes de la ecuacón (5.6) por el vector. El producto con el segundo térmno se anula y el producto con el prmer térmno da Î dt Î d d De esta manera se obtene el teorema de energía para un cuerpo rígdo según el cual la dervada de la energía cnétca es gual al producto escalar de los vectores de la frecuenca angular y del torque N : dt N (5.7) Ahora aplcaremos las ecuacones de Euler para analzar El movmento lbre de un cuerpo rígdo. 5. El movmento lbre de un cuerpo rígdo. En ausenca del momento aplcado, cuando N las ecuacones dferencales (5.6) se transforman a unas ecuacones homogéneas, las cuales pueden resolverse en una forma explícta para un caso partcular cuando el cuerpo rígdo es un trompo smétrco. En este caso I I y desde últma ecuacón (5.6) tenemos const, mentras que las prmeras dos ecuacones se reducen a un par de las ecuacones lneales: d d I I ; ; (5.8) I Expresando desde la segunda ecuacón a través de la dervada de y susttuyendo en la prmera se puede obtener para y un par de las ecuacones desacopladas:
8 d d I I ; (5.9) I ; y la segunda por y las sumamos se obtene: Además s multplcaremos la prmera ecuacón (5.8) por d ; const; Es fácl de convencerse de que las funcones que satsfacen a las ecuacones (5.9) y (5.) son (5.) t ; sn t ; cos (5.) donde y son dos constantes arbtraras. El vector velocdad angular tene tres componentes, una de las cuales orentada a lo largo de ee e es constante y otras dos en el plano ortogonal osclan según las formulas (5.) y su resultante está grando en este plano de tal manera que el extremo del vector resultante forma una crcunferenca (vease la Fg.) del rado. El vector velocdad angular total efectúa, por tanto, un movmento de precesón alrededor del ee e con velocdad angular, descrbendo su extremo una crcunferenca del rado. La precesón es en el msmo sentdo que s I I y en sentdo opuesto en el caso contraro. Según las formulas anterores la rotacón de un cuerpo rígdo tene tres constantes arbtraras, y, ya que ecuacones de Euler son tres ecuacones dferencales de prmer orden. Estas constantes determnan por las condcones ncales. Fg. El ee nstantáneo de rotacón, determnado por el vector, cuando efectúa la precesón alrededor del ee de smetría descrbe un cono en el cuerpo (cono lgado o cono polar móvl). El valor absoluto de la frecuenca angular total const (5.) es una constante. El semángulo de este cono vene dado por tg (5.) Anotemos que los resultados anterores se referen a un sstema de coordenadas móvles lgados al cuerpo, mentras que es más fácl analzar el movmento espacal respecto a una dreccón fa del espaco. En caldad de tal dreccón es convenente utlzar el vector del momento angular M el cual es una constante debdo a que el momento de las fuerzas externas N. El ángulo entre dos vectores M y vene dado por M Î T cos (5.4) M M M Según el teorema de energía (5.7) y la formula (5. )T y son constantes y por eso el ee de rotacón descrbe un cono en el espaco, el cono polar fo. Este cono tene un semangulo dado por (5.4) y su ee tene la dreccón del vector momento angular M. La generatrz de contacto de los conos polares fo y móvl es el ee nstantáneo de rotacón (el vector ). Puesto que este ee está en el cono móvl nstantáneamente en repozo, el cono móvl rueda sn deslzar alrededor del cono fo. Ello consttuye una descrpcón completa del movmento (véase Fg.)
9 Fg. 5.4 Ángulos de Euler Descrpcón del movmento de un cuerpo rígdo se puede realzar a través de coordenadas de centro de masa y tres ángulos que defnen la orentacón de tres ees x,x, x de un sstema de coordenadas lgados con el cuerpo rígdo y con el orgen en el centro de masa respecto a un sstema de referenca x,y,z. En caldad de estos ángulos es convenente escoger los llamados ángulos de Euler. Los ees lgados con el cuerpo rígdo en la Fg.4 se denotan como, y. La línea de nterseccón de los planos xoy y x Ox en la Fg.4 se llama la línea de los nodos. cos, sn, sn sn cos sn sn, sn cos, cos sn cos sn,,,, cos Problemas. Fg.4 ) En los vértces de un cuadrado con el lado a están dspuestas masas m y M Hállense los componentes del tensor de nerca respecto a: a) los ees x,y,z, b) los ees x,y que concden con las dagonales del cuadrado, así como al ee z a a m M a m M m M a m M 4a m M 4a m 4a M a m M 4 ) Hállense los momentos de nerca prncpales para sguentes cuerpos rígdos homogéneos de masa M: a) cubo con lado a ( I I I / I Mb / ; I Ma / ; I M a b / ) I MR / 4; I MR / 4; I MR / ); I I M R / 4 H / / ; I MR / Ma ; b) paralelepípedo rectangular con lados a, b y c ( I Mb c / ; I Ma c / ; I Ma b ) c) placa angosta rectangular con lados a y b ( d) dsco angosto de rado R ( e) clndro de rado R y altura H: f) bola del rado R I I I MR 5 g) cono de rado de base R y altura H: I I / 8M 4R H / ; I / MR
10 ) Hállense los momentos de nerca prncpales para sguentes moléculas presentadas en la fgura: a)molécula lneal de tres átomos con masas guales / ma l al; I I I b)molécula de tres átomos de masa guales en forma de un trangulo sósceles I / ma ; I mh ; I m / ma mh c)molécula de cuatro átomos con masa guales en forma de un tetraedro. I I I ma 4) Demuéstrese que para cualquer cuerpo rígdo plano el tensor de nerca en J sstema coordenadas Oxyz con los ees Ox y Oy en el plano de obeto tene la forma xx J yx Como se camba el tensor al tener en cuenta el ancho del cuerpo rígdo? 5) El tensor de nerca de un cuerpo rígdo en cualquer sstema de coordenadas tene la forma Demuéstrese que los valores a) A+B+C, b)abc-ad -BE -CF -DEF; c)bc-d +AC-E +AB-F son nvarants al respecto de eleccón de sstema de coordenadas. J J yy xy A F E J xx J F B D yy E D C 6) Hállense los ees de nerca prncpales y los momentos de nerca prncpales de los sguentes sstemas: a) las masas m y M se encuentran en los vértces de un rectángulo con lados a y b (Fg a)), b) las masas m y m están en los vértces de un trángulo de catetos a y 4a (Fg. b)) 7) Un clndro homogéneo de masa m, longtud h y del rado R esta rotándose unformemente con una velocdad angular alrededor de ee AB que atravesa el centro de masa del clndro C y forma el ángulo con ee de smetría del clndro. Encuéntrese a) el valor del momento angular, b) el ángulo entre el momento angular y el ee de smetría, c) la energía cnétca. a) M m / R h sn 6R cos b) tg R h 6 R tg 8) Hállese ) la poscón del centro de masas, ) los ees prncpales y ) los momentos prncpales de nerca de una molécula que tene la forma de un trangulo sósceles presentado en la Fgura. Cual será 4) la energía y 5) el momento angular s molécula esta rotándose alrededor del ee CA (C es el centro de masas) que forma con el plano de molécula el ángulo 4 a a 5 / ; yc 4m h yc m ma ma ; my mh y 4mh 5 m4h 5 ) h 4a ; yc h 5 ) J xx m a J yy myc C C ma ; J zz ) I x J yy J zz ma ; I y J xx J zz ma ; I z J yy J xx 4ma ; 4 ) sn / ; cos sn; cos cos; tg a / y 5a h 5 cos tg 8; sn 5 8; x 5 ; y 9 ; 5 ) T I x x / I y y / I z z / ma 5 64 ma ma 8 4 ma 6 ) Lx I x x ma 5 6 4ma 5; Ly I y y ma 9 6 4ma ; L I 4ma / ma z z z z x y C 5 ;
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Dpto. Física y Mecánica
 Dpto. Físca y Mecánca Mecánca analítca Introduccón Notacón Desplazamento y fuerza vrtual Fuerza de lgadura Trabao vrtual Energía cnétca. Ecuacones de Lagrange Prncpode los trabaos vrtuales Prncpo de D
Dpto. Físca y Mecánca Mecánca analítca Introduccón Notacón Desplazamento y fuerza vrtual Fuerza de lgadura Trabao vrtual Energía cnétca. Ecuacones de Lagrange Prncpode los trabaos vrtuales Prncpo de D
Vectores en el espacio
 ectores en el espaco Los puntos y los vectores en el espaco se pueden representar como ternas de números reales (a,b,c) c b a Por el Teorema de Ptagoras, la norma del vector = (a,b,c) es = a 2 +b 2 +c
ectores en el espaco Los puntos y los vectores en el espaco se pueden representar como ternas de números reales (a,b,c) c b a Por el Teorema de Ptagoras, la norma del vector = (a,b,c) es = a 2 +b 2 +c
Coordenadas Curvilíneas
 Departamento: Físca Aplcada III Mecánca Raconal (Ingenería Industral) Curso 007-08 Coordenadas Curvlíneas 1. Introduccón a. Obetvo: Generalar los tpos de coordenadas conocdos. Cartesanas. Clíndrcas, Esfércas,
Departamento: Físca Aplcada III Mecánca Raconal (Ingenería Industral) Curso 007-08 Coordenadas Curvlíneas 1. Introduccón a. Obetvo: Generalar los tpos de coordenadas conocdos. Cartesanas. Clíndrcas, Esfércas,
Centro de Masa. Sólido Rígido
 Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Centro de Masa. Sólido Rígido
 Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
10. VIBRACIONES EN SISTEMAS CON N GRADOS DE LIBERTAD
 10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
Mecánica Clásica ( Partículas y Bipartículas )
 Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
Cinemática del Brazo articulado PUMA
 Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
2. EL TENSOR DE TENSIONES. Supongamos un cuerpo sometido a fuerzas externas en equilibrio y un punto P en su interior.
 . EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
. EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
Descripción de la deformación y de las fuerzas en un medio continuo
 Descrpcón de la deformacón y de las fuerzas en un medo contnuo Mecánca del Contnuo 15 de marzo de 2010 1. Temas tratados con anterordad: Descrpcón cualtatva de un medo contnuo Hpótess del contnuo Elementos
Descrpcón de la deformacón y de las fuerzas en un medo contnuo Mecánca del Contnuo 15 de marzo de 2010 1. Temas tratados con anterordad: Descrpcón cualtatva de un medo contnuo Hpótess del contnuo Elementos
PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemático y dinámico de un mecanismo plano articulado con un grado de libertad.
 Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Tema 3. Sólido rígido.
 Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
Una Reformulación de la Mecánica Clásica
 Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Apuntes de Mecánica Newtoniana: Sistemas de Partículas, Cinemática y Dinámica del
 Apuntes de Mecánca Newtonana: Sstemas de Partículas, Cnemátca y Dnámca del Rígdo. Arel Fernández Danel Marta Insttuto de Físca - Facultad de Ingenería - Unversdad de la Repúblca Índce general Contendos
Apuntes de Mecánca Newtonana: Sstemas de Partículas, Cnemátca y Dnámca del Rígdo. Arel Fernández Danel Marta Insttuto de Físca - Facultad de Ingenería - Unversdad de la Repúblca Índce general Contendos
Determinar el momento de inercia para un cuerpo rígido (de forma arbitraria).
 Unversdad de Sonora Dvsón de Cencas Exactas y Naturales Departamento de Físca Laboratoro de Mecánca II Práctca #3: Cálculo del momento de nerca de un cuerpo rígdo I. Objetvos. Determnar el momento de nerca
Unversdad de Sonora Dvsón de Cencas Exactas y Naturales Departamento de Físca Laboratoro de Mecánca II Práctca #3: Cálculo del momento de nerca de un cuerpo rígdo I. Objetvos. Determnar el momento de nerca
Tema 3-Sistemas de partículas
 Tema 3-Sstemas de partículas Momento lneal y colsones Momento lneal de un partícula Segunda ley de Newton dp F dt p mv Impulso I tb ta Fdt Teorema del mpulso I p B p A Centro de masas 1 r M m r con M m
Tema 3-Sstemas de partículas Momento lneal y colsones Momento lneal de un partícula Segunda ley de Newton dp F dt p mv Impulso I tb ta Fdt Teorema del mpulso I p B p A Centro de masas 1 r M m r con M m
Robótica Tema 4. Modelo Cinemático Directo
 UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industral ASIGNATURA: Robótca TEMA: Modelo Cnemátco Ttulacón: Grado en Ingenería Electrónca y Automátca Área: Ingenería de Sstemas y Automátca Departamento de
UNIVERSIDAD POLITÉCNICA DE MADRID E.U.I.T. Industral ASIGNATURA: Robótca TEMA: Modelo Cnemátco Ttulacón: Grado en Ingenería Electrónca y Automátca Área: Ingenería de Sstemas y Automátca Departamento de
Cinemática y dinámica del Cuerpo Rígido (no se incluye el movimiento de precesión y el del giróscopo)
 Cnemátca y dnámca del Cuerpo ígdo (no se ncluye el movmento de precesón y el del gróscopo) El cuerpo rígdo El cuerpo rígdo es un caso especal de un sstema de partículas. Es un cuerpo deal en el cual las
Cnemátca y dnámca del Cuerpo ígdo (no se ncluye el movmento de precesón y el del gróscopo) El cuerpo rígdo El cuerpo rígdo es un caso especal de un sstema de partículas. Es un cuerpo deal en el cual las
TRABAJO Y ENERGÍA INTRODUCCIÓN. requiere como varia la fuerza durante el movimiento. entre los conceptos de fuerza y energía mecánica.
 TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
Para dos variables x1 y x2, se tiene el espacio B 2 el que puede considerarse definido por: {0, 1}X{0, 1} = {(00), (01), (10), (11)}
 Capítulo 4 1 N-cubos 4.1. Representacón de una funcón booleana en el espaco B n. Los n-cubos representan a las funcones booleanas, en espacos n-dmensonales dscretos, como un subconjunto de los vértces
Capítulo 4 1 N-cubos 4.1. Representacón de una funcón booleana en el espaco B n. Los n-cubos representan a las funcones booleanas, en espacos n-dmensonales dscretos, como un subconjunto de los vértces
Herramientas Matemáticas para la localización espacial. Prof. Cecilia García
 Herramentas Matemátcas para la localzacón espacal Contendo I. Justfcacón 2. Representacón de la poscón 2. Coord. Cartesanas 2.2 Coord. Polares y Clíndrcas 2.3 Coord. Esfércas 3. Representacón de la orentacón
Herramentas Matemátcas para la localzacón espacal Contendo I. Justfcacón 2. Representacón de la poscón 2. Coord. Cartesanas 2.2 Coord. Polares y Clíndrcas 2.3 Coord. Esfércas 3. Representacón de la orentacón
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
CAMPOS DE VELOCIDADES DE LOS DISCOS
 CAMPOS DE VELOCIDADES DE LOS DISCOS Los dscos galáctcos se modelan como anllos crculares concéntrcos. S Ω es la velocdad angular del anllo y r el vector que va hasta el centro, sendo n el vector untaro
CAMPOS DE VELOCIDADES DE LOS DISCOS Los dscos galáctcos se modelan como anllos crculares concéntrcos. S Ω es la velocdad angular del anllo y r el vector que va hasta el centro, sendo n el vector untaro
CÁLCULO VECTORIAL 1.- MAGNITUDES ESCALARES Y VECTORIALES. 2.- VECTORES. pág. 1
 CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
3 LEYES DE DESPLAZAMIENTO
 eyes de desplazamento EYES DE DESPAZAMIENTO En el capítulo dos se expone el método de obtencón de las leyes de desplazamento dseñadas por curvas de Bézer para mecansmos leva palpador según el planteamento
eyes de desplazamento EYES DE DESPAZAMIENTO En el capítulo dos se expone el método de obtencón de las leyes de desplazamento dseñadas por curvas de Bézer para mecansmos leva palpador según el planteamento
Fuerzas distribuidas. 2. Momento de inercia
 Dpto. Físca y Mecánca Fuerzas dstrbudas d Centro de gravedad centro de masas. Centro de gravedad, centro de masas. Momento de nerca ntroduccón. Fuerzas dstrbudas Cálculo de centrodes y centros de gravedad
Dpto. Físca y Mecánca Fuerzas dstrbudas d Centro de gravedad centro de masas. Centro de gravedad, centro de masas. Momento de nerca ntroduccón. Fuerzas dstrbudas Cálculo de centrodes y centros de gravedad
Y ahora observamos que lo que está entre paréntesis es la derivada de un producto, de modo que
 Estas son ms notas para las clases del curso Mecánca Raconal (62.11) en la Facultad de Ingenería-UBA. Están aún en proceso de ser completadas, no tenen carácter de texto acabado, por el contraro seguramente
Estas son ms notas para las clases del curso Mecánca Raconal (62.11) en la Facultad de Ingenería-UBA. Están aún en proceso de ser completadas, no tenen carácter de texto acabado, por el contraro seguramente
Fuerzas ficticias Referencial uniformemente acelerado
 Capítulo 10 Fuerzas fctcas Las fuerzas fctcas son fuerzas que deben nclurse en la descrpcón de un sstema físco cuando la observacón se realza desde un sstema de referenca no nercal, a pesar de ello, se
Capítulo 10 Fuerzas fctcas Las fuerzas fctcas son fuerzas que deben nclurse en la descrpcón de un sstema físco cuando la observacón se realza desde un sstema de referenca no nercal, a pesar de ello, se
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Primer Semestre - Otoño 2014. Omar De la Peña-Seaman. Instituto de Física (IFUAP)
 MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
Pista curva, soporte vertical, cinta métrica, esferas metálicas, plomada, dispositivo óptico digital, varilla corta, nuez, computador.
 ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, son números ordenados en filas y columnas.
 MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
Cantidad de movimiento
 Cnétca 37 / 63 Cnétca Cantdad de momento Momento cnétco: Teorema de Koeng Energía cnétca: Teorema de Koeng Sóldo con punto fjo: Momento cnétco Sóldo con punto fjo: Energía cnétca Sóldo: Momento relato
Cnétca 37 / 63 Cnétca Cantdad de momento Momento cnétco: Teorema de Koeng Energía cnétca: Teorema de Koeng Sóldo con punto fjo: Momento cnétco Sóldo con punto fjo: Energía cnétca Sóldo: Momento relato
TEMA 4. TRABAJO Y ENERGIA.
 TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
Etáti Estática. 2.Centros de gravedad y 3.Momentos de inercia
 Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
Ecuación de Lagrange
 Capítulo 6 Ecuacón de Lagrange 6. Introduccón a las ecuacones de Lagrange La mecánca que nos presenta Lagrange en su Mécanque Analytque sgnfca un salto conceptual muy grande respecto de la formulacón Newtonana.
Capítulo 6 Ecuacón de Lagrange 6. Introduccón a las ecuacones de Lagrange La mecánca que nos presenta Lagrange en su Mécanque Analytque sgnfca un salto conceptual muy grande respecto de la formulacón Newtonana.
Campo eléctrico. Líneas de campo. Teorema de Gauss. El campo de las cargas en reposo. Campo electrostático
 qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
Mecánica del Sólido Rígido
 Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Física Curso: Física General
 UTP IMAAS ísca Curso: ísca General Sesón Nº 14 : Trabajo y Energa Proesor: Carlos Alvarado de la Portlla Contendo Dencón de trabajo. Trabajo eectuado por una uerza constante. Potenca. Trabajo eectuado
UTP IMAAS ísca Curso: ísca General Sesón Nº 14 : Trabajo y Energa Proesor: Carlos Alvarado de la Portlla Contendo Dencón de trabajo. Trabajo eectuado por una uerza constante. Potenca. Trabajo eectuado
CI42A: ANALISIS ESTRUCTURAL. Programa CI42A
 CI4A: ANALISIS ESTRUCTURAL Prof.: Rcardo Herrera M. Programa CI4A NÚMERO NOMBRE DE LA UNIDAD OBJETIVOS DURACIÓN 4 semanas Prncpo de los trabajos vrtuales y teoremas de Energía CONTENIDOS.. Defncón de trabajo
CI4A: ANALISIS ESTRUCTURAL Prof.: Rcardo Herrera M. Programa CI4A NÚMERO NOMBRE DE LA UNIDAD OBJETIVOS DURACIÓN 4 semanas Prncpo de los trabajos vrtuales y teoremas de Energía CONTENIDOS.. Defncón de trabajo
Introducción a Vacío
 Introduccón a Vacío Sstema de vacío Partes generales de un sstema de vacío: Fgura 1: Sstema de vacío con bomba mecánca y dfusora Fgura 2: Prncpo de funconamento de la bomba mecánca La Fg. 2 muestra el
Introduccón a Vacío Sstema de vacío Partes generales de un sstema de vacío: Fgura 1: Sstema de vacío con bomba mecánca y dfusora Fgura 2: Prncpo de funconamento de la bomba mecánca La Fg. 2 muestra el
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Ximénez & San Martín, 2004)
 FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Físca General 1 Proyecto PMME - Curso 2007 Insttuto de Físca Facultad de Ingenería UdelaR ANÁLISIS E INFLUENCIA DE DISTINTOS PARÁMETROS EN EL ESTUDIO DE LA ESTÁTICA DE CUERPOS RÍGIDOS. Sebastán Bugna,
Físca General 1 Proyecto PMME - Curso 2007 Insttuto de Físca Facultad de Ingenería UdelaR ANÁLISIS E INFLUENCIA DE DISTINTOS PARÁMETROS EN EL ESTUDIO DE LA ESTÁTICA DE CUERPOS RÍGIDOS. Sebastán Bugna,
Es el movimiento periódico de un punto material a un lado y a otro de su posición en equilibrio.
 1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
i=1 Demuestre que cumple los axiomas de norma. Calcule el límite Verifiquemos cada uno de los axiomas de la definición de norma: i=1
 CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6a)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
OSCILACIONES 1.- INTRODUCCIÓN
 OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
5ª Lección: Sistema de fuerzas gravitatorias. Cálculo de centros de gravedad de figuras planas: teoremas de Guldin.
 Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Números complejos. Actividades. Problemas propuestos. Matemáticas 1 Bachillerato? Solucionario del Libro
 Matemátcas Bachllerato? Soluconaro del Lbro Actvdades Dado el número complejo se pde: qué valor ha de tener x para que x? Calcula el opuesto de su conjugado Calcula el conjugado de su opuesto x x x El
Matemátcas Bachllerato? Soluconaro del Lbro Actvdades Dado el número complejo se pde: qué valor ha de tener x para que x? Calcula el opuesto de su conjugado Calcula el conjugado de su opuesto x x x El
CANTIDADES VECTORIALES: VECTORES
 INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO N FEH DURION 3 11 3 JULIO 26 DE 2013 9
INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO N FEH DURION 3 11 3 JULIO 26 DE 2013 9
Geometría convexa y politopos, día 1
 Geometría convexa y poltopos, día 1 Alexey Beshenov (cadadr@gmal.com) 8 de agosto de 2016 Los objetos geométrcos que nos nteresan en esta hstora son subconjuntos de R n. Voy a denotar los puntos de R n
Geometría convexa y poltopos, día 1 Alexey Beshenov (cadadr@gmal.com) 8 de agosto de 2016 Los objetos geométrcos que nos nteresan en esta hstora son subconjuntos de R n. Voy a denotar los puntos de R n
7º CONGRESO IBEROAMERICANO DE INGENIERIA MECANICA 7º CONGRESSO IBEROAMERICANO DE ENGENHARIA MECANICA México D.F., 12 al 14 de Octubre de 2005
 7º CONGRESO IBEROAMERICANO DE INGENIERIA MECANICA 7º CONGRESSO IBEROAMERICANO DE ENGENHARIA MECANICA Méxco D.F., 1 al 14 de Octubre de 005 ANÁLISIS DINÁMICO DE UN EQUIPO DE ENSAYO DE AMORTIGUADORES Zabalza
7º CONGRESO IBEROAMERICANO DE INGENIERIA MECANICA 7º CONGRESSO IBEROAMERICANO DE ENGENHARIA MECANICA Méxco D.F., 1 al 14 de Octubre de 005 ANÁLISIS DINÁMICO DE UN EQUIPO DE ENSAYO DE AMORTIGUADORES Zabalza
Disipación de energía mecánica
 Laboratoro de Mecáa y ludos Práctca 9 Dspacón de energía mecáa Objetvos El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Determnar los cambos de la energía cnétca de un
Laboratoro de Mecáa y ludos Práctca 9 Dspacón de energía mecáa Objetvos El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Determnar los cambos de la energía cnétca de un
Ejercicios Resueltos de Vectores
 Departamento de Matemátca y C C Coordnacón: Calculo II para Ingenería Semestre Eerccos Resueltos de Vectores Sean los vectores en IR : v,,, u,, 4, a,, y b,, 4 : a) Determne los vectores: UV y AB UV AB
Departamento de Matemátca y C C Coordnacón: Calculo II para Ingenería Semestre Eerccos Resueltos de Vectores Sean los vectores en IR : v,,, u,, 4, a,, y b,, 4 : a) Determne los vectores: UV y AB UV AB
Ejercicios y problemas (páginas 131/133)
 7 Calcula el opuesto y el conjugado de los sguentes números complejos, expresándolos en forma polar: a) z b) z (cos 00 sen 00 ) c) z Expresamos en prmer lugar los números complejos en forma Calcula las
7 Calcula el opuesto y el conjugado de los sguentes números complejos, expresándolos en forma polar: a) z b) z (cos 00 sen 00 ) c) z Expresamos en prmer lugar los números complejos en forma Calcula las
Perturbación de los valores propios simples de matrices de polinomios dependientes diferenciablemente de parámetros
 Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Mecánica del Sólido Rígido
 Mecánca del Sóldo ígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, otacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Mecánca del Sóldo ígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, otacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Resuelve. Unidad 6. Números complejos. BACHILLERATO Matemáticas I. [x ( )][x (2 3 1)] = Cómo operar con 1? Página 147
![Resuelve. Unidad 6. Números complejos. BACHILLERATO Matemáticas I. [x ( )][x (2 3 1)] = Cómo operar con 1? Página 147 Resuelve. Unidad 6. Números complejos. BACHILLERATO Matemáticas I. [x ( )][x (2 3 1)] = Cómo operar con 1? Página 147](/thumbs/62/47025176.jpg) Undad. Números complejos Matemátcas I Resuelve Págna 7 Cómo operar con? Vamos a proceder como los antguos algebrstas: cuando nos encontremos con seguremos adelante operando con ella con naturaldad y tenendo
Undad. Números complejos Matemátcas I Resuelve Págna 7 Cómo operar con? Vamos a proceder como los antguos algebrstas: cuando nos encontremos con seguremos adelante operando con ella con naturaldad y tenendo
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
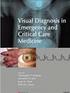 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
Cifrado de imágenes usando autómatas celulares con memoria
 Cfrado de mágenes usando autómatas celulares con memora L. Hernández Encnas 1, A. Hernández Encnas 2, S. Hoya Whte 2, A. Martín del Rey 3, G. Rodríguez Sánchez 4 1 Insttuto de Físca Aplcada, CSIC, C/Serrano
Cfrado de mágenes usando autómatas celulares con memora L. Hernández Encnas 1, A. Hernández Encnas 2, S. Hoya Whte 2, A. Martín del Rey 3, G. Rodríguez Sánchez 4 1 Insttuto de Físca Aplcada, CSIC, C/Serrano
16.21 Técnicas de diseño y análisis estructural. Primavera 2003 Unidad 8 Principio de desplazamientos virtuales
 16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
Métodos específicos de generación de diversas distribuciones discretas
 Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
FORMA TRADICIONAL DE CÁLCULO DE DESPLAZAMIENTOS Y FUERZAS EN ESTRUCTURAS SIN MAMPOSTERÍA RESUMEN
 CAPITULO 1 FORMA TRADICIONAL DE CÁLCULO DE DESPLAZAMIENTOS Y FUERZAS EN ESTRUCTURAS SIN MAMPOSTERÍA RESUMEN En la actualdad los métodos de dseño estructural y las consderacones que se realzan prevas al
CAPITULO 1 FORMA TRADICIONAL DE CÁLCULO DE DESPLAZAMIENTOS Y FUERZAS EN ESTRUCTURAS SIN MAMPOSTERÍA RESUMEN En la actualdad los métodos de dseño estructural y las consderacones que se realzan prevas al
EJERCICIOS RESUELTOS DE TRABAJO Y ENERGÍA
 JRCICIOS RSULTOS D TRABAJO Y NRGÍA. Un bloque de 40 kg que se encuentra ncalmente en reposo, se empuja con una uerza de 30 N, desplazándolo en línea recta una dstanca de 5m a lo largo de una superce horzontal
JRCICIOS RSULTOS D TRABAJO Y NRGÍA. Un bloque de 40 kg que se encuentra ncalmente en reposo, se empuja con una uerza de 30 N, desplazándolo en línea recta una dstanca de 5m a lo largo de una superce horzontal
CANTIDADES VECTORIALES: VECTORES
 INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
Tema 2 : DEFORMACIONES
 Tema : eformacones Tema : EFRMACINES F F 3 F / u u u 3 3 3 / 3 / F n Prof.: Jame Santo omngo Santllana E.P.S.-Zamora (U.SAL.) - 008 Tema : eformacones..- INTRUCCIÓN Los cuerpos se deforman debdo a la accón
Tema : eformacones Tema : EFRMACINES F F 3 F / u u u 3 3 3 / 3 / F n Prof.: Jame Santo omngo Santllana E.P.S.-Zamora (U.SAL.) - 008 Tema : eformacones..- INTRUCCIÓN Los cuerpos se deforman debdo a la accón
Capítulo V. Teoremas de Fermat, Euler y Wilson
 Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. x x0 y y0. Deducir la fórmula para el polinomio de Lagrange de grado a lo más uno que Interpola la tabla.
 EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. Consdere la sguente tabla, donde 0 : 0 y y0 y Deducr la fórmula para el polnomo de Lagrange de grado a lo más uno que Interpola la tabla.. Consdere la sguente
EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. Consdere la sguente tabla, donde 0 : 0 y y0 y Deducr la fórmula para el polnomo de Lagrange de grado a lo más uno que Interpola la tabla.. Consdere la sguente
Electricidad y calor
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electricidad y calor. Un repaso... Temas. 4. Primera ley de la Termodinámica. Webpage: Algunas definiciones
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
(p +Q 222 P +Q P +Q )
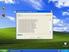 TEMA S.- PUNTOS. RECTAS Y PLANOS EN EL ESPACO. TEMA 5.- PUNTOS, RECTAS Y PLANOS EN EL ESPACO..- PUNTOS. Sstema de referenca: Un sstema de referenca en el espaco 93 consste en un conjunto formado por un
TEMA S.- PUNTOS. RECTAS Y PLANOS EN EL ESPACO. TEMA 5.- PUNTOS, RECTAS Y PLANOS EN EL ESPACO..- PUNTOS. Sstema de referenca: Un sstema de referenca en el espaco 93 consste en un conjunto formado por un
MODELADO CINEMÁTICO APLICADO AL SISTEMA DE NAVEGACIÓN DE UN ROBOT MÓVIL TIPO SKID STEER
 MODELADO CINEMÁTICO APLICADO AL SISTEMA DE NAVEGACIÓN DE UN ROBOT MÓVIL TIPO SKID STEER Danel E. Castblanco Jménez, Francy Carolna Barreto Ballesteros dcmdscrum9@gmal.com Ingenería Mecatrónca, Unversdad
MODELADO CINEMÁTICO APLICADO AL SISTEMA DE NAVEGACIÓN DE UN ROBOT MÓVIL TIPO SKID STEER Danel E. Castblanco Jménez, Francy Carolna Barreto Ballesteros dcmdscrum9@gmal.com Ingenería Mecatrónca, Unversdad
6.1 EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS
 TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
EQUILIBRIO DE UN CUERPO RIGIDO
 Manual e Laboratoro e ísca I C - UNMSM EQUILIBRIO E UN CUERPO RIGIO EXPERIENCIA Nº 6 Cuerpo rígdo: La dstanca entre dos puntos cualesquera del cuerpo permanece nvarante en el tempo. I. OBJETIVOS - Estudar
Manual e Laboratoro e ísca I C - UNMSM EQUILIBRIO E UN CUERPO RIGIO EXPERIENCIA Nº 6 Cuerpo rígdo: La dstanca entre dos puntos cualesquera del cuerpo permanece nvarante en el tempo. I. OBJETIVOS - Estudar
Clase 19: Estado Estacionario y Flujo de Potencia. EL Conversión de la Energía y Sistemas Eléctricos Eduardo Zamora D.
 Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
CESMA BUSINESS SCHOOL
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
Consideremos un sólido rígido sometido a un sistema de fuerzas en equilibrío, es decir
 1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
Propiedades efectivas de medios periódicos magneto-electroelásticos a través de funciones de Green
 Propedades efectvas de medos peródcos magneto-electroelástcos a través de funcones de Green utores: Lázaro Makel Sto Camacho Julán Bravo Castllero LOGO Renaldo Rodríguez Ramos Raúl Gunovart Díaz Introduccón
Propedades efectvas de medos peródcos magneto-electroelástcos a través de funcones de Green utores: Lázaro Makel Sto Camacho Julán Bravo Castllero LOGO Renaldo Rodríguez Ramos Raúl Gunovart Díaz Introduccón
Introducción a la mecánica analítica
 Prof. Jesús Hernández Trujllo Facultad de Químca, UNAM. Mecánca analítca y fscoquímca. La mecánca clásca estuda los movmentos de los cuerpos macroscópcos y las fuerzas que los orgnan. Hay dos tratamentos
Prof. Jesús Hernández Trujllo Facultad de Químca, UNAM. Mecánca analítca y fscoquímca. La mecánca clásca estuda los movmentos de los cuerpos macroscópcos y las fuerzas que los orgnan. Hay dos tratamentos
Los vectores y sus operaciones
 lasmatematcase Pedro Castro rtega Los ectores y ss operacones Un ector qeda determnado por dos pntos, el orgen, y el extremo Un ector qeda completamente defndo a traés de tres elementos: módlo, dreccón
lasmatematcase Pedro Castro rtega Los ectores y ss operacones Un ector qeda determnado por dos pntos, el orgen, y el extremo Un ector qeda completamente defndo a traés de tres elementos: módlo, dreccón
ESTADÍSTICA (GRUPO 12)
 ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
INGENIERÍA DE TELECOMUNICACIÓN BLOQUE 1
 INGENIERÍA DE TELECOMUNICACIÓN BLOQUE En el Aula Vrtual se encuentra dsponble: Materal nteractvo con teoría y ejerccos resueltos. Para acceder a ello deberá pulsar sobre los sguentes enlaces una vez dentro
INGENIERÍA DE TELECOMUNICACIÓN BLOQUE En el Aula Vrtual se encuentra dsponble: Materal nteractvo con teoría y ejerccos resueltos. Para acceder a ello deberá pulsar sobre los sguentes enlaces una vez dentro
SISTEMA DIÉDRICO I Intersección de planos y de recta con plano TEMA 8 INTERSECCIONES. Objetivos y orientaciones metodológicas. 1.
 Objetvos y orentacones metodológcas SISTEMA DIÉDRICO I Interseccón de planos y de recta con plano TEMA 8 Como prmer problema del espaco que presenta la geometría descrptva, el alumno obtendrá la nterseccón
Objetvos y orentacones metodológcas SISTEMA DIÉDRICO I Interseccón de planos y de recta con plano TEMA 8 Como prmer problema del espaco que presenta la geometría descrptva, el alumno obtendrá la nterseccón
PRÁCTICA Nº 5. CIRCUITOS DE CORRIENTE CONTINUA
 PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
Capítulo 3: Teoría Básica de los Convertidores Electromecánicos de Energía.
 . 3. Energía y coenergía en el campo magnétco En este capítulo se analzan los balances de energía en los convertdores electromecáncos de energía y se ntroduce la teoría básca del análss de las máqunas
. 3. Energía y coenergía en el campo magnétco En este capítulo se analzan los balances de energía en los convertdores electromecáncos de energía y se ntroduce la teoría básca del análss de las máqunas
CAPITULO 5 TRAYECTORIAS EN R 3. Platón.
 CAPITULO 5 La geometría es una cenca del conocmento del ser pero no de lo que esta sueto a la generacón o a la muerte. La geometría es una cenca de lo que sempre es Platón. TRAYECTORIAS EN R 5. Interpretacón
CAPITULO 5 La geometría es una cenca del conocmento del ser pero no de lo que esta sueto a la generacón o a la muerte. La geometría es una cenca de lo que sempre es Platón. TRAYECTORIAS EN R 5. Interpretacón
Tipología de nudos y extremos de barra
 Tpología de nudos y extremos de barra Apelldos, nombre Basset Salom, Lusa (lbasset@mes.upv.es) Departamento Centro ecánca de edos Contnuos y Teoría de Estructuras Escuela Técnca Superor de Arqutectura
Tpología de nudos y extremos de barra Apelldos, nombre Basset Salom, Lusa (lbasset@mes.upv.es) Departamento Centro ecánca de edos Contnuos y Teoría de Estructuras Escuela Técnca Superor de Arqutectura
NÚMEROS COMPLEJOS. y sabemos que no podemos calcular raíces de números negativos en R. Para resolver este problema introduciremos el valor i = 1
 NÚMEROS COMPLEJOS 1. Qué es un número complejo? Defncones. La ecuacón x + 1 = 0 no tene solucón en el campo real puesto que s ntentamos resolverla tendremos que x = ± 1 y sabemos que no podemos calcular
NÚMEROS COMPLEJOS 1. Qué es un número complejo? Defncones. La ecuacón x + 1 = 0 no tene solucón en el campo real puesto que s ntentamos resolverla tendremos que x = ± 1 y sabemos que no podemos calcular
Problemas sobre números complejos -1-
 Problemas sobre números complejos --.- Representa gráfcamente los sguentes números complejos y d cuáles son reales, cuáles magnaros y, de estos, cuáles magnaros puros: 5-5 + 4-5 7 0 -- -7 4.- Obtén las
Problemas sobre números complejos --.- Representa gráfcamente los sguentes números complejos y d cuáles son reales, cuáles magnaros y, de estos, cuáles magnaros puros: 5-5 + 4-5 7 0 -- -7 4.- Obtén las
ALN - SVD. Definición SVD. Definición SVD (Cont.) 29/05/2013. CeCal In. Co. Facultad de Ingeniería Universidad de la República.
 9/05/03 ALN - VD CeCal In. Co. Facultad de Ingenería Unversdad de la Repúblca Índce Defncón Propedades de VD Ejemplo de VD Métodos para calcular VD Aplcacones de VD Repaso de matrces: Una matrz es Untara
9/05/03 ALN - VD CeCal In. Co. Facultad de Ingenería Unversdad de la Repúblca Índce Defncón Propedades de VD Ejemplo de VD Métodos para calcular VD Aplcacones de VD Repaso de matrces: Una matrz es Untara
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
CAPITULO 2 VALORES, VECTORES PROPIOS y SVD. Ing. Diego A. Patiño M.Sc., Ph.D.
 CAPITULO VALORES, VECTORES PROPIOS y SVD Ing. Dego A. Patño M.Sc., Ph.D. Valores y Vectores Propos Muchas de las transformacones que se necestan en el dseño de sstemas de control se realzan sobre vectores
CAPITULO VALORES, VECTORES PROPIOS y SVD Ing. Dego A. Patño M.Sc., Ph.D. Valores y Vectores Propos Muchas de las transformacones que se necestan en el dseño de sstemas de control se realzan sobre vectores
5. DIAGONALIZACIÓN DE MATRICES
 Dagonalzacón Herraentas nforátcas para el ngenero en el estudo del algebra lneal 5. DIAGONALIZACIÓN DE MATRICES 5.1. INTRODUCCIÓN 5.2. VALORES Y VECTORES PROPIOS 5.3. MATRICES DIAGONALIZABLES 5.4. DIAGONALIZACIÓN
Dagonalzacón Herraentas nforátcas para el ngenero en el estudo del algebra lneal 5. DIAGONALIZACIÓN DE MATRICES 5.1. INTRODUCCIÓN 5.2. VALORES Y VECTORES PROPIOS 5.3. MATRICES DIAGONALIZABLES 5.4. DIAGONALIZACIÓN
