1. Las matrices se denotan con letras mayúsculas. Por ejemplo, A, B, C, X,...
|
|
|
- María Carmen Núñez Campos
- hace 5 años
- Vistas:
Transcripción
1 CAPÍTULO 1 ALGEBRA MATRICIAL 11 Introducción Definición 111 (Matriz) Definimos una matriz como un arreglo rectangular de elementos, llamados escalares, sobre un álgebra F Más que hacer referencia especifica al álgebra F, se asumirá que ésta es el álgebra de los números reales a menos que se establezca lo contrario Por lo tanto, un escalar será siempre un escalar a menos que se establezca lo contrario Notación 1 Las matrices se denotan con letras mayúsculas Por ejemplo, A, B, C, X, 2 Los elementos de la matriz, escalares, se denotan con letras minúsculas con 2 subíndices, es decir, a ij donde i se refiere a la fila y j a la columna Algunas veces se escribe A = [a ij ] 3 El conjunto de los números reales se denota con R o E 1 4 La traspuesta de A se denota por A 5 Si A tiene inversa, la inversa se denota por A 1 6 El determinantre de A, se denota por A o det(a) 1
2 2 Algebra Matricial 7 La matriz identidad se denota por I Se usa I n para denotar una matriz n n 8 El tamaño de una matriz es el número de sus filas por el número de columnas Por ejemplo, la matriz A m n, es una matriz con m filas y n columnas 9 Sean A m n y B n p, el producto de A y B se denota como AB 10 Sean A m n y B n p, la suma de A y B se denota como A + B 11 Sean A m n y k un escalar, el producto de k y A se denota como ka 12 La matriz diagonal D se define como una matriz cuadrada cuyos elementos fuera de la diagonal son cero, esto es, si D = [d ij ], entonces d ij = 0 si y sólo si i j 12 Inversa de una matriz Definición 121 (Matriz inversa) Sea A una matriz cuadrada Si existe una matriz B tal que BA = I, entonces B es llamada la inversa de A y se denota por A 1 Si A tiene inversa, A es llamada no singular; si A no tiene inversa, A es llamada singular Teorema 121 (La inversa A 1 es única) Si A es una matriz que tiene una inversa, la inversa es única Prueba 121 Sea B la matriz inversa de A, entonces BA = I Suponga que C es otra inversa de A, entonces CA = I, lo cual implica que C = B Teorema 122 Si A tiene una inversa, entonces A 1 tiene una inversa (A 1 ) 1 = A Prueba 122 Sea B la matriz inversa de A, entonces B = A 1 y BA = I Sea C la inversa de B entonces C = B 1 y BC = I, por lo tanto C = (A 1 ) 1 y C = A, así A = (A 1 ) 1 Teorema 123 Si A y B son matrices no singulares n n, entonces AB tiene una inversa (AB) 1 = B 1 A 1 : Esto puede extenderse a un número finito de matrices no singulares n n Prueba 123 Sea CD la inversa de AB, entonces (CD)(AB) = I, entonces C(DA)B = I Si D es la inversa de A entonces DA = I, por consiguiente CB = I, así D = A 1 y C = B 1 Por lo tanto, CD = B 1 A 1
3 13 Determinante de una matriz 3 Teorema 124 Si A es no singular y k es un escalar diferente de cero, entonces (ka) 1 = 1 k A 1 13 Determinante de una matriz Definición 131 (Determinante de una matriz) El determinante es una función que a cada matriz cuadrad An n le asigna un número, si los elementos de la matriz A son reales, el número que se asigna es un real y se denota por det(a) ó A 131 Cálculo del determinante de una matriz Definición 132 Si A es una matriz de tamaño 1, es decir A = [a], entonces det(a) = a Definición 133 Si A es una matriz 2 2, es decir A = se define como det(a) = a 11 a 22 a 12 a 21 ( a 11 a 12 a 21 a 22 ), entonces det(a) Definición 134 El determinante de una matriz 3 3 es a 11 a 12 a 13 det(a) = a 21 a 22 a 23 = a 11 a 22 a 33 +a 12 a 23 a 31 +a 13 a 21 a 32 a 13 a 22 a 31 a 11 a 23 a 32 a 12 a 21 a 33 a 31 a 32 a 33 Para calcular dicho determinante se usa comúnmente la regla de Sarrus La cual consiste en copiar la primera y segunda columna de la matriz y colocarlas inmediatamente a la derecha de la matriz Luego se calcula la suma de los productos de las diagonales a la derecha menos los productos de las diagonales hacia la izquierda Para calcular el determinante de matrices de tamaños superiores se deben tomar en cuenta las siguientes definiciones Definición 135 (Menor complementario) Sea A una matriz cuadrada y a ij el elemento ubicado en la fila i y la coluimna j de A El menor complementario de a ij se define como
4 4 Algebra Matricial el determinante de la matriz que se obtiene al eliminar la fila i y la columna j de A, y se denota por M ij Por ejemplo sea det(a) = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 entonces M 23 = a 11 a 12 a 31 a 32 = a 11a 32 a 31 a 12 Definición 136 Sea A una matriz cuadrada, se define el cofactor de un elemento a ij como el número C ij = ( 1) i+j M ij Es decir, el cofactor no es mas que el menor complementario correspondiente acompañado de un sigma mas o menos dependiendo de la fila y columna en la que se encuentre el elemento en cuestión Por ejemplo C 23 = ( 1) 5 M 23 = M Propiedades Teorema 131 Si A y B son matrices n n, entonces det(ab) = [det(a)][det(b)] Este resultado se puede extender a un número finito de matrices Teorema 132 Sea A ij el cofactor de a ij, entonces det(a) = a ij A ij j=1 Para algún i Teorema 133 Sea A una matriz n n; A = 0 si y sólo si A es una matriz singular
5 14 Traspuesta de una matriz 5 14 Traspuesta de una matriz Definición 141 Sea A una matriz La traspuesta de A, denotada por A, es la matriz con las filas y las columnas intercambiada Si A tiene tamaño m n, entonces A tiene tamaño n m 141 Propiedades Teorema 141 Si A y B son matrices m n, y a y b son escalares, entonces (aa) = (Aa) = A a = aa (aa + bb) = aa = bb Teorema 142 Si A y B son matrices tales que AB está definida, entonces (AB) = B A Teorema 143 Sea A una matriz cuadrad La inversa de la traspuesta de A es igual a la traspuesta de la inversa de A, es decir (A ) 1 = (A 1 ) 15 Matriz Simétrica Definición 151 Si A = A, entonces A es un matriz simétrica Esto implica que A debe ser cuadrada 151 Propiedades Teorema 151 Si A es cualquier matriz, entonces A A y AA son simétricas
6 6 Algebra Matricial 16 Rango de una matriz Definición 161 Sea A una matriz n m, se dice que A es de rango r si el tamaño de la submatriz cuadrada no singular mas grande es r 161 Propiedades Teorema 161 Si las matrices A y B son no singulares, entonces para cualquier matriz C, las matrices C, AC, CB y ACB tienen el mismo rango (Asumiendo que todo los productos están definidos) Teorema 162 Si A es una matriz m n de rango r, entonces existen matrices no singulares P y Q tales que donde I es r r PAQ = I, [ ] m = n = r; I 0 [ ], m = r < n; I, 0 [ ] m > r = n; I 0 0 0, m > r y n > r Corolario 1621 Si A es una matriz m n de rengo r > 0, entonces existen matrices A L y A R de tamaños m r y r n, respectivamente, y de rangos r tales que A = A L A R A L A R es llamada la factorización de rango completo de A Teorema 163 El rango del producto de las matrices A y B no pueden exceder el rango de A ni de B, es decir, r(ab) r(a) ó r(ab) r(b) Teorema 164 Una matriz no singular A puede siempre reducirse a I por transformaciones elementales de filas (columnas) Teorema 165 Si A es una matriz n n, entonces det(a) = 0 si y sólo si r(a) < n Teorema 166 Si C es una matriz m n de rango r, entonces el rango de CC y de C C es r
7 17 Matriz Idempotente 7 17 Matriz Idempotente Definición 171 Sea B una matriz n n tal que (1) B = B (2) B = B 2 entonces B se define como una matriz idempotente si (2) se satisface y una matriz simétrica idempotente si (1) y (2) se satisfacen 171 Propiedades Teorema 171 Si B es una matriz n n idempotente de rango n, entonces B = I Si B es una matriz simétrica idempotente de rango menor que n, entonces B es una matriz semidefinida positiva Teorema 172 Sea B una matriz n n de rango p 1 Si B es idempotente, entonces B tiene p raíces características distintas de cero y ellas son cada una igual a +1 2 Si B es simétrica, entonces una condición necesaria y suficiente para que B sea idempotente es que esta tenga p raíces características distintas de cero y cada una igual a +1 Teorema 173 Sea An n una matriz simétrica idempotente Entonces 1 A es una matriz simétrica idempotente 2 P AP es una matriz simétrica idempotente si P es ortogonal n n 3 PAP 1 es una matriz idempotente donde P es no singular n n 4 I A es una matriz simétrica idempotente Prueba 171 La prueba es como sigue
8 8 Algebra Matricial 1 Simetría: Como A es simétrica, entonces A = A Ahora (A ) = A, entonces A es simétrica Idempotente: A A = AA = A = A 2 Simetría: (P AP) = P A (P ) = P A P = P AP ya que A = A Idempotente: (P AP)(P AP) = P APP AP = P AAP = P AP ya que PP = I 3 Idempotente: (PAP 1 )(PAP 1 ) = PAP 1 PAP 1 = PAAP 1 = PAP 1 ya que P 1 P = I 4 Simetría: (I A) = I A = I A Idempotente: (I A)(I A) = I A A + AA = I A A + A = I A 18 Traza de una matriz Definición 181 La traza de una matriz An n, la cual escribimos como tr(a) se define como la suma de los elementos de la diagonal de A, esto es, tr(a) = i=1 a ii 181 Propiedades Teorema 181 Sean A y B matrices m n y n m respectivamente; entonces tr(ab) = tr(ba) Prueba 181 Sea AB = C, entonces c pq = n j=1 a pjb jq es el elemento de la fila p y la columna q Sea BA = G, entonces g rs = m i=1 b ria is Pero, m m tr(ab) = c pp = a pj b jp p=1 p=1 j=1
9 18 Traza de una matriz 9 y tr(ba) = = m g rr = b ri a is haciendo i = p, r = j r=1 r=1 i=1 m b jp a pj = m j=1 p=1 p=1 j=1 a pj b jp = tr(ab) Teorema 182 Sea A una matriz n n y P cualquier matriz n n no singular, entonces tr(a) = tr(p 1 AP) si P es una matriz ortogonal, entonces tr(a) = tr(p AP) Prueba 182 Por el teorema anterior tr(p 1 AP) = tr[p 1 (AP)] = tr[(ap)p 1 ] = tr(ai) = tr(a) igual con el otro Teorema 183 Sea A una matriz n n con raíces características λ 1, λ 2,, λ n, entonces tr(a) = i=1 λ i Esto es, la suma de los elementos de la diagonal de una matriz n n es igual a la suma de las raíces características de la matriz Prueba 183 Sea P una matriz no singular tal que P 1 AP = T donde T es una matriz triangular con raíces características λ i sobre la diagonal (P y T pueden no ser matrices reales), entonces tr(a) = tr(p 1 AP) = tr(t) = i=1 λ i
10 10 Algebra Matricial Teorema 184 Si A y B son matrices n n y a y b son escalares, entonces tr(aa + bb) = atr(a) + btr(b) Prueba 184 Sea C = aa+bb, entonces tr(c) = n i=1 c ii donde c ii = aa ii +bb ii entonces tr(aa + bb) = aa ii + bb ii = a a ii + b b ii = atr(a) + btr(b) i=1 i=1 i=1 Teorema 185 Si A es una matriz n n y A 2 = ma, entonces tr(a) = mr(a) Si A es idempotente, entonces m = 1 y tr(a) = r(a) Teorema 186 Sea A una matriz m n, entonces tr(aa ) = tr(a A) = n j=1 m i=1 a2 ij y tr(aa ) = tr(a A) = 0 si y sólo si A = 0 Prueba 185 tr(a A) = tr = tr a 11 a 21 a m1 a 11 a 12 a 1n a 12 a 22 a m2 a 21 a 22 a 2n a 1n a 2n a mn a m1 a m2 a mn m i=1 a2 i1 a m 12 i=1 a2 i2 m = j=1 i=1 m i=1 a2 in a 2 ij Por el teorema 182 tr(aa ) = tr(a A) Como tr(a A) = n j=1 m i=1 a2 ij = 0 sólo si a ij = 0, ij con lo cual A = 0 Teorema 187 Si A es una matriz n n, entonces tr(a) = tr(a )
11 19 Formas Cuadráticas 11 Prueba 186 tr(a) = n i=1 a ii Sea B = A, entonces tr(b) = n i=1 b ii, como b ii = a ii = a ii, entonces tr(a ) = tr(b) = n i=1 b ii = n i=1 a ii = tr(a) Teorema 188 Si A es una matriz n n y A es la g-inversa de A, entonces tr(a A) = tr(aa ) = r(a) 19 Formas Cuadráticas Definición 191 Una función f(x 1, x 2,, x n ) de n variables reales x 1, x 2,, x n se define a ser una forma cuadrática si la función es definida por f(x 1, x 2,, x n ) = a ij x i x j = X AX i=1 j=1 La matriz A es definida a ser la matriz de la forma cuadrática Teorema 191 La matriz de una forma cuadrática puede seleccionarse siempre a ser simétrica Debido a este teorema, toda forma cuadrática aquí será considerada a tener una matriz simétrica a menos que se establezca lo contrario En una forma cuadrática, X AX, es a menudo necesario cambiar las variables x i por las variables y i en el conjunto de ecuaciones lineales Y = C 1 X, donde C 1 es una matriz no singular n n Cuando esto se hace, la forma cuadrática X AX será X AX = (CY ) A(CY ) = Y C ACY = Y BY donde B = C AC En este caso se dice que A y B son congruentes 110 Derivada de funciones lineales y cuadráticas Definición 1101 (Derivada de una función con respecto a un vector) Sea f(x) una función de n variables reales independientes x 1, x 2,, x n La derivada de f(x) con
12 12 Algebra Matricial respecto al vector x, donde x = x 1 x 2 x n es denotado por f(x) x y se define por f(x) x = f(x) x 1 f(x) x 2 f(x) x n Ejemplo 1101 Sea f(x) = 6x 2 1 2x 1x 2 + 2x 2 3, < x i <, entonces f(x) x = f(x) x 1 f(x) x 2 f(x) x 3 = 12x 1 2x 2 2x 1 6x 3 Teorema 1101 (Derivada de una función lineal) Sea l(x) una función lineal de n variables independientes definida por l(x) n ( ) i=1 a ix i = a x = x a donde a = a 1 a 2 a n y los a i son constantes Entonces l(x) x = a Prueba 1101 l(x) x = l(x) x 1 l(x) x 2 l(x) x n = x 1 (a 1 x 1 + a 2 x a n x n ) x 2 (a 1 x 1 + a 2 x a n x n ) x n (a 1 x 1 + a 2 x a n x n ) = a 1 a 2 a n = a
13 110 Derivada de funciones lineales y cuadráticas 13 Teorema 1102 (Derivada de una función cuadrática) Sea q(x) una forma cuadrática en las n variables reales independientes x 1, x 2,, x n definida por q(x) = X AX donde A es una matriz simétrica de constantes Entonces q(x) x = 2AX Prueba 1102 X AX = = a 11 a 12 a 1n ( ) a x 1 x 2 x n 21 a 22 a 2n a n1 a n2 a nn ( n j=1 a 1jx j n j=1 a 2jx j ) n j=1 a njx j x 1 x 2 x n x 1 x 2 = x 1 a 1j x j + x 2 a 2j x j + + x n a nj x j = j=1 x i a ij x j = j=1 i=1 j=1 i=1 j=1 a ij x i x j j=1 x n
14 14 Algebra Matricial XA X X = = = XA X x 1 XA X x 2 XA X x n = x 1 n i=1 n j=1 a ijx i x j x 2 n i=1 n j=1 a ijx i x j x n n i=1 n j=1 a ijx i x j (a x 11 x a 12x 1 x a 1n x 1 x n + a 21 x 2 x 1 + a 22 x a 2nx 1 x n + a n1 x nx a nnx 2 n) (a x 11 x 2 n 1 + a 12x 1 x a 1n x 1 x n + a 21 x 2 x 1 + a 22 x a 2nx 1 x n + a n1 x nx a nnx 2 n ) 2a 11 x 1 + a 12 x a 1n x n + a 21 x 2 + a 31 x a n1 x n a 11 x 1 + 2a 22 x a 2n x n + a 21 x 1 + a 32 x a n2 x n a 1n x 1 + a 2n x a nn x n + a n1 x 1 + a n2 x x + + a (n 1)n x n 1 = 2a 11 x 1 + 2a 12 x 2 + 2a 13 x 3 + 2a 1n x n 2a 21 x 1 + 2a 22 x 2 + 2a 23 x 3 + 2a 2n x n 2a n1 x 1 + 2a n2 x 2 + 2a n3 x 3 + 2a nn x n = 2 a 11 a 12 a 1n a 21 a 22 a 2n x 1 x 2 = 2AX a n1 a n2 a nn x n 111 Inversa Generalizada En la sección 12 se definió la inversa de una matriz y se discutieron varias propiedades Se estableció que si una matriz A tiene inversa, la matriz debe ser cuadrada y el determinante debe ser cero La teoría de modelos lineales, la cual incluye una gran parte de estadística teórica y aplicada, envuelve las soluciones de un sistema de ecuaciones lineales de la forma AX = g (1111) y funciones de las soluciones Si A es una matriz n n no singular, la solución al sistema de ecuaciones de la ecuación
15 111 Inversa Generalizada existe, es única y esta dada por X = A 1 g Sin embargo, hay casos donde A no es una matriz cuadrada y otras situaciones donde A es una matriz cuadrada pero es singular En estas situaciones todavía puede haber una solución para el sistema, y una teoría unificada para tratar tales situaciones puede ser deseable Una de tales teorías envuelve el uso de inversa generalizada, la cuál es discutida en esta sección Sea A una matriz m n de rango r Se investiga una matriz denotada por A la cual tiene muchas de las propiedades que la inversa de la matriz A debería si la inversa existe Definición 1111 (Inversa Generalizada) Sea A una matriz m n Si una matriz denotada por A existe la cual satisface las 4 condiciones siguientes, será definida como una inversa generalizada de A 1 AA es simétrica; 2 A A es simétricas; 3 AA A = A; 4 A AA = A Se usa la terminología g inversa para inversa generalizada Si A es no singular, es claro que A 1 satisface las condiciones de una g inversa Sin embargo, si A es una matriz cuadrada y singular, o si A es una matriz no cuadrada, entonces el problema se trata como si una matriz A existe la cual satisface las condiciones de la definición 1111 A continuación se demuestra que para cada matriz A, una matriz g inversa existe y es única También se establecen y se prueban varias propiedades de esta g inversa Teorema 1111 Si una g inversa de una matriz A m n existe, esta tiene tamaño n m Prueba 1111 La prueba se sigue del hecho de que AA es simétrica y por lo tanto cuadrada, es decir, AA es una matriz m m por lo tanto la columna de A debe ser m y para que el producto este definido A debe tener n filas Así, A es un matriz n m Teorema 1112 Si A es la matriz nula de tamaño m n, entonces A es la matriz nula n m Prueba 1112 Claramente A = 0 satisface las condiciones de la definición 1111 si A = 0
16 16 Algebra Matricial Teorema 1113 Para cada matriz A existe una matriz A que satisface las condiciones de la definición 1111, es decir, cada matriz tiene una g inversa Prueba 1113 Si A = 0, entonces por el teorema 1112 A = 0 Asumamos A 0 Usando el corolario 1621, si A tiene rango r > 0, esta puede factorizarse como, digamos A = A L A R = BC (1112) donde B es una matriz m r de rango r y C es una matriz r n de rango r Note que B B y CC son ambas no singulares Si se define Av como A = C (CC ) 1 (B B) 1 B (1113) es fácil mostrar que esta satisface las condiciones de la definición 1111 Note también que si A es real, entonces A es real La factorización de A en 1112 no es única; sin embargo, la g-inversa A es única, esto se ve en el siguiente teorema Teorema 1114 Para cada matriz A existe una única matriz A que satisface las condiciones de la definición 1111, es decir, cada matriz tiene una única g inversa Prueba 1114 Asumamos que A 1 y A 2 son 2 g inversas de una matriz A Esto significa que A 1 y A 2 cada una satisface las condiciones de la definición 1111 Se demostrará que cuando este es el caso, se sigue que A 1 = A 2 Primero se demostrará que AA 1 = AA 2 Por el item 3 de la definición 1111 se tiene que A = AA 1 A Multiplicando a la derecha por A 2 se obtiene AA 2 = AA 1 AA 2 Por el item 1 de la definición 1111 AA 1 y AA 2 son simétricos y por lo tanto AA 1 AA 2 es simétrico, es decir de allí se obtiene que AA 1 AA 2 = (AA 1 AA 2 ) AA 2 = AA 1 AA 2 = [(AA 1 )(AA 2 )] = (AA 2 ) (AA 1 ) = (AA 2 )(AA 1 ) = (AA 1 )
17 111 Inversa Generalizada 17 ya que de manera similar por el item 3 se obtiene que A = AA 2 A lo cual implica que AvA 1 = AA 2 AA 1 Por lo tanto, AA 1 = AA 2 y por simetría A 2 A = A 1 A Por el item 4 se obtiene que A 1 = A 1 AA 1 = A 1 (AA 1 ) = A 1 (AA 2 ) = (A 1 A)A 2 = (A 2 A)A 2 = A 2 AA 2 = A 2 entonces A 1 = A 2 y esto completa la prueba Teorema 1115 La g inversa de la traspuesta de A es la traspuesta de la g inversa de A, es decir (A ) = (A ) Prueba 1115 La prueba consiste en demostrar que (A ) es la g inversa de A y ya que la g inversa de A es única, se sigue que (A ) = (A ) Sea A = BC como en la ecuación 1112, se obtiene A = C (CC ) 1 (B B) 1 B (1114) además y A = C B (A ) = (B ) [B (B )] 1 [(C ) C ] 1 (C ) = B(B B) 1 (CC ) 1 C tomando la traspuesta de A en 1114 se obtiene como en la ecuación 1112, se obtiene (A ) = B(B B) 1 (CC ) 1 C
18 18 Algebra Matricial por lo tanto, (A ) = (A ) y ya que la g-inversa de una matriz es única, el teorema es probado Teorema 1116 La g inversa de A es igual a A, es decir (A ) = A Prueba 1116 Por la definición 1111 la g inversa satisface los siguientes resultados 1 A (A ) = [A (A ) ] 2 (A ) A = [(A ) A ] 3 A (A ) A = A 4 (A ) A (A ) = (A ) Pero si se sustituye A por (A ), las 4 ecuaciones anteriores son exactamente las de la definición 1111 Por lo tanto, A es la única g inversa de A, es decir (A ) = A Teorema 1117 El rango de la g inversa de A es igual al rango de A Prueba 1117 Si se aplica el teorema 163 a AA A = A, se obtiene que r(a) = r(aa A) r(a ) Pero como A AA = A, se obtiene que r(a ) = r(a AA ) r(a) por lo tanto, r(a ) = r(a) Corolario Si el rango de la matriz A es igual a r, el rango de cada una de las matrices siguientes es igual a r: A, AA, A A, AA A, A AA Prueba 1118 Sólo falta probar AA y A A
19 111 Inversa Generalizada 19 Para AA Se sabe que A = AA A entonces r(a) = r(aa A) r(aa ) como r(a) = r(a ) se tiene que r(a ) = r(a AA ) r(aa ) por lo tanto, r(aa ) = r(a) Igual para A A Teorema 1118 Si A e una matriz simétrica, la g inversa de A es también simétrica; esto es, si A = A entonces A = (A ) Prueba 1119 Por el teorema 1115, se obtiene que (A ) = (A ), pero ya que A = A, se obtiene que A = (A ) Los próximos teoremas dan la forma de la g inversa de matrices especiales Teorema 1119 Si la matriz A es no singular, entonces A 1 = A Prueba Para probar que esto es cierto hay que ver que A 1 cumple las condiciones de la definición AA 1 = I la cual es simétrica; 2 A 1 A = I la cual es simétrica; 3 AA 1 A = IA = A 4 A 1 AA 1 = IA 1 = A 1 Teorema Si A es simétrica idempotente, entonces A = A, esto es, si A = A y A = A 2, entonces A = A Teorema Si A es una matriz m n de rango m, entonces A = A (AA ) 1 y AA = I Si el rango de A es n, entonces A = (A A) 1 A y A A = I
20 20 Algebra Matricial Teorema Las matrices AA, A A,I AA,I A A son todas simétricas idempotentes Prueba Se probará primera la simetría y luego la idempotencia Simetría: 1 (AA ) = (A ) A = (A ) 1 A = (A ) [(A ) ], se cumple por la condición 1 de 1111; 2 A A es simétrica; 3 (I AA ) = I (AA ) = I AA 4 (I A A) = I (A A) = I A A Idempotencia: 1 (AA )(AA ) = AA AA = AA ya que A AA = A ; 2 (A A)(AA) = A AA A = A A ya que AA A = A; 3 (I AA )(I AA ) = I AA AA AA +AA AA = I 2AA +AA = I AA ; 4 (I A A)(I A A) = I A A A A A A+A AA A = I 2A A+A A = I A A Nota 1111 No siempre es cierto que (GH) = H G para todas las matrices G y H Sin embargo, para ciertas matrices esta ecuación es correcta Ahora se establecen algunos teoremas relacionados con este asunto Teorema Sea B una matriz m r de rango r, (r > 0), y sea C una matriz r m de rango r, entonces (CB) = C B Prueba Por el teorema 11111, se obtiene que C = C (CC ) 1 y B = (B B) 1 B
21 111 Inversa Generalizada 21 Por lo tanto, C B = C (CC ) 1 (B B) 1 B Por la ecuación 1113 C (CC ) 1 (B B) 1 B = A = (BC) Teorema (A A) = A (A ) para cualquier matriz A Teorema (AA ) = AA y (A A) = A A para cualquier matriz A
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
Algebra lineal Matrices
 Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
23/10/14. Algebra Matricial $ $ ' ' ' $ & & & # # I 3 I 2 = 1 0 $ DEFINICION DE MATRIZ 2.1 CONCEPTOS DE MATRICES CONCEPTOS DE MATRICES. $ n. ! a.
 /0/ Algebra Matricial. OPERACIONES DE DEFINICION DE MATRIZ Si A es una matriz de m x n (esto es una matriz con m filas y n columnas) la entrada escalar en la i-ésima fila y la j-ésima columna de A se denota
/0/ Algebra Matricial. OPERACIONES DE DEFINICION DE MATRIZ Si A es una matriz de m x n (esto es una matriz con m filas y n columnas) la entrada escalar en la i-ésima fila y la j-ésima columna de A se denota
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Matrices. José Vicente Romero Bauset. ETSIT-curso 2009/2010. José Vicente Romero Bauset Tema 1.- Matrices. 1
 Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Estadística III Repaso de Algebra Lineal
 Repaso de Algebra Lineal Vectores Un vector columna de dimensión n 1 es una serie de números dispuestos como sigue: x 1 x 2 x =. x n Un vector fila de dimensión 1 p es una serie de números dispuestos como
Repaso de Algebra Lineal Vectores Un vector columna de dimensión n 1 es una serie de números dispuestos como sigue: x 1 x 2 x =. x n Un vector fila de dimensión 1 p es una serie de números dispuestos como
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES
 Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
MATRICES OPERACIONES BÁSICAS CON MATRICES
 MATRICES OPERACIONES BÁSICAS CON MATRICES ANTECEDENTES En el año 1850, fueron introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A.
MATRICES OPERACIONES BÁSICAS CON MATRICES ANTECEDENTES En el año 1850, fueron introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A.
Repaso de álgebra de matrices y probabilidad. Javier Santibáñez (IIMAS, UNAM) Regresión Semestre / 58
 Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Matrices y Determinantes. Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC
 Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
Es decir, det A = producto de diagonal principal producto de diagonal secundaria. Determinante de una matriz cuadrada de orden 3
 1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
2. Álgebra matricial. Inversa de una matriz O B 1 O B 1. Depto. de Álgebra, curso
 Depto de Álgebra, curso 2017-2018 2 Álgebra matricial Inversa de una matriz Ejercicio 21 Calcule la matriz inversa de cada una de las matrices siguientes: a 2 1 1 3 2 1 h e, b 2 1 1 5 2 3 2 0 1 1 2 1 1
Depto de Álgebra, curso 2017-2018 2 Álgebra matricial Inversa de una matriz Ejercicio 21 Calcule la matriz inversa de cada una de las matrices siguientes: a 2 1 1 3 2 1 h e, b 2 1 1 5 2 3 2 0 1 1 2 1 1
Métodos Estadísticos Multivariados
 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Matrices Particionadas Traza de una Matriz
 CAPÍTULO Matrices Particionadas Traza de una Matriz Este capítulo consta de tres secciones Las dos primeras versan sobre matrices particionadas La tercera sección trata sobre la traza de una matriz En
CAPÍTULO Matrices Particionadas Traza de una Matriz Este capítulo consta de tres secciones Las dos primeras versan sobre matrices particionadas La tercera sección trata sobre la traza de una matriz En
TEMA 7. Matrices y determinantes.
 TEMA 7 Matrices y determinantes. 1. Matrices. Generalidades Definición 1 Sea E un conjunto cualquiera, m, n IN. Definimos matriz de orden m n sobre E a una expresión de la forma: a 11 a 12... a 1n a 21
TEMA 7 Matrices y determinantes. 1. Matrices. Generalidades Definición 1 Sea E un conjunto cualquiera, m, n IN. Definimos matriz de orden m n sobre E a una expresión de la forma: a 11 a 12... a 1n a 21
ELEMENTOS DE ALGEBRA LINEAL
 ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; (A ) = A. 2. La inversa de A 1 es A; (A 1 ) 1 = A. 3. (AB) = B A.
 ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
 Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Matrices y determinantes
 Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
MATEMÁTICAS 2º BACH TECNOL. MATRICES. Profesor: Fernando Ureña Portero MATRICES
 CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
Determinantes. Definiciones básicas sobre determinantes. José de Jesús Angel Angel.
 Determinantes Definiciones básicas sobre determinantes wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2008 Contenido 1 Determinantes 2 11 Propiedades de determinantes 4 2 Inversa
Determinantes Definiciones básicas sobre determinantes wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2008 Contenido 1 Determinantes 2 11 Propiedades de determinantes 4 2 Inversa
Algebra de Matrices 1
 Algebra de Matrices Definición Una matriz es un arreglo rectangular de valores llamados elementos, organizados por filas y columnas. Ejemplo: Notas: A 6. Las matrices son denotadas con letras mayúsculas..
Algebra de Matrices Definición Una matriz es un arreglo rectangular de valores llamados elementos, organizados por filas y columnas. Ejemplo: Notas: A 6. Las matrices son denotadas con letras mayúsculas..
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Matrices y Determinantes.
 Tema II Capítulo 1 Matrices Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC Tema II Matrices y Determinantes 1 Matrices 1 Definiciones básicas Definición 11 Una matriz A de
Tema II Capítulo 1 Matrices Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC Tema II Matrices y Determinantes 1 Matrices 1 Definiciones básicas Definición 11 Una matriz A de
Matrices y determinantes
 Matrices y determinantes Las matrices y los determinantes son herramientas del álgebra de gran utilidad en muchas disciplinas. Los campos de aplicación de la teoría de las matrices y de los determinantes
Matrices y determinantes Las matrices y los determinantes son herramientas del álgebra de gran utilidad en muchas disciplinas. Los campos de aplicación de la teoría de las matrices y de los determinantes
Matrices y determinantes (Curso )
 ÁLGEBRA Práctica 3 Matrices y determinantes (Curso 2008 2009) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz triangular
ÁLGEBRA Práctica 3 Matrices y determinantes (Curso 2008 2009) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz triangular
ÁLGEBRA LINEAL I Práctica 3
 ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ALGEBRA y ALGEBRA LINEAL
 520142 ALGEBRA y ALGEBRA LINEAL Primer Semestre, Universidad de Concepción CAPITULO 7. MATRICES DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Matriz Sean
520142 ALGEBRA y ALGEBRA LINEAL Primer Semestre, Universidad de Concepción CAPITULO 7. MATRICES DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición: Matriz Sean
TEMA 1: MATRICES. Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas ...
 TEMA : MATRICES Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas a a a... a n a a a... an A... am am am... amn A los números reales a ij se les llama elementos
TEMA : MATRICES Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas a a a... a n a a a... an A... am am am... amn A los números reales a ij se les llama elementos
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
ÁLGEBRA LINEAL I Práctica 3
 ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2013 2014) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2013 2014) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
MATRICES. M(n) ó M nxn A =
 MTRICES Definición de matriz. Una matriz de orden m n es un conjunto de m n elementos pertenecientes a un conjunto, que para nosotros tendrá estructura de cuerpo conmutativo y lo denotaremos por K, dispuestos
MTRICES Definición de matriz. Una matriz de orden m n es un conjunto de m n elementos pertenecientes a un conjunto, que para nosotros tendrá estructura de cuerpo conmutativo y lo denotaremos por K, dispuestos
MATRICES. Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.
 MATRICES Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
MATRICES Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
 1 de 6 24/08/2009 9:54 MATRICES Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853 En
1 de 6 24/08/2009 9:54 MATRICES Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853 En
Lección 8. Matrices y Sistemas de Ecuaciones Lineales
 Lección 8 Matrices y Sistemas de Ecuaciones Lineales MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En
Lección 8 Matrices y Sistemas de Ecuaciones Lineales MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En
Una matriz es un arreglo rectangular de elementos. Por ejemplo:
 1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
Contenido. 2 Operatoria con matrices. 3 Determinantes. 4 Matrices elementales. 1 Definición y tipos de matrices
 elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Menor, cofactor y comatriz
 Menor, cofactor y comatriz Sea A una matriz cuadrada de orden n. Al quitarle la línea i y la columna j se obtiene una submatriz de orden n-1, que se denota habitualmente A i,j. Por ejemplo, con n = 4,
Menor, cofactor y comatriz Sea A una matriz cuadrada de orden n. Al quitarle la línea i y la columna j se obtiene una submatriz de orden n-1, que se denota habitualmente A i,j. Por ejemplo, con n = 4,
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
 CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
Matrices. Observación: Es usual designar una matriz por letras mayúsculas: A, B, C,... 3 B =
 Definición: A una ordenación o arreglo rectangular de ciertos objetos se define como matriz (en este curso nos interesa que los objetos de la matriz sean numeros reales. Observación: Es usual designar
Definición: A una ordenación o arreglo rectangular de ciertos objetos se define como matriz (en este curso nos interesa que los objetos de la matriz sean numeros reales. Observación: Es usual designar
Escuela de Matemáticas
 Escuela de Matemáticas Universidad de Costa Rica MA-004: Álgebra Lineal Prácticas Sistemas de ecuaciones lineales, Matrices Determinantes MSc Marco Gutiérrez Montenegro 07 Sistemas de ecuaciones lineales
Escuela de Matemáticas Universidad de Costa Rica MA-004: Álgebra Lineal Prácticas Sistemas de ecuaciones lineales, Matrices Determinantes MSc Marco Gutiérrez Montenegro 07 Sistemas de ecuaciones lineales
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Relación de problemas. Álgebra lineal.
 Relación de problemas Álgebra lineal Tema 1 Sección 1 Matrices Determinantes Sistemas lineales Matrices Ejercicio 11 Consideremos las siguientes matrices: ( 1 2 A = 1 1 ) ( 1 1 B = 0 1 ) C = 1 0 0 0 1
Relación de problemas Álgebra lineal Tema 1 Sección 1 Matrices Determinantes Sistemas lineales Matrices Ejercicio 11 Consideremos las siguientes matrices: ( 1 2 A = 1 1 ) ( 1 1 B = 0 1 ) C = 1 0 0 0 1
Capitulo 6. Matrices y determinantes
 Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Tema 1. 1 Álgebra lineal. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. 1.1 Vectores de R n. 1. Vectores. 2.
 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Matemáticas II. Prácticas: Matrices y Determinantes ; C = 1 3 5
 Matemáticas II Prácticas: Matrices y Determinantes. Sean las matrices cuadradas siguientes: 4 5 6 B = 9 8 7 6 5 4 C = 5 7 9 0 7 8 9 Se pide calcular: a A B + C. b A AB + AC. c A B AB + ACB.. Sean las matrices:
Matemáticas II Prácticas: Matrices y Determinantes. Sean las matrices cuadradas siguientes: 4 5 6 B = 9 8 7 6 5 4 C = 5 7 9 0 7 8 9 Se pide calcular: a A B + C. b A AB + AC. c A B AB + ACB.. Sean las matrices:
Matrices y determinantes
 Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
a) La adición y la multiplicación de matries cuadradas del mismo orden, están bien definidas.
 MATRICES CUADRADAS Definición: ( Cuadradas Una matriz A es una matriz cuadrada de orden n, si y solo si, A es de oreden n n, es decir, A tiene n filas y n columnas: a 11 a 1n a n1 a nn Observación: a La
MATRICES CUADRADAS Definición: ( Cuadradas Una matriz A es una matriz cuadrada de orden n, si y solo si, A es de oreden n n, es decir, A tiene n filas y n columnas: a 11 a 1n a n1 a nn Observación: a La
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
Matrices, determinantes y sistemas de ecuaciones lineales
 Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Capítulo 2. Determinantes Introducción. Definiciones
 Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
Bases y dimensión. Problemas teóricos. En todos los problemas se supone que V es un espacio vectorial sobre un campo F. p=1
 Bases y dimensión Problemas teóricos Bases de un espacio vectorial En todos los problemas se supone que V es un espacio vectorial sobre un campo F. Definición de base. Sean b 1,..., b n V. Se dice que
Bases y dimensión Problemas teóricos Bases de un espacio vectorial En todos los problemas se supone que V es un espacio vectorial sobre un campo F. Definición de base. Sean b 1,..., b n V. Se dice que
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE
 3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE
 3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS // Curso 2017-18 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS // Curso 2017-18 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
Matemática 2 MAT022. Clase 6 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María. Determinante de una matriz
 Matemática 2 MAT022 Clase 6 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María Tabla de Contenidos 1 Determinante de una matriz Sea A la matriz de orden 2 2 con coeficientes
Matemática 2 MAT022 Clase 6 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María Tabla de Contenidos 1 Determinante de una matriz Sea A la matriz de orden 2 2 con coeficientes
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn
![MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn](/thumbs/79/78966751.jpg) MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a [ 21 a 22 a 2n ] a m1 a m2 a mn con m renglones y n columnas, donde los a
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a [ 21 a 22 a 2n ] a m1 a m2 a mn con m renglones y n columnas, donde los a
Métodos directos para resolver sistemas de ecuaciones lineales
 Métodos directos para resolver sistemas de ecuaciones lineales Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el
Métodos directos para resolver sistemas de ecuaciones lineales Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales
 Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
DOCENTE: JESÚS E. BARRIOS P.
 DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
Matrices 3. Matrices. Verónica Briceño V. agosto 2012
 3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
 Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Práctica 1: Sistemas de Ecuaciones Lineales - Matrices
 ALGEBRA LINEAL Primer Cuatrimestre 2017 Práctica 1: Sistemas de Ecuaciones Lineales - Matrices En todas las prácticas, K es un cuerpo; en general K = Q (los números racionales, R (los números reales o
ALGEBRA LINEAL Primer Cuatrimestre 2017 Práctica 1: Sistemas de Ecuaciones Lineales - Matrices En todas las prácticas, K es un cuerpo; en general K = Q (los números racionales, R (los números reales o
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
 INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Apuntes de modelos lineales
 Apuntes de modelos lineales Clases Nos. 1 al 3 Ernesto Ponsot Balaguer Dr. en Estadística, MSc. en Estadística Aplicada, Ing. de Sistemas http://webdelprofesor.ula.ve/economia/ernesto E-mail: ernesto@ula.ve
Apuntes de modelos lineales Clases Nos. 1 al 3 Ernesto Ponsot Balaguer Dr. en Estadística, MSc. en Estadística Aplicada, Ing. de Sistemas http://webdelprofesor.ula.ve/economia/ernesto E-mail: ernesto@ula.ve
Matrices 2º curso de Bachillerato Ciencias y tecnología
 MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
TEMA 7: MATRICES. OPERACIONES.
 TEMA 7: MATRICES. OPERACIONES. 1. MATRICES. TIPOS DE MATRICES. Se llama matriz de orden m x n (m filas y n columnas) a un conjunto de m n elementos, distribuidos en m filas y n columnas y encerrados entre
TEMA 7: MATRICES. OPERACIONES. 1. MATRICES. TIPOS DE MATRICES. Se llama matriz de orden m x n (m filas y n columnas) a un conjunto de m n elementos, distribuidos en m filas y n columnas y encerrados entre
ALGEBRA LINEAL - Práctica N 2 - Segundo cuatrimestre de 2017 Matrices y coordenadas
 Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA 1 ALGEBRA LINEAL - Práctica N 2 - Segundo cuatrimestre de 2017 Matrices y coordenadas Ejercicio 1 Sean m n y r N i) Probar que
Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA 1 ALGEBRA LINEAL - Práctica N 2 - Segundo cuatrimestre de 2017 Matrices y coordenadas Ejercicio 1 Sean m n y r N i) Probar que
Teoría de Matrices. Julio Yarasca. 30 de junio de 2015. Julio Yarasca
 30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
Tema 1: Matrices y Determinantes
 Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Departamento de Matemática Segundo Cuatrimestre de 2002 ÁLGEBRA LINEAL
 Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Departamento de Matemática Segundo Cuatrimestre de 2002 ÁLGEBRA LINEAL Práctica N 2: Matrices Ejercicio 1 Probar que los siguientes
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Departamento de Matemática Segundo Cuatrimestre de 2002 ÁLGEBRA LINEAL Práctica N 2: Matrices Ejercicio 1 Probar que los siguientes
SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
1. Matrices. Operaciones con matrices
 REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
Álgebra lineal - Matriz inversa. Determinante. Farith J. Briceño N.
 Álgera lineal - Matriz inversa. Determinante. Farith J. Briceño N. Ojetivos a curir Matriz Inversa. Determinante. Calculo de determinantes. Propiedades de los determinantes. Adjunta de una matriz. Calculo
Álgera lineal - Matriz inversa. Determinante. Farith J. Briceño N. Ojetivos a curir Matriz Inversa. Determinante. Calculo de determinantes. Propiedades de los determinantes. Adjunta de una matriz. Calculo
2 - Matrices y Determinantes
 Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Elementos de una matriz.
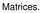 Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices y Determinantes
 Matrices y Determinantes Definición de matriz Matriz Una matriz es un ente matemático equivalente a una tabla; es decir, es un arreglo de elementos de cualquier naturaleza (aunque, en general, suelen ser
Matrices y Determinantes Definición de matriz Matriz Una matriz es un ente matemático equivalente a una tabla; es decir, es un arreglo de elementos de cualquier naturaleza (aunque, en general, suelen ser
Tema I. Matrices y determinantes
 Tema I. Matrices y determinantes 2007 Carmen Moreno Valencia 1. Matrices sobre un cuerpo 2. Operaciones con matrices 3. Determinante de una matriz cuadrada 4. Menor complementario y adjunto 5. Cálculo
Tema I. Matrices y determinantes 2007 Carmen Moreno Valencia 1. Matrices sobre un cuerpo 2. Operaciones con matrices 3. Determinante de una matriz cuadrada 4. Menor complementario y adjunto 5. Cálculo
ACTIVIDADES SELECTIVIDAD MATRICES
 ACTIVIDADES SELECTIVIDAD MATRICES Ejercicio 1 Para qué valores de m tiene solución la ecuación matricial? (b) Resuelve la ecuación matricial dada para. Ejercicio 2 Siendo I la matriz identidad de orden
ACTIVIDADES SELECTIVIDAD MATRICES Ejercicio 1 Para qué valores de m tiene solución la ecuación matricial? (b) Resuelve la ecuación matricial dada para. Ejercicio 2 Siendo I la matriz identidad de orden
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji
![a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji a n1 a n2 a nn x n a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x j x i = s ij x i x j + s ji x j x i 2 x i x j + a ij + a ji](/thumbs/84/89039875.jpg) 16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
16 Fundamentos de Matemáticas : Álgebra Lineal Capítulo 1 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado,
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel.
 Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
MATRICES. Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas. o simplemente A = (a.
 MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES
 ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
Matrices y determinantes
 Matrices y determinantes 1 Matrices Una matriz de orden m n es un conjunto de m n números ordenados en m filas y n columnas Por ejemplo, 1 1 2 0 2 0 2 1 1 1 2 1 3 0 2 es una matriz de orden 3 5 Una matriz
Matrices y determinantes 1 Matrices Una matriz de orden m n es un conjunto de m n números ordenados en m filas y n columnas Por ejemplo, 1 1 2 0 2 0 2 1 1 1 2 1 3 0 2 es una matriz de orden 3 5 Una matriz
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Estos apuntes se han sacado de la página de internet de vitutor con pequeñas modificaciones.
 TEMA 1: MATRICES Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
TEMA 1: MATRICES Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Matriz A = Se denomina MATRIZ a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.
 MATRICES Matriz Se denomina MATRIZ a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n A = a i1 a ij a in a m1 a
MATRICES Matriz Se denomina MATRIZ a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n A = a i1 a ij a in a m1 a
a n1 a n2 a nn Es decir, una forma cuadrática es un polinomio homogéneo de grado 2 y n variables.
 Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Capítulo 7 Formas cuadráticas. Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado de la norma de un vector
Tema 1. Preliminares. 1.1 Resultados algebraicos
 Tema 1 Preliminares 11 Resultados algebraicos Consideraremos habitualmente matrices con coeficientes en R y, ocasionalmente, en C Denotaremos por a i j a los elementos de una matriz A, donde el subíndice
Tema 1 Preliminares 11 Resultados algebraicos Consideraremos habitualmente matrices con coeficientes en R y, ocasionalmente, en C Denotaremos por a i j a los elementos de una matriz A, donde el subíndice
1 Vectores de R n. Tema 1. Álgebra matricial. 1.2 Dependencia lineal
 Diplomatura en Estadística 1 Tema 1. Álgebra matricial 1. Vectores 1.1 Definiciones básicas 1.2 Dependencia lineal 2. Matrices 2.1 Rango de una matriz 2.2 Matrices cuadradas 3. Vectores y valores propios
Diplomatura en Estadística 1 Tema 1. Álgebra matricial 1. Vectores 1.1 Definiciones básicas 1.2 Dependencia lineal 2. Matrices 2.1 Rango de una matriz 2.2 Matrices cuadradas 3. Vectores y valores propios
Tema 3: MATRICES. Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada
 Tema 3: MATRICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura: Matemáticas
Tema 3: MATRICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura: Matemáticas
Resumen de Teoría de Matrices
 Resumen de Teoría de Matrices Rubén Alexis Sáez Morcillo Ana Isabel Martínez Domínguez 1 de Octubre de 2004 1. Matrices. Generalidades. Definición 1.1. Se llama matriz de orden m n sobre un cuerpo K a
Resumen de Teoría de Matrices Rubén Alexis Sáez Morcillo Ana Isabel Martínez Domínguez 1 de Octubre de 2004 1. Matrices. Generalidades. Definición 1.1. Se llama matriz de orden m n sobre un cuerpo K a
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
