DERIVADES. TÈCNIQUES DE DERIVACIÓ
|
|
|
- María Pilar Villalobos Quintero
- hace 5 años
- Vistas:
Transcripción
1 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres tres punts en què la derivada sigui positiva. La derivada també és positiva en x 4, x, x 0 Digues un altre punt en què la derivada sigui zero. La derivada també és zero en x. Digues uns altres dos punts en què la derivada sigui negativa. La derivada també és negativa en x 4, x 5 Digues un interval [a, b] en el qual es compleixi que si x [a, b], llavors f'(x) >0. Per exemple, en l interval [ 5, ] es compleix que, si x [ 5, ], aleshores f'(x) > 0. 65
2 Pàgina 57 Funció derivada y f (x) Continua escrivint les raons per les quals g (x) és una funció el comportament de la qual respon al de la derivada de f (x). a b En l interval (a, b), f (x) és decreixent. Per tant, la seva derivada és negativa. És el que li passa a g(x) en (a, b). La derivada de f a b és 0: f'(b) 0. I també és g(b) 0. a b y g(x) f'(x) En general: g(x) f'(x) 0 on f (x) té tangent horitzontal. g(x) f'(x) > 0 on f (x) és creixent. g(x) f'(x) < 0 on f (x) és decreixent. A Les gràfiques A, B i C són les funcions derivades de les gràfiques, i, però en un altre ordre. Respon raonadament quina és la de cadascuna. ) B ) A ) C La derivada s anul la en els punts de tangent horitzontal, és positiva on la funció és creixent, i és negativa on la funció decreix. B C 66
3 Pàgina 59 EXERCICIS PROPOSATS x, x. f (x) És derivable en x 0? x, x > lím f (x) lím ( x) 4 x x lím f (x) lím (x ) x + x + La funció no és contínua en x, ja que: lím f (x) lím f (x). x x + Per tant, tampoc no és derivable en x. x, x. f (x) És derivable en x 0? x 8, x > lím f (x) lím ( x) 4 x x lím f (x) lím (x 8) 4 x + x + La funció és contínua, ja que: lím f (x) lím f (x) f () 4 x x + si x < f'(x) x si x > f'( ) f'( + ) 4 Per tant, f (x) no és derivable en x. Pàgina 6. Calcula la derivada de cada una de les funcions següents: x x a) f (x) b) f (x) + x + x x tg x c) f (x) ln d) f (x) + x + tg x tg x e) f (x) + tg x f ) f (x) ln e tg x g) f (x) x + h) f (x) log (sin x cos x) i) f (x) sin x + cos x + x j) f (x) sin x + cos x k) f (x) 7 sin(x + ) l) f (x) sin(x 5 x + x ) m) f (x) sin x + x + n) f (x) cos x + ( x) 67
4 a) f'(x) ( + x) ( x) x + x ( + x) ( + x) ( + x) b) Utilitzem el resultat obtingut a a): f'(x) ( + x) x + x ( x)( + x) c) Utilitzem el resultat obtingut a a): f'(x) ( + x) x ( + x) ( x)( + x) + x D una altra manera: Si agafem logaritmes prèviament: f (x) ln ( x) ln ( + x). Derivem: f'(x) x + x x + x x x d) f'(x) ( + tg x)( + tg x) ( tg x) ( + tg x) ( + tg x) ( + tg x)[ tg x + tg x] ( + tg x) ( + tg x) ( + tg x) x D una altra manera: Si tenim en compte el resultat obtingut a a): f'(x) D [tg x] ( + tg x) ( + tg x) ( + tg x) ( + tg x) ( + tg x) e) Tenint en compte el que hem obtingut a d): f'(x) ( + tg ( + tg x) x) ( + tg x) ( tg x)( + tg x) tg x + tg x També podríem haver arribat a aquest resultat utilitzant el que hem obtingut a b). f) f (x) ln ln e (tg x) / f'(x) e tg x + tg x tg x x + g) f (x) (x + ) / f'(x) (x + ) / ln ln h) f (x) log (sin x cos x) [log (sin x) +log (cos x)] cos x sin x ln 0 sin x cos x x + ln 0 ln 0 cos x sin x sin x cos x f'(x) [ + ] 68
5 D una altra manera: 4 cos x sin x 4 cos x 4 ln 0 sin x cos x ln 0 sin x ln 0 tg x f (x) log (sin x cos x) sin x log ( ) f'(x) cos x ln 0 sin x i) f (x) sin x + cos x + x + x f'(x) 4 ln 0 tg x cos x + cos x j) f'(x) + x + x sin x + ( sin x ) cos x + cos x x + sin x + sin x x k) f'(x) 7 sin(x + ) ln 7 D(sin (x + )) 7 sin(x + ) ln 7 x cos(x + ) l) f'(x) cos (x 5 x + x ) ( 5x4 + ) x x m) f'(x) (cos x + x) sin x + x + cos x + x sin x + x + + ( x) ( ) n) f'(x) cos x + ( x) [ sin x + ( x) ] (x + ( x) ) cos x +( x) sin x +( x) (x 5) (x + ( x) ) (5 x) sin ( x + ( x) ) (x + ( x) ) 4. Troba les derivades a, a i a de les funcions següents: a) y x 5 b) y x cos x c) y sin x + cos x + x a) y x 5 y' 5x 4 ; y'' 0x ; y''' 60x b) y x cos x y' cos x x sin x 69
6 y'' sin x sin x x cos x sin x x cos x y''' cos x cos x + x sin x cos x + x sin x c) y sin x + cos x + x + x y' ; y'' 0; y''' 0 5. Calcula f'() essent: f (x) x x e 4 5 x 5 f (x) x x e 4 x / / x / e 4 /5 e 4 x /0 9 e 4 x /0 x 5 /5 x /5 5 9 e f'(x) 4 x 7/ e x 7 Per tant: f'() 5 9 e Calcula f'(π/6) essent: f (x) (cos x sin x) sin 6x f (x) (cos x sin sin x x) sin 6x cos 6x sin 6x cos x f'(x) 6cos x π π Per tant: f'( ) 6 cos 6 cos(π) Calcula f'(0) essent: f (x) ln x + x + (x + ) f (x) ln (x + ) ln (x x + x + + x + ) (x + ) f'(x) x + (x + ) x + 8x + 4 x + x + x + x + x + (6x + 4x + 4x + 8) (x + x + ) 6x 4x + ( 4)x + 8 (x + x + ) Per tant: f'(0) 8 70
7 Pàgina Estudia la derivabilitat en x 0 de la funció: f (x) Continuïtat en x 0 : lím f (x) lím (x x) 0 lím f (x) f () 0 x x x lím f (x) lím (x 9) 0 Per tant, f (x) és contínua en x 0. x + x Derivabilitat en x 0 : x x, x x 9, x > lím f'(x) lím (x ) f'( ) x x lím f'(x) lím () f'( + ) x + x + Les derivades laterals existeixen i coincideixen. Per tant, f (x) és derivable en x 0. A més, f'(). 9. Calcula m i n perquè f (x) sigui derivable en Á: f (x) Si x 0, la funció és contínua i derivable, ja que està formada per dos polinomis. Continuïtat en x 0: lím f (x) lím (x mx + 5) 5 x 0 x 0 lím f (x) lím ( x + n) n x 0 + x 0 f (0) 5 Derivabilitat en x 0: lím f'(x) lím (x m) m f'(0 ) x 0 x 0 lím f'(x) lím ( x) 0 f'(0 + ) x 0 + x 0 + Per tant, f (x) és derivable en Á per a m 0 i n 5. Perquè f (x) sigui contínua en x 0, ha de ser: n 5 x mx + 5, x 0 x + n, x > 0 Perquè sigui derivable en x 0, ha de ser: m 0 m 0 7
8 Pàgina 68 EXERCICIS I PROBLEMES PROPOSATS PER PRACTICAR Definició de derivada 0. Troba la taxa de variació mitjana (TVM) de les funcions següents en els intervals: [, ]; [0, ]; [, 5]; [, + h] a) f(x) x + b) f(x) 7x 5 c) f(x) d) f(x) x En quines és constant la TVM? Quin tipus de funcions són? a) f(x) x + f ( ) f ( ) En [, ] TVM 4 f () f (0) En [0, ] TVM f (5) f () En [, 5] TVM 7 f ( + h) f () h En [, + h] TVM + h h + h h b) f(x) 7x 5 f ( ) f ( ) En [, ] TVM 7 f () f (0) En [0, ] TVM 7 f (5) f () En [, 5] TVM 7 f ( + h) f () En [, + h] TVM 7h 7 h h c) f(x) f ( ) f ( ) En [, ] TVM 0 f () f (0) En [0, ] TVM 0 En [, 5] TVM f (5) f () 0 En [, + h] TVM f ( + h) f () 0 h 7
9 d) f(x) x En [, ] TVM f ( ) f ( ) En [0, ] TVM f () f (0) En [, 5] TVM f (5) f () En [, + h] TVM f ( + h) f () (h ) h h La funció b) f(x) 7x 5 és una funció afí i la TVM és constant. La funció c) f(x) és una funció constant i la TVM és 0 (constant) Troba la TMV de la funció f(x) x + 5x en l interval [, + h] i, amb el resultat obtingut, calcula f' (). f(x) x + 5x en [, + h] f ( + h) f () h + h h + h h f'() lím ( h + ) h 0. Utilitzant la definició de derivada, calcula f' () en les funcions següents: x a) f(x) b) f(x) x 4 c) f(x) (x 5) + x d) f(x) x a) f'() lím f ( + h) f () lím (h/7) 7 b) f'() lím f ( + h) f () h lím + 6h 6 c) f'() lím f ( + h) f () h lím 4h 4 d) f'() lím f ( + h) f () lím h h 0 9h + h 9. Calcula la funció derivada de les funcions següents, utilitzant la definició: 5x + a) f(x) b) f(x) x c) f(x) d) f(x) x x x a) f'(x) lím f (x + h) f (x) lím 5h/ 5 h 0 9 7
10 b) f'(x) lím f (x + h) f (x) h lím 6xh 6x c) f'(x) lím f (x + h) f (x) lím h h 0 (x ) (x + h ) h lím h 0 (x ) (x + h ) (x ) d) f'(x) lím f (x + h) f (x) h lím + xh h x x 4. Calcula, aplicant la definició de derivada, f' (), f' ( ) i f' (x), si f(x). x f '(x) lím f (x + h) f (x) lím h 0 x + xh x per tant, f '() 4 i f '( ). 5. Comprova, utilitzant la definició de derivada, que la funció f(x) x no té derivada en x 0. h h f '(x) lím f (0 + h) f (0) lím lím h 0 x ; no existeix. 6. Troba la taxa de variació mitjana de la funció f(x) e x en l interval [;,00] i comprova que el seu valor és molt proper a e. f '() lím f (x 0 + h) f (x 0 ) lím f ( + 0,00) f () 7,9 e h 0 0,00 x si x < 7. Donada f(x), troba f' () i f' () utilitzant la definició x si x de derivada. f '() lím f ( + h) f () lím ( + h) + f '() lím f ( + h) f () lím + h Regles de derivació 8. Calcula la derivada de les funcions següents: a) y x x + b) y c) y x d) y ( ) 0,5 x 4 x + ( x) x + x 0 74
11 a) y' x (x + ) (x ) x x + 6x x + 6x x (x + ) (x + ) (x + ) b) y' ( x) + (x + ) ( x) ( x) 4 6x (x + x) x ( + ) x c) y' (x + x) d) y' 4 ( ) 0,5 x ( ) 0,5 x x + 4 ( x) 0 9x + 6x x x (x + x) 9. Troba la derivada d aquestes funcions: x sin x a) y b) y ( ) c) y d) y (x + ) x + x sin x cos x a) y' x (x + ) x (x + ) (x + ) 4 x (x + ) (x + ) x + x x (x + ) x x c) y' cos x sin x d) y' cos x + sin x cos x cos x x + x b) y' ( ) ( ) x x 0. Deriva les funcions següents: a) y e 4x (x ) b) y ( x) c) y x d) y ln(x ) e x a) y' 4 e 4x (x ) + e 4x e 4x (4x ) b) y' ( x) e x ( x) e x ( x) ( x) c) y' x ln x d) y' x e x x ln x e x x + 4x e x. Deriva aquestes funcions: a) y ln (x ) b) y ln x ln x c) y d) y sin x a) y' x x e x 75
12 b) y ln x ln ( x) / ln ( x) y' ( x) x c) y' /x e x ln x e x /x ln x x ln x e x e x x e x d) y' x sin x cos x 4x sin x cos x. Calcula la derivada d aquestes funcions: a) y sin x cos x b) y sin x + cos x c) y e x + d) y cos (x + ) a) y' cos x sin x cos x b) y' sin x cos x ( + cos x) + sin x cos x sin x ( + cos x) c) y' x e x + 4sin x cos x ( + cos x) d) y' cos (x + ) sin(x + ) 6 cos (x + ) sin(x + ). Deriva les funcions següents: + x a) y log b) y sin x c) y d) y x + x x x a) y log log x y' x ln b) y' x cos x sin x ( x) + ( + x) 4 ( x) ( x) c) y' + x + x ( x) + x x x x ( x) ( + x) + x x + d) y' x + 4 x x x + x x + 4 x + x x 76
13 4. Troba la derivada de: a) y x x b) y ln x x + c) y ln(sin e x ) d) y x x + b) Aplica les propietats dels logaritmes abans de derivar. 4 a) y x y' 4 x 4 b) y (ln x ln (x + )) x x + y' ( ) x + x c) y' e x/ cos e x sin e x x + x + d) y' (x ) x x + (x ) (x + ) Pàgina 69 Continuïtat i derivabilitat 5. Estudia la continuïtat i derivabilitat de les funcions següents en els punts que s indiquen, i representa-les. x si x < a) f (x) en x x + x si x x b) f (x) si x < 0 en x 0 x si x 0 x si x < c) f (x) en x x 4 si x x si x d) f (x) en x x + si x > a) Continuïtat en x : lím f (x) lím (x ) x x lím f (x) lím (x + x) x + f (x) és contínua en x. x f () 77
14 Derivabilitat en x : lím f'(x) lím f'( ) x x lím f'(x) lím (x + ) f'( + ) x + x Per tant, f (x) és derivable en x. A més, f'(). Així f(x) és contínua i derivable en tot Á. f'(0) f'() + 7 a) La funció és contínua, perquè lím f (x) lím f (x) f () x x + f '( ) lím ( + h) lím h f '( + ) lím ( + h) + + h + lím (h + ) h 0 Per tant, és derivable en x Les derivades laterals existeixen i coincideixen. y x + x y x b) La funció és contínua, perquè lím f (x) lím f (x) f (0) 0 x 0 x 0 + f '(0 ) lím h lím h 0 h 0 h f '(0 + ) lím lím h 0 h 0 Per tant, és derivable en x 0 y x y x 78
15 c) La funció és contínua, perquè lím f (x) lím f (x) f () 5 x x + f '( ) lím ( + h) 5 lím h f '( + ) lím ( + h) 4 5 lím h h 0 Per tant, no és derivable en x, és un punt angulós. y x 4 y x d) La funció no és contínua, perquè lím f (x) lím f (x) f () x x + Per tant, no és derivable. y x + y x 79
16 6. Comprova que f(x) és contínua però no derivable en x. f (x) ln(x ) si x < x 6 si x Continuïtat en x : lím f (x) lím ln (x ) ln 0 x x lím f (x) lím (x 6) 0 x + f és contínua en x. x f () 0 Derivabilitat en x : lím f'(x) lím f'( ) x x x lím f'(x) lím f'( + ) x + x Les derivades laterals existeixen, però no coincideixen. f (x) no és derivable en x. 7. Considera la funció següent: 0 si x < 0 f (x) x si 0 x < x si x a) Estudia n la continuïtat. b) Estudia n la derivabilitat. Continuïtat: Si x 0 i x És contínua, ja que està formada per funcions contínues. En x 0: lím f (x) lím 0 0 x 0 x 0 lím f (x) lím x 0 x 0 + x 0 f (0) 0 lím f (x) f (0). Així doncs, la funció és contínua x 0 en x 0. 80
17 En x : lím f (x) lím x x x lím f (x) lím x x + x f () La funció és contínua en Á. Derivabilitat: Si x 0 i x La funció és derivable. La seva derivada és, en aquests punts: 0 si x < 0 f'(x) x si 0 < x < si x > lím f (x) f (). Així doncs, la funció és contínua x en x. En x 0: f'(0 ) 0 f'(0 + ). Per tant, f (x) és derivable en x 0; i f'(0) 0. En x : f'( ) f'( + ). Per tant, f (x) no és derivable en x. La funció és derivable en Á {}. La seva derivada és: 0 si x < 0 f'(x) x si 0 x < si x > 8. Prova que la funció f(x) x + no és derivable en x. f '( ) i f '( + ), per tant, no és derivable en x. 9. Estudia la continuïtat i derivabilitat de la funció: f (x) En x : La funció és contínua, perquè està formada per dues funcions contínues. En x : La funció és contínua, perquè lím x f (x) lím x + f (x) f () Derivabilitat: Si x : La funció és derivable: f' (x) x + x si x x + si x x + si x < si x > 8
18 Si x : f' ( ) 4 per tant, no és derivable en x. f' ( + ) 0. Donada la funció f (x) e x si x 0 x si x > 0 estudia n la continuïtat i la derivabilitat. Continuïtat: En x 0 La funció és contínua, ja que està formada per dues funcions contínues. En x 0: lím f (x) lím e x x 0 x 0 lím f (x) lím ( x) x 0 + x 0 f (0) La funció és contínua en tot Á. Derivabilitat: Si x 0 La funció és derivable. A més: f'(x) e x si x < 0 si x > 0 lím f (x) f (0). Per tant, la funció és contínua en x x 0 0. En x 0: f'(0 ) f'(0 + ) Així doncs, f (x) és derivable en x 0 i f'(0). La funció és derivable en tot Á. La seva derivada seria: f'(x) e x si x < 0 si x 0. En quins punts no són derivables les funcions següents: a) f (x) x 4 b) f (x) x a) En x i x. b) Primerament cal mirar si és contínua. f (x) x és contínua ja que és una funció polinòmica (el valor absolut només en pot canviar el signe). 8
19 Per veure si és o no derivable caldrà convertir el valor absolut: El valor absolut no actua si x > 0 x > El valor absolut actua si x > 0 x < Així podem escriure la funció com: x si x / f (x) x si x < / f lím f (x) lím f (x) 0 ( ) x / x / + La derivem: si x > / f'(x) si x < / La funció serà derivable excepte en x, on: + f' ( ) f' ( No és derivable en x ) PER RESOLDRE. Donada f (x) x si x x + si x > a) Calcula f'() i f'(). b) Comprova que f'( ) f'( + ). si x < f'(x) x si x > a) Com que < f'() Com que > f'() 6 b) f '( ) 4 f '( + ). Aquí sota tenim la gràfica d una funció y f (x). Calcula, observant-la: f'( ), f'() i f'() En quins punts no és derivable? 4 8
20 f'( ) 0; f'() 0; f'() No és derivable en x 0 ni en x. 4. Quants punts que no tinguin derivada hi ha en la funció y x + 6x + 8? x 6 ± 6 6 ± 4 6 ± + 6x +8 0 x x + 6x +8 si x < 4 x + 6 si x < 4 y x 6x 8 si 4 x y' x 6 si 4 < x < x + 6x +8 si x > x + 6 si x > La funció és contínua, ja que és el valor absolut d una funció contínua. En x 4 y'( 4 ) y'( 4 + ) En x y'( ) y'( + ) x x 4 La funció no és derivable en x 4 ni en x ; és a dir, en ( 4, 0) i en (, 0). Són dos punts angulosos. 5. Calcula a i b perquè la funció següent sigui derivable en tot Á: f (x) ax + x si x x bx 4 si x > Perquè sigui derivable, en primer lloc, ha de ser contínua. Si x La funció és contínua, ja que està formada per dos polinomis. En x : lím f (x) lím (ax + x) 4a + 6 x x lím f (x) lím (x bx 4) b x + x f () 4a + 6 Perquè sigui contínua, ha de ser 4a + 6 b, és a dir, a + b; o bé b a. Derivabilitat: Si x la funció és derivable. A més: ax + si x < f'(x) x b si x > En x : f'( ) 4a + f'( + ) 4 b Perquè sigui derivable ha de ser 4a + 4 b, és a dir, b 4a +. 84
21 Tenint en compte les dues condicions obtingudes: b a b 4a + a 4a + a 4 a b 7 Per tant, perquè f (x) sigui derivable en tot Á, ha de ser a i b Observa les gràfiques de les funcions següents i indica en quins punts no són derivables. a) b) c) Alguna d aquestes és derivable en tot Á? a) No és derivable en x (té un punt angulós ) ni en x (no està definida la funció). b) És derivable en tot Á. c) No és derivable en x 0 (té un punt angulós ). 7. La funció f (x) està definida per: f (x) x x si x 0 ax + b si x > 0 Calcula a i b perquè f sigui contínua i derivable. Continuïtat: En x 0 La funció és contínua, ja que està formada per dos polinomis. En x 0: lím f (x) lím (x x) 0 x 0 x 0 lím f (x) lím (ax + b) b Perquè sigui contínua ha de ser b 0 x 0 + x 0 f (0) 0 Derivabilitat: Si x 0 La funció és derivable. A més: f'(x) x si x < 0 a si x > 0 En x 0: f'(0 ) f'(0 + ) a Perquè sigui derivable, ha de ser a. Així doncs, f (x) serà contínua i derivable si a i b 0. 85
22 8. La funció f (x) està definida de la manera següent: e x, x 0 f (x), 0 < x < x + x +, x Estudia n la continuïtat i derivabilitat. Si x 0 i x, la funció és contínua i derivable. Continuïtat en x 0: lím f (x) lím e x x 0 x 0 lím f (x) lím x 0 + f (x) és contínua en x 0. x 0 f (0) Continuïtat en x : lím f (x) lím x x lím f (x) lím ( x + x + ) x + x f () Derivabilitat en x 0: lím f'(x) lím e x f'(0 ) x 0 x 0 lím f'(x) lím 0 0 f'(0 + ) x 0 + x 0 + f (x) no és derivable en x 0. Els límits per la dreta i per l esquerra no coincideixen. La funció no és contínua en x. Les derivades laterals existeixen, però no coincideixen. Derivabilitat en x : Com que f (x) no és contínua en x, f (x) no és derivable en x. Pàgina Esbrina per quins valors de x és f'(x) 0 en cadascuna de les funcions següents: x a) f(x) (x 8) b) f(x) x 4 + x c) f(x) d) f(x) e x (x ) x + a) y x4 8x 86
23 x f'(x) 4x x x f'(x) 0 x (x ) 0 x 0 y 0 x y (4/) f' < 0 f' < 0 f' > 0 4 Hi ha un mínim en (, ). b) f'(x) 4x 6x f'(x) 0 x (4x 6) 0 x 0 y 0 x / y (7/6) 7 6 Hi ha un mínim en (, ). f' < 0 f' < 0 f' > 0 c) f'(x) x (x + ) f'(x) 0 x 0 x 0 y 0 f' > 0 f' < 0 0 Hi ha un màxim en (0, ). d) f'(x) e x (x ) + e x e x (x + ) xe x f'(x) 0 xe x 0 x 0 (ja que e x 0 per a tot x) y f'' < 0 f'' > 0 0 Hi ha un mínim en (0, ). 87
24 40. Troba els punts en què el pendent de la recta tangent és igual a 0 en cada una de les funcions següents: a) f(x) x + b) f(x) x x x x c) f(x) x d) f(x) x x + x a) f (x) f'(x) x (x ) (x + ) x 0 x x x x 0 x 0 (x ) + f (0) ; Per tant, en (0, ) el pendent de la tangent val 0. b) f (x) x + x x x f'(x) x (x ) x x (x ) 0 x 4 x x 4 0 x (x ) 0 x 0, x i x 0 f (0) 0; f ( ) ; f ( ) Per tant, en (0, 0), (, ) ( ) i, el pendent de la tangent val 0. c) f (x) f'(x) x x x (4x ) ( x) (x x) ( ) ( x) 0 8x 4x 6 + x + x x 0 x 4x + 0 x ; x 9 f () ; f () 9 + Per tant, en (, ) i (, 9) el pendent de la tangent val 0. d) f (x) x + x f'(x) x x (x + ) 0 x x 0 x ; x x 88
25 + f () ; f ( ) Per tant, en (, ) i (, ) el pendent de la tangent val Esbrina si en les funcions següents existeixen punts en els quals f'(x) 0. x a) f(x) b) f(x) x + c) f(x) ln(x + ) d) f(x) 0 (x ) 4 5 a) No n existeix cap ja que f'(x) i mai f'(x) 0 x + x + b) f'(x) 6 6x 0 (x + ) 6 6x 0 x i x 6x x + c) No n existeix cap ja que f'(x) i mai f'(x) 0 x + d) f'(x) 4x + 4x x 4. Les funcions següents tenen alguns punts en què la derivada no existeix. Troba ls en cada cas. a) f(x) x b) f(x) x + c) f(x) x d) f(x) x e) f(x) f) f(x) x x a) x 0 b) x c) x + d) x 5 e) x 4 f) x 0 i x 4x 5 89
26 4. Aquesta és la gràfica d una funció y f(x). 4 4 Estudia n la continuïtat i derivabilitat. És una funció contínua en els intervals (, ), (, + ) i discontínua en x. És derivable en els intervals (, 0), (0, ) i (, + ), i no derivable en x 0 i x. 44. Considera la funció: f (x) x 5x + m si x x + nx si x > Calcula els valors de m i n perquè f sigui derivable en tot Á. Perquè sigui derivable, en primer lloc ha de ser contínua. Si x, la funció és contínua, ja que està formada per dos polinomis. En x : lím f (x) x lím f (x) x + f () 4 + m (x 5x + m) 4 + m ( x + nx) + n Perquè sigui contínua en x, ha de ser: 4 + m + n; és a dir: m n +. Derivabilitat: lím x lím x Si x, la funció és derivable. A més: x 5 si x < f'(x) x + n si x > En x : f'( ) f'( + ) + n Perquè sigui derivable en x, ha de ser + n, és a dir, n. Per tant, la funció serà derivable en tot Á si m i n. En aquest cas, la derivada seria: x 5 si x < f'(x) x si x 90
27 45. Estudia la continuïtat i derivabilitat de la funció: x f (x) + x si x x + si x Existeix algun punt en el qual f'(x) 0? Representa-la gràficament. Continuïtat: En x : La funció és contínua, ja que està formada per dos polinomis. En x : lím f (x) lím (x + x ) x x lím f (x) lím (x + ) x + x f () La funció és contínua en tot Á. Derivabilitat: Si x : La funció és derivable. A més: x + si x < f'(x) si x > En x : f'( ) 4 f'( + ) La funció no és derivable en x. Per tant, la funció és derivable en Á {}. Punts en els quals f'(x) 0: f'(x) x + si x < x + 0 x f'(x) si x > f'(x) 0 si x > Per tant, la derivada s anul la a x. Gràfica de f (x): lím f (x) f (). Per tant, la funció és x contínua en x. 9
28 46. Troba a i b perquè la funció f (x) sigui contínua: x + a si x < f (x) ax + b si x < 0 x + si 0 x Estudia la derivabilitat de f per als valors de a i b obtinguts. Si x i x 0: La funció és contínua, ja que està formada per polinomis. En x : lím f (x) lím (x + a) + a x x lím f (x) lím (ax + b) a + b x + x f ( ) a + b En x 0: lím f (x) lím (ax + b) b x 0 x 0 lím f (x) lím (x + ) Perquè sigui contínua, ha de ser b. x 0 + x 0 f (0) Així doncs, f (x) serà contínua si a i b. Per a aquests valors, queda: x + si x < f (x) x + si x < 0 ; és a dir: x + si 0 x Derivabilitat: x + si x < 0 f (x) x + si x 0 Si x 0: És derivable. A més: si x < 0 f'(x) 6x si x > 0 En x 0: f'(0 ) f'(0 + ) 0 La funció no és derivable en x 0. Per tant, és derivable en Á {0}. Perquè sigui contínua, ha de ser + a a + b, és a dir: b a. 9
29 47. Calcula f'(0) si f (x) ln ex + e x x +. Aplica les propietats dels logaritmes abans de derivar. (x )e f'(x) x + ( x )e x (x + )e x + (x + )e x f '(0) 48. Troba el pendent de la recta tangent a les corbes següents en els punts indicats. a) y sin x cos x en π x 4 b) y xlnx en x e x e x c) y en x 0 i en x d) e x en x a) f'(x) sin x + cos x π 4 f '( ) 0 b) f'(x) lnx + f '(e) c) f'(x) f '(0) 0 i f '() d) f'(x) x e x f '() x lnx x ln x e 49. Aquestes gràfiques representen les funcions derivades de les funcions f, g, h i j: f' g' h' 4 j' 9
30 a) Quines d aquestes funcions tenen punts en què f '(x) 0? b) Quina d aquestes gràfiques és la funció derivada d una funció polinòmica de primer grau? c) Quina d aquestes correspon a una funció polinòmica de segon grau? a) Els punts de tangent horitzontal són els punts en els quals s anul la la derivada. f té un punt de tangent horitzontal en x, ja que f'( ) 0. j té dos punts de tangent horitzontal en x i en x, ja que j'() j'() 0. g i h no tenen cap punt de tangent horitzontal. b) La derivada d una funció polinòmica de primer grau és una funció constant. Per tant, és g'. c) La derivada d una funció polinòmica de segon grau és una funció polinòmica de primer grau. Per tant, és f'. Pàgina 7 QÜESTIONS TEÒRIQUES 50. Una funció polinòmica de tercer grau, quants punts de derivada nul la pot tenir? En pot tenir un o cap? La derivada d una funció polinòmica de tercer grau és una funció polinòmica de segon grau. Així doncs, pot haver-hi dos punts, un punt o cap punt amb derivada nul la. Per exemple: x f (x) x x f'(x) x 0 Dos punts x f (x) x f'(x) x 0 x 0 Un punt f (x) x + x f'(x) x + 0 per a tot x Cap punt 94
31 5. Justifica que una funció polinòmica de segon grau té sempre un punt de tangent horitzontal. La seva derivada és una funció polinòmica de primer grau, que s anul la sempre en un punt. 5. Si una funció té un punt angulós en x a, què podem dir de f'(a)? Que f '(a) no existeix, perquè f (x) no és derivable en x a. 5. Sigui f una funció de la qual sabem que: f'( ) lím f( + h) f() h 0 h f'( + ) lím f( + h) f() h 0 + h És f derivable en x? No, cal que f '( ) f '( + ). 54. La funció f(x) x és contínua en x i f'() +. Com és la recta tangent a f en x? La tangent és vertical. 55. Donada la funció f(x), troba f'(x) i f''(x) aplicant dues vegades la definició de derivada. Tingues en compte que f''(x) lím h 0 x f'(x + h) f'(x) h (x + h) x f '(x) lím lím x + h x h 0 h 0 f ''(x) lím x + h x lím h 0 PER APROFUNDIR 56. Sigui la funció: f (x) x x a) Troba f'(x). b) Troba f''(x). c) Representa f' i f''. x si x 0 x si x > 0 95
32 x si x < 0 a) f'(x) x si x 0 En x 0 existeix la derivada, ja que f (x) és contínua, i, a més, f'(0 ) f'(0 + ). si x < 0 b) f''(x) si x > 0 En x 0 no existeix la segona derivada, ja que f''(0 ) f''(0 + ). c) f'(x) f''(x) 57. Prova que la funció f (x) x + x no és derivable en x. x x + si x < f (x) x + x si x 0 si x < f'(x) si x > si x < x si x f'( ) 0 f'( + ). Per tant, la funció no és derivable en x. 58. Calcula la derivada d ordre n de la funció f (x) e x. f'(x) e x f''(x) 4e x e x f'''(x) 8e x e x f n (x) n e x Ho demostrem per inducció: Per a n, n, n, veiem que es compleix. Suposem que és cert per a n ; és a dir, que f n (x) n e x ; aleshores, derivant, tenim que: f n (x) n e x n e x. Per tant, l expressió obtinguda és certa per a tot n. 96
33 59. Donada la funció f (x) e x + ln ( x), comprova que f'(0) 0 i f''(0) 0. Serà també f'''(0) 0? f'(x) e x f'(0) 0 x f''(x) e x f''(0) 0 ( x) f'''(x) e x f'''(0) 0 ( x) 60. Quina d aquestes gràfiques representa la funció f i la seva derivada f'? Justifica la teva resposta. a) b) c) a) La funció és una recta que té pendent. Per tant, la seva derivada és y. Així doncs, aquesta gràfica sí representa una funció i la seva derivada. b) En x 0, la funció té un màxim; la derivada s anul la. La recta hauria de passar per (0, 0). No representa, per tant, una funció i la seva derivada. c) En x, la funció té un màxim; la derivada s anul la, i hauria de passar per (, 0). Aquesta tampoc no representa una funció i la seva derivada. Per tant, només la primera és vàlida. 6. La funció f (x) x + ax + bx + c verifica que f (), f'() 0 i f''() 0. Calcula a, b i c. f (x) x + ax + bx + c f'(x) x + ax + b f''(x) 6x +a f () + a + b + c f'() 0 + a + b 0 f''() a 0 a b c 0 f (x) x x + x 97
34 6. Determina el valor de k que fa que la funció f (x) tingui només un punt en el qual es verifiqui f'(x) 0. x + k f'(x) e x (x + k) xe x (x x + k) e x (x + k) (x + k) f'(x) 0 x ± 4 4k x + k 0 x Perquè hi hagi una sola solució, ha de ser 4 4k 0; és a dir, k. e x 6. Calcula a, b i c perquè es compleixi que la funció f (x) ax + bx + c passi pel punt (0, ) i verifiqui f'() i f'() 0. f (0) f'() f'() 0 c a + b a 4a + b 0 b 4 f (x) x 4x Troba els punts de la funció y x x en què el pendent de la recta tangent és igual a. (x ) x x x y' (x ) (x ) y' (x ) (x ) (x ) x 0 x 65. Troba a i b perquè la funció f (x) sigui contínua: x + a si x < f (x) ax + b si x < 0 x + si 0 x Per als valors de a i b obtinguts, estudia la derivabilitat de f. Si x i x 0: La funció és contínua, ja que està formada per polinomis. En x : lím f (x) lím (x + a) + a x x lím f (x) lím (ax + b) a + b x + x f ( ) a + b Perquè sigui contínua, ha de ser + a a + b, és a dir: b a. 98
35 En x 0: lím f (x) lím (ax + b) b x 0 x 0 lím f (x) lím (x + ) Perquè sigui contínua, ha de ser b. x 0 + x 0 f (0) Així doncs, f (x) serà contínua si a i b. Per a aquests valors, queda: x + si x < f (x) x + si x < 0 ; és a dir: x + si 0 x x + si x < 0 f (x) x + si x 0 Derivabilitat: Si x 0: És derivable. A més: si x < 0 f'(x) 6x si x > 0 En x 0: f'(0 ) f'(0 + ) 0 La funció no és derivable en x 0. Per tant, és derivable en Á {0}. 66. Hi ha algun punt en què f (x) +x no sigui derivable? Justifica la teva resposta. si x 0 + x f (x) si x < 0 x Es comprova que és contínua en tot Á, ja que els punts que anul len el denominador són del domini de l altre tros. si x > 0 ( + x) f'(x) si x < 0 ( x) Si x 0 serà derivable. Si x 0 f'(0 + ) f'(0 ) f (x) no és derivable en x 0 99
36
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 55 REFLEXIONA I RESOL Tangents a una corba y f ( 5 5 Troba, mirant el gràfic i les rectes traçades, f'(, f'( y f'(. f'( 0; f'( ; f'( Digues uns altres tres punts
DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 55 REFLEXIONA I RESOL Tangents a una corba y f ( 5 5 Troba, mirant el gràfic i les rectes traçades, f'(, f'( y f'(. f'( 0; f'( ; f'( Digues uns altres tres punts
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
11 Límits de funcions. Continuïtat i branques infinites
 Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
Institut Jaume Balmes Aplicacions de les derivades I
 MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
UNITAT DIDÀCTICA 10 L ÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
SOLUCIONARI Unitat 2. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Data de lliurament: divendres 8 d abril de 2016
 INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
ANÀLISI. MATEMÀTIQUES-2
 1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
REPRESENTACIÓ DE FUNCIONS
 1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Al ser un quocient, el denominador no pot ser 0 i al ser una arrel d index senars no hi ha problema Dom = R\{x 3 +3x 2-6x-8=0}= R\{-4, 2, -1}.
 Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
INTEGRACIÓ: resolució exercicis bàsics ex res I.1
 INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra.
 UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
QUADERN D ESTIU 4t ESO MATEMÀTIQUES
 QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
Aplicacions de la derivada
 Aplicacions de la derivada 1 Aplicacions de la derivada Les aplicacions de la derivada són molt àmplies; entre les més importants hi ha: Localització d extrems (màxims i mínims) d una funció Un màxim és
Aplicacions de la derivada 1 Aplicacions de la derivada Les aplicacions de la derivada són molt àmplies; entre les més importants hi ha: Localització d extrems (màxims i mínims) d una funció Un màxim és
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Exercicis de derivades
 Variació mitjana d'una funció 1. Calcula la variació mitjana de la funció f (x) = x 2 2 x als següents intervals: a) [ 1, 3 ] b) [0, 4 ] c) [1, 5 ] 2. Donada la funció següent: a) Quina és la variació
Variació mitjana d'una funció 1. Calcula la variació mitjana de la funció f (x) = x 2 2 x als següents intervals: a) [ 1, 3 ] b) [0, 4 ] c) [1, 5 ] 2. Donada la funció següent: a) Quina és la variació
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. MATEMÀTIQUES-1
 FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
Apunts de Càlcul Tema 2. Derivació de funcions d una variable
 Apunts de Càlcul Tema 2. Derivació de funcions d una variable Lali Barrière, Josep M. Olm Departament de Matemàtica Aplicada 4 - UPC Enginyeria de Sistemes de Telecomunicació Enginyeria Telemàtica EETAC
Apunts de Càlcul Tema 2. Derivació de funcions d una variable Lali Barrière, Josep M. Olm Departament de Matemàtica Aplicada 4 - UPC Enginyeria de Sistemes de Telecomunicació Enginyeria Telemàtica EETAC
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
Unitat 2 EQUACIONS DE PRIMER GRAU. Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 EQUACIONS DE PRIMER GRAU
 Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
TEMA 5 : Límits de funcions. Continuïtat
 TEMA : Límits de uncions. Continuïtat.. LÍMIT D UNA FUNCIÓ EN UN PUNT... Conceptes bàsics a c signiica que pren valors cada vegada més pròims a c. Es llegei tendei a c : ;.9;.8;..., ;.9;.99;.999... c -
TEMA : Límits de uncions. Continuïtat.. LÍMIT D UNA FUNCIÓ EN UN PUNT... Conceptes bàsics a c signiica que pren valors cada vegada més pròims a c. Es llegei tendei a c : ;.9;.8;..., ;.9;.99;.999... c -
SOLUCIONARI Unitat 1. Exercicis. Comencem. 1. La gràfica velocitat-temps corresponent a dos mòbils és la que pots veure a la dreta (fig. 1.3).
 SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
1. Continuïtat i ĺımit de funcions de vàries variables
 Càlcul 2 1. Continuïtat i ĺımit de funcions de vàries variables Dept. de Matemàtica Aplicada I www.ma1.upc.edu Universitat Politècnica de Catalunya 12 Febrer 2012 Copyleft c 2012 Reproducció permesa sota
Càlcul 2 1. Continuïtat i ĺımit de funcions de vàries variables Dept. de Matemàtica Aplicada I www.ma1.upc.edu Universitat Politècnica de Catalunya 12 Febrer 2012 Copyleft c 2012 Reproducció permesa sota
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
2.2 Continuïtat i representació de funcions
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 20 gener 2016 Continuïtat i representació de funcions exercicis 2.2 Continuïtat i representació de funcions 20. Calcula la derivada que s indica en cadascun
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 20 gener 2016 Continuïtat i representació de funcions exercicis 2.2 Continuïtat i representació de funcions 20. Calcula la derivada que s indica en cadascun
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
Cognoms i Nom: Examen parcial de Física - ELECTRÒNICA 1 de desembre de 2016
 1 de desembre de 016 Model A Qüestions: 50% de l examen A cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.5 punts, en blanc =
1 de desembre de 016 Model A Qüestions: 50% de l examen A cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.5 punts, en blanc =
MATEMÀTIQUES SOLUCIONARI. Autors del llibre de l alumne Àngela Jané Jordi Besora Josep M. Guiteras. Revisió tècnica Antoni Giménez
 SOLUCIONARI MATEMÀTIQUES Autors del llibre de l alumne Àngela Jané Jordi Besora Josep M. Guiteras Revisió tècnica Antoni Giménez BARCELONA - MADRID - BUENOS AIRES - CARACAS GUATEMALA - LISBOA - MÈXIC -
SOLUCIONARI MATEMÀTIQUES Autors del llibre de l alumne Àngela Jané Jordi Besora Josep M. Guiteras Revisió tècnica Antoni Giménez BARCELONA - MADRID - BUENOS AIRES - CARACAS GUATEMALA - LISBOA - MÈXIC -
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
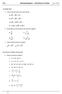 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
UNITAT DIDÀCTICA 11 I NICIACIÓ AL CÀLCUL DE DERIVADES. APLICACIONS
 0 Matemàtiques UNITAT DIDÀCTICA Pàgina 80. a 0 km/h b 88 km/h Hi accedirà suaument. Pàgina 8. a Intenta assolir la velocitat de l autobús per accedir-hi suaument. b El passatger accedei suaument a l autobús;
0 Matemàtiques UNITAT DIDÀCTICA Pàgina 80. a 0 km/h b 88 km/h Hi accedirà suaument. Pàgina 8. a Intenta assolir la velocitat de l autobús per accedir-hi suaument. b El passatger accedei suaument a l autobús;
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
QUADERN d ESTUDI de RECTES TANGENTS
 QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES
 FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
Matemàtiques 1 - FIB
 Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
Generalitat de Catalunya. 12 3x. x x x. lim. lim. 2 x. + = e) x +
 1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
SOLUCIONARI Unitat 3. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
PROBLEMES DE SELECTIVITAT - MATEMÀTIQUES I - SOLUCIONS
 Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
Unitat 4. Fraccions algèbriques
 Unitat 4. Fraccions algèbriques Curs d Anivellament de Matemàtiques Montserrat Corbera / Vladimir Zaiats montserrat.corbera@uvic.cat / vladimir.zaiats@uvic.cat c 2012 Universitat de Vic Sagrada Família,
Unitat 4. Fraccions algèbriques Curs d Anivellament de Matemàtiques Montserrat Corbera / Vladimir Zaiats montserrat.corbera@uvic.cat / vladimir.zaiats@uvic.cat c 2012 Universitat de Vic Sagrada Família,
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
Derivació Funcions Vàries Variables
 Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
Institut d Educació Secundària Funcions IV i estadística d'una variable
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
3. FUNCIONS DE RECERCA I REFERÈN- CIA
 1 RECERCA I REFERÈN- CIA Les funcions d aquest tipus permeten fer cerques en una taula de dades. Les funcions més representatives són les funcions CONSULTAV i CONSULTAH. Aquestes realitzen una cerca d
1 RECERCA I REFERÈN- CIA Les funcions d aquest tipus permeten fer cerques en una taula de dades. Les funcions més representatives són les funcions CONSULTAV i CONSULTAH. Aquestes realitzen una cerca d
Cognoms i Nom: Examen parcial de Física - CORRENT CONTINU 5 d octubre de 2017
 xamen parcial de ísica - CONT CONTINU Model Qüestions: 50% de l examen cada qüestió només hi ha una resposta correcta. ncercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.25 punts,
xamen parcial de ísica - CONT CONTINU Model Qüestions: 50% de l examen cada qüestió només hi ha una resposta correcta. ncercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.25 punts,
Nom i Cognoms: Grup: Data:
 n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
Sigui un carreró 1, d amplada A, que gira a l esquerra i connecta amb un altre carreró, que en direm 2, que és perpendicular al primer i té amplada a.
 ENUNCIAT: Sigui un carreró 1, d amplada A, que gira a l esquerra i connecta amb un altre carreró, que en direm 2, que és perpendicular al primer i té amplada a. Dos transportistes porten un vidre de longitud
ENUNCIAT: Sigui un carreró 1, d amplada A, que gira a l esquerra i connecta amb un altre carreró, que en direm 2, que és perpendicular al primer i té amplada a. Dos transportistes porten un vidre de longitud
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
Propietats de les desigualtats.
 Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Unitat 1. Nombres reals.
 Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
E.1. Extrems de funcions. Fonaments Matemàtics de l Enginyeria II Yolanda Vidal, Francesc Pozo, Núria Parés
 E.1 Extrems de funcions Extrems de funcions E. Recordatori extrems lliures funcions una variable. Sigui f : [a, b] R derivable en l interval (a, b) i x 0 [a, b] un extrem de la funció f(x). En un entorn
E.1 Extrems de funcions Extrems de funcions E. Recordatori extrems lliures funcions una variable. Sigui f : [a, b] R derivable en l interval (a, b) i x 0 [a, b] un extrem de la funció f(x). En un entorn
2. FUNCIONS MATEMÀTIQUES, TRIGO- NOMÈTRIQUES I ESTADÍSTIQUES
 1 2. FUNCIONS MATEMÀTIQUES, TRIGO- NOMÈTRIQUES I ESTADÍSTIQUES Les funcions matemàtiques permeten realitzar càlculs d aquest tipus sobre cel les i sobre intervals de valors, retornant sempre valors numèrics.
1 2. FUNCIONS MATEMÀTIQUES, TRIGO- NOMÈTRIQUES I ESTADÍSTIQUES Les funcions matemàtiques permeten realitzar càlculs d aquest tipus sobre cel les i sobre intervals de valors, retornant sempre valors numèrics.
Examen FINAL M2 FIB-UPC 11 de gener de 2017
 Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
