1. Indicar el lenguaje aceptado por los siguientes autómatas :
|
|
|
- Julia Giménez Calderón
- hace 8 años
- Vistas:
Transcripción
1 Universidd Rey Jun Crlos Grdo en Ingenierí de Computdores Máquins Secuenciles, Autómts y Lengujes Hoj de Prolems: Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio, ( ) vnzdo.. Indicr el lenguje ceptdo por los siguientes utómts : () ( ) q q El lenguje que reconoce este utómt es un lenguje inrio donde ls plrs ceptds contienen un número pr de unos: L = {w w {,}, n (w) mod 2 = } q q q 2, () ( ) El lenguje ceptdo por este utómt es un lenguje inrio donde tods ls plrs ceptds tienen todos los ceros situdos delnte de todos los unos: L = { n m n, m } q, q q 2, (c) ( ) El lenguje reconocido por este utómt, es un lenguje inrio que está formdo por plrs compuests por un cierto número de ceros y finlizds con un uno: L = { n n } Págin de 4
2 Hoj de Prolems: Autómts Finitos Determinists (cont.) q q q 2, (d) ( ) El utómt nterior cept plrs inris que contienen l secuenci : L = {w w {,}, w contiene } (e) ( ) q q q 2 q 3 Ddo un plr x culquier. Ovimente, el utómt, l procesr x se quedrí en lguno de sus estdos. Se puede oservr que desde culquier estdo se lleg q 3 con l cden. Por tnto, el lenguje reconocido por el utómt es el conjunto de plrs inris que finlizn con l secuenci : L = {xy x {,}, y = } q q 2 q q 3 (f) ( ) El lenguje reconocido por el utómt corresponde ls siguientes cdens inris:. Si l cden no tiene ningún uno, se reconocen cdens con un número de ceros pr. 2. Sielnúmerodeunosespr(ymyorquecero),lcdendeeterminr con un número de ceros impr. Págin 2 de 4
3 Hoj de Prolems: Autómts Finitos Determinists (cont.) 3. Si el número de unos es impr, l cden dee terminr con un número de ceros pr. Es decir: L = { 2m m } {x 2m x {,}, n (x) mod 2 =, m } {x 2m+ x {,}, n (x) mod 2 =, m } q q (g) ( ) q 2 q 3, El lenguje reconocido por este utómt es el cierre de l unión de otros dos lengujes. Un primer lenguje que reconoce cdens formds por l conctención de l secuenci. Un segundo lenguje que hce lo mismo pero con l secuenci. Si definimos estos lengujes: L = {() n n } L 2 = {() m m } L 3 = L L 2 Por lo tnto, el lenguje ceptdo por este utómt es: L = L 3 (h) ( ) q q q 2 q 3 Págin 3 de 4
4 Hoj de Prolems: Autómts Finitos Determinists (cont.) El lenguje reconocido por el utómt es l unión de los lengujes siguientes: L = {x() 2n+ x {,} y n } L 2 = {x() 2n+ x {,} y n } L 3 = {() 2n+ n } L 4 = {() 2n+ n } L(AUT) = L L 2 L 3 cupl 4 2. Ddo el lfeto Σ = {,}, construye un utómt pr cd uno de los siguientes lengujes : () ( ) Ls cdens que terminn en. A = ({,},{q,q,q 2,q 3 },f,q,{q 3 }) Donde f está definid por el siguiente grfo de trnsición: q q q 2 q 3 () ( ) Ls cdens que no contengn l secuenci. A = ({,},{q,q,q 2,q 3,q 4 },f,q,{q,q,q 2,q 3 }) Donde f está definid por el siguiente grfo de trnsición: q q q 2 q 3 q 4, (c) ( ) Ls cdens tl que cd loque de cinco símolos consecutivos contienen l menos dos s. Págin 4 de 4
5 Hoj de Prolems: Autómts Finitos Determinists (cont.) A c = ({,},{q,q,q 2,q 3,q 4,q 6,q 7,q 8,q 9,q,q,q 2,q 3 },f c,q,{q 3 }) Donde f c está definid por el siguiente grfo de trnsición:,,, q q q 2 q 3 q q 5 q 6 q 7 q 8 q 9, q q 2 q 3 q 4, Como comentmos en clse de ejercicios, lo más sencillo es dotr de semántic cd uno de los estdos del utómt, de est form será más fácil el diseño del mismo. En este ejercicio, por un ldo deemos llevr l cuent del número de crcteres que hemos leido y por otro ldo, el número de s necesris pr reconocer l cden (dos en este cso). Por ello, el utómt se h dispuesto en tres zons horizontles. L primer división horizontl (q..q 4 ), se refiere los posiles estdos donde todví no hemos leído ningún crácter. L segund líne (q 5..q 9 ), lmcen informción cerc de que hemos leído un. Y l tercer zon (q..q 3 ), nos indic que hemos leído dos o más s. Por otro ldo, tmién deemos llevr informción cerc del número de crcteres leídos. Por ejemplo, q y q 5 indicn que se h leído un crácter; q 2, q 6 y q nos informn que se hn leído dos crcteres y sí sucesivmente. Oservemos que no son necesrios cinco estdos por líne pr gurdr informción cerc de los crcteres leídos. Así, l primer líne sólo contiene cutro estdos, y que si no hemos leído previmente ningun letr, el último crácter que reconozcmos nos es indiferente, y que es cden no v ser reconocid y, en vez de crer un estdo sumidero dicionl, reutilizmos el estdo q 9. Lo último que deeremos tener en cuent son ls trnsiciones que slen desde el estdo finl y que nos indicn que se empiez reconocer otr ristr de cinco crcteres(y por lo tnto, se dee trnsitr los estdos correspondientes). (d) ( ) Ls cdens con un número de s múltiplo de tres. A d = ({,},{q,q,q 2 },f d,q,{q }) Págin 5 de 4
6 Hoj de Prolems: Autómts Finitos Determinists (cont.) Donde f d está definid por el siguiente grfo de trnsición: q 2 q q (e) ( ) Ls cdens con un número pr de s y un número de s múltiplo de tres. A e = ({,},{q,p,i,p,i,2p,2i,3p,3i},f,q,{q,p,3p}) Donde f e está definid por el siguiente grfo de trnsición: p p 2p 3p q i i 2i 3i Al igul que en el prtdo nterior, en este utómt deemos recordr vris coss. Por un ldo, deemos ser si el número de s leíds son pres y por otro ldo, deemos ser si el número de s es múltiplo de tres. Pr diseñr el utómt procederemos de form nálog l cso nterior. En este prtdo, se h decidido nomrr los estdos del utómt de form que conozcmos l semátic de cd uno de los mismos. De est form, si l letr p form prte del nomre del utómt significrá que el número de letrs es pr (y l contrrio si tenemos l letr i ). Y por otr prte, en el nomre del utómt tmién definimos el número de letrs que hemos ido reconociendo. Si queremos ser más correctos, siempre podemos renomrr los estdos l finlizr el diseño, de form que los nomres sen los hitules (q,q,...). (f) ( ) L(m,n) := {w Σ n (w) mod m = y n (w) mod n = }. Pr poder dr un solución genéric como se pide en el ejercicio, es más fácil generr unos cuntos utómts pr intentr identificr el ptrón que Págin 6 de 4
7 Hoj de Prolems: Autómts Finitos Determinists (cont.) siguen: m=2,n=2 m=3,n=3 q 2 q 2 Podemos oservr que de form genéric, donde X = (n ) e Y = (m ), se puede relizr l siguiente representción: q 2... Y 2... Y Y X X 2X... YX Por lo tnto, el utómt puede ser definido como: A f = ({,},{q,,2,...,,2,...,(m )(n )},f f,q,{q }) Donde f f está definid por el grfo de trnsición nterior. 3. ( ) Compror si los siguientes AFD son equivlentes : Págin 7 de 4
8 Hoj de Prolems: Autómts Finitos Determinists (cont.) AFD = AFD2 = ({,,c},{p,q,r,s,t,u,v},f,p,{s,t,u,v}) ({,,c},{p,q,r,s,t},f 2,p,{r,s,t}) f c p r t q f c q q v p r p u r *s q t u *t t v u *u t t v p s q p q t p q *r q t s *s s t s *t t s s *v u u t Pr compror que los dos utómts son equivlentes, lo primero que deeremos hcer es hllr sus respectivos utómts mínimos equivlentes. Minimizción de f : Primero eliminmos los estdos inccesiles. Por lo tnto, s se elimin de l tl de trnsiciones. Después, clculremos el conjunto cociente Q/E: Q/E = Q/E Q/E = {{p,q,r},{t,u,v}} Q/E = {{p,q,r},{t,u,v}} por lo tnto Q/E = Q/E Si renomrmos los conjuntos de estdos equivlentes y cremos un nuev tl de trnsiciones, nos qued el siguiente utómt: f c A A B A *B B B B,c,,c A B Minimizción de f 2 : Primero eliminmos los estdos inccesiles. Por lo tnto, r se elimin de l tl de trnsiciones. Después, clculremos el conjunto cociente Q/E: Q/E = {{p,q},{s,t}} Págin 8 de 4
9 Hoj de Prolems: Autómts Finitos Determinists (cont.) Q/E = Q/E Q/E = {{p,q},{s,t}} por lo tnto Q/E = Q/E Si renomrmos los conjuntos de estdos equivlentes y cremos un nuev tl de trnsiciones, nos qued el siguiente utómt: f 2 c A B A A *B B B B,c,,c A B Como se desprende de sus tls de trnsición, estos dos utómts no son isomorfos y por lo tnto, no son equivlentes. 4. ( ) Compror cuáles de los siguientes AFD son equivlentes entre sí. Págin 9 de 4
10 Hoj de Prolems: Autómts Finitos Determinists (cont.) AFD = AFD2= ({,},{p,q,r,s,t,u},f,p,{q,r}) ({,},{p,q,r,s,t,u},f 2,p,{u}) f f 2 p q p *q r s *r q t s t u t s u u q u p q u q r t r s t s r t t u s *u u q AFD3 = AFD4 = ({,},{p,q,r,s,t,u},f 3,p,{s,t,u}) ({,},{p,q,r,s,t,u},f 4,p,{r,s}) f 3 f 4 p u q q t r r s r *s t r *t u q *u s p p r q q r q *r s t *s r t t t q u u p AFD5 = AFD6 = ({,},{p,q,r,s,t},f 5,p,{r,s}) ({,},{p,q,r,s,t,u},f 6,p,{r,s,t}) f 5 p q r q q t *r s q *s r q t r q f 4 p q r q p s *r t u *s t u *t t u u u u Al igul que en el ejercicio nterior, hllremos el utómt mínimo equivlente de cd uno de ellos. Minimizción de f : No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Q/E = {{p,s,t,u},{q,r}} Q/E 2 = Q/E Q/E = {{p,u},{s,t},{q,r}} Q/E 2 = {{p,u},{s,t},{q,r}} por lo tnto Q/E = Q/E {p,u},{s,t},{q,r} } {{ } }{{} } {{ } A B C Págin de 4
11 Hoj de Prolems: Autómts Finitos Determinists (cont.) f A C A B B A *C C B Minimizción de f 2 : No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Q/E = {{p,q,r,s,t},{u}} Q/E = {{p},{q,r,s},{t},{u}} Q/E 2 = {{p},{q,r,s},{t},{u}} Q/E 2 = Q/E por lo tnto Q/E = Q/E {p},{q,r,s}, {t}, {u} }{{} } {{ } }{{} }{{} A B C D f 2 A B D B B C C D B *D D B Minimizción de f 3 : No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Q/E = {{p,q,r},{s,t,u}} Q/E = Q/E Q/E = {{p,q,r},{s,t,u}} por lo tnto Q/E = Q/E {p,q,r},{s,t,u} } {{ } } {{ } A B f 3 A B A *B B A Minimizción de f 4 : No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Págin de 4
12 Hoj de Prolems: Autómts Finitos Determinists (cont.) Minimizción de f 5 : Q/E 2 = Q/E Q/E = {{p,q,t,u},{r,s}} Q/E = {{p,q},{t,u},{r,s}} Q/E 2 = {{p,q},{t,u},{r,s}} por lo tnto Q/E = Q/E {p,q},{t,u},{r,s} } {{ } } {{ } } {{ } A B C f 4 A C A B B A *C C B No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Q/E 2 = Q/E Q/E = {{p,q,t},{r,s}} Q/E = {{p},{q},{t},{r,s}} Q/E 2 = {{p},{q},{t},{r,s}} por lo tnto Q/E = Q/E {p}, {q}, {t},{r,s} }{{} }{{} }{{} } {{ } A B C D f 5 A B D B B C C D B *D D B Minimizción de f 6 : No tiene estdos inccesiles,por lo tnto, psmos clculr el conjunto cociente Q/E: Q/E = {{p,q,u},{r,s,t}} Q/E 2 = Q/E Q/E = {{p,q},{u},{r,s,t}} Q/E 2 = {{p,q},{u},{r,s,t}} por lo tnto Q/E = Q/E {p,q}, {u},{r,s,t} } {{ } }{{} } {{ } A B C Págin 2 de 4
13 Hoj de Prolems: Autómts Finitos Determinists (cont.) f 6 A A C B B B *C C B Si compromos ls tls de trnsición correspondientes, el resultdo del prolem es el siguiente: AF es equivlente AF4 AF2 es equivlente AF5 5. ( ) Se Σ = {,} un lfeto y se L el lenguje de ls cdens que considerds como números inrios tienen un vlor entero múltiplo de 5. Demuestr que L es regulr. Deemos encontrr un utómt que reconozc el lenguje, poyándonos en l definición: L es regulr si existe un utómt finito que lo reconoce L construcción del utómt se s en ls siguientes ides: El utómt tendrá 5 estdos uno pr cd posile vlor del modulo de un cden inri culquier. Sen los nomres de estos estdos {q,q,q 2,q 3,q 4 } tl que con un plr x con x mod 5 = i el utómt un pr o trnsit l estdo q i. Ovimente, el estdo q será finl. Definimos ls trnsiciones de form recursiv. Pr ello se supone que el utómt hy ledio un cden inri x (x mod 5 = i) y se encontrrá en el estdoq i (pri {,,2,3,4}).Lcuestión seráqueestdotendrá que trnsitr el utómt l ñdir un nuevo it ( o ) l finl de l cden, es decir, como cmirí el modulo y conocido de x l ñdir un nuevo it. Relizmos el nlisis correspondiente: Sexlcdendeitsyleidporelutómtyseq i el estdolquehy trnsitdo. Suponemos que x = x n x n x...x (x i {,}. Ovimente, el vlor deciml de x es v x = x n 2 n +x n 2 n +...+x 2 y, ddo que el utómt hy trnsitdo q i, se cumple v x mod 5 = i. Cómo tendrí que cmir el módulo si ñdimosun nuevo it ( o) l finl dex. Anlizmos los dos csos posiles: Se ñde un : L cuestión es que estdo hy que trnsitr desde el estdo q i si leemos un. L nuev plr serí x = x n x n x...x. El vlor deciml serí v x = 2(x n 2 n +x n 2 n +...+x 2 ). Respecto l módulo de x podemos oservr que v x mod 5 = (2v x ) mod 5 = Págin 3 de 4
14 Hoj de Prolems: Autómts Finitos Determinists (cont.) 2(v x mod 5) mod 5 y si v x mod 5 = i, se cumple: v x mod 5 = (2i) mod 5. Est formul nos d el estdo l que hy que trnsitr desde el estdo q i con el. Así desde q 3, por ejemplo, hy que trnsitr q ((2 3) mod 5 = ), etc. Se ñde un : L cuestión es que estdo hy que trnsitr desde el estdo q i si leemos un. L nuev plr serí x = x n x n x...x. El vlor deciml serí v x = 2(x n 2 n +x n 2 n +...+x 2 )+. Respecto l módulo de x podemos oservr que v x mod 5 = (2v x + ) mod 5 = 2(v x mod 5) + mod 5 y si v x mod 5 = i, se cumple: v x mod 5 = (2i+) mod 5. Est formul nos d el estdo l que hy que trnsitr desde el estdo q i con el. Así desde q 3, por ejemplo, hy que trnsitr q 2 ((2 3+) mod 5 = 2), etc. Con est ide construimos el siguiente utómt: A = ({,},{q,q,q 2,q 3,q 4 },f,q,{q }) Donde f está definid por el siguiente grfo de trnsición: q q q 2 q 3 q 4 Págin 4 de 4
1. Indicar el lenguaje aceptado por los siguientes autómatas :
 Universidd Rey Jun Crlos Curso 27 28 Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Hoj de Prolems 4 Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio,
Universidd Rey Jun Crlos Curso 27 28 Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Hoj de Prolems 4 Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio,
Fundamentos de Algoritmos y Computabilidad
 Fundmentos de Algoritmos y Computilidd * Autómts finitos * Autómts finitos determinists * Autómts finitos no determinists * Equivlenci entre AFD y AFN Lengujes regulres Tipo Lengujes Tipo de máquin 0 Recursivmente
Fundmentos de Algoritmos y Computilidd * Autómts finitos * Autómts finitos determinists * Autómts finitos no determinists * Equivlenci entre AFD y AFN Lengujes regulres Tipo Lengujes Tipo de máquin 0 Recursivmente
Informática Teórica. Tema 4: Autómatas Finitos
 Informátic Teóric Tem 4: Autómts Finitos 1 Autómts Finitos. Biliogrfí M. Alfonsec, J. Sncho y M. Mrtínez. Teorí de Lengujes, Grmátics y Autómts, R.A.E.C., Mdrid, (1998). P. Issi, P. Mrtínez y D. Borrjo.
Informátic Teóric Tem 4: Autómts Finitos 1 Autómts Finitos. Biliogrfí M. Alfonsec, J. Sncho y M. Mrtínez. Teorí de Lengujes, Grmátics y Autómts, R.A.E.C., Mdrid, (1998). P. Issi, P. Mrtínez y D. Borrjo.
Capítulo 8: Propiedades de Lenguajes Regulares
 Cpítulo 8: Propieddes de Lengujes Regulres 8.1. Identificción de lengujes no regulres 8.1.1. Lem de Boeo 8.1.2. Aplicciones del lem de omeo 8.2. Propieddes de Cierre 8.2.1. Unión, Conctención, Clusur 8.2.2.
Cpítulo 8: Propieddes de Lengujes Regulres 8.1. Identificción de lengujes no regulres 8.1.1. Lem de Boeo 8.1.2. Aplicciones del lem de omeo 8.2. Propieddes de Cierre 8.2.1. Unión, Conctención, Clusur 8.2.2.
Autómatas finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS. Ejemplo 2. Ejemplo 1
 Autómts finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Autómts finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Resolución de circuitos complejos de corriente continua: Leyes de Kirchhoff.
 Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
Temas. Objetivo. Definición de autómata finito. Autómata finito determinístico y no determinístico. Autómata finito de estados mínimos 14:17
 0 Tems Definición de utómt finito Autómt finito determinístico y no determinístico Autómt finito de estdos mínimos Ojetivo Que el estudinte logre: 1) Identificr conceptos constructivos de l Teorí de l
0 Tems Definición de utómt finito Autómt finito determinístico y no determinístico Autómt finito de estdos mínimos Ojetivo Que el estudinte logre: 1) Identificr conceptos constructivos de l Teorí de l
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
AUTÓMATAS DE PILA. Dpto. de Informática (ATC, CCIA y LSI). Univiersidad de Valladolid.
 Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
AUTOMATAS FINITOS Traductores
 Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
Minimización de AFDs, método y problemas
 Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
AUTOMATAS FINITOS CIENCIAS DE LA COMPUTACION I 2009
 AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
Modelo 2014. Problema 1B.- (Calificación máxima: 2 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro real a:
 odelo. Proble B.- (Clificción ái puntos) Se consider el siste linel de ecuciones dependiente del práetro rel ) Discútse en función de los vlores del práetro R. b) Resuélvse pr.. l siste se clsific en función
odelo. Proble B.- (Clificción ái puntos) Se consider el siste linel de ecuciones dependiente del práetro rel ) Discútse en función de los vlores del práetro R. b) Resuélvse pr.. l siste se clsific en función
q 2 q 3 b q 3 q 4 a, b
 M = (Σ E, Q, q, f, F ) donde Reconocedor finito determinist Slide Σ E : lfeto de entrd Q : conjunto de estdos, f inito q Q : estdo inicil f : Q Σ E Q función prcil de trnsición F Q : estdos finles o de
M = (Σ E, Q, q, f, F ) donde Reconocedor finito determinist Slide Σ E : lfeto de entrd Q : conjunto de estdos, f inito q Q : estdo inicil f : Q Σ E Q función prcil de trnsición F Q : estdos finles o de
Clase Auxiliar 5. Aútomatas Finitos Determinísticos (Diagramas de Estado)
 CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
Ejercicios resueltos de Lenguajes, Gramáticas y Autómatas ( )
 Ejercicios resueltos de Lengujes, Grmátics y utómts (-2-4). Encuentr el FD mínimo que reconoce el lenguje representdo por l ER ( + + ) ( + ) Pr otener el FD mínimo correspondiente (+ +ɛ) (+) tenemos que
Ejercicios resueltos de Lengujes, Grmátics y utómts (-2-4). Encuentr el FD mínimo que reconoce el lenguje representdo por l ER ( + + ) ( + ) Pr otener el FD mínimo correspondiente (+ +ɛ) (+) tenemos que
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
5. Lenguajes Regulares
 5. Lengujes Regulres Arceli Snchis de Miguel Agpito Ledezm Espino José A. Iglesis Mr
5. Lengujes Regulres Arceli Snchis de Miguel Agpito Ledezm Espino José A. Iglesis Mr
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO
 PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
x 2 + ( x + 1 ) 2 + ( x + 2 ) 2 = 365 x 2 + x 2 + 2 x + 1 + x 2 + 4x + 4 = 365 3 x 2 + 6x 360 = 0
 Ecuciones cudrátics con un incógnit Sen, 1 y los tres números nturles consecutivos uscdos. El prolem nos indic que ( 1 ) ( ) 365 Un número con misterio! El número 365 tiene l crcterístic de ser l sum de
Ecuciones cudrátics con un incógnit Sen, 1 y los tres números nturles consecutivos uscdos. El prolem nos indic que ( 1 ) ( ) 365 Un número con misterio! El número 365 tiene l crcterístic de ser l sum de
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
Problemas de Lenguajes y Autómatas
 Trjo VIII Semestre A2005 Prolems Prolems de Lengujes y Autómts 1. Pr los lengujes ddos sore Σ = {, } construir un expresión regulr de él y un Autómt Finito que lo cepte: ) L = {w w tiene un numero pr de
Trjo VIII Semestre A2005 Prolems Prolems de Lengujes y Autómts 1. Pr los lengujes ddos sore Σ = {, } construir un expresión regulr de él y un Autómt Finito que lo cepte: ) L = {w w tiene un numero pr de
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Tema 4: Operaciones sobre lenguajes regulares
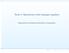 Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I
 INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 18 de enero de 2008 APELLIDOS Y NOMBRE: DURACIÓN: 3 hors. SOLUCIÓN del EXAMEN L primer pregunt es un test, que const de 8 supregunts corts y puntú
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 18 de enero de 2008 APELLIDOS Y NOMBRE: DURACIÓN: 3 hors. SOLUCIÓN del EXAMEN L primer pregunt es un test, que const de 8 supregunts corts y puntú
AUTÓMATAS PUSH-DOWN Y MÁQUINAS DE TURING
 1 FACULTAD REGIONAL ROSARIO AUTÓMATAS PUSH-DOWN Y MÁQUINAS DE TURING GUÍA TEÓRICO-PRÁCTICA PARA ALUMNOS DE LA CÁTEDRA SINTAXIS Y SEMÁNTICA DE LOS LENGUAJES DE LA CARRERA DE INGENIERÍA EN SISTEMAS DE INFORMACIÓN
1 FACULTAD REGIONAL ROSARIO AUTÓMATAS PUSH-DOWN Y MÁQUINAS DE TURING GUÍA TEÓRICO-PRÁCTICA PARA ALUMNOS DE LA CÁTEDRA SINTAXIS Y SEMÁNTICA DE LOS LENGUAJES DE LA CARRERA DE INGENIERÍA EN SISTEMAS DE INFORMACIÓN
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
Autómatas Finitos. Programación II Margarita Álvarez 0,1 0,1. q 3
 Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
Tema 25. AP con dos pilas. Más allá del autómata de pila. No-LLC. Máquina de Turing, Problema del paro y Tesis de Church
 Tem 25 Máquin de Turing, Prolem del pro y Tesis de Church No-LLC LLC no-miguos LLC-Det LR Pl mrk Pl i i c i Dr. Luis A. Pined ISBN: 970-32-2972-7 LLC Proceso de i i c i : AP con dos pils Push tods ls s
Tem 25 Máquin de Turing, Prolem del pro y Tesis de Church No-LLC LLC no-miguos LLC-Det LR Pl mrk Pl i i c i Dr. Luis A. Pined ISBN: 970-32-2972-7 LLC Proceso de i i c i : AP con dos pils Push tods ls s
Función de transición δ. Tema 6. Función de transición extendida. Función de transición extendida. Función de transición extendida
 Tem 6 El lenguje eptdo por un FA Funión de trnsiión δ p j p l Dr. Luis A. Pined ISBN: 970-32-2972-7 Σ Q p i p k n Pr todo en Q & Σ, δ(, ) = p Funión de trnsiión etendid δ permite moverse the un estdo otro
Tem 6 El lenguje eptdo por un FA Funión de trnsiión δ p j p l Dr. Luis A. Pined ISBN: 970-32-2972-7 Σ Q p i p k n Pr todo en Q & Σ, δ(, ) = p Funión de trnsiión etendid δ permite moverse the un estdo otro
DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES
 DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES PROGRAMA EDUCATIVO: INGENIERÍA EN COMPUTACIÓN ESPACIO ACADÉMICO: FACULTAD DE INGENIERÍA
DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES PROGRAMA EDUCATIVO: INGENIERÍA EN COMPUTACIÓN ESPACIO ACADÉMICO: FACULTAD DE INGENIERÍA
Relaciones de equivalencia
 Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Facultad de Informática Universidad Complutense de Madrid PROBLEMAS DE FUNDAMENTOS DE COMPUTADORES TEMA 5. Problemas básicos:
 Fcultd de Informátic Universidd Complutense de Mdrid Prolems ásicos: PROBLEMAS DE FUNDAMENTOS DE COMPUTADORES TEMA 5 1. Especifique como máquin de Moore un sistem secuencil cuy slid z se comport, en función
Fcultd de Informátic Universidd Complutense de Mdrid Prolems ásicos: PROBLEMAS DE FUNDAMENTOS DE COMPUTADORES TEMA 5 1. Especifique como máquin de Moore un sistem secuencil cuy slid z se comport, en función
Determinización: Construcción de Safra
 Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL
 3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TEORÍA DE AUTÓMATAS I Informática de Sistemas. Soluciones a las cuestiones de examen del curso 2010/11
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2/ Ferero, ª semn. Indique cuál de ls siguientes firmciones referentes los operdores sore símolos *, y es FALSA:
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2/ Ferero, ª semn. Indique cuál de ls siguientes firmciones referentes los operdores sore símolos *, y es FALSA:
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I
 INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 22 de Junio de 2009 SOLUCIONES 1. (0,5 puntos) Sobre el lfbeto {,b}, d expresiones regulres que denoten los siguientes lengujes: ) El lenguje formdo
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 22 de Junio de 2009 SOLUCIONES 1. (0,5 puntos) Sobre el lfbeto {,b}, d expresiones regulres que denoten los siguientes lengujes: ) El lenguje formdo
Autómatas finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS. Ejemplo 2. Ejemplo 1
 Autómts finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Autómts finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
TEORÍA DE AUTÓMATAS I Informática de Sistemas
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 25/6 Ferero 26, ª semn. Se un utómt finito M={S, Σ, δ, ι, F,}. Sen p,q S;, Σ. Indique cuál de ls siguientes firmciones
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 25/6 Ferero 26, ª semn. Se un utómt finito M={S, Σ, δ, ι, F,}. Sen p,q S;, Σ. Indique cuál de ls siguientes firmciones
Módulo 12 La División
 Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
O(0, 0) verifican que. Por tanto,
 Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Relación de ejercicios hechos en clase en los últimos días previos al examen de febrero
 Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
1. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN
 http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
SISTEMAS DE ECUACIONES LINEALES: Igualación y Sustitución
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0
Exámenes de Teoría de Autómatas y Lenguajes Formales. David Castro Esteban
 Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
Examen Parcial de Autómatas y Lenguajes Formales 12 de diciembre de 2003
 Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Caracterización de lenguajes regulares con expresiones regulares
 Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
Ejercicios de Lenguajes Gramáticas y Autómatas. Curso 2004 / 2005
 Ejercicios de Lengujes Grmátics y Autómts Curso 24 / 25 Lengujes Regulres... 2 A. Ejercicio ásicos... 2 B. Ejercicios de exmen... 5 Lengujes Independientes del Contexto... 9 C. Ejercicio ásicos... 9 D.
Ejercicios de Lengujes Grmátics y Autómts Curso 24 / 25 Lengujes Regulres... 2 A. Ejercicio ásicos... 2 B. Ejercicios de exmen... 5 Lengujes Independientes del Contexto... 9 C. Ejercicio ásicos... 9 D.
7 DE LA EXPRESIÓN REGULAR AL AUTÓMATA FINITO
 7 DE LA EXPRESIÓN REGULAR AL AUTÓMATA FINITO En los cpítulos nteriores se hn construído diversos AFDs y AFNs que reconocen distintos LRs. Pero no siempre result tn sencillo ni tn seguro diseñr un Autómt
7 DE LA EXPRESIÓN REGULAR AL AUTÓMATA FINITO En los cpítulos nteriores se hn construído diversos AFDs y AFNs que reconocen distintos LRs. Pero no siempre result tn sencillo ni tn seguro diseñr un Autómt
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA
 MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 12, N o 1. Agosto Febrero 2012.
 Artículo de sección Revist digitl Mtemátic, Educción e Internet www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
TEORÍA DE AUTÓMATAS I Informática de Sistemas. Soluciones a las cuestiones de examen del curso 2011/12
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2011/12 Ferero 12, 1ª semn 1. Considere el lenguje { 2n n c / 0}. Indique cuál de ls siguientes firmciones es fls:
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2011/12 Ferero 12, 1ª semn 1. Considere el lenguje { 2n n c / 0}. Indique cuál de ls siguientes firmciones es fls:
Venta de 6 frigoríficos a 1.000 cada uno. Las ventas del ejercicio son ingresos. Banco Clientes a Ventas de mercaderías 6000
 Solución Ejercicio 3: A. Registro de l vent. Vent de 6 frigoríficos 1.000 cd uno. Ls vents del ejercicio son ingresos. 5400 Bnco Clientes Vents de mercderís 0 (+) Bnco (-) (-) Resultdo Ejer (+) 0 (+) Clientes
Solución Ejercicio 3: A. Registro de l vent. Vent de 6 frigoríficos 1.000 cd uno. Ls vents del ejercicio son ingresos. 5400 Bnco Clientes Vents de mercderís 0 (+) Bnco (-) (-) Resultdo Ejer (+) 0 (+) Clientes
CONTROL DE PROCESOS FACET UNT TEMA 1 Nota Auxiliar B ÁLGEBRA DE BLOQUES
 Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Soluciones a los ejercicios
 Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
MÉTODO DE KARNAUGH MÉTODO DE KARNAUGH... 1
 MÉTODO DE KARNAUGH Jesús Pizrro Peláez MÉTODO DE KARNAUGH... 1 1. INTRODUCCIÓN... 1 2. MÉTODO DE KARNAUGH... 2 3. EJEMPLO DE APLICACIÓN (I)... 4 4. ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS... 6 5. EJEMPLO
MÉTODO DE KARNAUGH Jesús Pizrro Peláez MÉTODO DE KARNAUGH... 1 1. INTRODUCCIÓN... 1 2. MÉTODO DE KARNAUGH... 2 3. EJEMPLO DE APLICACIÓN (I)... 4 4. ESTADOS NO IMPORTA EN LAS FUNCIONES LÓGICAS... 6 5. EJEMPLO
OBTENCIÓN DEL DOMINIO DE DEFINICIÓN A PARTIR DE LA GRÁFICA
 . DOMINIO inio de o cmpo de eistenci de es el conjunto de vlores pr los que está deinid l unción, es decir, el conjunto de vlores que tom l vrible independiente. Se denot por. { R / y R con y } OBTENCIÓN
. DOMINIO inio de o cmpo de eistenci de es el conjunto de vlores pr los que está deinid l unción, es decir, el conjunto de vlores que tom l vrible independiente. Se denot por. { R / y R con y } OBTENCIÓN
Concepto clave. La derivada de una función se define principalmente de dos maneras: 1. Como el límite del cociente de Fermat ( )( )
 Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
MATRICES DE NÚMEROS REALES
 MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
Autómatas Finitos. Leopoldo Altamirano, Eduardo Morales. Verano, 2011 INAOE. Introducción a. Autómatas. Definición formal de un. Finito Determinístico
 los s s s s Leopoldo Altamirano, Eduardo Morales INAOE Verano, 2011 (INAOE) Verano, 2011 1 / 60 Contenido los s s 1 los s 2 3 4 s 5 (INAOE) Verano, 2011 2 / 60 los s los s los s s : Conjunto de estados
los s s s s Leopoldo Altamirano, Eduardo Morales INAOE Verano, 2011 (INAOE) Verano, 2011 1 / 60 Contenido los s s 1 los s 2 3 4 s 5 (INAOE) Verano, 2011 2 / 60 los s los s los s s : Conjunto de estados
7. Integrales Impropias
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Bsdo en el punte del curso Cálculo (2d semestre), de Roerto Cominetti, Mrtín Mtml y Jorge
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Bsdo en el punte del curso Cálculo (2d semestre), de Roerto Cominetti, Mrtín Mtml y Jorge
Espacios vectoriales y Aplicaciones Lineales II: Núcleo e imagen. Diagonalización. Ker(f) = {x V f(x) = 0} Im(f) = {f(x) x V}.
 UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
Y f. Para ello procederemos por aproximaciones sucesivas, de modo que cada una de ellas constituya un término de una sucesión G n cuyo límite
 INTEGRALES LECCIÓN Índice: El prolem del áre. Ejemplos. Prolems..- El prolem del áre Se f un función continu y no negtiv en [,]. Queremos clculr el áre S de l región del plno limitd por l gráfic de f,
INTEGRALES LECCIÓN Índice: El prolem del áre. Ejemplos. Prolems..- El prolem del áre Se f un función continu y no negtiv en [,]. Queremos clculr el áre S de l región del plno limitd por l gráfic de f,
(lo podemos visualizar como el área de un cuadrado de lado 4) Pues bien, diremos que la base de dicha potencia, 4, es su raíz cuadrada exacta: 16 = 4.
 Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN)
 Lortorio Tercero Básico Centro Integrl Empresril por Mdurez CIEM INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN). Identific los elementos que se piden: ) Los términos de 5r +s ) Los términos
Lortorio Tercero Básico Centro Integrl Empresril por Mdurez CIEM INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN). Identific los elementos que se piden: ) Los términos de 5r +s ) Los términos
GRAMATICAS REGULARES - EXPRESIONES REGULARES
 CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
Tema 9: Memorias y Dispositivos programables
 Tem 9: Memoris Dispositivos prormles Prolem. Implemente l siuiente unción multislid hciendo uso de un. F = Σ(,,,7,9,,5) G = Π(,,,5,6,,) H = (X + X). (X + X + X) Prolem. Diseñe l unción multislid hciendo
Tem 9: Memoris Dispositivos prormles Prolem. Implemente l siuiente unción multislid hciendo uso de un. F = Σ(,,,7,9,,5) G = Π(,,,5,6,,) H = (X + X). (X + X + X) Prolem. Diseñe l unción multislid hciendo
NOTAS DE CLASE TEORIA DE LA COMPUTACIÓN. Autora: Dra. Cecilia Poblete Ibaceta. Revisión Técnica: Ing. David Jiménez Mimila
 NOTAS DE CLASE TEORIA DE LA COMPUTACIÓN Autor: Revisión Técnic: Ing. Dvid Jiménez Mimil Edición Corregid y Aumentd de Enero de 2006 TABLA DE CONTENIDOS CONJUNTOS... 3 RELACIONES Y FUNCIONES.... 10 GRAMÁTICAS...
NOTAS DE CLASE TEORIA DE LA COMPUTACIÓN Autor: Revisión Técnic: Ing. Dvid Jiménez Mimil Edición Corregid y Aumentd de Enero de 2006 TABLA DE CONTENIDOS CONJUNTOS... 3 RELACIONES Y FUNCIONES.... 10 GRAMÁTICAS...
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE
 CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE CONCEPTOS CLAVE: FUNCIONES, GRAFICA DE UNA FUNCIÒN, COMPOSICIÒN DE FUNCIONES, INVERSA DE UNA FUNCIÒN, LIMITE DE UNA FUNCIÒN, LIMITES LATERALES, TEOREMAS
CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE CONCEPTOS CLAVE: FUNCIONES, GRAFICA DE UNA FUNCIÒN, COMPOSICIÒN DE FUNCIONES, INVERSA DE UNA FUNCIÒN, LIMITE DE UNA FUNCIÒN, LIMITES LATERALES, TEOREMAS
EJERCICIOS del TEMA 2: Lenguajes Regulares
 EJERCICIOS de MAC 1 ALF (Tem 2) Curso 2010/2011 EJERCICIOS del TEMA 2: Lengujes Regulres Sore AFDs (utómts finitos determinists): 1. Rzon l vercidd o flsedd de l siguientes firmción, poyándote en l teorí
EJERCICIOS de MAC 1 ALF (Tem 2) Curso 2010/2011 EJERCICIOS del TEMA 2: Lengujes Regulres Sore AFDs (utómts finitos determinists): 1. Rzon l vercidd o flsedd de l siguientes firmción, poyándote en l teorí
Universidad de Valladolid
 Universidd de Vlldolid Deprtmento de Informátic Teorí de utómts y lengujes formles. 2 o I.T.Informátic. Gestión. Exmen de segund convoctori, 5 de septiemre de 2007 Apellidos, Nomre... Grupo:... Firm: 1
Universidd de Vlldolid Deprtmento de Informátic Teorí de utómts y lengujes formles. 2 o I.T.Informátic. Gestión. Exmen de segund convoctori, 5 de septiemre de 2007 Apellidos, Nomre... Grupo:... Firm: 1
I.3.1.3 Hidroformilación bifásica de 1-octeno con sistemas de Rh/fosfina perfluorada P(C 6 H 4 -p-och 2 C 7 F 15 ) 3
 I.3 Discusión de resultdos I.3.1.3 Hidroformilción ifásic de 1-octeno con sistems de Rh/fosfin perfluord P(C 6 H 4 -p-och 2 C 7 F 15 ) 3 Como y se h comentdo en l introducción l ctálisis ifásic en sistems
I.3 Discusión de resultdos I.3.1.3 Hidroformilción ifásic de 1-octeno con sistems de Rh/fosfin perfluord P(C 6 H 4 -p-och 2 C 7 F 15 ) 3 Como y se h comentdo en l introducción l ctálisis ifásic en sistems
Resolución de triángulos rectángulos
 Resoluión de triángulos retángulos Ejeriio nº 1.- Uno de los tetos de un triángulo retángulo mide 4,8 m y el ángulo opuesto este teto mide 4. Hll l medid del resto de los ldos y de los ángulos del triángulo.
Resoluión de triángulos retángulos Ejeriio nº 1.- Uno de los tetos de un triángulo retángulo mide 4,8 m y el ángulo opuesto este teto mide 4. Hll l medid del resto de los ldos y de los ángulos del triángulo.
IES Fernando de Herrera 23 de octubre de 2013 Primer trimestre - Primer examen 4º ESO NOMBRE:
 IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer emen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, eplicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer emen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, eplicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernando de Herrera 23 de octubre de 2013 Primer trimestre - Primer examen 4º ESO NOMBRE:
 IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
7.1. Definición de integral impropia y primeras propiedades
 Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Fórmulas de cuadratura.
 PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
AUTÓMATAS FINITOS y LENGUAJES REGULARES
 Dpto. de nformátic (ATC, CCA y LS. Universidd de Vlldolid. TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES ngenierí Técnic en nformátic de Sistems. Curso 2011-12. AUTÓMATAS FNTOS y LENGUAJES REGULARES 1. Sen
Dpto. de nformátic (ATC, CCA y LS. Universidd de Vlldolid. TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES ngenierí Técnic en nformátic de Sistems. Curso 2011-12. AUTÓMATAS FNTOS y LENGUAJES REGULARES 1. Sen
2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR
 1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
Álgebra de Boole y circuitos con puertas lógicas
 Tem 3 Álger de Boole y circuitos con puerts lógics Los circuitos que componen un computdor son muy diversos: los hy destindos portr l energí necesri pr ls distints prtes que componen l máquin y los hy
Tem 3 Álger de Boole y circuitos con puerts lógics Los circuitos que componen un computdor son muy diversos: los hy destindos portr l energí necesri pr ls distints prtes que componen l máquin y los hy
PROBLEMAS DE ELECTRÓNICA DIGITAL
 Prolems de Eletróni Digitl 4º ESO PROLEMS DE ELECTRÓNIC DIGITL 1. En l gráfi siguiente se muestr l rterísti de l resisteni de un LDR en funión de l luz que reie. Qué tipo de mgnitud es est resisteni? 2.
Prolems de Eletróni Digitl 4º ESO PROLEMS DE ELECTRÓNIC DIGITL 1. En l gráfi siguiente se muestr l rterísti de l resisteni de un LDR en funión de l luz que reie. Qué tipo de mgnitud es est resisteni? 2.
Curso ON LINE Tema 5. x + y + z = 5 1200x + 600y = 2000 + m z 1200x = 3 m z
 Curso ON LINE Tem 5 Un gente inmobilirio puede relir tipos de operciones: vent de un piso nuevo, vent de un piso usdo lquiler. Por l vent de cd piso nuevo recibe un prim de. Si l operción es l vent de
Curso ON LINE Tem 5 Un gente inmobilirio puede relir tipos de operciones: vent de un piso nuevo, vent de un piso usdo lquiler. Por l vent de cd piso nuevo recibe un prim de. Si l operción es l vent de
a) Decimales finitos: Corresponden a los cuocientes exactos entre el numerador y el denominador. Ejemplo: : 8 = (b)
 Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
INTEGRAL DEFINIDA. El hallar el área aproximada bajo la curva por suma de n áreas rectangulares de igual ancho x
 en INTEGRAL DEFINIDA El concepto de integrl definid está relciondo con el vlor que determin el áre jo l curv dd por un función f (x) el [, ]. (ve l intervlo gráfic) Uno de los primeros psos pr llegr este
en INTEGRAL DEFINIDA El concepto de integrl definid está relciondo con el vlor que determin el áre jo l curv dd por un función f (x) el [, ]. (ve l intervlo gráfic) Uno de los primeros psos pr llegr este
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EJERCICIOS PAUS MATEMÁTICAS II (DESDE EL CURSO 07-08 AL 11-12) ÁLGEBRA: TEMAS 1-2-3
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID EJERCICIOS PUS MTEMÁTICS II (DESDE EL CURSO 78 L ) ÁLGEBR: TEMS (Los ejercicios de selectividd resueltos los podéis encontrr en l págin web clsesdepooco) http://wwwclsesdepooco/docuents/es_serch
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID EJERCICIOS PUS MTEMÁTICS II (DESDE EL CURSO 78 L ) ÁLGEBR: TEMS (Los ejercicios de selectividd resueltos los podéis encontrr en l págin web clsesdepooco) http://wwwclsesdepooco/docuents/es_serch
