Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
|
|
|
- Eduardo Carrizo Alarcón
- hace 7 años
- Vistas:
Transcripción
1 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria
2 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable E el siguiete gráfico se cosidera ua fució y= f. Represeta la derivada e el puto, el icremeto de y= f para u icremeto de,, y la diferecial de y = f e para. Calcula estos dos valores para y= e el puto =. f(+ ) f() α f(+ )-f() α + Solució: = y log= logy Derivado implícitamete Para = y ' log + = y ' = y log+ y ' = log+ y y ' = log+ dy = log + Deduce la derivada de la fució y= arcse Solució: Sea y = arcse etoces Profesora: Elea Álvarez Sáiz
3 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I sey = Derivado respecto a : cos y y ' = y ' = = = cosy se y Hallar la derivada eésima de f se cos águlo doble) = e =0 (utilizar fórmula del seo del Solució: Teiedo e cueta que: f = se cos = se( 4) se tiee: Luego, para todo = f ' cos 4 = f '' 4se 4 = f ''' 4 cos 4 iv = 4 ( 4 ) f se = ( ) 4 ( 4 ) ( f se + = 4 cos( 4 ) ( f Otra forma: Teiedo e cueta que: se tiee que: π cos( α) = se α+ π f ' = cos( 4) = se 4+ f '' 4cos 4 π π π = + = 4 se 4+ + π π f ''' = 4 cos 4+ = 4 se 4+ Profesora: Elea Álvarez Sáiz S
4 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Fórmula que se demuestra por iducció sobre. - 4 Se cosidera la ecuació: d y dy 4 6y d d + = t y se realiza el cambio = e. Escribir la ecuació después de haber realizado el cambio cosiderado la variable y depediete de t. Solució: Se tiee el siguiete árbol de depedecia: y t Aplicado la regla de la cadea: dy dy d dy dy t = = e () dt d dt d dt Aplicado uevamete la regla de la cadea derivado respecto de sabiedo que -----t d y d dy d dy dt dy d y d d d dt dt d dt d t t t t t = e e e = = + e t= log dt t = = e d () Sustituyedo e la ecuació dada: 4 Profesora: Elea Álvarez Sáiz
5 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I e e e e e y e dt d t dt t t dy t d y t t dy t = dy d y dy + dt + = d t dt t 4 6y e d y dy t 5 6y e d t dt + = 5 Sea g = f( se), sabiedo que f '( 0) = 0 calcular g '( π ). Comprueba además el resultado obteido para ua fució f cocreta. Solució: Aplicado la regla de la cadea, ( π) ( π) π g ' = f ' se cos g ' = f ' se cos = f ' 0 = 0 Por ejemplo, podemos cosiderar f = g = f( se) = ( se) Se tedría para este ejemplo ( π) g ' = se cos g ' = seπ cosπ= 0 6 Dada la curva + y + 6y+ 6= 0, se pide represetarla y calcular la recta tagete y ormal a dicha curva e el puto P(, + ). Solució: Completado cuadrados ( ) ( + ) + y + 6y+ 6= + y + 6y + 6= + y 9+ 6 Se tiee que Profesora: Elea Álvarez Sáiz S 5
6 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable + y + 6 y+ 6 = 0 + y+ = 4 luego la curva es ua circuferecia cetrada e el puto (, -) y de radio. Para calcular la pediete de la recta tagete calculamos la derivada e el puto P. Derivado implícitamete: e el puto P + yy ' + 6 y ' = 0 y ' = y + 6 y ' la ecuació de la recta tagete es: P = = y la de la recta ormal y = + ( ) ( ) y ( ) ( ) = + + y recta ormal recta tagete P Profesora: Elea Álvarez Sáiz
7 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I 7 U puto P se mueve sobre la parábola = y situada e el primer cuadrate de forma que su coordeada está aumetado a razó de 5 cm/seg. Calcular la velocidad a la que el puto P se aleja del orige cuado =9. Solució: Se trata de u problema de razó de cambio relacioadas. La fució distacia de u puto situado e las coordeadas (, y) al orige es: = + d t t y t Si el puto (, y) está e la parábola = y será: = + d t t t Profesora: Elea Álvarez Sáiz S 7
8 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable y =y - y(t) d(t) (t) La velocidad a la que se aleja del orige aplicado la regla de la cadea es: d '( t) = ( t) + ( t) t ' t + ' t / E el istate e que =9 y teiedo e cueta que '( t) = 5 cm / seg se cocluye que la velocidad a la que el puto P se aleja del orige es: / ( 9 + 9) ( ) = = Determia el puto de corte de la recta tagete a la gráfica de log co el eje X. f = e el puto =e 8 Profesora: Elea Álvarez Sáiz
9 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Utilizado la regla de la cadea (derivació logarítmica) ' f log log log f = log( ) = ( log) = f f ' luego la recta tagete es: e ' = = e log log loge log = f ( e) e y e= ( e) que corta al eje X e el puto e e 0 e= e =,0 9 E ua empresa la fuerza laboral L se mide e horas-trabajador y es ua fució del tiempo, L= f( t). Sea M= g( t) la producció media por persoa. Supoga que la producció Q está dada por el producto LM. E cierto mometo la fuerza laboral L está creciedo a u ritmo de 4% aual y la producció media está creciedo a ua razó de 5% al año. Ecotrar la razó de cambio de la producció total cuado Q=0. Solució: Datos del problema: Se pide: Q= LM= f( t) g( t) dl = 0'04 L dt dm = 0'05 M dt Profesora: Elea Álvarez Sáiz S 9
10 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable dq dl dm = M+ L dt dt dt dq = 0'04 L M+ L 0'05M = 0'09 L M= 0'09 Q= 0,9 dt = Q 0 0 Calcular dy d arctgy supoiedo que y() está dada implícitamete por la ecuació = ych. Solució: Tomado logaritmos a ambos lados de la epresió: arctgy = ych se obtiee arctgy log= log y+ log( Ch ) Derivado implícitamete respecto de : Reagrupado los térmios e y : y 'log arctgy y ' Sh + = + + y y Ch y 'log y ' Sh arctgy = + y y Ch Despejado y ( + y ) dy Th arctgy y y ' = = d y log y 0 Profesora: Elea Álvarez Sáiz
11 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Nota: El ejercicio se puede resolver derivado respecto de a ambos lados de la igualdad implícitamete: d d arctgy ( ) = ( ych) d d Derivació implícita del térmio de la izquierda: arctgy ( ) h = log h = arctgy log y + y h ' ' = log+ arctgy h arctgy y ' ' log h = + arctgy + y Derivado implícitamete el térmio de la derecha: y ' Ch y Sh y + Etoces se tedrá: Despejado y : arctgy y ' log + arctgy = y ' Ch+ y Sh y + y arctgy log arctgy y ' Ch = y Sh y y + arctgy y ' = arctgy arctgy y Sh log Ch + y y arctgy Operado se puede llegar al resultado: Profesora: Elea Álvarez Sáiz S
12 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable ( + y ) dy Th arctgy y y ' = = d y log y U depósito de agua es cóico, co el vértice hacia arriba, y tiee 40 m. de alto y 0 m. de radio e la base. El depósito se llea a 80 m / mi. A qué velocidad se eleva el ivel de agua cuado la profudidad del agua es de m.? Nota: El volume de u coo de altura h y radio de la base r es: V = π r h Solució: E cualquier istate de tiempo el volume V es V = π 0 40 π r 40 h dode r y h so fucioes del tiempo. Además estás dos fucioes está relacioadas de la maera siguiete: h = r= 40 h r 40- h h r 40 0 Profesora: Elea Álvarez Sáiz
13 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I E cosecuecia el volume e u istate t es: 40 h t V t π 0 40 π = 4 Derivado respecto de t e ambos lados de la igualdad dv dt = π 40 h t 4 dh dt E el istate e el que h= m el deposito se llea a 80 m / mi luego, π dh dh 0 80= 40 0' m / mi 4 = dt dt 49π Ejemplo: f = se( ) + log( + ) Poliomio de Taylor de grado (recta tagete) e =0 ( ) T f,0 = 0 Profesora: Elea Álvarez Sáiz S
14 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Poliomio de Taylor de grado : ( ) = T f,0 ( ) f = + R f,0 R f,0 =Ο para = 0 4 Profesora: Elea Álvarez Sáiz
15 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Poliomio de Taylor de grado 4: T4 f 4 (,0) = f = 4 + R ( ) ( ) ( 4 4 f,0 R4 f,0 =Ο ) para = 0 Profesora: Elea Álvarez Sáiz S 5
16 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Se cosidera la fució f = + (a) Calcula ua estimació del error de la aproimació de f = + por su poliomio de Taylor de grado e el puto a= 0 cuado perteece al itervalo 0 (b) Calcula para esta fució la diferecial e 0 fució y represeta el valor obteido. a= e 0.5 =. Haz u bosquejo de esta (c) Puedes dar ua cota del error que se comete al aproimar por? Solució 6 Profesora: Elea Álvarez Sáiz
17 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I (a) Cosideramos la fució f = derivado + / f = + f 0 = / f ' = ( + ) f '( 0) = 5/ f '' = ( + ) f ''( 0) = 4 El poliomio de Taylor de grado es: Utilizado el resto de Lagrage el error es T f 8 (,0) = + ( ) ( c) ''' f 5 7/ f T f ; 0 = = + c c puto itermedio a 0 y a!! Si 0 el error ua estimació del error es 5 7/ 5 5 ( + c) 6 = c + c + 7/ 7/ + + ( c) (b) La diferecial es: dy= f '( 0) = 0,5= 0,5 Profesora: Elea Álvarez Sáiz S 7
18 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable.5 Recta tagete Diferecial 0.5 (o,f(o) alfa y=f() h y=f(o+h)-f(o) (o+h,f(o+h) dy Para que se vea mejor la gráfica correspode a u icremeto de valor. (c) Se está pidiedo calcular ua cota del error de sustituir f = = + que sabemos que para icremetos pequeños se por f ( 0) =. Es decir acotar y puede aproimar por la diferecial, luego, y 0.5. Otra forma es utilizar el resto de Lagrage es decir, '( c) f y= f f( 0) = co 0< c<! f f( 0) ( c) / co 0 c = + < < Por el mismo razoamieto que ates f f 0 ( c) / = + = 0, 5 Sea f ( ) = log( + ). Se pide: (a) Escribir la fórmula de Taylor para f() e =0 de orde co el resto de Lagrage. 8 Profesora: Elea Álvarez Sáiz
19 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I 0 0 (b) Dar ua cota del error al aproimar log de grado. mediate el poliomio de Taylor Solució: (a) = log( + ) f E primer lugar calculamos la derivada -ésima. Método : Calculamos las derivadas sucesivas f ' = log( + ) + + ( ) + f '' = + = iv = ( )( + ) + ( )( + ) f ''' = ( )( )( + ) + ( )( )( + ) 4 f ( ) ( f =! + +! + = ( + )! + = ( ) ( )! + = ( ) ( + + ) ( + ) = ( ) ( ) ( f 0! ( ) = ( ) ( f 0! Método : Aplicado la fórmula de Leibiz Profesora: Elea Álvarez Sáiz S 9
20 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable ( f = log( ) log( ) ( ( Calculamos etoces la derivada -ésima de g = log( + ) g ' + = = ( + ) = ( )( + ) g '' = ( )( )( + ) g ''' + ( g =! + + E el orige g '( 0) =, ( g 0 =! Nota: E esta última epresió si cosideramos = se obtiee la derivada primera e el orige por lo que puede cosiderarse válida para + ( g 0 =! Por lo tato, + ( ) ( )!! ( f = + = ( + ) ( + ) ( ( ) ( ) )!! + = + + = + + = ( ) ( ) ( f 0! ( ) = ( ) ( f 0! La fórmula de Taylor será: ( + ( ) f ( t ) ( + )! + log + = co t etre 0 y 0 Profesora: Elea Álvarez Sáiz
21 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Como el resto es: f ( + = ( + + ( ) ( )(! + + ) ( + ) + + ( ) ( + + ) f t t R = = +! + + t Apartado (b) Si cosideramos = la aproimació por este poliomio es 0 ( ) log cometiédose por error, ( ) ( t ) Error= R = co t etre 0 y ( + ) ( + t) Ua cota del error para = es: Error ( t ) = 4 ( ) 0 + t t 4 0 = < < Dode se ha teido e cueta que: 4 0< < + 4 < + 4= Si t ( t ) < < < + < 0 0 Si 0 t ( t) 4 4 < ( + t) < < < ( + t) 0 Profesora: Elea Álvarez Sáiz S
22 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Por lo tato ua cota del error podría ser: 4 Error Cosidera la fució f = +. (a) Determia la epresió del resto -ésimo del poliomio de Taylor de la fució e =0 (b) Determia el grado del poliomio de Taylor de la fució f e =0 que permite aproimar co u error meor que ua décima. Solució: (a) Aplicado la fórmula de Leibiz para obteer la derivada -ésima de f = + Se tiee que ( ( ( f g g siedo g 0 = + = + = ( + ) / Por iducció puede probarse que g ( Podemos cosiderar que la derivada... ( ) ( ) + = ( + ) = ( )... ( ) ( g = + N tomado como coveio que e la fórmula aterior se tomará Luego, ( ) si ( )... < Profesora: Elea Álvarez Sáiz
23 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I ( ) + + ( ) ( f = La epresió del resto -ésimo es: (, ) ( + f ( t) ( + )! R f = + co t u puto itermedio etre 0 y sustituyedo f t ( ) ( ) ( t) ( t ) ( = t + +! + + +! + + co t u puto itermedio etre 0 y. (b) Se tiee que f que = luego se trata de determiar el valor de de forma R ( f ) ( + f ( t) ( + ) +, = <! 0 siedo t u puto itermedio a 0 y a. Se tiee, aplicado la desigualdad triagular, ( ) + + ( t) ( ) R( f,) = t + ( + )! ( t) t ( ) ( t) ( ) ( t) ! + +! siedo t u puto itermedio a 0 y a. k Como 0< t< < + t < < + t < si k es atural k k Profesora: Elea Álvarez Sáiz S
24 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable k k k = < + < si k es atural < ( t) ( + t) k Luego, R ( f,) + ( ) ( ) ! +! Para resolver el problema basta ecotrar el úmero que hace que: + ( ) ( ) ! +! 0 Dado valores a vemos que se cumple para =, es decir, R ( f,) 5 + 4! 4! 0 4 y el poliomio que se ha de tomar es de grado. 5 Calcular mediate el poliomio de Taylor co u error meor que ua décima el valor de Represetar de forma aproimada la gráfica de la fució y del poliomio de e Taylor obteido e el apartado aterior. Solució: / (a) Observamos que = e. Ua posibilidad para hacer el ejercicio es e f = e. El puto dode desarrollaremos será a=0 y tomar como fució el puto dode aproimaremos la fució por el poliomio de Taylor será = Como ( ( f = e N f 0 = N es secillo ver que la fórmula de Taylor es 4 Profesora: Elea Álvarez Sáiz
25 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I f R f!! = (, ) dode R ( f, ) = t + e ( + )! siedo t u puto itermedio a 0 y a / Haciedo = se tiee que el error al sustituir f = e poliomio de Taylor de grado e el puto / es por el + t e R f, = +! ( ) siedo < t< 0 Como + + t e + R f, = = +! +! +! Hay que ecotrar el valor de que hace ( ) ( + ) ( ) << t 0 t 0 e< e = < 0 < ( + )! +! 0 ( + ) (I) ya que así se tedrá: Dado valores a e la desigualdad (I) + R f, < +! ( ) + 0 = 0 <! NO = 0 <! SI Luego el poliomio buscado es el segudo / 5 = e + + = + = e! 9 9 Profesora: Elea Álvarez Sáiz S 5
26 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable 6 La fórmula de Machi π= 4arctg arctg puede usarse para aproimar los valores de π. Utilizar el desarrollo de Taylor de la fució arctg( ) hasta tercer orde y la fórmula de Machi para calcular el valor de π. Dar ua cota para el error de la aproimació justificado adecuadamete la respuesta. Nota: E el caso de cálculos fiales se puede dejar idicada la operació. Solució: Se cosidera la fució f = arctg a= 0 Las derivadas ecesarias so: f ' = f '( 0) = + f '' = f '' 0 = 0 ( + ) ( + ) 4( ) 4 ( + ) 6 f ''' = f ''' 0 = f iv = El poliomio de Taylor e a=0 es: P = El error: 6 Profesora: Elea Álvarez Sáiz
27 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I t t ( + t ) 4 f P = R = + 4! siedo t u puto itermedio etre 0 y. 4 4 (*) El valor aproimado es: π= 6arctg 4arctg 6P 4P = y ua estimació del error es: error = Luego: π=.406± Observació: E la acotació (*) se ha utilizado la desigualdad triagular. Podía haberse obteido otra cota por ejemplo, cosiderado la t t fució g( t) = y observado que es creciete e el itervalo [0, /5]. + ( t ) Para valores de e este itervalo se podrá acotar: g t t t = g ( + t ) 0< t< E este caso, para valores de e el itervalo [0, /5] se tedrá: ( ) ( ) ( ) 5 4 f P = R = + + Profesora: Elea Álvarez Sáiz S 7
28 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable De esta maera para =/5, =/ arctg P = f P = R = arctg P = f P = = R = ( ) (a) Calcular la derivada eésima de la fució f log ( ) =. (b) Calcular el cojuto de úmeros reales de maera que el poliomio de MacLauri 5 4 de f = log ( ) de grado permita aproimar f() co u error meor que 0 5 (c) Calcular de forma aproimada el valor de log( ' ) co la aproimació de la ordeada de la recta tagete dado ua estimació del error Solució: (a) Derivado 5 f = log = 5 log f 0 = 0 5 f ' = = 5( ) f '( 0) = 5 ' f '' = 5( ) = 5( ) f ''( 0) = 5 f ''' = 5 f ''' 0 = 0 ( ( f = 5! f 0 = 5! 8 Profesora: Elea Álvarez Sáiz
29 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I (a) El poliomio de Taylor de grado es: f = ( t) siedo t itermedio a 0 y : 5 error = f T = < Para que ( t) 4 4 basta que: Si >0. Como el logaritmo solo está defiido para valores positivos se tiee que se deberá cumplir: > 0 <. Por lo tato supodremos que 0< < Etoces 0<t<< 0<-<-t< como error= < = ( t) ( ) 4 Basta hacer < < < < < = A Es decir, A < A < ( ) A < + A Si <0 etoces <t<0 <-t<- como Basta hacer 5 5 error= < ( t) < 0 < < Profesora: Elea Álvarez Sáiz S 9
30 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable (b) Si se aproima por la recta tagete: Se tiee que: ( ) 5 log = 5 5 ( t) co t itermedio etre 0 y Luego ( ) 5 5 log ' = log '= = 0' 5 5log( ') = 5 ( 0') 0' t El valor aproimado es: ( ) co t itermedio etre 0 y -0 y ua cota del error: 5log( ') 0'5 error '<< t 0 t = 5log ' 0'5 = 0'0 < 0< < t 0' t ' < < < t 8 Sea f log( ) = +. Se pide: (a) Escribir la fórmula de Taylor para f() e =0 de orde co el resto de Lagrage. 0 0 (b) Dar ua cota del error al aproimar log grado. mediate el poliomio de Taylor de Solució: Apartado (a) = log( + ) f 0 Profesora: Elea Álvarez Sáiz
31 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I E primer lugar calculamos la derivada -ésima. Método : Calculamos las derivadas sucesivas f ' = log( + ) + + ( ) + f '' = + = iv = ( )( + ) + ( )( + ) f ''' = ( )( )( + ) + ( )( )( + ) 4 f ( ) ( f =! + +! + = ( + )! + = ( ) ( )! + = ( ) ( + + ) ( + ) = ( ) ( ) ( f 0! ( ) = ( ) ( f 0! Método : Aplicado la fórmula de Leibiz ( f = log( ) log( ) ( ( Calculamos etoces la derivada -ésima de g = log( + ) g ' + = = ( + ) = ( )( + ) g '' = ( )( )( + ) g ''' Profesora: Elea Álvarez Sáiz S
32 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable + ( g =! + + E el orige g '( 0) =, ( g 0 =! Nota: E esta última epresió si cosideramos = se obtiee la derivada primera e el orige por lo que puede cosiderarse válida para + ( g 0 =! Por lo tato, + ( ) ( )!! ( f = + = ( + ) ( + ) ( ( ) ( ) )!! + = + + = + + = ( ) ( ) ( f 0! ( ) = ( ) ( f 0! La fórmula de Taylor será: ( + ( ) f ( t ) ( + )! + log + = co t etre 0 y Como el resto es: f ( + = ( + + ( ) ( )(! + + ) ( + ) + + ( ) ( + + ) f t t R = = +! + + t Profesora: Elea Álvarez Sáiz
33 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Apartado (b) Si cosideramos = la aproimació por este poliomio es 0 ( ) log cometiédose por error, ( ) ( t ) Error= R = co t etre 0 y ( + ) ( + t) Ua cota del error para = es: Error ( t ) = 4 ( ) 0 + t = 0 t 4 0 < < Dode se ha teido e cueta que: 4 0< < + 4 < + 4= Si t ( t ) < < < + < 0 0 Si 0 t ( t) 4 4 < ( + t) < < < ( + t) 0 Por lo tato ua cota del error podría ser: 4 Error 0 5 se 9 Ecuetra u ifiitésimo equivalete a la fució f = e e e =0 Solució: Profesora: Elea Álvarez Sáiz S
34 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Utilizado poliomios de Taylor aalizamos el orde de la primera derivada o ula e =0. Se tiee que: se f ' = e e cos f ' 0 = 0 se se f '' = e e cos + e se f '' 0 = 0 se se se se f ''' = e e cos + e cosse+ e se cos+ e cos f ''' = 0 Aplicado la fórmula de Taylor: f ' 0 f '' 0 f f = f ''' 0 + R = + R!!! 6 dode el resto es u ifiitésimo de orde superior a tres. Por lo tato f() es u ifiitésimo de orde. Poliomio de Taylor f = e e se Poliomio de Taylor de grado 5 e =0 T5 f (,0) = Profesora: Elea Álvarez Sáiz
35 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I 0 Calcular la parte pricipal de los ifiitésimos: (a) arctg (b) se cos Solució: Poliomio de Taylor: Apartado (a) f = arctg Poliomio de Taylor de grado 4 e =0 T4 f 4 4 ( ( 4 ),0) = Profesora: Elea Álvarez Sáiz S 5
36 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Poliomio de Taylor: Apartado (b) f = se cos Poliomio de Taylor de grado 5 e =0 T5 f 0 5 ( ( 4 ),0) = 6 Profesora: Elea Álvarez Sáiz
37 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Utilizado poliomios de Taylor calcular los siguietes límites: (a) arctg lim cos se 0 = (b) 8 se cos lim = cos 0 ( ) ( c) lim e = e + se 0 Solució: Fució f = arctg ( ) cos se El poliomio de Taylor e =0 es: Profesora: Elea Álvarez Sáiz S 7
38 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Fució: f = arctg Fució: f = ( se ) cos 8 Profesora: Elea Álvarez Sáiz
39 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Fució f se cos = ( cos) Profesora: Elea Álvarez Sáiz S 9
40 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Fució: f = se cos Fució: f = ( ) cos 40 Profesora: Elea Álvarez Sáiz
41 Ejercicios: Fucioes ua variable Igeiería de Telecomuicació Fudametos Matemáticos I Fució f se = Las derivadas so: f ' f se 0 = lim = 0 cos se = f ( 0+ ) ( 0) f f f ' 0 = lim = 0 h 0 h se cos se f ' 0 + f f ' 0 f ' = + f ''( 0) = lim h 0 h cos se cos se f ''' = El poliomio de Taylor de orde es T = 6 Profesora: Elea Álvarez Sáiz S 4
42 Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios: Fucioes ua variable Nota: Si e la solució de algú ejercicio crees que hay algú error pote e cotacto co la profesora para su correcció. 4 Profesora: Elea Álvarez Sáiz
Apellidos y Nombre: Aproximación lineal. dy f x dx
 INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
Material interactivo con teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguientes enlaces una vez dentro de la asignatura
 E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 16 de julio de 2015 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
(3 ) (6 ) 5 (3 x ) 5 81x. log (3 4) log 5 3log 5 5 (3log 5) y x x. cos 7 4 ( 1) 2 (3 ) 2 4
 E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
Fórmula de Taylor. Si f es continua en [a,x y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) f(x) f(a) f '(c)(x a)
 Aproimació de ua fució mediate u poliomio Cuado y=f tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado y=f tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:...CURSO:...
 EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
DERIVACIÓN Y DIFERENCIACIÓN DE FUNCIONES DE UNA VARIABLE REAL. APROXIMACIÓN POLINÓMICA. DESARROLLOS EN SERIE
 DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
L lim. lim. a n. 5n 1. 2n lim. lim. lim. 1 Calcula: Solución: a) 2
 Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
INGENIERÍA DE TELECOMUNICACIÓN PRÁCTICA 7
 E esta práctica se aalizará la aproximació de ua ució mediate su poliomio de Taylor estimado esta aproximació. Los coceptos y resultados que se utilizará so los siguietes: Supogamos que ( x ) es ua ució
E esta práctica se aalizará la aproximació de ua ució mediate su poliomio de Taylor estimado esta aproximació. Los coceptos y resultados que se utilizará so los siguietes: Supogamos que ( x ) es ua ució
1ª Prueba de Evaluación Continua 20 de septiembre de 2011 Tipo I
 1ª Prueba de Evaluació Cotiua 0 de septiembre de 011 Tipo I 1.- La medida del radio de ua pieza circular ha dado 15cm co ua cota de error de 0,0cm. a. Aproximar, mediate difereciales, el porcetaje del
1ª Prueba de Evaluació Cotiua 0 de septiembre de 011 Tipo I 1.- La medida del radio de ua pieza circular ha dado 15cm co ua cota de error de 0,0cm. a. Aproximar, mediate difereciales, el porcetaje del
1 Definición de derivada
 Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Sucesiones y series numéricas
 PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
Prueba 18 de octubre. c) x=0:0.1:4; x1=x 2; plot(x1,(x1.^3+sin(x1))./(x1+1)) d) x= 2:0.2:2; plot(x,(x^3+sin(x))/(x+1))
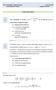 E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
Ejercicios Resueltos de Clasificación de Funciones
 Istituto Tecológico de Ciudad Madero Uidad I. Complejidad Computacioal Capitulo. Clasificació de Algoritmos Ejercicios Resueltos de Clasificació de Fucioes.. Determie si f ( ) perteece a la clase idicada
Istituto Tecológico de Ciudad Madero Uidad I. Complejidad Computacioal Capitulo. Clasificació de Algoritmos Ejercicios Resueltos de Clasificació de Fucioes.. Determie si f ( ) perteece a la clase idicada
EJERCICIOS DE SERIES DE FUNCIONES
 EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
Soluciones de los problemas de la HOJA 2B
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
Sesión de Preparación de Olimpiada Matemática.
 Sesió de Preparació de Olimpiada Matemática 6 de Diciembre de 06 Ferado Mayoral Desigualdades (y Poliomios y otras fucioes) (I) -Alguas desigualdades básicas ) x 0 para cualquier x R La igualdad sólo se
Sesió de Preparació de Olimpiada Matemática 6 de Diciembre de 06 Ferado Mayoral Desigualdades (y Poliomios y otras fucioes) (I) -Alguas desigualdades básicas ) x 0 para cualquier x R La igualdad sólo se
MATE1214 -Calculo Integral Parcial -3
 MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
MATE114 -Calculo Itegral Parcial -3 Duració: 60 miutos 1. Cosidere la curva paramétrica descrita por = te t, y = 1 + t. Halle la pediete de la recta tagete a esta curva cuado t = 0.. Calcular la logitud
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE INGENIERIA DEPARTAMENTO DE MATEMATICA APLICADA. Temas 5 y 6 Sucesiones y Series. Series de Potencias
 Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
= 2n 4 n distancia a 2 es menor que 0,1. = 4n 1 n distancia a 4 es menor que 0,001. 4n 1 = 3 4 0,01. 4 la sucesión son menores que un millón.
 IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS 4º ESO ALUMNO: TRABAJO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE: La mayoría de estos ejercicios está hechos e clase o e los aputes. Estúdiate primero los aputes
IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS 4º ESO ALUMNO: TRABAJO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE: La mayoría de estos ejercicios está hechos e clase o e los aputes. Estúdiate primero los aputes
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 Matemáticas II - º Bachillerato INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN Método de itegració por cambio de variable Cosiste e sustituir por ua fució adecuada para que la epresió resultate sea más secilla
Matemáticas II - º Bachillerato INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN Método de itegració por cambio de variable Cosiste e sustituir por ua fució adecuada para que la epresió resultate sea más secilla
Profr. Efraín Soto Apolinar. Área bajo una curva
 Profr. Efraí Soto Apoliar. Área bajo ua curva Nosotros coocemos muchas fórmulas para calcular el área de diferetes figuras geométricas. Por ejemplo, para calcular el área A de u triágulo co base b altura
Profr. Efraí Soto Apoliar. Área bajo ua curva Nosotros coocemos muchas fórmulas para calcular el área de diferetes figuras geométricas. Por ejemplo, para calcular el área A de u triágulo co base b altura
Prueba Integral Lapso / Área de Matemática Fecha: MODELO DE RESPUESTA (Objetivos del 01 al 11)
 Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN 2 1+ x dx
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN Método de itegració por cambio de variable Cosiste e sustituir por ua fució adecuada para que la epresió resultate sea más secilla de itegrar que la primera.
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN Método de itegració por cambio de variable Cosiste e sustituir por ua fució adecuada para que la epresió resultate sea más secilla de itegrar que la primera.
Cálculo I (Grado en Ingeniería Informática) Examen final, enero de 2014
 Cálculo I (Grado e Igeiería Iformática 03-4 Exame fial, eero de 04 PUNTUACIÓN DEL EXAMEN: P. P. P. 3 P. 4 P. 5 P. 6 TOTAL Iicial del primer apellido: NOMBRE: APELLIDOS: D.N.I. O PASAPORTE: FIRMA: Notas
Cálculo I (Grado e Igeiería Iformática 03-4 Exame fial, eero de 04 PUNTUACIÓN DEL EXAMEN: P. P. P. 3 P. 4 P. 5 P. 6 TOTAL Iicial del primer apellido: NOMBRE: APELLIDOS: D.N.I. O PASAPORTE: FIRMA: Notas
Cálculo. 1 de septiembre de Cuestiones
 Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 5. Series.
 CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
CÁLCULO Igeiería Idustrial. Curso 2009-200. Departameto de Matemática Aplicada II. Uiversidad de Sevilla. Lecció 5. Series. Resume de la lecció. 5.. Sucesioes y series. Sucesió covergete. Se de e ua sucesió
Tema 2. Tema 2: Aproxim mación de funciones por po olinomios
 Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
Tema 8. Derivabilidad y reglas de derivación. 8.1 Derivada de una función
 Tema 8 Derivabilidad y reglas de derivació 8. Derivada de ua fució f : I R es derivable e a I si eiste el límite que llamaremos f 0 (a) f() f(a) lim a a Ejercicio 8.. Si f() 3 calcular f 0 () f(a + ) f(a)
Tema 8 Derivabilidad y reglas de derivació 8. Derivada de ua fució f : I R es derivable e a I si eiste el límite que llamaremos f 0 (a) f() f(a) lim a a Ejercicio 8.. Si f() 3 calcular f 0 () f(a + ) f(a)
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Una sucesión es un conjunto infinito de números ordenados de tal forma que se puede decir cuál es el primero, cuál el segundo, el tercero, etc.
 Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
De esta forma, el problema de encontrar la mejor recta se concentra en calcular los valores de la pendiente (m) y de la ordenada al origen (b)
 MÉTODO DE MÍNIMOS CUADRADOS E muchos de los experimetos que se realiza e Física, se obtiee u cojuto de parejas de úmeros (abscisa, ordeada) por los cuales ecesitamos, para obteer u modelo matemático que
MÉTODO DE MÍNIMOS CUADRADOS E muchos de los experimetos que se realiza e Física, se obtiee u cojuto de parejas de úmeros (abscisa, ordeada) por los cuales ecesitamos, para obteer u modelo matemático que
1 Definición de derivada
 Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
EJERCICIOS RESUELTOS. t +
 BXX5744_07 /6/09 4: Págia 49 EJERCICIOS RESUELTOS Calcula la tasa de variació media de la fució f() = + e los itervalos [, 0] y [0, ], aalizado el resultado obteido y la relació co la fució. La fució f()
BXX5744_07 /6/09 4: Págia 49 EJERCICIOS RESUELTOS Calcula la tasa de variació media de la fució f() = + e los itervalos [, 0] y [0, ], aalizado el resultado obteido y la relació co la fució. La fució f()
Métodos Numéricos (SC 854) Ajuste a curvas. 2. Ajuste a un polinomio mediante mínimos cuadrados
 Métodos Numéricos SC 854 Auste a curvas c M Valezuela 007 008 7 de marzo de 008 1 Defiició del problema E el problema de auste a curvas se desea que dada ua tabla de valores i,f i ecotrar ua curva que
Métodos Numéricos SC 854 Auste a curvas c M Valezuela 007 008 7 de marzo de 008 1 Defiició del problema E el problema de auste a curvas se desea que dada ua tabla de valores i,f i ecotrar ua curva que
Unidad 1: Las Ecuaciones Diferenciales y Sus Soluciones
 Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)
![Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a) Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)](/thumbs/19/223892.jpg) Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Cálculo II (0252) TEMA 6 SERIES DE POTENCIAS. Semestre
 Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
TEMA 2 CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE
 TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles 10 de agosto del Solucionario
 SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
Cód. Carrera: Área de Matemática Fecha: MODELO DE RESPUESTAS Objetivos 1 al 11.
 rueba Itegral Lapso 03-7-76-77 /0 Uiversidad Nacioal Abierta Matemática I (Cód. 7-76-77) icerrectorado Académico Cód. Carrera: 6-36-80-08- -60-6-6-63 Fecha: 0 0-0 MODELO DE RESUESTAS Objetivos al. OBJ
rueba Itegral Lapso 03-7-76-77 /0 Uiversidad Nacioal Abierta Matemática I (Cód. 7-76-77) icerrectorado Académico Cód. Carrera: 6-36-80-08- -60-6-6-63 Fecha: 0 0-0 MODELO DE RESUESTAS Objetivos al. OBJ
OBJETIVOS. Objetivos Generales. Objetivos Específicos. Profesora: María Martel Escobar. Una función f es creciente (estrictamente) si x, y Dom(f), con
 Curso -3 OBJETIVOS Objetivos Geerales Itroducir el cálculo de fucioes de ua variable como fudameto del aálisis ecoómico margial y los problemas de optimizació. Matemáticas Empresariales Doble Grado e ADE
Curso -3 OBJETIVOS Objetivos Geerales Itroducir el cálculo de fucioes de ua variable como fudameto del aálisis ecoómico margial y los problemas de optimizació. Matemáticas Empresariales Doble Grado e ADE
IES Fco Ayala de Granada Soluciones Germán-Jesús Rubio Luna INTERVALOS DE CONFIANZA PARA PROPORCIONES (2007)
 IS Fco Ayala de Graada Solucioes Germá-Jesús Rubio Lua INTRVALOS D CONFIANZA PARA PROPORCIONS (007) jercicio 1- Tomada, al azar, ua muestra de 10 estudiates de ua Uiversidad, se ecotró que 54 de ellos
IS Fco Ayala de Graada Solucioes Germá-Jesús Rubio Lua INTRVALOS D CONFIANZA PARA PROPORCIONS (007) jercicio 1- Tomada, al azar, ua muestra de 10 estudiates de ua Uiversidad, se ecotró que 54 de ellos
TRABAJO DE GRUPO Series de potencias
 DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
CAPÍTULO VIII. CONVERGENCIA DE SUCESIONES. SECCIONES A. Criterios de convergencia. B. Ejercicios propuestos.
 CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
CAPÍTULO VIII CONVERGENCIA DE SUCESIONES SECCIONES A Criterios de covergecia B Ejercicios propuestos 347 A CRITERIOS DE CONVERGENCIA Ua fució cuyo domiio es el cojuto de los úmeros aturales se dice sucesió
TEMA 26 DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS. APLICACIONES.
 Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
4. Con b = ( 1) 1 n. 6. Con c = n = p = 1, 1, ( 1) 1 2, ( 1) 1 3, ( 1) 1 4, ( 1) 1 5, ( 1) , 1 3, 1 2, 1 6 6, 5, 1.
 Respuestas Respuestas al desarrollo de la competecia del capítulo E los problemas del al, ecuetra los primeros 6 térmios de la sucesió dada. Verifica tus respuestas co el comado Secuecia[ , ,
Respuestas Respuestas al desarrollo de la competecia del capítulo E los problemas del al, ecuetra los primeros 6 térmios de la sucesió dada. Verifica tus respuestas co el comado Secuecia[ , ,
INSTRUCCIONES PARA LA REALIZACIÓN DE ESTE EXAMEN
 Uiversidad de Las Palmas de Gra Caaria ETSIT CÁLCULO - 09004-9 horas CONVOCATORIA ORDINARIA Profesores A Plaza y K Sadaragai Colocar el DNI e lugar visible El exame se divide e dos partes de hora 30 miutos,
Uiversidad de Las Palmas de Gra Caaria ETSIT CÁLCULO - 09004-9 horas CONVOCATORIA ORDINARIA Profesores A Plaza y K Sadaragai Colocar el DNI e lugar visible El exame se divide e dos partes de hora 30 miutos,
ACTIVIDADES NO PRESENCIALES
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
Aproximar numéricamente la derivada de una función a partir de valores conocidos de la función. f a h f a f a h R
 PÁCTICA APOXIMACIÓN DE LA DEIVADA Prácticas Matlab Práctica 5: Aproximació de la derivada Objetivos Aproximar uméricamete la derivada de ua fució a partir de valores coocidos de la fució. Comados de Matlab
PÁCTICA APOXIMACIÓN DE LA DEIVADA Prácticas Matlab Práctica 5: Aproximació de la derivada Objetivos Aproximar uméricamete la derivada de ua fució a partir de valores coocidos de la fució. Comados de Matlab
1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE
 1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE 1. Cocepto de límite 1.1 Defiició de etoro o vecidad: Si a es u úmero real (supógase que a está e el eje X), etoces, u etoro o vecidad de a de radio es u itervalo
1. INTRODUCCIÓN AL CONCEPTO DE LÍMITE 1. Cocepto de límite 1.1 Defiició de etoro o vecidad: Si a es u úmero real (supógase que a está e el eje X), etoces, u etoro o vecidad de a de radio es u itervalo
Hoja de Problemas Tema 3. (Sucesiones y series)
 Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
8 Derivadas. Página 239. Página 247. Función derivada
 8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
Tema 7 (IV). Aplicaciones de las derivadas (2). Representación gráfica de curvas y fórmula de Taylor
 Tema 7 (IV) Aplicacioes de las derivadas () Represetació gráfica de curvas y fórmula de Taylor Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos
Tema 7 (IV) Aplicacioes de las derivadas () Represetació gráfica de curvas y fórmula de Taylor Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos
LIMITES DE FUNCIONES. Ejemplo: Sea la función F(x) = 3X 2, evalúe la función para valores de X cercanos a 2, es decir
 PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
Tema 8 Límite de Funciones. Continuidad
 Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS SERIES DE POTENCIAS
 UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asigatura : Cálculo Numérico, MAT-23. Profesor : Emilio Cariaga L. Periodo : er. Semestre 205. SERIES DE POTENCIAS
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asigatura : Cálculo Numérico, MAT-23. Profesor : Emilio Cariaga L. Periodo : er. Semestre 205. SERIES DE POTENCIAS
x 4 1 x 2 T2)a) Analice si alguna de las siguientes integrales es impropia. Justifique. Si encuentra alguna que lo sea, resuélvala:
 Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 22 de Mayo 2013 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
Material del que dispone:
 Prueba experimetal. El vuelo del capacillo Cuado u cuerpo se mueve e el seo de u fluido co velocidad v, su movimieto se ve freado por ua fuerza, llamada de resistecia. Supogamos que esta fuerza depede
Prueba experimetal. El vuelo del capacillo Cuado u cuerpo se mueve e el seo de u fluido co velocidad v, su movimieto se ve freado por ua fuerza, llamada de resistecia. Supogamos que esta fuerza depede
DERIVADA DE FUNCIONES DEL TIPO f ( x) c, donde c es una constante, la derivada de esta función es siempre cero, es decir:
 DERIVADA DE FUNCIONES DEL TIPO f ( ) c Coceptos clave: 1. Derivada de la fució costate f ( ) c, dode c es ua costate, la derivada de esta fució es siempre cero, es decir: f '( ) 0 c. Derivada de ua fució
DERIVADA DE FUNCIONES DEL TIPO f ( ) c Coceptos clave: 1. Derivada de la fució costate f ( ) c, dode c es ua costate, la derivada de esta fució es siempre cero, es decir: f '( ) 0 c. Derivada de ua fució
Sucesiones de números reales
 Sucesioes de úmeros reales Sucesioes Ejercicio. Prueba que si x
Sucesioes de úmeros reales Sucesioes Ejercicio. Prueba que si x
Ejercicios Matemáticas I Pendientes 1 BCT
 Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
1. Serie de Potencias
 . Serie de Potecias Recordemos que dada ua sucesió {b } N, podemos defiir ua serie: E el caso particular e que b = a (x c) b la serie tedría la forma b = a (x c) y es llamada serie de potecias cetrada
. Serie de Potecias Recordemos que dada ua sucesió {b } N, podemos defiir ua serie: E el caso particular e que b = a (x c) b la serie tedría la forma b = a (x c) y es llamada serie de potecias cetrada
Por: Lic. Eleazar J. García. República Bolivariana de Venezuela Tinaco.- Estado Cojedes. INTEGRALES INDEFINIDAS
 Por: Lic. Eleazar J. García. República Bolivariaa de Veezuela Tiaco.- Estado Cojedes. INTEGRALES INDEFINIDAS Usted está familiarizado co alguas operacioes iversas. La adició y la sustracció so operacioes
Por: Lic. Eleazar J. García. República Bolivariaa de Veezuela Tiaco.- Estado Cojedes. INTEGRALES INDEFINIDAS Usted está familiarizado co alguas operacioes iversas. La adició y la sustracció so operacioes
1. Sucesiones y series numéricas
 ITINFORMÁTICA GESTIÓN BOLETÍN DE PROBLEMAS CÁLCULO INFINITESIMAL CURSO 00- Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3, 3 4, 3 4 5, c),,
ITINFORMÁTICA GESTIÓN BOLETÍN DE PROBLEMAS CÁLCULO INFINITESIMAL CURSO 00- Sucesioes y series uméricas Escribir ua expresió para el -ésimo térmio de la sucesió: +, + 3 4, + 7 8, + 5 6, 3, 3 4, 3 4 5, c),,
INTERÉS SIMPLE COMO FUNCIÓN LINEAL.
 INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
INTERÉS SIMPLE COMO FUNCIÓN LINEAL. EJERCICIOS PROPUESTOS. 1.- Grafica las fucioes Moto e Iterés: a) C = + 0, co C e miles de pesos ; : meses y R. Para graficar estar fucioes, debemos dar valores a, por
CALCULO DIFERENCIAL E INTEGRAL II
 CALCULO DIFERENCIAL E INTEGRAL II TEMA 5 (Última modificació 8-7-015) TEOREMA DEL VALOR MEDIO TEOREMA DEL VALOR MEDIO O DE LAGRANGE O DE LOS INCREMENTOS FINITOS PARA FUNCIONES DE UNA VARIABLE INDEPENDIENTE.
CALCULO DIFERENCIAL E INTEGRAL II TEMA 5 (Última modificació 8-7-015) TEOREMA DEL VALOR MEDIO TEOREMA DEL VALOR MEDIO O DE LAGRANGE O DE LOS INCREMENTOS FINITOS PARA FUNCIONES DE UNA VARIABLE INDEPENDIENTE.
Universidad Nacional Autónoma de Honduras Facultad de Ciencias Económicas Guía de Ejercicios No. 2 DET 385, Métodos Cuantitativos III
 .: Derivadas de orde superior: Elaborada por: Wilfredo Saravia M. Uiversidad Nacioal Autóoma de Hoduras Facultad de Ciecias Ecoómicas Guía de Ejercicios No. DET 85, Métodos Cuatitativos III E los ejercicios
.: Derivadas de orde superior: Elaborada por: Wilfredo Saravia M. Uiversidad Nacioal Autóoma de Hoduras Facultad de Ciecias Ecoómicas Guía de Ejercicios No. DET 85, Métodos Cuatitativos III E los ejercicios
Listado para la Evaluación 2 Cálculo II (527148)
 Uiversidad de Cocepció Facultad de Ciecias Físicas y Matemáticas Departameto de Matemática Área, Volume y Logitud de arco. Listado para la Evaluació Cálculo II (5748). Calcular el área ecerrada por la
Uiversidad de Cocepció Facultad de Ciecias Físicas y Matemáticas Departameto de Matemática Área, Volume y Logitud de arco. Listado para la Evaluació Cálculo II (5748). Calcular el área ecerrada por la
una sucesión de funciones de A. Formemos una nueva sucesión de funciones {S n } n=1 de A de la forma siguiente:
 Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
METODO DE ITERACION DE NEWTON
 METODO DE ITERACION DE NEWTON Supogamos que queremos resolver la ecuació f( ) y lo que obteemos o es la solució eacta sio sólo ua buea aproimació, para obteer esta aproimació observemos la siguiete figura
METODO DE ITERACION DE NEWTON Supogamos que queremos resolver la ecuació f( ) y lo que obteemos o es la solució eacta sio sólo ua buea aproimació, para obteer esta aproimació observemos la siguiete figura
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL 1 FUNCIONES DE VARIAS VARIABLES.
 FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
FUNCIONES DE VARIAS VARIABLES: DOMINIO, RANGO, CURVAS DE NIVEL FUNCIONES DE VARIAS VARIABLES. DEFINICIONES DE FUNCIONES EN VARIAS VARIABLES. Ua fució de variable es u cojuto de pares ordeados de la forma
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Objetivo: Concepto de Límite
 --0 Sesió Coteidos: Cocepto ituitivo de límite. > Coceptos básicos propiedades de alguos límites. > Cálculo de límite de alguas fucioes. Objetivo: Determia límite de fucioes, sólo por reemplazo. Determia
--0 Sesió Coteidos: Cocepto ituitivo de límite. > Coceptos básicos propiedades de alguos límites. > Cálculo de límite de alguas fucioes. Objetivo: Determia límite de fucioes, sólo por reemplazo. Determia
Prácticas de Matemáticas I y Matemáticas II con DERIVE 136
 Prácticas de Matemáticas I y Matemáticas II co DERIVE 6. DIGONLIZCIÓN... PRINCIPLES FUNCIONES DE DERIVE PR L DIGONLIZCION: CLCULO DE UTOVLORES Y UTOVECTORES. tes de iiciar el estudio de los pricipales
Prácticas de Matemáticas I y Matemáticas II co DERIVE 6. DIGONLIZCIÓN... PRINCIPLES FUNCIONES DE DERIVE PR L DIGONLIZCION: CLCULO DE UTOVLORES Y UTOVECTORES. tes de iiciar el estudio de los pricipales
ORGANIZACIÓN DE LOS DATOS.
 ORGANIZACIÓN DE LOS DATOS. La toma de datos es ua de las partes de mayor importacia e el desarrollo de ua ivestigació. Así los datos obteidos mediate u primer proceso recibe el ombre de datos si tratar
ORGANIZACIÓN DE LOS DATOS. La toma de datos es ua de las partes de mayor importacia e el desarrollo de ua ivestigació. Así los datos obteidos mediate u primer proceso recibe el ombre de datos si tratar
Tema II: Interpolación. Polinomios de Lagrange Diferencias Divididas Interpolación Lineal
 Poliomios de Lagrage Dierecias Divididas Iterpolació Lieal Deiició: es el cálculo de valores para ua ució tabulada, e putos que o se tiee Posició X =?? 4 7 78 48 8 Tiempo Supogamos la cúbica de la siguiete
Poliomios de Lagrage Dierecias Divididas Iterpolació Lieal Deiició: es el cálculo de valores para ua ució tabulada, e putos que o se tiee Posició X =?? 4 7 78 48 8 Tiempo Supogamos la cúbica de la siguiete
Tema 2. Medidas descriptivas de los datos
 Tema 2. Medidas descriptivas de los datos Resume del tema 2.1. Medidas de posició So valores que os sirve para idicar la posició alrededor de la cual se distribuye las observacioes. 2.1.1. Mediaa La mediaa
Tema 2. Medidas descriptivas de los datos Resume del tema 2.1. Medidas de posició So valores que os sirve para idicar la posició alrededor de la cual se distribuye las observacioes. 2.1.1. Mediaa La mediaa
Preguntas de examen. Apéndice A. A.1 Abril de 2008 (Examen parcial) Preguntas de test (30%) Teoría (10 %)
 Apédice A Pregutas de exame A. Abril de 2008 (Exame parcial) Pregutas de test (30%) A. Se cosidera las sucesioes ( ) a b. Etoces: (a) Si b coverge, etoces a tambié coverge y sus límites coicide. (b) Si
Apédice A Pregutas de exame A. Abril de 2008 (Exame parcial) Pregutas de test (30%) A. Se cosidera las sucesioes ( ) a b. Etoces: (a) Si b coverge, etoces a tambié coverge y sus límites coicide. (b) Si
Desigualdad entre las medias Aritmética y Geométrica
 Desigualdad etre las medias Aritmética y Geométrica Jorge Tipe Villaueva Dados reales positivos a 1, a,..., a, defiimos la media aritmética de a 1, a,..., a como el úmero a 1 + a +... + a y la media geométrica
Desigualdad etre las medias Aritmética y Geométrica Jorge Tipe Villaueva Dados reales positivos a 1, a,..., a, defiimos la media aritmética de a 1, a,..., a como el úmero a 1 + a +... + a y la media geométrica
Unidad 10: LÍMITES DE FUNCIONES
 Uidad 1: LÍMITES DE FUNCIONES LÍMITES 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Ua sucesió de úmeros reales es u cojuto ordeado de iiitos úmeros reales. Los úmeros reales a1, a,..., a,... se llama térmios,
Uidad 1: LÍMITES DE FUNCIONES LÍMITES 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Ua sucesió de úmeros reales es u cojuto ordeado de iiitos úmeros reales. Los úmeros reales a1, a,..., a,... se llama térmios,
Series Numéricas. Una forma de definir e es a través de la suma: 1. 1 0! + 1 1! + 1 2! + 1 3! + 1 4! + + 1 n. cuyo límite es e, es decir:
 Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
Capítulo Series Numéricas Las series uméricas so sucesioes muy particulares ya que se defie (o se geera) a partir de otra sucesió. Dos ejemplos secillos aparece e la defiició de e y el la Paradoja de Zeó.
R. Urbán Introducción a los métodos cuantitativos. Notas de clase Sucesiones y series.
 R. Urbá Itroducció a los métodos cuatitativos. Notas de clase Sucesioes y series. SUCESIONES. Ua sucesió es u cojuto umerable de elemetos, dispuestos e u orde defiido y que guarda ua determiada ley de
R. Urbá Itroducció a los métodos cuatitativos. Notas de clase Sucesioes y series. SUCESIONES. Ua sucesió es u cojuto umerable de elemetos, dispuestos e u orde defiido y que guarda ua determiada ley de
SESIÓN 8 DESCRIPCIONES DE UNA RELACIÓN
 SESIÓN 8 DESCRIPCIONES DE UNA RELACIÓN I. CONTENIDOS: 1. Regresió lieal simple.. Iterpretació de gráficas de regresió. 3. Cálculo de coeficiete de correlació. 4. Iterpretació del coeficiete de correlació.
SESIÓN 8 DESCRIPCIONES DE UNA RELACIÓN I. CONTENIDOS: 1. Regresió lieal simple.. Iterpretació de gráficas de regresió. 3. Cálculo de coeficiete de correlació. 4. Iterpretació del coeficiete de correlació.
CÁLCULO Ejercicios Resueltos Semana 1 30 Julio al 3 Agosto 2007
 CÁLCULO Ejercicios Resueltos Semaa 0 Julio al Agosto 007 Ejercicios Resueltos. Estime el área ecerrada por la curva de ecuació y, el eje X y, para ello, divida el itervalo [0,] e cico partes iguales, y
CÁLCULO Ejercicios Resueltos Semaa 0 Julio al Agosto 007 Ejercicios Resueltos. Estime el área ecerrada por la curva de ecuació y, el eje X y, para ello, divida el itervalo [0,] e cico partes iguales, y
Cálculo de límites Criterio de Stolz. Tema 8
 Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Tema 8 Cálculo de límites El presete tema tiee u iterés emietemete práctico, pues vamos a estudiar alguos métodos cocretos para resolver idetermiacioes. Etre ellos destaca el criterio de Stolz, del que
Problemas de cálculo
 Problemas Estimació estadística Vicete Mazao-Arrodo, 2012,2013 Problemas de cálculo Ejercicio 1 resuelto Observamos e mometos al azar e ua cocurrida calle de la ciudad. Nos iteresa registrar cuátas persoas
Problemas Estimació estadística Vicete Mazao-Arrodo, 2012,2013 Problemas de cálculo Ejercicio 1 resuelto Observamos e mometos al azar e ua cocurrida calle de la ciudad. Nos iteresa registrar cuátas persoas
a n = Ejemplo: Representa las gráficas de las funciones f(x) = 1/x, g(x) = x 2 y h(x) =
 TEMA 9: LÍMITE Y CONTINUIDAD DE UNA FUNCIÓN. 9. Cocepto de límite lateral. Límite. 9. Operacioes co fucioes covergetes. 9.3 Cálculo de límites. 9.4 Cotiuidad de ua fució. 9.5 Asítotas: Verticales, horizotales
TEMA 9: LÍMITE Y CONTINUIDAD DE UNA FUNCIÓN. 9. Cocepto de límite lateral. Límite. 9. Operacioes co fucioes covergetes. 9.3 Cálculo de límites. 9.4 Cotiuidad de ua fució. 9.5 Asítotas: Verticales, horizotales
5. Aproximación de funciones: polinomios de Taylor y teorema de Taylor.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
Tema 5. APLICACIONES DE LAS DERIVADAS: REPRESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR
 Tema. ALICACIONES DE LAS DERIVADAS: RERESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos de crecimieto
Tema. ALICACIONES DE LAS DERIVADAS: RERESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos de crecimieto
Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 138
 Prácticas de Matemáticas I y Matemáticas II co DERIVE-5 8. DIGONLIZCIÓN... PRINCIPLES FUNCIONES DE DERIVE PR L DIGONLIZCION: CLCULO DE UTOVLORES Y UTOVECTORES. tes de iiciar el estudio de los pricipales
Prácticas de Matemáticas I y Matemáticas II co DERIVE-5 8. DIGONLIZCIÓN... PRINCIPLES FUNCIONES DE DERIVE PR L DIGONLIZCION: CLCULO DE UTOVLORES Y UTOVECTORES. tes de iiciar el estudio de los pricipales
DESIGUALDADES CLÁSICAS
 DESIGUALDADES CLÁSICAS PARA EL SEMINARIO DE PROBLEMAS (CURSO 017/018) ALBERTO ARENAS 1 Desigualdades etre medias La estrategia más geeral para probar desigualdades es trasformar la desigualdad a la que
DESIGUALDADES CLÁSICAS PARA EL SEMINARIO DE PROBLEMAS (CURSO 017/018) ALBERTO ARENAS 1 Desigualdades etre medias La estrategia más geeral para probar desigualdades es trasformar la desigualdad a la que
Universidad Simón Bolıvar. Departamento de Matemáticas puras y aplicadas. Autoevaluación No. 1 MA2115 Enero 2009
 Uiversidad Simó Bolıvar. Departameto de Matemáticas puras y aplicadas. Autoevaluació No. MA25 Eero 2009 I. Evaluació Teórica.. Diga la defiició de ua sucesió covergete, la defiició de ua sucesió divergete
Uiversidad Simó Bolıvar. Departameto de Matemáticas puras y aplicadas. Autoevaluació No. MA25 Eero 2009 I. Evaluació Teórica.. Diga la defiició de ua sucesió covergete, la defiició de ua sucesió divergete
Problema 34. Evaluar lim(2x. Solución: Problema 35. Calcular lim. lim x x. Solución: Problema 36. Determinar lim. lim 5 4(2)
 Si la fució f es u poliomio o ua fució racioal y a perteece al domiio de f, etoces f ( ) f( a) siempre que el valor del deomiador para a o sea cero, e el a caso de ua fució racioal Problema. Evaluar (
Si la fució f es u poliomio o ua fució racioal y a perteece al domiio de f, etoces f ( ) f( a) siempre que el valor del deomiador para a o sea cero, e el a caso de ua fució racioal Problema. Evaluar (
Marco Teórico n = i = 2. Deducción: Si la serie se suma dos veces de la siguiente forma:
 Uiversidad de Sa Carlos de Guatemala Teoría de Cojutos Estudiate: Roald Oliverio Chubay Gallia -6 de mayo 0- Marco Teórico Para el presete texto se deduce alguas expresioes y luego se demuestra, para otras
Uiversidad de Sa Carlos de Guatemala Teoría de Cojutos Estudiate: Roald Oliverio Chubay Gallia -6 de mayo 0- Marco Teórico Para el presete texto se deduce alguas expresioes y luego se demuestra, para otras
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES
 RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
