APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
|
|
|
- José Manuel Roldán Rivas
- hace 7 años
- Vistas:
Transcripción
1 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos Máimos y mínimos locales. Puntos críticos Monotonía y concavidad. Más asíntotas horizontales, verticales y oblícuas Trazado de curvas. Máimos y mínimos absolutos. Problemas de optimización Ejercicios a resolver en la práctica 5 1. Dada la unción deinida por ( ) +. Determina y clasiica los puntos o valores críticos.. Dada la unción deinida por ( ) arctan( ). Indica el dominio, los puntos críticos, los intervalos en los cuales la unción dada crece o decrece, indica, si eisten, los valores etremos locales, estudia la concavidad de la gráica, e indica, si eisten, los puntos de inleión.. Esboza la gráica de la unción deinida por ( ) ( + 1) 4. Sea una unción continua tal que la gráica de la unción es la siguiente:
2 a) En cuáles intervalos es la unción creciente y en cuáles es decreciente? Justiica tu respuesta. b) Indica, si eisten, los etremos locales. c) En cuáles intervalos la gráica de es cóncava hacia arriba y en cuáles es cóncava hacia abajo? Justiica tu respuesta. d) Indica, si eisten, los puntos de inleión. 5. Sea ( ) a + b + c+ d. Halla los valores de a, b, c y d para los que la unción tenga un máimo local en 1, y un mínimo local 1 en Dada si ( ) si 4 - < 0 0< < a) Indica el dominio el dominio de la unción b) Halla, si eisten, las asíntotas horizontales y verticales de la gráica de la unción. c) Indica los intervalos de crecimiento y decrecimiento. d) Indica, si eisten, los valores etremos locales. e) Determina los intervalos donde la gráica de la unción es creciente y donde es decreciente. ) Has un bosquejo de la gráica.
3 7. Halla el máimo absoluto y el mínimo absoluto de la unción deinida por ( ) + 1 en el intervalo [ 1, ]. 8. Una caja con base cuadrada y parte superior abierta debe tener un volumen de 000 cm. Determina las dimensiones de la caja que minimicen la cantidad de material usado. 9. a) Si ( ), calcula () y () para todo número real, y demuestra que (0) no eiste. b) Estudia los intervalos de crecimiento y decrecimiento de la unción '. c) Estudia la concavidad de la gráica de la unción de la unción ', y determina si eisten puntos de inleión. d) Graica las unciones, y y veriica los resultados obtenidos en a), b), c) y d). ()
4 Releiona Qué es un punto o valor crítico? Qué pasos debes seguir para hallar los puntos o valores críticos de una unción? b ' > Qué característica se puede deducir de una unción en el intervalo ( a, ) si ( ) 0 para toda ( a, b)? Qué característica se puede deducir de una unción en el intervalo ( a, b) si '( ) < 0 para toda ( a, b)? Qué pasos debes seguir para determinar los intervalos en los cuales una unción es creciente? Qué pasos debes seguir para determinar los intervalos en los cuales una unción es decreciente? Qué es un máimo local? Qué es un mínimo local? Si Dom ' > para toda ( a, 0 ) y '( ) < 0 para toda ( 0, b), 0 y además ( ) 0 qué puedes airmar con respecto a ( 0 )? Si 0 Dom y además '( ) < 0 qué puedes airmar con respecto a ( 0 )? para toda ( ) y '( ) > 0 para toda (, b) a, 0 Qué pasos debes seguir para determinar los máimos locales de una unción? Qué pasos debes seguir para determinar los mínimos locales de una unción?, Qué característica se puede deducir de la gráica de una unción en el intervalo ( a, b) si ''( ) > 0 para toda ( a, b)? Qué característica se puede deducir de la gráica de una unción en el intervalo ( a, b) si ''( ) < 0 para toda ( a, b)? Qué pasos debes seguir para determinar los intervalos en que la gráica de una unción es cóncava hacia arriba? Qué pasos debes seguir para determinar los intervalos en que la gráica de una unción es cóncava hacia abajo? Qué es un punto de inleión? Si Dom '' > para toda ( a, 0 ) y ''( ) < 0 para toda 0 y además ( ) 0 ( 0 b), qué puedes airmar con respecto al punto ( 0, ( 0) )? 0 Dom y además ''( ) < 0 para toda ( a, 0 ) y ''( ) > 0 ( b), qué puedes airmar con respecto al punto ( ( ))?, Si para toda 0, 0, 0 Qué pasos debes seguir para determinar los puntos de inleión de la gráica de una unción? 0 4
5 Ejercicios propuestos 1. Para cada una de las unciones que se deinen a continuación determina el dominio, los valores críticos, los intervalos en los cuales la unción dada crece o decrece, los valores etremos locales, discute la concavidad de la gráica, e indica, si eisten, los puntos de inleión. a) ( ) + sen b) ( ) + arctan( ) c) ( ) ( )5 d) 4 ( ) 1. Para cada una de las unciones que se deinen a continuación: i) Indica el dominio. ii) Halla, si eisten, los cortes con los ejes. iii) Determina las ecuaciones de las asíntotas horizontales y verticales de la gráica de. iv) Estudia los intervalos de crecimiento y decrecimiento. v) Determina, si eisten, los valores etremos locales vi) Estudia la concavidad. vii) Indica, si eisten, puntos de inleión viii) Graica la unción dada. a) d) ( ) b) 4 ( ) + e) 1 ( ) + c) ( ) + 4+ ( ) ) 1+ + ( ) 9 4. Sea una unción continua tal que ( 1) 5 y ( ) 4, si la gráica de la unción es la siguiente: 5
6 a) En cuáles intervalos es la unción creciente y en cuáles es decreciente? Justiica tu respuesta. b) Indica los etremos locales. Releiona Qué es el valor máimo absoluto de una unción? Qué es el valor mínimo absoluto de una unción? En cuáles puntos o valores del dominio puede alcanzar una unción su máimo o mínimo absoluto? Toda unción alcanza el máimo o mínimo absoluto en algún punto de su dominio? Qué puedes airmar acerca de los valores etremos absolutos de una unción continua deinida en un intervalo cerrado y acotado? Qué pasos debes seguir para hallar los valores etremos absolutos de una unción continua en un intervalo cerrado y acotado? 4. Para cada una de las unciones que se deinen a continuación: halla el máimo y mínimo absoluto de cada una de las unciones en el intervalo indicado. a) g( ) cos en π π, 4 b) 4 1 en [ 1,1] ( ) en 1, 1 d) c) ( ) arcsen( ) + ( ) + 5 g en [ 6,8] 5. Una empresa constructora está diseñando una zona de descanso para automovilistas al lado de una carretera principal. La zona será rectangular, tendrá m de área y estará cercada por los tres lados no adyacentes a la carretera. Cuál es la menor cantidad de metros de cerca necesaria para realizar el trabajo? 6. Halla la distancia del punto (, 0) a la gráica de la unción deinida por ( ). 7. Halla las dimensiones de un rectángulo de área 64cm para que la distancia de un vértice al punto medio de uno de sus lados no adyacentes sea mínima. 6
7 . Halla a y b si (, ) 8. Sea una unción deinida por ( ) a + b inleión de la gráica de. es un punto de 9. Sea una unción impar de dominio R { 1,1} tal que, es continua en su dominio, ( 0) 0, lim ( ), lim ( ), lim ( ) 1, es decreciente en ( 0,1), la gráica de es 1 ( 1) cóncava hacia abajo en (, 0) a) lim ( ) + 1 b) lim ( ) c) La recta de ecuación y 1 es una asíntota horizontal. d) lim ( ) 1 e) La gráica de es cóncava hacia arriba en ( 0, + ) ) es creciente en ( 1, 0),. Cuáles de las airmaciones siguientes son verdaderas? 7
8 Respuestas de los ejercicios propuestos 1) a) Dom R ; puntos críticos: ( 1+ k) π k Z los intervalos de la orma ( k π,( k+ 1) π) con Z (( k + 1) π,( k+ ) π) con Z b) Dom R ; punto crítico: 0 k. Puntos de inleión: kπ, k Z hacia abajo en ( 0, + ) y es cóncava hacia arriba en (, 0) ; (,) c) Dom R ; punto crítico: ; es creciente en(, ) máimo local. La gráica de es cóncava hacia arriba en todo su dominio. d) Dom [ 1,1] ; puntos críticos: 1 1 creciente en, ; ; es creciente en R. La gráica es cóncava hacia abajo en k y es cóncava hacia arriba en los intervalos de la orma ; es decreciente en R; no tiene valores etremos locales. La gráica es cóncava 1 1 y 0 es un punto de inleión. y es decreciente en (, + ) 1 1 ; es decreciente en 1, y en ; ( ) es un 1,1 y es 1 1 es un máimo local y es un mínimo local. La gráica 1, 0,1 0, 0 es un punto de inleión. de es cóncava hacia arriba en ( ) y cóncava hacia abajo en ( 0 ) ; ( ) ) a) i) R {, } ii) ( 0, 0) iii) Verticales: y y 1 iv) la unción es creciente en (, ) y en (, 0) en( 0, ) y en (, + ) v) ( 0) 0 locales vi) La gráica es cóncava hacia arriba en (, ) y en (, + ) es cóncava hacia abajo en (, ). Horizontal: y es decreciente es un máimo local. No tiene mínimos y vii) La gráica no tiene puntos de inleión. b) i) R { } ii) (, 4), 0 5, 0 ii) Vertical: y + iv) La unción es creciente en (, ) y en (, + ) etremos locales vi) La gráica es cóncava hacia arriba en (, ) cóncava hacia abajo en (, + ) viii) 0, ( 5 ) y ( ) Oblícua: v) No tiene y es vii) La gráica no tiene puntos de inleión 8
9 c) i) ( ) (, + ) Verticales:, ii) No interseca a los ejes coordenados iii) y. Oblícuas: y y y iv) La unción es, y en (, ) y es decreciente en(, ) y creciente en ( ) en (, + ) v) ( ) 4 y ( ) 4 son máimos locales. No tiene mínimos locales vi) La gráica de es cóncava hacia abajo en (, ) y en (, + ) vii) La gráica no tiene puntos de inleión R ii) (, 0) d) i) { 0} iii) Vertical: 0. Horizontales: no tiene Oblícuas: No tiene iv) La unción es creciente en (, + ) (, 0) y ( 0,1) v) ( 1) 1 y es decreciente es un mínimo local. No tiene máimos locales vi) La gráica de es cóncava hacia arriba en (, ) cóncava hacia abajo en(, 0) vii) Punto de inleión: (, 0) y en (, + ) 0 y e) i) R ii) ( 0, ) y ( 1, 0) iii) Verticales: no tiene Horizontal: La unción es creciente en ( 1,1) y es decreciente (, 1) y en (, + ) y iv) 1 v) ( 1) 4 es un máimo local y ( 1) 0 es un mínimo local vi) La gráica de es cóncava hacia arriba en (, 0) y en (, + ) en(, ) y en (, ) y (, + ) 0 vii) Puntos de inleión: (, ) y cóncava hacia abajo 0, (, ) 1 ii) 0, iii) Vertical:. Horizontal: y 0 iv) es creciente en (, ) en (, ) y en (, + ) v) No tiene valores etremos locales vi) La gráica de es cóncava hacia arriba en (, ) y en(, ) y cóncava hacia abajo en(, + ) vii) No tiene puntos de inleión ) i) R {, } 9
10 ) a) Creciente en (, 1) y en (, + ) ; creciente en ( 1, ) ( ) 4. 4) a) Máimo absoluto ( π) g(0) 1 π g, mínimo absoluto g 1 b) máimo local : ( 1) 5 ; mínimo local: 1 1 b) Máimo absoluto, mínimo absoluto π c) Máimo absoluto ( 1), mínimo absoluto ( 0 ) 0 d) Máimo absoluto ( 6 ) 15 g, mínimo absoluto g ( 5 + ) ) 00m 6) 7 7) 4 y y 16 8) a 1 y b 9) a), c) y e) 10
11 Halla el error Como la unción es creciente en ( 1,1) es un mínimo local. es decreciente en(, 1) se tiene que 1 Como la gráica de la unción es cóncava hacia arriba en (, 0) abajo en (, ) se tiene que es un punto de inleión. y es cóncava hacia 1 Sea ( ) entonces como la gráica de la unción es cóncava hacia arriba en 1 ( 1, + ) y es cóncava hacia abajo en (,1) en 1 hay un punto de inleión. La unción seno tiene ininitos máimos y mínimos absolutos, que son π π + kπ, k Z y + kπ, k Z respectivamente. La gráica de una unción puede intersecar (cortar) las asíntotas verticales. La gráica de una unción no puede intersecar (cortar) una asíntota horizontal. Para resolver un problema de optimización es suiciente deinir la unción correspondiente y luego basta determinar los puntos o valores críticos. 11
12 Problemas Etras Parte única: 1 Halla los intervalos de crecimiento y de decrecimiento de la unción: ( ) ( + ) Estudia y representa la unción: ( ) Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: 4 Dada la unción: ( ) + 1 ( ) estudia sus aspectos más relevantes y represéntala gráicamente. 5 Estudia y representa la siguiente unción: ( ) 4 6 Estudia el crecimiento y el decrecimiento de la siguiente unción: ( ) Estudia y representa la unción: ( ) + 1 1
13 8 Representa gráicamente la siguiente unción, estudiando los aspectos que consideres más relevantes: ( ) + 9 Estudia y representa la unción: ( ) 1 10 Estudia dónde crece y dónde decrece la unción: ( ) Resuelva los siguientes problemas: a) Encuentre dos números que sumados den 100 y cuyo producto sea máimo. b) Muestre que de todos los rectángulos con un área dada, el cuadrado es que tiene menor perímetro. c) Encuentre el área del mayor rectángulo que se pueda inscribir en un semicírculo de radio r. d) Encuentre el punto de la parábola y más cercano al punto (1, 4). e) Un hombre está en A, a la orilla de un río recto de km de ancho, quiere llegar al punto D, 8 km más abajo en la otra orilla, lo más rápido posible. Podría remar en su km bote directamente al rente (B) y correr a D, o A B podría remar directamente a D, o podría remar a un punto C cualquiera entre B y D y luego correr. Si el C hombre puede remar a 6 km/hr y correr a 8 km/hr, hasta donde debe llegar en bote para llegar a D lo D más rápido posible? Asuma que la rapidez del agua es 0 km/hr. 8 km ) Un cilindro circular recto se inscribe en un cono de altura h y base de radio r. 1
14 Encuentre el volumen máimo posible de dicho cilindro. g) Los márgenes superior e inerior de un poster miden 6 cm y los márgenes laterales 4 cm cada uno. Si el área impresa debe ser de 84 cm, encuentre las dimensiones del poster de área mínima. 1 Considera la unción: () a) Estudia su crecimiento y halla sus máimos y mínimos. b) Estudia su curvatura y obtén sus puntos de inleión. 1 Halla los máimos, mínimos y puntos de inleión de la unción: () ( -) ( + 1) Di dónde es creciente, decreciente, cóncava y convea. 14 Un heladero ha comprobado que, a un precio de 50 céntimos de euro la unidad, vende una media de 00 helados diarios. Por cada céntimo que aumenta el precio, vende dos helados menos al día. Si el coste por unidad es de 40 céntimos, a qué precio de venta es máimo el beneicio diario que obtiene el heladero? Cual será ese beneicio? 15 Halla los intervalos de crecimiento y los máimos y mínimos de la unción: + ( ) 1 16 Estudia el crecimiento y la curvatura de la siguiente unción. Halla sus máimos, mínimos y puntos de inleión: 4 ( ) Una huerta tiene actualmente 4 árboles, que producen 600 rutos cada uno. Se calcula que, por cada árbol adicional plantado, la producción de cada árbol disminuye en 15 rutos. Cuál debe ser el número total de árboles que debe tener la huerta para que la producción sea máima? Cuál será esa producción? 14
15 18 Estudia los intervalos de crecimiento y los máimos y mínimos de la unción: 4 1 ( ) ( ) 19 Un depósito abierto de latón con base cuadrada y capacidad para litros, qué dimensiones debe tener para que su abricación sea lo más económica posible? Practica elaborada por la Pro: Aida Montezuma. Ampliada por Pro Antonio Di Teodoro (Basada en prácticas anteriores de la USB-Matemáticas), en Especial las prácticas de la Proa Diasparra Maikol. Formato doc->pd 15
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL
 EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
 REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
Aplicaciones de la derivada.
 Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de funciones. Extremos
 (Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
REPRESENTACIÓN GRÁFICA DE FUNCIONES
 REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Representación de funciones
 Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción,
Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción,
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días 5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg) . [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
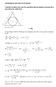 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN
 BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN Crecimiento y decrecimiento. Extremos absolutos y relativos. Concavidad y convexidad. Asíntotas.
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN Crecimiento y decrecimiento. Extremos absolutos y relativos. Concavidad y convexidad. Asíntotas.
Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PRÁCTICA DE LA SEMANA 2
 UNIVERSIDAD SIMÓN BOLÍVAR Trimestre: Ene-Mar DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-) Fecha de publicación: 3// Contenido para el parcial: I PRÁCTICA DE LA SEMANA Contenidos Sistemas
UNIVERSIDAD SIMÓN BOLÍVAR Trimestre: Ene-Mar DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-) Fecha de publicación: 3// Contenido para el parcial: I PRÁCTICA DE LA SEMANA Contenidos Sistemas
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas Función Derivada Función compuesta Derivada y f x y f x y f g x
 Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN
 TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y () en un intervalo Variación
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y () en un intervalo Variación
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
ANÁLISIS (Selectividad)
 ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
Rectas y Parábolas. Sistemas de coordenadas rectangulares (Plano Cartesiano)
 Rectas y Parábolas Prof. Gabriel Rivel Pizarro Sistemas de coordenadas rectangulares (Plano Cartesiano) El sistemas de coordenadas rectangulares se representa en un plano, mediante dos rectas perpendiculares.
Rectas y Parábolas Prof. Gabriel Rivel Pizarro Sistemas de coordenadas rectangulares (Plano Cartesiano) El sistemas de coordenadas rectangulares se representa en un plano, mediante dos rectas perpendiculares.
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
Ejercicios Resueltos de Derivadas y sus aplicaciones:
 Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
Las superficies serán: Tapa y superficie lateral S 1 = ( x 2 +4xy ) cm 2 Superficie de la base: S 2 = x 2 cm 2
 MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 29-OCTUBRE-1996. (1) 2x 3 > 4.
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1
 Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1 EJERCICIO : A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1 EJERCICIO : A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición
Apuntes de A. Cabañó. Matemáticas II REPRESENTACIÓN GRÁFICA DE FUNCIONES.
 REPRESENTACIÓN GRÁFICA DE FUNCIONES. TEORÍA - ESQUEMA A SEGUIR EN LA REPRESENTACIÓN DE FUNCIONES. Para dibujar la curva (C) de la unción :->y() se estudiará sucesivamente los siguientes puntos: * Dominio
REPRESENTACIÓN GRÁFICA DE FUNCIONES. TEORÍA - ESQUEMA A SEGUIR EN LA REPRESENTACIÓN DE FUNCIONES. Para dibujar la curva (C) de la unción :->y() se estudiará sucesivamente los siguientes puntos: * Dominio
Matemática I - Problemas de Máximos y Mínimos
 Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
APLICACIONES DE LAS DERIVADAS
 0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
Teorema de máximos y mínimos para funciones continuas:
 Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
1. f(x) = x3 1 x 2. 2. f(x) = x2 9 x 2 4. 3. f(x) = x 3 x + 2. x 3 (x 1) 2. 4. f(x) = 5. f(x) = x + 5 x 2 9. 6. f(x) = x2 3 x 2. x 2 3 x 2. 7.
 . f() =. f() = 9. f() =. f() = ( ). f() = 9 6. f() = 7. f() =. f() = 9. f() = p. f() =. f() =. f() = ( ). f() = 9. f() = ( ) . f() = Función racional con asíntota oblícua. Einamos los puntos que anulan
. f() =. f() = 9. f() =. f() = ( ). f() = 9 6. f() = 7. f() =. f() = 9. f() = p. f() =. f() =. f() = ( ). f() = 9. f() = ( ) . f() = Función racional con asíntota oblícua. Einamos los puntos que anulan
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
ANÁLISIS. d) No, se podrían haber considerado infinitas funciones diferenciadas en una constante.
 Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
PENDIENTES 2º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 2º ESO Curso 2013-2014
 014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
f(x) = xe para x -1 y x 0, MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio 1. (Reserva 1 Septiembre 2013 Opción A) Sea f la función definida por
 MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
{( ) ( ) ( ) ( )} 4. FUNCIONES. B y f es una función de A en B definida por y = x 2 1, = x + 3, encuentra 5 pares que pertenezcan a la
 4 FUNCIONES 4 Conceptos básicos Sean A y B dos conjuntos dados, una unción de A en B es una regla de correspondencia que asigna a cada elemento de A uno y solamente uno de B En una unción: A es el dominio
4 FUNCIONES 4 Conceptos básicos Sean A y B dos conjuntos dados, una unción de A en B es una regla de correspondencia que asigna a cada elemento de A uno y solamente uno de B En una unción: A es el dominio
SECUELA SUGERIDA PARA RESOLVER PROBLEMAS DE EXTREMOS
 (Apuntes en revisión para orientar el aprendizaje) SECUELA SUGERIDA PARA RESOLVER PROBLEMAS DE EXTREMOS - Leer cuidadosamente el enunciado para comprender la problemática presentada y ver qué se pretende
(Apuntes en revisión para orientar el aprendizaje) SECUELA SUGERIDA PARA RESOLVER PROBLEMAS DE EXTREMOS - Leer cuidadosamente el enunciado para comprender la problemática presentada y ver qué se pretende
PROBLEMAS DE RECTA TANGENTE. 6 en el punto de abscisa 2. Halla la ecuación de la recta tangente a. ( en el punto de abscisa. x 3x
 PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
4.2. Continuidad de una función en un punto. (A) Una función f es continua en un punto x=a, cuando se cumplen las siguientes condiciones:
 4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
EJERCICIOS RESUELTOS. x )
 BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
UNIDAD 5: FUNCIONES. CARACTERÍSTICAS
 I.E.S. Ramón Giraldo UNIDAD 5: FUNCIONES. CARACTERÍSTICAS. CONCEPTO DE FUNCIÓN Una unción real de variable real es una correspondencia de un conjunto D en el conjunto de los números reales, es decir, una
I.E.S. Ramón Giraldo UNIDAD 5: FUNCIONES. CARACTERÍSTICAS. CONCEPTO DE FUNCIÓN Una unción real de variable real es una correspondencia de un conjunto D en el conjunto de los números reales, es decir, una
APLICACIONES DE LAS DERIVADAS 2º Bachillerato
 APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
SOLUCIONES ( ) ( ) ( ) 2 ( ) ( ) Fecha: La pendiente de la recta es m = = x = 4. x = 2 2x. Ejercicio nº 1.- Solución: La recta será:
 Ejercicio nº.- Halla la ecuación de la recta tangente a la curva que sea paralela a la recta y. SOLUCIONES ' Fecha: La pendiente de la recta es m Cuando, y La recta será: Ejercicio nº.- y ( ) Averigua
Ejercicio nº.- Halla la ecuación de la recta tangente a la curva que sea paralela a la recta y. SOLUCIONES ' Fecha: La pendiente de la recta es m Cuando, y La recta será: Ejercicio nº.- y ( ) Averigua
Universidad de Buenos Aires. Instituto Libre de Segunda Enseñanza MATEMÁTICA GUÍA DE TRABAJOS PRÁCTICOS QUINTO AÑO
 Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA GUÍA DE TRABAJOS PRÁCTICOS QUINTO AÑO Se agradece el aporte de los proesores María Inés Sáinz y Daniel Dacunti TRABAJO PRÁCTICO
Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA GUÍA DE TRABAJOS PRÁCTICOS QUINTO AÑO Se agradece el aporte de los proesores María Inés Sáinz y Daniel Dacunti TRABAJO PRÁCTICO
x 0 1 0,5 0,3 0,1 0,1 f(x) 2 x 1 2 1,41421 1,23114 1,07177 0,93303
 Solucionario Derivada de una unción en un punto 0.0. Considera la unción (). Usa la calculadora para completar la siguiente tabla: 0 0,5 0, 0, 0, (),44,4,0777 0,90 Calcula la tasa de variación media en
Solucionario Derivada de una unción en un punto 0.0. Considera la unción (). Usa la calculadora para completar la siguiente tabla: 0 0,5 0, 0, 0, (),44,4,0777 0,90 Calcula la tasa de variación media en
en el intervalo - 1-cos(x) 2 si x > 0 sen(x)
 . [04] [ET-A] Sea la función f() = e -. Determinar sus intervalos de crecimiento y decrecimiento, etremos relativos, intervalos de concavidad y conveidad, puntos de infleión y asíntotas. Esbozar su gráfica..
. [04] [ET-A] Sea la función f() = e -. Determinar sus intervalos de crecimiento y decrecimiento, etremos relativos, intervalos de concavidad y conveidad, puntos de infleión y asíntotas. Esbozar su gráfica..
CARACTERÍSTICAS DE UNA FUNCIÓN
 . DOMINIO CARACTERÍSTICAS DE UNA FUNCIÓN inio de o campo de eistencia de es el conjunto de valores para los que está deinida la unción, es decir, el conjunto de valores que toma la variable independiente.
. DOMINIO CARACTERÍSTICAS DE UNA FUNCIÓN inio de o campo de eistencia de es el conjunto de valores para los que está deinida la unción, es decir, el conjunto de valores que toma la variable independiente.
, 0 ; Decrece: 0 2, 0 ; 0, 2. d f x x x x. a f x. b f x. Solucionario tema 9: Estudio de Funciones. Ejercicio 1. Ejercicio 2
 Solucionario tema 9: Estudio de Funciones Ejercicio Estudia la gráica siguiente: Dominio Recorrido 0, 4 Puntos de corte con los Ejes Con el Eje Y: 0, 4 Puntos máimos y mínimos: Máimo absoluto: 0, No hay
Solucionario tema 9: Estudio de Funciones Ejercicio Estudia la gráica siguiente: Dominio Recorrido 0, 4 Puntos de corte con los Ejes Con el Eje Y: 0, 4 Puntos máimos y mínimos: Máimo absoluto: 0, No hay
. Matemáticas aplicadas CCSS. Ejercicios modelo Selectividad 2000-2011
 1. CÁLCULO DE DERIVADAS Ejercicio 1. (001) Calcule las funciones derivadas de las siguientes: Lx a) (1 punto) f ( x) = (Lx indica logaritmo neperiano de x) x 3 b) (1 punto) g( x) = (1 x ) cos x 3 1 c)
1. CÁLCULO DE DERIVADAS Ejercicio 1. (001) Calcule las funciones derivadas de las siguientes: Lx a) (1 punto) f ( x) = (Lx indica logaritmo neperiano de x) x 3 b) (1 punto) g( x) = (1 x ) cos x 3 1 c)
Repaso general de matemáticas I. 2) 4 e indica el dominio e imagen de p. D x,,
 . Sea F( ) arcsen. Repaso general de matemáticas I π π a) Obtén la gráfica de h ( ) = F ( ) - e indica el dominio e imagen de h. D, ; I, π π b) Obtén la gráfica de g( ) F( ) e indica el dominio e imagen
. Sea F( ) arcsen. Repaso general de matemáticas I π π a) Obtén la gráfica de h ( ) = F ( ) - e indica el dominio e imagen de h. D, ; I, π π b) Obtén la gráfica de g( ) F( ) e indica el dominio e imagen
03 Ejercicios de Selectividad Continuidad y derivabilidad de funciones. Ejercicios propuestos en 2009
 0 Ejercicios de Selectividad Continuidad y derivabilidad de unciones Ejercicios propuestos en 009 1- [009-1-A-] a) [1 5] Halle las unciones derivadas de las unciones deinidas por las siguientes ln epresiones:
0 Ejercicios de Selectividad Continuidad y derivabilidad de unciones Ejercicios propuestos en 009 1- [009-1-A-] a) [1 5] Halle las unciones derivadas de las unciones deinidas por las siguientes ln epresiones:
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INTRODUCCIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 INTRODUCCIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES CONTENIDOS.- INTRODUCCIÓN....- EJEMPLO....- TASA DE VARIACIÓN... 4.- CONCEPTO DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y DE FUNCIÓN DERIVADA. DERIVADAS
INTRODUCCIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES CONTENIDOS.- INTRODUCCIÓN....- EJEMPLO....- TASA DE VARIACIÓN... 4.- CONCEPTO DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y DE FUNCIÓN DERIVADA. DERIVADAS
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
 FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
Máximo o mínimo de una función. Solución: El mínimo de una función se da en los puntos que anulan su derivada y tiene derivada segunda positiva.
 Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
EJERCICIOS. + 1 en el punto en que la abscisa es x = 2
 EJERCICIOS,.Calcular las ecuaciones de la tangente y de la normal a la parábola y en el punto en que la abscisa es Punto de tangencia,, ' Tangente... y y y y y Normal... y y y 8.- Calcular la ecuación
EJERCICIOS,.Calcular las ecuaciones de la tangente y de la normal a la parábola y en el punto en que la abscisa es Punto de tangencia,, ' Tangente... y y y y y Normal... y y y 8.- Calcular la ecuación
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA
 CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
TEMAS 10 LAS FUNCIONES ELEMENTALES 1º BACH MATE I
 TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
. (Nota: ln x denota el logaritmo neperiano de x).
 e - si 0. [04] [ET-A] Sea la función f() = k si = 0 a) Determine razonadamente el valor del parámetro k para que la función sea continua para todos los números reales. b) Estudie si esta función es derivable
e - si 0. [04] [ET-A] Sea la función f() = k si = 0 a) Determine razonadamente el valor del parámetro k para que la función sea continua para todos los números reales. b) Estudie si esta función es derivable
, siendo ln(1+x) el logaritmo neperiano de 1+x. x
 Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO
 EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
derivable en x = 0. b) Para los valores encontrados, calcula la ecuación de la recta tangente a la gráfica de f(x) en el punto de abscisa x = 0.
 . [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
. [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
PROBLEMAS DE REPASO. Solución: Si llamamos x e y a las longitudes de cada uno de los catetos, sabemos que: x 2 y 2 1 y 2 1 x 2 El volumen del cono es:
 PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
CÁLCULO DIFERENCIAL 9. UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS
 CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
( ) ( ( ) ( ) ) ( ( ) ( x) ( 2) ( ) ( ) ( )
 Modelo. Problema B.- Caliicación máima: puntos) La igura representa la gráica de una unción : [ 6; 5] R. Contéstese razonadamente a las preguntas planteadas.? a) Para qué valores de es > b) En qué puntos
Modelo. Problema B.- Caliicación máima: puntos) La igura representa la gráica de una unción : [ 6; 5] R. Contéstese razonadamente a las preguntas planteadas.? a) Para qué valores de es > b) En qué puntos
Tema 7. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización
 Tema 7 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Aplicaciones de la derivada primera para el estudio de la variación de una función El signo de la derivada primera
Tema 7 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Aplicaciones de la derivada primera para el estudio de la variación de una función El signo de la derivada primera
Aplicaciones de la derivada
 CAPÍTULO 8 Aplicaciones de la derivada 8. Máimos mínimos locales Si f. 0 / f./ para cada cerca de 0, es decir, en un intervalo abierto que contenga a 0, diremos que f alcanza un máimo local o un máimo
CAPÍTULO 8 Aplicaciones de la derivada 8. Máimos mínimos locales Si f. 0 / f./ para cada cerca de 0, es decir, en un intervalo abierto que contenga a 0, diremos que f alcanza un máimo local o un máimo
5 GUÍA PARA REALIZAR ESTUDIO DE FUNCIÓN
 5 GUÍA PARA REALIZAR ESTUDIO DE UNCIÓN ) Determinar el Dominio de la función. ) Hallar, si eisten, las Intersecciones con los Ejes de Coordenadas Signo. ( Int. con eje y, hacer = Int. con eje, hacer y
5 GUÍA PARA REALIZAR ESTUDIO DE UNCIÓN ) Determinar el Dominio de la función. ) Hallar, si eisten, las Intersecciones con los Ejes de Coordenadas Signo. ( Int. con eje y, hacer = Int. con eje, hacer y
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Colegio Portocarrero. Curso 2014-2015. Departamento de matemáticas. Análisis y programación lineal
 Análisis y programación lineal Problema 1: La gráfica de la función derivada de una función f es la parábola de vértice (0, 2) que corta al eje de abscisas en los puntos ( 3, 0) y (3, 0). A partir de dicha
Análisis y programación lineal Problema 1: La gráfica de la función derivada de una función f es la parábola de vértice (0, 2) que corta al eje de abscisas en los puntos ( 3, 0) y (3, 0). A partir de dicha
x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1
![x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1 x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1](/thumbs/80/80474947.jpg) Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
PAU: Aplicaciones de la derivada MATEMÁTICAS II 1. 2cos. x 0 x 0
 PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2008 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva,
