Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados:
|
|
|
- Pilar Serrano Olivares
- hace 7 años
- Vistas:
Transcripción
1 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica y, por tanto, no tiene asíntotas. ) f ( ) Dom( ) R { f / } R {} ASÍNTOTAS VERTICALES f ( ) de f ( ) f ( ) f ( ) y es A.H. de f ( ) ; por la izquierda está por debajo de la asíntota y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O.
2 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) f ( ) Dom( f ) R { / } R {,} ASÍNTOTAS VERTICALES f ( ) de f ( ) f ( ) de f ( ) f ( ) ( Ι) f ( ) ( Ι) y es A.H. de f ( ) ; por la izquierda está por encima de la asíntota y por la derecha está por debajo. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O.
3 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4) f ( ) Dom( f ) R { / } R {} ASÍNTOTAS VERTICALES f ( ) de f ( ) f ( ) f ( ) No hay asíntotas horizontales ( Ι) ( Ι) ( ) ( ) ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n f ( ) m ( Ι) n [ f ( ) m] ( ) ( Ι) n m Por tanto, y es A.O.de f () POSICIÓN Izquierda ( ) ( ) Función y y 99 99, f ( ) está por encima de la A.O.
4 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Derecha () () 98 Función y, 97 f ( ) está por debajo de la A.O. y 5) f ( ) Dom( f ) R { / } R {, } ASÍNTOTAS VERTICALES f ( ) de f ( ) f ( ) es A.V. de f ( ) 4
5 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ( Ι) f ( ) ( Ι) y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 6) f ( ) Dom( f ) R { / } R ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) ( Ι) f ( ) ( Ι) 5
6 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS y es A.H. de f ( ) ; por la izquierda está por debajo de la asíntota y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 4 7) f ( ) Dom( f ) R { / 8 ASÍNTOTAS VERTICALES 8 } R { } 4 f ( ) de f () 4 f ( ) ( Ι) 8 4 f ( ) ( Ι) 8 y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 6
7 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 8) f ( ) Dom( f ) R { / ASÍNTOTAS VERTICALES } R {,} f ( ) de f ( ) f ( ) Observación f ( ) f () ( )( ) ( Ι) ( ) Discontinuidad evitable ( punto en blanco ) NO de f ( ) f ( ) f ( ) ( Ι) ( Ι) y es A.H. de f ( ) 7
8 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS POSICIÓN ( ) Función y Izquierda ( ) ( ) y 9999,99 f ( ) está por debajo de la A.H. () Función y Derecha () y , f ( ) está por encima de la A.H. y es A.H. de f ( ) ; por la izquierda está por debajo de la asíntota y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 8
9 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 9) f ( ) Dom( f ) R {} ASÍNTOTAS VERTICALES f ( ) es A.V. de f ( ) f ( ) ( Ι) f ( ) ( Ι) No hay asíntotas horizontales () () ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n f ( ) m ( Ι) m n [ f ( ) m] 5 ( 5) 5 n ( Ι) Por tanto, y 5 es A.O.de f () POSICIÓN Izquierda ( Función y ) ( ) 99 5,9 98 f ( ) está por debajo de la A.O. y ( ) 5 5 9
10 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Derecha () Función y ) () ,9 f ( ) está por encima de la A.O. y () ) 5 95 ) f ( ) Dom( f ) R { /( ) ( ) ASÍNTOTAS VERTICALES } R { / } R {} f ( ) ( ) ( ) ( ) de f ( ) f ( ) ( )
11 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ( ) y es A.H. de f ( ) ; tanto por la izquierda como por la derecha la función está por debajo de la A.H. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. ) f ( ) Dom( f ) R { /( ) } R { / } R { } ( ) ASÍNTOTAS VERTICALES f ( ) ( ) ( ) ( ) de f ( ) f ( ) ( ) ( Ι)
12 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ( ) ( Ι) y es A.H.de f ( ) POSICIÓN ( ) Función y Izquierda ( ) y () Función y Derecha ( ) y 9998, ,98 f ( ) está por debajo de la A.H. f ( ) está por encima de la A.H. y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O.
13 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) ( ) f Dom( ) R ( ) f { /( ) } R { / } R { } ASÍNTOTAS VERTICALES f ( ) ( ) ( ) ( ) de f () f ( ) ( ) ( Ι) f ( ) ( ) ( Ι) No hay asíntotas horizontales ASÍNTOTAS OBLICUAS: Como f () ambos lados. y m n es una función racional, si tiene asíntota oblicua es la misma por f ( ) m n [ f ( ) m] ( Ι) ( Ι) ( ) n m Por tanto, y es A.O.de f ( ) POSICIÓN ( ) Función y, Izquierda ( ) y.( ) f ( ) está por debajo de la A.O.
14 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS () Función y 98, Derecha ( ) y 98 f ( ) está por encima de la A.O. 7 ) f ( ) Dom( ) R 5 f { / ASÍNTOTAS VERTICALES f ( ) } R { 5,5} de f () f ( ) de f ( ) 4
15 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 7 7 f ( ) f ( ) 5 y es A.H. de f ( ) ; tanto por la izquierda como por la derecha f ( ) está por encima de la A.H. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 4 4) f ( ) Dom( f ) R { / 4 4 } R ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) 4 ( Ι) 4 4 5
16 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4 f ( ) ( Ι) 4 4 No tiene A.H. ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n m f ( ) ( Ι) 4 4 no hay A.O. f ( ) ± f ( ) ± f ( ) tiene tanto por la izquierda como por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) 4 5) f ( ) Dom( f ) R { / 6 ASÍNTOTAS VERTICALES 6 } R { 4,4} 4 f ( ) es A.V. de f ( ) 6
17 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4 f ( ) de f () 4 f ( ) 6 4 f ( ) 6 y es A.H.de f ( ) ( Ι) Ι) ( ( ) ( ) POSICIÓN 4 ( ) Función y Izquierda ( ) 6 y 9996, 9984 f ( ) está por debajo de la A.H. 4 () Función y Derecha () 6 y 9996, 9984 f ( ) está por debajo de la A.H. y es A.H. de f ( ) ; tanto por la izquierda como por la derecha está por debajo de la A.H. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 7
18 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 6) f ( ) Dom( f ) R { / } R ± 4 solución real ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) ( Ι) f ( ) ( Ι) y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 8
19 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 7) f ( ) Dom( f ) R { / ASÍNTOTAS VERTICALES f ( ) } R {, } de f ( ) f ( ) es A.V. de f ( ) ( ) f ( Ι) f ( ) ( Ι) y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 9
20 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 5 8) f ( ) Dom( f ) R { / ASÍNTOTAS VERTICALES } R {, } 5 4 f ( ) de f ( ) 5 f ( ) 5 5 es A.V. de f ( ) 5 f ( ) 5 f ( ) y es A.H.de f ( ) ( Ι) ( Ι)
21 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS POSICIÓN Izquierda ( ) 5 Función y ( ) ( ) y ,98 f ( ) está por encima de la A.H. () 5 Función y Derecha () () y ,99 f ( ) está por debajo de la A.H. y es A.H. de f ( ) ; por la izquierda está por encima de la A.H. y por la derecha está por debajo. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 9) f ( ) Dom( f ) R { / ASÍNTOTAS VERTICALES: No tiene A.V. } R
22 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) f ( ) ( Ι) y es A.H.de f ( ) Ι) ( POSICIÓN Izquierda ( ) ( ) Función y ( ) y,96 f ( ) está por encima de la A.H. () () Función y Derecha () y 99,99 f ( ) está por debajo de la A.H. y es A.H. de f ( ) ; por la izquierda está por encima de la A.H. y por la derecha está por debajo. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O.
23 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) f ( ) Dom( f ) R { / } R {} ASÍNTOTAS VERTICALES f ( ) de f ( ) f ( ) ( Ι) f ( ) ( Ι) No hay asíntotas horizontales ( ) ( ) ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n f ( ) m n [ f ( ) m] ( ) ( ) n ( Ι) ( ) m ( Ι) Por tanto, y es A.O.de f () POSICIÓN ( ) Función y 97, Izquierda ( ) y ( ) 97 f ( ) está por encima de la A.O.
24 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS () Función y, Derecha () 99 y () f ( ) está por debajo de la A.O ) f ( ) Dom( f ) R { / 4 6 : ± 4 6 ASÍNTOTAS VERTICALES f ( ) } R {,} ± de f ( ) f ( ) de f ( ) 4
25 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) f ( ) No tiene A.H ( Ι) ( Ι) 4 6 ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n m f ( ) ( Ι) 4 6 no hay A.O. f ( ) ± f ( ) ± f ( ) tiene tanto por la izquierda como por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) 5
26 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) f ( ) Dom( f ) R { / 9 ASÍNTOTAS VERTICALES 9 } R {,} f ( ) de f ( ) 6 f ( ) de f ( ) f ( ) 9 f ( ) 9 ( Ι) ( Ι) No hay asíntotas horizontales ASÍNTOTAS OBLICUAS: Como f () ambos lados. es una función racional, si tiene asíntota oblicua es la misma por y m n f ( ) m 9 ( ) Ι 9 n [ f ( ) m] ( Ι) n 9 m Por tanto, y es A.O.de f ( ) 6
27 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS POSICIÓN Izquierda ( ) ( ) 9997 Función y,6 ( ) f () está por debajo de la A.O. y Derecha () () Función y,6 () f ( y ) está por encima de la A.O. ) f ( ) Dom( f ) Dom y R {} ASÍNTOTAS VERTICALES f ( ) de f ( ) por la derecha 7
28 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) f () "punto en blanco" ( ) f ( ) f y es A.H.de f ( ) POSICIÓN Izquierda Función y Asíntota y,99 f ( ) está por debajo de la A.H. 99 Derecha Función y Asíntota y,7 f ( ) está por encima de la A.H. y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 8
29 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4) f ( ) Dom( f ) { / ASÍNTOTAS VERTICALES: : No tiene A.V. } (, ] [, ) f ( ) f ( ) ( ( ) ) f () NO tiene A.H. ASÍNTOTAS OBLICUAS: Como f () no tiene A.H. puede que tenga A.O. m f ( ) [ ] y m n ( ) n [ f ( ) m] ( ( Ι) [ ( ) ( Ι) n ] [ ] [ )( ) ( ( ) ) m ] ( ) ) Por tanto, y es A.O.por la izquierda de f ( ) POSICIÓN Función y ( ) 99,9 f ( ) está por debajo de la A.O. Asíntota y ( ) y m n m f ( ) ( Ι) m 9
30 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS n [ f ( ) m] ( )( ) [ n ( ] [ ] [ ] ) ) ( Ι) Por tanto, y es A.O.por la derecha de f ( ) POSICIÓN Función y () 99,9 f ( ) está por debajo de la A.O. Asíntota y 5) f ( ) Dom( f ) / (,] (, ) ASÍNTOTAS VERTICALES f ( ) de f ( ) por la derecha
31 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ( ) ( ) ( Ι) f ( ) ) ( ) ( Ι) ( y es A.H.de f ( ) POSICIÓN Función y,995 Izquierda y f ( ) está por debajo de la A.H. Función y,5 Derecha y f ( ) está por encima de la A.H. y es A.H. de f ( ) ; por la izquierda está por debajo de la A.H. y por la derecha está por encima. ASÍNTOTAS OBLICUAS: Como f () tiene A.H. no tiene A.O.
32 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 6) f ( ) Dom( f ) [, ) (, ) y Dominio { / } [, ) y Dominio R ya que anula al denominador ASÍNTOTAS VERTICALES f ( ) de f ( ) No hay pues Dom ( f ) [,) (, ) f ( ) y es A.H.de f ( ) por la derecha y la función está por encimade la asíntota
33 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ASÍNTOTAS OBLICUAS: No hay pues Dom ( f ) [,) (, ) Como f () tiene A.H. no tiene A.O. ( ) 7) f ( ) Dom( f ) R { / ASÍNTOTAS VERTICALES: : No tiene A.H. } R ( ) f ( ) ( ) f ( ) y es A.H.de f ( ) ( Ι) ( Ι)
34 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS POSICIÓN ( ) Función y, Izquierda ( ) y f ( ) está por encima de la A.H. ( ) Función y Derecha () y 98,98 f ( ) está por debajo de la A.H. y es A.H. de f ( ) ; por la izquierda está por encima de la A.H. y por la derecha está por debajo. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 8) f ( ) Dom( f ) R { } ASÍNTOTAS VERTICALES f ( ) f ( ) f () "punto en blanco" de f ( ) por la izquierda f ( ) 4
35 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) y es A.H.de f ( ) POSICIÓN Izquierda Función y y, f ( ) está por encima de la A.H. Derecha Función y y,98 f ( ) está por debajo de la A.H. y es A.H. de f ( ) ; por la izquierda está por encima de la A.H. y por la derecha está por debajo. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. 5
36 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 9) f ( ) Dom( f ) R ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) f ( ) y es A.H.de f ( ) y tantopor la izquierdacomo por la derechala función está por encimade la A.H. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. ln ) f ( ) Dom( f ) (, ) ASÍNTOTAS VERTICALES ln de f ( ) por la derecha f ( ) No hay pues Dom ( f ) (, ) 6
37 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ln f ( ) ( Ι) ( ) (*) Las potencias de son infinitos de orden superior a cualquier función logarítmica. ASÍNTOTAS OBLICUAS: No hay pues Dom ( f ) (, ) Como f () y es A.H. de f ( ) por la derecha y la función está por encima de la asíntota tiene A.H. no tiene A.O. ) f ( ) Dom( f ) (,) (, ) ln ASÍNTOTAS VERTICALES f ( ) ln ln ln de f ( ) No hay pues Dom ( f ) (,) (, ) f ( ) ( Ι) f () NO tiene A.H.de por la derecha ln Las potencias de son infinitos de orden superior a cualquier función logarítmica. 7
38 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ASÍNTOTAS OBLICUAS: No hay pues Dom ( f ) (,) (, ) Como no hay A.H. puede que haya A.O. f ( ) ln m NO hay A.O.por la derecha ln ln f ( ) f ( ) f ( ) tiene por la derecha una rama parabólica en la dirección del eje de abscisas (eje OX) ) f ( ) ln( 4) Dom( f ) { / ASÍNTOTAS VERTICALES f ( ) ln( 4 > } (, ) (, ) 4) ln( ) de f ( ) por la izquierda f ( ) ln( 4) ln( ) de f ( ) por la derecha f ( ) ln(( ) 4) ln( 4) f ( ) f ( ) es PAR y, por tanto,su comportamiento en es el mismo que en f ( ) ± ln( ± 4) f () NO tiene A.H. 8
39 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ASÍNTOTAS OBLICUAS: f ( ) ln(( ) 4) ln( 4) f ( ) f ( ) es PAR y, por tanto,su comportamiento en es el mismo que en f ( ) ln( 4) m ( Ι) f ( ) NO tiene A.O. Las potencias de son infinitos de orden superior a cualquier función logarítmica. ± ± f ( ) f ( ) f ( ) tiene por ambos lados una rama parabólica en la dirección del eje de abscisas (eje OX) ) f ( ) e Dom( f ) R ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) e ( ) e f ( ) f ( ) es PAR y, por tanto, su comportamiento en es el mismo que en ± f ( ) ln e ± e y es A.H.de f ( ); y la función está por encima de la asíntota por por ambos lados ASÍNTOTAS OBLICUAS: : Como hay A.H. no hay A.O. 9
40 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4) f ( ) e f ( ) Dom ( f ) R e ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) f () NO tiene A.H.por la izquierda e e f ( ) e ( ) (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. y es A.H.de f ( ) por la derecha y la función está por encimade la A.H. ASÍNTOTAS OBLICUAS: Como no hay A.H. puede que haya A.O. y m n f ( ) e m ( Ι) f ( ) NO tiene A.O. e e ( ) (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. 4
41 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) f ( ) f ( ) tiene por la derecha una rama parabólica en la dirección del eje de abscisas (eje OX) Como hay A.H. no hay A.O. 5) f ( ) e Dom( f ) R ASÍNTOTAS VERTICALES: : No tiene A.V. e ( ) f ( ) e ( Ι) ( Ι) e e L Hôpital e y es A.H.de f ( ) por la izquierda y la función está por debajo de la asíntota ( ) (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. 4
42 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) e ( ) ( ) f ( ) NO tiene A.H.por la derecha ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. Como no hay A.H. puede que haya A.O. y m n m f ( ) e e e f () NO tiene A.O.por la derecha f ( ) f ( ) f ( ) tiene por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) e 6) f ( ) e f ( ) Dom ( f ) R {} ASÍNTOTAS VERTICALES e f ( ) e e de f ( ) 4
43 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) f ( ) e e y es A.H. de f ( ) por la izquierda y la función está por debajo de la asíntota e e ( Ι ) f ( ) NO tiene A.H.por la derecha (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. ASÍNTOTAS OBLICUAS: Como hay A.H. no hay A.O. Como no hay A.H. puede que haya A.O. y m n ( ) e f ( ) e m ( Ι) f ( ) NO tiene A.O.por la derecha ( ) (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. f ( ) f ( ) f ( ) tiene por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) 4
44 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 7) f ( ) e f ( ) Dom ( f ) R e ASÍNTOTAS VERTICALES: : No tiene A.V. f ( ) f () NO tiene A.H. por la izquierda e e f ( ) e (*) Las funciones eponenciales de base mayor que uno son infinitos de orden superior a cualquier potencia de. y es A.H.de f ( ) por la derecha y la función está por encima de la A.H. ASÍNTOTAS OBLICUAS: Como no hay A.H. puede que haya A.O. y m n m f ( ) e e e e f ( ) NO tiene A.O.por la izquierda. f ( ) f ( ) f ( ) tiene por la izquierda una rama parabólica en la dirección del eje de ordenadas (eje OY) Como hay A.H. no hay A.O. 44
45 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 8) f ( ) e Dom( f ) R { } ASÍNTOTAS VERTICALES e e e e f ( ) e e e de f ( ) por la derecha e e e Simplificar e e ( )( Ι) L Hôpital f ( ) f () "punto en blanco" f ( ) e ( ) e ( ) e ( ) f ( ) NO tiene A.H. por la izquierda 45
46 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) e ( ) e ( ) e ( ) f ( ) NO tiene A.H. por la derecha ASÍNTOTAS OBLICUAS: Como no hay A.H. puede que haya A.O. y m n m f ( ) e e n [ f ( ) m] e e e e e n m ( e ) ( ) ( Ι) e ( ) Ι L Hôpital Por tanto, y es A.O.por la izquierda de f ( ) POSICIÓN Función y e 99,5 f ( ) está por debajo de la A.O. Asíntota y 99 Como no hay A.H. puede que haya A.O. y m n m f ( ) e e n [ f ( ) m] e e e e e n m ( e ) ( ) ( Ι) e ( ) Ι L Hôpital Por tanto, y es A.O.por la derecha de f ( ) 46
47 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS POSICIÓN Función y e,5 f ( ) está por encima de la A.O. Asíntota y 9) f ( ) ln Dom( f ) (, ) ASÍNTOTAS VERTICALES ln f ( ) ln ( )( Ι) NO de f ( ) ( Ι) L Hôpital ( ) f ( ) f () "punto en blanco" f () NO tiene A.V. No hay ya que Dom ( f ) (, ) 47
48 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ln ( ) ( ) f ( ) NO tiene A.H.por la derecha ASÍNTOTAS OBLICUAS: No hay ya que Dom( f ) (, ) Como no hay A.H. puede que haya A.O. y m n m f ( ) f ( ) f ( ) ln ln f ( ) NO tiene A.O. por la derecha f ( ) tiene por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) 4) f ( ) ln Dom( f ) (, ) ASÍNTOTAS VERTICALES ln f ( ) ln ( )( Ι) NO de f ( ) ( Ι) L Hôpital f () NO tiene A.V. f ( ) f () "punto en blanco" No hay ya que Dom ( f ) (, ) 48
49 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ln ( ) ( ) f ( ) NO tiene A.H.por la derecha ASÍNTOTAS OBLICUAS: No hay ya que Dom( f ) (, ) Como no hay A.H. puede que haya A.O. y m n m f ( ) f ( ) f ( ) ln ln ( ) ( ) f ( ) NO tiene A.O. por la derecha f ( ) tiene por la derecha una rama parabólica en la dirección del eje de ordenadas (eje OY) 49
50 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) si f ( ) Dom ( f ) R si > ASÍNTOTAS VERTICALES f ( ) es A.V. por la derecha de f ( ) ASÍNTOTAS HORIZONTALES f ( ) no tiene f ( ) y es A.H. por la derecha y f ( ) está por encima de la A.H. ASÍNTOTAS OBLICUAS f () es una función constante no hay A.O.por la izquierda Como hay A.H. no hay A.O. A.H. por la izquierda 5
51 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) f ( ) si si < Dom ( f ) R ASÍNTOTAS VERTICALES f ( ) ASÍNTOTAS HORIZONTALES f ( ) ( Ι) y es A.H. por la izquierda Función y,99 Posición: y f ( ) ( ) por la izquierda f ( ) está por debajo de la A.H. y es A.H. por la derecha y f ( ) está por encima de la A.H. ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. Como hay A.H. no hay A.O. 5
52 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ) si < f ( ) Dom ( f ) R { } si ASÍNTOTAS VERTICALES f ( ) ASÍNTOTAS HORIZONTALES f ( ) f ( ) ( Ι) ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. Como no hay A.H. puede que haya A.O. y m n m y es A.H. por la izquierda y f ( ) está por debajo de la A.H. f ( ) ( Ι) no hay A.H.por la derecha n [ f ( ) m] m n Por tanto, y es A.O.por la derecha de f ( ) Función y 99,99 Posición: f ( ) está por debajo de la A.O. y 5
53 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 4) f ( ) si si si < < < Dom ( f ) R {,,} ASÍNTOTAS VERTICALES f ( ) f ( ) ASÍNTOTAS HORIZONTALES f ( ) ( Ι) y es A.H.por la izquierda ( ) Función y, Posición: 97 y f ( ) está por debajo de la A.H. 5
54 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS f ( ) ( Ι) no hay A.H.por la derecha ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. Como no hay A.H. puede que haya A.O. y m n m f ( ) n [ f ( ) m] n ( Ι) m ( Ι) Por tanto, y es A.O.por la derecha de f ( ) Función y,4 Posición: 98 f ( ) está por encima de la A.O. y 54
55 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 5) 9 si 9 f ( ) Dom ( f ) R {,} si > 4 ASÍNTOTAS VERTICALES 9 ( ) f ( ) ( Ι) f ( ) NO 9 ( )( ) Observación f ( ) discontinu idad evitable ("punto en blanco") f ( ) f ( ) es A.V. ASÍNTOTAS HORIZONTALES 9 f ( ) ( Ι) es A.H. 9 y por la izquierda y está por debajo de la A.H. f ( ) 4 ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. Como hay A.H. no hay A.O. f ( ) y es A.H. por la derecha y f ( ) está por encima de la A.H. 55
56 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS 6) f si < ) Dom ( f ) R {} si ( ASÍNTOTAS VERTICALES f ( ) por la izquierda f ( ) ASÍNTOTAS HORIZONTALES f ( ) ( Ι) f ( ) ( Ι) es y A.H. por la izquierda y por encima de la A.H. no hay A.H.por la derecha f ( ) está ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. 56
57 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Como no hay A.H. puede que haya A.O. y m n m f ( ) ( Ι) n [ f ( ) m] n m ( Ι) Por tanto, y es A.O.por la derecha de f ( ) Función y, Posición: 99 f ( ) está por encima de la A.O. y 7) si h( ) Dom ( f ) R { } si > 57
58 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS ASÍNTOTAS VERTICALES 4 4 f ( ) 4 f ( ) ASÍNTOTAS HORIZONTALES f ( ) ( Ι) ( ) Función y,4 Posición: 97 y f ( ) por encima de la A.H. por la derecha ( ) y es A.H. por la izquierda y f ( ) f ( ) está por debajo de la A.H. ( Ι) es A.H.por y la derecha y f ( ) está ASÍNTOTAS OBLICUAS Como hay A.H. no hay A.O. Como hay A.H. no hay A.O. 58
Procedimiento para determinar las asíntotas verticales de una función
 DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
Límites y continuidad
 Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
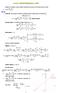 Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
 REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Procedimiento para determinar las asíntotas verticales de una función
 DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
Procedimiento para determinar las asíntotas verticales de una función
 DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
REPRESENTACIÓN GRÁFICA DE FUNCIONES
 REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
REPRESENTACIÓN DE CURVAS
 ºBachillerato REPRESENTACIÓN DE CURVAS Esquema Para representar gráficamente una función se debe estudiar:. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
ºBachillerato REPRESENTACIÓN DE CURVAS Esquema Para representar gráficamente una función se debe estudiar:. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
LÍMITES Y CONTINUIDAD. 1º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN LÍMITE DE UNA FUNCIÓN EN UN PUNTO CONCEPTO DE LÍMITE DE UNA FUNCIÓN
 LÍMITES Y CONTINUIDAD º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN Sea f() =. Vamos a darle valores a cercanos a y vamos a ver cómo se comporta f()..9.99.999.9999.99999 f() 4.8 4.98 4.998 4.9998
LÍMITES Y CONTINUIDAD º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN Sea f() =. Vamos a darle valores a cercanos a y vamos a ver cómo se comporta f()..9.99.999.9999.99999 f() 4.8 4.98 4.998 4.9998
TEMA 2: CONTINUIDAD DE FUNCIONES
 TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
Asíntotas en una función.
 Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Tipos de Funciones. 40 Ejercicios para practicar con soluciones. 1 Representa en los mismos ejes las siguientes funciones: 1 x
 Tipos de Funciones. 40 Ejercicios para practicar con soluciones Representa en los mismos ejes las siguientes funciones: a) y = ; b) y = ; c) y = y= y= y= Representa las siguientes funciones: a) y = b)
Tipos de Funciones. 40 Ejercicios para practicar con soluciones Representa en los mismos ejes las siguientes funciones: a) y = ; b) y = ; c) y = y= y= y= Representa las siguientes funciones: a) y = b)
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
 Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Límites y continuidad
 Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
= y. Así pues, el domino lo forman los números x para los cuales existe el valor de f (x)
 UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
REPRESENTACIÓN DE CURVAS - CCSS
 REPRESENTACIÓN DE CURVAS - CCSS Esquema Para representar gráficamente una función se debe estudiar: 1. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
REPRESENTACIÓN DE CURVAS - CCSS Esquema Para representar gráficamente una función se debe estudiar: 1. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN
 ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN Problema Datos Procedimiento Ejemplo Dominio de una La ecuación de Casos en los que en dominio no es IR: función la función Irracionales (ecluir valores
ANÁLISIS DE FUNCIONES, LÍMITES Y CONTINUIDAD. RESUMEN Problema Datos Procedimiento Ejemplo Dominio de una La ecuación de Casos en los que en dominio no es IR: función la función Irracionales (ecluir valores
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
 Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Tema 4: Representación de funciones Índice:. Información obtenida de la función... Dominio de la función.. Simetrías..3. Periodicidad.4. Puntos de corte con los ejes..5. Ramas
REPRESENTACIÓN DE FUNCIONES Tema 4: Representación de funciones Índice:. Información obtenida de la función... Dominio de la función.. Simetrías..3. Periodicidad.4. Puntos de corte con los ejes..5. Ramas
CONTINUIDAD DEFINICIÓN CONTINUIDAD LATERAL. es continua en un punto. Una función. si:
 CONTINUIDAD DEFINICIÓN Una función 1) l a ) f (a) ) f ( a) a un punto a Si una función no cumple alguna de estas condiciones es discontinua en : a CONTINUIDAD LATERAL Ejemplo a por la izquierda f ( a)
CONTINUIDAD DEFINICIÓN Una función 1) l a ) f (a) ) f ( a) a un punto a Si una función no cumple alguna de estas condiciones es discontinua en : a CONTINUIDAD LATERAL Ejemplo a por la izquierda f ( a)
SOLUCIÓN. BLOQUE DE FUNCIONES.
 SOLUCIÓN. BLOQUE DE FUNCIONES. Análisis de funciones 1. a) y c) son funciones, porque para cada valor de hay un único valor de y. b) no es una función, porque para cada valor de hay dos valores de y. 2.
SOLUCIÓN. BLOQUE DE FUNCIONES. Análisis de funciones 1. a) y c) son funciones, porque para cada valor de hay un único valor de y. b) no es una función, porque para cada valor de hay dos valores de y. 2.
I.- Representación gráfica de una función polinómica
 Los campos a considerar en el estudio de una representación gráfica son; Dominio de la función Continuidad y derivabilidad Simetrías Periodicidad Asíntotas Verticales Horizontales Oblicuas Posición de
Los campos a considerar en el estudio de una representación gráfica son; Dominio de la función Continuidad y derivabilidad Simetrías Periodicidad Asíntotas Verticales Horizontales Oblicuas Posición de
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
SOLUCIONES DE LAS ACTIVIDADES Págs. 239 a 257
 TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL
 TEMA. FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL . FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL.5.1. DOMINIO, CORTES CON LOS
TEMA. FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL . FUNCIONES REALES DE VARIABLE REAL.5. GRÁFICAS DE FUNCIONES REALES DE VARIABLE REAL.5.1. DOMINIO, CORTES CON LOS
Apuntes Matemáticas 2º de bachillerato. Tema 5. Estudio de funciones
 Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
TEMA 10.-LÍMITES DE FUNCIONES Y CONTINUIDAD
 TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
I.- Límite de una función
 I.- Límite de una función a) En un punto En la mayoría de las funciones que vas a encontrarte, el límite, cuando tiende a un número real c, coincide con el valor numérico f(c), siempre que c pertenezca
I.- Límite de una función a) En un punto En la mayoría de las funciones que vas a encontrarte, el límite, cuando tiende a un número real c, coincide con el valor numérico f(c), siempre que c pertenezca
1 Elabora una tabla de valores de la función f(x) = x 2-4x + 3 en puntos x próximos a x = 2. Sugiere la tabla
 Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 1 PROBLEMAS PROPUESTOS 1 Elabora una tabla de valores de la función f() - + en puntos próimos a. Sugiere la tabla que f() es continua en? 1 9 1 99 1 999 1 01
Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 1 PROBLEMAS PROPUESTOS 1 Elabora una tabla de valores de la función f() - + en puntos próimos a. Sugiere la tabla que f() es continua en? 1 9 1 99 1 999 1 01
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES IDEA INTUITIVA DE LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Ejemplo : Consideremos la función: f Su gráfica: si < si > Si toma valores próimos a, distintos de y menores que ej.: 9, 99, 999,,
LÍMITES DE FUNCIONES IDEA INTUITIVA DE LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Ejemplo : Consideremos la función: f Su gráfica: si < si > Si toma valores próimos a, distintos de y menores que ej.: 9, 99, 999,,
TEMA 9: FUNCIONES, LÍMITES Y CONTINUIDAD
 º CONCEPTOS PREVIOS Ejercicio º Valor absoluto a,b, TEMA 9: FUNCIONES, LÍMITES Y CONTINUIDAD º Intervalos: a, b, a, b, a, b Semirrectas:, a, -,a, a,, a, Representa gráficamente las siguientes funciones,
º CONCEPTOS PREVIOS Ejercicio º Valor absoluto a,b, TEMA 9: FUNCIONES, LÍMITES Y CONTINUIDAD º Intervalos: a, b, a, b, a, b Semirrectas:, a, -,a, a,, a, Representa gráficamente las siguientes funciones,
CÁLCULO DIFERENCIAL 9. UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS
 CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
9.11. Gráficas con poco
 9 - Gráficas con poco. 21 9.11. Gráficas con poco 9.11.1. Asíntotas Las asíntotas son rectas a las que la curva tiende a unirse en situaciones especiales. Unas (verticales) tienen que ver con las discontinuidades
9 - Gráficas con poco. 21 9.11. Gráficas con poco 9.11.1. Asíntotas Las asíntotas son rectas a las que la curva tiende a unirse en situaciones especiales. Unas (verticales) tienen que ver con las discontinuidades
Límites de funciones. Continuidad
 Límites de funciones. Continuidad 1. Calcula los siguientes límites: a) f(x) = 1 x x 4 b) f(x) = 2x2 +x x 2 +1 c) f(x) = x2 +x +2x 4x 2 +1 d) f(x) = x +x +2x 4x 2 +1 2. Calcula los límites cuando x + de
Límites de funciones. Continuidad 1. Calcula los siguientes límites: a) f(x) = 1 x x 4 b) f(x) = 2x2 +x x 2 +1 c) f(x) = x2 +x +2x 4x 2 +1 d) f(x) = x +x +2x 4x 2 +1 2. Calcula los límites cuando x + de
Continuidad, límites y asíntotas. Funciones
 9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
MATE 3031. Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 77
 MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN
 TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN ESTUDIO DE LA MONOTONÍA DEF.- Una función es CRECIENTE en un intervalo I del dominio de la función si: x1 < x2 I f ( x1 ) f ( x2). Si se cumple
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN ESTUDIO DE LA MONOTONÍA DEF.- Una función es CRECIENTE en un intervalo I del dominio de la función si: x1 < x2 I f ( x1 ) f ( x2). Si se cumple
Matemáticas 1º Bachillerato ASÍNTOTAS Colegio La Presentación
 ASÍNTOTA Es una recta imaginaria que nosotros calculamos y representamos con una línea discontinua. Esta recta tiene la propiedad de que en el infinito no puede ser traspasada por la gráfica de la función,
ASÍNTOTA Es una recta imaginaria que nosotros calculamos y representamos con una línea discontinua. Esta recta tiene la propiedad de que en el infinito no puede ser traspasada por la gráfica de la función,
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1
 TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
Tema 4. Representación de Funciones. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 4
 Tema 4 Representación de Funciones 0.- Introducción.- Estudio de una función...- Dominio...- Simetrías...- Periodicidad..4.- Continuidad..5.- Puntos de Corte con los ejes..6.- Asíntotas y ramas infinitas..7.-
Tema 4 Representación de Funciones 0.- Introducción.- Estudio de una función...- Dominio...- Simetrías...- Periodicidad..4.- Continuidad..5.- Puntos de Corte con los ejes..6.- Asíntotas y ramas infinitas..7.-
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A
 Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
Tipos de funciones. Clasificación de funciones. Funciones algebraicas
 Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
a) p = ½. b) p = 0. c) Ninguna de las anteriores. Solución: Para que sea continua en x = 0 debe cumplirse que lím
 Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
lím x 1 r x a, donde a es un nº que cumple que el ) es algún 1. ASÍNTOTAS DE UNA FUNCIÓN
 . ASÍNTOTAS DE UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición más formal
. ASÍNTOTAS DE UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición más formal
IES Fernando de Herrera Curso 2015 / 16 Tercer trimestre - Prueba de observación continua nº 1 1º Bach CT NOMBRE:
 IES Fernando de Herrera Curso 0 / 6 Tercer trimestre - Prueba de observación continua nº º Bach CT NOMBRE: Instrucciones: ) Todos los folios deben tener el nombre y estar numerados en la parte superior.
IES Fernando de Herrera Curso 0 / 6 Tercer trimestre - Prueba de observación continua nº º Bach CT NOMBRE: Instrucciones: ) Todos los folios deben tener el nombre y estar numerados en la parte superior.
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
MATEMÁTICAS APLICADAS A LAS CCSS I Actividades de refuerzo Curso:
 MATEMÁTICAS APLICADAS A LAS CCSS I Actividades de refuerzo -. Curso: 0-0. Realiza la siguiente suma racionalizando previamente los denominadores + +. Calcula utilizando las propiedades de los logaritmos
MATEMÁTICAS APLICADAS A LAS CCSS I Actividades de refuerzo -. Curso: 0-0. Realiza la siguiente suma racionalizando previamente los denominadores + +. Calcula utilizando las propiedades de los logaritmos
APUNTES DE FUNCIONES PARA 4º ESO
 APUNTES DE FUNCIONES PARA 4º ESO - DEFINICIÓN: Una función es una relación entre dos magnitudes, X e Y, de forma que a cada valor de la magnitud X corresponde un único valor y de la magnitud Y. : variable
APUNTES DE FUNCIONES PARA 4º ESO - DEFINICIÓN: Una función es una relación entre dos magnitudes, X e Y, de forma que a cada valor de la magnitud X corresponde un único valor y de la magnitud Y. : variable
Matemáticas II TEMA 7 Límites y continuidad de funciones Problemas Propuestos
 Matemáticas II TEMA 7 Límites y continuidad de funciones Problemas Propuestos Definición de ites Demuestra, aplicando la definición, que ( ) Demuestra, aplicando la definición, que + + 8 Cálculo de ites
Matemáticas II TEMA 7 Límites y continuidad de funciones Problemas Propuestos Definición de ites Demuestra, aplicando la definición, que ( ) Demuestra, aplicando la definición, que + + 8 Cálculo de ites
1) La función no está definida para x = 0 ya que anula el denominador de su exponente, por tanto, D = R- {0}.
 6. Estudiar y representar gráficamente las siguientes funciones: a) ( ) f e b) Solución f( ) + 3 + c) f( ) ln + a) Para estudiar la función e se realizan los siguientes pasos: f( ) ) La función no está
6. Estudiar y representar gráficamente las siguientes funciones: a) ( ) f e b) Solución f( ) + 3 + c) f( ) ln + a) Para estudiar la función e se realizan los siguientes pasos: f( ) ) La función no está
LÍMITES Y CONTINUIDAD
 LÍMITES Y CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Dada una función f(), diremos que el ite de f() cuando tiende a a es el número real L y lo escribiremos f() = L, si al tomar cada vez valores más
LÍMITES Y CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Dada una función f(), diremos que el ite de f() cuando tiende a a es el número real L y lo escribiremos f() = L, si al tomar cada vez valores más
Tema 4: Representación de Funciones
 Tema 4: Representación de Funciones.- Dominio y recorrido: Dominio: Valores de para los que está definida (eiste) f () Recorrido: Valores que toma f () Funciones Polinómicas, son de la forma f ( ) ao a...
Tema 4: Representación de Funciones.- Dominio y recorrido: Dominio: Valores de para los que está definida (eiste) f () Recorrido: Valores que toma f () Funciones Polinómicas, son de la forma f ( ) ao a...
Considermos la función
 Considermos la función f x = x2 9 x 3 Qué sucede si reemplazamos a x por 3? f x = x2 9 x 3 = 32 9 3 3 = 0 0 Tenemos lo que se denomina UNA INDETERMINACIÓN En matemática hay 7 indeterminaciones básicas
Considermos la función f x = x2 9 x 3 Qué sucede si reemplazamos a x por 3? f x = x2 9 x 3 = 32 9 3 3 = 0 0 Tenemos lo que se denomina UNA INDETERMINACIÓN En matemática hay 7 indeterminaciones básicas
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 2º BACHILLERATO
 LÍMITES: OPERACIONES CON INFINITOS LÍMITES: RESOLUCIÓN DE INDETERMINACIONES DEL TIPO 1 Estas indeterminaciones están relacionadas con el número e se calculan de la siguiente forma: 1 DOMINIO E IMAGEN DE
LÍMITES: OPERACIONES CON INFINITOS LÍMITES: RESOLUCIÓN DE INDETERMINACIONES DEL TIPO 1 Estas indeterminaciones están relacionadas con el número e se calculan de la siguiente forma: 1 DOMINIO E IMAGEN DE
FUNCIONES REALES DE VARIABLE REAL
 FUNCIONES REALES DE VARIABLE REAL Función: Es toda aplicación definida entre conjuntos numéricos. Cuando el conjunto inicial y final son los números Reales, se llaman funciones reales de variable real.
FUNCIONES REALES DE VARIABLE REAL Función: Es toda aplicación definida entre conjuntos numéricos. Cuando el conjunto inicial y final son los números Reales, se llaman funciones reales de variable real.
Tema 9 Funciones elementales
 Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
? Sí es un infinito. Comparación de infinitos
 Infinitos: límites infinitos. Comparación de infinitos Ejercicio. Cuáles de las siguientes expresiones son infinitas ( ± 4 ) cuando x 6 + 4? Sí es un infinito?????? Comparación de infinitos < Dadas dos
Infinitos: límites infinitos. Comparación de infinitos Ejercicio. Cuáles de las siguientes expresiones son infinitas ( ± 4 ) cuando x 6 + 4? Sí es un infinito?????? Comparación de infinitos < Dadas dos
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Opción A. teorema se puede aplicar también si sale /, y cuando x. Como. , la recta x = 0 es una A.V. de la función f.
 Opción A 1 Ejercicio 1. [ 5 puntos] Sea f la función definida, para 0, por f e. Determina las asíntotas de la gráfica de f. La recta = a es una asíntota vertical (A.V.) de la función f si lim f Veamos
Opción A 1 Ejercicio 1. [ 5 puntos] Sea f la función definida, para 0, por f e. Determina las asíntotas de la gráfica de f. La recta = a es una asíntota vertical (A.V.) de la función f si lim f Veamos
1.5 Límites infinitos
 SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN
 ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN La gráfica de una función elemental puede presentar ninguna una o varias asíntotas verticales y además puede presentar a lo sumo una asíntota horizontal o una asíntota
ASÍNTOTAS DE LA GRÁFICA DE UNA FUNCIÓN La gráfica de una función elemental puede presentar ninguna una o varias asíntotas verticales y además puede presentar a lo sumo una asíntota horizontal o una asíntota
1.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO.
 º Bachillerato Matemáticas I Tema 8:Límites y continuidad.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. En ocasiones interesa saber hacia qué valor se aproima una función cuando la variable
º Bachillerato Matemáticas I Tema 8:Límites y continuidad.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. En ocasiones interesa saber hacia qué valor se aproima una función cuando la variable
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
Representación gráfica de funciones
 Gráfica de una fución Representación gráfica de funciones La gráfica de una función está formada por el conjunto de puntos (x, y) para todos los valores de x pertenecientes al Dominio de la función gráfica
Gráfica de una fución Representación gráfica de funciones La gráfica de una función está formada por el conjunto de puntos (x, y) para todos los valores de x pertenecientes al Dominio de la función gráfica
2.1. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable x)
 Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
= 1. x = 3: Lím = Asíntota vertical en x = 3: = 0 ; No se anula nunca. Punto de corte con OY es (0, 3) 3 x
 Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
1. f(x) = x3 1 x 2. 2. f(x) = x2 9 x 2 4. 3. f(x) = x 3 x + 2. x 3 (x 1) 2. 4. f(x) = 5. f(x) = x + 5 x 2 9. 6. f(x) = x2 3 x 2. x 2 3 x 2. 7.
 . f() =. f() = 9. f() =. f() = ( ). f() = 9 6. f() = 7. f() =. f() = 9. f() = p. f() =. f() =. f() = ( ). f() = 9. f() = ( ) . f() = Función racional con asíntota oblícua. Einamos los puntos que anulan
. f() =. f() = 9. f() =. f() = ( ). f() = 9 6. f() = 7. f() =. f() = 9. f() = p. f() =. f() =. f() = ( ). f() = 9. f() = ( ) . f() = Función racional con asíntota oblícua. Einamos los puntos que anulan
SOLUCIONES HOJA 5: APLICACIONES DE LA DERIVADA 1
 MATEMÁTICAS:º BACHILLERATO SOLUCIONES HOJA 5: APLICACIONES DE LA DERIVADA.- Calcular los etremos relativos de las siguientes funciones: a) f ( ) D(f) (Por ser polinómica) ; Posibles máimos o mínimos 6
MATEMÁTICAS:º BACHILLERATO SOLUCIONES HOJA 5: APLICACIONES DE LA DERIVADA.- Calcular los etremos relativos de las siguientes funciones: a) f ( ) D(f) (Por ser polinómica) ; Posibles máimos o mínimos 6
Límite, continuidad, asíntotas. Rápidamente aparecen las indeterminaciones y aplicamos las principales herramientas para su
 UNIDAD 4 Límite, continuidad, asíntotas a presente Unidad es la base del denominado L Cálculo Infinitesimal, que es a su vez el sustento del Análisis Matemático Los temas de la Unidad ya fueron tratados
UNIDAD 4 Límite, continuidad, asíntotas a presente Unidad es la base del denominado L Cálculo Infinitesimal, que es a su vez el sustento del Análisis Matemático Los temas de la Unidad ya fueron tratados
2.1 CONTINUIDAD EN UN PUNTO 2.2 CONTINUIDAD DE FUNCIONES CONOCIDAS 2.3 CONTINUIDAD EN OPERACIONES CON
 Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
4.2. Continuidad de una función en un punto. (A) Una función f es continua en un punto x=a, cuando se cumplen las siguientes condiciones:
 4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES GRÁFICA DE UNA FUNCIÓN: Conjunto de puntos del plano (,y), en los que y = f(), es decir, conjunto de puntos del plano en los que la segunda coordenada es la imagen de la primera.
REPRESENTACIÓN DE FUNCIONES GRÁFICA DE UNA FUNCIÓN: Conjunto de puntos del plano (,y), en los que y = f(), es decir, conjunto de puntos del plano en los que la segunda coordenada es la imagen de la primera.
Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10
 página 1/20 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10 Hoja 2. Problema 2 Resuelto por Carmen Jiménez Cejudo (diciembre 2014)
página 1/20 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10 Hoja 2. Problema 2 Resuelto por Carmen Jiménez Cejudo (diciembre 2014)
Denominadores: un denominador nunca se puede hacer cero. Ejemplo: 𝑓 𝑥 =
 1. Continuidad de funciones. Una función es continua en 𝑥 = 𝑎, si se cumple: Existe 𝑓(𝑎). lim!! 𝑓 𝑥 = lim!!! 𝑓(𝑥) = lim!!! 𝑓 𝑥 𝒇 𝒂 = 𝐥𝐢𝐦𝒙 𝒂 𝒇 𝒙 Las funciones definidas por expresiones analíticas elementales
1. Continuidad de funciones. Una función es continua en 𝑥 = 𝑎, si se cumple: Existe 𝑓(𝑎). lim!! 𝑓 𝑥 = lim!!! 𝑓(𝑥) = lim!!! 𝑓 𝑥 𝒇 𝒂 = 𝐥𝐢𝐦𝒙 𝒂 𝒇 𝒙 Las funciones definidas por expresiones analíticas elementales
EXAMEN DE FUNCIONES ELEMENTALES
 EXAMEN DE FUNCIONES ELEMENTALES Se recomienda: a) Antes de hacer algo, leer todo el eamen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta.
EXAMEN DE FUNCIONES ELEMENTALES Se recomienda: a) Antes de hacer algo, leer todo el eamen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta.
TEMA 1: Funciones elementales
 MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
Representación de funciones
 Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción,
Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción,
A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. ( (
 A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. 1. Calcula el dominio de las siguientes funciones: ( ( ( ( ( ( 2. Calcula la imagen de las siguientes
A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. 1. Calcula el dominio de las siguientes funciones: ( ( ( ( ( ( 2. Calcula la imagen de las siguientes
1. Definición y formas de de definir una función
 Tema 7. Funciones 1. Definición y formas de definir una función 1.1. Definición de una función 1.. Formas de definir una función 1..1. A Partir de gráfica 1... Epresión algebraica 1..3. Tabla. Dominio
Tema 7. Funciones 1. Definición y formas de definir una función 1.1. Definición de una función 1.. Formas de definir una función 1..1. A Partir de gráfica 1... Epresión algebraica 1..3. Tabla. Dominio
Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 01 - Problemas 8, 9
 Asignatura: Matemáticas II ºBachillerato página 1/8 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 01 - Problemas 8, 9 Hoja 1. Problema 9 Resuelto por José Antonio Álvarez
Asignatura: Matemáticas II ºBachillerato página 1/8 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 01 - Problemas 8, 9 Hoja 1. Problema 9 Resuelto por José Antonio Álvarez
