Lógica Proposicional. Sergio Stive Solano Sabié. Marzo de 2012
|
|
|
- María Concepción Paz Fidalgo
- hace 7 años
- Vistas:
Transcripción
1 Lógica Proposicional Sergio Stive Solano Sabié Marzo de 2012
2 Lógica Proposicional Sergio Stive Solano Sabié Marzo de 2012
3 Proposiciones Definición 1.1 Una proposición (o declaración) es una oración declarativa que es verdadera o falsa, pero no ambas. Comúnmente se denotan con las letras minúsculas p, q, r, s, t,..., las cuales reciben el nombre de letras o variables proposicionales, de esta forma, el lenguaje proposicional se hace más simple y exacto que el lenguaje natural.
4 Proposiciones Ejemplo 1.1 Los siguientes ejemplos ilustran cómo se pueden simbolizar las proposiciones: 1 p : Hoy es sábado. 2 q : Estudio ingeniería de sistemas. 3 r : New York es llamada la capital del mundo. 4 s : 1 no es un número primo. 5 t : = v : 3 > 5 7 w : El sol es amarrillo
5 Proposiciones Ejemplo 1.2 Las siguientes expresiones NO son proposiciones: 1 Viajar en el día. 2 x + 3 = 7. 3 Mirar T.V. 4 De qué color es la mesa? Toda afirmación es verdadera o falsa y no hay una que sea verdadera y falsa al mismo tiempo. Esta suposición la llamamos la Ley del tercero excluido. Una consecuencia de esta suposición es que si una afirmación no es falsa tendrá que ser verdadera.
6 Operaciones básicas En el lenguaje cotidiano se encuentran expresiones como: Ejemplo Las rosas son rojas y tienen espinas. 2 El tablero es verde o es blanco. 3 En el país no hay violencia. 4 Si estudio lógica matemática entonces seré un destacado ingeniero de sistemas. 5 4 es un número par si y sólo si se puede dividir por 2.
7 Operaciones básicas Los términos de enlace, y, o, no, si,...,entonces, si y sólo si, reciben el nombre de Conectivos lógicos, y estas nuevas proposiciones que se obtienen uniendo dos o más proposiciones simples mediante conectivos lógicos se conocen como proposiciones compuestas. Al igual que a las proposiciones, los conectivos lógicos también se les asignan un lenguaje simbólico, así: LENGUAJE NATURAL LENGUAJE FORMAL NOMBRE y Conjunción o Disyunción No Negación Si... entonces Condicional Si y sólo si Bicondicional
8 Operaciones básicas Ejemplo p : Las rosas son rojas, q : Las rosas tienen espinas, p q : Las rosas son rojas y tienen espinas.
9 Operaciones básicas Ejemplo r : El tablero es verde, s : El tablero es blanco, r s : El tablero es verde o es blanco.
10 Operaciones básicas Ejemplo t : En el país hay violencia, t : En el país no hay violencia.
11 Operaciones básicas Ejemplo x : Estudio lógica matemática, y : Seré un destacado ingeniero de sistemas, x y : Si estudio lógica matemática entonces seré un destacado ingeniero de sistemas.
12 Operaciones básicas Ejemplo u : 4 es un número par, v : 4 es divisible por 2, u v : 4 es un número par si y sólo si es divisible por 2.
13 Si conocemos los valores de verdad, (V ó F) de las proposiciones simples p y q que componen las proposiciones compuestas p q, p, p q, p q y p q, entonces podremos deducir el valor de verdad de estas. Lo anterior se logra mediante la elaboración de una tabla de verdad, la cual depende del conectivo lógico utilizado y de los valores de verdad (V ó F) de las proposiciones p y q.
14 Conjunción ( ) p q p q V V V V F F F V F F F F La proposición p q es verdadera si p y q son verdaderas, y falsa si alguna de ellas es falsa. Negación ( ) p V F p F V p es falso cuando p es verdadero y p es verdadero cuando p no lo es. Disyunción ( ) p q p q V V V V F V F V V F F F La proposición p q es falsa si las proposiciones p y q lo son, y verdadera en cualquier otro caso.
15 Conjunción ( ) p q p q Se pueden simbolizar los valores de verdad de una proposición; asignando 1 al valor verdadero y 0 al valor falso. Negación ( ) p p utilizando el sistema binario, mediante el cual se le asigna1 al valor verdadero y 0 al valor falso. Disyunción ( ) p q p q Se pueden simbolizar los valores de verdad de una proposición; asignando 1 al valor verdadero y 0 al valor falso.
16 Condicional ( ) p q p q V V V V F F F V V F F V La proposición p q es verdadera si nunca ocurre que p sea verdadera y que q sea falso. Bicondicional( ) p q p q V V V V F F F V F F F V La proposición p q es verdadera si p y q son ambas verdaderas o falsas, y falso en caso contrario.
17 Condicional ( ) p q p q Se pueden simbolizar los valores de verdad de una proposición; asignando 1 al valor verdadero y 0 al valor falso. Bicondicional( ) p q p q Se pueden simbolizar los valores de verdad de una proposición; asignando 1 al valor verdadero y 0 al valor falso.
18 Ejemplo 3.1 Elaborar la tabla de verdad de (p q) r. Solución. p q r q r p q (p q) r V V V F F V F V V F F V V V V F V V F V F V F F V V V V F V V F F F F F V F F V F F F F V V F V F F F F V V V V
19 Ejemplo 3.1 Elaborar la tabla de verdad de (p q) r. Solución. p q r q r p q (p q) r V V V F F V F V V F F V V V V F V V F V F V F F V V V V F V V F F F F F V F F V F F F F V V F V F F F F V V V V
20 Ejemplo 3.2 Elaborar la tabla de verdad de (p q) r. Solución. p q r p q (p q) r V V V V V V V F V F V F V F F V F F F V F V V V V F V F V F F F V V V F F F V F
21 Ejemplo 3.2 Elaborar la tabla de verdad de (p q) r. Solución. p q r p q (p q) r V V V V V V V F V F V F V F F V F F F V F V V V V F V F V F F F V V V F F F V F
22 Tautología Definición 4.1 Una tautología es una proposición que siempre es verdadera sin importar el valor de verdad de sus componentes. Ejemplo 4.1 Demostrar que la proposición (p q) ( q p) es una tautología. Demostración. Para verificar la validez de esta proposición es necesario realizar la tabla de verdad de ella:
23 Tautología Definición 4.1 Una tautología es una proposición que siempre es verdadera sin importar el valor de verdad de sus componentes. Ejemplo 4.1 Demostrar que la proposición (p q) ( q p) es una tautología. Demostración. Para verificar la validez de esta proposición es necesario realizar la tabla de verdad de ella:
24 Tautología Definición 4.1 Una tautología es una proposición que siempre es verdadera sin importar el valor de verdad de sus componentes. Ejemplo 4.1 Demostrar que la proposición (p q) ( q p) es una tautología. Demostración. Para verificar la validez de esta proposición es necesario realizar la tabla de verdad de ella:
25 Tautología p q p q q q p (p q) ( q p) Nótese que en la última columna solamente aparecen valores verdaderos. Luego, por definición la proposición dada es una tautología.
26 Absurdo o contradicción Definición 4.2 Un absurdo o contradicción es una proposición que siempre es falsa sin importar el valor de verdad de sus componentes. Ejemplo 4.2 Verifique que la proposición (p q) q es una contradicción.
27 Absurdo o contradicción Definición 4.2 Un absurdo o contradicción es una proposición que siempre es falsa sin importar el valor de verdad de sus componentes. Ejemplo 4.2 Verifique que la proposición (p q) q es una contradicción.
28 Absurdo o contradicción Solución. Construyamos la tabla de verdad de la proposición dada, así: p q q p q (p q) q V V F F F V F V V F F V F F F F F V F F Por lo tanto esta proposición es una contradicción.
29 Absurdo o contradicción Solución. Construyamos la tabla de verdad de la proposición dada, así: p q q p q (p q) q V V F F F V F V V F F V F F F F F V F F Por lo tanto esta proposición es una contradicción.
30 Proposiciones equivalentes Definición 4.3 Dos proposiciones compuestas P y Q se consideran logicamente equivalentes o simplemente equivalentes, y se denota P Q si y sólo si tienen los mismos valores de verdad para cada una de las opciones en la tabla de verdad. Note que lo anteior implica que P Q si y sólo si P Q es una tautología. Ejemplo 4.3 Las proposiciones (p q) y ( q p) son equivalentes puesto que en el ejemplo 4.1 se verificó que (p q) ( q p) es una tautología.
31 Proposiciones equivalentes Definición 4.3 Dos proposiciones compuestas P y Q se consideran logicamente equivalentes o simplemente equivalentes, y se denota P Q si y sólo si tienen los mismos valores de verdad para cada una de las opciones en la tabla de verdad. Note que lo anteior implica que P Q si y sólo si P Q es una tautología. Ejemplo 4.3 Las proposiciones (p q) y ( q p) son equivalentes puesto que en el ejemplo 4.1 se verificó que (p q) ( q p) es una tautología.
32 Equivalencias importantes Las siguientes equivalencias son ciertas (es decir los bicondicionales correspondientes son tautologías), y serán muy usadas en la construcción de argumentos validos. Sean P, Q y R proposiciones, entonces: Doble negación ( P ) P Idempotencia 1 P P P 2 P P P Conmutativa 1 P Q Q P 2 P Q Q P Asociativa 1 P (Q R) (P Q) R 2 P (Q R) (P Q) R
33 Equivalencias importantes Las siguientes equivalencias son ciertas (es decir los bicondicionales correspondientes son tautologías), y serán muy usadas en la construcción de argumentos validos. Sean P, Q y R proposiciones, entonces: Doble negación ( P ) P Idempotencia 1 P P P 2 P P P Conmutativa 1 P Q Q P 2 P Q Q P Asociativa 1 P (Q R) (P Q) R 2 P (Q R) (P Q) R
34 Equivalencias importantes Las siguientes equivalencias son ciertas (es decir los bicondicionales correspondientes son tautologías), y serán muy usadas en la construcción de argumentos validos. Sean P, Q y R proposiciones, entonces: Doble negación ( P ) P Idempotencia 1 P P P 2 P P P Conmutativa 1 P Q Q P 2 P Q Q P Asociativa 1 P (Q R) (P Q) R 2 P (Q R) (P Q) R
35 Equivalencias importantes Distributiva 1 P (Q R) (P Q) (P R) 2 P (Q R) (P Q) (P R) Leyes de De Morgan 1 (P Q) P Q 2 (P Q) P Q La prueba de todas estas equivalencias se realizan a través de tablas de verdad mostrando que los bicondicionales correspondientes son tautologías.
36 Equivalencias importantes La siguientes equivalencias se pueden probar a través de tablas de verdad mostrando que los bicondicionales correspondientes son tautologías o derivando resultados de las equivalencias que conocemos hasta el momento. Ejercicios 1 (P Q) ( P Q) (Condicional-negación y disyunción) 2 (P Q) (P Q) (Negación del condicional). 3 (P Q) ( Q P ) (Contrarrecíproco). 4 (P (Q Q)) P (Absorción). 5 (P (Q Q)) P (Absorción). 6 (P Q) ((P Q) (Q P )) (Bicondicional-condicional)
37 Equivalencias importantes La siguientes equivalencias se pueden probar a través de tablas de verdad mostrando que los bicondicionales correspondientes son tautologías o derivando resultados de las equivalencias que conocemos hasta el momento. Ejercicios 1 (P Q) ( P Q) (Condicional-negación y disyunción) 2 (P Q) (P Q) (Negación del condicional). 3 (P Q) ( Q P ) (Contrarrecíproco). 4 (P (Q Q)) P (Absorción). 5 (P (Q Q)) P (Absorción). 6 (P Q) ((P Q) (Q P )) (Bicondicional-condicional)
38 Equivalencias importantes Solución 1 Veamos que (P Q) ( P Q) es una tautología. Elaboremos su tabla de verdad: P Q P P Q P Q (P Q) ( P Q) V V F V V V V F F F F V F V V V V V F F V V V V 2 Usando las equivalencias vistas, tenemos: (P Q) ( P Q) Ejercicio 1 ( P ) Q Leyes de De Morgan P Q Doble negación.
39 Inferencias lógicas Para definir las inferencias lógicas es necesario precisar algunos conceptos tales como razonamiento y demostración. Razonamiento Es el proceso que se realiza para obtener una demostración. Demostración es el encadenamiento de proposiciones que permiten obtener otra proposición, llamada conclusión, a partir de ciertas proposiciones iniciales supuestas como verdaderas, que reciben el nombre de premisas.
40 Inferencias lógicas Inferencias lógicas Son las conclusiones que se pueden obtener después de realizar un razonamiento, este razonamiento solamente es verdadero si se cumplen las siguientes condiciones: 1 Las premisas deben ser verdaderas. 2 Durante el proceso de deducción las premisas deben relacionarse sujetas a las leyes de la lógica.
41 Reglas de inferencia A continuación se muestran las Reglas de Inferencia más utilizadas en la derivación de un argumento. La prueba de todas estas implicaciones se realizan a través de tablas de verdad mostrando que los bicondicionales correspondientes son tautologías. Simplificación (S) De P Q podemos inferir P. Esquematicamente, Adición (A) De P podemos inferir P Q. Esquematicamente, P Q P P P Q
42 Reglas de inferencia Modus Ponendo Ponens (MP) De P Q y P podemos inferir Q. Esquematicamente, P Q P Q Modus Tollendo Tollens (MT) De P Q y Q podemos inferir P. Esquematicamente, P Q Q P
43 Reglas de inferencia Silogismo Disyuntivo (SD) De P Q y Q podemos inferir P. Esquematicamente, P Q Q P Silogismo Hipotético (SH) De P Q y Q R podemos inferir P R. Esquematicamente, P Q Q R P R
44 Reglas de inferencia Adjunción (AD) De P y Q podemos inferir P Q. Esquematicamente, P Q P Q Dilema Constructivo (DC) De P Q, R S y P R podemos inferir Q S. Esquematicamente, P Q R S P R Q S
45 Reglas de inferencia Ejemplo 6.1 Demostrar c a partir de las premisas dadas. Premisa 1: b Premisa 2: a b Premisa 3: a c Demostración. 1. b (P) 2. a b (P) 3. a MT(1,2) 4. a c (P) 5. c MP(3,4)
46 Reglas de inferencia Ejemplo 6.2 Si un hombre se orienta siempre por su sentido del deber, tiene que renunciar al goce de muchos placeres, y si se guía siempre por su deseo de placer, a menudo olvidará su deber. O bien un hombre se guía siempre por su sentido del deber, o bien siempre se orienta por su deseo de placer. Si un hombre se guía siempre por su sentido del deber, no descuidará a menudo su deber, y si siempre se guía por su deseo de placer, no renunciará al goce de muchos placeres. Luego, un hombre debe renunciar al goce de muchos placeres si y sólo si no descuida a menudo su deber.
47 Reglas de inferencia Solución. Tomando el siguiente lenguaje formal: P : se orienta por su sentido del deber Q: renuncia al goce de placeres R: se guía por su deseo de placer S: olvidará su deber Las premisas quedan así: 1. P Q 2. R S 3. P R 4. P S 5. R Q Conclusión: Q S.
48 Reglas de inferencia 1. P R (P) 2. P Q (P) 3. R S (P) 4. Q S DC(1,2,3) 5. P S (P) 6. R Q (P) 7. S Q DC (1,5,6) 8. Q ( S) Doble nagación aplicada en Q S Condicional-negación y disyunción aplicada en S Q Condicional-negación y disyunción aplicada en (Q S) ( S Q) AD(9,10) 12. Q S Bicondicional-condicional aplicado a (10,11)
49 Funciones proposicionales Definición 7.1 Sea A un conjunto dado. Una función proposicional definida sobre A es una expresión p(x), la cual tiene la propiedad que p(a) es verdadera o falsa para cada a A. El conjunto A es llamado dominio de p(x), y el conjunto T p de todos los elemento de A para los cuales p(a) es verdadero es llamado el conjunto de verdad de p(x). En otras palabras, T p = {x : x A, p(x) es verdadera} Frecuentemente, cuando A es algún conjunto de números, la condició p(x) tiene la forma de una ecuación o inecuación que involucra la variable x.
50 Funciones proposicionales Ejemplo 7.1 Hallar el conjunto de verdad de cada función proposicional p(x) definida sobre el conjunto N de números naturales. 1 Sea p(x) : x + 2 > 7. El conjunto de verdad es T p = {x : x N, x + 2 > 7} = {6, 7, 8,...} que consiste de todos los naturales mayores que 5. 2 Sea p(x) : x + 5 < 3. El conjunto de verdad es T p = {x : x N, x + 5 < 3} = el conjunto vacío.
51 Cuantificador universal Sea p(x) una función proposicional definida sobre un conjunto A. Considere la expresión ( x A)p(x) o xp(x) la cual se lee Para todo x en A, p(x) es una declaración verdadera o, simplemente, Para todo x, p(x). El símbolo el cual se lee para todo o para cada es llamado el cuantificador universal.
52 Cuantificador universal Ejemplo La proposición ( n N)(n + 4 > 3) es verdadera 2 La proposición ( n N)(n + 2 > 8) es falsa
53 Cuantificador existencial Sea p(x) una función proposicional definida sobre un conjunto A. Considere la expresión ( x A)p(x) o x, p(x) la cual se lee Existe un x en A tal que p(x) es una declaración verdadera o, simplemente, Para algún x, p(x). El símbolo el cual se lee existe o para algún es llamado el cuantificador existencial.
54 Cuantificador existencial Ejemplo La proposición ( n N)(n + 4 < 7) es verdadera 2 La proposición ( n N)(n + 6 < 4) es falsa
55 Negación de declaraciones cuantificadas Teorema 7.1 (De Morgan) ( x A)p(x) ( x A) p(x) Teorema 7.2 (De Morgan) ( x A)p(x) ( x A) p(x) Ejemplo ( n N)(n + 4 > 3) ( n N)(n + 4 3). 2 ( n N)(n + 4 < 7) ( n N)(n + 4 7).
56 GRACIAS POR SU ATENCIÓN
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO I LOGICA Y CONJUNTOS.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
Introducción a la Lógica
 Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
MATEMÁTICAS BÁSICAS. 23 de febrero de Universidad Nacional de Colombia MATEMÁTICAS BÁSICAS
 23 de febrero de 2009 Parte I Lógica Proposiciones Considere las siguientes frases Páseme el lápiz. 2 + 3 = 5 1 2 + 1 3 = 2 5 Qué hora es? En Bogotá todos los días llueve Yo estoy mintiendo Maradona fue
23 de febrero de 2009 Parte I Lógica Proposiciones Considere las siguientes frases Páseme el lápiz. 2 + 3 = 5 1 2 + 1 3 = 2 5 Qué hora es? En Bogotá todos los días llueve Yo estoy mintiendo Maradona fue
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Módulo I: s Válidos Departamento de Matemáticas ITESM Módulo I: s Válidos Matemáticas Discretas - p. 1/50 En matemáticas y en lógica un argumento no es una disputa. Más bien,
Matemáticas Discretas TC1003 Módulo I: s Válidos Departamento de Matemáticas ITESM Módulo I: s Válidos Matemáticas Discretas - p. 1/50 En matemáticas y en lógica un argumento no es una disputa. Más bien,
Cálculo Proposicional
 Universidad Técnica ederico Santa María Departamento de Informática undamentos de Informática 1 Cálculo Proposicional Dr. Gonzalo Hernández Oliva Dr. Gonzalo Hernández USM I-1 Cálculo Proposicional 1 1)
Universidad Técnica ederico Santa María Departamento de Informática undamentos de Informática 1 Cálculo Proposicional Dr. Gonzalo Hernández Oliva Dr. Gonzalo Hernández USM I-1 Cálculo Proposicional 1 1)
REGLAS Y LEYES LOGICAS
 LOGICA II REGLAS Y LEYES LOGICAS Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente ciertos enunciados a partir de otros.
LOGICA II REGLAS Y LEYES LOGICAS Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente ciertos enunciados a partir de otros.
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo. Contenidos
 Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
2. Si P; Q; R son verdaderas y S; T son falsas, determine el valor de verdad de la proposición: [P =) (R =) T )] () [(:P ^ S) =) (Q =) :T )]
![2. Si P; Q; R son verdaderas y S; T son falsas, determine el valor de verdad de la proposición: [P =) (R =) T )] () [(:P ^ S) =) (Q =) :T )] 2. Si P; Q; R son verdaderas y S; T son falsas, determine el valor de verdad de la proposición: [P =) (R =) T )] () [(:P ^ S) =) (Q =) :T )]](/thumbs/52/30304807.jpg) Instituto Tecnológico de Costa Rica Escuela de Matemática I semestre 2012 Cálculo Diferencial e Integral. Prof. Juan José fallas. 1 Leyes de la lógica y reglas de inferencia 2 Ejercicios 1 Leyes de la
Instituto Tecnológico de Costa Rica Escuela de Matemática I semestre 2012 Cálculo Diferencial e Integral. Prof. Juan José fallas. 1 Leyes de la lógica y reglas de inferencia 2 Ejercicios 1 Leyes de la
RAZONAMIENTO LÓGICO LECCIÓN 1: ANÁLISIS DEL LENGUAJE ORDINARIO. La lógica se puede clasificar como:
 La lógica se puede clasificar como: 1. Lógica tradicional o no formal. 2. Lógica simbólica o formal. En la lógica tradicional o no formal se consideran procesos psicológicos del pensamiento y los métodos
La lógica se puede clasificar como: 1. Lógica tradicional o no formal. 2. Lógica simbólica o formal. En la lógica tradicional o no formal se consideran procesos psicológicos del pensamiento y los métodos
Ampliación Matemática Discreta. Justo Peralta López
 Justo Peralta López UNIVERSIDAD DE ALMERíA DEPARTAMENTO DE ÁGEBRA Y ANÁLISIS MATEMÁTICO 1 Introducción 2 Definición semántica de las proposiciones 3 Diagrama de valores de certeza 4 Evaluación de fórmulas.
Justo Peralta López UNIVERSIDAD DE ALMERíA DEPARTAMENTO DE ÁGEBRA Y ANÁLISIS MATEMÁTICO 1 Introducción 2 Definición semántica de las proposiciones 3 Diagrama de valores de certeza 4 Evaluación de fórmulas.
LICENCIATURA EN MATEMÁTICA. Práctico N 1 Lenguaje de la lógica. proposicional VICTOR GALARZA ROJAS 1 5 / 0 5 /
 Práctico N 1 Lenguaje de la lógica LICENCIATURA EN MATEMÁTICA proposicional VICTOR GALARZA ROJAS 1 5 / 0 5 / 2 0 1 0 PRÁCTICO N 1 1. Fundamentación: fundamentar la expresión Por lo tanto del siguiente
Práctico N 1 Lenguaje de la lógica LICENCIATURA EN MATEMÁTICA proposicional VICTOR GALARZA ROJAS 1 5 / 0 5 / 2 0 1 0 PRÁCTICO N 1 1. Fundamentación: fundamentar la expresión Por lo tanto del siguiente
Capítulo 1 Lógica Proposicional
 Capítulo 1 Lógica Proposicional 1.1 Introducción El ser humano, a través de su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de frases
Capítulo 1 Lógica Proposicional 1.1 Introducción El ser humano, a través de su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de frases
Capítulo 4. Lógica matemática. Continuar
 Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
SOBRE LOGICA MATEMATICA. Sandra M. Perilla-Monroy. Departamento de Ciencias Básicas, Universidad Santo Tomás, Bogotá, Colombia.
 SOBRE LOGICA MATEMATICA Sandra M. Perilla-Monroy Departamento de Ciencias Básicas, Universidad Santo Tomás, Bogotá, Colombia. Resumen. sandraperilla@usantotomas.edu.co Carrera 9 No 51-11 Bogotá Colombia
SOBRE LOGICA MATEMATICA Sandra M. Perilla-Monroy Departamento de Ciencias Básicas, Universidad Santo Tomás, Bogotá, Colombia. Resumen. sandraperilla@usantotomas.edu.co Carrera 9 No 51-11 Bogotá Colombia
RAZONAMIENTO MATEMÁTICO
 RAZONAMIENTO MATEMÁTICO I. LÓGICA PROPOSICIONAL A. Proposiciones B. Conectivos proposicionales B.. Negación B.2. Conjunción B.3. Disyunción B.4. Condicional B.5. Bicondicional B.6. Otros conectivos C.
RAZONAMIENTO MATEMÁTICO I. LÓGICA PROPOSICIONAL A. Proposiciones B. Conectivos proposicionales B.. Negación B.2. Conjunción B.3. Disyunción B.4. Condicional B.5. Bicondicional B.6. Otros conectivos C.
MATERIAL DE APOYO PARA EL PRIMER CURSO DE MATEMÁTICAS COMPUTACIONALES.
 MATERIAL DE APOYO PARA EL PRIMER CURSO DE MATEMÁTICAS COMPUTACIONALES. Ing. HUGO HUMBERTO MORALES PEÑA MAESTRÍA EN ENSEÑANZA DE LAS MATEMÁTICAS Línea de Matemáticas Computacionales UNIVERSIDAD TECNOLÓGICA
MATERIAL DE APOYO PARA EL PRIMER CURSO DE MATEMÁTICAS COMPUTACIONALES. Ing. HUGO HUMBERTO MORALES PEÑA MAESTRÍA EN ENSEÑANZA DE LAS MATEMÁTICAS Línea de Matemáticas Computacionales UNIVERSIDAD TECNOLÓGICA
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN
 INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
1.1.1 Conectivos lógicos, formas proposicionales y tablas de verdad.
 Tema 1 Lógica. 1.1 Cálculo proposicional. Definición 1.1 Una proposición es una frase o sentencia declarativa que es verdadera o falsa pero no ambas cosas a la vez. Los dos posibles valores de verdad que
Tema 1 Lógica. 1.1 Cálculo proposicional. Definición 1.1 Una proposición es una frase o sentencia declarativa que es verdadera o falsa pero no ambas cosas a la vez. Los dos posibles valores de verdad que
APENDICE REGLAS Y LEYES DE LA LOGICA DE PRIMER ORDEN
 LOGICA (FCE-UBA) APENDICE REGLAS Y LEYES DE LA LOGICA DE PRIMER ORDEN Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente
LOGICA (FCE-UBA) APENDICE REGLAS Y LEYES DE LA LOGICA DE PRIMER ORDEN Una regla lógica, o regla de inferencia (deductiva), es una forma válida de razonamiento que es empleada para inferir deductivamente
Inteligencia en Redes de Comunicaciones. Razonamiento lógico. Julio Villena Román.
 Inteligencia en Redes de Comunicaciones Razonamiento lógico Julio Villena Román jvillena@it.uc3m.es Índice La programación lógica Lógica de predicados de primer orden Sistemas inferenciales IRC 2009 -
Inteligencia en Redes de Comunicaciones Razonamiento lógico Julio Villena Román jvillena@it.uc3m.es Índice La programación lógica Lógica de predicados de primer orden Sistemas inferenciales IRC 2009 -
Benemérita Universidad Autónoma de Puebla
 Tarea No. 1 Matemáticas Elementales Profesor Fco. Javier Robles Mendoza Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Lógica y Conjuntos 1. Considere las proposiciones
Tarea No. 1 Matemáticas Elementales Profesor Fco. Javier Robles Mendoza Benemérita Universidad Autónoma de Puebla Facultad de Ciencias de la Computación Lógica y Conjuntos 1. Considere las proposiciones
ANOTACIONES BÁSICAS SOBRE LÓGICA PROPOSICIONAL FILOSOFÍA 1º BACHILLERATO
 Pág. 1 Lógica Proposicional La lógica proposicional es la más antigua y simple de las formas de lógica. Utilizando una representación primitiva del lenguaje, permite representar y manipular aserciones
Pág. 1 Lógica Proposicional La lógica proposicional es la más antigua y simple de las formas de lógica. Utilizando una representación primitiva del lenguaje, permite representar y manipular aserciones
No ~ Si entonces Sí y sólo si
 Principios de lógica. Principios de la lógica y o Objetivo general Establecer el valor de verdad de muchos de los enunciados lógicos, utilizando las leyes de la lógica y las de las inferencias, ya sea
Principios de lógica. Principios de la lógica y o Objetivo general Establecer el valor de verdad de muchos de los enunciados lógicos, utilizando las leyes de la lógica y las de las inferencias, ya sea
LÓGICA MATEMÁTICA O FORMAL O SIMBÓLICA
 LÓGICA MATEMÁTICA O FORMAL O SIMBÓLICA La lógica formal o simbólica, a diferencia de la lógica clásica, utiliza un lenguaje artificial, es decir, está rigurosamente construido, no admite cambios en el
LÓGICA MATEMÁTICA O FORMAL O SIMBÓLICA La lógica formal o simbólica, a diferencia de la lógica clásica, utiliza un lenguaje artificial, es decir, está rigurosamente construido, no admite cambios en el
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Lógica : Proposiciones, Conectivos, Tablas de Verdad y Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Lógica Matemáticas Discretas - p. 1/43 En esta lectura
Matemáticas Discretas TC1003 Lógica : Proposiciones, Conectivos, Tablas de Verdad y Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Lógica Matemáticas Discretas - p. 1/43 En esta lectura
MATEMÁTICA 1 JRC El futuro pertenece a aquellos que creen en la belleza de sus sueños
 MATEMÁTICA 1 JRC LÓGICA Es la ciencia formal que estudia los principios y procedimientos que permiten demostrar la validez o invalidez de una inferencia, es decir, reconocer entre un razonamiento correcto
MATEMÁTICA 1 JRC LÓGICA Es la ciencia formal que estudia los principios y procedimientos que permiten demostrar la validez o invalidez de una inferencia, es decir, reconocer entre un razonamiento correcto
Notas de Álgebra y Matemática Discreta
 Libros de Cátedra Notas de Álgebra y Matemática Discreta Liliana Alcón FACULTAD DE CIENCIAS EXACTAS NOTAS DE ÁLGEBRA Y MATEMÁTICA DISCRETA Liliana Alcón 2014 Alcón, Liliana Notas de algebra y matemática
Libros de Cátedra Notas de Álgebra y Matemática Discreta Liliana Alcón FACULTAD DE CIENCIAS EXACTAS NOTAS DE ÁLGEBRA Y MATEMÁTICA DISCRETA Liliana Alcón 2014 Alcón, Liliana Notas de algebra y matemática
LÓGICA PROPOSICIONAL
 LÓGICA PROPOSICIONAL QUE ES LA LÓGICA? El sentido ordinario de la palabra lógica se refiere a lo que es congruente, ordenado, bien estructurado. Lo ilógico es lo mismo que incongruente, desordenado, incoherente.
LÓGICA PROPOSICIONAL QUE ES LA LÓGICA? El sentido ordinario de la palabra lógica se refiere a lo que es congruente, ordenado, bien estructurado. Lo ilógico es lo mismo que incongruente, desordenado, incoherente.
Más sobre Leyes de implicación
 Más sobre Leyes de implicación Dilema constructivo. Se abrevia d.c. Se considera que si hay una disyunción que contiene los antecedentes de dos condicionales, la conclusión será la disyunción de los consecuentes.
Más sobre Leyes de implicación Dilema constructivo. Se abrevia d.c. Se considera que si hay una disyunción que contiene los antecedentes de dos condicionales, la conclusión será la disyunción de los consecuentes.
Taller Matemático. Lógica. Cristóbal Pareja Flores antares.sip.ucm.es/cpareja Facultad de Estadística Universidad Complutense de Madrid
 Taller Matemático Lógica Cristóbal Pareja Flores antares.sip.ucm.es/cpareja Facultad de Estadística Universidad Complutense de Madrid 1. Lógica 14 amigos aportan la misma cantidad de dinero, sobre un fondo
Taller Matemático Lógica Cristóbal Pareja Flores antares.sip.ucm.es/cpareja Facultad de Estadística Universidad Complutense de Madrid 1. Lógica 14 amigos aportan la misma cantidad de dinero, sobre un fondo
En general, un conjunto A se define seleccionando los elementos de un cierto conjunto U de referencia que cumplen una determinada propiedad.
 nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
Ejercicios de Lógica Proposicional *
 Ejercicios de Lógica Proposicional * FernandoRVelazquezQ@gmail.com Notación. El lenguaje proposicional que hemos definido, aquel que utiliza los cinco conectivos,,, y, se denota como L {,,,, }. Los términos
Ejercicios de Lógica Proposicional * FernandoRVelazquezQ@gmail.com Notación. El lenguaje proposicional que hemos definido, aquel que utiliza los cinco conectivos,,, y, se denota como L {,,,, }. Los términos
Tema 6: Teoría Semántica
 Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Conjuntos. () April 4, / 32
 Conjuntos En general, un conjunto A se de ne seleccionando los elementos de un cierto conjunto U de referencia (o universal) que cumplen una determinada propiedad. () April 4, 2014 1 / 32 Conjuntos En
Conjuntos En general, un conjunto A se de ne seleccionando los elementos de un cierto conjunto U de referencia (o universal) que cumplen una determinada propiedad. () April 4, 2014 1 / 32 Conjuntos En
Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos
 Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos Material preparado por: Prof. Ana María Tosetti Revisado y complementado por: Ing. Freddy Rabín Catedrático
Parte 1: Introducción a la lógica funcional Parte 2: Introducción a la teoría intuitiva de conjuntos Material preparado por: Prof. Ana María Tosetti Revisado y complementado por: Ing. Freddy Rabín Catedrático
Material diseñado para los estudiantes del NUTULA, alumnos del profesor Álvaro Moreno.01/10/2010 Lógica Proposicional
 Lógica Proposicional INTRODUCCIÓN El humano se comunica con sus semejantes a través de un lenguaje determinado (oral, simbólico, escrito, etc.) construido por frases y oraciones. Estas pueden tener diferentes
Lógica Proposicional INTRODUCCIÓN El humano se comunica con sus semejantes a través de un lenguaje determinado (oral, simbólico, escrito, etc.) construido por frases y oraciones. Estas pueden tener diferentes
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria) TEMA 70 LÓGICA PROPOSICIONAL. EJEMPLOS Y APLICACIONES AL RAZONAMIENTO MATEMÁTICO. 1. Introducción. 2. El Lenguaje para la Lógica de Proposiciones. 2.1.
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria) TEMA 70 LÓGICA PROPOSICIONAL. EJEMPLOS Y APLICACIONES AL RAZONAMIENTO MATEMÁTICO. 1. Introducción. 2. El Lenguaje para la Lógica de Proposiciones. 2.1.
Facultad de Informática. Módulo 1 Lógica. Matemática 0 UNLP. Curso de Ingreso 2013 Matemática 0 Página 1
 Matemática 0 UNLP Curso de Ingreso 2013 Matemática 0 Página 1 Contenido 1.1 Álgebra de proposiciones 3 Expresiones No Proposicionales 4 Enunciados Abiertos 4 Clasificación de las Proposiciones 4 1.2 Conectivos
Matemática 0 UNLP Curso de Ingreso 2013 Matemática 0 Página 1 Contenido 1.1 Álgebra de proposiciones 3 Expresiones No Proposicionales 4 Enunciados Abiertos 4 Clasificación de las Proposiciones 4 1.2 Conectivos
Lógica Proposicional. Guía Lógica Proposicional. Tema III: Cuantificadores
 Guía Lógica Proposicional Tema III: Cuantificadores 1.7.2. CUANTIFICADORES Los cuantificadores permiten afirmaciones sobre colecciones enteras de objetos en lugar de tener que enumerar los objetos por
Guía Lógica Proposicional Tema III: Cuantificadores 1.7.2. CUANTIFICADORES Los cuantificadores permiten afirmaciones sobre colecciones enteras de objetos en lugar de tener que enumerar los objetos por
Matemáticas Discretas. Oscar Bedoya
 Matemáticas Discretas Oscar Bedoya oscar.bedoya@correounivalle.edu.co http://eisc.univalle.edu.co/~oscarbed/md/ * Lógica proposicional * Concepto de proposición * Valores de verdad * Operadores lógicos
Matemáticas Discretas Oscar Bedoya oscar.bedoya@correounivalle.edu.co http://eisc.univalle.edu.co/~oscarbed/md/ * Lógica proposicional * Concepto de proposición * Valores de verdad * Operadores lógicos
Matemáticas Básicas para Computación
 Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 5 Nombre: Tablas de verdad Objetivo Al término de la sesión el participante aplicará los conceptos de lógica a través
Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 5 Nombre: Tablas de verdad Objetivo Al término de la sesión el participante aplicará los conceptos de lógica a través
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
L OGICA Proposiciones
 CAPíTULO 4 LÓGICA Uno de los procesos por los cuales adquirimos conocimiento es el proceso de razonamiento. A su vez, hay una variedad de modos o formas mediante las cuales razonamos o argumentamos a favor
CAPíTULO 4 LÓGICA Uno de los procesos por los cuales adquirimos conocimiento es el proceso de razonamiento. A su vez, hay una variedad de modos o formas mediante las cuales razonamos o argumentamos a favor
Una proposición es una afirmación que debe ser cierta o falsa (aunque no lo sepamos).
 Lógica intuitiva Una proposición es una afirmación que debe ser cierta o falsa (aunque no lo sepamos). A : Las águilas vuelan B : El cielo es rosa C : No existe vida extraterrestre D : 5 < 3 E : Algunos
Lógica intuitiva Una proposición es una afirmación que debe ser cierta o falsa (aunque no lo sepamos). A : Las águilas vuelan B : El cielo es rosa C : No existe vida extraterrestre D : 5 < 3 E : Algunos
Capítulo 2 Conjuntos. 2.1 Introducción. 2.2 Determinación de conjuntos. Definición:
 Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Lógica. Matemática discreta. Matemática discreta. Lógica
 Lógica Matemática discreta Lógica: rama de las matemáticas instrumento para representar el lenguaje natural proporciona un mecanismo de deducción 2 y de predicados Razonamientos Cálculo proposicional Cálculo
Lógica Matemática discreta Lógica: rama de las matemáticas instrumento para representar el lenguaje natural proporciona un mecanismo de deducción 2 y de predicados Razonamientos Cálculo proposicional Cálculo
Resumen de deducción natural
 Resumen de deducción natural F. Javier Gil Chica 2010 1. Orientación de estas notas El cálculo de argumentos mediante tablas de verdad es un método rápido y seguro. También mecánico, puesto que se puede
Resumen de deducción natural F. Javier Gil Chica 2010 1. Orientación de estas notas El cálculo de argumentos mediante tablas de verdad es un método rápido y seguro. También mecánico, puesto que se puede
UNIDAD 4: INTRODUCCIÓN A LA LÓGICA
 UNIDAD 4: INTRODUCCIÓN A LA LÓGICA Bien! hemos pasado a la segunda parte de los contenidos, espero que esos ánimos sigan predispuestos a continuar con el estudio de estos nuevos contenidos. Lo invitamos
UNIDAD 4: INTRODUCCIÓN A LA LÓGICA Bien! hemos pasado a la segunda parte de los contenidos, espero que esos ánimos sigan predispuestos a continuar con el estudio de estos nuevos contenidos. Lo invitamos
Capítulo 1 Lógica y Conjuntos
 Capítulo Lógica y Conjuntos Introducción Todos estamos familiarizados con la idea de que algunas personas poseen una mentalidad lógica mientras que otras no. No siempre resulta sencillo seguir razonamientos
Capítulo Lógica y Conjuntos Introducción Todos estamos familiarizados con la idea de que algunas personas poseen una mentalidad lógica mientras que otras no. No siempre resulta sencillo seguir razonamientos
INTRODUCCION AL ALGEBRA.
 INTRODUCCION AL ALGEBRA. 2- TEORIA DE CONJUNTOS. Apuntes de la Cátedra. Alberto Serritella. Colaboraron: Cristian Mascetti. Vanesa Bergonzi Edición Previa CECANA CECEJS CET Junín 2010. UNNOBA Universidad
INTRODUCCION AL ALGEBRA. 2- TEORIA DE CONJUNTOS. Apuntes de la Cátedra. Alberto Serritella. Colaboraron: Cristian Mascetti. Vanesa Bergonzi Edición Previa CECANA CECEJS CET Junín 2010. UNNOBA Universidad
John Venn Matemático y filósofo británico creador de los diagramas de Venn
 Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6]
![ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6] ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6]](/thumbs/51/28877791.jpg) ALGEBRA DE BOOLE El álgebra booleana, como cualquier otro sistema matemático deductivo, puede definirse con un conjunto de elementos, un conjunto de operadores y un número de axiomas no probados o postulados.
ALGEBRA DE BOOLE El álgebra booleana, como cualquier otro sistema matemático deductivo, puede definirse con un conjunto de elementos, un conjunto de operadores y un número de axiomas no probados o postulados.
Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional
![Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional](/thumbs/49/25492005.jpg) Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional 1. Responda las siguientes preguntas: a) Qué es un lenguaje formal? b) Qué es lenguaje matemático? c)
Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional 1. Responda las siguientes preguntas: a) Qué es un lenguaje formal? b) Qué es lenguaje matemático? c)
LÓGICA PROPOSICIONAL
 MATEMÁTICA I AÑO LÓGICA PROPOSICIONAL LÓGICA PROPOSICIONAL Nadie aprende si no se ha equivocado al intentarlo... - DE QUÉ TRATA LA LÓGICA? La lógica investiga la relación de consecuencia que se da entre
MATEMÁTICA I AÑO LÓGICA PROPOSICIONAL LÓGICA PROPOSICIONAL Nadie aprende si no se ha equivocado al intentarlo... - DE QUÉ TRATA LA LÓGICA? La lógica investiga la relación de consecuencia que se da entre
encontramos dos enunciados. El primero (p) nos afirma que Pitágoras era griego y el segundo (q) que Pitágoras era geómetra.
 Álgebra proposicional Introducción El ser humano, a través de su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de frases u oraciones. Estas
Álgebra proposicional Introducción El ser humano, a través de su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de frases u oraciones. Estas
Universidad Nacional Abierta y a Distancia UNAD-Lógica Matemática - Georffrey Acevedo G. A que viene la lógica?
 A que viene la lógica? Autor: Georffrey Acevedo G. Noviembre 16 de 2008. Los conceptos de proposiciones, conectivos e inferencias confluyen al analizar un razonamiento. Para tener claridad sobre los conceptos
A que viene la lógica? Autor: Georffrey Acevedo G. Noviembre 16 de 2008. Los conceptos de proposiciones, conectivos e inferencias confluyen al analizar un razonamiento. Para tener claridad sobre los conceptos
Lógica proposicional. Ivan Olmos Pineda
 Lógica proposicional Ivan Olmos Pineda Introducción Originalmente, la lógica trataba con argumentos en el lenguaje natural es el siguiente argumento válido? Todos los hombres son mortales Sócrates es hombre
Lógica proposicional Ivan Olmos Pineda Introducción Originalmente, la lógica trataba con argumentos en el lenguaje natural es el siguiente argumento válido? Todos los hombres son mortales Sócrates es hombre
Proposicional. Curso Mari Carmen Suárez de Figueroa Baonza
 Semántica Proposicional Curso 2014 2015 Mari Carmen Suárez de Figueroa Baonza mcsuarez@fi.upm.es Contenidos Introducción Interpretación de FBFs proposicionales Validez Satisfacibilidad Validez y Satisfacibilidad
Semántica Proposicional Curso 2014 2015 Mari Carmen Suárez de Figueroa Baonza mcsuarez@fi.upm.es Contenidos Introducción Interpretación de FBFs proposicionales Validez Satisfacibilidad Validez y Satisfacibilidad
Introd. al Pens. Científico Nociones básicas de la lógica ClasesATodaHora.com.ar
 ClasesATodaHora.com.ar > Exámenes > UBA - UBA XXI > Introd. al Pensamiento Científico Introd. al Pens. Científico Nociones básicas de la lógica ClasesATodaHora.com.ar Razonamientos: Conjunto de propiedades
ClasesATodaHora.com.ar > Exámenes > UBA - UBA XXI > Introd. al Pensamiento Científico Introd. al Pens. Científico Nociones básicas de la lógica ClasesATodaHora.com.ar Razonamientos: Conjunto de propiedades
Escuela de Ingeniería - Universidad de Chile Escuela de Verano 2011 Matemáticas III. Guía de Problemas N 1 *
 Escuela de Ingeniería - Universidad de Chile Escuela de Verano 2011 Matemáticas III Profesor: Pablo Dartnell Auxiliares: Roberto Castillo y Andrés Zúñiga Guía de Problemas N 1 * P1.- Sean p, q y r proposiciones.
Escuela de Ingeniería - Universidad de Chile Escuela de Verano 2011 Matemáticas III Profesor: Pablo Dartnell Auxiliares: Roberto Castillo y Andrés Zúñiga Guía de Problemas N 1 * P1.- Sean p, q y r proposiciones.
Lógica Matemática, Sistemas Formales, Cláusulas de Horn
 Lógica Matemática, Sistemas Formales, Cláusulas de Horn Lic. José Manuel Alvarado La lógica se ocupa de las argumentaciones válidas. Las argumentaciones ocurren cuando se quiere justificar una proposición
Lógica Matemática, Sistemas Formales, Cláusulas de Horn Lic. José Manuel Alvarado La lógica se ocupa de las argumentaciones válidas. Las argumentaciones ocurren cuando se quiere justificar una proposición
Negación Conjunción Dis junción. P -ip P Q P & Q P Q P V Q C F C C C C C C F C C F F C F C F C F F C C F F F F F F P Q P Q
 APITULO 4 TABLAS DE ERTEZA 4.1 Tablas de certeza Un método en general más conveniente que el diagrama para analizar los valores de certeza de proposiciones, es el de poner todas las posabilidades de certeza
APITULO 4 TABLAS DE ERTEZA 4.1 Tablas de certeza Un método en general más conveniente que el diagrama para analizar los valores de certeza de proposiciones, es el de poner todas las posabilidades de certeza
Apuntes de Lógica Proposicional
 Apuntes de Lógica Proposicional La lógica proposicional trabaja con expresiones u oraciones a las cuales se les puede asociar un valor de verdad (verdadero o falso); estas sentencias se conocen como sentencias
Apuntes de Lógica Proposicional La lógica proposicional trabaja con expresiones u oraciones a las cuales se les puede asociar un valor de verdad (verdadero o falso); estas sentencias se conocen como sentencias
Introducción. Lógica de proposiciones: introducción. Lógica de proposiciones. P (a) x. Conceptos
 Introducción César Ignacio García Osorio Lógica y sistemas axiomáticos 1 La lógica ha sido históricamente uno de los primeros lenguajes utilizados para representar el conocimiento. Además es frecuente
Introducción César Ignacio García Osorio Lógica y sistemas axiomáticos 1 La lógica ha sido históricamente uno de los primeros lenguajes utilizados para representar el conocimiento. Además es frecuente
Apuntes de Lógica Introducción Nociones de Lógica elemental Tablas de verdad Tautología y Contradicción Equivalencia lógica Algebra de proposiciones
 Apuntes de Lógica 1. Introducción 2. Nociones de Lógica elemental.proposiciones.conjunción.disyunción.negación.condicional.bicondicional.ejercicios 3. Tablas de verdad.construcción de tablas de verdad
Apuntes de Lógica 1. Introducción 2. Nociones de Lógica elemental.proposiciones.conjunción.disyunción.negación.condicional.bicondicional.ejercicios 3. Tablas de verdad.construcción de tablas de verdad
Forma lógica de enunciados
 Forma lógica de enunciados Marisol Miguel Cárdenas Lenguaje natural y lenguaje formal El lenguaje natural es aquel que utilizamos cotidianamente. Surge históricamente dentro de la sociedad y es aprendido
Forma lógica de enunciados Marisol Miguel Cárdenas Lenguaje natural y lenguaje formal El lenguaje natural es aquel que utilizamos cotidianamente. Surge históricamente dentro de la sociedad y es aprendido
Métodos de Inteligencia Artificial
 Métodos de Inteligencia Artificial L. Enrique Sucar (INAOE) esucar@inaoep.mx ccc.inaoep.mx/esucar Tecnologías de Información UPAEP Contenido Lógica proposicional Lógica de predicados Inferencia en lógica
Métodos de Inteligencia Artificial L. Enrique Sucar (INAOE) esucar@inaoep.mx ccc.inaoep.mx/esucar Tecnologías de Información UPAEP Contenido Lógica proposicional Lógica de predicados Inferencia en lógica
10.4 Sistemas de ecuaciones lineales
 Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 001 y MATE 02 Clase #11: martes, 14 de junio de 2016. 10.4 Sistemas de ecuaciones lineales
Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 001 y MATE 02 Clase #11: martes, 14 de junio de 2016. 10.4 Sistemas de ecuaciones lineales
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: ASIGNATURA: MATEMATICAS. NOTA
 INSTITUCION EDUCATIA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS. NOTA DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO ECHA N DURACION 1
INSTITUCION EDUCATIA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS. NOTA DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO ECHA N DURACION 1
INTRODUCCIÓN A LA LÓGICA
 UNIVERSIDAD NACIONAL DE RÍO CUARTO FACULTAD DE CIENCIAS EXACTAS, FÍSICO-QUÍMICAS Y NATURALES DEPARTAMENTO DE MATEMÁTICA INTRODUCCIÓN A LA LÓGICA Para el ingreso a las carreras de Matemática Material preparado
UNIVERSIDAD NACIONAL DE RÍO CUARTO FACULTAD DE CIENCIAS EXACTAS, FÍSICO-QUÍMICAS Y NATURALES DEPARTAMENTO DE MATEMÁTICA INTRODUCCIÓN A LA LÓGICA Para el ingreso a las carreras de Matemática Material preparado
ESCUELA MILITAR DE INGENIERÍA MISCELÁNEAS DE PROBLEMAS 2013 ÁLGEBRA I
 ESCUELA MILITAR DE INGENIERÍA Elaborado por: Lic. Bismar Choque Nina MISCELÁNEAS DE PROBLEMAS 2013 ÁLGEBRA I A pesar de que la refutación por ejemplo del contrario es un procedimiento válido, los teoremas
ESCUELA MILITAR DE INGENIERÍA Elaborado por: Lic. Bismar Choque Nina MISCELÁNEAS DE PROBLEMAS 2013 ÁLGEBRA I A pesar de que la refutación por ejemplo del contrario es un procedimiento válido, los teoremas
RAZONAMIENTO LÓGICO PARA LA ARGUMENTACIÓN JURÍDICA
 ESCUELA DEL MINISTERIO PÚBLICO Dr. Gonzalo Ortiz de Zevallos Roedel RAZONAMIENTO LÓGICO PARA LA ARGUMENTACIÓN JURÍDICA Dr. Luis Alberto Pacheco Mandujano Gerente Central de la Escuela del Ministerio Público
ESCUELA DEL MINISTERIO PÚBLICO Dr. Gonzalo Ortiz de Zevallos Roedel RAZONAMIENTO LÓGICO PARA LA ARGUMENTACIÓN JURÍDICA Dr. Luis Alberto Pacheco Mandujano Gerente Central de la Escuela del Ministerio Público
Unidad 2.- Lógica y tablas de verdad. Lógica
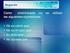 Lógica Algebra Booleana Las álgebras booleanas, estudiadas por primera vez en detalle por George Boole, constituyen un área de las matemáticas que ha pasado a ocupar un lugar prominente con el advenimiento
Lógica Algebra Booleana Las álgebras booleanas, estudiadas por primera vez en detalle por George Boole, constituyen un área de las matemáticas que ha pasado a ocupar un lugar prominente con el advenimiento
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS
 CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
La Lógica estudia la forma del razonamiento. La Lógica Matemática es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la
 LÓGICA MATEMÁTICA OBJETIVOS Definirás proposición simple. Definirás proposiciones compuestas: Disyunción y conjunción. Relacionarás dichas proposiciones con las operaciones de conjuntos: unión e intersección.
LÓGICA MATEMÁTICA OBJETIVOS Definirás proposición simple. Definirás proposiciones compuestas: Disyunción y conjunción. Relacionarás dichas proposiciones con las operaciones de conjuntos: unión e intersección.
CURSO NIVELACIÓN LÓGICA MATEMÁTICA PROYECTO UNICOMFACAUCA TU PROYECTO DE VIDA LAS PROPOSICIONES
 LAS PROPOSICIONES Objetivo Brindar al estudiante un concepto claro en la formulación, interpretación y aplicabilidad de las proposiciones. La interpretación de las proposiciones compuestas permite al estudiante
LAS PROPOSICIONES Objetivo Brindar al estudiante un concepto claro en la formulación, interpretación y aplicabilidad de las proposiciones. La interpretación de las proposiciones compuestas permite al estudiante
PRINCIPIOS DE LÓGICA. 1.1 CONCEPTO Y PROPÓSITO DE LA DE LÓGICA. UNIDAD 1. FUNDAMENTOS DE LÓGICA. Competencias:
 UNIDAD 1. FUNDAMENTOS DE LÓGICA. MAPA CONCEPTUAL LÓGICA MATEMÁTICA Como Es Ciencia de la razón Aporta Desarrolla Acción Pedagógica Genera Nuevos Saberse Que desarrollan Habilidades de Pensamiento Aprendizaje
UNIDAD 1. FUNDAMENTOS DE LÓGICA. MAPA CONCEPTUAL LÓGICA MATEMÁTICA Como Es Ciencia de la razón Aporta Desarrolla Acción Pedagógica Genera Nuevos Saberse Que desarrollan Habilidades de Pensamiento Aprendizaje
DEPARTAMENTO DE MATEMÁTICAS Página 1
 DEPARTAMENTO DE MATEMÁTICAS Página 1 APROBADO EN EL CONSEJO DE LA FACULTAD DE CIENCIAS EXACTAS ACTA 13 DEL 21 ABRIL 2010 PROGRAMAS DEL DEPARTAMENTO DE MATEMÁTICAS El presente formato tiene la finalidad
DEPARTAMENTO DE MATEMÁTICAS Página 1 APROBADO EN EL CONSEJO DE LA FACULTAD DE CIENCIAS EXACTAS ACTA 13 DEL 21 ABRIL 2010 PROGRAMAS DEL DEPARTAMENTO DE MATEMÁTICAS El presente formato tiene la finalidad
LÓGICA DE PROPOSICIONES. a) El rumor y el ir y venir incesante de las abejas. b) No te vayas! c) Hoy es martes.
 LÓGICA DE PROPOSICIONES 1. Cuál de las siguientes oraciones es una proposición lógica? a) El rumor y el ir y venir incesante de las abejas. b) No te vayas! c) Hoy es martes. La opción a) no es una proposición
LÓGICA DE PROPOSICIONES 1. Cuál de las siguientes oraciones es una proposición lógica? a) El rumor y el ir y venir incesante de las abejas. b) No te vayas! c) Hoy es martes. La opción a) no es una proposición
Matemáticas Discretas, Lógica: Predicados y Cuantificadores
 Matemáticas Discretas, Lógica: Predicados y Cuantificadores Prof. Víctor Bravo 1 1 Universidad de los Andes A-2008 Licencia de Uso Copyright (c), 2007. 2008, ULA. Permission is granted to copy, distribute
Matemáticas Discretas, Lógica: Predicados y Cuantificadores Prof. Víctor Bravo 1 1 Universidad de los Andes A-2008 Licencia de Uso Copyright (c), 2007. 2008, ULA. Permission is granted to copy, distribute
Introducción. El uso de los símbolos en matemáticas.
 Introducción El uso de los símbolos en matemáticas. En el estudio de las matemáticas lo primero que necesitamos es conocer su lenguaje y, en particular, sus símbolos. Algunos símbolos, que reciben el nombre
Introducción El uso de los símbolos en matemáticas. En el estudio de las matemáticas lo primero que necesitamos es conocer su lenguaje y, en particular, sus símbolos. Algunos símbolos, que reciben el nombre
Lógica Simbólica y Demostraciones
 Lógica Simbólica y Demostraciones Introducción al álculo Diego lejandro Mejía Guzmán El estudio de las formas de pensamiento y los métodos de razonamiento se remonta desde el siglo V a.. en las civilizaciones
Lógica Simbólica y Demostraciones Introducción al álculo Diego lejandro Mejía Guzmán El estudio de las formas de pensamiento y los métodos de razonamiento se remonta desde el siglo V a.. en las civilizaciones
Pregunta 1 Es correcta esta definición? Por qué?
 TEORÍA DE CONJUNTOS. En un libro de COU de 1975 puede leerse la siguiente definición de conjunto: Un conjunto es una colección de objetos, cualquiera que sea su naturaleza. Pregunta 1 Es correcta esta
TEORÍA DE CONJUNTOS. En un libro de COU de 1975 puede leerse la siguiente definición de conjunto: Un conjunto es una colección de objetos, cualquiera que sea su naturaleza. Pregunta 1 Es correcta esta
Un subconjunto no vacío H de un espacio vectorial V es un subespacio de V si se cumplen las dos reglas de cerradura:
 4 Subespacios 29 b) x 5 [25;5], 5 [;24], z 5 [4;4] Use a 5 2, a 5 / a 5 2 / 2 c) Su propia elección de x,, z /o a 2 a) Elija algunos valores para n m genere tres matrices aleatorias de n m, llamadas X,
4 Subespacios 29 b) x 5 [25;5], 5 [;24], z 5 [4;4] Use a 5 2, a 5 / a 5 2 / 2 c) Su propia elección de x,, z /o a 2 a) Elija algunos valores para n m genere tres matrices aleatorias de n m, llamadas X,
Lógica Proposicional
 Existen en la realidad un número considerable de problemas con los que una persona se enfrenta y de los cuales se deben deducir ciertos datos para poder resolverlos. Generalmente la forma en que las personas
Existen en la realidad un número considerable de problemas con los que una persona se enfrenta y de los cuales se deben deducir ciertos datos para poder resolverlos. Generalmente la forma en que las personas
Operaciones con conjuntos (ejercicios)
 Operaciones con conjuntos (ejercicios) Ejemplo: Definición de la diferencia de conjuntos. Sean y conjuntos. Entonces \ := { x: x x / }. Esto significa que para todo x tenemos la siguiente equivalencia:
Operaciones con conjuntos (ejercicios) Ejemplo: Definición de la diferencia de conjuntos. Sean y conjuntos. Entonces \ := { x: x x / }. Esto significa que para todo x tenemos la siguiente equivalencia:
Algoritmos y Estructura de Datos I
 Clase práctica de Especificación - Lógica proposicional Viernes 20 de Marzo de 2015 Menú del día Fórmulas bien formadas Tablas de verdad Tautologías, Contingencias y Contradicciones Relación de fuerza
Clase práctica de Especificación - Lógica proposicional Viernes 20 de Marzo de 2015 Menú del día Fórmulas bien formadas Tablas de verdad Tautologías, Contingencias y Contradicciones Relación de fuerza
Tema 9: Cálculo Deductivo
 Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 9: Cálculo Deductivo Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 24/10/2012 Introducción a la
Facultad de Informática Grado en Ingeniería Informática Lógica PARTE 2: LÓGICA DE PRIMER ORDEN Tema 9: Cálculo Deductivo Profesor: Javier Bajo jbajo@fi.upm.es Madrid, España 24/10/2012 Introducción a la
EJERCICIOS SOBRE PROPOSICIÓN. DEFINICIÓN Y CLASES
 INSTRUCCIÓN. Resuelve los problemas propuestos del modo siguiente: primero en forma individual, luego en forma grupal y por último preséntalo en forma grupal en un máximo de cinco (05) integrantes. EJERCICIOS
INSTRUCCIÓN. Resuelve los problemas propuestos del modo siguiente: primero en forma individual, luego en forma grupal y por último preséntalo en forma grupal en un máximo de cinco (05) integrantes. EJERCICIOS
GUIA DE TRABAJOS TEORICO PRACTICO N 1: LÓGICA DE LAS PROPOSICIONES
 CENTRO EDUCATIVO DE NIVEL TERCIARIO N 2 INTRODUCCIÓN A LA LOGICA SIMBOLICA PRIMER AÑO AÑO: 2005 GUIA DE TRABAJOS TEORICO PRACTICO N 1: LÓGICA DE LAS PROPOSICIONES La lógica es una ciencia formal, o sea,
CENTRO EDUCATIVO DE NIVEL TERCIARIO N 2 INTRODUCCIÓN A LA LOGICA SIMBOLICA PRIMER AÑO AÑO: 2005 GUIA DE TRABAJOS TEORICO PRACTICO N 1: LÓGICA DE LAS PROPOSICIONES La lógica es una ciencia formal, o sea,
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE CIENCIAS CARRERA DE MATEMÁTICO CONJUNTOS Y LÓGICA
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE CIENCIAS CARRERA DE MATEMÁTICO CONJUNTOS Y LÓGICA SEMESTRE: Segundo a cuarto CLAVE: 0271 HORAS A LA SEMANA/SEMESTRE TEÓRICAS PRÁCTICAS CRÉDITOS 5/80
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE CIENCIAS CARRERA DE MATEMÁTICO CONJUNTOS Y LÓGICA SEMESTRE: Segundo a cuarto CLAVE: 0271 HORAS A LA SEMANA/SEMESTRE TEÓRICAS PRÁCTICAS CRÉDITOS 5/80
Lógica, conjuntos, relaciones y funciones
 Lógica, conjuntos, relaciones y funciones Álvaro Pérez Raposo Universidad Autónoma de San Luis Potosí Universidad Politécnica de Madrid Publicaciones Electrónicas Sociedad Matemática Mexicana A la memoria
Lógica, conjuntos, relaciones y funciones Álvaro Pérez Raposo Universidad Autónoma de San Luis Potosí Universidad Politécnica de Madrid Publicaciones Electrónicas Sociedad Matemática Mexicana A la memoria
personal.us.es/elisacamol Elisa Cañete Molero Curso 2011/12
 Teoría de conjuntos. Teoría de Conjuntos. personal.us.es/elisacamol Curso 2011/12 Teoría de Conjuntos. Teoría de conjuntos. Noción intuitiva de conjunto. Propiedades. Un conjunto es la reunión en un todo
Teoría de conjuntos. Teoría de Conjuntos. personal.us.es/elisacamol Curso 2011/12 Teoría de Conjuntos. Teoría de conjuntos. Noción intuitiva de conjunto. Propiedades. Un conjunto es la reunión en un todo
Tópicos de Matemáticas Discretas
 Tópicos de Matemáticas Discretas Proposiciones Lógicas y Tablas de Verdad Raquel Torres Peralta Universidad de Sonora Matemáticas Discretas Proposiciones Lógicas Matemáticas Discretas Lógica - La lógica
Tópicos de Matemáticas Discretas Proposiciones Lógicas y Tablas de Verdad Raquel Torres Peralta Universidad de Sonora Matemáticas Discretas Proposiciones Lógicas Matemáticas Discretas Lógica - La lógica
Si..., siempre que, con tal que, puesto que, ya que, porque, cuando, de, a menos que, a no ser que, salvo que, solamente.
 1.2 Proposiciones condicionales y equivalencia lógica. Proposición Condicional o implicación lógica Una proposición condicional, es aquella que está formada por dos proposiciones atómicas o moleculares,
1.2 Proposiciones condicionales y equivalencia lógica. Proposición Condicional o implicación lógica Una proposición condicional, es aquella que está formada por dos proposiciones atómicas o moleculares,
Matemáticas Básicas para Computación
 Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 6 Nombre: Álgebra Booleana Objetivo Durante la sesión el participante identificará las principales características
Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 6 Nombre: Álgebra Booleana Objetivo Durante la sesión el participante identificará las principales características
Funciones y Cardinalidad
 Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Guía para el estudiante
 Guía para el estudiante Guía realizada por Jefferson Bustos Profesional en Matemáticas Master en Educación Nombre: Fecha: Curso: Dentro del lenguaje común, las palabras y frases pueden tener diversas interpretaciones.
Guía para el estudiante Guía realizada por Jefferson Bustos Profesional en Matemáticas Master en Educación Nombre: Fecha: Curso: Dentro del lenguaje común, las palabras y frases pueden tener diversas interpretaciones.
