Los pesos de las partículas pueden reemplazarse por una única (equivalente) resultante con un punto de aplicación G bien definido.
|
|
|
- Manuel Valdéz Serrano
- hace 7 años
- Vistas:
Transcripción
1 UNIDAD 2 EQUILIBRIO DE CUERPOS RÍGIDOS. CENTROS DE GRAVEDAD GENERALIDADES.- El centro de gravedad es aquel que localiza el peso resultante de un sistema de partículas y el centro de masas de un sistema de partículas discretas. Para ello consideraremos un sistema de n partículas fijo dentro de una región del espacio. Los pesos de las partículas pueden reemplazarse por una única (equivalente) resultante con un punto de aplicación G bien definido. Es decir, un sistema de fuerzas paralelas entre sí, puede ser sustituido por una fuerza única resultante, como la suma algebraica (W R ) que actúa sobre un punto específico. UNELLEZ - INGENIERÍA CIVIL 14
2 Ese es el punto de aplicación que tendrá por coordenadas x, y y z, y se le denominará Centro de Gravedad (G). El Peso resultante = peso total de las n partículas La suma de los momentos de los pesos de todas las partículas respecto a los ejes x, y, z ejes = momento del peso resultante respecto a esos ejes. La Suma de momentos respecto al eje x. La Suma de momentos respecto al eje y. Aunque los pesos no producen momento sobre el eje z, podemos rotar el sistema de coordenadas 90 respecto al eje x (o y) con las partículas fijas y sumar los momentos respecto al eje x (o y), Ya que el Peso = m.g Esto implica que el centro de gravedad coincide con el centro de masas. Las partículas tienen peso solo bajo la influencia de una atracción gravitatoria, mientras que el centro de masas es independiente de la gravedad. UNELLEZ - INGENIERÍA CIVIL 15
3 CENTROS DE GRAVEDAD DE ÁREAS SIMÉTRICAS Y REGULARES El centro de gravedad de áreas regulares y/o simétricas de cuerpos rígidos, tales como: cuadrados, rectángulos, triángulos, círculos, entre otros, coinciden su centro geométrico de tal forma: r G. a G h G a b Momentos de Primer Orden. Si se tiene un área cualquiera, referidos a un sistema de ejes cartesianos, a su vez, esta puede subdividirse en varias áreas conocidas A 1, A 2, A 3 A n. Entonces se denomina momento de primer orden al producto de dicho eje al considerado. S x = A 1. Y 1 + A 2. Y 2 + A 3. Y A n. Y n En resumen: S x = n i=1 A i. Y i De forma similar con respecto al eje Y: n S y = A i. X i i=1 UNELLEZ - INGENIERÍA CIVIL 16
4 Un cuerpo rígido está compuesto por un número infinito de partículas. Si consideramos una partícula arbitraria de peso d W. Por otra parte, si un área definida por el contorno y = f (x) ; se lleva a un elemento infinitesimal, teniendo: Donde x, y y z respectivamente, se denominan momentos estáticos de primer orden respecto a los ejes x, y y z. Centro de Gravedad para un Sistema de Partículas. Si se considera un sistema de n partículas fijas contenidas en un espacio de coordenadas x, y y z. Para el centroide de la superficie de un objeto, tal como una placa o un disco, subdividimos el área en elementos diferenciales d A. UNELLEZ - INGENIERÍA CIVIL 17
5 CENTROIDE DE UNA LÍNEA. Si la geometría de un objeto (rígido), por ejemplo una varilla o un alambre, que tenga la forma de una línea continua y homogénea, se elige un diferencial de longitud d L, que tiene coordenadas x, y y z respectivamente En este caso el centro de gravedad del objeto no necesariamente debe estar sobre la línea, sino fuera de ella, tal como se muestra en la figura. Entonces se tiene que: UNELLEZ - INGENIERÍA CIVIL 18
6 Eje de Simetría. En el caso de figuras plana, el centro de gravedad G, necesariamente se encuentra dentro de esa área. UNELLEZ - INGENIERÍA CIVIL 19
7 Ejemplo # 1. Centros de Gravedad de Áreas Demostrar que el centro de gravedad de un rectángulo es b h y h 2 respectivamente. y Solución: d y h Los lados de b y h se tiene d A = b.dy Aplicando la definición, se tiene: b y x Aŷ = y. d A ; ŷ = ŷ = b. y 2 2 b.h h 0 = b.h2 2.b.h h 0 y.b dy A pero como A = b.h ; ŷ = h 2 Demostramos a X Aplicando la definición, se tiene: d A = h.dx ; x = b 0 X da A pero como d A = h.dx b 0 X.hdx b.h ŷ = h. x2 2 b.h b 0 = h.b 2 2.b.h ; x = b 2 Ejemplo # 2. Determinar el centro de gravedad de un triángulo. Solución: y d A = s.dy Dado que A = ½ b.h, aplicando la definición se tiene: d y I h s y ŷ = s = b h y.d A d A por semejanza de triángulo b s = h h y => (h y) sustituyendo el valor de G b x ŷ = h y. b 0 h (h y ) d y h 0 b h (h y ) d y = b h b h h 0 (h y 2 ) d y h 0 (h y) d y ŷ = h.y y 3 h.y y 2 2 h 0 h = centro de gravedad a 1/3h de la base y a una distancia 2/3h del vértice h3 1 ; ŷ = 1. h identifica el 2 h2 3 UNELLEZ - INGENIERÍA CIVIL 20
8 UNELLEZ - INGENIERÍA CIVIL 21
9 Ejemplo # 3. Determinar el centro de gravedad de la figura compuesta que se muestra. Solución: C1 C2 UNELLEZ - INGENIERÍA CIVIL 22
10 Ejemplo # 4. Determinar el centro de gravedad de la figura. Solución:. Ejemplo # 5. Localice el centro de gravedad de la figura compuesta. UNELLEZ - INGENIERÍA CIVIL 23
11 Ejemplo # 6. Localice el centro de gravedad de la figura compuesta. UNELLEZ - INGENIERÍA CIVIL 24
12 Ejemplo # 7. Determinar el centro de gravedad de la figura. UNELLEZ - INGENIERÍA CIVIL 25
13 Ejemplo # 8. Determinar el centro de gravedad de la figura. Un cuarto de Elipse Ejemplo # 9. Determinar el centro de gravedad de la figura. UNELLEZ - INGENIERÍA CIVIL 26
14 Ejemplo # 10. Determinar el centro de gravedad de la figura. UNELLEZ - INGENIERÍA CIVIL 27
15 Usando Y de un arco de radio En el límite como Δ 0 Así que: UNELLEZ - INGENIERÍA CIVIL 28
16 Ejemplo # 11. El eje horizontal x señala el centroide del área mostrada y divide el área en dos componentes A 1 y A 2. Determine el primer momento para cada componente de área respecto al eje x, y explique los resultados obtenidos. Primero, se localiza y en la figura Área 1 Área 2 UNELLEZ - INGENIERÍA CIVIL 29
17 Centros de Gravedad de Líneas Ejemplo # 12. Determinar la distancia de x al centro de gravedad de una varilla homogénea de forma parabólica. Si la varilla tiene un peso por unidad de longitud de 0.5 lb/ft. Determine la reacción al soporte de apoyo O. Solución: = 0 UNELLEZ - INGENIERÍA CIVIL 30
18 Ejemplo # 13. Una varilla uniforme de acero es doblada en un arco circular con radio de 500 mm. La varilla está apoyada por un vínculo A y una cuerda BC. Determine la tensión de la cuerda y la reacción en A. Solución: Primero, por definición sabemos que: También note que la deflexión ABD es un triángulo equilátero. Equilibrando se tiene:: UNELLEZ - INGENIERÍA CIVIL 31
19 Ejemplo # 14. Un alambre homogéneo de acero es doblada en un arco parabólico. Determine por integración la coordenada x de su centroide. Solución: Primero, notemos que debido a que el alambre es homogéneo, su centro de gravedad coincide con el centroide de la línea correspondiente se tiene: Luego: Entonces: Entonces: UNELLEZ - INGENIERÍA CIVIL 32
20 Ejemplo # 15. Un alambre homogéneo de acero es doblada en un arco parabólico. Determine por integración la coordenada x de su centroide. Solución: Primero, notemos que debido a que el alambre es homogéneo, su centro de gravedad coincide con el centroide de la línea correspondiente Ahora: Luego: Y: Entonces: UNELLEZ - INGENIERÍA CIVIL 33
21 Centros de Gravedad de Volúmenes Ejemplo # 16. Determine el volumen y área del sólido obtenido por rotación del área del ejemplo # 4. a) referente al eje x, b) a la línea x = 165 mm. Solución: De la solución del Ejemplo # 4, tenemos: Área Aplicando el Teorema de Pappus-Guldinus, tenemos: Línea (b) La Rotación referente al eje x: (a) La Rotación referente a x= 165 mm: UNELLEZ - INGENIERÍA CIVIL 34
22 Ejemplo # 17. En un agujero de 15 mm de díametro se introduce un tornillo de acero de 20 mm de espesor, el orificio luego es compensado por el tornillo, tal como se muestra. Determine el volumen del acero removido durante el proceso de atornillado Solución: El volumen requerido puede ser generado por la rotación del área mostrada referenten al eje y. aplicando el segundo Teorema de Pappus-Guldinus, tenemos: UNELLEZ - INGENIERÍA CIVIL 35
23 Ejemplo # 18. Determine el volumen y el área de superficie de la figura mostrada, el cual está hecha de 2 in (pulgadas) de diámetro. Si R = 3 in y L = 10 in. Solución: Notemos que el área A y la circunferencia C del cruce de la sección del tubo es: Observemos que el final de la sección semicircular puede ser obtenida por la rotación al cruce de la sección a través del arco semicircular del radio R. Luego aplicando el segundo Teorema de Pappus-Guldinus, tenemos: UNELLEZ - INGENIERÍA CIVIL 36
CENTRO DE GRAVEDAD Y CENTROIDE. Considerando el sistema de n partículas fijo dentro de una región del espacio,
 CENTRO DE GRAVEDAD Y CENTROIDE Centro de gravedad y centro de masa para un sistema de partículas Centro de gravedad Considerando el sistema de n partículas fijo dentro de una región del espacio, Los pesos
CENTRO DE GRAVEDAD Y CENTROIDE Centro de gravedad y centro de masa para un sistema de partículas Centro de gravedad Considerando el sistema de n partículas fijo dentro de una región del espacio, Los pesos
TEMA II CENTRO DE GRAVEDAD Y CENTROIDES
 Universidad de los Andes Facultad de Ingeniería Departamento de Ciencias Aplicadas y Humanísticas. Mecánica Racional 10 TEMA II CENTRO DE GRAVEDAD Y CENTROIDES Apuntes de clases, de la profesora Nayive
Universidad de los Andes Facultad de Ingeniería Departamento de Ciencias Aplicadas y Humanísticas. Mecánica Racional 10 TEMA II CENTRO DE GRAVEDAD Y CENTROIDES Apuntes de clases, de la profesora Nayive
Si se incrementa el número de elementos en los cuales se ha dividido la placa y simultáneamente se disminuye el tamaño de cada elemento se obtiene
 Capítulo 5 Fuerzas distribuidas. Centroides y centros de gravedad Introducción La acción de la Tierra sobre un cuerpo rígido debe representarse por un gran número de pequeñas fuerzas distribuidas sobre
Capítulo 5 Fuerzas distribuidas. Centroides y centros de gravedad Introducción La acción de la Tierra sobre un cuerpo rígido debe representarse por un gran número de pequeñas fuerzas distribuidas sobre
ESTÁTICA. Mecánica vectorial para ingenieros: Centroides y Centros de Gravedad. Novena edición CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
 Novena edición CAPÍTULO : ESTÁTICA Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University Centroides y Centros de Gravedad 2010 The McGraw-Hill Companies, Inc. All
Novena edición CAPÍTULO : ESTÁTICA Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University Centroides y Centros de Gravedad 2010 The McGraw-Hill Companies, Inc. All
CENTRO DE GRAVEDAD, CENTRO DE MASA Y CENTROIDE
 UNIERSIDD NION DE O FUTD DE INGENIERÍ EÉTRI Y EETRÓNI ESUE PROFESION DE INGENIERÍ EÉTRI ENTRO DE GREDD, ENTRO DE MS Y ENTROIDE ING. JORGE MONTÑO PISFI O, 2010 ENTRO DE GREDD, ENTRO DE MSYY ENTROIDE ENTRO
UNIERSIDD NION DE O FUTD DE INGENIERÍ EÉTRI Y EETRÓNI ESUE PROFESION DE INGENIERÍ EÉTRI ENTRO DE GREDD, ENTRO DE MS Y ENTROIDE ING. JORGE MONTÑO PISFI O, 2010 ENTRO DE GREDD, ENTRO DE MSYY ENTROIDE ENTRO
DIVISIÓN DE INGENIERÍAS CIVIL Y GEOMÁTICA DEPARTAMENTO DE ESTRUCTURAS
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE INGENIERÍAS CIVIL Y GEOMÁTICA DEPARTAMENTO DE ESTRUCTURAS ASIGNATURA: TEMA: ESTÁTICA ESTRUCTURAL CENTROIDES CENTROIDES: CENTRO
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE INGENIERÍAS CIVIL Y GEOMÁTICA DEPARTAMENTO DE ESTRUCTURAS ASIGNATURA: TEMA: ESTÁTICA ESTRUCTURAL CENTROIDES CENTROIDES: CENTRO
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Centro de gravedad de un cuerpo bidimensional
 Centro de gravedad de un cuerpo bidimensional Al sumar las fuerzas en la dirección z vertical y los momentos alrededor de los ejes horizontales y y x, Aumentando el número de elementos en que está dividida
Centro de gravedad de un cuerpo bidimensional Al sumar las fuerzas en la dirección z vertical y los momentos alrededor de los ejes horizontales y y x, Aumentando el número de elementos en que está dividida
Centro de masa. Centro de gravedad. Centroides.
 Centro de masa. Centro de gravedad. Centroides. MOMENTOS Hasta ahora se han calculado momentos de fuerzas. Sin embargo, en muchos problemas de ingeniería aparecen momentos de masas, fuerzas, volúmenes,
Centro de masa. Centro de gravedad. Centroides. MOMENTOS Hasta ahora se han calculado momentos de fuerzas. Sin embargo, en muchos problemas de ingeniería aparecen momentos de masas, fuerzas, volúmenes,
Problemas propuestos: Estatica condiciones de equilibrio,centro de gravedad
 Problemas propuestos: Estatica condiciones de equilibrio,centro de gravedad Curso Fisica I 1. Una barra de masa M y de largo L se equilibra como se indica en la figura 1. No hay roce. Determine el ángulo
Problemas propuestos: Estatica condiciones de equilibrio,centro de gravedad Curso Fisica I 1. Una barra de masa M y de largo L se equilibra como se indica en la figura 1. No hay roce. Determine el ángulo
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
Monday, March 26, 12
 cómo puede influir la sección transversal de un objeto en su equilibrio? es importante para la construcción de estructuras? fuerzas distribuidas: centroides centros de gravedad areas líneas centro de gravedad
cómo puede influir la sección transversal de un objeto en su equilibrio? es importante para la construcción de estructuras? fuerzas distribuidas: centroides centros de gravedad areas líneas centro de gravedad
TRABAJO DE INVESTIGACIÓN
 TRABAJO DE INVESTIGACIÓN TEMA: 3.7.- CENTROIDES DE GRAVEDAD DE LÍNEAS, ÁREAS Y VOLÚMENES DE CUADROS COMPUESTOS UTILIZANDO TABLAS.. GRUPO: 402 UNIDAD: 3 FECHA: 25/abril/2016 INTEGRANTES: Barrios Flores
TRABAJO DE INVESTIGACIÓN TEMA: 3.7.- CENTROIDES DE GRAVEDAD DE LÍNEAS, ÁREAS Y VOLÚMENES DE CUADROS COMPUESTOS UTILIZANDO TABLAS.. GRUPO: 402 UNIDAD: 3 FECHA: 25/abril/2016 INTEGRANTES: Barrios Flores
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ALGEBRA I GUÍA N o 2 DE GEOMETRÍA ANALÍTICA Profesor: David Elal Olivero Primer año Plan Común de Ingeniería Primer Semestre 2009
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ALGEBRA I GUÍA N o 2 DE GEOMETRÍA ANALÍTICA Profesor: David Elal Olivero Primer año Plan Común de Ingeniería Primer Semestre 2009
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
SEMEJANZA Y PROPORCIONALIDAD
 SEMEJANZA Y PROPORCIONALIDAD Teorema de Pitágoras En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. congruencia ( ) : Dos figuras son congruentes
SEMEJANZA Y PROPORCIONALIDAD Teorema de Pitágoras En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. congruencia ( ) : Dos figuras son congruentes
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS
 CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 4.- ESTATICA. 3.1.- Centro de gravedad de un cuerpo. Un cuerpo de masa M, se puede considerar compuesto por multitud de partículas
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 4.- ESTATICA. 3.1.- Centro de gravedad de un cuerpo. Un cuerpo de masa M, se puede considerar compuesto por multitud de partículas
Sólido Rígido. Momento de Inercia 17/11/2013
 Sólido ígido Un sólido rígido es un sistema formado por muchas partículas que tiene como característica que la posición relativa de todas ellas permanece constante durante el movimiento. A B El movimiento
Sólido ígido Un sólido rígido es un sistema formado por muchas partículas que tiene como característica que la posición relativa de todas ellas permanece constante durante el movimiento. A B El movimiento
5.1 a Localícese el centroide del área plana mostrada en la figura. Fig. 5.1 Fig. 5.2 Fig. 5.3
 5.1 a 5.7.- Localícese el centroide del área plana mostrada en la figura. Fig. 5.1 Fig. 5.2 Fig. 5.3 Fig. 5.4 Fig. 5.5 Fig. 5.6 Fig. 5.7 5.8.- El primer momento del área sombreada con respecto del eje
5.1 a 5.7.- Localícese el centroide del área plana mostrada en la figura. Fig. 5.1 Fig. 5.2 Fig. 5.3 Fig. 5.4 Fig. 5.5 Fig. 5.6 Fig. 5.7 5.8.- El primer momento del área sombreada con respecto del eje
4. PROPIEDAD DE ÁREAS PLANAS Y LINEAS Centroides de áreas compuestas
 4. PROPIEDAD DE ÁREAS PLANAS Y LINEAS 4.1. Centroides de áreas compuestas 4.1.1. Centros de gravedad de un cuerpo bidimensional Para iniciar, considere una placa plana horizontal (figura 5.1). La placa
4. PROPIEDAD DE ÁREAS PLANAS Y LINEAS 4.1. Centroides de áreas compuestas 4.1.1. Centros de gravedad de un cuerpo bidimensional Para iniciar, considere una placa plana horizontal (figura 5.1). La placa
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
PROBLEMAS PROPUESTOS
 PROBLEMAS PROPUESTOS En los problemas que a continuación se proponen, el campo gravitacional de intensidad g actúa verticalmente en el plano que coincide con la hoja de papel. 1.- La esfera A de radio
PROBLEMAS PROPUESTOS En los problemas que a continuación se proponen, el campo gravitacional de intensidad g actúa verticalmente en el plano que coincide con la hoja de papel. 1.- La esfera A de radio
PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO.
 PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO. FACULTAD DE MATEMATICAS UNIVERSIDAD VERACRUZANA 2010 Xalapa, Ver. México 1 1. La distancia entre dos puntos en la recta real es 5. Si uno de los puntos
PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO. FACULTAD DE MATEMATICAS UNIVERSIDAD VERACRUZANA 2010 Xalapa, Ver. México 1 1. La distancia entre dos puntos en la recta real es 5. Si uno de los puntos
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω
 ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
4.3 - Determine el punto (distinto del infinito) en el cual el campo eléctrico es igual a cero.
 Unidad Nº 4 Electrostática Ley de Coulomb Campo eléctrico 4.1 - En las esquinas de un triángulo equilátero existen tres cargas puntuales, fijas, como se ve en la figura, cuyos valores son: q1=2µc, q2=-4µc
Unidad Nº 4 Electrostática Ley de Coulomb Campo eléctrico 4.1 - En las esquinas de un triángulo equilátero existen tres cargas puntuales, fijas, como se ve en la figura, cuyos valores son: q1=2µc, q2=-4µc
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
 1 1.1. INTRODUCCIÓN Se ha supuesto que la atracción ejercida por la tierra sobre un cuerpo rígido puede representarse por una sola fuerza W, esta fuerza, denominada fuerza de gravedad o peso del cuerpo,
1 1.1. INTRODUCCIÓN Se ha supuesto que la atracción ejercida por la tierra sobre un cuerpo rígido puede representarse por una sola fuerza W, esta fuerza, denominada fuerza de gravedad o peso del cuerpo,
ALTURAS DE UN TRIÁNGULO
 TRIÁNGULO Polígono de tres lados. Según la longitud de sus lados, los triángulos se clasifican en equiláteros, si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escálenos, si los
TRIÁNGULO Polígono de tres lados. Según la longitud de sus lados, los triángulos se clasifican en equiláteros, si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escálenos, si los
Índice 1. Conocimientos básicos de dibujo geométrico... 1
 Índice 1. Conocimientos básicos de dibujo geométrico... 1 1.1 Trazado de una perpendicular (mediatriz) en el punto medio de una recta (AB)... 1 1.2 Trazado de una perpendicular en un punto cualquiera (C)
Índice 1. Conocimientos básicos de dibujo geométrico... 1 1.1 Trazado de una perpendicular (mediatriz) en el punto medio de una recta (AB)... 1 1.2 Trazado de una perpendicular en un punto cualquiera (C)
Sistema Bidimensional
 Capítulo 7 Sistema Bidimensional 7.1. Sistema Cartesiano La correspondencia entre pares ordenados de números reales y puntos en el plano, idea inicial que se debe a Renato Descartes (1596-1650), es lo
Capítulo 7 Sistema Bidimensional 7.1. Sistema Cartesiano La correspondencia entre pares ordenados de números reales y puntos en el plano, idea inicial que se debe a Renato Descartes (1596-1650), es lo
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
TEMA 6: GEOMETRÍA EN EL PLANO
 TEMA 6: GEOMETRÍA EN EL PLANO Definiciones/Clasificaciones Fórmulas y teoremas Dem. Def. y Clasificación de polígonos: Regular o irregular Cóncavo o convexo Por número de lados: o Triángulos: clasificación
TEMA 6: GEOMETRÍA EN EL PLANO Definiciones/Clasificaciones Fórmulas y teoremas Dem. Def. y Clasificación de polígonos: Regular o irregular Cóncavo o convexo Por número de lados: o Triángulos: clasificación
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA
 SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera Soluciones del boletín de problemas 6
 2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
8 GEOMETRÍA DEL PLANO
 8 GEOMETRÍ DEL PLNO EJERIIOS PR ENTRENRSE Ángulos y triángulos 8.6 Halla la medida del ángulo p en el siguiente triángulo. 6 4 180 6 p 4 p 180 6 4 11 8.7 alcula la suma de los ángulos interiores de un
8 GEOMETRÍ DEL PLNO EJERIIOS PR ENTRENRSE Ángulos y triángulos 8.6 Halla la medida del ángulo p en el siguiente triángulo. 6 4 180 6 p 4 p 180 6 4 11 8.7 alcula la suma de los ángulos interiores de un
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Estática. Centro de Gravedad y Centroide
 Estática 9 Centro de Gravedad y Centroide Objetivos Concepto de centro de gravedad, centro de masas y centroide Determinar la localización del centro de gravedad y del centroide para un sistema de partículas
Estática 9 Centro de Gravedad y Centroide Objetivos Concepto de centro de gravedad, centro de masas y centroide Determinar la localización del centro de gravedad y del centroide para un sistema de partículas
Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31)
 Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
El cálculo de la viga superior no presenta mayores problemas, ya que su volumen corresponde al de un prisma recto cuyas dimensiones se indican:
 Consideremos el problema: Usted es un ingeniero civil y se le ha encargado la tarea de construir un puente. Para ello necesita cubicar (dimensionar), para saber la cantidad de material necesario para hacer
Consideremos el problema: Usted es un ingeniero civil y se le ha encargado la tarea de construir un puente. Para ello necesita cubicar (dimensionar), para saber la cantidad de material necesario para hacer
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Introducción a la geometría
 Introducción a la geometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares. Plan de estudios (217 temas)
Introducción a la geometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares. Plan de estudios (217 temas)
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA
 Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA ASIGNATURA: Cálculo Diferencial e Integral I PROFESOR: José Alexander Echeverría Ruiz CUATRIMESTRE: Segundo TÍTULO DE LA
Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA ASIGNATURA: Cálculo Diferencial e Integral I PROFESOR: José Alexander Echeverría Ruiz CUATRIMESTRE: Segundo TÍTULO DE LA
Aplicaciones físicas
 Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
UNIVERSIDAD AUTÓNOMA DE CHIAPAS FACULTAD DE INGENIERÍA CAMPUS I ESTATICA
 UNIVERSIDAD AUTÓNOMA DE CHIAPAS FACULTAD DE INGENIERÍA CAMPUS I ESTATICA NIVEL: LICENCIATURA CRÉDITOS: 9 CLAVE: ICAC24.500917 HORAS TEORÍA: 4.5 SEMESTRE: TERCERO HORAS PRÁCTICA: 0 REQUISITOS: CINEMATICA
UNIVERSIDAD AUTÓNOMA DE CHIAPAS FACULTAD DE INGENIERÍA CAMPUS I ESTATICA NIVEL: LICENCIATURA CRÉDITOS: 9 CLAVE: ICAC24.500917 HORAS TEORÍA: 4.5 SEMESTRE: TERCERO HORAS PRÁCTICA: 0 REQUISITOS: CINEMATICA
VIII. MOMENTOS DE INERCIA
 VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
27.- La diferencia entre el lado de un triangulo equilátero y su altura es 12 cm. Cuanto mide el perímetro del triangulo?
 EJERCICIOS 1.- Calcular la altura a la hipotenusa de un triángulo rectángulo cuyos catetos miden 6 y 8 cm. 5 2.- En un triángulo rectángulo, un cateto mide 15 cm., y la proyección del otro sobre la hipotenusa
EJERCICIOS 1.- Calcular la altura a la hipotenusa de un triángulo rectángulo cuyos catetos miden 6 y 8 cm. 5 2.- En un triángulo rectángulo, un cateto mide 15 cm., y la proyección del otro sobre la hipotenusa
PÁGINA 88. Pág. 1. Unidad 9. Problemas métricos en el plano
 Soluciones a las actividades de cada epígrafe PÁGINA 88 1 En los siguientes triángulos rectángulos, se dan dos catetos y se pide la hipotenusa (si su medida no es eacta, dala con una cifra decimal): a)
Soluciones a las actividades de cada epígrafe PÁGINA 88 1 En los siguientes triángulos rectángulos, se dan dos catetos y se pide la hipotenusa (si su medida no es eacta, dala con una cifra decimal): a)
Mecánica de Fluidos y Máquinas Hidráulicas
 Mecánica de Fluidos y Máquinas Hidráulicas Tema 02. Está-ca de Fluidos Severiano F. Pérez Remesal Carlos Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica bajo Licencia:
Mecánica de Fluidos y Máquinas Hidráulicas Tema 02. Está-ca de Fluidos Severiano F. Pérez Remesal Carlos Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica bajo Licencia:
4- Fuerzas Distribuidas
 4- Fuerzas Distribuidas Prof. JOSÉ BENJUMEA ROYERO Ing. Civil, Magíster en Ing. Civil Contenido 4. Fuerzas distributivas 4.1 Centro de gravedad de un cuerpo bidimensional. 4.2 Centroide de áreas y líneas.
4- Fuerzas Distribuidas Prof. JOSÉ BENJUMEA ROYERO Ing. Civil, Magíster en Ing. Civil Contenido 4. Fuerzas distributivas 4.1 Centro de gravedad de un cuerpo bidimensional. 4.2 Centroide de áreas y líneas.
UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS.
 UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS. Área de un sector en coordenadas polares. Área de una superficie de revolución. Volumen de un sólido de revolución. Objetivos Instructivos. Con esta
UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS. Área de un sector en coordenadas polares. Área de una superficie de revolución. Volumen de un sólido de revolución. Objetivos Instructivos. Con esta
Péndulo de torsión y momentos de inercia
 Prácticas de Física Péndulo de torsión y momentos de inercia 1 Objetivos Curso 2009/10 Determinar la constante de un muelle espiral Determinar el momento de inercia de varios sólidos rígidos Comprobar
Prácticas de Física Péndulo de torsión y momentos de inercia 1 Objetivos Curso 2009/10 Determinar la constante de un muelle espiral Determinar el momento de inercia de varios sólidos rígidos Comprobar
Formulario: Geometría Analítica
 Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
Unidad III. Si f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida :
![Unidad III. Si f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida : Unidad III. Si f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida :](/thumbs/62/48065993.jpg) Unidad III Aplicaciones de la integral. 3.1 Áreas. 3.1.1 Área bajo la gráfica de una función. Si f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida
Unidad III Aplicaciones de la integral. 3.1 Áreas. 3.1.1 Área bajo la gráfica de una función. Si f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 17 Indice. 1. Líneas y Curvas. 2. Ángulos en el plano. 3. Medida de un ángulo. 4. Tipos de Ángulos. 5. Teorema de
Geometría del Plano. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 17 Indice. 1. Líneas y Curvas. 2. Ángulos en el plano. 3. Medida de un ángulo. 4. Tipos de Ángulos. 5. Teorema de
Unidad 6. Objetivos. Equilibrio, momento de una fuerza. Al término de la unidad, el alumno:
 Unidad 6 Equilibrio, momento de una fuerza Objetivos Al término de la unidad, el alumno: Definir e identificar los brazos de palanca que se generan por la aplicación de fuerzas que se aplican sobre algunos
Unidad 6 Equilibrio, momento de una fuerza Objetivos Al término de la unidad, el alumno: Definir e identificar los brazos de palanca que se generan por la aplicación de fuerzas que se aplican sobre algunos
INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES
 INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES Hasta el momento hemos tratado integrales dobles en las cuales la región de integración es una región rectangular de la forma *(
INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES Hasta el momento hemos tratado integrales dobles en las cuales la región de integración es una región rectangular de la forma *(
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Tema 5: Tensor de Inercia
 Tema 5: Tensor de Inercia Mecánica Racional, 2º, Grado en Ingeniería Civil Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Índice Introducción Momentos de inercia de cuerpos continuos Tensor
Tema 5: Tensor de Inercia Mecánica Racional, 2º, Grado en Ingeniería Civil Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Índice Introducción Momentos de inercia de cuerpos continuos Tensor
TRIÁNGULOS Y CUADRILÁTEROS.
 TRIÁNGULOS Y CUADRILÁTEROS. 1. Triángulos. Al polígono de tres lados se le llama triángulo. Clasificación: Según sus lados, un triángulo puede ser Equilátero, si tiene los tres lados iguales Isósceles,
TRIÁNGULOS Y CUADRILÁTEROS. 1. Triángulos. Al polígono de tres lados se le llama triángulo. Clasificación: Según sus lados, un triángulo puede ser Equilátero, si tiene los tres lados iguales Isósceles,
GEOMETRÍA PLANA 3º E.S.O. Un polígono es una figura geométrica plana y cerrada limitada por tres o más segmentos llamados lados.
 GEOMETRÍA PLANA 3º E.S.O. POLÍGONO.- Un polígono es una figura geométrica plana y cerrada limitada por tres o más segmentos llamados lados. El triángulo (tres lados), el cuadrilátero (cuatro lados), el
GEOMETRÍA PLANA 3º E.S.O. POLÍGONO.- Un polígono es una figura geométrica plana y cerrada limitada por tres o más segmentos llamados lados. El triángulo (tres lados), el cuadrilátero (cuatro lados), el
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD NACIONAL EXPERIMENTAL DE LOS LLANOS OCCIDENTALES EZEQUIEL ZAMORA VICERRECTORADO DE INFRAESTRUCTURAS Y PROCESOS INDUSTRIALES
 UNELLEZ UNIVERSIDAD NACIONAL EXPERIMENTAL DE LOS LLANOS OCCIDENTALES EZEQUIEL ZAMORA VICERRECTORADO DE INFRAESTRUCTURAS Y PROCESOS INDUSTRIALES PROGRAMA DE INGENIERÍA, ARQUITECTURA Y TECNOLOGÍA INGENIERÍA
UNELLEZ UNIVERSIDAD NACIONAL EXPERIMENTAL DE LOS LLANOS OCCIDENTALES EZEQUIEL ZAMORA VICERRECTORADO DE INFRAESTRUCTURAS Y PROCESOS INDUSTRIALES PROGRAMA DE INGENIERÍA, ARQUITECTURA Y TECNOLOGÍA INGENIERÍA
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
 EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO
 Liceo Pedro de Valdivia La Calera PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO - 2015 Nombre del Profesor: Eduardo Hernán Guerra Cuevas Título: Geometría euclidiana Tiempo estimado: 65 horas pedagógicas UNIDAD
Liceo Pedro de Valdivia La Calera PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO - 2015 Nombre del Profesor: Eduardo Hernán Guerra Cuevas Título: Geometría euclidiana Tiempo estimado: 65 horas pedagógicas UNIDAD
El Geoplano como Herramienta Didáctica para la Enseñanza de la Geometría
 como Herramienta Didáctica para la Enseñanza de la Geometría Luis F. Cáceres Ph.D César A. Barreto Universidad de Puerto Rico, Recinto Universitario de Mayagüez Abril 30 de 2011 Que es el Geoplano? El
como Herramienta Didáctica para la Enseñanza de la Geometría Luis F. Cáceres Ph.D César A. Barreto Universidad de Puerto Rico, Recinto Universitario de Mayagüez Abril 30 de 2011 Que es el Geoplano? El
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
Guía de estudio Nº 3: Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas
 U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
TRANSFORMACIONES EN EL PLANO
 ACADEMIA SABATINA TRANSFORMACIONES EN EL PLANO Llamaremos transformación geométrica a una operación que permite producir una nueva figura (imagen) de la dada originalmente. Las podemos clasificar en directas,
ACADEMIA SABATINA TRANSFORMACIONES EN EL PLANO Llamaremos transformación geométrica a una operación que permite producir una nueva figura (imagen) de la dada originalmente. Las podemos clasificar en directas,
GEOMETRÍA ANALÍTICA PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES
 PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
Repaso de Geometría. Ahora formulamos el teorema:
 Repaso de Geometría Preliminares: En esta sección trabajaremos con los siguientes temas: I. El Teorema de Pitágoras. II. Fórmulas básicas de geometría: perímetro, área y volumen. I. El Teorema de Pitágoras.
Repaso de Geometría Preliminares: En esta sección trabajaremos con los siguientes temas: I. El Teorema de Pitágoras. II. Fórmulas básicas de geometría: perímetro, área y volumen. I. El Teorema de Pitágoras.
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
TALLER 5. GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER 5. GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 01-1 Profesor: Jaime Andres Jaramillo González. jaimeaj@conceptocomputadores.com Parte de este documento es tomado
TALLER 5. GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 01-1 Profesor: Jaime Andres Jaramillo González. jaimeaj@conceptocomputadores.com Parte de este documento es tomado
Matemáticas II Magisterio (Primaria) Curso Problemas de repaso
 Matemáticas II Magisterio (rimaria) urso 2013-2014 1. alcula la medida del ángulo a de la figura. roblemas de repaso 116 105 a Sol: a = 49. 2. Sabiendo que los puntos, y R están sobre una circunferencia
Matemáticas II Magisterio (rimaria) urso 2013-2014 1. alcula la medida del ángulo a de la figura. roblemas de repaso 116 105 a Sol: a = 49. 2. Sabiendo que los puntos, y R están sobre una circunferencia
A RG. Diédrico 22. Sección 3. Cilindro recto por un proyectante Hoja 1/2
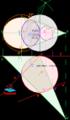 Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
3.1. Distancia entre dos puntos. Definición 3.1. Sean a, b e, se llama distancia entre los números a y b que se denota por d (a, b), a la cantidad:
 III. UNIDAD: GEOMETRIA ANALITICA LANA. La Geometría Analítica permite usar los métodos algebraicos en la solución de problemas geométricos, recíprocamente, los métodos de la geometría analítica pueden
III. UNIDAD: GEOMETRIA ANALITICA LANA. La Geometría Analítica permite usar los métodos algebraicos en la solución de problemas geométricos, recíprocamente, los métodos de la geometría analítica pueden
CUERPOS DE REVOLUCIÓN
 PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA
 Departamento de Física Aplicada Universidad de Castilla-La Mancha Escuela Técnica Superior Ing. Agrónomos PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA Materiales * Varilla delgada con orificios practicados
Departamento de Física Aplicada Universidad de Castilla-La Mancha Escuela Técnica Superior Ing. Agrónomos PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA Materiales * Varilla delgada con orificios practicados
LA PARADOJA DE BERTRAND: Un problema y varias soluciones.
 LA PARADOJA DE BERTRAND: Un problema y varias soluciones. Juan Manuel Valderas Jaramillo {valderas@us.es} Elena Olmedo Fernández {olmedo@us.es} Luis Franco Martín {lfranco@us.es} Departamento de Economía
LA PARADOJA DE BERTRAND: Un problema y varias soluciones. Juan Manuel Valderas Jaramillo {valderas@us.es} Elena Olmedo Fernández {olmedo@us.es} Luis Franco Martín {lfranco@us.es} Departamento de Economía
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
ESCUELA PREPARATORIA OFICIAL NÚM. 11 PROGRAMA DEL ESTUDIANTE POR MATERIA PRIMER PERIODO DE TRABAJO DEL SEGUNDO SEMESTRE DEL CICLO ESCOLAR
 EPO 11 ESCUELA PREPARATORIA OFICIAL NÚM. 11 CUAUTITLAN IZCALLI, MEX. PROGRAMA DEL ESTUDIANTE POR MATERIA PRIMER PERIODO DE TRABAJO DEL SEGUNDO SEMESTRE DEL CICLO ESCOLAR 2014-2015 Materia: GEOMETRÍA ANALÍTICA_
EPO 11 ESCUELA PREPARATORIA OFICIAL NÚM. 11 CUAUTITLAN IZCALLI, MEX. PROGRAMA DEL ESTUDIANTE POR MATERIA PRIMER PERIODO DE TRABAJO DEL SEGUNDO SEMESTRE DEL CICLO ESCOLAR 2014-2015 Materia: GEOMETRÍA ANALÍTICA_
2 =0 (3.146) Expresando, las componentes del tensor de esfuerzos en coordenadas cartesianas como: 2 ; = 2 2 ; =
 3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
3.7. Función de Airy Cuando las fuerzas de cuerpo b son constantes en un sólido con estado de deformación o esfuerzo plano, el problema elástico se simplifica considerablemente mediante el uso de una función
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 CTIVIDDES DE GEMETRÍ PR 4º ES DE EPV Nombre y apellidos: Curso: TEM 1: TRZDS BÁSICS. 1. RECTS PRLELS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar. 1.1. Trazado
CTIVIDDES DE GEMETRÍ PR 4º ES DE EPV Nombre y apellidos: Curso: TEM 1: TRZDS BÁSICS. 1. RECTS PRLELS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar. 1.1. Trazado
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
Universidad Nacional del Litoral Facultad de Ingeniería y Ciencias Hídricas GUÍA DE PROBLEMAS
 UNIDAD V: CUERPO RÍGIDO GUÍA DE PROBLEMAS 1) a) Calcular los valores de los momentos de cada una de las fuerzas mostradas en la figura respecto del punto O, donde F1 = F = F3 = 110N y r1 = 110 mm, r =
UNIDAD V: CUERPO RÍGIDO GUÍA DE PROBLEMAS 1) a) Calcular los valores de los momentos de cada una de las fuerzas mostradas en la figura respecto del punto O, donde F1 = F = F3 = 110N y r1 = 110 mm, r =
El teorema de Euclides tiene dos enunciados que conocemos con los nombres de teorema del cateto y teorema de la altura.
 El teorema de Euclides tiene dos enunciados que conocemos con los nombres de teorema del cateto y teorema de la altura. Teorema del cateto: El cateto de un triángulo rectángulo es media proporcional entre
El teorema de Euclides tiene dos enunciados que conocemos con los nombres de teorema del cateto y teorema de la altura. Teorema del cateto: El cateto de un triángulo rectángulo es media proporcional entre
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S GEOMETRÍA ANALÍTICA
 IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S DE GEOMETRÍA ANALÍTICA CONCEPTOS BÁSICOS 1.- Hallar la distancia entre los pares de puntos cuyas coordenadas son: a) A (4, 1), B (3, 2)
IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S DE GEOMETRÍA ANALÍTICA CONCEPTOS BÁSICOS 1.- Hallar la distancia entre los pares de puntos cuyas coordenadas son: a) A (4, 1), B (3, 2)
CONTENIDO SÓLIDO RÍGIDO I. CINEMÁTICA. Definición de sólido rígido. Cálculo de la posición del centro de masas. Movimiento de rotación y de traslación
 CONTENIDO Definición de sólido rígido Cálculo de la posición del centro de masas Movimiento de rotación y de traslación Movimiento del sólido rígido en el plano Momento de inercia Teorema de Steiner Tema
CONTENIDO Definición de sólido rígido Cálculo de la posición del centro de masas Movimiento de rotación y de traslación Movimiento del sólido rígido en el plano Momento de inercia Teorema de Steiner Tema
Cuáles son las imágenes de los puntos M,N,O,P respecto eje x?
 Guía N 3 Nombre: Curso: 1 Medio A-B-C-D Unidad Geometría Fecha: Profesora: Odette Castro M. Contenidos: Transformaciones isométricas en el plano cartesiano Simetría Axial 1. Dibuja la figura simétrica,
Guía N 3 Nombre: Curso: 1 Medio A-B-C-D Unidad Geometría Fecha: Profesora: Odette Castro M. Contenidos: Transformaciones isométricas en el plano cartesiano Simetría Axial 1. Dibuja la figura simétrica,
