Instituto Superior del Profesorado Dr. Joaquín V. González Departamento de Matemática - Curso de Nivelación A N E X O T E Ó R I C O
|
|
|
- Manuela Rodríguez Rivero
- hace 7 años
- Vistas:
Transcripción
1 A N E X O T E Ó R I C O Coteido Cojutos uméricos... 2 Módulo o Vlor bsoluto... 5 PROPIEDADES DE LA POTENCIACIÓN... 6 PROPIEDADES DE LA RADICACIÓN... 7 Logritmció... 8 Expresioes lgebrics... 8 Poliomios... 8 Opercioes co poliomios... 9 Ríces y Fctorizció de poliomios Expresioes lgebrics rcioles Itervlos reles Fucioes FUNCIONES POLINÓMICAS FUNCIÓN CONSTANTE FUNCIÓN LINEAL FUNCIÓN CUADRÁTICA Águlos Polígoos Triágulos Triágulo rectágulo Trigoometrí e el triágulo rectágulo Cudriláteros Circufereci y círculo Perímetro y Áre de Figurs Pls Cuerpos Áre y Volume de cuerpos geométricos... 20
2 Cojutos uméricos NÚMEROS NATURALES Los úmeros turles so quellos que se us pr cotr y umerr. El cojuto se simboliz co N y uque el cero puede o o ser cosiderdo como úmero turl, veces pr evitr duds se simboliz N 0 l cojuto que lo icluye N= {0; 1; 2; 3; 4; 5;.} Algus propieddes importtes so: N tiee u primer elemeto (el cero) o tiee u último elemeto, es por lo tto, u cojuto ifiito N es u cojuto discreto porque etre dos úmeros turles siempre hy u úmero fiito de úmeros turles. Todo úmero turl, tiee su sucesor +1. OPERACIONES Ls opercioes siempre posibles e el cojuto de los úmeros turles so: Sum, Producto y Potecició U úmero turl se puede expresr como producto de otros úmeros turles, que se llm fctores o divisores del primero. Ls opercioes posibles e lguos csos so: -Rest (si el miuedo es myor que el sustredo e N, y si el miuedo es myor o igul que el sustredo e N 0 ). -Cociete (Si el dividedo es múltiplo del divisor y éste es distito de cero). -Rdicció (Podemos extrer ríces cudrds de cudrdos perfectos, ríces cúbics de cubos perfectos, etc.). NÚMEROS ENTEROS El cojuto de los úmeros eteros es u mplició del cojuto de los úmeros turles. L ecesidd de relizr l operció 3-8, por ejemplo, justificó l creció de los úmeros egtivos. Al cojuto formdo por los úmeros turles, sus correspodietes egtivos y el cero se lo llm cojuto de los úmeros eteros. L otció que se us pr idetificr l cojuto de los úmeros eteros es: Z = {.,-4,-3,-2,-1, 0, 1, 2, 3,.} Propieddes importtes: OPERACIONES Z o tiee primero i último elemeto Cd úmero tiee u tecesor y u sucesor. Z es u cojuto discreto. Todo úmero etero tiee su opuesto -, tl que + (-) = 0 Al relizr ls opercioes de sum, rest y multiplicció de úmeros eteros,
3 siempre se obtiee como resultdo u úmero etero. Pr el producto y el cociete se debe teer e cuet l regl de los sigos. L potecició es posible si l bse es eter pero el expoete es turl Números Pres e Impres U umero pr es quel etero que se puede escribir de l form: 2k, dode k es u etero (los úmeros pres so los múltiplos del úmero 2). Los úmeros eteros que o so pres, se llm úmeros impres y se puede escribir como 2k+1 Los úmeros pres so: { -4, -2, 0, 2, 4, 6, } y los impres: { -5, -3, -1, 1, 3, 5, } Divisibilidd e Z U úmero etero 0 es divisor de otro úmero etero b si existe u tercer úmero etero tl que se verific. = b. E símbolos: b Z /b=. (se lee es divisor de b ) Decir que es divisor de b es equivlete decir que b es divisible por o bie que b es u múltiplo de. Ejemplo: 32 es divisible por 4 puesto que 32= 4.8 Etoces 4 32 U umero etero b, distito de 0, 1 y 1, se llm PRIMO si y solo si dmite solo cutro divisores: 1, 1, el mismo úmero y su opuesto. Por ejemplo: 3 es u úmero primo pues sus divisores so -3; - 1; 1; 3 A los úmeros distitos de 0, 1 y -1 que dmite más de cutro divisores se los llm úmeros COMPUESTOS Observció: 1 y 1 o so úmeros primos i compuestos. Dos úmeros eteros so COPRIMOS ó PRIMOS ENTRE SI, cudo solo tiee como divisor comú 1 y - 1. Tegmos e cuet que si bie dos úmeros primos so siempre coprimos, o es ecesrio que los úmeros ddos se primos pr que resulte coprimos. NÚMEROS RACIONALES Los úmeros rcioles so quellos que se puede escribir como cociete de dos úmeros eteros (co divisor distito de cero) Simbólicmete: b, dode y b so eteros y b 0 recibe el ombre de umerdor y b se llm deomidor.
4 Eteros positivos +1; +2; +3; egtivos -1; -2; -3; = {0} Rcioles Frcciorios Decimles exctos 2,5 = Puros Periódicos Periódicos Mixtos 0,6 = 2,333 = 2, 3 = 2,132 = 4,323 = 0, 12 = 0,214 = Propieddes importtes de este cojuto umérico: Etre dos úmeros rcioles existe ifiitos rcioles, por eso se dice que o es discreto sio que es u cojuto deso. Como cosecueci de esto, o puede hblrse de úmeros rcioles cosecutivos. Expresió deciml de u rciol Q o tiee primero i último elemeto. Pr expresr u frcció como úmero deciml es suficiete efectur el cociete etre el umerdor y el deomidor. Tl como se muestr e el cudro terior, l expresió deciml obteid puede teer u úmero fiito de cifrs decimles, o bie, u úmero ifiito de cifrs decimles que se repite ifiitmete. OPERACIONES - SUMA c + = b d. d b. c b. d co b, d 0 - RESTA: pr restr dos frccioes, simplemete summos l miuedo el opuesto del sustredo: - PRODUCTO c - = + c. d b. c = b d b d b. d c. c. = b d b. d co b, d 0 - COCIENTE: el cociete se resuelve multiplicdo el dividedo por el recíproco o iverso del divisor: c d : =. = b d b c Recordr: Dos úmeros rcioles so recíprocos o iversos multiplictivos si su producto es igul 1. Hy u úmero rciol que o tiee recíproco... Cuál es?. d b. c
5 - POTENCIACION: l potecició puede hcerse e el cojuto de los úmeros rcioles pr bse rciol y expoete etero b b b b b -RADICACION: b c d c d b NÚMEROS IRRACIONALES Hy úmeros que se crcteriz porque tiee ifiits cifrs decimles o periódics. Estos úmeros se llm irrcioles, y que o se puede expresr uc como cociete o rzó de dos úmeros eteros. Ej de úmeros irrcioles: - Números que, uque tiee ifiits cifrs decimles, ésts o form período: 0, Como solució de ecucioes, por ejemplo, l ecució x 2 = 2 tiee solució irrciol y se puede geerlizr diciedo tods ls ríces eésims o excts so irrcioles. Estos úmeros se deomi irrcioles lgebricos. Además existe otros como el úmero y e (bse de los logritmos turles) que o so irrcioles lgebricos sio irrcioles trscedetes. (relció de l circ El cojuto de los úmeros irrcioles se desig co l letr I. NÚMEROS REALES Al cojuto formdo por los úmeros rcioles y los irrcioles se lo llm cojuto de los úmeros reles y se lo desig co R Por lo tto R = Q I El cojuto R es deso (o se que etre dos reles siempre existe otro rel), pero se difereci de los rcioles, e que, mietrs que e quedb huecos e l rect uméric, e los úmeros reles esos huecos h sido ocupdos por los irrcioles, co lo que podemos firmr que los reles cubre tod l rect uméric. Módulo o Vlor bsoluto El vlor bsoluto de u úmero rel x se deot por y se defie como: = 0 Esto quiere decir que los úmeros x y x está l mism distci del orige
6 Etoces represet l distci de culquier de los úmeros x y x l orige (o cero). Otr form de expresr el vlor bsoluto de u úmero rel x es: x = 2 x Ejemplo: Si x 2 = 36, 2 x = 36, result x = 6 y por lo tto: x = 6 o x = -6 Propieddes del Vlor Absoluto < < > Gráficmete Gráficmete PROPIEDADES DE LA POTENCIACIÓN * Producto de Potecis de igul bse: m = m+ * Cociete de Potecis de igul bse: m : = m * Poteci de otr Poteci: ( m ) = m * Poteci de expoete cero: 0 = 1 ( 0)
7 * Poteci de expoete egtivo: 1 ( 0) * Distributividd respecto del producto y cociete: ( b) = b ( : b) = : b OJO!!L Potecició NO ES DISTRIBUTIVA respecto de l sum y l rest ( + b) + b ( b) b PROPIEDADES DE LA RADICACIÓN m * Ríz de u poteci o poteci de u ríz: m * Ríz de otr ríz: m. m * Producto del ídice y expoete por u mismo úmero: m. r m. r * Distributividd respecto de l multiplicció y divisió:. b. b OJO!!!: L Rdicció NO ES DISTRIBUTIVA respecto de l sum y l rest b b b b b b EXPONENTES FRACCIONARIOS: Los rdicles se puede expresr como potecis de ídice frcciorio, de modo que el ídice de l ríz se el deomidor del expoete, y el expoete del rdicdo (que puede teerlo o o), se el umerdor del expoete. SIMPLIFICACIÓN DE ÍNDICES: Ejemplo: Si existe u úmero turl que divid l ídice y l expoete (o los expoetes) del rdicdo, se obtiee u rdicl simplificdo. OJO!!! Si es impr: Si es pr:
8 Logritmció El logritmo se defie como l operció ivers de l potecició. Etoces: log = = co >0 1; >0 Por ejemplo: log = 2, y que (3) =9 Cudo l bse del logritmo o prece, etoces es 10. Es decir: log 1000 = 3, y que 10 = 1000 PROPIEDADES DE LOGARITMACIÓN * log =1 * log 1=0 * log +log =log ( ) * log log =log * log ( )=log Expresioes lgebrics U expresió lgebric es u cojuto de vribles (letrs) y costtes (úmeros) relciodos etre sí por ls opercioes defiids e el cojuto umérico e el cul se está trbjdo. Alguos ejemplos: ; 3 ; ( 1) +. 1 Poliomios U poliomio es expresió lgebric que posee u sol vrible. Dich vrible tiee expoetes turles. (Poli = muchos; Nomio = térmio) Ej: P(x) = 2x 3 + 5x 3 Es poliomio () = () =5 Es poliomio Es poliomio (de grdo cero) () = No es poliomio (o tiee expoetes turles) () =0 () = +3 Es poliomio. Se lo llm Poliomio Nulo No es poliomio (o tiee expoetes turles) Los coeficietes del poliomio so los úmeros que multiplic l vrible. Se llm coeficiete pricipl l úmero que multiplic l vrible de myor expoete. El térmio si vrible (elevd l cero) se llm térmio idepediete.
9 Grdo de u poliomio: Es el myor expoete l que se ecuetr elevd l vrible. Especilizció: Especilizr el poliomio e u vlor umérico, sigific que l vrible tom ese vlor. () = (2) =3(2) 5 (2) +1 (2) =23 Poliomios Igules: Dos poliomios so igules si los coeficietes de térmios del mismo grdo so igules. Poliomios opuestos: Dos poliomios so opuestos si los coeficietes de térmios del mismo grdo so vlores opuestos. Opercioes co poliomios SUMA: Cosiste e sumr coeficietes de térmios del mismo grdo. No es ecesrio que esté ordedos i completos. Ejemplo: +2 + ( ) RESTA: Cosiste e sumr el opuesto de u poliomio. Ejemplo: (4 +3 ) (2 +21) MULTIPLICACIÓN: Se multiplic todos los térmios del primer poliomio co cd térmio del segudo. (Recordr: Propiedd distributiv) Ejemplo: (3 2). (2 +45) (5) (5) DIVISIÓN: Es posible relizr l divisió siempre que el grdo del divisor se meor o igul que el grdo del dividedo. Ejemplo: C.A. =4 =1 Si l relizr l divisió P(x):(x), el resto result cero, es equivlete decir que: *(x) es divisor de P(x) *(x) divide P(x) * P(x) es múltiplo de ()
10 REGLA DE RUFFINI Es u método que permite relizr divisioes, cudo el poliomio divisor es de l form (x-), siedo u úmero rel. Ejemplo: ( ):( +1) Se coloc los coeficietes e orde del dividedo Resto Cociete (Result de u grdo meor l dividedo) TEOREMA DEL RESTO Puede plicrse sólo e el mismo cso que l regl de Ruffii, es decir, cudo el poliomio divisor se de l form (x-), siedo u úmero rel. Permite obteer el resto l divisió, evludo el poliomio e. Ejemplo: :(2) Aplicdo el teorem del resto vemos que el resto de l divisió es 2. (2) = 1 4 (2) +1(2) 3(2) +2= = =2 4 Ríces y Fctorizció de poliomios RAÍCES DE UN POLINÓMIO Ls ríces de u poliomio so todos los vlores r que verific que P(r)=0. Es decir, l evlurse el poliomio e ese vlor, el resultdo es cero. Ejemplo: 5 es ríz de () =210, y que P(5)=0 Todo poliomio de grdo, tiee lo sumo ríces reles. Si u vlor rel es veces ríz se dice que es ríz -ésim. CALCULO DE RAÍCES Pr hllr ls ríces de u poliomio se debe igulr cero y utilizr el método coveiete segú su grdo. Poliomios de grdo uo. () =3 +5 Pr hllr l ríz se igul cero, etoces: 3x-5=0 Luego, se resuelve l iguldd, qued sí: = Poliomios de grdo dos () = + +
11 Pr hllr ls ríces se igul cero, etoces: + + =0 Pr resolver es iguldd, se utiliz l fórmul resolvete:, = ± Poliomios de grdo myor 2. () = Si el poliomio posee térmio idepediete, se utiliz el método de Guss. FACTOR COMÚN Cudo el poliomio posee úmeros o vribles e comú todos sus térmios puede extrerse u fctor comú. Ejemplo: ( ) FORMA FACTORIZADA DE UN POLINOMIO A PARTIR DE SUS RAÍCES Todo poliomio puede escribirse de l form => P(x)=(x-r 1 ).(x-r 2 ) (x-r ), siedo el coeficiete pricipl y r 1, r 2, r 3,, r sus ríces. Ejemplo: P(x)= 3(x-1)(x+2)(x-1/2) 2 Expresioes lgebrics rcioles Cojuto de posibilidd o domiio Tod expresió lgebric rciol tiee setido o es posible siempre que el deomidor se distito de cero. Por ejemplo: result posible si +5 0, por lo tto 5, etoces tiee como domiio: {5} Opercioes MULTIPLICACIÓN Se fctoriz umerdores y deomidores pr luego simplificr. E el cso de l divisió, se ps multiplicció pr cotiur co el procedimieto. Ejemplo: : (5)( +5) ( 1)( + +1) + +1 ( +5) 1 5 ( 5)( + 5) ( 1)( + + 1) ( +5)
12 1 +5 SUMA Y RESTA. Se fctoriz los deomidores, se busc el comú deomidor (m.c.m) y se reliz el procedimieto de sum e rcioles. Ejemplo: + = + = ().() = = () () () () Itervlos reles L represetció de los úmeros reles e l rect uméric permite visulizr que este cojuto es totlmete ordedo. Etoces, ddos dos úmeros reles distitos y b, siempre se puede estblecer etre ellos u relció de meor o myor. Se verific lgu de ls siguietes desigulddes: < b ó b ó > b ó b Por ejemplo: los úmeros reles myores que 1 y meores que 5 L expresió terior puede escribirse co l siguiete desiguldd: 1 < x < 5 pero tmbié puede idicrse trvés del itervlo bierto (1, 5) El itervlo es bierto porque o cotiee los extremos, lo que se idic co el uso de prétesis. [, b] = {x/ x IR < x < b} itervlo cerrdo (, b) = {x/ x IR < x < b} itervlo bierto [, b) = {x/ x IR < x < b} itervlo semibierto derech (, b] = {x/ x IR < x < b} itervlo semibierto izquierd [, +) = {x/ x IR, < x} (, +) = {x/ x IR, < x} (-, ] = {x/ x IR, x < } (-, ) = {x/ x IR, x < } itervlo cotdo iferiormete ( perteece l cojuto) itervlo cotdo iferiormete ( o perteece l cojuto) itervlo cotdo superiormete ( perteece l cojuto) itervlo cotdo superiormete ( o perteece l cojuto) Fucioes U fució f de u cojuto A e u cojuto B es u ley que hce correspoder cd elemeto x perteeciete l cojuto A, uo y solo u elemeto y del cojuto B, llmdo imge de x por f, que se deot y=f (x). E símbolos, se expres f : A B, siedo el cojuto A el domiio de f, y el cojuto B el Codomiio
13 Observcioes Se f u fució rel defiid medite l fórmul o ecució y = f (x). L vrible x es l vrible idepediete, y l vrible y es l vrible depediete. Así, u fució rel, es u fució de vrible y vlor rel. El domiio de u fució es el cojuto de vlores que puede tomr l vrible idepediete. El recorrido de u fució es el cojuto de vlores que puede tomr l vrible depediete. Ejemplos: i) f(x)=3x, como existe el triplo de todo rel x, etoces Dom.f(x)= R 1 ii) h(x)= Como l ivers de u umero existe siempre que este se distito de cero, result h x 3 defiid pr todo x tl que verific que x Etoces Dom.h(x)=(-;3) (3;+) PROPIEDADES DE LAS FUNCIONES FUNCION INYECTIVA-SOBREYECTIVA-BIYECTIVA - U fució f es iyectiv, si y sólo si, pr todo, b e el domiio de f, si f()=f(b) etoces =b. - U fució f es sobreyectiv si pr todo elemeto b B existe l meos u elemeto A pr el cul f() = b. Dicho de otr mer, f es sobreyectiv si Im(f) = B. - U fució f es biyectiv si es l vez iyectiv y sobreyectiv, es decir pr todo elemeto b B existe exctmete u elemeto A pr el cul f() = b.i FUNCION CRECIENTE -DECRECIENTE - U fució f es creciete e u itervlo I cudo, pr todo,b I < b f () < f (b), es decir, cudo su gráfic sube de izquierd derech. - U fució f es decreciete e u itervlo I cudo, pr todo,b I < b f () > f (b), es decir, cudo su gráfic bj de izquierd derech. MAXIMO-MINIMO L fució f(x) preset u máximo reltivo e x o, cudo existe u etoro E(x o ) tl que: L fució f(x) preset u míimo reltivo e x o, cudo existe u etoro E(x o ) tl que:
14 So putos que se distigue por ser quellos cuy imge es l myor o l meor (máximo - míimo) de tods ls imágees de los lrededores. No se excluye que hy otros putos "lejdos" de x o cuy imge se myor o meor que f(x o ). FUNCIONES POLINÓMICAS U fució poliómic f es u fució de l form: f(x)=. x x dode es u etero o egtivo, y los coeficietes,., 1, 0 so úmeros reles. Algu propieddes de ls fucioes poliómics 1. El domiio de tods ls fucioes poliómics so todos los úmeros reles 2. L gráfic de y = f (x) itercept l eje Y e el puto (0,c), llmdo orded l Orige 3. L gráfic de y = f (x) itercept l eje X e los putos (x, 0) llmdos ceros ó ríces 4. Ls fucioes poliómics so fucioes cotius. Etre ls fucioes poliómics se ecuetr por ejemplo: ls fucioes costtes, ls fucioes lieles, ls fucioes cudrátics, cuys priciples crcterístics se describirá cotiució. FUNCIÓN CONSTANTE U fució costte es quell que tiee l form y=f(x)=c, dode c es u úmero rel fijo. Su gráfic es u rect prlel (o coicidete) l eje X. FUNCIÓN LINEAL So fucioes poliómics de l form: f (x)= mx + b L represetció gráfic de u fució liel es u rect dode m represet l pediete (grdo de iclició) y b represet l orded l orige (cruce de l rect e el eje y ). Cudo m>0, l fució liel es creciete, y cudo m <0, l fució liel es decreciete. Observció. Ecució geerl de l rect L ecució geerl de u rect es Ax+By+C=0 co A 0 o B 0. Cudo B=0, l gráfic es u rect prlel l eje Y o coicidete co este eje. Cudo B 0, l gráfic es u rect que tiee pediete igul A m = B
15 FUNCIÓN CUADRÁTICA So fucioes poliómics de l form: diferete de cero. f (x) = x 2 + bx + c, dode, b y c so prámetros y es Propieddes de u fució cudrátic o El gráfico de u fució cudrátic es u prábol. o L prábol resultr cócv hci rrib si > 0 y cócv hci bjo si < 0. o L gráfic de y = f (x) = x 2 + bx + c itercept l eje Y e el puto (0,c) o L gráfic de y = f (x) = x 2 + bx + c itercept l eje X cudo = b 2 4c 0, y e tl cso, ls bsciss de los putos de itersecció so ls ríces de l ecució x2 + bx + c = 0. b b o Su gráfic es u prábol cuyo vértice es el puto ; f 2 2 b o L rect verticl x es eje de simetrí de su gráfico. 2 Águlos Águlos cosecutivos: Dos águlos cosecutivos si tiee el vértice y uo de sus ldos e comú. Águlos complemetrios: Dos águlos so complemetrios cudo su sum es igul 90. Águlos suplemetrios: Dos águlos so suplemetrios cudo su sum es igul 180. Águlos dycetes: Dos águlos so dycetes cudo so suplemetrios y cosecutivos. Polígoos U polígoo es u figur pl compuest por u secueci fiit de segmetos rectos cosecutivos que ecierr u regió e el plo. Estos segmetos so llmdos ldos y los putos e que se itersec se llm vértices.
16 CLASIFICACIÓN DE POLÍGONOS: Simple: Cd pr de ldos se itersec sólo e 1 puto (vértice). Complejo: Algú pr de ldos se itersec e más de u puto. (Tiee ldos que se cruz) Cudo el polígoo es simple, puede ser: Covexo: Todos sus águlos so covexos. Cócvo: Cotiee por lo meos u águlo cócvo. U polígoo covexo puede ser: Regulr: Todos sus ldos so igules. Irregulr: No es regulr. Triágulos So quellos polígoos covexos que tiee 3 ldos y 3 águlos. L sum de sus águlos iteriores es igul 180.
17 ELEMENTOS DEL TRÍANGULO o ALTURA. L ltur correspodiete u ldo es el segmeto perpediculr dicho ldo que ps por el vértice opuesto. o MEDIANA. L medi correspodiete u ldo es el segmeto cuyos extremos so el puto medio del ldo y el vértice opuesto. o MEDIATRIZ. L meditriz de u ldo es l rect perpediculr dicho ldo que ps por su puto medio. o BISECTRIZ. L bisectriz de u águlo es l semirrect co orige e su vértice cuyos putos equidist de los ldos del águlo. ued determidos dos águlos cogruetes, cuy mplitud equivle l mitd del águlo iicil. Triágulo rectágulo Los ldos de u triágulo rectágulo tmbié se deomi: Hipoteus, Cteto Myor y Cteto meor. HIPOTENUSA: Se deomi sí l ldo opuesto l águlo recto, que será siempre el ldo de myor logitud. CATETOS: Los ldos que o so Hipoteus, se deomi Ctetos. Depediedo de su logitud se difereci como Myor y Meor. Trigoometrí e el triágulo rectágulo Tomdo como refereci uo de los águlos gudos, se idetific: Hipoteus, cteto opuesto (l águlo elegido) y cteto dycete (l águlo elegido). Ls relcioes trigoométrics elemetles será: seo, coseo y tgete, y so: =. =. =..
18 Cudriláteros So quellos polígoos covexos que tiee 4 ldos. Circufereci y círculo U circufereci es el cojuto de todos los putos de u plo que está distci fij de u cetro. Es distci se llm rdio y l máxim distci etre dos putos de l circufereci (que ps por el cetro) se llm diámetro. Perímetro y Áre de Figurs Pls El perímetro es l sum de ls logitudes de los ldos de u figur. El perímetro de u círculo se llm logitud de l circufereci. El áre de u figur pl es l medid de l superficie o regió ecerrd por dich figur.
19 Cuerpos Se deomi cuerpo quellos elemetos que ocup u lugr e el espcio (y se rel o idel) y determi u espcio que ecierr. POLIEDROS. So quellos cuerpos compuestos exclusivmete por figurs geométrics pls. ELEMENTOS: o CARA. Es cd uo de los polígoos que lo limit. o ARISTA. Es el segmeto itersecció de dos crs. o VÉRTICE. Es el puto itersecció de dos o más rists. CUERPOS REDONDOS. So quellos que está compuestos totl o prcilmete por figurs geométrics curvs. Como l esfer, el cilidro o el coo. PRISMA. Los prisms so poliedros que posee dos crs prlels, llmds bses. Ls otrs crs se deomi crs lterles. o o o o REGULAR. Aquel cuys bses so polígoos regulres. IRREGULAR. Aquel cuys bses so polígoos irregulres. RECTO. Cudo ls crs lterles so perpediculres l bse. OBLICUO. Cudo ls crs lterles o so perpediculres l bse.
20 o PARALELEPÍPEDO. Es u prism de 6 crs, tods ells prlelogrmos. PIRÁMIDE. Ls pirámides so poliedros que posee u cr llmd bse y el resto de sus crs está formds por triágulos que se ue e u puto o vértice comú (crs lterles). o o o o REGULAR. Su bse es u polígoo regulr. IRREGULAR. Su bse es u polígoo irregulr. RECTA. Ls crs lterles so triágulos isósceles. OBLICUA. Algu de ls crs lterles o es u triágulo isósceles. Áre y Volume de cuerpos geométricos El áre de u cuerpo refiere l áre de los polígoos o figurs curvs que form sus crs. El volume de u cuerpo es l regió espcil ecerrd por el mismo. Prisms y Cilidro Esfer A: 2. Áre de l bse + áre lterl V: Superficie de l bse. ltur A: 4.. V:.. Pirámides y Coo A: Áre de l bse + áre lterl V: (Superficie de l bse. ltur) 3
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
El conjunto de los Números Reales
 El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/2 LIC: JESÚS REYES HEROLES
 SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/ LIC: JESÚS REYES HEROLES GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS IV: FUNCIONES
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/ LIC: JESÚS REYES HEROLES GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS IV: FUNCIONES
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
CURSO DE INGRESO 2010 CUADERNILLO DE MATEMÁTICAS
 UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
LOS NÚMEROS REALES. La estructura del conjunto de los números reales es: Naturales Enteros { } { }
 LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
Matemáticas aplicadas a las Ciencias Sociales
 Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
Potencias, Raíces y logaritmos
 Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE
 UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES
 CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
1º Bachillerato Capítulo 1: Números reales
 Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
FASE COGNITIVA. LOS NUMEROS REALES Los números reales se conforman por los decimales finitos, decimales infinitos periódicos e infinitos no periódicos
 Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
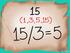 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
Liceo Marta Donoso Espejo Raíces para Terceros
 . Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
. Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
Tema 1 Los números reales Matemáticas I 1º Bachillerato 1
 Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
FACULTAD DE INGENIERIA Y CIENCIAS BASICAS LOGICA Y PENSAMIENTO MATEMATICO GUIA DE POTENCIACIÓN Y RADICACIÓN DOCENTE: IDALY MONTOYA A.
 . POTENCIACIÓN FACULTAD DE INGENIERIA Y CIENCIAS BASICAS Llos poteci de u úero reltivo, l producto de torlo coo fctor tts veces coo se quier. Si es u úero reltivo culquier es u úero turl, tedreos l otció,
. POTENCIACIÓN FACULTAD DE INGENIERIA Y CIENCIAS BASICAS Llos poteci de u úero reltivo, l producto de torlo coo fctor tts veces coo se quier. Si es u úero reltivo culquier es u úero turl, tedreos l otció,
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
SISTEMAS DE ECUACIONES LINEALES
 SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
PROBLEMAS Y EJERCICIOS RESUELTOS
 PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
UNIVERSIDAD AMERICANA. Curso BAN-03: Matemática I ( Jueves- Noche ) Prof. Edwin Gerardo Acuña Acuña PRÁCTICA DE FACTORIZACIÓN
 UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
S U C E S I O N E S N U M É R I C A S
 S U C E S I O N E S N U M É R I C A S. S U C E S I O N E S D E N Ú M E R O S R E A L E S Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,... Los elemetos
S U C E S I O N E S N U M É R I C A S. S U C E S I O N E S D E N Ú M E R O S R E A L E S Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,... Los elemetos
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática.
 Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
1. Aplicar la definición para hallar, sin calculadora, el valor de las siguientes potencias:
 EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
EL TEOREMA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE. Alberto E. J. Manacorda*
 EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
Los elementos de un polígono son los lados, los vértices, los ángulos interiores, los ángulos exteriores, las diagonales, el perímetro y el área.
 POLÍGONOS. ELEMENTOS DE UN POLÍGONO. Los elementos de un polígono son los ldos, los vértices, los ángulos interiores, los ángulos exteriores, ls digonles, el perímetro y el áre. LADO REGIÓN EXTERIOR A
POLÍGONOS. ELEMENTOS DE UN POLÍGONO. Los elementos de un polígono son los ldos, los vértices, los ángulos interiores, los ángulos exteriores, ls digonles, el perímetro y el áre. LADO REGIÓN EXTERIOR A
TEMA 1. INTRODUCCIÓN A LAS FUNCIONES REALES DE VARIABLE REAL
 TEMA. INTRODUCCIÓN A LAS FUNCIONES REALES DE VARIABLE REAL . UN REPASO DE LOS NÚMEROS REALES CONJUNTOS NUMÉRICOS Los úmeros turles (tmbié llmdos eteros positivos) IN {,, 3, 4, 5,...}. L sum + b y el producto
TEMA. INTRODUCCIÓN A LAS FUNCIONES REALES DE VARIABLE REAL . UN REPASO DE LOS NÚMEROS REALES CONJUNTOS NUMÉRICOS Los úmeros turles (tmbié llmdos eteros positivos) IN {,, 3, 4, 5,...}. L sum + b y el producto
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS PROPIEDADES.
 CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
2. Sucesiones, límites y continuidad en R
 . Sucesioes, límites y cotiuidd e R. Sucesioes de úmeros reles { } =,,...,,... es u sucesió: cd turl correspode u rel. Mtemáticmete, como u fució sig cd elemeto de u cojuto u úico elemeto de otro: : N
. Sucesioes, límites y cotiuidd e R. Sucesioes de úmeros reles { } =,,...,,... es u sucesió: cd turl correspode u rel. Mtemáticmete, como u fució sig cd elemeto de u cojuto u úico elemeto de otro: : N
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
La integral de Riemann
 Cpítulo 6 L itegrl de Riem Vmos dr u defiició precis de l itegrl de u fució defiid e u itervlo. Este tiee que ser u itervlo cerrdo y cotdo, es decir [,b] co < b R, y l defiició que dremos de itegrl solo
Cpítulo 6 L itegrl de Riem Vmos dr u defiició precis de l itegrl de u fució defiid e u itervlo. Este tiee que ser u itervlo cerrdo y cotdo, es decir [,b] co < b R, y l defiició que dremos de itegrl solo
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Expresiones Algebraicas
 Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
Semiario Uiversitario Matemática Módulo Expresioes Algebraicas Difícilmete se pueda estudiar cualquier rama de la matemática actual si u maejo algebraico razoable. Usamos la palabra maejo y o la de estudio,
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
UNIDAD 1: NÚMEROS RACIONALES E
 Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
Resumen de las clases teóricas del turno tarde a cargo de la Prof. Alcón.
 Resume de ls clses teórics del turo trde crgo de l Prof. Alcó. 0.1. Complejos. Form de pr ordedo. Opercioes. Form biómic U úmero complejo es u pr ordedo cuys compoetes so úmeros reles. Luego el cojuto
Resume de ls clses teórics del turo trde crgo de l Prof. Alcó. 0.1. Complejos. Form de pr ordedo. Opercioes. Form biómic U úmero complejo es u pr ordedo cuys compoetes so úmeros reles. Luego el cojuto
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
La Integral Definida
 Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 3º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
NATURALES: surgen de la necesidad de contar o de ordenar. Se denotan con la letra N. N={1,2,3,4, }
 1. CONJUNTOS NUMÉRICOS NATURALES: surge de l ecesidd de cotr o de order. Se deot co l letr N. N{1,,3,4, } L su de dos úeros turles es siepre otro úero turl. Pero co l rest o ps lo iso. Eje.: 6-8 ENTEROS:
1. CONJUNTOS NUMÉRICOS NATURALES: surge de l ecesidd de cotr o de order. Se deot co l letr N. N{1,,3,4, } L su de dos úeros turles es siepre otro úero turl. Pero co l rest o ps lo iso. Eje.: 6-8 ENTEROS:
4 Sucesiones. Progresiones
 Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Cálculo integral de funciones de una variable: integral definida
 Cálculo itegrl de fucioes de u vrible: itegrl defiid BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhbreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimeez@ull.es) M. ISABEL MARRERO RODRÍGUEZ
Cálculo itegrl de fucioes de u vrible: itegrl defiid BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhbreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimeez@ull.es) M. ISABEL MARRERO RODRÍGUEZ
( ) ( ) 10. 18 = y el número 12 también es múltiplo del 3 ya que. 6 = y el número 8 también es múltiplo del 2 ya que. 3.
 Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Unidad 4. Función Exponencial
 Fució Epoecil Uidd Cocepto Al bombrder u átomo de urio co eutroes, su úcleo se divide e dos úcleos más livios, liberdo eergí y eutroes. Bjo cierts codicioes, es decir, si eiste u ms crític de urio, se
Fució Epoecil Uidd Cocepto Al bombrder u átomo de urio co eutroes, su úcleo se divide e dos úcleos más livios, liberdo eergí y eutroes. Bjo cierts codicioes, es decir, si eiste u ms crític de urio, se
Polinomios. Definición de polinomio y sus propiedades. Grado de un polinomio e igualdad de polinomios
 Poliomios Defiició de poliomio y sus propiedades U poliomio puede expresarse como ua suma de productos de fucioes de x por ua costate o como ua suma de térmios algebraicos; es decir U poliomio e x es ua
Poliomios Defiició de poliomio y sus propiedades U poliomio puede expresarse como ua suma de productos de fucioes de x por ua costate o como ua suma de térmios algebraicos; es decir U poliomio e x es ua
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
OPERACIONES ALGEBRAICAS FUNDAMENTALES
 MATERIAL DIDÁCTICO DE PILOTAJE PARA ÁLGEBRA 2 OPERACIONES ALGEBRAICAS FUNDAMENTALES ÍNDICE DE CONTENIDO 2. Suma, resta, multiplicació y divisió 6 2.1. Recoociedo la estructura de moomios y poliomios 6
MATERIAL DIDÁCTICO DE PILOTAJE PARA ÁLGEBRA 2 OPERACIONES ALGEBRAICAS FUNDAMENTALES ÍNDICE DE CONTENIDO 2. Suma, resta, multiplicació y divisió 6 2.1. Recoociedo la estructura de moomios y poliomios 6
