C.1 Pares de series básicas de Fourier en tiempo discreto
|
|
|
- María Luz Ortega Ávila
- hace 7 años
- Vistas:
Transcripción
1 impo Coiua ( Discra [ FS Prióica (, [] X X [] prioo DFS [ Ω x Ω y prioo Ω Discra ( o prióica (, X ( D X X ( Ω ( X ( X ( i prioo Coiua (,Ω o prióica (, Prióica (,Ω Frcucia C. Pars sris básicas Fourir impo iscro Domiio l impo Ω + ] ; prioo, M {, M < / 2 Domiio la frcucia X x Ω [ ] [ ] ; Ω Ω s (2M + 2 Ω s 2 pω, p, p ±, p ± 2, {, oro caso / 2, ± p, ± p ±, ± p ± 2, cos( pω {, oro caso / 2, p, p ±, p ± 2, s ( pω { / 2, p, p ±, p ± 2,, oro caso,, ±, ± 2, {, oro caso [ p p x [ ] x [ δ ]
2 C.2 Pars básicos sris Fourir Domiio l impo Domiio la frcucia ; prioo ( Ω ] ( ; x { (, s x, < / 2 s x s( s p δ[ p] cos( p x ( s ( p x ( δ ( p p X [ δ[ p] + δ[ + p] 2 2 X [ δ[ p] δ[ + p] 2 2 C.3 Pars básicos rasformaas Fourir impo iscro Domiio l impo Domiio la frcucia X ( Ω Ω X ( 2 2M + s, M Ω Ω 2 { X (, oro caso Ω s 2 α u[, α < X ( Ω α δ[ X ( X ( Ω p x [ u[ + δ ( p, Ω W Ω x s( W, < W < ( s, W < Ω ; [ X prióica ( + α u[ X ( Ω 2 ( α 2
3 C.4 Pars básicos rasformaas Fourir Domiio l impo Domiio la frcucia x X ( ( X 2 (, 2s( { X (, oro caso s( W, W X ( {, oro caso δ ( X ( X ( δ ( x ( u( X ( + δ ( ( a x u(, R{ a} > X ( a + ( a x u(, R{ a} > X ( ( a + 2 C.5 Pars rasformaas Fourir para sñals prióicas Sñal prióica l rasformaa Fourir omiio l impo X ( δ ( x ( cos( X ( δ ( ( + δ + cos( X ( δ ( δ ( + X ( δ ( x ( δ ( Τ X ( δ, s 2s( s { X ( δ (, < < / 2 + s 3
4 C.6 Pars rasformaas Fourir impo iscro para sñals prióicas Sñal prióica l omiio l impo Ω rasformaa Fourir impo iscro ( 2 X δ ( Ω Ω cos( Ω X ( δ ( Ω Ω + δ ( Ω + Ω s( Ω X ( δ ( Ω Ω δ ( Ω + Ω x [ δ ( X ( δ ( Ω Ω X ( δ ( Ω C.7. Propias la rasformaa Fourir Propias X ( ; y( Y ( Lialia Corrimio l impo Corrimio la frcucia Escalamio Difrciació l impo Difrciació la frcucia Igració / sumaoria Covolució Moulació (Sumaoria Dualia ( a + by( Z( ax ( + by ( X ( γ X ( ( γ a X a a X ( X ( τ τ X ( + X ( δ ( * y( τ y( τ τ X ( Y ( ( X ( υ Y( ( υ X ( υ 4
5 C.7.2 Propias la Sri Fourir FS: FS: Propias ; y( Lialia Corrimio l impo Corrimio la frcucia Escalamio Difrciació l impo Difrciació la frcucia Igració / sumaoria Covolució Moulació (Sumaoria Dualia Y[ ; prio ( a + by( a + by[ a ] a y( τ y( τ τ l x ( y( * Y[ D ( ; X ( C.7.3 Propias la impo iscro D D Propias ( ; y( Y ( Lialia Corrimio l impo Corrimio la frcucia Escalamio Difrciació l impo Difrciació la frcucia Igració / sumaoria Covolució Moulació (Sumaoria Dualia D [ a + b Z( ] Γ D x ( p D D X ( X ( Ω/ p ax ( X ( ( Ω Γ + by ( ; x (, l p D X ( Ω D X ( x [ + X ( Ω δ ( Ω D * X ( Y ( l D Γ ( Ω Γ [ X ( Y ( Γ D ( ; X ( 5
6 C.7.4 Propias la FS impo iscro DFS: Ω Propias ( DFS [ ] ; ( : Ω x y Y[ ; pr. Lialia Corrimio l impo Corrimio la frcucia Escalamio Difrciació l impo Difrciació la frcucia Igració / sumaoria Covolució Moulació (Sumaoria Dualia [ a + b D Ω D Ω Ω ] D Ω Ω D p x ( p ] a + by[ Ω px [ ; x (, l p D Ω l D x [ ( Y ( D Ω l C.8 Rlacios las cuaro rprsacios Fourir. Rprsació la para ua sñal prióica impo coiuo ( FS g( G[ G( G[ δ ( Rprsació la D para ua sñal prióica impo iscro ( DFS Ω D w[ W[ W ( W[ δ ( Ω Ω Rprsació la para ua sñal o prióica impo iscro ( D ( Ω v[ δ ( Vδ ( V v ( ] δ / g( G[ D Ω / w[ W[ D v[ V ( Rprsació la para ua sñal prióica impo iscro Ω wδ ( w[ δ ( Wδ ( W [ δ ; 6
7 C.9 Rlacios musro y raslap Musro por impulsos para sñals prióicas impo coiuo x ( ( ( ( ( δ x s δ s X δ X ; s s Musro ua sñal impo iscro q D ( Ω m / q v[ q Y ( V ( ; q m Musro la D frcucia DFS ; Ω / ; [ ] [ ] 2 Ω w v + m W[ V ( m Musro la frcucia 2 / ; g( + m G[ X ( X ( D v[ V ( s 7
CAPITULO 3.- Representaciones de Fourier para señales.
 CAPIULO 3.- Rprsacios Fourir para sñals. 3. Iroucció. 3. Sñals prióicas impo iscro: la sri Fourir impo iscro. 3.3 Sñals prióicas impo coiuo: la sri Fourir. 3.4 Sñals o prióicas impo iscro: la rasformaa
CAPIULO 3.- Rprsacios Fourir para sñals. 3. Iroucció. 3. Sñals prióicas impo iscro: la sri Fourir impo iscro. 3.3 Sñals prióicas impo coiuo: la sri Fourir. 3.4 Sñals o prióicas impo iscro: la rasformaa
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Problemas Tema 2: Sistemas
 SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
SEÑALES Y SISTEMAS I TABLAS. Dpto. Teoría de la Señal y Comunicaciones
 SEÑALES Y SISEMAS I ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s () ( s) ( s) Lilidd () + b ( ) ( s) b ( s) Dsplzmio l impo ( ) Dsplzmio
SEÑALES Y SISEMAS I ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s () ( s) ( s) Lilidd () + b ( ) ( s) b ( s) Dsplzmio l impo ( ) Dsplzmio
SISTEMAS LINEALES TABLAS. Dpto. Teoría de la Señal y Comunicaciones
 SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
Análisis de Fourier para Señales y Sistemas de Tiempo Discreto
 Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
TEMA 1 INTRODUCCIÓN A LA TEORÍA DE LA SEÑAL
 EMA INRODUCCIÓN A LA EORÍA DE LA SEÑAL Vicor Moisés Hrádz Cham hdzcham@ux.s Sismas d rasmisió d Daos.ELEMENOS BÁSICOS DE UN SISEMA DE COMUNICACIÓN U sisma d comuicació básico sá compuso por: - fu - caal
EMA INRODUCCIÓN A LA EORÍA DE LA SEÑAL Vicor Moisés Hrádz Cham hdzcham@ux.s Sismas d rasmisió d Daos.ELEMENOS BÁSICOS DE UN SISEMA DE COMUNICACIÓN U sisma d comuicació básico sá compuso por: - fu - caal
MUESTREO Y RECONSTRUCCIÓN DE SEÑALES. Teoría de circuitos y sistemas
 MUESREO Y RECONSRUCCIÓN DE SEÑALES oría d circuios y sismas Inroducción Sabmos modlar sismas coninuos Laplac o sismas discros Z. Pro n muchos casos los sismas coninn ano bloqus coninuos como bloqus discros.
MUESREO Y RECONSRUCCIÓN DE SEÑALES oría d circuios y sismas Inroducción Sabmos modlar sismas coninuos Laplac o sismas discros Z. Pro n muchos casos los sismas coninn ano bloqus coninuos como bloqus discros.
Análisis de Señales. Descripción matemática de señales
 Análisis d Sñals Dscripción mamáica d sñals Sñals Las sñals son funcions d variabls indpndins, poradoras d información Sñals lécricas:nsions y corrins n un circuio Sñals acúsicas: audio Sñals d vido: variación
Análisis d Sñals Dscripción mamáica d sñals Sñals Las sñals son funcions d variabls indpndins, poradoras d información Sñals lécricas:nsions y corrins n un circuio Sñals acúsicas: audio Sñals d vido: variación
Tema 0 Repaso de Señales y Sistemas Discretos. 4º Ing. Telecomunicación EPS Univ. San Pablo CEU
 Tma Rpaso d Sñals y Sistmas Discrtos 4º Ig. Tlcomuicació EPS Uiv. Sa Pablo CEU Lcturas complmtarias Opp., Pro (sólo hasta.: Itroducció a TDS Importacia d TDS la igiría Prspctiva histórica Esquma d u sistma
Tma Rpaso d Sñals y Sistmas Discrtos 4º Ig. Tlcomuicació EPS Uiv. Sa Pablo CEU Lcturas complmtarias Opp., Pro (sólo hasta.: Itroducció a TDS Importacia d TDS la igiría Prspctiva histórica Esquma d u sistma
ANÁLISIS DE FOURIER CAPÍTULO CUATRO TIEMPO DISCRETO Introducción
 CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
Universidad Carlos III de Madrid. 3.4 Sistemas LIT. SLIT: Sistemas Lineales e Invariantes con el Tiempo Linealidad
 Uiversidad Carlos III de Madrid 3.4 Sisemas LIT SLIT: Sisemas Lieales e Ivariaes co el Tiempo Liealidad Supogamos que la señal se puede expresar como ua combiació lieal de señales más simples ( x i ()
Uiversidad Carlos III de Madrid 3.4 Sisemas LIT SLIT: Sisemas Lieales e Ivariaes co el Tiempo Liealidad Supogamos que la señal se puede expresar como ua combiació lieal de señales más simples ( x i ()
Ing. Mario R. Modesti
 UNIVERSIDAD ECNOLOGICA NACIONAL FACULAD REGIONAL CORDOBA DEPARAMENO ELECRONICA Carrra Asignaura : Ingniría Elcrónica : Análisis d Sñals y Sismas.P.N : Sris y ransformada d Fourir, ransformada invrsa d
UNIVERSIDAD ECNOLOGICA NACIONAL FACULAD REGIONAL CORDOBA DEPARAMENO ELECRONICA Carrra Asignaura : Ingniría Elcrónica : Análisis d Sñals y Sismas.P.N : Sris y ransformada d Fourir, ransformada invrsa d
Respuesta en frecuencia. Procesado Digital de Señales.4º Ingeniería Electrónica. Universitat de València. Profesor Emilio Soria.
 Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
Tema 2: Sistemas. 2.1 Introducción
 Tema : Sisemas Tema : Sisemas. Iroducció U sisema respode co uas deermiadas señales a la acció de oras. x() sisema y ( ) = T x( ) Ejemplo Tiempo coiuo: sisema mecáico () dy b d y() T{ } { } d y() dy()
Tema : Sisemas Tema : Sisemas. Iroducció U sisema respode co uas deermiadas señales a la acció de oras. x() sisema y ( ) = T x( ) Ejemplo Tiempo coiuo: sisema mecáico () dy b d y() T{ } { } d y() dy()
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
 Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Buscapalabras Circula las palabras que escribiste como respuestas
 El cocinero babilónico está cocinando algo más rico que sopa de verduras. Es sopa de la Palabra de Dios. Encuentra y marca solo las palabras del versículo en la sopa y escribe el versículo de Lucas 11:28
El cocinero babilónico está cocinando algo más rico que sopa de verduras. Es sopa de la Palabra de Dios. Encuentra y marca solo las palabras del versículo en la sopa y escribe el versículo de Lucas 11:28
CAPÍTULO 2.- Representaciones en el dominio del tiempo para sistemas lineales e invariantes con el tiempo
 Sigls Ssms, /E Simo i Brr V V Coprig Jo Wil & Sos Ic All rigs rsrv CAPÍTULO - Rprscios l omiio l impo pr sisms lils ivris co l impo Irocció Covolció: rprsció l rsps l implso Propis l rprsció l rsps l implso
Sigls Ssms, /E Simo i Brr V V Coprig Jo Wil & Sos Ic All rigs rsrv CAPÍTULO - Rprscios l omiio l impo pr sisms lils ivris co l impo Irocció Covolció: rprsció l rsps l implso Propis l rprsció l rsps l implso
Régimen transitorio. Respuesta a funciones elementales
 Régie rasiorio Vibració Trasioria: Desaparece co el paso el iepo, pero puee ser iporae e respuesa a fuerzas o perióicas (golpes, explosioes...). Respuesa a fucioes eleeales c () x ució escaló ució rapa
Régie rasiorio Vibració Trasioria: Desaparece co el paso el iepo, pero puee ser iporae e respuesa a fuerzas o perióicas (golpes, explosioes...). Respuesa a fucioes eleeales c () x ució escaló ució rapa
Nicolás Rivera. 20 de Marzo de 2012
 Gramáticas Libre de Contexto Aleatorias. Nicolás Rivera 20 de Marzo de 2012 Pontificia Universidad Católica de Chile Tabla de Contenidos 1 Introducción Gramáticas Libres de Contexto Sistema de Producción
Gramáticas Libre de Contexto Aleatorias. Nicolás Rivera 20 de Marzo de 2012 Pontificia Universidad Católica de Chile Tabla de Contenidos 1 Introducción Gramáticas Libres de Contexto Sistema de Producción
1. Sumar monomios semejantes:
 HOJA 1: Monomios 1. Sumar monomios semejantes: a) 3x + 4x 5x b) 6x 3 x 3 + 3x 3 c) x 5 + 4x 5 7x 5 d) x 4 + 6x 4 + 3x 4 5x 4 e) 7x + 9x 8x + x f) y + 5y 3y g) 3x y 6x y + 5x y h) 4xy xy 7xy i) a 6 3a 6
HOJA 1: Monomios 1. Sumar monomios semejantes: a) 3x + 4x 5x b) 6x 3 x 3 + 3x 3 c) x 5 + 4x 5 7x 5 d) x 4 + 6x 4 + 3x 4 5x 4 e) 7x + 9x 8x + x f) y + 5y 3y g) 3x y 6x y + 5x y h) 4xy xy 7xy i) a 6 3a 6
DISEÑO MECÁNICO RODAMIENTOS NORMALIZACIÓN DE LOS RODAMIENTOS CINEMÁTICA DISTRIBUCIÓN DE CARGA EN EL RODAMIENTO
 DISEÑO MECÁNICO RODAMIENTOS NORMALIZACIÓN DE LOS RODAMIENTOS CINEMÁTICA DISTRIBUCIÓN DE CARGA EN EL RODAMIENTO REPRESENTACIÓN SIMPLIFICADA DE LOS RODAMIENTOS 2 q q q q q q q q q 3 q q q q q q q q q q q
DISEÑO MECÁNICO RODAMIENTOS NORMALIZACIÓN DE LOS RODAMIENTOS CINEMÁTICA DISTRIBUCIÓN DE CARGA EN EL RODAMIENTO REPRESENTACIÓN SIMPLIFICADA DE LOS RODAMIENTOS 2 q q q q q q q q q 3 q q q q q q q q q q q
UNIDAD 3 Transformadas de Laplace
 Traformada de aplace 3. Defiicioe a raformada de aplace de ua fució () f, repreeada co el ímbolo, e la operació maemáica defiida mediae la iguiee iegral impropia: { ()} lim b f e f () d b Por lo geeral,
Traformada de aplace 3. Defiicioe a raformada de aplace de ua fució () f, repreeada co el ímbolo, e la operació maemáica defiida mediae la iguiee iegral impropia: { ()} lim b f e f () d b Por lo geeral,
ALGEBRA III (Curso ) Teoría de conjuntos José A. Alonso Jiménez Ejercicio 1. Probar que para cualesquiera conjuntos a, b y c se tiene que:
 ALGEBRA III (Curso 1989-90) Teoría de conjuntos José A. Alonso Jiménez Ejercicio 1. Probar que para cualesquiera conjuntos a, b y c se tiene que: (1) a a. (2) a b b a = a = b. (3) a b b c = a c. (4) a.
ALGEBRA III (Curso 1989-90) Teoría de conjuntos José A. Alonso Jiménez Ejercicio 1. Probar que para cualesquiera conjuntos a, b y c se tiene que: (1) a a. (2) a b b a = a = b. (3) a b b c = a c. (4) a.
Respuesta al escalón unitario
 Rpua al caló uiario Epcificacio l domiio dl impo La ampliud duració d la rpua raioria db mar dro d lími olrabl dfiido E ima d corol lial la caracrizació dl raiorio comúm raliza uilizado u caló uiario a
Rpua al caló uiario Epcificacio l domiio dl impo La ampliud duració d la rpua raioria db mar dro d lími olrabl dfiido E ima d corol lial la caracrizació dl raiorio comúm raliza uilizado u caló uiario a
Análisis Geostadístico. de datos funcionales
 á í á - á é í : í é : á ó í ( ). é í á ó,,,., í é.,, é ó., í á. í., ó, ó. é ó., á, ó.., ó - ()., é á í. é á., á. ó, ó á. é ó é. í á ó. : ; ; ó ; ; ; ó. ó í............................... á..............................................................
á í á - á é í : í é : á ó í ( ). é í á ó,,,., í é.,, é ó., í á. í., ó, ó. é ó., á, ó.., ó - ()., é á í. é á., á. ó, ó á. é ó é. í á ó. : ; ; ó ; ; ; ó. ó í............................... á..............................................................
Ampliación Matemática Discreta. Justo Peralta López
 Justo Peralta López UNIVERSIDAD DE ALMERíA DEPARTAMENTO DE ÁGEBRA Y ANÁLISIS MATEMÁCO 1 Código Bloque y Distancia Mínima 2 cíclicos 3 Codificación 4 BCH Código Bloque y Distancia Mínima Si A es un alfabeto,
Justo Peralta López UNIVERSIDAD DE ALMERíA DEPARTAMENTO DE ÁGEBRA Y ANÁLISIS MATEMÁCO 1 Código Bloque y Distancia Mínima 2 cíclicos 3 Codificación 4 BCH Código Bloque y Distancia Mínima Si A es un alfabeto,
Superficies cuádricas
 Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Intersección Cono-Esfera - Oposición Hoja 1/3. NOTA: Por razones de espacio, los dibujos se han realizado a la escala 3:4.
 NOTA: Por razones de espacio, los dibujos se han realizado a la escala 3:4. V 2 En la intersección del cono y de la esfera, dada la posición de sus ejes, que son paralelos y están contenidos en un proyectante
NOTA: Por razones de espacio, los dibujos se han realizado a la escala 3:4. V 2 En la intersección del cono y de la esfera, dada la posición de sus ejes, que son paralelos y están contenidos en un proyectante
Distribuciones unidimensionales continuas
 Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
Topologías. Segundo cuatrimestre Práctica Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos.
 Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Topología Segundo cuatrimestre - 2011 Práctica 1 Topologías Ejemplos de topologías 1. Encuentre todas las topologías sobre conjuntos de a lo sumo cuatro elementos. 2. Sea X un conjunto. (a) Sea τ = {U
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
UNIDAD 5 ACTIVIDAD 5.3 El alfabeto griego M.A. Rosa María Funderburk Razo Autor
 UNIDAD 5 ACTIVIDAD 5.3 El alfabeto griego M.A. Rosa María Funderburk Razo Autor El alfabeto griego El alfabeto griego es un alfabeto utilizado para escribir la lengua griega. Desarrollado alrededor del
UNIDAD 5 ACTIVIDAD 5.3 El alfabeto griego M.A. Rosa María Funderburk Razo Autor El alfabeto griego El alfabeto griego es un alfabeto utilizado para escribir la lengua griega. Desarrollado alrededor del
TEMA 4. Anillos de polinomios.
 TEMA 4 Anillos de polinomios. Ejercicio 4.1. Encontrar un polinomio f(x) de grado 3 tal que: f(0) = 6, f(1) = 12 y f(x) (3x + 3) mod (x 2 + x + 1). Ejercicio 4.2. Demostrar que en un D.E. todos los ideales
TEMA 4 Anillos de polinomios. Ejercicio 4.1. Encontrar un polinomio f(x) de grado 3 tal que: f(0) = 6, f(1) = 12 y f(x) (3x + 3) mod (x 2 + x + 1). Ejercicio 4.2. Demostrar que en un D.E. todos los ideales
UNIDAD 3 Transformadas de Laplace. { ( )} lim b st ( ) f t = e f t dt
 UNIDAD 3 Traformada de aplace 3. Defiicioe a traformada de aplace de ua fució f ( t ), repreetada co el ímbolo, e la operació memática defiida mediate la iguiete itegral impropia: { lim b t e dt b Por
UNIDAD 3 Traformada de aplace 3. Defiicioe a traformada de aplace de ua fució f ( t ), repreetada co el ímbolo, e la operació memática defiida mediate la iguiete itegral impropia: { lim b t e dt b Por
Materiales-G704/G742. Jesús Setién Marquínez Jose Antonio Casado del Prado Soraya Diego Cavia Carlos Thomas García. Lección 2.
 -G704/G742 Lección 2. Ley de Hooke Jesús Setién Marquínez Jose Antonio Casado del Prado Soraya Diego Cavia Carlos Thomas García Departamento de Ciencia e Ingeniería del Terreno y de los Este tema se publica
-G704/G742 Lección 2. Ley de Hooke Jesús Setién Marquínez Jose Antonio Casado del Prado Soraya Diego Cavia Carlos Thomas García Departamento de Ciencia e Ingeniería del Terreno y de los Este tema se publica
Transformada de Laplace
 Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
Una Versión de ACO para Problemas con Grafos de. muy Gran Extensión. Enrique Alba y Francisco Chicano. Introducción. ACOhg.
 1/22 Puerto de La Cruz, Tenerife, España, 14 a 16 de Febrero de 2007 Una Versión de ACO para s con Grafos de muy Gran Extensión Enrique Alba y Francisco Chicano Puerto de La Cruz, Tenerife, España, 14
1/22 Puerto de La Cruz, Tenerife, España, 14 a 16 de Febrero de 2007 Una Versión de ACO para s con Grafos de muy Gran Extensión Enrique Alba y Francisco Chicano Puerto de La Cruz, Tenerife, España, 14
Universidad Carlos III de Madrid
 Uiversidad Carlos III de Madrid. El mudo físico: represeació co señales y sisemas Señales: Fucioes co las que represeamos variacioes de ua magiud física Volaje, iesidad, fuerza, emperaura, posició r ()
Uiversidad Carlos III de Madrid. El mudo físico: represeació co señales y sisemas Señales: Fucioes co las que represeamos variacioes de ua magiud física Volaje, iesidad, fuerza, emperaura, posició r ()
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Ejercicios de Teoría de conjuntos
 Ejercicios de Teoría de conjuntos José A. Alonso Jiménez Mario J. Pérez Jiménez Sevilla, Octubre de 1992 Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla 1 Contenido
Ejercicios de Teoría de conjuntos José A. Alonso Jiménez Mario J. Pérez Jiménez Sevilla, Octubre de 1992 Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla 1 Contenido
SOBRE LA ECUACIÓN DE ONDAS
 Eu C í Sb uó s SOBE A ECUACIÓN DE ONDAS Eu C í -Iuó p. - suó uó s u só. -Ipó ís suó uó s. -Os Ess. 5-E Fu uó. 6- uó s ss. 7-Os sés. 8-ó uó p uó s. 9-E pp Hugs ó. -Os ss s ss. -Os gus. -Os u u gu. -Cuó
Eu C í Sb uó s SOBE A ECUACIÓN DE ONDAS Eu C í -Iuó p. - suó uó s u só. -Ipó ís suó uó s. -Os Ess. 5-E Fu uó. 6- uó s ss. 7-Os sés. 8-ó uó p uó s. 9-E pp Hugs ó. -Os ss s ss. -Os gus. -Os u u gu. -Cuó
FACULTAD DE INGENIERÍA
 FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
PRÁCTICA 1: Análisis en el dominio del tiempo de sistemas continuos simples
 Sismas Sñals Crso 4/5 Igiría Iformáia PRÁCTICA : Aálisis l omiio l impo sismas oios simpls I.- Prosamio sñal Malab Tal omo s vio l rso arior Malab rabaa o úio ipo lmos: las maris. Los ipos aos básios o
Sismas Sñals Crso 4/5 Igiría Iformáia PRÁCTICA : Aálisis l omiio l impo sismas oios simpls I.- Prosamio sñal Malab Tal omo s vio l rso arior Malab rabaa o úio ipo lmos: las maris. Los ipos aos básios o
LISTA DE SÍMBOLOS. Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro
 LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
Ejercicios de Teoría de conjuntos
 Dpto. de Álgebra, Computación, Geometría y Topología Universidad de Sevilla Ejercicios de Teoría de conjuntos José A. Alonso Jiménez (jalonso@us.es) Sevilla, 1991 Contenido 1 La teoría de conjunto de Zermelo
Dpto. de Álgebra, Computación, Geometría y Topología Universidad de Sevilla Ejercicios de Teoría de conjuntos José A. Alonso Jiménez (jalonso@us.es) Sevilla, 1991 Contenido 1 La teoría de conjunto de Zermelo
OSCILADOR ARMÓNICO SIMPLE
 OSIDOR RÓNIO SIPE 0409 1 ey e Hooe rterzón e ovmento rmóno Sme (..S.) Veo y eerón en e..s. Ejemo. Reorte en oón horzont y vert Pénuo me Pénuo fo Energ en e movmento rmóno ovmento rmóno mortguo ey e Hooe
OSIDOR RÓNIO SIPE 0409 1 ey e Hooe rterzón e ovmento rmóno Sme (..S.) Veo y eerón en e..s. Ejemo. Reorte en oón horzont y vert Pénuo me Pénuo fo Energ en e movmento rmóno ovmento rmóno mortguo ey e Hooe
Álgebra II Primer Cuatrimestre 2016
 Álgebra II Primer Cuatrimestre 2016 Práctica 3: Anillos Ejemplos construcciones 1. Probar que los siguientes conjuntos son anillos con las operaciones indicadas. Decidir en cada caso si son conmutativos,
Álgebra II Primer Cuatrimestre 2016 Práctica 3: Anillos Ejemplos construcciones 1. Probar que los siguientes conjuntos son anillos con las operaciones indicadas. Decidir en cada caso si son conmutativos,
Flexión de placas planas
 Método de los Elementos Finitos para Análisis Estructural Fleión de placas planas Teoría clásica Definición Dominio continuo plano (XY), espesor pequeño h. Fuerzas (F z ) y deformaciones (w) perpendiculares
Método de los Elementos Finitos para Análisis Estructural Fleión de placas planas Teoría clásica Definición Dominio continuo plano (XY), espesor pequeño h. Fuerzas (F z ) y deformaciones (w) perpendiculares
Tema 1. Clasificación de las EDP. Características
 Tema 1. Clasificación de las EDP. Características 1.1. Definiciones y notación En este curso vamos a seguir y a ampliar el estudio de las Ecuaciones en Derivadas Parciales (EDP) iniciado en la asignatura
Tema 1. Clasificación de las EDP. Características 1.1. Definiciones y notación En este curso vamos a seguir y a ampliar el estudio de las Ecuaciones en Derivadas Parciales (EDP) iniciado en la asignatura
Tema 2: Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 Tema 2: Espacios vectoriales Ejercicios 1. En R 2 se definen las siguientes operaciones: (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 Tema 2: Espacios vectoriales Ejercicios 1. En R 2 se definen las siguientes operaciones: (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Resultados de los Problemas: Práctico Nº 1
 Resultados de los Problemas: Práctico Nº 1 1. (a) 0,19 m; (b) 7,50 10 7 cl; (c) 10-3 Gbyte; (d) 1,9740 10-8 m; (e) 4500 pulsaciones/h; (f) 11,11 m/s; (g) 5,0 10 3 kg/m 3 2. 0,7 nm; 7 Å 3. (a) Dos; (b)
Resultados de los Problemas: Práctico Nº 1 1. (a) 0,19 m; (b) 7,50 10 7 cl; (c) 10-3 Gbyte; (d) 1,9740 10-8 m; (e) 4500 pulsaciones/h; (f) 11,11 m/s; (g) 5,0 10 3 kg/m 3 2. 0,7 nm; 7 Å 3. (a) Dos; (b)
Estimación de variables no observables para la economía peruana
 Estimación de variables no observables para la economía peruana XXX Encuentro de Investigación del BCRP Ismael Ignacio Mendoza Mogollón imendoza@mef.gob.pe Octubre 2012 XXX Encuentro de Economistas (Institute)
Estimación de variables no observables para la economía peruana XXX Encuentro de Investigación del BCRP Ismael Ignacio Mendoza Mogollón imendoza@mef.gob.pe Octubre 2012 XXX Encuentro de Economistas (Institute)
Sistemas continuos. Francisco Carlos Calderón PUJ 2010
 Sistemas continuos Francisco Carlos Calderón PUJ 2010 Objetivos Definir las propiedades básicas de los sistemas continuos Analizar la respuesta en el tiempo de un SLIT continuo Definición y clasificación
Sistemas continuos Francisco Carlos Calderón PUJ 2010 Objetivos Definir las propiedades básicas de los sistemas continuos Analizar la respuesta en el tiempo de un SLIT continuo Definición y clasificación
Coordenadas geográficas
 Cálculos de radiación sobre superficies inclinadas Coordenadas geográficas Ingenieros Industriales 1 VARIABLES DEL SISTEMA Se definen a continuación todas las variables tanto geográficas como temporales-
Cálculos de radiación sobre superficies inclinadas Coordenadas geográficas Ingenieros Industriales 1 VARIABLES DEL SISTEMA Se definen a continuación todas las variables tanto geográficas como temporales-
SOBRE UNIFORMIDADES DEFINIDAS POR CUBRIMIENTOS Y COMPLETADO FIBRA A FIBRA HECTOR ANTONIO RICAURTE MONCALEANO
 SOBRE UNIFORMIDADES DEFINIDAS POR CUBRIMIENTOS Y COMPLETADO FIBRA A FIBRA HECTOR ANTONIO RICAURTE MONCALEANO 830219 UNIVERSIDAD NACIONAL DE COLOMBIA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS BOGOTÁ,
SOBRE UNIFORMIDADES DEFINIDAS POR CUBRIMIENTOS Y COMPLETADO FIBRA A FIBRA HECTOR ANTONIO RICAURTE MONCALEANO 830219 UNIVERSIDAD NACIONAL DE COLOMBIA FACULTAD DE CIENCIAS DEPARTAMENTO DE MATEMÁTICAS BOGOTÁ,
LISTA DE SÍMBOLOS. Bajada, movimiento que realiza el palpador al acercarse al centro de rotación de la
 LISTA DE SÍMBOLOS a bu ( ) B Bi n af u b i Ancho de la huella de contacto Curva de Bézier no paramétrica Bajada, movimiento que realiza el palpador al acercarse al centro de rotación de la Polinomio de
LISTA DE SÍMBOLOS a bu ( ) B Bi n af u b i Ancho de la huella de contacto Curva de Bézier no paramétrica Bajada, movimiento que realiza el palpador al acercarse al centro de rotación de la Polinomio de
Tema 4: Aplicaciones lineales
 Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 4: Aplicaciones lineales Ejercicios 1 Estudia la linealidad de las siguientes aplicaciones: (a) f : R R 3, definida por f(x, y) =
Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 4: Aplicaciones lineales Ejercicios 1 Estudia la linealidad de las siguientes aplicaciones: (a) f : R R 3, definida por f(x, y) =
INGENIERÍA DE SISTEMAS Y AUTOMÁTICA. Fundamentos de Regulación y Automática. Análisis de Sistemas
 INGENIERÍA DE SISTEMAS Y AUTOMÁTIA Fudao d Rgulació y Auoáica Aálii d Sia FUNDAMENTOS DE REGULAIÓN AUTOMÁTIA Aálii d Sia Jua Lui Roja Ojda Igiría d Sia y Auoáica Uivridad d ádiz Spibr 00 ANEXO B : Traforada
INGENIERÍA DE SISTEMAS Y AUTOMÁTIA Fudao d Rgulació y Auoáica Aálii d Sia FUNDAMENTOS DE REGULAIÓN AUTOMÁTIA Aálii d Sia Jua Lui Roja Ojda Igiría d Sia y Auoáica Uivridad d ádiz Spibr 00 ANEXO B : Traforada
Tema 5. Análisis de Fourier para Señales y Sistemas Discretos.
 Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
Problemas con soluciones
 Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Multiplicación de Matrices Naïve
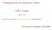 Multiplicación de Matrices Naïve Carl C. Cowen IUPUI (Indiana University Purdue University Indianapolis) Universidad de Zaragoza, 6 julio 2009 Los estudiantes de álgebra lineal aprenden, para matrices
Multiplicación de Matrices Naïve Carl C. Cowen IUPUI (Indiana University Purdue University Indianapolis) Universidad de Zaragoza, 6 julio 2009 Los estudiantes de álgebra lineal aprenden, para matrices
Métodos de Pareo FN1. Fernanda Ruiz Nuñez Noviembre, 2006 Buenos Aires
 Métodos de Pareo FN1 Fernanda Ruiz Nuñez Noviembre, 2006 Buenos Aires Slide 1 FN1 Fernanda Nunez, 11/17/2006 Asignación aleatoria vs. Selección en observables Supuesto bajo asignación aleatoria: Y (1),
Métodos de Pareo FN1 Fernanda Ruiz Nuñez Noviembre, 2006 Buenos Aires Slide 1 FN1 Fernanda Nunez, 11/17/2006 Asignación aleatoria vs. Selección en observables Supuesto bajo asignación aleatoria: Y (1),
Primera Escuela de Verano de Matemática y Física Universidad Central del Ecuador. Espacios Algebraicos de Probabilidad y Aplicaciones
 Primera Escuela de Verano de Matemática y Física Universidad Central del Ecuador Espacios Algebraicos de Probabilidad y Aplicaciones 12 de junio 2013 Sean: El conjunto Ω = {ω 1, ω 2,, ω n}, La función
Primera Escuela de Verano de Matemática y Física Universidad Central del Ecuador Espacios Algebraicos de Probabilidad y Aplicaciones 12 de junio 2013 Sean: El conjunto Ω = {ω 1, ω 2,, ω n}, La función
MUNICIPIO DE MEDELLÍN GRADO 10 CONCEPTOS BÁSICOS DE TRIGONOMETRÍA
 GUÍA DE CONCEPTOS BÁSICOS DE TRIGONOMETRÍA ÁREA MATEMÁTICAS PERÍODO 01 FECHA: 16 de enero de 2017 LOGROS: MUNICIPIO DE MEDELLÍN GRADO 10 Construir y clasificar los diferentes tipos de ángulos, expresando
GUÍA DE CONCEPTOS BÁSICOS DE TRIGONOMETRÍA ÁREA MATEMÁTICAS PERÍODO 01 FECHA: 16 de enero de 2017 LOGROS: MUNICIPIO DE MEDELLÍN GRADO 10 Construir y clasificar los diferentes tipos de ángulos, expresando
Convolución discreta cíclica
 Covolució discreta cíclica Estos aputes está escritos por Darío Coutiño Aquio y Egor Maximeko. Objetivos. Defiir la covolució discreta cíclica y demostrar el teorema sobre la covolució discreta cíclica
Covolució discreta cíclica Estos aputes está escritos por Darío Coutiño Aquio y Egor Maximeko. Objetivos. Defiir la covolució discreta cíclica y demostrar el teorema sobre la covolució discreta cíclica
Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula:
 PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
Espacio métrico 2º Bachillerato
 Espacio métrico 2º Bachillerato Presentación elaborada por la profesora Ana Mª Zapatero a partir de los materiales utilizados en el centro (Editorial SM) Ángulo entre dos rectas El ángulo de dos rectas
Espacio métrico 2º Bachillerato Presentación elaborada por la profesora Ana Mª Zapatero a partir de los materiales utilizados en el centro (Editorial SM) Ángulo entre dos rectas El ángulo de dos rectas
TEMA 2: DISTRIBUCIONES DE PROBABILIDAD
 ESTADÍSTICA, CURSO 008 009 TEMA : DISTRIBUCIONES DE PROBABILIDAD LEYES DE PROBABILIDAD. SUCESOS ALEATORIOS Experimetos aleatorios, espacio muestral. Sucesos elemetales y compuestos. Suceso imposible Ø,
ESTADÍSTICA, CURSO 008 009 TEMA : DISTRIBUCIONES DE PROBABILIDAD LEYES DE PROBABILIDAD. SUCESOS ALEATORIOS Experimetos aleatorios, espacio muestral. Sucesos elemetales y compuestos. Suceso imposible Ø,
La Recta. Hermes Pantoja Carhuavilca. Matemática I. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 La Recta Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matemática I Hermes Pantoja Carhuavilca 1 de 11 CONTENIDO Ecuaciones de la recta en R 2 Ecuación
La Recta Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matemática I Hermes Pantoja Carhuavilca 1 de 11 CONTENIDO Ecuaciones de la recta en R 2 Ecuación
Formulaciones equivalentes del Axioma de Elección
 Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Ecuaciones fundamentales en Física general. Cinemática de una partícula
 Ecuacies fudametales de la Física Ecuacies fudametales e Física geeal Ciemática de ua patícula v d a dv.r.u. v cte a 0 s s + v.t.r.u.a. a cte s s + v.t + ½.a.t v v + a.t v v +.a.s vimiet cicula s φ.r dϕ
Ecuacies fudametales de la Física Ecuacies fudametales e Física geeal Ciemática de ua patícula v d a dv.r.u. v cte a 0 s s + v.t.r.u.a. a cte s s + v.t + ½.a.t v v + a.t v v +.a.s vimiet cicula s φ.r dϕ
Curso Curso
 Problema 98. Dos chicos juegan a partir una tableta de chocolate de m n pastillas. Cada uno de ellos parte la tableta por alguna de las ĺıneas marcadas. Pierde el que no pueda partir. Quién ganará, el
Problema 98. Dos chicos juegan a partir una tableta de chocolate de m n pastillas. Cada uno de ellos parte la tableta por alguna de las ĺıneas marcadas. Pierde el que no pueda partir. Quién ganará, el
SISMOLOGÍA E INGENIERÍA SISMICA Tema II. Propagación de ondas sísmicas: Ondas internas.
 SISMOLOGÍA E INGENIERÍA SISMICA Tema II. Propagación de ondas sísmicas: Ondas internas. I. Introducción II. Mecánica de un medio elástico. Ecuación del desplazamiento en un medio elástico, isótropo, homogéneo
SISMOLOGÍA E INGENIERÍA SISMICA Tema II. Propagación de ondas sísmicas: Ondas internas. I. Introducción II. Mecánica de un medio elástico. Ecuación del desplazamiento en un medio elástico, isótropo, homogéneo
Macroeconomía Dinámica
 Macroeconomía Dinámica Bloque 2. El modelo básico de equilibrio general dinámico Departamento de Economía Este tema se publica bajo Licencia: Crea8ve Commons BY- NC- SA 4.0 1 Introducción 2 El hogar representativo
Macroeconomía Dinámica Bloque 2. El modelo básico de equilibrio general dinámico Departamento de Economía Este tema se publica bajo Licencia: Crea8ve Commons BY- NC- SA 4.0 1 Introducción 2 El hogar representativo
Ecuaciones diferenciales de Equilibrio
 Ecuaciones diferenciales de Equilibrio 28 de marzo de 2006 1. Elasticidad en una dimensión 1.1. Esfuerzo σ y carga lineal b(x) Para examinar un cuerpo desde el contínuo, que es la primera hipótesis (a),
Ecuaciones diferenciales de Equilibrio 28 de marzo de 2006 1. Elasticidad en una dimensión 1.1. Esfuerzo σ y carga lineal b(x) Para examinar un cuerpo desde el contínuo, que es la primera hipótesis (a),
Teoría Espectral. Stephen B. Sontz. Centro de Investigación en Matemáticas, A.C. (CIMAT) Guanajuato, Mexico
 Teoría Espectral Stephen B. Sontz Centro de Investigación en Matemáticas, A.C. (CIMAT) Guanajuato, Mexico Mini-curso impartido en Colima 29 septiembre 2016 - Tercer día Introducción Hay dos dichos populares
Teoría Espectral Stephen B. Sontz Centro de Investigación en Matemáticas, A.C. (CIMAT) Guanajuato, Mexico Mini-curso impartido en Colima 29 septiembre 2016 - Tercer día Introducción Hay dos dichos populares
( ) C P 2. : Realizo todas las tareas solo si no estudio diariamente. : Es necesario que realice todas las tareas para que no apruebe el curso.
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN INTENSIVO 015 PRIMERA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN INTENSIVO 015 PRIMERA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y
5 MECÁNICA ESTADÍSTICA CUÁNTICA DE GASES IDEALES
 ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
MATRICES,DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES
 Departamento de Matemática Aplicada II EEI ÁLGEBRA Y ESTADÍSTICA Boletín n o 1 (2010-2011 MATRICES,DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES 1 Sean A, B, C, D y E matrices de tamaño 4 5, 4 5, 5 2,
Departamento de Matemática Aplicada II EEI ÁLGEBRA Y ESTADÍSTICA Boletín n o 1 (2010-2011 MATRICES,DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES 1 Sean A, B, C, D y E matrices de tamaño 4 5, 4 5, 5 2,
ARMADURA DE CORTE VERIFICACION Y DIMENSIONAMIENTO. Zona a: Zona en la cual no es de esperar fisuras por flexión.
 HORMIGÓN II 74.5 ARMADURA DE CORTE VERIFICACION Y DIMENSIONAMIENTO Definición de zonas a y b Zona a: Zona en la cual no es de esperar fisuras por flexión. Zona b: Zona en la cual las fisuras por corte
HORMIGÓN II 74.5 ARMADURA DE CORTE VERIFICACION Y DIMENSIONAMIENTO Definición de zonas a y b Zona a: Zona en la cual no es de esperar fisuras por flexión. Zona b: Zona en la cual las fisuras por corte
Ejercicios de Teoría de conjuntos
 Ejercicios de Teoría de conjuntos José A. Alonso Jiménez Mario J. Pérez Jiménez Sevilla, Octubre de 1993 Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla 1 TEORÍA DE
Ejercicios de Teoría de conjuntos José A. Alonso Jiménez Mario J. Pérez Jiménez Sevilla, Octubre de 1993 Dpto. de Ciencias de la Computación e Inteligencia Artificial Universidad de Sevilla 1 TEORÍA DE
PROCESAMIENTO DIGITAL DE SEÑALES
 PROCESAMIENTO DIGITAL DE SEÑALES Profsor: Mg. Ig. Rafal Bustamat Alvarz Itroducció: El procsamito digital d sñals ti su orig los años 60 co l mplo d las primras computadoras digitals. El dsarrollo d la
PROCESAMIENTO DIGITAL DE SEÑALES Profsor: Mg. Ig. Rafal Bustamat Alvarz Itroducció: El procsamito digital d sñals ti su orig los años 60 co l mplo d las primras computadoras digitals. El dsarrollo d la
Tarea 2 de Álgebra Superior II
 Tarea 2 de Álgebra Superior II Divisibilidad 1. Sean a, b, c, d Z. Determine si los siguientes enunciados son verdaderos o falsos. Si son verdaderos, probar el resultado, y si son falsos, dar un contraejemplo.
Tarea 2 de Álgebra Superior II Divisibilidad 1. Sean a, b, c, d Z. Determine si los siguientes enunciados son verdaderos o falsos. Si son verdaderos, probar el resultado, y si son falsos, dar un contraejemplo.
Objetos en equilibrio - Ejemplo
 Objetos en equilibrio - Ejemplo Una escalera de 5 m que pesa 60 N está apoyada sobre una pared sin roce. El extremo de la escalera que apoya en el piso está a 3 m de la pared, ver figura. Cuál es el mínimo
Objetos en equilibrio - Ejemplo Una escalera de 5 m que pesa 60 N está apoyada sobre una pared sin roce. El extremo de la escalera que apoya en el piso está a 3 m de la pared, ver figura. Cuál es el mínimo
Respuesta en Frecuencia de Sistemas Continuos
 espuesta en Frecuencia e Sisteas Continuos UeC - DIE Problea Caso Ilustrar el Diagraa e Boe a partir e una F. e T. y/o e una representación {A, b, c, }. Masa suspenia. Paráetros l o :=.5 :=.5 k:= x(t k
espuesta en Frecuencia e Sisteas Continuos UeC - DIE Problea Caso Ilustrar el Diagraa e Boe a partir e una F. e T. y/o e una representación {A, b, c, }. Masa suspenia. Paráetros l o :=.5 :=.5 k:= x(t k
CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen
 CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
TEMA 2: CINEMÁTICA Y DINÁMICA DE UNA PARTÍCULA
 EA : CINEÁICA Y DINÁICA DE UNA PAÍCULA. Desipión del oiieno: ipos de sises de efeeni.. gniudes del oiieno: eo posiión, yeoi, eo desplzieno, eloidd, eleión. 3. Esudio de lgunos oiienos: oiienos eilíneos,
EA : CINEÁICA Y DINÁICA DE UNA PAÍCULA. Desipión del oiieno: ipos de sises de efeeni.. gniudes del oiieno: eo posiión, yeoi, eo desplzieno, eloidd, eleión. 3. Esudio de lgunos oiienos: oiienos eilíneos,
Un resultado de H convergencia para operadores tipo elpticos fraccionarios
 Un resultado de H convergencia para operadores tipo elpticos fraccionarios Julián Fernández Bonder Universidad de Buenos Aires e IMAS-CONICET http://mate.dm.uba.ar/~jfbonder Trabajo conjunto con Antonella
Un resultado de H convergencia para operadores tipo elpticos fraccionarios Julián Fernández Bonder Universidad de Buenos Aires e IMAS-CONICET http://mate.dm.uba.ar/~jfbonder Trabajo conjunto con Antonella
Parte 2: Definición y ejemplos de topologías.
 Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Tema 4: Probabilidad y Teoría de Muestras
 Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Sistemas de ayuda a la decisión Modelización de la incertidumbre Tema 2. Incertidumbre y Probabilidad
 Sistemas de ayuda a la decisión Modelización de la incertidumbre Tema 2. Incertidumbre y Probabilidad Indice 1) Sucesos aleatorios. Espacio muestral. 2) Operaciones con sucesos. 3) Enfoques de la Probabilidad.
Sistemas de ayuda a la decisión Modelización de la incertidumbre Tema 2. Incertidumbre y Probabilidad Indice 1) Sucesos aleatorios. Espacio muestral. 2) Operaciones con sucesos. 3) Enfoques de la Probabilidad.
Teoría de Lenguajes. Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014
 Teoría de Lenguajes Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014 aterial compilado por el Profesor Julio Jacobo, a lo largo de distintas ediciones
Teoría de Lenguajes Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014 aterial compilado por el Profesor Julio Jacobo, a lo largo de distintas ediciones
Transformada Z. Ejemplos. Ejemplos de cálculo [ ] = [ ] ( ) ( ) 1. Transformada Z. α = α α α si α. α α α
![Transformada Z. Ejemplos. Ejemplos de cálculo [ ] = [ ] ( ) ( ) 1. Transformada Z. α = α α α si α. α α α Transformada Z. Ejemplos. Ejemplos de cálculo [ ] = [ ] ( ) ( ) 1. Transformada Z. α = α α α si α. α α α](/thumbs/56/38404012.jpg) Trasformada Ejemplos Ejemplos de cálculo. Trasformada... Calcular la trasformada, por defiició, idicado la regió de coergecia p u [ ] h h p u cos u Solució: Para calcular la Trasformada por defiició, resulta
Trasformada Ejemplos Ejemplos de cálculo. Trasformada... Calcular la trasformada, por defiició, idicado la regió de coergecia p u [ ] h h p u cos u Solució: Para calcular la Trasformada por defiició, resulta
Cálculo numérico. Sistemas de ecuaciones lineales.
 José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
José Luis Morales http://allman.rhon.itam.mx/ jmorales Departamento de Matemáticas. ITAM. 2010. Las raíces de x 2 bx + c = 0. r = b ± b 2 4c 2 b = 3.6778, c = 0.0020798 r 1 = 3.67723441190... r 2 = 0.00056558809...
Lógica e Inteligencia Artificial: Una Historia sin Fin
 Lógica e Inteligencia Artificial: Una Historia sin Fin UCAB / USB Detractores de Lógica L en IA... Búsqueda del del razonamiento lógico desde Aristóteles, con con su su consolidación por por Peano, Frege,
Lógica e Inteligencia Artificial: Una Historia sin Fin UCAB / USB Detractores de Lógica L en IA... Búsqueda del del razonamiento lógico desde Aristóteles, con con su su consolidación por por Peano, Frege,
Probabilidad y Estadística
 Probabilidad y Estadística Grado en Ingeniería Informática Tema 4 Vectores aleatorios Javier Cárcamo Departamento de Matemáticas Universidad Autónoma de Madrid javier.carcamo@uam.es Javier Cárcamo PREST.
Probabilidad y Estadística Grado en Ingeniería Informática Tema 4 Vectores aleatorios Javier Cárcamo Departamento de Matemáticas Universidad Autónoma de Madrid javier.carcamo@uam.es Javier Cárcamo PREST.
Ejercicio 1. Calcule y grafique la densidad espectral de potencia de la salida del filtro y el valor de potencia total. Ejercicio 2.
 Guía de Ejercicios Ejercicio El circuito RC de la figura es excitado por ua señal de ruido blaco co desidad espectral de potecia costate e igual a N /. R w(t) C v(t) Calcule y grafique la desidad espectral
Guía de Ejercicios Ejercicio El circuito RC de la figura es excitado por ua señal de ruido blaco co desidad espectral de potecia costate e igual a N /. R w(t) C v(t) Calcule y grafique la desidad espectral

