Herramientas digitales de auto-aprendizaje para Matemáticas
|
|
|
- José María Alberto Herrera Alcaraz
- hace 7 años
- Vistas:
Transcripción
1 ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura
2 ir
3 ir Índice. Definiciones y propiedades Método de por partes Integración de funciones Integración de funciones Integración de funciones ir Bibliografía
4 ir
5 . Definiciones y propiedades El cálculo integral formaliza conceptos bastantes sencillos e intuitivos: el de área de una región, volumen de un cuerpo, y longitud de curvas entre otras aplicaciones. ir Los orígenes del cálculo de áreas se pueden encontrar en el método de exhaución desarrollado por los griegos hace más de 2000 años. Sin embargo fueron Newton y Leibnitz quienes le dieron el enfoque riguroso actual.
6 . Definiciones y propiedades ir
7 . Definiciones y propiedades ir Definición Dadas dos funciones f y F, decimos que F es una primitiva de la función f en un conjunto de valores D si: Ejemplo Si f(x) = 2x, entonces F (x) = f(x), x D. F (x) = x 2 es una primitiva de f(x) en R, porque F (x) = (x 2 ) = 2x = f(x). Del mismo modo, F (x) = x es una primitiva de f(x) en R, porque F (x) = (x 2 + 7) = 2x = f(x). Se deduce fácilmente que Observación Si F es una primitiva de f en D, entonces F (x) + C es primitiva de f(x) en D, siendo C cualquier número real.
8 . Definiciones y propiedades ir Definición Al conjunto de todas las primitivas de f se le llama integral indefinida de f y se denota por f(x)dx. De la observación anterior se deduce que si F (x) es una primitiva de f(x), entonces f(x)dx = F (x) + C, C R. Propiedades (de la integral indefinida) Sea f : I R R. Se tiene que 1 Si k R, entonces k f(x)dx = k f(x)dx. 2 (f(x) ± g(x)) dx = f(x)dx ± g(x)dx.
9 ir
10 ir Definición Se llaman integrales a aquellas que se deducen directamente de las reglas de derivación. En la tabla de la página siguiente se muestran algunas integrales.
11 Algunas integrales ir k dx = kx k R (n 1) x n dx = xn+1 1 x dx = ln x e x dx = e x a x dx = ax ln a sen(x) dx = cos(x) cos(x) dx = sen(x) 1 n+1 f(x) n f (x) dx = f(x)n+1 f (x) f(x) sen 2 (x) dx = cotg(x) f (x) 1 n+1 dx = ln f(x) e f(x) f (x) dx = e f(x) a f(x) f (x) dx = af(x) ln a sen(f(x))f (x) dx = cos(f(x)) cos(f(x))f (x) dx = sen(f(x)) sen 2 (f(x)) dx = tg(x) f (x) cos 2 (x) f dx = arctg(x) (x) 1+x x 2 dx = arcsen(x) f cos 2 (f(x)) 1+(f(x)) 2 (x) 1 (f(x)) 2 dx = cotg(f(x)) dx = tg(f(x)) dx = arctg f(x) dx = arcsen f(x)
12 ir
13 Integración por sustitución o cambio ir
14 : sustitución o cambio ir Consiste en hacer un cambio que transforme la integral en otra que sepamos calcular. Una vez resuelta, hay que deshacer el cambio. Teorema Sea x = φ(t) derivable respecto de t (entonces dx = φ (t)dt). Podremos calcular f(x)dx así: f(x)dx = f(φ(t))φ (t)dt Encontraremos solución siempre que sepamos calcular la última primitiva de la igualdad anterior. Ejemplo { t = 2x; x = t/2 cos(2x)dx = dt = 2dx } = { e cosx t = cosx sen(x) dx = dt = sen(x) dx cos(t) dt 2 = 1 2 sen(t)+c = 1 2 sen(2x)+c } = e t dt = e t +C = e cos(x) +C
15 Integración por partes ir
16 : por partes ir Integración por partes Sea u(x) y v(x) dos funciones derivables. Dado que se deduce que (u(x) v(x)) = u(x) v (x) + u (x) v(x) u(x) v (x) = (u(x) v(x)) u (x) v(x) y por tanto, si se puede integrar respecto de x: u(x)v (x)dx = u(x)v(x) v(x)u (x)dx Ejemplo { u(x) = ln x du(x) = 1 x n x ln x dx = dx } dv(x) = x n = dx v(x) = xn+1 n+1 = xn+1 n + 1 ln x x n ( xn+1 dx = ln x 1 ) + C. n + 1 n + 1 n + 1
17 : por partes Ejemplo ir { u = arctg(x) du = dx arctg(x)dx = 1+x 2 dv = dx v = x = x arctg(x) } = x 1 + x 2 dx = x arctg(x) 1 2 ln x C.
18 Integración de funciones ir
19 Integración de funciones Integración de funciones Son integrales de la forma f(x)dx = p(x) q(x) dx, ir donde p(x) y q(x) son polinomios. Si grado(p) < grado(q), aplicaremos el método de descomposición descrito a continuación. En otro caso, debemos efectuar la división de polinomios: f(x) = p(x) r(x) = c(x) + q(x) q(x), donde c(x) y r(x) son respectivamente el polinomio cociente y el polinomio resto de la división.
20 Integración de funciones ir Ejemplo Calculemos x 2 x 1 dx. Dividiendo se obtiene que x2 = (x + 1)(x 1) + 1, por tanto: x 2 [ x 1 dx = (x + 1) + 1 ] dx = x 1 1 (x + 1) dx + x 1 dx = x2 /2 + x + ln( x 1 + C)
21 Integración de funciones Método de descomposición (grado(p) < grado(q)) Caso 1. grado(q) = n con todas las raíces reales y simples: q(x) = a 0(x x 1)(x x 2)... (x x n) ir Se realizará una descomposición en fracciones simples como sigue: p(x) q(x) = A 1 a 0(x x 1) + A2 x x An x x n, A i R, i = 1... n. A continuación se integrarán los sumandos de la descomposición obtenida: p(x) q(x) dx = A 1 a 0(x x dx + A 2 A n dx dx = 1) x x 2 x x n = A1 a 0 ln x x 1 + A 2 ln x x A n ln x x n + C.
22 Integración de funciones Ejemplo Calcula 2x 3 x 2 3x+2 dx ir
23 Integración de funciones ir Ejemplo Calcula 2x 3 x 2 3x+2 dx Puesto que x 2 3x + 2 = (x 1)(x 2), se tiene que 2x 3 x 2 3x + 2 = A1 x 1 + { 2x 3 = A 1(x 2) + A 2(x 1) Por tanto 2x 3 x 2 3x + 2 dx = A2 x 2 2x 3 A1(x 2) + A2(x 1) = x 2 3x + 2 (x 2)(x 1)) 1 x 1 dx + 2 = A 1 + A 2 3 = 2A 1 A 2 { A1 = 1 A 2 = 1 1 dx = ln x 1 +ln x 2 +C x 2
24 Integración de funciones Ejemplo 2x 3 2x 3 x 2 x dx = ir
25 Integración de funciones ir Ejemplo { 2x 3 Teniendo en cuenta: 2x 3 x 2 x dx = 2x 3 x 2 x = x(x 1)(2x + 1) ( A = x + B x 1 + C ) = 2x + 1 = 3 ln x 1 3 ln x 1 8 ln 2x C, 3 donde los coeficientes A, B y C se han calculado resolviendo: 2x 3 2x 3 x 2 x = A x + B x 1 + } = C 2x+1 = A(x 1)(2x+1)+Bx(2x+1)+Cx(x 1) = x(x 1)(2x+1) = x2 (2A+2B+C)+x( A+B C) A 2x 3 x 2, x para lo que se debe cumplir que: 0 = 2A + 2B + C 2 = A + B C 3 = A A = 3 B = 1 3 C = 16 3
26 Integración de funciones Método de descomposición (grado(p) < grado(q)) Caso 2. grado(q) = k con alguna raíz real de multiplicidad k: q(x) = a 0(x x 0) k ir Descomposición en fracciones simples: p(x) q(x) = A 1 a 0(x x 0) + A 2 (x x 0) 2 + A 3 (x x 0) A k (x x 0) k. Integración de los sumandos obtenidos: p(x) q(x) dx = A 1 a 0(x x 0) dx + = A1 a 0 A 2 (x x dx + 0) 2 ln x x 0 +A 2 (x x 0) 1 1 A 3 (x x dx ) 3 +A 3 (x x 0) 2 2 A k (x x 0) k dx (x x 0) k A k +C. k + 1
27 Integración de funciones Ejemplo Calcula 3x+5 x 3 x 2 x+1 dx ir
28 Integración de funciones ir Ejemplo Calcula 3x+5 x 3 x 2 x+1 dx Puesto que x 3 x 2 x + 1 = (x + 1)(x 1) 2, se tiene que: 3x+5 x 3 x 2 x+1 = A 1 x+1 + A 2 (x 1) + A 3 (x 1) 2 3x+5 x 3 x 2 x+1 = A 1(x 1) 2 +A 2 (x 1)(x+1)+A 3 (x+1) (x+1)(x 1) 2 y en consecuencia, como los denominadores de las fracciones anteriores también son iguales, los numeradores también lo serán: de donde Por tanto 3x + 5 = A 1 (x 1) 2 + A 2 (x 1)(x + 1) + A 3 (x + 1) 3x + 5 x 3 x 2 x + 1 dx = 0 = A 1 + A 2 3 = 2A 1 + A 3 5 = A 1 A 2 + A 3 1/2 x + 1 dx + A 1 = 1/2 A 2 = 1/2 A 3 = 4 1/2 (x 1) dx + 1/2 ln x + 1 1/2 ln x 1 3 (x 1) 2 dx = 4 (x 1)
29 Integración de funciones ir Ejemplo donde : { } 2x 3 Teniendo en cuenta: x 3 3x 2 + 3x 1 dx = x 3 3x 2 + 3x 1 = (x 1) 3 = ( = A x 1 + ) B (x 1) 2 + C (x 1) 3 dx = ( 0 = x (x 1) ) 1 (x 1) 3 dx = 2 (x 1) + 1/2 (x 1) 2 + C 2x 3 x 3 3x 2 +3x 1 = A x 1 + B (x 1) 2 + lo que implica que A = 0, B = 2 y C = 1. Observación C (x 1) 3 = Ax2 +x( 2A+B)+(A B+C) (x 1) 3 Hay otras muchas combinaciones, como mezcla de raíces reales y complejas (simples y/o múltiples). Aquí sólo se tratará el caso anterior, y el caso en que la raíz compleja es de multiplicidad 1.
30 Integración de funciones ir Método de descomposición (grado(p) < grado(q)) Caso 3. q(x) tiene alguna raíz compleja simple. q(x) = k(x x 1) α 1... (x x p) αp [(x b 1) 2 + c 2 1]... [(x b k ) 2 + c 2 k] con k, x i, a j, c j R y α i N. Siempre es posible descomponer la fracción de esta forma: ( p(x) A 1 q(x) dx = 1 A α x x 1 (x x ) α 1 siendo M j, N j R + A1 p A αp p + + x x p (x x + p) αp M1x + N1 + [(x b 1) 2 + c 2 1 ] + + M kx + N k [(x b k ) 2 + c 2 k ] ) dx
31 Integración de funciones Ejemplo 1 x 3 +1 dx ir
32 Integración de funciones ir Ejemplo 1 x 3 +1 dx Puesto que x = (x + 1)(x 2 x + 1), se tiene que: 1 x 3 +1 = A 1 x+1 + A 2x+A 3 x 2 x+1 = A 1(x 2 x+1)+(a 2 x+a 3 )(x+1) (x+1)(x 2 x+1) 1 = A 1 (x 2 x + 1) + (A 2 x + A 3 )(x + 1) Igualando los coeficientes de los polinomios anteriores Por tanto 0 = A 1 + A 2 0 = A 1 + A 2 + A 3 1 = A 1 + A 3 A 1 = 1/3 A 2 = 1/3 A 3 = 2/3 1 dx = 1/3 dx + 1/3x+2/3 dx = x 3 +1 x+1 x 2 x+1 = 1 ln x /3x+2/3 dx 3 x 2 x+1 = 1 ln x + 1 1/6 2x 4 dx = 3 x 2 x+1
33 Integración de funciones ir Ejemplo (continuación) 1 x 3 +1 dx = = 1 3 ln x + 1 1/6 2x x 2 x+1 dx = = 1 3 ln x + 1 1/6 2x 1 x 2 x+1 + 1/6 3 x 2 x+1 dx = = 1 3 ln x + 1 1/6 ln(x2 x + 1) + 1/6 3 x 2 x+1 dx = = 1 3 ln x + 1 1/6 ln(x2 x + 1) + 1/6 3 (x 1/2) 2 +3/4 dx = = 1 3 ln x + 1 1/6 ln(x2 x + 1) + 1/6 3 4/3 4/3[(x 1/2) 2 +3/4] dx = = 1 3 ln x + 1 1/6 ln(x2 x + 1) + 1/6 4 ) 2+1 dx = 1 3 ln x + 1 1/6 ln(x2 x + 1) ( 2x / 3 ( ) 2x dx = 3 = 1 3 ln x + 1 1/6 ln(x2 x + 1) + 1 2/ 3 ( ) 3 2x dx = 3 ( ) = 1 3 ln x + 1 ln x2 x arctg 2x
34 Integración de funciones Método de descomposición (grado(p) < grado(q)) Caso 3.q(x) tiene alguna raíz compleja múltiple Por ejemplo, 2x 3 2x x(x 2 +4) 2 dx ir Para resolver integrales como la del ejemplo se puede emplear el método de Hermite (no lo veremos en este curso), que permite calcular primitivas de cocientes de polinomios rebajando el grado de los polinomios implicados en sucesivos pasos.
35 Integración de funciones ir
36 Integración de funciones ir -: f(sen(x), cos(x))dx Se convierten en integrales mediante la sustitución trigonométrica t = tan( x ), como sigue: 2 f(sen(x), cos(x))dx = = que es la integral de racional. Ejemplo dx sen(x) dx = = { t = tan( x 2dt ) dx = 2 1+t 2 sen(x) = 2t 1+t 2 cos(x) = 1 t2 1+t 2 ( 2t f 1 + t 2, 1 ) t t t 2 dt, { t = tan( x 2 sen(x) = ) dx = 2dt 1+t 2 2t cos(x) = 1 t2 1+t 2 1+t 2 1 t dt = ln t + C = ln tan( x 2 ) + C. } } = =
37 Integración de funciones ir Observaciones Existen varios tipos de integrales que se pueden racionalizar con cambios más sencillos. Son los siguientes: 1 f(sen(x), cos(x))dx, donde f( sen(x), cos(x)) = f(sen(x), cos(x)). Cambio t = cos(x). 2 f(sen(x), cos(x))dx, donde f(sen(x), cos(x)) = f(sen(x), cos(x)). Cambio t = sen(x). 3 f(sen(x), cos(x))dx, donde f( sen(x), cos(x)) = f(sen(x), cos(x)). Cambio t = tan(x).
38 Integración de funciones ir Ejemplo = dx sen(x) dx = { t = cos(x) dx = dt 1 t 2 sen(x) = 1 t 2 cos(x) = t 1 1 t dt = ln t 1 t C = 1 2 ln cos(x) 1 cos(x) C. Ejemplo t = sen(x) dx = dt cos 3 1 t 2 (x) dx = cos(x) = = 1 t 2 sen(x) = t = 1 t 2 dt = t t3 3 + C = sen(x) sen3 (x) + C. 3 } =
39 Integración de funciones ir ir
40 Integración de funciones ir ir del tipo f(x, x 2 ± a 2 )dx, f(x, a 2 x 2 )dx con a R, se convierten en integrales mediante los cambios 1 f(x, a 2 x 2 )dx: cambio x = a sen(t). 2 f(x, x 2 a 2 )dx: cambio x = a sen(t). 3 f(x, x 2 + a 2 )dx: cambio x = a tan(t).
41 Integración de funciones ir Ejemplo a { x = a sen(t) 2 x 2 dx = dx = a cos(t)dt } = a 2 que aplicando la igualdad 1 + cos(2t) = 2cos 2 (t) se transforma en cos 2 (t)dt ir a 2 cos 2 (t) dt = a 2 2 t + a2 a2 sen(2t) + C = 4 2 t + a2 2sen(t) cos(t) + C = 4 a 2 2 t + a2 4 2 sen(t) 1 sen 2 (t) + C = a 2 2 arc sen x a + x a 2 x 2 + C. 2
42 Integración de funciones ir Ejemplo x2 + a 2 dx = ir
43 Integración de funciones ir ir Ejemplo = x2 { } x = a tan(t) + a 2 dx = = a 2 dx = adt cos 2 (t) { y = sen(t) dt = dy 1 y 2 cos(t) = 1 y 2 sen(t) = y = a2 4 } = a 2 1 cos 3 (t) dt = 1 (1 y 2 ) 2 dt = ( ) 1 (1 y) (1 y) + 1 (1 + y) + 1 dt = 2 (1 + y) = a2 4 ( 2y 1 y 2 + ln y+1 y 1 ) + C = { } Deshaciendo los cambios: = y = sen t = 1 tan tan(t) = x = 2 (t) x 2 a 2 = x 2 x2 + a 2 + a2 ln x+ 4 x x 2 +a 2 x 2 +a 2 + C
44 Integración de funciones ir ir del tipo ( ) ax + b f x, n dx cx + d Se convierten en integrales mediante el cambio Ejemplo dx x + 1 dx = = 3 (t 1)dt + 3 Cambio: t = 3 x + 1 dx = 3t 2 dt t = n ax + b cx + d = 3 t 2 dt 1 + t = dt 1 + t = 3 t(t 2) + 3 ln(t + 1) + C = 2 = 3 3 x + 1( 3 x + 1 2) + 3 ln( 3 x ) + C 2
Proposición Si F es una primitiva de f en I, entonces todas las primitivas de f en I son de la forma F (x) + C con C R
 Tema 8 Cálculo de Primitivas. 8.. Definición y propiedades Definición 8... Sea f : I R R. Una primitiva de f en I es una función F : I R R derivable en I y tal que F (x) = f(x) para todo x I. Proposición
Tema 8 Cálculo de Primitivas. 8.. Definición y propiedades Definición 8... Sea f : I R R. Una primitiva de f en I es una función F : I R R derivable en I y tal que F (x) = f(x) para todo x I. Proposición
Matemáticas Empresariales I. Cálculo de Primitivas
 Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
TeleAcademia. Tu Academia Online. Tabla Resumen de Integrales. Nivel: Bachillerato y Universidad Versión: 0.1
 TeleAcademia Tu Academia Online www.teleacademia.es Tabla Resumen de Integrales Nivel: Bachillerato y Universidad Versión: 0.1 Todos los derechos reservados c 015 TeleAcademia Tu Academia Online. http://www.teleacademia.es
TeleAcademia Tu Academia Online www.teleacademia.es Tabla Resumen de Integrales Nivel: Bachillerato y Universidad Versión: 0.1 Todos los derechos reservados c 015 TeleAcademia Tu Academia Online. http://www.teleacademia.es
Contenidos de los preliminares
 Preliminares del tema Contenidos de los preliminares Propiedades de los logaritmos Un par de primitivas elementales Algunas ideas sobre la función arcotangente Funciones hiperbólicas Descomposición en
Preliminares del tema Contenidos de los preliminares Propiedades de los logaritmos Un par de primitivas elementales Algunas ideas sobre la función arcotangente Funciones hiperbólicas Descomposición en
CÁLCULO DE PRIMITIVAS
 CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
1. CÁLCULO DE PRIMITIVAS
 1 1. CÁLCULO DE PRIMITIVAS Definición 1.1. Primitiva. Una función F (x) es primitiva de f(x) si F (x) = f(x) para todo x del dominio de f. Obsérvese que si F (x) es primitiva de f(x), entonces F (x) +
1 1. CÁLCULO DE PRIMITIVAS Definición 1.1. Primitiva. Una función F (x) es primitiva de f(x) si F (x) = f(x) para todo x del dominio de f. Obsérvese que si F (x) es primitiva de f(x), entonces F (x) +
5.1. Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Cálculo de Primitivas
 . Primitivas de una función Sea I un intervalo y f : I IR. Se dice que f tiene tiene una primitiva en I si existe una función G : I IR, continua en I, derivable en el interior de I y verificando que G
. Primitivas de una función Sea I un intervalo y f : I IR. Se dice que f tiene tiene una primitiva en I si existe una función G : I IR, continua en I, derivable en el interior de I y verificando que G
2. La fórmula de la derivada de un producto de dos funciones, aplicada a f(x) g(x), permite escribir,
 INTRO. MÉTODOS DE INTEGR. ( II ) En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones
INTRO. MÉTODOS DE INTEGR. ( II ) En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones
Antiderivada o Primitiva
 Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Funciones racionales. Tema 5: Integración. Integrales reducibles a racionales. Primera reducción. Primeros ejemplos. Definición
 Funciones racionales Funciones racionales Tema 5: Integración. Integrales racionales y reducibles a racionales Análisis Matemático Grado en Física Definición Una función f se dice que es racional si f
Funciones racionales Funciones racionales Tema 5: Integración. Integrales racionales y reducibles a racionales Análisis Matemático Grado en Física Definición Una función f se dice que es racional si f
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES
 INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
MÉTODOS DE INTEGRACION
 MÉTODOS DE INTEGRACION En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones elementales
MÉTODOS DE INTEGRACION En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones elementales
B. Cálculo de primitivas.
 50CAPÍTULO 5. INTEGRAL DEFINIDA. CÁLCULO DE PRIMITIVAS y y f(x) x y y F (x) x F (x) 8 >< >: x si x [0, ] x + six (, ] x si x (, ] Figura 5.5: B. Cálculo de primitivas. 5.. Integración inmediata. Definición
50CAPÍTULO 5. INTEGRAL DEFINIDA. CÁLCULO DE PRIMITIVAS y y f(x) x y y F (x) x F (x) 8 >< >: x si x [0, ] x + six (, ] x si x (, ] Figura 5.5: B. Cálculo de primitivas. 5.. Integración inmediata. Definición
Capítulo 3: Cálculo integral
 (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos La integral indefinida Propiedades básicas de la integral indefinida Métodos de integración: por
(Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos La integral indefinida Propiedades básicas de la integral indefinida Métodos de integración: por
1. Algunas primitivas inmediatas (o casi inmediatas).
 Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
Integrales indefinidas. Teoremas 2º Bachillerato. Editorial SM
 Integrales indefinidas. Teoremas º Bachillerato Editorial SM Esquema Primitiva de una función La función G(x) es una primitiva de la función f(x) en un intervalo I si G'(x) = f(x) para todo x del intervalo
Integrales indefinidas. Teoremas º Bachillerato Editorial SM Esquema Primitiva de una función La función G(x) es una primitiva de la función f(x) en un intervalo I si G'(x) = f(x) para todo x del intervalo
5.1 Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 8. Introducción a la integración INTEGRAL INDEFINIDA
 INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
Antiderivada o Primitiva
 Antiderivada o Promitiva agosto 2012 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada. En esta Presentación... En esta Presentación veremos: Definición de Antiderivada.
Antiderivada o Promitiva agosto 2012 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada. En esta Presentación... En esta Presentación veremos: Definición de Antiderivada.
RESUMEN DE INTEGRALES. Concepto de Función primitiva: La función F es una función primitiva de f, si la derivada de F es f, es decir: = x 2
 RESUMEN DE INTEGRALES Concepto de Función primitiva: La función F es una función primitiva de f, si la derivada de F es f, es decir: F(x) es una función primitiva de f(x) F (x)=f(x) Ejemplo: f(x)=x 2 F(x)=
RESUMEN DE INTEGRALES Concepto de Función primitiva: La función F es una función primitiva de f, si la derivada de F es f, es decir: F(x) es una función primitiva de f(x) F (x)=f(x) Ejemplo: f(x)=x 2 F(x)=
Unidad Temática Cálculo de primitivas
 Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
Método de integración por fracciones parciales
 Método de integración por fracciones parciales Temas Fracciones parciales. Método de integración por fracciones parciales. Capacidades Descomponer una fracción en suma de fracciones parciales. Conocer
Método de integración por fracciones parciales Temas Fracciones parciales. Método de integración por fracciones parciales. Capacidades Descomponer una fracción en suma de fracciones parciales. Conocer
Colegio San Agustín (Santander) Página 1
 Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 3º Evaluación Integrales PRIMITIVA Integración es el proceso Recíproco de la Derivación Primitiva de una función f(x): F(x) es una primitiva
Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 3º Evaluación Integrales PRIMITIVA Integración es el proceso Recíproco de la Derivación Primitiva de una función f(x): F(x) es una primitiva
Tema 9: Cálculo integral
 Tema 9: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 9: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
integración de funciones racionales
 VIII 1 / 6 Ejercicios sugeridos para : los temas de las clases del 26 de febrero y 2 de marzo de 2004. Tema : Integración de funciones racionales. 1.- Diga, justificando, cuales de las siguientes fórmulas
VIII 1 / 6 Ejercicios sugeridos para : los temas de las clases del 26 de febrero y 2 de marzo de 2004. Tema : Integración de funciones racionales. 1.- Diga, justificando, cuales de las siguientes fórmulas
Cálculo de primitivas.
 Cálculo de primitivas. Isabel María Elena Fernández y Celia Rodríguez Alfama * 8 de septiembre de 005 Resumen Vamos a intentar mostrar una introducción al cálculo integral, que es el tema que nos ha quedado
Cálculo de primitivas. Isabel María Elena Fernández y Celia Rodríguez Alfama * 8 de septiembre de 005 Resumen Vamos a intentar mostrar una introducción al cálculo integral, que es el tema que nos ha quedado
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
UNIVERSIDAD DE SEVILLA CALCULO DE PRIMITIVAS. PRIMER CURSO
 UNIVERSIDD DE SEVILL DEPRTMENTO DE ECONOMÍ PLICD I CLCULO DE PRIMITIVS. PRIMER CURSO CLCULO DE PRIMITIVS Conceptos generales. Definición. Dada f : D IR IR decimos que F : D IR IR es una primitiva de f
UNIVERSIDD DE SEVILL DEPRTMENTO DE ECONOMÍ PLICD I CLCULO DE PRIMITIVS. PRIMER CURSO CLCULO DE PRIMITIVS Conceptos generales. Definición. Dada f : D IR IR decimos que F : D IR IR es una primitiva de f
INTEGRALES. EL PROBLEMA DEL ÁREA I
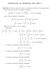 INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
1. PRIMITIVA DE UNA FUNCIÓN 2. PROPIEDADES DE LA INTEGRAL INDEFINIDA 3. INTEGRALES INMEDIATAS Ejemplos de integrales inmediatas tipo potencia
 Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
Funciones de Una Variable Real II: Cálculo de Primitivas
 Universidad de Murcia Departamento Matemáticas Funciones de Una Variable Real II: Cálculo de Primitivas B. Cascales, J. M. Mira y L. Oncina Universidad de Murcia http://webs.um.es/beca Grado en Matemáticas
Universidad de Murcia Departamento Matemáticas Funciones de Una Variable Real II: Cálculo de Primitivas B. Cascales, J. M. Mira y L. Oncina Universidad de Murcia http://webs.um.es/beca Grado en Matemáticas
Universidad de Chile Integración por partes. Ingeniería Matemática SEMANA 6: PRIMITIVAS
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Cálculo II
 - Fernando Sánchez - - 3 Cálculo Cálculo II de primitivas 0 03 07 Si f es una función elemental, se trata de encontrar una función F que cumpla F (x) = f (x). Para una clase amplia de funciones ya se ha
- Fernando Sánchez - - 3 Cálculo Cálculo II de primitivas 0 03 07 Si f es una función elemental, se trata de encontrar una función F que cumpla F (x) = f (x). Para una clase amplia de funciones ya se ha
INTEGRALES INDEFINIDAS
 INTEGRALES INDEFINIDAS Índice: 1. Primitiva de una función--------------------------------------------------------------------------- 2 2. Interpretación geométrica. Propiedades de la integral indefinida--------------------------
INTEGRALES INDEFINIDAS Índice: 1. Primitiva de una función--------------------------------------------------------------------------- 2 2. Interpretación geométrica. Propiedades de la integral indefinida--------------------------
CAPITULO 5. Integral Indefinida. Licda. Elsie Hernández Saborío. Instituto Tecnológico de Costa Rica Escuela de Matemática
 CAPITULO 5 Integral Indefinida 1 Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr) Créditos
CAPITULO 5 Integral Indefinida 1 Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr) Créditos
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Cálculo II
 - Fernando Sánchez - - 3 Cálculo Cálculo II de primitivas 04 03 06 Si f es una función elemental, se trata de encontrar una función F que cumpla F (x = f (x. Para una clase amplia de funciones ya se ha
- Fernando Sánchez - - 3 Cálculo Cálculo II de primitivas 04 03 06 Si f es una función elemental, se trata de encontrar una función F que cumpla F (x = f (x. Para una clase amplia de funciones ya se ha
Métodos de integración
 Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
INTEGRALES INMEDIATAS
 INTEGRALES INMEDIATAS Hay casos en los que la integral indeinida se calcula de orma inmediata, ya que la unción integrando es la derivada de una unción conocida. Se llaman integrales inmediatas a aquellas
INTEGRALES INMEDIATAS Hay casos en los que la integral indeinida se calcula de orma inmediata, ya que la unción integrando es la derivada de una unción conocida. Se llaman integrales inmediatas a aquellas
sobre un intervalo si para todo de se tiene que. Teorema 1 Sean y dos primitivas de la función en. Entonces,
 Integral indefinida Primitiva e integral indefinida. Cálculo de primitivas: métodos de integración. Integración por cambio de variable e integración por partes. Integración de funciones racionales e irracionales.
Integral indefinida Primitiva e integral indefinida. Cálculo de primitivas: métodos de integración. Integración por cambio de variable e integración por partes. Integración de funciones racionales e irracionales.
Tema 10: Cálculo integral
 Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Familiarizarse con las propiedades y las principales técnicas de integración.
 Capítulo 7 Integración Objetivos Familiarizarse con las propiedades y las principales técnicas de integración. 7.1. Definición y propiedades Sea f(x) una función real. Una primitiva o integral indefinida
Capítulo 7 Integración Objetivos Familiarizarse con las propiedades y las principales técnicas de integración. 7.1. Definición y propiedades Sea f(x) una función real. Una primitiva o integral indefinida
Tema 10: Cálculo Integral
 . Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
. Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Cálculo integral de funciones de una variable: integral indefinida
 Cálculo integral de funciones de una variable: integral indefinida BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M. ISABEL
Cálculo integral de funciones de una variable: integral indefinida BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M. ISABEL
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
 ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
, se denomina primitiva de esta función a otra F(x)
 1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
CÁLCULO DE PRIMITIVAS
 2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
1 El número x = 0, es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x.
 El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
Un resumen de la asignatura. Junio, 2015
 Un resumen de la asignatura Departamento de Matemática Aplicada a las Tecnologías de la Información y las Comunicaciones ETSIT (UPM) Junio, 2015 1 Los Números Reales(R) Los números Irracionales Continuidad
Un resumen de la asignatura Departamento de Matemática Aplicada a las Tecnologías de la Información y las Comunicaciones ETSIT (UPM) Junio, 2015 1 Los Números Reales(R) Los números Irracionales Continuidad
Análisis Matemático I (Lic. en Cs. Biológicas)
 Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Polinomios (II) Polinomios reales irreducibles. Pares de raíces conjugadas. Sesión teórica 4 (págs ) 27 de septiembre de 2010
 Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
Polinomios (II) 1 Sesión teórica 4 (págs. 3-9) 7 de septiembre de 010 Pares de raíces conjugadas irreducibles Consideremos un polinomio f (x) =a0 + a1x + ax + + anx n R[x], es decir, con coeficientes reales
Integrales indenidas
 Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Definición. Se denomina primitiva de la función f(x) en un intervalo (a, b) a toda función F (x) diferenciable en (a, b) y tal que F (x) = f(x).
 Tema 5 Integración 5.1 Integral Indefinida Definición. Se denomina primitiva de la función f(x) en un intervalo (a, b) a toda función F (x) diferenciable en (a, b) y tal que F (x) = f(x). Ejemplos: La
Tema 5 Integración 5.1 Integral Indefinida Definición. Se denomina primitiva de la función f(x) en un intervalo (a, b) a toda función F (x) diferenciable en (a, b) y tal que F (x) = f(x). Ejemplos: La
5. Métodos de integración y aplicaciones de la integral denida 5.5 Fracciones parciales. Métodos de Integración. Integración por fracciones parciales
 Métodos de Integración Integración por fracciones parciales P x) Consideremos la función racional donde P, Q son polinomios. Si derivamos una función racional Qx) obtenemos una funciòn racional. Si integramos
Métodos de Integración Integración por fracciones parciales P x) Consideremos la función racional donde P, Q son polinomios. Si derivamos una función racional Qx) obtenemos una funciòn racional. Si integramos
TEMA 12.- CÁLCULO DE PRIMITIVAS
 TEMA.- CÁLCULO DE PRIMITIVAS.-.- PRIMITIVA DE UNA FUNCIÓN Definición de Función Primitiva Una función F() se dice que es primitiva de otra función f() cuando F'() f() Ejemplos: F() es primitiva de f()
TEMA.- CÁLCULO DE PRIMITIVAS.-.- PRIMITIVA DE UNA FUNCIÓN Definición de Función Primitiva Una función F() se dice que es primitiva de otra función f() cuando F'() f() Ejemplos: F() es primitiva de f()
Ejercicios de Integrales resueltos
 Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
2 ln x dx. Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = 1 x dx dv = dx v = x y por tanto
 Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
CÁLCULO INTEGRAL INTEGRAL INDEFINIDA
 CÁLCULO INTEGRAL INTEGRAL INDEFINIDA Función primitiva : Una función F( se dice que es primitiva de otra función f( cuando F'( f( Por ejemplo F( es primitiva de f( Otra primitiva de f( podría ser F( +
CÁLCULO INTEGRAL INTEGRAL INDEFINIDA Función primitiva : Una función F( se dice que es primitiva de otra función f( cuando F'( f( Por ejemplo F( es primitiva de f( Otra primitiva de f( podría ser F( +
INTEGRAL INDEFINIDA. CÁLCULO DE PRIMITIVAS
 urso 07-08 TEMA 0 INTEGRAL INDEFINIDA. ÁLULO DE PRIMITIVAS ÍNDIE I. INTRODUIÓN II. PRIMITIVA DE UNA FUNIÓN. INTEGRAL INDEFINIDA III. INTEGRALES INMEDIATAS IV. MÉTODOS DE INTEGRAIÓN A. MÉTODO DE SUSTITUIÓN.
urso 07-08 TEMA 0 INTEGRAL INDEFINIDA. ÁLULO DE PRIMITIVAS ÍNDIE I. INTRODUIÓN II. PRIMITIVA DE UNA FUNIÓN. INTEGRAL INDEFINIDA III. INTEGRALES INMEDIATAS IV. MÉTODOS DE INTEGRAIÓN A. MÉTODO DE SUSTITUIÓN.
CAPÍTULO VII. INTEGRACIÓN INDEFINIDA
 CAPÍTULO VII. INTEGRACIÓN INDEFINIDA SECCIONES A. Integrales inmediatas. B. Integración por sustitución. C. Integración por partes. D. Integración por fracciones simples. E. Aplicaciones de la integral
CAPÍTULO VII. INTEGRACIÓN INDEFINIDA SECCIONES A. Integrales inmediatas. B. Integración por sustitución. C. Integración por partes. D. Integración por fracciones simples. E. Aplicaciones de la integral
Curso 0: Matemáticas Año académico
 Curso 0: Matemáticas Año académico 2014-2015 Ana García González Miguel Martínez Panero Luis Carlos Meneses Poncio Teresa Peña García UniversidaddeValladolid Departamento de Economía Aplicada 1. Aritmética
Curso 0: Matemáticas Año académico 2014-2015 Ana García González Miguel Martínez Panero Luis Carlos Meneses Poncio Teresa Peña García UniversidaddeValladolid Departamento de Economía Aplicada 1. Aritmética
Cálculo de Primitivas
 Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición de primitiva Primitivas Integral
Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición de primitiva Primitivas Integral
du = ln u + NOTA: En las integrales 11, 12, 17 y 18 α significa la raíz cuadrada positiva de α 2. Escribimos
 CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Unidad 1 Integrales Indefinidas 1.1 Diferenciales Aproximaciones Anti derivada
 Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Métodos de Integración
 CAPÍTULO Métodos de Integración.6 Integración de funciones racionales. Fracciones parciales.6. Introcción En la sección anterior vimos que aplicando el cambio de variable x a sen se obtiene: a x a ln a
CAPÍTULO Métodos de Integración.6 Integración de funciones racionales. Fracciones parciales.6. Introcción En la sección anterior vimos que aplicando el cambio de variable x a sen se obtiene: a x a ln a
Soluciones de los ejercicios del examen de Cálculo del 29 de junio de 2007 Primero de Ingeniería de Telecomunicación
 Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
UNIVERSIDAD SIMON BOLIVAR MA1112 enero-marzo de 2004 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 IV / UNIVERSIDAD SIMON BOLIVAR MA enero-marzo de Ejercicios sugeridos para : los temas de la clase del 7 de enero de. Temas : Algunas integrales trigonomètricas; integraciòn por sustituciòn. Algunos ejercicios
IV / UNIVERSIDAD SIMON BOLIVAR MA enero-marzo de Ejercicios sugeridos para : los temas de la clase del 7 de enero de. Temas : Algunas integrales trigonomètricas; integraciòn por sustituciòn. Algunos ejercicios
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M.
 INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción En este capítulo vamos a abordar y estudiar el concepto de integral definida. Empezaremos planteando algunos ejemplos sencillos
INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción En este capítulo vamos a abordar y estudiar el concepto de integral definida. Empezaremos planteando algunos ejemplos sencillos
INTEGRACIÓN DE RACIONALES. Siendo p(x) y q(x) dos polinomios. Nos podemos encontrar dos casos:
 INTEGRACIÓN DE RACIONALES Nos hallamos ante una racional cuando estamos atacando un problema y nos encontramos con un cociente de polinomios que tenemos que integrar. Hemos de resolver: f(x) = p(x) q(x)
INTEGRACIÓN DE RACIONALES Nos hallamos ante una racional cuando estamos atacando un problema y nos encontramos con un cociente de polinomios que tenemos que integrar. Hemos de resolver: f(x) = p(x) q(x)
Integración de funciones de una variable
 Capítulo 3 Integración de funciones de una variable LA INTEGRAL INDEFINIDA. CÁLCULO DE PRIMITIVAS El cálculo de primitivas se puede pensar como la operación inversa de la derivación. El objetivo es que
Capítulo 3 Integración de funciones de una variable LA INTEGRAL INDEFINIDA. CÁLCULO DE PRIMITIVAS El cálculo de primitivas se puede pensar como la operación inversa de la derivación. El objetivo es que
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 17/01/2013
 MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
Cálculo de primitivas
 73 Fundamentos de Matemáticas : Cálculo integral en R 4. Primitiva de una función Capítulo 4 Cálculo de primitivas Definición 6.- Diremos ue la función F continua en [a, b], es una primitiva de la función
73 Fundamentos de Matemáticas : Cálculo integral en R 4. Primitiva de una función Capítulo 4 Cálculo de primitivas Definición 6.- Diremos ue la función F continua en [a, b], es una primitiva de la función
Tema 6: Ecuaciones diferenciales lineales.
 Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Capítulo 5: Cálculo integral
 Capítulo 5: Cálculo integral 1. Lección 18. La integral indefinida 1.1. Concepto de integral indefinida En el capítulo 3 hemos visto la diferencial de una función: dada y = f(x), su diferencial es una
Capítulo 5: Cálculo integral 1. Lección 18. La integral indefinida 1.1. Concepto de integral indefinida En el capítulo 3 hemos visto la diferencial de una función: dada y = f(x), su diferencial es una
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x):
 1 FUNCIONES ELEMENTALES CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x): Lo denotamos por : f : Dom -----> R x
1 FUNCIONES ELEMENTALES CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x): Lo denotamos por : f : Dom -----> R x
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Contenidos de los preliminares
 Preliminares del tema 3 Contenidos de los preliminares Algunas primitivas Una primitiva por cambio de variable Igualdades notables Ecuaciones bicuadradas Construcción de un polinomio de segundo grado a
Preliminares del tema 3 Contenidos de los preliminares Algunas primitivas Una primitiva por cambio de variable Igualdades notables Ecuaciones bicuadradas Construcción de un polinomio de segundo grado a
Convocatoria de Septiembre 9 de Septiembre de Nombre y Apellidos: (6 p.) 1) Se considera la función f : R R definida por
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre 9 de Septiembre de 26 Nombre y Apellidos: DNI: (6 p. Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre 9 de Septiembre de 26 Nombre y Apellidos: DNI: (6 p. Se considera la función f : R R definida
METODO DE FRACCIONES PARCIALES
 METODO DE FRACCIONES PARCIALES Este método consiste en epresar una fracción propia como la suma de fracciones más simples que puedan integrarse en forma inmediata o casi inmediata. Para convertir una fracción
METODO DE FRACCIONES PARCIALES Este método consiste en epresar una fracción propia como la suma de fracciones más simples que puedan integrarse en forma inmediata o casi inmediata. Para convertir una fracción
Repaso de integración
 TABLA DE INTEGRALES INMEDIATAS Repaso de integración. Tabla de integrales inmediatas n d = n+ + C, si n n + f() n f () d = f()n+ n + + C, si n d = ln + C f() f () d = ln f() + C e d = e + C e f() f ()
TABLA DE INTEGRALES INMEDIATAS Repaso de integración. Tabla de integrales inmediatas n d = n+ + C, si n n + f() n f () d = f()n+ n + + C, si n d = ln + C f() f () d = ln f() + C e d = e + C e f() f ()
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
1. CÁLCULO DE PRIMITIVAS
 . CÁLCULO DE PRIMITIVAS. Calcular las siguientes integrales indefinidas:. ( + Es inmediata. ( = (ln ln + + C +. + + + Descomponemos el integrando en fracciones parciales y obtenemos. + + = + arc tg + =
. CÁLCULO DE PRIMITIVAS. Calcular las siguientes integrales indefinidas:. ( + Es inmediata. ( = (ln ln + + C +. + + + Descomponemos el integrando en fracciones parciales y obtenemos. + + = + arc tg + =
TEMA. 29 Cálculo de primitivas * ( ) = ( ) ( ) + ( ) ( ) Primitivas de las funciones racionales. P x Q x C x R x
 TEMA 9 álculo de primitivas * Primitivas de las funciones racionales. omo ya sabemos ver tema ) una función racional es una función de la forma P f =, Q 0 Q donde P y Qson funciones polinómicas. omo ya
TEMA 9 álculo de primitivas * Primitivas de las funciones racionales. omo ya sabemos ver tema ) una función racional es una función de la forma P f =, Q 0 Q donde P y Qson funciones polinómicas. omo ya
Tema 10: Cálculo integral
 Tema 10: Cálculo integral 1. Introducción El matemático inglés Isaac Barrow (1630-1677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 10: Cálculo integral 1. Introducción El matemático inglés Isaac Barrow (1630-1677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
LÍMITES. Ing. Ronny Altuve
 UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE CIENCIAS ADMINISTRATIVAS Unidad Curricular: Matemática II LÍMITES Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Enero de 2016 INDICADOR DE LOGRO Aplicar la definición
UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE CIENCIAS ADMINISTRATIVAS Unidad Curricular: Matemática II LÍMITES Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Enero de 2016 INDICADOR DE LOGRO Aplicar la definición
1.1. Primitivas inmediatas
 1.1. Primitivas inmediatas Sólo sabiendo derivar podemos conocer la primitiva de una amplia variedad de funciones, el conocimiento de dichas primitivas (elementales) junto con algunas técnicas serán suficientes
1.1. Primitivas inmediatas Sólo sabiendo derivar podemos conocer la primitiva de una amplia variedad de funciones, el conocimiento de dichas primitivas (elementales) junto con algunas técnicas serán suficientes
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
La integral indefinida
 Apuntes Matemáticas º de bachillerato Leibniz Tema 7 La integral indefinida Matemáticas º de bachillerato 7. Introducción Def.: Dadas dos funciones, F() y f(), si se verifica que: F () f(), para un cierto
Apuntes Matemáticas º de bachillerato Leibniz Tema 7 La integral indefinida Matemáticas º de bachillerato 7. Introducción Def.: Dadas dos funciones, F() y f(), si se verifica que: F () f(), para un cierto
DERIVACIÓN DE LAS FUNCIONES ELEMENTALES
 DERIVACIÓN DE LAS FUNCIONES ELEMENTALES 2 El procedimiento mediante el cuál se obtiene la derivada de una función se conoce como derivación. Llamaremos funciones elementales a las funciones polinómicas,
DERIVACIÓN DE LAS FUNCIONES ELEMENTALES 2 El procedimiento mediante el cuál se obtiene la derivada de una función se conoce como derivación. Llamaremos funciones elementales a las funciones polinómicas,
