NÚMEROS COMPLEJOS. Autor: Patrici Molinàs Mata José Francisco Martínez Boscá NÚMEROS COMPLEJOS

Transcripción

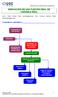
1 Númros complos NÚMEROS COMPLEJOS Autor: Patrici Molinàs Mata José Francisco Martín Boscá MAPA CONCEPTUAL Dfinición Fórmula d Cardano NÚMEROS COMPLEJOS Rsolución d cuacions d sgundo y trcr grado Opracions aritméticas n forma binómica: Propidads suma, rsta, producto y división Torma d D Moivr n forma polar: Fórmula d Eulr producto, división, potnciación y radicación Funcions hiprbólicas Proycto -Math

2 Númros complos INTRODUCCIÓN A mnudo los más pquños nos prguntan: Y cuánto val la raí d un númro ngativo? y dbmos rspondrls: No xist Est math-block prtnd dar rspusta a stas prguntas a partir d la rsolución d la cuacions introducindo lo qu llamamos los númros complos. Para llo partimos d la cuación sin solución ral más sncilla qu xist y qu no pos solución n los númros rals: 0. Sus solucions son la unidad imaginaria ( -) qu nos prmit rsolvr la raí cuadrada d cualquir númro ral ngativo, n particular dl. Sólo con sta información somos capacs d obtnr todas las solucions d cuacions d sgundo y trcr grado, utiliando la fórmula d sgundo grado y la fórmula d Cardano, rspctivamnt. A partir d aquí prsntarmos la aritmética n los complos qu incluyn a los númros rals así como algunas propidads d intrés. OBJETIVOS DOCENTES Proporcionar una primra introducción a los númros complos, como solucions d cuacions algbraicas. Dsarrollar cirta soltura para calcular con llos n los distintos formalismos. Ilustrar la rsolución d cuacions y l cálculo con númros complos, n gnral, con l programa Mathcad. CONOCIMIENTOS PREVIOS Es rcomndabl qu, prviamnt, s dominn los siguints apartados: Ecuación d sgundo grado. Su rsolución. Gráfica a la qu corrspond. Asimismo también s muy aconsabl qu s tnga un conociminto mínimo dl programa Mathcad. Por lo tanto s rcominda la lctura prvia d los Mathblocks: Uso básico dl Mathcad n Análisis (I): cálculo simbólico y analítico, Funcions d una variabl y Sris d potncias. CONCEPTOS FUNDAMENTALES Los númros rals El sistma numérico, como nosotros lo conocmos n la actualidad, s l rsultado d una volución gradual n la historia d las Matmáticas. Dscribimos brvmnt los tipos d númros qu la humanidad ha ido dscubrindo []. Los númros naturals:,,,..., o también llamados ntros positivos. Furon usados primro para contar. Los símbolos han cambiado con las épocas, pus los romanos, por mplo, utiliaban I, II, III, IV,.... La suma, a b, y l producto, a b, d dos númros naturals són también númros naturals, lo cual s pud xprsar dicindo qu l conunto d los númros naturals s crrado rspcto a las opracions d suma y producto o qu cumpl la propidad d clausura con rlación a stas opracions. Los ntros ngativos y l cro, dspués dnotados por, -, -,... y 0, rspctivamnt, qu prmitn rsolvr cuacions como x b a con a y b naturals, llvan a la Proycto -Math

3 Númros complos opración d rsta, qu s scrib x a b. El conunto d ntros positivos y ngativos con l cro s llama l conunto d los ntros y s crrado bao las opracions d suma, producto y rsta. Los númros racionals o fraccions, tals como /, -8/,... prmitn rsolvr cuacions d la forma bx a para ntros cualsquira a y b, con b 0, los cuals conducn a la opración d división o invrsa dl producto, qu s rprsnta como x a / b (llamado cocint d a y b ) dond a s l numrador y b l dnominador. El conunto d los ntros s un subconunto d los númros racionals, pusto qu los ntros corrspondn a los númros racionals conb. El conunto d númros racionals s crrado bao las opracions d suma, sustracción, multiplicación y división, xcluyndo la división por cro. Los númros irracionals, tals como,... y, son númros qu no son racionals, s dcir, no pudn sr xprsados como a / b dond a y b son ntros y b 0. El conunto d númros racionals irracionals s llamado l conunto d los númros rals. S supon qu l studiant stá ya familiariado con las divrsas opracions con númros rals. Es conocido qu los númros rals pudn rprsntars por puntos d una rcta infinita qu llamamos o rcta ral. El punto corrspondint al cro, s llama orign. Rcíprocamnt, para cada punto sobr la rcta hay uno y solamnt un númro ral. Si un punto A corrspondint a un númro ral a stá ubicado a la drcha d un punto B corrspondint a un númro ral b, dcimos qu a s mayor qu b o qu b s mnor qu a y scribimos rspctivamnt a > b o b < a y a 0 si a 0. Dcimos qu l conunto d los númros rals satisfacn una rlación d ordn. El conunto d todos los valors d x, tal qu a < x < b s llama un intrvalo abirto sobr l ral, mintras qu a x b, l cual incluy los xtrmos a y b, s llama un intrvalo crrado. El símbolo x, qu pud rprsntar a cualquir lmnto dl conunto d númros rals, s llamado una variabl ral. El valor absoluto d un númro ral a, dnotado por a s igual a a si a > 0, a a si a < 0 y a 0 si a 0. La distancia ntr dos puntos a y b sobr l ral s a b. Dfinición d un númro complo [] No xist un númro ral x qu satisfaga la cuación polinómica x 0. Para rsolvr st tipo d cuacions, s ncsario introducir los númros complos. S dfin un númro complo,, mdiant la siguint xprsión: x dond x y son una para cualquira d númros rals. Llamamos a la unidad imaginaria compla. Dfinimos d la siguint manra:. y Proycto -Math

4 Númros complos Si a b, a s llama la part ral d y b la part imaginaria d y s dnominan mdiant a R() y b I(), rspctivamnt. El símbolo, qu pud rprsntar cualquir lmnto dl conunto d númros complos, s llamado una variabl compla. Dos númros complos a b y c d son iguals si y solamnt si a c y b d. Podmos considrar los númros rals como l subconunto dl conunto d los númros complos con b 0. En st caso por mplo, los númros complos 0 0 y 0 rprsntan los númros rals 0 y, rspctivamnt. Si a 0, l númro complo 0 b o b s llama un númro imaginario puro. El conugado d un númro complo indica frcuntmnt por * o. a b s a b. El conugado d un númro complo s Opracions aritméticas con númros complos n forma binómica Suma ( a b) ( c d ) ( a c) ( b d ) Rsta ( a b) ( c d ) ( a c) ( b d ) Producto ( a b) ( c d ) ac ad bc bd ( ac bd ) ( ad bc) División ( a b) ( c d ) ( a b) ( c d ) ( c d )( c d ) ac ad bc c d bd ac bd c d ( bc ad ) ac bd c d bc ad c d El curpo d los númros complos S pud probar qu si, y prtncn al conunto d los númros complos, C,, ntoncs, satisfacn las siguints propidads:. y prtncn a C Ly d clausura. Ly conmutativa d la suma Proycto -Math

5 Númros complos Ly asociativa d la suma. ( ) ( ). Ly conmutativa dl producto Ly asociativa dl producto 5. ( ) ( ) Ly distributiva. ( ) , 0 s llamado l lmnto nutro d la suma y s l llamado lmnto nutro dl producto. 8. Para cualquir númro complo,, distinto d cro, xist un númro único n C tal qu 0 ; s llama l opusto d con rspcto a la suma y s dnota por. 9. Para cualquir 0, xist un númro único n C tal qu ; s llama l invrso d con rspcto al producto y s dnotado por o. En gnral, cualquir conunto, como C, cuyos lmntos satisfagan las propidads antriors, s dic qu s un curpo. Rprsntación gráfica d los númros complos Si s lign s rals sobr dos rctas prpndiculars (los s x y, rspctivamnt), podmos situar cualquir punto dl plano dtrminado por stas rctas mdiant la para ordnada d númros rals ( x, y) o coordnadas cartsianas dl punto. Como un númro complo x y s pud considrar como una para ordnada d númros rals, podmos rprsntar stos númros por puntos n l plano xy, llamado l plano complmntario o diagrama d Argand. Por mplo, l númro complo también s pud lr, ntoncs, como l par ordnado (,). Así, a cada númro complo corrspond uno y solamnt un punto n l plano y rcíprocamnt a cada punto n l plano l corrspond uno y solamnt un númro complo. A causa d sto, a mnudo mncionamos al númro complo como l punto. Nos rfrimos a los s x y y como los s ral imaginario, rspctivamnt y al plano complo como al plano. La distancia ntr dos puntos x y y x y n l plano complo vin dada por ( ) ( ) x x y y. Módulo y argumnto d un númro complo Si P s un punto n l plano complo corrspondint al númro complo ( x, y) o x y, ntoncs podmos dfinir l módulo, mod ( ) o, d dicho complo d la siguint forma: x y. También podmos dfinir l argumnto d st complo, arg ( ) o φ ( ), como l ángulo qu forma la rcta OP con l OX positivo. A partir d la trigonomtria s dduc qu: x y r cosφ sinφ ( ) Proycto -Math 5

6 Númros complos φ rcibn l nombr d coordnadas polars. Para cualquir númro complo 0 corrspond solamnt un valor d φ n 0 φ <. No obstant, cualquir otro intrvalo d longitud, por mplo, φ <, s pud mplar. Esta Esta última s la llamada forma polar o módulo-argumntal dl númro complo r y ( ) lcción particular rcib l nombr d la part principal y l valor d φ s llama valor principal. Producto, división y potnciación [] El módulo d un producto d númros complos x y r ( cosφ sinφ ) x y r ( cosφ φ ) y sin s igual al producto d los módulos d sos númros mintras qu l argumnto dl producto s igual a la suma d los argumntos d sos númros complos. Es dcir: arg( ) φ φ arg( ) arg( ) r r para comprobarlo basta con vr qu: [( cosφ cosφ sinφ sinφ ) ( sinφ cosφ cosφ φ )] r r sin [ cos( φ φ ) ( φ φ )] r r sin En l caso d la división d dos númros complos, l módulo s l cocint ntr los módulos d los dos númros, mintras qu l argumnto dl cocint s igual a la difrncia d los argumntos dl dividndo y dl divisor. El lctor pud comprobar l rsultado bin mdiant l uso d xprsions trigonométricas o rcordando qu dividir s multiplicar por l invrso. El invrso d un númro complo tin por módulo l invrso dl módulo y, por argumnto mnos l argumnto dl complo considrado. Así pus: r arg( ) φ φ arg( ) arg( ) r Torma d Moivr [] Si multiplicamos n númros complos, a partir d la xprsión dl producto d dos númros complos obtnmos qu l producto d n númros complos quival a un complo cuyo módulo s l producto d los n módulos y l argumnto, la suma d los n argumntos. D sta forma: { cos ( φ φ φ L φ ) ( φ φ φ φ )} Ln r r r Lrn n sin L Tomando todos los complos iguals como: n r n { cos ( nφ ) sin( nφ )} L n, la xprsión antrior quda Por otro lado, la n-ésima potncia dl númro complo también pud xprsars, lógicamnt como: n Proycto -Math

7 Númros complos n { r( cos ( φ ) sin( φ ))} n y igualando las dos últimas xprsions llgamos al Torma d Moivr: n n n { r( cos ( φ ) sin( φ ))} r ( cos( nφ ) sin( nφ )) Radicación [] El torma d Moivr nos prmit calcular fácilmnt la xprsión para las raícs d cualquir númro complo. Un númro w s una d las n raícs n-ésimas d un númro complo, si / n w. Dl Torma d Moivr, podmos dmostrar qu las n raícs d, w k son: w k n n { r( cos( φ ) sin( φ ))} r n φ k φ k cos sin n n con k 0,,, K, n Estos n valors distintos surgn dbido a la posibilidad d obtnr un mismo númro complo sumando vultas ntras (d ) al argumnto. Fórmula d Eulr [] La xtnsión compla d la función xponncial vin dfinida a partir d la sri d potncias x x x! x! K Substituyndo la variabl x por θ, llgamos al rsultado siguint: θ ( θ )! ( θ )! ( θ )! θ K ( θ! θ! K ) ( θ θ ) cosθ θ K sin dond,788k. Esta fórmula rcib l nombr d fórmula d Eulr. A partir d sta xprsión y dfinindo la xponncial d un númro complo como: x y x y y utiliando la fórmula d Eulr, obtnmos: x y x y x ( cosθ sinθ ) Un caso particular d la fórmula d Eulr s: 0 Proycto -Math 7

8 Númros complos qu rlaciona lmntos matmáticos tan difrnts como l 0 y l natural, los irracionals y, y l imaginario puro. Funcions trigonométricas complas y funcions hiprbólicas [] Las funcions hiprbólicas introducidas n l Mathblock Funcions d una variabl s pudn xprsar a partir d funcions trigonométricas n l plano complo. Amplimos las dfinicions d las funcions sno y cosno n l plano complo: cos sin Cuando s ral, stas fórmulas coincidn con las funcions sno y cosno ordinarias. Cuando s imaginario puro, sto s y, obtnmos: cos y sin y y y y y y y y y y y y y y y con lo cual podmos stablcr la rlación xistnt ntr las funcions trigonométricas d argumnto complo y las funcions hiprbólicas: cos y cosh y sin y sinh y CASOS PRÁCTICOS CON SOFTWARE Rsolución d cuacions d trcr grado. Solucions rals y complas La busquda d todas las raícs o solucions d un polinomio cualquira d grado mayor o igual qu dos s n gnral un problma sin solución n los númros rals. En particular, la cuación x 0 no prsntan ninguna solución n R. Sabmos por l Mathblock Funcions d una variabl dond tratamos la intrscción d las parábolas con l d las x, qu sta cuación corrspond a buscar la intrscción ntr una parábola qu pasa por ncima dl d las x y st. Como la intrscción no xist, la cuación no tin ninguna solución n R. Vamos a continuación un mplo d rsolución d cuacions d trcr grado y su intrprtación gráfica. Vamos a ncontrar las solucions d la siguint cuación d trcr grado: 0. Aplicarmos la fórmula d Cardano [] qu proporciona las solucions d cualquir cuación d trcr grado con coficints rals: a a a a0 0, substituyndo a -, a y a 0 -., En primr lugar, calculmos los parámtros q, r, s y s : Proycto -Math 8

9 Númros complos a a q 9 9 a a a0 a r s r q r s r q r Entoncs tnmos: a s s s s a s s ( ) s s a 0 08 ( s s ) Las trs solucions d la cuación son:, y. Y por lo tanto, tnmos qu l polinomio - - también pud xprsars como (-)(-)(). Utilicmos Mathcad para ncontrar las solucions d la cuación - -. La instrucción polyroots prmit a partir dl conociminto d los coficints d un polinomio, obtnr todas sus raícs, ya san rals o complas. Para llo, basta con habr construido l vctor d coficints y aplicarl la instrucción mncionada. v : polyroots ( v) Proycto -Math 9

10 Númros complos Rprsntmos la función ral yx -x x- asociada a la cuación compla S obsrva qu la función tind a mnos infinito cuando la variabl tind a mnos infinito, y, a más infinito, cuando la variabl tind a más infinito. x x x x En particular, una ampliación crca dl orign d coordnadas nos prmit comprobar qu l único cruc con l x s produc n x y0. x x x 0 0 Suma, rsta, producto y división d númros complos n forma binómica Con l propósito d ilustrar las opracions aritméticas con complos n forma binómica, vamos a fctuar las siguints opracions a) b) c) R( ) d) Im( ) con los complos -,. a) En primr lugar fctumos las sumas n l numrador y l dnominador: Como l módulo d un cocint d complos corrspond al cocint d los rspctivos módulos, no s ncsario multiplicar numrador y dnominador por l conugado dl dnominador. Basta con buscar l módulo d cada part d la fracción: ( ) Proycto -Math 0

11 Númros complos Utilicmos Mathcad para vrificar sta opración. En primr lugar dfinamos los complos - y. Lugo calculmos l complo dl cual dsamos obtnr l módulo mdiant l Evaluat Symbolically. Dspués d calcular l módulo, también con la instrucción Evaluat Symbolically, utiliamos l Evaluat Numrically para conocr l valor numérico d dicho módulo. : : ( ) ( ) ( ) ( ) i.8 b) Aplicando la dfinición d módulo d un númro complo, podmos scribir: ( ) ( ) ( ) ( ) ( ) ( ) ( ( ) ) dond hmos multiplicado numrador y dnominador por l conugado dl dnominador y obtnmos: ( ( ) ) Con Mathcad vrificamos sta opración. : Dspués d dfinir los complos y, introducimos la xprsión a valuar. : Utiliando la instrucción d simplificación Symbolic Complx Evaluation comprobamos l rsultado. complx i Proycto -Math

12 Númros complos c) Evalumos la xprsión dntro d la opración part ral (R()): ( ) ( ) ( ) cuya part ral s cro. Vrificamos st rsultado también con Mathcad. Dspués d dfinir los complos y, introducimos la xprsión a valuar. : Utiliando la instrucción d simplificación Symbolic Complx Evaluation comprobamos l valor dl complo, cuya part ral s nula como podmos vr utiliando la instrucción R, qu xtra la part ral d un complo. : ( ) complx i R( ) 0 d) La part imaginaria (Im()) d un númro complo s l coficint ral qu multiplica a la unidad imaginaria. Así pus: ( ) Im( ( ) Im( ) ) Im Vrifiqumos st último rsultado con Mathcad. : Dspués d dfinir los complos y, introducimos la xprsión a valuar. : Utiliando la instrucción d simplificación Symbolic Complx Evaluation comprobamos l valor dl complo, cuya part imaginaria s igual a como podmos vr utiliando la instrucción Im, qu xtra la part imaginaria d un complo. complx i Im( ) Proycto -Math

13 Númros complos Producto, división y potnciación d númros complos n forma polar Como ilustración dl cálculo con númros complos n forma polar, vamos primro a convrtir complos n forma binómica a polar para lugo fctuar opracions con llos. En primr lugar, convrtirmos los siguints complos xprsados n forma binómica: -, ( )/ a su forma polar y lugo buscarmos l rsultado d las siguints xprsions: a ) a ) 5 0 Para convrtir a forma polar los complos y dbmos calcular sus módulos: ( ) y sus argumntos: φ φ arctan 0º arctan 0º 00º dond hmos utiliado, n la dtrminación unívoca dl argumnto, l hcho d qu stá n l cuarto cuadrant y, n l primro. En forma polar, stos complos corrspondn a: 0º ( cos( 0º ) sin( 0º )) 0º ( cos( 0º ) sin( 0º )) Proycto -Math

14 Númros complos a) Efctumos la división ntr y n forma polar. El módulo d sta división srá l cocint d módulos, s dcir, ntr /,. El argumnto corrspondrá a la rsta d los argumntos d y, s dcir, d 0º y 0º, pus tnmos qu tomar l signo opusto al d al star conugado. Por lo tanto, l argumnto dl cocint srá 0º. El complo qu stamos buscando s, pus: 0º ( cos( 0º ) sin( 0º )) a Vrifiqumos los cálculos n forma polar con Mathcad. Dspués d dfinir los complos y, introducimos la xprsión a valuar. : : Utiliando la instrucción d simplificación Symbolic Complx Evaluation obtnmos l rsultado n forma binómica. Para obtnr la forma polar y xponncial d st complo, basta con buscar l módulo y l argumnto ayudándonos d la instrucción Simplify. complx i i simplify ( ) simplify arg i Fiaos qu l argumnto / n radians quival a 0º pusto qu radians quivaln a 80º. a) Calculmos la xprsión n forma xponncial. Como 5 0 0º y 0º, tnmos: º 5 0º 5 00º 00º 0 ( ) 0 5 Proycto -Math

15 Númros complos a Vrifiqumos los cálculos n forma polar con Mathcad. Dspués d dfinir los complos y, introducimos la xprsión a valuar. Utiliando la instrucción d simplificación Symbolic Complx Evaluation obtnmos l rsultado n forma binómica. Al sr ral y positivo, l módulo coincid con l complo y l argumnto s cro como vmos ayudándonos d la instrucción Simplify. : : 5 0 complx simplify Radicación d un númro complo n forma polar [5] Como ilustración d la radicación d númros complos, vamos a calcular la raícs qu aparcn al rsolvr la cuación: 0 Dspando obtnmos la siguint cuación: cuyas solucions vinn dadas por las raícs cúbicas d qu n forma polar quival a: cos sin. Efctumos sta opración d radicación mdiant la fórmula qu hmos drivado dl Torma d Moivr: w,, k cos sin k Proycto -Math 5

16 Númros complos Proycto -Math k k sin cos 0,, k Así pus las raícs son: sin cos w 5 5 sin cos w sin 9 cos w Si dibuamos los puntos w, w y w, vmos qu rprsntan trs puntos quidistants situados ncima d una circumfrncia d radio. Vrifiqumos los cálculos n forma polar con Mathcad. Dspués d intoducir las trs raícs w, w y w, calculamos sus cubos. w : w 5 5 : w 5 5 : w ( ) w ( ) w ( )

17 Númros complos Podmos rprsntar los puntos n l plano complo qu rprsntan las trs raícs (puntos roos). w : 5 5 Coordnadas_x : w r : t : 0, 0... xt ( ) : r cos () t Coordnadas_y : w y( t) : r sin () t Estan situados ncima d una circumfrncia d radio (n trao continuo aul) y sparados 0º ntr si. Coordnadas_y y( t) 0 0 Coordnadas_x, x( t) CONCLUSIONES Dntro dl curpo d los númros complos, toda cuación polinómica tin solución. Hmos mostrado qu mdiant la fórmula d Cardano y la unidad imaginaria, podmos obtnr la solución d cualquir cuación d trcr grado. Una v introducidos los númros complos n sus formas binómica y polar, hmos visto qu tanto la suma como la rsta s fctuan con xtraordinaria facilidad n forma binómica, mintras qu l producto y la división s ralian más facilmnt n forma polar. Una v hmos dducido la Torma d Eulr, hmos podido construir la rgla para la radicación d un númro complo cualquir. Todas stas opracions s han ido acompañando d mplos con l programa Mathcad, qu constituy una hrraminta útilisima para l cálculo con númros complos. Proycto -Math 7

18 Númros complos BIBLIOGRAFÍA [] M. R. Spigl (970): Toría y problmas d Variabl Compla, Sri d Compndios Schaum, McGraw-Hill, Mxico. [] V.A. Kudryasvtsv and B.P. Dmidovich (98): A brif cours of Highr Mathmatics, Mir Publishrs, Moscú, p. 5-. [] T.A. Apostol (98): Calculus: Cálculuo con funcions d una variabl, con una introducción al álgbra linal, Rvrté, Barclona, p. 5. [] M. R. Spigl (970): Manual d Fórmulas y Tablas Matmáticas, Sri d Compndios Schaum, McGraw-Hill, Mxico, p.. [5] R. Calm, N. Coll, y M.R. Estla (99): Problmas d cálculo, Micromar, Barclona, p.. [] R. Courant and F. John (97): Introducción al Cálculo y al Análisis Matmático, Limusa, México, p.. [7] T.M. Apostol, (979): Análisis Matmático, Rvrté, Barclona, p. 9-. ENLACES [W] [W] [W] [W] [W5] [W] [W7] Introducción amna intrsant a los númros complos. Incluy una animación a propósito d las raícs d un complo. Rsumn conciso y muy manabl sobr las opracions y propidads d los númros complos. Opracions con númros complos. Incluy l cálculo dl logaritmo d un númro complo qu no hmos prsntado aquí. Los númros complos n la historia d las matmáticas. Artículo d divulgación sobr la historia d las matmáticas a caballo d los grands movimintos culturals. Los comntarios sobr los númros complos mpian con la solución d la cuación d sgundo grado por Cardano, n plno Rnaciminto. Extnso compndio d rcicios con númros complos. Proycto -Math 8

19 Númros complos Prsntación n Powr Point sobr los númros complos. Ilustra las propidads d stos i númros con mplos intrsants como i. [W8] [W9] Monografía sobr los númros complos, sus opracions y sus aplicacions. Introducción a los númros complos. Axiomática y propidads (n inglés). [W0] Aproximación práctica a los númros complos (n inglés). Proycto -Math 9