UNIDAD 14 LA ELIPSE Y LA HIPÉRBOLA
|
|
|
- Juana Lucero Barbero
- hace 6 años
- Vistas:
Transcripción
1 UNIDAD 1 LA ELIPSE Y LA HIPÉRBOLA Ojetivo generl. Al terminr est Unidd plirás ls definiiones los elementos que rterizn l elipse l hipérol en ls soluiones de ejeriios prolems. Ojetivos espeífios: 1. Reordrás plirás l definiión de l elipse omo un lugr geométrio su euión en l form nóni.. Reordrás plirás l definiión de l hipérol omo un lugr geométrio, su euión en l form nóni.. Reordrás plirás l form generl de l euión de un elipse de un hipérol ls rterístis de los oefiientes de un euión de segundo grdo que represent un elipse o un hipérol.
2 Ojetivo 1. Reordrás plirás l definiión de l elipse omo un lugr geométrio su euión en l form nóni en l form generl. Definiión. L elipse es el lugr geométrio de un punto que se mueve en un plno de tl mner que l sum de sus distnis dos puntos fijos, situdos en el mismo plno, llmdos foos, es un ntidd onstnte mor que l distni entre los foos. Se llm eje fol l ret que ps por los foos (F F ) que ort l elipse en dos puntos llmdos vérties (V V ). L porión del eje fol omprendid entre los vérties: se llm eje mor su longitud VV ' se design omo. L longitud del eje fol es FF '. L ret perpendiulr l eje fol en el entro de l elipse se llm eje norml, ort l urv en dos puntos, A A. El segmento longitud es. AA ' es el eje menor de l elipse su L posiión del eje fol define l posiión de l elipse: horizontl, si su eje fol es prlelo o oinide on el eje (Figur 6.1); vertil, si su eje fol es prlelo o oinide on el eje (Figur 6.1); o inlind. Si l posiión de l elipse es inlind, se reurre l rotión de ejes pr nlizrl. Figur 1.1.
3 Figur 1.1. L elipse es un urv simétri on respeto sus dos ejes, que tiene dos ldos retos: ls dos rets perpendiulres l eje mor que psn por los foos unen dos puntos de l urv. L elipse tiene dos diretries: ls rets perpendiulres l eje fol que se enuentrn l mism distni de los vérties que los foos, pero en el ldo opuesto, es deir fuer de l elipse. Pr determinr l euión del lugr geométrio que define l elipse, en el so en que l urv tiene su entro en el origen su eje fol oinide on el eje, omo los foos se enuentrn sore el eje de ls siss, sus oordends son F(, 0), F (, 0), siendo un onstnte positiv. Si P(, ) es un punto ulquier de l elipse, de uerdo on l definiión de est urv P dee stisfer l ondiión: FP F' P ; donde > Al sustituir en l fórmul pr lulr l distni de d segmento se tiene: 0 0
4 Desrrollndo: Como, l epresión 0 puede ser reemplzd por un número positivo : Sustituendo: Y dividiendo por : 1 Ést es l euión de un elipse on ls siguientes rterístis: Centro: C(0, 0) Eje fol: eje
5 Vérties: V(, 0) V (, 0) Foos: F(, 0), F (, 0) Distni fol: Longitud del eje mor: Longitud del eje menor: Longitud de d ldo reto: Eentriidd: e < 1 En el so de l elipse l eentriidd siempre será menor 1 que >. Cundo el eje fol de l elipse oinide on el eje, l urv es vertil, ls oordends de los foos serán F(0, ), F (0, ) ls de los vérties V(0, ) V (0, ). En este so su euión es: Y sus elementos son: 1 Centro: C(0, 0) Eje fol: eje Vérties: V(0, ) V (0, ) Foos: F(0, ), F (0, ) Distni fol: Longitud del eje mor: Longitud del eje menor: Longitud de d ldo reto: Eentriidd: e < 1
6 Ejemplos: 1.) Pr enontrr l euión de l elipse on entro en el origen, un foo en el punto (0, ) semieje mor igul 5, por ls oordends del foo se se que el eje fol es el eje, que l distni del entro l foo es =. Además, = 5. L euión de l urv es del tipo 1, pr l ul se neesit tener el vlor de, el semieje menor. Puesto que se onoen, se determin de l epresión que ls relion: 5 16 Al sustituir estos vlores, l euión de l elipse es ) Se pueden determinr todos los elementos que rterizn l elipse del ejemplo nterior representrl en el plno oordendo: Centro: C(0, 0) Eje fol: eje Vérties: V(0, 5) V (0, 5) Foos: F(0, ), F (0, ) Distni fol: = 6 Longitud del eje mor: = 10 Longitud del eje menor: = 8 Longitud de d ldo reto: Eentriidd: = e = < 1 5
7 Figur E 1. 1.) L euión de l elipse on vérties V(, 0) V (, 0) eentriidd se puede otener de l siguiente mner: Por los vérties se se que es un elipse on entro en el origen, que su eje fol es el eje, que =. Por l definiión de l eentriidd: Entones e, por lo tnto,, =. 7 L euión es
8 .) Pr l elipse uo eje mor oinide on el eje ps por los puntos (, ) (6, ), l onsiderr l fórmul 1 omo los puntos deen stisfer l euión, se tiene: Pr (, ): ; 1... (1) Pr (6, ): ; 1... () Éste es un sistem de euiones on dos inógnits:. Pr resolverlo se puede despejr de ls dos euiones e igulr los vlores pr determinr el vlor de : 16 9 De (1): () De (): () 6 6 Igulndo () ():
9 Este vlor se sustitue, por ejemplo, en (): L euión de l elipse es: Pr definir sus elementos se requiere onoer el vlor de. Utilizndo l epresión: Los elementos de l elipse son: Centro: C(0, 0) Eje fol: Eje Vérties: V( 5, 0) V ( 5, 0) Foos: F( 9, 0), F ( 9, 0) Distni fol: = 9 Longitud del eje mor: = 5 Longitud del eje menor: = 1 Longitud de d ldo reto: = 6 1 5
10 Eentriidd: e = 9 5 su gráfi es: F'( 9,0) F( 9,0) V' (- 5,0) V( 5, 0) Figur E 1. Cundo un elipse tiene su entro en otro punto ulquier (h, k) del plno su eje fol es prlelo l eje, l euión que l define se enuentr suponiendo que los ejes se trsldn de mner que el nuevo origen O oinid on el entro (h, k) de l urv. Figur 1.
11 Entones l euión de l elipse referid los nuevos ejes es ' ' Est euión puede referirse los ejes originles usndo ls euiones de trnsformión h, ' k de donde ' h, k Al sustituir estos vlores en l epresión de l elipse se otiene l euión referid los ejes originles: 1 h k 1 En este so, lo únio que se modifi son ls oordends de los foos de los vérties, Centro: C(h, k) Eje fol: prlelo l eje Vérties: V(h +, k), V (h, k) Foos: F(h +, k), F (h, k) Cundo el eje fol es prlelo l eje, l elipse es vertil su euión, referid los ejes, es: ' ' 1 Aplindo ls euiones de trnsformión se otiene h k 1 Sus elementos son: Centro: C(h, k) Eje fol: prlelo l eje Vérties: V(h, k + ), V (h, k ) Foos: F(h, k + ), F (h, k )
12 En mos sos los demás elementos de l urv permneen igul: Distni fol: Longitud del eje mor: Longitud del eje menor: Longitud de d ldo reto: Eentriidd: e < 1 Ejemplos: 5.) Pr l elipse uos vérties son V(6, ) V (, ) sus foos los puntos F(5, ) F ( 1, ), omo los vérties los foos tienen l mism ordend, l elipse tiene su eje mor prlelo l eje, de mner que l fórmul utilizr es h k 1 El entro de l elipse está en el punto medio de los vérties ( de los foos) por lo tnto sus oordends son 1 = 6 1 = C(, ) L distni del entro ulquier de los vérties es el vlor de, de modo que: 6 Y es l distni del entro ulquier de los foos: 5 Pr determinr l euión es neesrio onoer el vlor de :
13 Y se tom > 0 puesto que es un distni. Se sustituen estos vlores en l euión orrespondiente qued: Pr determinr su gráfi se lolizn los vérties, los foos el entro, se se que su eje mor mide = () = 8 su eje menor, = 7, de mner que los puntos de interseión de l elipse on su eje menor son B, 7 B ', 7. Cd uno de sus ldos retos mide 1 =. 5 Pr = 0 Pr = Otros puntos de l elipse, on vlores proimdos de l ordend, son: ; ; ; 0 ; 1 = 6. ; = ; 1 = (0, 6.) (0, 1.7) (, 6.) (, 1.7)
14 Pr = 1 = 6. ; = 1.7 1; ; ; (, 6.65) (, 1.5) ; 1 = 6.65 ; = 1.5 Con estos puntos los demás elementos luldos, se puede grfir de mner proimd l elipse. Figur E 1. 6.) Si los vérties de un elipse son los puntos (, 7) (, 1) l longitud de d ldo reto es, omo los vérties tienen l mism sis l elipse es vertil que el eje mor, el fol, son prlelos l eje. L euión que le orresponde es: h k 1
15 El entro es el punto medio del eje mor vérties su ordend es 1 = 7 1 VV ': su sis es l mism de los C(, ) L longitud de su eje mor es l distni entre sus vérties: = Como l longitud de d uno de sus ldos retos es, se tiene: l longitud de su eje menor es = = 8 L euión de est elipse es: 16 1 Pr determinr ls oordends de los foos se lul el vlor de prtir de l epresión: Por lo tnto, los foos son los puntos: F,, ', F su eentriidd es e
16 Figur E 1. 7.) Pr enontrr l euión de l elipse que tiene entro en (1, ), uno de los foos es (6, ) ps por el punto (, 6), se puede proeder de l siguiente mner: Como el entro el foo tienen l mism ordend, el eje fol el eje mor son prlelos l eje. Por tnto, l euión que orresponde est urv es: h k 1 Al sustituir ls oordends del entro (h, k) = (1, ): H que determinr. 1 1 Como el punto (, 6) pertenee l elipse, stisfe su euión:
17 Pr otener un euión on un sol inógnit, se he l sustituión, puesto que es l distni del entro l foo: de modo que: Ést es un euión en, que se puede resolver omo sigue: Al sustituir ls dos ríes en l epresión pr : Sólo l primer ríz es válid que no puede ser negtiv, por lo tnto = 5, = 0 l euión de l elipse es: ) L Tierr desrie un tretori elípti lrededor del Sol que se enuentr en uno de los foos. Si se se que el semieje mor de l elipse es de kilómetros que l eentriidd es proimdmente 1 6, se pueden enontrr
18 ls distnis máim mínim de l Tierr l Sol l onsiderr que, omo entones: ,500,000 e 18,500,000 6 =,00,000 (proimdo) Por tno, l distni máim es + = 18,500,000 +,00,000 = 150,900,000 = kilómetros. l distni mínim es = 18,500,000,00,000 = 16,100,000 = kilómetros. Ojetivo. Reordrás plirás l definiión de l hipérol omo un lugr geométrio su euión en l form nóni. Definiión. L hipérol es el lugr geométrio de un punto que se mueve en un plno de tl mner que el vlor soluto de l difereni de sus distnis dos puntos fijos del plno llmdos foos, es siempre igul un ntidd onstnte menor que l distni entre los foos. Se llm eje fol de l hipérol l ret de longitud que ps por los foos F F que ort l urv en dos puntos V V llmdos vérties. L porión VV ' del eje fol omprendid entre los vérties se llm eje trnsverso. El punto medio del eje trnsverso es el entro de l hipérol se denot omo C (Fig..1). Tmién se definen el eje norml, que es l ret perpendiulr l eje trnsverso en C el eje onjugdo, que es un segmento AA ' del eje norml que tiene C omo punto medio (más delnte se preis l lolizión de los puntos A A'). L hipérol tiene dos ldos retos que son ls rets perpendiulres l eje fol que psn por los foos unen dos
19 puntos de l urv. L hipérol es un urv simétri on respeto sus ejes tiene dos síntots que se ortn en el entro de l hipérol. (Fig..). Figur.1 Figur. L posiión del eje fol define l posiión de l hipérol: es horizontl, si su eje fol es prlelo o oinide on el eje ; es vertil, si su eje fol es prlelo o oinide on el eje. Tmién puede estr inlind en el plno, en uo so se reurre l rotión de ejes pr onvertirl uno de los dos sos nteriores.
20 Pr determinr l euión del lugr geométrio que define l hipérol, en el so en que l urv tiene su entro en el origen su eje fol oinide on el eje, omo los foos se enuentrn sore el eje de ls siss uniddes l dereh l izquierd del entro, sus oordends son F,0, F ',0, donde es un onstnte positiv. Si P, es un punto ulquier de l hipérol, por l definiión se dee stisfer l ondiión: Est epresión es equivlente FP F ' P ; donde FP F' P FP F' P Al sustituir en l fórmul pr lulr l distni de d segmento, en ms epresiones, se tiene: (1) () Simplifindo l epresión (1):
21 Como, 0 puede reemplzrse por un número positivo,, que l sustituirse en l últim epresión dej: Y dividiendo por : 1 Se puede ompror que prtir de l epresión () siguiendo el proedimiento nterior l euión que se otiene es l mism: 1. En el so de l hipérol, ls onstntes, están ligds por l relión: = por lo que Del nálisis del lugr geométrio que define l euión 1, se otiene que: 1. Es un urv simétri on respeto los ejes oordendos l origen.. En el intervlo no eisten vlores reles pr.. L longitud de d ldo reto es. L eentriidd, e, es mor que l unidd que >
22 L hipérol tiene dos síntots. Pr el so que se está presentndo, si se despej de l euión 1 se otiene: 1 Si ument indefinidmente, l urv se prolong hi el infinito prtir del vértie el oiente d vez más ls rets tiende ero, por lo que el rdindo tiende l vlor de 1 l urv se er, que son ls euiones de ls dos síntots de l hipérol. En resumen, l hipérol u euión en l form nóni es 1 es horizontl, tiene ls siguientes rterístis elementos: Centro C(0, 0) Eje fol El eje Vérties V(, 0) V (, 0) Foos F(, 0), F (, 0) Distni fol Longitud del eje trnsverso Longitud del eje onjugdo*
23 Longitud de d ldo reto Eentriidd Asíntots e = > 1 ; *Aun undo l hipérol no interset l eje, los puntos A (0, ) A (0, ), se tomn omo etremos del eje onjugdo. Cundo el eje fol oinide on el eje l hipérol es vertil, ls oordends de los foos son F(0, ), F (0, ), ls de los vérties: V(0, ) V (0, ), su euión: 1 Sus rterístis elementos son: Centro C(0, 0) Eje fol Vérties Foos Distni fol Longitud del eje trnsverso el eje V(0, ) V (0, ) F(0, ), F (0, ) Longitud del eje onjugdo* Longitud de d ldo reto Eentriidd Asíntots e = > 1 ; *Ahor no h interseión on el eje, pero los puntos A (, 0) A (, 0), se onsidern los etremos del eje onjugdo.
24 Ejemplos: 1.) Pr enontrr l euión de l hipérol uos vérties son V(, 0) V (, 0) sus foos F(5, 0), F ( 5, 0) se puede proeder omo sigue. Por ls oordends de los vérties los foos se se que l hipérol tiene su entro en el origen su eje fol está sore el eje, por lo tnto, su euión es de l form 1. L distni de los vérties l entro es de uniddes, =, l distni de los foos l entro es de 5 uniddes, = 5, por lo que = = (5) () = 5 9 = 16 = L euión de l hipérol es: ) Los elementos que rterizn l hipérol del ejemplo nterior son: Distni fol = 10 Longitud del eje trnsverso = 6 Longitud del eje onjugdo = 8 Longitud de d ldo reto Eentriidd Asíntots = 16 5 e = = ; =
25 Figur E.1.) Si los etremos del eje onjugdo de un hipérol son los puntos (0, ) (0, ) l longitud de d ldo reto es 6, entones de ls oordends dds (que orresponden los puntos A A') se se que l hipérol tiene su entro en el origen, que su eje fol está sore el eje, que su semieje onjugdo,, es igul. Pr determinr l euión se dee onoer el vlor de, el semieje trnsverso, que puede enontrrse on el dto de l longitud del ldo reto que = LR LR = 6 = 18 6 Entones l euión de l hipérol es: 1 9 9
26 Su eentriidd es: e = = 9 9 = = Figur E..) Pr un hipérol on entro en el origen eje onjugdo sore el eje, su euión es del tipo 1. Si l longitud de d ldo reto es ps por el punto 1,, se puede enontrr su euión de l siguiente mner: El punto 1, pertenee l urv, por lo tnto stisfe su euión: Por otr prte, () ( 1) LR 6 Al sustituir l epresión pr en l euión de l hipérol:
27 resolviendo est euión se otiene: = El vlor negtivo de se desrt ddo que es un longitud. Entones = 1 : Con estos vlores l euión de l hipérol es: Figur E. Dependiendo de l relión entre los ejes trnsverso onjugdo, se definen dos tipos prtiulres de hipérols:
28 . Se llm hipérol equiláter l hipérol uos ejes trnsverso onjugdo tienen l mism longitud, es deir =, su euión se redue 1 1 Ls síntots de est urv:,, reduen su epresión :, Como ests rets son perpendiulres entre sí, l urv tmién reie el nomre de hipérol retngulr.. Se llmn hipérols onjugds dos hipérols en ls que el eje trnsverso de un es igul l eje onjugdo de l otr, por lo que tmién se die que d hipérol es onjugd de l otr. Si l euión de un hipérol es l euión de su hipérol onjugd es: on 1 1. Dos hipérols onjugds tienen un entro omún, dos síntots omunes todos sus foos equidistn del entro. Ejemplo: 5.) Pr l hipérol , su hipérol onjugd es Pr 1, que es horizontl, = 9, = 16, sus síntots son 9 16
29 Pr 1, que es vertil, , 1 que son ls misms síntots de l primer hipérol , sus síntots son El semieje fol tiene l mism longitud en ms hipérols: Por lo tnto, los foos de l hipérol son F(5, 0) F ( 5, 0) los de l hipérol onjugd son F(0, 5) F (0, 5) Figur E. L euión de un hipérol uo entro no está en el origen, pero sus ejes son prlelos los ejes oordendos, puede otenerse medinte trslión de los ejes rtesinos de mner que el origen del sistem oordendo oinid on el entro de l urv. Si ls oordends
30 del entro de l hipérol son (h, k) su eje trnsverso es prlelo l eje, l euión de l hipérol on respeto los nuevos ejes oordendos es ( ') ( ') 1, ddo que l trslión de ejes es tl que ' h ' k Al sustituir en l euión se otiene h k 1 Ést es l euión de un hipérol on Centro C(h, k) Eje fol prlelo l eje Vérties V(h +, k) V (h, k) Foos F(h +, k), F (h, k) Distni fol Longitud del eje trnsverso Longitud del eje onjugdo Longitud de d ldo reto Eentriidd e = Asíntots h k ; h k > 1 Si el entro de l hipérol está en (h, k) el eje fol es prlelo l eje, l euión es k h sus rterístis: Centro C(h, k) Eje fol ( eje trnsverso) prlelo l eje 1
31 Vérties V(h, k + ) V (h, k ) Foos F(h, k + ), F (h, k ) Distni fol Longitud del eje trnsverso Longitud del eje onjugdo Longitud de d ldo reto Eentriidd Asíntots e = > 1 h k ; h k Ejemplos: 6.) Pr otener l euión de l hipérol que tiene su entro en (, 1) un vértie en (, 1) su semieje onjugdo es igul, omo el entro el vértie tienen l mism ordend, l hipérol tiene su eje fol prlelo l eje, l euión será h k 1 Su semieje onjugdo es =, l distni del entro l vértie es 6 De modo que su euión es ) Los demás elementos de l hipérol del ejemplo nterior se pueden otener prtir de que h = ; k = 1; = 6, = ; = Vérties V(, 1), V ( 10, 1) Foos F( + 5, 1), F ( 5, 1) Distni fol 5 = 1 Longitud del eje trnsverso 1
32 Longitud del eje onjugdo 8 Longitud de d ldo reto Eentriidd Asíntots = e = = 6 8.) Si un hipérol tiene eentriidd de sus vérties son los puntos (, 1),, omo los vérties tienen l mism sis, l hipérol tiene su eje trnsverso prlelo l eje, su entro está en el punto medio de este segmento: C(, 1). L longitud del semieje trnsverso es: 1, omo e, entones =. Con estos vlores se puede lulr 9 5 L euión de l hipérol es ls oordends de los foos son F(, ) F (, ) l longitud del ldo reto LR 10 5
33 Ojetivo. Reordrás plirás l form generl de l euión de un elipse de un hipérol ls rterístis de los oefiientes de un euión de segundo grdo que represent un elipse o un hipérol. De l form nóni de l euión de un elipse o de un hipérol es posile otener l form generl desrrollndo ls operiones indids por los oientes los inomios l udrdo (si l urv tiene su entro fuer del origen), pr después reduir términos semejntes e igulr ero l euión. En el so de un elipse en l que el eje mor se horizontl: h k h h 1 k 1 h h k k h k h k 0 Comprndo est euión on l form generl de un euión de segundo grdo, en que no prez el término en : se otiene que: A C D E F 0 A ; C ; D h ; E k ; F h k Un desrrollo similr pr l elipse on eje mor vertil llev que: A ; C ; D h ; E k ; F h k Así, l euión udráti de l form A C D E F 0, on A C, pero on el mismo signo, orresponde un elipse. Si A C l elipse es horizontl si A C, es vertil. Ejemplos:
34 1.) Pr l elipse : A = 1; C = ; D = ; E = 1; F = 6 Como A C son diferentes pero del mismo signo A < C, l elipse es horizontl tiene, es deir, su eje mor prlelo l eje. Pr determinr sus elementos se puede otener l euión en l form nóni, pr lo ul se ompletn los trinomios se igul 1 l euión De quí se se que: ) Su entro está en C 1, ) Como =, =, los vérties son V 1, = 1, V ' 1, =, ) De,, los foos están en F 1, F ' 1, d) L longitud del eje mor es = ; l longitud del eje menor es = ; l longitud de d ldo reto es LR = 1 1
35 e) L eentriidd es e.) Dd l euión de l elipse 9 8 0, se pueden determinr todos sus elementos sin psr por l form nóni. Pr otener ls oordends del entro, los vérties, los foos, ls longitudes de sus ejes de sus ldos retos, l eentriidd, se deen onoer los vlores de h, k,,, prtir de los de A, C, D, E F. De l euión: A 9, C, D 0, E 8, F Como A > C, l elipse tiene su eje mor vertil por lo que: A = 9, = ; C =, = D 0 D h ; h = 0 18 E E k ; k = 8 = Con estos vlores se determinn: ) Centro: (h, k) = (0, 1) ) Vérties: (h, k ± ) V(0, 1 + ) = (0, ) V (0, 1 ) = (0, ) ) Foos: (h, k ± ) F 0,1 5 F ' 0,1 5 d) Eje mor: = 6 e) Eje menor: = f) Ldo reto (d uno): g) Eentriidd: e 5 8
36 Un euión de segundo grdo A C D E F 0 on A C pero del mismo signo represent, en generl, un elipse, pero tmién puede ourrir que se sólo un punto, o inluso que no represente un lugr geométrio rel. Esto dependerá del vlor de de l epresión CD AE ACF omo se indi: ) Si ( CD AE ACF ) > 0, l euión represent un elipse de ejes prlelos los oordendos. D E ) Si ( CD AE ACF ) = 0, represent un punto de oordends, A C ) Si ( CD AE ACF ) < 0, no represent ningún lugr geométrio rel. Ejemplos:.) L euión 6 0 no represent un elipse puesto que: Si ien A =, C = 1, 1 mos son positivos, omo D =, E =, F 6, entones = CD AE ACF = = 6 < 0 Este resultdo indi que l euión no represent un lugr geométrio rel. 5.) El lugr geométrio de los puntos P(, ) u sum de distnis los puntos fijos (, 1) (-5, 1) se igul 10 es un elipse, omo se muestr ontinuión: 1 Distni de P (, 1) = 1 5 Distni de P (-5, 1) = L sum de ls distnis es igul 10: = 10
37 Pr simplifir est euión, se puede psr un rdil l segundo miemro, elevr l udrdo tod l euión, desrrollr los inomios udrdos reduir términos semejntes: 1 = = Se puede dividir por utro tod l euión, elevr nuevmente l udrdo pr eliminr el rdil, volver desrrollr los inomios udrdos reduir términos semejntes: Ést es l euión del lugr geométrio. Por ls rterístis de A de C pree ser un elipse on eje mor prlelo l eje (horizontl). Pr omprorlo se evlú CD AE ACF omo A = 9, C = 5, D = 18, E = 50, F = 191: CD AE ACF = (5) (18) + (9) ( 50) (9) (5) ( 191) = = > 0 Por lo tnto el lugr geométrio es un elipse.
38 Siguiendo un proedimiento similr l que se siguió en el so de l elipse, pr l euión de un hipérol on entro en (h, k) eje fol prlelo l eje : h k l desrrollr udrdos, eliminr denomindores e igulr ero se otiene: h h 1 k 1 h h k k h k h k 0 Al omprr est euión on l form generl de un euión de segundo grdo, sin el término en : A C D E F 0 se otiene que: A ; C ; D h ; E k ; F h k Pr un hipérol vertil on entro en (h, k), se otiene que: A ; C ; D h ; E k ; F k h En generl, si los oefiientes de A C difieren en signo, un euión de segundo grdo, sin término en, representrá un hipérol uos ejes son prlelos los oordendos. Si A es positivo, se trtrá de un hipérol horizontl, si A es negtivo será un hipérol vertil. Ejemplos: 6.) En l hipérol , omo el término positivo es el de, l hipérol es horizontl (su eje fol es prlelo l eje ). Pr determinr sus elementos se pueden ompletr los trinomios udrdos e igulr 1 l euión: ( ( ) 5( ) 5( ) 9 1)
39 ( ) 5( 1) 0 Pr igulr 1 se divide entre 0 l euión: 5 De est euión se otiene que: 1 1 de modo que sus rterístis son: C(, 1); = 5; = ; 5 Centro C(, 1) Eje fol Prlelo l eje Vérties V( + 5, 1) V ( 5, 1) Foos F(5, 1) F ( 1, 1) Distni fol 6 Longitud del eje trnsverso 5 Longitud del eje onjugdo Longitud de d ldo reto Eentriidd = e = Asíntots ) En l hipérol 6 1 0, el oefiiente de es positivo, por lo tnto l hipérol es vertil l relión entre los oefiientes de l euión en l form nóni l form generl es: A ; C ; D h ; E k ; F k h Entones: A = = ; C = = Longitud del eje trnsverso: =, longitud del eje onjugdo: =, :
40 7 Pr ls oordends del entro: El entro es C 1, D = 6 = h; E = = k; D 6 E h 1; k 6 8 Los vérties son: V( 1, + ), V ( 1, ) Los foos son: F( 1, + 7 ), F ( 1, 7 ) Figur E.1 En osiones, l euión A C D E F 0 on A C de signos diferentes, no represent un hipérol sino un pr de rets que se ortn. Si en est euión, undo A > 0 C < 0, se he C C ', entones C ' será positivo. Al ompletr los udrdos perfetos en A C D E F ' 0
41 se otiene que es igul A D A D A C' E E C' C' D E F A C' D ' E A C D E F A C ' A C ' Si el segundo miemro de est euión es positivo o negtivo, l euión represent un hipérol on ejes prlelos los ejes oordendos; pero si el segundo miemro es igul ero, l epresión tiene l form D E A C ' 0 A C ', omo d uno de los dos términos del primer miemro es positivo, se tiene un difereni de udrdos que se puede ftorizr omo D E D E A C ' A C ' 0 A C ' A C ' Al igulr d uno de los ftores ero se otienen dos rets que se ortn. En osiones este pr de rets se les llm hipérol degenerd. Pr el so en que A < 0 C > 0, l euión A C D E F 0 represent un pr de rets que se ruzn undo E D F 0, en donde A A'. C A' Ejemplo: 8.) En l euión 6 9 0, se tiene que: A, C 1, D 0, E 6, F 9 entones, A' E D 6 0 F 9 C A' 1
42 por lo que l euión represent dos rets que se ruzn. Como se se, tnto pr l irunfereni omo pr l práol, se requieren tres ondiiones pr determinr su euión, porque d un tiene tres prámetros independientes que deen onoerse. En el so de l elipse, de ulquier de sus euiones: h k 1 ó h k se oserv que son utro los prámetros que l definen: h, k,. Por tnto, pr determinr l euión de un elipse se neesitn utro ondiiones, por ejemplo utro puntos de l urv. 1 De l mism mner, pr el so de l hipérol se neesitn tmién utro ondiiones pr determinr su euión puesto que, igulmente, en ulquier de sus euiones preen utro prámetros. Ejemplo: 9.) L euión de l elipse uos ejes son prlelos los ejes oordendos que ps por los puntos ( 6, ), ( 8, 1), (, ), (8, ), por l uiión de los puntos en el plno, orresponde un en l que el eje fol es prlelo l eje. Figur E.
43 Cd uno de los puntos por los que ps l urv stisfe su euión. Entones, en l euión 0 F E D C se sustituen los puntos: ( 6, 8): F E D C ( 8, 1): F E D C (, ): 0 F E D C (8, ): F E D C se otiene entones un sistem de utro euiones on utro inógnits que se puede resolver on lgún pquete de ómputo. L soluión es: C =, D =, E = 8, F = 9 por lo que l euión de l elipse es: en l form nóni:
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
B 1. d 1 d 2 B 2 XI.2 ECUACIÓN ORDINARIA DE LA HIPÉRBOLA HORIZONTAL CON CENTRO EN EL ORIGEN
 Págin del Colegio de Mtemátis de l ENP-UNAM Hipérol Autor: Dr. José Mnuel Beerr Espinos HIPÉRBOLA UNIDAD XI XI.1 DEFINICIÓN DE HIPÉRBOLA Un hipérol es el lugr geométrio de todos los puntos P del plno,
Págin del Colegio de Mtemátis de l ENP-UNAM Hipérol Autor: Dr. José Mnuel Beerr Espinos HIPÉRBOLA UNIDAD XI XI.1 DEFINICIÓN DE HIPÉRBOLA Un hipérol es el lugr geométrio de todos los puntos P del plno,
X. LA ELIPSE DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO. La recta que pasa por el punto medio del segmento el, se llama EJE MENOR de la elipse.
 X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
7.1 Ecuación en forma común o canónica de la hipérbola. En la gráfica dada a continuación (Fig. 1) es posible encontrar los elementos siguientes:
 UNIDAD VII. LA HIPÉRBOLA. DEFINICIÓN: L Hipérol es el onjunto de puntos en el plno u difereni de sus distnis dos puntos fijos en el mismo plno, llmdos foos, es onstnte e igul. 7.1 Euión en form omún o
UNIDAD VII. LA HIPÉRBOLA. DEFINICIÓN: L Hipérol es el onjunto de puntos en el plno u difereni de sus distnis dos puntos fijos en el mismo plno, llmdos foos, es onstnte e igul. 7.1 Euión en form omún o
Matemática Diseño Industrial Cónicas Ing. Avila Ing. Moll CÓNICAS. Directriz. Generatriz
 Mtemáti Diseño Industril Cónis Ing. Avil Ing. Moll CÓNICAS Diretriz Genertriz Un superfiie óni está generd por un ret (genertriz) que se mueve poyándose en un urv fij (diretriz) y que ps por un punto fijo
Mtemáti Diseño Industril Cónis Ing. Avil Ing. Moll CÓNICAS Diretriz Genertriz Un superfiie óni está generd por un ret (genertriz) que se mueve poyándose en un urv fij (diretriz) y que ps por un punto fijo
MATEMÁTICAS BÁSICAS ELIPSE. B 2B 1 del eje mayor es el eje menor. Cada extremo del eje mayor V 1 y V 2 se llama vértice. El punto DEFINICIÓN DE ELIPSE
 Fultd de ontdurí dministrión. UN lipse utor: r. José nuel Beerr spinos TÁTIS BÁSIS LIPS FINIIÓN LIPS Un elipse es el lugr geométrio de todos los puntos P del plno, tles que l sum de sus distnis dos puntos
Fultd de ontdurí dministrión. UN lipse utor: r. José nuel Beerr spinos TÁTIS BÁSIS LIPS FINIIÓN LIPS Un elipse es el lugr geométrio de todos los puntos P del plno, tles que l sum de sus distnis dos puntos
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
m 2 9 8 La fórmula cuadrática que se usó para construir el ejemplo anterior es un caso particular
 Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
8. La elipse. 9/ Las cónicas.
 9/ Ls ónis. 8. L elipse. Definiión: Ddos dos puntos un distni 2 mor que l distni, se llm elipse de foos prámetro 2, l lugr geométrio de los puntos del plno u sum de distnis es 2. Dee umplirse pues que,
9/ Ls ónis. 8. L elipse. Definiión: Ddos dos puntos un distni 2 mor que l distni, se llm elipse de foos prámetro 2, l lugr geométrio de los puntos del plno u sum de distnis es 2. Dee umplirse pues que,
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE
 DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
se llama ecuación polinómica de primer grado con una incógnita. Dos ecuaciones son equivalentes cuando admiten el mismo conjunto solución.
 Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Cuestionario Respuestas
 Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
LA ELIPSE EJERCICIOS RESUELTOS. Colegio Sor Juana Inés de la Cruz Sección Preparatoria Matemáticas III Bloque VII Ing. Jonathan Quiroga Tinoco
 LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
La hipérbola es el lugar geométrico de todos los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante e igual a 2a.
 INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
Los triángulos se clasifican según la magnitud de sus lados y de sus ángulos internos. SEGÚN SUS LADOS EQUILÁTERO ISÓSCELES ESCALENO
 Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
SenB. SenC. c SenC = 3.-
 TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
3.1 Circunferencia 3.2 Parábola 3.3 Elipse 3.4 Hiperbola
 Moisés Villen Muñoz Cónis. Cirunfereni. Prábol. Elipse. Hiperbol Objetivos. Se persigue que el estudinte: Identifique, grfique determine los elementos de un óni onoiendo su euión generl. Ddo elementos
Moisés Villen Muñoz Cónis. Cirunfereni. Prábol. Elipse. Hiperbol Objetivos. Se persigue que el estudinte: Identifique, grfique determine los elementos de un óni onoiendo su euión generl. Ddo elementos
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
SISTEMAS DE ECUACIONES LINEALES
 UNEFA C.I.N.U. Mtemátis Mteril dptdo on fines instruionles por Teres Gómez, de: Oho, A., González N., Lorenzo J. Gómez T. (008) Fundmentos de Mtemátis, Unidd 5: Euiones e Ineuiones, CIU 008, UNEFA, Crs.
UNEFA C.I.N.U. Mtemátis Mteril dptdo on fines instruionles por Teres Gómez, de: Oho, A., González N., Lorenzo J. Gómez T. (008) Fundmentos de Mtemátis, Unidd 5: Euiones e Ineuiones, CIU 008, UNEFA, Crs.
TRIGONOMETRÍA (4º OP. A)
 SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
Fracciones equivalentes
 6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
UNIVERSIDAD CRISTIANA AUTONOMA DE NICARAGUA UCAN FACULTAD DE INGENIERÍAS. Ingeniería en Sistemas de Computación. Ing. Enmanuel de Jesús Fonseca Alfaro
 CARRERA: Ingenierí en Sistems de Computión PLAN DE ESTUDIOS: 00 ASIGNATURA: AÑO ACADÉMICO: DOCENTE: MATEMATICA BASICA I Año Ing. Enmnuel de Jesús Fonse Alfro UNIDAD I: ALGEBRA Al finlir est unidd el estudinte
CARRERA: Ingenierí en Sistems de Computión PLAN DE ESTUDIOS: 00 ASIGNATURA: AÑO ACADÉMICO: DOCENTE: MATEMATICA BASICA I Año Ing. Enmnuel de Jesús Fonse Alfro UNIDAD I: ALGEBRA Al finlir est unidd el estudinte
XI. LA HIPÉRBOLA LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO
 XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE ZARAGOZA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
UNIDAD I. El Punto y la Recta
 SSTEMS E REPRESENTÓN 10 UN SESÓN 3 L Ret: efiniión, trzs y posiiones notles ORE L. LERÓN S. SSTEMS E REPRESENTÓN 10 1.5 L RET Es el eleento geoétrio unidiensionl y puede deterinrse trés de un segento de
SSTEMS E REPRESENTÓN 10 UN SESÓN 3 L Ret: efiniión, trzs y posiiones notles ORE L. LERÓN S. SSTEMS E REPRESENTÓN 10 1.5 L RET Es el eleento geoétrio unidiensionl y puede deterinrse trés de un segento de
1.6. BREVE REPASO DE LOGARITMOS.
 .. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
.. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
Triángulos y generalidades
 Geometrí Pln y Trigonometrí (ldor) Septiemre Diiemre 2008 INOE 5/1 pítulo 5. Ejeriios Resueltos (pp. 62 63) (1) Los ldos de un triángulo miden 6 m, 7 m y 9 m. onstruir el triángulo y lulr su perímetro
Geometrí Pln y Trigonometrí (ldor) Septiemre Diiemre 2008 INOE 5/1 pítulo 5. Ejeriios Resueltos (pp. 62 63) (1) Los ldos de un triángulo miden 6 m, 7 m y 9 m. onstruir el triángulo y lulr su perímetro
ECUACIONES DE PRIMER GRADO
 IES Jun Grí Vldemor Deprtmento de Mtemátis TEMA : ECUACIONES º ESO Mtemátis B ECUACIONES DE PRIMER GRADO PASOS PARA RESOLVER UNA ECUACIÓN DE PRIMER GRADO. Eliminr préntesis si los hy). Eliminr denomindores
IES Jun Grí Vldemor Deprtmento de Mtemátis TEMA : ECUACIONES º ESO Mtemátis B ECUACIONES DE PRIMER GRADO PASOS PARA RESOLVER UNA ECUACIÓN DE PRIMER GRADO. Eliminr préntesis si los hy). Eliminr denomindores
FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS Hemos visto el prolem de enontrr el produto, ddos los ftores. L ftorizión es enontrr los ftores, ddo el produto. Se llmn ftores de un epresión lgeri quellos que multiplidos
FACTORIZACIÓN DE POLINOMIOS Hemos visto el prolem de enontrr el produto, ddos los ftores. L ftorizión es enontrr los ftores, ddo el produto. Se llmn ftores de un epresión lgeri quellos que multiplidos
GEOMETRÍA ANALÍTICA LA HIPÉRBOLA. 1. Ecuación de la hipérbola horizontal con centro en el origen
 LA HIPÉRBOLA CONTENIDO. Ecución de l hipérol horizontl con centro en el origen. Análisis de l ecución. Asíntots de l hipérol Ejemplo 3. Ecución de l hipérol verticl con centro en el origen Ejemplo 4. Hipérols
LA HIPÉRBOLA CONTENIDO. Ecución de l hipérol horizontl con centro en el origen. Análisis de l ecución. Asíntots de l hipérol Ejemplo 3. Ecución de l hipérol verticl con centro en el origen Ejemplo 4. Hipérols
Taller de Matemáticas III
 Tller de Mtemátis III Semn 3 4 Tller de Mtemátis III Universidd CNCI de Méio Tller de Mtemátis III Semn 3 4 Temrio. L práol.. Crterizión geométri... L práol omo lugr geométrio... Elementos soidos on l
Tller de Mtemátis III Semn 3 4 Tller de Mtemátis III Universidd CNCI de Méio Tller de Mtemátis III Semn 3 4 Temrio. L práol.. Crterizión geométri... L práol omo lugr geométrio... Elementos soidos on l
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS
 TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
1. Conceptos previos. Traslación gráficas en los ejes de coordenadas
 Tem 8. Cónis. Coneptos previos. Trslión gráfis en los ejes de oordends.... L irunfereni... 3.. Definiión euión de l irunfereni... 3.. Euión de l rets tngentes normles l irunfereni.... 6.3 Posiiones reltivs
Tem 8. Cónis. Coneptos previos. Trslión gráfis en los ejes de oordends.... L irunfereni... 3.. Definiión euión de l irunfereni... 3.. Euión de l rets tngentes normles l irunfereni.... 6.3 Posiiones reltivs
Triángulos congruentes
 Leión#4 Triángulos ongruentes y triángulos similres Ojetivos Aplir ls propieddes de triángulos ongruentes Aplir ls propieddes de ongrueni Aplir ls propieddes de triángulos similres Aplir el teorem de Pitágors
Leión#4 Triángulos ongruentes y triángulos similres Ojetivos Aplir ls propieddes de triángulos ongruentes Aplir ls propieddes de ongrueni Aplir ls propieddes de triángulos similres Aplir el teorem de Pitágors
Sistemas de Ecuaciones lineales Discusión con parámetros. Discutir el siguiente sistema de ecuaciones lineales según el valor del parámetro a:
 ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
MATEMÁTICAS APLICADAS A CC.SS. I TEMA 1 Y 2: LOS NÚMEROS RADICALES. LOGARITMOS
 http://olmo.pnti.me.es/dms000 MATEMÁTICAS APLICADAS A CC.SS. I TEMA Y : LOS NÚMEROS RADICALES. LOGARITMOS HOJA Nº Feh de entreg: Viernes, de Oture de 00 Ejeriios. 7. Etre ftores y simplifi l máimo l epresión
http://olmo.pnti.me.es/dms000 MATEMÁTICAS APLICADAS A CC.SS. I TEMA Y : LOS NÚMEROS RADICALES. LOGARITMOS HOJA Nº Feh de entreg: Viernes, de Oture de 00 Ejeriios. 7. Etre ftores y simplifi l máimo l epresión
Cónicas y Cuádricas. Tema V. 2 Intersección de una recta y una cónica. 1 Definición y ecuaciones.
 Tem V Cpítulo Cónis Álgebr Deprtmento de Métodos Mtemátios de Representión UDC Tem V Cónis Cuádris Cónis En todo este pítulo trbjremos en el plno fín eulídeo E 2 on respeto un refereni retngulr {O; ē,
Tem V Cpítulo Cónis Álgebr Deprtmento de Métodos Mtemátios de Representión UDC Tem V Cónis Cuádris Cónis En todo este pítulo trbjremos en el plno fín eulídeo E 2 on respeto un refereni retngulr {O; ē,
GEOMETRÍA ANALÍTICA DEL ESPACIO
 CAPITULO Espero que l posteridd me jugue on enevoleni no solo por ls oss que he eplido sino tmién por quells que he omitido inteniondmente pr dejr los demás el pler de desurirls René Desrtes. GEOMETRÍA
CAPITULO Espero que l posteridd me jugue on enevoleni no solo por ls oss que he eplido sino tmién por quells que he omitido inteniondmente pr dejr los demás el pler de desurirls René Desrtes. GEOMETRÍA
CIRCUNFERENCIA: Definición: Es el lugar geométrico de los puntos que equidistan de un punto llamado Centro y esa distancia es el radio.
 Ls cónics responden l ecución generl del tipo F, ) 0 L ecución generl de un cónic es: A B C D E F 0 I) tér min oc cudráti cos tér min os lineles tér min o independiente B término rectngulr, cundo prece
Ls cónics responden l ecución generl del tipo F, ) 0 L ecución generl de un cónic es: A B C D E F 0 I) tér min oc cudráti cos tér min os lineles tér min o independiente B término rectngulr, cundo prece
Resumen creado por Hernán Verdugo Fabiani, profesor de Matemática y Física, abril 2011.
 Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
Figura 1. Teoría y prática de vectores
 UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio UDB Físi Cátedr FÍSICA I VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo
UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio UDB Físi Cátedr FÍSICA I VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo
La Elipse. B( 0, b ) P( x, y ) a b. B'( 0, -b ) PF' PF VV ' (x + c) + y = 2a (x c) + y elevando al cuadrado (x + c) + y = 2a (x c) + y
 L Elipse Regresr Wikispces L elipse es el conjunto de todos los puntos P de un plno, tles que l sum de ls distncis de culquier punto dos puntos fijos del plno es constnte y su ecución se llm ecución ordinri.
L Elipse Regresr Wikispces L elipse es el conjunto de todos los puntos P de un plno, tles que l sum de ls distncis de culquier punto dos puntos fijos del plno es constnte y su ecución se llm ecución ordinri.
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
Razones trigonométricas de un ángulo agudo. Relaciones fundamentales
 B C Mtemátis I - º Billerto Rzones trigonométris de un ángulo gudo. Reliones fundmentles En todo triángulo retángulo BC ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este
B C Mtemátis I - º Billerto Rzones trigonométris de un ángulo gudo. Reliones fundmentles En todo triángulo retángulo BC ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este
Definiciones de seno, coseno OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Definiciones de seno, coseno y tangente.
 89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
9 Proporcionalidad geométrica
 82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
Nombre y apellidos:... Curso:... Fecha:... TEOREMA DE PITÁGORAS SEMEJANZA FIGURAS SEMEJANTES
 8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
Propuesta sobre la enseñanza de los números racionales Geovany Sanabria Brenes
 Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Sinopsis. Caracterización de ángulos en su entorno. Se recomienda recurso interactivo. Adobe Edge Animator. Para dibujos: Adobe Illustrator Corel Draw
 AN_M_G08_U04_L02_03_04 Se reomiend reurso intertivo Sinopsis Un vtr similr Ninj expli el tem ángulos lternos internos y externos, olterles, orrespondientes y opuestos l vértie. Adoe Edge Animtor Pr diujos:
AN_M_G08_U04_L02_03_04 Se reomiend reurso intertivo Sinopsis Un vtr similr Ninj expli el tem ángulos lternos internos y externos, olterles, orrespondientes y opuestos l vértie. Adoe Edge Animtor Pr diujos:
F(x,y,z)=0 (2) Es decir la superficie S está formada por dos planos paralelos al plano coordenado xy
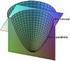 Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
Hl = {P = (x, y) 1 d(p, Fl) - d(p, 4) = -2a} 4.2 NOTACION Y PROPIEDADES
 4.1 DEFINICION. Un hipérol es el conjunto de todos los puntos del plno euclideno R~ tles que que l diferenci de sus distncis dos puntos fijos es en vlor soluto un constnte. Así, si F, y F, son dos puntos
4.1 DEFINICION. Un hipérol es el conjunto de todos los puntos del plno euclideno R~ tles que que l diferenci de sus distncis dos puntos fijos es en vlor soluto un constnte. Así, si F, y F, son dos puntos
VECTORES Magnitudes escalares y vectoriales Vectores Figura 1.1 Figura 1-1 vector. Año: 2010
 UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio --- UDB Físi Cátedr VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo de su
UNIVERSIDAD TECNOLÓGICA NACIONAL Fultd Regionl Rosrio --- UDB Físi Cátedr VECTORES Mgnitudes eslres vetoriles Ls mgnitudes eslres son quells que quedn determinds dndo un solo número rel, resultdo de su
Integrales dobles y triples
 Integrles dobles y triples 1 Integrles dobles Integrles triples 3 Cmbios de vrible R: retángulo R = [, b [, d f : R R: mpo eslr e dos vribles. Si f es ontinu en R f x : [, d R y f y : [, b R son funiones
Integrles dobles y triples 1 Integrles dobles Integrles triples 3 Cmbios de vrible R: retángulo R = [, b [, d f : R R: mpo eslr e dos vribles. Si f es ontinu en R f x : [, d R y f y : [, b R son funiones
Teorema de Pitágoras
 Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
 Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Semejanza. 2. Relación entre perímetros, áreas y volúmenes de figuras semejantes 51
 Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Area Académica: Licenciatura en Sistemas Computacionales. Profesor: I.E.C. Roxana Sifuentes Carrillo
 Are Adémi: Lienitur en Sistems Computionles Asigntur: Álger Linel Profesor: I.E.C. Ron Sifuentes Crrillo Periodo: Julio-Diiemre 0 Tem: Determinnts Astrt A determinnt is mthemtil nottion onsists of squre
Are Adémi: Lienitur en Sistems Computionles Asigntur: Álger Linel Profesor: I.E.C. Ron Sifuentes Crrillo Periodo: Julio-Diiemre 0 Tem: Determinnts Astrt A determinnt is mthemtil nottion onsists of squre
UNIDAD Nº 1: LAS RELACIONES TRIGONOMETRICAS Y SUS APLICACIONES, GUIA 2 DOCENTE: LIC ROSMIRO FUENTES ROCHA
 REPUBLICA DE COLOMBIA SECRETARIA DE EDUCACION DISTRITAL DE SANTA MARTA INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluión Nº 88 de noviemre.8/ Emnd de l Seretri De Eduión Distritl DANE Nº7-99
REPUBLICA DE COLOMBIA SECRETARIA DE EDUCACION DISTRITAL DE SANTA MARTA INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluión Nº 88 de noviemre.8/ Emnd de l Seretri De Eduión Distritl DANE Nº7-99
344 MATEMÁTICAS 2. ESO MATERIAL FOTOCOPIABLE SANTILLANA EDUCACIÓN, S. L. OBJETIVO 1 LA RAZÓN DE DOS SEGMENTOS NOMBRE: CURSO: FECHA:
 LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
INTEGRAL INDEFINIDA. Derivación. Integración
 Integrión. Cálulo de áres. INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA F() es un primitiv de f() si F ()= f(). Esto se epres sí: f() = F'() = F() L integrión es l operión invers l derivión, de modo que: FUNCIONES
Integrión. Cálulo de áres. INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA F() es un primitiv de f() si F ()= f(). Esto se epres sí: f() = F'() = F() L integrión es l operión invers l derivión, de modo que: FUNCIONES
Matemática Diseño Industrial Trigonometría Ing. Avila Ing. Moll
 Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TEMA 2 INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS
 Frnisnos T.O.R. Cód. 867 TEMA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS. INTEGRAL DEFINIDA El álulo de l integrl definid, que se denot por: f ( d, onsiste en lulr l integrl de l funión f( en el intervlo [, ].
Frnisnos T.O.R. Cód. 867 TEMA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS. INTEGRAL DEFINIDA El álulo de l integrl definid, que se denot por: f ( d, onsiste en lulr l integrl de l funión f( en el intervlo [, ].
Haga clic para cambiar el estilo de título
 Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
UNIDAD 2 Geometría 2.2 Triángulos 10
 UNI Geometrí. Triánguos 10. Triánguos OJETIVOS ur e áre e perímetro de triánguos. Otener os dos ánguos de triánguos utiizndo s reiones entre otros ánguos en figurs geométris. ur os dos de un triánguo usndo
UNI Geometrí. Triánguos 10. Triánguos OJETIVOS ur e áre e perímetro de triánguos. Otener os dos ánguos de triánguos utiizndo s reiones entre otros ánguos en figurs geométris. ur os dos de un triánguo usndo
GRAMATICAS REGULARES - EXPRESIONES REGULARES
 CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
ECUACIONES DE LA RECTA EN EL PLANO CARTESIANO
 Jie Brvo Feres ECUACIONES DE LA RECTA EN EL PLANO CARTESIANO Teore: A tod ret L del plno rtesino está soid l enos un euión de l for: x + + 0, en donde, son núeros reles; 0 ó 0, (x, ) represent un punto
Jie Brvo Feres ECUACIONES DE LA RECTA EN EL PLANO CARTESIANO Teore: A tod ret L del plno rtesino está soid l enos un euión de l for: x + + 0, en donde, son núeros reles; 0 ó 0, (x, ) represent un punto
ALGEBRA. 1. Si A y B son matrices cuadradas de orden n, se cumple la relación (A-B) 2 = A 2-2AB+B 2?
 ejeriiosemenes.om. Si A B son mtries udrds de orden n, se umple l relión (AB) A ABB?. Siendo que d e f. Hllr el vlor de: g h i ( e) i h g d g i d f ) (d e) f i e h ) h e ) h/ / e/ e i h i f i f. Enuni
ejeriiosemenes.om. Si A B son mtries udrds de orden n, se umple l relión (AB) A ABB?. Siendo que d e f. Hllr el vlor de: g h i ( e) i h g d g i d f ) (d e) f i e h ) h e ) h/ / e/ e i h i f i f. Enuni
UNIDAD 7 Trigonometría
 UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
UNIDAD 7 Trigonometría
 UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
Resolución de Triángulos Rectángulos
 PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) exigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) exigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
que verifican A 2 = A.
 . Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
. Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
UNIVERSIDAD DE CANTABRIA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA NÚMEROS COMPLEJOS. Miguel Angel Rodríguez Pozueta
 DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 6:CÓNICAS 1º BACHILLERATO ÍNDICE 1. INTRODUCCIÓN... 1.1. SUPERFICIE CÓNICA... 1.. CURVAS CÓNICAS... 5. CIRCUNFERENCIA... 6.1. ECUACIÓN COMPLETA DE UNA CIRCUNFERENCIA... 6.1.1.
APUNTES DE MATEMÁTICAS TEMA 6:CÓNICAS 1º BACHILLERATO ÍNDICE 1. INTRODUCCIÓN... 1.1. SUPERFICIE CÓNICA... 1.. CURVAS CÓNICAS... 5. CIRCUNFERENCIA... 6.1. ECUACIÓN COMPLETA DE UNA CIRCUNFERENCIA... 6.1.1.
6. Variable aleatoria continua
 6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
Nombre y apellidos:... Curso:... Fecha:... TEOREMA DE PITÁGORAS SEMEJANZA FIGURAS SEMEJANTES
 8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
2. Integrales iteradas dobles.
 2 Integrles prmétris e integrles dobles y triples. Eleonor Ctsigers. 9 Julio 26. 2. Integrles iterds dobles. 2.. Integrles iterds en dominios simples respeto de x. Se omo en l subseión.2, el retángulo
2 Integrles prmétris e integrles dobles y triples. Eleonor Ctsigers. 9 Julio 26. 2. Integrles iterds dobles. 2.. Integrles iterds en dominios simples respeto de x. Se omo en l subseión.2, el retángulo
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA
 MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
Apéndice V. Ing. José Cruz Toledo M. Vectores tridimensionales
 Apéndie V Ing. José Cruz Toledo M. Vetores tridimensionles En este péndie se present un resúmen de ls reliones vetoriles que son referenidos en este liro. y(j) (x,y,z) y Simologí (Ver Fig. V-1): ( x i
Apéndie V Ing. José Cruz Toledo M. Vetores tridimensionles En este péndie se present un resúmen de ls reliones vetoriles que son referenidos en este liro. y(j) (x,y,z) y Simologí (Ver Fig. V-1): ( x i
Función de transición δ. Tema 6. Función de transición extendida. Función de transición extendida. Función de transición extendida
 Tem 6 El lenguje eptdo por un FA Funión de trnsiión δ p j p l Dr. Luis A. Pined ISBN: 970-32-2972-7 Σ Q p i p k n Pr todo en Q & Σ, δ(, ) = p Funión de trnsiión etendid δ permite moverse the un estdo otro
Tem 6 El lenguje eptdo por un FA Funión de trnsiión δ p j p l Dr. Luis A. Pined ISBN: 970-32-2972-7 Σ Q p i p k n Pr todo en Q & Σ, δ(, ) = p Funión de trnsiión etendid δ permite moverse the un estdo otro
CAPÍTULO 4: RELACIÓN ENTRE ÁNGULOS Y ARCOS DE CIRCUNFERENCIA (III)
 PÍTULO 4: RELIÓN ENTRE ÁNGULOS Y ROS DE IRUNFERENI (III) Dnte Guerrero-hnduví Piur, 2015 FULTD DE INGENIERÍ Áre Deprtmentl de Ingenierí Industril y de Sistems PÍTULO 4: RELIÓN ENTRE ÁNGULOS Y ROS DE IRUNFERENI
PÍTULO 4: RELIÓN ENTRE ÁNGULOS Y ROS DE IRUNFERENI (III) Dnte Guerrero-hnduví Piur, 2015 FULTD DE INGENIERÍ Áre Deprtmentl de Ingenierí Industril y de Sistems PÍTULO 4: RELIÓN ENTRE ÁNGULOS Y ROS DE IRUNFERENI
GUIA DE TRABAJO # 28. Materia: Matemáticas. Tema: Múltiplos y divisores. Fecha: Profesor: Fernando Viso. Nombre del alumno: Sección del alumno:
 GUIA DE TRABAJO # 28. Mteri: Mtemátis. Tem: Múltiplos y divisores. Feh: Profesor: Fernndo Viso Nombre del lumno: Seión del lumno: CONDICIONES: Trbjo individul. Sin libros, ni udernos, ni nots. Sin elulres.
GUIA DE TRABAJO # 28. Mteri: Mtemátis. Tem: Múltiplos y divisores. Feh: Profesor: Fernndo Viso Nombre del lumno: Seión del lumno: CONDICIONES: Trbjo individul. Sin libros, ni udernos, ni nots. Sin elulres.
Sistemas de Ecuaciones lineales Discusión con parámetros. Discutir el siguiente sistema de ecuaciones lineales según el valor del parámetro a:
 ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
UNIDAD 12.- Productos vectorial y mixto. Aplicaciones. (tema 7 del libro)
 UNIDAD.- Produto etoril mixto. Apliione. (tem 7 del liro). PRODUCTO VECTORIAL DE DOS VECTORES LIBRES Definiión: El produto etoril de do etore lire - Si 0 ó 0 ó on proporionle, entone - En o ontrrio, etore
UNIDAD.- Produto etoril mixto. Apliione. (tem 7 del liro). PRODUCTO VECTORIAL DE DOS VECTORES LIBRES Definiión: El produto etoril de do etore lire - Si 0 ó 0 ó on proporionle, entone - En o ontrrio, etore
LEY DE SENOS Y COSENOS
 FULTD DE IENIS EXTS Y NTURLES SEMILLERO DE MTEMÁTIS GRDO: 10 TLLER Nº: 1 SEMESTRE 1 LEY DE SENOS Y OSENOS RESEÑ HISTÓRI Menelo de lejndrí L trigonometrí fue desrrolld por strónomos griegos que onsidern
FULTD DE IENIS EXTS Y NTURLES SEMILLERO DE MTEMÁTIS GRDO: 10 TLLER Nº: 1 SEMESTRE 1 LEY DE SENOS Y OSENOS RESEÑ HISTÓRI Menelo de lejndrí L trigonometrí fue desrrolld por strónomos griegos que onsidern
PROBLEMAS DE ÁLGEBRA DE MATRICES
 Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
Resolución del examen de Matemáticas II de Selectividad Andalucía Junio de 2006
 Resolución del emen de Mtemátics II de Selectividd Andlucí Junio de 6 Antonio Frncisco Roldán López de Hierro * de junio de 6 Opción A Ejercicio [ 5 puntos] Determin un punto de l curv de ecución y e pendiente
Resolución del emen de Mtemátics II de Selectividd Andlucí Junio de 6 Antonio Frncisco Roldán López de Hierro * de junio de 6 Opción A Ejercicio [ 5 puntos] Determin un punto de l curv de ecución y e pendiente
Profr. Efraín Soto Apolinar. Ley de senos
 Profr. Efrín Soto Apolinr. Ley de senos Hst hor hemos resuelto triángulos retángulos, pero tmién es omún enontrr prolems on triángulos que no son retángulos, omo utángulos u otusángulos. Pr resolver estos
Profr. Efrín Soto Apolinr. Ley de senos Hst hor hemos resuelto triángulos retángulos, pero tmién es omún enontrr prolems on triángulos que no son retángulos, omo utángulos u otusángulos. Pr resolver estos
4. Trigonometría II. c) c 2 b 2 a 2 2ba cos C c 11,17 cm a A 61,84. B 38,11 se n B sen C d) A B C 180 A 70 a b 5,32. l 40 sen.
 9 ) os 11,17 m se n 61,84 38,11 se n d) 180 70 se n 5,3 se n 10,48 lul un ulquier de ls lturs de los triángulos resueltos en el ejeriio nterior y utilízl después pr lulr su áre. Pr resolver este ejeriio
9 ) os 11,17 m se n 61,84 38,11 se n d) 180 70 se n 5,3 se n 10,48 lul un ulquier de ls lturs de los triángulos resueltos en el ejeriio nterior y utilízl después pr lulr su áre. Pr resolver este ejeriio
CALCULO DE CENTROS DE MASA: PLACAS
 CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
