Mecánica Estadística: Estadística de Maxwell-Boltzmann
|
|
|
- Eva María Rodríguez Vázquez
- hace 6 años
- Vistas:
Transcripción
1 Ludwg Boltzmann James Clerk Maxwell E. Martínez 1
2 Lápda de Boltzmann en el cementero de Vena S=k ln W E. Martínez 2
3 S=k ln W Entropía, una propedad termodnámca Una medda de nuestra gnoranca de un sstema físco-químco Conexón entre las propedades termodnámcas macroscópcas del sstema y las propedades mcroscópcas de sus elementos E. Martínez 3
4 La entropía de un sstema aslado tende a crecer (o por lo menos no decrece) como consecuenca de cualquer transformacón termodnámca. Consdere usted un cubo de helo, aslado en una habtacón a una temperatura constante, dgamos 17 grados celcus... He aquí el helo: E. Martínez 4
5 En el nstante msmo que dejamos el helo en la habtacón tenemos absoluto conocmento de la poscón de cada molécula del helo. E. Martínez 5
6 ... Sn embargo, en un proceso cuasestátco este helo se fundrá, transformándose en agua líquda. Y este proceso de fusón ha destrudo el orden en que se encontraban las moléculas en el sóldo. Ha aumentado, al gual que la entropía, nuestra gnoranca sobre la poscón de las partículas, producto del desorden. E. Martínez 6
7 Entropía e gnoranca Vamos a asocar la entropía con total gnoranca, en vez de asocarla sólo con la gnoranca de la poscón de los elementos. Por lo tanto, el problema es dar un sgnfcado precso al concepto de gnoranca, y hallar la relacón funconal que lo vncule con la entropía (y así, tambén, poder entender cabalmente porqué está esa relacón funconal en la lápda de Ludwg Boltzmann) E. Martínez 7
8 Consderemos por analogía un mazo de nape El mazo representa el sstema... y los napes, los elementos E. Martínez 8
9 S los elementos (napes) se encuentran orgnalmente ordenados (por pnta y valores), ello corresponderá a un estado de orden total (correspondendo a un estado de entropía cero). Es decr, que exste una únca dsposcón posble de los elementos del sstema, y conocemos perfectamente la poscón de cada nape. S se barajan las cartas (correspondendo a una agtacón térmca debda a un aumento de la temperatura) aumenta nuestra gnoranca respecto de la poscón de un nape dado (correspondendo a un aumento de la entropía). Cómo medremos esta gnoranca? E. Martínez 9
10 Consderemos el mazo ordenado, extragamos una carta al azar y coloquémosla en una poscón cualquera del mazo. S el número de cartas es N, tendremos N poscones dstntas gualmente posbles. Supongamos ahora que son dos los napes que se extrajeron y se han vuelto a colocar en otra poscón cualquera. El número de dsposcones dstntas e gualmente posbles es ahora N(N-1) E. Martínez 10
11 Sacamos un nape... Q Q N napes ordenados... y lo colocamos en una de las N poscones Habrán N poscones, gualmente posbles, donde la carta puede ubcarse! E. Martínez 11
12 Sacamos ahora dos napes... K Q Q N napes ordenados Este lugar ya está ocupado!... y volvemos a colocar los dos napes K Habrán N(N-1) poscones, gualmente posbles, donde los dos napes pueden ubcarse! E. Martínez 12
13 Se observa que el aumento de nuestra gnoranca acerca de la dsposcón de los napes en el mazo (que se corresponde con el aumento del desorden) está asocado con el número de dsposcones dstntas gualmente posbles. Podemos proponer, entonces, como medda de nuestra gnoranca el número de dsposcones dstntas de los napes, gualmente posbles, para el estado que se consdere. Es mportante consderar que, a pror, todas las poscones dstntas son gualmente posbles E. Martínez 13
14 El número de dsposcones dstntas de los elementos de un sstema dado se denotará por W Consderemos ahora dos mazos que se barajan ndependentemente Cuál es el número W de dsposcones gualmente probables del sstema formado por los dos mazos? W = W W 1 2 Sea W 1 el número de... y W para este dsposcones gualmente sstema 2 probables de este sstema E. Martínez 14
15 Por otro lado, termodnámcamente s S 1 y S 2 ndcan la entropía de dos sstemas ndependentes, la entropía total S está dada por S = S + S 1 2 Hemos encontrado una nterrelacón entre W y S, tal que: a) A un aumento de S corresponde un aumento de W, y vceversa b) Cuando se consderan dos sstemas ndependentes, a la propedad adtva de S le corresponde la propedad multplcatva de W E. Martínez 15
16 Por lo tanto, la funcón que vncule a S y W deberá ser tal que f(w W ) = f(w ) + f(w ) Exste una, y solo una, funcón que verfca la condcón anteror y es la que fue puesta en la lápda de Boltzmann S = k lnw E. Martínez 16
17 S = k lnw Para el caso de un sstema físco-químco, W representará, al gual que los napes de la baraja, el número de todas las posbles poscones de sus elementos. Supongamos que el sstema tene N partículas, una funcón de volumen V, y una energía nterna U Uno de lo objetvo de la mecánca estadístca es calcular la gnoranca W como funcón de W = W(U, V, N) E. Martínez 17
18 Vamos a calcular W para un sstema aslado de elementos ndependentes localzados. Por localzado se entenderá que el elemento se puede encontrar en el entorno de una poscón fja en el espaco; además se puede encontrar uno, y solo un, elemento en tal poscón. Por ndependente se entenderá que el estado del elemento en un nstante dado no está afectado por el estado de los restantes elementos. E. Martínez 18
19 Supongamos entonces que tenemos un sstema aslado con N partículas déntcas. Cada partícula puede ocupar un nvel de energía E, E, La energía (constante) de este sstema aslado es U Defnamos una dstrbucón del sstema de partículas medante la notacón (n, n,..., n,... ) 1 2 E. Martínez 19
20 (n, n,..., n,... ) 1 2 número de partículas en el nvel, donde cada una de ellas tene una energía E Entonces n E=U y además n =N E. Martínez 20
21 Defnamos el conjunto de todas estas dstrbucones como Ω= (n 1, n2,..., n,...) / n =N, n E=U Cada elemento de Ω se dce que es un macroestado Ahora, cada macroestado tene varas maneras de confgurarse, y una manera asocada a un determnado macroestado se llamará mcroestado Luego W es el número de mcroestados posbles del sstema E. Martínez 21
22 Macroestado y mcroestado Supongase que el sstema tene N = 4 partículas, y que la energía nterna es U = 6, y los nveles de energía van desde 0, 1, 2,... He aquí tres posbles macroestados A B C E. Martínez 22
23 E. Martínez 23 Mecánca Estadístca: Estadístca de Maxwell-Boltzmann A Como el sstema es localzado, esto sgnfca que las partículas son dstngubles, luego algunas manfestacones (mcroestados) para el macroestado A son las sguentes: A A
24 E. Martínez 24 Mecánca Estadístca: Estadístca de Maxwell-Boltzmann Algunos mcroestados asocados al macroestado B son los sguentes: B B B B
25 La pregunta es entonces dado un determnado macroestado, cuántos mcroestados asocados tene? La respuesta no es senclla. Sn embargo s la respondemos tenemos calculado el conjunto W. En efecto, sea ω Ω un macroestado Defnamos por asocados a ω Entonces ω como el número de mcroestados W= ω ω Ω E. Martínez 25
26 Insstmos en la pregunta entonces, dado un determnado macroestado, cuántos mcroestados asocados tene? La respuesta no es senclla. Sn embargo s por un momento olvdamos la condcón n E=U podemos responder a la pregunta, Dado N objetos, de cuántas maneras podemos repartr estos objetos en k cajas que tengan capacdad para n,n,..., n, objetos 1 2 k respectvamente?, donde n + n n = N 1 2 k E. Martínez 26
27 ... N boltas... n n 1 + n k = N ( N ) ( N - n 1 ) n 1 ( ) N - (n n ) 1 k-1 n 2 n k E. Martínez 27
28 No resulta complcado demostrar que ( N )( N - n 1 ) n 1 ( ) N - (n n )... 1 k-1 = n 2 n k N! n! n!... n! 1 2 k Son todos los mcroestados posbles para el macroestado (n, n,..., n ) 1 2 k pero que no necesaramente tenen la condcón n E + n E n E = U k k E. Martínez 28
29 De otra forma, la cardnaldad de un macroestado partcular (n, n,..., n ) 1 2 k es (n, n,..., n ) 1 2 k = N! n! n!... n! 1 2 k Sn consderar la condcón n E + n E n E = U k k E. Martínez 29
30 De manera que podemos conclur que donde W= ω Ω N! n1! n2! L n k! Ω= ω=(n 1, n 2,..., n k ) / k n =N, n E=U =1 =1 k E. Martínez 30
31 Así como toda ubcacón del nape extraído del mazo es gualmente probable, toda confguracón de un mcroestado es gualmente probable. En rgor, es el postulado fundamental de la mecánca estadístca: Todo sstema en equlbro tene la msma probabldad de estar en cualquera de sus mcroestados permtdos. De esta manera, el macroestado que tenga mayor número de mcroestados es, obvamente, el macroestado más probable. Y, en consecuenca, será (en probabldad) el estado de equlbro. E. Martínez 31
32 A la búsqueda del macroestado más probable Supongamos que exste una dstrbucón ω Ω tal que ω ω ω Ω Nuestro nterés es calcular entonces ω E. Martínez 32
33 A la búsqueda del macroestado más probable Encontrar ω sgnfca N! max n 1! L n k! sujeto a las condcones extremas k k =1 n =N, =1 n E =U E. Martínez 33
34 A la búsqueda del macroestado más probable Maxmzar la funcón N! ω= n 1! L n k! Es equvalente a maxmzar ln ω=ln N! -ln (n 1! L nk! ) E. Martínez 34
35 A la búsqueda del macroestado más probable Utlzando el método de los multplcadores de Lagrange, defnmos ( ) ( ) n -N - n E -U T( ω)=ln ω+ α β Dervando parcalmente e gualando a cero T(w) n =0 T(w) α =0 ; ; T(w) β =0 E. Martínez 35
36 A la búsqueda del macroestado más probable Para obtener las dervadas de ln n ω = n utlzamos la fórmula de Strlng ( ln N! -(ln n! + L+ln n! )) 1 ln M! =M ln M-M k y obtenemos ln w n =-ln n E. Martínez 36
37 A la búsqueda del macroestado más probable Obtenemos T( ω) =-ln n + + E =0 n α β De modo que, s dentfcamos por tenemos n =e α+ βe βe =c n e los máxmos, E. Martínez 37
38 A la búsqueda del macroestado más probable La constante c se encuentra sumando los n, esto es n =N=c e βe de modo que c= N β E e E. Martínez 38
39 A la búsqueda del macroestado más probable Conclumos que la dstrbucón más probable es ω ( n, n, ) = L 1 2, nk donde n =N e βe k β E e j=1 j Contnuará... E. Martínez 39
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
3. VARIABLES ALEATORIAS.
 3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
Electricidad y calor
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Electricidad y calor. Un repaso... Temas. 4. Primera ley de la Termodinámica. Webpage: Algunas definiciones
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Fundamentos de Física Estadística: Problema básico, Postulados
 Fundamentos de Físca Estadístca: Problema básco, Postulados y Formalsmos. Problema básco de la Mecánca Estadístca del Equlbro (MEE) El problema básco de la MEE es la determnacón de la relacón termodnámca
Fundamentos de Físca Estadístca: Problema básco, Postulados y Formalsmos. Problema básco de la Mecánca Estadístca del Equlbro (MEE) El problema básco de la MEE es la determnacón de la relacón termodnámca
TEMA 3. VARIABLE ALEATORIA
 TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
Métodos específicos de generación de diversas distribuciones discretas
 Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Problemas donde intervienen dos o más variables numéricas
 Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Reconciliación de datos experimentales. MI5022 Análisis y simulación de procesos mineralúgicos
 Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
4. PROBABILIDAD CONDICIONAL
 . ROBBILIDD CONDICIONL La probabldad de que ocurra un evento B cuando se sabe que ha ocurrdo algún otro evento se denomna robabldad Condconal, Se denota como (B/) y se lee como la probabldad de que ocurra
. ROBBILIDD CONDICIONL La probabldad de que ocurra un evento B cuando se sabe que ha ocurrdo algún otro evento se denomna robabldad Condconal, Se denota como (B/) y se lee como la probabldad de que ocurra
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
Consideremos un sólido rígido sometido a un sistema de fuerzas en equilibrío, es decir
 1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
Mecánica Clásica ( Partículas y Bipartículas )
 Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
Mecánca lásca ( Partículas y Bpartículas ) Alejandro A. Torassa Lcenca reatve ommons Atrbucón 3.0 (0) Buenos Ares, Argentna atorassa@gmal.com Resumen Este trabajo consdera la exstenca de bpartículas y
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
PROBABILIDAD Y ESTADÍSTICA
 PROBABILIDAD Y ESTADÍSTICA 1. S A es un suceso de probabldad 0.3, la probabldad de su suceso contraro es: a) 0. b) 1.0 c) 0.7 (Convocatora juno 006. Eamen tpo H) S A es un suceso, la probabldad de su suceso
PROBABILIDAD Y ESTADÍSTICA 1. S A es un suceso de probabldad 0.3, la probabldad de su suceso contraro es: a) 0. b) 1.0 c) 0.7 (Convocatora juno 006. Eamen tpo H) S A es un suceso, la probabldad de su suceso
Perturbación de los valores propios simples de matrices de polinomios dependientes diferenciablemente de parámetros
 Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
TERMODINÁMICA FUNDAMENTAL. TEMA 3. Primer principio de la termodinámica
 TERMODINÁMIA FUNDAMENTAL TEMA 3. Prmer prncpo de la termodnámca 1. alor 1.1. oncepto de calor alor: orma de transerenca de energía entre dos sstemas termodnámcos, o entre un sstema y su entorno, como consecuenca
TERMODINÁMIA FUNDAMENTAL TEMA 3. Prmer prncpo de la termodnámca 1. alor 1.1. oncepto de calor alor: orma de transerenca de energía entre dos sstemas termodnámcos, o entre un sstema y su entorno, como consecuenca
TERMODINÁMICA AVANZADA
 TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Propiedades Asintóticas
 Capítulo 3 Propedades Asntótcas 3.. Dstrbucones Estaconaras Defncón 3. Sea X n, n, una cadena de Markov con espaco de estados E y matrz de transcón P. Sea π(), E, una dstrbucón de probabldad, es decr,
Capítulo 3 Propedades Asntótcas 3.. Dstrbucones Estaconaras Defncón 3. Sea X n, n, una cadena de Markov con espaco de estados E y matrz de transcón P. Sea π(), E, una dstrbucón de probabldad, es decr,
i=1 Demuestre que cumple los axiomas de norma. Calcule el límite Verifiquemos cada uno de los axiomas de la definición de norma: i=1
 CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
Efectos fijos o aleatorios: test de especificación
 Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Lección: Disoluciones
 Leccón: Dsolucones TEMA: Introduccón 1 Adolfo Bastda Pascual Unversdad de Murca. España. I. Caracterzacón de las dsolucones.......2 I.A. Composcón de una dsolucón....... 2 I.B. Magntudes molares parcales.........
Leccón: Dsolucones TEMA: Introduccón 1 Adolfo Bastda Pascual Unversdad de Murca. España. I. Caracterzacón de las dsolucones.......2 I.A. Composcón de una dsolucón....... 2 I.B. Magntudes molares parcales.........
2.1. Sustancias puras. Medida de los cambios de entalpía.
 2 Metalurga y termoquímca. 7 2. Metalurga y termoquímca. 2.1. Sustancas puras. Medda de los cambos de entalpía. De acuerdo a las ecuacones (5 y (9, para un proceso reversble que ocurra a presón constante
2 Metalurga y termoquímca. 7 2. Metalurga y termoquímca. 2.1. Sustancas puras. Medda de los cambos de entalpía. De acuerdo a las ecuacones (5 y (9, para un proceso reversble que ocurra a presón constante
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL.
 VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un expermento, un número real.
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un expermento, un número real.
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA
 LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
Aplicación de la termodinámica a las reacciones químicas Andrés Cedillo Departamento de Química Universidad Autónoma Metropolitana-Iztapalapa
 Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Capítulo V. Teoremas de Fermat, Euler y Wilson
 Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
Capítulo V Teoremas de Fermat, Euler y Wlson En este capítulo utlzamos los conceptos desarrollados en dvsbldad y conteo para deducr tres teoremas báscos de la teoría de números. En el próxmo capítulo,
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Una Reformulación de la Mecánica Clásica
 Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
TEMA 4 Variables aleatorias discretas Esperanza y varianza
 Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y A c se les ha asociado los sucesos B y B c.
 Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA
 INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA LABORATORIO 1-008 PRACTICA 4: LEYES DE LOS GASES 1. OBJETIVOS ) Comprobacón expermental de las leyes de los gases. En este caso nos vamos a concentrar en el estudo
INSTITUTO DE FÍSICA FACULTAD DE INGENIERÍA LABORATORIO 1-008 PRACTICA 4: LEYES DE LOS GASES 1. OBJETIVOS ) Comprobacón expermental de las leyes de los gases. En este caso nos vamos a concentrar en el estudo
Continua: Corriente cuyo valor es siempre constante (no varía con el tiempo). Se denota como c.c.
 .. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
.. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
EXPERIMENTACIÓN COMERCIAL(I)
 EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
ESTADÍSTICA BIDIMENSIONAL ÍNDICE GENERAL
 ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
Pregunta Hoy está nublado, cuál es la probabilidad de que mañana continúe nublado? cuál es la probabilidad de que está nublado pasado mañana?
 Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, son números ordenados en filas y columnas.
 MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
Fisicoquímica CIBEX Guía de Trabajos Prácticos 2010. Trabajo Práctico N 7. - Medida de la Fuerza Electromotriz por el Método de Oposición-
 Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Campo eléctrico. Líneas de campo. Teorema de Gauss. El campo de las cargas en reposo. Campo electrostático
 qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
INTRODUCCIÓN. Técnicas estadísticas
 Tema : Estadístca Descrptva Undmensonal ITRODUCCIÓ Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. (Ejemplo: lómetros recorrdos en un ntervalo de tempo a una velocdad
Tema : Estadístca Descrptva Undmensonal ITRODUCCIÓ Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. (Ejemplo: lómetros recorrdos en un ntervalo de tempo a una velocdad
TEMA 1: PROBABILIDAD
 robabldad TEM : ROBBILIDD Índce del tema Índce del tema.. Introduccón 2.2. Defncón de probabldad 3.2.. ropedades nmedatas 3 Ejemplo 7 Ejemplo 2 8 Ejemplo 3 9.3. robabldad condconada 0.3.. Introduccón 0.3.2.
robabldad TEM : ROBBILIDD Índce del tema Índce del tema.. Introduccón 2.2. Defncón de probabldad 3.2.. ropedades nmedatas 3 Ejemplo 7 Ejemplo 2 8 Ejemplo 3 9.3. robabldad condconada 0.3.. Introduccón 0.3.2.
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA. Ingeniería Química
 UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA Ingenería Químca Undad I. Introduccón a los cálculos de Ingenería Químca
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA Ingenería Químca Undad I. Introduccón a los cálculos de Ingenería Químca
1. Actividad y Coeficientes de actividad
 ermodnámca. ema Dsolucones Reales. Actvdad y Coecentes de actvdad Se dene el coecente de actvdad,, de manera que: ( ( ln Actvdad ( Esta epresón es análoga a la de las dsolucones deales. Sn embargo, es
ermodnámca. ema Dsolucones Reales. Actvdad y Coecentes de actvdad Se dene el coecente de actvdad,, de manera que: ( ( ln Actvdad ( Esta epresón es análoga a la de las dsolucones deales. Sn embargo, es
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Tema 1: Análisis de datos unidimensionales
 Tema : Análss de datos undmensonales. Varables estadístcas undmensonales. Representacones gráfcas.. Característcas de las dstrbucones de frecuencas undmensonales.. Varables estadístcas undmensonales. Representacones
Tema : Análss de datos undmensonales. Varables estadístcas undmensonales. Representacones gráfcas.. Característcas de las dstrbucones de frecuencas undmensonales.. Varables estadístcas undmensonales. Representacones
Reconocimiento de Locutor basado en Procesamiento de Voz. ProDiVoz Reconocimiento de Locutor 1
 Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
Cinemática del Brazo articulado PUMA
 Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
Modelos unifactoriales de efectos aleatorizados
 Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
Disoluciones. Disolución ideal. Disolución ideal. Disolución ideal. Disolución ideal
 Dsolucones TEM. Dsolucones reales. otencal químco en dsolucones reales. Concepto de actvdad. Una dsolucón es una mezcla homogénea de un componente llamado dsolvente () que se encuentra en mayor proporcón
Dsolucones TEM. Dsolucones reales. otencal químco en dsolucones reales. Concepto de actvdad. Una dsolucón es una mezcla homogénea de un componente llamado dsolvente () que se encuentra en mayor proporcón
Colección de problemas de. Poder de Mercado y Estrategia
 de Poder de Mercado y Estratega Curso 3º - ECO- 0-03 Iñak Agurre Jaromr Kovark Marta San Martín Fundamentos del Análss Económco I Unversdad del País Vasco UPV/EHU Tema. Olgopolo y competenca monopolístca.
de Poder de Mercado y Estratega Curso 3º - ECO- 0-03 Iñak Agurre Jaromr Kovark Marta San Martín Fundamentos del Análss Económco I Unversdad del País Vasco UPV/EHU Tema. Olgopolo y competenca monopolístca.
Variable aleatoria: definiciones básicas
 Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
1. Modelos Expresados en Variables de Estado 1
 2 3 Modelo en Varables de Estado.doc 1 1. Modelos Exresados en Varables de Estado 1. Modelos Exresados en Varables de Estado 1 1.1. Introduccón 2 1.2. Defncón 2 1.3. Forma General 9 1.4. Solucón 1 1.5.
2 3 Modelo en Varables de Estado.doc 1 1. Modelos Exresados en Varables de Estado 1. Modelos Exresados en Varables de Estado 1 1.1. Introduccón 2 1.2. Defncón 2 1.3. Forma General 9 1.4. Solucón 1 1.5.
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA
 EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Primer Semestre - Otoño 2014. Omar De la Peña-Seaman. Instituto de Física (IFUAP)
 MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
Sistemas de Varias Partículas.
 Capítulo 6 Sstemas de Varas Partículas. Al estudar los sstemas con varas partículas surgen varos elementos adconales, como son los enlaces o lgaduras entre puntos, tanto nternos al sstema como externos,
Capítulo 6 Sstemas de Varas Partículas. Al estudar los sstemas con varas partículas surgen varos elementos adconales, como son los enlaces o lgaduras entre puntos, tanto nternos al sstema como externos,
TEMA 4. TRABAJO Y ENERGIA.
 TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
Tema 3. Sólido rígido.
 Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
Tema 3. Sóldo rígdo. Davd Blanco Curso 009-010 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca 3 1.1. Condcón cnemátca de rgdez............................ 3 1.. Movmento de traslacón...............................
NÚMEROS COMPLEJOS. y sabemos que no podemos calcular raíces de números negativos en R. Para resolver este problema introduciremos el valor i = 1
 NÚMEROS COMPLEJOS 1. Qué es un número complejo? Defncones. La ecuacón x + 1 = 0 no tene solucón en el campo real puesto que s ntentamos resolverla tendremos que x = ± 1 y sabemos que no podemos calcular
NÚMEROS COMPLEJOS 1. Qué es un número complejo? Defncones. La ecuacón x + 1 = 0 no tene solucón en el campo real puesto que s ntentamos resolverla tendremos que x = ± 1 y sabemos que no podemos calcular
OSCILACIONES 1.- INTRODUCCIÓN
 OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
LABORATORIO DE OPERACIONES UNITARIAS I
 UNIVERSIA EL ZULIA FACULTA E INGENIERÍA ESCUELA E INGENIERÍA QUÍMICA EPARTAMENTO E INGENIERÍA QUÍMICA BÁSICA LABORATORIO E OPERACIONES UNITARIAS I TRANSFERENCIA E CALOR EN INTERCAMBIAORES Profesora: Maranela
UNIVERSIA EL ZULIA FACULTA E INGENIERÍA ESCUELA E INGENIERÍA QUÍMICA EPARTAMENTO E INGENIERÍA QUÍMICA BÁSICA LABORATORIO E OPERACIONES UNITARIAS I TRANSFERENCIA E CALOR EN INTERCAMBIAORES Profesora: Maranela
En un mercado hay dos consumidores con las siguientes funciones de utilidad:
 En un mercado hay dos consumdores con las sguentes funcones de utldad: U ( + y, y = ln( + U ( = + y con a >,, y a ln( + donde, =,, es la cantdad del ben consumda por el ndvduo, y es la cantdad de renta
En un mercado hay dos consumdores con las sguentes funcones de utldad: U ( + y, y = ln( + U ( = + y con a >,, y a ln( + donde, =,, es la cantdad del ben consumda por el ndvduo, y es la cantdad de renta
Simulación y Optimización de Procesos Químicos. Titulación: Ingeniería Química. 5º Curso Optimización.
 Smulacón y Optmzacón de Procesos Químcos Ttulacón: Ingenería Químca. 5º Curso Optmzacón. Programacón Cuadrátca Métodos de Penalzacón Programacón Cuadrátca Sucesva Gradente Reducdo Octubre de 009. Programacón
Smulacón y Optmzacón de Procesos Químcos Ttulacón: Ingenería Químca. 5º Curso Optmzacón. Programacón Cuadrátca Métodos de Penalzacón Programacón Cuadrátca Sucesva Gradente Reducdo Octubre de 009. Programacón
Introducción a las Subastas de Múltiples Objetos
 Introduccón a las Subastas de Múltples Objetos Alvaro J. Rascos Vllegas Unversdad de los Andes Abrl de 2010 lvaro J. Rascos Vllegas (Unversdad de losintroduccón Andes) a las Subastas de Múltples Objetos
Introduccón a las Subastas de Múltples Objetos Alvaro J. Rascos Vllegas Unversdad de los Andes Abrl de 2010 lvaro J. Rascos Vllegas (Unversdad de losintroduccón Andes) a las Subastas de Múltples Objetos
LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION
 Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
Unversdad Católca Los Ángeles de Chmbote LECTURA 06: MEDIDAS DE TENDENCIA CENTRAL (PARTE I) LA MEDIA ARITMÉTICA TEMA 15: MEDIDAS ESTADISTICAS: DEFINICION Y CLASIFICACION 1. DEFINICION: Las meddas estadístcas
Tema 3. Trabajo, energía y conservación de la energía
 Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA
 Ing. Federco G. Salazar Termodnámca del Equlbro TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA Contendo 1. Conversón y Coordenada de Reaccón. 2. Ecuacones Independentes y Regla
Ing. Federco G. Salazar Termodnámca del Equlbro TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA Contendo 1. Conversón y Coordenada de Reaccón. 2. Ecuacones Independentes y Regla
Laboratorio de Electricidad PRACTICA - 8 SHUNTS PARA INSTRUMENTOS DE MEDICIÓN DE CORRIENTE
 PRACTCA - 8 HUNT PARA NTRUMNTO D MDCÓN D CORRNT - Fnaldades 1.- Convertr un dspostvo fundamental de medcón (alvanómetro) en un mlamperímetro con márenes de medda más elevados. 2.- Calcular el valor del
PRACTCA - 8 HUNT PARA NTRUMNTO D MDCÓN D CORRNT - Fnaldades 1.- Convertr un dspostvo fundamental de medcón (alvanómetro) en un mlamperímetro con márenes de medda más elevados. 2.- Calcular el valor del
Introducción al riesgo de crédito
 Introduccón al resgo de crédto Estrella Perott Investgador Senor Bolsa de Comerco de Rosaro eperott@bcr.com.ar. Introduccón El resgo credtco es el resgo de una pérdda económca como consecuenca de la falta
Introduccón al resgo de crédto Estrella Perott Investgador Senor Bolsa de Comerco de Rosaro eperott@bcr.com.ar. Introduccón El resgo credtco es el resgo de una pérdda económca como consecuenca de la falta
ALINEAMIENTO DE DOS SECUENCIAS (pairwise alignment)
 ALINEAMIENTO DE DOS SECUENCIAS (parwse algnment) El alneamento de una pareja de secuencas permte cuantfcar el grado de smltud que hay entre ellas y determnar s exste algún tpo de relacón entre ambas. Para
ALINEAMIENTO DE DOS SECUENCIAS (parwse algnment) El alneamento de una pareja de secuencas permte cuantfcar el grado de smltud que hay entre ellas y determnar s exste algún tpo de relacón entre ambas. Para
MÁQUINAS TÉRMICAS. Aspectos Fundamentales de Termodinámica. Mayo 2012 ASPECTOS FUNDAMENTALES
 MÁQUINAS TÉRMICAS Aspectos Fundamentales de Termodnámca rof. Mguel ASUAJE Mayo 2012 Contendo ASECTOS FUNDAMENTALES Breve revsón de los conceptos de Termodnámca Trabajo y Calor rmera Ley d Segunda Ley Cclo
MÁQUINAS TÉRMICAS Aspectos Fundamentales de Termodnámca rof. Mguel ASUAJE Mayo 2012 Contendo ASECTOS FUNDAMENTALES Breve revsón de los conceptos de Termodnámca Trabajo y Calor rmera Ley d Segunda Ley Cclo
Población: Es el conjunto de todos los elementos cuyo conocimiento nos interesa y serán objeto de nuestro estudio.
 Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
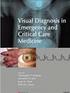 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
Fuerzas ficticias Referencial uniformemente acelerado
 Capítulo 10 Fuerzas fctcas Las fuerzas fctcas son fuerzas que deben nclurse en la descrpcón de un sstema físco cuando la observacón se realza desde un sstema de referenca no nercal, a pesar de ello, se
Capítulo 10 Fuerzas fctcas Las fuerzas fctcas son fuerzas que deben nclurse en la descrpcón de un sstema físco cuando la observacón se realza desde un sstema de referenca no nercal, a pesar de ello, se
EJERCICIO 1 1. VERDADERO 2. VERDADERO (Esta afirmación no es cierta en el caso del modelo general). 3. En el modelo lineal general
 PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
VARIABLES ALEATORIAS BIDIMENSIONALES. DISTRIBUCIONES
 Gestón Aeronáutca: Estadístca Teórca Facultad Cencas Económcas Empresarales Departamento de Economía Aplcada Profesor: Santago de la Fuente Fernández VARIABLES ALEATORIAS BIDIMENSIONALES. DISTRIBUCIONES
Gestón Aeronáutca: Estadístca Teórca Facultad Cencas Económcas Empresarales Departamento de Economía Aplcada Profesor: Santago de la Fuente Fernández VARIABLES ALEATORIAS BIDIMENSIONALES. DISTRIBUCIONES
CESMA BUSINESS SCHOOL
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
http://www.rubenprofe.com.ar biofisica@rubenprofe.com.ar RESISTENCIAS EN PARALELO
 bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
Análisis estadístico de incertidumbres aleatorias
 Análss estadístco de ncertdumbres aleatoras Errores aleatoros y sstemátcos La meda y la desvacón estándar La desvacón estándar como error de una sola medda La desvacón estándar de la meda úmero de meddas
Análss estadístco de ncertdumbres aleatoras Errores aleatoros y sstemátcos La meda y la desvacón estándar La desvacón estándar como error de una sola medda La desvacón estándar de la meda úmero de meddas
Apuntes de Mecánica Newtoniana: Sistemas de Partículas, Cinemática y Dinámica del
 Apuntes de Mecánca Newtonana: Sstemas de Partículas, Cnemátca y Dnámca del Rígdo. Arel Fernández Danel Marta Insttuto de Físca - Facultad de Ingenería - Unversdad de la Repúblca Índce general Contendos
Apuntes de Mecánca Newtonana: Sstemas de Partículas, Cnemátca y Dnámca del Rígdo. Arel Fernández Danel Marta Insttuto de Físca - Facultad de Ingenería - Unversdad de la Repúblca Índce general Contendos
Trabajo y Energía Cinética
 Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS
 CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
Tema 8 - Estadística - Matemáticas CCSSI 1º Bachillerato 1
 Tema 8 - Estadístca - Matemátcas CCSSI 1º Bachllerato 1 TEMA 8 - ESTADÍSTICA 8.1 NOCIONES GENERALES DE ESTADÍSTICA 8.1.1 INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para
Tema 8 - Estadístca - Matemátcas CCSSI 1º Bachllerato 1 TEMA 8 - ESTADÍSTICA 8.1 NOCIONES GENERALES DE ESTADÍSTICA 8.1.1 INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para
Mecánica del Sólido Rígido
 Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Mecánca del Sóldo Rígdo 1.- Introduccón Cnemátca, Dnámca y Estátca 2.- Cnemátca. Tpos de movmento del sóldo: Traslacón, Rotacón Movmento Plano General Movmento General 3.- Cnétca. Fuerzas y aceleracones.
Conceptos fundamentales de Termodinámica
 CAPÍTULO Conceptos fundamentales de Termodnámca ESQUEMA DEL CAPÍTULO. Qué es la Termodnámca y por qué es útl?. Defncones báscas necesaras para descrbr los sstemas termodnámcos.3 Termometría.4 Ecuacones
CAPÍTULO Conceptos fundamentales de Termodnámca ESQUEMA DEL CAPÍTULO. Qué es la Termodnámca y por qué es útl?. Defncones báscas necesaras para descrbr los sstemas termodnámcos.3 Termometría.4 Ecuacones
Ejercicio nº 1. a) Elabora una tabla de frecuencias. b) Representa gráficamente la distribución.
 Ejercco nº En una empresa de teleonía están nteresados en saber cuál es el número de aparatos teleóncos (ncludos teléonos móvles) que se tene en las vvendas. Se hace una encuesta y, hasta ahora, han recbdo
Ejercco nº En una empresa de teleonía están nteresados en saber cuál es el número de aparatos teleóncos (ncludos teléonos móvles) que se tene en las vvendas. Se hace una encuesta y, hasta ahora, han recbdo
Es el movimiento periódico de un punto material a un lado y a otro de su posición en equilibrio.
 1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
