1 Magnitudes y circuitos eléctricos.
|
|
|
- Óscar Montes Godoy
- hace 6 años
- Vistas:
Transcripción
1 Magntudes y crcutos eléctrcos.. Introduccón Alguna vez nos habremos preguntado porqué funconan como lo hacen los aparatos de rado, las calculadoras de bolsllo, o los ordenadores. Estas máqunas, y muchas otras, utlzan la energía eléctrca y nos ayudan a realzar determnadas tareas, o smplemente nos entretenen. Sabemos que en su nteror hay crcutos eléctrcos, que conssten en una sere de componentes undos por cables, que procesan o tratan, de una manera prefjada, certa nformacón codfcada en forma de campos eléctrcos y magnétcos. La manera en que hay que unr (o conectar) dchos componentes, e ncluso la eleccón de los componentes electróncos a conectar, para que el crcuto resultante funcone conforme a nuestros deseos es, en últma nstanca, el objetvo de la electrónca. El propósto de estas notas es apoyar el aprendzaje de los fundamentos de la electrónca. Nos centraremos en el análss de los crcutos electróncos. O sea, deberemos aprender a predecr cómo funconará un determnado crcuto electrónco s conocemos cómo está realzado. En otros cursos se estará en dsposcón de sntetzar un crcuto: elegr los componentes y la manera de conectarlos de modo que el resultado sea un crcuto que funcone conforme a determnadas especfcacones de partda. Este prmer capítulo es marcadamente ntroductoro. En él se presentan conceptos y magntudes fundamentales de teoría de crcutos. Trataremos de dar un sentdo precso a lo que se entende por componente electrónco y crcuto eléctrco. Tambén aprenderemos técncas para predecr el funconamento de estos crcutos.. Objetvos del tema El tema se dstrburá en 9 partes cuyos objetvos pasamos a descrbr a contnuacón Presentacón de las magntudes fundamentales que van a ser la base del estudo de la asgnatura, se defnen la corrente eléctrca, la tensón y la potenca. De momento estas magntudes son abstractas sn relacón entre ellas Interrelacón entre las magntudes fundamentales para los dspostvos pasvos báscos como son la resstenca el condensador y el nductor. Introduccón a los conceptos que defnen estos componentes a partr de las relacones para cada uno de ellos de las magntudes
2 fundamentales. Tambén son objetvos mportantes la presentacón de los símbolos de cada uno de los componentes tanto actvos (fuentes) como pasvos El sguente objetvos es ver como las relacones entre magntudes fundamentales se solapan para pasar de los componentes a los crcutos. Presentacón de las leyes de Krchoff. Como objetvo ddáctco se presentan las relacones entre la corrente y la tensón de forma gráfca para resstencas, fuentes de almentacón y conjuntos de ambos. Defncón de crcuto equvalente Thevenn y Norton. Este es otro objetvo fundamental que se presenta ahora pero que se ra afanzando a los largo del curso. Todos los objetvos vstos hasta ahora partían de stuacones estátcas, se ntroduce el concepto de señal varable en el tempo Una vez ntroducdo el concepto de señal varable se llega al análss somero de crcutos ya no sólo compuestos de resstencas y fuentes sno tambén condensadores e nductores. Concepto de mpedanca. El últmo objetvo de este tema es la ntroduccón de las fuentes dependentes deales para completar todas las posbldades a falta de ntroducr más adelante los componentes no lneales..3 Magntudes fundamentales. Hemos dcho que exsten unas entdades, llamadas crcutos eléctrcos, capaces de tratar campos eléctrcos y magnétcos. Los campos eléctrcos y magnétcos caracterzan a una de las cuatro fuerzas conocdas en la naturaleza: la fuerza electromagnétca (las otras tres son la gravtatora, la nuclear fuerte y la nuclear débl). Así como la masa gravtatora, por ejemplo, es la causa que produce la aparcón de las fuerzas gravtatoras, la carga eléctrca es la causa que produce los campos electromagnétcos (en reposo produce fenómenos eléctrcos puros y en movmento produce tambén fenómenos magnétcos). Como en determnadas ocasones trataremos con efectos cas puramente eléctrcos y, en otras, nos nteresarán los efectos cas puramente magnétcos, necestamos defnr una cantdad responsable de los efectos magnétcos puros en lugar de hacer referenca a cargas en movmento (es más fácl así), esta cantdad será el flujo magnétco. En lo que sgue daremos detalles de estas magntudes, de otras que se dervan de ellas y algunas de sus característcas.
3 .3. Carga eléctrca. Corrente eléctrca. La carga eléctrca es la responsable de la exstenca de los campos eléctrcos. La cantdad de carga contenda en un objeto (q) se mde en Culombos (C) en el Sstema Internaconal de undades. Así, cuanto mayor sea la carga de un objeto más ntensos serán los efectos eléctrcos que produzca. En la naturaleza se encuentran dos tpos dstntos de cargas eléctrcas, las postvas y las negatvas. Además la carga total contenda en un objeto es sempre un múltplo entero de la cantdad fundamental C, que es la carga contenda en un protón, o, cambada de sgno, la que posee un electrón. El movmento de las cargas, o con mayor generaldad, la varacón con el tempo de la cantdad de carga presente en certo lugar se denomna ntensdad de corrente eléctrca (), y se calcula dervando la carga frente al tempo, dq dt La corrente es tambén una magntud fundamental. La undad de la corrente eléctrca en el Sstema Internaconal es el Ampero (A). Esta magntud caracterza el movmento de las cargas. Una buena magen de la corrente eléctrca es la del agua líquda crculando por un crcuto hdráulco y atravesando dversos dspostvos que son los elementos de crcuto: tuberías, bombas de mpulsón, recpentes, curvas. Este flujo de agua se especfca asgnando un sentdo de movmento de la msma. En el caso de la corrente eléctrca tambén deberemos asgnar un sentdo a esta crculacón que, tradconalmente, concde con el movmento de las cargas postvas. Esto se hará utlzando una flecha. Algunos materales permten la crculacón de la corrente eléctrca con mayor facldad que otros. Aquellos para los que el paso de las cargas es "fácl" se denomnan buenos conductores y suelen ser metales. Por el contraro los que presentan una gran dfcultad al paso de la corrente, es decr, los malos conductores se llaman aslantes..3. Flujo magnétco. Tensón eléctrca. Análogamente a la carga, el flujo magnétco (ϕ) se puede nterpretar como el agente que caracterza los campos magnétcos. Su undad en el Sstema Internaconal es el Weber (Wb). La varacón con el tempo del flujo magnétco se denomna tensón eléctrca (v), s esa varacón es constante tambén se puede llamar potencal eléctrco. Es decr 3
4 v dϕ dt La undad de la tensón eléctrca en el Sstema Internaconal es el olto (). La tensón eléctrca es una magntud fundamental. El valor de la tensón se puede magnar como la altura de un salto de agua en el modelo del crcuto hdráulco, como algo proporconal a la energía del líqudo en el crcuto. Para ndcar el sentdo en que el líqudo es mpulsado se utlzarán sgnos + y - de modo que desde el punto ndcado con + hasta el ndcado con menos "cae" el agua. Este sentdo de la caída se ndca en los crcutos eléctrcos expresando la "polardad" con sgnos + y. Colocaremos el sgno + donde la tensón eléctrca sea mayor. La caída de tensón se mde sempre respecto a un valor de referenca. Sólo tene sentdo hablar de caída de tensón o de dferenca de potencal y cuando dgamos que la tensón en tal o cual elemento es tanto debe estar clara la referenca. La referenca puede ser un punto del propo elemento o uno stuado en algún lugar del resto del crcuto eléctrco..3.3 Potenca y energía eléctrcas. La medda de la energía eléctrca consumda o entregada por un elemento en la undad de tempo se realza evaluando la potenca eléctrca. Su expresón es p v donde p es la potenca eléctrca medda en Watos (W) que, en general, depende del tempo. S la potenca calculada para un elemento, en certo ntervalo de tempo, es postva dcho elemento está absorbendo energía del resto del crcuto, es decr la consume (esta energía transferda se dspará en forma de calor o se almacenará). S la potenca resulta negatva, el elemento entrega energía al crcuto en ese ntervalo de tempo. Conocda la potenca, la energía ntercambada (E) se evalúa a partr de la propa defncón de potenca escrta en forma ntegral de p dt E t 0 p dτ S el valor de esta ntegral es postvo se dce que el elemento es pasvo: consume energía; s la ntegral resultase negatva se dce que el elemento es actvo: entrega energía. 4
5 Es frecuente utlzar valores medos para expresar la potenca ntercambada por un determnado elemento..4 Teoría de crcutos eléctrcos..4. Elementos de crcuto: relacones consttutvas En los apartados anterores se han defndo las magntudes fundamentales de la teoría de crcutos: carga (q), tensón (v), flujo magnétco (ϕ) y corrente () Estas cuatro magntudes dan cuenta de la presenca de fenómenos eléctrcos y magnétcos en los crcutos. El lugar en que se encuentren, o mejor dcho, el medo y la forma del materal en que estén defndas, ejerce una nfluenca muy mportante sobre ellas hacendo que, en determnadas ocasones estén relaconadas unas con otras. S el medo mpone algún tpo de relacón matemátca entre las magntudes, dcha relacón se denomna ecuacón consttutva del medo. En este apartado nos preguntamos por ellas. Así por ejemplo, estarán relaconadas en algún medo la carga y la tensón eléctrcas?. S dcha relacón exstese podríamos escrbr una ecuacón que lgue ambas magntudes. Esa ecuacón será, en general, del tpo qf(v) donde f() representa a una funcón cualquera. En este caso dcha funcón se llama capactor. Además s la f() es lneal, entonces q y v serán proporconales q C v donde C será una constante de proporconaldad. Esta relacón se llamará capactor lneal y la constante se denomna capactanca del capactor. La undad de la capactanca es el Farado (F). Esta relacón se consgue en la práctca con determnadas estructuras consstentes en dos conductores muy próxmos separados por un materal aslante. Dcha estructura se denomna, coloqualmente, condensador y es uno de los elementos que pueden utlzarse al realzar un crcuto electrónco. La ecuacón consttutva de los capactores se puede expresar en térmnos de correntes y tensones sn más que tomar dervadas respecto al tempo y tener en cuenta la defncón de la corrente dq d ( C v) dv C dt dt dt s C no depende del tempo. 5
6 Segumos buscando relacones entre las magntudes fundamentales y nos preguntamos ahora por la exstenca de algún medo que establezca una relacón entre la tensón y la corrente eléctrca. S dcha relacón exstese escrbríamos vf(). Al gual que en el caso anteror f() puede adoptar cualquer forma. Una funcón de ese tpo se llama resstor. S es lneal, entonces v e serán proporconales v ecuacón que se denomna ley de Ohm. Llamaremos a esta relacón resstor lneal y la constante de proporconaldad, que se smbolza por la letra, resstenca del resstor. La undad de la resstenca es el Ohmo (Ω). Esta relacón se consgue en la práctca hacendo pasar la corrente eléctrca por materales que no son buenos conductores. La resstenca de un elemento mde la dfcultad que éste opone al paso de la corrente eléctrca a su través. Para el resstor podemos escrbr v G v La nversa de la resstenca, que se suele smbolzar con la letra G, se denomna conductanca. Su undad es el mhos o Semens, la undad nversa del Ohmo. Fnalmente hablaremos de la relacón que puede mponer el medo entre el flujo magnétco y la corrente eléctrca. Es decr, nos preguntamos por la exstenca de una funcón tal que ϕf(). Exsten estos elementos de crcuto y su nombre más general es el de nductores. De nuevo, s la funcón es lneal, entonces ϕ L y se trata de nductores lneales. L es la nductanca medda en Henros (H). Estos elementos se suelen fabrcar medante arrollamentos de materales conductores, tambén se les denomna bobnas. La ecuacón consttutva de los nductores se puede expresar en térmnos de correntes y tensones sn más que tomar dervadas respecto al tempo y tener en cuenta la defncón de la tensón d d(l ) d v ϕ L dt dt dt en la anteror ecuacón se asume que L no depende del tempo. 6
7 Podríamos establecer aún otras tres relacones entre varables. Una es la relacón entre la carga y la corrente, otra es la que relacona el flujo magnétco y la tensón, y la tercera relacona la carga y el flujo magnétco. La prmera de ellas es una de las ecuacones fundamentales: carga y corrente eléctrca se relaconan por una dervada. Por otro lado el flujo magnétco están relaconadas medante otra de las llamadas ecuacones fundamentales, en partcular con la utlzada para defnr la tensón eléctrca. Con la últma se defnrían unos elementos de crcuto denomnados memrstores, pero no tenen aplcacón práctca. Exsten, además, unos elementos de crcuto que sumnstran una corrente fja con ndependenca de la tensón que caga en ellos. Estos elementos se llaman fuentes ndependentes de corrente y se caracterzan por la ecuacón consttutva sendo I un valor que no depende de la tensón. I Otros elementos, las fuentes ndependentes de tensón, establecen una caída de tensón fja en los lugares donde se conectan, con ndependenca de la corrente que fluya por ellos. La relacón consttutva de las fuentes ndependentes de tensón es donde es ndependente de la corrente. v En el síml hdráulco ambas fuentes serían las bombas de mpulsón del agua en el crcuto, esta mpulsón se logra a costa de certo consumo de energía. Hay fuentes en las que la corrente o tensón puede depender de otra varable del crcuto que se llaman fuentes controladas o dependentes, a ellas nos referremos más adelante..4. Símbolos de crcuto. En el apartado anteror hemos defndo las relacones consttutvas de los resstores lneales (resstencas), capactores lneales (condensadores) e nductores lneales (bobnas). Además de dchas relacones es precso conocer una sere de símbolos utlzados para ndcar la presenca de estos elementos en los crcutos bajo estudo. Junto a los símbolos se debe ndcar la "polardad" de la tensón (medante sgnos + y - que asgnamos al elemento para ndcar la manera en que cae la tensón) y la ntensdad de la corrente (medante una flecha). 7
8 Los símbolos de crcuto de las resstencas, los condensadores, las bobnas y las fuentes ndependentes son los ndcados en la Fgura -. Para las fuentes de tensón ndcamos dos símbolos alternatvos. Las ecuacones consttutvas, tal y como han sdo escrtas, son correctas cuando la polardad y la corrente son las ndcadas en la fgura correspondente. Nótese que para las resstencas, los condensadores y las bobnas, la corrente "entra" por el termnal "+" del elemento, mentras, para las fuentes la corrente "sale" por el termnal "+". Esta eleccón tene que ver con la manera en que estos elementos ntercamban energía con el resto del crcuto, ya que los tres prmeros son elementos pasvos y los dos últmos son actvos. Fgura -. Símbolos de crcuto..4.3 Crcutos eléctrcos. Un crcuto eléctrco es la conexón, medante conductores (cables), de dstntos elementos. En la Fgura - se muestra un crcuto, y en la Fgura -3 se muestra otro con la msma "topología" (o forma) que el anteror (en éste los elementos son genércos). Las cajas, referencadas con letras mayúsculas, representan a cualquera de los elementos vstos: resstencas, condensadores, bobnas, fuentes ndependentes de ntensdad y fuentes ndependentes de tensón. Fgura -. Crcuto eléctrco. 8
9 Fgura -3. Crcuto genérco. Las líneas contnuas que unen los dstntos elementos representan los conductores que conectan eléctrcamente los dstntos elementos del crcuto. En estos cables no cae tensón alguna. Los puntos en los que se conectan dos o más elementos del crcuto se denomnan nudos. En nuestro crcuto hay exactamente cnco nudos ndcados con los números del al 5. El nudo 4, por ejemplo es un punto que conecta eléctrcamente a 4 elementos, los C, D, F y G. Es un error muy común nterpretar que en las proxmdades del nudo 4 hay otros nudos separados de éste exclusvamente por cables. Desde el punto de vsta eléctrco todos los puntos que estén undos por el msmo cable son equvalentes, así el nudo 4 podría haberse dbujado debajo del elemento C, debajo del G o en cualquer otro lugar de ese cable aunque no sea un "ángulo". De modo que dos nudos son dstntos s entre ellos hay algún elemento (alguna caja). Algo smlar podría decrse del nudo 3. Llamaremos nudo smple a aquel nudo que conecta sólo a dos elementos y nudos prncpales a los que conectan a más de dos elementos. Puede ocurrr que en un determnado crcuto nos muestren algún elemento que no esté conectado a otro, en ese caso hablaremos de nudo termnal. En nuestro crcuto son nudos smples los y 5 y son prncpales el resto. No hay nudos termnales. Una rama es cualquer camno que conecte dos nudos sucesvos. Es decr, una rama está consttuda por un par de nudos y un solo elemento de crcuto. El concepto de rama se puede extender para abarcar más de un elemento s los nudos que se ncluyen son todos smples. Llamaremos bucle a cualquer camno cerrado que pueda trazarse en un crcuto a condcón de no pasar más de una vez por un msmo elemento. Como su nombre ndca un camno cerrado es el conjunto de ramas y nudos recorrdos partendo de un nudo arbtraro y volvendo a él. En el crcuto de las cajas hay tres bucles que contenen al nudo : el prmer bucle está formado por los elementos B, C, D y A, el segundo por los B, E, F, D y A, y el tercero contene a B, E, G, D y A. 9
10 Una malla es un bucle que no contene ramas en su nteror. En el crcuto de la Fgura -3 hay tres mallas que contenen los elementos sguentes: malla : A, B, C y D malla : C, E y F malla 3: F y G. Como paso prevo al análss de cualquer crcuto deberemos asgnar unas polardades a cada elemento y un sentdo a las correntes en las ramas. La asgnacón es arbtrara, sn embargo es útl acostumbrarse a respetar el que las correntes salgan por el nudo + de las fuentes (elementos actvos) y entren por el nudo + a las resstencas, condensadores y bobnas (elementos pasvos). En la Fgura -4 se asgnan polardades y sentdos para las correntes. Fgura -4. Asgnacón de polardades a las tensones y sentdos de corrente..5 elacones topológcas: leyes de Krchoff. Dos leyes dervadas de la teoría electromagnétca nos van a permtr analzar los crcutos eléctrcos. Estas leyes son rgurosamente váldas sólo cuando nnguna de las correntes o tensones presente varacones con el tempo. Sn embargo para un buen número de aplcacones son muy precsas, ncluso cuando hay varacones más o menos rápdas (frecuencas bajas y moderadas) de las señales de corrente o tensón. La prmera es una expresón de que el campo electrostáctco es conservatvo. Se denomna ley de Krchoff de las tensones (en nglés se abreva por KL) y se enunca así: "La suma algebraca de las tensones de los elementos de un crcuto en un bucle es nula". La palabra "algebraca" expresa la necesdad de tener en cuenta las polardades al realzar la suma. Por ejemplo en el crcuto de la Fgura -4 elegmos las tres mallas para escrbr 0
11 v a v c v f + v b + v e + v + v + v g c f 0 + v d 0 0 en cada malla se elgen arbtraramente un nudo de partda y un sentdo para escrbr la ecuacón. Al recorrer la malla en el sentdo elegdo se consgna en la ecuacón el sgno de la tensón por el que se alcanza el elemento de crcuto. Podemos escrbr muchas ecuacones, pero sólo unas pocas son ndependentes. El número de ecuacones ndependentes concdrá con el número de mallas del crcuto. Esto no es completamente general, es certo para los crcutos planares y conexos, a esa clase pertenecen todos los que aquí se proponen. Los detalles se estudarán en cursos posterores. La segunda le expresa el prncpo de conservacón de la carga. Se trata de la ley de Krchoff de las ntensdades (KCL): "La suma de las correntes que entran en un nudo es gual a la suma de las correntes que salen de él". Para el crcuto del ejemplo tenemos que al nudo 4, por ejemplo, entran las correntes c, f e g y sale la corrente d, con esto se puede escrbr + + c f g d Para los nudos restantes, +, +, a b b c e e f g d a Una vez planteadas las ecuacones topológcas (que son las dervadas de las leyes de Krchoff) se debe hacer uso de las consttutvas para determnar las tensones y correntes de nterés..5. Método de análss por nudos. En este apartado y en el sguente vamos a presentar dos métodos sstemátcos de análss de crcutos; conssten en una sere de pasos a segur para llegar a la resolucón de un crcuto. esolver un crcuto quere decr expresar los valores de todas las correntes en las ramas y las tensones que caen en todos sus elementos. El método de análss por nudos utlza como ncógntas las tensones en todos los nudos del crcuto. Dado un crcuto, el procedmento de análss por mallas consste en lo sguente
12 Prmero: elegr un nudo de referenca al que llamaremos terra. El nudo terra puede ser cualquera. Es convenente, sn embargo, elegr aquél en que se nterconecten más elementos de crcuto. A este nudo asocaremos la tensón de referenca, es decr le asgnamos el valor de tensón nulo. Segundo: enumerar el resto de los nudos del crcuto y defnr las tensones en los nudos. Estas tensones son las que caen entre cada uno de los nudos y el de terra. Tercero: elegr polardades para cada elemento del crcuto y asgnar un sentdo a las correntes en las ramas que sea coherente (s es posble) con las polardades elegdas (la corrente entra por el nudo + en los elementos pasvos y sale por el nudo + en los actvos). Cuarto: escrbr las ecuacones dervadas de la ley de Krchoff de las ntensdades en los nudos enumerados, expresando las ntensdades en funcón de las tensones en los nudos medante las ecuacones consttutvas de los elementos. Las fuentes de tensón ntroducen datos en las ecuacones. S en el crcuto hubese alguna fuente de corrente se ntroduce una ecuacón adconal que expresa el valor conocdo de la corrente en esa rama. Qunto: resolver el sstema de ecuacones. Como ejemplo del método resolveremos el crcuto de la Fgura -5 en el que son conocdos los valores de todas las resstencas y fuentes ndependentes. Este crcuto es bastante general en el sentdo que contene los dos tpos de fuentes ndependentes conocdos. Fgura -5. Aplcacón del método de análss por nudos. El nudo de terra en nuestro ejemplo será el que está en la parte nferor del esquemátco del crcuto pues en él se unen cuatro elementos. En la Fgura -6 repetmos la anteror ntroducendo un símbolo especal para ndcar que este nudo es el de terra.
13 Fgura -6. Enumeramos los nudos restantes y resulta que tenemos sete. De ello dos son prncpales y cnco son smples. Asocamos las tensones en los nudos,, 3, 4, 5, 6 y 7 que serán las ncógntas a determnar (Fgura -7). Es decr, tendremos que escrbr sete ecuacones utlzando las leyes de Krchoff. Fgura -7. Dbujamos arbtraramente las polardades en todos los elementos. Aunque tengamos plena lbertad para decdr las polardades es aconsejable ser metódco y acostumbrarse a determnadas reglas de conducta, es usual decdr que las tensones caerán de zquerda a derecha y de arrba abajo, con ello las tensones caen como se ndca en la Fgura -8. Fgura -8. 3
14 Conforme a la regla ndcada en el parágrafo anteror, para asgnar el sentdo de las correntes basta dbujarlas en cada nudo fluyendo de zquerda a derecha o de arrba abajo (Fgura -9). Fgura -9. Fnalmente escrbremos en prmer lugar las ecuacones que relaconan las tensones en los nudos con los valores conocdos de las tensones de las fuentes de tensón con KL, para el nudo tenemos y para el nudo 5 A + B 5 6 la prmera de éstas expresa que la caída de tensón desde el nudo hasta terra es justamente la que fuerza la fuente A. La segunda ecuacón contene un sgno menos delante de B porque la polardad que hemos asgnado a esta fuente es contrara a la que realmente tene. Escrbmos ahora las ecuacones dervadas de KCL para los nudos, 3 y 4 (el resto de los nudos se tratan más adelante). amos a escrbr relacones entre correntes pero expresadas en térmnos de las tensones en los nudos, estas correntes son cocentes entre caídas de tensón (respetando las polardades) y valores de resstencas (ley de Ohm). La ecuacón para el nudo es La correspondente al nudo 3 resulta ser Y para el nudo 4 tenemos que 4
15 La corrente en la rama que contene al nudo 7 es la opuesta a la que fja la fuente, por ello escrbmos I A el sgno negatvo delante de I A expresa el hecho ndcado. La presenca entre los nudos 5 y 6 de una fuente de tensón mpde expresar en térmnos de tensones el valor de la corrente que entra al nudo 6. Sn embargo, medante la observacón del crcuto podremos relaconar esta corrente con la que fluye por otros elementos. En este caso la corrente de rama es la que pasa por la resstenca 5, de modo que En resumen, hemos escrto un conjunto de sete ecuacones con sete ncógntas. La solucón de este sstema arroja el valor de todas las tensones en los nudos y con ellas se pueden calcular todas las correntes de rama o las caídas de tensón en cada elemento..5. Método de análss por mallas. Con este método expresaremos el sstema de ecuacones algebracas en funcón de las correntes de malla. Estas correntes son las que fluyen por cada una de las mallas de un crcuto. El procedmento a segur consste en Prmero: determnar las mallas del crcuto y defnr las correntes de malla asgnándoles un sentdo arbtraro. Estas correntes serán las ncógntas a determnar. Segundo: escrbr las ecuacones de la ley de Krchoff de las tensones para cada una de las mallas del crcuto en funcón de las correntes de malla, recorrendo cada malla en el sentdo ndcado por la corrente de malla correspondente. La corrente que fluye por un elemento es la suma algebraca de las correntes de las mallas a las que pertenezca. S hubese alguna fuente de tensón se utlza su valor y s es de corrente se expresa la relacón entre su valor y las correntes de malla para elmnar una ncógnta. Tercero: resolver el sstema ecuacones
16 esolvemos ahora el msmo crcuto del apartado anteror utlzando este método. El crcuto posee tres mallas a las que asgnamos las correntes a, b e c. El sentdo de las msmas es arbtraro (Fgura -0). Fgura -0. Para escrbr las ecuacones KL en la malla la recorremos desde el nudo de terra y en el sentdo de a. Hemos de tener en cuenta las polardades de las fuentes para decdr el sgno que lleva su tensón en la ecuacón. S en el sentdo de recorrdo de la malla entramos por el termnal postvo colocaremos un sgno + en la ecuacón, s entramos por el negatvo colocaremos un sgno -. Con esto A + a + ( a b) 4 + IA 0 notamos que la corrente que fluye por la resstenca 4 es a - b cuando recorremos esta rama desde arrba haca abajo. Se escrbe así porque a baja (postva pues su sentdo es a favor del de recorrdo) e b sube (negatva por la razón contrara), esto es el sgnfcado de suma algebraca. Por otro lado, la caída de tensón en la fuente de corrente es una ncógnta adconal, IA, sn embargo podemos escrbr la sguente ecuacón I I + a b ecorremos la malla empezando de nuevo por el nudo de terra, resulta la ecuacón Fnalmente la ecuacón KL de la malla 3 es -IA + (b-a ) c ) c A b 4 + b + (b + c )5-B + (b c3 + (c + b )5-B + (b + c )7 Hemos escrto un sstema de cuatro ecuacones en las ncógntas a, b, c y IA. Su solucón permte el cálculo de todas las magntudes eléctrcas de crcuto. A a 0 0 6
17 Con el ejemplo planteado parece que el método de análss por mallas es más smple que el de nudos, pero esto no es sempre así. Depende de la forma y la consttucón de los crcutos..6 Curvas característcas -v. Hemos caracterzado los elementos de crcuto por sus ecuacones consttutvas. En el caso de los resstores ésta es una ecuacón que expresa la relacón que lga a la corrente y la tensón. La representacón gráfca de dcha ecuacón en un dagrama v- es lo que llamaremos curva característca -v del elemento. Tambén se puede hablar de otras curvas característcas como las q-v o las ϕ-. Pero en esta seccón nos ocuparemos de las prmeras pues son las que más se utlzan. Hemos descrto la resstenca por v esta ecuacón está representada en la Fgura -. Se trata de una línea recta con pendente - que pasa por el orgen del dagrama v-, observamos que cuanto mayor es el valor de la resstenca menor es el de la pendente. Fgura -. Característca -v de una resstenca. En la Fgura - mostramos la curva característca de las fuentes de tensón, cuya ecuacón consttutva es v v D donde 0 no depende de la corrente. Nótese que se trata de nuevo de una línea recta, pero esta vez vertcal, corta al eje v en v D. 7
18 Fgura -. Característca -v de una fuente ndependente de tensón. Para el caso de la fuente ndependente de ntensdad, que posee la ecuacón consttutva I D sendo I D un valor ndependente de la tensón. La curva característca -v es una línea recta horzontal (Fgura -3). Ambos tpos de fuentes son resstores en el sentdo que poseen una curva característca -v. Fgura -3. Característca -v de la fuente ndependente de corrente. Observemos de nuevo la ecuacón consttutva de la resstenca y hagamos tender a nfnto. En ese caso la curva característca que obtendríamos es una línea horzontal (el eje v, esto es 0), ya que la pendente sería cero. Un elemento así permte que entre sus termnales la caída de tensón sea cualquera pero la corrente que fluye a su través es sempre nula. Una resstenca de valor nfnto mpde el paso de la corrente y se llama crcuto aberto. Podemos smbolzar el crcuto aberto tal y como se ndca en la Fgura -4. Análogamente una resstenca de valor nulo tendría una pendente nfnta y su característca -v es una línea vertcal (el eje, osea v0). Este otro elemento se denomna cortocrcuto y permte que fluya cualquer corrente a su través a condcón que la caída de tensón sea nula. Un cortocrcuto es un cable. 8
19 9 Fgura -4. Crcuto aberto. Tambén podemos construr curvas característcas -v de la asocacón de varos elementos resstvos. Es decr, de crcutos que contengan fuentes y resstencas. Podemos ver esto analzando el subcrcuto resstvo del crcuto de la Fgura -5 en el que son conocdos los valores de, y. Fgura -5. Dcho subcrcuto se traza de nuevo en la Fgura -6 y los nudos y pasan a ser nudos termnales, admtremos que por el nudo entra certa corrente. Por la ley de Krchoff de las tensones, consderando las ecuacones consttutvas de las resstencas v v b b b a b a Fgura -6. Aplcando ahora la ley de Krchoff de las ntensdades al nudo, junto con las anterores v v v a b b a
20 que es la característca -v buscada. Esta expresón es la línea recta con pendente y con ordenada en el orgen + mostrada en la Fgura -7. Esta ecuacón descrbe completamente el funconamento del crcuto. S hacemos, por ejemplo, Ω, tenemos que la ecuacón es v Fgura Crcutos equvalentes. Consderaremos ahora la sguente cuestón: será posble que dos crcutos dstntos funconen exactamente gual?. eremos que la respuesta es sí. Tales crcutos se dce que son equvalentes desde el punto de vsta eléctrco. Sea por ejemplo el crcuto de la fgura Fgura -8. Fgura -8. 0
21 De las leyes de Krchoff junto a las ecuacones consttutvas tenemos + a b a A v v b v esta ecuacón es la característca -v del crcuto de la Fgura -8. esulta ser exactamente gual a la del últmo crcuto del apartado anteror. Por lo tanto estos dos crcutos funconan exactamente gual y son equvalentes. En el próxmo apartado veremos técncas generales de cálculo de crcutos equvalentes cuando se trate de redes resstvas. La utldad de este concepto estrba en que nos permte smplfcar mucho el análss de determnados crcutos..7. Asocacón de resstencas en sere. S varos elementos de crcuto están conectados de manera que la corrente que fluye por todos ellos es la msma, esto es s los elementos se conectan unos con otros medante nudos smples, entonces están en sere. Fgura -9. esstencas en sere. En el crcuto de la Fgura -9 tenemos n resstencas conectadas en sere. Es claro, por la ley de Krchoff de las ntensdades aplcada a cada nudo que las correntes que fluyen a través de cada una de ellas es la msma, sea esta corrente n k, k,,, n Por otro lado, aplcando la ley de Krchoff de las tensones tenemos que v v + v + + v v n n v k k como quera que para la resstenca k se tene que vk k k, k,,, n podemos escrbr
22 v n k k n k s hacemos ahora n T k habremos escrto la ecuacón de una únca resstenca de valor la suma de todas cuya curva característca es la msma que la asocacón de todas las que están conectadas en sere. Por lo tanto la resstenca T es equvalente al crcuto completo. Conocda esta resstenca equvalente a la asocacón en sere podemos susttur todas aquellas por una sola. Esto smplfca los cálculos necesaros para resolver los crcutos. Sn embargo perdemos los detalles de cada una de ellas por separado, es decr, s nos preguntan por la caída de tensón, la corrente o la potenca dspada en una de las resstencas orgnales no podremos responder a la pregunta mas que volvendo al crcuto orgnal y hacer cálculos adconales..7. Asocacón de resstencas en paralelo. aros elementos de crcuto están conectados en paralelo s la tensón que cae en todos es la msma. Esto se consgue hacendo que estén conectados entre los msmos nudos del crcuto. Fgura -0. esstencas en paralelo. El crcuto de la Fgura -0 está consttudo por n resstencas conectadas en paralelo. Es claro, por la ley de Krchoff de las tensones aplcada a cada camno cerrado que podamos trazar que las tensones que caen en cada resstenca son las msmas, sea v esta tensón v v v vn v vk, k,,, n Por otro lado, aplcando la ley de Krchoff de las correntes tenemos que n n k k como quera que para la resstenca k se tene que
23 vk k k podemos escrbr n vk k v n k s hacemos ahora n T habremos escrto la ecuacón de un únca resstenca cuya nversa es la suma de las nversas de todas y cuya curva característca es la msma que la asocacón de todas las que están conectadas en paralelo. Por lo tanto la resstenca T es equvalente al crcuto completo. Como djmos en el apartado anteror es muy mportante tener presente que esta resstenca contene la nformacón del conjunto de resstencas que representa pero no los detalles de cada una de ellas..7.3 esstenca equvalente. En los dos apartados anterores hemos calculado la resstenca equvalente en confguracones partculares: la asocacón en sere y en paralelo. Ahora generalzaremos el concepto y expondremos un método de cálculo de la resstenca equvalente de una sere de resstencas conectadas arbtraramente (no sólo en sere o en paralelo). Para ello consderaremos un crcuto consttudo por fuentes y resstencas conectadas de cualquer manera. Para calcular la resstenca equvalente tendremos que ndcar un par de nudos que consderaremos termnales y desde los que realzaremos el cálculo de dcha resstenca equvalente. Pronto comprobaremos que la resstenca equvalente de un crcuto no tene que ser la msma desde cualquer par de nudos termnales. Por lo tanto sempre deberemos especfcar el par de nudos desde el que vemos esa resstenca equvalente. De modo que tenemos un crcuto cualquera con dos nudos termnales como el de la Fgura -. k 3
24 Fgura -. El procedmento de cálculo consste en tres pasos que detallamos a contnuacón: Prmero: anular todas las fuentes ndependentes. Para ello susttumos las de tensón por cortocrcutos y las de corrente por crcutos abertos, (más adelante veremos otro tpo de fuentes llamadas controladas, éstas no se anulan) Segundo: conectar entre el par de nudos termnales una fuente ndependente de valor v x que entrega al crcuto una corrente x y analzar el crcuto resultante. Tercero: calcular el valor del cocente v T x x que es la resstenca equvalente buscada. Fgura -. Por ejemplo en el crcuto de la Fgura -. estamos nteresados en el cálculo de la resstenca equvalente vsta por la resstenca de Ω, sn nclurla. Por ello en prmer lugar dbujamos el crcuto sn dcha resstenca y anulamos las fuentes hacendo la de tensón un cortocrcuto y la de corrente un crcuto aberto. El crcuto resultante es el ndcado en la Fgura -3. Fgura -3 Ahora conectamos entre los nudos 3 y 5 una fuente de tensón de valor desconocdo v x y asummos que entrega una corrente x (Fgura -4). 4
25 Fgura -4 esolvemos el crcuto resultante + pero a 0 porque esta rama tene un crcuto aberto. De modo que de la ley de Krchoff de las tensones x a x b b v x + v 6 + v4 0 utlzamos ahora las ecuacones consttutvas de las resstencas nvolucradas con todo tenemos que v 6 6 x; v4 4 b v x vx 6 x + 4 x 0 x T 0Ω x Este ejemplo es muy sencllo, desde el nco podíamos ver que la resstenca equvalente es la asocacón en sere de las de 4Ω y 6Ω. Sn embargo es váldo para mostrar el procedmento de cálculo. Fgura -5 Mostramos ahora que desde otro par de termnales en el msmo crcuto podemos obtener una resstenca equvalente dstnta. Calculemos, por ejemplo, la resstenca que ve la fuente 5
26 ndependente de corrente. Para ello anulamos las fuentes y dbujamos de nuevo el crcuto resultante reorganzando la dsposcón de las resstencas. La nueva dstrbucón de los nudos es la psta que permte comprobar que la reorganzacón está ben hecha. Los nudos y 5 son ahora equvalentes porque hemos anulado la fuente de tensón. Los nudos termnales son el 4 y el 5, por tanto conectamos entre ellos una fuente de tensón de valor desconocdo v x y asummos que entrega una corrente x al resto del crcuto una corrente. El conjunto de ecuacones fruto de las leyes de Krchoff son x a + b a c ; v x v8 + v4; vx v8 + v6 + con las ecuacones consttutvas podemos escrbr por lo tanto x x b ; v v (6 + ) 4 8 x a b a b a x a vx 8 x + x x T Ω 3 valor que es dstnto al que anterormente encontrado..7.4 Los dvsores de tensón y de corrente. En este apartado nos ocupamos de dos crcutos que aparecen con bastante frecuenca en los problemas de análss y que es convenente conocer y recordar pues gracas a ello se ahorrará tempo en la solucón de algunos problemas. El prmero de ellos, que se llama dvsor de tensón, es el crcuto cuyo esquemátco es el de la fgura Fgura -6. Aclaramos que la corrente que fluye por la rama de la derecha, que llamaremos corrente de salda, es necesaramente nula, en otro caso este crcuto no sería un dvsor de tensón. Fgura -6 La justfcacón de este nombre se obtene calculando el valor de la tensón v, conocda por tensón de salda. Aplcando el método de análss por nudos escrbmos 6
27 A v v v + notamos que v tene por valor el de la fuente dvddo por la cantdad + que es mayor que la undad y por lo tanto v es sempre menor que A. El segundo crcuto es el dvsor de corrente que podemos ver en la Fgura -7. De nuevo en este caso la corrente de salda debe ser nula. A Fgura -7 Calculemos el valor de la corrente. Por KCL v v I + ; v A I + A luego el dvsor de corrente equvale a una fuente de corrente cuyo valor es el ndcado..8 Teoremas relatvos a los crcutos lneales. Llamaremos crcuto lneal a aquel crcuto consttudo por elementos lneales. En este momento la defncón parece no tener sentdo pues todos los elementos de crcuto que se han presentado son lneales: resstencas, condensadores, bobnas y fuentes ndependentes. Sn embargo en próxmos temas se verá que exsten determnados elementos cuya ecuacón consttutva es no lneal (su característca -v no es una línea recta que pasa por el orgen), para esos crcutos no es váldo lo que se presenta en esta seccón..8. Teorema de superposcón. S en un crcuto lneal hay más de una fuente ndependente (de tensón o de corrente) cualquer tensón o corrente del crcuto se puede calcular superponendo (sumando) los valores de dcha tensón o corrente calculados al r anulando todas las fuentes menos una hasta consderarlas todas. 7
28 Así, para calcular la tensón v en el nudo ndcado en el crcuto propuesto en el esquemátco mostrado en la Fgura -8 podríamos proceder medante el método de mallas o de nudos. Sn embargo, dado que hay tres fuentes ndependentes nos planteamos la aplcacón del teorema de superposcón. En prmer lugar nos preguntamos s este crcuto es lneal. Dado que sólo contene resstencas y fuentes ndependentes podemos asegurar que lo es. Fgura -8 Aplquemos el teorema de superposcón. Para ello tenemos que proceder en tres pasos, en cada uno de ellos anularemos dos fuentes de tensón y calcularemos el valor de la tensón pedda. Al fnal sumamos los valores obtendos en cada paso. amos a ello!. Anulamos B y C. El crcuto resultante es el de la Fgura -9. Fgura -9 Llamamos v a a la tensón que estamos calculando. Notamos que las resstencas y 3 están en paralelo, de modo que podemos asocarlas y el crcuto nos queda como el de la Fgura -30, donde el valor de la resstenca equvalente es 3 A + 3 8
29 9 Fgura -30 Pero este crcuto es un dvsor de tensón, por lo tanto A a a a v + Anulamos ahora A y C, el crcuto pasa a ser el mostrado en la Fgura -3. Fgura -3 Este crcuto lo podemos dbujar con la msma dsposcón del de la Fgura -9 y podemos verlo en la Fgura -3. Fgura -3 Tenemos entonces que resolver el msmo crcuto que antes pero ahora las resstencas y 3 están en paralelo. Calculamos la resstenca equvalente al paralelo de estas dos y obtenemos 3 3 b + De modo que el valor de la tensón buscada es B b b b v + Fnalmente anulamos A y B. Por razones obvas C c c c c v + + 3
30 Para termnar sumamos las tres tensones parcales que hemos obtendo y resolvemos el problema v v a + v b + v c a + a A b + + b B c c C Este ejercco nos ha permtdo comprobar la utldad del teorema de superposcón junto al conocmento de la expresón del dvsor de tensón. Hemos ahorrado bastante tempo en el cálculo..8. Teoremas de Thévenn y Norton. Sea un crcuto lneal consttudo por resstencas y fuentes ndependentes del que se selecconan un par de nudos termnales y como el de la Fgura -33que puede estar conectado a otro crcuto no necesaramente lneal. Fgura -33. Crcuto genérco. El teorema de Thévenn establece que dcho crcuto equvale a otro como el representado en la Fgura -34, consttudo por la asocacón en sere de una resstenca y una fuente de tensón. El valor de la resstenca E es el de la resstenca equvalente vsta desde los nudos termnales. El valor de la fuente de tensón, llamada tensón Thévenn ( Th ), se determna calculando la tensón que cae entre los nudos termnales, desde el nudo al nudo, cuando se hallan en crcuto aberto. Fgura -34. Crcuto equvalente Thévenn. El teorema de Norton, análogo al anteror, establece que el crcuto de la fgura Fgura -33 equvale a otro como el representado en la Fgura -35, consttudo por la asocacón en paralelo de una resstenca y una fuente de ntensdad ndependente. El valor de la resstenca es el msmo que en el caso del equvalente Thévenn. El de la fuente de corrente Norton (I N ) se determna calculando la 30
31 corrente que fluye entre los nudos termnales cuando están cortocrcutados. El sentdo de dcha corrente es desde el nudo al nudo. Este cálculo no es necesaro s la tensón Thévenn es conocda prevamente ya que el valor de la corrente Norton se puede calcular como I N Th E Fgura -35. Crcuto equvalente Norton. Como ejemplo de aplcacón calculamos el crcuto equvalente Thévenn de la parte recuadrada en la Fgura -36. Fgura -36. Crcuto para el cálculo del equvalente Thévenn. Obtengamos en prmer lugar la resstenca equvalente. Para ello debemos anular la fuente y calcular el valor de la resstenca vsta desde los nudos termnales. Al anular la fuente el crcuto queda como se ndca en la Fgura -37. Fgura -37. Crcuto para el cálculo de la resstenca equvalente. 3
32 En este caso, en lugar de ntroducr la fuente v x que entrega la corrente x, es más sencllo aplcar las expresones de la asocacón de resstencas sere/paralelo. emos que, y 3 están en sere y su asocacón se encuentra en paralelo con 4. Luego ( + + 3) E Para el cálculo la tensón Thévenn obtengamos la tensón v que cae entre los nudos termnales cuando éstos están en crcuto aberto (Fgura -38) Fgura -38. Crcuto para el cálculo de la tensón Thévenn. Por el método de análss por nudos I A Th Th 4 0 Y la solucón para la tensón Thévenn de este sstemas de ecuacones es 3 4 Th I A Th.9 Señales. Las fuentes ndependentes ya presentadas fjan, en el tempo, el valor de la tensón o la ntensdad. Sn embargo, podemos utlzar otras fuentes ndependentes de tensón (o de corrente) cuyo valor dependa del tempo. En ese caso las fuentes se denomnan de señal. Las señales exctan los crcutos y no es raro que un crcuto tenga a la vez fuentes ndependentes y fuentes de señal. En este apartado vamos a ndcar algunas de las posbles formas (llamadas formas de onda) en que pueden varar las exctacones, es decr, ndcaremos, para los casos más usuales, cómo dependen 3
33 las tensones o correntes del tempo. Pero antes de pasar a la descrpcón de las señales trataremos de dstngur dos grandes grupos de señales: las analógcas y las dgtales. Fgura -39. Señal analógca. Una señal analógca es aquella cuyos valores pueden ser todos los de un determnado ntervalo. Aclaremos esto. La señal de tensón v(t) de la Fgura -39 varía en el tempo de manera arbtrara. Los posbles valores que puede tomar se encuentran sempre entre, dgamos, 0 y 5 voltos. v(t) es analógca s todos los posbles valores de tensón desde el 0 hasta el 5 (en voltos) son dstntos para el crcuto en que opera. Así el crcuto responderá de dstnta manera s la tensón es.3 que s es de.4 o s es de.36. El concepto matemátco que está debajo de la dea de señales analógcas es el de funcón contnua en el tempo. Por últmo dremos que los crcutos que convven con señales analógcas (es mejor decr procesan señales analógcas ) se llaman crcutos analógcos. Fgura -40. Señal dgtal. Por contra, una señal dgtal no es contnua, es dscreta. Es decr, es la que sólo posee unos pocos valores dstngubles dentro de un ntervalo. S se trata de una señal dgtal bnara los valores dstngubles en el ntervalo que sea son dos. En la Fgura -40 se muestra una señal bnara en los 33
34 valores 0 y 5 voltos. S por cualquer fallo aparece el valor.4 el crcuto lo nterpretará como un 0. Los crcutos que operan con señales dgtales se llaman crcutos dgtales. Qué es mejor: analógco o dgtal?. Depende. Cada tpo de crcuto tene sus ventajas e nconvenentes. Algunas tareas se realzan mejor en el mundo analógco y otras en el dgtal..9. Señal escalón y señal cuadrada. La señal escalón y la señal cuadrada son deales. Esto quere decr que en la práctca no se pueden consegur. Aún así, resulta muy útl conocerlas y utlzarlas en los análss pues la cuadrada es la señal bnara por excelenca. La señal escalón se defne a partr de la llamada escalón untaro, u(t-t 0 ), que es una funcón cuya forma es la representada en la Fgura -4 y que se descrbe por u( t t 0 0 ) s s t < t t t 0 0 Fgura -4. Señal escalón untaro. Una señal escalón de salto A, esto es f tene la forma ndcada en la Fgura -4 ( 0 t) A u( t t ), 34
35 35 Fgura -4. Señal escalón de subda. Los escalones de bajada poseen un sgno menos delante del escalón untaro ) ( ) ( 0 t t A u t f Su forma está representa en la Fgura -43. Fgura -43. Señal escalón de bajada. Un pulso de ampltud A y duracón T 0 se defne como un escalón de subda (o bajada) segudo por otro de bajada (o subda). El de subda aparece en la Fgura -44. Fgura -44. Pulso de ampltud A. La expresón en funcón de señales escalón de ambos tpos de pulsos es [ ] [ ] ) ( ) ( ) ( ) ( ) ( ) ( T t t u t t u A t t p T t t u t t u A t t p Fnalmente una señal cuadrada es un tren de pulsos. Esta señal es peródca y su forma de onda se muestra en la Fgura -45.
36 Fgura -45. Señal cuadrada..9. Señales snusodales Una señal snusodal se escrbe medante cualquera de las funcones v( t) A sen( ωt ± θ ) v( t) A cos( ωt ± θ ) A se denomna ampltud de la señal, ω representa la frecuenca angular (medda en rad/s), llamaremos a la cantdad (ωt+θ) fase de la señal y a θ, medda en radanes, la denomnaremos desfase. Esta señal es peródca y en la Fgura -46 mostramos su forma de onda. Fgura -46. Señal snusodal. La frecuenca angular está relaconada con la frecuenca f medda en hertzos (Hz) por f ω π y el perodo T de la señal, que expresamos en segundos es 36
37 T f S la señal snusodal es una tensón se llama tensón pco a pco al valor pp A.0 Crcutos CL. Impedanca. Los crcutos en los que estén presentes, además de fuentes y resstencas, condensadores y bobnas se denomnan crcutos CL. Inclumos algunos aspectos báscos de estos dos elementos lneales, que son necesaros para una compresón senclla del funconamento de los msmos. Los condensadores están defndos por la ecuacón consttutva sguente C donde C es la capactanca del condensador. Es evdente que s la tensón, v, no depende del tempo (esto se denomna régmen de corrente contnua) su dervada es nula y por tanto la corrente que fluye a su través es tambén nula. De modo que s la tensón que cae entre los termnales de un condensador es constante el condensador opera como un crcuto aberto. Por otro lado, s la tensón depende del tempo tene que ser una funcón contnua. En otro caso su dervada tendería a nfnto y por ende la corrente sería nfnta que es una stuacón nadmsble en un crcuto. Por últmo ndcamos que el condensador es un elemento capaz de almacenar certa carga. Podemos calcular la cantdad de carga almacenada medante la conocda ecuacón dv dt q C v así, para certo valor de tensón a mayor capactanca mayor es la carga que almacena el elemento. Por su parte, las bobnas están defndas por la ecuacón consttutva sguente d v L dt donde L es la nductanca del elemento. S la corrente no depende del tempo su dervada es nula y por tanto la tensón que cae entre los termnales de la bobna es nula y funcona como un cortocrcuto. Además la corrente debe ser una funcón contnua del tempo ya que en otro caso se establecería una tensón nfnta a través de la bobna. Es decr, las bobnas no permten cambos bruscos en los valores de las correntes que fluyen a su través. 37
38 Las bobnas almacenan flujo magnétco (campo magnétco) ϕ L la nductanca es una medda de la cantdad de campo magnétco capaz de almacenar un nductor. olvendo a los crcutos CL, su análss se realza aplcando las leyes de Krchoff junto con las ecuacones consttutvas. Esto nos permte escrbr una ecuacón dferencal, llamada ecuacón dnámca del crcuto, que una vez resuelta descrbe su funconamento. Cuando la exctacón es snusodal, se pueden aplcar técncas de análss en las que los elementos del crcuto se representan medante números complejos llamados fasores. No vamos a entrar aquí a realzar una descrpcón exhaustva de la técnca. Nos basta con ndcar que con ella se defnen unas magntudes llamadas mpedancas de los elementos y meddas en óhmos, que son, en general, números complejos y que podemos nterpretar como cantdades análogas a la resstenca de los elementos, de hecho son el cocente entre el fasor tensón y el fasor corrente en estos crcutos. La mpedanca de una resstenca de valor la defnremos por Z La mpedanca de un condensador de capactanca C depende de la frecuenca de la señal snusodal de exctacón, s ω es dcha frecuenca Z C jωc aquí utlzamos j para que no haya confusón con el símbolo de la corrente eléctrca. Notamos que cuanto mayor es la frecuenca o la capactanca, menor es la mpedanca de un condensador. Por lo tanto a frecuencas grandes o con capactancas grandes la resstenca de un condensador es pequeña y, en algunos casos, podremos desprecar su nfluenca para smplfcar los análss. Por contra a frecuencas muy bajas la mpedanca es grande. Esto está de acuerdo con lo dcho anterormente: s la señal no depende del tempo (corrente contnua, o lo que es lo msmo ω0) el condensador es un crcuto aberto. Fnalmente ndcaremos que la mpedanca de una bobna de nductanca L exctada por una fuente snusodal de frecuenca ω es Z L jωl notamos que en corrente contnua la bobna presenta una mpedanca nula. 38
Bloque 2 Análisis de circuitos alimentados en corriente continua. Teoría de Circuitos
 Bloque Análss de crcutos almentados en corrente contnua Teoría de Crcutos . Métodos sstemátcos de resolucón de crcutos : Método de mallas Métodos sstemátcos de resolucón de crcutos Permten resolver los
Bloque Análss de crcutos almentados en corrente contnua Teoría de Crcutos . Métodos sstemátcos de resolucón de crcutos : Método de mallas Métodos sstemátcos de resolucón de crcutos Permten resolver los
Tallerine: Energías Renovables. Fundamento teórico
 Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Circuitos eléctricos en corriente continúa. Subcircuitos equivalentes Equivalentes en Serie Equivalentes en Paralelo Equivalentes de Thevenin y Norton
 ema II Crcutos eléctrcos en corrente contnúa Indce Introduccón a los crcutos resstvos Ley de Ohm Leyes de Krchhoff Ley de correntes (LCK) Ley de voltajes (LVK) Defncones adconales Subcrcutos equvalentes
ema II Crcutos eléctrcos en corrente contnúa Indce Introduccón a los crcutos resstvos Ley de Ohm Leyes de Krchhoff Ley de correntes (LCK) Ley de voltajes (LVK) Defncones adconales Subcrcutos equvalentes
PRÁCTICA Nº 5. CIRCUITOS DE CORRIENTE CONTINUA
 PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
Continua: Corriente cuyo valor es siempre constante (no varía con el tiempo). Se denota como c.c.
 .. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
.. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
Tema 3. Teoremas de la Teoría de Circuitos
 Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton 3.6 Máxma transferenca de potenca Th Th L nálss de Crcutos
Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton 3.6 Máxma transferenca de potenca Th Th L nálss de Crcutos
v i CIRCUITOS ELÉCTRICOS (apuntes para el curso de Electrónica)
 IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
ÍNDICE FUNDAMENTOS UNIDAD DIDÁCTICA 1. Capítulo 1. Presentación...15
 ÍNDICE Presentacón...5 UNIDAD DIDÁCTICA Capítulo FUNDAMENTOS. Crcuto eléctrco... 2 2. Símbolos lterales... 2 3. Convenos para el sentdo de referenca de la corrente eléctrca... 23 4. Convenos para la polardad
ÍNDICE Presentacón...5 UNIDAD DIDÁCTICA Capítulo FUNDAMENTOS. Crcuto eléctrco... 2 2. Símbolos lterales... 2 3. Convenos para el sentdo de referenca de la corrente eléctrca... 23 4. Convenos para la polardad
PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I
 PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I 1. Objetvo El objetvo de esta práctca es el estudo del funconamento del amplfcador operaconal, en partcular de dos de sus montajes típcos que son como amplfcador
PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I 1. Objetvo El objetvo de esta práctca es el estudo del funconamento del amplfcador operaconal, en partcular de dos de sus montajes típcos que son como amplfcador
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6a)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
Dpto. Física y Mecánica
 Dpto. Físca y Mecánca Mecánca analítca Introduccón Notacón Desplazamento y fuerza vrtual Fuerza de lgadura Trabao vrtual Energía cnétca. Ecuacones de Lagrange Prncpode los trabaos vrtuales Prncpo de D
Dpto. Físca y Mecánca Mecánca analítca Introduccón Notacón Desplazamento y fuerza vrtual Fuerza de lgadura Trabao vrtual Energía cnétca. Ecuacones de Lagrange Prncpode los trabaos vrtuales Prncpo de D
El diodo Semiconductor
 El dodo Semconductor J.I. Hurcán Unversdad de La Frontera Aprl 9, 2012 Abstract Se plantean procedmentos para analzar crcutos con dodos. Para smpl car el trabajo, el dodo semconductor es reemplazado por
El dodo Semconductor J.I. Hurcán Unversdad de La Frontera Aprl 9, 2012 Abstract Se plantean procedmentos para analzar crcutos con dodos. Para smpl car el trabajo, el dodo semconductor es reemplazado por
Figura 1
 5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
Capítulo 11. Movimiento de Rodamiento y Momentum Angular
 Capítulo 11 Movmento de Rodamento y Momentum Angular 1 Contendos: Movmento de rodamento de un cuerpo rígdo. Momentum Angular de una partícula. Momentum Angular de un sstema de partículas. Momentum Angular
Capítulo 11 Movmento de Rodamento y Momentum Angular 1 Contendos: Movmento de rodamento de un cuerpo rígdo. Momentum Angular de una partícula. Momentum Angular de un sstema de partículas. Momentum Angular
CAPÍTULO 1: VARIABLES ALEATORIAS Y SUS DISTRIBUCIONES
 CAÍTULO : VARIABLES ALEATORIAS SUS DISTRIBUCIONES En este capítulo el alumno debe abordar el conocmento de un mportante concepto el de VARIABLE ALEATORIA tpos de varables aleatoras cómo se dstrbue la funcón
CAÍTULO : VARIABLES ALEATORIAS SUS DISTRIBUCIONES En este capítulo el alumno debe abordar el conocmento de un mportante concepto el de VARIABLE ALEATORIA tpos de varables aleatoras cómo se dstrbue la funcón
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
Capítulo 11. Movimiento de Rodamiento y Momentum Angular
 Capítulo 11 Movmento de Rodamento y Momentum Angular 1 Contendos: Movmento de rodamento de un cuerpo rígdo. Momentum Angular de una partícula. Momentum Angular de un sstema de partículas. Momentum Angular
Capítulo 11 Movmento de Rodamento y Momentum Angular 1 Contendos: Movmento de rodamento de un cuerpo rígdo. Momentum Angular de una partícula. Momentum Angular de un sstema de partículas. Momentum Angular
ESTÁTICA DEL SÓLIDO RÍGIDO
 DSR-1 ESTÁTICA DEL SÓLIDO RÍGIDO DSR-2 ESTÁTICA DEL SÓLIDO RÍGIDO La estátca estuda las condcones bajo las cuales los sstemas mecáncos están en equlbro. Nos referremos úncamente a equlbro de tpo mecánco,
DSR-1 ESTÁTICA DEL SÓLIDO RÍGIDO DSR-2 ESTÁTICA DEL SÓLIDO RÍGIDO La estátca estuda las condcones bajo las cuales los sstemas mecáncos están en equlbro. Nos referremos úncamente a equlbro de tpo mecánco,
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
TEMA 6 AMPLIFICADORES OPERACIONALES
 Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Clase 19: Estado Estacionario y Flujo de Potencia. EL Conversión de la Energía y Sistemas Eléctricos Eduardo Zamora D.
 Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
TEMA 8 CIRCUITOS SIMPLES EN REGIMEN ESTACIONARIO SENOIDAL
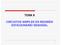 TEMA 8 UTOS SMPLES EN EGMEN ESTAONAO SENODAL TEMA 8:UTOS SMPLES EN EGMEN ESTAONAO SENODAL 8. ntroduccón 8. espuesta senodal de los elemetos báscos: espuesta del crcuto espuesta del crcuto L espuesta del
TEMA 8 UTOS SMPLES EN EGMEN ESTAONAO SENODAL TEMA 8:UTOS SMPLES EN EGMEN ESTAONAO SENODAL 8. ntroduccón 8. espuesta senodal de los elemetos báscos: espuesta del crcuto espuesta del crcuto L espuesta del
Problemas donde intervienen dos o más variables numéricas
 Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemático y dinámico de un mecanismo plano articulado con un grado de libertad.
 Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED
 Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
ESTADÍSTICA DESCRIPTIVA
 Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
10. VIBRACIONES EN SISTEMAS CON N GRADOS DE LIBERTAD
 10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
10. VIBRACIONES EN SISEMAS CON N GRADOS DE LIBERAD 10.1. Matrces de rgdez, nerca y amortguamento Se puede demostrar que las ecuacones lneales del movmento de un sstema dscreto de N grados de lbertad sometdo
CURSO INTERNACIONAL: CONSTRUCCIÓN DE ESCENARIOS ECONÓMICOS Y ECONOMETRÍA AVANZADA. Instructor: Horacio Catalán Alonso
 CURSO ITERACIOAL: COSTRUCCIÓ DE ESCEARIOS ECOÓMICOS ECOOMETRÍA AVAZADA Instructor: Horaco Catalán Alonso Modelo de Regresón Lneal Smple El modelo de regresón lneal representa un marco metodológco, que
CURSO ITERACIOAL: COSTRUCCIÓ DE ESCEARIOS ECOÓMICOS ECOOMETRÍA AVAZADA Instructor: Horaco Catalán Alonso Modelo de Regresón Lneal Smple El modelo de regresón lneal representa un marco metodológco, que
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II
 UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
Pista curva, soporte vertical, cinta métrica, esferas metálicas, plomada, dispositivo óptico digital, varilla corta, nuez, computador.
 ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
Tema 6. Estadística descriptiva bivariable con variables numéricas
 Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
SEGUNDA PARTE RENTAS FINANCIERAS
 SEGUNDA PARTE RENTAS FINANCIERAS 5 INTRODUCCIÓN A LA TEORÍA DE RENTAS 5.1 CONCEPTO: Renta fnancera: conjunto de captales fnanceros cuyos vencmentos regulares están dstrbudos sucesvamente a lo largo de
SEGUNDA PARTE RENTAS FINANCIERAS 5 INTRODUCCIÓN A LA TEORÍA DE RENTAS 5.1 CONCEPTO: Renta fnancera: conjunto de captales fnanceros cuyos vencmentos regulares están dstrbudos sucesvamente a lo largo de
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Gráficos de flujo de señal
 Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
Tema 1: Jerarquía Digital Síncrona, SDH Disponibilidad de Sistemas
 Tema : Jerarquía Dgtal Síncrona, SDH Dsponbldad de Sstemas Tecnologías de red de transporte de operadora MÁSTER EN INGENIERÍ TELEMÁTIC Profesor: Espín Defncones Fabldad (Relablty): Probabldad de que el
Tema : Jerarquía Dgtal Síncrona, SDH Dsponbldad de Sstemas Tecnologías de red de transporte de operadora MÁSTER EN INGENIERÍ TELEMÁTIC Profesor: Espín Defncones Fabldad (Relablty): Probabldad de que el
Tallerine: Energías Renovables
 Tallerne: Energías Renoables Fundamento Teórco Parte II: Curas de crcutos Autores: Carlos Brozzo Agustín Castellano Versón 0.1 Tallerne2017 Energías Renoables 2 Índce 1. Curas de crcutos 3 1.1. Fuente
Tallerne: Energías Renoables Fundamento Teórco Parte II: Curas de crcutos Autores: Carlos Brozzo Agustín Castellano Versón 0.1 Tallerne2017 Energías Renoables 2 Índce 1. Curas de crcutos 3 1.1. Fuente
Corriente alterna. (a) no cambia, (b) el valor de X no cambia, y X L = Z sen = 433 L= 1,38 H (c) no cambia, (d) no cambia, (e) C=1,83 F; (f) no cambia
 Corrente alterna Ejercco 1: un generador de corrente alterna que entrega 100V de tensón efcaz a 50 Hz se halla conectado a un crcuto C sere. Por el crcuto crcula una corrente efcaz ef = 0,2 sen (2 50 t
Corrente alterna Ejercco 1: un generador de corrente alterna que entrega 100V de tensón efcaz a 50 Hz se halla conectado a un crcuto C sere. Por el crcuto crcula una corrente efcaz ef = 0,2 sen (2 50 t
Leyes de tensión y de corriente
 hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
http://www.rubenprofe.com.ar biofisica@rubenprofe.com.ar RESISTENCIAS EN PARALELO
 bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
INSTRUMENTACIÓN Y TÉCNICAS DE MEDIDA. EL AMPLIFICADOR DE POTENCIA
 PÁCTICA 1. INSTUMENTACIÓN Y TÉCNICAS DE MEDIDA. EL AMPLIFICADO DE POTENCIA 1.1 Objetvos El objetvo de esta práctca consste en presentar los nstrumentos y las técncas de medda habtualmente utlzadas para
PÁCTICA 1. INSTUMENTACIÓN Y TÉCNICAS DE MEDIDA. EL AMPLIFICADO DE POTENCIA 1.1 Objetvos El objetvo de esta práctca consste en presentar los nstrumentos y las técncas de medda habtualmente utlzadas para
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Cinemática del Brazo articulado PUMA
 Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades 5 4.3 Carga y corrente.4 Tensón.5 Potenca y energía 3.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades 5 4.3 Carga y corrente.4 Tensón.5 Potenca y energía 3.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de
MÁQUINAS DE CORRIENTE CONTINUA
 MÁQUINAS D CORRINT CONTINUA n esta stuacón, la energía producda por el motor que funcona como generador es transformada en calor por efecto Joule en las resstencas de carga conectadas al nducdo del motor.
MÁQUINAS D CORRINT CONTINUA n esta stuacón, la energía producda por el motor que funcona como generador es transformada en calor por efecto Joule en las resstencas de carga conectadas al nducdo del motor.
Ejercicios y problemas (páginas 131/133)
 7 Calcula el opuesto y el conjugado de los sguentes números complejos, expresándolos en forma polar: a) z b) z (cos 00 sen 00 ) c) z Expresamos en prmer lugar los números complejos en forma Calcula las
7 Calcula el opuesto y el conjugado de los sguentes números complejos, expresándolos en forma polar: a) z b) z (cos 00 sen 00 ) c) z Expresamos en prmer lugar los números complejos en forma Calcula las
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Variables Aleatorias
 Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Electricidad y calor
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
TEMA 4. TRABAJO Y ENERGIA.
 TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
Electricidad y calor. Un repaso... Temas. 4. Primera ley de la Termodinámica. Webpage: Algunas definiciones
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Reconciliación de datos experimentales. MI5022 Análisis y simulación de procesos mineralúgicos
 Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
Reconclacón de datos expermentales MI5022 Análss y smulacón de procesos mneralúgcos Balances Balances en una celda de flotacón En torno a una celda de flotacón (o un crcuto) se pueden escrbr los sguentes
En el capítulo correspondiente a Inducción Magnética, vimos que un cuadro de hilo
 VII. Corrente Alterna Introduccón: Cas la totaldad de la energía eléctrca utlzada actualmente se produce medante generadores eléctrcos de corrente alterna, la cual tene la gran ventaja sobre la corrente
VII. Corrente Alterna Introduccón: Cas la totaldad de la energía eléctrca utlzada actualmente se produce medante generadores eléctrcos de corrente alterna, la cual tene la gran ventaja sobre la corrente
La representación Denavit-Hartenberg
 La representacón Denavt-Hartenberg José Cortés Parejo. Marzo 8 Se trata de un procedmeto sstemátco para descrbr la estructura cnemátca de una cadena artculada consttuda por artculacones con. un solo grado
La representacón Denavt-Hartenberg José Cortés Parejo. Marzo 8 Se trata de un procedmeto sstemátco para descrbr la estructura cnemátca de una cadena artculada consttuda por artculacones con. un solo grado
16.21 Técnicas de diseño y análisis estructural. Primavera 2003 Unidad 8 Principio de desplazamientos virtuales
 16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
16.21 Técncas de dseño y análss estructural Prmavera 2003 Undad 8 Prncpo de desplazamentos vrtuales Prncpo de desplazamentos vrtuales Tengamos en cuenta un cuerpo en equlbro. Sabemos que el campo de esfuerzo
Ecuación de Lagrange
 Capítulo 6 Ecuacón de Lagrange 6. Introduccón a las ecuacones de Lagrange La mecánca que nos presenta Lagrange en su Mécanque Analytque sgnfca un salto conceptual muy grande respecto de la formulacón Newtonana.
Capítulo 6 Ecuacón de Lagrange 6. Introduccón a las ecuacones de Lagrange La mecánca que nos presenta Lagrange en su Mécanque Analytque sgnfca un salto conceptual muy grande respecto de la formulacón Newtonana.
Objetivos de aprendizaje. Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 epartamento de Físca, UTFSM Físca General II / Prof: A. Brunel. FIS120: FÍSICA GENERAL II GUÍA#6: Campo magnétco, efectos. Objetvos de aprendzaje. Esta guía es una herramenta que usted debe usar para lograr
epartamento de Físca, UTFSM Físca General II / Prof: A. Brunel. FIS120: FÍSICA GENERAL II GUÍA#6: Campo magnétco, efectos. Objetvos de aprendzaje. Esta guía es una herramenta que usted debe usar para lograr
DISTRIBUCIONES BIDIMENSIONALES
 Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
TRABAJO Y ENERGÍA INTRODUCCIÓN. requiere como varia la fuerza durante el movimiento. entre los conceptos de fuerza y energía mecánica.
 TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
Electromagnetismo. El campo de las cargas en reposo: el campo electrostático. Campo eléctrico
 Electromagnetsmo El campo de las cargas en reposo: el campo electrostátco Andrés Cantarero. Curso 2005-2006. ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electrostátco.
Electromagnetsmo El campo de las cargas en reposo: el campo electrostátco Andrés Cantarero. Curso 2005-2006. ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electrostátco.
RESISTENCIAS EN SERIE Y LEY DE LAS MALLAS V 1 V 2 V 3 A B C
 RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
Organización y resumen de datos cuantitativos
 Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
+ V i - V o - Filtro Supresor de Banda
 Fltro Supresor de Banda Los fltros supresor de banda o banda de atenuacón tambén se construyen usando un fltro pasa bajos y uno pasa altos. Sn embargo, en lugar de la confguracón en cascada empleada para
Fltro Supresor de Banda Los fltros supresor de banda o banda de atenuacón tambén se construyen usando un fltro pasa bajos y uno pasa altos. Sn embargo, en lugar de la confguracón en cascada empleada para
Variables Aleatorias. Variables Aleatorias. Variables Aleatorias. Objetivos del tema: Al final del tema el alumno será capaz de:
 Varables Aleatoras Varables Aleatoras Objetvos del tema: Concepto de varable aleatora Al fnal del tema el alumno será capaz de: Varables aleatoras dscretas y contnuas Funcón de probabldad Funcón de dstrbucón
Varables Aleatoras Varables Aleatoras Objetvos del tema: Concepto de varable aleatora Al fnal del tema el alumno será capaz de: Varables aleatoras dscretas y contnuas Funcón de probabldad Funcón de dstrbucón
Laboratorio de Análisis de Circuitos. Práctica 10. Medición de la potencia eléctrica y corrección del factor de potencia con Maple y Proteus ISIS
 aboratoro de Análss de Crcutos Práctca 10 Medcón de la potenca eléctrca y correccón del factor de potenca con Maple y Proteus ISIS 1 Objetos 1 Calcular con el empleo de programas de cómputo las ntensdades
aboratoro de Análss de Crcutos Práctca 10 Medcón de la potenca eléctrca y correccón del factor de potenca con Maple y Proteus ISIS 1 Objetos 1 Calcular con el empleo de programas de cómputo las ntensdades
Tipos de amplificadores según su ganancia
 Tpos de amplfcadores según su gananca Electrónca nalógca: ealmentacón Todo amplfcador que posea unas resstencas de entrada () y de salda (o) dstntas de cero y dstntas de nfnto se puede representar de cuatro
Tpos de amplfcadores según su gananca Electrónca nalógca: ealmentacón Todo amplfcador que posea unas resstencas de entrada () y de salda (o) dstntas de cero y dstntas de nfnto se puede representar de cuatro
Introducción a Vacío
 Introduccón a Vacío Sstema de vacío Partes generales de un sstema de vacío: Fgura 1: Sstema de vacío con bomba mecánca y dfusora Fgura 2: Prncpo de funconamento de la bomba mecánca La Fg. 2 muestra el
Introduccón a Vacío Sstema de vacío Partes generales de un sstema de vacío: Fgura 1: Sstema de vacío con bomba mecánca y dfusora Fgura 2: Prncpo de funconamento de la bomba mecánca La Fg. 2 muestra el
Cálculo y EstadísTICa. Primer Semestre.
 Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
Práctica 12 - Programación en C++ Pág. 1. Practica Nº 12. Prof. Dr. Paul Bustamante. Informática II Fundamentos de Programación - Tecnun
 Práctca 1 - Programacón en C++ Pág. 1 Práctcas de C++ Practca Nº 1 Informátca II Fundamentos de Programacón Prof. Dr. Paul Bustamante Práctca 1 - Programacón en C++ Pág. 1 INDICE ÍNDICE... 1 1.1 Ejercco
Práctca 1 - Programacón en C++ Pág. 1 Práctcas de C++ Practca Nº 1 Informátca II Fundamentos de Programacón Prof. Dr. Paul Bustamante Práctca 1 - Programacón en C++ Pág. 1 INDICE ÍNDICE... 1 1.1 Ejercco
60 EJERCICIOS de NÚMEROS COMPLEJOS
 60 EJERCICIOS de NÚMEROS COMPLEJOS. Resolver las sguentes ecuacones en el campo de los números complejos a) x -x+=0 (Soluc ) b) x +=0 (Soluc ) c) x -x+=0 (Soluc ) d) x +x+=0 (Soluc ) e) x -6x +x-6=0 (Soluc,
60 EJERCICIOS de NÚMEROS COMPLEJOS. Resolver las sguentes ecuacones en el campo de los números complejos a) x -x+=0 (Soluc ) b) x +=0 (Soluc ) c) x -x+=0 (Soluc ) d) x +x+=0 (Soluc ) e) x -6x +x-6=0 (Soluc,
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
2. EL TENSOR DE TENSIONES. Supongamos un cuerpo sometido a fuerzas externas en equilibrio y un punto P en su interior.
 . EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
. EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
ESTADÍSTICA. Definiciones
 ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
Universidad de Pamplona Facultad de Ciencias Básicas Física para ciencias de la vida y la salud
 Unversdad de Pamplona Facultad de Cencas Báscas Físca para cencas de la vda y la salud AÁLISIS GRÁFICO DE DATOS EXPERIMETALES OBJETIVO: Representar gráfcamente datos expermentales. Ajustar curvas a datos
Unversdad de Pamplona Facultad de Cencas Báscas Físca para cencas de la vda y la salud AÁLISIS GRÁFICO DE DATOS EXPERIMETALES OBJETIVO: Representar gráfcamente datos expermentales. Ajustar curvas a datos
TEMA 8: PRÉSTAMOS ÍNDICE
 TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
Introducción a la Física. Medidas y Errores
 Departamento de Físca Unversdad de Jaén Introduccón a la Físca Meddas y Errores J.A.Moleón 1 1- Introduccón La Físca y otras cencas persguen la descrpcón cualtatva y cuanttatva de los fenómenos que ocurren
Departamento de Físca Unversdad de Jaén Introduccón a la Físca Meddas y Errores J.A.Moleón 1 1- Introduccón La Físca y otras cencas persguen la descrpcón cualtatva y cuanttatva de los fenómenos que ocurren
Facultad de Ciencias Básicas
 Facultad de Cencas Báscas ANÁLISIS GRÁFICO DE DATOS EXPERIMENTALES OBJETIVO: Representar gráfcamente datos expermentales. Ajustar curvas a datos expermentales. Establecer un crtero para el análss de grafcas
Facultad de Cencas Báscas ANÁLISIS GRÁFICO DE DATOS EXPERIMENTALES OBJETIVO: Representar gráfcamente datos expermentales. Ajustar curvas a datos expermentales. Establecer un crtero para el análss de grafcas
OSCILACIONES 1.- INTRODUCCIÓN
 OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
AMPLIFICADORES CON BJT.
 Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
Convertidores Digital-Analógico y Analógico-Digital
 Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
TEMA 4 Amplificadores realimentados
 TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
3.1 Resolver mediante el método de la transformada de Laplace el problema 1.1.
 rcutos y Sstemas Dnámcos Ejerccos tema 3 Método de la transformada de aplace 3. esolver medante el método de la transformada de aplace el problema.. 3. esolver medante el método de la transformada de aplace
rcutos y Sstemas Dnámcos Ejerccos tema 3 Método de la transformada de aplace 3. esolver medante el método de la transformada de aplace el problema.. 3. esolver medante el método de la transformada de aplace
TEORÍA DE CIRCUITOS ADAPTADO A LOS GRADOS DE INGENIERÍA
 arlos Roldán Porta Gullermo Escrvá Escrvá arlos Roldán Blay TEORÍA DE IRUITOS ADAPTADO A LOS GRADOS DE INGENIERÍA EDITORIAL UNIVERSITAT POLITÈNIA DE VALÈNIA Los contendos de esta publcacón han sdo revsados
arlos Roldán Porta Gullermo Escrvá Escrvá arlos Roldán Blay TEORÍA DE IRUITOS ADAPTADO A LOS GRADOS DE INGENIERÍA EDITORIAL UNIVERSITAT POLITÈNIA DE VALÈNIA Los contendos de esta publcacón han sdo revsados
5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA.
 Programacón en Pascal 5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA. Exsten numerosas stuacones que pueden representarse medante relacones de recurrenca; entre ellas menconamos las secuencas y las
Programacón en Pascal 5. PROGRAMAS BASADOS EN RELACIONES DE RECURRENCIA. Exsten numerosas stuacones que pueden representarse medante relacones de recurrenca; entre ellas menconamos las secuencas y las
EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. x x0 y y0. Deducir la fórmula para el polinomio de Lagrange de grado a lo más uno que Interpola la tabla.
 EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. Consdere la sguente tabla, donde 0 : 0 y y0 y Deducr la fórmula para el polnomo de Lagrange de grado a lo más uno que Interpola la tabla.. Consdere la sguente
EJERCICIOS SOBRE INTERPOLACIÓN POLINOMIAL. Consdere la sguente tabla, donde 0 : 0 y y0 y Deducr la fórmula para el polnomo de Lagrange de grado a lo más uno que Interpola la tabla.. Consdere la sguente
Análisis de Resultados con Errores
 Análss de Resultados con Errores Exsten dos tpos de errores en los expermentos Errores sstemátcos errores aleatoros. Los errores sstemátcos son, desde lejos, los más mportantes. Errores Sstemátcos: Exsten
Análss de Resultados con Errores Exsten dos tpos de errores en los expermentos Errores sstemátcos errores aleatoros. Los errores sstemátcos son, desde lejos, los más mportantes. Errores Sstemátcos: Exsten
Cinemática del movimiento rotacional
 Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
