ESTADISTICA APLICADA Y ECONOMETRIA
|
|
|
- Alicia Ríos Torregrosa
- hace 6 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE CHILE MAGISTER EN GESTION Y POLITICAS PUBLICAS ESTADISTICA APLICADA Y ECONOMETRIA Sara Arancba C 01 1 Objetvos Comprender y aplcar los conceptos báscos de Econometría y metodologías de Análss Multvarante, fundamentales para el análss de nformacón. Conocer y manejar el software estadístco SPSS, con énfass en la resolucón de estudos de casos aplcados a la gestón y polítcas públcas. Metodología Clases teórcas y práctcas. Apoyo de materal; transparencas, guías, lecturas complementaras Manejo del software SPSS En los laboratoros se realzarán estudos de casos apoyados de guías. 1
2 Evaluacón Tareas semanales ( 30%), un control (30%), examen (40%) Bblografía: Introduccón a la Econometría. Un enfoque moderno. Jeffrey y Wooldrdge. Ed Thomson Learnng Econometría. Cuarta Edcón Gujarat Ed. Mc Graw Hll Análss Multvarable para las Cencas Socales. Lévy y Varela Ed Pearson Análss multvarante Har-Anderson-Tatham-Black. Ed Prentce Hall. Análss de datos con SPSS 13 Base Pardo y Ruz. Ed Mc Graw Hll. Análss Estadístco con SPSS para wndows. Estadístca Multvarante. Vsauta y Martor. Ed Mc Graw Hll. Segunda Edcón 3 Contendos Prmera sesón Introduccón a la Econometría Introduccón al Análss Multvarable Análss de varanza Análss no paramétrco de H de Kruskall-Walls Guía 1-Estudos de casos Segunda y Tercera Sesón Análss de regresón lneal smple Modelos ln-log y log-ln y semlogartmcos Guía - Estudos de casos Cuarta y Qunta Sesón Análss de regresón múltple Guía 3- Estudos de casos 4
3 Contendos Sexta Sesón Modelos de regresón múltple con varables cualtatvas ( dam) Estmacón ponderada Guía 4- Estudos de casos Séptma Sesón Regresón logístca Guía 5- Estudos de casos Octava Sesón Análss Factoral Guía 6- Estudos de casos 5 Introduccón Introduccón a la Econometría Introduccón al Análss Multvarante 6 3
4 Introduccón a la Econometría Naturaleza de la Econometría y de los datos económcos Qué es la Econometría? Funcones de la Econometría La metodología de la Econometría La regresón es una herramenta fundamental de la Econometría. Estructura de los datos económcos Relacones estadístcas vs. Relacones determnístcas Regresón vs. Causaldad Regresón vs. Correlacón Termnología 7 Introduccón Naturaleza de la econometría y de los datos económcos Qué es la econometría? Lteralmente, econometría sgnfca medcón económca. La econometría se basa en métodos estadístcos para estmar las relacones económcas, poner a prueba teorías económcas y evaluar y poner en práctca polítcas gubernamentales y comercales. Aplcacones de la econometría Pronóstco de varables macroeconómcas ( nflacón, el producto nterno bruto ) Estudos aplcados a dversos campos de la economía (Ej: estudo de los efectos de los gastos de las campañas polítcas en los resultados de las votacones, en el efecto de los gastos en educacón en el rendmento de los estudantes, etc) 8 4
5 Cuáles son las funcones de la econometría? La econometría tene báscamente tres funcones estrechamente nterrelaconadas. 1) Probar teorías económcas o hpótess. Por ejemplo, está el consumo drectamente relaconado con el ngreso?, está la cantdad demandada de un artículo nversamente relaconada con su preco?. ) Dar estmacones numércas de los coefcentes de las relacones económcas. Estos son esencales en la toma de decsones. Por ejemplo, un asesor gubernamental necesta tener una estmacón exacta del coefcente de la relacón entre consumo e ngreso con el fn de determnar el efecto estmulante de una reduccón de mpuestos propuesta. 3) La predccón de sucesos económcos La Econometría da contendo empírco a gran parte de la teoría económca 9 La metodología de la Econometría En térmnos generales, el análss econométrco sgue las sguentes líneas generales de accón: 1. Enuncado de la teoría o hpótess. Especfcacón del modelo econométrco drgdo a probar la teoría 3. Estmacón de los parámetros del modelo 4. Verfcacón o nferenca estadístca 5. Predccones o pronóstcos 6. Utlzacón del modelo para fnes de control o formulacón de polítcas 10 5
6 Ejemplo Consderemos a contnuacón la teoría keynesana de la funcón consumo Enuncado de la teoría o hpótess Keynes plantea La ley scológca fundamental consste en que los hombres están dspuestos, por regla general y en promedo, a aumentar su consumo a medda que aumenta su ngreso, aunque no en la msma proporcón al ncremento en dcho ngreso. Keynes afrma que la propensón margnal a consumr (PMC), la tasa de cambo del consumo ante un cambo de una undad en el ngreso, es mayor que cero pero menor que uno. 11 Especfcacón del modelo econométrco Para smplfcar, un economsta matemátco puede sugerr la sguente forma para la funcón de consumo de Keynes: Y 0 1X (1) en donde Y gastos de consumo X ngreso 0 nt erseccón con el eje Y 1 pendente El coefcente de la pendente 1 representa la propensón margnal a consumr (PMC) 1 6
7 La ecuacón (1), que afrma que el consumo está relaconado lnealmente con el ngreso, es un ejemplo de un modelo matemátco. S el modelo, como del ejemplo anteror, consta de una sola ecuacón, recbe el nombre de modelo unecuaconal; s tene más de una ecuacón, se denomna modelo multecuaconal o modelo de ecuacones smultáneas. El modelo matemátco de la funcón de consumo (1) es de lmtado nterés para el econometrsta, por cuanto supone una relacón exacta o determnístca entre el consumo y el ngreso. Sn embargo, las relacones exstentes entre las varables económcas son generalmente nexactas 13 Para tener en cuenta la exstenca de una relacón nexacta entre las varables económcas, el econometrsta debe modfcar la funcón de consumo determnístca de (1), de la sguente manera Y o 1X u () En la que u representa el térmno de perturbacón o de error, que es una varable aleatora ( estocástca) con propedades probablístcas ben defndas. El térmno perturbacón, u, suele representar todas aquellas fuerzas que afectan el consumo pero que no se tenen en cuenta de manera explícta en la ecuacón 14 7
8 Estmacón Habendo especfcado el modelo econométrco, la tarea sguente del econometrsta consste en obtener estmacones (valores numércos) de los parámetros del modelo, a partr de la nformacón dsponble, generalmente proporconada por el estadístco económco. Estas estmacones le conferen un contendo empírco a la teoría económca. Así por ejemplo, s en el estudo de la funcón de consumo anterormente expuesta, se encuentra que 1 0,8, este valor no sólo proporcona una estmacón numérca de la PMC sno que corrobora la hpótess keynesana según la cual la PMC es menor que 1. Cómo se estman los parámetros? La técnca utlzada para obtener dchas estmacones es el análss de regresón 15 Verfcacón ( nferenca estadístca) Habendo obtendo ya estmacones de los parámetros, la tarea sguente consste en desarrollar crteros apropados drgdos a establecer s las estmacones obtendas están de acuerdo con lo que se espera de la teoría que se está verfcando. La refutacón o confrmacón de las teorías económcas, basándose en la evdenca empírca, se fundamenta en la nferenca estadístca ( prueba de hpótess) Predccones o pronóstcos S el modelo escogdo confrma la hpótess o teoría que se está nvestgando, se puede entonces proceder a predecr el (los) valor(es) futuro(s) de la varable dependente Y con base en valores futuros, conocdos o esperados, para la(s) varable(s) explcatva(s) X. 16 8
9 Utlzacón de los modelos para fnes de control o formulacón de polítcas Supóngase que un economsta del goberno estma la funcón de consumo keynesana, obtenendo los sguentes resultados Y= 5+0,7X donde el gasto de consumo Y y el ngreso X se mden en mles de mllones de dólares. Adconalmente se supone que el goberno cree que un nvel de gastos de 1060 ( mles de mllones de dólares) mantendrá la tasa de desempleo a un nvel relatvamente bajo, del orden del 5%. Qué nvel de ngresos (X) garantzará que se obtenga la cantdad presupuestada ncalmente de gastos de consumo?. Suponendo que el modelo es aceptable, se tene que: 1060=5+0,7X o X=1055/ 0,7 =1507 Lo anteror mplca que un nvel de ngresos de 1507 (mles de mll de dólares), dada una PMC=0,7, generará un gasto de 1060 (mles de mllones de dólares) 17 La regresón es una herramenta fundamental de la econometría. Interpretacón moderna de la regresón El análss de regresón está relaconado con el estudo de la dependenca de una varable, la varable dependente, de una o más varables adconales, las varables explcatvas con la perspectva de estmar y/ o predecr el valor (poblaconal) medo o promedo de la prmera en térmnos de valores conocdos o fjos ( en muestreos repetdos) de las segundas. Debe tenerse sempre en mente que el éxto del análss de regresón depende de la dsponbldad de nformacón adecuada. 18 9
10 Estructura de los datos económcos Las estructuras de datos más comunes en la econometría aplcada son las de los datos de corte transversal, de seres de tempo, de combnacón de cortes transversales, y de panel. Datos de corte transversal Un conjunto de datos de corte transversal consta de una muestra de ndvduos, hogares, empresas, cudades, estados, países u otras dversas undades, tomada en un momento determnado. A veces, los datos de todas las undades no corresponden con exacttud al msmo perodo; por ejemplo, es posble entrevstar a varas famlas durante semanas dstntas del año. En un análss de seccón cruzada pura, gnoraríamos cualquer dferenca de tempo mínma en la recoplacón de los datos. S se entrevstó a un grupo de famlas en semanas dstntas del msmo año, aún veríamos esta nformacón como un conjunto de datos de corte transversal. 19 Tabla 1.1 Conjunto de datos de corte transversal sobre salaro y otras característcas ndvduales Obs sala educ exper sexo ecvl
11 Tabla 1. Conjunto de datos sobre las tasas de crecmento económco y característcas de los países obs país tpb Consgob60 Secund60 1 Argentna Austra Bélgca Bolva Zmbabwe Datos de seres de tempo Un conjunto de datos de seres de tempo (o datos de seres temporales) consta de observacones, de una o más varables, hechas en el tempo. Entre los ejemplos de este tpo de nformacón se encuentran los precos de las accones, el índce de precos al consumdor, el producto nterno bruto, los índces anuales de homcdos y las cfras de venta de automóvles. Como los hechos del pasado pueden tener nfluenca en los del futuro y los rezagos en el comportamento son comunes en las cencas socales, el tempo es un factor mportante en los datos de seres de tempo. A dferenca del ordenamento de los datos de corte transversal, la dsposcón cronológca de las observacones en una sere temporal proporcona nformacón potencalmente mportante. 11
12 Tabla 1.3 Salaro mínmo, desempleo y datos relaconados para Puerto Rco obs año salamn cob desem pb Combnacón de cortes transversales Algunos conjuntos de datos tenen característcas tanto de corte transversal como de seres temporales. Por ejemplo, supongamos que se realzaron a escala naconal dos encuestas transversales de hogares, una en 1985 y otra en En 1985 se entrevstó a una muestra aleatora de hogares sobre varables como ngreso, ahorro, tamaño de la famla, etc. En 1990 se realzó una nueva muestra aleatora con las msmas preguntas. Con el objeto de aumentar el tamaño de nuestra muestra, podemos formar una combnacón de cortes transversales para los dos años. Como las muestras aleatoras se tomaron cada año, sería mera casualdad que el msmo hogar aparecera en la muestra de ambos años. (Por lo regular, el tamaño de la muestra será muy pequeño, en comparacón con el de todos los hogares del país). Este mportante factor dstngue a la combnacón de cortes transversales de los conjuntos de datos de panel. 4 1
13 Tabla 1.4 Combnacones de cortes transversales: dos años de precos de la vvenda obs año preco mptos pecuad habt Baños Datos de panel o longtudnales Un conjunto de datos de panel (o longtudnales) consta de una sere temporal para cada membro del corte transversal en el conjunto de datos. Como ejemplo, supongamos que tenemos salaro, educacón y antecedentes de empleo de un grupo de ndvduos a los que se ha dado segumento durante 10 años; o tambén podríamos reunr nformacón, como datos fnanceros y de nversones, sobre el msmo conjunto de empresas durante un perodo de cnco años. De gual forma es posble recoplar datos de panel en undades geográfcas. Por ejemplo, podemos reunr datos de los msmos muncpos de un país sobre flujos de mgracón, tasas mpostvas, nveles de salaros, gastos gubernamentales, etc., para los años 1980, 1985 Y La característca fundamental de los datos de panel, que los dstnguen de las combnacones de cortes transversales, es el hecho de que se da segumento a las msmas undades 6 13
14 Tabla 1.5 Conjunto de datos de panel de dos años sobre estadístcas de delncuenca urbana obs cudad año homcd os poblacó n desem Polcía Nota: Los conjuntos de datos que ncluyen la dmensón del tempo, como los de seres temporales y de panel, exgen un tratamento especal por la correlacón con el paso del tempo de la mayor parte de las seres de tempo económcas. Otros temas, como las tendencas y la estaconaldad, surgen en el análss de los datos de seres temporales, pero no en los de corte transversal. 8 14
15 Relacones estadístcas vs. Relacones determnístcas En el análss de regresón nos nteresa lo que se conoce como dependenca estadístca entre varables, pero no la funconal o determnístca propa de la físca clásca. En las relacones estadístcas entre varables tratamos esencalmente con varables aleatoras o estocástcas, esto es varables que tenen dstrbucones de probabldad. Por otra parte, en la dependenca funconal o determnístca tambén manejamos varables, pero éstas no son aleatoras o estocástcas. NOTA: La palabra estocástca vene de la palabra grega stokhos que sgnfca "centro del blanco". El resultado de lanzar dardos sobre un tablero es un proceso estocástco, esto es, un proceso que permte errores. 9 Relacones estadístcas vs. Relacones determnístcas La dependenca del producto de una cosecha respecto a la temperatura ambente, la lluva, el sol y los fertlzantes, por ejemplo, es de naturaleza estadístca en el sentdo que las varables explcatvas, s ben son mportantes, no permtrán al agrónomo predecr en forma exacta el producto de la cosecha debdo a los errores nvolucrados en la medcón de estas varables y en razón de otra sere de factores (varables), que afectan colectvamente la produccón pero pueden ser dfícles de dentfcar ndvdualmente. De esta manera habrá alguna varabldad "ntrínseca" o aleatora en la varable dependente, produc to de la cosecha, que no puede ser explcada en su totaldad sn mportar cuán tas otras varables explcatvas consderemos
16 Regresón vs Causaldad S ben el análss de regresón tene que ver con la dependenca de una varable respecto a otras varables, esto no mplca causaldad necesaramente. En palabras de Kendall y Stuart: "Una relacón estadístca, sn mportar qué tan fuerte y sugestva sea, nunca podrá establecer una conexón causal: nuestras deas de causaldad deben venr de estadístcas externas y, en últmo térmno, de una u otra teoría." Por ejemplo s consderamos el producto de una cosecha, no hay una razón estadístca para suponer que la lluva no depende del producto de la cosecha. El hecho de que se trata el producto de la cosecha como dependente de la lluva (entre otras cosas) es debdo a consderacones no estadístcas: el sentdo común sugere que la relacón no puede revertrse, ya que no podemos contro lar la lluva modfcando la produccón de la cosecha. 31 Regresón vs Correlacón El análss de correlacón está estrechamente relaconado con el de regresón aunque conceptualmente los dos son muy dferentes. En el análss de correlacón el objetvo prncpal es medr la fuerza o el grado de asocacón lneal entre dos varables. El coefcente de correlacón, mde esta fuerza de asocacón (lneal). Por ejemplo, se puede estar nteresado en encontrar la correlacón (el coefcente) entre el hábto de fumar y el cáncer del pulmón; entre las calfcacones obtendas en exámenes de estadístca y las obtendas en exámenes de matemátcas; entre las altas calfcacones obtendas en la escuela secundara y en la unversdad, y así sucesvamente. 3 16
17 Regresón vs Correlacón En el análss de regresón, como ya se menconó, no estamos nteresados en ese tpo de medcón. En cambo, se trata de estmar o de predecr el valor promedo de una varable sobre la base de valores fjos de otras varables. Así, quzás se desee saber s se puede predecr el promedo de las calfcacones en un examen de estadístca, conocendo la calfcacón de un estudante en un examen de matemátcas. 33 Termnología Y X X n X n En la teoría económca los térmnos varable dependente y varable ndependente están descrtos de varas maneras; a contnuacón se presenta una lsta representatva de ellas: y Varable dependente Varable explcada Varable de respuesta Varable predcha Regresada X 1, X, X 3,. X k Varable ndependente Varable explcatva Varables de control Varables predctora Regresora 34 17
18 Introduccón al Análss Multvarante Conceptos y técncas del Análss Multvarable Qué es el Análss Multvarable? Utldad del Análss Multvarable Los datos en el Análss Multvarable Varables y escalas de medda Análss ncal de datos Las técncas de Análss Multvarable Técncas de análss de la dependenca Técncas de análss de la nterdependenca 35 Qué es el Análss Multvarable? Qué es el Análss Multvarable? El análss multvarable puede defnrse como el conjunto de métodos o técncas, dseñados con el fn de maxmzar e nterpretar la nformacón contenda en un conjunto de varables, sn perder la nteraccón o grado en que se afectan unas con otras El análss multvarable permte llevar a cabo la resolucón de problemas y la toma de decsones con un enfoque analítco sobre todas las varables que llegan a nflur sobre el o los problemas en cuestón
19 Utldad del Análss Multvarable La complejdad de la realdad socoeconómcoempresaral y el hecho de que en su conocmento confluyan dscplnas centífcas de orgen dverso hacen que el contendo de los métodos multvarables se proyecte como un cuerpo de conocmentos de naturaleza nterdscplnara. Las necesdades de nformacón de los nvestgadores y decdores para la planfcacón, ejecucón de accones o el control de resultados son cada vez mayores. En el análss multvarable, se puede encontrar una herramenta práctca, versátl y adaptable a todo tpo de análss, al permtr extraer nformacón relevante, y efcente. 37 Los datos en el Análss Multvarable Varables y escalas de medda Datos Análss Multvarable Valores que toman las Varables Magntudes que representan dstntos conceptos o atrbutos de ndvduos u objetos La precsón de tal representacón dependerá drectamente de la escala de medda 38 19
20 Los datos en el Análss Multvarable Escalas de medda La tpología de escalas de medda dstngue cuatro báscas Nomnal Ordnal Escalas no métrcas o cualtatvas Intervalo Razón Escalas métrcas o cuanttatvas 39 Los datos en el Análss Multvarable Escalas de medda Una varable no métrca puede ser convertda en varable fctcas bnaras (dummy). Sería necesaro contar con un número de ellas gual al número de categorías de la varable no métrca menos uno. Ejemplo: Supóngase que se pretende transformar la varable medos de transporte más comunes de tres categorías: 1=autobús, =tren y 3=avón. La conversón podría efectuarse por medo de dos varables fctcas, F1 y F. Los valores que éstas tomarían para representar cada categoría serían los sguentes: Categoría F1 F Autobús 1 0 Tren 0 1 Avón
21 Los datos en el Análss Multvarable Análss ncal de datos Antes de comenzar con el análss multvarable, es esencal realzar un examen exhaustvo de los datos. La deteccón de problemas ocultos en las matrces de datos supondrá un gran avance en la consecucón de resultados lógcos y consstentes. Es fundamental nspecconar: Análss de datos ausentes (mssng values) Analzar s es relevante para el análss obtener los datos perddos. Determnar s la nformacón que falta puede ser completada. Susttur los datos por valores estmados 41 Los datos en el Análss Multvarable Análss ncal de datos Es fundamental nspecconar: Representacones gráfcas para el análss de datos Hstogramas de cada varable Gráfcos de dspersón Gráfco de cajas ( Boxplot) Tablas Deteccón de outlers Tablas de frecuenca Tablas de contngenca Estudar los casos atípcos 4 1
22 Los datos en el Análss Multvarable Análss ncal de datos Es fundamental nspecconar: Supuestos subyacentes en los métodos multvarables Normaldad de las varables Lnealdad ( exstenca de asocacones lneales entre varables) Homocedastcdad (Varanza de los errores es constante) 43 Las técncas del Análss Multvarable Tpología de las técncas De análss de la dependenca De análss de la nterdependenca Otras técncas 44
23 Las técncas del Análss Multvarable De análss de la dependenca De análss de la nterdependenca Técncas aplcables cuando una o varas varables dependentes van a ser explcadas por un conjunto de varables ndependentes que actúan como predctoras Técncas que otorgan la msma consderacón a todas las varables objeto de estudo, sn dstngur entre dependentes e ndependentes, y que tenen como fn descubrr las nterrelacones entre ellas. Son técncas de clasfcacón. Otras técncas Técncas novedosas que permten un tratamento más efcaz y efcente en grandes cantdades de datos, como análss con redes neuronales, data mnng. 45 Técncas de análss de la dependenca Técnca Análss de la varanza y la covaranza Varable dependente Métrca Varables ndependentes No métrcas Análss dscrmnante No métrca Métrcas Regresón lneal múltple ídem con varables fctcas Modelos de eleccón dscreta ídem con varables fctcas Métrca Métrca No métrca No métrca Análss conjunto Métrca o no métrca Segmentacón Jerárquca No métrca o métrca Métrcas No métrcas Métrcas No métrcas No métrcas No métrcas Análss de ecuacones estructurales Métrca Métrcas o no métrcas Análss con clases latentes No métrca latente No métrcas observables 46 3
24 Termnología Varable fctca Varable bnara que se suele emplear para representar una categoría de una varable no métrca. Varable métrca (o cuanttatva) Varable medda en escala de ntervalo o de razón, capaz de reflejar, por tanto, dferencas de grado o cantdad entre sus elementos. La dferenca entre dos elementos consecutvos es constante a lo largo de toda la escala. Varable no métrca (o cualtatva) Varable medda en escala nomnal u ordnal que dentfca categorías o propedades. S es ordnal, los números asgnados a cada categoría guardan una relacón de orden; pero, por lo demás, son smples etquetas sn nngún otro sgnfcado. 47 ANOVA (o análss de la varanza) Método para contrastar s dversas muestras proceden de poblacones con gual meda. ANCOVA (o análss de la covaranza) Proceso que comenza por emplear la regresón para elmnar la varacón expermentada por la varable dependente producda por una varable ndependente no controlada (covarable) cuyos efectos se consderan ndeseados, y sgue con un ANOVA sobre la varable dependente ajustada. 48 4
25 Análss dscrmnante Técnca de clasfcacón que permte agrupar a los elementos de una muestra en dos o más categorías dferentes, predefndas en una varable dependente no métrca, en funcón de una sere de varables ndependentes métrcas combnadas lnealmente. Regresón lneal múltple Técnca que pretende determnar la combnacón lneal de varables ndependentes cuyos cambos son los mejores predctores de los cambos expermentados por la varable dependente. Todas las varables que ntervenen en la regresón son métrcas, aunque admte la posbldad de trabajar con varables ndependentes no métrcas s se emplean varables fctcas para su transformacón en varables dam. 49 Modelo logt Modelo de eleccón dscreta en el que la funcón de dstrbucón de probabldad de la varable perturbacón es la funcón logístca. Modelo logt multnomal Modelo logt en el que la varable dependente es poltómca en lugar de dcotómca. Modelo probt Modelo de eleccón dscreta en el que la funcón de dstrbucón de probabldad de b, varable perturbacón es la funcón normal. 50 5
26 Análss conjunto Técnca que se emplea para entender cómo conforman los ndvduos sus preferencas haca los objetos, normalmente marcas o productos. Segmentacón jerárquca Técnca de análss de la dependenca que tene por objeto dstngur grupos de elementos homogéneos en una poblacón a través de un proceso teratvo descendente de partcón de la muestra total en sucesvos grupos en vrtud del valor adoptado por la varable dependente, el cual es funcón de los valores presentados por las varables ndependentes. 51 Análss con clases latentes Técnca que busca dstngur en una muestra grupos de elementos homogéneos en funcón de los valores que adopta una varable latente no métrca. Tales valores son las categorías de esa varable, las cuales recben el nombre de clases latentes. Análss con ecuacones estructurales (o análss de estructuras de covaranzas) Técnca que permte analzar varas relacones de dependenca que se presentan smultáneamente. 5 6
27 Técncas de análss de la nterdependenca Se ncluyen en esta categoría las sguentes: el análss factoral y por componentes prncpales, el análss de correspondencas, el análss de conglomerados, el escalamento multdmensonal y el análss con clases latentes. En el cuadro sguente se observan algunas característcas dferencadoras entre ellas, como son el tpo de varables que permten manejar y qué clase de elementos componen los grupos que resultan de la aplcacón de cada una. 53 Técncas de análss de la nterdependenca. Técnca Varable Forma grupos de Análss factoral y por componentes prncpales Análss correspondencas de Métrca No métrca Análss de conglomerados Métrca y no métrca Escalamento multdmensonal Métrca y no métrca Varables Categorías de varables Objetos Objetos Análss con clases latentes No métrcas Objetos y categorías de varables 54 7
28 Análss factoral Técnca de análss de la nterdependenca presentada por un certo número de varables susceptble de ser sntetzada en un conjunto de factores comunes que subyacen tras ella. Dchos factores pueden ser comunes (captan la varabldad compartda por todas las varables), o específcos (captan la varabldad propa de cada varable, sn relacón con las demás). Análss por componentes prncpales Técnca de análss de la nterdependenca presentada por un certo número de varables susceptble de ser sntetzada en un conjunto de factores comunes que subyacen tras ella. Dchos factores o componentes buscan explcar la mayor proporcón posble de la varabldad total, lo que quere decr que, a dferenca de lo que ocurre en análss factoral. no exsten factores específcos. 55 Análss de correspondencas Técnca basada en el estudo de la asocacón entre las categorías de múltples varables no métrcas, que persgue la elaboracón de un mapa perceptual que ponga de manfesto dcha asocacón en modo gráfco. Análss de conglomerados (o análss cluster) Técnca cuyo fn es clasfcar sujetos u objetos en funcón de certas característcas de modo que los elementos de cada grupo sean muy smlares entre sí. 56 8
29 Escalamento multdmensonal Técnca cuyo fn es elaborar una representacón gráfca que permta conocer la magen que los ndvduos se crean de un conjunto de objetos por posconamento de cada uno en relacón a los demás. Análss con clases latentes Técnca que busca dstngur en una muestra grupos de elementos homogéneos en funcón de los valores que adopta una varable latente no métrca. Tales valores son las categorías de esa varable, las cuales recben el nombre de clases latentes. 57 Otras técncas Eleccón multcrtero dscreta Conjunto de métodos de ayuda en la resolucón de problemas de decsón en los que se han de tener en cuenta dferentes puntos de vsta o crteros y en los que se baraja un número fnto de alternatvas. Data mnng (o mnería de datos o extraccón de datos) Proceso medante el cual se explora y analza un gran volumen de datos con el fn de descubrr relacones, reglas o patrones de comportamento en ellos que sean de utldad para el usuaro en la toma de decsones. Análss con redes neuronales Técnca cuya forma de proceder pretende replcar el funconamento del cerebro humano, ntentando aprender de los errores cometdos en aras de la consecucón del mejor resultado posble. 58 9
30 La eleccón de una técnca concreta A la luz de lo expuesto en este apartado se deduce que la eleccón de una determnada técnca de análss multvarable pasa por dar respuesta preva a preguntas como Sgue un fn predctvo o clasfcatoro? Se puede dstngur entre varables dependente e ndependentes? Cuántas varables dependentes hay? Qué tpo de escalas de medda presentan las varables? Estas se dstrbuyen normalmente? 59 TECNICAS DE ANÁLISIS DE LA DEPENDENCIA VARIABLE INDEPENDIENTE Métrca No métrca VARIABLE DEPENDIENTE VARIABLE DEPENDIENTE Métrca No métrca Métrca No métrca Smple Múltple Smple Múltple Regresón Lneal múltple Análss con ecuacones estructurales¹ Análss Dscrmnante Modelos de Eleccón dscreta ANOVA, ANCOVA Análss conjunto Segmentacón Jerárquca Regresón lneal con varable fctcas MANOVA MANCOCA² Análss con Ecuacones estructurales¹ Modelo de eleccón dscreta con varable Fctcas Análss conjunto Segmentacón Jerárquca Análss con Clases latentes³ 60 30
31 TÉCNICAS DE ANÁLISIS DE LA INTERDEPENCIA VARIABLES Métrcas No métrca Análss factoral Análss por componentes prncpales Análss de conglomerados Escalamento multdmensonal Análss de correspondencas Análss de conglomerados Escalamento multdmensonal Análss con clase latentes OTRAS TÉCNICAS Eleccón multcrtero dscreta Redes neuronales Data mnng 61 Técncas a estudar Análss de varanza de un factor Regresón lneal smple Regresón lneal múltple Regresón logístca Análss Factoral De análss de la dependenca En SPSS menú Analzar/Comparar Medas De análss de la dependenca En SPSS menú Analzar/Regresón De análss de la dependenca En SPSS menú Analzar/Regresón De análss de la dependenca En SPSS menú Analzar/Regresón/Logístca De análss de la nterdependenca En SPSS menú Analzar/Reduccón de datos 6 31
32 Análss de Varanza de un factor El análss ANOVA de un factor Datos y supuestos Prueba de homogenedad de Varanzas. Comparacones post-hoc Prueba no parámetrca H de Kruskal-Walls 63 Análss de Varanza Análss de varanza de un factor El análss ANOVA de un factor es una generalzacón de la prueba T para dos muestras ndependentes al caso de dseños con más de dos muestras. Srve para comparar varos grupos en una varable cuanttatva. Varable Independente (VI) o factor Varable Dependente (VD) Varable categórca (Nomnal u ordnal) que defne los grupos Varable cuanttatva en la que se desea comparar los grupos 64 3
33 Análss de varanza de un factor Datos. Los valores de la varable de factor deben ser enteros y la varable dependente debe ser cuanttatva (nvel de medda de ntervalo). Supuestos. Cada grupo es una muestra aleatora ndependente procedente de una poblacón normal. El análss de varanza es robusto a las desvacones de la normaldad, aunque los datos deberán ser smétrcos. Los grupos deben proceder de poblacones con varanzas guales. Para contrastar este supuesto, utlce la prueba de Levene de homogenedad de varanzas. 65 Análss de varanza de un factor La hpótess que se pone a prueba en el ANOVA de un factor es que las medas poblaconales ( las medas de la VD en cada nvel de la VI) son guales. H... 0 : 1 3 n S las medas poblaconales son guales, eso sgnfca que los grupos no dferen en la VD y que, en consecuenca, la VI o factor es ndependente de la VD. El procedmento para poner a prueba la Ho consste en obtener un estadístco, llamado F, que refleja el grado de parecdo exstente entre las medas que se están comparando. F 1 n S Y j 66 33
34 Análss de varanza de un factor F 1 n S Y j El numerador del estadístco F es una estmacón de la varanza poblaconal basada en la varabldad exstente entre las medas de cada grupo El denomnador del estadístco F es una estmacón de la varanza poblaconal, basada en la varabldad exstente dentro de cada grupo ( j se refere a los dstntos grupos o nveles del factor) S las medas poblaconales son guales, las medas muestrales de los dferentes grupos serán parecdas, exstendo entre ellas tan sólo dferencas atrbubles al azar. En ese caso, la estmacón ( basada en las dferencas entre las medas muestrales) reflejará el msmo grado de varacón que la estmacón basada en las dferencas entre las puntuacones ndvduales dentro de cada grupo) y el cuocente F tomará un valor próxmo a Análss de varanza de un factor Por el contraro, s las medas muestrales son dstntas, la estmacón reflejará mayor grado de varacón que la estmacón caso el cuocente F tomará un valor mayor que 1. Cuanto más, en cuyo dferentes sean las medas muestrales, mayor será el valor de F. 1 F 1 n S Y j S las poblacones muestreadas son normales y sus varanzas guales, el estadístco F se dstrbuye según el modelo de probabldad F de Fsher Snedecor Los grados de lbertad del numerador son el número de grupos menos 1;los del denomnador el número total de observacones menos el número de grupos
35 Análss de varanza de un factor Ejemplo: ANOVA de un factor Consderemos el archvo de Datos de empleados Varable dependente: Salaro actual (salaro) Factor: Categoría laboral (catlab) Salaro actual Descrptvos Admnstratvo Segurdad Drectvo Total Desvacón N Meda típca Mínmo Máxmo 363 $7, $7, $15,750 $80,000 7 $30, $, $4,300 $35,50 84 $63, $18, $34,410 $135, $34, $17, $15,750 $135, Análss de varanza de un factor ANOVA Salaro actual Inter-grupos Intra-grupos Total Suma de cuadrados gl Meda cuadrátca F Sg , , ,481, , , La tabla ANOVA muestra el resultado del estadístco F ( cuocente entre dos estmadores dferentes de la varanza poblaconal. Uno de los estmadores se obtene a partr de la varacón exstente entre las medas de los grupos (varacón Inter-grupos). El otro estmador se obtene a partr de la varacón exstente entre las puntuacones dentro de cada grupo (varacón Intra-grupos) La tabla ofrece una cuantfcacón de ambas fuentes de varacón (Suma de cuadrados), los grados de lbertad asocados a cada suma de cuadrados (gl) y el valor concreto que adopta cada estmador de la varanza poblaconal (medas cuadrátcas, que se obtenen dvdendo las sumas de cuadrados entre sus correspondentes grados de lbertad) 70 35
36 Análss de varanza de un factor ANOVA Salaro actual Inter-grupos Intra-grupos Total Suma de cuadrados gl Meda cuadrátca F Sg , , ,481, , , El cuocente entre las dos medas cuadrátcas (la nter-grupos y la ntra-grupos) proporcona el valor del estadístco F, el cual aparece acompañado de su correspondente nvel de sgnfcacón observado (Sg) Puesto que el nvel crítco (Sg=0,000) es menor que 0,05, debe rechazarse la hpótess de gualdad de medas Puede conclurse que las poblacones defndas por la varable catlab no poseen el msmo salaro medo: hay al menos una poblacón cuyo salaro medo dfere del de al menos otra. 71 Análss de varanza de un factor Prueba de homogenedad de las varanzas El estadístco F del ANOVA de un factor se basa en el cumplmento de dos supuestos fundamentales: normaldad y homocedastcdad Normaldad sgnfca que la varable dependente se dstrbuye normalmente en la J poblacones muestreadas (tantas como grupos defndos por la varable factor); s los tamaños de los grupos son grandes, el estadístco F se comporta razonablemente ben ncluso con dstrbucones poblaconales sensblemente alejadas de la normaldad Homocedastcdad o gualdad de varanzas sgnfca que la J poblacones muestreadas poseen la msma varanza; con grupos de dstnto, tamaño el ncumplmento de este supuesto debe ser cudadosamente vglado. 7 36
37 Prueba de homogenedad de las varanzas. Prueba de Levene La prueba de Levene permte contrastar el supuesto de homogenedad de varanzas, es decr permte contrastar la hpótess de que los grupos defndos por la varable factor proceden de poblacones con las msma varanza Prueba de homogenedad de varanzas Salaro actual Estadístco de Levene gl1 gl Sg. 59, ,000 La tabla contene el estadístco de Levene. Puesto que el nvel crítco es menor que 0,05, se debe rechazar la hpótess de gualdad de varanzas y conclur, que en las poblacones defndas por las tres categorías laborales, las varanzas de la varable salaro no son guales. 73 Salaro actual Welch Brown-Forsythe Pruebas robustas de gualdad de las medas Estadístco a gl1 gl Sg. 16,00 117,31, ,810 93,906,000 a. Dstrbudos en F asntótcamente. El estadístco de Welch y el de Brown-Forsythe contrasta la gualdad de las medas de grupo. Este estadístco es preferble al estadístco F cuando no se puede mantener el supuesto de gualdad de varanzas. Puesto que el nvel crítco asocado a ambos estadístcos es menor que 0,05, se puede rechazar la hpótess de gualdad de medas y conclur que los promedos salarales de las poblacones no son guales 74 37
38 Comparacones post-hoc El estadístco F del ANOVA úncamente permte contrastar la hpótess general de que los J promedos comparados son guales. Rechazar esa hpótess sgnfca que las medas poblaconales comparadas no son guales, pero no permte precsar dónde en concreto se encuentran las dferencas detectadas. Para saber qué meda dfere de qué otra se debe utlzar un tpo partcular de contrastes denomnados comparacones múltples post-hoc Asumendo varanzas guales Exsten varos métodos, el más utlzado es la opcón Tukey 75 No asumendo varanzas guales Exsten varos métodos, el más utlzado es la opcón Games -Howell En nuestro ejemplo por la prueba de Levene, no podemos asumr que las varanzas poblaconales sean guales por tanto debe prestarse atencón a la opcón de Games- Howell Varable dependente: Salaro actual Games-Howell Comparacones múltples (I) Categoría laboral Admnstratvo Segurdad Drectvo (J) Categoría laboral Segurdad Drectvo Admnstratvo Drectvo Admnstratvo Segurdad *. La dferenca entre las medas es sgnfcatva al nvel.05. Intervalo de confanza al 95% Dferenca de Límte medas (I-J) Error típco Sg. Límte nferor superor -$3, * $ ,000 -$4, $1, $36,139.58* $,09.91,000 -$40, $31, $3, * $ ,000 $1, $4, $33, * $, ,000 -$37, $8, $36,139.58* $,09.91,000 $31, $40, $33, * $, ,000 $8, $37, Puede conclurse que todos los promedos comparados dferen sgnfcatvamente
39 Análss no paramétrco Prueba de H de Kruskal-Walls La prueba de Mann- Whtney para dos muestras ndependentes fue extendda al caso de más de dos muestras por Kruskal y Walls (195). La stuacón expermental que permte resolver esta prueba es smlar a la estudada a propósto del ANOVA de un factor completamente aleatorzado: J muestras son aleatora e ndependentemente extraídas de J poblacones para averguar s las J poblacones son déntcas o alguna de ellas presenta promedos mayores que otra. Las ventajas fundamentales de esta prueba frente al estadístco F del ANOVA de un factor son dos: (1) no necesta establecer supuestos sobre las poblacones orgnales tan exgentes como los del estadístco F (normaldad, homocedastcdad); y () permte trabajar con datos ordnales. S se cumplen los supuestos en los que se basa el estadístco F, la potenca de éste es mayor que la que es posble alcanzar con el estadístco H de Kruskal- Walls. 77 Ejemplo: Pruebas no paramétrcas /Varas muestras ndependentes H de Kruskal-Walls Rangos Esta dístcos de contraste a,b Salaro actual Categoría laboral Admnstratvo Segurdad Drectvo Total Rango N promedo , , , Ch-cuadrado gl Sg. asntót. Salaro actual 07,679,000 a. Prueba de Kruskal-Walls b. Varable de agrupacón: Categoría laboral La prmera tabla ofrece el tamaño de cada grupo (N) y los rangos promedos resultantes de la asgnacón de rangos a las puntuacones de los tres grupos. En la segunda tabla, puesto que el nvel crítco es menor que 0,05, se puede rechazar la hpótess de gualdad de medas poblaconales y conclur que las poblacones comparadas dferen en salaro actual
40 Análss de regresón lneal Análss de regresón lneal smple Análss de regresón lneal múltple 79 Análss de regresón lneal smple Análss de regresón con dos varables: Algunas deas báscas Concepto de funcón de regresón poblaconal Sgnfcado del térmno lneal Especfcacón estocástca de la FRP Funcón de regresón muestral (FRM) Análss de regresón con dos varables: problema de estmacón. Método de Mínmos cuadrados ordnaros (MCO) Modelo clásco: Supuestos detrás del método MCO Precsón o errores estándar de MCO Propedades de los estmadores de MCO Coefcente de determnacón r:una medda de bondad de ajuste Coefcente de correlacón muestral y propedades de r Interpretacón de la pendente 80 40
41 Análss de regresón lneal smple Modelo clásco de regresón lneal normal (MCRLN) Regresón con dos varables: estmacón de ntervalos y pruebas de hpótess. Intervalos de confanza Pruebas t Aplcacón problemas de predccón Predccón del valor de la meda condconal Predccón de un valor ndvdual Formas funconales de los modelos de regresón Modelo log-lneal Modelos semlogartmcos 81 Análss de regresón lneal smple Algunas deas báscas El análss de regresón se relacona en gran medda con la estmacón y/o predccón de la meda (de la poblacón) o valor promedo de la varable dependente, con base en los valores conocdos o fjos de las varables explcatvas. Consderemos los datos de la tabla sguente, la que se refere a la poblacón total de 60 famlas de una comundad hpotétca, así como a su ngreso semanal (X) y a su gasto de consumo semanal (Y), dados en dólares. 8 41
42 Algunas deas báscas Tabla 1 Gastos de consumo famlar semanal Y,$. Ingreso famlar semanal X,$ Y\X Total Medas Las 60 famlas se dvden en 10 grupos de ngresos (de $80 a $60). Se tenen 10 valores fjos de X y los correspondentes valores de Y para cada uno de los valores X; así que hay 10 subpoblacones Y 83 Algunas deas báscas Se tenen 10 valores medos para las 10 subpoblacones de Y. A estos valores medos se les denomna valores esperados condconales, en vsta de que dependen de los valores dados a la varable condconal X. Se denota por E(Y/X) Resulta mportante dstngur dchos valores condconales esperados del valor esperado ncondconal del gasto de consumo semanal, E(Y). E(Y)=77/60=11, Es ncondconal en el sentdo de que para obtener esta cfra se omten los nveles de ngresos de las dversas famlas 84 4
43 Algunas deas báscas Cuál es el valor esperado del gasto de consumo semanal de una famla? La meda ncondconal: $11,0 Cuál es el valor esperado del gasto de consumo semanal de una famla cuyo ngreso mensual es, dgamos, $140? La meda condconal: $101 Saber el nvel de ngreso nos permte predecr mejor el valor medo del gasto de consumo 85 Algunas deas báscas Se puede observar en él gráfco de dspersón, al unr las medas condconales la recta de regresón poblaconal (RRP). ( o regresón de Y sobre X). El adjetvo poblaconal se debe al hecho de que en este ejemplo se consderó una poblacón de 60 famlas. Gráfco de dspersón Gasto de consumo v/s Ingreso A pesar de la varabldad del gasto para cada ngreso, en promedo el consumo semanal se ncrementa en la msma medda que el ngreso Ingreso semanal 86 43
44 Curva de regresón poblaconal Desde el punto de vsta geométrco, una curva de regresón poblaconal es smplemente el lugar geométrco de las medas condconales de la varable dependente para los valores fjos de la (s) varables explcatva(s). Es la curva que conecta las medas de las subpoblacones de Y que corresponden a los valores del regresor X 87 Concepto de funcón de regresón poblaconal (FRP) Es claro que cada meda condconal E(Y/X) es funcón de X, donde X es un valor dado de X. E(Y/X)=f(X) (1) y f(x) denota alguna funcón de la varable explcatva X. Qué forma toma la funcón f(x)? En una stuacón real no tenemos la totaldad de la poblacón para efectuar el análss. La forma funconal de la FRP es, una pregunta empírca, aunque en casos específcos la teoría puede tener algo que decr. Por ejemplo, un economsta podría plantear que el gasto de consumo está relaconado lnealmente con el ngreso. Por tanto, como una prmera aproxmacón podemos suponer que la FRP es una funcón lneal de X E ( Y / X ) 1 X 88 44
45 Ecuacón de regresón poblaconal FRP E ( Y / X ) 1 X Ecuacón de regresón poblaconal FRP () Donde 1 y son parámetros no conocdos pero fjos que se denomnan coefcentes de regresón. En el análss de regresón el nterés es estmar la FRP, es decr estmar los valores de no 1 y conocdos con base en las observacones de Y y X 89 Sgnfcado del térmno lneal Lnealdad en las varables Se dce que una funcón Y=f(X) es lneal en X s X aparece elevado a una potenca o índce de 1 solamente y dcha varable no está multplcada n dvdda por alguna otra varable E ( Y / X ) X 1 es lneal en X. Geométrcamente la curva de regresón es una línea recta Lnealdad en los parámetros Se dce que una funcón es lneal en el parámetro, 1 por ejemplo s 1 aparece elevado a una potenca o índce de 1 solamente y no está multplcado n dvddo por nngún otro parámetro. E ( Y / X ) 1 X Es lneal en los parámetros pero no es lneal en la varable X 90 45
46 Especfcacón estocástca de la FRP Qué podemos decr sobre la relacón entre el gasto de consumo de una famla ndvdual y un nvel dado de ngresos? Se observa en la fgura, que dado el nvel de ngresos de X, el gasto de consumo de una famla ndvdual está agrupado alrededor del consumo promedo de todas las famlas en ese nvel de X, esto es, alrededor de su esperanza condconal. Por consguente, podemos expresar la desvacón de un Y ndvdual alrededor de su valor esperado de la sguente manera: u Y E( Y / X ) o Y E( Y / X ) u (3) Donde la desvacón u es una varable aleatora no observable que toma valores postvos o negatvos. Técncamente, u es conocda como perturbacón estocástca o térmno de error estocástco. 91 Especfcacón estocástca de la FRP Se puede decr que el gasto de una famla ndvdual, dado su nvel de ngresos, puede ser expresado como la suma de dos componentes Y E( Y / X ) u (4) La meda del gasto de consumo de todas las famlas con el msmo nvel de ngresos. Componente aleatoro. Es un susttuto para todas aquellas varables que son omtdas del modelo pero que colectvamente afectan a Y 9 46
47 Especfcacón estocástca de la FRP S se supone que E( Y / X ) es lneal en X como en la ec () la ecuacón (3) puede escrbrse como Y E( Y / X ) u 1 X u (5) La ecuacón plantea que el gasto de consumo de una famla está relaconado lnealmente con su ngreso, más el térmno de perturbacón. Así los gastos de consumo ndvdual, dado X=US$80, pueden ser expresados como Y Y Y Y Y u u u u u Ahora, s se toma el valor esperado de (5), obtenemos Y E( Y Especfcacón estocástca de la FRP E( Y / X / X ) Puesto que ) u E E( Y / X ) E( Y/X ) (5) E( u E( u / X / X E Y / X ) es lo msmo que E Y / X ) ( Implca que E u / X ) 0 (6) ( ) ) ( Así, el supuesto de que la recta de regresón pasa a través de las medas condconales de Y mplca que los valores de la meda condconal de u son cero
48 Especfcacón estocástca de la FRP La especfcacón estocástca Y E( Y / X ) u 1 X u (7) Tene la ventaja que muestra claramente otras varables además del ngreso, que afectan el gasto de consumo y que un gasto de consumo de famlas ndvduales no puede ser explcado en su totaldad solamente por la(s) varable(s) ncluda(s) en el modelo de regresón. 95 Funcón de regresón muestral (FRM) En la práctca lo que se tene al alcance no es más que una muestra de valores de Y que corresponden a algunos valores fjos de X. Por consguente la labor ahora es estmar la FRP con base en nformacón muestral. Supóngase que no se conocía la poblacón de la tabla 1 y que la únca nformacón que se tenía era una muestra de valores de Y selecconada aleatoramente para valores dados de X tal como se presenta en la tabla Y X De la muestra de la tabla, se puede predecr el gasto de consumo semanal promedo Y para la poblacón correspondente a los valores de X selecconados? Se puede estmar la forma FRP a partr de la nformacón muestral? Tabla Prmera muestra 96 48
49 Funcón de regresón muestral (FRM) Consderemos otra muestra tomada de la poblacón de la tabla 1. Las rectas de la fgura se conocen como rectas de regresón muestral. En general, se podrían obtener N FRM dferentes para N muestras dferentes y estas FRM no necesaramente son guales Y X Tabla 3 Segunda muestra 97 Ahora, en forma análoga a la FRP en la cual se basa la recta de regresón poblaconal, se puede desarrollar el concepto de funcón de regresón muestral. La contraparte muestral de (1) puede escrbrse como Donde Y Y 1 X estmador de E(Y/X) Es la contraparte de E( Y / ) 1 X X 1 estmador de 1 estmador de Un estmador, conocdo tambén como estadístco (muestral) es smplemente una regla, o método que dce cómo estmar el parámetro poblaconal a partr de la nformacón sumnstrada por la muestra dsponble. Un valor numérco partcular obtendo por el estmador en una aplcacón es conocdo como estmado
50 Funcón de regresón muestral (FRM) en su forma estocástca La FRM en su forma estocástca se puede expresar como Y 1 X (8) denota el térmno resdual (muestral) Donde Conceptualmente es análogo a u y puede ser consderado como un estmado de u El objetvo prncpal en el análss de regresón es estmar la FRP Y 1 X Con base en la FRM Y 1 X 99 Rectas de regresón muestral y poblaconal Debdo a fluctuacones muestrales el estmado de la FRP basado en FRM es, en el mejor de los casos, una aproxmacón
51 Rectas de regresón muestral y poblaconal Para X=X, se tene una observacón muestral Y=Y. En térmnos de la FRM, la Y observada puede ser expresada como Y Y Y en térmnos de la FRP, puede ser expresada como Y E( Y / ) X Dado que la FRM es apenas una aproxmacón de la FRP, se puede dseñar un método que haga que esta aproxmacón sea lo más ajustada posble? 101 Funcón de regresón smple: problema de estmacón La tarea consste en estmar la funcón de regresón poblaconal (FRP) con base en la funcón de regresón muestral (FRM) en la forma más precsa posble. Los dos métodos de estmacón que suelen utlzarse son: 1) Los mínmos cuadrados ordnaros (MCO) ) La máxma verosmltud (MV). El método de MCO es el que más se emplea en el análss de regresón por ser en gran medda más ntutvo y matemátcamente más smple
52 Método de mínmos cuadrados ordnaros (MCO) El método MCO se atrbuye a Carl Fredrch Gauss un matemátco alemán. Bajo certos supuestos el método tene algunas propedades estadístcas muy atractvas que lo han convertdo en uno de los más efcaces y populares del análss de regresón. Prmero se estma u Y 1 X (9) que muestra que los resduos son smplemente las dferencas entre los valores observados y los estmados de Y. Ahora, dados n pares de observacones de Y y X, se está nteresado en determnar la FRM de tal manera que esté lo más cerca posble a la Y observada. 103 Método de mínmos cuadrados ordnaros (MCO) Con este fn se puede adoptar el sguente crtero: selecconar la FRM de tal manera que la suma de los resduos : sea la menor posble. u Y Y Este crtero, no es muy bueno porque a todos los resduos se les da la msma mportanca sn consderar qué tan cerca o qué tan dspersas estén las observacones ndvduales de la FRM. Debdo a lo anteror, es muy posble que la suma algebraca de los resduos sea pequeña (aun cero) a pesar de que las están bastante dspersas alrededor de FRM. u 104 5
53 Valores ajustados y resduos 105 Método de mínmos cuadrados ordnaros (MCO) Se puede evtar este problema s se adopta el crtero de mínmos cuadrados, el cual establece que la FRM puede determnarse en forma tal que u Y Y Y 1 X (10) sea la menor posble. Este método da más peso a los resduos tales como 1 y u 4 que a los resduos u y u u 3 El procedmento de MCO genera las sguentes ecuacones para estmar 1 y donde n es el tamaño de la muestra
54 Método de mínmos cuadrados ordnaros (MCO) Y Y X n 1 1 X X X Ecuacones normales Resolvendo las ecuacones normales smultáneamente se obtene x y x 1 Y - X Estmadores de mínmos cuadrados 107 Modelo clásco de regresón lneal: supuestos detrás del método MCO El modelo de Gauss, modelo clásco o estándar de regresón lneal (MCRL) el cual es el cmento de la mayor parte de la teoría econométrca, plantea 10 supuestos. Supuesto 1: Modelo de regresón lneal El modelo de regresón es lneal en los parámetros Y 1 X modelo smple Supuesto : Los valores de X son fjos en muestreo repetdo. Sgnfca que el análss de regresón es un análss de regresón condconal, esto es, condconado a los valores dados del (los) regresor X
55 Supuesto 3: El valor medo de la perturbacón u es gual a cero. Dado el valor de X, el valor esperado del térmno aleatoro de perturbacón u es cero. E( u / X ) 0 Nótese que el supuesto E(u/X)=0 mplca que E ( Y / X ) 1 X 109 Supuesto 4: Homocedastcdad o gual varanza de u. Dado el valor de X, la varanza de u es la msma para todas las observacones, es decr, las varanzas condconales de u son déntcas. var( u/ X) Homocedastcdad Heterocedastcdad
56 Supuesto 5: No exste auto correlacón entre las perturbacones. Dados dos valores cualquera de X, X y Xj, la correlacón entre dos u y uj es cero. cov( u, uj / X, X j ) Supuesto 6: La covaranza entre u y X es cero o E(uX)=0 cov( u, X Supuesto 7: El número de observacones n debe ser mayor que el número de parámetros por estmar. ) 0 Supuesto 8: Varabldad en los valores de X. No todos los valores de X en una muestra dada deben ser guales. var( X ) 0 Recordar que la varanza muestral de X es var( X ) X n 1 X 11 56
57 Supuesto 9: El modelo de regresón está correctamente especfcado. Supuesto 10:No hay multcolnealdad perfecta. No hay relacones perfectamente lneales entre las varables explcatvas. 113 Precsón o errores estándar de los mínmos cuadrados estmados Lo que se requere es alguna medda de confabldad o precsón de los estmadores. En estadístca la precsón de un valor estmado es medda por su error estándar (ee). Los errores estándar de los MCO estmados pueden obtenerse de la sguente manera var( 1 y ) ee( ) x x (11) Nota: El error estándar es la desvacón estándar de la dstrbucón muestral del estmador, y la dstrbucón muestral es una dstrbucón del conjunto de valores del estmador obtendos de todas las muestras posbles de gual tamaño de una poblacón dada
58 Precsón o errores estándar de los mínmos cuadrados estmados Nota: es estmada medante la fórmula n u Suma de resduos al cuadrado (SRC) Número de grados de lbertad (1) Donde. es el estmador de MCO de la verdadera El térmno número de grados de lbertad sgnfca el número total de observacones n menos el número de restrccones puestas en ellas. 115 Error estándar de la regresón n u (13) Es la desvacón estándar de los valores de Y alrededor de la recta de regresón estmada, la cual es utlzada como una medda resumen de la bondad del ajuste de dcha recta
59 Propedades de los estmadores de mínmos cuadrados: Teorema de Gauss-Markov Dados los supuestos del modelo de regresón lneal clásca, los estmatvos de mínmos cuadrados poseen propedades deales u óptmas, las cuales se encuentran resumdas en el teorema de Gauss Markov Un estmador de MCO es el mejor estmador lneal nsesgado (MELI) de s: 1. Es lneal, es decr, una funcón lneal de una varable aleatora tal como la varable dependente Y en el modelo de regresón. 117 Propedades de los estmadores de mínmos cuadrados: Teorema de Gauss-Markov. Es nsesgado, es decr, su valor promedo o esperado, E ( ) es gual al valor verdadero, E( ) 3. Tene varanza mínma entre la clase de todos los estmadores lneales nsesgados; a un estmador nsesgado con varanza mínma se le conoce como estmador efcente
60 Teorema de Gauss-Markov En el contexto del análss de regresón se puede demostrar que los estmadores de MCO son MELI Teorema de Gauss-Markov: Dados los supuestos del modelo clásco de regresón lneal, los estmadores de mínmos cuadrados, en la clase de estmadores lneales nsesgados, tenen varanza mínma; es decr son MELI 119 Coefcente de determnacón r Una medda de la bondad del ajuste La cantdad r se conoce como coefcente de determnacón (muestral) y es la medda más frecuente utlzada de la bondad del ajuste de una recta de regresón. Mde la proporcón o el porcentaje de la varacón total en Y explcada por el modelo de regresón 10 60
61 Coefcente de determnacón r Para calcular r, para cada se escrbe: y y Elevando la expresón al cuadrado en ambos lados y sumando sobre la muestra, se obtene (14) puesto que y ˆ ˆ u 0 y ˆ ˆ x y 11 Coefcente de determnacón r Las dversas sumas de cuadrados que aparecen en la expresón anteror pueden descrbrse de la manera sguente y Y Y (STC) varacón total de los valores reales de y con respecto a su meda muestral, los cuales pueden ser llamados suma total de cuadrados (STC) ˆ ˆ ˆ ˆ y ˆ Y Y Y Y x (SEC) varacón de los valores Y estmados alrededor de su meda Ŷ que apropadamente puede llamarse la suma de los cuadrados debda a la regresón [es decr, debda a la(s) varable(s) explcatva(s)], o explcada por ésta, o smplemente la suma explcada de cuadrados (SEC). Y 1 61
62 Coefcente de determnacón r u ˆ Así, (14) es STC = SEC + SRC (SRC) la varacón resdual o no explcada de los valores de Y alrededor de la recta de regresón, o smplemente la suma de resduos al cuadrado (SRC). 13 Coefcente de determnacón r muestra que la varacón total en los valores Y observados alrededor del valor de su meda puede ser dvdda en dos partes, una atrbuble a la recta de regresón y la otra a fuerzas aleatoras, puesto que no todas las observacones Y caen sobre la recta ajustada. Ahora dvdendo por la STS en ambos lados, se obtene STC = SEC + SRC Ahora, se defne r como r Y Y Y Y SEC STC 14 6
63 Coefcente de determnacón r O en forma alterna r Y u 1 Y 1 SRC STC (15) Coefcente de determnacón La cantdad r así defnda se conoce como el coefcente de determnacón (muestral) y es la medda más frecuentemente utlzada de la bondad del ajuste de una recta de regresón r mde la proporcón o el porcentaje de la varacón total en Y explcada por el modelo de regresón. 15 Coefcente de correlacón muestral Una cantdad estrechamente relaconada con r pero conceptualmente muy dferente de ésta es el coefcente de correlacón, el cual, es una medda del grado de asocacón entre dos varables. Puede ser calculado a partr de O a partr de su defncón r r r x x y y n x n x y x n x y y y (16) 16 63
64 Propedades de r Puede tener sgno postvo o negatvo, dependendo del sgno del térmno en el numerador de (16), el cual mde la covaracón muestral de dos varables. Cae entre los límtes de -1 y 1 Es smétrco por naturaleza; es decr, el coefcente de correlacón entre X y Y (r xy ) es el msmo que entre Y y X (r yx ). Es ndependente del orgen y de la escala S X y Y son estadístcamente ndependentes, el coefcente de correlacón entre ellos es cero; pero s r = O, esto no sgnfca que las dos varables sean ndependentes. En otras palabras, una correlacón gual a cero no necesaramente mplca ndependenca. Es una medda de asocacón lneal o dependenca lneal solamente; su uso en la descrpcón de relacones no lneales no tene sgnfcado. 17 Coefcente de correlacón muestral 18 64
65 Interpretacón de la pendente: Puesto que el coefcente de la pendente es smplemente la tasa de cambo, se mde en las undades de la sguentes proporcón undades de la varabl e dependente (Y) undades de la varable explcatva (X) La nterpretacón del coefcente de la pendente es que s X camba en una undad, la Y camba en promedo en undades 19 Ejemplo; Gasto de consumo famlar e ngreso famlar Consderando una muestra de una poblacón donde X representa ngreso famlar por semana e Y gastos de consumo famlar por semana, se obtenen los sguentes cálculos Y X r 1 4,4545 0,5091 0,961 r se( se( 1 ) ) 0,9809 6,4138 0,0357 Por tanto la línea de regresón estmada es Y 4,4545 0, 5091 X
66 Ejemplo; Gasto de consumo famlar e ngreso famlar Resultados en SPSS Modelo 1 Resumen del modelo R cuadrado Error típ. de la R R cuadrado corregda estmacón,981 a,96,957 6,493 a. Varables predctoras: (Constante), X Modelo 1 (Constante) X a. Varable dependente: Y Coefcentes no estandarzados Coe fcentes a Coefcentes estandarzad os B Error típ. Beta t Sg. 4,455 6,414 3,813,005,509,036,981 14,43, Ejemplo; Gasto de consumo famlar e ngreso famlar Interpretacón: El valor de 1 0,5091 que mde la pendente de la línea, muestra que dentro del rango de la muestra de X comprenddo entre $80 y $60 semanales, a medda que X aumenta, dgamos en $1, el aumento estmado en el promedo de gastos de consumo semanales es de aproxmadamente 51 centavos. El valor de, el cual 1 4,45 corresponde a la nterseccón de la línea, ndca el nvel promedo de los gastos de consumo semanales cuando el ngreso semanal es cero. No obstante, esta es una nterpretacón mecánca de la nterseccón. En el análss de regresón esta nterpretacón lteral del ntercepto no es sempre sgnfcatva, aunque en el ejemplo que estamos consderando se puede argumentar que una famla sn ngreso alguno( ya sea por desempleo, despdo, etc.) puede mantener algún nvel mínmo de gastos de consumo, ya sea tomando dnero prestado o utlzando sus ahorros
67 Ejemplo; Gasto de consumo famlar e ngreso famlar Sn embargo en general, se debe apelar al sentdo común para nterpretar la nterseccón puesto que es muy común que el rango que ha tomado la muestra de valores de X no haya ncludo el valor cero como uno de los valores observados. Quzá sea mejor nterpretar la nterseccón como el efecto medo o promedo que tenen todas las varables omtdas del modelo de regresón sobre el valor de Y. El valor de 0,961 para r cuadrado sgnfca que cerca del 96% de la varacón en los gastos de consumo semanales se explca por la varable ngreso; puesto que r cuadrado puede tener un valor máxmo de 1 solamente, el r cuadrado observado sugere que la línea de regresón muestral se ajusta muy ben a la nformacón. El coefcente de correlacón de 0,9809 muestra que las dos varables, gastos de consumo e ngreso, están muy postvamente correlaconadas. 133 Ejemplo: Salaro y educacón De la poblacón de trabajadores en 1976, sea y = sala, en la que sala se mde, en dólares por hora. Así, para una persona cualquera, s sala = 6.75, el salaro por hora es de 6.75 dólares. Sea x = educ los años de escolardad; por ejemplo, educ = 1 corresponde a la educacón preparatora completa. Puesto que el salaro promedo de la muestra es de 5.90 dólares, el índce de precos al consumdor ndca que esta suma es equvalente a dólares de Con los datos de SALA 1.RAW, en los que n = 56 ndvduos, obtenemos la sguente línea de regresón de MCO (o funcón de regresón muestra!): sala ˆ educ
68 Ejemplo: Salaro y educacón Debemos nterpretar con cudado la ecuacón. La ntercepcón sgnfca lteralmente que una persona sn nstruccón recbe un salaro pronostcado de -90 centavos de dólar por hora, lo que, desde luego, es una tontería. Resulta que nngún membro de la muestra tene menos de ocho años de educacón, lo que explca el pronóstco descabellado de una escolardad de 0 años. Para una persona con ocho años de escolardad, el salaro pronostcado es sala ˆ = (8) = 3.4, o 3.4 dólares por hora (en dólares de 1976). La estmacón de la pendente mplca que un año más de educacón aumenta el salaro promedo en 54 centavos de dólar por hora. 135 Ejemplo: Resultados electorales y gastos de campaña El archvo VOTE 1.RAW contene datos sobre los resultados electorales y los gastos de campaña de 173 contendas bpartdstas para la Cámara de los Representantes estadoundense en En cada contenda hay dos canddatos, A y B. Sea votoa el porcentaje de los votos recbdos por el canddato A y parta el porcentaje de partcpacón de los gastos de su campaña, ambos en el total correspondente. Además de parta, muchos otros factores nfluyen en los resultados electorales (entre ellos la caldad de los canddatos y posblemente las sumas gastadas por A y B). No obstante, podemos estmar un modelo de regresón smple para averguar s gastar más que el contraro produce un porcentaje mayor en la votacón
69 Ejemplo: Resultados electorales y gastos de campaña La ecuacón estmada con las 173 observacones es voˆ toa = parta. Esto sgnfca que, s la partcpacón de los gastos del canddato A aumenta un punto porcentual, éste cas obtene un terco de punto porcentual más de la R votacón total. En la ecuacón de los resultados electorales = Así, la partcpacón en los gastos de campaña explca algo más de 50 por cento de la varacón en los resultados de esta muestra, lo cual es una proporcón bastante consderable. 137 El supuesto de normaldad: El modelo clásco de regresón lneal normal Recordemos que con los supuestos vstos anterormente los estmadores de MCO 1,, satsfacían dferentes propedades estadístcas muy deseables, tales como nsesgamento y varanza mínma. S nuestro objetvo es úncamente la estmacón puntual el método de MCO será sufcente, sn embargo la estmacón puntual es sólo la formulacón de un aspecto de la nferenca estadístca. Nuestro nterés no consste solamente en estmar la funcón muestral de regresón (FRM), sno tambén en utlzarla para obtener nferencas respecto a la funcón de regresón poblaconal (FRP)
70 El supuesto de normaldad: El modelo clásco de regresón lneal normal La regresón lneal normal clásca supone que cada u, está normalmente dstrbuda con Meda: Varanza: Cov( u, u ) : j E(u E u E u ) 0 E( u ) E( u ) u E( u ) j E( u ) j E( u u ) j 0 j Estos supuestos pueden expresarse en forma más compacta como u ~ N(0, ) 139 El supuesto de normaldad La regresón lneal normal clásca supone que la dstrbucón probabílstca de u es normal. La suposcón de normaldad permte utlzar las pruebas estadístcas t, F, Consderemos el ejemplo consumo e ngreso. Obtuvmos que la PMC estmada es de 0,5091, correspondente a una sola estmacón puntual de la PMC de la poblaconal desconocda. Qué tan confable es esta estmacón?. Debdo a fluctuacones muestrales, es posble que una sola estmacón dfera del valor verdadero, aunque en un muestreo repetdo se espera que su valor medo sea gual al valor verdadero E( ) Y 4,4545 0, 5091 X
71 Estmacón de ntervalos Ahora, en estadístca, la confabldad de un estmador puntual se mde por su error estándar. Por consguente, en lugar de depender de un solo estmador puntual, se puede construr un ntervalos alrededor del estmador puntual, por ejemplo, dentro de dos o tres errores estándar a cada lado del estmador puntual, tal que este ntervalo tenga, dgamos, 95% de probabldad de nclur el verdadero valor del parámetro. Esta es la dea básca de la estmacón de ntervalos. 141 Estmacón de ntervalos Consderemos el ejemplo hpotétco consumo-ngreso. La ecuacón Y 4,4545 0, 5091 X muestra que la propensón margnal a consumr (PMC) estmada es 0,5091, la cual consttuye una únca estmacón (puntual) de la PMC poblaconal desconocda que es un (punto) estmado de la poblacón desconocda PMC. Qué tan confable es esta estmacón? Debdo a las fluctuacones muestrales, es probable que una sola estmacón dfera del valor verdadero, aunque en un muestreo repetdo se espera que el valor de su meda sea gual al valor verdadero (Nota: E( ) ) 14 71
72 Estmacón de ntervalos Ahora, en estadístca, la confabldad de un estmador puntual se mde por su error estándar. Por consguente, en lugar de depender de un solo estmador puntual, se puede construr un ntervalo alrededor del estmador puntual, por ejemplo, dentro de dos o tres errores estándar a cada lado del estmador puntual, tal que este ntervalo tenga, dgamos, 95% de probabldad de nclur el verdadero valor del parámetro. Ésta es, a grandes rasgos, la dea básca de la estmacón de ntervalos. Para ser más específco, supóngase que se desea encontrar qué tan" cerca" está por ejemplo, de Con este fn, tratamos de encontrar dos números postvos, y, este últmo stuado entre 0 y 1, tal que la probabldad de que el ntervalo aleatoro, - contenga el verdadero sea Estmacón de ntervalos Smbólcamente Pr - 1 Tal ntervalo, s exste, se conoce como ntervalo de confanza; a 1 - se le denomna coefcente de confanza; y (0 < < 1) se conoce como el nvel de sgnfcanca. Los puntos extremos del ntervalo de confanza se conocen como límtes de confanza (tambén denomnados valores crítcos), sendo el límte de confanza nferor y - el límte de confanza superor. Obsérvese que en la práctca y 1 - son expresados frecuentemente en forma porcentual como 100 y 100(1 - )%
73 Intervalos de confanza para los coefcentes de regresón 1 y Intervalo de confanza de 100(1- ) por cento para - t /se( ) Al regresar a nuestro ejemplo lustratvo de consumo e ngreso encontramos que 0,5091 se( ) 0,0357 S suponemos que que =5%, es decr un coefcente de confanza del 95% entonces la tabla t muestra que para 8 gl, el t crítco es. 306 t 0, Intervalos de confanza para los coefcentes de regresón 1 y Al susttur esos valores se obtene que el ntervalo de confanza del 95% para es el sguente: 0,468 0,5914 La nterpretacón de este ntervalo de confanza es: dado un coefcente de confanza del 95%, a largo plazo, en 95 de cada cen casos, ntervalos como (0,468 ; 0,5914) contendrán el verdadero. Como se advrtó antes, obsérvese que no se puede decr que la probabldad de que el ntervalo específco (0,468 ; 0,5914) contenga el verdadero. de 95% porque este ntervalo es ahora fjo y no aleatoro;por consguente se encontrará o no dentro de él
74 Intervalos de confanza para los coefcentes de regresón 1 y Para el ejemplo consumo-ngreso, el ntervalo de confanza para 1 al 95% es: Utlzando 9, t /se( 39,448 ) Se tene 4,4545 -,306(6,4138) Se debe ser cauteloso al nterpretar el ntervalo de confanza ( 9,6643; 39,448). A largo plazo, en 95 de cada 100 casos, ntervalos como ( 9,6643; 39,448) contendrán el verdadero 1; la probabldad de que este ntervalo fjo ncluya el verdadero 1 es 1 o Prueba de hpótess. Prueba t La dea fundamental detrás de las pruebas de sgnfcanca consste en utlzar un estadístco de prueba ( estmador). Bajo el supuesto de normaldad la varable t 1 1 se( 1 ) sgue la dstrbucón t con N- grados de lbertad. S el valor verdadero de 1 se especfca en la hpótess nula, el valor t puede calcularse fáclmente a partr de la muestra dsponble, pudendo servr por tanto como estadístco de prueba
75 Prueba de hpótess. Prueba t Consderemos nuevamente el ejemplo de consumo -ngreso. Sabemos que 1 0,5091 se( 1) 0,0357 t S 0,5091 0,3 0,0357 5%,,, gl S Ho: 1=0,3 y H1: 1 0,3 5,86 8 entonces t 0,05 luego el t calculado es mayor al t de tabla.306 y por lo tanto se rechaza la hpótess nula El procedmento anteror se denomna prueba t. En el lenguaje de pruebas de sgnfcanca, se dce que un estadístco es estadístcamente sgnfcatvo s el valor del estadístco de prueba se encuentra en la regón crítca. En nuestro ejemplo, el estadístco t es sgnfcatvo y procedemos a rechazar la hpótess nula. 149 Aplcacón problema de predccón Con base en los datos muestrales, se obtuvo la sguente regresón muestral. t Y 4,4545 0, 5091 X Yˆ E( Y ) Donde es el estmador del verdadero correspondente a X dada. Qué uso se puede dar a esta regresón hstórca? Uno es predecr o pronostcar el gasto de consumo futuro Y correspondente a algún nvel dado de ngreso X. Ahora, hay dos clases de predccones: 1) la predccón del valor de la meda condconal de Y correspondente a un valor escogdo X, por ejemplo, que es el punto sobre la recta de regresón poblaconal msma, y ) predccón de un valor ndvdual Y correspondente a X 0. Se llamarán estas dos predccones de predccón meda y la predccón ndvdual
76 Aplcacón problema de predccón Supóngase que Xo = 100 y se desea predecr E(Y I Xo = 100). Ahora, puede demostrarse que la regresón hstórca Y 4,4545 0, 5091 X proporcona la estmacón puntual de esta predccón meda de la sguente forma: Y 0 X (100) Donde Y 0 = estmador de E(Y I Xo). Puede demostrarse que este predctor puntual es el mejor estmador lneal e nsesgado (MELI). Puesto que Y 0 es un estmador, es probable que éste sea dferente de su verdadero valor. La dferenca entre los dos valores dará alguna dea sobre el error de predccón o de pronóstco. 151 Aplcacón problema de predccón se demuestra que en la ecuacón Y 0 X Y está normalmente dstrbuda con meda 0 0 y con una varanza dada por la sguente fórmula: 1 X 0 X var( Y0 ) n X Al reemplazar desconocda por su estmador nsesgado se cumple que la varable Y 0 1 X 0 t ee( Y 0) sgue una dstrbucón t con n - g de l. La dstrbucón t puede ser utlzada por consguente para construr ntervalos de confanza para el verdadero E(Yo I Xo) y para hacer pruebas de hpótess acerca de tal valor de la manera usual, a saber, 1 X 0 - t / Y ee( 0) x 15 76
77 Aplcacón problema de predccón Para los datos del ejemplo (tabla 3.3 anexo 1) var( Y ) y ee(y ) Por consguente, el ntervalo de confanza al 95% para el verdadero E Y / X 0 ) X ( 1 0 es E( Y / X 100) Por tanto, dada X 0 =100, en muestreo repetdo, en 95 de cada 100 ntervalos como el anteror estará ncludo el verdadero valor medo; la mejor estmacón del verdadero valor medo es, por supuesto, la estmacón puntual Predccón ndvdual S nuestro nterés está en predecr un valor ndvdual Y, Y 0 correspondente a un valor dado X, dgamos X 0, entonces el mejor estmador lneal nsesgado de Y 0 está dado tambén por Y 0 X (100) (17) Pero su varanza es la sguente var( Y 0 Y 0 ) E( Y 0 Y 0 ) 1 1 n X 0 X x (18) Puede demostrarse además que Y 0 tambén sgue una dstrbucón normal con meda y varanza dadas por (17) y (18), respectvamente. Susttuyendo desconocda por se cumple que t Y 0 ee( Y Y0) 0 Y 0 tambén sgue una dstrbucón t
78 Predccón ndvdual Por consguente, la dstrbucón t puede utlzarse para hacer nferenca sobre la verdadera Y o. Al contnuar con nuestro ejemplo consumo-ngreso, se ve que la predccón puntual de Y o es , gual a Y y su varanza es Por consguente, el 0 ntervalo de confanza al 95% para Y o correspondente a Xo =100 es ( Y 0 / X 0 100) ) Comparando este ntervalo con E( Y / X 100) Se ve que el ntervalo de confanza para el Y 0 ndvdual es más amplo que el ntervalo para el valor medo de Y Intervalos de confanza para Y meda y para valores ndvduales de Y
79 Formas funconales de los modelos de regresón Consderemos algunos modelos de regresón que pueden ser no lneales en las varables pero que son lneales en los parámetros o que pueden serio medante transformacones apropadas de las varables. En partcular, consderemos los modelos de regresón: 1. El modelo log-lneal. Modelos semlogarítmcos 157 Cómo medr la elastcdad: Modelo Log-Lneal Consdérese el sguente modelo, conocdo como el modelo de regresón exponencal: Y 1 X e El cual puede ser expresado alternatvamente lny ln β1 β ln X μ S escrbmos como lny β ln X μ Donde ln β 1 este modelo es lneal en los parámetros y lneal en los logartmos de las varables Y y X y puede ser estmado por regresón MCO y β
80 Cantdad demandada ln de cantdad demandada Cómo medr la elastcdad: Modelo Log-Lneal Una característca mportante del modelo log-iog, que lo ha hecho muy popular en el trabajo empírco, es que el coefcente de la pendente mde la elastcdad de Y con respecto a X, es decr, el cambo porcentual en Y ante un pequeño cambo porcentual en X dado. Así, s Yrepresenta la cantdad demandada de un ben y X su preco untaro, mde la elastcdad-preco de la demanda, un parámetro de gran nterés en economía. 159 Modelo de elastcdad constante S la relacón entre la cantdad demandada y el preco es como se muestra en la fgura (a ) la transformacón doble-iog presentada en la fgura ( b) dará entonces la estmacón de la elastcdad-preco (- ) Y Y 1 X e lny lny ln β1 β ln X Preco X Ln del Preco lnx
81 Ejemplo Gasto en benes duraderos respecto al gasto de consumo personal total Consderemos datos sobre el gasto de consumo personal total (GCPERT), el gasto en benes duraderos (GASBD), el gasto en benes perecederos (GASBPER) y el gasto en servcos (GASERV), todos meddos en mllones de dólares de 199. (tabla 6.3-Anexo 1) Su póngase que se desea calcular la elastcdad del gasto en benes durables respecto al gasto de consumo personal total. Al grafcar el logartmo del gasto en benes durables en comparacón con el logartmo del gasto de consumo personal total, se observará que la relacón entre las dos varables es lneal. Por tanto, el modelo del doble logartmo podría resultar adecuado. Los resultados de la regresón son: 161 In GASBD = In GCPERT, ee = (0.4341) (0.0514) t = (-.3370)* (37.096)* r² = donde * ndca que el valor p es extremadamente pequeño. Todos estos resultados muestran que la elastcdad de GASBD respecto a GCPERT es de cas 1.90, lo que sugere que s el gasto personal total aumenta 1 %, en promedo, el gasto en benes duraderos se ncrementa cas 1.90%. En consecuenca, el gasto en benes duraderos es muy sensble a los cambos en el gasto de consumo personal. Ésta es una razón por la que los productores de benes duraderos sguen muy de cerca los cambos en el ngreso personal y el gasto de consumo personal
82 Ejemplo: Salaro y ventas Podemos estmar un modelo de elastcdad constante que relacone el salaro del drector ejecutvo con las ventas de la empresa. Sea vtas las ventas anuales de la compañía, meddas en mllones de dólares. Un modelo de elastcdad constante es ln sala 0 1 ln vtas en el que es la elastcdad de sala en relacón con vtas. Este modelo se encuentra entre los de regresón smple, al defnr la varable dependente como y = log(sala) y la ndependente como x = log(vtas). La estmacón de esta ecuacón medante MCO da ln sala ˆ n , R u 0.57 ln vtas El coefcente de ln(vtas) es la elastcdad estmada de sala con respecto a vtas. Implca que un ncremento de uno por cento en las ventas de la compañía aumenta el salaro del drector ejecutvo en alrededor de 0.57 por cento, que es la nterpretacón usual de elastcdad. 163 Cómo medr la tasa de crecmento: Modelo Log-Ln Los economstas, la gente de negocos y los gobernos frecuentemente están nteresados en encontrar la tasa de crecmento de certas varables económcas. tales como poblacón, PNB, oferta monetara, empleo, productvdad, défct comercal. etc. Supóngase que se desea saber la tasa de crecmento del gasto de consumo personal en servcos. Sea Y, el gasto real en servcos en el tempo t, y Yo el valor ncal del gasto en servcos. Recordemos la muy conocda fórmula del nterés compuesto, vsta en los cursos báscos de economía. Y Y 0 (1 r) t (1) Donde r es la tasa de nterés compuesta de Y 164 8
83 Cómo medr la tasa de crecmento: Modelo Log-Ln Tomando el logartmo natural, podemos escrbr lny lny0 t ln(1 r) () Ahora sea 1 lny0 ln(1 r) Se puede escrbr () así lny 1 t (3) Agregando el térmno de perturbacón, se obtene ln Y 1 t (4) Este modelo es gual a cualquer otro modelo de regresón lneal en el sentdo de que los parámetros 1 y son lneales. La únca dferenca es que la varable dependente o regresada es el logartmo de Y y el regresor o varable explcatva es el "tempo", que adquere valores de 1,,3, etc. 165 Cómo medr la tasa de crecmento: Modelo Log-Ln Modelos como ln Y 1 t se denomnan modelos semlog porque solamente una varable (en este caso la regresada) aparece en forma logarítmca. Para fnes descrptvos, un modelo en el cual la varable regresada es logarítmca se denomnará modelo log-ln. En este modelo el coefcente de la pendente mde el cambo proporconal constante o relatvo en Y para un cambo absoluto dado en el valor del regresor (en este caso la varable t ), es decr; cambo cambo relatvo en Y absoluto en X
84 Cómo medr la tasa de crecmento: Modelo Log-Ln S se multplca el cambo relatvo en Y por 100, nos dará entonces el cambo porcentual, o la tasa de crecmento, en Y ocasonada por un cambo absoluto en X, el regresor. Es decr, 100 por da como resultado la tasa de crecmento en Y; 100 por se conoce en la lteratura como la semelastcdad de Y respecto a X. 167 Cómo medr la tasa de crecmento: Modelo Log-Ln Ejemplo: Para lustrar el modelo de crecmento ln Y 1 t consderemos los datos sobre el gasto en servcos proporconados en (tabla 6.3-Anexo 1). Los resultados de la regresón son los sguentes: ln GES T = t ee = (0.003) ( ) t = ( )* (44.86)* r = Nota: GES sgnfca gasto en servcos y el astersco (*) denota que el valor p es extremadamente pequeño
85 Cómo medr la tasa de crecmento: Modelo Log-Ln La nterpretacón de la ecuacón es que durante un perodo de un trmestre, el gasto en servcos se ncrementó a una tasa (trmestral) de 0.743%. Aproxmadamente esto es gual a un crecmento anual de.97%. Puesto que = ln(ges) al comenzo del perodo de análss, s se toma su antlogartmo se tene (bllones de dólares), como el valor ncal de GES (es decr, el valor al fnal del últmo trmestre de 199). 169 Cómo medr la tasa de crecmento: Modelo Log-Ln Ejemplo: Salaro y educacón Recuerde el ejemplo del salaro y la educacón, en el que hcmos la regresón del salaro por hora sobre los años de escolardad. Obtuvmos una estmacón de la pendente de 0.54, que sgnfca que pronostcamos que cada año adconal de nstruccón aumenta en. promedo el salaro por hora en 54 centavos de dólar. A causa del carácter lneal de sala ˆ educ. 0, 54 centavos es el ncremento tanto para el prmer año como para el vgésmo, lo que acaso no sea razonable. Ahora, consderemos ln(sala) como la varable dependente, obtenemos la sguente relacón: ln sala ˆ n 56, R educ
86 Cómo medr la tasa de crecmento: Modelo Log-Ln El coefcente de educ tene una nterpretacón porcentual cuando se multplca por 100: sala aumenta 8.3 por cento por cada año adconal de escolardad. Es lo que entenden los economstas cuando se referen al "rendmento de otro año de estudos". Es mportante recordar que la prncpal razón para tomar el logartmo de sala es mponer un efecto porcentual constante de la educacón en sala. La ntercepcón no es muy sgnfcatva, ya que da el log(sala) pronostcado cuando educ = 0. La R cuadrada muestra que educ explca alrededor de 18.6 por cento de la varacón en log(sala) (que no es sala). 171 El modelo Ln-Log A dferenca del modelo de crecmento recén estudado, en el cual se estaba nteresado en encontrar el crecmento porcentual en Y, ante un cambo untaro absoluto en X, ahora hay nterés en encontrar el cambo absoluto en Y debdo a un cambo porcentual en X. Un modelo que puede lograr este propósto puede escrbrse como Y 1 lnx Para fnes descrptvos, llamamos a este modelo un modelo ln-iog
87 El modelo Ln-Log Interpretacón de la pendente cambo en Y cambo en ln X cambo en Y cambo relatvo en X Smbólcamente, se tene Y X / X En forma equvalente Y X / X Esta ecuacón plantea que el cambo absoluto en Y (= Y) es gual a la pendente multplcada por el cambo relatvo en X. 173 El modelo Ln-Log S este últmo es multplcado por 100 entonces da el cambo absoluto en Y ocasonado por un cambo porcentual en X. Así, s X/X camba en 0.01 undades (o 1%), el cambo absoluto en Y es 0.01( ). Por tanto, s en una aplcacón se encuentra que = 500, entonces el cambo absoluto en Y es (0.01)(500), o 5.0. Por consguente, cuado se utlza MCO para estmar regresones como en Y Y X / 1 lnx se debe multplcar el valor del coefcente de la pendente estmado, por 0.01 o, dvddo entre 100. X
88 El modelo Ln-Log Ejemplo: Como ejemplo del modelo ln-iog, consderemos el gasto almentco en Inda, (tabla.8-anexo 1). S se grafcan los datos, se obtene la gráfca de la fgura. Tal y como esta fgura sugere, el gasto almentco se ncrementa en forma más lenta, conforme el gasto total aumenta, lo cual quzá proporcone sustento a la ley de Engels. Nota: Cuándo resulta útl un modelo ln-log? Se ha encontrado una nteresante aplcacón en los así conocdos modelos de gasto Engel [nombrados en honor del estadístco alemán Emst Engel ( ). Engel postuló que "el gasto total que se dedca a los almentos tende a ncrementarse en progresón artmétca, mentras que el gasto total aumenta en progresón geométrca. 175 El modelo Ln-Log Los resultados de ajustar el modelo ln-iog a los datos son los sguentes: GASAL I = ln GASTOT t = ( )* (5.665)* r = Interpretado de la forma antes descrta, el coefcente de la pendente, que vale cas 57, sgnfca que un ncremento en el gasto total en almentos de 1%, en promedo, propca un ncremento de cas.57 rupas en el gasto en almento de las 55 famlas ncludas en la muestra. (Nota: se dvdó el coefcente estmado de la pendente entre 100.)
89 Análss de regresón múltple Análss de regresón múltple: problema de la estmacón Notacón y supuestos Interpretacón de la ecuacón de regresón múltple Sgnfcado de los coefcentes de regresón parcal Estmacón MCO de los coefcentes de regresón parcal El coefcente de determnacón múltple R El coefcente de correlacón múltple R Análss de regresón múltple: el problema de la nferenca El supuesto de normaldad Prueba de hpótess en regresón múltple Prueba t para coefcentes ndvduales Prueba F de sgnfcacón global Modelos de regresón con varables dcotómcas Problemas en el análss de regresón Estmacón ponderada 177 Análss de regresón múltple El modelo de dos varables, con frecuenca es nadecuado en la práctca. Es el caso del ejemplo consumo ngreso, en donde se supuso mplíctamente que solamente el ngreso X afecta el consumo Y. Pero la teoría económca rara vez es tan smple, ya que, además del ngreso, exsten muchas otras varables que probablemente afectan el gasto de consumo. Por consguente, se necesta amplar el modelo smple de regresón con dos varables para consderar modelos que contengan más de dos varables. La adcón de varables conduce al análss de los modelos de regresón múltple, es decr, a modelos en los cuales la varable dependente, o regresada, Y, depende de dos o más varables explcatvas, o regresoras
90 Modelo de tres varables Generalzando la funcón de regresón poblaconal (FRP) de dos varables se puede escrbr la FRP de tres varables así: Y 1 X 3 X 3 donde Y es la varable dependente, X y X 3 las varables explcatvas (o regresoras). u es el térmno de perturbacón estocástca, e la ésma observacón. Los coefcentes se denomnan coefcentes de regresón parcal Se contnúa operando dentro del marco del modelo clásco de regresón lneal (MCRL). 179 Modelo de tres varables Supuestos Específcamente. se supone lo sguente Valor medo de u, gual a cero E( u / X, X 3 ) 0 para cada No correlacón seral cov( u, u j ) 0 j Homocedastcdad var( u )
91 Supuestos Covaranza entre u y cada varable X gual a cero cov( u, X ) cov( u, X 3 ) 0 No hay sesgo de especfcacón El modelo está especfcado correctamente No hay colnealdad exacta entre las varables X No hay relacón lneal exacta entre X y X 3 Adconalmente, se supone que el modelo de regresón múltple es lneal en los parámetros, que los valores de las regresoras son fjos en muestreos repetdo y que hay sufcente varabldad en dchos valores Interpretacón de la ecuacón de regresón múltple Dados los supuestos del modelo de regresón clásco, se cumple que, al tomar la esperanza condconal de Y a ambos lados de se obtene Y 1 X E( Y / X, X 3 ) 1 X 3X3 Expresado en palabras, de la expresón anteror se obtene la meda condconal o el valor esperado de Y condconado a los valores dados o fjos de las varables X y X 3. Por consguente, gual que en el caso de dos varables, el análss de regresón múltple es el análss de regresón condconal, sobre los valores fjos de las varables explcatvas, y lo que obtenemos es el valor promedo o la meda de Y, o la respuesta meda de Y a valores dados de las regresoras X. Nota: Las propedades de los estmadores MCO del modelo de regresón múltples son smlares a aquellas del modelo con dos varables 3 X
92 Sgnfcado de los coefcentes de regresón parcal Los coefcentes de regresón y coefcentes de regresón parcal. 3 se denomnan mde el cambo en el valor de la meda de Y, E(Y) por undad de cambo en X permanecendo X 3 constante. 3 mde el cambo en el valor medo de Y, E(Y) por undad de cambo en X 3 cuando el valor de X se conserva constante. 183 El coefcente de determnacón múltple R En el caso de tres varables nos gustaría conocer la proporcón de la varacón en Y explcada por las varables X y X conjuntamente. La medda que da esta nformacón es conocda como el coefcente de determnacón múltple y se denota por R ;conceptualmente se asemeja a r. R 1 SRC STC 1 u y R, al gual que r, se encuentra entre 0 y 1. Se dce que el ajuste del modelo es mejor entre más cerca esté R de
93 El coefcente de correlacón múltple R Recuérdese que en el caso de dos varables, se defnó r como el coefcente de correlacón y se ndcó que éste mde el grado de asocacón (lneal) entre las dos varables. El análogo de r para tres o más varables es el coefcente de correlacón múltple, denotado por R, el cual es una medda del grado de asocacón entre Y y todas las varables explcatvas conjuntamente. Aun cuando r puede ser postvo o negatvo, R sempre se consdera postvo. En la práctca, sn embargo, R tene poca mportanca. La medda de mayor sgnfcado es R. 185 Ejemplo: Mortaldad Infantl respecto al PIB per cápta y a la tasa de alfabetzacón en las mujeres Consderemos como ejemplo el comportamento de la mortaldad nfantl (MI) en relacón con el PIB per cápta (PIBPC) y el alfabetsmo femenno meddo por la tasa de alfabetzacón en las mujeres (TAM). A pror. se espera que la TAM tambén ejerza un mpacto negatvo en la MI al gual que el PIBPC. cuando se ntroducen ambas varables en el modelo, se requere elmnar la nfluenca neta de cada regresora. Es decr. se necesta estmar los coefcentes de regresón (parcal) de cada regresora. Por lo tanto. el modelo es: MI 1 PIBPC 3 TAM u
94 Ejemplo: Mortaldad Infantl respecto al PIB per cápta y a la tasa de alfabetzacón en las mujeres Téngase en cuenta que MI es el número de muertes de nños menores de 5 años por cada nacmentos vvos. el PIBPC es el PIB per cápta en 1980 y que la TAM se mde en porcentaje. La muestra se realzó en 64 países. Utlzando un paquete estadístco se obtenen los sguentes resultados: MI ee 63,6416 (11,593) 0,0056PIBPC (0,0019),316TAM R 0,7077 R 0, Interpretacón El coefcente de regresón parcal -0,0056 del PIBPC ndca que s la nfluenca de la TAM se mantene constante, conforme el PIBPC se ncrementa, dgamos en un dólar, en promedo, la mortaldad nfantl dsmnuye en undades. Para hacerlo nterpretable desde el punto de vsta económco, s el PIB per cápta se ncrementara ml dólares, en promedo, el número de muertes de nños menores de 5 años se reducría a 5.6 por cada 1000 nacmentos vvos. El coefcente señala que s la nfluenca del PIBPC se mantene constante, el número de muertes de nños menores de 5 años dsmnuría, en promedo,.3 por cada ml nacmentos vvos, en tanto que la tasa de alfabetzacón en las mujeres subría un punto porcentual. El valor de la nterseccón de cas 63, s se nterpretara de una forma mecancsta, sgnfcaría que s los valores del PIBPC y de la TAM fuesen cero, la mortaldad nfantl promedo sería de aproxmadamente 63 muertes por cada ml nacmentos vvos
95 El valor de la nterseccón de cas 63, s se nterpretara de una forma mecancsta, sgnfcaría que s los valores del PIBPC y de la TAM fuesen cero, la mortaldad nfantl promedo sería de aproxmadamente 63 muertes por cada ml nacmentos vvos. Por supuesto, tal nterpretacón debería tomarse con mucho cudado. El valor de R de cas 0.71 sgnfca que cas 71 % de la varacón en la mortaldad nfantl se explca medante el PIBPC y la TAM, lo cual es un gran porcentaje s se consdera que el valor máxmo que puede tener R es 1l. De todo lo dcho hasta aquí, los resultados de la regresón tenen sentdo. 189 Análss de regresón múltple: el problema de la nferenca El supuesto de normaldad Como ya se sabe, s el únco objetvo es la estmacón puntual de los parámetros de los modelos de regresón, será sufcente el método de mínmos cuadrados ordnaros (MCO), el cual no hace supuestos sobre la dstrbucón de probabldad de las perturbacones u. Pero s el objetvo no sólo es la estmacón sno además la nferenca, entonces, como se analzó para el modelo de regresón smple, se debe suponer que las u sguen alguna dstrbucón de probabldad. Se supuso que las u seguían la dstrbucón normal con meda cero y varanza constante. Se mantene el msmo supuesto para los modelos de regresón múltple. Con el supuesto de normaldad, se halla que los estmadores MCO de los coefcentes de regresón parcal, son los mejores estmadores lneales nsesgados (MELI)
96 El supuesto de normaldad Consderemos nuevamente el ejemplo de la regresón de la mortaldad nfantl (MI) sobre el PIB per cápta (PIBP) y la tasa de analfabetsmo en las mujeres (TAM) para una muestra de 64 países. Los resultados de la regresón se reproducen a contnuacón. MI ee 63,6416 (11,593) 0,0056PIBPC (0,0019),316TAM R 0,7077 R 0,6981 Qué hay respecto a la sgnfcanca estadístca de los resultados observados? Consdérese por ejemplo el coefcente del PIBP ( ). Es estadístcamente sgnfcatvo este coefcente; es decr, es estadístcamente dferente de cero? Ambos coefcentes son estadístcamente sgnfcatvos? 191 Prueba de hpótess sobre coefcentes ndvduales de regresón parcal u ~ N(0, Bajo el supuesto de que entonces, se puede utlzar la prueba t para demostrar una hpótess sobre cualquer coefcente de regresón parcal ndvdual. Para lustrar el procedmento, consdérese la regresón sobre la mortaldad nfantl. La hpótess nula establece que, mantenendo X3 constante (la tasa de alfabetsmo en las mujeres), el ngreso personal dsponble no tene nfluenca (lneal) sobre el gasto personal de consumo. Para probar la hpótess nula, se utlza la prueba t donde: H 0 : 0 y H1 : 0 ) 19 96
97 Prueba de hpótess sobre coefcentes ndvduales de regresón parcal Para el ejemplo consderado se tene t Prueba de hpótess sobre coefcentes ndvduales de regresón parcal Puesto que el valor t calculado de.8187 (en térmnos absolutos) excede el valor crítco t de, se puede rechazar la hpótess nula de que el PIBP no tene nngún efecto sobre la mortaldad nfantl. Para expresarlo en térmnos más postvos, s se mantene la tasa de analfabetsmo para las mujeres constante, el PIB per cápta tene un efecto sgnfcatvo (negatvo) sobre la mortaldad nfantl, como se podría esperar a pror. De forma gráfca, la stuacón es la que se muestra en la fgura anteror. En la práctca, no se tene que suponer un valor partcular de para llevar a cabo la prueba de hpótess. Uno smplemente utlza el valor p dado, que en el caso actual es de La nterpretacón de este valor p (es decr, el nvel exacto de sgnfcanca) es que s la hpótess nula fuese verdadera, la probabldad de obtener un valor t gual a.8187 o mayor (en térmnos absolutos ) es de sólo o 0.65%. que de hecho es una probabldad pequeña, mucho menor que el valor artfcal mente adoptado de = 5%
98 Prueba de hpótess sobre coefcentes ndvduales de regresón parcal Exste una conexón muy estrecha entre la prueba de hpótess y la estmacón del ntervalo de confanza. Para este ejemplo, el ntervalo de 95% de confanza para es - t /se( ) que para de este ejemplo se converte en o sea, el ntervalo de a ncluye al verdadero coefcente con un coefcente de confanza del 95%. Por tanto, s 100 muestras de tamaño 64 se selecconan y 100 ntervalos de confanza como el anteror se forman, entonces se espera que 95 de ellos contengan el verdadero parámetro de poblacón.puesto que el ntervalo no ncluye el valor cero de la hpótess nula, se puede rechazar tal hpótess (que el verdadero es cero con 95% de confanza). 195 Prueba de la sgnfcacón global de la regresón La prueba t hace referenca a la prueba de sgnfcanca ndvdual de los coefcentes de regresón parcal estmados, es decr, bajo la hpótess separada de que cada uno de los verdaderos coefcentes de regresón parcal de la poblacón era cero. Pero ahora consdérese la sguente hpótess: H 0 : 3 Esta hpótess nula es conjunta de que y 3 son guales a cero en forma conjunta o smultánea. Una prueba de tal hpótess se denomna prueba de sgnfcanca global de la recta de regresón observada o estmada, es decr, s Y está relaconada o no lnealmente con X y X 3 a la vez
99 Prueba de la sgnfcacón global de la regresón La sgnfcacón global de la regresón se puede probar con la relacón de la varanza explcada a la varanza no explcada: Esta sgue una dstrbucón F con k-1 y n-k grados de lbertad, donde n es el número de observacones y k es el número de parámetros estmados. R /( k 1) F k 1, n k (1 R ) /( n S la relacón F calculada excede el valor tabulado de F al nvel especfcado de sgnfcacón y grados de lbertad, se acepta la hpótess de que los parámetros de la regresón no son todos guales a cero y que R cuadrado es sgnfcatvamente dferente de cero. H 0 : k) n 0 H 1 : No todas las son cero 197 Modelos de regresón con varables dcotómcas En el análss de regresón, la varable dependente o regresada, está nfluda frecuentemente no sólo por varables de razón de escala (por ejemplo: ngreso, produccón, precos, costos, estatura y temperatura), sno tambén por varables que son esencalmente cualtatvas por naturaleza, o de escala nomnal (por ejemplo, sexo, raza, color, relgón, naconaldad, regón geográfca, trastornos polítcos y aflacón a un partdo). Por ejemplo, mantenendo los demás factores constantes, se ha encontrado que las trabajadoras ganan menos que sus colegas masculnos y que las personas de color ganan menos que las blancas. Este patrón puede resultar de la dscrmnacón sexual o racal, pero cualquera que sea la razón, las varables cualtatvas tales como sexo y raza sí nfluyen sobre la varable dependente y es claro que deben ser ncludas dentro de las explcatvas, o regresoras
100 Modelos de regresón con varables dcotómcas Puesto que tales varables usualmente ndcan la presenca o ausenca de una "cualdad" o atrbuto, tal como femenno o masculno, negro o blanco, católco o no católco, demócrata o republcano son varables de escala nomnal esencalmente. Se podrían "cuantfcar" tales atrbutos medante la elaboracón de varables artfcales que tomaran los valores 0 y 1, donde 1 ndcara la presenca (o la posesón) de ese atrbuto y 0 la ausenca de tal atrbuto. Por ejemplo, el 1 puede ndcar que una persona es de sexo masculno y 0 puede desgnar una de sexo femenno; o el 1 puede ndcar que una persona se ha graduado en la unversdad y 0 que no lo ha hecho y así sucesvamente. Las varables que adqueren tales valores 0 y 1 se llaman varables dcótomas. Tales varables son, por tanto, esencalmente un recurso para clasfcar datos en categorías mutuamente excluyentes, como masculno o femenno. 199 Modelos de regresón con varables dcotómcas Las varables fctcas se pueden usar para establecer cambos en la ordenada en el orgen, cambos en la pendente y cambos tanto en la ordenada en el orgen como en la pendente. Y b b X b D u Y Y b b b X 1 b X 1 b XD b D u b DX u
101 Modelos de regresón con varables dcotómcas S una varable cualtatva tene m categorías, sólo hay que agregar (m-1) varables dcotómcas Ejemplo: Consdérese el sguente modelo: Y 1 D 3D3 X u donde Y = salaro por hora en dólares X = educacón (años de escolardad) D = 1 s es mujer; 0 en otro caso D3 = 1 s no es blanco y no hspano; 0 en otro caso 01 Modelos de regresón con varables dcotómcas En este modelo el sexo y la raza son regresoras cualtatvas y la escolardad es cuanttatva. Está mplícta en este modelo la suposcón de que el efecto dferencal de la varable dcótoma sexo, D, es constante en las dos categorías de raza y el efecto dferencal de la varable dcótoma raza, D3, tambén es constante en los dos sexos. Es decr, s el salaro medo es mayor para los hombres que para las mujeres, se debe a que pertenezcan o no pertenezcan a la categoría de no hspanos n blancos. De gual forma, s por ejemplo los no blancos n hspanos tenen salaros medos menores, se debe a que son hombres o mujeres
102 Modelos de regresón con varables dcotómcas En muchas aplcacones, dcha suposcón puede ser nsostenble. Una mujer no blanca n hspana tal vez gane menor salaro que un hombre de esa msma categoría. En otras palabras, quzá haya una nteraccón entre las dos varables cualtatvas D y D3. Por tanto, su efecto sobre la meda quzá no sea smplemente adtvo, sno multplcatvo, como en el sguente modelo: Y 1 D 3D3 4 DD3 de donde E( Y / D 1, D3 1, X ) Que es la funcón salaro medo por hora para las trabajadoras no blancas n hspanas. X u X 03 Obsérvese que Modelos de regresón con varables dcotómcas = efecto dferencal de ser mujer 3 = efecto dferencal de ser no blanco n hspano 4 = efecto dferencal de ser mujer no blanca n hspana lo cual muestra que el salaro medo por hora de las mujeres no blancas n hspanas es dferente (en una cantdad gual a 4 ) del salaro medo por hora de las mujeres blancas o hspanas. S por ejemplo los tres coefcentes de las varables dcótomas son negatvos, mplcaría que las trabajadoras no blancas n hspanas ganan un salaro medo por hora mucho más bajo que las trabajadoras blancas o hspanas, s se compara con la categoría base, la cual en el ejemplo presente es la de hombres blancos o hspanos
103 Modelos de regresón con varables dcotómcas Ejemplo: Ingresos promedo por hora en comparacón con la escolardad, sexo y raza Los resultados de la regresón basados en el modelo son Y 1 D 3D3 donde Y = salaro por hora en dólares X = educacón (años de escolardad) D = 1 s es mujer; 0 en otro caso D3 = 1 s no es blanco y no hspano; 0 en otro caso Y t R ( ) 0.03 **.3606D n * ( ) 58 X u 1.737D * (-.1803) X * (9.9094) 05 Modelos de regresón con varables dcotómcas donde * ndca los valores p menores que el 5%, y ** señala los valores p mayores que 5%. Los coefcentes dferencales de la nterseccón son estadístcamente sgnfcatvos y tenen los sgnos que se esperaban y la escolardad tene un gran efecto postvo sobre el salaro por hora. Como lo muestra la ecuacón, ceters parbus, los ngresos promedo por hora de las mujeres son nferores por cas $.36;además, los ngresos promedo por hora de los trabajadores no blancos n hspanos tambén son menores por $
104 Modelos de regresón con varables dcotómcas Ahora consderemos los resultados del modelo Y 1 D 3D3 4 DD3 Que ncluye la varable dcotómca de nteraccón. X u Y t ( ) **.3606D * ( ) 1.737D 3 * (-.1803).189 D D (1.740) ** X (9.9095) ** R 0.03 n 58 donde * ndca los valores p menores que el 5%, y ** señala los valores p mayores que 5%. Como se observa las dos varables dcotómcas adtvas sguen sendo estadístcamente sgnfcatvas, pero la varable dcotómca nteractva no está al nvel convenconal del 5% 07 S se consdera estadístcamente sgnfcatva entonces se nterpreta de la sguente manera. S se mantene constante el nvel de educacón y s se añaden los tres coefcentes de las varables dcotómcas entonces se obtendrá -1,964=-,3605-1,73+,18 Lo cual sgnfca que los salaros medos por hora de las trabajadoras no blancas n hspanas es menor por cas $1,96, valor que está entre -,3605 (dferenca sólo debda a sexo) y -1,737 ( dferenca sólo debda a la raza)
105 Problemas en el análss de regresón Multcolnealdad: Se refere al caso en el cual dos o más varables explcatoras en el modelo de regresón están altamente correlaconadas, hacendo dfícl o mposble aslar sus efectos ndvduales sobre la varable dependente. Con multcolnealdad, los coefcentes de MCO estmados pueden ser estadístcamente nsgnfcantes (y aún tener el sgno contraro) aunque R cuadrado puede ser alto. La multcolnealdad puede ser superada a veces o reducrse colecconando más datos, usando nformacón a pror, transformando la relacón funconal, o reducendo una de las varables altamente colneales. 09 Heteroscedastcdad S no se mantene la suposcón de MCO de que la varanza del térmno de error es constante para todos los valores de las varables ndependentes, enfrentamos el problema de la heterocedastcdad. Esto conduce a estmacones sesgadas e nefcentes (es decr, con varanza mayor que la mínma) de los errores estándar ( y así pruebas estadístcas ncorrectas e ntervalos de confanza tambén ncorrectos)
106 Autocorrelacón: Cuando el térmno de error en un período está correlaconado postvamente con el térmno de error en el período anteror, enfrentamos el problema de autocorrelacón (de prmer orden postva). Esto es común en análss de seres de tempo. La presenca de autocorrelacón de prmer orden se prueba utlzando la tabla del estadístco de Durbn- Watson a los nveles de sgnfcacón del 5% o 1% para n observacones y k, varables explcatoras 11 Estmacón ponderada ( MCP- WLS) Los modelos de regresón lneal típcos asumen que la varanza es constante en la poblacón objeto de estudo. Cuando éste no es el caso (por ejemplo cuando los casos con puntuacones mayores en un atrbuto muestran más varabldad que los casos con puntuacones menores en ese atrbuto), la regresón lneal medante mínmos cuadrados ordnaros (MCO, OLS) deja de proporconar estmacones óptmas para el modelo
107 Estmacón ponderada ( MCP- WLS) S las dferencas de varabldad se pueden pronostcar a partr de otra varable, el procedmento Estmacón ponderada permte calcular los coefcentes de un modelo de regresón lneal medante mínmos cuadrados ponderados (MCP, WLS), de forma que se les dé mayor ponderacón a las observacones más precsas (es decr, aquéllas con menos varabldad) al determnar los coefcentes de regresón. Ejemplo. Cuáles son los efectos de la nflacón y el paro sobre los cambos en el preco de las accones? Debdo a que los valores con mayor valor de cotzacón suelen mostrar más varabldad que aquellos con menor valor de cotzacón, la estmacón de mínmos cuadrados ordnaros no generará estmacones que sean óptmas. El método de Estmacón ponderada permte capturar el efecto del preco de cotzacón sobre la varabldad de los cambos en el preco, al calcular el modelo lneal. 13 Estmacón ponderada ( MCP- WLS) Consderacones sobre los datos Datos. Las varables dependente e ndependentes deben ser cuanttatvas. Las varables categórcas, como la relgón, la edad o el lugar de resdenca, han de recodfcarse como varables bnaras (dummy). La varable de ponderacón deberá ser cuanttatva y estar relaconada con la varabldad de la varable dependente Supuestos. Para cada valor de la varable ndependente, la dstrbucón de la varable dependente debe ser normal. La relacón entre la varable dependente y cada varable ndependente debe ser lneal y todas las observacones deben ser ndependentes. La varanza de la varable dependente puede cambar según los nveles de la varable o varables ndependentes, pero las dferencas se deben poder pronostcar en funcón de la varable de ponderacón
108 Regresón Logístca Consderacones sobre los datos Fases fundamentales Fundamentos Funcón logístca Cálculo de las probabldades pronostcadas Interpretacón de los coefcentes El problema de clasfcacón Estadístcos: Puntuacón de Rao, Ch cuadrado, Wald Regresón logístca versus análss dscrmnante 15 Regresón Logístca La regresón logístca resulta útl para los casos en los que se desea predecr la presenca o ausenca de una característca o resultado según los valores de un conjunto de varables predctoras. Es smlar a un modelo de regresón lneal pero está adaptado para modelos en los que la varable dependente es dcotómca. Los coefcentes de regresón logístca pueden utlzarse para estmar la razón de las ventajas (odds rato) de cada varable ndependente del modelo. La regresón logístca se puede aplcar a un rango más amplo de stuacones de nvestgacón que el análss dscrmnante
109 Regresón logístca: Consderacones sobre los datos Datos. La varable dependente debe ser dcotómca. Las varables ndependentes pueden estar a nvel de ntervalo o ser categórcas; s son categórcas, deben ser varables dummy o estar codfcadas como ndcadores (exste una opcón en el procedmento para recodfcar automátcamente las varables categórcas). Supuestos. La regresón logístca no se basa en supuestos dstrbuconales en el msmo sentdo en que lo hace el análss dscrmnante. Sn embargo, la solucón puede ser más estable s los predctores tenen una dstrbucón normal multvarante. Adconalmente, al gual que con otras formas de regresón, la multcolnealdad entre los predctores puede llevar a estmacones sesgadas y a errores típcos nflados. El procedmento es más efcaz cuando la pertenenca a grupos es una varable categórca auténtca. 17 Regresón Logístca El análss de regresón logístca tene como fnaldad prncpal pronostcar la pertenenca a un grupo a partr de una sere de varables ndependentes. Varables ndependentes Grupo 1 Grupo Varable dependente dcotómca Para llevar a cabo un análss de regresón logístca bnara es necesaro dsponer de una varable categórca que defna dos grupos: Los clentes que devuelven un crédto y los que no Los cudadanos que votan y los que no Los pacentes que tenen una determnada enfermedad y los que no
110 Regresón Logístca Varables ndependentes o predctoras (covarables) Grupo 1 Grupo Varable dependente dcotómca Las varables en las que se supone que se dferencan los grupos La varable dcotómca es la varable dependente del análss, es decr, la varable cuyos valores se desea pronostcar. El análss de regresón logístca genera una sere de pesos o coefcentes que: (1) Informan sobre la capacdad ndvdual de cada varable ndependente para dferencar entre los grupos. () Permten obtener pronóstcos que srven para clasfcar a los sujetos 19 Fases fundamentales Un análss de regresón logístca consta de cuatro fases fundamentales: La seleccón de las varables de análss. La estmacón de los pesos o coefcentes de las varables selecconadas. La clasfcacón de los casos. El análss de los resduos. La seleccón de las varables puede realzarse a partr de crteros teórcos o puede obedecer a crteros estadístcos La estmacón de los pesos o coefcentes asocados a cada varable se realza medante una algortmo teratvo de máxma verosmltud. La clasfcacón de los casos se realza a partr de los pronóstcos del modelo estmado. El análss de los resduos permte detectar posbles casos atípcos o predccones anómalas
111 Fundamentos Funcón Logístca Y 1 1 e ( B B X ) 0 1 El coefcente Bo representa la poscón de la curva sobre el eje horzontal o las abscsas (más haca la zquerda o más haca la derecha). Y el coefcente B1 representa la pendente de la curva medda en la zona de nflexón de la curva. Y 1 B0 B1 B X BkX k 1 e ( ) 0<Y<1 El exponente del número e es una ecuacón lneal múltple en la que cada varable ndependente recbe una ponderacón proporconal a su capacdad para predecr Y. 1 Fundamentos Funcón Logístca S dos sucesos son exclusvos entre sí (no se solapan) y exhaustvos (agotan el espaco muestral de posbles sucesos), la probabldad de aparcón de cualquera de ellos es gual a 1 menos la probabldad de aparcón del otro. Supongamos que la varable Y puede tomar sólo dos valores (0 y 1) Sea P(Y = 1) la probabldad de que la varable Y tome el valor 1, entonces la probabldad de que Y tome el valor 0 será: P(Y = 0) = 1-P (Y = 1). 111
112 Ejemplo Supongamos que nteresa explcar y predecr s una persona ha votado o no en las últmas eleccones a partr de un conjunto de característcas soco-demográfcas. La varable que dstngue a los sujetos que manfestan haber votado de aquellos que manfestan no haber votado es la varable voto. Votó en 199? Váldos Perddos Total Sí votó No votó Total Sstema Porcentaje Porcentaje Frecuenca Porcentaje váldo acumulado ,8 71,1 71,1 40 8,0 8,9 100, ,8 100,0 48 3, ,0 3 Ejemplo Consderemos en prmer lugar la varable lee como varable ndependente ( Lee el peródco?) Lee el peródco? Váldos Perddos Total Sí lee No lee Total Sstema Porcentaje Porcentaje Frecuenca Porcentaje váldo acumulado 86 57,5 85,3 85, ,9 14,7 100, ,3 100, , ,0 En el ejemplo propuesto, el fenómeno que nteresa estudar es la abstencón, es decr, el hecho de que una persona no acuda a votar. Una buena estmacón de la probabldad de este fenómeno es la frecuenca relatva de abstencón observada en la muestra. 4 11
113 Ejemplo Tabla de contngenca Votó en 199? * Lee el peródco? Votó en 199? Total Sí votó No votó Recuento % de Lee el peródco? Recuento % de Lee el peródco? Recuento % de Lee el peródco? Lee el peródco? Sí lee No lee Total ,9% 47,6% 70,9% ,1% 5,4% 9,1% ,0% 100,0% 100,0% En las frecuencas margnales de la tabla puede aprecarse que se ha abstendo de votar el 9,1% de los encuestados. La estmacón de la probabldad del suceso No votó será P(Y = 1) = 0,91. Por tanto, la probabldad del suceso Sí votó será P(Y = 0) = 0, Ejemplo Se sabe que aproxmadamente una tercera parte de los sujetos encuestados se abstene y que, por tanto, cabe esperar que una de cada tres personas no acuda a las urnas; pero no se sabe nada acerca de las característcas de las personas que se abstenen. La pregunta que nteresa responder en este momento es: es posble utlzar alguna otra varable, preva a la votacón, que permta pronostcar adecuadamente la probabldad de que un sujeto no vote?. Es decr, es posble construr un modelo de regresón que permta pronostcar la probabldad de abstencón a partr de una o varas varables ndependente?
114 Ecuacón logístca S exsten varables capaces de predecr la abstencón, entonces es posble nclurlas en un modelo de regresón y utlzarlas para corregr las estmacones de proporcón de votantes y no votantes. El problema que surge en una stuacón de estas característcas es que, al tener que pronostcar una probabldad (es decr, un valor comprenddo entre 0 y 1), un modelo de regresón lneal puede plantear seros problemas de predccón por no tener máxmo n mínmo teórcos en los pronóstcos que arroja. Por esta razón es más apropado recurrr a un modelo de tpo logístco. Consdérese la sguente ecuacón logístca: PY ( 1) 1 1 e ( B B X ) Defnda la ecuacón que puede utlzarse, el objetvo consste en encontrar una varable que dscrmne ben entre los dos posbles valores de Y. La fgura muestra cuatro curvas logístcas correspondentes a cuatro posbles varables ndependentes o predctoras
115 Las curvas se encuentran ordenadas por orden crecente de capacdad dscrmnatva. Puesto que el coefcente que controla la pendente de la curva es B1, una buena varable predctora será aquella que genere una curva con mucha pendente (es decr, una varable que tenga asocado un coefcente muy alto, en valor absoluto), mentras que una mala varable predctora será aquella que genere una curva sn pendente o con muy poca pendente (es decr, que tenga asocado un coefcente B1 próxmo a 0, en valor absoluto). El objeto de análss de regresón logístca es encontrar las varables con mayor (en valor absoluto) coefcente asocado. 9 Supongamos, por smplcdad, que para clasfcar a un sujeto como votante o abstenconsta se decde establecer como punto de corte el valor de probabldad 0, ,5 Los sujetos con un pronóstco mayor que 0,5 son Los sujetos con un pronóstco menor o gual que 0,5 son clasfcados como votantes clasfcados como abstenconsta Una buena varable predctora (podría decrse óptma) será aquella que permta obtener pronóstcos (probabldades) guales a 0 para el suceso Y=0 y pronóstcos guales a 1 para el suceso Y=
116 Cálculo de las probabldades pronostcadas Utlzando los datos de la tabla ( software SPSS) del ejemplo; Paso 1 a LEE Constante Varables en la ecuacón B E.T. Wald gl Sg. Exp(B) 1,19,186 41,58 1,000 3,93-1,094, ,316 1,000,335 a. Varable(s) ntroducda(s) en el paso 1: LEE. la ecuacón de regresón logístca toma la forma : PY ( 1) 1 Donde Y=0 Sí votó X=0 Sí lee Y=1 No votó X=1 No lee 1 1 e 1 e B0 B1 X ( 1,094 1,19 X ) 31 Cálculo de las probabldades pronostcadas En el caso de que un encuestado no lea el peródco, la probabldad pronostcada por la ecuacón de regresón logístca para la categoría No votó vale: 1 1 P( Y 1 X 1) 1,094 1,19 1 0,098 1 e 1 e 0, 545 Y en el caso de que un encuestado lea el peródco, la probabldad pronostcada para la categoría No votó vale: P Y 1 X 0 = 1 1 1,094 1,19 0 1,094 1 e 1 e 0,
117 Cálculo de las probabldades pronostcadas Por tanto, a partr de los pronóstcos dervados de la ecuacón de regresón logístca, se puede afrmar que, entre los sujetos que manfestan no leer el peródco, la probabldad de abstencón en las eleccones es mayor (aproxmadamente el doble) que entre los sujetos que manfestan leer el peródco. Es muy mportante tener en cuenta que los pronóstcos obtendos con la ecuacón de regresón logístca sempre se referen a una de las dos categorías de la varable dependente: aquella codfcada con el valor mayor y que es la que el procedmento Regresón logístca codfca nternamente con el valor 1. En el ejemplo, la categoría No votó. 33 Interpretacón de los coefcentes Cómo nterpretar los coefcentes de un modelo de regresón logístca? Ya se ha dcho que P( Y 0) 1 P( Y 1) Dvdendo la probabldad de uno de los sucesos por su probabldad complementara y smplfcando se obtene el cuocente denomnado la ventaja (odds) del suceso Y=1 frente al suceso Y=0 : PY PY 1 1/ 1 e / 1 B0 B1X e B0 B1X e B0 B1X La ventaja de un suceso es el cuocente entre la probabldad de que el suceso ocurra y la probabldad de que no ocurra
118 Interpretacón de los coefcentes Tomando el logartmo neperano de la ventaja se obtene la transformacón logt: ln PY PY 1 0 B B X 0 1 Este modelo se ajusta a un modelo de regresón lneal. Por tanto, el coefcente de regresón de un modelo logístco puede nterpretarse como el cambo que se produce en la transformacón logt (en el logartmo de la ventaja del suceso Y = 1) por cada undad de cambo que se produce en la varable ndependente. Un coefcente postvo debe nterpretarse como un ncremento en la probabldad que el ndvduo tome el valor 1 debdo a una varacón untara en la varable, mentras que un valor negatvo debe nterpretarse como una dsmnucón en la msma probabldad 35 Interpretacón de los coefcentes Con los datos del ejemplo, la transformacón logt del suceso No votó (Y = 1), cuando el encuestado Lee el peródco (X = 0) vale: P Y 1 X 0 0, 509 ln B0 ln ln 0,335 1, 094 P Y 0 X 0 1 0, 509 Y la transformacón logt del suceso No votó cuando el encuestado No lee el peródco (X = 1) vale: P Y 1 X 1 0,545 ln B0 B1 ln ln 1,103 0, 098 P Y 0 X 1 1 0,545 Por tanto, la dferenca entre ambos logartmos permte obtener el valor del coefcente: B 1 0, 098 1, 094 1,
119 Interpretacón de los coefcentes Así, en el modelo de regresón logístca, el coefcente de regresón asocado a una varable ndependente representa el cambo producdo en la transformacón logt por undad de cambo en la varable ndependente. Es preferble nterpretar drectamente el cambo en las ventajas y no en los logartmos de las ventajas. Volvendo a la expresón de la ventaja: PY 1 B0 B1 X B0 BX 1 e e e P Y 0 Se ve claramente que una ventaja se puede expresar en térmnos de potencas del número e. Por ello se suele nformar del valor exponencal de los coefcentes de regresón. 37 Interpretacón de los coefcentes En los resultados de la regresón logístca se ncluye tanto el valor del coefcente de regresón (B) como el de Exp(B). En el ejemplo, la ventaja del suceso No votó cuando el encuestado No lee el peródco vale 1,103, mentras que la ventaja de ese msmo suceso cuando el encuestado Sí lee el peródco vale 0,335. S se expresa el cambo proporconal de la ventaja en térmnos de un cocente (como una razón) se obtene 1,103/0,335 = 3,93, que es justamente el valor de Exp(B). A este cambo proporconal se le denomna razón de las ventajas (odds rato en nglés), dado que es el resultado de dvdr dos ventajas. Y se nterpreta en térmnos del cambo proporconal (ya sea aumento o dsmnucón) que se produce en la ventaja del suceso o evento de nterés ( No vota en el ejemplo) por cada undad de cambo que se produce en la varable ndependente (VI)
120 El problema de la clasfcacón Una ecuacón de regresón logístca raramente arroja pronóstcos con valores 0 y 1, es decr, raramente genera una curva en forma de escalón Lo habtual es encontrar que la probabldades pronostcadas adoptan valores comprenddos entre 0 y 1. Este es el motvo que oblga a tener que establecer un punto de corte para poder tomar la decsón de clasfcar a los sujetos en uno u otro grupo a partr de las probabldades pronostcadas. Cuando la varable ndependente es dcotómca, como en el ejemplo, establecer el punto de corte es una tarea bastante senclla. Puesto que una varable dcotómca sólo adopta dos valores (en el ejemplo: 0 = S lee el peródco y 1 = No lee el peródco ), sólo es posble obtener dos pronóstcos. (0,509 y 0,545). 39 Tambén se ha vsto que la probabldad del suceso No votó vale 0,91 Así parece razonable pensar que el punto del corte debería encontrarse entre las dos probabldades pronostcadas; ese punto de corte ben podría ser, por ejemplo 0, ,91 Los sujetos con un pronóstco menor o gual que el punto de corte son clasfcados en el grupo que sí votan Los sujetos con un pronóstco mayor que el punto de corte son clasfcados en el grupo que no votan 40 10
121 En los modelos con más de una varable ndependente se ncrementa el número de valores dstntos que es posble pronostcar Exsten dos camnos alternatvos para determnar el punto de corte óptmo, es decr, para encontrar cuál es el valor (la probabldad) a partr del cual se consgue dferencar al máxmo a los sujetos de uno y otro grupo y, consecuentemente, para efectuar la mejor clasfcacón posble. El prmero de estos camnos consste en generar múltples tablas de clasfcacón varando en cada una de ellas el punto de corte hasta optmzar el porcentaje de casos correctamente clasfcados. El segundo camno para determnar el punto de corte óptmo consste en utlzar la curva COR. 41 Tablas de clasfcacón con dstntos valores de corte Tabla de clasfca cón a Pronostcado Paso 1 Observado Votó en 199? Porcentaje global a. El valor de corte es,500 Sí votó No votó Votó en 199? Porcentaje Sí votó No votó correcto , ,4 71,6 Tabla de clasfca cón a Pronostcado Paso 1 Observado Votó en 199? Porcentaje global a. El valor de corte es,300 Sí votó No votó Votó en 199? Porcentaje Sí votó No votó correcto , ,4 71,6 4 11
122 Tabla de clasfca cón a Pronostcado Paso 1 Observado Votó en 199? Porcentaje global a. El valor de corte es,60 Sí votó No votó Votó en 199? Porcentaje Sí votó No votó correcto , ,4 71,6 Tabla de clasfca cón a Pronostcado Paso 1 Observado Votó en 199? Porcentaje global a. El valor de corte es,50 Sí votó No votó Votó en 199? Porcentaje Sí votó No votó correcto 0 69, ,0 9,1 43 Regresón logístca múltple Nos nteresa nterpretar un análss de regresón logístca utlzando más de una varable ndependente. Varable dependente Voto Varables ndependentes Leer Edad Hjos Educ Ingfam91 Consderemos la msma varable dependente que en el prmer ejemplo (voto) y, además de la varable ndependente allí utlzada (leer), otras cuatro nuevas: edad (Edad del encuestado), hjos (Número de hjos), educ (Años de escolarzacón) e ngfam91 (Ingresos famlares en 1991) 44 1
123 Estadístco de puntuacón de Rao La tabla sguente contene los valores del estadístco de puntuacón de Rao. Este estadístco mde la contrbucón ndvdual de cada varable a la mejora del ajuste global del modelo. El nvel crítco (Sg) asocado a cada estadístco ndca qué varables contrbuyen sgnfcatvamente al ajuste. Puede verse que, exceptuando la varable hjos, todas las varables ncludas en el análss son sgnfcatvas; por tanto, buenas canddatas para formar parte del modelo de regresón. La últma línea, Estadístcos globales, contene una valoracón global de todas las varables ndependentes tomadas juntas. Varables que no están en la ecuacón Paso 0 Varables Estadístcos globales LEE EDAD EDUC INGFAM91 HIJOS Puntuacón gl Sg. 45,137 1,000 0,956 1,000 60,910 1,000 53,935 1,000,188 1, ,954 5, El estadístco ch-cuadrado Pruebas omnbus sobre los coefcentes del modelo Paso 1 Paso Bloque Modelo Ch-cuadrado gl Sg. 143,754 5, ,754 5, ,754 5,000 El estadístco ch-cuadrado permte contrastar la hpótess de que el ncremento obtendo en el ajuste global del modelo es nulo. Este estadístco srve para determnar s, al ntroducr las cnco varables ndependentes en el modelo, se consgue un ncremento sgnfcatvo del ajuste global. Este ncremento se valora tomando como punto de referenca el modelo nulo. Puesto que el modelo se construye en un únco paso (pues se está utlzando el método ntroducr; ver sguente apartado), todas las seccones de tabla nforman del msmo valor; la mejora respecto al modelo nulo, es decr, respecto al modelo del paso 0 (Ch-cuadrado = 143,754). En el ejemplo, esta mejora es sgnfcatva: 46 13
124 Paso 1 Resumen de los modelos R cuadrado - log de la R cuadrado de verosmltud de Cox y Snell Nagelkerke 970,39 a,143,05 a. La estmacón ha fnalzado en el número de teracón 5 porque las estmacones de los parámetros han cambado en menos de,001. La tabla ofrece un resumen del modelo. Contene tres estadístcos que permten valorar el ajuste global del modelo en el paso 1, es decr, del modelo que ncluye todas las varables. Los parámetros están estmados a través del método de máxma verosmltud (-LL), de modo que sus valores tenderán a 0 s la verosmltud tende a máxma y al revés s ésta es baja.en el ejemplo se observa un un bajo ajuste del modelo a los datos. Este resultado queda corroborado con el estadístco de Cox y Snell, que se nterpreta de la msma forma que el coefcente de determnacón de un modelo de regresón lneal. 47 Matrz de confusón Tabla de clasfcacón a Pronostcado Paso 1 Observado Votó en 199? Porcentaje global a. El valor de corte es,500 Sí votó No votó Votó en 199? Porcentaje Sí votó No votó correcto , ,7 74,0 La tabla muestra la matrz de confusón con los resultados de la clasfcacón. Aunque no es posble mejorar el porcentaje global de clasfcacón correcta sn nclur nuevas varables ndependentes, s es posble equlbrar la tasa de acertos en los dos grupos manpulando el punto de corte utlzado en la clasfcacón
125 Paso 1 a LEE EDAD EDUC INGFAM91 HIJOS Constante Varables en la ecuacón B E.T. Wald gl Sg. Exp(B),671,07 10,468 1,001 1,956 -,034,006 36,188 1,000,967 -,19,03 35,76 1,000,85 -,056,016 1,7 1,000,945,018,051,15 1,73 1,018 3,636,56 47,706 1,000 37,957 a. Varable(s) ntroducda(s) en el paso 1: LEE, EDAD, EDUC, INGFAM91, HIJOS. La tabla muestra las estmacones de los coefcentes (B) del modelo y los datos necesaros para valorar su sgnfcacón e nterpretarlos. La sgnfcacón de cada coefcente se evalúa a partr del estadístco de Wald. Este estadístco permte contrastar la hpótess nula de que el coefcente vale cero en la poblacón y se obtene elevando al cuadrado el cocente entre el valor estmado del coefcente (B) y su error típco (error tp). 49 Estadístco de Wald Estadístco de Wald Coefcente E.estándar Es un estadístco smlar a una t. Cuando el nvel crítco (Sg.) asocado al estadístco de Wald es menor que 0,05, se puede rechazar la hpótess nula y, por tanto, conclur que la correspondente varable ndependente está sgnfcatvamente relaconada con la varable dependente. Un nconvenente de este estadístco es que es demasado sensble al tamaño de los coefcentes; en general, cuando el valor de un coefcente es muy grande (en valor absoluto) el estadístco de Wald es poco fable. En estos casos es preferble evaluar la sgnfcacón de las varables utlzando un método por pasos 50 15
126 Razón de las ventajas La columna de la razón de las ventajas, Exp(B), permte cuantfcar en qué grado aumenta la abstencón cuando los sujetos no leen el peródco (y se mantenen constantes las restantes varables). Puesto que el punto de comparacón es el valor 1 y el Exp(B) de la varable leer vale 1,956, se puede conclur que la ventaja de la abstencón entre los sujetos que no leen el peródco es aproxmadamente el doble que entre los que sí lo leen. El sgno negatvo del resto de los coefcentes ndca que el ncremento en cualquera de las demás varables dsmnuye la probabldad de que un sujeto no vote: la abstencón es menos probable a medda que aumentan la edad, los ngresos famlares y los años de escolarzacón. 51 Análss de regresón logístca por pasos Cuando, se dspone de más de una varable ndependente, exsten varos métodos para selecconar la varable o varables que deben formar parte del modelo fnal. El método de ntroduccón forzosa hace que el modelo de regresón ncluya todas las varables ndependentes selecconadas. Los métodos de seleccón por pasos permten utlzar crteros estadístcos para, de forma automátca, nclur en el modelo las varables que son sgnfcatvas y dejar fuera las que no lo son. Los métodos de seleccón por bloques permten al usuaro manpular la nclusón y/o exclusón de varables medante la combnacón secuencada de dstntos procedmentos, pudendo generar modelos jerárqucos. 5 16
127 Regresón logístca multnomal La opcón Regresón logístca multnomal resulta útl en aquellas stuacones en las que desee poder clasfcar a los sujetos según los valores de un conjunto de varables predctoras. Este tpo de regresón es smlar a la regresón logístca, pero más general, ya que la varable dependente no está restrngda a dos categorías. Ejemplo. Para consegur una produccón y dstrbucón de películas más efcaz, los estudos de cne necestan predecr qué tpo de películas es más probable que vayan a ver los afconados. Medante una regresón logístca multnomal, el estudo puede determnar la nfluenca que la edad, el sexo y las relacones de pareja de cada persona tenen sobre el tpo de película que preferen. De esta manera, el estudo puede orentar la campaña publctara de una película concreta al grupo de la poblacón que tenga más probabldades de r a verla. 53 Regresón logístca versus análss dscrmnante La regresón logístca se puede aplcar a un rango más amplo de stuacones de nvestgacón que el análss dscrmnante. El análss dscrmnante resulta útl para las stuacones en las que se desea construr un modelo predctvo para pronostcar el grupo de pertenenca de un caso a partr de las característcas observadas de cada caso. El procedmento genera una funcón dscrmnante (o, para más de dos grupos, un conjunto de funcones dscrmnantes) basada en combnacones lneales de las varables predctoras que proporconan la mejor dscrmnacón posble entre los grupos. Las funcones se generan a partr de una muestra de casos para los que se conoce el grupo de pertenenca; posterormente, las funcones pueden ser aplcadas a nuevos casos que dspongan de meddas para las varables predctoras pero de los que se desconozca el grupo de pertenenca
128 Análss dscrmnante Datos. La varable de agrupacón debe tener un número lmtado de categorías dstntas, codfcadas como números enteros. Las varables ndependentes que sean nomnales deben ser recodfcadas a varables dummy o de contraste. Supuestos. Los casos deben ser ndependentes. Las varables predctoras deben tener una dstrbucón normal multvarada y las matrces de varanzas-covaranzas ntra-grupos deben ser guales en todos los grupos. Se asume que la pertenenca al grupo es mutuamente exclusva (es decr, nngún caso pertenece a más de un grupo) y exhaustva de modo colectvo (es decr, todos los casos son membros de un grupo). El procedmento es más efectvo cuando la pertenenca al grupo es una varable verdaderamente categórca; s la pertenenca al grupo se basa en los valores de una varable contnua (por ejemplo, un cocente de ntelgenca alto respecto a uno bajo), deberá consderar el uso de la regresón lneal para aprovechar la nformacón más rca ofrecda por la propa varable contnua. 55 Análss Factoral Datos y supuestos Técnca del análss factoral Fases del análss factoral Matrz de correlacones Extraccón de factores Métodos de Rotacón Puntuacones factorales 56 18
129 Análss Factoral El análss factoral es una técnca de reduccón de datos que srve para encontrar grupos homogéneos de varables a partr de un conjunto numeroso de varables. v1, v, v3,.vn v1, v5,v7 v,v8,v10. V3,v4,v9.. Esos grupos homogéneos se forman con las varables que correlaconan mucho entre sí y procurando, ncalmente, que unos grupos sean ndependentes de otros. 57 Datos y supuestos Objetvo Buscar el número mínmo de dmensones capaces de explcar el máxmo de nformacón contenda en los datos. Varables En el análss factoral no exste varable dependente. Todas las varables del análss tenen el msmo rango: todas ellas son ndependentes en el sentdo de que no exste a pror una dependenca conceptual de unas varables sobre otras. Las varables deberían ser cuanttatvas a nvel de ntervalo o de razón. Los datos categórcos (como la relgón o el país de orgen) no son adecuados para el análss factoral
130 Datos y supuestos Supuestos Los datos han de tener una dstrbucón normal bvarada para cada pareja de varables, y las observacones deben ser ndependentes. Ejemplo Qué acttudes subyacentes hacen que las personas respondan a las preguntas de una encuesta polítca de la manera en que lo hacen? Con el análss factoral, se puede nvestgar el número de factores subyacentes y, en muchos casos, se puede dentfcar lo que los factores representan conceptualmente. Adconalmente, se pueden calcular las puntuacones factorales para cada encuestado, que pueden utlzarse en análss subsguentes. 59 Técnca del análss factorai. Cada varable aparece como combnacón lneal de una sere de factores X A F A F A F donde F son los factores comunes a todas las varables y U es el factor únco referdo a la parte de la varable que no puede ser explcada por los factores comunes. Las A, son los coefcentes de cada uno de los factores. Los factores úncos se asume que están ncorrelaconados con el resto de factores úncos y con los factores comunes. Cada factor es una combnacón lneal de las varables orgnales F W X W X W X... j j1 1 j 3 j3 3 A k F k U W p X p Wj son los coefcentes de las puntuacones factorales P es el número de varables
131 Fases del Análss factoral El análss factoral consta de cuatro fases característcas: El cálculo de una matrz capaz de expresar la varabldad conjunta de todas las varable. La extraccón del número óptmo de factores. La rotacón de la solucón para facltar su nterpretacón. La estmacón de las puntuacones de los sujetos en las nuevas dmensones. Para ejecutar correctamente un análss factoral es necesaro tomar algunas decsones en cada una de estas fases. 61 Ejemplo Analcemos, por ejemplo, la pregunta del cuestonaro cuyos datos recoge el archvo trabajo.sav y referda a la evaluacón por parte de los encuestados de la mportanca que según su opnón pueden tener cada una de las causas que se enumeran, en el alto índce de paro en un país. B13: La crss económca. B14: La polítca de empleo del goberno. B15: La mala gestón de los empresaros. B16: La comoddad de la gente, que sólo quere buenos trabajos. B17: La falta de preparacón del trabajador. B18: Las pocas ganas de trabajar de la gente. B19: El no saber buscar trabajo. B0: Que hay mucho plurempleo. B1: Que el trabajo que hay no se reparte ben socalmente
132 El modelo matemátco que subyace a esta técnca es smlar al de la regresón smple y en él cada varable aparece como combnacón lneal de una sere de factores que no son en este momento observables. Por ejemplo, B13 (la crss económca) puede aparecer expresada como: B13 = a(sujeto) + b(externos al sujeto) + c(entorno) + U B13 donde sujeto, externos al sujeto y entorno no son varables ndependentes sno grupos de varables desconocdas por nosotros a pror, que pueden ser los factores subyacentes y que hemos denomnado «sujeto» como factor que puede englobar las varables referdas a causas del paro nherentes al propo sujeto, «externas al sujeto», en donde estarían como causantes del paro el goberno y los empresaros, por ejemplo, y el «entorno» en donde ben podrían estar la crss económca y el reparto del trabajo. 63 Descrptvos Estadístcos descrptvos Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Fgura 1 Desvacón Meda típca N del análss 3,93, ,91, ,53 1, ,0 1, ,9 1, ,85 1, ,77 1, ,57 1, ,87,
133 Matrz de correlacones Matrz de correla cones a Correlacón Sg. (Unlateral) a. Determnante =,40 Fgura Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Polítca de Ganas de Crss empleo Empresaros Comoddad Preparacón trabajar Búsqueda Plurempleo Reparto 1,000,397,185 -,10 -,003 -,157 -,101,019,084,397 1,000,0 -,077 -,050 -,104 -,078,054,103,185,0 1,000,08 -,010 -,04,044,101,161 -,10 -,077,08 1,000,336,559,387,14,043 -,003 -,050 -,010,336 1,000,45,345,115,045 -,157 -,104 -,04,559,45 1,000,451,195,071 -,101 -,078,044,387,345,451 1,000,31,134,019,054,101,14,115,195,31 1,000,376,084,103,161,043,045,071,134,376 1,000,000,000,000,457,000,001,73,004,000,000,007,057,000,006,044,001,000,000,185,373,1,08,001,000,000,007,185,000,000,000,000,087,457,057,373,000,000,000,000,077,000,000,1,000,000,000,000,01,001,006,08,000,000,000,000,000,73,044,001,000,000,000,000,000,004,001,000,087,077,01,000,000 Es mportante que todas las varables tengan al menos un coefcente de correlacón sgnfcatvo en la matrz. 65 El índce KMO Inversa de la matrz de correlacones Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Polítca de Ganas de Crss empleo Empresaros Comoddad Preparacón trabajar Búsqueda Plurempleo Reparto 1,39 -,441 -,134,061 -,115,138,059 -,008 -,049 -,441 1,3 -,153,014,034,04,048 -,043 -,059 -,134 -,153 1,086 -,063,03,054 -,058 -,038 -,18,061,014 -,063 1,548 -,148 -,674 -,07 -,160,080 -,115,034,03 -,148 1,90 -,376 -,31,005,005,138,04,054 -,674 -,376 1,740 -,361 -,067 -,07,059,048 -,058 -,07 -,31 -,361 1,380 -,144 -,086 -,008 -,043 -,038 -,160,005 -,067 -,144 1,47 -,47 -,049 -,059 -,18,080,005 -,07 -,086 -,47 1,01 Fgura 3 KMO y prueba de Bartlett Medda de adecuacón muestral de Kaser-Meyer-Olkn.,71 Prueba de esfercdad de Bartlett Ch-cuadrado aproxmado gl Sg. 1434,418 36,000 Fgura 4 En la tabla tenemos la nversa de la matrz de correlacones, los «KMO» (Kaser-Meyer-Olkn) y el test de Bartlett. Este últmo, es decr, el test de Bartlett, se utlza para verfcar s la matrz de correlacones es una matrz de dentdad, es decr, s todos los coefcentes de la dagonal son guales a la undad y los externos a la dagonal guales a O
134 El índce KMO Este estadístco se obtene a partr de la transforma cón X del determnante de la matrz de correlacones y cuanto mayor sea y por tanto menor el grado de sgnfcacón, más mprobable que la matrz sea una matrz de dentdad. En el ejemplo, con un valor 1434,418 y un grado de sgnfcacón p = 0,000 resulta evdente que no se trata de una matrz de dentdad. En el supuesto de que no se pudese rechazar esta hpótess, se desaconseja proceder a realzar un análss factoral con los datos. 67 El índce KMO El índce KMO nos compara los coefcentes de correlacón de Pearson obtendos en la Fgura con los coefcentes de correlacón parcal entre varables. Se obtene j j rj j KMO a r j j rj el coefcente de correlacón de Pearson entre las varables y j y aj es el coefcente de correlacón parcal entre las varables y j
135 Correlacón ant-magen Covaranza ant-magen Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto El índce KMO S la suma de los coefcentes de correlacón parcal al cuadrado es muy pequeña, KMO será un índce muy próxmo a la undad y por tanto el análss factoral un procedmento adecuado. En cambo, valores pequeños en este índce nos dan a entender todo lo contraro. De hecho para Kaser : 1 KMO > 0,90 son consderados excelentes. 0,90 KMO > 0,80 son consderados buenos. 0,80 KMO > 0,70 son consderados aceptables. 0,70 KMO > 0,60 son consderados medocres o regulares. 0,60 KMO > 0,50 son consderados malos. KMO < 0,50 son consderados naceptables o muy malos. En el ejemplo este valor es de 0,71 y por tanto se puede consderar como aceptable y contnuar con el análss factoral. 69 Matrces ant-magen Matrces ant-magen Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto a. Medda de adecuacón muestral,807 -,91 -,100,03 -,07,064,034 -,005 -,033 -,91,818 -,115,007,0,011,08 -,08 -,040 -,100 -,115,91 -,038,03,09 -,039 -,08 -,098,03,007 -,038,646 -,074 -,50 -,097 -,083,043 -,07,0,03 -,074,775 -,168 -,130,003,003,064,011,09 -,50 -,168,575 -,151 -,031 -,013,034,08 -,039 -,097 -,130 -,151,75 -,083 -,05 -,005 -,08 -,08 -,083,003 -,031 -,083,80 -,85 -,033 -,040 -,098,043,003 -,013 -,05 -,85,833,601 a -,358 -,116,044 -,091,094,045 -,006 -,040 -,358,609 a -,13,010,07,016,037 -,034 -,048 -,116 -,13,690 a -,049,07,039 -,047 -,033 -,11,044,010 -,049,744 a -,104 -,411 -,14 -,115,058 -,091,07,07 -,104,791 a -,51 -,173,004,004,094,016,039 -,411 -,51,71 a -,33 -,046 -,019,045,037 -,047 -,14 -,173 -,33,816 a -,109 -,067 -,006 -,034 -,033 -,115,004 -,046 -,109,669 a -,349 -,040 -,048 -,11,058,004 -,019 -,067 -,349,591 a Fgura 5 En la Fgura 5 tenemos las matrces ant-magen de covarancas y correlacones entre todas las varables del ejemplo. Serán los negatvos de los coefcentes de correlacón parcal entre cada par de varables, neutralzando el efecto de todas las restantes. Interesan por tanto coefcentes cuanto más pequeños, mejor
136 En la dagonal de esta últma tenemos los coefcentes MSA (Measures of Sam plng Adequacy) que venen a ser los KMO pero en este caso para cada varable por separado. La nterpretacón de sus valores es déntca a la realzada para los KMO. En resumen, tenemos: Coefcentes de correlacón de Pearson que en la mayoría de los casos son altamente sgnfcatvos. El determnante de la matrz de correlacones (0,40) relatvamente bajo. El índce KMO = 0,71 bastante aceptable. El resultado del test de Bartlett con un = 1434,418 Y p = 0,000. Valores muy bajos en la matrces ant-magen, MSA bastante altos en la dagonal de la matrz de correlacones ant-magen. Todo ello nos lleva a conclur que el análss factoral que sgue a contnuacón resulta a pror pertnente y puede proporconamos conclusones satsfactoras. 71 Extraccón de factores Método. Permte especfcar el método de extraccón factoral. Los métodos dsponbles son: Componentes prncpales, Mínmos cuadrados no ponderados, Mínmos cuadrados generalzados, Máxma verosmltud, factorzacón de Ejes prncpales, factorzacón Alfa y factorzacón Imagen. En SPSS el sstema coge por defecto el método de componentes prncpales que es el que hemos utlzado en esta prmera parte del ejemplo
137 Componentes prncpales (PC) Consste báscamente en llevar a cabo una combnacón lneal de todas las varables de modo que el prmer componente prncpal sea una combnacón que explque la mayor proporcón de varanca de la muestra, el segundo la segunda mayor y que a su vez esté ncorrelaconado con el prmero, y así sucesvamente hasta tantos componentes como varables. El método de extraccón de componentes prncpales, es el que actúa por defecto, asume que es posble explcar el 100% de la varanza observada y, por ello, todas las comunaldades ncales son guales a la undad (que es justamente la varanza de una varable en puntuacones típcas). 73 Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Comunaldades Comunaldades Incal Extraccón 1,000,644 1,000,60 1,000,39 1,000,59 1,000,53 1,000,684 1,000,519 1,000,646 1,000,693 Método de extraccón: Análss de Componentes prncpales. La comunaldad de una varable es la proporcón de su varanza que puede ser explcada por el modelo factoral obtendo. Fgura 6 En la Fgura 6 tenemos las comunaldades ncales de la solucón de componentes prncpales. Estos resultados se obtenen s en el subcuadro de dálogo «Descrptves» de la Fgura y dentro de «Statstcs» selecconamos «Intal Soluton». S utlzamos tantos componentes prncpales como varables, cada varable puede ser explcada por ella msma y por tanto toda la varabldad de cada varable, que expresada en undades de desvacón estandarzadas es gual a la undad, explcada a su vez por los factores comunes. Esta es la razón por la que en la Fgura 6 la comunaldad ncal es gual a la undad para todas las varables
138 Valores propos La decsón respecto al número de factores que deseamos para representar los datos puede adoptarse desde una doble vía que es la que aparece en el subcuadro de dálogo «Extracton. Por defecto el sstema extraerá tantos factores como haya en la solucón ncal con valores propos (egenvalues) superores a la undad. En la Fgura 7 vemos que hay tres factores con valores propos superores a 1 y que en defntva será el número que extraerá el sstema. Evdentemente, podemos cambar el valor por defecto correspondente al «egenvalue». La segunda posbldad corresponde al botón de rado «Number of factors» y consste sencllamente en fjar un número entero determnado de factores, sempre nferor, lógcamente, al número de varables. Los autovalores (o valores propos) expresan la cantdad de la varanza total que está explcada por cada factor; y los porcentajes de varanza explcada asocados a cada factor se obtenen dvdendo su correspondente autovalor por la suma de los autovalores (la cual concde con el número de varables 75 Componente Autovalores ncales Varanza total explcada % de la % de la % de la Total varanza % acumulado Total varanza % acumulado Total varanza % acumulado,449 7,11 7,11,449 7,11 7,11,74 5,65 5,65 1,684 18,714 45,95 1,684 18,714 45,95 1,553 17,5 4,518 1,116 1,395 58,30 1,116 1,395 58,30 1,4 15,80 58,30,848 9,46 67,747,705 7,834 75,580,616 6,84 8,4,597 6,69 89,051,568 6,314 95,365,417 4, ,000 Método de extraccón: Análss de Componentes prncpales. Fgura 7 Matrz Varanza total explcada Sumas de las saturacones al cuadrado de la extraccón Suma de las saturacones al cuadrado de la rotacón La Fgura 7 recoge, en porcentajes ndvduales y acumulados, la proporcón de varanca total explcada por cada factor, tanto para la solucón no rotada como para la rotada. En concreto, qué porcentaje supone,449 sobre el total de varabldad (nueve en el ejemplo) de toda la muestra. Los tres factores ncludos en el modelo son capaces de explcar exactamente un 58,3 por 100 de la varabldad total, lo que puede nterpretarse como un porcentaje aceptable
139 Gráfco de sedmentacón Fgura 8 El gráfco de sedmentacón srve para determnar el número óptmo de factores. Consste smplemente en una representacón gráfca del tamaño de los autovalores. Según se ha señalado ya, los autovalores ndcan la cantdad de varanza que está explcada por cada componente prncpal Tanto la tabla de porcentajes de varanza explcada como el gráfco de sedmentacón muestran los autovalores ordenados de mayor a menor: el prmer autovalor es el mayor de los posbles, el segundo autovalor es el mayor de los restantes, y así sucesvamente. S un autovalor se aproxma a cero, esto sgnfca que el factor correspondente a ese autovalor es ncapaz de explcar una cantdad relevante de la varanza total. Por tanto, un factor al que corresponde un autovalor próxmo a cero se cons dera un factor resdual y 77 carente de sentdo en el análss. Matrz de componentes Matrz de componentes a Crss Polítca de empleo Empresaros Comoddad Preparacón Ganas de trabajar Búsqueda Plurempleo Reparto Componente 1 3 -,9,640,46 -,185,668,373,00,569,070,748 -,036,177,69,00,357,804 -,085,174,718,045,040,436,437 -,515,36,551 -,577 Método de extraccón: Análss de componentes prncpales. a. 3 componentes extraídos Fgura 9 En la Fgura 9 tenemos los coefcentes utlzados para expresar cada varable estandarzada en térmnos de los tres factores del modelo. Estos coefcentes se conocen tambén con el nombre de pesos factorales, cargas, ponderacones factorales o saturacones factorales ya que nos ndcan la carga de cada varable en cada factor, de modo que los factores con unos pesos factorales más elevados en térmnos absolutos nos ndcan una relacón estrecha con las varables
140 Matrz de componentes El deal desde el punto de vsta del análss factoral es encontrar un modelo en el que todas las varables saturen en algún factor, es decr, pesos factorales altos en uno y bajos en el resto. Por ejemplo la varable B18 (Ganas de trabajar como posble explcacón del alto índce de desempleo en el país) es una varable con una elevada carga factoral en el prmero de los fac tores y mucho más pequeña en los dos restantes. Podríamos expresar la varable B18 como: B18 = 0,80408 F1-0,08519 F + 0,17407 F3 donde F1, F y F3 son los tres factores del modelo. 79 Matrz de componentes Ganas de trabajar Comoddad Búsqueda Preparacón Polítca de empleo Crss Empresaros Reparto Plurempleo Matrz de componentes a Componente 1 3,804 -,085,174,748 -,036,177,718,045,040,69,00,357 -,185,668,373 -,9,640,46,00,569,070,36,551 -,577,436,437 -,515 Método de extraccón: Análss de componentes prncpales. a. 3 componentes extraídos Ganas de trabajar Comoddad Búsqueda Preparacón Polítca de empleo Crss Empresaros Reparto Plurempleo Matrz de componentes a Componente 1 3,804,174,748,177,718,69,357 -,185,668,373 -,9,640,46,569,36,551 -,577,436,437 -,515 Método de extraccón: Análss de componentes prncpales. a. 3 componentes extraídos En la Fgura 9 aparecen ordenadas las varables tal y como están en la base de datos. La segunda tabla de esta fgura es la que corres ponde a la opcón que hemos selecconado en el subcuadro de dálogo Optons al selecconar «Sorted by sze» el sstema ordena las varables en la matrz de mayor a menor peso o carga factoral y sempre comenzando por el prmer factor, posterormente el segundo, y así sucesvamente. Fnalmente la opcón del msmo subcuadro de dálogo «Suppress absolute values less than» nos permte una lectura todavía más clara de la matrz puesto que permte elmnar de la msma aquellos coefcentes con valores nferores a uno dado (0,10 por defecto)
141 Matrz de componentes Para determnar en qué medda los tres factores son capaces de explcar las varables orgnales, podemos sumar la proporcón de varanca de la varable explcada por cada uno de ellos (es decr, los coefcentes al cuadrado) y de este modo obtener las comunaldades que aparecen en la dagonal de la Fgura 10. Cojamos de nuevo la varable B18 (Ganas de trabajar) y calculemos este sumatora: B 18 = 0, , ,17407 = 0,68410 Cas el 70 por 100 de la varabldad de B18 es explcada por los tres factores del modelo, en tanto que por ejemplo en la varable BI5 (Empresaros) los msmos úncamente explcan en torno al 33 por 100. Reteramos que esta proporcón de la varabldad de cada varable explcada por los factores del modelo es lo que se conoce con el nombre de comunaldad de la varable. Obvamente su valor oscla entre 0 y 1 y la parte de varanca no explcada por el modelo factoral, es decr, 1- comunaldad, es lo que se conoce con el nombre de factor únco o uncdad. 81 Rotacón La fnaldad de la rotacón es la de ayudamos a nterpretar. En el subcuadro de dálogo Rotacón exsten varos procedmentos. VARIMAX, EQUAMAX y QUARTlMAX son procedmentos ortogonales es decr que los factores se mantenen ncorrelaconados y los ejes forman ángulos rectos. El PROMAX y el DlRECT OBLlMIN pertenecen al grupo de los denomnados oblcuos o no ortogonales. La rotacón no afecta a la comunaldad y al porcentaje de varanca explcada por el modelo, aunque sí puede cambar la de cada factor
142 Métodos de Rotacón Varmax. Método de rotacón ortogonal que mnmza el número de varables que te nen saturacones altas en cada factor. Smplfca la nterpretacón de los factores opt mzando la solucón por columna. Quartmax. Método de rotacón ortogonal que mnmza el número de factores nece saros para explcar cada varable. Smplfca la nterpretacón de las varables obser vadas optmzando la nterpretacón por flas. Equamax. Método de rotacón que es combnacón del método Varmax, que smpl fca los factores, y del método Quartmax, que smplfca las varables. Se mnmza tanto el número de varables que saturan alto en un factor como el número de factores necesaros para explcar una varable. 83 Métodos de Rotacón Oblmn drecto. Método para la rotacón oblcua (no ortogonal). Cuando delta es gual a cero (el valor por defecto), las solucones son las más oblcuas. A medda que delta se va hacendo más negatvo, los factores son menos oblcuos. Para anular el va lor por defecto de delta, puede ntroducrse un número menor o gual que 0,8. Delta. El valor de delta permte controlar el grado de oblcudad que pueden lle gar a alcanzar los factores de la solucón. Promax. Rotacón oblcua que permte que los factores estén correlaconados. Puede calcularse más rápdamente que una rotacón oblmn drecta, por lo que es útl para grandes conjuntos de datos. Kappa. Parámetro que controla el cálculo de la rotacón Promax. El valor por de fecto es 4. Este valor es adecuado para la mayoría de los análss
143 Matrz factoral En resumen, todos los métodos tratan de obtener una matrz factoral que se aproxme al prncpo de estructura smple. Según este prncpo, la matrz factoral debe reunr las sguentes característcas: Cada factor debe tener unos pocos pesos altos y el resto próxmos a 0. Cada varable no debe estar saturada mas que en un solo factor. No deben exstr factores con la msma dstrbucón. El método utlzado en todos los casos ha sdo el de componentes prncpales. Todos ellos concden a grandes rasgos en la sguente asgnacón: 85 Matrz factoral Factor 1 Varables: B18: Pocas ganas de trabajar de la gente. B16: La comoddad de la gente, que sólo quere buenos trabajos. B19: El no saber buscar trabajo. B17: La falta de preparacón del trabajador. Factor Varables: B 14: La polítca de empleo del goberno. B 13: La crss económca. B15: La mala gestón de los empresaros. Factor 3 Varables: B1: Que el trabajo que hay no se reparte ben socalmente. B: Que hay mucho plurempleo
144 Matrz de pesos factorales Ganas de trabajar Comoddad Preparacón Búsqueda Crss Polítca de empleo Empresaros Reparto Plurempleo Matrz de componentes rotados a Componente 1 3,818 -,111,055,765 -,058,06,71,085 -,095,688 -,056,05 -,090,795 -,059 -,067,784,010,07,51,57,014,19,8,6,033,771 Método de extraccón: Análss de componentes prncpales. Método de rotacón: Normalzacón Quartmax con Kaser. a. La rotacón ha convergdo en 5 teracones. Ganas de trabajar Comoddad Preparacón Búsqueda Crss Polítca de empleo Empresaros Reparto Plurempleo Matrz de componentes rotados a Componente 1 3,813 -,1,088,761 -,069,094,716,077 -,063,678 -,068,33 -,077,797 -,051 -,057,785,019,03,508,65 -,019,117,84,194,019,780 Método de extraccón: Análss de componentes prncpales. Método de rotacón: Normalzacón Equamax con Kaser. a. La rotacón ha convergdo en 5 teracones. Ganas de trabajar Comoddad Preparacón Búsqueda Crss Polítca de empleo Empresaros Reparto Plurempleo Matrz de componentes rotados a Componente 1 3,815 -,118,076,76 -,065,083,715,080 -,074,68 -,064,4 -,081,796 -,053 -,061,785,017,04,509,63 -,008,10,83,05,03,777 Método de extraccón: Análss de componentes prncpales. Método de rotacón: Normalzacón Varmax con Kaser. a. La rotacón ha convergdo en 5 teracones. Ganas de trabajar Comoddad Preparacón Búsqueda Crss Polítca de empleo Empresaros Reparto Plurempleo Matrz de confguracón ạ Componente 1 3,813 -,085 -,014,76 -,035 -,01,740,1,146,664 -,048 -,17 -,06,806,106 -,013,790,036,08,496 -,9 -,091,056 -,834,14 -,08 -,775 Método de extraccón: Análss de componentes prncpales. Metodo de rotacón: Normalzacón Oblmn con Kaser. a. La rotacón ha convergdo en 5 teracones. 87 Ganas de trabajar Comoddad Preparacón Búsqueda Crss Polítca de empleo Empresaros Reparto Plurempleo Matrz de pesos factorales Matrz de confguracón ạ Componente 1 3,815 -,068 -,00,765 -,019,009,751,136 -,154,663 -,034,161 -,006,804 -,080,005,789 -,010,034,497,46 -,111,057,841,105 -,0,776 Método de extraccón: Análss de componentes prncpales. Método de rotacón: Normalzacón Promax con Kaser. a. La rotacón ha convergdo en 5 teracones. Analzando someramente estos resultados, ben podría tratarse de tres factores claramente dferencados y referdos: 1) Al trabajador ) Goberno y empresaros 3) Reparto o redstrbucón del trabajo
145 Gráfco de componentes en espaco rotado Gráfcamente podemos ver estos msmos resultados en la Fgura que corresponde al gráfco trdmensonal de la solucón rotada VARIMAX y componentes prncpales. 89 Gráfco de componentes en espaco rotado
CURSO INTERNACIONAL: CONSTRUCCIÓN DE ESCENARIOS ECONÓMICOS Y ECONOMETRÍA AVANZADA. Instructor: Horacio Catalán Alonso
 CURSO ITERACIOAL: COSTRUCCIÓ DE ESCEARIOS ECOÓMICOS ECOOMETRÍA AVAZADA Instructor: Horaco Catalán Alonso Modelo de Regresón Lneal Smple El modelo de regresón lneal representa un marco metodológco, que
CURSO ITERACIOAL: COSTRUCCIÓ DE ESCEARIOS ECOÓMICOS ECOOMETRÍA AVAZADA Instructor: Horaco Catalán Alonso Modelo de Regresón Lneal Smple El modelo de regresón lneal representa un marco metodológco, que
Medidas de Variabilidad
 Meddas de Varabldad Una medda de varabldad es un ndcador del grado de dspersón de un conjunto de observacones de una varable, en torno a la meda o centro físco de la msma. S la dspersón es poca, entonces
Meddas de Varabldad Una medda de varabldad es un ndcador del grado de dspersón de un conjunto de observacones de una varable, en torno a la meda o centro físco de la msma. S la dspersón es poca, entonces
Tema 6. Estadística descriptiva bivariable con variables numéricas
 Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
EXPERIMENTACIÓN COMERCIAL(I)
 EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
Problemas donde intervienen dos o más variables numéricas
 Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Figura 1
 5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
Inferencia en Regresión Lineal Simple
 Inferenca en Regresón Lneal Smple Modelo de regresón lneal smple: Se tenen n observacones de una varable explcatva x y de una varable respuesta y, ( x, y)(, x, y),...,( x n, y n ) el modelo estadístco
Inferenca en Regresón Lneal Smple Modelo de regresón lneal smple: Se tenen n observacones de una varable explcatva x y de una varable respuesta y, ( x, y)(, x, y),...,( x n, y n ) el modelo estadístco
H 0 : La distribución poblacional es uniforme H 1 : La distribución poblacional no es uniforme
 Una hpótess estadístca es una afrmacón con respecto a una característca que se desconoce de una poblacón de nterés. En la seccón anteror tratamos los casos dscretos, es decr, en forma exclusva el valor
Una hpótess estadístca es una afrmacón con respecto a una característca que se desconoce de una poblacón de nterés. En la seccón anteror tratamos los casos dscretos, es decr, en forma exclusva el valor
Ejemplo: Consumo - Ingreso. Ingreso. Consumo. Población 60 familias
 Ejemplo: Consumo - Ingreso Ingreso Consumo Poblacón 60 famlas ( YX ) P = x [ YX ] E = x Línea de regresón poblaconal 80 60 Meda Condconal 40 20 00 [ X = 200] EY o o o o [ X = 200] EY 80 o o o 60 o 40 8
Ejemplo: Consumo - Ingreso Ingreso Consumo Poblacón 60 famlas ( YX ) P = x [ YX ] E = x Línea de regresón poblaconal 80 60 Meda Condconal 40 20 00 [ X = 200] EY o o o o [ X = 200] EY 80 o o o 60 o 40 8
Problema: Existe relación entre el estado nutricional y el rendimiento académico de estudiantes de enseñanza básica?
 Relacones entre varables cualtatvas Problema: xste relacón entre el estado nutrconal y el rendmento académco de estudantes de enseñanza básca? stado Nutrconal Malo Regular Bueno TOTAL Bajo 13 95 3 55 Rendmento
Relacones entre varables cualtatvas Problema: xste relacón entre el estado nutrconal y el rendmento académco de estudantes de enseñanza básca? stado Nutrconal Malo Regular Bueno TOTAL Bajo 13 95 3 55 Rendmento
Análisis cuantitativo aplicado al Comercio Internacional y el Transporte
 Máster de Comerco, Transporte y Comuncacones Internaconales Análss cuanttatvo aplcado al Comerco Internaconal y el Transporte Ramón úñez Sánchez Soraya Hdalgo Gallego Departamento de Economía Introduccón
Máster de Comerco, Transporte y Comuncacones Internaconales Análss cuanttatvo aplcado al Comerco Internaconal y el Transporte Ramón úñez Sánchez Soraya Hdalgo Gallego Departamento de Economía Introduccón
Muestra: son datos de corte transversal correspondientes a 120 familias españolas.
 Capítulo II: El Modelo Lneal Clásco - Estmacón Aplcacones Informátcas 3. APLICACIONES INFORMÁTICAS Fchero : cp.wf (modelo de regresón smple) Seres: : consumo famlar mensual en mles de pesetas RENTA: renta
Capítulo II: El Modelo Lneal Clásco - Estmacón Aplcacones Informátcas 3. APLICACIONES INFORMÁTICAS Fchero : cp.wf (modelo de regresón smple) Seres: : consumo famlar mensual en mles de pesetas RENTA: renta
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
MODELOS DE ELECCIÓN BINARIA
 MODELOS DE ELECCIÓN BINARIA Econometría I UNLP http://www.econometra1.depeco.econo.unlp.edu.ar/ Modelos de Eleccón Bnara: Introduccón Estamos nteresados en la probabldad de ocurrenca de certo evento Podemos
MODELOS DE ELECCIÓN BINARIA Econometría I UNLP http://www.econometra1.depeco.econo.unlp.edu.ar/ Modelos de Eleccón Bnara: Introduccón Estamos nteresados en la probabldad de ocurrenca de certo evento Podemos
Econometría de corte transversal. Pablo Lavado Centro de Investigación de la Universidad del Pacífico
 Econometría de corte transversal Pablo Lavado Centro de Investgacón de la Unversdad del Pacífco Contendo Defncones báscas El contendo mínmo del curso Bblografía recomendada Aprendendo econometría Defncones
Econometría de corte transversal Pablo Lavado Centro de Investgacón de la Unversdad del Pacífco Contendo Defncones báscas El contendo mínmo del curso Bblografía recomendada Aprendendo econometría Defncones
1.Variables ficticias en el modelo de regresión: ejemplos.
 J.M.Arranz y M.M. Zamora.Varables fctcas en el modelo de regresón: ejemplos. Las varables fctcas recogen los efectos dferencales que se producen en el comportamento de los agentes económcos debdo a dferentes
J.M.Arranz y M.M. Zamora.Varables fctcas en el modelo de regresón: ejemplos. Las varables fctcas recogen los efectos dferencales que se producen en el comportamento de los agentes económcos debdo a dferentes
Tema 1: Estadística Descriptiva Unidimensional
 Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. Fenómeno aleatoro: no es posble predecr el resultado. La estadístca se ocupa de aquellos fenómenos no determnstas donde
Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. Fenómeno aleatoro: no es posble predecr el resultado. La estadístca se ocupa de aquellos fenómenos no determnstas donde
A. Una pregunta muy particular que se puede hacer a una distribución de datos es de qué magnitud es es la heterogeneidad que se observa.
 MEDIDA DE DIPERIÓ A. Una pregunta muy partcular que se puede hacer a una dstrbucón de datos es de qué magntud es es la heterogenedad que se observa. FICHA º 18 Las meddas de dspersón generalmente acompañan
MEDIDA DE DIPERIÓ A. Una pregunta muy partcular que se puede hacer a una dstrbucón de datos es de qué magntud es es la heterogenedad que se observa. FICHA º 18 Las meddas de dspersón generalmente acompañan
INTRODUCCIÓN. Técnicas estadísticas
 Tema : Estadístca Descrptva Undmensonal ITRODUCCIÓ Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. (Ejemplo: lómetros recorrdos en un ntervalo de tempo a una velocdad
Tema : Estadístca Descrptva Undmensonal ITRODUCCIÓ Fenómeno determnsta: al repetrlo en déntcas condcones se obtene el msmo resultado. (Ejemplo: lómetros recorrdos en un ntervalo de tempo a una velocdad
Pronósticos. Humberto R. Álvarez A., Ph. D.
 Pronóstcos Humberto R. Álvarez A., Ph. D. Predccón, Pronóstco y Prospectva Predccón: estmacón de un acontecmento futuro que se basa en consderacones subjetvas, en la habldad, experenca y buen juco de las
Pronóstcos Humberto R. Álvarez A., Ph. D. Predccón, Pronóstco y Prospectva Predccón: estmacón de un acontecmento futuro que se basa en consderacones subjetvas, en la habldad, experenca y buen juco de las
Modelos unifactoriales de efectos aleatorizados
 Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
Capítulo 4 Modelos unfactorales de efectos aleatorzados En el modelo de efectos aleatoros, los nveles del factor son una muestra aleatora de una poblacón de nveles. Este modelo surge ante la necesdad de
CARTAS DE CONTROL. Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones para el control del proceso.
 CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
EJERCICIO 1 1. VERDADERO 2. VERDADERO (Esta afirmación no es cierta en el caso del modelo general). 3. En el modelo lineal general
 PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general. 3. En el modelo lneal general Y =X β + ε, explcar la forma que
GERENCIA DE OPERACIONES Y PRODUCCIÓN DISEÑO DE NUEVOS PRODUCTOS Y SERVICIOS ESTRATEGIAS DE OPERACIONES
 GERENCIA DE OPERACIONES Y PRODUCCIÓN DISEÑO DE NUEVOS PRODUCTOS Y SERVICIOS ESTRATEGIAS DE OPERACIONES PRONÓSTICOS PREDICCIÓN, PRONÓSTICO Y PROSPECTIVA Predccón: estmacón de un acontecmento futuro que
GERENCIA DE OPERACIONES Y PRODUCCIÓN DISEÑO DE NUEVOS PRODUCTOS Y SERVICIOS ESTRATEGIAS DE OPERACIONES PRONÓSTICOS PREDICCIÓN, PRONÓSTICO Y PROSPECTIVA Predccón: estmacón de un acontecmento futuro que
Lo que nos interesa en el análisis de varianza de una vía es extender el test t para dos muestras independientes, para comparar más de dos muestras.
 Capítulo : Comparacón de varos tratamentos o grupos Muchas preguntas de nvestgacón en educacón, pscología, negocos, ndustra y cencas naturales tenen que ver con la comparacón de varos grupos o tratamentos.
Capítulo : Comparacón de varos tratamentos o grupos Muchas preguntas de nvestgacón en educacón, pscología, negocos, ndustra y cencas naturales tenen que ver con la comparacón de varos grupos o tratamentos.
IN540: Métodos Estadísticos para economía y gestión Profesores: Marcelo Henríquez, Felipe Avilés Auxiliares: José Miguel Carrasco
 Departamento de Ingenería Industral Facultad de Cs. Físcas y Matemátcas Unversdad de Chle IN540: Métodos Estadístcos para economía y gestón Profesores: Marcelo Henríquez, Felpe Avlés Auxlares: José Mguel
Departamento de Ingenería Industral Facultad de Cs. Físcas y Matemátcas Unversdad de Chle IN540: Métodos Estadístcos para economía y gestón Profesores: Marcelo Henríquez, Felpe Avlés Auxlares: José Mguel
Mª Dolores del Campo Maldonado. Tel: :
 Mª Dolores del Campo Maldonado Tel: : 918 074 714 e-mal: ddelcampo@cem.mtyc.es Documentacón de referenca nternaconalmente aceptada ISO/IEC GUIDE 98-3:008 Uncertanty of measurement Part 3: Gude to the n
Mª Dolores del Campo Maldonado Tel: : 918 074 714 e-mal: ddelcampo@cem.mtyc.es Documentacón de referenca nternaconalmente aceptada ISO/IEC GUIDE 98-3:008 Uncertanty of measurement Part 3: Gude to the n
Efectos fijos o aleatorios: test de especificación
 Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
TEMA III EL ANÁLISIS DE REGRESIÓN LINEAL MÚLTIPLE
 TEMA III EL ANÁLISIS DE REGRESIÓN LINEAL MÚLTIPLE LECTURA OBLIGATORIA Regresón Lneal Múltple. En Ral, A. y Varela, J. (008). Estadístca Práctca para la Investgacón en Cencas de la Salud. Coruña: Netbblo.
TEMA III EL ANÁLISIS DE REGRESIÓN LINEAL MÚLTIPLE LECTURA OBLIGATORIA Regresón Lneal Múltple. En Ral, A. y Varela, J. (008). Estadístca Práctca para la Investgacón en Cencas de la Salud. Coruña: Netbblo.
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Ximénez & San Martín, 2004)
 FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
Población 1. Población 1. Población 2. Población 2. Población 1. Población 1. Población 2. Población 2. Frecuencia. Frecuencia
 MAT-3 Estadístca I Tema : Meddas de Dspersón Facltador: Félx Rondón, MS Insttuto Especalzado de Estudos Superores Loyola Introduccón Las meddas de tendenca central son ndcadores estadístcos que resumen
MAT-3 Estadístca I Tema : Meddas de Dspersón Facltador: Félx Rondón, MS Insttuto Especalzado de Estudos Superores Loyola Introduccón Las meddas de tendenca central son ndcadores estadístcos que resumen
Análisis de Regresión y Correlación
 1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
Tema 9. Análisis de Varianza de un factor. Análisis de la Varianza (ANOVA) Conceptos generales
 Tema 9 Análss de la Varanza (ANOVA) Conceptos generales La técnca del Análss de la Varanza consste en descomponer la varabldad de una poblacón (representada por su varanza) en dversos sumandos según los
Tema 9 Análss de la Varanza (ANOVA) Conceptos generales La técnca del Análss de la Varanza consste en descomponer la varabldad de una poblacón (representada por su varanza) en dversos sumandos según los
ESTADÍSTICA DESCRIPTIVA
 Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
Estadístca descrptva. ESTADÍSTICA DESCRIPTIVA POBLACIÓN Y MUESTRA. VARIABLES ESTADÍSTICAS DISTRIBUCIÓN DE FRECUENCIAS DE UNA MUESTRA AGRUPACIÓN DE DATOS REPRESENTACIONES GRÁFICAS DE LAS MUESTRAS PRINCIPALES
SEMANA 5 MEDIDAS DE TENDENCIA CENTRAL Y POSICIÓN
 Estadístca SEMANA 5 MEDIDAS DE TENDENCIA CENTRAL Y POSICIÓN LOGRO DE APRENDIZAJE: Al fnalzar la sesón, el estudante estará en la capacdad de calcular e nterpretar meddas de tendenca central y poscón de
Estadístca SEMANA 5 MEDIDAS DE TENDENCIA CENTRAL Y POSICIÓN LOGRO DE APRENDIZAJE: Al fnalzar la sesón, el estudante estará en la capacdad de calcular e nterpretar meddas de tendenca central y poscón de
1 EY ( ) o de E( Y u ) que hace que g E ( Y ) sea lineal. Por ejemplo,
 Modelos lneales generalzados En los modelos no lneales (tanto en su formulacón con coefcentes fjos o coefcentes aleatoros) que hemos vsto hasta ahora, exsten algunos que se denomnan lnealzables : son modelos
Modelos lneales generalzados En los modelos no lneales (tanto en su formulacón con coefcentes fjos o coefcentes aleatoros) que hemos vsto hasta ahora, exsten algunos que se denomnan lnealzables : son modelos
TODO ECONOMETRIA. Variables cualitativas
 TODO ECONOMETRIA Varables cualtatvas Índce Defncón de las varables dummy (o varables fctcas) Regresón con varables explcatvas dummy Varables dummy S queremos estudar s los hombres ganan más que las mujeres,
TODO ECONOMETRIA Varables cualtatvas Índce Defncón de las varables dummy (o varables fctcas) Regresón con varables explcatvas dummy Varables dummy S queremos estudar s los hombres ganan más que las mujeres,
Cada uno da lo que recibe, Y luego recibe lo que da, Nada es más simple, No hay otra norma: Nada se pierde, Todo se transforma.
 Cada uno da lo que recbe, Y luego recbe lo que da, Nada es más smple, No hay otra norma: Nada se perde, Todo se transforma. Todo se transforma (Jorge Drexler, cantautor uruguayo) Estadístca Básca - Manuel
Cada uno da lo que recbe, Y luego recbe lo que da, Nada es más smple, No hay otra norma: Nada se perde, Todo se transforma. Todo se transforma (Jorge Drexler, cantautor uruguayo) Estadístca Básca - Manuel
REGRESION LINEAL SIMPLE
 REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una muestra de observacones formadas por pares de varables: (x 1, y 1 ), (x, y ),.., (x n, y n ) A través de esta muestra, se desea estudar la relacón
REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una muestra de observacones formadas por pares de varables: (x 1, y 1 ), (x, y ),.., (x n, y n ) A través de esta muestra, se desea estudar la relacón
Algunas aplicaciones del test del signo
 43 Algunas aplcacones del test del sgno Test de Mc emar para sgnfcacón de cambos: En realdad este test se estuda en detalle en Métodos no Paramétrcos II, en el contexto de las denomnadas Tablas de Contngenca.
43 Algunas aplcacones del test del sgno Test de Mc emar para sgnfcacón de cambos: En realdad este test se estuda en detalle en Métodos no Paramétrcos II, en el contexto de las denomnadas Tablas de Contngenca.
REGRESION LINEAL SIMPLE
 REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Relación 2: Regresión Lineal.
 Relacón 2: Regresón Lneal. 1. Se llevó a cabo un estudo acerca de la cantdad de azúcar refnada (Y ) medante un certo proceso a varas temperaturas dferentes (X). Los datos se codfcan y regstraron en el
Relacón 2: Regresón Lneal. 1. Se llevó a cabo un estudo acerca de la cantdad de azúcar refnada (Y ) medante un certo proceso a varas temperaturas dferentes (X). Los datos se codfcan y regstraron en el
TRABAJO 1: Variables Estadísticas Unidimensionales (Tema 1).
 TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Introducción a la Física. Medidas y Errores
 Departamento de Físca Unversdad de Jaén Introduccón a la Físca Meddas y Errores J.A.Moleón 1 1- Introduccón La Físca y otras cencas persguen la descrpcón cualtatva y cuanttatva de los fenómenos que ocurren
Departamento de Físca Unversdad de Jaén Introduccón a la Físca Meddas y Errores J.A.Moleón 1 1- Introduccón La Físca y otras cencas persguen la descrpcón cualtatva y cuanttatva de los fenómenos que ocurren
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Midiendo la Asociación lineal entre dos variables
 Unversdad de Sonora XVIII Semana Regonal de Investgacón y Docenca en Matemátcas Mdendo la Asocacón lneal entre dos varables Rosa Ma. Montesnos Csneros Adán Durazo Armenta Departamento de Matemátcas Hermosllo,
Unversdad de Sonora XVIII Semana Regonal de Investgacón y Docenca en Matemátcas Mdendo la Asocacón lneal entre dos varables Rosa Ma. Montesnos Csneros Adán Durazo Armenta Departamento de Matemátcas Hermosllo,
MUESTREO EN POBLACIONES FINITAS
 MUESTREO EN POBLACIONES FINITAS Antono Morllas A.Morllas: Muestreo 1 MUESTREO EN POBLACIONES FINITAS 1. Conceptos estadístcos báscos. Etapas en el muestreo 3. Tpos de error 4. Métodos de muestreo 5. Tamaño
MUESTREO EN POBLACIONES FINITAS Antono Morllas A.Morllas: Muestreo 1 MUESTREO EN POBLACIONES FINITAS 1. Conceptos estadístcos báscos. Etapas en el muestreo 3. Tpos de error 4. Métodos de muestreo 5. Tamaño
REGRESION Y CORRELACION
 nav Estadístca (complementos) 1 REGRESION Y CORRELACION Fórmulas báscas en la regresón lneal smple Como ejemplo de análss de regresón, descrbremos el caso de Pzzería Armand, cadena de restaurantes de comda
nav Estadístca (complementos) 1 REGRESION Y CORRELACION Fórmulas báscas en la regresón lneal smple Como ejemplo de análss de regresón, descrbremos el caso de Pzzería Armand, cadena de restaurantes de comda
Correlación y regresión lineal simple
 . Regresón lneal smple Correlacón y regresón lneal smple. Introduccón La correlacón entre dos varables ( e Y) se refere a la relacón exstente entre ellas de tal manera que a determnados valores de se asocan
. Regresón lneal smple Correlacón y regresón lneal smple. Introduccón La correlacón entre dos varables ( e Y) se refere a la relacón exstente entre ellas de tal manera que a determnados valores de se asocan
ESTADÍSTICA. Definiciones
 ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
ESTADÍSTICA Defncones - La Estadístca es la cenca que se ocupa de recoger, contar, organzar, representar y estudar datos referdos a una muestra para después generalzar y sacar conclusones acerca de una
DISTRIBUCIONES BIDIMENSIONALES
 Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
Regresión y correlación simple 113
 Regresón y correlacón smple 113 Captulo X ANALISIS DE REGRESION Y CORRELACION El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes
Regresón y correlacón smple 113 Captulo X ANALISIS DE REGRESION Y CORRELACION El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes
Investigación y Técnicas de Mercado. Previsión de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): Ajustes de Tendencia
 Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
EL ANÁLISIS DE LA VARIANZA (ANOVA) 2. Estimación de componentes de varianza
 EL ANÁLSS DE LA VARANZA (ANOVA). Estmacón de componentes de varanza Alca Maroto, Rcard Boqué Grupo de Qumometría y Cualmetría Unverstat Rovra Vrgl C/ Marcel.lí Domngo, s/n (Campus Sescelades) 43007-Tarragona
EL ANÁLSS DE LA VARANZA (ANOVA). Estmacón de componentes de varanza Alca Maroto, Rcard Boqué Grupo de Qumometría y Cualmetría Unverstat Rovra Vrgl C/ Marcel.lí Domngo, s/n (Campus Sescelades) 43007-Tarragona
Regresión Binomial Negativa
 Regresón Bnomal Negatva Resumen El procedmento Regresón Bnomal Negatva está dseñado para ajustar un modelo de regresón en el cual la varable dependente Y consste de conteos. El modelo de regresón ajustado
Regresón Bnomal Negatva Resumen El procedmento Regresón Bnomal Negatva está dseñado para ajustar un modelo de regresón en el cual la varable dependente Y consste de conteos. El modelo de regresón ajustado
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
Unversdad de Cádz Departamento de Matemátcas MATEMÁTICAS para estudantes de prmer curso de facultades y escuelas técncas Tema 13 Dstrbucones bdmensonales. Regresón y correlacón lneal Elaborado por la Profesora
Variables Aleatorias
 Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS
 CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
PRÁCTICA 16: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN
 PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general). 3. En el modelo lneal general Y = X b + e, explcar la forma
PRÁCTICA 6: MODELO DE REGRESIÓN MÚLTIPLE SOLUCIÓN EJERCICIO. VERDADERO. VERDADERO (Esta afrmacón no es certa en el caso del modelo general). 3. En el modelo lneal general Y = X b + e, explcar la forma
Introducción a los Modelos de Pronósticos
 Introduccón a los Modelos de Pronóstcos Dra. Fernanda Vllarreal Unversdad Naconal del Sur- Departamento de Matemátca Septembre 2016 - fvllarreal@uns.edu.ar Introduccón Planeacón del futuro, un aspecto
Introduccón a los Modelos de Pronóstcos Dra. Fernanda Vllarreal Unversdad Naconal del Sur- Departamento de Matemátca Septembre 2016 - fvllarreal@uns.edu.ar Introduccón Planeacón del futuro, un aspecto
T. 9 El modelo de regresión lineal
 1 T. 9 El modelo de regresón lneal 1. Conceptos báscos sobre el análss de regresón lneal. Ajuste de la recta de regresón 3. Bondad de ajuste del modelo de regresón Modelos predctvos o de regresón: la representacón
1 T. 9 El modelo de regresón lneal 1. Conceptos báscos sobre el análss de regresón lneal. Ajuste de la recta de regresón 3. Bondad de ajuste del modelo de regresón Modelos predctvos o de regresón: la representacón
6 Impacto en el bienestar de los beneficiarios del PAAM
 6 Impacto en el benestar de los benefcaros del PAAM Con el fn de evaluar el efecto del PAAM sobre sus benefcaros, se consderó como hpótess que el Programa ha nfludo en el mejoramento de la caldad de vda
6 Impacto en el benestar de los benefcaros del PAAM Con el fn de evaluar el efecto del PAAM sobre sus benefcaros, se consderó como hpótess que el Programa ha nfludo en el mejoramento de la caldad de vda
Guía para el Trabajo Práctico N 5. Métodos Estadísticos en Hidrología
 Guía para el Trabajo Práctco 5 Métodos Estadístcos en Hdrología er. PASO) Realzar el ajuste de la funcón de dstrbucón normal a una muestra de datos totales anuales de una varable (caudal, precptacón, etc.)
Guía para el Trabajo Práctco 5 Métodos Estadístcos en Hdrología er. PASO) Realzar el ajuste de la funcón de dstrbucón normal a una muestra de datos totales anuales de una varable (caudal, precptacón, etc.)
Objetivo del tema. Esquema del tema. Economía Industrial. Tema 2. La demanda de la industria
 Economía Industral Tema. La demanda de la ndustra Objetvo del tema Entender el modelo económco de comportamento del consumdor, fnalmente resumdo en la funcón de demanda. Comprender el carácter abstracto
Economía Industral Tema. La demanda de la ndustra Objetvo del tema Entender el modelo económco de comportamento del consumdor, fnalmente resumdo en la funcón de demanda. Comprender el carácter abstracto
FORMULARIO PARA LA PRESENTACIÓN DE RESUMEN DE PONENCIA
 FORMULARIO PARA LA PRESENTACIÓN DE RESUMEN DE PONENCIA TÍTULO DE LA PONENCIA: Heterogenedad en los perfles de ngreso y retornos a la educacón superor en el Perú AUTOR: Gustavo Yamada, Juan F. Castro y
FORMULARIO PARA LA PRESENTACIÓN DE RESUMEN DE PONENCIA TÍTULO DE LA PONENCIA: Heterogenedad en los perfles de ngreso y retornos a la educacón superor en el Perú AUTOR: Gustavo Yamada, Juan F. Castro y
2.2 TASA INTERNA DE RETORNO (TIR). Flujo de Caja Netos en el Tiempo
 Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Econometría. Ayudantía # 01, Conceptos Generales, Modelo de Regresión. Profesor: Carlos R. Pitta 1
 Escuela de Ingenería Comercal Ayudantía # 01, Conceptos Generales, Modelo de Regresón Profesor: Carlos R. Ptta 1 1 cptta@spm.uach.cl Escuela de Ingenería Comercal Ayudantía 01 Parte 01: Comentes Señale
Escuela de Ingenería Comercal Ayudantía # 01, Conceptos Generales, Modelo de Regresón Profesor: Carlos R. Ptta 1 1 cptta@spm.uach.cl Escuela de Ingenería Comercal Ayudantía 01 Parte 01: Comentes Señale
3. VARIABLES ALEATORIAS.
 3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
ESTADÍSTICA BIDIMENSIONAL ÍNDICE GENERAL
 ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
ESTADÍSTICA BIDIMESIOAL ÍDICE GEERAL 1.-Varable Estadístca Bdmensonal. Tablas de frecuenca... 1.1.- Concepto de varable estadístca bdmensonal. Eemplos.... 1..-Tablas bdmensonales de frecuencas. Tablas
Modelos triangular y parabólico
 Modelos trangular y parabólco ClassPad 0 Prof. Jean-Perre Marcallou INTRODUCCIÓN La calculadora CASIO ClassPad 0 dspone de la Aplcacón Prncpal para realzar los cálculos correspondentes a los modelos trangular
Modelos trangular y parabólco ClassPad 0 Prof. Jean-Perre Marcallou INTRODUCCIÓN La calculadora CASIO ClassPad 0 dspone de la Aplcacón Prncpal para realzar los cálculos correspondentes a los modelos trangular
Estadísticos muéstrales
 Estadístcos muéstrales Una empresa dedcada al transporte y dstrbucón de mercancías, tene una plantlla de 50 trabajadores. Durante el últmo año se ha observado que 5 trabajadores han faltado un solo día
Estadístcos muéstrales Una empresa dedcada al transporte y dstrbucón de mercancías, tene una plantlla de 50 trabajadores. Durante el últmo año se ha observado que 5 trabajadores han faltado un solo día
Tema 1. Conceptos generales
 Análss de Datos I Esquema del Tema Tema. Conceptos generales. COCEPTOS PREVIOS. DEFIICIÓ DE MEDICIÓ 3. DEFIICIÓ DE ESCALAS DE MEDIDA 4. VARIABLES CLASIFICACIÓ Y OTACIÓ REGLAS DEL SUMATORIO 5. EJERCICIOS
Análss de Datos I Esquema del Tema Tema. Conceptos generales. COCEPTOS PREVIOS. DEFIICIÓ DE MEDICIÓ 3. DEFIICIÓ DE ESCALAS DE MEDIDA 4. VARIABLES CLASIFICACIÓ Y OTACIÓ REGLAS DEL SUMATORIO 5. EJERCICIOS
Tema 2: El modelo clásico de regresión
 CURSO 010/011 Tema : El modelo clásco de regresón Aránzazu de Juan Fernández ECONOMETRÍA I ESQUEMA DEL TEMA Presentacón del modelo Hpótess del modelo Estmacón MCO Propedades algebracas de los estmadores
CURSO 010/011 Tema : El modelo clásco de regresón Aránzazu de Juan Fernández ECONOMETRÍA I ESQUEMA DEL TEMA Presentacón del modelo Hpótess del modelo Estmacón MCO Propedades algebracas de los estmadores
Tallerine: Energías Renovables. Fundamento teórico
 Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Economía de la Empresa: Financiación
 Economía de la Empresa: Fnancacón Francsco Pérez Hernández Departamento de Fnancacón e Investgacón de la Unversdad Autónoma de Madrd Objetvo del curso: Dentro del contexto de Economía de la Empresa, se
Economía de la Empresa: Fnancacón Francsco Pérez Hernández Departamento de Fnancacón e Investgacón de la Unversdad Autónoma de Madrd Objetvo del curso: Dentro del contexto de Economía de la Empresa, se
EL MODELO DE REGRESIÓN LINEAL SIMPLE
 Unversdad Carlos III de Madrd César Alonso ECONOMETRIA EL MODELO DE REGRESIÓN LINEAL SIMLE Índce 1. Relacones empírcas y teórcas......................... 1 2. Conceptos prevos................................
Unversdad Carlos III de Madrd César Alonso ECONOMETRIA EL MODELO DE REGRESIÓN LINEAL SIMLE Índce 1. Relacones empírcas y teórcas......................... 1 2. Conceptos prevos................................
Las hipótesis en las que vamos a basar el funcionamiento del Modelo Lineal General
 CAPÍULO. EL MODELO LINEAL GENERAL. Introduccón. Hpótess del modelo Las hpótess en las que vamos a basar el funconamento del Modelo Lneal General son las sguentes. Suponemos que tenemos una muestra de valores
CAPÍULO. EL MODELO LINEAL GENERAL. Introduccón. Hpótess del modelo Las hpótess en las que vamos a basar el funconamento del Modelo Lneal General son las sguentes. Suponemos que tenemos una muestra de valores
EJERCICIOS. Ejercicio 1.- Para el modelo de regresión simple siguiente: Y i = βx i + ε i i =1,..., 100. se tienen las siguientes medias muestrales:
 EJERCICIOS Tema 2: MODELO DE REGRESION LINEAL SIMPLE Ejercco 1.- Para el modelo de regresón smple sguente: Y = βx + ε =1,..., 100 se tenen las sguentes medas muestrales: ( P y ) /n =0.3065 ( P y 2 ) /n
EJERCICIOS Tema 2: MODELO DE REGRESION LINEAL SIMPLE Ejercco 1.- Para el modelo de regresón smple sguente: Y = βx + ε =1,..., 100 se tenen las sguentes medas muestrales: ( P y ) /n =0.3065 ( P y 2 ) /n
Reconocimiento de Locutor basado en Procesamiento de Voz. ProDiVoz Reconocimiento de Locutor 1
 Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
Reconocmento de Locutor basado en Procesamento de Voz ProDVoz Reconocmento de Locutor Introduccón Reconocmento de locutor: Proceso de extraccón automátca de nformacón relatva a la dentdad de la persona
EXPERIMENTOS ANIDADOS O JERARQUICOS NESTED
 EXPERIMENTOS ANIDADOS O JERARQUICOS NESTED Exsten ocasones donde los nveles de un factor B son smlares pero no déntcos para dferentes nveles del factor A. Es decr, dferentes nveles del factor A ven nveles
EXPERIMENTOS ANIDADOS O JERARQUICOS NESTED Exsten ocasones donde los nveles de un factor B son smlares pero no déntcos para dferentes nveles del factor A. Es decr, dferentes nveles del factor A ven nveles
Introducción al riesgo de crédito
 Introduccón al resgo de crédto Estrella Perott Investgador Senor Bolsa de Comerco de Rosaro eperott@bcr.com.ar. Introduccón El resgo credtco es el resgo de una pérdda económca como consecuenca de la falta
Introduccón al resgo de crédto Estrella Perott Investgador Senor Bolsa de Comerco de Rosaro eperott@bcr.com.ar. Introduccón El resgo credtco es el resgo de una pérdda económca como consecuenca de la falta
Estadística Descriptiva y Analisis de Datos con la Hoja de Cálculo Excel. Números Índices
 Estadístca Descrptva y Analss de Datos con la Hoja de Cálculo Excel úmeros Índces úmeros Índces El número índce es un recurso estadístco para medr dferencas entre grupos de datos. Un número índce se puede
Estadístca Descrptva y Analss de Datos con la Hoja de Cálculo Excel úmeros Índces úmeros Índces El número índce es un recurso estadístco para medr dferencas entre grupos de datos. Un número índce se puede
ESTADISTÍCA. 1. Población, muestra e individuo. 2. Variables estadísticas. 3. El proceso que se sigue en estadística
 ESTADISTÍCA. Poblacón, muestra e ndvduo Las característcas de una dstrbucón se pueden estudar drectamente sobre la poblacón o se pueden nferr a partr de l estudo de una muestra. Poblacón estadístca es
ESTADISTÍCA. Poblacón, muestra e ndvduo Las característcas de una dstrbucón se pueden estudar drectamente sobre la poblacón o se pueden nferr a partr de l estudo de una muestra. Poblacón estadístca es
Visión moderna del modelo de transporte clásico
 Vsón moderna del modelo de transporte clásco Zonfcacón y Red Estratégca Datos del Año Base Datos de Planfcacón Para el Año de Dseño Base de Datos año base futuro Generacón de Vajes Demanda Dstrbucón y
Vsón moderna del modelo de transporte clásco Zonfcacón y Red Estratégca Datos del Año Base Datos de Planfcacón Para el Año de Dseño Base de Datos año base futuro Generacón de Vajes Demanda Dstrbucón y
Histogramas: Es un diagrama de barras pero los datos son siempre cuantitativos agrupados en clases o intervalos.
 ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
Descripción de una variable
 Descrpcón de una varable Tema. Defncones fundamentales. Tabla de frecuencas. Datos agrupados. Meddas de poscón Meddas de tendenca central: meda, medana, moda Ignaco Cascos Depto. Estadístca, Unversdad
Descrpcón de una varable Tema. Defncones fundamentales. Tabla de frecuencas. Datos agrupados. Meddas de poscón Meddas de tendenca central: meda, medana, moda Ignaco Cascos Depto. Estadístca, Unversdad
Métodos cuantitativos de análisis gráfico
 Métodos cuanttatvos de análss gráfco Método de cuadrados mínmos Regresón lneal Hemos enfatzado sobre la mportanca de las representacones gráfcas hemos vsto la utldad de las versones lnealzadas de los gráfcos
Métodos cuanttatvos de análss gráfco Método de cuadrados mínmos Regresón lneal Hemos enfatzado sobre la mportanca de las representacones gráfcas hemos vsto la utldad de las versones lnealzadas de los gráfcos
Tema 6 El mercado de bienes y la función IS
 Tema 6 El mercado de benes y la funcón IS Macroeconomía I Prof. Anhoa Herrarte Sánchez Curso 2007-08 Bblografía para preparar este tema Apuntes de clase Capítulo 3, Macroeconomía, O. Blanchard Prof. Anhoa
Tema 6 El mercado de benes y la funcón IS Macroeconomía I Prof. Anhoa Herrarte Sánchez Curso 2007-08 Bblografía para preparar este tema Apuntes de clase Capítulo 3, Macroeconomía, O. Blanchard Prof. Anhoa
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y A c se les ha asociado los sucesos B y B c.
 Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Diseño y Análisis de Experimentos en el SPSS 1
 Dseño y Análss de Expermentos en el SPSS EJEMPLO. Los sguentes datos muestran las meddas de hemoglobna (gramos por 00 ml) en la sangre de 40 ejemplares de una espece de truchas marrones. Las truchas se
Dseño y Análss de Expermentos en el SPSS EJEMPLO. Los sguentes datos muestran las meddas de hemoglobna (gramos por 00 ml) en la sangre de 40 ejemplares de una espece de truchas marrones. Las truchas se
Boletín de la Tendencia Laboral del Desarrollo Humano
 Boletín de la Tendenca Laboral del Desarrollo Humano Notas técncas AÑO 05 NÚMERO 6 PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO MÉXICO Nota técnca Índce de Compettvdad Socal (cs) El cs es una medda
Boletín de la Tendenca Laboral del Desarrollo Humano Notas técncas AÑO 05 NÚMERO 6 PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO MÉXICO Nota técnca Índce de Compettvdad Socal (cs) El cs es una medda
Especialista en Estadística y Docencia Universitaria REGRESION LINEAL MULTIPLE
 Especalsta en Estadístca y Docenca Unverstara REGRESION LINEAL MULTIPLE El modelo de regresón lneal múltple El modelo de regresón lneal múltple con p varables predctoras y basado en n observacones tomadas
Especalsta en Estadístca y Docenca Unverstara REGRESION LINEAL MULTIPLE El modelo de regresón lneal múltple El modelo de regresón lneal múltple con p varables predctoras y basado en n observacones tomadas
Población: Es el conjunto de todos los elementos cuyo conocimiento nos interesa y serán objeto de nuestro estudio.
 Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para el conocmento
Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN Objetvo: La estadístca tene por objeto el desarrollo de técncas para el conocmento
Economía Aplicada. Estimador de diferencias en diferencias. Ver Wooldridge cap.13. Departamento de Economía Universidad Carlos III de Madrid 1 / 19
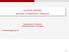 Economía Aplcada Estmador de dferencas en dferencas Departamento de Economía Unversdad Carlos III de Madrd Ver Wooldrdge cap.13 1 / 19 Análss de Polítca: Dferencas-en-Dferencas En muchos casos la varable
Economía Aplcada Estmador de dferencas en dferencas Departamento de Economía Unversdad Carlos III de Madrd Ver Wooldrdge cap.13 1 / 19 Análss de Polítca: Dferencas-en-Dferencas En muchos casos la varable
Apéndice A: Metodología para la evaluación del modelo de pronóstico meteorológico
 Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
Tema 3. Estadísticos univariados: tendencia central, variabilidad, asimetría y curtosis
 Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
