c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
|
|
|
- Gonzalo Vidal Fuentes
- hace 6 años
- Vistas:
Transcripción
1 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g de vitamina B i 0,15 g de calci, també per cada 100 g. Escriu la matriu corresponent. æ0,06 0,3 0, ö 0,1 0, 0,15 La representació matricial d una xarxa de transport per carretera, segons el conveni anterior, és donada per la matriu: æ ö Dibuixa un esquema que hi estigui relacionat. Resposta oberta. Per exemple: c) C = (c ij ) de tres files i tres columnes per a c ij = j i.. ndica els vectors que determinen cadascuna de les matrius de l exercici anterior. a) u r = (1,, 3, 4), r æ1 3 ö v= r æ1 4ö,1,, i w=,,1, r b) a r = c r = (, 0) i b r = d = (0, ) c) u r = (1, 1, 1), v r = (, 4, 8) i w r = (3, 9, 7) 3. Escriu una matriu que representi vectors de V, i una altra que representi 4 vectors de V 3. ndica l ordre de cadascuna. Resposta oberta. Per exemple: æ 1ö A = 1 1 æ1 3ö C = æ1 1 1ö B = La matriu A és d ordre (, ) i la matriu B d ordre (3, 4). 4. Escriu una matriu A d ordre (3, 4). Resposta oberta. Per exemple: Exercicis 1. Escriu les matrius següents: i a) A = (a ij ) i = 1,, 3, 4; j = 1,, 3 per a ij =. j æ1 1/ 1/3 ö 1 /3 A = 3 3/ 1 4 4/3 b) B = (b ij ) d ordre (, 4) sabent que b ij = = ( 1) i + ( 1) j. æ- 0-0ö B = 0 0 æ1 1 ö A = a) Troba n la matriu oposada i la matriu transposada. Comprova que la matriu oposada de la transposada és igual a la matriu transposada de l oposada. æ 1 1ö - A = t A æ 1 0 0ö 1 = 1 1 Mcraw-ill/nteramericana de España, S.A.U. Matemàtiques. Batxillerat 95
2 æ 0 0ö ( t A) = t ( A) = b) Comprova que t ( t A) = A. æ1 1 ö t ( t A) = 0 1 = A Donades les matrius següents: æ x 3zö æ 4y -t ö A = i B = x - y y z 3x + 4 Troba els valors de x, y, z i t sabent que A = = B. (1) x = 4y () 3z = t (3) x y = z (4) y = 3x + 4 De (1) i (4) x =, y = 1, substituint a (3) z = 1, i substituint a () t = Escriu una matriu quadrada d ordre 3 que sigui triangular superior. ndica els vectors de V 3 que defineixen la matriu. Calcula n la traa. Resposta oberta. Per exemple: æ 3 ö A = u r = (, 0, 0), v r = (3, 1, 0) i w r = ( 1,, 1) tra(a) = = 7. Escriu una matriu quadrada d ordre 4 que sigui alhora simtrica i antisimtrica. i ha moltes matrius que tinguin aquesta característica? La matriu quadrada nul la d ordre quatre. Només aquesta. 8. Qualsevol matriu diagonal és simtrica? antisimtrica? ustifica n les respostes. Sí, ja que si A és una matriu diagonal t A = A A és simtrica. No, perqu si és una matriu diagonal, els elements de la diagonal principal no són zero, i per tant no pot ser antisimtrica. Mcraw-ill/nteramericana de España, S.A.U. 9. Per qu han de ser zero els elements de la diagonal principal d una matriu antisimtrica? Perqu sigui una matriu antisimtrica, els elements de la diagonal principal han de verificar que a ii = a ii, d on s obté que a ii = Tenim la matriu: a) Com és aquesta matriu? És una matriu simtrica. b) Troba la matriu transposada de la matriu oposada. c) Com són entre elles la matriu que has trobat en l apartat anterior i la matriu inicial? Són oposades. d) Es pot enunciar, en aquest sentit, alguna propietat general? En una matriu simtrica, la transposada de l oposada coincideix amb la matriu oposada. 11. Donades les matrius: æ 6 1 4ö æ 1ö æ 1 1 ö A = B = æ0-3 1ö C = a) Comprova les propietats de la suma i del producte de matrius. Suma: associativa: A + (B + C) = (A + B) + C = Matemàtiques. Batxillerat 96
3 existncia d element neutre: - A + O = O + A = = A, sent O la matriu quadrada nul la d ordre tres. existncia d element simtric: A + ( A) = ( A) + A = O, 1 - sent A = 0-0 commutativa: A + B = B + A = Producte: associativa: æ ö (AB)C = A(BC) = distributiva: æ 7 16ö A(B + C) = AB + AC = æ 9 3 6ö (A + B)C = AC + BC = b) Prenent el valors k = i h = 3, comprova les propietats del producte d un nombre per una matriu. æ 0 6 0ö (A + B) = A + B = æ ö 5A = A + 3A = æ-6 1 6ö (3A) = æ 1ö 1A = = A 1 0 Mcraw-ill/nteramericana de España, S.A.U. c) Amb el mateix valor de k de l apartat anterior, comprova les propietats de la transposició de matrius. 0 t (A + B) = t A + t B = t (A) = ( t A) = t (AB) = ( t B)( t A) = t (A )+ = ( t A) = 1. Amb les matrius de l exercici anterior, calcula: a) A 3B + 4C b) AB + C c) 3A CB d) C(A B) e) A 3 f) (BC) Matemàtiques. Batxillerat 97
4 . Es diu que dues matrius A i B commuten quan AB = BA. Comprova, amb matrius quadrades d ordre 3, que: Respostes obertes. Per exemple: a) Una matriu diagonal commuta amb qualsevol matriu del seu mateix ordre. A = 1 1 B = 1 1 AB = BA = b) Si és la matriu unitat, A = A = A. A = A = 14. Siguin A i B dues matrius quadrades d ordre, tals que: A = (a ij ); a 11 = a = 1, a 1 =, a 1 = 0 B = (b ij ); b 11 = b = a 1, b 1 = b , b 1 = 0 a) Escriu les dues matrius. 1 3 A = B = b) Les matrius A i B commuten? Sí, ja que AB = BA = c) Comprova que (A + B) (A B) = A B. Per qu creus que passa això? ustifica n la resposta. (A + B)(A B) = A B = Si commuten, vol dir que AB = BA, d on tenim que: (A + B)(A B) = AA + BA AB BB = A + BA BA B = A B 15. Demostra que si A i B no commuten, aleshores (A + B) ¹ A + AB + B Si no commuten, tenim que AB ¹ BA, i per tant BA + AB ¹ AB, d on: (A + B) = (A + B)(A + B) = AA + BA + AB + BB = A + BA + AB + B Mcraw-ill/nteramericana de España, S.A.U. 16. Siguin A, B i C matrius quadrades d ordre 3 i no nul les. a) És possible que AB doni la matriu nul la d ordre 3? Sí, ja que el producte de dues matrius no nul les pot donar la matriu nul la. b) Si es verifica que AB = AC, podem assegurar que B = C? No, AB = AC AB AC = 0 A(B C) = 0 i pot ser que A ¹ 0 i B C ¹ 0 d on B ¹ C. 17. Donades les matrius: æ 8 5ö æ 3 5 -ö A = i B = calcula els productes AB i ( t B) ( t A) AB = ( t B)( t A) = Calcula els determinants d ordre següents: - 1 a) = cos a -sin a b) = 1 sina cos a c) 3 4 = / x e 1 d) = 0 x 1 e æ 1 3 ö 19. Considera les matrius: A = 0 3, 4 1 æ - 1 4ö æ3-5 1ö B = 1 7 i C = Calcula A, B, C i A + B + C. A =19, B =6, C =, A + B + C =17. Matemàtiques. Batxillerat 98
5 0. Comprova les igualtats següents: t - 10 t - 5 a) = (t 1)(t 5) 1+ t t = t 6t + 5 = (t 1)(t 5) b) x y z = (y x)(z x)(z y) x y z (y x)(z x)(z y) = yz xz + x z y z + + xy x y. 1. Resol les equacions: a) b) t 0 t t t x y z =yz +x z+xy x y xz y z x y z 1+ x x 1 =0 + x x 3 + 3x = 0 x = 0, x = 3 x - 1 x + 4 = x x 6x 4 = 10 x = 1 r. Considera els vectors de V 3, = ( 1,, 1), r v r u = (, 3, ) i w = (0, 1, 3); i calcula: D ( u r + v r + w r, u r v r + w r, u r + v r w r ) r r r - u + v + u = (3,0,0) ü r r r ï u - v + w = (-3,-,6) ý;0-6 = r r r u + v - w = (1,6,-4) ïþ = 3 = 3(8-36) = Considerant la matriu A de l exemple anterior, calcula A i A*. Quina relació s estableix entre els dos determinants? A = 14, A* =196, A* = A 4. Sigui A = (a ij ) una matriu quadrada d ordre 3, definida per a ij = i j + 1. Troba la matriu A* i comprova que t (A*) = ( t A)*. A* = Mcraw-ill/nteramericana de España, S.A.U. t (A*) = ( t A)* = 5. Sigui B la matriu definida pels vectors u r = r = (1, ) i v = ( 1, 1) de V. a) Troba B*. B* = b) Les matrius B i B* commuten? ustifica n la resposta. No, perqu BB* = -3-3 B*B = 3 0 c) Calcula B, B*, BB* i B*B. 6. Calcula el determinant B = B* =3, BB* = B*B =9. a) Per la regla de Sarrus = 9 b) Desenvolupant-lo pels elements de la segona fila. ( ) ( 1) = = 9 c) Desenvolupant-lo pels elements de la tercera columna. c) ( 7) + 5( 1) = 14 5 = Desenvolupa, per la columna o la fila més adequada, els determinants: a) b) c) æ1 -ö a columna 5 3a fila 0 a fila Matemàtiques. Batxillerat i 99
6 8. Comprova amb determinants d ordre 3 i utilitzant la regla de Sarrus les propietats a), b), c), g) i j). Resposta oberta. Per exemple: a) = = 1 0 b) 1 0 = 3; 1 0 = c) - 0 = 6; 1 0 = 3 = f ) = g) = = = + 1 = Esbrina, emprant determinants, la dependncia o independncia lineal dels vectors següents: a) u r = (3, 1, ), v r = ( 1, 1, ), w r = (0,, 3) 3 0 =- 10 ¹ 0 1 linealment independents -3 b) u r = ( 1, 1, 4), v r = (, 1, 1), w r = (, 0, ) = 0 linealment dependents 4 1 c) u r = (1, 0, 1), v r = (,, 1), w r = (1,, ) = 0 linealment dependents 1 - d) u r = (1, 1, 1), v r = (1, 1, 1), w r = ( 1, 1, 1) =- 4 ¹ linealment independents 1 1 Mcraw-ill/nteramericana de España, S.A.U. 30. Utilitzant determinants, troba els valors de a, per tal que els vectors de V 3 següents siguin linealment dependents: a) u r = (1, 1, a), v r = (, 3, ), w r = (5, a, 8) a = a + 17a + 30; a = 5 =- =- a 17a 30 0 a1, a 6 b) u r = (1, 3, ), v r = (, 1, a), w r = (,, ) = 7a+ 35; 7a + 35 = 0 a a = Calcula el determinant següent, calculant només un determinant d ordre : Resposta oberta. Per exemple, deixant la 1a fila igual i canviant les altres dues per f ' = f + + f 1 i f 3 ' = f 3 f 1 i desenvolupant-lo pels elements de la segona columna nova queda: 3 6 = Troba el rang de les matrius següents: æ3 1 ö a) A = æ3 1 5ö b) B = æ3 1 5ö 1 5 c) C = æ 1ö d) D = rang A =, rang B = rang C = rang D = 3 Matemàtiques. Batxillerat 100
7 æ 1 a 1 ö 33. Considera la matriu A = a a. Tro- 1 ba els valors de a pels quals rang A ¹ 3. A = 0 a + 3a = 0 a = 1, a = 34. Sigui A una matriu quadrada regular. Demostra: a) Si AX = B, aleshores X = A 1 B AX = B A 1 (AX) = A 1 B (A 1 A)X = A 1 B X = A 1 B X = A 1 B b) Si XA = C, aleshores X = CA 1 XA = C (XA)A 1 = CA 1 X(AA 1 ) = CA 1 X = CA 1 X = CA 1 c) Aplica-ho a les matrius: 35. De les matrius: æ 3ö æ 4 1ö A = ; B = 5 0 æ 1 0ö i C = X = A 1 B = 8 - X = CA 1 = æ 1 0ö æ 1 3ö A = ; B = æ3-1ö i C =. a) ndica n una que tingui inversa. La matriu A. b) Troba aquesta inversa. es-ne la comprovació A 1 = 1 AA 1 = A 1 A = Mcraw-ill/nteramericana de España, S.A.U. 36. Amb les matrius de l exercici anterior, troba una matriu X tal que AX B = C. X = A 1 (C + B) = 37. Troba la inversa de la matriu: i comprova-ho. æ 1 3ö A = Calcula A 1 i compara-ho amb A. Qu observes? A 1 = AA 1 = A 1 A = A 1 = 1/11 = 1/ A 38. Troba una matriu B, tal que BA = (1 0), essent A la matriu de l exercici anterior. B = ( 10/11 6/11 9/11) 39. Comprova que la inversa de æa bö 1 æ d -bö A = és A 1 = c d ad - bc -c a Demostra que A 1 = A A d b da bc = = = ( ad -bc) -c a ( ad -bc ) 1 1 = = ad - bc A Amb les matrius A i B, comprova: (BA) 1 =(A 1 )(B 1 ) i (AB) 1 = (B 1 )(A 1 ) æ3 1 ö æ0 0 1ö A = 0 1 ; B = Matemàtiques. Batxillerat 101
8 Acabem (BA) 1 = (A 1 )(B 1 ) = (AB) 1 = (B 1 )(A 1 ) = Donades les matrius: æ 1 3ö æ 4 0ö A = 1 0, B = 1 3 i troba, si existeix, la ma- æ 1 ö C = triu X: a) A B + X = C 1 b) X 3B = A C c) XB = C d) AX = B Mcraw-ill/nteramericana de España, S.A.U. æ 3 4ö. Sigui A = troba una altra matriu - quadrada B d ordre tal que AB = 3A. B = 3. Calcula el determinant d una matriu quadrada A d ordre 3, definida per les condicions: a ij = 3 (i = j), a ij = 1 (i ¹ j) A = A = Resol l equació següent: x + 1 3x - 1 4x = 0 3x - 1 4x 6x - 1 6x + 3x = 0 x = 0, x = 1/. 5. Demostra que les arrels del polinomi següent són 4, 8 i 1. p(x) = p(x) = x 3 11x = (x 4)(x 8)(x + 1). 6. Calcula: x x + 1 x + 1 æ 1 4 ö æ 1 0ö x x x Troba les matrius inverses de: æ 1-3ö æ 3ö A = 0 1, B = 1 0 i æ 4 3ö C = 0 1. Matemàtiques. Batxillerat 10
9 es-ne la comprovació. A 1 = B 1 = C 1 = AA 1 = A 1 A = BB 1 = B 1 B = CC 1 = C 1 C = = De les matrius: 1-7 æ 1 0 0ö æ 1 3ö A = 0 1 0, B = 1 3 i æ3-1ö C = 1-4 indica n una que tingui inversa i troba-la. Troba una matriu X tal que XA + B = C La matriu A, A = ; X = (C B)A = Les matrius: æ a bö æ c dö A = i B = -b a -d c commuten? ustifica n la resposta. Sí, ja que AB = BA = ac - bd ad + bc -bc -ad - bd + ac 10. Decideix, segons els valors de k, el rang de la matriu: æ1 k k ö k 5k + 6 = 0 k =, k = 3. Si k ¹ i k ¹ 3, el rang és 3; i si k = o k = 3, aleshores el rang és. 11. Troba el rang de les matrius següents: æ 1ö æ 1 1 1ö -3 - A = B = æö æ ö C = D = rang A = 3, rang B =, rang C = i rang D = Troba A n si: æ a 1- aö A = 1+ a -a Si n és parell A n =, si n és senar A n = A. Mcraw-ill/nteramericana de España, S.A.U. Matemàtiques. Batxillerat 103
10
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
E0. Exercicis comentats.
 ETSAV-UPC Matemàtiques I [títol_ ] Exercicis de matemàtiques I. Lliçó 0. [versió_ ] Setembre 200 [matèria_ ] Operacions amb matrius i determinants. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura
ETSAV-UPC Matemàtiques I [títol_ ] Exercicis de matemàtiques I. Lliçó 0. [versió_ ] Setembre 200 [matèria_ ] Operacions amb matrius i determinants. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Al consejero A no le gusta ninguno de sus colegas como presidente. Dos consejeros (C y E) están de acuerdo en los mismos candidatos (B, C y D).
 ÁLGEBRA DE MATRIU Pàgina 48 Ajudant-te de la taula... De la tabla podemos deducir muchas cosas: Al consejero A no le gusta ninguno de sus colegas como presidente. B solo tiene un candidato el C. Dos consejeros
ÁLGEBRA DE MATRIU Pàgina 48 Ajudant-te de la taula... De la tabla podemos deducir muchas cosas: Al consejero A no le gusta ninguno de sus colegas como presidente. B solo tiene un candidato el C. Dos consejeros
Nom i Cognoms: Grup: Data:
 n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
n BATX MA ) Raoneu la certesa o falsedat de les afirmacions següents: a) Si A és la matriu dels coeficients d'un sistema d'equacions lineals i Ampl és la matriu ampliada del mateix sistema. Rang(A) Rang
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
SOLUCIONARI Unitat 9. Comencem. Exercicis
 SOLUCIONARI Unitat 9 Comencem Les edats de tres nens sumades de dues en dues donen 6, 8 i 12 anys, respectivament. Troba les edats de cada nen. + y = 6 El sistema és: x + z = 8 îy + z 2 Es pot resoldre
SOLUCIONARI Unitat 9 Comencem Les edats de tres nens sumades de dues en dues donen 6, 8 i 12 anys, respectivament. Troba les edats de cada nen. + y = 6 El sistema és: x + z = 8 îy + z 2 Es pot resoldre
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Matemàtiques 1 - FIB
 Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
1. SISTEMA D EQUACIONS LINEALS
 1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
Apèndix Àlgebra lineal amb wxmaxima
 Apèndix Àlgebra lineal amb wxmaxima Objectius 1. Definir matrius amb wxmaxima. 2. Aplicar amb wxmaxima operacions amb matrius. 3. Aplicar transformacions elementals de matrius. 4. Calcular el determinant
Apèndix Àlgebra lineal amb wxmaxima Objectius 1. Definir matrius amb wxmaxima. 2. Aplicar amb wxmaxima operacions amb matrius. 3. Aplicar transformacions elementals de matrius. 4. Calcular el determinant
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
SOLUCIONARI Unitat 1
 SOLUCIONARI Unitat Comencem En un problema de física es demana el temps que triga una pilota a assolir una certa altura. Un estudiant, que ha resolt el problema correctament, arriba a la solució t s. La
SOLUCIONARI Unitat Comencem En un problema de física es demana el temps que triga una pilota a assolir una certa altura. Un estudiant, que ha resolt el problema correctament, arriba a la solució t s. La
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Anells i cossos. Definició i exemples. Donat un conjunt A i dues operacions binàries que denotarem per + i, direm que (A, +, ) és un anell si
 Anells i cossos Definició i exemples Donat un conjunt A i dues operacions binàries que denotarem per + i, direm que (A, +, ) és un anell si (A, +) és un grup commutatiu, l operació és tancada, associativa
Anells i cossos Definició i exemples Donat un conjunt A i dues operacions binàries que denotarem per + i, direm que (A, +, ) és un anell si (A, +) és un grup commutatiu, l operació és tancada, associativa
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Propietats de les desigualtats.
 Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
TEMA 1: EXPRESSIONS ALGEBRAIQUES. Activitats
 TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
Les Arcades. Molló del terme. Ermita la Xara. Esglèsia Sant Pere
 Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
VECTORS EN L ESPAI. Pàgina 130. Pàgina 131. Problema 1. Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 5 sen α = 40 sen α cm 2
 VECTORS EN L ESPAI Pàgina 130 Problema 1 Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 sen α = 40 sen α cm cm α 8 cm Troba l àrea d aquest triangle en funció de l angle β: β a b
VECTORS EN L ESPAI Pàgina 130 Problema 1 Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 sen α = 40 sen α cm cm α 8 cm Troba l àrea d aquest triangle en funció de l angle β: β a b
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
4. EQUACIONS DE PRIMER GRAU AMB UNA INCÒGNITA
 Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
Fonaments Matemàtics
 Departament de Matemàtiques EPSEVG Universitat Politècnica de Catalunya BarcelonaTech Copyright 2011, 2016 Carles Batlle (carles.batlle@upc.edu) This work is licensed under a Creative Commons Attribution-Share
Departament de Matemàtiques EPSEVG Universitat Politècnica de Catalunya BarcelonaTech Copyright 2011, 2016 Carles Batlle (carles.batlle@upc.edu) This work is licensed under a Creative Commons Attribution-Share
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
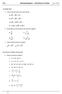 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
SOLUCIONARI Unitat 8. a) De tercer grau i amb dos termes. Comencem. b) De quart grau i amb cinc termes. c) De segon grau i amb un terme.
 SOLUCIONARI Unitat 8 Comencem Utilitza les potències de base 0 per descompondre aqests nombres: 56;,05;,; 005 i tres milions i mig. 56 0 5 0 6 0,05 0 5 0 0, 0 005 0 5 milions i mig 0 6 5 0 5 Troba el valor
SOLUCIONARI Unitat 8 Comencem Utilitza les potències de base 0 per descompondre aqests nombres: 56;,05;,; 005 i tres milions i mig. 56 0 5 0 6 0,05 0 5 0 0, 0 005 0 5 milions i mig 0 6 5 0 5 Troba el valor
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos
 DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
TEMA 2: Múltiples i Divisors
 TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial
 Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial Títol de l activitat MATRIU INVERSA Mestre/a - Professor/a Nom i Cognoms Adreça electrònica Cristina Steegmann
Fitxa per recollir informació sobre activitats d aula realitzades amb TAC d interès especial Títol de l activitat MATRIU INVERSA Mestre/a - Professor/a Nom i Cognoms Adreça electrònica Cristina Steegmann
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
7. Calcula P (x ) Q (x ): P (x ) = 5x 4 + x 3 2x 2 5 Q (x ) = 7x 4 5x 2 + 3x + 2 P (x ) Q (x ) = 2x 4 + x 3 + 3x 2 3x 7
 50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
SOLUCIONARI Unitat 10
 SOLUCIONARI Unitat 1 Comencem Donades dues ectes que tenen la mateixa diecció, quants plans hi ha que siguin pependiculas a les dues ectes a la vegada? Hi ha infinits plans, que són paal lels. Donats un
SOLUCIONARI Unitat 1 Comencem Donades dues ectes que tenen la mateixa diecció, quants plans hi ha que siguin pependiculas a les dues ectes a la vegada? Hi ha infinits plans, que són paal lels. Donats un
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
SOLUCIONARI Unitat 2. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
SOLUCIONARI Unitat 1. Exercicis. Comencem. 1. La gràfica velocitat-temps corresponent a dos mòbils és la que pots veure a la dreta (fig. 1.3).
 SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
ETSAV-UPC Matemàtiques I 5
 ETSAV-UPC Matemàtiques I 5 [títol_ ] Lliçó 3. Exercicis [versió_ ] Octubre 8 [matèria_ ] Sistemes de referència. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura del Vallès - Universitat
ETSAV-UPC Matemàtiques I 5 [títol_ ] Lliçó 3. Exercicis [versió_ ] Octubre 8 [matèria_ ] Sistemes de referència. [assignatura_ ] Matemàtiques I [centre_ ] E. T. S. d'arquitectura del Vallès - Universitat
Unitat didàctica 2. Polinomis i fraccions algebraiques
 Unitat didàctica. Polinomis i fraccions algebraiques Refleiona L Andrea té una bona col lecció d espelmes que decoren la seva habitació. Totes les espelmes cilíndriques tenen la mateia alçària: cm. Epressa,
Unitat didàctica. Polinomis i fraccions algebraiques Refleiona L Andrea té una bona col lecció d espelmes que decoren la seva habitació. Totes les espelmes cilíndriques tenen la mateia alçària: cm. Epressa,
Equacions i sistemes de primer grau
 Equacions i sistemes de primer grau Equacions de primer grau amb una incògnita. Resolució 1. a) Llegeix atentament l endevinalla numèrica següent i resol-la començant amb tres nombres diferents: Pensa
Equacions i sistemes de primer grau Equacions de primer grau amb una incògnita. Resolució 1. a) Llegeix atentament l endevinalla numèrica següent i resol-la començant amb tres nombres diferents: Pensa
Àmbit de les matemàtiques, de la ciència i de la tecnologia M14 Operacions numèriques UNITAT 2 LES FRACCIONS
 M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
Matemàtiques 1 - FIB
 Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS. 1) PAU 1999 Sèrie 1 Qüestió 1: Resoleu el sistema següent per als valors de k que el facin compatible.
 PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
EXERCICIS - SOLUCIONS
 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
Unitat 2 EQUACIONS DE PRIMER GRAU. Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 EQUACIONS DE PRIMER GRAU
 Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Elements d àlgebra lineal i geometria
 Elements d àlgebra lineal i geometria Espais vectorials, matrius, determinants, espai afí i euclidià Gerard Fortuny Anguera Ángel Alejandro Juan Pérez PID_151931 FUOC PID_151931 Elements d àlgebra lineal
Elements d àlgebra lineal i geometria Espais vectorials, matrius, determinants, espai afí i euclidià Gerard Fortuny Anguera Ángel Alejandro Juan Pérez PID_151931 FUOC PID_151931 Elements d àlgebra lineal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
1- Preguntes breus (resposta correcta del apartat són 0.5 punts. Total de punts, 5 sobre 10).
 UPF, Anàlisi Multivariant, Examen Final, de desembre de, De. a 7.,Aula 4. Professor: Albert Satorra Instruccions: Aquest examen consta de tres apartats. El primer són preguntes breus sobre temes diversos.
UPF, Anàlisi Multivariant, Examen Final, de desembre de, De. a 7.,Aula 4. Professor: Albert Satorra Instruccions: Aquest examen consta de tres apartats. El primer són preguntes breus sobre temes diversos.
(1,2) (1,2) (1,3) (3,0) (0,3) (2,1) (3,0) (1,3) (1,3) (2,3) (3,1) (3,0) (0,3) (1,2) (1,3) (4,0) (3,1) (3,1) (1,2) (1,3)
 1. DISTRIBUCIONS BIDIMENSIONALS Distribucions bidimensionals Moltes vegades interessa estudiar dues variables alhora dels elements d una població o mostra. En aquests casos, es recopilen dues dades per
1. DISTRIBUCIONS BIDIMENSIONALS Distribucions bidimensionals Moltes vegades interessa estudiar dues variables alhora dels elements d una població o mostra. En aquests casos, es recopilen dues dades per
Àlgebra lineal i equacions diferencials. Curs 2001/02 Exemple de diagonalització.
 Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes
 Genealitat de Catalunya Depatament d Educació Institut d Educació Secundàia Jaume Balmes Depatament de Matemàtiques 2n BATX MA Geometia Nom i Cognoms: Gup: Data: 5x y+ z= 0 1) Donat el pla π: ax 6y + 4z
Genealitat de Catalunya Depatament d Educació Institut d Educació Secundàia Jaume Balmes Depatament de Matemàtiques 2n BATX MA Geometia Nom i Cognoms: Gup: Data: 5x y+ z= 0 1) Donat el pla π: ax 6y + 4z
LES FRACCIONS Una fracció és part de la unitat Un tot es pren com a unitat La fracció expressa un valor amb relació a aquest tot
 LES FRACCIONS Termes d una fracció: a b Numerador Denominador 1.- ELS TRES SIGNIFICATS D UNA FRACCIÓ 1.1. Una fracció és part de la unitat Un tot es pren com a unitat La fracció expressa un valor amb relació
LES FRACCIONS Termes d una fracció: a b Numerador Denominador 1.- ELS TRES SIGNIFICATS D UNA FRACCIÓ 1.1. Una fracció és part de la unitat Un tot es pren com a unitat La fracció expressa un valor amb relació
Geometria Analítica del pla
 Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES
 TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departaent d Educació Institut d Educació Secundària Jaue Bales Departaent de Mateàtiques n BATX MA Àlgebra i vectors No i Cognos: Grup: Data: 1) Discutiu i resoleu en els casos
Generalitat de Catalunya Departaent d Educació Institut d Educació Secundària Jaue Bales Departaent de Mateàtiques n BATX MA Àlgebra i vectors No i Cognos: Grup: Data: 1) Discutiu i resoleu en els casos
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES
 FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
6. Potències i arrel quadrada
 43 6. Potències i arrel quadrada 1. POTÈNCIES Completa la taula següent en el quadern: 1 2 3 4 5 6 7 8 9 10 1 4 49 1 2 3 4 5 6 7 8 9 10 1 4 9 16 25 36 49 64 81 100 a) 5 600 b) 0,00795 11. Tenim una finca
43 6. Potències i arrel quadrada 1. POTÈNCIES Completa la taula següent en el quadern: 1 2 3 4 5 6 7 8 9 10 1 4 49 1 2 3 4 5 6 7 8 9 10 1 4 9 16 25 36 49 64 81 100 a) 5 600 b) 0,00795 11. Tenim una finca
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 1 SÈRIE 3 1.- Digueu per a quin valor del paràmetre m els plans π 1 : x y +mz = 1, π 2 : x y +z = m, π 3 : my +2z = 3, tenen com a
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 1 SÈRIE 3 1.- Digueu per a quin valor del paràmetre m els plans π 1 : x y +mz = 1, π 2 : x y +z = m, π 3 : my +2z = 3, tenen com a
REPÀS D ALGEBRA 2n BATXILLERAT
 REPÀS D LGEBR n BTXILLERT VECTORS Un vector v és combinació lineal (C.L.) dels vectors { v,v,,vk} { v,v,,vk} { v,v,,vk} { v,v,,v } és base d un espai vectorial V { v,v,,v } quan v = av + av + + ak vk,
REPÀS D LGEBR n BTXILLERT VECTORS Un vector v és combinació lineal (C.L.) dels vectors { v,v,,vk} { v,v,,vk} { v,v,,vk} { v,v,,v } és base d un espai vectorial V { v,v,,v } quan v = av + av + + ak vk,
2. Espais vectorials, matrius, determinants i sistemes d equacions lineals
 2. Espais vectorials, matrius, determinants i sistemes d equacions lineals 2.1 Definicions Un espai vectorial és una estructura algebraica com també ho són el concepte de grup, d anell o el de cos. Ací
2. Espais vectorials, matrius, determinants i sistemes d equacions lineals 2.1 Definicions Un espai vectorial és una estructura algebraica com també ho són el concepte de grup, d anell o el de cos. Ací
POLINOMIS. Divisió. Regla de Ruffini.
 POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
Sistemes d equacions. Bloc 2
 Bloc 08 Sistemes d equacions En un mosaic com aquest cal col locar estratègicament les peces perquè tot encaixi i es formi el dibuix desitjat. Però podem fer-ho de diverses maneres: hi haurà algú que comenci
Bloc 08 Sistemes d equacions En un mosaic com aquest cal col locar estratègicament les peces perquè tot encaixi i es formi el dibuix desitjat. Però podem fer-ho de diverses maneres: hi haurà algú que comenci
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES
 EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES Suma de monomis. 1. Realitza les següents operacions: + 8 4 9 9 6 + 4 5 5 1 + 4 4 4 11 7 f) 6 7 1 8. Realitza les següents operacions: 1 + 5 5 + 1 y + y + y
EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES Suma de monomis. 1. Realitza les següents operacions: + 8 4 9 9 6 + 4 5 5 1 + 4 4 4 11 7 f) 6 7 1 8. Realitza les següents operacions: 1 + 5 5 + 1 y + y + y
