Estructuras de acero: Problemas 1 Pandeo local

Transcripción

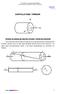
1 Esrucuras de acero: Problemas Pandeo local Se han unido or soldadura res chaas de acero que consiuyen una sección comuesa en Ι simérica sólo or el eje de la chaa del alma. La sección que reresena la figura se uede someer a esfuerzo axial o a flexión. El acero de odas las chaas que comonen la sección es de calidad S55. Se oma una resisencia a la fluencia de cálculo igual a la ensión mínima de fluencia, es decir, f y 55 N/. ε 5 fy 0,8 El roblema consise en hallar las roiedades de la sección efeciva que se vaya a escoger ara comrobar el esfuerzo axial y la flexión resecivamene. Figura. Sección ransversal brua Elemenos Esrucurales. Tomo 9. (999). Insiuo Técnico de la Esrucura en Acero. San Sebasián Esrucuras de acero. Problemas. Pandeo local.

2 Se hacen las siguienes hióesis: Figura. Soldadura en ángulo a. Las soldaduras de cordón que unen el alma a ambas alas se desrecian ara calcular las roiedades de la sección: área de la sección, segundo momeno de inercia, ec. b. Las soldaduras de cordón de la unión alma-alas se han reresenado con riángulos isósceles como se ve en la figura ; or ano, el cano neo del alma medido enre la soldadura suerior e inferior es de 790. c. Los límies de las relaciones b/ que se mencionan son los del CTE. d. El crierio de cálculo es la aarición de la ensión de fluencia de cálculo en el cenroide del ala más alargada, ero no en la fibra exrema más ensada; los módulos de la sección se calcularán consecuenemene. En rimer lugar se deermina la osición del cenro de gravedad (cdg) de la sección, y oseriormene el momeno de inercia (reseco al eje fuere y-y). Para ello (figura ), se denomina con G, G y G los cdg del ala suerior, ala inferior y alma, resecivamene, y con G T el cdg de la sección. Del mismo modo, A, A, A y A T reresenan las secciones del ala suerior, ala inferior, alma y de la sección comlea. Para deerminar la osición del cenroide de la sección, se oman momenos reseco a G. Denominando d a la disancia enre los cdg de las alas, d a la disancia enre el cdg del alma y del ala inferior, y d T a la disancia del cdg de la sección y el cdg del ala inferior, se iene: Esrucuras de acero. Problemas. Pandeo local.

3 G GT G d d dt G Figura. Deerminación del cenroide de la sección y momeno de inercia. A T d T A d + A d A A A T d d Con odos esos valores se deermina la osición del cdg de la sección, ues d A d + A A d T T 49 ). Por ano, el cdg se encuenra siuado a 444 de la fibra inferior (z g 444 El momeno de inercia de la sección reseco al eje y-y es: Ι 4000 ( ) ( 76 5) ( 444 5) ( ) cm 4 Esrucuras de acero. Problemas. Pandeo local.

4 Figura 4. Deerminación del cenroide. Los módulos resisenes de la sección son: Relaivo al cenroide del ala suerior: W u cm 7, Relaivo al cenroide del ala inferior: W u cm 4,9 Sección efeciva ara la comresión axial Deerminación de la clase de sección Relaciones b/ Ala suerior c 0, c 00 0 Ala inferior 0 c 0, Esrucuras de acero. Problemas. Pandeo local. 4

5 c Alma c c 790 6,7 Los valores límie de las relaciones b/ de las secciones de Clase son: c En alas, 4 ε, 4 lim c En alma, 4 ε 4, lim Todas las chaas rebasan el límie indicado. Por ano, la sección erenece a la Clase 4 y hay que reducir la sección de cada chaa. Deerminación de las anchuras efecivas La eficacia de la zona de comresión de cada chaa se halla or medio de: ρ 0, 88 ( ) donde la esbelez normalizada de la chaa viene dada or: f y cr b 8,4 ε - Para el ala suerior c 0 ψ 0,57 0, ψ + 0,07 ψ 0,4 0,578 0,578 0,4 ψ + 0,4,4 Esrucuras de acero. Problemas. Pandeo local. 5

6 0 8,4 0,8 0,4, ρ 0,88 ( ), 0,88, 0,650 b eff ρ b 0, Para el ala inferior c 5 ψ 0,57 0, ψ + 0,07 ψ 0,4 0,578 0,578 0,4 ψ + 0,4,4 5 8,4 0,8 0,4 0,99 ρ 0,88 ( ) 0,99 0,88 0,99 0,88 b eff ρ b 0, ,4 - Para el alma c,7 ψ 4,7 8,4 0,8 4,84 ρ 0,88 ( ),84 0,88,84 0,9 h eff ρ h 0, , Esa magniud se asigna a ares iguales (5 ) a ambos exremos. Esrucuras de acero. Problemas. Pandeo local. 6

7 Proiedades de la sección G ,4 00 Figura 5. Sección ransversal efeciva or comresión axial. Área de la sección A eff,n A , eff,n Posición del cenroide z, N g 49 Deslazamieno del cenroide en zg zg, n Ese deslazamieno genera un momeno de flexión secundario que se suerone a M Ed, de valor M N Ed e N Sección efeciva ara la flexión Deerminación de la clase de sección Las relaciones b/ de las chaas han sido calculadas en el aarado anerior. Esrucuras de acero. Problemas. Pandeo local. 7

8 El valor límie del ala en comresión de las secciones de Clase es: c lim 4 ε,4 Ese valor resula suerado. Por ano, la sección erenece a la Clase 4. Como las alas aoran más a la rigidez a flexión que el alma, se recomienda reducir el ala en comresión anes de calcular el rearo de ensiones en el cano de la sección, en esecial la relación de ensiones en el alma de la que deende su valor límie (d/) lim. La anchura efeciva del ala en comresión se ha calculado en el aarado anerior, y vale b eff 60. Figura 6. Sección ransversal brua uilizada ara valorar el radio de ensión del alma (sección sujea a flexión). La sección que se va a esudiar en cuano a la relación de ensiones en el ala es la de la figura 6. Área de la sección A eff,m A eff,m Posición del cenroide z, M g 94 Esrucuras de acero. Problemas. Pandeo local. 8

9 La relación de ensiones Ψ es como sigue, eniendo en cuena que reresena el cociene enre la máxima ensión y la máxima comresión: ψ ,9 El valor límie del alma (c/) lim de la Clase (abla 5.) ara ese valor de Ψ es: 4 ε 0,67 + 0, ψ 9 Ese valor es inferior a,7. Por ano, la sección erenece a la Clase 4, or lo que ambién hay que reducir el alma. Deerminación de las anchuras efecivas La anchura efeciva del ala en comresión ya se ha calculado en el aarado anerior. El ala en racción es oalmene efeciva. El alma, someida a comresión y flexión, viene caracerizada en rimera aroximación or Ψ-0,9. El coeficiene de andeo de la chaa del alma es (abla 5.6): 7,8 6,9 ψ + 9,78 ψ,7 de donde la esbelez normalizada del alma,7 8,4 0,8 y la eficacia del alma,7, ρ 0,88 ( ), 0,88, 0,69 Esa eficacia corresonde a la are del cano c c que exerimena ensiones de comresión. Por consiguiene, la zona de comresión es efeciva en un cano: ( c ) 0, c eff Esrucuras de acero. Problemas. Pandeo local. 9

10 La zona que se ierde en el alma comrimida es: La zona más comrimida es: 0,4 88 5, medida a arir del reborde del cordón de soldadura suerior. La zona menos comrimida es: 0, Proiedades de la sección G 9 00 Figura 7. Sección ransversal efeciva ara flexión. Área de la sección A eff,m A (800 8) eff,m Posición del cenroide z, M g 9 Momeno de inercia en el eje y-y Ι ( ) Los módulos resisenes de la sección son: cm Esrucuras de acero. Problemas. Pandeo local. 0

11 Relaivo al cenroide del ala suerior: W u cm 4. Relaivo al cenroide del ala inferior: W u 94 9cm 8.8 Esrucuras de acero. Problemas. Pandeo local.