SUCESIONES DE POTENCIAS ITERATIVAS GENERADAS POR a.
|
|
|
- Juan Luis Sebastián Ortega Benítez
- hace 6 años
- Vistas:
Transcripción
1 SUCESIONES DE POTENCIAS ITERATIVAS GENERADAS POR. Jorg E. Hráz U. Eith C. Hráz Uivri Pá, Ctro Rgiol Uivritrio Vrgu, Ecul Mtátic. RESUMEN E l prt trjo tui l ució i i potci itrtiv gr por, > 0; í coo l oluili l cució rgo S tlc qu to prol tá trcht ligo co l coportito l fucio f ), h ) co l tiguo prol trir l olucio l cució =. Filt, tui l coportito l fució g ) clcul u ivr cotru u gráfic. Tcocici, Vol., N 7
2 PALABRAS CLAVES Sucio potci itrtiv, pr Broulli, pr Eulr. ABSTRACT I thi ppr w tu th quc i i of itrt potil, > 0; wll th rg of olvilit of th qutio W tt tht th two prol r clol rlt with th hvior of th fuctio f ) h ) with th ol prol of fiig th olutio of th qutio =. w tu th hvior of th fuctio Fill, g ) clcult it ivr rw it grph. KEYWORDS Squc of itrt potil, Broulli pir, Eulr pir. 8 Hráz U., J. Hráz, E.
3 . Lo Oríg Do u úro rl > 0, potci itr :,, pu coirr l ució, Si =, toc vit qu t ució covrgt; i rgo, pr = l ució ivrgt. U prgut turl : Pr qué vlor l ució potci itr covrgt? Et prol t rlcioo irctt co l cució, l fucio f ), h ) l cució = l cul fu rult prirt por Golch Cho, 00; Hurwitz, 96, Sv, 990). Rlt, l hitori t prol coiz co u crt Dil Brouilli Chriti Golch fch l 9 juio 78 Hurwitz, 96). El fil t crt ic: Triré co u prol l cul cotré u itrt h rulto. Aquí tá: Ecutr o úro ifrt tl qu =. H ólo u co cuo to o úro o tro, r =, = 4 qu 4 = 4 ), pro uo pu cotrr u ifii úro quro qu tifc t cució. H tié otro tipo cti l cul o iré. Si á tr Golch l rpoió Broulli icluo u rput u rivció l olució, for prtric. Su rguto puir r tlcio coo igu: Supogo qu =, > > 0; por lo tto =, pr lgú >. Etoc = ) Tcocici, Vol., N 9
4 o por coiguit Aí pu - = =, i Eulr, i l coociito l couicció tr Broulli Golch Cho, 00; Sloi, 9), uo l i rlció = rolvió l cució =,, or R + Z +, prto l olucio rciol, L rlcio Golch h io rcuirt por u úro plurl utor tr lo cul cutr Eulr, Eiti, Kol, Brrow, Lägr, Strhir Crutz Cho, 00; Sv, 990, Hráz, 004). Aprtt, iguo to tático tí coociito l olució origil Golch. Auqu t oto l prol Broulli prcir o tr rlcioo co l covrgci l ucio potci itr, vro qu l olucio l prol Broulli o rá l iforció pr trir l covrgci t ucio.. L fució f) = L cució = quivlt l cució ; por lo tto, l tuio l coportito l fució f) = prioril pr trir l olucio l cució =. 0 Hráz U., J. Hráz, E.
5 Coiro l fució coo ti qu l f ) f: 0,) R fii por: f) = 0 f ) = 0 í ólo í, =, Aá f ) > 0 i 0, ) f ) < 0 i, ) Por lo tto, f trictt crcit l itrvlo 0, ). f trictt crcit l itrvlo,). f lcz u vlor áio = f) = li f ) li 0 0 li f ) li 0 0 < f) f), pr too 0, ) D lo rulto trior, poo tr cotiut f l itrvlo [0, ) l iguit r f: [0, ) R 0, f) =, 0 0 Tcocici, Vol., N
6 u gráfic l iguit 0 Not qu f cotiu l itrvlo [0, ). f ictiv l itrvlo [0, ] l itrvlo [, ) Si 0 < < toc 0 < f) <. f0) = 0, f) = f) = Si < < toc Si < < toc Pr c, ) it u úico, ) tl qu f) = f), rcíproct f ) f ) Aí poo firr qu l cució =, o quivltt ) o ti olució pr 0 < < ó 0 < < ; pr c, ) it u úico,) tl qu =. Coo l úico tro poitivo tr, t álii utr qu =, = 4 l úic olució tr poitiv l cució =. Hráz U., J. Hráz, E.
7 . Pr Broulli Rcoro qu Golch prtó l iguit olució prtric l cució = : > 0, l cul prit cotruir olucio, ) t cució, coo por jplo: Vo qu ocurr co l olucio prtric cuo proi. Pr to too l líit cuo hgo l utitució = t + ; li t t t li lit ) lit )t ) lit ) t0 t0 t0 li t ) t0 Not qu i 0 < <, toc t itr qu i >, toc < <, 0 < < 0 < <, < <. L prtrizció Golch prit fácilt crctrizr cirt olucio iportt. Por jplo, Eulr fu l priro trir l olucio rciol l cució =, l cul oti too Tcocici, Vol., N
8 4 Hráz U., J. Hráz, E. Pr oti l olucio: Pr oti l olucio: Dfiició : S, o úro rl poitivo itito, <. El cojuto {, } u pr Broulli i =. Si {, } u pr Broulli, toc < < < {, 4} l úico pr Broulli foro por tro Lo úico pr Broulli rciol o l for pr N. Por l prtrizció Golch, lo pr Broulli o pr >. ),,,
9 4. L Sució S > 0 u úro fijo. Dfio rcurivt l ució por i i Lo tério t ució o,,, El propóito t trjo trir lo úro pr lo cul t ució covrg, l igul qu u líit. Pr to prto l iguit otció [], [],, [ ] [ ] Aí, l ució pu rprtr coo [ ] [ Tor : S > 0. Si ] li, toc =, Dotrció: Supogo qu toc [ ] li [ ] li li [ ] Tcocici, Vol., N 5
10 li [ ] Aí pu = Aá, coo f ) =, ti qu f ) Dfio hor l fució g) por g) = li [ ] Si u lto l oiio g, toc por l Tor, fg)) =. og) Rgf) = 0, Por lo tto, l ució ivrg í >. [ ] Tor : S [ ] toc l ució covrgt. Aá, i [ ] li toc <. 6 Hráz U., J. Hráz, E.
11 Dotrció: Si 0 < p < q, toc p < q. Por lo tto, o <, < = [], [] = < [ -] < [ ], pr too, [] [],... Lugo [ ] u ució crcit. Por otro lo, coo ti qu [ ] igult, grl, [] < [] <, pr too. [ ] Eto iplic qu u ució crcit cot upriort por l úro. Por lo tto, l ució trior, i toc <. [ ] [ ] li covrgt. Aí, por l tor Tcocici, Vol., N 7
12 Orvció: Si >, toc Lugo, por l tor trior, l ució Pro [ ] li covrgt. [ ] qu >. El líit l ució l úro c, < c <, tl qu c c ; o qu {c, } u pr Broulli. [ ] Etuio hor l coportito l ució, cuo 0 < <. Not qu t co, i 0 < p < q, toc q < p. Por lo tto, 0 < [] = < = [] < 0 < [] = < = [] < = [] < [ ] 0 < [] = < [] [] < [] [4] < = [] < 0 < [] = < [] < [4] [5] < [] [4] < [] < 0 < [] < [] < [5] < [6] < [4] < [] < por u rguto iuctivo ti qu 0 < [-] < [+] <... < [+] < [] < pr too úro turl. [ ] D lo trior ti qu l ució crcit cot upriort por lo tério l ució []. [] D igul r, l ució crcit cot ifriort por lo tério l ució [ ]. Aí, t o ucio o covrgt. Doto i li [], 8 Hráz U., J. Hráz, E. p li [ ]
13 Etoc 0 < i p < á, l ució [ ] covrgt í ólo í i = p. Por otro lo, coo [ ] [ ] [] [] Aplico líit cuo oto i p p i Por coiguit o i p p i p p i i Et iti o ugir tuir l coportito l fució h: [0, ] R 0 h ) 0 Drivo l fució h oto h ) = [ l + ] lugo Aá h) = 0 í ólo í h) < 0 pr 0, - ) h) > 0 pr -, ) Tcocici, Vol., N 9
14 Por coiguit h0) = h) = f trictt crcit l itrvlo 0, - ). f trictt crcit l itrvlo -, ). f lcz u vlor íio = - li h ) li. 0 0 h ) h ), pr too [0,]. L gráfic l fució h) = l iguit - Not qu l fució h o uo l itrvlo [0, ]. Dl álii l gráfic h) = ti qu i 0 < < l ució toc i < p lo rulto trior ivrgt, 0 Hráz U., J. Hráz, E. [ ]
15 0 < i < - < p < qu h i ) = h p ). El prol trir l covrgci l ució [ ], co 0 < <, quivl prgutr qu i 0 < c < < c c, toc pu r l co qu c = i = p. E t tio v irigio l iguit tor. Tor : S 0 < <. Si 0 < c < < c c toc [] [ ] 0 i c p pr c turl, l ució [ ] ivrgt. Dotrció: Si c <. toc coo ti qu c lo qu u cotricció, por lo tto < c. D lo trior ti qu = c < = [] lugo l gráfic h) = uc qu c Nuvt, coo 0 < <, c [ ] [ ] c [ ] Tcocici, Vol., N
16 por lo tto, ] c [ 4] c D igul r, [5] [4] c c Aplico rptit t rguto oto por coiguit, l ució [ [ ] [ ] 0 c [] [ ] 0 i c p [ ] ivrgt. Dfiició: El cojuto {c, } u pr Eulr i Ejplo: 0 < c < < c c =, u pr Eulr, qu 4 4 E l iguit tor rlcioo lo pr Eulr co lo pr Broulli Tor 4: El cojuto {c, } u pr Eulr í ólo í u pr Broulli, c Dotrció: Supogo qu 0 < c < < too =, = c 4 4 Hráz U., J. Hráz, E.
17 toc < <, á c c c = c c =. Orvcio:. Si {c, } u pr Eulr, toc 0 < c < < < [ ]. Si 0 < < l ució ivrgt, toc { i, p } u pr Eulr.. D lo o últio tor uc qu i 0 < < i it u pr Eulr {c, } tl qu c toc l ució c [ ] c ivrgt. Dl tor trior uo l rprtció prtric Golch pr l olucio l cució =, poo cocluir qu lo pr Eulr {c, } ti l for c c ), ), Si upoo qu c c toc coo c ) ) ) c ) ti qu ) ) c ) c ) ),. Tcocici, Vol., N
18 [ ] Por lo tto, l ució ivrg or l rgo l fució ), fii or l oiio, ). Aí qu iportt trir l rgo l fució ). Coiro l fucio c:, ) R c ) :, ) R ) :, ) R ) c ) ) ) c ) Aplico l rgl L Hopitl o lizo l gráfic l fució h) =, qu hc)) = h))) oto qu: li c ) li li ) li li c ) li 0 Por lo tto, li ) li li ) li ) 0 Aá, coo c) ) o cotiu l itrvlo, ), ti qu ) cotiu l itrvlo, ). 4 Hráz U., J. Hráz, E.
19 Tcocici, Vol., N 5 Lugo por l Tor l Vlor Itrio, ti qu 0, - ) rg )). Nutr tr coit toc trir l rgo l fució ). Pr to to l iguit tor. Tor 5: L fució crcit l itrvlo, ). Dotrció: Proo qu ) < 0 pr >. E fcto, Coo ) = uo riv logrític oto qu ) l ) l ) ) o ) l ) ) ) Por otro lo, coo c )) ) ti qu ) ) ) ) ) ) c c ) ) )
20 Uo riv logrític oto qu ) ) l )) ) ) por coiguit l )) ) ) )) )l )) )) ) ) ) l )) ) )l )) )) rplzo l vlor ) t cució oto qu ) ) ) ) l )) )) ) ) )l )) l ) l ) ) )) )l ) )l ))l )l )) ) l )) ) ) pro coo l l l )) = oto qu ) l l l l ) ) ) ) ) ) ) l )l ) l )l ) ) ) l l l l l ) l l l ) ) ) ) ) l ) 6 Hráz U., J. Hráz, E.
21 O Not qu ) ) ) ) ) ) ) l ) 0, pr >. Dfio hor l fució t: [, ) R Etoc t) = l ) t) = l + l ) l t ) l t ) Coo t) < 0 pr t, ), ti qu t) trictt crcit l itrvlo [, ). Pro coo t) = 0, t) gtiv l itrvlo, ). Eto iplic qu l fució t) trictt crcit l itrvlo [, ). Pro t) = 0, lo qu iplic qu t) gtiv l itrvlo, ). Por coiguit, l fució t) trictt crcit l itrvlo [, ). Filt, coo t) = 0, ti qu l fució t) gtiv l itrvlo, ). D too lo trior uc qu l fució ) < 0 pr too t, ). Por coiguit, l fució ) trictt crcit l itrvlo [, ). Orvció: Coo l fució ) cotiu trictt crcit l itrvlo, ), ll ictiv t itrvlo. Aá coo li ), li ) 0 Tcocici, Vol., N 7
22 ti qu rg)) = 0, - ) [ ] por lo tto, l ució ivrgt i 0, - ). Tor 6: S 0 < <. L ució ólo í - <. covrg í Dotrció: [ ] Supogo qu l ució covrgt qu 0 < < -. Etoc rg)). Eto iplic qu it u pr Eulr {c), )} tl qu [ ] c ) ) ) c ) ) Lugo por l Tor, l ució qu u cotricció. Aí, - <. [ ], ivrgt. Lo Rcíproct, upogo qu - < upogo qu l [ ] ució ivrgt. Etoc 0 i li p i li i p p { i, p } u pr Eulr. Por lo tto, it u, ) tl qu i = c), p = ) = ) Eto iplic qu cotricció. Aí rg)) = 0, - ), lo qu u [ ] u ució covrgt. Corolrio : Si < [ ] li <. toc 8 Hráz U., J. Hráz, E.
23 Dotrció: Por Tor ti qu = Lugo, l gráfic l fució f) = ti qu <. Aá, coo l gráfic l fució f) trictt crcit l itrvlo [0, ] f ) ti qu <. Corolrio : Si 0 < < toc it u úico pr Eulr { i, p } tl qu 0 < i < < < p < p, i i p Dotrció: Coo 0 < < [ ], por l Tor 6 l ució ivrgt. Lugo, por l Tor á 0 li li p i i i p { i, p } u pr Eulr. Tié, coo 0 < < -, l gráfic l fució f ) ti qu p 0 < < < p Por otro lo, coo 0 < < =, i p, < p ti qu i <. Por coiguit, 0 < i < < < p <. Tcocici, Vol., N 9
24 Corolrio : El oiio l fució l itrvlo i. fg)) = i, g ) li [ ] ii. gf)) = i Dotrció: Por lo Tor, 6, l ució í, por lo tto og) = Aá, por l Tor,, [ ] covrg í ólo fg)) = i Por otro lo, upogo qu = f) = Etoc l gráfic l fució f) = Eto iplic qu og). S ti qu c = li toc por lo Tor l Corolrio ti qu c c c 0 Hráz U., J. Hráz, E.
25 Por lo tto f) = f c) = Pro coo, l gráfic l fució f) ti qu = c. Aí li =. D lo rulto trior ti qu l fucio f: [, ], g:, [, ] f) = g) = li o ictiv, á g = f. Por lo cul pu otr l gráfic l fució g prtir l gráfic l fució f. CONCLUSIONES [] Si > 0 li, toc. Por lo tto, l ució [ ] ivrg i [ ] L ució covrg í ólo í., L cució t co ti olució í ólo í [ -, ]. E Si > [ ] toc, l ució covrgt, pro o u líit. Tcocici, Vol., N
26 REFERENCIAS Cho, Y. & K. Prk. 00. Ivr Fuctio of = Mthticl Mothl 08, , Th Aric Hráz, J. E. & E. C. Hráz Solucio rciol l cució =, Hurwitz, S. 96. O th rtiol olutio of = with, Th Aric Mthticl Mothl 74. Kol, R. A. 98. Epotil ritrt, Th Aric Mthticl Mothl 88, 5-5. Lgr, H A ltr proof of th covrgc of itrt potil, El. Mth Sloi, H. L. 9. Th olutio of =, > 0, > 0,, thir grphicl rprttio, Th Aric Mthticl Mothl 8, Sv, M O th rtiol olutio of =, Mth gzi 6. Rciio ptir 00, cpto octur 0. Hráz U., J. Hráz, E.
FRACCIONARIOS Y DECIMALES
 FRACCIONARIOS Y DECIMALES Hg clck obr l t qu coultr: 1. Núro Frccoro - Frccoro grl - Frccoro hoogéo y htrogéo - Clfccó lo frccoro - Frcco quvlt - Ruccó frcco (plfccó) - Covró frccoro cl 2. Núro Dcl Núro
FRACCIONARIOS Y DECIMALES Hg clck obr l t qu coultr: 1. Núro Frccoro - Frccoro grl - Frccoro hoogéo y htrogéo - Clfccó lo frccoro - Frcco quvlt - Ruccó frcco (plfccó) - Covró frccoro cl 2. Núro Dcl Núro
Formulario de matemáticas
 Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
UNIDAD 7 SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
Análisis de Fourier para Señales y Sistemas de Tiempo Discreto
 Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
(esta notación fue elegida por el matemático Leonhar Euler) De hecho la función f ( x)
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
7ma Guía de Estudio 2do Parcial Estudio de Series de Potencia SOLUCIONARIO Guía Complementaria No.07
 álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
 Cátdr Mtátic II Espcilidds Mcáic - Quíic Ejrcicios d Aplicció d l drivd co rcts tgts orls ϕ Dds ls ucios ϕ S Hllr ϕ cos ϕ ϕ cos ϕ cos ϕ Qué águlo or co l j o ls tgts l curv puto cu scis s? θ θ. pr θ θ
Cátdr Mtátic II Espcilidds Mcáic - Quíic Ejrcicios d Aplicció d l drivd co rcts tgts orls ϕ Dds ls ucios ϕ S Hllr ϕ cos ϕ ϕ cos ϕ cos ϕ Qué águlo or co l j o ls tgts l curv puto cu scis s? θ θ. pr θ θ
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INGENIEÍA MECÁNICA Y ELÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONOL M.C. ELIZABEH GPE. LAA HDZ. M.C. OSÉ MANUEL OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO LEÓN
UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INGENIEÍA MECÁNICA Y ELÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONOL M.C. ELIZABEH GPE. LAA HDZ. M.C. OSÉ MANUEL OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO LEÓN
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
es divergente. es divergente.
 .- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
.- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
Enfrentando. cesantía INUND. ntía INUNDAC
 frto i F f I C D tí IU o B t B o t tr it D D o I o CS SUICID F i F i f f I C tí IUD B to B o t t i D D tr o o CS SUICIDI F F i i f f tí IUDCI to B B o t t tr i D o I ID IC U o FCS S i i f f I CI tí IUDC
frto i F f I C D tí IU o B t B o t tr it D D o I o CS SUICID F i F i f f I C tí IUD B to B o t t i D D tr o o CS SUICIDI F F i i f f tí IUDCI to B B o t t tr i D o I ID IC U o FCS S i i f f I CI tí IUDC
Z = número atómico o número de protones del núcleo Z = 1 (H); 2 (He + ); 3 (Li 2+ ).
 CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
ALGUNAS FÓRMULAS ESTÁNDAR DE CÁLCULO DIFERENCIAL E INTEGRAL. e = log. d dx. d v v dv. d dx. en particular: ( log v) = 1
 ALGUNAS FÓRMULAS ESTÁNDAR DE CÁLCULO DIFERENCIAL E INTEGRAL Síolos. E ls tls siguits,, c, y ot costts, itrs qu u, v, w y so vrils, u, v, y w so tos fucios. L s l sist Npirio o tié llo turl logritos s ot
ALGUNAS FÓRMULAS ESTÁNDAR DE CÁLCULO DIFERENCIAL E INTEGRAL Síolos. E ls tls siguits,, c, y ot costts, itrs qu u, v, w y so vrils, u, v, y w so tos fucios. L s l sist Npirio o tié llo turl logritos s ot
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l. U l a d i s l a o G á m e z S o l a n o
 1 A n t o l o g í a : P r o m o c i ó n y A n i m a c i ó n d e l a l e c t u r a M i n i s t e r i o d e E d u c a c i ó n P ú b l i c a I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l.
1 A n t o l o g í a : P r o m o c i ó n y A n i m a c i ó n d e l a l e c t u r a M i n i s t e r i o d e E d u c a c i ó n P ú b l i c a I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l.
1.2 INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (1.2_CvR_T_062, Revisión: , C2, C3, C4)
 . INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
. INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
2. MÉTODO DE COEFICIENTES INDETERMINADOS.
 . MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
. MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
Geodesia Matemática.
 Godsi Mtátic Sist d coordds crtsis Sist crtsio triplt ortogol vctors uitrios ls dirccios d los js coorddos O r r r r Distci tr dos putos Trsforcios lils tr sists crtsios X Y Z Trslció c b Giro lrddor dl
Godsi Mtátic Sist d coordds crtsis Sist crtsio triplt ortogol vctors uitrios ls dirccios d los js coorddos O r r r r Distci tr dos putos Trsforcios lils tr sists crtsios X Y Z Trslció c b Giro lrddor dl
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Resumen: Límites, Continuidad y Asíntotas
 Resue: Líites, Cotiuidd y Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. : *? ** *
Resue: Líites, Cotiuidd y Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. : *? ** *
3.- Solución de sistemas de ecuaciones lineales
 .- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
.- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
Construyendo la función exponencial
 Costrdo l ció ocil Cr SÁNCHZ DÍZ Pd costrirs l ció ocil ri o trl coo l ció ivrs d l ció logrito trl r d idtiicrs co l ocil d s úro rl os d ror tl coicidci l cso d ot tro tié rciol l cso d ot rl d diirs
Costrdo l ció ocil Cr SÁNCHZ DÍZ Pd costrirs l ció ocil ri o trl coo l ció ivrs d l ció logrito trl r d idtiicrs co l ocil d s úro rl os d ror tl coicidci l cso d ot tro tié rciol l cso d ot rl d diirs
Q, entonces b equivale a un radical. Es decir:
 UNIDAD : POTENCIACIÓN, RADICACIÓN Y LOGARITMACIÓN. POTENCIACIÓN L potecició se utili pr epresr u producto de fctores igules. Es u operció teátic etre dos térios deoidos se epoete... Eleetos de l potecició
UNIDAD : POTENCIACIÓN, RADICACIÓN Y LOGARITMACIÓN. POTENCIACIÓN L potecició se utili pr epresr u producto de fctores igules. Es u operció teátic etre dos térios deoidos se epoete... Eleetos de l potecició
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Seguridad Sanitaria Internacional
 7 Abri 2007 Sguri Sitri Itrcio Oció pr ibiizr obr pcto cv u mui. E objtivo guri itri itr gobiro/orgizcio/ mpr ivrtir u pr forjr u porvir má guro. Efrm mrgt/pimióg y u brot; propgció VIH/SIDA, mrgci humitri
7 Abri 2007 Sguri Sitri Itrcio Oció pr ibiizr obr pcto cv u mui. E objtivo guri itri itr gobiro/orgizcio/ mpr ivrtir u pr forjr u porvir má guro. Efrm mrgt/pimióg y u brot; propgció VIH/SIDA, mrgci humitri
3. SISTEMAS DE ECUACIONES LINEALES
 Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
ADMINISTRACION DE OPERACIONES
 Ssió 3: Plció l AMINISTRACION E OPERACIONES Objtivo spcífico 1: El luo coocrá y plicr cut los étoos proóstico l pr plr l ctivi futur l prs.. Cocptos srrollr l ui: L clsificció los sists proucció, los sists
Ssió 3: Plció l AMINISTRACION E OPERACIONES Objtivo spcífico 1: El luo coocrá y plicr cut los étoos proóstico l pr plr l ctivi futur l prs.. Cocptos srrollr l ui: L clsificció los sists proucció, los sists
El dual tiene tantas restricciones como variables tiene el primal.
 .. EL MODELO DUAL A todo progr liel, lldo prole pril, le correspode otro que se deoi prole dul. Ls relcioes eistetes etre os proles so ls siguietes: El dul tiee tts vriles coo restriccioes eiste e el pril.
.. EL MODELO DUAL A todo progr liel, lldo prole pril, le correspode otro que se deoi prole dul. Ls relcioes eistetes etre os proles so ls siguietes: El dul tiee tts vriles coo restriccioes eiste e el pril.
ESTABILIDAD. estable, si sometido a una perturbación, éste, luego de un tiempo, vuelve a su
 ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
fundada en 1996 México Nueva York Los Angeles
 f 1996 Méxic Nv Yrk L Agl r pii pr llv p cr v. gt tj L Crp Prii l t r iñ p c. C r F c ú i b b cfé ILLY t prpr l i c p Tbié v p pii igrit r j tr cr l tr clit, c frt lbl. c fr pr i rrll pr tr f cr pé hbr
f 1996 Méxic Nv Yrk L Agl r pii pr llv p cr v. gt tj L Crp Prii l t r iñ p c. C r F c ú i b b cfé ILLY t prpr l i c p Tbié v p pii igrit r j tr cr l tr clit, c frt lbl. c fr pr i rrll pr tr f cr pé hbr
( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:
![( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término: ( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:](/thumbs/40/21276395.jpg) Fult Cotuí Aiitió. UNAM Pouto otl Auto: D. Joé Mul B Eio MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES CONCEPTO DE PRODUCTO NOTABLE Tto l ultiliió li oo l itéti iu u loito uo o ou l ulto. Si o, it outo lio u
Fult Cotuí Aiitió. UNAM Pouto otl Auto: D. Joé Mul B Eio MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES CONCEPTO DE PRODUCTO NOTABLE Tto l ultiliió li oo l itéti iu u loito uo o ou l ulto. Si o, it outo lio u
MANUAL MATEMÁTICAS PARA ESTUDIANTES DE FINANZAS. Exponentes
 _ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
_ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
a su fin. la Bolivariana.
 i t q j i f Sii h z 18 hí ii ó 27 f i ijtii t q t Pti i í i z v há 2010. Pit H 28 vi izió 2 1 ñ tiií D vt i í itió q iit t vz v ii i i if t t x i ít. z it i i ó tt h i Biit Ni. Ahiv Aivi t 8 1 t. t V L
i t q j i f Sii h z 18 hí ii ó 27 f i ijtii t q t Pti i í i z v há 2010. Pit H 28 vi izió 2 1 ñ tiií D vt i í itió q iit t vz v ii i i if t t x i ít. z it i i ó tt h i Biit Ni. Ahiv Aivi t 8 1 t. t V L
TALKINGISTEACHING.ORG
 l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
Índice General. Disposiciones iniciales y definiciones generales
 Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
Índice General Int r o d u c c i ó n... xxvii CAPÍTULO I Disposiciones iniciales y definiciones generales Dis p o s i c i o n e s iniciales y de f i n i c i o n e s ge n e r a l e s... 1 Capítulo II Trato
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Programación lineal. m a x i mizar o m i n im i z ar f u n c i o n e s q ue s e e nc u e ntran s u j e ta s a d e terminad as
 Programación lineal L a p r o g r a m ac i ó n l i ne al d a r e s pu e s t a a s i t u aciones e n l as q ue s e e xi g e m a x i mizar o m i n im i z ar f u n c i o n e s q ue s e e nc u e ntran s u
Programación lineal L a p r o g r a m ac i ó n l i ne al d a r e s pu e s t a a s i t u aciones e n l as q ue s e e xi g e m a x i mizar o m i n im i z ar f u n c i o n e s q ue s e e nc u e ntran s u
n o ó i Mi nombre: Mi numero de orden: Cuadernillo 1 periodo II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR LA MEJORA DE LOS APRENDIZAJES
 l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES
 EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES EDDY ABREU, AIDA MONTEZUMA Y JAIME RANGEL Uivrsidd Mtropolit, Crcs, Vzul, 7 Hcho l dpósito d Ly Dpósito Lgl: ISBN: Formto:, X 7,9 cms. Nº d págis: 7 Rsrvdos
EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES EDDY ABREU, AIDA MONTEZUMA Y JAIME RANGEL Uivrsidd Mtropolit, Crcs, Vzul, 7 Hcho l dpósito d Ly Dpósito Lgl: ISBN: Formto:, X 7,9 cms. Nº d págis: 7 Rsrvdos
TEMA 2 SUCESIONES. Tema 2 Sucesiones Matemáticas I 1º Bach. 1 SUCESIONES Y TÉRMINOS
 Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
MatemáticasI. 1. Basta con mover el cuadrado para ver que el área de la región limitada es la cuarta parte del cuadrado.
 MtmáticsI UNIDAD : Límits d fucios. Cotiuidd ACTIVIDADES-PÁG. 76. Podmos dcir lo siguit: ) Pr l gráfic dl prtdo I): f ) tid cudo tid f ) tid + cudo tid por l izquird f ) tid - cudo tid por l drch f ) tid
MtmáticsI UNIDAD : Límits d fucios. Cotiuidd ACTIVIDADES-PÁG. 76. Podmos dcir lo siguit: ) Pr l gráfic dl prtdo I): f ) tid cudo tid f ) tid + cudo tid por l izquird f ) tid - cudo tid por l drch f ) tid
TEMA 2 - FUNCIONES DE VARIAS VARIABLES (I): LÍMITES Y CONTINUIDAD. 1. Conceptos topológicos previos en el espacio euclídeo R n.
 Fucioes de varias variables (I TEMA - FUNCIONES DE VARIAS VARIABLES (I: LÍMITES Y CONTINUIDAD. Coceptos topológicos previos e el espacio euclídeo R. Sea R el espacio euclídeo de dimesioes. U puto a de
Fucioes de varias variables (I TEMA - FUNCIONES DE VARIAS VARIABLES (I: LÍMITES Y CONTINUIDAD. Coceptos topológicos previos e el espacio euclídeo R. Sea R el espacio euclídeo de dimesioes. U puto a de
En imprenta: Anuario Martiano. Revista del Centro de Estudios Martianos. (La Habana, Cuba). Sección Estudios y aproximaciones
 Publicado en: Revista Cubana de Filosofía. Edición Digital No. 15. Junio - Septiembre 2009. ISSN: 1817-0137 En: http://revista.filosofia.cu/articulo.php?id=549 En imprenta: Anuario Martiano. Revista del
Publicado en: Revista Cubana de Filosofía. Edición Digital No. 15. Junio - Septiembre 2009. ISSN: 1817-0137 En: http://revista.filosofia.cu/articulo.php?id=549 En imprenta: Anuario Martiano. Revista del
FACULTAD DE INGENIERÍA
 FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Definiciones de estabilidad BIBO
 Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
Clase-11. Raíces: Sea n número natural mayor que 1 con a, números reales. Si n =a, se tiene
 Ríces: Clse- Se úero turl or que co, úeros reles. Si =, se tiee que es l ríz eési de l que se deot ; es decir: dode es el ídice; l ctidd surdicl es l ríz; es decir l ríz es quel rel tl que elevdo l ídice,
Ríces: Clse- Se úero turl or que co, úeros reles. Si =, se tiee que es l ríz eési de l que se deot ; es decir: dode es el ídice; l ctidd surdicl es l ríz; es decir l ríz es quel rel tl que elevdo l ídice,
TEMA 1. OPERACIONES BANCARIAS A CORTO
 1 E 6 TEMA 1. OPERACIONES BANCARIAS A CORTO PLAZO (I) 1.1. Itrouccó 1.2. Cuts corrts 1.3. Cuts corrts bcrs 1.4. Cuts créto 1.5. Cálculo los ttos fctvos 1. INTROUCCIÓN Toos los rchos rsrvos. Qu prohb l
1 E 6 TEMA 1. OPERACIONES BANCARIAS A CORTO PLAZO (I) 1.1. Itrouccó 1.2. Cuts corrts 1.3. Cuts corrts bcrs 1.4. Cuts créto 1.5. Cálculo los ttos fctvos 1. INTROUCCIÓN Toos los rchos rsrvos. Qu prohb l
FAyA Licenciatura en Química Física III año 2006 MECANICA CUANTICA
 FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/74/71224437.jpg) IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
Axonometria, calculos y artefactos
 , o9 r t di do 2 o d c ln ln i t b li po tiro o r c o 3 d cid n s ri ln io ñ o b ofus C tir r, D s T CIA: 9 Sig TAN DIS C n D ri s Sig tiro b d DIS s T ln cro TA ro c po li NC d IA: fusio o 2 til,3 n tiro
, o9 r t di do 2 o d c ln ln i t b li po tiro o r c o 3 d cid n s ri ln io ñ o b ofus C tir r, D s T CIA: 9 Sig TAN DIS C n D ri s Sig tiro b d DIS s T ln cro TA ro c po li NC d IA: fusio o 2 til,3 n tiro
La identidad de la obra artística
 L i F i F u ul lt t A ti A i Al U C lf U Ci f iv i v r i E r i E i B H B N C Hu g N C N u g l C N t N tá 2 b á, 20 b i C 01 l G, C 14 l G, D l 4 z l D z D b C bi b V C rt b V l t b l br r r rg b g bi t
L i F i F u ul lt t A ti A i Al U C lf U Ci f iv i v r i E r i E i B H B N C Hu g N C N u g l C N t N tá 2 b á, 20 b i C 01 l G, C 14 l G, D l 4 z l D z D b C bi b V C rt b V l t b l br r r rg b g bi t
Índice alfabético. página: 565 a b c d e f g h i j k l m n o p q r s t u v w x y z. búsqueda contenido imprimir última pantalla atrás siguiente
 Í é á: 565 á é ú ú á í é á: 566 A A é, 376 A, 378 379 Aé, 309 310 Aé ( ), 311 Aé, 305 308 Aé, 305 A, 463 A á B, 470 A á, 384 385 A,, Bç, 338 340 A é, 337 A, 333 334 A, 410 419 A K, 466 A, 123 A í, 205
Í é á: 565 á é ú ú á í é á: 566 A A é, 376 A, 378 379 Aé, 309 310 Aé ( ), 311 Aé, 305 308 Aé, 305 A, 463 A á B, 470 A á, 384 385 A,, Bç, 338 340 A é, 337 A, 333 334 A, 410 419 A K, 466 A, 123 A í, 205
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
3.11 Trasformada de Laplace de una función periódica 246
 3. Trformd d plc d un función priódic 46 3. Trformd d plc d un función priódic Dfinición 3.. Un función f llmd priódic i y olo i, it un númro no nulo f tl qu impr y cundo té n l dominio d f, tmbién lo
3. Trformd d plc d un función priódic 46 3. Trformd d plc d un función priódic Dfinición 3.. Un función f llmd priódic i y olo i, it un númro no nulo f tl qu impr y cundo té n l dominio d f, tmbién lo
Seminario Universitario de Ingreso Números reales
 Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
Exportación e Importación en formato XML
 Exportcó Importcó formto XML Tléfoo (506) 2276-3380 Fx (506) 2276-3778 d@c.co.cr www.d.com 1 Exportcó d Iformcó formto XML Pr xportr dto dd lpho formto XML, l mú Admtrcó, cutr l opcó Exportr S motrrá l
Exportcó Importcó formto XML Tléfoo (506) 2276-3380 Fx (506) 2276-3778 d@c.co.cr www.d.com 1 Exportcó d Iformcó formto XML Pr xportr dto dd lpho formto XML, l mú Admtrcó, cutr l opcó Exportr S motrrá l
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/64/51459891.jpg) IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
I.E.S. Mediterráneo de Málaga Junio 2015 Juan Carlos Alonso Gianonatti OPCIÓN A
 I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
PRIMER CONGRESO LATINOAMERICANO DE AGENCIAS DE DESARROLLO LOCALCa rm e n d e Vib o ra l An tio q u ia -Co lo m b ia
 PRIMER CONGRESO LATINOAMERICANO DE AGENCIAS DE DESARROLLO LOCALCa rm e n d e Vib o ra l An tio q u ia -Co lo m b ia 2 8 y 2 9 d e m a yo d e l 2 0 0 9 Pa ís u n ita rio. Niv e le s d e Go b ie rn o : N
PRIMER CONGRESO LATINOAMERICANO DE AGENCIAS DE DESARROLLO LOCALCa rm e n d e Vib o ra l An tio q u ia -Co lo m b ia 2 8 y 2 9 d e m a yo d e l 2 0 0 9 Pa ís u n ita rio. Niv e le s d e Go b ie rn o : N
Tema 1: NÚMEROS REALES.
 I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
. De manera sucesiva, si x se multiplica por si misma n veces, se
 Fcultd de Cotdurí Adiistrció UNAM Lees de eoetes ritos Autor: Dr José Muel Becerr Esios MATEMÁTICAS BÁSICAS LEYES DE EXPONENTES Y LOGARITMOS LEYES DE EXPONENTES Se u úero rel Si se ultilic or sí iso se
Fcultd de Cotdurí Adiistrció UNAM Lees de eoetes ritos Autor: Dr José Muel Becerr Esios MATEMÁTICAS BÁSICAS LEYES DE EXPONENTES Y LOGARITMOS LEYES DE EXPONENTES Se u úero rel Si se ultilic or sí iso se
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
Programa. COLEGIO DE BIBLIOTECARIOS DE CHILE A.G. Diagonal Paraguay 383 of. 122 Santiago Telefono: 56 2 222 56 52 Mail: cbc@bibliotecarios.
 Programa COLEGIO DE BIBLIOTECARIOS DE CHILE A.G. Diagonal Paraguay 383 of. 122 Santiago Telefono: 56 2 222 56 52 Mail: cbc@bibliotecarios.cl Programa XVI Conferencia Internacional de Bibliotecología Buenas
Programa COLEGIO DE BIBLIOTECARIOS DE CHILE A.G. Diagonal Paraguay 383 of. 122 Santiago Telefono: 56 2 222 56 52 Mail: cbc@bibliotecarios.cl Programa XVI Conferencia Internacional de Bibliotecología Buenas
Tema 4: Regresiones lineales y no lineales TEMA 4. REGRESIONES LINEALES LINEALES Y NO. 1. 2. 3. Introducción 4. Nomenclatura
 T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
MATEMÁTICAS BÁSICAS RADICALES. 4 x, es exacto. OPERACIONES CON RADICALES. 16x es un radical racional porque su resultado,
 Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
Mg. Marco Antonio Plaza Vidaurre 1 LA TASA DE INTERÉS ANTICIPADA Y SUS APLICACIONES
 Mg. Mrco Atoio Plz Viurre LA TASA E ITERÉS ATICIPAA Y SUS APLICACIOES L ts e iterés veci es quell que se utiliz e u operció ficier cuy liquició se efectú l fil el u perioo y l ts e iterés ticip, ifereci
Mg. Mrco Atoio Plz Viurre LA TASA E ITERÉS ATICIPAA Y SUS APLICACIOES L ts e iterés veci es quell que se utiliz e u operció ficier cuy liquició se efectú l fil el u perioo y l ts e iterés ticip, ifereci
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
OPCIÓN A. c) (1 punto)
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
Ruta Alimentadora Sur
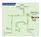 Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
Estado de conservación vs. estado ecológico de los ecosistemas fluviales en España. Hacia una sinergia de las Directivas Marco del Agua y Hábitats
 Ctr Etui Hirgráfic Smiri br l plicció cri l plític cmuitri Biivri, Agu y Mi Mri Mri, 9 y 10 Jui 2011 Et crvció v. t clógic l citm fluvil Epñ. Hci u irgi l Dirctiv Mrc l Agu y Hábitt 1 Mul Tr Ctr Etui Hirgrá
Ctr Etui Hirgráfic Smiri br l plicció cri l plític cmuitri Biivri, Agu y Mi Mri Mri, 9 y 10 Jui 2011 Et crvció v. t clógic l citm fluvil Epñ. Hci u irgi l Dirctiv Mrc l Agu y Hábitt 1 Mul Tr Ctr Etui Hirgrá
Proyecto de recuperación psicosocial de niñas y niños afectados por desastres naturales El retorno a la alegría
 i viit ió i j it U í fii A AMISTAD L E D E U Q S O pi E it j Pyt pió pii iñ y iñ ft p t t E t gí E F Ni Ui p Ifi-UNICEF, UNICEF-E Av Az N2889 y L Gj Téf: (593-2) 2460330 wwwifg/ Qit-E Si h, q ig pñ y z
i viit ió i j it U í fii A AMISTAD L E D E U Q S O pi E it j Pyt pió pii iñ y iñ ft p t t E t gí E F Ni Ui p Ifi-UNICEF, UNICEF-E Av Az N2889 y L Gj Téf: (593-2) 2460330 wwwifg/ Qit-E Si h, q ig pñ y z
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
Radicación en R - Potencia de exponente racional Matemática
 Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
2) En cualquier intervalo de la recta real hay infinitos número racionales, por ello se dice que el conjunto Q es denso.
 TEMA : NÚMEROS REALES. Clsificció de los úeros reles.. Itervlos y seirrects.. Vlor bsoluto de u úero rel.. Potecis y rdicles. Propieddes.. Clsificció de los úeros reles. No olvideos: ) Los úeros rcioles
TEMA : NÚMEROS REALES. Clsificció de los úeros reles.. Itervlos y seirrects.. Vlor bsoluto de u úero rel.. Potecis y rdicles. Propieddes.. Clsificció de los úeros reles. No olvideos: ) Los úeros rcioles
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
IES Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti
 IES Mediterráeo de Málg Juio Ju Crlos loso Giotti UNIVERSIDD DEL PIS VSCO PRUES DE CCESO L UNIVERSIDD CONVOCTORI DE JUNIO Este Eme tiee dos opcioes. Dees de cotestr u de ells No olvides icluir el código
IES Mediterráeo de Málg Juio Ju Crlos loso Giotti UNIVERSIDD DEL PIS VSCO PRUES DE CCESO L UNIVERSIDD CONVOCTORI DE JUNIO Este Eme tiee dos opcioes. Dees de cotestr u de ells No olvides icluir el código
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
Enterprise Architecture Offering for Telco. Diego Cotignola Sr Architect IBM Global Business Services
 Ei Ai Offi f Tl i il Ai I Gll i vi 1 A Iió Aqi Eil Qé? ál l vl i? Ei Ai Offi f Tl Al Ii lí 2 A Iió Aqi Eil Qé? ál l vl i? Ei Ai Offi f Tl Al Ii lí 3 Aqi Eil l víl l Ei Eil l Ejió Ei Eil Oi Ni Ei N. Ei
Ei Ai Offi f Tl i il Ai I Gll i vi 1 A Iió Aqi Eil Qé? ál l vl i? Ei Ai Offi f Tl Al Ii lí 2 A Iió Aqi Eil Qé? ál l vl i? Ei Ai Offi f Tl Al Ii lí 3 Aqi Eil l víl l Ei Eil l Ejió Ei Eil Oi Ni Ei N. Ei
CIENCIAS EXPERIMENTALES
 Fult CIENCIAS EXPERIMENTALES Gr Bilí Uivri Jé GRADO EN BIOLOGÍA PRESENTACIÓN DEL GRADO El Gr Bilí u titulió rátr itífi qu ti m bjtiv frmr l lum l imit l vi t u ft l ut vit mlulr ht l tui l itm rfi l l
Fult CIENCIAS EXPERIMENTALES Gr Bilí Uivri Jé GRADO EN BIOLOGÍA PRESENTACIÓN DEL GRADO El Gr Bilí u titulió rátr itífi qu ti m bjtiv frmr l lum l imit l vi t u ft l ut vit mlulr ht l tui l itm rfi l l
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
5 3 = (5)(5)(5) = 125
 Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
CAPITULO 6.- LA TRANSFORMADA DE LAPLACE.
 PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
POLITÉCNICA SUPERIOR DE LINARES
 El POLITÉCNICA SUPERIOR DE LINARES Gr Igirí Qíi Iil Uivri Jé GRADO EN INGENIERÍA QUÍMICA INDUSTRIAL PRESENTACIÓN DEL GRADO L titl Gr Igirí Qíi Iil hbilit r l jri l rf rgl Igir Té Iil ili Qíi Iil. Et títl
El POLITÉCNICA SUPERIOR DE LINARES Gr Igirí Qíi Iil Uivri Jé GRADO EN INGENIERÍA QUÍMICA INDUSTRIAL PRESENTACIÓN DEL GRADO L titl Gr Igirí Qíi Iil hbilit r l jri l rf rgl Igir Té Iil ili Qíi Iil. Et títl
2 J,, M L (M M), M, í L j g g í ñ gé ó ó:? Q g H g Y g g, j ó, é í é ó í gó í g, í g, j í,,, í g P j g g,, á? g g Pí gz T j gó ó g é M x j M ó é D U C
 U : w ww L ZO D MOR B RIN WI P RÓLOGO g V, é, G OTH 2 J,, M L (M M), M, í L j g g í ñ gé ó ó:? Q g H g Y g g, j ó, é í é ó í gó í g, í g, j í,,, í g P j g g,, á? g g Pí gz T j gó ó g é M x j M ó é D U
U : w ww L ZO D MOR B RIN WI P RÓLOGO g V, é, G OTH 2 J,, M L (M M), M, í L j g g í ñ gé ó ó:? Q g H g Y g g, j ó, é í é ó í gó í g, í g, j í,,, í g P j g g,, á? g g Pí gz T j gó ó g é M x j M ó é D U
Para ordenar números decimales debemos tener en cuenta la siguiente imagen:
 TEMA y NÚMEROS DECIMALES Y FRACCIONES. ORDENAR NÚMEROS DECIMALES Pr order úeros deciles deeos teer e cuet l siguiete ige: Lo que vos hcer es coprr priero l prte eter cifr cifr ver si so igules y si so
TEMA y NÚMEROS DECIMALES Y FRACCIONES. ORDENAR NÚMEROS DECIMALES Pr order úeros deciles deeos teer e cuet l siguiete ige: Lo que vos hcer es coprr priero l prte eter cifr cifr ver si so igules y si so
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
INVITACIÓN PÚBLICA No. 023 DE 2015
 INVITACIÓN PÚBLICA No. 023 DE 2015 RESPUESTA OBSERVACIONES AL PROYECTON DE PLIEGO DE CONDICIONES DE LA INVITACIÓN PÚBLICA RECTORIA COMITÉ DE CONTRATACIÓN UNIVERSIDAD PEDAGÓGICA Y TECNOLÓGICA DE COLOMBIA
INVITACIÓN PÚBLICA No. 023 DE 2015 RESPUESTA OBSERVACIONES AL PROYECTON DE PLIEGO DE CONDICIONES DE LA INVITACIÓN PÚBLICA RECTORIA COMITÉ DE CONTRATACIÓN UNIVERSIDAD PEDAGÓGICA Y TECNOLÓGICA DE COLOMBIA
