x b EXPONENTES Y LOGARITMOS Formulario Matemático para Economía III x = x x = Claudia Aburto 1 = x a A. Propiedades exponenciales: 1.
|
|
|
- María Jesús Contreras Zúñiga
- hace 5 años
- Vistas:
Transcripción
1 Formulrio Mtemático pr Economí III EXPONENTES Y LOGARITMOS Cludi Aurto A. Propieddes eponenciles:. Multiplicción 4. División Distriución con Multiplicción: () () Distriución con división 0 5. Potenci de un potenci ( ) ( ) 6 6. Potenci invers: 4 7. Potenci Ríz: 4 8. Potenci Rcionl
2 Formulrio Mtemático pr Economí III Cludi Aurto B. Propieddes logrítmics form logrítmic:. Form logrítmic: log, esto se lee como es el eponente l que se dee elevr pr otener. log00 0, 0 es el eponente l que se dee elevr pr otener 00 o Propieddes logrítmics: ) Multiplicción: log log + log ) División: log log log c) Propiedd de potenci: log * log d) Propiedd de identidd: si log log, entonces D. Gráfics de ecuciones eponenciles logrítmics : Ejemplo :, (/) en l mism gráfic. (5) Ejemplo : 9 +X (5) Ejemplo : - (5) Ejemplo 4: - + (54) Ejemplo 5: log (+) (55) Ejemplo 6: log (-) (56) Ejemplo 7: log (-)+ (57) Ejemplo 8: log (+)- (58) F()9 + F() - + F() - - Asíntot en - Asíntot en Asíntot en F()log (-) F()log (-)+ F()log (+)- F()log (+) Asíntot en 57 Asíntot en 58 Asíntot en - Br Chrts, Inc. 00.
3 Formulrio Mtemático pr Economí III Cludi Aurto INTEGRALES L integrl indefinid F() SE LLAMA ANTIDERIVADA DE f(), SI F ()f().. L ntiderivd más generl está denotd por f()d.. f()d. tmién se llm integrl indefinid de f(). Teorem fundmentl de cálculo. Si F () f() f() es continu sore [,], entonces f ( ) d F( ) F( ) Fórmuls de Integrción. Si k es l constnte kd k + c d + c n n. d + c n + d Ln + c 5. d Ln + c. (integrl de ) n - 4. >0 6. k k d + c kln 7. k k e e d + c k kf ( ) d k f ( ) d [ ) g( ) ] d f ( ) d + f ( + g( ) d 0. f ( ) d f ( ) d 0 (q ln e). Si f() 0 sore [,], d el áre jo l curv. f ( ) d. Si f() g() sore [,], [ f ( ) g( ) ] d d el áre entre ls curvs f() g().. El vlor promedio de f() sore [,] es f ( ) d Integrción por prtes. Fctorice l integrl en prtes: u dv. Encuentre du v dv. Encuentre v du 4. Hg u dv uv - v du
4 Formulrio Mtemático pr Economí III Integrción por sustitución Pr resolver f ( g( )) g'( ) d Cludi Aurto Derivds:. Hg ug(), donde g() se escoge pr simplificr el integrndo.. Sustitu ug() dug ()d en el integrndo. ) Este pso por lo generl require multiplicr o dividir entre un constnte. Resuelv f(u)du F(u)+C 4. Sustitu ug() pr otener l respuest: F(g())+C L primer derivd nos hl de l pendiente de l función.. d Se un constnte 0. d. d Sen constntes demás se 0 d. dln d 4. d Ln d es un constnte de Cso prticulr: e d Suponemos f() g() son dos funciones de que f () g () eisten [ f ( ) + g( ) ] d f ' ( ) + g' ( ) d d[ f ( ). g( ) ] f ( ) g' ( ) + g( ) f d f ( ) d g( ) g( ) f '( ) f ( ) g'( ) d g( ) [ ] ' ( ) g ( ) 0 Suponemos f() g(z) que f () g (z) d d d g 8. Regl de l cden. f ' ( ). g' ( z) dz d dz z Se puede ver cómo un vrile (z) fect otr () trvés de l influenci de un intermediri (). z & +5 z z. 6 ( + 5)
5 Formulrio Mtemático pr Economí III Derivds Prciles Cludi Aurto f (,,...,n) ó Ó f ó f Derivd de con respecto, mnteniendo constntes TODAS ls demás vriles. lim f ( + h,,..., n ) f ( +,..., n ),... n h 0 h ejemplos: f ( + + c, ) + + c Derivds prciles de segundo orden (segunds derivds) Es l derivd prcil de un derivd prcil Nos hln de l curvtur de l función. ( i) / j z ó f i j i j Ejemplo nterior: f ( + + c, ) + + c Segunds derivds cruzds c Teorem de Young f i j f j i ó Diferencil totl f(,,...,n) 5
6 Formulrio Mtemático pr Economí III d d + d n dn Cludi Aurto Vrición Vrición de multiplicd por l pendiente de l función medid en dirección. + Vrición de multiplicd por l pendiente de l función medid en dirección Ejemplos: d Si f() d f () d f '( ) d Si f(,,...n) d f ()d + f ()d+...f (n)dn. Conveidd Estrict Conveidd Concvidd f () > 0 positiv f () > 0 positiv f () > 0 f () 0 f () > 0 f () < 0 constnte creciente positiv decreciente Crece tss constntes Crece tss crecientes Crece tss decrecientes f () < 0 f () 0 negtiv constnte f () < 0 f () > 0 negtiv creciente f () < 0 f () < 0 negtiv decreciente Decrece ts constnte Crece de - cero Decrece de 0-6
DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES
 DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES Deinición de derivd prcil en un punto lim + Se : A R con A R se un punto interior de A. Se denominn derivds prciles de respecto ls vriles e en el
DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES Deinición de derivd prcil en un punto lim + Se : A R con A R se un punto interior de A. Se denominn derivds prciles de respecto ls vriles e en el
CÁLCULO DIFERENCIAL E
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO COLEGIO DE CIENCIAS Y HUMANIDADES PLANTEL ORIENTE GUÍA PARA EL EXAMEN EXTRAORDINARIO CÁLCULO DIFERENCIAL E INTEGRAL II d f( ) d f () f ( ) d f( ) 1 1 1 0 ( ) < d
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO COLEGIO DE CIENCIAS Y HUMANIDADES PLANTEL ORIENTE GUÍA PARA EL EXAMEN EXTRAORDINARIO CÁLCULO DIFERENCIAL E INTEGRAL II d f( ) d f () f ( ) d f( ) 1 1 1 0 ( ) < d
TEMA 5: INTEGRACIÓN. f(x) dx.
 TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
Cálculo de áreas de figuras planas. Cálculo de volúmenes de sólidos de revolución. Cálculo de áreas de superficies de revolución.
 APLICACIONES DE LA INTEGRAL DEFINIDA Cálculo de áres de figurs plns. Cálculo de volúmenes de sólidos de revolución. Cálculo de longitud de rco de curv. Cálculo de áres de superficies de revolución. Cálculo
APLICACIONES DE LA INTEGRAL DEFINIDA Cálculo de áres de figurs plns. Cálculo de volúmenes de sólidos de revolución. Cálculo de longitud de rco de curv. Cálculo de áres de superficies de revolución. Cálculo
D I F E R E N C I A L
 D I F E R E N C I A L µ dy y = d Si un función y = f() dmite derivd finit en un punto su incremento puede epresrse como y = f () + ε, siendo ε un infinitésimo pr 0. Al primer término se lo llm diferencil
D I F E R E N C I A L µ dy y = d Si un función y = f() dmite derivd finit en un punto su incremento puede epresrse como y = f () + ε, siendo ε un infinitésimo pr 0. Al primer término se lo llm diferencil
La función logaritmo. Definición de la función logaritmo natural.
 L función logritmo Definición de l función logritmo nturl. Se se que un primitiv o ntiderivd de l función f() = n es l función F() n / (n+), es decir n n n cte. Est fórmul es válid sólo cundo n. Cundo
L función logritmo Definición de l función logritmo nturl. Se se que un primitiv o ntiderivd de l función f() = n es l función F() n / (n+), es decir n n n cte. Est fórmul es válid sólo cundo n. Cundo
INTEGRAL DEFINIDA. El hallar el área aproximada bajo la curva por suma de n áreas rectangulares de igual ancho x
 en INTEGRAL DEFINIDA El concepto de integrl definid está relciondo con el vlor que determin el áre jo l curv dd por un función f (x) el [, ]. (ve l intervlo gráfic) Uno de los primeros psos pr llegr este
en INTEGRAL DEFINIDA El concepto de integrl definid está relciondo con el vlor que determin el áre jo l curv dd por un función f (x) el [, ]. (ve l intervlo gráfic) Uno de los primeros psos pr llegr este
AREA DE CIENCIAS BÁSICAS - CÁLCULO INTEGRAL INTEGRAL DEFINIDA
 GUIA DE INTEGRALES DEFINIDAS INTEGRAL DEFINIDA. APLICACIONES DE LA INTEGRAL DEFINIDA Teorem Fundmentl del Cálculo Áre jo l curv de un región Áre entre dos regiones COMPETENCIA: Resolver integrles plicndo
GUIA DE INTEGRALES DEFINIDAS INTEGRAL DEFINIDA. APLICACIONES DE LA INTEGRAL DEFINIDA Teorem Fundmentl del Cálculo Áre jo l curv de un región Áre entre dos regiones COMPETENCIA: Resolver integrles plicndo
LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.
![LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b. LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.](/thumbs/52/29237757.jpg) Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES
 LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) 1-FUNCION LOGARITMO NATURAL
 FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) -FUNCION LOGARITMO NATURAL Definición propieddes L funcion logritmo nturl de un numero positivo se not ln su dominio es el conjunto de los números reles positivos
FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) -FUNCION LOGARITMO NATURAL Definición propieddes L funcion logritmo nturl de un numero positivo se not ln su dominio es el conjunto de los números reles positivos
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Muchos cálculos algebraicos, que son difíciles o imposibles por otros métodos, son fáciles de desarrollar por medio de los logaritmos.
 1.3. L función Logrítmic Con el uso de los ritmos, los procesos de multiplicción, división, elevción potencis extrcción de ríces entre números reles pueden simplificrse notorimente. El proceso de multiplicción
1.3. L función Logrítmic Con el uso de los ritmos, los procesos de multiplicción, división, elevción potencis extrcción de ríces entre números reles pueden simplificrse notorimente. El proceso de multiplicción
Tema 11: Integrales denidas
 Tem : Integrles denids My 9, 7 Denición y propieddes Denición. Si f ) es un función continu en un intervlo [, b] y denid positiv, f ), l integrl denid en ese intervlo l denimos como: f ). Si f ) > l integrl
Tem : Integrles denids My 9, 7 Denición y propieddes Denición. Si f ) es un función continu en un intervlo [, b] y denid positiv, f ), l integrl denid en ese intervlo l denimos como: f ). Si f ) > l integrl
Relación entre el cálculo integral y el cálculo diferencial.
 Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
2. LAS INTEGRALES DEFINIDA E INDEFINIDA
 2. LAS INTEGRALES DEFINIDA E INDEFINIDA Ojetivo: El lumno identificrá los conceptos de ls integrles definid e indefinid y los plicrá en el cálculo y otención de integrles Notción sum Se k un numero rel
2. LAS INTEGRALES DEFINIDA E INDEFINIDA Ojetivo: El lumno identificrá los conceptos de ls integrles definid e indefinid y los plicrá en el cálculo y otención de integrles Notción sum Se k un numero rel
INTEGRALES Curso , 2 tal que f(c) = k? ), para algún punto [a, b].
![INTEGRALES Curso , 2 tal que f(c) = k? ), para algún punto [a, b]. INTEGRALES Curso , 2 tal que f(c) = k? ), para algún punto [a, b].](/thumbs/68/58654060.jpg) INTEGRALES Curso 9-.- ) Enuncir el Teorem del vlor medio integrl y dr un interpretción del mismo. Cundo f(), cómo puede interpretrse geométricmente? cos si [-, ] ) Se f () = 4 + sen si (, ] ) Hllr I =
INTEGRALES Curso 9-.- ) Enuncir el Teorem del vlor medio integrl y dr un interpretción del mismo. Cundo f(), cómo puede interpretrse geométricmente? cos si [-, ] ) Se f () = 4 + sen si (, ] ) Hllr I =
DERIVADAS. I.E.S. Miguel de Cervantes (Granada) Departamento de Matemáticas - GBG
 DERIVADAS DERIVADAS TASA DE VARIACIÓN MEDIA Llmmos ts de vrición medi de l fnción f entre y b con < b, y lo representmos por TVM[, b], l cociente entre l vrición de f () y l de en el intervlo [, b]. f
DERIVADAS DERIVADAS TASA DE VARIACIÓN MEDIA Llmmos ts de vrición medi de l fnción f entre y b con < b, y lo representmos por TVM[, b], l cociente entre l vrición de f () y l de en el intervlo [, b]. f
Teorema fundamental del Cálculo.
 Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
Integral definida. Áreas MATEMÁTICAS II 1
 Integrl definid. Áres MATEMÁTICAS II APROXIMACIÓN AL VALOR DEL ÁREA BAJO UNA CURVA L integrl definid está históricmente relciond con el prolem de definir y clculr el áre de figurs plns. En geometrí se
Integrl definid. Áres MATEMÁTICAS II APROXIMACIÓN AL VALOR DEL ÁREA BAJO UNA CURVA L integrl definid está históricmente relciond con el prolem de definir y clculr el áre de figurs plns. En geometrí se
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL
 3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
Fundamentos Matemáticos de la Ingeniería. Tema 9: Cálculo integral de funciones de varias variables Curso
 Fundmentos Mtemáticos de l Ingenierí. (Tem 9) Hoj Escuel Técnic Superior de Ingenierí Civil e Industril (Esp. en Hidrologí) Fundmentos Mtemáticos de l Ingenierí. Tem 9: Cálculo integrl de funciones de
Fundmentos Mtemáticos de l Ingenierí. (Tem 9) Hoj Escuel Técnic Superior de Ingenierí Civil e Industril (Esp. en Hidrologí) Fundmentos Mtemáticos de l Ingenierí. Tem 9: Cálculo integrl de funciones de
Es una función exponencial con base 2. Veamos con la rapidez que crece:
 Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
3 HERRAMIENTAS DE MATEMÁTICAS
 HERRAMIENAS DE MAEMÁICAS Entre ls operciones mtemátics más comunes se encuentrn: Sum, Rest, Multiplicción, División, Elevción Potencis Etrcción de Ríces, que se indicn con los signos siguientes: -El signo
HERRAMIENAS DE MAEMÁICAS Entre ls operciones mtemátics más comunes se encuentrn: Sum, Rest, Multiplicción, División, Elevción Potencis Etrcción de Ríces, que se indicn con los signos siguientes: -El signo
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Tema 11: Integral definida. Aplicaciones al cálculo de áreas
 Tem : Integrl definid. Aplicciones l cálculo de áres. Introducción Ls integrles no vn permitir clculr áres de figurs no geométrics. En nuestro cso, nos limitremos clculr el áre jo un curv y el áre encerrd
Tem : Integrl definid. Aplicciones l cálculo de áres. Introducción Ls integrles no vn permitir clculr áres de figurs no geométrics. En nuestro cso, nos limitremos clculr el áre jo un curv y el áre encerrd
a x0 x x... x x b, con lo que los (n+1) números reales dividen al intervalo, 1. ÁREAS DE RECINTOS PLANOS. INTEGRAL DEFINIDA
 UNIDAD 6: Integrles Definids. Aplicciones. ÁREAS DE RECINTOS PLANOS. INTEGRAL DEFINIDA Nos plntemos el cálculo de áres de recintos limitdos por curvs que vienen dds por funciones reles,como por ejemplo
UNIDAD 6: Integrles Definids. Aplicciones. ÁREAS DE RECINTOS PLANOS. INTEGRAL DEFINIDA Nos plntemos el cálculo de áres de recintos limitdos por curvs que vienen dds por funciones reles,como por ejemplo
Tema 3 La elasticidad y sus aplicaciones Relación elasticidad-precio y gasto en la curva de demanda lineal
 Introducción l Teorí Económic Crmen olores Álvrez Alelo Miguel Becerr omínguez Ros Mrí Cáceres Alvrdo Mrí del ilr Osorno del Rosl Olg Mrí Rodríguez Rodríguez http://it.ly/8l8u Tem 3 L elsticidd y sus plicciones
Introducción l Teorí Económic Crmen olores Álvrez Alelo Miguel Becerr omínguez Ros Mrí Cáceres Alvrdo Mrí del ilr Osorno del Rosl Olg Mrí Rodríguez Rodríguez http://it.ly/8l8u Tem 3 L elsticidd y sus plicciones
Tema 10: Integral definida. Aplicaciones al cálculo de áreas
 Tem : Integrl definid. Aplicciones l cálculo de áres. Introducción Ls integrles nos vn permitir clculr áres de figurs no geométrics. En nuestro cso, nos limitremos clculr el áre jo un curv y el áre encerrd
Tem : Integrl definid. Aplicciones l cálculo de áres. Introducción Ls integrles nos vn permitir clculr áres de figurs no geométrics. En nuestro cso, nos limitremos clculr el áre jo un curv y el áre encerrd
LOGARITMOS. John Neper ( ) Henry Briggs ( )
 LOGARITMOS John Neper (550-67) Henry Briggs (56-630) MATEMÁTICAS CCSS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que
LOGARITMOS John Neper (550-67) Henry Briggs (56-630) MATEMÁTICAS CCSS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que
UNIDAD 6.- Integrales Definidas. Aplicaciones (tema 15 del libro)
 UNIDAD 6.- Integrles Definids. Aplicciones (tem 5 del liro). ÁREAS DE RECINTOS PLANOS. INTEGRAL DEFINIDA Nos plntemos el cálculo de áres de recintos limitdos por curvs que vienen dds por funciones reles,como
UNIDAD 6.- Integrles Definids. Aplicciones (tem 5 del liro). ÁREAS DE RECINTOS PLANOS. INTEGRAL DEFINIDA Nos plntemos el cálculo de áres de recintos limitdos por curvs que vienen dds por funciones reles,como
SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES
 Junio 009 SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES PR-.- Un cmpo de tletismo de 00 metros de perímetro consiste en un rectángulo y dos semicírculos en dos ldos opuestos, según
Junio 009 SELECTIVIDAD CASTILLA Y LEÓN/ MATEMÁTICAS / ANÁLISIS DE FUNCIONES PR-.- Un cmpo de tletismo de 00 metros de perímetro consiste en un rectángulo y dos semicírculos en dos ldos opuestos, según
Función Cuadrática. 1. Si f ( x) x x 2, determine su forma canónica
 Función Cudrátic. Si f ( ), determine su form cnónic. Determine el ámbito de l función ( 4). Hlle l ecución de l prábol que tiene vértice V (,) y cort l eje y en el punto (0,5). 4. Grfique l función f
Función Cudrátic. Si f ( ), determine su form cnónic. Determine el ámbito de l función ( 4). Hlle l ecución de l prábol que tiene vértice V (,) y cort l eje y en el punto (0,5). 4. Grfique l función f
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
CONTENIDO PROGRAMÁTICO
 CONTENIDO PROGRAMÁTICO Fech Emisión: 205/09/30 Revisión No. 2 AC-GA-F-8 Págin de 5 NOMBRE DEL CONTENIDO PROGRAMÁTICO CÓDIGO 2202 PROGRAMA TECNOLOGÍA EN ELECTRÓNICA Y COMUNICACIONES ÁREA Y/O COMPONENTE
CONTENIDO PROGRAMÁTICO Fech Emisión: 205/09/30 Revisión No. 2 AC-GA-F-8 Págin de 5 NOMBRE DEL CONTENIDO PROGRAMÁTICO CÓDIGO 2202 PROGRAMA TECNOLOGÍA EN ELECTRÓNICA Y COMUNICACIONES ÁREA Y/O COMPONENTE
TEMA 5: Logaritmos y ecuaciones logarítmicas. Tema 5: Logaritmos y ecuaciones logarítmicas 1
 TEMA : Logritmos y ecuciones rítmics Tem : Logritmos y ecuciones rítmics ESQUEMA DE LA UNIDAD.- Logritmos...- Logritmo de un número rel...- Logritmos decimles y neperinos..- Propieddes de los ritmos..-
TEMA : Logritmos y ecuciones rítmics Tem : Logritmos y ecuciones rítmics ESQUEMA DE LA UNIDAD.- Logritmos...- Logritmo de un número rel...- Logritmos decimles y neperinos..- Propieddes de los ritmos..-
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
PRIMITIVA E INTEGRACIÓN INDEFINIDA
 TEMA CÁLCULO DE PRIMITIVAS. - PRIMITIVA E INTEGRACIÓN INDEFINIDA PRIMITIVA DE UNA FUNCIÓN f(): F() es un primitiv de f() si F () = f() Ejemplos: función: f() Primitiv: F() sen - cos Not: Un función tiene
TEMA CÁLCULO DE PRIMITIVAS. - PRIMITIVA E INTEGRACIÓN INDEFINIDA PRIMITIVA DE UNA FUNCIÓN f(): F() es un primitiv de f() si F () = f() Ejemplos: función: f() Primitiv: F() sen - cos Not: Un función tiene
una función acotada. a) Cuántas particiones puede tener el intervalo [ ab, ]?. c) Cuántos puntos como máximo puede tener una partición de [ ab, ]?.
![una función acotada. a) Cuántas particiones puede tener el intervalo [ ab, ]?. c) Cuántos puntos como máximo puede tener una partición de [ ab, ]?. una función acotada. a) Cuántas particiones puede tener el intervalo [ ab, ]?. c) Cuántos puntos como máximo puede tener una partición de [ ab, ]?.](/thumbs/77/74537816.jpg) Ejercicios del Tem de Integrles Cálculo Diferencil e Integrl II ) Sen A y B dos conjuntos no vcíos de números reles, tles que B A y A está cotdo superiormente Demostrr que B está cotdo superiormente y
Ejercicios del Tem de Integrles Cálculo Diferencil e Integrl II ) Sen A y B dos conjuntos no vcíos de números reles, tles que B A y A está cotdo superiormente Demostrr que B está cotdo superiormente y
LÍMITES CONCEPTO INTUITIVO DE LÍMITE
 Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
Tema V: CALCULO DE INTEGRALES
 http://selectividd.intergrnd.com Tem V: CALCULO DE INTEGRALES.- CONCEPTO DE PRIMITIVA DE UNA FUNCION: Como hemos visto hst hor, l derivción es un técnic prtir de l cul dd un función culquier f() podemos
http://selectividd.intergrnd.com Tem V: CALCULO DE INTEGRALES.- CONCEPTO DE PRIMITIVA DE UNA FUNCION: Como hemos visto hst hor, l derivción es un técnic prtir de l cul dd un función culquier f() podemos
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES En l epresión n c, puede clculrse un de ests tres cntiddes si se conocen dos de ells resultndo de este odo, tres operciones diferentes: º Potenci º Rdicción º Logrito
LOGARITMO º AÑO DEF. Y PROPIEDADES En l epresión n c, puede clculrse un de ests tres cntiddes si se conocen dos de ells resultndo de este odo, tres operciones diferentes: º Potenci º Rdicción º Logrito
La Integral de Riemann
 Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Lím. Lím. Lím. Lím 3. Lím Lím Lím. Lím Lím Lím Lím Lím Lím. Lím. Lím. Lím. Lím. Lím
 Universidd Ncionl Autónom de Hondurs Fcultd de Ciencis Económics Guí de Ejercicios No. DET 85, Métodos Cuntittivos III PARTE : Propieddes de límites: No. Teorem Form de reconocerlo C C ite de un constnte
Universidd Ncionl Autónom de Hondurs Fcultd de Ciencis Económics Guí de Ejercicios No. DET 85, Métodos Cuntittivos III PARTE : Propieddes de límites: No. Teorem Form de reconocerlo C C ite de un constnte
La hipérbola es el lugar geométrico de todos los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante e igual a 2a.
 INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
Teoría Tema 7 Integral definida. Área encerrada por una curva
 Colegio Mrist L Inmculd de Grnd Profesor Dniel Prtl Grcí www.dniprtl.net Asigntur: Mtemátics II 2ºBchillerto Teorí Tem 7: Integrl definid. Áre encerrd por un curv págin /0 Teorí Tem 7 Integrl definid.
Colegio Mrist L Inmculd de Grnd Profesor Dniel Prtl Grcí www.dniprtl.net Asigntur: Mtemátics II 2ºBchillerto Teorí Tem 7: Integrl definid. Áre encerrd por un curv págin /0 Teorí Tem 7 Integrl definid.
Fundamentos matemáticos. Tema 7 Integración. Aplicaciones
 Fundmentos mtemáticos Grdo en Ingenierí grícol y del medio rurl Tem 7 Integrción. Aplicciones José Brrios Grcí Deprtmento de Análisis Mtemático Universidd de L Lgun jrrios@ull.es 16 Licenci Cretive Commons
Fundmentos mtemáticos Grdo en Ingenierí grícol y del medio rurl Tem 7 Integrción. Aplicciones José Brrios Grcí Deprtmento de Análisis Mtemático Universidd de L Lgun jrrios@ull.es 16 Licenci Cretive Commons
UNIVERSIDAD ALAS PERUANAS FACULTAD DE MEDICINA HUMANA y CIENCIAS DE LA SALUD Escuela Académico Profesional de Nutrición Humana SILABO
 1. DATOS INFORMATIVOS. SILABO 1.1. Asigntur : Cálculo Diferencil e Integrl. 1.2. Código : 28-112 1.3 Áre : Formtivo 1.4 Fcultd : Ciencis de l Slud 1.5 Ciclo : Segundo 1.6 Créditos : 04. 1.7 Totl de hors
1. DATOS INFORMATIVOS. SILABO 1.1. Asigntur : Cálculo Diferencil e Integrl. 1.2. Código : 28-112 1.3 Áre : Formtivo 1.4 Fcultd : Ciencis de l Slud 1.5 Ciclo : Segundo 1.6 Créditos : 04. 1.7 Totl de hors
Integración de funciones reales de una variable real. 24 de octubre de 2014
 Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Integración de funciones racionales
 Integrción de funciones rcionles P() Se l integrl d donde P() y Q() son funciones polinómics. Si el grdo P() Q() se Q() divide P() entre Q() medinte el método de l cj y se otiene un cociente () y un resto
Integrción de funciones rcionles P() Se l integrl d donde P() y Q() son funciones polinómics. Si el grdo P() Q() se Q() divide P() entre Q() medinte el método de l cj y se otiene un cociente () y un resto
Primitiva de una función.
 Primitiv de un función. 1 / 29 Definición. Un función derivble F es primitiv de l función f en el intervlo I si F (x) = f(x), pr todo x I. Ejemplos 2 / 29 Ejemplo. Se f : R R tl que f(x) = 4x 3. i) F(x)
Primitiv de un función. 1 / 29 Definición. Un función derivble F es primitiv de l función f en el intervlo I si F (x) = f(x), pr todo x I. Ejemplos 2 / 29 Ejemplo. Se f : R R tl que f(x) = 4x 3. i) F(x)
X = x ) pierde su significado. Lo que se hace es sustituir la definida sólo para x,..., por una función f (x)
 rte Vriles letoris. Vriles letoris continus En l sección nterior se considerron vriles letoris discrets, o se vriles letoris cuo rngo es un conjunto finito o infinito numerle. ero h vriles letoris cuo
rte Vriles letoris. Vriles letoris continus En l sección nterior se considerron vriles letoris discrets, o se vriles letoris cuo rngo es un conjunto finito o infinito numerle. ero h vriles letoris cuo
Logaritmos y exponenciales de otras bases. La función. Tipo III: Si u y v son funciones diferenciables en x y u > 0,
 Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
accés a la universitat dels majors de 25 anys MATEMÀTIQUES UNIDAD DIDÁCTICA 4: LOGARITMOS
 Unitt d ccés ccés l universitt dels mjors de 25 ns Unidd de cceso cceso l universidd de los mores de 25 ños UNIDAD DIDÁCTICA 4: LOGARITMOS ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función
Unitt d ccés ccés l universitt dels mjors de 25 ns Unidd de cceso cceso l universidd de los mores de 25 ños UNIDAD DIDÁCTICA 4: LOGARITMOS ÍNDICE 1. Introducción 2. Potencis funciones eponenciles 3. Función
MÉTODOS DE INTEGRACIÓN
 Mtemátics II LE.Tem 4: Introducción l teorí de integrción Integrles inmedits MÉTODOS DE INTEGRACIÓN x α = xα+ α+ + C, si α - (f(x)) α f '(x) = (f(x))α+ + C, si α - α + x = x + C f '(x) = f(x) + C f(x)
Mtemátics II LE.Tem 4: Introducción l teorí de integrción Integrles inmedits MÉTODOS DE INTEGRACIÓN x α = xα+ α+ + C, si α - (f(x)) α f '(x) = (f(x))α+ + C, si α - α + x = x + C f '(x) = f(x) + C f(x)
c. m a t e m á t i c a s
 Guí de mtemátics ingeníeris Universidd Tecnológic de Agusclientes c. m t e m á t i c s Guí de estudio Educción...nuestr visión hci el futuro Eloro: M en C Mónic González Rmírez Guí de mtemátics ingeníeris
Guí de mtemátics ingeníeris Universidd Tecnológic de Agusclientes c. m t e m á t i c s Guí de estudio Educción...nuestr visión hci el futuro Eloro: M en C Mónic González Rmírez Guí de mtemátics ingeníeris
f x dx F(x) b = F(b) F(a) De esta manera se define la Integral definida 14. Propiedades de la integral definida
 Sugerencis pr quien imprte el curso Anteriormente se clculron lguns áres emplendo solmente fórmuls de l geometrí pln pr otener áres de triángulos, rectángulos y trpecios; Se utilizó tmién l proimción numéric.
Sugerencis pr quien imprte el curso Anteriormente se clculron lguns áres emplendo solmente fórmuls de l geometrí pln pr otener áres de triángulos, rectángulos y trpecios; Se utilizó tmién l proimción numéric.
La Integral Definida
 Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
b) Calcule el área del recinto limitado por la gráfica de la función f(x) y el eje de abscisas entre x = 1 e y x = e.
 MsMtescom Integrles Selectividd CCNN Murci [] [EXT-A] ) Clcule l integrl indefinid rctgd, donde rctg denot l función rco-tngente de ) De tods ls primitivs de l función f() = rctg, encuentre l que ps por
MsMtescom Integrles Selectividd CCNN Murci [] [EXT-A] ) Clcule l integrl indefinid rctgd, donde rctg denot l función rco-tngente de ) De tods ls primitivs de l función f() = rctg, encuentre l que ps por
MATE 3013 LA FUNCIÓN DERIVADA
 MATE 3013 LA FUNCIÓN DERIVADA Se quiere hllr l rect tngente l curv en el punto ( ; f()) = f() 8 Se tom un punto rbitrrio ( ; f()) se trz l rect secnte que ps por esos dos puntos (; f()) (; f()) 8 Cuál
MATE 3013 LA FUNCIÓN DERIVADA Se quiere hllr l rect tngente l curv en el punto ( ; f()) = f() 8 Se tom un punto rbitrrio ( ; f()) se trz l rect secnte que ps por esos dos puntos (; f()) (; f()) 8 Cuál
Definición de la función logaritmo natural.
 L función logritmo Definición de l función logritmo nturl. Se sbe que un primitiv o ntiderivd de l función f() = n es l función F() n / (n+), es decir n n n cte. Est fórmul es válid sólo cundo n. Cundo
L función logritmo Definición de l función logritmo nturl. Se sbe que un primitiv o ntiderivd de l función f() = n es l función F() n / (n+), es decir n n n cte. Est fórmul es válid sólo cundo n. Cundo
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
1. Cálculo de primitivas. 2. Reglas de cálculo de primitivas. (I Integrales inmediatas)
 Tem : L integrl definid. Cálculo de primitivs. Aplicciones.. Cálculo de primitivs. Definición. Dds f, F : D R R, decimos que F es un primitiv de l función f si: F ( f(, D. Está clro que si F es un primitiv
Tem : L integrl definid. Cálculo de primitivs. Aplicciones.. Cálculo de primitivs. Definición. Dds f, F : D R R, decimos que F es un primitiv de l función f si: F ( f(, D. Está clro que si F es un primitiv
INTEGRAL DEFINIDA. 6.1 Aproximación intuitiva al concepto de integral definida. Propiedades con respecto al integrando y al intervalo de integración.
 INTEGRAL DEFINIDA Apuntes de A. Cñó Mtemátics II 6. Aproimción intuitiv l concepto de integrl definid. Propieddes con respecto l integrndo y l intervlo de integrción. 6. El teorem fundmentl del cálculo
INTEGRAL DEFINIDA Apuntes de A. Cñó Mtemátics II 6. Aproimción intuitiv l concepto de integrl definid. Propieddes con respecto l integrndo y l intervlo de integrción. 6. El teorem fundmentl del cálculo
Descomposición elemental (ajustes por constantes)
 Descomposición elementl (justes por constntes) OBSERVACIONES. Ls primers integrles que precen se hn obtenido del libro de Mtemátics I (º de Bchillerto) McGrw-Hill, Mdrid 007.. Otros problems se hn obtenido
Descomposición elementl (justes por constntes) OBSERVACIONES. Ls primers integrles que precen se hn obtenido del libro de Mtemátics I (º de Bchillerto) McGrw-Hill, Mdrid 007.. Otros problems se hn obtenido
UNIVERSIDAD CARLOS III DE MADRID. Departamento de Matemáticas CAPÍTULO 4 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 UNIVERSIDAD CARLOS III DE MADRID Deprtmento de Mtemátics MATEMÁTICAS CAPÍTULO 4 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elbordo por Elen Romer Índice generl 4. Cálculo
UNIVERSIDAD CARLOS III DE MADRID Deprtmento de Mtemátics MATEMÁTICAS CAPÍTULO 4 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elbordo por Elen Romer Índice generl 4. Cálculo
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
5. Integral y Aplicaciones
 Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Estudio de funciones exponenciales y logarítmicas
 FUNCIÓN EXPONENCIAL Recomendciones l Docente: L ctividd proponer debe puntr que los lumnos puedn nlizr los siguientes spectos: 1. Cómo vrí el gráfico de l función eponencil y de qué depende su monotoní.
FUNCIÓN EXPONENCIAL Recomendciones l Docente: L ctividd proponer debe puntr que los lumnos puedn nlizr los siguientes spectos: 1. Cómo vrí el gráfico de l función eponencil y de qué depende su monotoní.
Universidad de Antioquia
 Fcultd de Ciencis Ects Nturles Instituto de Mtemátics Grupo de Semilleros de Mtemátics (Semátic) Funciones inverss gráfics Mtemátics Opertivs Tller 7 0 El concepto mtemático de función epres l ide intuitiv
Fcultd de Ciencis Ects Nturles Instituto de Mtemátics Grupo de Semilleros de Mtemátics (Semátic) Funciones inverss gráfics Mtemátics Opertivs Tller 7 0 El concepto mtemático de función epres l ide intuitiv
C u r s o : Matemática. Material N 25 GUÍA TEÓRICO PRÁCTICA Nº 20 UNIDAD: ÁLGEBRA Y FUNCIONES. Sean a, b lr {0} y m, n.
 C u r s o : Mtemátic Mteril N 5 GUÍA TEÓRICO PRÁCTICA Nº 0 UNIDAD: ÁLGEBRA Y FUNCIONES POTENCIAS ECUACIÓN EXPONENCIAL FUNCIÓN EXPONENCIAL PROPIEDADES DE POTENCIAS Sen, b lr {0} y m, n PRODUCTO DE POTENCIAS
C u r s o : Mtemátic Mteril N 5 GUÍA TEÓRICO PRÁCTICA Nº 0 UNIDAD: ÁLGEBRA Y FUNCIONES POTENCIAS ECUACIÓN EXPONENCIAL FUNCIÓN EXPONENCIAL PROPIEDADES DE POTENCIAS Sen, b lr {0} y m, n PRODUCTO DE POTENCIAS
Tema 11. La integral definida
 Mtemátics II (Bchillerto de Ciencis) Análisis: Integrl definid 5 Integrl definid: áre jo un curv Tem L integrl definid L integrl definid permite clculr el áre del recinto limitdo, en su prte superior por
Mtemátics II (Bchillerto de Ciencis) Análisis: Integrl definid 5 Integrl definid: áre jo un curv Tem L integrl definid L integrl definid permite clculr el áre del recinto limitdo, en su prte superior por
Tema 4: Integrales Impropias
 Prof. Susn López 1 Universidd Autónom de Mdrid Tem 4: Integrles Impropis 1 Integrl Impropi En l definición de un integrl definid f (x) se exigió que el intervlo [, b] fuese finito. Por otro ldo el teorem
Prof. Susn López 1 Universidd Autónom de Mdrid Tem 4: Integrles Impropis 1 Integrl Impropi En l definición de un integrl definid f (x) se exigió que el intervlo [, b] fuese finito. Por otro ldo el teorem
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO CALCULO DIFERENCIAL. Integral Indefinida
 Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
DERIVADA DE LA FUNCIÓN LOGARITMO DE CUALQUIER BASE Y LA DERIVACIÓN LOGARÍTMICA
 DERIVADA DE LA FUNCIÓN LOGARITMO DE CUALQUIER BASE Y LA DERIVACIÓN LOGARÍTMICA Sugerencis pr quien imprte el curso: Se esper que con l propuest didáctic presentd en conjunción con los prendizjes logrdos
DERIVADA DE LA FUNCIÓN LOGARITMO DE CUALQUIER BASE Y LA DERIVACIÓN LOGARÍTMICA Sugerencis pr quien imprte el curso: Se esper que con l propuest didáctic presentd en conjunción con los prendizjes logrdos
Integrales Impropias. Capítulo Introducción Integrales de Funciones No Acotadas
 Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
UNIDAD III INECUACIONES
 Licencitur en Administrción Mención Gerenci y Mercdeo UNIDAD III INECUACIONES Elordo por: Ing. Ronny Altuve Rg, Esp. Ciudd Ojed, mrzo de 2017 Universidd Alonso de Ojed s reles Los números que están ordendos
Licencitur en Administrción Mención Gerenci y Mercdeo UNIDAD III INECUACIONES Elordo por: Ing. Ronny Altuve Rg, Esp. Ciudd Ojed, mrzo de 2017 Universidd Alonso de Ojed s reles Los números que están ordendos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 06 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserv, Ejercicio, Opción A Reserv, Ejercicio, Opción B Reserv, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 06 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserv, Ejercicio, Opción A Reserv, Ejercicio, Opción B Reserv, Ejercicio,
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
a Y = X donde a 1 siendo Lg el logaritmo y
 Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
Cálculo integral de funciones de una variable
 Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua.
 Integrción indefinid y definid. Aplicciones de l integrl: vlor medio de un función continu. Jun Ruiz 1 Mrcos Mrvá 1 1 Deprtmento de Mtemátics. Universidd de Alclá de Henres. Contenidos Introducción 1 Introducción
Integrción indefinid y definid. Aplicciones de l integrl: vlor medio de un función continu. Jun Ruiz 1 Mrcos Mrvá 1 1 Deprtmento de Mtemátics. Universidd de Alclá de Henres. Contenidos Introducción 1 Introducción
Tecnólogo Mecánico-Cartografía
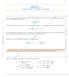 PRÁCTICO MATEMÁTICA II Tecnólogo Mecánico - Tecnólogo en Crtogrfí. Mtemátic II En los cursos re-universitrios rendimos derivr funciones. Dd un función f (derivble) se estudiron cierts técnics que nos ermitín
PRÁCTICO MATEMÁTICA II Tecnólogo Mecánico - Tecnólogo en Crtogrfí. Mtemátic II En los cursos re-universitrios rendimos derivr funciones. Dd un función f (derivble) se estudiron cierts técnics que nos ermitín
2. Derivada: tangente a una curva. Los teoremas de Rolle y Lagrange.
 . Derivd: tngente un curv. Los teorems de Rolle y Lgrnge. Se f : x I f( x) un función definid en un intervlo I y se un punto interior del intervlo I. L pendiente de l rect tngente l curv y f( x), f( )
. Derivd: tngente un curv. Los teorems de Rolle y Lgrnge. Se f : x I f( x) un función definid en un intervlo I y se un punto interior del intervlo I. L pendiente de l rect tngente l curv y f( x), f( )
Integral de línea de campos escalares.
 Integrl de líne de cmpos esclres. Sen f : R n R un cmpo esclr y un curv prmetrizd por σ : [, b] R n de modo que i) σ (1) [, b]. ii) σ([, b]) D(f). iii) f σ es continu en [, b]. Se define l integrl de f
Integrl de líne de cmpos esclres. Sen f : R n R un cmpo esclr y un curv prmetrizd por σ : [, b] R n de modo que i) σ (1) [, b]. ii) σ([, b]) D(f). iii) f σ es continu en [, b]. Se define l integrl de f
ÁLGEBRA: Propiedades para la Simplificación
 Sludmed 016, por Prof. Edgr Loptegui Corsino ( http://www.sludmed.com/ ), se encuentr bjo un licenci CC: Cretive Commons : Atribución-No Comercil-Sin Derivds 3.0 PR: http://cretivecommons.org/licenses/by-nc-nd/3.0/pr/
Sludmed 016, por Prof. Edgr Loptegui Corsino ( http://www.sludmed.com/ ), se encuentr bjo un licenci CC: Cretive Commons : Atribución-No Comercil-Sin Derivds 3.0 PR: http://cretivecommons.org/licenses/by-nc-nd/3.0/pr/
UNIVERSIDAD DE CANTABRIA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA NÚMEROS COMPLEJOS. Miguel Angel Rodríguez Pozueta
 DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
Módulo 12 La División
 Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
La Integral Multiplicativa
 Universidd del Pís Vsco Mtemátic Aplicd y Estdístic L Integrl Multiplictiv Jun-Miguel Grci Extrcto: Se nliz l relción de l integrl multiplictiv de Volterr con l derivd logrítmic y los sistems diferenciles
Universidd del Pís Vsco Mtemátic Aplicd y Estdístic L Integrl Multiplictiv Jun-Miguel Grci Extrcto: Se nliz l relción de l integrl multiplictiv de Volterr con l derivd logrítmic y los sistems diferenciles
TEMA 4. Cálculo integral
 TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
Matemáticas Aplicadas a las Ciencias Sociales II. Análisis: Integrales 171. Tema 8. Integrales. , es fácil hallar su derivada F (x)
 Mtemátics Aplicds ls Ciencis Sociles II Análisis: Integrles 7 Concepto de integrl indefinid Tem 8 Integrles L derivd de un función permite conocer l ts de vrición (el cmio instntáneo) de un determindo
Mtemátics Aplicds ls Ciencis Sociles II Análisis: Integrles 7 Concepto de integrl indefinid Tem 8 Integrles L derivd de un función permite conocer l ts de vrición (el cmio instntáneo) de un determindo
0 PRELIMINARES. NÚMEROS REALES
 ACCESO A LA UNIVERSIDAD MATEMÁTICAS VOLUMEN II PRELIMINARES. NÚMEROS REALES. El conjunto de los número reles L representción más común de hce ver l conjunto como un líne rect del plno.,, 4, 8,.7,... 3
ACCESO A LA UNIVERSIDAD MATEMÁTICAS VOLUMEN II PRELIMINARES. NÚMEROS REALES. El conjunto de los número reles L representción más común de hce ver l conjunto como un líne rect del plno.,, 4, 8,.7,... 3
IES Fernando de Herrera 23 de octubre de 2013 Primer trimestre - Primer examen 4º ESO NOMBRE:
 IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
5. Aplicación de la Integral de Riemann
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 8-2 Ingenierí Mtemátic Universidd de Chile SEMANA 9: APLICACIONES DE LA INTEGRAL 5. Aplicción
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 8-2 Ingenierí Mtemátic Universidd de Chile SEMANA 9: APLICACIONES DE LA INTEGRAL 5. Aplicción
Sean dos funciones f y g de variable real definidas en un dominio DŒÑ Definición g es una primitiva de f si f(x)=g (x) "x D
 INTEGRAL DE RIEMANN 1- Primitivs e integrl indefinid - Integrl de Riemnn 3- Interpretción geométric de ls integrles de Riemnn 4- Propieddes de ls integrles de Riemnn 5- Cmio de vrile en ls integrles de
INTEGRAL DE RIEMANN 1- Primitivs e integrl indefinid - Integrl de Riemnn 3- Interpretción geométric de ls integrles de Riemnn 4- Propieddes de ls integrles de Riemnn 5- Cmio de vrile en ls integrles de
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
6. Variable aleatoria continua
 6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
