PROVES PAU. matemàtiques Material recollit per Maite Gorriz i Santi Vilches
|
|
|
- Pilar Poblete Rey
- hace 5 años
- Vistas:
Transcripción
1 PROVES PAU matemàtiques Títol: Paràbola convexa Autor: Francisco Javier Perez Padilla Material recollit per Maite Gorriz i Santi Vilches
2 Proves d accés a la universitat Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu el sistema d equacions lineals següent, que depèn del paràmetre λ: a) Estudieu per a quins valors del paràmetre λ el sistema és incompatible. b) Resoleu el sistema per al cas λ = Considereu els plans π 1 : 5x y 7z = 1 i π 2 : 2x + 3y + z = 5. a) Determineu l equació general (és a dir, la que té la forma Ax + By + Cz = D) del pla que passa per l origen de coordenades i és perpendicular als plans π 1 i π 2. b) Calculeu l angle que formen els plans π 1 i π 2. Convocatòria Sigui la funció, en què k és un paràmetre real diferent de 0. Per als diferents valors del paràmetre k: a) Calculeu el domini i les asímptotes de la funció. b) Calculeu els punts amb un màxim o un mínim relatiu.
3 4. Sabem que el sistema d equacions lineals següent té una única solució: a) Comproveu que a 0. b) Trobeu la solució del sistema en funció del paràmetre a. 5. Considereu les matrius quadrades d ordre 2 de la forma, amb x i y nombres reals. a) Comproveu que la matriu M és sempre invertible, independentment dels valors de x i de y. b) Per a x = 1 i y = 1, calculeu M Considereu un con de 120 cm 3 de volum que té una altura h, un radi de la base x i una aresta a, com el de la figura següent: a) Comproveu que b) Calculeu l altura del con que té l aresta de longitud mínima. Nota: Recordeu que el volum del con és un terç del volum del cilindre recte que té la mateixa base i la mateixa altura que el con. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
4 Proves d accés a la universitat Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Siguin les rectes de R 3 i. a) Comproveu que són paraŀleles. b) Calculeu l equació vectorial del pla que les conté. 2. Considereu el sistema d equacions lineals següent: en què k és un paràmetre real. a) Discutiu el sistema per als diferents valors de k. b) Resoleu el sistema per al cas k = 2. Convocatòria Responeu a les qüestions següents: a) Comproveu que la recta tangent a la corba y = x 2 en el punt d abscissa x = 2 és la recta y = 4x 4 i calculeu els punts d intersecció d aquesta recta amb els eixos de coordenades. b) Calculeu l àrea limitada per la corba de l apartat anterior, la recta tangent en x = 2 i l eix de les abscisses.
5 4. Considereu la matriu. a) Calculeu les potències A 2, A 3 i A 6. b) Calculeu la inversa de la matriu A Sigui la matriu ampliada d un sistema d equacions lineals. a) Discutiu el sistema segons els valors del paràmetre a, i interpreteu el resultat geomètricament. b) Per a a = 1 trobeu la forma paramètrica del pla solució i doneu un punt i dos vectors directors d aquest pla. 6. El croquis de sota representa la paret d unes golfes amb el sostre inclinat, en la qual es vol construir un armari rectangular com el de la zona ombrejada. a) Expresseu l àrea del rectangle en funció de la longitud x del segment AB. b) Determineu les dimensions del rectangle si volem que tingui una superfície màxima i calculeu aquesta superfície màxima. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
6 Proves d accés a la universitat Matemàtiques Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu el pla π: x + y + z = 1 i la recta r que passa pels punts P = (0, 0, 6) i Q = (1, 2, 3). a) Estudieu la posició relativa de la recta r i el pla π. b) Calculeu la distància entre la recta r i el pla π. Nota: Podeu calcular la distància d un punt de coordenades (x 0, y 0, z 0 ) al pla d equa- ció Ax + By + Cz + D = 0 amb l expressió. 2. Siguin les matrius i. a) Comproveu que satisfan la igualtat, en què I és la matriu identitat d ordre 3. b) Fent servir la igualtat anterior, trobeu la matriu inversa de A: A 1. Convocatòria Considereu el sistema d equacions lineals següent: a) Discutiu el sistema per als diferents valors del paràmetre real a. b) Resoleu el sistema per al cas a = 2.
7 4. De les funcions f (x), f (x), g (x) i g (x), en coneixem els valors següents: x f (x) f (x) x g(x) g (x) a) De la funció f (x) sabem també que el pendent de la recta tangent a un punt d abscissa x és 4x 3 9x 2 2x + 1. Trobeu f (x). b) Calculeu (g f ) (1). 5. A R 3, siguin la recta i el punt P = (0, 1, 1). a) Calculeu l equació general (és a dir, la que té la forma Ax + By + Cz = D) del pla π perpendicular a la recta r i que passa pel punt P. b) Calculeu el punt simètric del punt P respecte del pla x + y + z = Sigui la funció. a) Calculeu una primitiva de la funció f (x). b) Calculeu l àrea limitada per la funció f (x) i l eix de les abscisses entre les abscisses x = 0 i. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
8 Proves d accés a la universitat Convocatòria 2016 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Siguin la recta r: (x, y, z) = (5 + k, k, 2 2k) i els punts P = (1, 0, 1) i Q = (2, 1, 1). a) Calculeu l equació paramètrica de la recta que passa pel punt Q i és perpendicular al pla determinat per la recta r i el punt P. b) Calculeu el punt de la recta r que equidista dels punts P i Q. 2. Tres nombres, x, y i z, compleixen dues condicions: que el primer és la suma dels altres dos, i que el segon és la suma de la meitat del primer i el doble del tercer. a) Comproveu que el càlcul dels tres nombres, x, y i z, té una infinitat de solucions. b) Trobeu una expressió general de les solucions. 3. Volem fer un envàs de gelat amb forma de prisma regular de base quadrada i amb una capacitat de 80 cm 3. Per a elaborar-ne la tapa i la superfície lateral, farem servir un material determinat que costa 1 /cm 2, però per a la base haurem d utilitzar un material que és un 50 % més car. a) Si x és la mesura, en cm, del costat de la base, comproveu que la funció que determina el preu de l envàs és. b) Calculeu les mides que ha de tenir l envàs perquè el preu sigui el mínim possible.
9 4. Sigui la funció f(x) = sin (x). a) Calculeu l equació de les rectes tangents a la funció f en els punts d abscissa x = 0 i x = π, respectivament. Trobeu les coordenades del punt en què es tallen les dues rectes. b) Calculeu l àrea de la regió limitada per la gràfica de la funció f i les rectes tangents de l apartat anterior (en cas de no haver resolt l apartat anterior, suposeu que les rectes són y = x i y = x + π, respectivament). 5. Responeu a les qüestions següents: a) Trobeu l única matriu de la forma que satisfà que A 2 = A, i comproveu que A i A I no són invertibles. b) Justifiqueu raonadament que si A és una matriu quadrada d ordre n diferent de la matriu nuŀla, 0, i de la matriu identitat, I, i satisfà la igualtat A 2 = A, aleshores les matrius A i A I no són invertibles. 6. Responeu a les qüestions següents: a) Calculeu l equació cartesiana (és a dir, que té la forma Ax + By + Cz = D) del pla que passa pel punt de coordenades (0, 0, 1) i és perpendicular als plans 3x + y z = 1 i x + y + 2z = 5. b) Suposeu que un pla π 1 és perpendicular a un segon pla π 2 i que el pla π 2 és a la vegada perpendicular a un tercer pla π 3. Expliqueu raonadament si necessàriament els plans π 1 i π 3 han de ser perpendiculars entre ells. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
10 Proves d accés a la universitat Convocatòria 2016 Matemàtiques Sèrie 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu el sistema d equacions lineals següent: a) Discutiu el sistema per als diferents valors del paràmetre real k. b) Resoleu el sistema per al cas k = A R 3, siguin la recta r que té per equació (x, y, z) = (1 + λ, λ, 1 λ) i el pla π d equació 2x y + z = 2. a) Determineu la posició relativa de la recta r i el pla π. b) Calculeu la distància entre la recta r i el pla π. Nota: Podeu calcular la distància d un punt de coordenades (x 0, y 0, z 0 ) al pla d equació Ax + By + Cz + D = 0 amb l expressió. 3. Sigui la funció f(x) = x e x 1. a) Calculeu l equació de la recta tangent a la gràfica de la funció f en el punt d abscissa x = 1. b) Determineu en quins intervals la funció f és creixent i en quins intervals és decreixent.
11 4. Responeu a les qüestions següents: a) Calculeu totes les matrius de la forma que satisfan la igualtat A 2 + A = 2I, en què I és la matriu identitat,. b) Justifiqueu que si A és una matriu quadrada que compleix la igualtat A 2 + A = 2I, aleshores A és invertible, i calculeu l expressió de A 1 en funció de les matrius A i I. 5. Considereu el tetraedre que té per vèrtexs els punts A = (x, 0, 1), B = (0, x, 1), C = (3, 0, 0) i D = (0, x, 0), amb 0 < x < 3. a) Comproveu que el volum del tetraedre és donat per l expressió. b) Determineu el valor de x que fa que el volum sigui màxim i calculeu aquest volum màxim. Nota: Podeu calcular el volum del tetraedre de vèrtexs A, B, C i D amb l expressió. 6. Siguin les paràboles f(x) = x 2 + k 2 i g(x) = x 2 + 9k 2. a) Calculeu les abscisses, en funció de k, dels punts d intersecció entre les dues paràboles. b) Calculeu el valor del paràmetre k perquè l àrea compresa entre les paràboles sigui de 576 unitats quadrades. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
12 Proves d accés a la universitat Convocatòria 2016 Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu el sistema d equacions lineals. Expliqueu raonadament si les afirmacions següents són vertaderes o falses: a) Si, el sistema és compatible determinat i la solució és. b) Si, el sistema és compatible indeterminat. 2. Siguin a R 3 el pla π d equació x y + 2z = 2 i els punts A = (3, 1, 2) i B = (1, 1, 2). a) Comproveu que els punts A i B són simètrics respecte del pla π. b) Si r és la recta dels punts P que té per equació P = B + λν, en què λ és un paràmetre real i ν = (1, 1, 0), verifiqueu que els punts mitjans dels segments pertanyen al pla π.
13 3. Responeu a les qüestions següents: a) Calculeu els màxims relatius, els mínims relatius i els punts d inflexió de la funció f(x) = 2x 3 9x x 4. b) Expliqueu raonadament que si f(x) és una funció amb la derivada primera contínua en l interval [a, b] i satisfà que f (a) > 0 i f (b) < 0, aleshores hi ha, com a mínim, un punt de l interval (a, b) en què la recta tangent a la gràfica de f(x) en aquest punt és horitzontal. 4. Sigui A una matriu quadrada d ordre n que satisfà la igualtat A (A I) = I, en què I és la matriu identitat. a) Justifiqueu que la matriu A és invertible i que A 1 = A I. b) Calculeu el valor de a que fa que la matriu compleixi la igualtat A (A I) = I. Calculeu A 1 i comproveu que es correspon amb la matriu calculada a partir del resultat de l apartat anterior. 5. Siguin les rectes r: (x, y, z) = (2, 3, 3) + λ(1, 1, 0) i. a) Estudieu si les rectes r i s són paraŀleles o perpendiculars. b) Determineu la posició relativa de les rectes r i s i calculeu l equació paramètrica de la recta t que talla perpendicularment la recta r i la recta s. 6. Sabem que una funció f(x) té per derivada f (x) = (x + 1)e x i que f(0) = 2. a) Trobeu l equació de la recta tangent a y = f(x) en el punt de la corba d abscissa x = 0. b) Calculeu l expressió de f(x). L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
14 Proves d accés a la universitat Convocatòria 2015 Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Sigui la matriu. a) Determineu per a quins valors de a existeix A 1. b) Calculeu A 1 per a a = A l espai tridimensional considereu la recta r: (x, y, z) = (3 + 2α, α, 3 α) i els plans π 1 : x + y + z = 1 i π 2 : (x, y, z) = (2 + λ, 1 λ + μ, μ). a) Calculeu l equació cartesiana (és a dir, que té la forma Ax + By + Cz = D) del pla π 2. b) Trobeu els dos punts de la recta r que equidisten dels plans π 1 i π 2. Nota: Podeu calcular la distància d un punt de coordenades (x 0, y 0, z 0 ) al pla d equació Ax + By + Cz + D = 0 amb l expressió 3. Sigui la funció f(x) = e x x 2. a) Demostreu que la funció f té una arrel (un zero) en l interval [0, 2]. b) Comproveu que la funció és monòtona en l interval [0, 2] i calculeu les coordenades dels punts mínim absolut i màxim absolut de la funció en aquest interval.
15 4. Siguin els plans de R 3 π 1 : y + z = 2, π 2 : 2x + y + z = 1 i π 3 : 2x 2z = 1. a) Calculeu la posició relativa dels tres plans. b) Comproveu que el pla π 3 és paraŀlel a la recta definida per la intersecció dels plans π 1 i π Siguin x i y les mesures dels costats d un rectangle inscrit en una circumferència de diàmetre 2. a) Comproveu que la superfície del rectangle, en funció de x, és donada per l expressió b) Calculeu els valors de les mesures x i y per als quals la superfície del rectangle és màxima i calculeu el valor d aquesta superfície màxima. 6. Trobeu totes les matrius de la forma que siguin inverses d elles mateixes, és a dir, que [2 punts] L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
16 Proves d accés a la universitat Convocatòria 2015 Matemàtiques Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu el sistema d equacions lineals següent: a) Calculeu per a quins valors del paràmetre a el sistema té més d una solució. b) Resoleu el sistema per al cas a = Sigui r la recta de l espai que té per equació i sigui P el punt de coordenades (6, 0, 1). a) Trobeu l equació cartesiana (és a dir, que té la forma Ax + By + Cz = D) del pla que passa pel punt P i talla perpendicularment la recta r. b) Trobeu l equació paramètrica del pla que passa pel punt P i conté la recta r. 3. Responeu a les qüestions següents: a) Determineu l equació de la recta tangent a la corba y = x 3 en el punt d abscissa x = 2. b) Calculeu l àrea de la regió plana finita limitada per la corba y = x 3 i la recta y = 3x 2.
17 4. Considereu a R 3 la recta que té per equació r: (x, y, z) = ( 4 + 2λ, 2, 1 λ) i els plans π 1 i π 2 d equacions π 1 : x + 2y + 2z = 1 i π 2 : x 2y + 2z = 3, respectivament. a) Determineu la posició relativa de π 1 i π 2. b) Comproveu que tots els punts de la recta r estan situats a la mateixa distància dels plans π 1 i π 2. Nota: Podeu calcular la distància d un punt de coordenades (x 0, y 0, z 0 ) al pla d equació Ax + By + Cz + D = 0 amb l expressió 5. Responeu a les qüestions següents: a) Calculeu la matriu de la forma que satisfà A 2 A = I, en què I és la matriu identitat,. b) Calculeu A 1 i comproveu que el resultat es correspon amb el que obteniu de deduir la matriu A 1 a partir de la igualtat A 2 A = I. 6. La portalada d una catedral està formada, en la part superior, per un arc de mitja circumferència que recolza sobre dues columnes, com iŀlustra la figura adjunta, en què x és el diàmetre de la circumferència, és a dir, la distància entre columnes, i y és l alçària de cada columna. x/2 x y a) Comproveu que la funció determina l àrea d aquesta portalada. b) Si el perímetre de la portalada fa 20 m, determineu les mides x i y de la portalada que en maximitzen l àrea. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
18 Proves d accés a la universitat Convocatòria 2014 Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Siguin r i s les rectes de R 3 que tenen les equacions següents: 2. Siguin les funcions i. a) b) Calculeu per a quins valors de a i de b les gràfiques de les dues funcions són tangents (és a dir, tenen la mateixa recta tangent) en el punt d abscissa x = Considereu el sistema d equacions lineals, per a m R. a) Discutiu el sistema d equacions per als diferents valors del paràmetre m. b) Resoleu el sistema en aquells casos en què el sistema sigui compatible. i. a) Estudieu el paraŀlelisme i la perpendicularitat entre les rectes r i s. b) Trobeu l equació general (és a dir, que té la forma Ax + By + Cz = D) del pla π que conté la recta r i és paraŀlel a la recta s. Calculeu la distància entre la recta s i el pla π obtingut. Determineu el domini i el recorregut de la funció g. Districte Universitari de Catalunya
19 4. Sabem que una funció f té per derivada la funció f (x) = (3x 2) 2 (x 2). a) Calculeu els valors de x en què la funció f té un màxim relatiu, un mínim relatiu o un punt d inflexió, i indiqueu en cada cas de què es tracta. b) Determineu la funció f sabent que s anuŀla en el punt d abscissa x = Donats els vectors u = (2, 1, 0), v = ( 1, 3, 4) i w = (0, 3a 1, 4a), a) Calculeu els valors del paràmetre a perquè els vectors u, v i w siguin linealment dependents. b) Calculeu els valors del paràmetre a perquè un tetraedre d arestes u, v i w tingui un volum de 2/3 d unitats cúbiques. 6. Considereu l equació matricial X A = B, en què i. a) Per a quins valors del paràmetre a l equació matricial té una solució única? b) Trobeu la matriu X que satisfà l equació matricial quan a = 3. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
20 Proves d accés a la universitat Convocatòria 2014 Matemàtiques Sèrie 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu la matriu per a a R. a) Calculeu el rang de la matriu M en funció dels valors del paràmetre a. b) Discutiu i resoleu el sistema d equacions lineals segons els valors del paràmetre a. 2. Considereu el punt A = (1, 2, 3). a) Calculeu el punt simètric del punt A respecte de la recta d equació r: (x, y, z) = (3 + λ, 1, 3 λ). b) Calculeu el punt simètric del punt A respecte del pla que té per equació π: x + y + z = 3. Districte Universitari de Catalunya
21 3. Un nedador és al mar en un punt N, situat a 3 km d una platja recta, i just al davant d un punt S, situat a la platja arran de l aigua; i vol anar a un punt A, situat també arran de l aigua i a 6 km del punt S, de manera que el triangle NSA és rectangle en el vèrtex S. El nedador neda a una velocitat constant de 3 km/h i camina a una velocitat constant de 5 km/h. a) Si P és un punt entre el punt S i el punt A que està a una distància x de S, demostreu que el temps, en hores, que necessita el nedador per a nedar del punt N al punt P i caminar des del punt P fins al punt A és determinat per l expressió. b) Calculeu el valor de x que determina el temps mínim que cal per a anar del punt N al punt A, passant per P. Quin és el valor d aquest temps mínim? 4. Calculeu l àrea de la regió del pla limitada en el primer quadrant per les gràfiques de les funcions y = x 2, y = 4x 2 i y = 9. [2 punts] 5. Siguin r i s les rectes de R 3 d equacions i s: (x, y, z) = (1 + 2α, 3 α, 4 + 3α), amb α R. a) Comproveu que els punts mitjans dels segments que tenen un extrem situat sobre la recta r i l altre extrem situat sobre la recta s formen un pla. b) Trobeu l equació general (és a dir, que té la forma Ax + By + Cz = D) del pla de l apartat anterior. 6. Responeu a les qüestions següents: a) Demostreu que si A és una matriu quadrada que satisfà la igualtat A 2 = I, on I és la matriu identitat, aleshores A és invertible i A 1 satisfà (A 1 ) 2 = I. b) Calculeu l expressió general de les matrius de la forma amb b 0 que satisfan la igualtat A 2 = I. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
22 Proves d accés a la universitat Convocatòria 2014 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu la funció a) Calculeu les asímptotes verticals, horitzontals i obliqües de la funció f. b) Trobeu l equació de la recta tangent a la gràfica de la funció f en aquells punts en què la recta tangent sigui paraŀlela a la recta y = 5x Responeu a les qüestions següents: a) Discutiu el sistema d equacions lineals en funció dels valors de k. b) Resoleu el sistema per a k = Siguin els punts P = (1, 1, 0), Q = (1, 0, 1) i R = (0, 1, 1) i el pla π: x + y + z = 4. a) Trobeu l equació general (és a dir, que té la forma Ax + By + Cz = D) del pla que passa pels punts P, Q i R. b) Si S és un punt de π, comproveu que el volum del tetraedre de vèrtexs P, Q, R i S no depèn del punt S. Districte Universitari de Catalunya
23 4. Donats els plans π 1 : x 4y + z = 2m 1 i π 2 : 2x (2m + 2)y + 2z = 3m + 1, a) Determineu els valors de m perquè els plans π 1 i π 2 s intersequin en una recta i calculeu un vector director de la recta resultant que no depengui de m. b) Sigui el pla π: 3x 2y + 3z = 8. Estudieu la posició relativa del pla π amb la recta r definida per la intersecció dels plans π 1 i π 2 quan m = Responeu a les qüestions següents: a) Si A i B són dues matrius quadrades d ordre n, demostreu que (A + B) 2 = A 2 + 2AB + B 2 AB = BA. b) Si M 1 i M 2 són dues matrius de la forma, amb a, b R, comproveu que el producte M 1 M 2 té també la mateixa forma i que M 1 M 2 = M 2 M Responeu a les qüestions següents: a) La funció f(x) = (b x)e ax, amb a i b constants, té la representació gràfica següent i sabem que passa pels punts A = (0, 2) i B = (2, 0), i que en el punt A la recta tangent a la gràfica és horitzontal. Calculeu els valors de a i b. b) Calculeu L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
24 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Sigui V = {( 1, 1, 1), ( 2, 1, 0), (1, 2, a)} un conjunt de vectors de R 3. a) Trobeu el valor o els valors de a perquè V sigui linealment dependent. b) Quan a = 4, expresseu el vector v = (3, 9, 14) com a combinació lineal dels vectors de V. 2. De la funció polinòmica P(x) = x 3 + ax 2 + bx + 2 sabem que té un extrem relatiu en el punt d abscissa x = 3; la integral definida en l interval [0, 1] val. Calculeu el valor dels paràmetres a i b. [2 punts] 3. Donats el pla π: x + 2y z = 3 i la recta, a) Comproveu que el vector característic (o normal) de π i el vector director de r són perpendiculars. b) Estudieu la posició relativa de π i r en funció del paràmetre m. Districte Universitari de Catalunya
25 4. Siguin les matrius, on a, b i c són paràmetres reals. Calculeu el valor d aquests paràmetres perquè cap de les tres matrius tingui inversa. [2 punts] 5. Donats el pla π: 2x y + 3z 8 = 0 i el punt P = (6, 3, 7), a) Trobeu l equació contínua de la recta que passa per P i és perpendicular a π. b) Trobeu el punt del pla π que està més proper al punt P. 6. Volem construir una tenda en forma de piràmide regular de base quadrada. Disposem de 300 m 2 de tela per a la fabricació de les quatre cares de la tenda (se suposa que en l elaboració de les cares no es perd gens de tela). Designem x la longitud d un costat de la base de la tenda. a) Sabent que el volum d una piràmide és igual a un terç del producte de l àrea de la base per l altura, comproveu que, en aquest cas, b) Determineu el valor de x perquè el volum sigui el més gran possible (no cal que comproveu que el valor obtingut correspon realment a un màxim). LInstitut destudis Catalans ha tingut cura de la correcció lingüística i de ledició daquesta prova daccés
26 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Sabem que el vector (2, 1, 1) és una solució del sistema Calculeu el valor dels paràmetres a, b i c. [2 punts] 2. La corba y = x 2 i la recta y = k, amb k > 0, determinen una regió plana. a) Calculeu el valor de l àrea d aquesta regió en funció del paràmetre k. b) Trobeu el valor de k perquè l àrea limitada sigui. [1,5 punts per lapartat a; 0,5 punts per lapartat b] 3. Sigui. a) Què significa que la matriu B sigui la matriu inversa de A? b) Trobeu el valor del paràmetre p perquè la matriu inversa de A i la matriu transposada de A coincideixin. Nota: No aproximeu les arrels mitjançant valors amb decimals; treballeu amb els radicals. [0,5 punts per lapartat a; 1,5 punts per lapartat b] Districte Universitari de Catalunya
27 4. Es vol construir un canal que tingui com a secció un trapezi isòsceles de manera que l amplària superior del canal sigui el doble de l amplària inferior i que els costats no paraŀlels siguin de 8 metres. A la dreta teniu un esquema de la secció del canal. a) Trobeu el valor del segment L de la gràfica en funció de la variable x (amplària inferior del canal). b) Sabem que l àrea d un trapezi és igual a l altura multiplicada per la semisuma de les bases. Comproveu que, en aquest cas, l àrea de la secció és donada per c) Calculeu el valor de x perquè l àrea de la secció del canal sigui màxima (no cal que comproveu que és realment un màxim). [0,5 punts per lapartat a; 0,5 punts per lapartat b; 1 punt per lapartat c] 5. Donats els punts P = (1, 0, 1) i Q = ( 1, 2, 3), trobeu un punt R de la recta que compleixi que el triangle de vèrtexs P, Q i R és isòsceles, en què i [2 punts] són els costats iguals del triangle. 6. La funció f(x) és derivable i passa per l origen de coordenades. La gràfica de la funció derivada és la que veieu aquí dibuixada, essent fʹ(x) creixent als intervals (, 3] i [2, + ). a) T robeu l equació de la recta tangent a la gràfica de la funció f(x) en el punt d abscissa x = 0. b) Indiqueu les abscisses dels extrems relatius de la funció f(x) i classifiqueu aquests extrems. LInstitut destudis Catalans ha tingut cura de la correcció lingüística i de ledició daquesta prova daccés
28 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Sigui π: 3x 2y + z = 10. a) Trobeu l equació contínua de la recta r perpendicular a π que passa pel punt P = ( 1, 3, 2). b) Trobeu també l equació cartesiana (és a dir, de la forma Ax + By + Cz + D = 0) del pla π 1 paraŀlel a π que passa pel mateix punt P. 2. Considereu la matriu. Sigui I la matriu identitat d ordre 2. a) Trobeu el valor del paràmetre a perquè es compleixi que A 2 2A = I. b) Calculeu la matriu inversa de la matriu A quan a = Donada la funció i la recta horitzontal y = k, amb k > 0, a) Feu un esbós del recinte limitat per les gràfiques de la funció i la recta, i els eixos de coordenades. b) Trobeu el valor de k sabent que l àrea d aquest recinte és igual a 14/3. [0,5 per lapartat a; 1,5 per lapartat b] Districte Universitari de Catalunya
29 4. Un triangle d àrea 3/2 té dos dels vèrtexs als punts P = (0, 0, 0) i Q = (2, 0, 1). El tercer vèrtex, R, és un punt de la recta i té la primera coordenada no nul la. Cal culeu les coordenades del vèrtex R. [2 punts] 5. En una semiesfera de radi R inscrivim un con situant el vèrtex al centre de la semiesfera, tal com es veu en el dibuix. a) Sabent que el volum d un con és igual a l àrea de la base multiplicada per l altura i dividida per 3, comproveu que, en aquest cas, podem expressar el volum com b) Trobeu les dimensions d aquest con (el radi de la base i l altura) perquè el seu volum sigui màxim i comproveu que es tracta realment d un màxim. [0,5 punts per lapartat a; 1,5 punts per lapartat b] 6. Sigui f(x) = x 3 + ax 2 + bx + c. Sabem que la gràfica d aquesta funció és tangent a la recta r: y = x + 3 en el punt d abscissa x = 1, i que en el punt d abscissa x = 1 la recta tangent és paraŀlela a la recta r. Calculeu el valor dels paràmetres a, b i c. [2 punts] LInstitut destudis Catalans ha tingut cura de la correcció lingüística i de ledició daquesta prova daccés
30 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Siguin π 1 el pla 2x + 3y z = 4 i π 2 el pla x 2y 4z = 10. a) Comproveu que els plans π 1 i π 2 són perpendiculars. b) Trobeu l equació contínua de la recta paraŀlela als plans π 1 i π 2 i que passa pel punt P = ( 1, 3, 2). 2. La matriu de coeficients d un sistema d equacions lineals homogeni és a) Per a quins valors del paràmetre a el sistema té una sola solució? Quina és aquesta solució única? b) Resoleu el sistema si a = Donats els punts P = (1, 1, 2), Q = (2, 0, 1) i R = (3, 2, 1), a) Trobeu l equació cartesiana (és a dir, de la forma Ax + By + Cz + D = 0) del pla que determinen. b) Trobeu un punt S pertanyent a la recta, de manera que el tetraedre de vèrtexs P, Q, R i S tingui un volum igual a 1/2. Districte Universitari de Catalunya
31 4. Per a x 1, considereu la funció. a) Trobeu l equació de la recta tangent a la gràfica de f(x) en el punt d abscissa igual a 10. b) Calculeu l àrea del recinte limitat per la gràfica de f(x), la recta d equació x = 5 i l eix OX. 5. Considereu els punts A = ( 1, 2, 4) i B = (3, 0, 2). a) Trobeu l equació del pla format per tots els punts que equidisten de A i B. b) Donat un punt C = (x, y, z), dividim el segment en tres parts iguals i obtenim els punts A, A 1, B i C. Trobeu el punt C. 6. Un triangle rectangle situat en el primer quadrant té el vèrtex A en l origen de coordenades, el vèrtex B = (x, 0) en el semieix positiu d abscisses i el vèrtex C pertany a la recta x + 2y = 8. L angle recte és el que correspon al vèrtex B. a) Comproveu que l àrea del triangle es pot expressar de la manera següent:. b) Trobeu els vèrtexs B i C perquè l àrea del triangle sigui màxima i comproveu que es tracta realment d un màxim. LInstitut destudis Catalans ha tingut cura de la correcció lingüística i de ledició daquesta prova daccés
32 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Determineu el rang de la matriu en funció del paràmetre k. [2 punts] 2. Sigui, en què a 0. a) Determineu si té alguna asímptota vertical, en funció del paràmetre b. b ) Indiqueu el valor dels paràmetres a i b perquè la funció f(x) tingui la recta y = 2x 4 com a asímptota obliqua a Considereu el sistema d equacions lineals següent: a) Calculeu el valor o els valors del paràmetre a per al qual o per als quals el sistema és compatible indeterminat. b) Quantes solucions té aquest sistema quan a = 3? [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] Districte Universitari de Catalunya
33 4. Una fàbrica produeix diàriament x tones d un producte A i (40 5x)/(10 x) tones d un producte B. La quantitat màxima de producte A que es pot produir és 8 tones. El preu de venda del producte A és 100 per tona i el del producte B és 250 per tona. a) Construïu la funció de la variable x que ens proporciona els ingressos diaris, suposant que es ven tota la producció. b) Calculeu quantes tones de cada producte s han de produir diàriament per a obtenir el màxim d ingressos, i comproveu que és realment un màxim relatiu. [0,5 punts per lʼapartat a; 1,5 punts per lʼapartat b] 5. Considereu les rectes de l espai següents: a) Comproveu que són secants. b) Calculeu l equació contínua de la recta que les talla i que és perpendicular a totes dues. 6. Donades la recta y = ax + 1 i la paràbola y = 3x x 2, a) Calculeu els valors del paràmetre a perquè siguin tangents. b) Calculeu els punts de tangència. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
34 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Digueu per a quin valor del paràmetre m els plans tenen com a intersecció una recta. [2 punts] π 1 :x y+mz= 1, π 2 :x y+z=m i π 3 :my+2z= 3 2. Donades la recta y = 3x + b i la paràbola y = x 2, a) Calculeu l abscissa del punt on la recta tangent a la paràbola és paraŀlela a la recta donada. b) Calculeu el valor del paràmetre b perquè la recta sigui tangent a la paràbola. [1 punt per apartat] 3. Donats el pla π: x y + 2z 5 = 0 i la recta, a) Calculeu el punt d intersecció entre el pla i la recta. b) Trobeu l equació contínua de la recta s continguda en el pla π, que és perpendicular a la recta r i talla la recta r. [1 punt per apartat] Districte Universitari de Catalunya
35 4. Donades les matrius, a) Comproveu que es compleix la igualtat (A + B) (A B) = A 2 B 2. b) És certa aquesta igualtat per a qualsevol parell de matrius quadrades A i B del mateix ordre? Responeu raonadament utilitzant les propietats generals de les operacions entre matrius, sense utilitzar matrius A i B concretes. [1 punt per apartat] 5. Un triangle equilàter de vèrtexs A, B i C té els costats de 8 cm. Situem un punt P sobre una de les altures del triangle, a una distància x de la base corresponent. a) Calculeu l altura del triangle de vèrtexs A, B i C. b) Indiqueu la distància del punt P a cadascun dels vèrtexs (en funció de x). c) Determineu el valor de x perquè la suma dels quadrats de les distàncies del punt P a cadascun dels tres vèrtexs sigui mínima. [0,5 punts per lʼapartat a; 0,5 punts per lʼapartat b; 1 punt per lʼapartat c] 6. Donats els punts P = (1, 0, 0), Q = (0, 2, 0), R = (0, 0, 3) i S = (1, 2, 3), a) Calculeu l equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla que conté els punts P, Q i R. b) Comproveu si els quatre punts són coplanaris (és a dir, si els quatre estan continguts en un mateix pla). [1 punt per apartat] LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
36 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no s autoritzarà l ús de calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Donats els plans π 1 :3x+y 2z+15=0 i π 2 :x+y+2z 103=0, a) Comproveu que són perpendiculars. b) Calculeu l equació cartesiana (és a dir, de la forma Ax+By+Cz+D=0) del pla perpendicular a π 1 i π 2, que passa pel punt P=(1, 3, 2). 2. La gràfica de la funció és la següent: a) Trobeu el punt de tall, (a, 0), de la funció amb la part positiva de l eix OX. b) Calculeu l àrea del recinte limitat per la gràfica de f(x) i l eix OX en el primer quadrant. [0,5 punts per lʼapartat a; 1,5 punts per lʼapartat b] Districte Universitari de Catalunya
37 3. Sigui A una matriu quadrada d ordre n de manera que A 2 = O, en què O és la matriu nuŀla (la formada completament per zeros). a) Comproveu que (A + I n ) 2 = 2A + I n. b) Comproveu que les matrius B = I n A i C = A + I n són l una inversa de l altra. 4. Un rectangle és inscrit en el triangle que té els costats en les rectes d equacions y = x, x + y = 8, y = 0, i té un costat sobre la recta y = 0. Trobeu-ne els vèrtexs perquè la superfície sigui màxima. [2 punts] y = x x + y = 8 5. Contesteu les preguntes següents: a) Expliqueu raonadament si una matriu d ordre 3 i una matriu d ordre 2 poden tenir el mateix determinant. b) Considereu les matrius següents: Calculeu, si és possible, el valor del paràmetre p perquè det A = det B. 6. Siguin π: x 3y + 2z = 1 i. Estudieu-ne la posició relativa segons el valor del paràmetre m. [2 punts] LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
38 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Donada la matriu : a) Calculeu els valors del paràmetre k per als quals la matriu M no és invertible. b) Per a k=0, calculeu M Donada la recta, calculeu l equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla perpendicular a la recta que passa pel punt P = (1, 0, 1). [2 punts] 3. Donada la funció f(x)=x 3 + ax 2 + bx+ c: a) Determineu la relació que han de complir els paràmetres a, b i c perquè f(x) tingui un extrem relatiu en el punt d abscissa x= 1. b) Calculeu el valor del paràmetre a perquè hi hagi un punt d inflexió de la funció f(x) en el punt d abscissa x=0. c) Determineu la relació entre els paràmetres a, b i c sabent que la gràfica de f(x) talla l eix OX en el punt d abscissa x= 2. d) Calculeu el valor dels paràmetres a, b i c perquè es compleixin les tres propietats anteriors alhora. [0,5 punts per cada apartat] Districte Universitari de Catalunya
39 4. Sigui la matriu a) Calculeu A 2 i A 3. b) Deduïu el valor de A 101. NOTA: Treballeu amb radicals; no utilitzeu la representació decimal dels elements de la matriu. 5. Considereu la recta i el pla π : 2x+ y 5z=5. a) Estudieu la posició relativa de la recta r i el pla π en funció del paràmetre a. b) Quan a=3, calculeu la distància de la recta r al pla π. 6. Sigui per a > 0. a) Comproveu que b) Calculeu el valor del paràmetre a perquè la funció f(a) tingui un mínim relatiu. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
40 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Donada la recta : a) Trobeu-ne un vector director. b) Calculeu l equació contínua de la recta paral lela a r que passa pel punt P=(1, 0, 1). 2. Si tenim la matriu invertible A i l equació matricial X A+B=C: a) Aïlleu la matriu X. b) Trobeu la matriu X quan 3. Definim les funcions f(x)=a(1 x 2 ) i, en què a > 0. a) Comproveu que l àrea del recinte limitat per les gràfiques de les funcions és: b) Calculeu el valor del paràmetre a perquè aquesta àrea sigui mínima. Districte Universitari de Catalunya
41 4. Considereu el sistema d equacions següent: a) Calculeu els valors del paràmetre a perquè el sistema no sigui compatible determinat. b) Hi ha algun valor de a per al qual x=1, y= 3, z= 1 sigui l única solució del sistema? 5. Siguin i. a) Comproveu que r 1 i r 2 són perpendiculars. b) Comproveu que es tallen mitjançant la determinació del punt de tall. 6. Sigui f(x)=x 2 e ax quan a 0. a) Calculeu el valor de a perquè aquesta funció tingui un extrem relatiu en el punt d abscissa x=2. b) Quan a = 2, classifiqueu-ne els extrems relatius. L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
42 Proves d Accés a la Universitat. Curs Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Calculeu l àrea del recinte limitat per les corbes d equació f(x) = x 2 x + 2 i g(x)=5 3x. [2 punts] 2. Donat el pla π:2x+y z= 5: a) Calculeu l equació del pla paral lel al pla π que passa pel punt P=(1, 0, 1). b) Determineu també la distància entre el punt P i el pla π. 3. La gràfica corresponent a la derivada d una funció f(x) és la següent: a) Expliqueu raonadament quins valors de x corresponen a màxims o a mínims relatius de f(x). b) Determineu els intervals de creixement i decreixement de la funció f(x). [1,5 punts per l apartat a; 0,5 punts per l apartat b] Districte Universitari de Catalunya
43 4. Analitzeu, segons els valors del paràmetre k, el caràcter (és a dir, si és compatible o no i si és determinat o no) del sistema d equacions següent: [2 punts] 5. Calculeu l equació general (és a dir, de la forma Ax+By+Cz+D=0) dels plans que contenen la recta i que formen un angle de 45 amb el pla z=0. [2 punts] 6. Dins d un triangle rectangle, de catets 3 i 4 cm, hi ha un rectangle. Dos costats del rectangle estan situats en els catets del triangle i un dels vèrtexs del rectangle és a la hipotenusa del triangle. a) Feu un esbós de la situació descrita. b) Si x és la longitud del costat del rectangle que està situat en el catet petit i y és l altre costat del rectangle, comproveu que es compleix que 4x+3y=12. c) Determineu les dimensions del rectangle perquè l àrea sigui màxima. [0,5 punts per l apartat a; 0,5 punts per l apartat b; 1 punt per l apartat c] L Institut d Estudis Catalans ha tingut cura de la correcció lingüística i de l edició d aquesta prova d accés
44 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Trobeu les asímptotes de la funció. [2 punts] 2. Donats el pla π:5x + y + 3z = 4 i la recta, estudieu-ne la posició relativa en funció del paràmetre a. [2 punts] 3. Considereu tots els prismes rectes de base quadrada amb un volum V fixat. Anomeneu x el costat de la base del prisma i y la seva altura. a) Trobeu l expressió del volum i de l àrea total del prisma en funció de les variables x i y. b) Comproveu que el que té àrea total mínima és en realitat un cub. [0,5 punts per lʼapartat a; 1,5 punts per lʼapartat b] 4. Considereu la matriu. a) Comproveu que compleix la igualtat A 2 5A = I 2, on I 2 és la matriu identitat d ordre 2. b) Utilitzeu aquesta igualtat per a calcular la matriu inversa de A. c) Resoleu l equació matricial, utilitzant la matriu inversa de A. [0,5 punts per lʼapartat a; 0,75 punts per lʼapartat b; 0,75 per lʼapartat c] Districte Universitari de Catalunya
45 5. Sigui. Trobeu l àrea del recinte limitat per la gràfica d aquesta funció, l eix OX i les rectes x = 0 i x = 2. [2 punts] 6. Considereu la recta. a) Trobeu els dos punts, A i B, de la recta r que estan situats a una distància d = 6 del punt P = ( 1, 1, 2). b) Trobeu l àrea del triangle de vèrtexs A, B i P. LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
46 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Trobeu l equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que conté la recta i és paral lel a la recta. [2 punts] 2. Donat el sistema d equacions lineals : a) Estudieu-ne el caràcter (és a dir, si és compatible o no i si és determinat o no) en funció del paràmetre p. b) Comproveu que si p 5 la solució del sistema no depèn del valor d aquest paràmetre. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] 3. Un segment de longitud fixada m recolza sobre els eixos de coordenades. Calculeu el valor de l angle α que forma el segment amb l eix OX perquè el triangle rectangle determinat pel segment amb els eixos i del qual m és la hipotenusa tingui àrea màxima. Comproveu que es tracta realment d un màxim. [2 punts] Districte Universitari de Catalunya
47 4. Donades les rectes i : a) Comproveu que són paral leles. b) Trobeu l equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté. 5. La gràfica de la funció f(x) = x sin(x) és la següent: a) Trobeu-ne una primitiva. b) Aplicant el resultat de l apartat anterior, calculeu l àrea del recinte limitat per la gràfica de la funció f(x) i l eix d abscisses des de x = 0 fins a x = π. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] 6. Sigui. Trobeu els valors de les variables x i y perquè es compleixi que A 2 = A. [2 punts] LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
48 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Donats el pla π :x + 2y + 3z 4 = 0 i els punts P = (3, 1, 2) i Q = (0, 1, 2): a) Calculeu l equació contínua de la recta perpendicular al pla π que passa pel punt P. b) Calculeu l equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla perpendicular a π que passa pels punts P i Q. 2. Considereu la igualtat matricial (A + B) 2 = A 2 + 2AB + B 2. a) Comproveu si les matrius i compleixen o no la igualtat anterior. b) En general, donades dues matrius qualssevol A i B quadrades del mateix ordre, expliqueu raonadament si hi ha alguna condició que hagin de complir perquè la igualtat de l enunciat sigui certa. 3. Sigui P(x) = ax 2 + bx + c un polinomi qualsevol de segon grau. a) Trobeu la relació existent entre els paràmetres a, b i c sabent que es compleix que P(1) = 0 i P(2) = 0. b) Quan es compleix la condició anterior, indiqueu quins valors pot tenir P (3/2). Districte Universitari de Catalunya
49 4. Hem escalonat la matriu ampliada d un sistema d equacions lineals, A X = b, i hem obtingut: a) Discutiu aquest sistema en funció del paràmetre a. b) Resoleu-lo quan a = 2. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] 5. En la figura següent es representen dues funcions. L una és la derivada de l altra. Decidiu si la funció f(x) és la derivada de la funció g(x) o és a l inrevés, estudiant què passa en els punts x = a, x = b i x = c. [2 punts] 6. Siguin u = ( 1, 3, 2), 1 u = (2, 1, 4) i 2 u = (a + 1, a 1, 4a + 2) tres vectors de l espai vectorial 3. 3 a) Trobeu el valor del paràmetre a per al qual el vector u és combinació lineal dels 3 vectors u i 1 u. 2 b) Comproveu que per a a = 0 el conjunt {u, 1 u, 2 u } és linealment independent. 3 LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
50 Proves dʼaccés a la Universitat. Curs Matemàtiques Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar calculadora, però no es poden fer servir calculadores o altres aparells que portin informació emmagatzemada o que puguin transmetre o rebre informació. 1. Considereu un sistema qualsevol de dues equacions amb tres incògnites. Responeu raonadament a les qüestions següents: a) És possible que el sistema considerat sigui compatible determinat? b) Pot ser incompatible? 2. Donats el punt P = (1, 0, 2) i la recta : a) Trobeu l equació contínua de la recta que passa pel punt P i talla perpendicularment la recta r. b) Calculeu la distància del punt P a la recta r. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b] 3. Determineu el valor dels paràmetres a, b i c perquè la gràfica de la funció [2 punts] sigui la següent: Districte Universitari de Catalunya
51 4. Siguin A, B i C matrius quadrades d ordre n. a) Expliqueu raonadament si és possible que det A 0, det B 0 i det (A B) = 0. Si és possible, poseu-ne un exemple. b) Si sabem que det A 0 i que A B = A C, expliqueu raonadament si podem assegurar que B = C. 5. Siguin r i s dues rectes d equacions a) Trobeu el valor del paràmetre a perquè aquestes rectes es tallin. b) En el cas en què es tallen, trobeu l equació general (és a dir, de la forma Ax + By + Cz + D = 0) del pla que les conté. [1,5 punts per lʼapartat a; 0,5 punts per lʼapartat b]. 3. En la figura es mostra la corba y = x(4 x) i una recta r que passa per l origen i talla la corba en un punt P d abscissa k, amb 0 < k < 4. a) Trobeu l àrea ombrejada, delimitada per la corba i la recta, en funció de k. b) Trobeu per a quin valor de k l àrea de la regió ombrejada és la meitat de l àrea del recinte limitat per la corba i l eix OX. [1 punt per apartat] LʼInstitut dʼestudis Catalans ha tingut cura de la correcció lingüística i de lʼedició dʼaquesta prova dʼaccés
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
PROVES PAU. matemàtiques Material recollit per Maite Gorriz i Santi Vilches
 PROVES PAU matemàtiques 2010-2016 Títol: Paràbola convexa Autor: Francisco Javier Perez Padilla Material recollit per www.mat3.cat Maite Gorriz i Santi Vilches Proves d accés a la universitat Convocatòria
PROVES PAU matemàtiques 2010-2016 Títol: Paràbola convexa Autor: Francisco Javier Perez Padilla Material recollit per www.mat3.cat Maite Gorriz i Santi Vilches Proves d accés a la universitat Convocatòria
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
Convocatòria Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 1. Fase específica
 Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010
 Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 2. Fase específica. Convocatòria 2015
 Proves d accés a la universitat per a més grans de 25 anys Convocatòria 2015 Matemàtiques Sèrie 2 Fase específica Qualificació 1 2 Exercicis 3 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Convocatòria 2015 Matemàtiques Sèrie 2 Fase específica Qualificació 1 2 Exercicis 3 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu
Proves dʼaccés a la Universitat. Curs 2009-2010 Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val 2 punts. Podeu
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Deduce razonadamente en que casos los planos π 1 y π 2 son o no paralelos:
 GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
TEMA 1 : Aplicacions de les derivades. Problemes de funcions
 TEMA 1 : Aplicacions de les derivades Problemes de funcions 1. Determineu els coeficients d un polinomi de tercer grau, P(x) = ax 3 + bx 2 + cx + d, sabent que P(1) = 0, que P(0) = -3, i que la seva gràfica
TEMA 1 : Aplicacions de les derivades Problemes de funcions 1. Determineu els coeficients d un polinomi de tercer grau, P(x) = ax 3 + bx 2 + cx + d, sabent que P(1) = 0, que P(0) = -3, i que la seva gràfica
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Oficina d Accés a la Universitat Pàgina 1 de 12 PAU 2015
 Oficina d Accés a la Universitat Pàgina 1 de 12 Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 12 Sèrie 5 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 22 PAU 2014
 Oficina d Accés a la Universitat Pàgina 1 de 22 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 22 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
PRIMERA MODEL B Codi B2. A1. C
 TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 13 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 13 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 1 SÈRIE 3 1.- Digueu per a quin valor del paràmetre m els plans π 1 : x y +mz = 1, π 2 : x y +z = m, π 3 : my +2z = 3, tenen com a
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 1 SÈRIE 3 1.- Digueu per a quin valor del paràmetre m els plans π 1 : x y +mz = 1, π 2 : x y +z = m, π 3 : my +2z = 3, tenen com a
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina de Sèrie Responeu a CINC de les sis qüestions següents. En les respostes, epliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar calculadora,
Oficina d Accés a la Universitat Pàgina de Sèrie Responeu a CINC de les sis qüestions següents. En les respostes, epliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar calculadora,
Problemes d Anàlisi. Problema 4 Un granger desitja tancar en un terreny rectangular adjacent a un riu.
 Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
Oficina d Accés a la Universitat Pàgina 1 de 21 PAU 2016
 Oficina d Accés a la Universitat Pàgina 1 de 21 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 21 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 22 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 22 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 16 PAU cx by + 2z = b. 2a+b c = a+c 2b 1 b = a b c
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 6 PAU 0 SÈRIE 4.- Sabem que el vector (,, ) és solució del sistema ax + by + cz = a+c bx y + bz = a b c. cx by + z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 6 PAU 0 SÈRIE 4.- Sabem que el vector (,, ) és solució del sistema ax + by + cz = a+c bx y + bz = a b c. cx by + z = b Calculeu el valor
Districte Universitari de Catalunya
 Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
SÈRIE 2 Pautes de correcció (PAAU2001) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 2016 Criteris de correcció
 Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 1 SÈRIE 1 1.- Trobeu l equació general (és a dir, de la forma Ax+By+Cz+D = ) del pla que conté la recta r 1 : x 1 { x y z =
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 1 SÈRIE 1 1.- Trobeu l equació general (és a dir, de la forma Ax+By+Cz+D = ) del pla que conté la recta r 1 : x 1 { x y z =
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Matemàtiques. Proves d accés a la Universitat per a més grans de 25 anys. Sèrie. el polinomi 2. Solució: tercera arrel. i , i.
 Pàgina 1 5 Proves d accés a la Universitat per a més grans 5 anys Abril 015 Sèrie Exercicis Opció A A1.- Consireu el polinomi 7 6. Justifiqueu que 1 i són dues arrels l polinomi. Determineu la tercera
Pàgina 1 5 Proves d accés a la Universitat per a més grans 5 anys Abril 015 Sèrie Exercicis Opció A A1.- Consireu el polinomi 7 6. Justifiqueu que 1 i són dues arrels l polinomi. Determineu la tercera
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS. 1) PAU 1999 Sèrie 1 Qüestió 1: Resoleu el sistema següent per als valors de k que el facin compatible.
 PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010
 Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
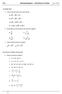 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2005
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
ANÁLISIS. 1 Junio Junio 98. y = 1al dar vuelta
 ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 2005 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
GEOMETRIA ANALÍTICA DEL PLA. MATEMÀTIQUES-1
 GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Exercici 2: Exercici 3: OPCIÓ A OPCIÓ B OPCIÓ A OPCIÓ B OPCIÓ A OPCIÓ B Etiqueta identificadora
Proves dʼaccés a la Universitat. Curs 2009-2010 Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Exercici 2: Exercici 3: OPCIÓ A OPCIÓ B OPCIÓ A OPCIÓ B OPCIÓ A OPCIÓ B Etiqueta identificadora
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 PAU SÈRIE 3 Pautes de correcció (PAU 2002) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
Problemes d optimització de les Pau s de València
 Problemes d optimització de les Pau s de València 00-01 Problema 1 Siga T un triangle de perímetre 60cm. Un dels costats del triangle T té x cm i els altres dos costats tenen la mateixa longitud. a) Obteniu
Problemes d optimització de les Pau s de València 00-01 Problema 1 Siga T un triangle de perímetre 60cm. Un dels costats del triangle T té x cm i els altres dos costats tenen la mateixa longitud. a) Obteniu
Districte Universitari de Catalunya
 Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
Proves d accés a la universitat Convocatòria 2014 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Opció B Exercici 2: Opció A Opció B Exercici 3: Opció A Opció B Qualificació 1
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2007-2008 Dibuix tècnic Sèrie 2 Indiqueu les opcions triades: Exercici 2: Exercici 3: Opció A Opció B Opció A Opció B Etiqueta identificadora de lʼalumne/a Etiqueta
Proves dʼaccés a la Universitat. Curs 2007-2008 Dibuix tècnic Sèrie 2 Indiqueu les opcions triades: Exercici 2: Exercici 3: Opció A Opció B Opció A Opció B Etiqueta identificadora de lʼalumne/a Etiqueta
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
Col legi Maristes Sants-Les Corts. Departament de matemàtiques. té per asímptotes les rectes =
 Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades:
 Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1
Proves d accés a la universitat Convocatòria 2016 Dibuix tècnic Sèrie 3 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1
Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Convocatòria 2017
 Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1 Exercicis 2 3 Suma
Proves d accés a la universitat Dibuix tècnic Sèrie 1 Indiqueu les opcions triades: Exercici 1: Opció A Exercici 2: Opció A Exercici 3: Opció A Opció B Opció B Opció B Qualificació 1 Exercicis 2 3 Suma
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
IES CTEIB. Departament de Matemàtiques. Matemàtiques II. Problemes proposats en les PAU. José Luis Bernal Garcías. Curs
 IES CTEIB Departament de Matemàtiques Matemàtiques II Problemes proposats en les PAU José Luis Bernal Garcías Curs 016-17 Índex 1 Límits, continuïtat i derivabilitat 5 1.1 Enunciats.................................................
IES CTEIB Departament de Matemàtiques Matemàtiques II Problemes proposats en les PAU José Luis Bernal Garcías Curs 016-17 Índex 1 Límits, continuïtat i derivabilitat 5 1.1 Enunciats.................................................
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
Tècniques elementals de
 Dept. Matemàtica Aplicada IV Tècniques elementals de Càlcul i Àlgebra Exercicis bàsics Presentació Aquest document va adreçat als estudiants de nou ingrés de les escoles d enginyeria en les quals imparteix
Dept. Matemàtica Aplicada IV Tècniques elementals de Càlcul i Àlgebra Exercicis bàsics Presentació Aquest document va adreçat als estudiants de nou ingrés de les escoles d enginyeria en les quals imparteix
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU z y 2
 Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 014 SÈRIE 3 1. En Pol, la Júlia i la Maria han comprat un regal. La Júlia ha gastat la meitat que la Maria, i en Pol n ha gastat el triple que la Júlia.
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 014 SÈRIE 3 1. En Pol, la Júlia i la Maria han comprat un regal. La Júlia ha gastat la meitat que la Maria, i en Pol n ha gastat el triple que la Júlia.
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Matemàtiques 1 - FIB
 Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
f =. El pendent de la recta tangent
 Oficina d'organització de Proves d'accés a la Universitat Pàgina 1 de 11 PAU 004 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d'organització de Proves d'accés a la Universitat Pàgina 1 de 11 PAU 004 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2008
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 008 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 008 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d'organització de Proves d'accés a la Universitat Pàgina 1 de 8 PAU 2004
 Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
