Escuela Técnica Superior de Ingenieros de Telecomunicación. Electrónica. Prueba parcial JUEVES, 9 DE DICIEMBRE DE 1999
|
|
|
- Luz Rey Miguélez
- hace 5 años
- Vistas:
Transcripción
1 Escuela écnca Superor de Ingeneros de elecomuncacón. Electrónca. Prueba parcal JUEES, 9 DE DICIEMBE DE 1999 pelldos: Nombre: Cuestón 1 Dbujar el esquemátco del modelo en pequeña señal de un dodo. Indcar para qué se utlza. (1,5 puntos) Solucón El esquemátco en pequeña señal es r d C DQ este esquemátco se utlza para calcular la relacón funconal entre los ncrementos de corrente y de tensón entre los termnales del dodo cuando las varacones son pequeñas y nos permte separarlas de los valores de tensón y corrente contnuas del crcuto. 1
2 Cuestón 2 Para cada uno de los crcutos de la fgura la tensón de entrada es y. Consderar que "! y dbujar, cualtatvamente, la forma de onda de salda de cada uno de ellos. (1,5 puntos) v v v (a) (b) (c) (d) v Solucón En todos los crcutos anterores tenendo en cuenta que no tenemos el dato de # podemos suponer que el dodo nunca estará en la regón zener y por tanto el crcuto equvalente del dodo en drecta será γ s y cuando esté en nversa será como sempre un crcuto aberto, por tanto en cada uno de los crcutos deberemos ver cuando está en drecta y en nversa. Empecemos por el crcuto (a). La tensón de salda será $&%'($ ) cuando el dodo no esté conducendo ya que la corrente será cero y por tanto no cae tensón en la resstenca y $*%'(,/ cuando el dodo conduzca. El valor de $*) para el que se produce el cambo de conduccón a corte será cuando $&89':24 ya que en ese momento no hay corrente, por tanto s resolvemos la malla del crcuto nos queda $*);'<26=02>4 para tencones en el generador superores a esa el dodo estará en conduccón y para valores menores estará en corte, así pues $*%?'@$*) $&%?'(,/.B02>45026 CED $*)GFH26I02>4 D $ )KJ(26I02>4 la forma de onda de salda está clara cuando estamos en corte y cuando estamos en conduccón?. S calculamos la corrente que crcula por el crcuto es este caso tenemos que G' $ )7LM26NLO24,0,P. 2
3 t y s susttumos *Q? * > SS/U S/UB s SPU es mucho menor que que es lo habtual el prmer termno desaparece y la forma de onda queda o γ s /W no es tan pequeño entonces tenemos un dvsor de tensón que se quedará con parte de la tensón que cae en la resstenca con lo cual la forma de onda será o γ Cualquera de las dos solucones se da como válda. El resto de los crcuto una vez hecho este son nmedatos, en el caso del (d) vemos que los componentes son los msmos y el dodo está en la msma dreccón en la malla por tanto los valores de X*Y para conduccón y corte del dodo serán los msmos. Cuanto vale X&Z?. Pues en este caso. X*Z5[@\] X*Z[_^`ba\c]d[fehgj kml> kon ] pc] q `Ha\c]srut X YKvH\]wa\>x X Yzy@\]wa\>x por tanto cuando el dodo esté en corte la tensón de salda es \c] y cuando está en conduccón (` {}`/~ ) la forma de onda queda X&Z[(X Y\ x
4 Ž t γ o en caso de que /W no sea tan pequeño tenemos gual el dvsor de tensón y el pco de señal sería un poco más bajo pero la forma de onda sería la msma. eamos ahora el crcuto (b), es como el (d) salvo que el dodo está puseto en la dreccón opuesta, así pues la solucón será como en el (d) pero cambando el sgno de y las zonas de conduccón y corte, así pues ƒ* ƒ* _ f hšj Œm ŽcŒ Hˆ c bˆ s E ƒ z ƒ zš > N por tanto cuando el dodo esté en corte la tensón de salda es c y cuando está en conduccón ( }/W ) la forma de onda queda o ƒ& _ƒ ˆ γ Fnalmente queda el crcuto (c) y será como el (a) pero cambando tambén los sgnos de \ x y las zonas de conduccón y corte. de forma que nos queda X*Z[_X Y X*Z5[_^`/~K\ xœa\c] ret s `/~ es mucho menor que la forma de onda queda X*YG _\c]n\ x X YKž@\c]NO\ x 4
5 o γ 5
6 Problema 1 Para el crcuto de la fgura, calcular: 1. Las tensones en todos los nodos. (1 punto) 2. El equvalente hévenn vsto desde los termnales B. (1 punto). La potenca entregada por todos los elementos del crcuto. Indcar s se conserva la energía por undad de tempo. (1 punto) 10Ω 6 4Ω 4Ω P1 2 B Ω 1 Solucón Cálculo de las tensones en todos los nodos. Para calcular las tensones en todos los nodos vamos a defnr los nodos y a decdr cual es nuestro nodo de referenca, podemos verlo en la sguente fgura Ν 10Ω Ν Ν Ν a b c d 6 4Ω 4Ω Ν e 2 Ω 1 donde el Ÿ lo vamos a poner como referenca. En la fgura tambén hemos redbujado una resstenca para aprecar ben que hay dos resstencas de en paralelo. amos a calcular los valores de las tensones, para ello ncalmente vamos a asocar las dos resstencas de en paralelo resultando una de &. demás vamos a resolver el problema medante la ley de nudos (para ello los hemos puesto), por lo que damos nombre a las correntes 6
7 ª ª Ν 10Ω Ν Ν Ν a b c d 6 a b c 2 d Ω e 1 y planteamos las ecuacones de los nodos y que son los úncos en los que confluye 7 ª«ª ªG ± sustuttumos cada corrente por su valor y nos queda más de una corrente y además una ecuacón adconal por la exstenca de una fuente ndependente ª ª 7²c³ 7² µ u m»h¼ ³o º¹ m ³o»h¼ m ½ m»h¼ ³ m¾»h¼ m¾»h¼ ½ m Àh¼ º¹ m¾ À Á ² ³ ² tenemos dos ecuacones con tres ncogntas pero podemos poner otra relacón s despejamos obtenemos que y de aquí sacamos el resto de los valores ²³ ² 7² 7² ³ à ² ² ª«²cÅ 7² µ à Equvalente hévenn Para este cálculo necestamos cæèç y S ÆÈÇ, el crcuto que tenemos s reorganzamos la gráfca es el que sgue 6 10Ω Ω 2 b 2 Ω 1 B 7
8 Ë S Ä Ã Ä Ã así que tenemos que la cæèç es la tensón que hay entre los nodos B (vamos a calcular por smplcdad la tensón B ya que la referenca la elegmos en ), pero ya conocemos la tensón del nodo B respecto a, ya que lo calculamos en el apartado anteror, este nodo es el que antes llamamos y por tanto ÆÈÇ 7É 7² nos queda la S ÆÈÇ para calcularla anularemos las fuentes ndependentes y ÆÈÇ?Ê&Ë donde e I están expresadas en la fgura 10Ω Ω 1 I por la resstenca de no va a pasar corrente y por tanto no nfluye en nuestro crcuto, s aplcamos la ley de Krchoff para las correntes para el nodo con tensón ± Ë Ì 7 Ì Ä además tenemos que hay una relacón entre 7 y dadas por un dvsor de tensón entre las dos resstencas de & 7 & ± y por tanto s susttumos en la ecuacón anteror tenemos Ë Ì Ì S ÆÈÇ s hubesemos calculado los valores entre los nodos B tendríamos que cæèç tendría el sgno cambado pero S ÆÈÇ valdría lo msmo. Fnalmente nos queda el cálculo de las potencas para cada uno de los componentes y ya que conocemos las tensones de todos los nodos es smple el cálculo 1 1 odas las tensones han sdo consderadas postvas, el sgno de la corrente dependerá de s la corrente entra por el termnal postvo (postva) o por el negatvo (negatva) Ä Ì Ä 8
9 Ä Ä Ì ««Componente esstenca ensón Corrente P. entregada P. Consumda Fuente de W. de W 1 a. de Ä W 2 a. de Ä ± & W. de 4 2 8W. de Ì W Fuente de W Fuente dependente W Potenca total 408W 408W como vemos las potencas entregadas y y consumdas son guales y por tanto se conserva la energía por undad de tempo. 9
10 ª ª Problema 2 En el crcuto rectfcador de la fgura se pde: 1. La expresón matemátca de la señal de salda Qz. ( puntos) 2. Dbujar la forma de onda de Qz Í. (1 punto) Los valores de los componentes son: Dodo deal, L=50mH; S S v D L c v o () t(s) P2 Solucón En este problema tratamos la carga y descarga de corrente en una bobna y para ello tenemos que conocer las correntes ncales y fnales para cada carga o descarga y los valores de la resstenca a través de la que se producrá esta carga o descarga. eamos cuales con las condcones ncales y fnales del crcuto para cada valor de tensón. En el nstante t=0 la corrente por la bobna será 0, ya que el sstema está en reposo, las condcones ncales son pues ªÎ ( cuando el generador de tensón tene un valor * = el dodo estará en drecta, ya que la corrente crcula en la dreccón de conduccón del dodo, y como es deal será un cortocrcuto, así pues el crcuto queda como 1 2 L c la tensón sobre la resstenca es ya que comparte el nodo con la fuente de tensón, así pues la corrente que pasa por la bobna ( y cuando lleguemos al regmen estaconaro la corrente será ªÏÎ À ) es la msma que pasa por la resstenca S À 10 S
11 ª ª ¹ ª Ü Ê ª S Ü Ê S ya que la bobna se comportará como un cortocrcuto, la ecuacón para el tramo de tempo entre 0s y 0.1s será ªÏÎ Í Ð ªÎ ªÏÎ ÒÑ K( Í ÓQm K ªÏÎ ÒÑ >ÔÖÕ ÙØ ÚÛ ÓQ ±Ý ªÎ S ( S ÚÞ >ÔÖÕ ÙØ Ý fß ÞÔmÕ ß à&ádâ>ãbã las condcones fnales de este tramo son smples ya que como la constante de tempo es ä à&ádâ así pues tenemos que la carga completa se realzará en Ä ä ªÎ ÒÑ* å y entonces conocemos la tensón de salda y Í Ð ªÎ S ß ªÏÎ æômõ> ß > &Qç ÒÑ* å@ *Qè Ï â S ádâ à&ádâ ãbã ß å que es mucho menos que 0.1s, æôöõ ß à&ádâ ãzã hora vamos a por el tramos desde 0.1 a 0.2s, ya conocemos las condcones ncales, veamos ahora el crcuto que tenemos. Como la corrente de la fuente ahora camba de sentdo ya que camba su polardad el dodo estará cortado y se comportará como un crcuto aberto, el crcuto que nos queda es pues ahora» e 2 L c À son las úncas correntes y según la ley de Krchoff de las correntes tenemos À» ( así pues podemos pntar el crcuto de la sguente forma L c 11
12 ¹ Ü podemos ver que los tres elementos (la bobna y las dos resstencas) están recorrdos por la msma corrente lo que sgnfca que están en sere. demá conocemos la corrente ncal (que la fnal del otro tramo) y la fnal de este que es de 0 ya que no hay almentacón. sí pues la ecuacón de la corrente en la bobna será ªÎ (é( S Mê >ÔÖÕ dø GM> Ê SS Ý ÔmÕ ß Gæ> à&ádâåã las condcones fnales de este tramo son smples ya que como la constante de tempo es ä à&ádâ tenemos que la carga completa se realzará en Ä ä ádâ así pues ªÎ ªÏÎ ÒÑ* å > â ( que es mucho menos que 0.1s, y entonces conocemos la tensón de salda y Í å ªÎ S ÔÖÕ ß GM> à*ádâ ã *Qè Í ÒÑ& å( &Qç Ï> hora ya podemos representar la ÔÖÕ ß à&ádâ ã v t(s) 12
Tallerine: Energías Renovables. Fundamento teórico
 Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO.
 APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO. Dado un numero n de puntos del plano ( a, b ) es posble encontrar una funcón polnómca
APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO. Dado un numero n de puntos del plano ( a, b ) es posble encontrar una funcón polnómca
El diodo Semiconductor
 El dodo Semconductor J.I. Hurcán Unversdad de La Frontera Aprl 9, 2012 Abstract Se plantean procedmentos para analzar crcutos con dodos. Para smpl car el trabajo, el dodo semconductor es reemplazado por
El dodo Semconductor J.I. Hurcán Unversdad de La Frontera Aprl 9, 2012 Abstract Se plantean procedmentos para analzar crcutos con dodos. Para smpl car el trabajo, el dodo semconductor es reemplazado por
Bloque 2 Análisis de circuitos alimentados en corriente continua. Teoría de Circuitos
 Bloque Análss de crcutos almentados en corrente contnua Teoría de Crcutos . Métodos sstemátcos de resolucón de crcutos : Método de mallas Métodos sstemátcos de resolucón de crcutos Permten resolver los
Bloque Análss de crcutos almentados en corrente contnua Teoría de Crcutos . Métodos sstemátcos de resolucón de crcutos : Método de mallas Métodos sstemátcos de resolucón de crcutos Permten resolver los
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
Figura 22. Diagrama en bloques de un generador triangular.
 GENEADOES DE ONDA TIANGULA En la fgura 22 se puede aprecar el dagrama de bloques de un crcuto generador onda trangular, este crcuto es uno de los más smples, y es porque se dspone de un generador onda
GENEADOES DE ONDA TIANGULA En la fgura 22 se puede aprecar el dagrama de bloques de un crcuto generador onda trangular, este crcuto es uno de los más smples, y es porque se dspone de un generador onda
Capítulo 3 Unidad de Potencia
 apítulo 3 Undad de Potenca Una fuente de almentacón de corrente drecta cd converte la energía de una línea de corrente alterna ca en corrente contnua ó drecta, que es una voltaje constante a un valor deseado.
apítulo 3 Undad de Potenca Una fuente de almentacón de corrente drecta cd converte la energía de una línea de corrente alterna ca en corrente contnua ó drecta, que es una voltaje constante a un valor deseado.
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
El circuito eléctrico de la figura está formado por un conjunto de Resistencias, condensadores, bobinas y una fuente de tensión.
 El crcuto eléctrco de la fgura está formado por un conjunto de esstencas, condensadores, bobnas y una fuente de tensón. L L Para el sstema de la fgura, se pde: Modelo de bond graph del sstema, ncluyendo
El crcuto eléctrco de la fgura está formado por un conjunto de esstencas, condensadores, bobnas y una fuente de tensón. L L Para el sstema de la fgura, se pde: Modelo de bond graph del sstema, ncluyendo
PRÁCTICA Nº 5. CIRCUITOS DE CORRIENTE CONTINUA
 PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
PÁCTICA Nº 5. CICUITOS DE COIENTE CONTINUA OBJETIVO Analzar el funconamento de dferentes crcutos resstvos empleando la Ley de Ohm y las Leyes de Krchhoff. FUNDAMENTO TEÓICO Corrente Eléctrca Una corrente
Tema 3. Teoremas de la Teoría de Circuitos
 Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton 3.6 Máxma transferenca de potenca Th Th L nálss de Crcutos
Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton 3.6 Máxma transferenca de potenca Th Th L nálss de Crcutos
Problemas resueltos. Problema 6.1. E e1 R4 B R3. D Figura P6.1. Para la red de la figura P6.1:
 1 Problemas resueltos. Problema 6.1 Para la red de la fgura P6.1: j R e Fgura P6.1. a) etermnar la red pasa Norton entre y, sta por la resstenca. b) etermnar la fuente equalente Théenn entre y, sta por
1 Problemas resueltos. Problema 6.1 Para la red de la fgura P6.1: j R e Fgura P6.1. a) etermnar la red pasa Norton entre y, sta por la resstenca. b) etermnar la fuente equalente Théenn entre y, sta por
RESISTENCIAS EN SERIE Y LEY DE LAS MALLAS V 1 V 2 V 3 A B C
 RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
Sistemas Lineales de Masas-Resortes 2D
 Sstemas neales de Masas-Resortes D José Cortés Pareo. Novembre 7 Un Sstema neal de Masas-Resortes está consttudo por una sucesón de puntos (de ahí lo de lneal undos cada uno con el sguente por un resorte
Sstemas neales de Masas-Resortes D José Cortés Pareo. Novembre 7 Un Sstema neal de Masas-Resortes está consttudo por una sucesón de puntos (de ahí lo de lneal undos cada uno con el sguente por un resorte
TEMA 8 CIRCUITOS SIMPLES EN REGIMEN ESTACIONARIO SENOIDAL
 TEMA 8 UTOS SMPLES EN EGMEN ESTAONAO SENODAL TEMA 8:UTOS SMPLES EN EGMEN ESTAONAO SENODAL 8. ntroduccón 8. espuesta senodal de los elemetos báscos: espuesta del crcuto espuesta del crcuto L espuesta del
TEMA 8 UTOS SMPLES EN EGMEN ESTAONAO SENODAL TEMA 8:UTOS SMPLES EN EGMEN ESTAONAO SENODAL 8. ntroduccón 8. espuesta senodal de los elemetos báscos: espuesta del crcuto espuesta del crcuto L espuesta del
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
Matemáticas II. Segundo Curso, Grado en Ingeniería Electrónica Industrial y Automática Grado en Ingeniería Eléctrica. 17 de febrero de
 Matemátcas II Segundo Curso, Grado en Ingenería Electrónca Industral y Automátca Grado en Ingenería Eléctrca 7 de febrero de 0. Conteste las sguentes cuestones: Ã! 0 (a) (0.5 ptos.) Escrba en forma bnómca
Matemátcas II Segundo Curso, Grado en Ingenería Electrónca Industral y Automátca Grado en Ingenería Eléctrca 7 de febrero de 0. Conteste las sguentes cuestones: Ã! 0 (a) (0.5 ptos.) Escrba en forma bnómca
Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Solucón. Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador,
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Solucón. Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador,
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
sea un nº real. Hallar su cociente. Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
sea un nº real. Hallar su cociente. Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
Circuitos eléctricos en corriente continúa. Subcircuitos equivalentes Equivalentes en Serie Equivalentes en Paralelo Equivalentes de Thevenin y Norton
 ema II Crcutos eléctrcos en corrente contnúa Indce Introduccón a los crcutos resstvos Ley de Ohm Leyes de Krchhoff Ley de correntes (LCK) Ley de voltajes (LVK) Defncones adconales Subcrcutos equvalentes
ema II Crcutos eléctrcos en corrente contnúa Indce Introduccón a los crcutos resstvos Ley de Ohm Leyes de Krchhoff Ley de correntes (LCK) Ley de voltajes (LVK) Defncones adconales Subcrcutos equvalentes
Números Reales y Complejos
 Apéndce C Números Reales Complejos Ejerccos resueltos Halla los números reales que cumplen la condcón a a S a 0 : a a a 0 No este solucón S a < 0 : a a a a Halla todos los números r tales que r < a) S
Apéndce C Números Reales Complejos Ejerccos resueltos Halla los números reales que cumplen la condcón a a S a 0 : a a a 0 No este solucón S a < 0 : a a a a Halla todos los números r tales que r < a) S
3.1 Resolver mediante el método de la transformada de Laplace el problema 1.1.
 rcutos y Sstemas Dnámcos Ejerccos tema 3 Método de la transformada de aplace 3. esolver medante el método de la transformada de aplace el problema.. 3. esolver medante el método de la transformada de aplace
rcutos y Sstemas Dnámcos Ejerccos tema 3 Método de la transformada de aplace 3. esolver medante el método de la transformada de aplace el problema.. 3. esolver medante el método de la transformada de aplace
UNIVERSIDAD SIMON BOLIVAR Departamento de Conversión y Transporte de Energía Sección de Máquinas Eléctricas Prof. E. Daron B. REGIMEN DESBALANCEADO DE
 UVESDAD SMO BOLVA Seón de Máqunas Eléctrcas Prof. E. Daron B. EGME DESBALACEADO DE Hoja º 77 TASFOMADOES TFASCOS 4.6 Transformadores trfáscos con cargas desbalanceadas: 4.6 Conexón Estrella-Estrella sn
UVESDAD SMO BOLVA Seón de Máqunas Eléctrcas Prof. E. Daron B. EGME DESBALACEADO DE Hoja º 77 TASFOMADOES TFASCOS 4.6 Transformadores trfáscos con cargas desbalanceadas: 4.6 Conexón Estrella-Estrella sn
Problemas Adicionales. Capítulo 3: Diodos (II)
 Problemas dconales. Capítulo : Dodos (II). Problemas esueltos de Componentes y Crcutos Electróncos. E. Fgueres, M. Pascual, J.. Martínez e I. Mró. SPUPV- 000.475 Problema _er Problemas dconales. Capítulo
Problemas dconales. Capítulo : Dodos (II). Problemas esueltos de Componentes y Crcutos Electróncos. E. Fgueres, M. Pascual, J.. Martínez e I. Mró. SPUPV- 000.475 Problema _er Problemas dconales. Capítulo
Figura 1
 5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
5 Regresón Lneal Smple 5. Introduccón 90 En muchos problemas centífcos nteresa hallar la relacón entre una varable (Y), llamada varable de respuesta, ó varable de salda, ó varable dependente y un conjunto
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA
 EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
EL MÉTODO DE DIFERENCIAS FINITAS POR GUILLERMO HERNÁNDEZ GARCÍA . El Método de Dferencas Fntas El Método consste en una aproxmacón de las dervadas parcales por expresones algebracas con los valores de
+ V i - V o - Filtro Supresor de Banda
 Fltro Supresor de Banda Los fltros supresor de banda o banda de atenuacón tambén se construyen usando un fltro pasa bajos y uno pasa altos. Sn embargo, en lugar de la confguracón en cascada empleada para
Fltro Supresor de Banda Los fltros supresor de banda o banda de atenuacón tambén se construyen usando un fltro pasa bajos y uno pasa altos. Sn embargo, en lugar de la confguracón en cascada empleada para
Unidad 6-. Números complejos 1
 Undad -. Números complejos ACTIVIDADES FINALES EJERCICIOS Y PROBLEMAS Efectúa las sguentes operacones: aa (-(-(- aa (-(-(- cc ( -(-( bb ( ( - - (- 7 dd ( - - (- / ( - ( ( (. ( Sumamos algebracamente por
Undad -. Números complejos ACTIVIDADES FINALES EJERCICIOS Y PROBLEMAS Efectúa las sguentes operacones: aa (-(-(- aa (-(-(- cc ( -(-( bb ( ( - - (- 7 dd ( - - (- / ( - ( ( (. ( Sumamos algebracamente por
PRÁCTICA 4. INDUCCIÓN ELECTROMAGNÉTICA. A. Observación de la fuerza electromotriz inducida por la variación de flujo magnético
 A. Observacón de la fuerza electromotrz nducda por la varacón de flujo magnétco Objetvo: Observacón de la presenca de fuerza electromotrz en un crcuto que sufre varacones del flujo magnétco y su relacón
A. Observacón de la fuerza electromotrz nducda por la varacón de flujo magnétco Objetvo: Observacón de la presenca de fuerza electromotrz en un crcuto que sufre varacones del flujo magnétco y su relacón
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
1 Magnitudes y circuitos eléctricos.
 Magntudes y crcutos eléctrcos.. Introduccón Alguna vez nos habremos preguntado porqué funconan como lo hacen los aparatos de rado, las calculadoras de bolsllo, o los ordenadores. Estas máqunas, y muchas
Magntudes y crcutos eléctrcos.. Introduccón Alguna vez nos habremos preguntado porqué funconan como lo hacen los aparatos de rado, las calculadoras de bolsllo, o los ordenadores. Estas máqunas, y muchas
ELECTRÓNICA Y AUTOMATISMOS
 ELECTRÓNICA Y AUTOMATISMOS 2º Curso de Instalacones Electromecáncas Mneras Tema 2: Electrónca Analógca Amplfcadores operaconales Profesor: Javer Rbas Bueno Electrónca analógca: Conceptos generales de amplfcacón
ELECTRÓNICA Y AUTOMATISMOS 2º Curso de Instalacones Electromecáncas Mneras Tema 2: Electrónca Analógca Amplfcadores operaconales Profesor: Javer Rbas Bueno Electrónca analógca: Conceptos generales de amplfcacón
Consideremos un sólido rígido sometido a un sistema de fuerzas en equilibrío, es decir
 1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
1. PRINIPIO E TRJOS VIRTULES El prncpo de los trabajos rtuales, en su ertente de desplazamentos rtuales, fue ntroducdo por John ernoull en 1717. La obtencón del msmo dera de la formulacón débl (o ntegral)
Guía de ejercicios #1
 Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
ESTÁTICA DEL SÓLIDO RÍGIDO
 DSR-1 ESTÁTICA DEL SÓLIDO RÍGIDO DSR-2 ESTÁTICA DEL SÓLIDO RÍGIDO La estátca estuda las condcones bajo las cuales los sstemas mecáncos están en equlbro. Nos referremos úncamente a equlbro de tpo mecánco,
DSR-1 ESTÁTICA DEL SÓLIDO RÍGIDO DSR-2 ESTÁTICA DEL SÓLIDO RÍGIDO La estátca estuda las condcones bajo las cuales los sstemas mecáncos están en equlbro. Nos referremos úncamente a equlbro de tpo mecánco,
http://www.rubenprofe.com.ar biofisica@rubenprofe.com.ar RESISTENCIAS EN PARALELO
 bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
ÍNDICE FUNDAMENTOS UNIDAD DIDÁCTICA 1. Capítulo 1. Presentación...15
 ÍNDICE Presentacón...5 UNIDAD DIDÁCTICA Capítulo FUNDAMENTOS. Crcuto eléctrco... 2 2. Símbolos lterales... 2 3. Convenos para el sentdo de referenca de la corrente eléctrca... 23 4. Convenos para la polardad
ÍNDICE Presentacón...5 UNIDAD DIDÁCTICA Capítulo FUNDAMENTOS. Crcuto eléctrco... 2 2. Símbolos lterales... 2 3. Convenos para el sentdo de referenca de la corrente eléctrca... 23 4. Convenos para la polardad
Sistemas de Amortización de Deudas MATEMÁTICA FINANCIERA
 Sstemas de Amortzacón de Deudas MATEMÁTICA FINANCIERA SISTEMA FRANCÉS Lus Alcalá UNSL Segundo Cuatrmeste 2016 Como hpótess ncal de trabajo suponemos que la tasa de nterés cobrada por el prestamsta (acreedor)
Sstemas de Amortzacón de Deudas MATEMÁTICA FINANCIERA SISTEMA FRANCÉS Lus Alcalá UNSL Segundo Cuatrmeste 2016 Como hpótess ncal de trabajo suponemos que la tasa de nterés cobrada por el prestamsta (acreedor)
2. ANÁLISIS DE CIRCUITOS RESISTIVOS
 . Análss de crcutos resstos Índce. Análss de crcutos resstos.. Concepto de resstenca. ANÁLISIS DE CICUITOS ESISTIVOS dos tpos de resstencas físcas Elemento resstenca.. Concepto de resstenca.. Análss de
. Análss de crcutos resstos Índce. Análss de crcutos resstos.. Concepto de resstenca. ANÁLISIS DE CICUITOS ESISTIVOS dos tpos de resstencas físcas Elemento resstenca.. Concepto de resstenca.. Análss de
TEMA 3 Amplificadores Operacionales
 TEMA 3 Amplfcadores Operaconales mbología. Característcas del amplfcador operaconal deal. Modelos. Análss de crcutos con amplfcadores operaconales deales: nversor y no nversor. Aplcacones de los amplfcadores
TEMA 3 Amplfcadores Operaconales mbología. Característcas del amplfcador operaconal deal. Modelos. Análss de crcutos con amplfcadores operaconales deales: nversor y no nversor. Aplcacones de los amplfcadores
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6a)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
Tema 3. Teoremas de la Teoría de Circuitos
 Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton V Th Th L 3.6 Máxma transferenca de potenca José. Pereda,
Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton V Th Th L 3.6 Máxma transferenca de potenca José. Pereda,
Circuito Monoestable
 NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
Continua: Corriente cuyo valor es siempre constante (no varía con el tiempo). Se denota como c.c.
 .. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
.. TIPOS DE CORRIENTES Y DE ELEMENTOS DE CIRCUITOS Contnua: Corrente cuyo valor es sempre constante (no varía con el tempo). Se denota como c.c. t Alterna: Corrente que varía snusodalmente en el tempo.
Clase 19: Estado Estacionario y Flujo de Potencia. EL Conversión de la Energía y Sistemas Eléctricos Eduardo Zamora D.
 Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
Clase 19: Estado Estacionario y Flujo de Potencia. EL Conversión de la Energía y Sistemas Eléctricos Eduardo Zamora D.
 Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
Clase 9: Estado Estaconaro y Flujo de Potenca EL400 - Conversón de la Energía y Sstemas Eléctrcos Eduardo Zamora D. Temas - Líneas de Transmsón - El Sstema Eléctrco - Matrz de Admtanca - Flujo de Potenca
EL BJT TRANSISTOR DE UNIÓN BIPOLAR
 L BJT TANSSTO D UNÓN BPOLA TPOS D TANSSTOS BJT NPN PNP onstruccón Dspostvo semconductor de tres capas: dos de materal tpo n y una tpo p, llamado transstor npn; o dos de materal tpo p y una de tpo n, llamado
L BJT TANSSTO D UNÓN BPOLA TPOS D TANSSTOS BJT NPN PNP onstruccón Dspostvo semconductor de tres capas: dos de materal tpo n y una tpo p, llamado transstor npn; o dos de materal tpo p y una de tpo n, llamado
SEGUNDA PARTE RENTAS FINANCIERAS
 SEGUNDA PARTE RENTAS FINANCIERAS 5 INTRODUCCIÓN A LA TEORÍA DE RENTAS 5.1 CONCEPTO: Renta fnancera: conjunto de captales fnanceros cuyos vencmentos regulares están dstrbudos sucesvamente a lo largo de
SEGUNDA PARTE RENTAS FINANCIERAS 5 INTRODUCCIÓN A LA TEORÍA DE RENTAS 5.1 CONCEPTO: Renta fnancera: conjunto de captales fnanceros cuyos vencmentos regulares están dstrbudos sucesvamente a lo largo de
CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED
 Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
Modelo en red para la smulacón de procesos de agua en suelos agrícolas. CAPÍTULO IV: MODELOS MATEMÁTICOS Y MODELOS EN RED IV.1 Modelo matemátco 2-D Exsten dos posbldades, no ndependentes, de acuerdo con
PROBLEMAS RESUELTOS DE MÁQUINAS DE CORRIENTE CONTINUA
 UIVERSIDAD DE CATABRIA DEARTAMETO DE IGEIERÍA ELÉCTRICA Y EERGÉTICA ROBLEMAS RESUELTOS DE MÁQUIAS DE CORRIETE COTIUA Mguel Angel Rodríguez ozueta Doctor Ingenero Industral RESETACIÓ Esta coleccón de problemas
UIVERSIDAD DE CATABRIA DEARTAMETO DE IGEIERÍA ELÉCTRICA Y EERGÉTICA ROBLEMAS RESUELTOS DE MÁQUIAS DE CORRIETE COTIUA Mguel Angel Rodríguez ozueta Doctor Ingenero Industral RESETACIÓ Esta coleccón de problemas
Amplificador Operacional Ejercicios Resueltos
 Amplfcador Operaconal. Aplcacones lneales. Amplfcador Operaconal > Segudor de tensón (buffer, adaptador de mpedancas) onsste en realmentar la entrada negata con la señal de salda e ntroducr tensón por
Amplfcador Operaconal. Aplcacones lneales. Amplfcador Operaconal > Segudor de tensón (buffer, adaptador de mpedancas) onsste en realmentar la entrada negata con la señal de salda e ntroducr tensón por
CAPITULO 3º SOLUCIÓN ECUACIÓN DE ESTADO- 01. Ing. Diego A. Patiño G. M.Sc, Ph.D.
 CAPITULO 3º SOLUCIÓN ECUACIÓN DE ESTADO- 0 Ing. Dego A. Patño G. M.Sc, Ph.D. Solucón de la Ecuacón de Estado Solucón de Ecuacones de Estado Estaconaras: Para el caso estaconaro (nvarante en el tempo),
CAPITULO 3º SOLUCIÓN ECUACIÓN DE ESTADO- 0 Ing. Dego A. Patño G. M.Sc, Ph.D. Solucón de la Ecuacón de Estado Solucón de Ecuacones de Estado Estaconaras: Para el caso estaconaro (nvarante en el tempo),
Corriente alterna. (a) no cambia, (b) el valor de X no cambia, y X L = Z sen = 433 L= 1,38 H (c) no cambia, (d) no cambia, (e) C=1,83 F; (f) no cambia
 Corrente alterna Ejercco 1: un generador de corrente alterna que entrega 100V de tensón efcaz a 50 Hz se halla conectado a un crcuto C sere. Por el crcuto crcula una corrente efcaz ef = 0,2 sen (2 50 t
Corrente alterna Ejercco 1: un generador de corrente alterna que entrega 100V de tensón efcaz a 50 Hz se halla conectado a un crcuto C sere. Por el crcuto crcula una corrente efcaz ef = 0,2 sen (2 50 t
EL AMPLIFICADOR OPERACIONAL.
 Tema 6. El mplfcador peraconal. Tema 6 EL MPLIFICD PECINL.. Introduccón... Símbolos y termnales del amplfcador operaconal... El amplfcador operaconal como amplfcador de tensón..3. Conceptos báscos de realmentacón..4.
Tema 6. El mplfcador peraconal. Tema 6 EL MPLIFICD PECINL.. Introduccón... Símbolos y termnales del amplfcador operaconal... El amplfcador operaconal como amplfcador de tensón..3. Conceptos báscos de realmentacón..4.
COMPARADOR CON AMPLIFICADOR OPERACIONAL
 COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
Universidad Simón Bolívar Conversión de Energía Eléctrica - Prof. José Manuel Aller
 Unversdad Smón Bolívar Conversón de Energía Eléctrca Prof José anuel Aller 41 Defncones báscas En este capítulo se estuda el comportamento de los crcutos acoplados magnétcamente, fjos en el espaco El medo
Unversdad Smón Bolívar Conversón de Energía Eléctrca Prof José anuel Aller 41 Defncones báscas En este capítulo se estuda el comportamento de los crcutos acoplados magnétcamente, fjos en el espaco El medo
60 EJERCICIOS de NÚMEROS COMPLEJOS
 60 EJERCICIOS de NÚMEROS COMPLEJOS. Resolver las sguentes ecuacones en el campo de los números complejos a) x -x+=0 (Soluc ) b) x +=0 (Soluc ) c) x -x+=0 (Soluc ) d) x +x+=0 (Soluc ) e) x -6x +x-6=0 (Soluc,
60 EJERCICIOS de NÚMEROS COMPLEJOS. Resolver las sguentes ecuacones en el campo de los números complejos a) x -x+=0 (Soluc ) b) x +=0 (Soluc ) c) x -x+=0 (Soluc ) d) x +x+=0 (Soluc ) e) x -6x +x-6=0 (Soluc,
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tallerine: Energías Renovables
 Tallerne: Energías Renoables Fundamento Teórco Parte III: Componentes no lneales Autores: Carlos Brozzo Carolna Cabrera Agustín Castellano Versón 0.1 Tallerne2017 Energías Renoables 2 Índce 1. Introduccón
Tallerne: Energías Renoables Fundamento Teórco Parte III: Componentes no lneales Autores: Carlos Brozzo Carolna Cabrera Agustín Castellano Versón 0.1 Tallerne2017 Energías Renoables 2 Índce 1. Introduccón
TEORÍA. PREGUNTA 1 (1 p). La ecuación del movimiento de un péndulo simple está dada por θ = A cos
 FÍIC PLICD. EXMEN FINL ORDINRIO JUNIO 16 TEORÍ PREGUNT 1 (1 p). La ecuacón el movmento e un pénulo smple está aa por θ = cos, seno = 5º. (a) Qué ángulo formará este pénulo con la vertcal cuano el tempo
FÍIC PLICD. EXMEN FINL ORDINRIO JUNIO 16 TEORÍ PREGUNT 1 (1 p). La ecuacón el movmento e un pénulo smple está aa por θ = cos, seno = 5º. (a) Qué ángulo formará este pénulo con la vertcal cuano el tempo
Método De Lazos (contenido) Ecuaciones de Lazo. Variables y ecuaciones. Fundamentos Teóricos. Teoría y Principios Establecimiento general.
 Método De Lazos (contendo) Ecuacones de Lazo Teoría y Prncpos Establecmento general Fuentes de voltajee y resstencas solamente Con fuentes de voltaje dependentes Con fuentes de corrente Reduccón Fundamentos
Método De Lazos (contendo) Ecuacones de Lazo Teoría y Prncpos Establecmento general Fuentes de voltajee y resstencas solamente Con fuentes de voltaje dependentes Con fuentes de corrente Reduccón Fundamentos
PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemático y dinámico de un mecanismo plano articulado con un grado de libertad.
 Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Electrónica Analógica. 5 Resolución de Circuitos Eléctricos. Profesor: Javier Salgado
 Electrónca Analógca 5 esolucón de Crcutos Eléctrcos Profesor: Jaer Salgado . Es un sstema tecnológco de naturaleza eléctrca formado por : CICUITO ELECTONICO Elementos aportadores de energía: Generan la
Electrónca Analógca 5 esolucón de Crcutos Eléctrcos Profesor: Jaer Salgado . Es un sstema tecnológco de naturaleza eléctrca formado por : CICUITO ELECTONICO Elementos aportadores de energía: Generan la
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
2003/2004. Boletín de Problemas MÁQUINAS ELÉCTRICAS: MÁQUINA DE CORRIENTE CONTINUA 3º DE INGENIEROS INDUSTRIALES. Dpto. de Ingeniería Eléctrica
 Dpto. de Ingenería Eléctrca E.T.S. de Ingeneros Industrales Unversdad de Valladold 2003/2004 MÁQUINAS ELÉCTRICAS: MÁQUINA DE CORRIENTE CONTINUA 3º DE INGENIEROS INDUSTRIALES Boletín de Problemas MÁQUINA
Dpto. de Ingenería Eléctrca E.T.S. de Ingeneros Industrales Unversdad de Valladold 2003/2004 MÁQUINAS ELÉCTRICAS: MÁQUINA DE CORRIENTE CONTINUA 3º DE INGENIEROS INDUSTRIALES Boletín de Problemas MÁQUINA
CAPÍTULO 5 MÉTODO DE LA FUNCIÓN ELÍPTICA DE JACOBI
 CAPÍTULO 5: MÉTODO DE LA FUNCIÓN ELÍPTICA DE JACOBI 57 CAPÍTULO 5 MÉTODO DE LA FUNCIÓN ELÍPTICA DE JACOBI 5. Resumen Se busca solucón a las ecuacones acopladas que descrben los perfles de onda medante
CAPÍTULO 5: MÉTODO DE LA FUNCIÓN ELÍPTICA DE JACOBI 57 CAPÍTULO 5 MÉTODO DE LA FUNCIÓN ELÍPTICA DE JACOBI 5. Resumen Se busca solucón a las ecuacones acopladas que descrben los perfles de onda medante
UNIDAD 12: Distribuciones bidimensionales. Correlación y regresión
 Matemátcas aplcadas a las Cencas Socales UNIDAD 1: Dstrbucones bdmensonales. Correlacón regresón ACTIVIDADES-PÁG. 68 1. La meda la desvacón típca son: 1,866 0,065. Los jugadores que se encuentran por encma
Matemátcas aplcadas a las Cencas Socales UNIDAD 1: Dstrbucones bdmensonales. Correlacón regresón ACTIVIDADES-PÁG. 68 1. La meda la desvacón típca son: 1,866 0,065. Los jugadores que se encuentran por encma
Circuitos y Sistemas Dinámicos Ejercicios tema 4 Respuesta en frecuencia y circuitos resonantes
 rcutos y Sstemas Dnámcos Ejerccos tema 4 espuesta en frecuenca y crcutos resonantes 4. Dada la sguente funcón de transferenca: G(j ω ) 5jω (jω.5) (j ω ) 4jω Escrbrla en forma estándar. b) Trazar el dagrama
rcutos y Sstemas Dnámcos Ejerccos tema 4 espuesta en frecuenca y crcutos resonantes 4. Dada la sguente funcón de transferenca: G(j ω ) 5jω (jω.5) (j ω ) 4jω Escrbrla en forma estándar. b) Trazar el dagrama
En el circuito de la figura se han determinado los siguientes valores:
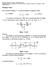 Probleas Adconales. Capítulo 7: Aplfcadores FET Probleas esueltos de Coponentes y Crcutos Electróncos. E. Fgueres, M. Pascual, J.A. Martínez e I. Mró. Problea 7.1er1 En el crcuto de la fgura 7.1.1 se han
Probleas Adconales. Capítulo 7: Aplfcadores FET Probleas esueltos de Coponentes y Crcutos Electróncos. E. Fgueres, M. Pascual, J.A. Martínez e I. Mró. Problea 7.1er1 En el crcuto de la fgura 7.1.1 se han
Utilizar sumatorias para aproximar el área bajo una curva
 Cálculo I: Guía del Estudante Leccón 5 Apromacón del área bajo la curva Leccón 5: Apromacón del área bajo una curva Objetvo: Utlzar sumatoras para apromar el área bajo una curva Referencas: Stewart: Seccón
Cálculo I: Guía del Estudante Leccón 5 Apromacón del área bajo la curva Leccón 5: Apromacón del área bajo una curva Objetvo: Utlzar sumatoras para apromar el área bajo una curva Referencas: Stewart: Seccón
Tema 6. Estadística descriptiva bivariable con variables numéricas
 Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
Clase 6 Tema 6. Estadístca descrptva bvarable con varables numércas Estadístca bvarable: tpos de relacón Relacón entre varables cuanttatvas Para dentfcar las característcas de una relacón entre dos varables
v i CIRCUITOS ELÉCTRICOS (apuntes para el curso de Electrónica)
 IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
TEMA 6 AMPLIFICADORES OPERACIONALES
 Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
315 M/R Versión 1 Integral 1/ /1 UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA
 35 M/R Versón Integral / 28/ UNIVERSIDAD NACIONAL AIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA MODELO DE RESPUESTA ASIGNATURA: Investgacón de Operacones I CÓDIGO: 35 MOMENTO: Prueba Integral FECHA DE
35 M/R Versón Integral / 28/ UNIVERSIDAD NACIONAL AIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA MODELO DE RESPUESTA ASIGNATURA: Investgacón de Operacones I CÓDIGO: 35 MOMENTO: Prueba Integral FECHA DE
PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I
 PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I 1. Objetvo El objetvo de esta práctca es el estudo del funconamento del amplfcador operaconal, en partcular de dos de sus montajes típcos que son como amplfcador
PRÁCTICA 11. AMPLIFICADOR OPERACIONAL I 1. Objetvo El objetvo de esta práctca es el estudo del funconamento del amplfcador operaconal, en partcular de dos de sus montajes típcos que son como amplfcador
Pista curva, soporte vertical, cinta métrica, esferas metálicas, plomada, dispositivo óptico digital, varilla corta, nuez, computador.
 ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
ITM, Insttucón unverstara Guía de Laboratoro de Físca Mecánca Práctca : Colsones en una dmensón Implementos Psta curva, soporte vertcal, cnta métrca, eseras metálcas, plomada, dspostvo óptco dgtal, varlla
SISTEMAS DE ECUACIONES DIFERENCIALES
 DIVISIÓN DE CIENCIAS FÍSICAS Y MATEMÁTICAS DTO. TERMODINÁMICA Y FENÓMENOS DE TRANSFERENCIA MÉTODOS AROXIMADOS EN ING. QUÍMICA TF-33 SISTEMAS DE ECUACIONES DIFERENCIALES Esta guía fue elaborada por: rof.
DIVISIÓN DE CIENCIAS FÍSICAS Y MATEMÁTICAS DTO. TERMODINÁMICA Y FENÓMENOS DE TRANSFERENCIA MÉTODOS AROXIMADOS EN ING. QUÍMICA TF-33 SISTEMAS DE ECUACIONES DIFERENCIALES Esta guía fue elaborada por: rof.
TTL LSTTL ALSTTL CMOS HCMOS
 TECNOLOGÍA ELECTRÓNICA TEMAS 9 Y 10 CMOS Y TTL EJEMPLOS RESUELTOS JULIO BRÉGAINS, DANIEL IGLESIA, JOSÉ LAMAS DEPARTAMENTO DE ELECTRÓNICA E SISTEMAS FACULTADE DE INFORMÁTICA, UNIERSIDADE DA CORUÑA Pensa
TECNOLOGÍA ELECTRÓNICA TEMAS 9 Y 10 CMOS Y TTL EJEMPLOS RESUELTOS JULIO BRÉGAINS, DANIEL IGLESIA, JOSÉ LAMAS DEPARTAMENTO DE ELECTRÓNICA E SISTEMAS FACULTADE DE INFORMÁTICA, UNIERSIDADE DA CORUÑA Pensa
CORRIENTE CONTINUA Y ALTERNA: TEOREMAS FUNDAMENTALES Y METODOS GENERALES DE ANÁLISIS Y CÁLCULO DE CIRCUITOS.
 E L E T D D OENTE ONTN Y LTEN: TEOEMS FNDMENTLES Y METODOS GENELES DE NÁLSS Y ÁLLO DE TOS. Ω Ω Ω V V VV Ω Ω VV Ω V s u(t) Ω L mh u Z - jω u(t) u. E. S. N D É S D E V N D E L V J. Garrgós ul TENOLOGÍ NDSTL
E L E T D D OENTE ONTN Y LTEN: TEOEMS FNDMENTLES Y METODOS GENELES DE NÁLSS Y ÁLLO DE TOS. Ω Ω Ω V V VV Ω Ω VV Ω V s u(t) Ω L mh u Z - jω u(t) u. E. S. N D É S D E V N D E L V J. Garrgós ul TENOLOGÍ NDSTL
Problemas de Control e Instrumentación de procesos químicos 4º Ingeniería Química
 Problemas de Control e Instrumentacón de procesos químcos 4º Ingenería Químca Problema 9 La presón de un sstema de almacenamento de un certo gas se regula por medo de un sstema como el reflejado en la
Problemas de Control e Instrumentacón de procesos químcos 4º Ingenería Químca Problema 9 La presón de un sstema de almacenamento de un certo gas se regula por medo de un sstema como el reflejado en la
Resolución Numérica de Problemas de Transmisión de Calor. Método de las diferencias finitas.
 Resolucón Numérca de Problemas de ransmsón de Calor. Método de las dferencas fntas.. Dvsón del espaco consderado en una sere de elementos cuas propedades venen representadas por un punto central (nodo)..
Resolucón Numérca de Problemas de ransmsón de Calor. Método de las dferencas fntas.. Dvsón del espaco consderado en una sere de elementos cuas propedades venen representadas por un punto central (nodo)..
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades 5 4.3 Carga y corrente.4 Tensón.5 Potenca y energía 3.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades 5 4.3 Carga y corrente.4 Tensón.5 Potenca y energía 3.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de
TRABAJO Y ENERGÍA INTRODUCCIÓN. requiere como varia la fuerza durante el movimiento. entre los conceptos de fuerza y energía mecánica.
 TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
TRABAJO Y ENERGÍA INTRODUCCIÓN La aplcacón de las leyes de Newton a problemas en que ntervenen fuerzas varables requere de nuevas herramentas de análss. Estas herramentas conssten en los conceptos de trabajo
5 Centrales Hidráulicas
 Curso SmSEE IIE 2012 Cap. 5 pág 1/6 5 Centrales Hdráulcas 5.1 Centrales Hdráulcas con Embalse En el caso de centrales con embalses, tendremos que agregar restrccones adconales para mponer los límtes de
Curso SmSEE IIE 2012 Cap. 5 pág 1/6 5 Centrales Hdráulcas 5.1 Centrales Hdráulcas con Embalse En el caso de centrales con embalses, tendremos que agregar restrccones adconales para mponer los límtes de
Si consideramos un sistema PVT con N especies químicas π fases en equilibrio se caracteriza por: P v =P L = =P π
 EQUILIBRIO DE FASES Reglas de las fases. Teorema de Duhem S consderamos un sstema PVT con N especes químcas π fases en equlbro se caracterza por: P, T y (N-1) fraccones mol tal que Σx=1 para cada fase.
EQUILIBRIO DE FASES Reglas de las fases. Teorema de Duhem S consderamos un sstema PVT con N especes químcas π fases en equlbro se caracterza por: P, T y (N-1) fraccones mol tal que Σx=1 para cada fase.
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Perspectiva inversa para Ray Tracing
 erspectva nversa para Ray Tracng efncón de la cámara José ortés areo, Abrl 7 a cámara vrtual suele defnrse en funcón de un conunto de parámetros ntutvos: Observador unto Focal: unto de Mra: stanca Focal:
erspectva nversa para Ray Tracng efncón de la cámara José ortés areo, Abrl 7 a cámara vrtual suele defnrse en funcón de un conunto de parámetros ntutvos: Observador unto Focal: unto de Mra: stanca Focal:
Magnetostática
 Magnetostátca Ejercco 1: un haz de sótopos (masa m=8,96 x 10 27 kg; carga q=+3,2 10 19 ) ngresa por el punto A de la fgura a una regón del espaco donde exste un campo magnétco de valor B = 0,1T. La energía
Magnetostátca Ejercco 1: un haz de sótopos (masa m=8,96 x 10 27 kg; carga q=+3,2 10 19 ) ngresa por el punto A de la fgura a una regón del espaco donde exste un campo magnétco de valor B = 0,1T. La energía
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
DISTRIBUCIONES BIDIMENSIONALES
 Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
Matemátcas 1º CT 1 DISTRIBUCIONES BIDIMENSIONALES PROBLEMAS RESUELTOS 1. a) Asoca las rectas de regresón: y = +16, y = 1 e y = 0,5 + 5 a las nubes de puntos sguentes: b) Asgna los coefcentes de correlacón
2. EL TENSOR DE TENSIONES. Supongamos un cuerpo sometido a fuerzas externas en equilibrio y un punto P en su interior.
 . EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
. EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
