Tècniques elementals de
|
|
|
- Natalia Aguirre Venegas
- hace 5 años
- Vistas:
Transcripción
1 Dept. Matemàtica Aplicada IV Tècniques elementals de Càlcul i Àlgebra Exercicis bàsics
2 Presentació Aquest document va adreçat als estudiants de nou ingrés de les escoles d enginyeria en les quals imparteix docència el Departament de Matemàtica Aplicada IV de la UPC, és a dir, l ETSETB, l EPSC i l EPSEVG. Conté un recull de les tècniques bàsiques de Càlcul i Àlgebra que cal dominar per poder seguir les assignatures de Matemàtiques de primer curs. Els temes presents en el document haurien de formar part de la cultura general matemàtica de qualsevol estudiant d enginyeria de les escoles esmentades. L objectiu és que un estudiant a punt de començar els seus estudis superiors pugui comprovar si les seves habilitats matemàtiques són suficients i, si li cal, completar-les en els aspectes necessaris abans de començar el curs. Els continguts es presenten en forma de llistes d exercicis bàsics; les solucions del exercicis s inclouen en una secció a part al final del document. Els continguts teòrics necessaris per resoldre els exercicis formen part del currículum de Matemàtiques de l ESO i el Batxillerat, de forma que es poden trobar en els llibres de Matemàtiques d aquests cursos; qualsevol d ells serà una bona referència complementària. AUTORS: F. Aguiló, M. Claverol, F. Comellas, I. Gracia, J. Guàrdia, S.C. López, J. Martí, S. Martín, X. Muñoz, A. Ras, M. Zaragozá Barcelona, Castelldefels i Vilanova i la Geltrú, Juny de 00 (C Dept. de Matemàtica Aplicada Universitat Politècnica de Catalunya
3 Índex. Manipulacions algebraiques elementals. Conceptes bàsics 5. Polinomis 6. Funcions elementals 7 5. Límits de funcions 9 6. Derivades 0 7. El mètode de Gauss 8. Operacions amb matrius 9. Determinants 5 0. Sistemes d equacions lineals 7. Solucions 8
4 Tema : Manipulacions algebraiques elementals. Opereu i simplifiqueu les fraccions: (a /7 = (b / = (c + = (d =. Simplifiqueu les expressions següents: (a = (f 8 = (k = 7 (b = (g 6 8 = (l = (c /5 9 / = (h = (m = (d = (i = (n = (e ( 8 = (j ( 5 = (o x =. Simplifiqueu les expressions següents: (a log a a m = (d ln e x = (g e ln x = (b log ( = (e e ln ln 0 = (h e +ln x = (c log ( + = (f ln ex ln(e x = (i ln e x =. Resoleu les equacions i inequacions següents: (a e x+ = (c x > 0 (e x < (b 5 ln e+ln x = 5 (d (x x(x + 0
5 Tema : Conceptes bàsics. Construïu la taula de les raons trigonomètriques dels angles més usuals i usant les propietats de les funcions trigonomètriques calculeu (sense calculadora: ( ( 5π (a cos = (c tan 5π = (e sec ( 7π = ( 5π (b sin = (d cosec ( 5π = (f cotan ( 5π =. Trobeu els angles α [0, π que compleixen: (a cos α = (b tan α = (c sin α =. Doneu les solucions reals de les equacions següents: (a sin(x = 0 (b cos(x = 0 (c sin(x cos(x = 0. Donades les funcions f(x = sin(x+ i g(x = x, calculeu les funcions compostes f g i g f..5 Trobeu l equació de la recta en el pla que passa pels punts (, i (0,. És la mateixa que la recta que passa pel punt (, i té vector director (,?.6 Trobeu l equació de la recta que passa pel punt (, i té pendent..7 Dóneu l equació de la recta vertical v i de la horitzontal h que passen pel punt (,..8 Trobeu el pendent de la recta r : x y + = 0. Busqueu una recta s paral lela a r que passi pel punt (, i una recta t perpendicular a r que passi pel punt (, 5..9 Calculeu el producte escalar dels vectors u = (, 0, i v = (,, 0. Quin angle formen?.0 Calculeu la distància entre els punts (, i (,.. Determineu un vector perpendicular al pla x + y + 5z =. Determineu la recta perpendicular al pla que passa pel punt (,,. 5
6 Tema : Polinomis. Trobeu les arrels dels polinomis següents i, en cada cas, doneu la descomposició en factors irreductibles. (a x 9x + 0. (b x x x +. (c 6x 7x + 6x + 8. (d x x + x. (e x 5x +. (f x 8x + x x Comproveu que és una arrel del polinomi x + x + x +, i que és una arrel del polinomi x ( + x + ( x +. Quines altres arrels tenen aquests polinomis?. Determineu un polinomi p(x de grau tres que tingui com arrel doble, com arrel simple i tal que p(0 =.. Per a quins valors de a el polinomi x + ax + no té arrels reals? Per a quins valors de a té una arrel doble?.5 Trobeu el quocient q i el residu r de la divisió del polinomi x 5 x + x x + pel polinomi x. Comproveu la igualtat x5 x + x x + = q + r x x. (x +.6 Expresseu la suma x x + x x x + Simplifiqueu l expressió que heu trobat. com un quocient de polinomis p q. 6
7 Tema : Funcions elementals. Determineu el domini de les funcions següents: (a f(x = ln(x + (b g(x = ( xx (c h(x = x x (d m(x = x x. Quines de les funcions següents són parelles, senars o no tenen cap d aquestes dues simetries? (a tan x (b sin x + cos x (c x (d x x +. Quin és el període de les funcions següents? (a tan x (b cos(x (c sin(πx (d cos(x/π. Sigui f una funció amb domini [, ], que té la gràfica la de la Figura. Dibuixeu, aproximadament, les gràfiques de les funcions f(x, f( x, f(x, f(x i f(x/ i doneu-ne el domini. Figura : Gràfica de f.5 Feu l esquema d una gràfica que compleixi: f(x = +, f(x = +, x x f(x =, f(x = + i f(x = 0 x x + x + Doneu les equacions de les asímptotes verticals i horitzontals, si en té. 7
8 .6 Les gràfiques següents corresponen a les funcions f (x = x, f (x = x, f (x = x, f (x = e x, f 5 (x = e x, f 6 (x = sin x, f 7 (x = cos x, f 8 (x = ln x i f 9 (x = x. Relacioneu cadascuna de les funcions amb la seva gràfica , , , , ,5,
9 Tema 5: Límits de funcions 5. Calculeu els límits següents: e x (a x x (b x x ln(x (c (d x + ln(x x + + x x + 5. Calculeu els límits següents de quocients de polinomis: (a x 0 x + x (b x + x x (c x x + x (d x x x x + x (e x 0 x x x x (f x x (x + (g x x x + x x (h x x + x x x 5. Calculeu els límits següents de quocients de polinomis: (a (b (c x + x + x + x + x + x + 5x 5 + x + x + x + x x + x 5 + x + x + x + 5x x + x + x + x x 0x 5x (d (e (f 5x x + 5x + x + 5x x + 5x + 5x x + 5x + x 5x x + 5x + x 7 x 6 x 7x 7 + 9
10 Tema 6: Derivades 6. Calculeu la derivada de les funcions següents. (a f(x = sin(x + cos(x (b f(x = e x cos x (c f(x = cos x x x (d f(x = (x x (e f(x = 9 x (f f(x = x (g f(x = tan(x (h f(x = tan x (i f(x = arctan ( x (j f(x = ln x ( (k f(x = x arccos x 6. Sense desenvolupar les expressions entre parèntesis, calculeu la derivada de les funcions següents: (a f(x = ( 5x 6 (b g(x = ( x 5 + x (c h(x = (x + (x 5 6. En cadascun dels apartats següents, calculeu l equació de la recta tangent a la gràfica de la funció f, en el punt d abscissa x = a: (a f(x = x 5 + 5x 0x + 6, a = (b f(x = x + x + 5, a = (c f(x = x + 6 x, a =. (d f(x = ( + x x /, a = 0. (e f(x = x + x +, a =. 6. En quins punts de la corba y = x + 5 la seva recta tangent és paral lela a la recta d equació x y = 7? 0
11 6.5 Estudieu els màxims i mínims de les funcions següents: (a f(x = x + x (b f(x = x + x x 8 (c f(x = ( x (d f(x = (x (e f(x = (x (x +
12 Tema 7: El mètode de Gauss 7. Calculeu el rang de les matrius següents, utilitzant el mètode de Gauss: ( 0 0 (a 0 (d 0 0 (f (b 0 (g (c 0 0 (e (h Aplicant operacions elementals per files, fem la transformació següent de la matriu A: A = Determineu quina operació hem fet en cada pas. 7. Calculeu el rang de les matrius A = i B =. 8 5 Podem obtenir la matriu B a partir de la matriu A aplicant operacions elementals per files?.
13 Tema 8: Operacions amb matrius 8. Calculeu, en el cas en què sigui possible, la matriu suma A + B i la matriu producte AB de les parelles de matrius següents: 0 (a A =, B = (b A =, B = Sigui A = ( 0 i sigui B = (a Comproveu que AB BA. ( (b Comproveu que (A + B A + AB + B. (c Comproveu que (A B A AB + B. (d Comproveu que A B (A + B(A B.. ( a 8. Calculeu A on A = quins valors de a es té que A = 0?. Per a quins valors de a es té que A = Id? Per a 8. Calculeu, quan sigui possible, la inversa de la matriu A, de la matriu B, de la matriu suma A + B i de la matriu producte AB, on: ( ( (a A =, B =. ( ( (b A =, B = (c A = 0, B = (d A = 8.5 Sigui A = ( 0, B = i sigui B = 0 0 ( 0 (a Comproveu que (A + B A + B... (b Comproveu que A B (AB = B A.
14 8.6 Comproveu que les matrius A = l una de l altra. 0 0 i B = són inverses
15 Tema 9: Determinants 9. Calculeu el determinant de les matrius que s indiquen: ( ( (, sin α cos α, cos α sin α 7 5, 5 0, 5 6, Relacioneu la matriu A = C = 5 0, D = i E = 5. amb les matrius B = ,. Calculeu el determinant d aquestes matrius i relacioneu el determinant de A amb el determinant de les altres quatre matrius Considereu les matrius A = 0 i B =. Comproveu 0 que: (a det(a + B det(a + det(b. (b det(ab = det(a det(b. (c det(a = (det(a (d det(a = / det(a. (e det(a det(a. (f det(7a = 7 det(a. 9. Per a quins valors d a la matriu a 5 0 a 0 5 a + té determinant nul? 5
16 Tema 0: Sistemes d equacions lineals 0. Resoleu els sistemes següents: (a (c { x +y = x +y = x y +7z = x +y z = x +y +z = (b (d x y +z = x +y z = x +y +z = 7 x +y +z = y +z = x +y = 0. Considerem els sistemes d equacions: { x +y = x +5y = { x +y +z = 0 x +5y +z = 0 x +y = 0 x +5y = 0 x +y = 0 Escriviu matricialment aquests sistemes. Quina relació tenen les matrius associades a aquests sistemes? Quins d aquests sistemes són compatibles determinats? 0. Expresseu cada una de les equacions vectorials següents com un sistema d equacions lineals i calculeu-ne la solució: (a x(, + y(, = (, 6. (b x(, + y(, + z(, 6 = (0, 0. (c x(,, + y(,, 6 = (0, 0, Discutiu els sistemes següents en funció del paràmetre a: (a { x y = a ax +y = (b x +y z = 5 x y +az = ax y +z = 0.5 Determineu els valors de a per als quals x = y = z = és una solució del sistema x +y +z = d equacions lineals x +y +z =. Quan x = y = z = és l única solució x +y +a z = a + del sistema? 0.6 Existeixen tres nombres reals que sumats dos a dos donen, 5 i 7? En cas afirmatiu, determineu-los. 6
17 Tema : Solucions Tema : Manipulacions algebraiques elementals. (a = 0 (b 5/7 / = 5 (c + + = (d = 5 5. (a = 7 (f 8 = (k = 0 7 (b = 675 (g 6 8 = (l = (c /5 9 / = (h = 5 (m = (d = (i = 5 (n = (e ( 8 = 8 (j ( 5 = ( 5 (o x = x.. (a log a a m = m (d ln e x = x (g e ln x = /x (b log ( = 7 (e e ln ln 0 = /0 (h e +ln x = x/e (c log ( + = (f ln ex ln(e x = x/ (i ln e x = x.. (a x = / (c x (, (, + (e x (, (b x = e (d x (, ] [0, ] Tema : Conceptes bàsics. (a cos ( 5π = ( (c tan 5π = 0 (e sec ( 7π = ( 5π (b sin = (d cosec ( 5π = (f cotan ( 5π =. 7
18 . (a α = 0 (b α = π 6, α = 7π 6 (c α = 5π, α = 7π. (a x = kπ, k Z (b x = (k + π, k Z (c x = k π, k Z. f g(x = sin(x, g f(x = sin (x + = cos (x +..5 y = x. Sí..6 y = x..7 v : x =, h : y =..8 El pendent és /. Les rectes demanades són s : y = x + 5 i t : y = x El producte escalar és u v = ; el cosinus de l angle α que formen és cos α = /, i per tant α = ±π/ Un vector normal al pla és v = (,, 5; la recta és x = y = z 5. Tema : Polinomis. (a Les arrels són i 5, i la factorització és x 9x + 0 = (x (x 5. (b Les arrels són, i, i la factorització és x x x + = (x (x (x +. (c Arrels: /, /, ; factorització 6x 7x +6x+8 = 6(x (x /(x+/ = (x (x + (x. (d Arrels: 0 i (doble; factorització: x x + x = x(x. (e Arrels: ±, ±; factorització: x 5x + = (x (x (x + (x +. (f Arrels dobles i ; factorització: x 8x + x x + 9 = (x (x.. El polinomi x + x + x + = (x + (x + només té la real real. El polinomi x ( + x + ( x + = ( x (x x té com arrels, +,.. p(x = (x (x +.. El discriminant del polinomi és a 6 = (a 6(a + 6; si 6 < a < 6 el polinomi no té arrels reals; si a = ±6 el polinomi té una sola arrel doble. 8
19 .5 q = x x +, r = x x +..6 (x + x x + x x x + = x 5x + 8. x Tema : Funcions elementals. Dom(f = (, +, Dom(g = [0, ], Dom(h = (, (, +, Dom(m = (, (, (, ].. Les tres primeres funcions són senars i la darrera és parella.. (a El període és π. (b El període és π. (c El període és. (d El període és π.. La funció original està representada en color vermell i la transformada en color blau. f(x f( x f(x Dom( f(x = [, ] Dom(f( x = [, ] Dom(f(x = [, ] f(x f(x/ Dom(f(x = [, ] Dom(f(x/ = [, ] 9
20 .5 Dues solucions possibles: Totes les funcions que compleixin les condicions demanades tindran les assimptotes verticals x = i en x =, i l assímptota horitzontal y = 0 quan x , , y = x y = cos x y = e x - 7 0, , y = sin x x y = x y = e ,5, y = x y = ln x y = x Tema 5: Límits de funcions 5. (a e x x x = 0 (b x x ln(x = 0 (c (d x + ln(x = 0 x + + x = + x + 0
21 5. (a x 0 x + x = (b x + x x = 0 (c x x + x = (d x x x x + x = 0 (e x 0 x x x x = (f x x (x + = (g x x x + x x (h x x + x x x = / =. 5. (a (b (c x + x + x + x + x + x + = 5x 5 + x + x + x + x x + x 5 + x + x + x + 5x = 5 x + x + x + x x 0x 5x = 0 (d (e (f 5x x + 5x + x + 5x x + 5x + = + 5x x + 5x + x 5x x + 5x + = x 7 x 6 x 7x 7 + = /7. Tema 6: Derivades 6. (a f (x = cos(x sin(x (b f (x = e x cos x e x sin x (c f x sin x + cos x (x = x (d f (x = x (x 8 (x (e f (x = 9 (9 x 9 x (f f (x = (ln x x (g f (x = x cos(x (h f (x = tan x cos (x = ( + tan x tan x (i f (x = x + 9 (j f (x = x x (k f (x = x ( x + x arccos x 6. (a f (x = 0( 5x 5 (b g (x = 5 ( x + x ( + x = 5x ( + x 6 (c h (x = 8x(x + (x 5 + 8x (x + (x 5 = x(x + (x 5 (7x + 7x 0
22 6. (a y = 5x + 5 (b y = 6 x + (c y = x + (d y = ( x + (e y = 5x + 6. En els punts d abscissa x = ±. 6.5 (a Mínim absolut en x =. (b Màxim relatiu en x =, mínim relatiu en x = /. (c La funció no té extrems relatius ni absoluts. (d Mínims absoluts en x = ±, màxim relatiu en x = 0. (e Màxim relatiu en x = 0, mínim relatiu en x =. Tema 7: El mètode de Gauss 7. (a rg (b rg ( 0 (c rg (d rg 0 = = = = (e rg (f rg (g rg (h rg = = = =
23 7. Primer pas: Hem intercanviat la primera i la tercera files. Segon pas: Hem restat a la tercera fila la suma de les dues anteriors. Tercer pas: Hem dividit la tercera fila per. Quart pas: Hem restat la primera fila a la segona. Cinquè pas: Hem multiplicat la segona fila per. 7. El rang d A és i el rang de B és ; com el rang és diferent, no podem obtenir una de l altra mitjançant operacions elementals per files. Tema 8: Operacions amb matrius 8. (a A + B = 0. El producte AB no es pot fer. (b La suma A + B no es pot fer. AB =. 8. ( (a AB = ( (b (A + B = 0 0 ( (c (A B = 6 ( 0 (d A B = (, BA =., A + AB + B =, A AB + B =, (A + B(A B = ( 5. ( 7 ( ( a A =. La igualtat A 0 a + = Id es té només per a a = 0, mentre que A = 0 si, i només si, a =. 8. ( / / (a A =, B / / = ( / (AB =. / 0 ( (b A = 0 invertible. 0 0 (c A = 0 ( / / / /., B no és invertible, (A + B =., B, A + B i AB no són invertibles., A + B no és invertible. (, AB no és
24 (d A, B i AB no són invertibles, (A + B = 8.5 (a (A + B = (b A B = ( ( (, A + B =, (AB = ( 0. = B A. 8.6 Només cal comprovar que AB = Id, o bé que BA = Id.. Tema 9: Determinants 9. det det ( 5 7 det ( ( = 9, det sin α cos α =, det + cos α sin α = 5. =, det = 90, det = 0, =, 9. La matriu B és la matriu A amb les dues darreres columnes intercanviades. La matriu C és la matriu A posant la tercera columna com a primera. La matriu D és la transposada d A. La matriu E és la matriu A amb la tercera columna multiplicada per -. És det A =, det B = det A =, det C = det D = det A, det E = det A =. 9. És det(a =, det(b =. (a det(a + B = det(a + det(b. (b det(ab = det(a det(b. (c det(a = = (det(a (d det(a = / = / det(a. (e det(a = 6 = det(a. (f det(7a = 986 = 7 det(a. 9. a = ±.
25 Tema 0: Sistemes d equacions lineals 0. (a x =, y =. (b x =, y =, z =. (c Sistema compatible indeterminat amb un grau de llibertat, i solució x = λ, y = λ, z = λ, λ R. (d Sistema incompatible. 0. ( 5 ( 5 5 ( ( x = y x 0 y = 0 z 0 ( 0 x = 0 y 0 La matriu del segon sistema és la matriu ampliada del primer sistema. La matriu del tercer sistema és la transposada de la matriu del segon. Només el primer i el tercer sistemes són compatibles determinats. 0. (a { x +y = x +y = 6, sistema ćompatible determinat amb solució: x =, y =. (b (c 0. { x +y +z = 0 ; sistema compatible indeterminat amb un grau de llibertat, i solució: x = λ, y = λ, z = λ, λ R. x +y +6z = 0 x y = 0 x +y = 0, sistema ćompatible determinat amb solució: x = 0, y = 0. x +6y = 0 (a Si a 6, el sistema és compatible determinat. Si a = 6 el sistema és incompatible. (b Si a 0, el sistema és compatible determinat Si a = 0 el sistema és compatible indeterminat amb un grau de llibertat. 0.5 El sistema admet la solució x = y = z = quan a = 0 o a =, i aquesta és l única solució només quan a = Els tres nombres són, 5, 9. 5
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010
 Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Matemàtiques 1 - FIB
 Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
PRIMERA MODEL B Codi B2. A1. C
 TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Al ser un quocient, el denominador no pot ser 0 i al ser una arrel d index senars no hi ha problema Dom = R\{x 3 +3x 2-6x-8=0}= R\{-4, 2, -1}.
 Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
IES CTEIB. Departament de Matemàtiques. Matemàtiques II. Problemes proposats en les PAU. José Luis Bernal Garcías. Curs
 IES CTEIB Departament de Matemàtiques Matemàtiques II Problemes proposats en les PAU José Luis Bernal Garcías Curs 016-17 Índex 1 Límits, continuïtat i derivabilitat 5 1.1 Enunciats.................................................
IES CTEIB Departament de Matemàtiques Matemàtiques II Problemes proposats en les PAU José Luis Bernal Garcías Curs 016-17 Índex 1 Límits, continuïtat i derivabilitat 5 1.1 Enunciats.................................................
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
QUADERN D ESTIU 4t ESO MATEMÀTIQUES
 QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES
 TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
TEXTOS DOCENTS 199 ÀLGEBRA LINEAL I GEOMETRIA. PROBLEMES Robert Estalella Guillem Anglada Rosendo Vílchez Rosario López Ferran Sala Departament d Astronomia i Meteorologia U UNIVERSITAT DE BARCELONA B
Convocatòria Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 1. Fase específica
 Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
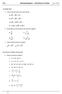 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010
 Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Prova d accés a Cicles formatius de grau superior de formació professional, Ensenyaments d esports i Ensenyaments d arts plàstiques i disseny 2010 Matemàtiques Sèrie 1 Dades de la persona aspirant Qualificació
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 2011 Matemàtiques Sèrie 1 Dades de la persona
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS. 1) PAU 1999 Sèrie 1 Qüestió 1: Resoleu el sistema següent per als valors de k que el facin compatible.
 PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
POLINOMIS. Divisió. Regla de Ruffini.
 POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
1. SISTEMA D EQUACIONS LINEALS
 1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
1. SISTEMA D EQUACIONS LINEALS 1.1 Equacions lineals Una equació lineal està composta de coeficients (nombres reals) acompanyats d incògnites (x, y, z,t..o ) s igualen a un terme independent, i les solucions
TOT 1r /15 INDEX PRÈVIA. PRIMERA Global 1a Recuperació 1a. SEGONA Global 2a Recuperació 2a. TERCERA Global 3a JUNY ÍNDEX
 TOT 1r 11-1 -1/15 INDEX PRÈVIA PRIMERA Global 1a Recuperació 1a SEGONA Global a Recuperació a TERCERA Global a JUNY TOT 1r 11-1 -/15 PREVIA MODEL A Codi B1.A0.11-1 1.- Calculeu les següents expressions,
TOT 1r 11-1 -1/15 INDEX PRÈVIA PRIMERA Global 1a Recuperació 1a SEGONA Global a Recuperació a TERCERA Global a JUNY TOT 1r 11-1 -/15 PREVIA MODEL A Codi B1.A0.11-1 1.- Calculeu les següents expressions,
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 2016 Criteris de correcció
 Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2005
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Derivació Funcions Vàries Variables
 Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
TEMA 6. POLINOMIS II. a n a 2 a 1 a Teorema del residu. 4. Polinomis irreductibles. 6. Fraccions algebraiques
 . REGLA DE RUFFINI És s un mètode m de divisió entre polinomis, més m s senzill que l algoritme l de la divisió i que permet la divisió només quan el divisor és s de la forma Q(x) x b. TEMA 6. S II Professor
. REGLA DE RUFFINI És s un mètode m de divisió entre polinomis, més m s senzill que l algoritme l de la divisió i que permet la divisió només quan el divisor és s de la forma Q(x) x b. TEMA 6. S II Professor
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 PAU SÈRIE 3 Pautes de correcció (PAU 2002) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
DOSSIER DE RECUPERACIÓ 3r ESO
 DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
PROBLEMES DE SELECTIVITAT - MATEMÀTIQUES I - SOLUCIONS
 Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
Si a=, compatible indeterminat amb un grau de llibertat (una recta) Si a, compatible determinat (un punt) x+y-z=6 Per a positiu: 6a) No b) Es demostra (Bolzano) 7a) Si a=-, són paral lels Si a -, es tallen
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
Unitat 4. Fraccions algèbriques
 Unitat 4. Fraccions algèbriques Curs d Anivellament de Matemàtiques Montserrat Corbera / Vladimir Zaiats montserrat.corbera@uvic.cat / vladimir.zaiats@uvic.cat c 2012 Universitat de Vic Sagrada Família,
Unitat 4. Fraccions algèbriques Curs d Anivellament de Matemàtiques Montserrat Corbera / Vladimir Zaiats montserrat.corbera@uvic.cat / vladimir.zaiats@uvic.cat c 2012 Universitat de Vic Sagrada Família,
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B
 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 4t d ESO A I B A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar en
MATEMÀTIQUES FEINES DE SETEMBRE QUART D ESO Acadèmiques CURS Nom i Llinatges:
 IES SANT AGUSTÍ MATEMÀTIQUES FEINES DE SETEMBRE QUART D ESO Acadèmiques CURS 2017-2018 Nom i Llinatges: RECULL D EXERCICIS DE 4t ESO OPCIÓ ACADÈMIQUES 1a AVALUACIÓ NOMBRES REALS. RADICALS I POTÈNCIES 1.
IES SANT AGUSTÍ MATEMÀTIQUES FEINES DE SETEMBRE QUART D ESO Acadèmiques CURS 2017-2018 Nom i Llinatges: RECULL D EXERCICIS DE 4t ESO OPCIÓ ACADÈMIQUES 1a AVALUACIÓ NOMBRES REALS. RADICALS I POTÈNCIES 1.
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
Deduce razonadamente en que casos los planos π 1 y π 2 son o no paralelos:
 GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRIA ANALÍTICA DEL PLA. MATEMÀTIQUES-1
 GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES
 EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES Suma de monomis. 1. Realitza les següents operacions: + 8 4 9 9 6 + 4 5 5 1 + 4 4 4 11 7 f) 6 7 1 8. Realitza les següents operacions: 1 + 5 5 + 1 y + y + y
EXERCICIS POLINOMIS I FRACCIONS ALGEBRAIQUES Suma de monomis. 1. Realitza les següents operacions: + 8 4 9 9 6 + 4 5 5 1 + 4 4 4 11 7 f) 6 7 1 8. Realitza les següents operacions: 1 + 5 5 + 1 y + y + y
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 2. Fase específica. Convocatòria 2015
 Proves d accés a la universitat per a més grans de 25 anys Convocatòria 2015 Matemàtiques Sèrie 2 Fase específica Qualificació 1 2 Exercicis 3 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Convocatòria 2015 Matemàtiques Sèrie 2 Fase específica Qualificació 1 2 Exercicis 3 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Àlgebra lineal i equacions diferencials. Curs 2001/02 Exemple de diagonalització.
 Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
INTEGRACIÓ: resolució exercicis bàsics ex res I.1
 INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 009 SÈRIE 4 QÜESTIONS 1. Considereu el sistema d inequacions següent: x 0, y 0 x+ 5y 10 3x+ 4y 1 a) Dibuixeu la regió de solucions
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 1 SÈRIE 1 1.- Trobeu l equació general (és a dir, de la forma Ax+By+Cz+D = ) del pla que conté la recta r 1 : x 1 { x y z =
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 14 PAU 1 SÈRIE 1 1.- Trobeu l equació general (és a dir, de la forma Ax+By+Cz+D = ) del pla que conté la recta r 1 : x 1 { x y z =
SÈRIE 2 Pautes de correcció (PAAU2001) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
QUADERN d ESTUDI de RECTES TANGENTS
 QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
PROVES PAU. matemàtiques Material recollit per Maite Gorriz i Santi Vilches
 PROVES PAU matemàtiques 2010-2016 Títol: Paràbola convexa Autor: Francisco Javier Perez Padilla Material recollit per www.mat3.cat Maite Gorriz i Santi Vilches Proves d accés a la universitat Convocatòria
PROVES PAU matemàtiques 2010-2016 Títol: Paràbola convexa Autor: Francisco Javier Perez Padilla Material recollit per www.mat3.cat Maite Gorriz i Santi Vilches Proves d accés a la universitat Convocatòria
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
Oficina d Accés a la Universitat Pàgina 1 de 22 PAU 2014
 Oficina d Accés a la Universitat Pàgina 1 de 22 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 22 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Tema 3: EQUACIONS I INEQUACIONS
 Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
