PLAN DE ESTUDIO DE MATEMÁTICA
|
|
|
- Esteban Bustamante Espinoza
- hace 5 años
- Vistas:
Transcripción
1
2 PLAN DE ESTUDIO DE MATEMÁTICA 2
3 3
4 RÉGIMEN DE CORRELATIVIDADES UNIDADES Pr cursr debe tener Pr creditr debe tener Año CURRICULARES Regulrizd Aprobd Regulrizd Aprobd P R I M E R O Pedgogí Alfbetizción Acdémic Didáctic Generl Algebr I Geometrí I Histori de l Mtemátic Sujeto de l Educción Secundri Práctic Docente I Álgebr II Álgebr I Algebr I Geometrí II Algebr I Geometrí I Algebr I Geometrí I S E G U N D O Análisis Mtemático Algebr I Algebr I Psicologí Educcionl Didáctic Generl Sujeto de l Educción Secundri Filosofí TIC en Educción Cultur y Lengu Originri 4
5 Práctic Docente I Algebr I Didáctic Generl Sujeto de l Educción Secundri Psicologí Educcionl Práctic Docente II Geometrí I Pedgogí Práctic Docente I Alfbetizción Acdémic UNIDADES Pr cursr debe tener Pr creditr debe tener Año CURRICULARES Regulrizd Aprobd Regulrizd Aprobd Didáctic Generl Didáctic Generl Didáctic de l Mtemátic I Algebr I Geometrí I Alfbetizción Acdémic Alfbetizción Acdémic Análisis Mtemático II Análisis Mtemático I Geometrí I Análisis Mtemático I Geometrí I Geometrí I T Probbilidd y Estdístics Algebr II Algebr I Algebr II E R C E R O Algebr y Geometrí III Didáctic de l Mtemátic II Algebr II Geometrí II Didáctic de l Mtemátic I Algebr II Geometrí II Algebr II Geometrí II Didáctic de l Mtemátic I Algebr II Geometrí II 5
6 Histori y Fundmento de l Mtemátic Histori y Fundmento de l Mtemátic Didáctic de l Mtemátic I Didáctic de l Mtemátic I L Enseñnz de l Mtemátic con TIC Algebr II Geometrí II Análisis Mtemático Algebr II Geometrí II Análisis Mtemático TIC en Educción TIC en Educción Histori y Polític de l Educción Ltinomericn Argentin y Chqueñ Pedgogí Pedgogí Sociologí Algebr II Práctic Docente I Práctic Docente I Geometrí II Práctic Docente III Análisis Mtemático Didáctic de l Mtemátic I TIC en Educción Didáctic de l Mtemátic I Didáctic de l Mtemátic I 6
7 UNIDADES Pr cursr debe tener Pr creditr debe tener Año CURRICULARES Regulrizd Aprobd Regulrizd Aprobd Modelizción Mtemátic Uniddes Curriculres de Cmpo Disciplinr de 2º Año Didáctic de l Mtemátic II Probbilidd y Estdístics Uniddes Curriculres de Cmpo Disciplinr de 1º Año Uniddes Curriculres de Cmpo Disciplinr de 2º Año Algebr II Algebr I Algebr II C U A R T O Físic Generl Geometrí II Análisis Mtemático Didáctic de l Mtemátic II Geometrí I Análisis Mtemático I Algebr I Geometrí II Análisis Mtemático Análisis Mtemático Algebr II Didáctic de l Mtemátic II Metodologí de l Investigción Eductiv en Mtemátic Probbilidd y Estdístics Práctic Docente III Uniddes Curriculres de Cmpo Disciplinr de 1º Año Probbilidd y Estdístics Práctic Docente III Uniddes Curriculres de Cmpo Disciplinr de 2º Año Uniddes Curriculres de Cmpo Disciplinr de 2º Año Formción en Derechos Filosofí Filosofí 7
8 Humnos, Étic y Ciuddní Residenci Pedgógic Uniddes Curriculres de Cmpo Disciplinr de 3º Año Práctic Docente III Uniddes Curriculres de Cmpo Disciplinr de 1º Año Uniddes Curriculres de Cmpo Disciplinr de 2º Año Práctic Docente III 8
9 Profesordo en Mtemátic 9
10 10
11 Operciones con Números Reles- Propieddes Ls propieddes son: Asocitiv de l sum: Ejemplo: (4-100)+ 4,7 + ( ,3) El mismo ejercicio, pero socido en form conveniente, result: ( ) + (4,7 + 1,3) +4 + (-7-3 ) = Elemento neutro pr l sum: es el 0 Opuesto de un número: todo número rel tiene opuesto. Lo llmmos Ejemplos: ) =0 b) 345 (-345) 0 Conmuttiv: = 5 + (-6) Asocitiv del producto: (-3).[(-5).(+7)] =[(-3).(-5)].7 Elemento neutro: es el 1 (es frecuente dr por obvio que 1.x = x) Inverso de un número: todo número rel (excepto el 0) tiene inverso multiplictivo. Lo llmmos y lo definimos como: -1=1/ -5. 5/1 =1 Distributiv del producto con respecto l sum de números reles: ) -5.( ,5) = -5 +(-5).(-9) +(-5).3 +(-5).(-0,5) = ,5 b) (-6x +3).(5 9)= Conmuttiv: = 5.(-6) = 5(-6) Cudro resumen de ls propieddes de Números reles Complet el cudro colocndo l form simbólic correspondiente los xioms de cd operción definid, usndo, b, c y d como representción de números reles culesquier. Propieddes de l sum Form simbólic Asocitiv Número neutro Numero opuesto Conmuttiv 11
12 Propieddes del producto Form simbólic Asocitiv Numero neutro Numero inverso Conmuttiv Distributiv respecto l sum Actividd 1: Aplic l propiedd distributiv y resuelve en los csos que sen posibles: ) b) c) Actividd 2: Resuelve ls siguientes operciones combinds: ) b) = Potencición: L potencición es l operción que expres en form brevid un multiplicción en l cul los fctores se repiten......= Bse Exponente n veces 12
13 Regls de signo de l potencición: Si el exponente es pr, el resultdo de l potenci es. Ejemplo: Si el exponente es impr, el resultdo de l potenci es. Ejemplo: Propieddes de l potencición: Distributiv con respecto l producto = Distributiv con respecto l cociente = Producto de potencis de igul bse Cociente de potencis de igul bse Potenci de otr potenci Actividd 3: Aplic propieddes de l potencición y resuelve cundo se posible: ) b) = c) d). e) = f) = g) = Actividd 4: ) : = b) = c) = d) = e) = f) = g) = h) = 13
14 Rdicción: Índice Ríz si se cumple que Signo RdiclRdicndo Propieddes de l Potencición: L rdicción es distributiv respecto de l multiplicción: L rdicción es distributiv respecto de l división: Reciproc de l distributiv: Ríz de otr ríz: Simplificción del índice de un ríz: b 0 Amplificción del índice de un ríz: c 0 Cncelción de los índices: Actividd 5: Aplic ls propieddes de l rdicción y resuelve cundo se posible. ) b) c) = d) = e) = f) = 14
15 g) = Actividd 6: Resolver los siguientes ejercicios combindos: ) b) -24 : c) -12 d) e) f) 2(-7-1) [(-12+3):9-5]= g) h) i) {-[-(-15-19)+(3-16)]+14-(-1)}= Rdicles Ls expresiones formds por el signo rdicl y un expresión numéric o literl debjo del mismo, se llm rdicl. Ejemplo: 1 2 5x 2 2 5x Es el rdicl. 1 2 Es el coeficiente del rdicl. Si el índice y el exponente de un rdicl de rdicndo positivo se multiplicn o dividen por un mismo número, el resultdo es el mismo. En símbolo: Extrcción de fctores del rdicl. s r s: n r: n s r s. n r. n Cundo el exponente es myor o igul que el índice se puede simplificr el rdicl extryendo fctores. Ejemplo 1: Se: 8 Podemos expresr 8 como un potenci: No podemos simplificr dividiendo el índice y el exponente por un mismo número. En cmbio podemos descomponer el rdicndo en potencis de igul bse, de modo que el exponente de uno de ells se múltiplo del índice, y el otro exponente menor que el índice. 15
16 Distribuyendo: Simplificndo: Hemos extrído el fctor 2 y el rdicl queddo simplificdo. Ejemplo 2: Se: 3 14 No es posible simplificr el índice 3 con el exponente 14, pero podemos descomponer el rdicndo en potencis de igul bse de modo que uno quede múltiplo de 3 y el otro menor que Ejemplo 3: Se:. b. c Si el rdicndo es un producto de vrios fctores se plic l regl cd uno de los fctores, plicndo l propiedd distributiv b. c. b. c. c Los exponentes 6 y 15 son múltiplos de 3. El exponente 2 es menor que b. c. b. c. c b. c. c. b. c El rdicl h queddo simplificdo. Todos los exponente del rdicndo son menores que el índice. Ejemplo 4: Se: Se descompone el rdicndo en fctores primos
17 Entonces: Ahor se procede como el cso nterior Operciones con rdicles Se considern solo los rdicles de rdicndo positivos. Rdicles semejntes: Dos rdicles son semejntes cundo tienen igul índice y el mismo rdicndo. 3 2 y 5 2 ; 3 y -5 son los coeficientes. Los rdicles semejntes solo difieren en sus coeficientes ADICION Y SUSTRACCION DE RADICALES Ejemplo 1: 5 Pr sumr se extre fctor común Ejemplo 2: b b b REGLA: L sum o diferenci de dos rdicles semejntes es otro rdicl semejnte los ddos, cuyo coeficiente es l sum o diferenci de los coeficientes ddos. b Ejemplo 3: Pr sber si dos rdicles son semejntes se pueden trnsformr en rdicles semejntes equivlentes los ddos, se extren los fctores positivos de cd rdicl. 17
18 (6 8) Ejemplo 4: Lo mismo que en el ejemplo nterior, extremos todos los fctores posibles pr determinr si los rdicles son semejntes No se puede seguir operndo y que los rdicles obtenidos no se pueden reducir rdicles semejntes. MULTIPLICACION DE RADICALES Considerndo dos csos: Multiplicción de rdicles de igul índice Pr multiplicr rdicles de igul índice se plic l propiedd distributiv de l rdicción con respecto l multiplicción Ejemplo: b. b EN SIMBOLO: n r n s n r. b. b s REGLA: El producto de dos rdicles de igul índice es otro rdicl: Cuyo índice es el mismo. Cuyo rdicndo es el producto de los rdicndos. Multiplicción de rdicles de distinto índice Se: Pr poder operr tenemos que encontrr dos rdicles de igul índice, equivlentes los ddos. Clculmos el m.c.m. de los índices. 18
19 m.c.m. (4,6) = es el índice común menor Buscmos dos rdicles equivlentes los ddos con índice Se multiplic índice y exponente por un mismo número. Entonces: REGLA: El producto de dos rdicles de distintos índice es igul otro l producto de otros tntos rdicles del mismo índice, equivlentes los ddos, tl que: ) Múltiplo común menor de los índices de los rdicles ddos. b) Los exponentes de los rdicndo se obtiene de multiplicr cd uno de ellos por el mismo número por el cul se multiplic el índice de dicho rdicl. DIVISION DE RADICALES L regl pr dividir rdicles son semejntes l multiplicción. División de rdicles del mismo índice: Ejemplo: : 4 32: División de rdicles de distinto índice: Pr dividir rdicles de distinto índice se procede en form nálog l multiplicción. Se clcul el índice común menor y se hlln dos rdicles equivlentes los ddos con el índice común. Ejemplo: : : 5. : : ) Extrign los fctores del rdicl. 2) Sumen y resten los términos con rdicles semejntes. 19
20 3) Resuelvn plicndo l propiedd distributiv 4) Reduzcn un índice común y resuelvn ls siguientes multiplicciones y divisiones. 5) Resuelvn ls siguientes operciones combinds. 6) Rcionlicen ls siguientes expresiones. 7) Resuelvn los siguientes cálculos hst encontrr su mínim expresión. Polinomios Denominmos polinomio en un indetermind x (puede ser otr letr), tod expresión lgebric enter con términos que tienen lo sumo un letr. Ejemplos: A (x) = 2 x x x x 16 +4x 3 20
21 P (y) = 4y 5 2y 3 + y 1 Cd uno de los monomios que componen el polinomio se llm término. Si un polinomio tiene 2, 3, 4. términos se llm binomio, trinomio, cutrinomio, etc. El grdo de un polinomio es el myor de los grdos de los términos que los formn. Ejemplo: -32 y + 5x - x + 1 es un polinomio de grdo 4 Un polinomio const de: Grdo P (y) = 4y 5 2y 3 + y 1 Termino I. Coeficiente P. Vrible. Grdo: exponente b. Vrible: letr (y) c. Coeficiente principl: es el coeficiente del myor grdo del polinomio. d. Termino independiente: es el número rel que no tiene vrible. Polinomios completos y ordendos: Identificdo el grdo de un polinomio, si en los otros términos están presentes todos Los de grdo nteriores él, se dice que el polinomio est completo. Porejemplo: Q(x)= 6 + x 3 + 3x x 2 Está completo A(x) = 2 x x x 2 3 Está Incompleto +4x Un polinomio está ordendo si sus términos están ordendos de cuerdo sus grdos. Esto es, en form creciente, de menor myor grdo o decreciente de myor menor. Por Ej.: Q (x)= 6 + x 3 + 3x x 2 est desordendo y completo Q(x) = x 3 x 2 + 3x+6 está ordendo en form decreciente y completo Pr completr, se gregn con sums (o rests) los términos que fltn con coeficientes 0. Por ejemplo: A(x) = 2 x x x x x 3 (ntes) A(x) = 7x 6 + 0x x 4 + 4x 3 + 3x 2 + 0x + 5 (completo y ordendo en formdecreciente) 21
22 Not: El 0 es unque no lo prezc un polinomio. Se llm polinomio nulo. TÉRMINO SEMEJANTES: Dos o más términos son semejntes cundo tiene l mism prte literl y el mismo grdo. Porejemplo:3x 4, ½ x 4,-x 4, 0,45x 4 sonsemejntes En cmbio: x 2, 2x, -x 4 no son semejntes Ejercicio: Propone pr cd cso un expresión que cumpl con ls siguientes condiciones: ) Binomio degrdo3.. b) Trinomio degrdo2 c) Monomio degrdo5. d) Cutrinomio degrdo6... e) Polinomio completo degrdo5 Ejercicio. Ddos los siguientes polinomios: A(x) = 5 -x 3 + 3x 2 ½x B(x) = 3x 4-2x 2 3/2 + x P(x) = 2x 2 + 4x 3 0,25 ) Cuáles son sus coeficientes principles y su términosindependientes? b) Completr los polinomios que consideresincompletos. c) Ordenr los polinomios que no lo estén en form decreciente. Sum (rest): OPERACIONES CON POLINOMIOS L sum (rest) de dos polinomios P(x) y Q(x) es otro polinomio que se cuyos términos se Obtienen sumndo (restndo) sus términos semejntes. Por ejemplo: Sen los polinomios: A(x) = 7 x x x 4 + 4x 3 + 3x x+5 Q(x) = 6 x x 4 + 8x 3 9x x -2 Y se dese sumr: A(x)+ Q(x). 22
23 Un form es colocr uno debjo del otro hciendo que coincidn los términos semejntes, de l siguiente A(x)= 7 x x x 4 + 4x 3 + 3x x +5 + Q(x)= 6 x x 4 + 8x 3 9x x -2 A(x)+Q(x)= 7x 6 6 x x x 3-6x x +3 En el cso de relizr l rest: A(x) Q(x), se cmbi de signo el sustrendo: A(x)=7 x x x 4 + 4x 3 + 3x x +5 -Q(x)= 6 x 5-3 x 4-8x 3 + 9x 2-0 x +2 A(x)+Q(x) = 7x x 5 x 4 4x x x +7 Observciones: Dos polinomios son igules si los coeficientes de los términos semejntes son igules. L dición de polinomios cumple ls propieddes socitiv y conmuttiv. El polinomio neutro es el polinomio nulo (todos sus coeficientes vlen 0), pues l sumrlo culquier polinomio, no lo cmbi este. Ejercicio: Ddos los siguientes polinomios: R(x) = 4x 3 2x+3 S(x) = -3x+ 6x 2 1 T(x) = 2x 2 5x 3 3 Clculen: ) R(x) + S(x) + T(x) = b) R(x) + S(x) T(x) = c) S(x) {R(x) + T(x)} = 23
24 Producto de Polinomios: Pr multiplicr dos polinomios se multiplic término término plicndo l propiedd distributiv, de mner que se multiplicn los coeficientes y ls indeterminds entre sí, plicndo l regl de los signos en los números y l propiedd de l potencición en ls Letrs: producto de potenci de igul bse. Por ejemplo: 3x.( 4x 2 ) = 12x 3-1/2 x 3.(-6x 4 ) = 3x 7 Posteriormente, se sumn los monomios semejntes. A continución, un ejemplo, de cómo se procede pr efectur el producto entre: P(x). Q(x) = (5x - 11) (x 2 + 2x + 4) = P(x) = 5x 11 y Q (x) = x 2 + 2x +4 P(x).Q(x) = 5x x x 11x 2 22x 44.Q(x) = 5x 3 + (10-11) x 2 + (20 22) x 44.Q(x) = 5x 3 x 2 2x 44 (plicmos lpropiedddistributiv) P(x) (grupmos lostérminossemejntes) P(x) FormPráctic: 5x 11 * x 2 + 2x+4 20x 44 10x 2-22x 5x 3 11x 2 5x 3 1x 2-2x 44 Ejercicio 10. Ddos los siguientes polinomios: P(x) = 2x - 5x 2 +4 Q(x) = 3x x 2 S(x) = 3x x Obtener:)P(x).Q(x) b)q(x).s(x) c) S(x).P(x)+Q(x) Ejercicio - Efectur los siguientes productos: 24
25 ) (6x2+ 5x 4).(-2x) = b) x 3 2x 2 + x 1).( x +2) = c) (5x+1). (-5x 1) = d) (x 2 + 0,5x 1). ( x 2 0,5x )= e) (-x 3 +3x 1). (x 2 x ) = f) (5x 2 x 3 + 4x).(-3x + 3 x 3 ) División depolinomios: Ddos dos polinomios P(x) (llmdo dividendo) y Q(x) (llmdo divisor) de modo que el grdo de P(x) se myor que el grdo de Q(x) 0 siempre hllremos dos polinomios C(x) (llmdo cociente) y R(x) (llmdo resto) tl que se verific. P(x)= Q(x).C(x) + R(x) Importnte: Antes de efectur l división hy que ordenr y completr los polinomios. Ejemplo: 5 x x 3-6x 2-2 x+6 x 2 + 0x x-16 2 x 3-16 x 2-2 x +6-2 x 3 +0x 2-4 x 16x x 2-6 x x +38 Ejercicio: Ddos: P(x)=2 x 3-4x 2 +x-2 Q(x) =-3 x 3 +4 x 2 -x-2 R(x) = - x 2 +2 S(x) = x 2-3 x-10 Clcule: ) P: R b) Q:S c) (P + Q):R d) (P - Q).S Regl de Ruffini En los csos prticulres de división donde el divisor es de lform x - sepuede 25
26 obtener el cociente y el resto, medinte un método sintético siguiendoel lgoritmo que continución se detll con unejemplo. Ejemplo: Q(x) = x + 3 P(x):Q(x) con P(x) = 2x 4-4x 3 + 3x 2-5x+6 Observmos que el divisor tiene l form x - con = -3, disponemos y opermos con los coeficientes de l siguiente mner: Resto C(x) = 2x 3-10x x 104 El cociente C(x) es un polinomio con coeficientes los cutro primeros números y con indetermind x, de grdo 3 (uno menos que P). En generl el polinomio cociente es otro polinomio de l mism indetermind con el grdo n-1 del dividendo y los coeficientes son los números que se obtienen en el último renglón menos el último número, que es el Resto. Psos: 1) Se escriben los coeficientes del dividendo completo y ordendo 2) A l izquierd se escribe ( es -3) 3) El primer coeficiente qued igul (2) 4) El segundo coeficiente se obtiene efectundo 2.(-3) y sumndo este resultdo -4 (es - 10) 5) El tercer coeficiente se obtiene efectundo (-10). (-3) y sumndo este resultdo 3 ( es 33) 6) El curto coeficiente se obtiene efectundo (33). (-3) y sumndo -5 se obtiene ) Por último, lo multiplicmos (-104). (-3) y le summos 6 y si obtenemos el resto (318). Actividd: Efectur los siguientes ejercicios: ) b) c) d) 26
27 27
28 28
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA:
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: EDISON MEJÍA MONSALVE. TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA DURACION 8
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: EDISON MEJÍA MONSALVE. TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA DURACION 8
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS
 CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
UNIDAD N 3: EXPRESIONES ALGEBRAICAS POLINOMIOS
 Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Álgebra 1 de Secundaria: I Trimestre. yanapa.com. a n. a m = a n+m. (a. b) n = a n. b n. ;. (a n ) m = a n. m.
 Álgebr 1 de Secundri: I Trimestre I: EXPRESIONES ALGEBRAICAS R Sen 1 Son epresiones lgebrics T 1 log R',, z 3 z A 1 TÉRMINO ALGEBRAICO TÉRMINOS SEMEJANTES ) 3z ; - 3z ; 6z Son términos semejntes b) b;
Álgebr 1 de Secundri: I Trimestre I: EXPRESIONES ALGEBRAICAS R Sen 1 Son epresiones lgebrics T 1 log R',, z 3 z A 1 TÉRMINO ALGEBRAICO TÉRMINOS SEMEJANTES ) 3z ; - 3z ; 6z Son términos semejntes b) b;
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: EDISON MEJÍA MONSALVE.
 INSTITUCION EDUCATIVA LA RESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIO DE GUIA: MATEMATICAS MATEMATICAS EDISON MEJÍA MONSALVE. CONCETUAL - EJERCITACION ERIODO GRADO 8 A/B N FECHA Enero / 0
INSTITUCION EDUCATIVA LA RESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIO DE GUIA: MATEMATICAS MATEMATICAS EDISON MEJÍA MONSALVE. CONCETUAL - EJERCITACION ERIODO GRADO 8 A/B N FECHA Enero / 0
TEMA 0: CONCEPTOS BÁSICOS.
 TEMA : CONCEPTOS BÁSICOS.. Intervlos:. Intervlos. 2. Propieddes de ls potencis.. Propieddes de los rdicles. Operciones con rdicles. Rcionlizción. 4. Conceptos de un polinomio. Fctorizción de polinomios..
TEMA : CONCEPTOS BÁSICOS.. Intervlos:. Intervlos. 2. Propieddes de ls potencis.. Propieddes de los rdicles. Operciones con rdicles. Rcionlizción. 4. Conceptos de un polinomio. Fctorizción de polinomios..
a n =b Si a es múltiplo de b, entonces b es divisor de a. Números primos: son números cuyos únicos divisores son ellos mismos y el 1.
 1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
EXPRESIONES ALGEBRAICAS: MONOMIOS Y POLINOMIOS
 EXPRESIONES LGERIS: MONOMIOS Y POLINOMIOS EXPRESIÓN LGERI.- Un epresión lgeric es culquier cominción de números letrs unidos por ls operciones ritmétics (sum, rest, multiplicción, división, potenci, (o)
EXPRESIONES LGERIS: MONOMIOS Y POLINOMIOS EXPRESIÓN LGERI.- Un epresión lgeric es culquier cominción de números letrs unidos por ls operciones ritmétics (sum, rest, multiplicción, división, potenci, (o)
Polinomios 3º Año Cód P r o f. Ma r í a d e l L u j á n Matemática M a r t í n e z P r o f. Mi r t a R o s i t o Dpto.
 Polinomios Mtemátic º Año Cód. 0-8 P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrible,
Polinomios Mtemátic º Año Cód. 0-8 P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrible,
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
2 cuando a y b toman los valores 2 y -1,
 COLEGIO PEDAGÓGICO DE LOS ANDES TALLER DE NIVELACIÓN DE MATEMÁTICAS SEGUNDO PERIODO GRADO OCTAVO ALGEBRA...- - LLeenngguuj jjee l llggee ri r iiccoo El lenguje numérico sirve pr epresr operciones en ls
COLEGIO PEDAGÓGICO DE LOS ANDES TALLER DE NIVELACIÓN DE MATEMÁTICAS SEGUNDO PERIODO GRADO OCTAVO ALGEBRA...- - LLeenngguuj jjee l llggee ri r iiccoo El lenguje numérico sirve pr epresr operciones en ls
Potencias y radicales
 Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
Módulo 14 Multiplicación de expresiones algebraicas. Exponentes
 Módulo 14 Multiplicción de expresiones lgebrics. Exponentes OBJETIVO: Identificr potenci, bse exponente de un expresión lgebric. Multiplicr dividir polinomios. Recordemos lguns definiciones básics. Un
Módulo 14 Multiplicción de expresiones lgebrics. Exponentes OBJETIVO: Identificr potenci, bse exponente de un expresión lgebric. Multiplicr dividir polinomios. Recordemos lguns definiciones básics. Un
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
TEMA 1. LOS NÚMEROS REALES
 TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
2 es racional y se llegará a una contradicción.
 Instituto de Enseñnz Superior Simón Bolívr Profesordo pr l Educción Secundri en Mtemátic Profesores: Olg Peñloz y Víctor Plzzesi. Espcio Curriculr: Elementos de l Aritmétic y el Álgebr. Clse 4: Si se pudiern
Instituto de Enseñnz Superior Simón Bolívr Profesordo pr l Educción Secundri en Mtemátic Profesores: Olg Peñloz y Víctor Plzzesi. Espcio Curriculr: Elementos de l Aritmétic y el Álgebr. Clse 4: Si se pudiern
73 ESO. E = m c 2. «El que pregunta lo que no sabe es ignorante un. día. El que no lo pregunta será ignorante toda la vida»
 73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
73 ESO dí. «El que pregunt lo que no se es ignornte un El que no lo pregunt será ignornte tod l vid» E = m c ÍNDICE: MENSAJES OCULTOS 1. EXPRESIONES ALGEBRAICAS. VALOR NUMÉRICO DE UNA EXPRESIÓN ALGEBRAICA
POLINOMIO GRADO TERM. INDEP. ORDENAR COMPLETAR 2x-x x 3 8-x 4 x+4x 4 2x-1+x 5
 SECRETARIA DE EDUCACIÓN DE BOGOTÁ D.C. COLEGIO CARLOS ALBÁN HOLGUÍN I.E.D. Resolución de Aproción (SED N 8879 de Dic. 7 de 001 Resolución de Jornd Complet (SED N 08 de Nov. 17 de 01 En sus niveles Preescolr,
SECRETARIA DE EDUCACIÓN DE BOGOTÁ D.C. COLEGIO CARLOS ALBÁN HOLGUÍN I.E.D. Resolución de Aproción (SED N 8879 de Dic. 7 de 001 Resolución de Jornd Complet (SED N 08 de Nov. 17 de 01 En sus niveles Preescolr,
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Las expresiones algebraicas provienen de fórmulas físicas, geométricas, de economía, etc. Son expresiones
 Definición de Polinomio Epresiones Algerics Epresión lgeric es tod cominción de números letrs ligdos por los signos de ls operciones ritmétics: dición, sustrcción, multiplicción, división potencición.
Definición de Polinomio Epresiones Algerics Epresión lgeric es tod cominción de números letrs ligdos por los signos de ls operciones ritmétics: dición, sustrcción, multiplicción, división potencición.
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
En general, si. son números racionales, la suma es un número racional.
 ... SUMA DE FRACCIONES. Al relizr sums con números rcionles encontrmos csos muy específicos, como son los siguientes: Sum de números rcionles con el mismo denomindor. Pr resolver este tipo de ejercicios
... SUMA DE FRACCIONES. Al relizr sums con números rcionles encontrmos csos muy específicos, como son los siguientes: Sum de números rcionles con el mismo denomindor. Pr resolver este tipo de ejercicios
1. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN
 http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
POLINOMIOS. se denominan coeficientes.
 POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile, tod epresión de l form: tl que: 0... n n 0 R; R; R;... ; n R n 0 siendo n N0 En tl epresión, l letr represent un número rel
POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile, tod epresión de l form: tl que: 0... n n 0 R; R; R;... ; n R n 0 siendo n N0 En tl epresión, l letr represent un número rel
I.E.S. Historiador Chabás -1- Juan Bragado Rodríguez
 Polinomios Operciones Regl de Ruffini Ríces o ceros Descomposición Frcciones lgebrics Ecuciones rcionles Repso de polinomios Ejercicios Ddos los polinomios P(, Q( R( clculr: P( Q( Q( R( P( Q( R( d P( Q
Polinomios Operciones Regl de Ruffini Ríces o ceros Descomposición Frcciones lgebrics Ecuciones rcionles Repso de polinomios Ejercicios Ddos los polinomios P(, Q( R( clculr: P( Q( Q( R( P( Q( R( d P( Q
Polinomios 3º Año Cód P r of. M a r í a d el L u já n Matemática M a r t í n ez P r of. M ir t a R o s i t o Dpto.
 Polinomios Mtemátic º Año Cód. 0- P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile,
Polinomios Mtemátic º Año Cód. 0- P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile,
Guía de álgebra básica para alumnos de nuevo ingreso. Academia de ciencias básicas
 Guí de álgebr básic pr lumnos de nuevo ingreso Acdemi de ciencis básics ÁLGEBRA Álgebr es l rm de l Mtemátic que emple números, letrs signos pr poder hcer referenci múltiples operciones ritmétics. El término
Guí de álgebr básic pr lumnos de nuevo ingreso Acdemi de ciencis básics ÁLGEBRA Álgebr es l rm de l Mtemátic que emple números, letrs signos pr poder hcer referenci múltiples operciones ritmétics. El término
Clase 2: Expresiones algebraicas
 Clse 2: Expresiones lgebrics Operr expresiones lgebrics usndo ls propieddes lgebrics de ls operciones sum y producto, propieddes de ls potencis, regls de signos y préntesis. Evlur expresiones lgebrics
Clse 2: Expresiones lgebrics Operr expresiones lgebrics usndo ls propieddes lgebrics de ls operciones sum y producto, propieddes de ls potencis, regls de signos y préntesis. Evlur expresiones lgebrics
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
NÚMEROS REALES, R. Es el conjunto de números que se obtiene al unir el conjunto de los números racionales con el conjunto de los números irracionales.
 NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
open green road Guía Matemática FRACCIONES ALGEBRAICAS profesor: Nicolás Melgarejo .co
 Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
GUIA DE MATEMATICA. Coeficiente numérico. Es toda combinación de números y letras ligados por los signos de las operaciones aritméticas.
 www.colegiosntcruzrioueno.cl Deprtmento de Mtemátic GUIA DE MATEMATICA Unidd: Álger en R Contenidos: - Conceptos lgericos ásicos - Operciones con epresiones lgerics - Vlorción de epresiones lgerics - Notción
www.colegiosntcruzrioueno.cl Deprtmento de Mtemátic GUIA DE MATEMATICA Unidd: Álger en R Contenidos: - Conceptos lgericos ásicos - Operciones con epresiones lgerics - Vlorción de epresiones lgerics - Notción
MATRICES Y DETERMINANTES
 MTRICES Y DETERMINNTES. Definición de mtriz.. Tipos de mtrices.. Sum de mtrices.. Producto de un número rel por un mtriz.. Producto de mtrices.. Ejercicios. Determinnte de un mtriz. 8. Menor complementrio
MTRICES Y DETERMINNTES. Definición de mtriz.. Tipos de mtrices.. Sum de mtrices.. Producto de un número rel por un mtriz.. Producto de mtrices.. Ejercicios. Determinnte de un mtriz. 8. Menor complementrio
El grado de un polinomio es el grado del monomio de mayor grado de los que lo forman.
 Lección 7:POLINOMIOS 7.- POLINOMIOS TÉRMINOS DE UN POLINOMIO Son cd uno de los monomios que formn un polinomio. Se identificn con l epresión término en (l prte literl que lo form). -6 se llmn términos
Lección 7:POLINOMIOS 7.- POLINOMIOS TÉRMINOS DE UN POLINOMIO Son cd uno de los monomios que formn un polinomio. Se identificn con l epresión término en (l prte literl que lo form). -6 se llmn términos
Módulo 12 La División
 Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
Módulo L División OBJETIVO: Epresrá lguns propieddes de l división usndo propieddes de l división los inversos; epresr un numero rcionl de l form deciml frcción común vicevers. L división es un operción
es una matriz de orden 2 x 3.
 TEMA 7: MATRICES. 7.. Introducción l concepto de mtriz. 7.. Tipos de mtrices. 7.. El espcio vectoril de ls mtrices de orden m x n. 7.. INTRODUCCIÓN AL CONCEPTO DE MATRIZ. Se define mtriz de orden m x n
TEMA 7: MATRICES. 7.. Introducción l concepto de mtriz. 7.. Tipos de mtrices. 7.. El espcio vectoril de ls mtrices de orden m x n. 7.. INTRODUCCIÓN AL CONCEPTO DE MATRIZ. Se define mtriz de orden m x n
Cálculo del valor decimal de una fracción Para obtener el valor de una fracción se divide el numerador entre el denominador. 2 5
 LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
Concepto clave. La derivada de una función se define principalmente de dos maneras: 1. Como el límite del cociente de Fermat ( )( )
 Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
PROPEDÉUTICO DE MATEMÁTICAS MODULO I
 PROPEDÉUTICO DE MATEMÁTICAS MODULO I ARITMÉTICA Y ALGEBRA Profesor: Dr. Luis G. Cbrl Rosetti Dr. Luis G. Cbrl Rosetti Págin 1 Dr. Luis G. Cbrl Rosetti Págin Dr. Luis G. Cbrl Rosetti Págin x b x b. cx d
PROPEDÉUTICO DE MATEMÁTICAS MODULO I ARITMÉTICA Y ALGEBRA Profesor: Dr. Luis G. Cbrl Rosetti Dr. Luis G. Cbrl Rosetti Págin 1 Dr. Luis G. Cbrl Rosetti Págin Dr. Luis G. Cbrl Rosetti Págin x b x b. cx d
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
56 CAPÍTULO 2. CÁLCULO ALGEBRAICO. SECCIÓN 2.4 Resolución de Ecuaciones de Segundo Grado
 56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
TEMA 3: Expresiones algebraicas. Polinomios. Tema 3: Expresiones algebraicas. Polinomios 1
 TEMA Epresiones lgerics. Polinomios Tem Epresiones lgerics. Polinomios ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum rest de polinomios...- Producto de polinomios...- Potenci de polinomios..-
TEMA Epresiones lgerics. Polinomios Tem Epresiones lgerics. Polinomios ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum rest de polinomios...- Producto de polinomios...- Potenci de polinomios..-
Módulo 16 Simplificación de fracciones
 Módulo 6 Simplificción de frcciones OBJETIVO: Mnejrá ls cutro operciones fundmentles con epresiones lgebrics frccionris, simplificrls hst trnsformrls en irreductibles y epresrá proposiciones en lenguje
Módulo 6 Simplificción de frcciones OBJETIVO: Mnejrá ls cutro operciones fundmentles con epresiones lgebrics frccionris, simplificrls hst trnsformrls en irreductibles y epresrá proposiciones en lenguje
TEMA 3: Polinomios y fracciones algebraicas. Tema 3: Polinomios y fracciones algebraicas 1
 TEMA Polinomios y frcciones lgerics Tem Polinomios y frcciones lgerics ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum y rest de polinomios...- Producto de polinomios...- División de polinomios..-
TEMA Polinomios y frcciones lgerics Tem Polinomios y frcciones lgerics ESQUEMA DE LA UNIDAD.- Operciones con polinomios...- Sum y rest de polinomios...- Producto de polinomios...- División de polinomios..-
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
IES Fernando de Herrera 23 de octubre de 2013 Primer trimestre - Primer examen 4º ESO NOMBRE:
 IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
IES Fernndo de Herrer de octure de 0 Primer trimestre - Primer exmen 4º ESO NOMBRE: ) Nomrr los principles conjuntos numéricos, explicitndo cuáles son sus elementos y ls relciones de inclusión entre ellos
NÚMEROS REALES 1º Bachillerato CC. SS.
 Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
ÁLGEBRA: Propiedades para la Simplificación
 Sludmed 016, por Prof. Edgr Loptegui Corsino ( http://www.sludmed.com/ ), se encuentr bjo un licenci CC: Cretive Commons : Atribución-No Comercil-Sin Derivds 3.0 PR: http://cretivecommons.org/licenses/by-nc-nd/3.0/pr/
Sludmed 016, por Prof. Edgr Loptegui Corsino ( http://www.sludmed.com/ ), se encuentr bjo un licenci CC: Cretive Commons : Atribución-No Comercil-Sin Derivds 3.0 PR: http://cretivecommons.org/licenses/by-nc-nd/3.0/pr/
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
Unidad 2. Fracciones y decimales
 Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
Mtemátics Múltiplo.º ESO / Resumen Unidd Unidd. Frcciones y decimles FRACCIONES NÚMEROS DECIMALES EXPRESIÓN, 8, 9 SIGNIFICADO FRACCIONES EQUIVALENTES 0 30 0 0 Prte de un unidd Prte de un cntidd ORDENACIÓN
Tema 1: Números reales.
 Tem : Números reles. Ejercicio. Representr los siguientes conjuntos numéricos: ) Números myores que. b) x / x c) x / x x d) Números menores que excluyendo el 0. e) / x x / x x / x ) (, ) b) [,) 0 c) [,]
Tem : Números reles. Ejercicio. Representr los siguientes conjuntos numéricos: ) Números myores que. b) x / x c) x / x x d) Números menores que excluyendo el 0. e) / x x / x x / x ) (, ) b) [,) 0 c) [,]
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
PRODUCTOS NOTABLES APELLIDOS Y NOMBRES
 PRODUCTOS NOTABLES APELLIDOS Y NOMBRES SECCIÓN Qué es un producto notble? L plbr "producto" hce referenci l resultdo de un multiplicción y l plbr "notble" hbl de lgo que se puede notr simple vist; por
PRODUCTOS NOTABLES APELLIDOS Y NOMBRES SECCIÓN Qué es un producto notble? L plbr "producto" hce referenci l resultdo de un multiplicción y l plbr "notble" hbl de lgo que se puede notr simple vist; por
DISTINGUIR E IDENTIFICAR ECUACIONES E IDENTIDADES
 REPASO Y APOYO OBJETIVO DISTINGUIR E IDENTIFICAR ECUACIONES E IDENTIDADES IDENTIDADES Y ECUACIONES Un iguldd lgebric está formd por dos expresiones lgebrics seprds por el signo igul (=). Un identidd es
REPASO Y APOYO OBJETIVO DISTINGUIR E IDENTIFICAR ECUACIONES E IDENTIDADES IDENTIDADES Y ECUACIONES Un iguldd lgebric está formd por dos expresiones lgebrics seprds por el signo igul (=). Un identidd es
La raíz cuadrada de un número es otro nº que al elevarlo al cuadrado nos da el radicando La raíz cuadrado de 9 es 3. Pues 3 2 es
 Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
3º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
º ESO NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números rcionles son lo que hbitulmente conocemos como frcciones. Un número rcionl o frcción está compuesto por
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN)
 Lortorio Tercero Básico Centro Integrl Empresril por Mdurez CIEM INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN). Identific los elementos que se piden: ) Los términos de 5r +s ) Los términos
Lortorio Tercero Básico Centro Integrl Empresril por Mdurez CIEM INTRODUCCIÓN AL ÁLGEBRA (TÉRMINOS, ADICIÓN Y SUSTRACCIÓN). Identific los elementos que se piden: ) Los términos de 5r +s ) Los términos
REGLAS DE LOS PRODUCTOS NOTABLES
 UNIDAD V.- PRODUCTOS NOTABLES Y FACTORIZACIO N Productos Notbles ( (b ( (d (e ( REGLAS DE LOS PRODUCTOS NOTABLES Un producto notble (multiplicción es quel que se puede obtener su resultdo sin necesidd
UNIDAD V.- PRODUCTOS NOTABLES Y FACTORIZACIO N Productos Notbles ( (b ( (d (e ( REGLAS DE LOS PRODUCTOS NOTABLES Un producto notble (multiplicción es quel que se puede obtener su resultdo sin necesidd
CURSO DE NIVELACIÓN 2012 EJERCITARIO TEÓRICO DE MATEMÁTICA I
 CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
a 11 a 12 a a 1n a 21 a 22 a a 2n a 31 a 32 a a 3n... a m1 a m2 a m3... a mn
 TEMA ÁLGEBRA DE MATRICES Mtemátics II º Bchillerto TEMA ÁLGEBRA DE MATRICES. NOMENCLATURA Y DEINICIONES.. - DEINICIÓN Ls mtrices son tbls numérics rectngulres ª column ª fil n n n.......... m m m mn (
TEMA ÁLGEBRA DE MATRICES Mtemátics II º Bchillerto TEMA ÁLGEBRA DE MATRICES. NOMENCLATURA Y DEINICIONES.. - DEINICIÓN Ls mtrices son tbls numérics rectngulres ª column ª fil n n n.......... m m m mn (
2 Números racionales positivos
 Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
EJERCICIOS DE RAÍCES
 EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
ECUACIONES (4º ESO Op B)
 ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
ECUACIONES ( ESO Op B) IDENTIDADES, IGUALDADES FALSAS Y ECUACIONES.- Un iguldd lgebric está formd por dos epresiones lgebrics (un de ells puede ser un número), seprds por el signo. Ejemplos.- + + 1 ( +
TEMA 5: Logaritmos y ecuaciones logarítmicas. Tema 5: Logaritmos y ecuaciones logarítmicas 1
 TEMA : Logritmos y ecuciones rítmics Tem : Logritmos y ecuciones rítmics ESQUEMA DE LA UNIDAD.- Logritmos...- Logritmo de un número rel...- Logritmos decimles y neperinos..- Propieddes de los ritmos..-
TEMA : Logritmos y ecuciones rítmics Tem : Logritmos y ecuciones rítmics ESQUEMA DE LA UNIDAD.- Logritmos...- Logritmo de un número rel...- Logritmos decimles y neperinos..- Propieddes de los ritmos..-
OPERACIONES CON FRACIONES
 LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
EXPONENTES Y RADICALES
 . UNIDAD EXPONENTES Y RADICALES Objetivo generl. Al terinr est Unidd resolverás ejercicios probles en los que pliques ls lees de los eponentes de los rdicles. Objetivos específicos:. Recordrás l notción
. UNIDAD EXPONENTES Y RADICALES Objetivo generl. Al terinr est Unidd resolverás ejercicios probles en los que pliques ls lees de los eponentes de los rdicles. Objetivos específicos:. Recordrás l notción
Conjuntos numéricos. Intervalos. Operaciones en el conjunto de números reales.
 Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
Fich Técnic Conjuntos numéricos Intervlos Operciones en el conjunto de números reles Índice de tems: Conjuntos numéricos Intervlos Operciones y propieddes Módulo o vlor bsoluto de un número rel Conjuntos
Apellidos: Nombre: Curso: 1º Grupo: C Día: 10 - XI- 14 CURSO Resuelve las siguientes ecuaciones y comprueba las soluciones obtenidas:
 EXAMEN DE MATEMÁTICAS ALGEBRA Apellidos: Nombre: Curso: º Grupo: C Dí: - XI- 4 CURSO 4-5. Hll el vlor de log log ), 4 log log b) log4 6 -log -log log 7 4 6. Clcul x pr que se cumpl: ) log 6,45,5 b) 5 +,58.
EXAMEN DE MATEMÁTICAS ALGEBRA Apellidos: Nombre: Curso: º Grupo: C Dí: - XI- 4 CURSO 4-5. Hll el vlor de log log ), 4 log log b) log4 6 -log -log log 7 4 6. Clcul x pr que se cumpl: ) log 6,45,5 b) 5 +,58.
Funciones Algebraicas
 1 1r Unidd s 1. Dominio de Polinomiles y Rcionles Cundo los pensmientos brumn nuestr mente es momento de tomr un pus, respirr, y reformulr ides. Unos minutos pr desconectrse resultn de provecho pr volver
1 1r Unidd s 1. Dominio de Polinomiles y Rcionles Cundo los pensmientos brumn nuestr mente es momento de tomr un pus, respirr, y reformulr ides. Unos minutos pr desconectrse resultn de provecho pr volver
TEMA 3. MATRICES Y DETERMINANTES
 TEMA. MATRICES Y DETERMINANTES. DEFINICIÓN Un mtriz es un tbl de números ordendos en fils y columns de l siguiente form: n A m mn que es un mtriz de m fils y n columns, donde el elemento ij es el número
TEMA. MATRICES Y DETERMINANTES. DEFINICIÓN Un mtriz es un tbl de números ordendos en fils y columns de l siguiente form: n A m mn que es un mtriz de m fils y n columns, donde el elemento ij es el número
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
IES Fernando de Herrera Curso 2012/13 Global 1ª evaluación 4º ESO 28 de noviembre de 2012 NOMBRE
 IES Fernndo de Herrer Curso 01/1 Globl 1ª evlución º ESO 8 de noviembre de 01 NOMBRE 1) Simplificr ls siguientes expresiones, rcionlindo el denomindor, en su cso: ( 1) ( ) ) ( puntos) 19 0 ( ) b) 8 c)
IES Fernndo de Herrer Curso 01/1 Globl 1ª evlución º ESO 8 de noviembre de 01 NOMBRE 1) Simplificr ls siguientes expresiones, rcionlindo el denomindor, en su cso: ( 1) ( ) ) ( puntos) 19 0 ( ) b) 8 c)
Tutorial MT-m3. Matemática Tutorial Nivel Medio. Función cuadrática
 12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
Propiedades de la Potencia. Observación: La potencia no es distributiva con respecto a la suma ni a la resta.
 Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
CAPÍTULO 1. Lenguaje algebraico
 CAPÍTULO Lenguje lgebrico El lenguje lgebrico se bs en el uso de letrs y relciones mtemátics pr generlizr diferentes situciones. Ejemplos: El perímetro P de un cudrdo de ldo P = 4. A lgebr en los números
CAPÍTULO Lenguje lgebrico El lenguje lgebrico se bs en el uso de letrs y relciones mtemátics pr generlizr diferentes situciones. Ejemplos: El perímetro P de un cudrdo de ldo P = 4. A lgebr en los números
UNIDAD 3 : ALGEBRA, POR FIN
 UNIDAD 3 : ALGEBRA, POR FIN JUSTIFICACIÓN : Y tenemos ide del trbjo de los números nturles, enteros, rcionles reles. Ahor plicremos su generlizción en los diversos ejercicios que nos present el álgebr
UNIDAD 3 : ALGEBRA, POR FIN JUSTIFICACIÓN : Y tenemos ide del trbjo de los números nturles, enteros, rcionles reles. Ahor plicremos su generlizción en los diversos ejercicios que nos present el álgebr
a) Decimales finitos: Corresponden a los cuocientes exactos entre el numerador y el denominador. Ejemplo: : 8 = (b)
 Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
Clse-06 Números rcionles expresdos en form deciml: Todo número rcionl con b 0 se puede trnsformr form deciml l dividir b el numerdor por su denomindor. En form deciml los siguientes rcionles quedn escritos
LECTURA N 7: OPERACIONES CON EXPRESIONES ALGEBRAICAS
 LECTURA N : OERACIONES CON EXRESIONES ALGEBRAICAS Mteril recopildo con fines instruccionles por: Gómez, B., Gómez, T., González, N., Moreno, E., Rojs, M. 00. Epresiones Algebrics. Crcs: UNEFA. Vlor Numérico
LECTURA N : OERACIONES CON EXRESIONES ALGEBRAICAS Mteril recopildo con fines instruccionles por: Gómez, B., Gómez, T., González, N., Moreno, E., Rojs, M. 00. Epresiones Algebrics. Crcs: UNEFA. Vlor Numérico
Multiplicar y dividir radicales
 Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
Manual de teoría: Álgebra Matemática Bachillerato
 Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
Clase 11 Tema: Multiplicación entre polinomios
 Bimestre: II Número de clse: Mtemátics 8 Clse Tem: Multiplicción entre polinomios Actividd 38 Hlle el volumen de cd cj. 2 8y 2 + 2 5 3y 2 5 9 3 y 4 2 y + 0 2y 2 y,8 3 y 4 + Actividd 39 Un fáric de empques
Bimestre: II Número de clse: Mtemátics 8 Clse Tem: Multiplicción entre polinomios Actividd 38 Hlle el volumen de cd cj. 2 8y 2 + 2 5 3y 2 5 9 3 y 4 2 y + 0 2y 2 y,8 3 y 4 + Actividd 39 Un fáric de empques
Factorización 3. FACTORIZACION
 UNIDAD Fctorizción. FACTORIZACION Sbemos que el orden de los fctores no lter el producto (propiedd conmuttiv). Recordemos que si (5)()=15 decimos que el 5 el son fctores de 15. Anteriormente recordmos
UNIDAD Fctorizción. FACTORIZACION Sbemos que el orden de los fctores no lter el producto (propiedd conmuttiv). Recordemos que si (5)()=15 decimos que el 5 el son fctores de 15. Anteriormente recordmos
DETERMINANTES. Determinante es la expresión numérica de una matriz. Según el orden de la matriz el determinante se resuelve de distintas formas:
 ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
DETERMINANTES K K. A cada matriz n-cuadrada A = (a ij ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), A o = K
 DETERMINANTES A cd mtriz ncudrd A ( ij ) se le sign un esclr prticulr denomindo determinnte de A, denotdo por det (A), A o n n n n nn K Un tbl ordend n n de esclres situd entre dos línes verticles, llmd
DETERMINANTES A cd mtriz ncudrd A ( ij ) se le sign un esclr prticulr denomindo determinnte de A, denotdo por det (A), A o n n n n nn K Un tbl ordend n n de esclres situd entre dos línes verticles, llmd
FICHA 1 3/2008. Propiedades Adición (+) Multiplicación (. ) Conmutativa A1 a + b = b + a M1 a.b =b.a
 FICHA 1 3/2008 Existe un conjunto de números llmdos reles en el que están definids 2 operciones: Adición (+) y multiplicción (.). Est estructur se indic sí: (R, +,. ) (Axiom de Cuerpo) Sen, b y c reles
FICHA 1 3/2008 Existe un conjunto de números llmdos reles en el que están definids 2 operciones: Adición (+) y multiplicción (.). Est estructur se indic sí: (R, +,. ) (Axiom de Cuerpo) Sen, b y c reles
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero. TEMA 2: actividades
 º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
Introducción. Objetivos de aprendizaje. Determinar las propiedades de las operaciones de números racionales
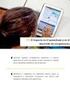 L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
INDICADORES DE DESEMPEÑO
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL-EJERCITACION PERIODO GRADO FECHA DURACION 8º A/B Myo
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL-EJERCITACION PERIODO GRADO FECHA DURACION 8º A/B Myo
