Ejercicios y problemas propuestos
|
|
|
- Andrés Espinoza Juárez
- hace 5 años
- Vistas:
Transcripción
1 Ejercicios problemas propuestos Página Para practicar Integral definida Calcula las siguientes integrales: a) d b) e d c) ln d d) d /e a) / ( ) d ( ) d / > H : D / / / b) d / / d ( ) d e o G < F / / d n d n d 8 n d n d n e c) ln d. Integramos por partes ln d: /e u ln 8 du d dv d 8 v ln d ln d ln e e ln 8 ln B ( e ln e e) d ln n e e e e / e / d) d ( e e) d ( ) n d n e e e e Calculamos una primitiva: d d d arc tg e o d 8 arc tg B c πm c πm π π π π/ Calcula: sen cos d π/ () / / * sen cos d t dt t G (*) Aplicamos el siguiente cambio: sen t ; cos d dt para ; t para π ; t 8
2 Halla el valor de la integral definida de la función f () I [, ]. Halla: sen( π) cos( π ) d ln( ) ln ln ln d n G π ( ) d G si < * ( ) si < si ( ) d d d ( ) d ( ) d G G d n cos (π) en el intervalo Calcula las siguientes integrales: si < a) f () d siendo f () * b) f () d siendo f () ) si si si < a) f () d d ( ) d G G d n b) f () d d ( ) d G G d n Área entre f (), eje X, a, b a) Calcula: ( ) d b) Halla el área que determina la curva con el eje X entre las abscisas. a) ( ) d 8 G d n b) Los puntos de corte de la curva con el eje X son:, De estos dos valores, uno se encuentra en el intervalo [, ] es. G () ( ) d G ( ) ; G( ) ; G( ) ( ) d G( ) G( ) ( ) d G( ) G( ) Área u
3 Calcula el área comprendida entre la curva, el eje X las rectas. I. Calculamos las soluciones de la ecuación: No tiene soluciones, por lo que no corta al eje X. II. Buscamos una primitiva de f (): G () ( ) d III. G (), G () IV. G () G () El área buscada es u. (La gráfica se ha incluido para entender el proceso, pero es innecesaria para obtener el área). 8 Calcula el área bajo la curva entre las rectas. I. Hallamos la solución de la ecuación. Es. II. Ordenamos los etremos del intervalo la raíz que ha entre ellos:,,. III. Buscamos una primitiva de f (): G () ( ) d IV. G ( ) ; Gd n ; G( ) V. Gd n G( ) G () G d n El área buscada es: u. (Se inclue la gráfica, aunque es innecesaria para obtener su área). 8 8 Halla el área bajo la curva entre. I. Buscamos la primitiva de la función f (). G () d II. G (), G () 8 III. G () G () El área buscada es: u. (Se inclue la gráfica, aunque es innecesaria para obtener su área).
4 Calcula el área de la región limitada por la curva ( ) ( ) las rectas,,. I. Hallamos las soluciones de la ecuación: ( ) ( ). Son. II. Ordenamos los etremos del intervalo las raíces que ha entre ellos:,,. III. Buscamos una primitiva de f (): G () ( ) ( ) d IV. G (), G( ) V. G () G () El área buscada es u. (Se adjunta la gráfica, aunque es innecesaria para resolver el ejercicio). ( ) ( ) Calcula el área de la región limitada por la curva las rectas,,. I. Hallamos la solución de. Es. II. Como esta solución se encuentra fuera del intervalo de integración, los etremos son. III. Buscamos la primitiva de la función f (), la cual es continua en dicho intervalo: G () d ln IV. G () ln ( ), G( ) ln ( ) V. G () G () [ ln ( ) ln ( )] El área buscada es: [ ln ( ) ln ( )] u. (Se adjunta la gráfica, aunque es innecesaria para la resolución del ejercicio). Cálculo de un área reconociendo la figura Las siguientes integrales se pueden calcular reconociendo, en cada caso, la curva cua ecuación está bajo el signo integral calculando, utilizando métodos de geometría elemental, el área pedida: a) d b) ( ) d c) d d) d Recuerda que el área de la elipse de semiejes a b es A πab. a) La recta, entre, limita con el eje X un triángulo. Por tanto: d 8 B 8 b) La recta, entre, limita con el eje X un trapecio. Por tanto: ( ) d G
5 c) La curva es una semicircunferencia centrada en el origen, de radio situada por encima del eje X. La integral pedida es un cuadrante de círculo, por tanto: d) d π π La función es la parte positiva de una elipse que corta a los ejes en (, ); (, ) (, ) la integral pedida es un cuadrante del área encerrada por la elipse. Por tanto, d π π Halla gráficamente las siguientes integrales: a) ( ) d b) ( ) C d a) La recta, entre, limita con el eje X un triángulo. Por tanto: ( ) d b) Como vemos en la gráfica siguiente, la integral es el resultado de restar al área del rectángulo el área del semicírculo de radio. Y X ( ( ) ) d π π Área entre dos curvas Halla, en cada caso, el área comprendida entre los siguientes pares de parábolas: a) e b) e a) I. Buscamos las soluciones de. Son Por tanto, estos van a ser nuestros límites de integración. II. Se obtiene la función diferencia: ( ) ( ) III. Buscamos su primitiva: G () ( ) d IV. G( ) G( ) El área buscada es: u. (Se inclue la gráfica, aunque es innecesaria para obtener el área).
6 b) I. Buscamos las soluciones de la ecuación:. Son. II. Calculamos la función diferencia: III. Buscamos su primitiva: G () ( ) d IV. G (), G () V. G () G () El área buscada es u. (Se adjunta la gráfica, aunque no es necesaria para la resolución del ejercicio). Calcula el área comprendida entre las curvas dadas en cada uno de los ejercicios siguientes: a) ; 8 b) ; c) ; d) ( ) ( ); e) ; f) ; g) ; a) I. Buscamos las soluciones de 8. Son. Por tanto, estos van a ser nuestros límites de integración. II. Calculamos la función diferencia: (8 ) ( ) III. Calculamos su primitiva: G () ( ) d IV. G ( ) 8 8 G () 8 8 V. G () G ( ) El área buscada es: d n u. 8 8 b) I. Buscamos las soluciones de la ecuación:. Son (nuestros límites de integración). II. Calculamos la función diferencia: ( ) III. Calculamos su primitiva: G () ( ) d 8 8 IV. G( ), G( ) 8 8 V. G( ) G( ) El área buscada es: u. (Se adjunta la gráfica, aunque es innecesaria para hallar el área).
7 c) I. Buscamos las soluciones de la ecuación:. Son,. II. Calculamos la función diferencia: ( ) III. Calculamos su primitiva: G () ( d ) IV. G (), G () G () G (), G () G () G () El área buscada es: u. (La gráfica que se adjunta es para entender mejor el ejercicio, pero es innecesaria para obtener el área). d) I. Buscamos las soluciones de: ( )( ). Son,. II. Calculamos la función diferencia: ( )( ) III. Calculamos su primitiva: G () ( )( ) d Resulta que se trata del mismo ejercicio que el apartado c). El área buscada es: u. e) I. Buscamos las soluciones de la ecuación:. Son. II. Calculamos la función diferencia: III. Calculamos su primitiva: G () ( ) d IV. G ( ), G () V. G () G ( ) El área buscada es: u. (Se adjunta la gráfica, aunque es innecesaria para resolver el ejercicio). f ) I. Buscamos las soluciones de la ecuación:. Son. II. Calculamos la función diferencia: ( ) ( ) III. Calculamos su primitiva: G () ( ) d IV. G (), G () V. G () G () El área buscada es: u. (Se adjunta la gráfica, aunque es innecesaria).
8 g) I. Buscamos las soluciones de:, Son. II. Calculamos la función diferencia: ( ) ( ) III. Calculamos su primitiva: G () ( ) d IV. G ( ), G () V. G () G ( ) El área buscada es: u. 8 (Se adjunta la gráfica, aunque es innecesaria para la resolución del ejercicio). Dibuja halla el área de la región limitada por la curva ( ) la recta. ( ) I. Buscamos las soluciones de la ecuación: ( ). Son. II. Calculamos la función diferencia: f () ( ) ( ) III. Calculamos su primitiva: G () ( ) d IV. G ( ), G( ) V. G () G ( ) El área buscada es u. Dibuja el recinto plano limitado por la parábola por la recta paralela a que pasa por el punto (, ). Calcula el área de ese recinto. Recta paralela a que pasas por (, ): m ( ) P(, ) Buscamos los puntos de corte de la curva la recta : Representamos el recinto lo descomponemos en dos partes: R limitado por, eje OX la recta R limitado por, eje OX la recta 8 8
9 Calculamos en primer lugar el área de R : Y R X / ( ) A R d ( ) d > H G / < ( ) F G 8 > d n d nh Calculamos ahora el área de R : R Y X u A R d ( ) d < ( ) F G Área total: R R u otra forma de resolverlo I. Calculamos las soluciones de la ecuación: (Esta ecuación resulta de despejar la en: ; ). Sus soluciones son,. Y X II. Calculamos la función diferencia: ( ) ( ) III. Buscamos su primitiva: G () ( ) d IV. G ( ) G( ) V. G () G ( ) El área buscada es u.
10 8 Halla el área limitada por la función sus tangentes en los puntos en los que su gráfica corta al eje de abscisas. I. Buscamos las soluciones de la ecuación:. Son. II. Calculamos la derivada de f (), que es f '(). La tangente que pasa por (, ) tiene pendiente f '() ; por tanto, es. La tangente que pasa por (, ) tiene pendiente f '() ; por tanto, es. III. Tenemos que distinguir dos intervalos de integración: entre entre. La función diferencia en el primer intervalo es: f () ( ) en el segundo intervalo es: f () ( ) IV. Sus primitivas son: G () d G () ( ) d V. G (), G (), G ( ) G ( ) G ( ), G ( ) 8, G ( ) G ( ) El área buscada es: u. (Se adjunta la gráfica, aunque no es necesaria para resolver el ejercicio). Página 8 Dadas la hipérbola la recta, calcula el área comprendida entre ellas. I. Buscamos las soluciones de la ecuación:. Son (nuestros límites de integración). II. Calculamos la función diferencia: III. Buscamos su primitiva: G () d n ln IV. G () G () ln () V. G () G () ln () ln () El área buscada es: ln () u (Se adjunta la gráfica, aunque no es necesaria para resolver el ejercicio).
11 Calcula el área limitada por la curva la recta tangente a ella en el origen de coordenadas. I. Calculemos la ecuación de la recta tangente en el punto (, ); para ello, calculamos la derivada de nuestra función: ' () (pendiente) La recta tangente tiene por ecuación. II. Calculamos las soluciones de:. Son (límites de integración). III. Obtenemos la función diferencia: IV. Buscamos su primitiva: G () ( ) d V. G (), G () G () G () El área buscada es: u. (Se adjunta la gráfica aunque no es necesaria para la resolución del ejercicio). Halla el área encerrada por la curva ln entre el punto de corte con el eje X el punto de abscisa e. La curva ln corta al eje X en el punto de abscisa. Área e Integramos por partes: * ln d u ln 8 du d dv d 8 v G () ln d ln d ln e Área ln d G() e G( ) ( ) u Halla el área limitada por las gráficas de las funciones que se indican. a) f () g () b) f () g () c) f () ( )( ) g () d) f () g () e) f () g () f ) f () g () a) Calculamos las abscisas de los puntos de corte de las dos curvas: f () g (), Llamamos la integral de h () f () g () Área u ( ) d G
12 b) Calculamos las abscisas de los puntos de corte: 8, Y 8, X Utilizamos la simetría respecto del eje vertical: e o [ ( )] d G e o ( ) d > H G e o Área e o u c) f () g () se cortan en los puntos de abscisas,,. d) Llamamos h () f () g () ( )( ) H () ( d ) H () ; H () Área ; H () ( d ) H( ) H( ) ( d ) H( ) H( ) u Área u 8, ( d ) G e) 8,, G () [ ( )] d e o e o e o Ge o ; G( ) e o e o e o G e o
13 ( d ) G( ) G e o ( d ) Ge o G( ) Área u f ) 8, ( ) d G d n Área u Volúmenes Calcula el volumen engendrado al girar alrededor del eje X los recintos siguientes: a) f () entre b) f () entre c) f () entre u d d G u u a) V π ( ) d π ( ) d π G 8π b) V π ( ) π π π c) V π ( ) d π ( ) d π G π Calcula el volumen engendrado al girar alrededor del eje X los recintos limitados por las gráficas que se indican: a) f (), g() b), a) I. Buscamos las soluciones de la ecuación:. Son. Estos son nuestros límites de integración. II. Calculamos la función diferencia: u f d d 88 B 8 III. V π ( ) ( ) d π ( ) d π G π u b) V π () π ( ) π π
14 Función integral Calcula las derivadas de las siguientes funciones: a) F () costdt b) G () ( t ) c) H () e t dt d) J () ( t ) Atención! La última es la más fácil. a) F '() cos b) F '() ( ) c) H '() e d) J '(), porque J () es constante. dt dt Para resolver Halla el área comprendida entre la curva: el eje de abscisas las rectas verticales que pasan por los puntos de infleión de dicha curva. I. Buscamos los puntos de infleión; para ello, calculamos las dos primeras derivadas: ' ( ) ( 8 ) '' ( ) Igualamos a cero para encontrar en qué valores de la segunda derivada es cero. Esto ocurre en II. Calculamos la primitiva de nuestra función: G () arc tg e o III. Ge o arc tg e o Ge o arc tg e o (puntos de infleión). Ge o Ge o farc tg e o arc tg e op El área buscada es: farc tg e o arc tg e op (Se adjunta la gráfica, aunque es innecesaria para la resolución del ejercicio).
15 Si f () g () : a) Dibuja las dos gráficas sobre unos mismos ejes halla sus puntos de intersección. b) Determina el área del recinto encerrado entre ambas gráficas. Y g() R R f() X a) Definimos g () por intervalos: g () ) si si > Buscamos los puntos de intersección resolviendo la siguiente ecuación: ( ) o bien ( ) Al elevar al cuadrado cualquiera de las dos ecuaciones, llegamos a: ± / Sus soluciones son (límites de integración). b) Tenemos que distinguir dos intervalos de integración: de a de a, porque en cambia la definición de g (). Tenemos, por tanto, dos recintos de integración, R R. I. La función diferencia en el primer intervalo es: h () ( ) La función diferencia en el segundo intervalo es: h ( ) II. Sus primitivas son: H () d n d n H () d n d n III. H d n ; H( ) H ( ) ; H ( ) IV. Área del recinto R : H ( ) H d n Área del recinto R : H ( ) H ( ) El área buscada es u.
16 8 Se considera la función: g () * si < si < si < Representa la función g calcula el valor de las siguientes integrales definidas: I gd () J gd () K gd () Y X I g() d d d G 8 B 8 J g() d d ( d ) 8 B G K g() d I J Dibuja el recinto comprendido entre las gráficas de las funciones,, 8, halla su área. Y 8 R R I. Buscamos los puntos de intersección de las funciones:. Su solución es Su solución es Su solución es. Tenemos dos intervalos de integración: de a de a. Corresponden a los recintos R R señalados en el gráfico. II. Hallamos la función diferencia en el primer intervalo: f () 8 Y en el segundo intervalo: f () X
17 III. Buscamos sus primitivas: G () d G () e d o IV. G (), G d n 8 G d n, G ( ) 8 V. Área de R : Gd n G ( ) Área de R : G () G d n 8 8 El área buscada es u Calcula el área del recinto plano limitado por la curva e las rectas. Buscamos una primitiva a nuestra función: G () e d ( ) e (aplicando el método de integración por partes). e G () G () e G () G () e El área buscada es (e ) u. (Se adjunta la gráfica, aunque no es necesaria para resolver el ejercicio). Dada la curva, halla el área limitada por la curva, la recta tangente en el punto donde la función tiene un etremo la tangente a la curva con pendiente. Buscamos el punto donde la curva tiene un etremo, hallando su derivada e igualando a cero: ', el punto es (, ). La ecuación de la recta tangente en dicho punto es. Por otro lado, la ecuación de la recta tangente con pendiente es. Buscamos los puntos de corte de la curva con ambas rectas, de con es (, ); de con es (, ); de con es d, n. Distinguimos dos intervalos de integración: de a de a. En el primer intervalo la función diferencia es: f () En el segundo: f () ( ) Buscamos sus primitivas: G () G ()
18 G ( ), G d n G d n, G( ) 8 G d n G ( ) G () G d n 8 El área buscada es: u / al dar una vuelta completa alre- Halla el volumen del cuerpo limitado por la elipse dedor de OX. u V π f p d π e o d π G π Calcula el área limitada por f (), el eje X las rectas a b, siendo a b las abscisas del máimo el mínimo de f. La función corta al eje X en. Por otro lado, tiene un mínimo en un máimo en. Tenemos que distinguir entre dos intervalos: de a de a. Hallamos la función primitiva: G () d ln ( ) El área en el primer intervalo es: G ( ) ln 8 G () ln G () G ( ) (ln ln 8) (ln ln 8) (ln 8 ln ) u El área en el segundo intervalo es: G () ln 8 G () G () (ln 8 ln ) (ln 8 ln ) u El área total es: (ln 8 ln ) (ln 8 ln ) (ln 8 ln ) u
19 Halla el área comprendida entre las curvas e, las rectas. I. Hallamos la función diferencia: e ( ) e II. Buscamos su primitiva: III. G () G () e G () e G () G () e El área buscada es: de n u. 8 e Página 8 La curva, los ejes de coordenadas la recta limitan una superficie S. Calcula el área de S el volumen de la figura engendrada por S al girar alrededor del eje X. Buscamos una primitiva: G () ln G () ln G () ln 8 G () G () (ln 8 ln ) El área buscada es (ln 8 ln ) u. V π d n d π < F π π u 8 Halla el polinomio de segundo grado que pasa por los puntos (, ) (, ), sabiendo que el área limitada por esa curva, el eje Y el eje X positivo es /. Como el polinomio pasa por el punto (, ), una raíz es, por tanto: ( )(a b ) Por otro lado, cuando, : ( b) b, b Luego queda: ( ) da n Puesto que pasa por los puntos indicados está limitado por los ejes X e Y (positivos), los límites de integración son.
20 Así, buscamos la primitiva del polinomio: G () ( ) a d a a d a a d n c m G () G () a a G () G () a a De donde sacamos que a. Por tanto, el polinomio es: ( ) d n Halla la ecuación de una parábola de eje vertical, tangente en el origen de coordenadas a una recta de pendiente que delimita con el eje X un recinto de base [, ] área. Del enunciado del problema se deduce que la parábola pasa por el origen de coordenadas. Supongamos que es de la forma f () a b. Como la pendiente de la recta tangente en el origen es f ' (). f '() a b, f '() b f () a Si la gráfica de la parábola queda por encima del eje X en el intervalo [, ], el área es: ( a d ) a G a 8, a 8 8 a La parábola buscada es f (), cua gráfica es positiva en el intervalo [, ]. 8 De la función f() a b c d se sabe que tiene un máimo relativo en, un punto de infleión en (, ) que f () d. Calcula a, b, c d. Hallamos f '() a b c f ''() a b Sabemos que f () pasa por el punto (, ), es decir, f (), de donde averiguamos que d. Por otro lado, sabemos que tiene un máimo relativo en, esto es que f ' (), es decir: a b c También tiene un punto de infleión en (, ), por lo que f ''(), de donde b. Como a b c b, se tiene que: a c c a Así, nuestra función queda reducida a la función: f () a a Buscamos su primitiva: G () a a G (), G () a a a G () G () a El resultado es a que es igual a, de donde deducimos que a, por tanto, c. La función buscada es f ().
21 Teniendo en cuenta que la función f () k toma valores positivos negativos, halla el valor de k de forma que el área de la región limitada por el eje X, las rectas, la curva f () quede dividida por el eje X en dos partes con igual área. Supongamos que a comprendido entre es el punto donde nuestra función corta al eje X; por tanto, tenemos que distinguir dos intervalos de integración: de a a de a a. Buscamos una primitiva de nuestra función: G () k k G ( ) k G () k Si suponemos que en el primer intervalo la función es negativa, el área es: G ( ) G (a) si en el segundo intervalo la función es positiva, el área es: G () G (a) Y como el área en los dos intervalos tiene que ser la misma, se tiene la siguiente igualdad: G ( ) G (a) G () G (a) es decir: G ( ) G () k k 8 k Observa que se obtiene el mismo resultado independientemente de qué intervalo consideremos en el que la función es positiva o negativa. Se consideran las curvas e a, donde < a <. Ambas curvas se cortan en el punto (, ) con abscisa positiva. Halla a sabiendo que el área encerrada entre ambas curvas desde hasta es igual a la encerrada entre ellas desde hasta. Hallamos los puntos de corte: a 8 a a a (no vale porque la abscisadebeser positiva). El punto de corte es ( aa., ) Dibujamos las áreas para tener una idea más clara de nuestro ejercicio: Tenemos dos intervalos de integración: de a a de a a, que determinan los recintos R R señalados en el gráfico. Y a R R a a X La función diferencia para el primer intervalo es: f () a
22 Su primitiva es: G () a G (), G ( a) El área del primer intervalo es a a a a a a a a u. La función diferencia en el segundo intervalo es: f () a Su primitiva es: G () a a a G ( a) a a, G ( ) a G () G ( a) a a a El área del segundo intervalo es a a a u. Como el área en los dos intervalos es igual, se tiene que: a a a a a De donde obtenemos que a. Sean a e a a las ecuaciones de una parábola p de una recta r, respectivamente. Demuestra las siguientes afirmaciones: a) Los puntos de corte de p r no dependen del valor de a. b) Si se duplica el valor de a, también se duplica el área encerrada entre p r. a) Los puntos de corte se obtienen al igualar ambas ecuaciones: a a a a a a a( ) Como suponemos a, para que sean ciertamente una parábola una recta, dividiendo toda la ecuación entre a, llegamos a: sus soluciones son: b) La función diferencia es: f () a a a a( ) Si llamamos h (), se tiene que: f () a h () (que no dependen de a). la primitiva de f () es a por la primitiva de h (), es decir: G () a H () El área comprendida es, por tanto: G e o G e o afhe o He op u
23 Si duplicamos a, se tiene que la función diferencia es ahora: f () a h () su primitiva: G () a H () Por lo que el área comprendida es: G e o Ge o afh e o H e op u Sabiendo que el área de la región comprendida entre la curva la recta b es igual a, calcula el valor de b. La curva la recta b se cortan en el punto de abscisa b en. Así, nuestros límites de integración son b. La función diferencia es: b Su primitiva es: G () b G () G (b) b G (b) G () b Como el área es, se tiene que: b, de donde obtenemos que b. 8 Calcula el valor de a para que el área de la región limitada por la curva a el eje X sea igual a. La curva corta al eje X en los puntos de abscisa a (estos son los límites de integración). Su primitiva es: G () a G () G (a) a G (a) G () a Como el área es, se tiene que: a, de donde averiguamos que a. 8
24 Dada la función calcula el valor de a para que el área limitada por esa curva las rectas a sea igual a. Buscamos su primitiva: G () ln ( ) G () G (a) ln (a ) G (a) G () ln (a ) Como el área es igual a, se tiene que: ln (a ) de donde averiguamos que a e. e e Epresa la función de posición de un móvil sabiendo que su aceleración es constante de 8 cm/s, que su velocidad es cuando t que está en el origen a los segundos. Llamamos S (t) a la posición del móvil al cabo de t segundos. Así: V (t) S' (t) a(t ) S ''(t) 8 cm/s Calculamos la velocidad V (t): Vt () at () dt 8dt 8t k V( ) k 8 k Calculamos S (t): V (t ) 8t S (t) Vt () dt ( 8t ) dt t t c S () c c Por tanto: S (t ) t t Un móvil se desplaza en línea recta, con movimiento uniformemente acelerado, con aceleración de m/s con velocidad inicial v m/s. Calcula compara las distancias recorridas entre t t entre t t. Calculamos la velocidad del móvil: Vt () at () dt dt t k V( ) k Distancia recorrida entre t t : V (t ) t d Vt () dt ( t ) dt 8t t B m Distancia recorrida entre t t : d Vt () dt 8t tb m Por tanto, recorre la misma distancia entre t t que entre t t.
25 Halla el volumen del cuerpo engendrado por la región del plano limitada por los ejes de coordenadas, la curva de ecuación e la recta, al girar alrededor del eje X. u V π ( e ) d π e d π e π ( e 8 B ) e 8 Calcula el volumen que se obtiene al hacer girar alrededor del eje X el recinto limitado por las gráficas de las funciones,,. Las curvas se cortan en el punto de abscisa. Por tanto, nuestros límites de integración son. El volumen buscado es el resultado de restar el volumen engendrado por la curva alrededor de OX entre, el volumen engendrado por la curva alrededor de OX entre los mismos límites. V π ( ) d π G π u V π dn d π < F π u El volumen buscado es: V V π π π u Calcula el volumen engendrado por la hipérbola cuando [, ]. u V π f ( ) d π e o d π G π 8π
26 Halla el volumen engendrado por la circunferencia al girar alrededor del eje X. El círculo del ejercicio tiene su centro en (, ) radio ; por tanto, corta al eje OX en (, ) (, ). Así, nuestros límites de integración son. ( ) u ( ) V π d π ( ( )) d π > H π Halla la derivada de las funciones que se dan en los siguientes apartados: a) F () cost dt b) F () ( t t) dt c) F () sen t dt sen d) F () ( tdt ) a) Como f es continua, podemos aplicar el teorema fundamental del cálculo: F '() cos b) Como f es continua, también podemos aplicar el teorema fundamental del cálculo: F '() [( ) ] c) Del mismo modo: F '() sen d) Análogamente: F '() ( sen ) (sen )' ( sen ) cos Sin resolver la integral, indica dónde ha máimo o mínimo relativo en la función: F () ( t ) dt Los máimos o mínimos relativos se obtienen para los valores de donde la primera derivada es cero, en nuestro caso, F '(). Como f es continua, podemos aplicar el teorema fundamental del cálculo: F '() F '() en, así en los puntos de abscisa ha máimos o mínimos relativos. Sabemos que f () t dt ( ), siendo continua en Á. Calcula f (). Aplicando el teorema fundamental del cálculo, se tiene que: f () ( ) f () Sea F () cos t dt. Halla los posibles etremos de dicha función en el intervalo [, π]. Como f () cos es continua en [, π], podemos aplicar el teorema fundamental del cálculo, así obtenemos la primera derivada de la función F (): F '() cos Esta tiene sus etremos en los valores de en que F '(), esto es en π π.
27 Página 8 Halla máimos mínimos relativos de las funciones: a) F () ( t ) ( t ) dt b) G () log t dt t a) F '() ( ) ( ) F '() ( ) ( ), Pero F '() > cuando por ser un cuadrado perfecto. Luego F () es creciente no tiene máimos ni mínimos relativos. b) G '() log con > G ' () log G' < G' > El mínimo relativo se alcanza en. log t, G () dt El mínimo relativo es el punto (, ). t Considera la región del plano que determinan las curvas e e e la recta k. a) Halla su área para k. b) Determina el valor de k > para que el área sea. a) Las funciones dadas se cortan en el punto,. Si k >, el área es: k k k k ( e e ) d e e e k e e k G d n e Si k <, el área es: k ( e e ) d e e k G e e k k b) e k e k k 8 e e Haciendo el cambio de variable z e k, obtenemos: z z z, z (no vale) e k k ln k Calcula el área encerrada entre la curva la cuerda de la misma que tiene por etremos los puntos de abscisas. Calculamos las coordenadas de los puntos:, (, ), (, ) La pendiente de la cuerda que pasa por ellos es: m La ecuación de la recta que contiene a la cuerda es: G () [( ) ( )] d [( ) ( )] d El área buscada es u.
28 Cuestiones teóricas 8 Calcula la derivada de la función dada por F () costdt de dos formas: a) Obteniendo de forma eplícita F (), después, derivando. b) Aplicando el teorema fundamental del cálculo. a) F () 8sen tb sen F ' () cos b) Como f es una función continua en todos los puntos, se puede aplicar el teorema fundamental del cálculo: F ' () f ( ) ( )' cos La gráficas I, II III corresponden, no necesariamente por ese orden, a las de una función derivable f, a su función derivada f a una primitiva F de f. Identifica cada gráfica con su función, justificando la respuesta. I II III La gráfica II es la de la función; la gráfica I, la de su derivada la gráfica III, la de su primitiva. La razón es: partiendo de la gráfica II, observamos que se trata de una función lineal (afín) con pendiente positiva, por lo que la función derivada tiene que ser una función constante (la pendiente de la función afín). Por otro lado, la primitiva de la función afín tiene que ser una función cuadrática, cua gráfica corresponde a la parábola. Sabemos que el área limitada por una función f, el eje de abscisas las rectas es igual a. Cuánto aumentará el área si trasladamos unidades hacia arriba la función f? f f Si trasladamos también el eje OX unidades hacia arriba, es fácil ver que el área añadida es la de un rectángulo u de base u de altura (su área es 8 u ). Y X Es decir, su área aumentará 8 u. (No depende de lo que mida el área señalada). Si una función f es positiva para todos los valores de su variable, cualquier función primitiva de ella es creciente en cada uno de sus puntos. Por qué? Cierto, puesto que si la primera derivada de una función es positiva, dicha función es creciente.
29 Halla las derivadas de: a) F () cos t dt b) F () ( t) dt a c) F () dt d) F () t (Observa que la puede salir fuera de la integral) a) F '() por ser una función constante. b) F () ( t ) dt F '() dt t a c) F () t dt a F '() t dt d) F () t dt F '() t dt t dt Cuál de las si guientes epresiones nos da el área limitada por la gráfica de f el eje de abscisas? f a b c c c b c b c a) f b) f c) f f d) f f a d) a a Dada la función, halla el punto c [, ] tal que el área d sea igual a la de un rectángulo de base altura f (c). Es decir, que cumpla lo siguiente: f (c) d Qué teorema asegura la eis tencia de c? d 8 Así pues, se tiene: f (c) 8, de donde averiguamos que c. El teorema que asegura la eistencia de c es el teorema del valor medio del cálculo integral. Sea F una función definida en [, ) tal que: F () ln ( tdt ) Analiza si es verdadera o falsa cada una de las siguientes afirmaciones: a) F () ln b) F ' (), c) F es creciente en su dominio. a) Calculamos G (t) ln ( tdt ) integrando por partes: u ln ( t) 8 du t dt dv dt 8 v t G (t) ln ( tdt ) t ln ( t) t dt t ln ( t) d ndt t t t ln ( t) t ln ( t) ( t ) ln ( t) t a b b
30 Por tanto: F () G () G () [( ) ln ( ) ] [ln ] ( ) ln ( ) ln F () ln ln La afirmación F () ln es falsa (basta ver, además, que en F () no ha área). b) Como f es continua para, aplicamos el teorema del cálculo integral: F '() ln ( ) También es falsa. c) Cierta, porque su derivada F ' es positiva en todo el dominio. Demuestra la desigualdad siguiente: En el intervalo ;, π E se cumple que: π/ sen d sen a que sen en dicho intervalo. Por tanto: π sen d π π d π ln ( ) ln π, d < F e o < De esta forma queda probada la desigualdad. Página 8 Para profundizar a) Halla el volumen del tronco de cono de radios cm cm altura cm. b) Obtén la fórmula: V π h ( r r r r ) que nos da el volumen de un tronco de cono de radios r, r altura h. Y B A X a) La recta pasa por los puntos (, ) (, ). Obtenemos su ecuación: m, la recta es Los límites de integración son.
31 b) El volumen será: V f () d d π ` j π d n π d nd π G π u r r h La recta pasa por los puntos (, r ) (h, r ). Obtenemos la ecuación: r r r r r r m 8 r d n h h h El volumen será: h r r V π > r d nh d h h r r π > r r r d n r d n H d h h r r r r r π > r d n d n H h h r r r r π r h h > d n r d n h H h h π r h < ( r r r r r r r F π r h < r rr rr F πh ( r r rr ) 8 a) Demuestra, utilizando el cálculo integral, que el área del círculo es π. b) Demuestra, utilizando el cálculo integral, que el volumen de la esfera de radio r es V π r. h a) Área d Calculamos G () d G () d c m d, mediante un cambio de variable:
32 Cambio: sent 8 sen t 8 d cos t dt G () sen t costdt cos t dt cos t dt t sen t t e o < F sen t arc sen c m c m arc sen c m c m arc sen c m Por tanto, el área será: A (G() G ()) π π u R R b) V π d π ( R ) d π R π R R G e R R o π R R R R R Calcula el área encerrada por la elipse. 8 e o 8 ± c m El área es: A d c m c m d Calculamos G () c m d : Cambio: sent 8 sen t 8 d cos t dt G () sen t costdt cos t dt e cos t odt ( cos t) dt t sen t arc sen c m arc sen c m 8 El área será: A [G () G ()] π
33 Demuestra, utilizando el cálculo integral, que el área de la elipse es π. Despejamos : 8 ± c m c m El área será: A c m d Calculamos G () c m d Cambio: sent 8 sen t 8 d cos t dt G () sen t costdt cos t dt e cos o ( cos ) t dt tdt t sen t arc sen arc sen c m c m c m El área será: A [G() G ()] π π Demuestra que el volumen del elipsoide obtenido al girar la elipse a es: b a) π a b si gira alrededor del eje X. b) π a b si gira alrededor del eje Y. a a) V π b b f p d π > b b H π e b a ab b a ab o π ab a a a b b) V π a a d π a a π a b ba f p > H e a b ba o πba b b b a a b b Halla la derivada de la función siguiente: F () sen tdt Si G () es una primitiva de la función g () sen, entonces sentdt G ( ) G ( ). La derivada, aplicando la regla de la cadena, es: D sen tdtg D [G( ) G ( )] G' ( ) G' ( ) sen ( ) sen ( ) Por tanto: F '() sentdt [ sen( ) sen ( )] sen tdt [ sen ( ) sen ( )]
34 Comprueba si eisten, en su caso, calcula las siguientes integrales impropias: a) dt b), t d r > c) dt d) e d r t e) d f ) d g) d h) du ( u ) a) dt 8arc tgtb arc tg t í π d lm dt lm í arc tg 8 8 t b) dt r r G r t ( rt ) ( r) r d lm í dt r 8 r t, a que r >, por tanto, la primera fracción tiende a. r c) dt 8arc tgtb arc tg arc tg ( ), con > t ( ) π π π d lm í dt lm í 8arc tg arc tg B c m 8 8 t t t d) e dt 8e B e, con > e) t 8 8 e d lím e dt lm í ( e ) t dt < t F / / d lm dt lm / í í d n 8 t 8 f ) ln ln t dt 8 t B g) h) lm í dt lm í ( ln ) t No eiste la integral. 8 8 t dt 8arc sen tb arc sen d lm í dt lm í arc sen π 8 t 8 du < F ( u ) u lm í du lm í 8 ( u ) d 8 n No eiste la integral. Si f () lm í e g () f () t dt, halla el siguiente límite: g () lm í 8 g () ( ) H '() lm í g lm í f () lm í ( ) e Por tanto, el límite dado vale.
35 Determina el valor del parámetro a > de tal manera que valga 8 el área de la región del plano limitada por el eje X la gráfica de la función siguiente: f () a( ) ( ) La función corta al eje X en los puntos de abscisa a. Nuestros límites de integración; buscamos una primitiva: G () [ ( ) ( )] ( ) a d a ( ) G (a ) a G ( ) G (a ) G () a Como el área tiene que ser 8, igualamos: a 8. De donde obtenemos que a.
36 Autoevaluación Página 8 Dada la función f (), calcula: a) El área encerrada por la gráfica de f (), el eje X las rectas. b) El área de cada uno de los dos recintos comprendidos entre las gráficas de f () de g (). a) Representamos el recinto: Cortes con el eje OX : Y ( ) Puntos singulares: f ' () ( ) X f '' () f ''( ) > 8 Mínimo: (, ) f ''( ) < 8 Má imo: (, ) Área ( ) d G d n ( 8 ) u b) Representamos f () g () : Hallamos los puntos de corte de f g : Y X Las gráficas se cortan en,. Calculamos el área entre el área entre : [( ) ( )] d ( ) d G d n d8 n d n u [( ) ( )] d ( ) d G d n d n d n u
37 Calcula el área del recinto limitado por f (), el eje Y la recta tangente a f en. Calculamos la tangente a f () en : Punto de tangencia:, f () (, ) Pendiente de la recta tangente: f '() m f ' () Ecuación de la recta tangente: ( ) Representamos el recinto: f () Y X Vértice de la parábola: f ' (), f () (, ) Corte con los ejes:, f () (, ) ± 8 No corta al eje OX. Calculamos el área: u A [( ) ( )] d ( ) d G Calcula: d La función se descompone de la siguiente manera: Por tanto: f () > * f () d ( ) d ( ) d 8 B 8 B / /
38 Halla el área de la región comprendida entre la gráfica de la función f () ( ),. Representamos la función f () ( ) : Asíntota vertical:, lm í f () 8 Asíntota horizontal: Puntos singulares: f '() para cualquier No tiene puntos singulares. ( ) Punto de corte con la recta : 8 ( ) ( ) 8 (, ) 8 (, ) Recinto: Y las rectas Área d ( ) G < F u X Calcula el área encerrada entre la gráfica de la función eponencial f () e la cuerda a la misma que une los puntos de abscisas. Ecuación de la cuerda: Área: 8 f ( ) e Recta que pasa por (, ) por (, e ): 8 f ( ) e m e 8 e e e e d e o e G ( e e ) ( e ) u Dada la función F () ln tdt con : a) Calcula F ' (e). b) Tiene F puntos de infleión? Justifica tu respuesta. a) F () ln td F '() (ln ) (ln ) ln F '(e) e ln e e b) F '' () ln ln ; ln ln e F no tiene puntos de infleión porque e < ; es decir, e no pertenece al dominio de F.
39 a) Halla, integrando la función adecuada en el intervalo que convenga, el volumen de un cono de radio cm altura cm. b) Procediendo de forma similar, deduce la fórmula del volumen de un cono de radio r altura a. a) La recta pasa por los puntos (, ) (, ). El cono dado se puede obtener girando el segmento que une los puntos anteriores alrededor del eje X. El volumen es: V π d π π d n G π u b) La recta a r pasa por los puntos (, ) (a, r ). El cono de altura a radio r se puede obtener girando el segmento que une los puntos anteriores alrededor del eje X. El volumen es: a V π r d π π r a c m G πr a u a ar a a
LA INTEGRAL DEFINIDA. APLICACIONES
 UNIDAD LA INTEGRAL DEFINIDA. APLICACIONES Página 78 Problema Interpreta lo que significa el área bajo la curva en cada uno de los siguientes casos: VELOCIDAD (km/h) VELOCIDAD DE UN TREN v = f (t) Gráfica
UNIDAD LA INTEGRAL DEFINIDA. APLICACIONES Página 78 Problema Interpreta lo que significa el área bajo la curva en cada uno de los siguientes casos: VELOCIDAD (km/h) VELOCIDAD DE UN TREN v = f (t) Gráfica
LA INTEGRAL DEFINIDA. APLICACIONES
 13 LA INTEGRAL DEFINIDA. APLICACIONES REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
13 LA INTEGRAL DEFINIDA. APLICACIONES REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
LA INTEGRAL DEFINIDA. APLICACIONES
 LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula
![x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula](/thumbs/55/37833821.jpg) . [] [ET-A] Calcula d. --. [] [ET-B] Calcula / d. (Sugerencia: integración por partes) cos. [] [JUN-A] Sean f: y g: las funciones definidas respectivamente por: f() = y g() = +. a) Esboza las gráficas
. [] [ET-A] Calcula d. --. [] [ET-B] Calcula / d. (Sugerencia: integración por partes) cos. [] [JUN-A] Sean f: y g: las funciones definidas respectivamente por: f() = y g() = +. a) Esboza las gráficas
ANÁLISIS DE FUNCIONES
 ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
( ) ( ) ( ) f h f h h h h. h 0 h h 0 h h 0 h h 0. f h f h h h h
 Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Matemáticas II. * Análisis III: Integrales * o) x x. p) 3. q) 5. r) 1. s) e 2x 3 dx. t) 5 dx. u) x2 5 x 4. v) x3 3x 2 x 1. z) 3
 I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
TREN DE PASAJEROS TREN DE MERCANCÍAS (en horas)
 Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 9 Dos trenes Un tren de pasajeros un tren de mercancías salen de la misma estación, por la misma vía en idéntica dirección, uno tras otro,
Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 9 Dos trenes Un tren de pasajeros un tren de mercancías salen de la misma estación, por la misma vía en idéntica dirección, uno tras otro,
TREN DE PASAJEROS TREN DE MERCANCÍAS (en horas)
 Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 9 Dos trenes Un tren de pasajeros un tren de mercancías salen de la misma estación, por la misma vía en idéntica dirección, uno tras otro,
Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 9 Dos trenes Un tren de pasajeros un tren de mercancías salen de la misma estación, por la misma vía en idéntica dirección, uno tras otro,
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad
 PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
4. [2012] [JUN-A] Sea f una función continua en el intervalo [2,3] y F una primitiva de f tal que F(2) = 1 y F(3) = 2. Calcula: 3 5f(x)-7 dx
![4. [2012] [JUN-A] Sea f una función continua en el intervalo [2,3] y F una primitiva de f tal que F(2) = 1 y F(3) = 2. Calcula: 3 5f(x)-7 dx 4. [2012] [JUN-A] Sea f una función continua en el intervalo [2,3] y F una primitiva de f tal que F(2) = 1 y F(3) = 2. Calcula: 3 5f(x)-7 dx](/thumbs/70/63743679.jpg) . [] [SEP-B] Sea f: la función definida por f() = 9-. a) Halla la ecuación de la recta tangente a la gráfica de f en el punto de abscisa =. b) Esboza el recinto limitado por la gráfica de f, la recta +y
. [] [SEP-B] Sea f: la función definida por f() = 9-. a) Halla la ecuación de la recta tangente a la gráfica de f en el punto de abscisa =. b) Esboza el recinto limitado por la gráfica de f, la recta +y
Integrales. 1. Calcular las siguientes integrales: dx x. iii) xsenx dx. ii) 3dx. Solución: i) Operando se tiene: x 2
 Integrales. Calcular las siguientes integrales: i) d ii) d 6 iii) sen d i) Operando se tiene: d = / / / / d = 7 / / / / / = c = c 7 7 ii) Ajustando constantes se tiene: d 6d = 6 c 6 6 iii) Haciendo el
Integrales. Calcular las siguientes integrales: i) d ii) d 6 iii) sen d i) Operando se tiene: d = / / / / d = 7 / / / / / = c = c 7 7 ii) Ajustando constantes se tiene: d 6d = 6 c 6 6 iii) Haciendo el
ACTIVIDADES INICIALES. 14.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 25, 25 5,...
 Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
INICIACIÓN A LAS INTEGRALES
 INICIACIÓN A LAS INTEGRALES Página REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
INICIACIÓN A LAS INTEGRALES Página REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
ln x dx = x ln x 2x ln x + 2x = (e 2e + 2e) 2 = (e 2) u
 Tema: Integrales definidas. Áreas Ejercicios PAU - JUNIO GENERAL Ejercicio.- Calcule d + Sea F() = d = + = + d d ln ln + = ln ln ln 5 + ln = A B + = + + = A( + ) + B = = A = = B A =, B = d = ln ln ln 5
Tema: Integrales definidas. Áreas Ejercicios PAU - JUNIO GENERAL Ejercicio.- Calcule d + Sea F() = d = + = + d d ln ln + = ln ln ln 5 + ln = A B + = + + = A( + ) + B = = A = = B A =, B = d = ln ln ln 5
a) Calcular las asíntotas, el máximo y el mínimo absolutos de f (x). 4. (SEP 04) Sabiendo que una función f (x) tiene como derivada
 Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
APLICACIONES DE LAS DERIVADAS
 APLICACIONES DE LAS DERIVADAS Apuntes de A. Cabañó. Calcula la tasa de variación media de la función +- en los intervalos: a) [-,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación
APLICACIONES DE LAS DERIVADAS Apuntes de A. Cabañó. Calcula la tasa de variación media de la función +- en los intervalos: a) [-,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación
Aplicaciones de la derivada
 Aplicaciones de la derivada º) Calcula los máimos y mínimos de la función f() = Máimo en P( 6, ) ; Mínimo en Q(0, 0) º) Determina el parámetro c para que la función f() = + + c tenga un mínimo igual a
Aplicaciones de la derivada º) Calcula los máimos y mínimos de la función f() = Máimo en P( 6, ) ; Mínimo en Q(0, 0) º) Determina el parámetro c para que la función f() = + + c tenga un mínimo igual a
De x = 1 a x = 6, la recta queda por encima de la parábola.
 Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Ejercicios de integración
 1. Calcular las siguientes integrales: 1) ) 8) + 1 d ) + 6 6 + 1 d 5) + + 1 + 1 7) d 8) + Ejercicios de integración d ) + + 1 d 6) ( + 1) + + d + d 9) ( + + 1) ln d + 1 + + 1) d 11) d 1) + + 1 d + 1 1)
1. Calcular las siguientes integrales: 1) ) 8) + 1 d ) + 6 6 + 1 d 5) + + 1 + 1 7) d 8) + Ejercicios de integración d ) + + 1 d 6) ( + 1) + + d + d 9) ( + + 1) ln d + 1 + + 1) d 11) d 1) + + 1 d + 1 1)
Autoevaluación. Bloque IV. Análisis. BACHILLERATO Matemáticas I. Página Observa la gráfica de la función y = f (x) y a partir de ella responde:
 Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
Matemáticas II TEMA 11 La integral definida Problemas Propuestos
 Análisis Integral Indefinida Matemáticas II TEMA La integral definida Problemas Propuestos Integrales definidas Halla el valor de: a) d b) 7 c) d 5 d d) e d Calcula la integral e ln( ) d Utilizando el
Análisis Integral Indefinida Matemáticas II TEMA La integral definida Problemas Propuestos Integrales definidas Halla el valor de: a) d b) 7 c) d 5 d d) e d Calcula la integral e ln( ) d Utilizando el
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
EJERCICIOS UNIDADES 3 y 4: INTEGRACIÓN DE FUNCIONES
 IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES a. (6-M-A-) (.5 puntos) Calcula el valor de a > para el que se verifica d. +. (6-M-B-) (.5 puntos) Considera la función : R R f
IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES a. (6-M-A-) (.5 puntos) Calcula el valor de a > para el que se verifica d. +. (6-M-B-) (.5 puntos) Considera la función : R R f
EJERCICIOS UNIDADES 3 y 4: INTEGRACIÓN DE FUNCIONES
 IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES (5-M-A-) (5 puntos) Calcula el valor de a > sabiendo que el área del recinto comprendido entre la parábola y + a y la recta y es
IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES (5-M-A-) (5 puntos) Calcula el valor de a > sabiendo que el área del recinto comprendido entre la parábola y + a y la recta y es
a) f(x) (x 1) 2 b) f(x) x c) h(x) 1 2 a) f (3) 8 0 f es creciente en x 3.
 6 Aplicando la definición de derivada, calcula la derivada de las siguientes funciones en los puntos que se indican: a) f() en Aplicando la definición de derivada, calcula f () en las funciones que se
6 Aplicando la definición de derivada, calcula la derivada de las siguientes funciones en los puntos que se indican: a) f() en Aplicando la definición de derivada, calcula f () en las funciones que se
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2002 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A
-, se pide: b) Calcula el área del recinto limitado por dicha gráfica, el eje horizontal y la vertical que pasa por el máximo relativo de la curva.
 EJERCICIOS PARA PREPARAR EL EXAMEN GLOBAL DE ANÁLISIS ln ) Dada la función f ( ) = +, donde ln denota el logaritmo - 4 neperiano, se pide: a) Determinar el dominio de f y sus asíntotas b) Calcular la recta
EJERCICIOS PARA PREPARAR EL EXAMEN GLOBAL DE ANÁLISIS ln ) Dada la función f ( ) = +, donde ln denota el logaritmo - 4 neperiano, se pide: a) Determinar el dominio de f y sus asíntotas b) Calcular la recta
Área entre curvas. Ejercicios resueltos. 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x.
 Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Unidad 14. Integral definida
 Unidad 4. Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la figura que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene exactamente 7,5 u y = x
Unidad 4. Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la figura que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene exactamente 7,5 u y = x
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2007 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2017 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Razonar si son ciertas o falsas las siguientes igualdades: Asociar cada función con su gráfica. (19) Si x 2 > 0, entonces x > 0.
 Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
ANTES DE COMENZAR RECUERDA
 ANTES DE COMENZAR RECUERDA 00 Determina cuáles de estos vectores son paralelos y cuáles son perpendiculares a v (, ). a) v ( 6, ) b) v (, ) c) v (, ) a) v v Los vectores son paralelos. b) v v 0 Los vectores
ANTES DE COMENZAR RECUERDA 00 Determina cuáles de estos vectores son paralelos y cuáles son perpendiculares a v (, ). a) v ( 6, ) b) v (, ) c) v (, ) a) v v Los vectores son paralelos. b) v v 0 Los vectores
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Apellidos: Nombre: Curso: 1º Grupo: C Día: 2- III- 16 CURSO
 EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
Selectividad hasta el año incluido = 0. Página 1 de 13 ANÁLISIS
 ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
Apellidos: Nombre: Curso: 2º Grupo: Día: CURSO
 EXAMEN DE MATEMATICAS II ª ENSAYO (ANÁLISIS) Apellidos: Nombre: Curso: º Grupo: Día: CURSO 56 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios
EXAMEN DE MATEMATICAS II ª ENSAYO (ANÁLISIS) Apellidos: Nombre: Curso: º Grupo: Día: CURSO 56 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Página 194 EJERCICIOS Y PROBLEMAS PROPUESTOS. Tasa de variación media PARA PRACTICAR UNIDAD
 UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
y = x ln x ; con los datos obtenidos representa su gráfica. f x es continua y derivable en 0, por ser producto de funciones continuas y derivables.
 Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
 INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA
 EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA. Calcular las siguientes integrales definidas: b) d e d c) + d d) d e) sen d f) + d d ( ) En primer lugar se ha calculado una primitiva de f() Barrow. y después
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA. Calcular las siguientes integrales definidas: b) d e d c) + d d) d e) sen d f) + d d ( ) En primer lugar se ha calculado una primitiva de f() Barrow. y después
Solución: Para calcular la pendiente, despejamos la y: La ordenada en el origen es n. 3 Puntos de corte con los ejes: 1 Eje Y 0, 3
 EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas de la recta 6y 0. Represéntala gráficamente. Para calcular la pendiente, despejamos la y: 6y 0
EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas de la recta 6y 0. Represéntala gráficamente. Para calcular la pendiente, despejamos la y: 6y 0
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
INICIACIÓN A LAS INTEGRALES
 9 INICIACIÓN A LAS INTEGRALES Página. Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente. Estas son las
9 INICIACIÓN A LAS INTEGRALES Página. Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente. Estas son las
INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx
![INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx](/thumbs/56/39119384.jpg) INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
1. INTEGRALES DEFINIDAS E IMPROPIAS
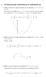 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Prueba º Bach C Análisis. Nombre:... 17/05/10. Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible 1 h. 30 min.
 Nota Prueba 3.04 º Bach C Análisis Nombre:... 7/05/0 Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible h. 30 min. OPCIÓN A. a) Calcula los siguientes límites: ln( + ) sen
Nota Prueba 3.04 º Bach C Análisis Nombre:... 7/05/0 Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible h. 30 min. OPCIÓN A. a) Calcula los siguientes límites: ln( + ) sen
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO
 EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
Tema 13 La integral definida. Aplicaciones
 Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Aplicaciones de la integral definida. Cálculo de áreas.
 ºBachillerato Aplicaciones de la integral definida. Cálculo de áreas.. Calcular el área del recinto limitado por la gráfica de la función f 4 abscisas y las rectas = y =. Sol: /., el eje de a) Buscamos
ºBachillerato Aplicaciones de la integral definida. Cálculo de áreas.. Calcular el área del recinto limitado por la gráfica de la función f 4 abscisas y las rectas = y =. Sol: /., el eje de a) Buscamos
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2013 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 03 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 03 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
1 + 3(0, 2) = ( 1, 2) + (0, 6) = ( 1, 4) ) ( = arc cos e 5
 utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
Idea de Derivada. Tasa de variación media e instantánea
 Idea de Derivada. Tasa de variación media e instantánea.- La variación de la altura de un niño con el paso de los años, se recoge en la guiente tabla: Edad (años) 0 6 9 8 Altura (cm.) 8 6 74 78 80 a) Representar
Idea de Derivada. Tasa de variación media e instantánea.- La variación de la altura de un niño con el paso de los años, se recoge en la guiente tabla: Edad (años) 0 6 9 8 Altura (cm.) 8 6 74 78 80 a) Representar
Lugares geométricos y cónicas
 Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
2. Calcula las velocidades medias anteriores tomando valores sobre la ecuación del movimiento de dicha partícula: s = 2
 Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. Estudia la continuidad derivabilidad de las funciones f() g() si f() si < Estudiamos la continuidad en. f() ( ) - - f() ( ) + + La función f() es continua
RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. Estudia la continuidad derivabilidad de las funciones f() g() si f() si < Estudiamos la continuidad en. f() ( ) - - f() ( ) + + La función f() es continua
Profesor: Fernando Ureña Portero
 MATEMÁTICAS º BACH CC. Y TECNOL. CURSO 13-14 1.-Dada la función a) (3p.) Dominio de f() b) (3 p.) Calcular. Es posible calcular? Por qué? c) (4p.) Calcular.- Estudiar la continuidad de la función: { 3.-a)
MATEMÁTICAS º BACH CC. Y TECNOL. CURSO 13-14 1.-Dada la función a) (3p.) Dominio de f() b) (3 p.) Calcular. Es posible calcular? Por qué? c) (4p.) Calcular.- Estudiar la continuidad de la función: { 3.-a)
EJERCICIOS RESUELTOS. x + ; a = 1; b = 1. x x x. x x
 B7_9 //9 : Página EJERIIOS RESUELTOS alcula las funciones primitivas, que toman el valor b cuando a, de las funciones f definidas por: f() + 7; a ; b. 7 f() + ; a ; b. F ( ) ( + 7 ) d + 7 + c omo debe
B7_9 //9 : Página EJERIIOS RESUELTOS alcula las funciones primitivas, que toman el valor b cuando a, de las funciones f definidas por: f() + 7; a ; b. 7 f() + ; a ; b. F ( ) ( + 7 ) d + 7 + c omo debe
a) Se trata de integrar una función racional cuyo denominador tiene raíces reales simples. Por tanto, se descompone en fracciones simples:
 . a.sen() e Sabiendo que lim es finito, calcula el valor de a y el de dicho límite. lim L'Hôpital a.sen() e a.cos (e e ) lim L'Hôpital a. sen e (e e ) a. sen e e lim lim L'Hôpital El parámetro a puede
. a.sen() e Sabiendo que lim es finito, calcula el valor de a y el de dicho límite. lim L'Hôpital a.sen() e a.cos (e e ) lim L'Hôpital a. sen e (e e ) a. sen e e lim lim L'Hôpital El parámetro a puede
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
derivable en x = 0. b) Para los valores encontrados, calcula la ecuación de la recta tangente a la gráfica de f(x) en el punto de abscisa x = 0.
 . [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
. [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA : FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA : FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS
 SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
INICIACIÓN A LAS INTEGRALES
 UNIDAD INICIACIÓN A LAS INTEGRALES Página. Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente. Éstas son
UNIDAD INICIACIÓN A LAS INTEGRALES Página. Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente. Éstas son
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. En las siguientes funciones estudia las características: dominio, los puntos de corte con los ejes, las simetrías, la periodicidad, las asíntotas, la monotonía,
RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. En las siguientes funciones estudia las características: dominio, los puntos de corte con los ejes, las simetrías, la periodicidad, las asíntotas, la monotonía,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
TRABAJO DE SEPTIEMBRE Matemáticas 1º Bachillerato
 Trabajo de Verano 04 º BACHILLERATO TRABAJO DE SEPTIEMBRE Matemáticas º Bachillerato. Página Trabajo de Verano 04 º BACHILLERATO BLOQUE I: CÁLCULO TEMA (UNIDAD DIDÁCTICA 9): Propiedades globales de las
Trabajo de Verano 04 º BACHILLERATO TRABAJO DE SEPTIEMBRE Matemáticas º Bachillerato. Página Trabajo de Verano 04 º BACHILLERATO BLOQUE I: CÁLCULO TEMA (UNIDAD DIDÁCTICA 9): Propiedades globales de las
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA : FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS II TEMA : FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
